优选空间力系的受力分析演示ppt
合集下载
理论力学课件:空间力系

空间力系
空间力系
4.1 空间汇交力系 4.2 力对点之矩及力对轴之矩 4.3 空间力偶系 4.4 空间力系向一点简化 主矢与主矩 4.5 空间力系的平衡方程及应用 4.6 物体的重心 思考题
空间力系
4.1 空间汇交力系
1.力在直角坐标轴上的投影与分解 1)直接投影法(一次投影法) 在图4-1所示的直角坐标系中,已知力F 与x 轴、y 轴、z
空间力系
2.空间力偶系的合成 作用面不共面的力偶系称为空间力偶系。由于力偶矩矢 是自由矢量,故空间力偶系合成的方法与空间汇交力系相同。 即空间力偶系合成的结果是一个合力偶,合力偶矩等于各分 力矩的矢量和,即
空间力系 将式(4-16)中的矩矢分别向x,y,z 上投影,有
即合力偶矩矢在x,y,z 轴上投影等于各分力偶矩矢在相应轴 上投影的代数和。
空间力系
图4-15
空间力系
空间力系
4)空间力系简化为力螺旋 当力系向一点简化时,R'≠0,MO ≠0,且R'与MO 不垂直而成 任一角α,这是最一般的情形。将 MO 分解为分别与R'平行、 垂直的两个分量 MO//、MO⊥ ,如图4-16(a)所示。其中, MO//=MOcosα、MO⊥ =MOsinα。 MO⊥ 与R'进一步合成为作用在A 点的一个力R, OA=MOsinα/R。由于力偶矩为自由矢量,将 MO//平移到A 点 与R重合,如图4-16(c)所示。最终的简化结果为一个力R 和一 个力偶MO//。这种由一个力和在与之垂直平面内的一力偶所 组成的力系称为力螺旋。
空间力系 合力偶矩矢的大小和方向为
式(4-18)中,α、β、γ 为M 在xyz 坐标系中的方向角。
空间力系 【例4-4】 在图4-12所示的直角三棱柱上,作用着力
空间力系
4.1 空间汇交力系 4.2 力对点之矩及力对轴之矩 4.3 空间力偶系 4.4 空间力系向一点简化 主矢与主矩 4.5 空间力系的平衡方程及应用 4.6 物体的重心 思考题
空间力系
4.1 空间汇交力系
1.力在直角坐标轴上的投影与分解 1)直接投影法(一次投影法) 在图4-1所示的直角坐标系中,已知力F 与x 轴、y 轴、z
空间力系
2.空间力偶系的合成 作用面不共面的力偶系称为空间力偶系。由于力偶矩矢 是自由矢量,故空间力偶系合成的方法与空间汇交力系相同。 即空间力偶系合成的结果是一个合力偶,合力偶矩等于各分 力矩的矢量和,即
空间力系 将式(4-16)中的矩矢分别向x,y,z 上投影,有
即合力偶矩矢在x,y,z 轴上投影等于各分力偶矩矢在相应轴 上投影的代数和。
空间力系
图4-15
空间力系
空间力系
4)空间力系简化为力螺旋 当力系向一点简化时,R'≠0,MO ≠0,且R'与MO 不垂直而成 任一角α,这是最一般的情形。将 MO 分解为分别与R'平行、 垂直的两个分量 MO//、MO⊥ ,如图4-16(a)所示。其中, MO//=MOcosα、MO⊥ =MOsinα。 MO⊥ 与R'进一步合成为作用在A 点的一个力R, OA=MOsinα/R。由于力偶矩为自由矢量,将 MO//平移到A 点 与R重合,如图4-16(c)所示。最终的简化结果为一个力R 和一 个力偶MO//。这种由一个力和在与之垂直平面内的一力偶所 组成的力系称为力螺旋。
空间力系 合力偶矩矢的大小和方向为
式(4-18)中,α、β、γ 为M 在xyz 坐标系中的方向角。
空间力系 【例4-4】 在图4-12所示的直角三棱柱上,作用着力
空间力系PPT课件

MO(F)
定位矢量
2. 力对轴的矩
Mz(F)
Mz(F) = MO(Fxy) =±Fxy h = ±2 △OAb
★ 力对轴的矩等于力在垂直于该 x 轴的平面上的投影对轴与平面交
点的矩。
z
O h
F
Fz
B
b
A
Fxy
y
力对轴之矩用来表征——力对刚体绕某轴的转动效应。
☆ 当力与轴在同一平面时,力对该轴的矩等于零。
M
z
(F
)
xFy
yFx
● 力对点的矩矢在通过 该点的某轴上的投影,等 于力对该轴的矩。
MO (F )x MO (F )y
M x(F) M y(F)
MO (F )z
M
z
(F )
MO (F ) 2OAB
Mz(F) = MO(Fxy) = ±2 △Oab
M=M1+M2+…+Mn=∑Mi
M Mxi My j Mzk
M x M1x M 2x L M nx Mix M y M1y M 2 y L M ny Miy M z M1z M 2z L M nz Miz
x
Fx Fy
F F
sin sin
cos sin
Fz F cos
F
Fx2
Fy2
Fz2
cos(F , i) Fx F
ห้องสมุดไป่ตู้
cos(F , j) Fy
F
cos(F , k) Fz F
空间力系(工程力学课件)

空间力系平衡方程的应用
二、空间力系平衡方程 空间汇交力系和空间平行力系是空间任意力系的特殊情况,由式(5-10) 可推出空间汇交力系的平衡方程为
空间力系平衡方程的应用
例1 如图5.8(a)所示,用起重杆吊起重物。起重杆的A端用球铰链固定在地 面上,而B端则用绳子CB和DB拉住,两绳分别系在墙上的点C和D,连线CD平行于 x轴。已知:CE=EB=DE,α=30°,CDB平面与水平面间的夹角∠EBF=30°(参见 图5.8(b)),物重P=l0kN。如起重杆的重量不计,试求起重杆所受的压力和绳
Fxy在与z轴垂直的xy面内
Mz (F ) MO (Fxy ) Fxyh 为代数量
即:力对轴之矩,等于力在垂直于该轴的平面
上的投影对轴与平面交点之矩。
x
特殊情况:
Oh Bh A
1、力与轴平行,矩为零。
y
2、力与轴相交,矩为零。
即: 力与轴位于同一平面内时,矩为零。
力对轴之矩及合力矩定理
1. 力对轴之矩
解:
2.由合力矩定理求F轴之矩FzFx Fra bibliotekxyFy
2F M x (F ) M x (Fx ) M x (Fy ) M x (Fz ) 0 0 2 6 10606.6N m
M y (F ) M y (Fx ) M y (Fy ) M y (Fz ) 0 0
2F 5 8838.8N m 2
例2 图5.4(a)所示为一圆柱斜齿轮,,, 其上受啮合力F作用。已知斜齿轮 的螺旋角β和压力角α。试求啮合力F在坐标轴x、y、z的投影。
解 先将啮合力F向坐标轴z和 坐标平面Oxy投影,如图5.4(b) 所示,得
Fz F sin Fxy F cos
第3章 空间力系简介(0.5周)——理论力学课件PPT

Z 0
——空间汇交力系的 平衡方程。
9
§3.2 空间力偶系
一、力偶矩用矢量表示: 由于空间力偶除大小、转向外,还必须确定力偶的作用面,
所以空间力偶矩必须用矢量表示。
末端
往下看
力偶的转向为右手螺旋定则。从力 偶矢末端看去,逆时针转动为正。 方法:先根据旋转效果定旋向(弧
线),再定力偶矩方向(直线)!
3
§3.1 空间汇交力系
一、力在空间轴上的投影与分解:
1.力在空间的表示:
力的三要素:
大小、方向、作用点(线)
g
O
Fxy
大小: F F
作用点:作用在物体的哪点。 方向:
由、、g三个方向角确定,
或:由仰角 与俯角 来确定。
4
2、一次投影法(直接投影法)
由图可知: X Fcos, Y Fcos , Z Fcosg
[证] ①作平面II//平面Ⅰ,cd // ab ②在E点作一对平衡力R =R' =2F1
(E点在ad和bc的中间位置)
③由反向平行力合成:F1与R合成得F2,作用在在对称的位 置d点;F1’与R’ 合成得F2’,作用在在对称的位置c点,
且F2 =F1,F2’ = F1’。即: ④ 在I内的力偶(F1,F1’)等效变成II内的新力偶( F2, 11
力对轴之矩: Mx (F) Mx (Fx ) Mx (Fy ) Mx (Fz ) Fz y Fy z
M y (F) M y (Fx ) M y (Fy ) M y (Fz ) Fx z Fz x Mz (F) Fy x Fx y
力对点之矩的投影:
MO (F)x yFz zFy M x (F ) MO (F ) y zFx xFz M y (F ) MO (F)z xFy yFx M z (F)
——空间汇交力系的 平衡方程。
9
§3.2 空间力偶系
一、力偶矩用矢量表示: 由于空间力偶除大小、转向外,还必须确定力偶的作用面,
所以空间力偶矩必须用矢量表示。
末端
往下看
力偶的转向为右手螺旋定则。从力 偶矢末端看去,逆时针转动为正。 方法:先根据旋转效果定旋向(弧
线),再定力偶矩方向(直线)!
3
§3.1 空间汇交力系
一、力在空间轴上的投影与分解:
1.力在空间的表示:
力的三要素:
大小、方向、作用点(线)
g
O
Fxy
大小: F F
作用点:作用在物体的哪点。 方向:
由、、g三个方向角确定,
或:由仰角 与俯角 来确定。
4
2、一次投影法(直接投影法)
由图可知: X Fcos, Y Fcos , Z Fcosg
[证] ①作平面II//平面Ⅰ,cd // ab ②在E点作一对平衡力R =R' =2F1
(E点在ad和bc的中间位置)
③由反向平行力合成:F1与R合成得F2,作用在在对称的位 置d点;F1’与R’ 合成得F2’,作用在在对称的位置c点,
且F2 =F1,F2’ = F1’。即: ④ 在I内的力偶(F1,F1’)等效变成II内的新力偶( F2, 11
力对轴之矩: Mx (F) Mx (Fx ) Mx (Fy ) Mx (Fz ) Fz y Fy z
M y (F) M y (Fx ) M y (Fy ) M y (Fz ) Fx z Fz x Mz (F) Fy x Fx y
力对点之矩的投影:
MO (F)x yFz zFy M x (F ) MO (F ) y zFx xFz M y (F ) MO (F)z xFy yFx M z (F)
【材料课件】04空间力系(1)

rr M o (F ) y zFx xFz
M o F z xFy yFx
(4–5)
2.力对轴的矩
r
r
Mz (F) Mo(Fxy ) Fxy h (4–6)
力与轴相交或与轴平行(力与轴在同一平面内),力对该轴 的矩为零.
3、 力对点的矩与力对过该点的轴的矩的关系
已知:力Fr ,力 标 x, y, z
结果: F1 3000N, F2 6000N,
FAx 10004N, FAz 9397N,
FBx 3348N, FBz 1799N,
例4-10
已知: F、P及各尺寸 求: 杆内力
解:研究对象,长方板
受力图如图 列平衡方程
r
M AB F 0
r
M AE F 0
r
M AC F 0
例4-3
已知:P=1000N ,各杆重不计. 求:三根杆所受力.
解:各杆均为二力杆,取球铰O,画受 力图建坐标系如图。
由 Fx 0 FOB sin 45 FOC sin 45 0
Fy 0 FOB cos 45 FOC cos 45 FOA cos 45 0
Fz 0
FOA sin 45 P 0
圆盘面O1垂直于z轴, 圆盘面O2垂直于x轴, 两盘面上作用有力偶, F1=3N,F2=5N,构件自重不计.
求:轴承A,B处的约束力.
解:取整体,受力图如图b所示.
由力偶系平衡方程
Mx 0
Mz 0
解得
F2 400 FAz 800 0
F1 400 FAx 800 0
FAx FBx 1.5N FAz FBz 2.5N
r F
在三根轴上的分力
Frx,Fry,Frz
,力
M o F z xFy yFx
(4–5)
2.力对轴的矩
r
r
Mz (F) Mo(Fxy ) Fxy h (4–6)
力与轴相交或与轴平行(力与轴在同一平面内),力对该轴 的矩为零.
3、 力对点的矩与力对过该点的轴的矩的关系
已知:力Fr ,力 标 x, y, z
结果: F1 3000N, F2 6000N,
FAx 10004N, FAz 9397N,
FBx 3348N, FBz 1799N,
例4-10
已知: F、P及各尺寸 求: 杆内力
解:研究对象,长方板
受力图如图 列平衡方程
r
M AB F 0
r
M AE F 0
r
M AC F 0
例4-3
已知:P=1000N ,各杆重不计. 求:三根杆所受力.
解:各杆均为二力杆,取球铰O,画受 力图建坐标系如图。
由 Fx 0 FOB sin 45 FOC sin 45 0
Fy 0 FOB cos 45 FOC cos 45 FOA cos 45 0
Fz 0
FOA sin 45 P 0
圆盘面O1垂直于z轴, 圆盘面O2垂直于x轴, 两盘面上作用有力偶, F1=3N,F2=5N,构件自重不计.
求:轴承A,B处的约束力.
解:取整体,受力图如图b所示.
由力偶系平衡方程
Mx 0
Mz 0
解得
F2 400 FAz 800 0
F1 400 FAx 800 0
FAx FBx 1.5N FAz FBz 2.5N
r F
在三根轴上的分力
Frx,Fry,Frz
,力
静力学 空间力系ppt课件

解:
Fz 5 F
35
Fy 3 F 35
Fx 1 F 35
M z(F ) M z(F x ) M z(F y ) M z(F z)
Fx(105 0)0Fy150
10.41(Nm)
1
20
2. 空间力偶 一、力偶矩用矢量表示:
由于空间力偶除大小、转向外,还必须确定力偶的作用面的方位,所以空间力偶矩必须用 矢量表示。
显然空间力偶系的平衡条件是:
MMi 0
∵ M Mx2My2Mz2
Mx 0 ∴ My 0
Mz 0
1
27
[例3]求合力偶 z
b
h
F2
y
F1
F1
x
F2
z
M1 M2 y
x
z M y
x
M 1 F1 b M 2 F2 h1
M M12 M22
28
§6-4 空间任意力系的平衡方程
一、空间任意力系向一点的简化 把研究平面一般力系的简化方法拿来研究空间一般力系的简化问题,但须把平面坐标系
1
3
§6–1 工程中的空间力系问题
a
a
A
P 2P
1
a 2P
B P
4
§6-2 力在空间坐标轴上的投影 ★一次投影法(直接投影法)
由图可知:
X F cos , Y F cos , Z F cos
z Z
F
Y
X
o
y
x
1
5
★ 二次投影法(间接投影法)
当力与各轴正向夹角不易
z
确定时,可先将 F 投影到xy
z a
解:
a
F
y
a
PPT3-1:空间力系课件
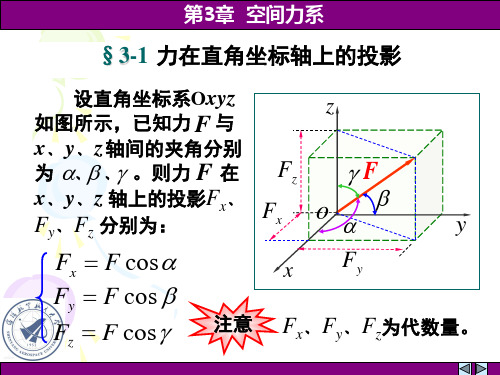
Mo (F ) M ox i M oy j M oz k
第 3章
空间力系
例3-1 构件OA在A点受到作用力F =1000N,方向 如图所示。图中A点在Oxy平面内,尺寸如图。试求: M y (F )、M z (F )。 力F 对x﹑y﹑z坐标轴的矩 M x (F )、 解:力 F 作用点 A 坐标为
y3 0
yC
Ai yi
i 1
A 7200 160 612.5 ( 46.67) (225 ) 0
47 .1mm
7200 612.5 (225 )
第 3章 5、试验法
空间力系
对于某些形状复杂的机械零部件,在工程实际 中常采用试验方法来测定其重心。试验法往往比计 算法直接、简便,并具有足够的准确性。常用的试 验方法有如下两种:
Ai yi
A
第 3章
空间力系
4、负面积法
形体组合法的推广
如果在规则形体上切去一部分,例如钻孔或开槽 等。当求这类形体的形心时,首先认为原形体是完整 的形体,然后把切去的部分视为负面积,运用公式求 出形心。 例3-4 已知振动器上用的 偏心块为等厚度的匀质形体, 如图所示。其上有半径为 r2 的圆孔。偏心块的几何尺寸 R=120mm,r1=35mm, r2=15mm。试求偏心块形心 的位置。
悬挂法:对于形状复杂 的薄平板求形心时可以 采用悬挂法。
AD 与 BE 的交点即 为薄平板的形心 C。
第 3章
空间力系
称重法:形状复杂或体积庞大的物体,可以采用 称重法求重心。
例3-5:内燃机的连杆,其重心必在对称中心线AB上。 将连杆的小端 A 放在水平面上,大端 B 放在台秤 上,使中心线 AB 处于水平位置。已知连杆重量为G, 小头支承点距重力G 的作用线的距离为 xC,由力矩平 衡方程得:
理论力学 第六章 空间力系.ppt

r = x i + y j + z k 则:
z
i x MO(F) = r F =
jk yz
B
MO(F)
F
Od y
Fx Fy Fz
rA
x
=( y·Fz - z ·Fy ) i + (z·Fx - x ·Fz ) j + (x·Fy - y ·Fx ) k
其中 [MO (F)] x = y·Fz - z ·Fy [MO (F)] z = x·Fy - y ·Fx
使-R=R')
③由反向平行力合成得:
F1与R合成得F2,作用在d点 F1'与R'合成得F2',作用在c点
且R-F1=F2 ,R'- F1'= F2'
④在I内的力偶(F1,F1')等效变成II内的( F2, F2' )
14
由此可得出,空间力偶矩是自由矢量,它有三个要素:
①力偶矩的大小= m
②力偶矩的方向——与力偶作用面法线方向相同 ③转向——遵循右手螺旋规则。 三、空间力偶系的合成与平衡 由于空间力偶系是自由矢量,只要方向不变,可移至任意 一点,故可使其滑至汇交于某点,由于是矢量,它的合成符合 矢量运算法则。
[MO (F)] y = z·Fx - x ·Fz 为力矩式在坐标轴上的投影。
19
二 力对轴的矩
z
力对物体绕轴转动效果的度量
1)定义:力对轴的矩等于此力在垂直
于矩轴的平面上的投影矢量对
于矩轴与这平面的交点的距 。
o
用FXY表示F在XY平面上的投影,
则力F对Z轴的矩为
x
mZ (F) Fxyd
各力偶矩矢在三个坐标轴的每一坐标轴上投影的代数和等于零.
工学工程力学空间力系PPT课件
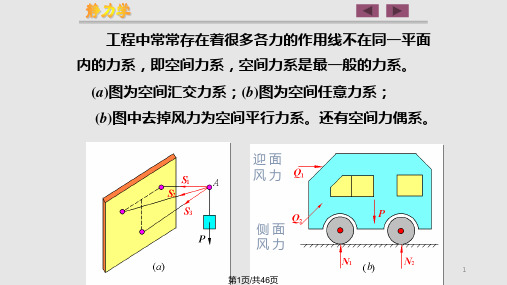
③合成 F '1,F2 ',F3'Fn ' 得主矢 R ' 即 R'Fi 'Fi(主矢 R ' 过简化中心O,
且与O点的选择无关) 合成 m1,m2,mn 得主矩 MO 即:mO mi mO (F(i) 主矩 MO与简化中心O有关)
31
第31页/共46页
§5-5 空间一般力系简化结果的讨论
空间一般力系向一点简化得一主矢和主矩,下面针对主 矢、主矩的不同情况分别加以讨论。
Fn
F2
M1
Fn
F2
F1
F1
F3
Mn
M2
29
第29页/共46页
①根据力线平移定理,将各力平行搬到O点得到一空间
汇交力系: F '1,F2 ',F3'F和n ' 附加力偶系
m1,m2 ,[m注n
意]
m1,m2,分m别n 是各力对O点的矩。
②由于空间力偶是自由矢量,总可汇交于O点。 30 第30页/共46页
矢量表示。
第18页/共46页
y
18
MO (F, F ') MO (F ) MO (F ') rA F rB F' (rA rB ) F
M rBA F 力偶矩矢与矩心无关
力偶矩矢的模等于三角形
ABC的面积。
力偶的转向为右手螺旋定则。
O1
从力偶矢末端看去,逆时针
转动为正。
空间力偶是一个自由矢量。
A为球铰链。
求:绳BE、BF的拉力和杆
AB的内力 解:分别研究C点和B点作 受力图
由C点:
Y 0,T1'sin15Qsin450,
《空间力系》课件

研究人体结构和生物力学特 性时,空间力系的概念和方 法也是重要的工具。
总结
通过本课件的学习,我们了解了空间力系的定义和重要性,以及其组成要素、 分类、特点和应用领域。空间力系是研究物体运动和变形的基础,对科学和 工程具有重要意义。
《空间力系》PPT课件
本课件将介绍空间力系的定义、重要性和组成要素,分类为线性、平面和立 体空间力系,以及其特点和应用领域。
空间力系的定义
空间力的概念与性质以及对物体或系统的影响。它是研究空间中物体相互作用和力的传递的力学分支。
空间力系的重要性
1 理解物体行为
2 解决实际问题更好地理解物体 在力的作用下的运动和 变形。
空间力系中的力可以以不同的强度作用于物体。
3 力的合成与分解
空间力系中的多个力可以通过合成和分解来影响物体的运动和形态。
空间力系的应用
机械力学中的应用
空间力系理论在机械设计、 工程结构分析和机器运动研 究中起着重要作用。
工程中的应用
空间力系的知识被广泛应用 于各种工程项目的设计和施 工中。
生物力学中的应用
力的方向是指力的作用方向,可以是直线、 平面或空间中的任意方向。
空间力系的分类
线性空间力系
力和物体的运动方向在同 一直线上。
平面空间力系
力和物体的运动方向在同 一平面上。
立体空间力系
力和物体的运动方向不在 同一平面上。
空间力系的特点
1 方向性
空间力系具有明确的力的方向,指示物体受力的作用方向。
2 力的大小
应用空间力系的知识, 可以帮助解决工程、力 学和生物力学中的实际 问题。
空间力系的研究对于推 动科学和技术的发展具 有重要意义。
空间力系的组成要素
总结
通过本课件的学习,我们了解了空间力系的定义和重要性,以及其组成要素、 分类、特点和应用领域。空间力系是研究物体运动和变形的基础,对科学和 工程具有重要意义。
《空间力系》PPT课件
本课件将介绍空间力系的定义、重要性和组成要素,分类为线性、平面和立 体空间力系,以及其特点和应用领域。
空间力系的定义
空间力的概念与性质以及对物体或系统的影响。它是研究空间中物体相互作用和力的传递的力学分支。
空间力系的重要性
1 理解物体行为
2 解决实际问题更好地理解物体 在力的作用下的运动和 变形。
空间力系中的力可以以不同的强度作用于物体。
3 力的合成与分解
空间力系中的多个力可以通过合成和分解来影响物体的运动和形态。
空间力系的应用
机械力学中的应用
空间力系理论在机械设计、 工程结构分析和机器运动研 究中起着重要作用。
工程中的应用
空间力系的知识被广泛应用 于各种工程项目的设计和施 工中。
生物力学中的应用
力的方向是指力的作用方向,可以是直线、 平面或空间中的任意方向。
空间力系的分类
线性空间力系
力和物体的运动方向在同 一直线上。
平面空间力系
力和物体的运动方向在同 一平面上。
立体空间力系
力和物体的运动方向不在 同一平面上。
空间力系的特点
1 方向性
空间力系具有明确的力的方向,指示物体受力的作用方向。
2 力的大小
应用空间力系的知识, 可以帮助解决工程、力 学和生物力学中的实际 问题。
空间力系的研究对于推 动科学和技术的发展具 有重要意义。
空间力系的组成要素
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z D
E
α
C B
α
F
A
y
x
解:取起重杆AB为研究对象
建坐标系如图,
C
z D
E
α F2
F1 α B
P
A
y
x FA
列平衡方程:
Fx 0
F1 sin 45 0 F2 sin 45 0 0
C
Fy 0
FA sin 300 F1 cos 450 cos 300
F2 cos 450 cos 300 0
3
0.6
BC
42 32
z
600
φ
4m
F2
2. 5m
F3 γ
B y
3m D
Fx F sin cos 1500 0.8944 0.6 805 N
Fy F sin sin 1500 0.8944 0.8 1073 N
Fz F cos 1500 0.4472 671N
二、空间汇交力系的合成和平衡
F1
F2
B
αP
Ay
FA
§3-2 力对轴的矩
一、空间力对点的矩
空间力对点的矩取决于:
(1)力矩的大小
z
(2)力矩作用面的方位
M
O
F
B
(3)力矩在作用面内的转向
F
这三个因素可以用一个矢量来
表示,记为:
M
O
F
x
rA
O
y
空间力对点的矩的计算
(1)力矩的大小为:
MO F F h 2OAB
(2)力矩矢通过O点
(3)力矩矢的方向:垂直 于OAB平面,指向由右手 螺旋法则决定之。
由矢量分析理论可知: MO F r F
M
O
F
x
z Oh r
B
F
A y
力矩矢量的方向
MO
r
F
按右手定则
MO r F
力对点之矩的矢量运算
由高等数学知:
i
jk
MO F r F = x y z
Fx Fy Fz
3 866 N 2
2. 5m
y 3m
对F3 应采用直接投影法
Fx F sin c os
Fy F sin sin
A
Fz F c os
sin BC
AB
42 32
F1
0.8944
42 32 2.52
cos 0.4472
C
sin CD
4
0.8
x
BC
42 32
cos BD
Mz
Fx
M
z
Fy
M z Fz
空间力对轴的矩等于零的条件
1、力通过轴线
F Fz
2、力与轴线平行
Fy Fx
力对轴之矩代数量的正负号
(按照右手螺旋法则决定之)
α
Fx
x
γ Fy
y
2、二次投影法
已知力 F 与 z 轴的夹角 γ
第一次投影:
Fxy F sin
Fz F c os
若再知道 Fxy 与x轴的夹角φ
第二次投影
z
FZ
F
γ
Fx Fxy cos Fy Fxy sin
φ
Fy y
最后得:
Fx
F sin
c os x
Fx
Fxy
Fy F sin sin
Fz 0
F1 cos 450 sin 300 F2 cos 450 sin 300 x
FA cos 300 P 0
解得:
F1
F2
10 2
3.54kN 2
FA 6F1 8.66kN
z D
E
α F2
F1 α B
P
A
y
FA
空间汇交力系在任一平面上的投 z D
影 →平面汇交力系
空间汇交 力系平衡, 投影得到的平面汇交 力系也必然平衡。
Fz F c os
例题 已知:F1 =500N,F2=1000N,F3=1500N,
求:各力在坐标轴上的投影
z
解: F1 、F2 可用直接投影法
Fx F cos Fy F cos
Fz F cos
F1
Fx1 0
Fy1 0 Fz1 F1 500N x
4m
600 F2
F3
Fx2 F2 sin 60 0 1000 Fy 2 F2 cos 60 0 500 N Fz 2 0
按照以下公式进行计算。
FR FRxi FRy j FRz k
合力的大小: FR FRx 2 FRy 2 FRz 2
Fxi 2 Fyi 2 Fzi 2
合力的方向:
COS( FR ,i )
FRx FR
COS( FR , j )
FRy FR
COS( FR , k )
(优选)空间力系的受力分析
空间力系:力的作用线不位于同一平面内。 空间力系包括: 空间汇交力系 空间力偶系 空间任意力系
§3-1 力在空间直角坐标轴上的投影
一、空间力沿直角坐标轴的投影和分解
1、直接投影法
已知力 F 与三个坐标 轴的夹角,则该力在 三个轴上的投影为
z
Fz
βF
Fx F cos Fy F cos Fz F cos
1、合成
空间汇交力系的合力等于各分力的矢量和,合力作
用点(线)通过汇交点。
n
FR F1 F2 Fn
Fi
i 1
空间合力投影定理:合力在某一轴上的投影等于
力系中各分力在同一轴上投影的代数和。
n
FRx
Fx i
i 1
n
FRy
Fy i
i 1
n
FRz
Fz i
i 1
根据空间合力投影定理,合力的大小和方向可
yFz zFy i zFx xFz j xFy yFx k
Fz F
Fx
r
Fy
二、力对轴之矩
1、定义:
力使物体绕某一轴 转动效应的量度,称 为力对该轴之矩.
F Fz
2、力对轴之矩实对轴之矩的计算
力F对z轴的矩等于该力在 通过O点垂直于z轴的平面 上的分量 对于O点的矩。
C E α F2
F1 α B
P
z
Fy 0,
FA sin 300 F1 cos 450 cos 300 F2 cos 450 cos 300 0
A x FA
Fz 0,
F1 cos 450 sin 300 F2 cos 450 sin 300 FA cos 300 P 0
yE
2 2
M z F M O Fxy
方法一 :
将力向垂直于该轴的平面投影 , 力对轴的矩等于力的投影与投影 至轴的垂直距离的乘积.
Mz (F) = Fxyd
= 2(OAB)
力对轴之矩的计算
方法二:
将力向三个坐标轴方向 分解,分别求三个分力对轴 之矩,然后将三个分力对 轴之矩的代数值相加。
M z F
FRz FR
2、空间汇交力系的平衡
空间汇交力系平衡的充要条件为:合力 = 0。
由于
n
FR
Fi 0
i 1
FR
Fxi 2
Fyi 2
Fzi 2
空间汇交力系的平衡条件:
Fx Fy
0 0
Fz 0
例题:已知: CE EB ED, 300 , F 10kN
求:起重杆AB及绳子的拉力.
E
α
C B
α
F
A
y
x
解:取起重杆AB为研究对象
建坐标系如图,
C
z D
E
α F2
F1 α B
P
A
y
x FA
列平衡方程:
Fx 0
F1 sin 45 0 F2 sin 45 0 0
C
Fy 0
FA sin 300 F1 cos 450 cos 300
F2 cos 450 cos 300 0
3
0.6
BC
42 32
z
600
φ
4m
F2
2. 5m
F3 γ
B y
3m D
Fx F sin cos 1500 0.8944 0.6 805 N
Fy F sin sin 1500 0.8944 0.8 1073 N
Fz F cos 1500 0.4472 671N
二、空间汇交力系的合成和平衡
F1
F2
B
αP
Ay
FA
§3-2 力对轴的矩
一、空间力对点的矩
空间力对点的矩取决于:
(1)力矩的大小
z
(2)力矩作用面的方位
M
O
F
B
(3)力矩在作用面内的转向
F
这三个因素可以用一个矢量来
表示,记为:
M
O
F
x
rA
O
y
空间力对点的矩的计算
(1)力矩的大小为:
MO F F h 2OAB
(2)力矩矢通过O点
(3)力矩矢的方向:垂直 于OAB平面,指向由右手 螺旋法则决定之。
由矢量分析理论可知: MO F r F
M
O
F
x
z Oh r
B
F
A y
力矩矢量的方向
MO
r
F
按右手定则
MO r F
力对点之矩的矢量运算
由高等数学知:
i
jk
MO F r F = x y z
Fx Fy Fz
3 866 N 2
2. 5m
y 3m
对F3 应采用直接投影法
Fx F sin c os
Fy F sin sin
A
Fz F c os
sin BC
AB
42 32
F1
0.8944
42 32 2.52
cos 0.4472
C
sin CD
4
0.8
x
BC
42 32
cos BD
Mz
Fx
M
z
Fy
M z Fz
空间力对轴的矩等于零的条件
1、力通过轴线
F Fz
2、力与轴线平行
Fy Fx
力对轴之矩代数量的正负号
(按照右手螺旋法则决定之)
α
Fx
x
γ Fy
y
2、二次投影法
已知力 F 与 z 轴的夹角 γ
第一次投影:
Fxy F sin
Fz F c os
若再知道 Fxy 与x轴的夹角φ
第二次投影
z
FZ
F
γ
Fx Fxy cos Fy Fxy sin
φ
Fy y
最后得:
Fx
F sin
c os x
Fx
Fxy
Fy F sin sin
Fz 0
F1 cos 450 sin 300 F2 cos 450 sin 300 x
FA cos 300 P 0
解得:
F1
F2
10 2
3.54kN 2
FA 6F1 8.66kN
z D
E
α F2
F1 α B
P
A
y
FA
空间汇交力系在任一平面上的投 z D
影 →平面汇交力系
空间汇交 力系平衡, 投影得到的平面汇交 力系也必然平衡。
Fz F c os
例题 已知:F1 =500N,F2=1000N,F3=1500N,
求:各力在坐标轴上的投影
z
解: F1 、F2 可用直接投影法
Fx F cos Fy F cos
Fz F cos
F1
Fx1 0
Fy1 0 Fz1 F1 500N x
4m
600 F2
F3
Fx2 F2 sin 60 0 1000 Fy 2 F2 cos 60 0 500 N Fz 2 0
按照以下公式进行计算。
FR FRxi FRy j FRz k
合力的大小: FR FRx 2 FRy 2 FRz 2
Fxi 2 Fyi 2 Fzi 2
合力的方向:
COS( FR ,i )
FRx FR
COS( FR , j )
FRy FR
COS( FR , k )
(优选)空间力系的受力分析
空间力系:力的作用线不位于同一平面内。 空间力系包括: 空间汇交力系 空间力偶系 空间任意力系
§3-1 力在空间直角坐标轴上的投影
一、空间力沿直角坐标轴的投影和分解
1、直接投影法
已知力 F 与三个坐标 轴的夹角,则该力在 三个轴上的投影为
z
Fz
βF
Fx F cos Fy F cos Fz F cos
1、合成
空间汇交力系的合力等于各分力的矢量和,合力作
用点(线)通过汇交点。
n
FR F1 F2 Fn
Fi
i 1
空间合力投影定理:合力在某一轴上的投影等于
力系中各分力在同一轴上投影的代数和。
n
FRx
Fx i
i 1
n
FRy
Fy i
i 1
n
FRz
Fz i
i 1
根据空间合力投影定理,合力的大小和方向可
yFz zFy i zFx xFz j xFy yFx k
Fz F
Fx
r
Fy
二、力对轴之矩
1、定义:
力使物体绕某一轴 转动效应的量度,称 为力对该轴之矩.
F Fz
2、力对轴之矩实对轴之矩的计算
力F对z轴的矩等于该力在 通过O点垂直于z轴的平面 上的分量 对于O点的矩。
C E α F2
F1 α B
P
z
Fy 0,
FA sin 300 F1 cos 450 cos 300 F2 cos 450 cos 300 0
A x FA
Fz 0,
F1 cos 450 sin 300 F2 cos 450 sin 300 FA cos 300 P 0
yE
2 2
M z F M O Fxy
方法一 :
将力向垂直于该轴的平面投影 , 力对轴的矩等于力的投影与投影 至轴的垂直距离的乘积.
Mz (F) = Fxyd
= 2(OAB)
力对轴之矩的计算
方法二:
将力向三个坐标轴方向 分解,分别求三个分力对轴 之矩,然后将三个分力对 轴之矩的代数值相加。
M z F
FRz FR
2、空间汇交力系的平衡
空间汇交力系平衡的充要条件为:合力 = 0。
由于
n
FR
Fi 0
i 1
FR
Fxi 2
Fyi 2
Fzi 2
空间汇交力系的平衡条件:
Fx Fy
0 0
Fz 0
例题:已知: CE EB ED, 300 , F 10kN
求:起重杆AB及绳子的拉力.
