动量守恒定律应用人船模型共20页文档
人船模型——应用平均动量守恒处理问题 PPT课件 人教课标版

23、天行健君子以自强不息;地势坤君子以厚德载物。
•
24、态度决定高度,思路决定出路,细节关乎命运。
•
25、世上最累人的事,莫过於虚伪的过日子。
•
26、事不三思终有悔,人能百忍自无忧。
•
27、智者,一切求自己;愚者,一切求他人。
•
28、有时候,生活不免走向低谷,才能迎接你的下一个高点。
•
29、乐观本身就是一种成功。乌云后面依然是灿烂的晴天。
•
44、仁慈是一种聋子能听到、哑巴能了解的语言。
•
45、不可能!只存在于蠢人的字典里。
•
46、在浩瀚的宇宙里,每天都只是一瞬,活在今天,忘掉昨天。
•
47、小事成就大事,细节成就完美。
•
48、凡真心尝试助人者,没有不帮到自己的。
•
49、人往往会这样,顺风顺水,人的智力就会下降一些;如果突遇挫折,智力就会应激增长。
0=m1v1-m2v2(其中v1、v2是平均速度)
得推论:m1s1=m2s2,使用时应明确s1、s2必须
是相对同一参照物体的大小。
人船模型
在静水上浮着一只长为L=3m、质量为m船=300kg的小 船,船尾站着一质量m人=60kg的人,开始时人和船都 静止。若人匀速从船尾走到船头,不计水的阻力。则
船将( )
•
30、经验是由痛苦中粹取出来的。
•
31、绳锯木断,水滴石穿。
•
32、肯承认错误则错已改了一半。
•
33、快乐不是因为拥有的多而是计较的少。
•
34、好方法事半功倍,好习惯受益终身。
•
35、生命可以不轰轰烈烈,但应掷地有声。
•
36、每临大事,心必静心,静则神明,豁然冰释。
人船模型(学生版)-动量守恒的十种模型
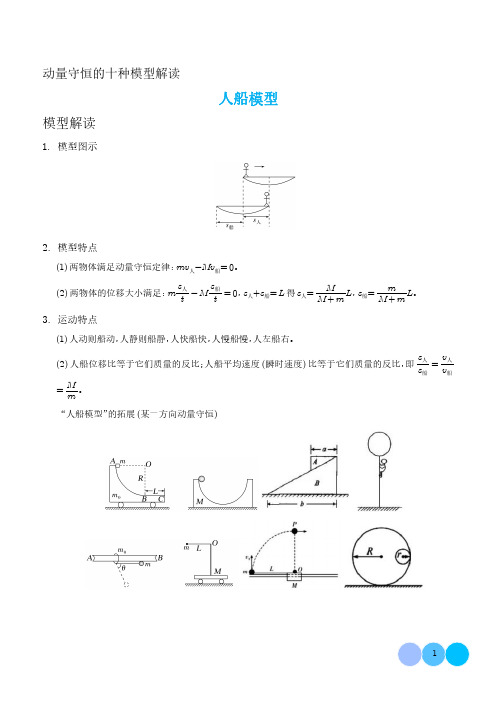
动量守恒的十种模型解读人船模型模型解读1.模型图示2.模型特点(1)两物体满足动量守恒定律:mv 人-Mv 船=0。
(2)两物体的位移大小满足:m s 人t -M s 船t =0,s 人+s 船=L 得s 人=M M +m L ,s 船=m M +mL 。
3.运动特点(1)人动则船动,人静则船静,人快船快,人慢船慢,人左船右。
(2)人船位移比等于它们质量的反比;人船平均速度(瞬时速度)比等于它们质量的反比,即s 人s 船=v 人v 船=M m 。
“人船模型”的拓展(某一方向动量守恒)【典例分析】1如图,质量为M 的匀质凹槽放在光滑水平地面上,凹槽内有一个半椭圆形的光滑轨道,椭圆的半长轴和半短轴分别为a 和b ,长轴水平,短轴竖直。
质量为m 的小球,初始时刻从椭圆轨道长轴的右端点由静止开始下滑。
以初始时刻椭圆中心的位置为坐标原点,在竖直平面内建立固定于地面的直角坐标系xOy ,椭圆长轴位于x 轴上。
整个过程凹槽不翻转,重力加速度为g 。
(1)小球第一次运动到轨道最低点时,求凹槽的速度大小;(2)凹槽相对于初始时刻运动的距离。
【针对性训练】1(2024河南名校联考).如图,棱长为a 、大小形状相同的立方体木块和铁块,质量为m 的木块在上、质量为M 的铁块在下,正对用极短细绳连结悬浮在平静的池中某处,木块上表面距离水面的竖直距离为h 。
当细绳断裂后,木块与铁块均在竖直方向上运动,木块刚浮出水面时,铁块恰好同时到达池底。
仅考虑浮力,不计其他阻力,则池深为()A.M +m M hB.M +m m (h +2a )C.M +m M (h +2a )D.M +m Mh +2a 2(2024全国高考模拟)一小船停靠在湖边码头,小船又窄又长(估计重一吨左右)。
一位同学想用一个卷尺粗略测定它的质量,他进行了如下操作:首先将船平行于码头自由停泊,轻轻从船尾上船,走到船头停下,而后轻轻下船。
用卷尺测出船后退的距离d ,然后用卷尺测出船长L 。
高中物理教研论文巧解人船模型问题(最全)word资料

高中物理教研论文巧解人船模型问题(最全)word资料巧解人船模型问题——平均动量守恒定律的应用1.平均动量守恒定律当系统在全过程中动量守恒时,则这一系统在全过程中的平均动量也守恒。
在符合动量守恒的条件下,如果物体做变速运动,为了求解位移,可用平均动量及其守恒规律来处理。
2. 人船模型如果系统是由两(或多)个物体组成的,合外力为零,且相互作用前合动量为零,我们称为人船模型。
(1)一人一船模型:如图1所示人由左端走到右端的过程中, 由动量守恒定律,得 02211=-v m v m由于在全过程动量都守恒,所以有 0211=---v m v m同乘以时间t ,得 0211=---t v m t v m即 2211s m s m =此为一人一船模型的平均动量守恒方程,且知位移与质量成反比。
又由图知 L s s =+21,解得两物体位移分别为L m m m s 2121+= Lm m m s 2112+=(2)二人一船模型:如图2所示,a 、b 两人交换位置过程中,设船c 向左运动,同理可得平均动量守恒定律的方程c c b b a a s m s m s m +=3.一题三法求解人船模型例题 如图2所示,a 、b 两人质量分别为a m 和b m ,船c 的质量为c m ,船长为L ,现在a 、b 交换位置,求船c 在该过程的位移?法1 由二人一船模型得 c c b b a a s m s m s m +=位移关系 L s s c a =+ L s s c b =-联立解得Lm m m m m s cb a ba c ++-=此解法作图较简单,但位移关系和解方程都较复杂。
法2 如图3所示,先令b 不动,a 走到右端,由一人一船模型,得 Lm m m m s cb a ac ++=1再令a 不动,让b 走到左端,在该过程中同理可得L m m m m s cb a bc ++=2由图知L m m m m m s s s cb a ba c c c ++-=-=21此解法把问题化为两个一人一船模型,根据位移和质量的反比关系可直得到结果。
动量守恒的条件 爆炸、反冲运动 人船模型(附精品解析)

动量守恒的条件爆炸、反冲运动人船模型考点一动量守恒的条件考点二爆炸、反冲运动考点三人船模型考点四连续射击问题1.动量守恒定律内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
2.动量守恒定律常用表达式:m1v1+m2v2=m1v1′+m2v2′.1)p=p′:相互作用前系统的总动量p等于相互作用后的总动量p′.2)m1v1+m2v2=m1v1′+m2v2′:相互作用的两个物体组成的系统,作用前动量的矢量和等于作用后动量的矢量和.3)Δp1=-Δp2:相互作用的两个物体组成的系统,一个物体的动量变化量与另一个物体的动量变化量大小相等、方向相反.4)Δp=0:系统总动量增量为零.考点一动量守恒的条件⑴系统不受外力或者所受外力之和为零;⑵系统受外力,但外力远小于内力,可以忽略不计;⑶系统在某一个方向上所受的合外力为零,则该方向上动量守恒。
⑷全过程的某一阶段系统受的合外力为零,则该阶段系统动量守恒。
附:机械能守恒的条件:只有重力、系统内弹力做功.1.下列四幅图所反映的物理过程中,说法正确的是()A.甲图中子弹射入木块过程中,子弹和木块组成系统动量守恒,能量不守恒B.乙图中M、N两木块放在光滑水平面上,剪断束缚M、N的细线,在弹簧从压缩状态恢复原长过程中,M、N与弹簧组成的系统动量不守恒,机械能守恒C.丙图中细线断裂后,木球和铁球在水中运动的过程,两球组成的系统动量不守恒,机械能守恒D.丁图中木块沿光滑固定斜面下滑,木块和斜面组成的系统动量守恒,机械能守恒2.如图所反映的物理过程中,以物体A和物体B为一个系统符合系统机械能守恒且水平方向动量守恒的是()A.甲图中,在光滑水平面上,物块B以初速度v0滑上上表面粗糙的静止长木板AB.乙图中,在光滑水平面上,物块B以初速度v0滑下靠在墙边的表面光滑的斜面AC.丙图中,在光滑水平上面有两个带正电的小球A、B相距一定的距离,从静止开始释放D.丁图中,在光滑水平面上物体A以初速度v0滑上表面光滑的圆弧轨道B3.(多选)如图所示,A、B两物体质量之比为m A∶m B=3∶2,原来静止在足够长的平板小车C上,A、B间有一根被压缩的弹簧,地面光滑.当两物体被同时释放后,则( )A.若A、B与平板车上表面间的动摩擦因数相同,则A、B组成系统的动量守恒B.若A、B与平板车上表面间的动摩擦因数相同,则A、B、C组成系统的动量守恒C.若A、B所受的摩擦力大小相等,则A、B组成系统的动量守恒D.若A、B所受的摩擦力大小相等,则A、B、C组成系统的动量守恒4. (2021·全国乙卷·T14)如图,光滑水平地面上有一小车,一轻弹簧的一端与车厢的挡板相连,另一端与滑块相连,滑块与车厢的水平底板间有摩擦。
人船模型——应用平均动量守恒处理问题PPT 人教课标版

1、聪明的人有长的耳朵和短的舌头。 ——弗莱格 2、重复是学习之母。 ——狄慈根 3、当你还不能对自己说今天学到了什么东西时,你就不要去睡觉。 ——利希顿堡 4、人天天都学到一点东西,而往往所学到的是发现昨日学到的是错的。 ——B.V 5、学到很多东西的诀窍,就是一下子不要学很多。 ——洛 克 6、学问是异常珍贵的东西,从任何源泉吸收都不可耻。 ——阿卜· 日· 法拉兹 7、学习是劳动,是充满思想的劳动。 ——乌申斯基 8、聪明出于勤奋,天才在于积累 --华罗庚 9、好学而不勤问非真好学者。 10、书山有路勤为径,学海无涯苦作舟。 11、人的大脑和肢体一样,多用则灵,不用则废 -茅以升 12、你想成为幸福的人吗?但愿你首先学会吃得起苦 --屠格涅夫 13、成功=艰苦劳动+正确方法+少说空话 --爱因斯坦 14、不经历风雨,怎能见彩虹 -《真心英雄》 15、只有登上山顶,才能看到那边的风光。 16只会幻想而不行动的人,永远也体会不到收获果实时的喜悦。 17、勤奋是你生命的密码,能译出你一部壮丽的史诗。 1 8.成功,往往住在失败的隔壁! 1 9 生命不是要超越别人,而是要超越自己. 2 0.命运是那些懦弱和认命的人发明的! 21.人生最大的喜悦是每个人都说你做不到,你却完成它了! 22.世界上大部分的事情,都是觉得不太舒服的人做出来的. 23.昨天是失效的支票,明天是未兑现的支票,今天才是现金. 24.一直割舍不下一件事,永远成不了! 25.扫地,要连心地一起扫! 26.不为模糊不清的未来担忧,只为清清楚楚的现在努力. 27.当你停止尝试时,就是失败的时候. 28.心灵激情不在,就可能被打败. 29.凡事不要说"我不会"或"不可能",因为你根本还没有去做! 30.成功不是靠梦想和希望,而是靠努力和实践. 31.只有在天空最暗的时候,才可以看到天上的星星. 32.上帝说:你要什么便取什么,但是要付出相当的代价. 33.现在站在什么地方不重要,重要的是你往什么方向移动。 34.宁可辛苦一阵子,不要苦一辈子. 35.为成功找方法,不为失败找借口. 36.不断反思自己的弱点,是让自己获得更好成功的优良习惯。 37.垃圾桶哲学:别人不要做的事,我拣来做! 38.不一定要做最大的,但要做最好的. 39.死的方式由上帝决定,活的方式由自己决定! 40.成功是动词,不是名词! 20、不要只会吃奶,要学会吃干粮,尤其是粗茶淡饭。
人船模型

O O ′ A B O ″ O bR 2R 人、船问题模型(C)动量守恒定律的两个推论:推论1:当系统的动量守恒时,任意一段时间内的平均动量也守恒;推论2:当系统的动量守恒时,系统的质心保持原来的静止或匀速直线运动状态不变。
例题、如图所示,长为l 、质量为M 的小船停在静水中,一个质量为m 的人立在船头,不计水的阻力。
当人从船头走到船尾的过程中,船和人对地的移位各是多大? 解一:设人行走的平均速度为v 1,在时间t 内从船头走到船尾对地位移为S 1,人行走时航速(平均)为v 2,位移为S 2,据动量守恒有 mv 1-Mv 2=0即 mS 1/t-MS 2/t=0 ∴S 1/S 2=M/m而S 1+S 2=l 解得S 1=Ml/(M+m) S 2=ml/(M+m)解二:系统质心位置保持不动,开始时人、船质心为O ′。
且OO ′=A O M m ', OO ′+O ′A=l/2 ∴ l m M M O O +=' 当人从船头走到船尾时,由于对称2l m M m O O ⋅+='' ∴ 船的位移l m M m O O S ⋅+='=22, l mM M S l S ⋅+=-=21 1.静止在空中的气球质量为M ,下面拖一条质量不计的软梯,质量为m 的人站在软梯上端距地面高为h 。
求:⑴人安全不能确定地面软梯的最小长度⑵若软梯长为h ,则人从软梯上端到下端时,人距地面还有多高?2.一质量为M 、底面边长为b 的三角形劈块静止于光滑水平地面上,如图。
有一质量为m 的物块由斜面顶部无初速滑到底部的过程中,劈块移动的距离是多少?3.某人在一只静止于水面上的小船上练习射出。
船、人连同枪(不包括子弹)及靶的总质量为M ,靶立于船头,枪内有n 颗质量均为m 的子弹,枪口到靶的距离为l ,子弹射出枪口时相对地面的速度为v ,在发射后一颗子弹时,前一颗子弹已陷入靶中,则在发射完n 颗子弹后小船后退的距离是多少?4.质量为m 、半径为R 的小球,放在半径为2R 、质量为2m 的大空心球内,大球开始静止在光滑水平面上。
动量中的人船模型精编版

M
解得:s2=mR/(M+m)
系统机械能守恒:mgR=mv12/2+Mv2/2
解得:
2ห้องสมุดไป่ตู้gR
v1 m M
4.某人在一只静止的小船上练习射击,船、人和枪(不包含子弹)及 船上固定靶的总质量为M,子弹质量m,枪口到靶的距离为L,子弹 射出枪口时相对于枪口的速率恒为V,当前一颗子弹陷入靶中时, 随即发射后一颗子弹,则在发射完全部n颗子弹后,小船后退的距 离多大?(不计水的阻力) 解:设子弹运动方向为正方向。 设发射第一颗子弹,小船后退距离为S,子弹飞行的距离为(L-S), 则由动量守恒定律有: m(L-S)-[M+(n-1)m]S=0 每颗子弹射入靶的过程中,小船后退距离都相同,n颗子弹全部射 入,小船后退的总距离为: nS=nmL/(M+nm)
模型特征:
1、运动特点:运动具有同时性
2、适用条件:一个原来处于静止状态的系统,由于其中一 个物体的运动而使两个物体发生相对运动
3、S人S船的大小与人运动的时间和运动的状态无关。
4、 在系统满足动量守恒的方向上,人船的位移与质量成反比;
5、m人v人-Mv船=0 故有:人走船走,人快船快,人慢船慢,人停船停.
M m甲 m乙
s s甲 s乙
3.如图所示,质量为M的小车静止在光滑的水平地面上,车上装有
半径为R的半圆形光滑轨道。现将质量为m的小球放于半圆形轨道的
边缘上,并由静止开始释放,当小球滑至半圆形轨道的最低位置时,
小车移动的距离为多少?此时小球的速率为多少?
m
系统水平方向动量守恒:mv1=Mv
则有:ms1=Ms2,s1+s2=R
解题要点
⑴ 分析题意看是否符合人船模型
⑵ 画出初末状态图,找出各自对地的位移
动量守恒的定律-人船模型

系统: 相互作用的几个物体
内力和外力: 内力:系统内个物体间的作用 外力:外界对系统的作用
人船模型
解题步骤:
动量守恒定律应用
(1)判断动量是否守恒(3个条件)
(2)确定正方向(一般以初速度的方向为正方向)
(3)相互作用前动量 m1v1+m2v2 (4)相互作用后动量 m1v1′+m2v2′ (5)列方程解答 m1v1+m2v2=m1v1′+m2v2′
学以致用
一题多练
变式2:载人气球原来静止在空中(如
图所示),质量为M,下面拖一条质量
不计的软梯,质量为m的人(可视为质
点)站在软梯上端距地面高度为H,若
人要沿轻绳梯返回地面,则绳梯的长度
h
L至少为多长?
根据动量守恒定律
mቤተ መጻሕፍቲ ባይዱ=Mh
H
(M+m)H 绳的长度至少为 L=H+h=
M
地面
学以致用
变式3、一个质量为M,底面边长 为 b 的劈静止在光滑的水平面 上,见右图,有一质量为m的物 块由斜面顶部无初速滑到底部时, 劈移动的距离S2是多少?
2、物体相互作用前均静止
解题步骤:
(1)判断是否符合动量守恒条件 (2)确定正方向 (3)划草图,找位移关系(相对统一参考系) (4)列式求解
一题多练
m
M
S2
S1
b
劈和小物块组成的系统水平方向动量守恒 根据动量守恒定律
mS1=MS2
又由几何关系可知:S1+S2=b
s2
m
m M
b
变式4、如图所示,一滑块B静止在光 滑水平面上,其上一部分为半径是R 的1/4光滑圆轨道,此滑块总质量为 m2,一个质量为m1的小球A(可视为 质点)由静止从最高点释放,当小球 从最低点水平飞出时,小球和滑块对 地的位移S1,S2分别为多大?
【课件】人船模型-应用动量守恒处理问题

气球和人
载人气球原来静止在空 中,与地面距离为h , 已知人的质量为m , 气球质量(不含人的质 量)为M。若人要沿轻 绳梯返回地面,则绳梯 的长度至少为多长?
L
解:取人和气球为对象,系统开始静止 且同时开始运动,人下到地面时,人相 对地的位移为h,设气球对地位移L, 则根据推论有
ML=mh
m
得L பைடு நூலகம் M h (M+m)h M
劈和物块
一个质量为M,底面 边长为 b 的劈静止 在光滑的水平面上, 见左图,有一质量 为 m 的物块由斜面 顶部无初速滑到底 部时,劈移动的距 离是多少?
m
M S1 b 分析和解答:劈和小球组成的系统水平方向不受外力, 故水平方向动量守恒,且初始时两物均静止,故由推论知 ms1=Ms2,其中s1和s2是m和M对地的位移,由上图很容易看 出:s1=b-s2代入上式得,m(b-s2)=Ms2, 所以 s2=mb/(M+m)即为M发生的位移。 可见,处理此类题,除熟记推论外,关键是画草图,确定 位移关系。 S2
1、表达式
0=m1v1-m2v2(其中v1、v2是平均速度) 2、推论: m1s1=m2s2
3、使用时应明确v1、 v2 、s1、s2必须是相对同一参照 物体的大小
s
解 设题述过程所用时间为 t,圆环的位移为s,则小滑块在水 平方向上对地的位移为(R-s),如图所示,取圆环的运动方向 为正,由动量守恒定律得 s 0=M - m (R-s) 即 Ms=m(R-s) t t m S= M+m R
小结
应用平均动量守恒解题的要点
如果系统是由两个物体组成,且相互作用前均静止, 相互作用后均发生运动,则
取人的走向为正方向
3.动量守恒定律的应用人船模型

3. 推论: m1s1=m2s2 4. 使用时应明确v1、 v2 、s1、s2 必须是 相对同一参照系(一般取地面)的大小.
例题9:某人在船上练习射击,人 在船的一端,靶在船的另一端,相
距为L,人、船、枪(不含子弹) 、靶的总质量为M,枪膛每颗子弹 的质量为m,共有子弹n发。当人把
2. 不需考虑过程的细节, 只需考虑初末
状态
教学目的
1、理解平均动量的概念及平均动量守 恒特点。 2、掌握“人船模型”的原理及方法。 3、会应用“人船模型”求位移等相关 物理问题。
人船模型
利用平均动量守恒求位移
播放动画
平均动量守恒求位移“模型”推导
解:以船和人为系统作为研究对象; 由于不计水的阻力,所以系统的动量守恒
课后讨论:
1.m越大,则S船也越大;反之,M越大, S船越小。
2.当M﹥﹥m时,S船→0;如:人在万吨 巨轮上行走时,S船→0;当M﹤﹤m时, 也可得到S船≈L
3.不论人怎样走动(匀速、变速),当
人从船头走至船尾时,船移动的距离 相同,而且人动船动,人停船停。
思考题:
1、一质量为M的船,静止于湖水 中,船身长L,船的两端点有质量 分别为m1和m2的人,且m1=m2,当 两人交换位置后,船身位移的大小 是多少?(不计水的阻力)
总结 :人船模型的综合 一发、散人船及人车模型(水平 二方、向劈)(斜面,弧面)和物块(水平 方三向、)气球和人(竖直方 四向、)圆环和球及圆环和环(水 处平理方此向类)题,除熟记推论外,关键是 画草图,确定位移s1和s2的关系。
作业
1.如图2所示,在光滑水平地面上,有两 个光滑的直角三形木块A和B,底边长 分别为a、b,质量分别为M、m,若M = 4m,且不计任何摩擦力,当B滑到底 部时,A向后移了多少距离?
高中物理《动量之人船模型》教学课件

【人快船快、人慢船慢、人停船停、人左船右】
03. 模型分析
情境简化:静止在水面上的小船长为L,质量为M,在船的最右端站有一质量为m的人, 当人从最右端走到最左端的过程中(不计水的阻力)小船移动的距离是多大? 【微元的思想:将全过程分成很多个极短的时段Δt ,每个Δt 内人与船的运动可视为匀速运动】
2、找位移之间的等量关系。
3、根据动量守恒定律列出方程。
4、代入数据求解。
反冲
05. 模型特点——总结归纳
1、速度的关系 :m v人 +M 船 v船=0
人动船动,人静船静,人快船快,人慢船慢,人左船右。
2、距离的关系 :S人 + S船 =L
S人
M mM
L
S船
m mM
L
3、比例的关系
:
v人 v船
S人 S船
M m
人船位移比等于它们质量的反比。 人船平均速度(瞬时速度)比等于它 们质量的反比。
4、适用的条件 :①某一方向上系统的初动量为0 ②在该方向上系统动量守恒
06. 模型拓展
类人船模型
分析该类问题时:画位移大小的等量关系图
07. “类人船模型”判断
1
人沿绳子下滑运动的过程
类人船模型
感受物理学之美
当堂演练
【例题1】西晋史学家陈寿在《三国志》中记载:“置象大船之上,而刻其水痕所 至,称物以载之,则校可知矣。”这就是著名的曹冲称象的故事。某同学欲挑 战曹冲,利用卷尺测定大船的质量。该同学利用卷尺测出船长为L,然后慢速 进入静止的平行于河岸的船的船头,再从船头行走至船尾,之后,慢速下船,
第一章:动量守恒定律 人船模型及应用
高中物理·选择性必修第一册
某方向上动量守恒 人船模型

(1)物体上升的最大高度。 (2)小车的最终速度; 解:当m与M相对静止时, 有最大速度h。
mv0 (m M )v 1 1 2 2 mv 0 (m M )v mgh 2 2 2 Mv0 hmax 2(m M )
分析可知,m返回水平面上时,M有最终的速度
动量守恒定律
某方向上动量守恒
1.如图所示,质量为M的三角形滑块置于水 平光滑地面上,高度为H,当质量为m的滑 块B沿斜面下滑的过程中,不计一切摩擦。 质量为m,凹形半圆槽的质量为M,各面 光滑,小球从静止开始下滑到槽的最低端时,小球和凹槽 的速度各为多大?半圆槽半径为R。 析:设当小球达最低端时的m、M速度分别为v1、v2, 由动量守恒得:
L
M
L M
S2
S1
解:以向右为正方向,设人速为V1 设船速为V2 0=m V1 -M V2 m V1 = M V2
由于人在走动过程中任意时刻人和船的速度和均满足上述 关系,所以运动过程中,人和船平均速度大小也应满足相 似的关系
m V1 = M V2 V1 = S1 /t
,
V2 =S2 /t
m S1 = M S2 S1 +S2=L S1 =ML/m+M
,
mv0 mv'Mv
1/2mV0
2=1/2mV!2+1/2MV2
2mv 0 v mM
平均动量守恒
人船模型
质量为M的船停在静止的水面上,船长为L,一质 量为m的人,由船头走到船尾,若不计水的阻力 ,则整个过程人和船相对于水面移动的距离?
分析:“人船模型”是由人和船 两个物体构成的系统; 该系统在人和船相互作用下各自 运动,运动过程中该系统所受到 的合外力为零;即人和船组成的 系统在运动过程中总动量守恒。
人船模型(解析版)—动量守恒的十种模型解读和针对性训练——2025届高考物理一轮复习

动量守恒的十种模型解读和针对性训练人船模型模型解读1.模型图示2.模型特点(1)两物体满足动量守恒定律:m v 人-M v 船=0。
(2)两物体的位移大小满足:m s 人t -M s 船t =0,s 人+s 船=L 得s 人=M M +m L ,s 船=mM +m L 。
3.运动特点(1)人动则船动,人静则船静,人快船快,人慢船慢,人左船右。
(2)人船位移比等于它们质量的反比;人船平均速度(瞬时速度)比等于它们质量的反比,即s 人s 船=v 人v 船=M m。
“人船模型”的拓展(某一方向动量守恒)【典例分析】【典例】 如图,质量为M 的匀质凹槽放在光滑水平地面上,凹槽内有一个半椭圆形的光滑轨道,椭圆的半长轴和半短轴分别为a 和b ,长轴水平,短轴竖直。
质量为m 的小球,初始时刻从椭圆轨道长轴的右端点由静止开始下滑。
以初始时刻椭圆中心的位置为坐标原点,在竖直平面内建立固定于地面的直角坐标系xOy ,椭圆长轴位于x 轴上。
整个过程凹槽不翻转,重力加速度为g 。
(1)小球第一次运动到轨道最低点时,求凹槽的速度大小;(2)凹槽相对于初始时刻运动的距离。
答案 (2)maM +m 解析 (1)小球从静止到第一次运动到轨道最低点的过程,小球和凹槽组成的系统水平方向上动量守恒,有0=m v 1-M v 2mgb =12m v 21+12M v 22联立解得v 2(2)根据人船模型规律,在水平方向上有mx 1=Mx 2又由位移关系知x 1+x 2=a解得凹槽相对于初始时刻运动的距离x 2=ma M +m。
【名师点拨】应用“人船模型”解题的两个关键点(1)“人船模型”的应用条件:相互作用的物体原来都静止,且满足动量守恒条件。
(2)人、船位移大小关系:m 人x 人=m 船x 船,x 人+x 船=L (L 为船的长度)。
【针对性训练】1. (2024河南名校联考).如图,棱长为a 、大小形状相同的立方体木块和铁块,质量为m 的木块在上、质量为M 的铁块在下,正对用极短细绳连结悬浮在平静的池中某处,木块上表面距离水面的竖直距离为h 。
人船模型
处理方法: 利用系统动量守衡的瞬时性和物体间 作用的
等时性,求解每个物体的对地位移.
m v1 = M v2
m v1 t = M v2 t
m s1 = M s2
---------------- ①
s1 + s2 = L
-----------②
结论: 人船对地位移为将二者相对位移按质量反比
分配关系
s人
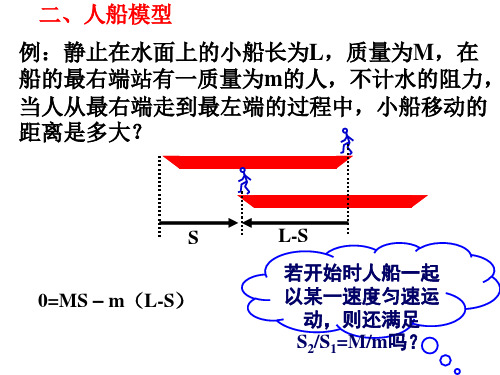
二、人船模型
例:静止在水面上的小船长为L,质量为M,在 船的最右端站有一质量为m的人,不计水的阻力, 当人从最右端走到最左端的过程中,小船移动的 距离是多大?
S 0=MS – m(L-S)
L-S
若开始时人船一起 以某一速度匀速运
动,则还满足 S2/S1=M/m吗?
条件: 系统动量守衡且系统初动量为零.
3、人船模型的适用条件是:两个物体组成的系统 动量守恒,系统的合动量为零。
例. 质量为m的人站在质量为M,长为L的静止小船的右 端,小船的左端靠在岸边。当他向左走到船的左端时, 船左端离岸多远?
解:先画出示意图。人、船系统动量守恒,总动
量始终为零,所以人、船动量大小始终相等。从
图中可以看出,人、船的位移大小之和等于L。
M mM
L
s船
m mM
L
1、“人船模型”是动量守恒定律的拓展应用,它 把速度和质量的关系推广到质量和位移的关系。 即:
m1v1=m2v2 则:m1s1= m2s2 2、此结论与人在船上行走的速度大小无关。不论 是匀速行走还是变速行走,甚至往返行走,只要 人最终到达船的左端,那么结论都是相同的。
设人、船位移大小分别为l1、l2 ,则:mv1=Mv2,
两边同乘时间t,ml1=Ml2,
人船模型

气球与猴子模型 已知目前猴子距地面的高度, 猴子的质量, 气球的质量, 若 要猴子能沿绳返回地面, 求绳 长的最小值。
斜劈与滑块模型 已知斜劈质量与底面边长, 水 平面光滑, 物块从顶部无初速 度滑到底部时, 求斜劈移动的 距离。
1
人船模型
平均动量守恒 若系统在全过程中动量守恒(包括单方向动量守恒) ,则这一系统在全过程中的平均动 量也守恒。 用平均动量守恒解决人船模型 如果系统是由两个物体组成的,且相互作用前均静止,相互作用后均发生运动,则有 0 m1v1 m2v2 ( v1、v2 表示平均速度的大小) 推论: m1于统一参照物位移的大小。 规律:你动我动,你停我停,你快我快,你慢我慢。 人船模型的延伸
