四年级图形的面积问题
小学四年级奥数思维问题之图形面积

图形面积问题教学目标:①知识与技能目标:借助所学知识计算组合图形的面积②过程与方法目标:通过对数量关系地分析,让学生在解决问题过程中掌握一些解决问题的基本策略③情感态度与价值观目标:感受所学知识与现实生活的紧密联系教学重点:图形面积公式的运用教学难点:组合图形的面积计算[知识引领与方法]1.细心观察,把握图形特点,合理的进行切拼,从而使问题得以顺利解答2.从整体上观察图形的特征,掌握图形本质,结合必要的分析,推理和计算,使隐蔽的数量关系明朗化[例题精选及训练]【例1】一块长方形铁板,长18分米,宽15分米。
若长和宽分别减少3分米,面积比原来的减少多少平方分米?练习:1.人民路小学操场长90米,宽45米,改造后,长和宽分别增加10米。
现在操场面积比原来增加了多少平方米?2.有一块长方形的木板,长22分米,宽8分米。
如果长和宽分别减少10分米和3分米,木板的面积比原来减少多少平方分米?3.一块长方形地,长是80米,宽是45米,如果把宽增加5米,要使面积不变,长应减少多少米?【例2】一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米;如果长不变,宽增加3米,那么它的面积增加48平方米。
问这个长方形原来的面积是多少平方米?练习:1.一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米;如果长不变,宽增加4米,那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米?2.一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减少36平方米。
问这个长方形原来的面积是多少平方米?3.一个长方形花圃,如果它的长减少5米,或它的宽减少6米,那么它的面积都减少60平方米。
求这个长方形花圃原来的面积。
【例3】下图是一个养鸡专业户用一段长17米的篱笆围成的一个长方形养鸡场,那么这个养鸡场的占地面积是多少平方米?练习:1.右图是某个养鸡专业户用一段长13米的篱笆围成一个长形的养鸡场,则养鸡场的占地面积有多大?2.用56米长的木栏围成长或宽是20米的长方形,其中一边利用围墙,怎样才能使围成的面积最大?【例4】街心花园中一个正方形的花坛四周有一条1米宽的水泥路,如果水泥路的总面积是12平方米,那么中间花坛的面积是多少平方米?练习:1.有一个正方形的水池,如右图阴影部分所示,在它的周围修了一个宽8米的花池,花池的面积是480平方米,求水池的边长。
四年级面积求解题技巧

四年级面积求解题技巧四年级学生面积求解题是数学学习中的重要内容之一。
通过解答面积求解题,学生可以培养自己的逻辑思维能力和问题解决能力。
下面将给出一些四年级面积求解题的技巧,帮助学生更好地完成这些题目。
一、认识面积的概念在讲解面积求解题技巧之前,首先要让学生掌握面积的概念。
面积是指平面上一个图形所占的两维空间的大小。
对于常见的图形,如矩形、正方形、三角形等,可以采用不同的公式来计算其面积。
二、理解面积的计算方法1.矩形的面积计算方法:矩形的面积等于底边的长度乘以高的长度,即S=a×h(a为底边的长度,h为高的长度)。
2.正方形的面积计算方法:正方形的面积等于边长的平方,即S=a×a(a为边长)。
3.三角形的面积计算方法:三角形的面积等于底边的长度乘以高的长度的一半,即S=(1/2)×a×h(a为底边的长度,h为高的长度)。
三、掌握面积求解题的常见算法1.直接计算法:根据题目给出的图形,直接使用相应的面积计算公式计算出面积。
2.分解法:将题目给出的图形分解为一些基本的图形,计算出每个基本图形的面积再求和。
3.相似图形法:根据相似图形的性质,利用已知面积和比例关系求解出未知图形的面积。
四、应用面积求解题技巧来解答问题以下是一些常见的面积求解题,我们可以利用上述技巧来解答。
例题1:一个正方形的边长是5米,求其面积。
解题思路:根据正方形的面积计算方法,直接计算出正方形的面积。
S = a × a = 5 × 5 = 25(平方米)。
所以正方形的面积是25平方米。
例题2:一个矩形的长是12厘米,宽是8厘米,求其面积。
解题思路:根据矩形的面积计算方法,直接计算出矩形的面积。
S = a × h = 12 × 8 = 96(平方厘米)。
所以矩形的面积是96平方厘米。
例题3:一个三角形的底边长是6厘米,高是4厘米,求其面积。
解题思路:根据三角形的面积计算方法,直接计算出三角形的面积。
小学数学四年级几何图形

小学数学四年级几何图形1、基本图形面积:正方形面积=边长×边长长方形面积=长×宽平行四边形面积=底×高三角形面积=底×高÷2梯形面积=(上底+下底)×高÷2例题1、如图,一张长方形纸片,长7厘米,宽5厘米。
把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?例题2、如图所示,7个完全相同的长方形拼成了图中的阴影部分,图中空白部分的面积是多少平方厘米?例题3、如图,在直角梯形ABCD中,三角形ABE和三角形CDE都是等腰直角三角形,且BC=20厘米,那么直角梯形ABCD的面积是多少?例题4、如图,小正方形ABCD放在大正方形EFGH上面,已知小正方形的边长为4厘米,且梯形AEHD的面积是28平方厘米,那么梯形AFGD的面积是多少平方厘米?2、计算面积基本原则:1)先基本图形2)如不是基本图形,则采用移、分、割、补的方法3)同底等高面积相等例题1、一个长方形被分成4个不同颜色的三角形,红色三角形的面积是9,黄色三角形的面积是21,绿色三角形的面积是10,那么蓝色三角形的面积是多少?例题2、如图,阴影部分的面积是多少?例题3、如图,正方形ABCD的边长为8,AE=2,CF=3。
长方形EFGH的面积为_______。
例题4、如图,ABCD是梯形,ABFD是平行四边形,CDEF是正方形,AGHF是长方形。
又知AD=14厘米,BC=22厘米,那么阴影部分的面积是多少平方厘米?3、格点图形采用皮克定理:S=n+s÷2-1n---代表在图形内部的格点数目s---代表在图形边上的格点数目第1题:第2题:第3题:4、勾股定理勾三股四弦5a2+b2=c2第1题:第2题:第3题:第4题:第5题:。
小学四年级必会图形求面积的10个方法!

我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形,我们的面积及周长都有相应的公式直接计算。
如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算。
一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例1:如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2:如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积。
一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD 面积的三分之一,也就是12厘米.解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3:两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形。
总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有1相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例如:求下图整个图形的面积。
一句话:半圆的面积+正方形的面积=总面积2相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
2024年数学四年级上册图形的周长与面积基础练习题(含答案)

2024年数学四年级上册图形的周长与面积基础练习题(含答案)试题部分一、选择题:1. 一个长方形的长是10厘米,宽是5厘米,它的周长是多少厘米?A. 15厘米B. 30厘米C. 50厘米D. 100厘米2. 一个正方形的边长是8厘米,它的面积是多少平方厘米?A. 16平方厘米B. 32平方厘米C. 64平方厘米D. 81平方厘米3. 下列哪个图形的周长与面积相等?A. 正方形B. 长方形C. 圆D. 三角形4. 一个圆的直径是10厘米,它的周长(圆周率取3.14)是多少厘米?A. 15.7厘米B. 31.4厘米C. 50厘米D. 157厘米5. 一个三角形的底是6厘米,高是4厘米,它的面积是多少平方厘米?A. 10平方厘米B. 12平方厘米C. 24平方厘米D. 48平方厘米6. 下列哪个图形的面积最大?A. 边长为10厘米的正方形B. 长为12厘米,宽为8厘米的长方形C. 半径为5厘米的圆D. 底为10厘米,高为6厘米的三角形7. 一个长方形的周长是40厘米,长是12厘米,宽是多少厘米?A. 8厘米B. 10厘米C. 16厘米D. 20厘米8. 下列哪个图形的周长最长?A. 边长为8厘米的正方形B. 长为10厘米,宽为6厘米的长方形C. 直径为10厘米的圆D. 底为10厘米,高为5厘米的三角形9. 一个圆的周长是31.4厘米,它的半径是多少厘米?A. 5厘米B. 10厘米C. 15厘米D. 20厘米10. 下列哪个图形的面积最小?A. 边长为3厘米的正方形B. 长为4厘米,宽为2厘米的长方形C. 半径为2厘米的圆D. 底为4厘米,高为3厘米的三角形二、判断题:1. 长方形的周长等于长和宽的和乘以2。
()2. 正方形的面积等于边长的平方。
()3. 圆的周长等于直径乘以圆周率。
()4. 三角形的面积等于底乘以高的一半。
()5. 长方形的面积等于长和宽的乘积。
()6. 正方形的周长等于边长的四倍。
()7. 圆的面积等于半径的平方乘以圆周率。
【详解】四年级下第04讲_格点图形面积计算
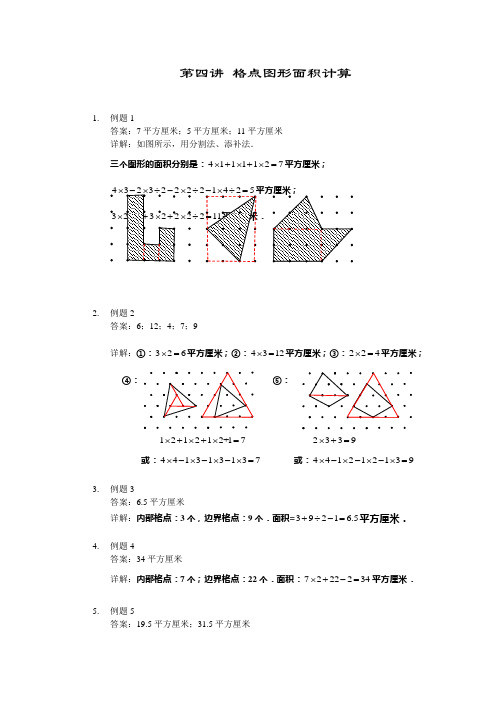
第四讲 格点图形面积计算1. 例题1答案:7平方厘米;5平方厘米;11平方厘米详解:如图所示,用分割法、添补法.三个图形的面积分别是:4111127⨯+⨯+⨯=平方厘米; 4⨯⨯÷32⨯⨯÷2. 例题2答案:6;12;4;7;9详解:①:326⨯=平方厘米;②:4312⨯=平方厘米;③:224⨯=平方厘米;3. 例题3答案:6.5平方厘米 详解:内部格点:3个,边界格点:9个.面积=3921 6.5+÷-=平方厘米.4. 例题4答案:34平方厘米详解:内部格点:7个;边界格点:22个.面积:7222234⨯+-=平方厘米.5.例题5答案:19.5平方厘米;31.5平方厘米④: ⑤: 121212+17⨯+⨯+⨯= 或:441313137⨯-⨯-⨯-⨯= 2339⨯+= 或:441212139⨯-⨯-⨯-⨯=详解:可以分割、添补,也可以用公式法:(1)内部格点:4个;边界格点:7个.面积:()7241319.5÷+-⨯=平方厘米;(2)内部格点:8个;边界格点:7个.面积:()7281331.5÷+-⨯=平方厘米.6. 例题6答案:28平方厘米;56平方厘米详解:可以分割、添补,也可以用公式法:(1)内部格点:4个;边界格点:8个.面积:()4282228⨯+-⨯=平方厘米;(2)内部格点:3个;边界格点:10个.面积:()32102456⨯+-⨯=平方厘米.7. 练习1答案:3平方厘米;10平方厘米详解:如图,分别用分割法、添补法.8. 练习2答案:12;20;5;18 详解:①:3412⨯=平方厘米; ②:直接数,每层4个,共5层,4520⨯=9. 练习3答案:13 简答:内部格点:1个,边界格点:13个.面积=()11321213+÷-⨯=.10. 练习4答案:17平方厘米简答:内部格点:1个;边界格点:17个.面积:1217217⨯+-=平方厘米. ③: ④:1112125⨯+⨯+⨯= 122312818⨯+⨯+⨯+=11.作业1答案:6;6.5简答:可用分割或添补法完成.12.作业2答案:7;12简答:使用割补法分别计算.13.作业3答案:56简答:大正三角形的面积是254100⨯=平方厘米,利用添补法可得.14.作业4答案:29简答:综合利用分割法与添补法.也可以用正方形格点图形面积公式计算.注意每个最小正方形面积是2.15.作业5答案:44简答:综合利用分割法与添补法.也可以用三角形格点图形面积公式计算.注意每个最小正三角形面积是2.。
小学四年级数学面积应用题及图形面积题

1.有一块菜地长37米,宽25米。
菜地中间留了宽1米的路,把菜地平均分成4块,每一块的面积是多少?
2.教室前面的墙壁,长6米,宽3米,墙上有一块黑板面积是3平方米,现在要粉刷这面墙壁,要粉刷的面积是多少?
3.学校安装教室玻璃。
每块玻璃长40厘米,宽35厘米。
每块玻璃的面积是多少平方分米?每平方分米玻璃是2角钱,一块玻璃多少钱?
4.一条人行道长20米,宽4米。
面积是多少?合多少平方分米?用面积是25平方分米的水泥砖铺地,需要这样的水泥砖几块?
5.一张写字台的台面长是13分米,宽是6分米。
他的面积是多少?合多少平方厘米?
6.在长为8米,宽为5米的土地上截一个最大的正方形,剩余土地的面积是多少?
7.有一块长为20米,宽为80分米的长方形土地要铺上地砖,每块地砖的边长是50分米。
至少需要多少块这样的地砖才能把这块地铺满?
8.有一块长30米,宽20米的长方形土地要铺上草皮,每块草皮的面积是9平方分米。
至少要多少块这样的草皮才能把这块地铺满?
9.一扇防盗门高20分米,宽12分米。
要给30扇这样的门涂油漆。
(涂两面)一共要涂多少平方米?
10.一间房间长4米,宽3米。
如果每平方米铺9块地砖,那么这间房需铺几块地砖?
四、(1)计算下面图形阴影部分的面积。
(单位:厘米)
3.如图:已知三角形的面积是60平方厘米,求梯形面积。
(阴影部分)(单位:厘米)。
小学四年级数学必会图形求面积的10个方法

我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算。
如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算。
一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
先看三道例题感受一下↓↓↓例1:如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2:如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积。
一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3:两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有↓↓↓一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
四年级奥数第三讲:图形面积问题

第三讲:图形面积问题
姓名:
例1、一块长方形铁板,长18分米,宽15分米。
若长和宽分别减少3分米,面积比原来减少多少平方分米?
练习1、人民路小学操场长90米,宽45米,改造后,场合宽分别增加10米。
现在操场面积比原来增加了多少平方米?
练习2、一块长方形地,长80米,宽45米,如果把宽增加5米,要使面积不变,长应该减少多少米?
例2、一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米;如果长不变,宽增加3米,那么它的面积增加48平方米。
问这个长方形原来的面积时多少平方米?
练习1、一个长方形花圃,如果它的长减少5米,或它的宽减少6米,那么它的面积都减少60平方米。
求这个长方形花圃原来的面积时多少平方米?
例3、右图是一个养鸡专业户用一段长17米的篱笆围成的一个长方形养鸡场,那么这个养鸡场的占地面积是多少平方米?
练习1、用56米长的木栏围成长或宽是20米的长方形,其中一边利用围墙,怎样才能使围成的面积最大?
例4、街心花园中一个正方形的花坛四周有一条1米宽的水泥路,如果水泥路的总面积是12平方米,那么中间花坛的面积是多少平方米?
练习1、有一个正方形的水池,如右图阴影部分所示,在它的周围修了一个宽8米的花池,花池的面积是480平方米,求水池的边长是多少米?
例5、一块正方形的钢板,先截去宽5分米的长方形,又截去宽8分米的长方形(如下图所示),这样面积就比原来的正方形减少了181平方分米。
原来正方形的边长是多少分米?
练习1、一个正方形一条边减少6分米,另一条边减少10分米后变成一个长方形,这个长方形的面积比正方形的面积少260平方分米,求原来正方形的边长是多少分米?。
四年级图形的面积问题

图形的面积问题【例题1】 人民路小学操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方米?场面积比原来增加了多少平方米?【思路导航】用操场现在的面积减去操场原来的面积,就得到增加的面积。
操场现在的面积是(90+1090+10)×()×()×(45+545+545+5))=5000平方米,操场原来的面积是9090××45=4050平方米。
所以,现在的面积比原来增加50005000--4050=950平方米。
平方米。
思考:还有其它的方法吗?练习1:1.1.有一块长方形的木板,有一块长方形的木板,有一块长方形的木板,长长22分米,宽8分米。
如果长和宽分别减少10分米、3分米,面积比原来减少多少平方分米?面积比原来减少多少平方分米?2.2.一块长方形地,长是一块长方形地,长是80米,宽是45米。
如果把宽增加5米,要使面积不变,长应减少多少米?米?【例题2】一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减少36平方米。
这个长方形原来的面积是多少平方米?【思路导航】由“宽不变,长增加6米,面积增加54平方米”可知,它的宽为5454÷÷6=9米;由“长不变,宽减少3米,面积减少36平方米”可知,它的长为3636÷÷3=12米。
所以,这个长方形原来的面积是1212××9=108平方米。
平方米。
警示:画图理解更深刻!!练习2:1.1.一个长方形,如果宽不变,长减少一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米;如果长不变,宽增加4米,那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米?2.2.一个长方形,如果它的长减少一个长方形,如果它的长减少3米,或它的宽减少2米,那么它的面积都减少36平方米。
四年级巧求面积练习题

四年级巧求面积演习题【1 】1.把一个长16米,宽9米的长方形的宽增长7米,可得到一个什么平面图形?面积是若干平方米?2.一个长方形的周长是40厘米,且宽比长短2厘米,求长方形的面积是若干?3.一个长62厘米,宽50厘米的长方形中截取一个最大的正方形,这个正方形的面积是若干?4.假如把一个边长是10厘米的正方形的边长增长3厘米,这个正方形的面积将增长若干平方厘米?5.有一个边长是20米的鱼塘,在它的周围有一条宽2米的道路,求道路的面积是若干平方米?6.求下面图形的面积是若干?(单位:厘米)7.大小两个正方形部分重合,边长分离是7厘米和5厘米,重合部分面积是10平方厘米,求两个正方形盖住的面积是若干?8.两个雷同的长方形,长是14厘米,宽是6厘米,把它们按如图叠放在一路,这个图形的面积是若干?B组9.一个长方形的长是30厘米,宽是20厘米,假如长和宽各增长5厘米,求面积增长若干平方厘米?10.有两个一样的正方形,拼成一个长方形,周长比本来削减8厘米,求拼成的长方形的面积?11.四个同样大小的长方形和一正方形拼成了一个大正方形,大正方形的面积是100平方厘米,小正方形的面积是4平方厘米,求长方形的宽是若干?12.有一个长方形,假如它的长削减2米,或宽削减3米,它的面积就削减24平方米,求本来的长方形的面积是若干?13.一个打谷场,长是60米,宽是45米,扩建后长增长了15米,宽增长了8米,那么打谷场的面积增长了若干平方米?6.如图分列着两个正方形,左边一个大正方形的边长是6厘米,求暗影部分的面积?14.如图长方形ABCD的长是12厘米,宽是6厘米,M.N分离为AB.CD的中点,求暗影部分的面积?15.假如长方形的长是9厘米,宽是6厘米,三角形ADE和DCF的面积都是长方形面积的三分之一,求暗影部分的面积?。
四年级图形的面积问题

四年级图形的面积问题 Document number:NOCG-YUNOO-BUYTT-UU986-1986UT图形的面积问题【例题1】人民路小学操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方米【思路导航】用操场现在的面积减去操场原来的面积,就得到增加的面积。
操场现在的面积是(90+10)×(45+5)=5000平方米,操场原来的面积是90×45=4050平方米。
所以,现在的面积比原来增加5000-4050=950平方米。
思考:还有其它的方法吗练习1:1.有一块长方形的木板,长22分米,宽8分米。
如果长和宽分别减少10分米、3分米,面积比原来减少多少平方分米2.一块长方形地,长是80米,宽是45米。
如果把宽增加5米,要使面积不变,长应减少多少米【例题2】一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减少36平方米。
这个长方形原来的面积是多少平方米【思路导航】由“宽不变,长增加6米,面积增加54平方米”可知,它的宽为54÷6=9米;由“长不变,宽减少3米,面积减少36平方米”可知,它的长为36÷3=12米。
所以,这个长方形原来的面积是12×9=108平方米。
警示:画图理解更深刻!!练习2:1.一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米;如果长不变,宽增加4米,那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米2.一个长方形,如果它的长减少3米,或它的宽减少2米,那么它的面积都减少36平方米。
求这个长方形原来的面积。
【例题3】下图是一个养禽专业户用一段16米的篱笆围成的一个长方形养鸡场,求它的占地面积。
【思路导航】根据题意,因为一面利用着墙,所以两条长加一条宽等于16米。
而宽是4米,那么长是(16-4)÷2=6米,占地面积是6×4=24平方米。
四年级数学上册面积应用题

四年级数学上册面积应用题一、长方形和正方形面积基础计算类(1 10题)1. 一个长方形花坛,长是12米,宽是8米,这个花坛的面积是多少平方米?解析:长方形的面积 = 长×宽,已知长为12米,宽为8米,所以花坛的面积= 12×8 = 96(平方米)。
2. 正方形手帕的边长是15厘米,它的面积是多少平方厘米?解析:正方形的面积 = 边长×边长,手帕边长15厘米,所以面积 = 15×15 = 225(平方厘米)。
3. 有一块长方形菜地,长18米,宽比长少6米,求这块菜地的面积。
解析:首先求出宽,宽比长少6米,那么宽 = 18 6 = 12(米)。
长方形面积= 长×宽,所以这块菜地的面积 = 18×12 = 216(平方米)。
4. 一个正方形的周长是48分米,它的面积是多少平方分米?解析:正方形的周长 = 边长×4,已知周长48分米,那么边长 = 48÷4 = 12(分米)。
正方形面积 = 边长×边长,所以面积 = 12×12 = 144(平方分米)。
5. 一间教室长9米,宽6米,如果用边长为3分米的地砖铺地,需要多少块地砖?解析:先算出教室的面积,教室面积 = 长×宽 = 9×6 = 54(平方米),54平方米 = 5400平方分米。
地砖为正方形,其面积 = 边长×边长 = 3×3 = 9(平方分米)。
需要地砖的块数 = 教室面积÷地砖面积 = 5400÷9 = 600(块)。
6. 一个长方形的长是15分米,宽是9分米,这个长方形的面积是多少平方分米?如果长增加3分米,宽不变,面积增加多少平方分米?解析:长方形原来的面积 = 长×宽 = 15×9 = 135(平方分米)。
长增加3分米后变为15 + 3 = 18分米,此时面积 = 18×9 = 162(平方分米)。
四年级奥数,图形面积的计算,讲义

中小学1对1课外辅导专家武汉龙文教育学科辅导讲义授课对象授课教师授课时间授课题目图形面积的计算课型使用教具教学目标掌握图形面积的计算教学重点和难点重点:图形面积公式的运用难点:组合图形的面积计算参考教材教学流程及授课详案温故知新解答有关“图形面积”问题时,应注意以下几点:1.细心观察,把握图形特点,合理地进行切拼,从而使问题得以顺利地解决;2.从整体上观察图形特征,掌握图形本质,结合必要的分析推理和计算,使隐蔽的数量关系明朗化。
知识讲解例题1.人民路小学操场长90米,宽45米,改造后,长增加10米,宽增加5米。
现在操场面积比原来增加多少平方米?【思路导航】用操场现在的面积减去操场原来的面积,就得到增加的面积,操场现在的面积是:(90+10)×(45+5)=5000(平方米),操场原来的面积是:90×45=4050(平方米)。
所以现在比原来增加5000-4050=950平方米。
(90+10)×(45+5)-(90×45)=950(平方米)题海拾贝1. 有一块长方形的木板,长22分米,宽8分米,如果长和宽分别减少10分米,3分米,面积比原来减少多少平方分米?2.一块长方形地,长是80米,宽是45米,如果把宽增加5米,要使面积不变,长应减少多少米?例题2:时间分配及备注一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米,如果长不变,宽减少3米,那么它的面积减少36平方米,这个长方形原来的面积是多少平方米?【思路导航】由:“宽不变,长增加6米,那么它的面积增加54平方米”可知它的宽是54÷6=9(米);又由“长不变,宽减少3米,那么它的面积减少了36平方米”,可知它的长为:36÷3=12(米),所以,这个长方形的面积是12×9=108(平方米)。
(36÷3)×(54÷9)=108(平方米)课堂练习1.一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米,如果长不变,宽增加4米,那么它的面积增加60平方米,这个长方形原来的面积是多少平方米?2.一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米,如果长不变,宽增加3米,那么它的面积增加48平方米,这个长方形的面积原来是多少平方米?3.一个长方形,如果它的长减少3米,或它的宽减少2米,那么它的面积都减少36平方米,求这个长方形原来的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图形的面积问题
【例题1】人民路小学操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方米?
【思路导航】用操场现在的面积减去操场原来的面积,就得到增加的面积。
操场现在的面积是(90+10)×(45+5)=5000平方米,操场原来的面积是90×45=4050平方米。
所以,现在的面积比原来增加5000-4050=950平方米。
思考:还有其它的方法吗?
练习1:1.有一块长方形的木板,长22分米,宽8分米。
如果长和宽分别减少10分米、3分米,面积比原来减少多少平方分米?
2.一块长方形地,长是80米,宽是45米。
如果把宽增加5米,要使面积不变,长应减少多少米?
【例题2】一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减少36平方米。
这个长方形原来的面积是多少平方米?
【思路导航】由“宽不变,长增加6米,面积增加54平方米”可知,它的宽为54÷6=9米;由“长不变,宽减少3米,面积减少36平方米”可知,它的长为36÷3=12米。
所以,这个长方形原来的面积是12×9=108平方米。
警示:画图理解更深刻!!
练习2:1.一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米;如果长不变,宽增加4米,那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米?
2.一个长方形,如果它的长减少3米,或它的宽减少2米,那么它的面积都减少36平方米。
求这个长方形原来的面积。
【例题3】下图是一个养禽专业户用一段16米的篱笆围成的一个长方形
养鸡场,求它的占地面积。
【思路导航】根据题意,因为一面利用着墙,所以两条长加一条宽等于
16米。
而宽是4米,那么长是(16-4)÷2=6米,占地面积是6×4=24平方
米。
练习3:1、用56米长的木栏围成长或宽是20米的长方形,其中一边利用围墙,怎样才能使围成的面积最大?
3.用15米长的栅栏沿着围墙围一个种植花草的长方形苗圃,其中一面利用着墙。
如果每边的长度都是整数,怎样才能使围成的面积最大?
思考:由练习3的两个题你得到了什么规律?
【例题4】街心花园中一个正方形的花坛四周有1米宽的水泥路,如果
水泥路的总面积是12平方米,中间花坛的面积是多少平方米?
【思路导航】把水泥路分成四个同样大小的长方形(如右图)。
因此,
一个长方形的面积是12÷4=3平方米。
因为水泥路宽1米,所以小长方形的
长是3÷1=3米。
从图中可以看出正方形花坛的边长是小长方形长与宽的差,
所以小正方形的边长是3-1=2米。
中间花坛的面积是2×2=4平方米。
练习4:1.四个完全相同的长方形和一个小正方形拼成了一个大正方形(如
图),大正方形的面积是64平方米,小正方形的面积是4平方米,长方形的短
边是多少米?
2.已知大正方形比小正方形的边长多4厘米,大正方形的面积比小正方形面积
大96平方厘米(如图)。
问大小正方形的面积各是多少?
【例题5】一块正方形的钢板,先截去宽5分米的长方形,又截去宽8分米的长方形(如图),面积比原来的正方形减少181平方分米。
原正方形的边长是多少?
【思路导航】把阴影部分剪下来,并把剪下的两个小长方形拼起来(如图),再被上长、宽分别是8分米、5分米的小长方形,这个拼合成的长方形的面积
是181+8×5=221平方分米,长是原来正方形的边长,宽是
8+5=13分米。
所以,原来正方形的边长是221÷13=17分米。
练习5:
1.一个正方形一条边减少6分米,另一条边减少10分米后
变为一个长方形,这个长方形的面积比正方形的面积少260平方米,求原来正方形的边长。
2.一个长方形的木板,如果长减少5分米,宽减少2分米,那么它的面积就减少66平方分米,这时剩下的部分恰好是一个正方形。
求原来长方形的面积。
3.一块正方形的的玻璃,长、宽都截去8厘米后,剩下的正方形比原来少448平方厘米,这块正方形玻璃原来的面积是多大?
【例题6】有9个小长方形,它们的长和宽分别相等,用这9个小长方形拼成的大长方形(如
图)的面积是45平方厘米,求这个大长方形的周长。
52
4
4
4
3
1
【思路导航】
从图上可以知道,小长方形的长的4倍等于宽的5倍,所以长是宽的5÷4=1.25倍。
每个小长方形的面积为45÷9=5平方厘米,所以1.25×宽×宽=5,所以宽为2厘米,长为2.5厘米。
练习:下图的长方形被分割成5个正方形,已知原长方形的面积为120平方厘米,求原长方形的长与宽。
【例题
7】一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米,则面积增
加9900平方米,问原来这块正方形苗圃的面积是多少平方米?
【思路导航】通过画图可以算出:小正方形的面积为:30×30=900平方米。
用增加的面积减去小正方形的面积就得到增加的两个长方形的面积之和,9900-900=9000平方米。
而增加的两个长方形的面积相等,于是其中一个长方形的面积为9000÷2=4500平方米。
练习:喜阳阳小学的操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方分米?
【例题7】如下图,用标号为1,2,3,4,5的五种大小不同的正方形
拼成一个大长方形,大长方形的长和宽分别是18,14,则标号为5的正方形的面积是多少?
【思路导航】如果标号为5的正方形的边长是a ,那么1号比
2号大a ,2号比3号大a ,所以1号比3号大2a ,又因为2号和3号的边长之和是14,1号和
厘米图a
2号的边长之和是18,所以1号比3号大18-14=4。
练习:小孙同学用编号为1,2,3,4,5的大小不同的正方形拼出一个长方形,如右图所示,则中间阴影部分正方形的周长是多少厘米?
1.如图是由5个相同的小长方形拼成的大长方形,大长方形的周长是44厘米,求大长方形的面
积。
2.一个正方形,相邻的两个边长增加4厘米,面积就增加96平方厘米,求原来正方形的面积?
3.如图
a 有一大一小两块正方形试验田,他们的周长相差40米,面积相
差220平方米,那么小正方形试验田的面积是多少平方米?。
