材料力学计算器
常用圆柱弹簧计算器-压缩与拉伸弹簧Excel计算表

有效圈数, n = 5
总圈数, N = 7
输出
线圈节距, p = (L - 3*d) / n
= 0.75
mm
压并高度, H = d * (N + 1)
= 3.125
mm
端部开放 + 未平切
输入
展开长度, L = 4.000
mm
线径, d = 0.125
mm
有效圈数, n = 5
总圈数, N = 7
输出
线圈节距, p = (L - d) / n
= 0.775
mm
压并高度, H = d * (N + 1)
= 3.125
mm
端部开放 + 平切
输入
展开长度, L = 4.000
mm
线径, d = 0.125
mm
有效圈数, n = 5
总圈数, N = 7
输出
线圈节距, p = L / n
= 0.8
mm
压并高度, H = d * (N + 1)
常用圆柱弹簧计算器
圆柱弹簧 - 圆线
压缩与拉伸弹簧强度计算
输入
试验载荷, P = 24.00
N
线径, d = 0.188
mm
弹簧中径, D = 2.000
mm
有效圈数, n = 10
-
材料的切变模量, G = 10,000,000
Mpa
输出
弹簧刚度系数, R = G*d^4 / (8*n*D^3)
= 19.52
= 3.125
mm
圆柱弹簧 - 方线
压缩与拉伸弹簧计算
试验载荷, 线截面厚, 线截面高, 弹簧中径, 有效圈数, 材料的切变模量,
新版吉林大学能源动力专业考研经验考研参考书考研真题

考研这个念头,我也不知道为什么,会如此的难以抑制,可能真的和大多数情况一样,我并没有过脑子,只是内心的声音告诉我:我想这样做。
得知录取的消息后,真是万分感概,太多的话想要诉说。
但是这里我主要想要给大家介绍一下我的备考经验,考研这一路走来,收集考研信息着实不易,希望我的文字能给师弟师妹们一个小指引,不要走太多无用的路。
其实在刚考完之后就想写一篇经验贴,不过由于种种事情就给耽搁下来了,一直到今天才有时间把自己考研的历程写下来。
先介绍一下我自己,我是一个比较执着的人,不过有时候又有一些懒散,人嘛总是复杂的,对于考研的想法我其实从刚刚大一的时候就已经有了,在刚刚进入大三的时候就开始着手复习了,不过初期也只是了解一下具体的考研流程以及收集一些考研的资料,反正说到底就是没有特别着急,就我个人的感受来说考研备考并不需要特别长的时间,因为如果时间太长的话容易产生疲惫和心理上的变化反而不好。
下面会是我的一些具体经验介绍和干货整理,篇幅总体会比较长,只因,考研实在是一项大工程,真不是一两句话可描述完的。
所以希望大家耐心看完,并且会有所帮助。
文章结尾处附上我自己备考阶段整理的学习资料,大家可以自取。
吉林大学能源动力初试科目:(101)思想政治理论(201)英语一(301)数学一(865)材料力学(需携带计算器)(自命题)或(101)思想政治理论(201)英语一(301)数学一(872)工程热力学(需携带计算器)(自命题)或(101)思想政治理论(202)俄语(301)数学一(865)材料力学(需携带计算器)(自命题)或(101)思想政治理论(202)俄语(301)数学一(872)工程热力学(需携带计算器)(自命题)或(101)思想政治理论(203)日语(301)数学一(865)材料力学(需携带计算器)(自命题)或(101)思想政治理论(203)日语(301)数学一(872)工程热力学(需携带计算器)(自命题)(865)材料力学参考书:《材料力学》第四版刘鸿文高等教育出版社(872)工程热力学参考书:(1)《工程热力学》第三版毕明树化学工业出版社,2016 年(2)《工程热力学》第五版沈维道高等教育出版社,2016 年先聊聊英语单词部分:我个人认为不背的单词再怎么看视频也没用,背单词没捷径。
压力容器焊材计算器
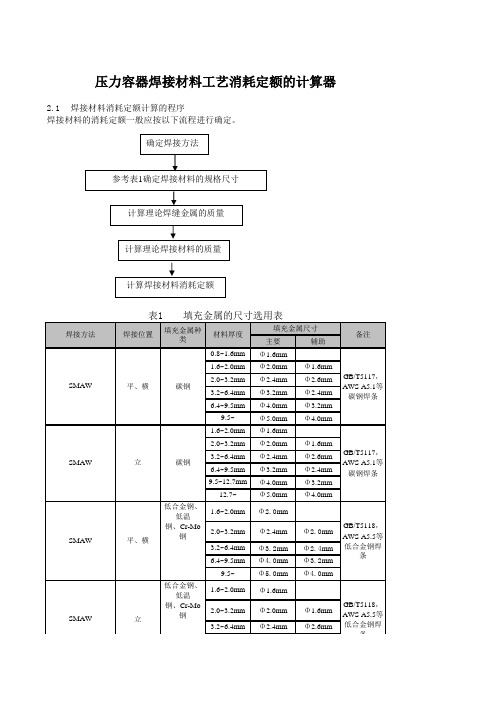
全位置
铝合金
9.5~
Φ1.6mm Φ1.2mm
平,横
碳钢
9.5~
Φ1.2mm Φ1.6mm 含FCAW
平,横
不锈钢
9.5~
Φ1.2mm Φ1.6mm 含FCAW
平,横 镍基合金
9.5~
碳钢、合金
全位置
钢、 不锈钢、镍
1.6~
基合金
Φ1.2mm Φ1.2mm
3.2~6.4mm Φ2.4mm
平
碳钢、低合
Φ1.2mm
AWS A5.11 等镍基合金
焊条
Φ2.0mm
Φ2.0mm Φ2.0mm Φ2.0mm Φ1.2mm Φ2.0mm Φ2.0mm Φ2.0mm Φ2.0mm Φ1.2mm Φ2.4mm Φ3.2mm Φ3.2mm Φ2.4mm Φ1.2mm Φ2.4mm Φ3.2mm
GTAW-AC
GTAW自动 GTAW药芯
GB/T5293, GB/T12470
, AWS A5.17, A5.23等
GB/T17854 ,AWS A5.9
等 AWS A5.14
等
Φ3.2mm
Φ1.6mm
Φ1.6mm
Φ1.6mm
Φ1.6mm
最小内径: 纵向
=200mm,环 向=300mm 最小外径:
纵向 =400mm,环
向=250mm 最小内径:
Φ1.6mm
Φ1.6mm
Φ2.4mm Φ2.4mm Φ2.4mm Φ1.6mm Φ1.6mm Φ2.4mm Φ2.4mm Φ2.4mm Φ1.6mm Φ1.6mm Φ2.4mm Φ2.4mm Φ3.2mm Φ1.6mm Φ1.6mm Φ2.4mm
Φ2.4mm Φ3.2mm Φ1.6mm Φ2.6mm Φ2.4mm Φ3.2mm Φ4.0mm
第一章 材料力学实验
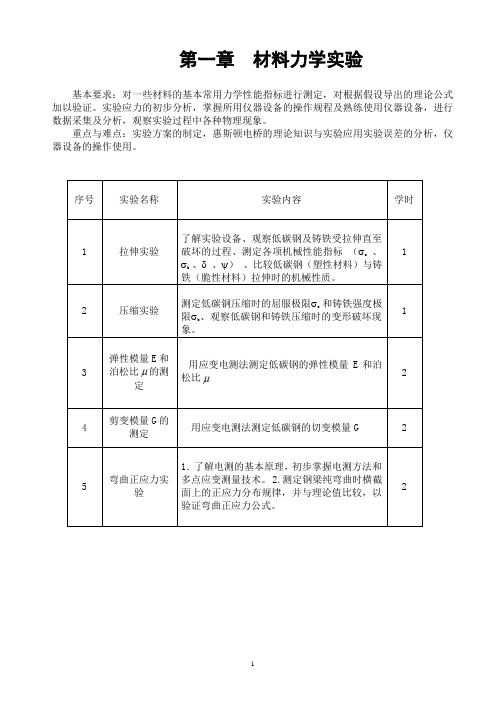
第一章材料力学实验基本要求:对一些材料的基本常用力学性能指标进行测定,对根据假设导出的理论公式加以验证。
实验应力的初步分析,掌握所用仪器设备的操作规程及熟练使用仪器设备,进行数据采集及分析,观察实验过程中各种物理现象。
重点与难点:实验方案的制定,惠斯顿电桥的理论知识与实验应用实验误差的分析,仪器设备的操作使用。
前言材料力学实验是材料力学课程的重要组成部分。
材料力学中的一些理论和公式是建立在实验、观察、推理、假设的基础上,它们的正确性还必须由实验来验证。
学生通过做实验,用理论来解释、分析实验结果,又以实验结果来证明理论,互相印证,以达到巩固理论知识和学会实验方法的双重目的。
本章是根据温州大学建筑与土木工程学院开设的材料力学实验内容和实验仪器设备情况而编写的,由材料的拉伸、压缩实验,弹性模量、泊松比和剪切模量的测定实验,弯曲正应力试验,以及相关仪器和设备的介绍组成。
编写时主要参考了刘鸿文、吕荣坤的《材料力学实验》、曹以柏、徐温玉的《材料力学测试原理及实验》,王绍铭等的《材料力学实验指导》,以及其他院校的有关实验教学资料。
由于水平和时间有限,本书难免有不足和错误,望广大读者给以批评指正。
主编:王军杨芳二00七年七月第一节实验简介§ 1-1-1 实验的意义和基本内容材料力学实验是教学中的一个重要的环节。
材料力学的结论及定律、材料的力学的性质(机械性质)都要通过实验来验证或测定;各种复杂构件的强度和刚度的研究,也需要通过实验才能解决。
故实验课能巩固、加强和应用基本理论知识,掌握测定材料机械性能及测定应力和变形的基本方法,学会使用有关的机器及仪表(如材料试验机、电阻应变仪等),初步培养独立确定实验方案、分析处理实验结果的能力。
通过实验还能培养严肃认真的工作态度,实事求是的科学作风和爱护财物的优良品质。
因此,实验是工程专业学生必须掌握的基本技能。
材料力学实验一般可以分为以下三类:一、测定材料的的力学性质构件设计时,需要了解所用材料的力学性质。
【建议收藏】压型钢板计算工具表格

q= 1.2D+1.4W= 0.80 kN/m
施工时板跨中临时支撑数量= 0 个
M= 1/8*q*l²= 1.516 kN*m
V=
强度验 算:
σ=
1/2*q*l=
M/Wef*1.05=
1.5552 kN 127.88 MPa
<
205 MPa
安全;
挠度验算:
q= 1.2D= 0.38 kN/m
批注本地保存成功开通会员云端永久保存去开通
压型钢板计算书 2703329582.xls2703329582.xls2703329582.xls
工程名称:XXX工程
(一 )
设计资料
压型钢底板采用YX130-600-600压型钢板;厚度为 0.8mm;
压型钢板材料为 Q235 钢;
楼板最大跨度: 3.9 m;
跨中挠度为:
dmax= 5/384*q*l4/2.06e5/I= 5.90 mm;
dmax/L= 0.00151 < 1/200
安全;
第 2 页,共 2 页
钢板重量= 截面积:A=
3.138 mm; 399.75 mm2/m
;
截面惯 性矩: 有效惯 性矩: 有效抗 弯模
600.0 68.3 1000
935070 827970 12450
mm; mm; mm;
mm4/m; mm4/m; mm3/m;
第 1 页,共 2 页
内力设计值:
2703329582.xls2703329582.xls2703329582.xls
肋高: h= 130.0 mm; 全截面形心高度:hcen= 59.5 mm;
厚度: t= 0.8 mm;
碳化硅器寿命计算

碳化硅器寿命计算全文共四篇示例,供读者参考第一篇示例:碳化硅器是一种常用的耐高温、耐酸碱腐蚀的耐磨材料,广泛应用于炼铁、电力、化工等工业领域。
在实际工作中,碳化硅器的寿命是一个重要的参数,它直接影响着设备的运行效率和成本。
对碳化硅器的寿命进行准确的计算和评估是非常重要的。
碳化硅器的寿命计算主要包括两方面的内容:一是机械寿命的计算,即碳化硅器在机械应力下的寿命;二是化学寿命的计算,即碳化硅器在化学腐蚀环境下的寿命。
下面我们将分别介绍这两方面的寿命计算方法。
一、机械寿命计算碳化硅器在高温条件下常常会受到机械应力的影响,如热膨胀、热震荷载等。
机械寿命的计算主要基于碳化硅器的材料力学性能和应力分析进行,常用的计算方法包括有限元分析、蠕变寿命分析等。
有限元分析是一种基于数值计算的方法,通过建立碳化硅器的有限元模型,对其受力情况进行模拟,计算碳化硅器在不同工况下的应力分布,从而预测碳化硅器的寿命。
蠕变寿命分析则是基于碳化硅器的蠕变特性,通过实验数据和理论模型,预测碳化硅器在高温条件下的寿命。
碳化硅器在化学腐蚀环境下也会发生损耗,因此化学寿命的计算也是十分重要的。
化学寿命的计算主要涉及碳化硅器的耐腐蚀性能、腐蚀速度和腐蚀机制等。
常用的计算方法包括浸泡实验、电化学测试等。
浸泡实验是一种通过将碳化硅器放入模拟腐蚀介质中进行实验,在一定时间内观察碳化硅器的损耗情况来评估化学寿命。
电化学测试则是通过电化学方法,测量碳化硅器在不同腐蚀条件下的腐蚀速度,从而预测碳化硅器的寿命。
综合上述所述,碳化硅器的寿命计算涉及多方面因素,其准确性取决于所选用的计算方法和参数。
在实际工程中,应根据具体的工作条件和要求,选择合适的计算方法,对碳化硅器的寿命进行科学评估,从而提高设备的使用效率和寿命,降低维护成本,保障设备的安全稳定运行。
第二篇示例:碳化硅器寿命计算是指通过一系列的理论推导和实验研究,来确定碳化硅器件在特定工作条件下的使用寿命。
历年北京科技大学材料力学C真题(2012,2006,2007)

一、 选择题(以下各题都提供(A)、(B)、(C)、(D)四个选项,只有一项正确。
试选出正确的答案。共 10 题,每题 5 分)
1、下面有关强度理论知识的几个论述,正确的是
。
(A) 需模拟实际应力状态逐一进行试验,确定极限应力;
(B) 无需进行试验,只需关于材料破坏原因的假说;
(C) 需要进行某些简单试验,但无需关于材料破坏原因的假说;
1-5.表示扭转变形程度的量__源自___A.是扭转角Φ,不是单位长度扭转角θ;B.是θ,不是Φ;
C.是Φ和θ;D.不是Φ和θ
1-6.低碳钢试件扭转破坏是_____
A.沿横截面拉断; B.沿 45°螺旋面拉断;
C .沿横截面剪断; D.沿 45°螺旋面剪断
1-7.当实心圆轴的直径增加 l 倍时,其抗扭强度、抗扭刚度分别增加到原来的____倍.
六、(统考题) 图示平面刚架 ABCD 各段的抗弯刚度 EI 相等,已知 P、L、EI、α,试用莫尔定理的图乘法求 解刚架上 A 点的水平位移δA 和截面 A 的转角θA。(20 分)
六、(单考题) 图示平面刚架各段的抗弯刚度 EI 相等,已知 P、a,试用莫尔定理的图乘法求解刚架上 A、B 两点的相对位移δAB。(20 分)
处的最大应力的增大倍数为 (A)2 倍; (B) 4 倍;
。 h
(C)8 倍; (D) 16 倍。
山东大学2018年《850-材料力学》考研大纲_山东大学考研网

山东大学2018年《850-材料力学》考研大纲一、考试性质《材料力学》是工程力学、固体力学、结构工程、岩土工程硕士(MPAcc)专业学位研究生入学统一考试的科目之一。
《材料力学》考试要力求反映上述专业学位的特点,科学、公平、准确、规范地测评考生的基本素质和综合能力,以利用选拔具有发展潜力的优秀人才入学,为国家的经济建设培养具有良好职业道德、具有较强分析与解决实际问题能力的高层次、应用型、复合型的会计专业人才。
二、考试要求测试考生对于与材料力学相关的基本概念、基础知识的掌握情况以及分析问题和解决问题的能力。
三、考试内容一、杆件的内力1.杆件内力的一般描述截面法1)轴力、剪力、扭矩和弯矩的概念2)截面法求杆的内力2.轴力与轴力图1)杆件轴向拉伸与压缩的概念2)截面法求杆的轴力3)轴力图画法3.扭矩与扭矩图1)扭转的概念2)外力偶矩与输出功率、传动轴的转速间的关系3)截面法求轴的扭矩4)扭矩图的画法4.弯曲内力与弯矩图1)平面弯曲的概念2)弯曲内力的概念3)截面法求杆件的剪力与弯矩4)剪力方程与弯矩方程5)剪力图与弯矩图的画法①载荷集度、剪力与弯矩之间的关系②简易法求剪力图和弯矩图5.平面刚架与平面曲杆的弯曲内力1)平面刚架的内力2)平面曲杆的内力二、杆件的应力与强度计算1.拉压杆的应力与强度1)拉压杆的应力计算2)拉压杆的强度校核、截面选择和许可载荷的计算。
2.圆轴扭转时的切应力及强度计算1)圆轴扭转切应力计算;①圆轴扭转切应力公式推导②切应力在横截面上分布规律③空心轴与实心轴的极惯性矩和扭转截面系数。
2)圆轴扭转时的强度校核、截面选择和许可载荷的计算3.梁的弯曲正应力及强度计算1)梁弯曲正应力公式计算①梁的弯曲应力公式推导②正应力在横截面上分布规律;中性轴的概念③矩形截面和圆截面对中性轴的惯性矩及弯曲截面系数。
2)梁弯曲时的强度校核、截面选择和许可载荷的计算;4.梁的弯曲切应力及强度计算1)梁弯曲切应力公式计算①梁弯曲时横截面上切应力计算公式应用②矩形截面梁曲切应力及最大切应力表达式③圆截面梁最大切应力表达式2)梁弯曲切应力的强度校核5.连接件的强度计算1)剪切的实用计算与强度校核2)挤压的实用计算与强度校核三、杆件的变形和简单超静定问题1.轴向拉伸与压缩时的变形1)轴向变形的计算2)横向变形与轴向变形之间的关系2.圆轴扭转变形与刚度条件1)圆轴扭转变形计算2)圆轴扭转的刚度条件与应用3.梁的弯曲变形1)梁挠曲线近似微分方程概念2)积分法求弯曲变形3)叠加法求弯曲变形(注:弯曲变形亦可用第七章中的卡氏定理或莫尔定理求解,考试中不作特殊规定,考生可自由选择自认为方便的方法。
悬臂梁的弯矩计算方法可参考材料力学

悬臂梁的弯矩计算⽅法可参考材料⼒学悬臂梁的弯矩计算⽅法可参考材料⼒学。
你没有说清楚悬臂梁上作⽤的是什么样的荷载形式,所以没有办法直接给答案,给你下以⼏种,让你参考吧(⼀)、受端部集中荷载作⽤时其悬臂梁上的弯矩值是Px,其中P是端部集中⼒,x是从端部到另⼀端的距离。
(⼆)、受均布荷载作⽤时其悬臂梁上的弯矩值是qx2/2,其中q是均布线荷载,x是从端部到另⼀端的距离。
设为均布荷载下。
悬臂梁悬臂净长L。
计算悬臂梁⾃重及其担负楼板⾯积的⾃重计g KN/m;(包括上下粉刷重)计算悬臂梁担负楼板⾯积上的活荷载q KN/m;(楼⾯活荷载标准值查荷载规范GB50009-2001)承载能⼒极限计算的荷载基本组合值为1.2g+1.4q=Q1正常使⽤极限计算的荷载标准组合值为g+q=Q2⽀座截⾯的弯矩=1/2Q×L^2。
(计算两种极限状态的弯矩分别代⼊Q1或Q2值)同问已知弯矩、板混凝⼟强度、钢筋型号,如何求板配筋??例如弯矩21.1KN/m,H=150mm,C25混凝⼟,⼆级钢求As2011-11-01 11:18 提问者:影⼦伯爵之⽻|浏览次数:808次我来帮他解答您还可以输⼊9999 个字推荐答案2011-11-01 14:02⼆、设计依据《混凝⼟结构设计规范》GB50010-2002三、计算信息1. ⼏何参数截⾯类型: 矩形截⾯宽度: b=1000mm截⾯⾼度: h=150mm2. 材料信息混凝⼟等级: C25 fc=11.9N/mm2 ft=1.27N/mm2钢筋种类: HRB335fy=300N/mm2最⼩配筋率: ρmin=0.200%纵筋合⼒点⾄近边距离: as=15mm3. 受⼒信息M=21.100kN*m4. 设计参数结构重要性系数: γo=1.0四、计算过程1. 计算截⾯有效⾼度ho=h-as=150-15=135mm2. 计算相对界限受压区⾼度ξb=β1/(1+fy/(Es*εcu))=0.80/(1+300/(2.0*105*0.0033))=0.5503. 确定计算系数αs=γo*M/(α1*fc*b*ho*ho)=1.0*21.100*106/(1.0*11.9*1000*135*135)= 0.0974. 计算相对受压区⾼度ξ=1-sqrt(1-2αs)=1-sqrt(1-2*0.097)=0.103≤ξb=0.550满⾜要求。
力学试验测试实验报告(3篇)

第1篇一、实验目的1. 了解力学试验的基本原理和方法。
2. 掌握拉伸试验、压缩试验、弯曲试验等力学试验的操作技能。
3. 培养学生严谨的实验态度和良好的实验习惯。
二、实验原理力学试验是研究材料力学性能的重要手段。
本实验主要研究材料的拉伸、压缩和弯曲性能。
通过测量材料在受力过程中的应力、应变等参数,可以了解材料的力学特性。
1. 拉伸试验:测量材料在拉伸过程中断裂时的最大应力,称为抗拉强度。
2. 压缩试验:测量材料在压缩过程中断裂时的最大应力,称为抗压强度。
3. 弯曲试验:测量材料在弯曲过程中断裂时的最大应力,称为抗弯强度。
三、实验仪器与材料1. 实验仪器:万能试验机、拉伸试验机、压缩试验机、弯曲试验机、测量仪器等。
2. 实验材料:钢棒、铜棒、铝棒等。
四、实验步骤1. 拉伸试验:(1)将材料固定在拉伸试验机上,调整夹具,使材料与试验机轴线平行。
(2)打开试验机,使材料缓慢拉伸,直到断裂。
(3)记录断裂时的最大应力值。
2. 压缩试验:(1)将材料固定在压缩试验机上,调整夹具,使材料与试验机轴线平行。
(2)打开试验机,使材料缓慢压缩,直到断裂。
(3)记录断裂时的最大应力值。
3. 弯曲试验:(1)将材料固定在弯曲试验机上,调整夹具,使材料与试验机轴线平行。
(2)打开试验机,使材料缓慢弯曲,直到断裂。
(3)记录断裂时的最大应力值。
五、实验数据与结果分析1. 拉伸试验:(1)材料:钢棒,直径为10mm,长度为100mm。
(2)实验数据:最大应力值为600MPa。
(3)结果分析:钢棒在拉伸试验中表现出良好的抗拉性能。
2. 压缩试验:(1)材料:铜棒,直径为10mm,长度为100mm。
(2)实验数据:最大应力值为200MPa。
(3)结果分析:铜棒在压缩试验中表现出较好的抗压性能。
3. 弯曲试验:(1)材料:铝棒,直径为10mm,长度为100mm。
(2)实验数据:最大应力值为150MPa。
(3)结果分析:铝棒在弯曲试验中表现出较好的抗弯性能。
材料力学计算器

弯曲刚度
μ
E*Iz
E*Iy
0
0
以下计算方法为图层法,需要自行画剪力图&弯矩图,最
弯矩Mz 应力σz1 应力σz2 应力σy
剪力 F(N)
弯矩与坐标轴面积 单位力下的剪力 单位力作用下的弯矩 单位力下形心处弯矩 单位力偶形心处弯矩
挠度z 挠度y 转角z 转角y
扭矩Mx 扭转切应力τ
剪力 F(N)
扭矩与坐标轴的面积 单位力作用下的剪力 单位力作用下的扭矩 单位力下形心处扭矩
只填写蓝色部分,其他区域自动计算,黄色区域为重点结果,部
截面参数 材料参数
面积 A 0
惯性矩
Iz
Iy
0
0
弯曲变形
抗弯截面系数
Wz=Iz/e
Wz1
Wz2
Wy
0
0
0
屈服极限应 力 σs
σ-1
材料 备注
弹性模量 E
弯曲极限应力 σb
切变模量 G 0
安全系数
许用应力
备注
塑性材料 强度校核 疲劳校核
0
0
泊松比
杆长 x(m)
0
0
0
0
凹
凸
0
0
0
0
0
1
0
0
0
0
0
0
0
0
均布载荷q作用
杆长 x(m)
0
0
凹
凸
0
0
0
0
0
计算结果
弯矩Mz
0
σz1
0
σz2
0
σy
0
计算结果
挠度z
0
挠度y
0
材料弯曲实验报告总结(3篇)

第1篇一、实验目的本次材料弯曲实验的主要目的是了解和掌握材料在弯曲过程中的力学性能,验证材料力学基本理论,提高对材料力学实验方法的认识。
通过实验,观察和分析不同材料在不同条件下的弯曲行为,为工程设计和材料选择提供理论依据。
二、实验原理材料在弯曲过程中,受到弯矩和剪力的影响,产生正应力和剪应力。
根据材料力学的基本理论,我们可以通过计算得到材料在弯曲过程中的应力分布和变形情况。
实验中,我们主要关注材料的弯曲正应力,即材料在弯曲过程中产生的垂直于中性轴的应力。
三、实验设备与材料1. 实验设备:弯曲试验机、万能材料试验机、测量仪器(如位移计、应变片等)、计算机等。
2. 实验材料:碳素钢、不锈钢、铝合金、塑料等。
四、实验步骤1. 根据实验要求,选择合适的材料,并进行加工处理,确保试样的尺寸和形状符合实验要求。
2. 将试样安装在弯曲试验机上,调整试验机的参数,如加载速度、加载方式等。
3. 对试样进行弯曲试验,记录实验过程中的数据,如位移、应变等。
4. 利用测量仪器对试样进行应变测量,通过应变片采集数据。
5. 对实验数据进行处理和分析,计算材料在弯曲过程中的应力分布和变形情况。
五、实验结果与分析1. 实验结果表明,不同材料在弯曲过程中的力学性能存在差异。
碳素钢具有较高的抗弯强度和刚度,适用于承受较大载荷的工程结构;不锈钢具有良好的耐腐蚀性能,适用于腐蚀性环境;铝合金具有较低的密度,适用于轻量化设计;塑料具有较好的韧性,适用于需要一定变形能力的场合。
2. 实验结果表明,材料在弯曲过程中的应力分布呈现非线性规律。
中性轴附近应力较大,远离中性轴的应力逐渐减小。
在材料弯曲过程中,最大应力出现在中性轴处。
3. 实验结果表明,材料在弯曲过程中的变形情况与材料的弹性模量和泊松比有关。
弹性模量较大的材料,其变形较小;泊松比较大的材料,其横向变形较大。
六、实验结论1. 通过本次材料弯曲实验,我们掌握了材料在弯曲过程中的力学性能,验证了材料力学基本理论。
考研讲义材料力学

2 梅花香自苦寒来,岁月共理想,人生齐高飞!
《材料力学》
1 基础课程学习缘由
1.1 这门课程适合什么院校和专业
材料力学适合 0802 机械工程、0805 材料科学与工程、0807 动力工程、0814 土木工程、 0815 水利工程、0830 环境科学与工程等专业,在推荐的院校当中,材料力学适合如下院校, 也就是说考生可以根据自己学习状况选择这些专业和院校:
初试科目
832 工程力学(理力、材力) 813 材料力学 C 867 材料力学(需携带计算器) 816 材料力学 830 材料力学 812 材料力学 801 材料力学 832 工程力学(理力、材力) 807 材料力学 867 材料力学(需携带计算器) 802 材料力学 812 材料力学 I 801 材料力学 801 材料力学 831 理论与材料力学
初试科目
952 热工基础 830 材料力学 816 材料力学(I) 824 材料力学 840 工程力学 867 材料力学
0814 土木工程专业之 33 所高校
序列
1
大学名称
北京航空航天大学
初试科目
831 工程力学
3 梅花香自苦寒来,岁月共理想,人生齐高飞!
《材料力学》 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 华北水利水电学院 华东交通大学 天津大学 同济大学 同济大学 西安建筑科技大学 西南交通大学 北京交通大学 大连海事大学 大连理工大学 东北电力大学 福州大学 哈尔滨工业大学 河海大学 华中科技大学 暨南大学 山东大学 上海交通大学 沈阳建筑大学 西北农林科技大学 厦门大学 浙江大学 中国矿业大学 中国农业大学 北方工业大学 西南科技大学 哈尔滨工程大学 河北工业大学 南京工业大学 南京航空航天大学 浙江工业大学 中南大学 重庆大学 905 材料力学 801 材料力学 802 工程力学 808 材料力学与结构力学 831 理论与材料力学 801 材料力学 923 材料力学 950 材料力学 817 材料力学 829 材料力学(土) 861 材料力学 829 材料力学(土木) 871 材料力学(B) 813 材料力学 841 工程力学 447 材料力学 850 材料力学 804 材料力学 801 材料力学 802 材料力学 855 材料力学 835 材料力学(乙) 807 材料力 832 工程力学(理力、材力) 872 材料力学 814 材料力学 805 材料力学 860 材料力学 831 材料力学(土) 816 材料力学 854 材料力学(II) 948 材料力学 846 材料力学一
迈达斯-截面特性值计算器

。状形面截拟模来面截的式形eniL或面截的式形enalP定 选意任要需据根以可户用中CPS在�状形面截拟模来式形种一ena lP或en iL以能只序程的往以
�
。写缩的”rotaluclaC ytreporP lanoitceS—器算计值性特面截“是CPSΒιβλιοθήκη 明 说 用 使 的 C PS
)rotaluclaC ytreporP lanoitceS( CPS/SADIM
�
。定设行进 gnitteS>slooT 在 者或 � ) g n i t t e S ( 击点里条具工在可等色颜定设、息信型模藏隐/示显、系体位单定设
。算计和模建行进来能功项各出调地便方 很以 可 户 用 � 能 功 的 关 相 算 计 面 截及 模 建 的 C P S 与 有 所 了 供 提 里 单 菜联 关 、 条 具 工 、 单 菜 形 树 在
)rotaluclaC ytreporP lanoitceS( CPS/SADIM
6
。面截的算计行进未和面截的算计面截行进已别区的然了目一以可色颜此过通 。色颜的线的成构所后算计面截成完定指 noitceS detaluclaC 。色颜的分部度厚的线的度厚有定指 :htdiW 。色颜的廓轮外线是的定指线的度厚有于对。色颜的线定指 :lamroN evruC 。色颜的线曲闭封定指 pooL desolC 。色颜景背的口窗作操定指 :dnuorgkcaB 。色颜的体个择选被定指 :ytitnE detceleS weiV � � �
yalpsiD
�
。改更、算换行进的动自而系体位单的定指照按会据数的有所�”)Y(是“ 击点如 ,框话对的下如现出会�系体位单改更果如。系体位单定指里这在 metsyS tinU 。整调的理合行进动自系体位单的定设据根会序程�下况情般一。差误许容定指里这在 ecnareloT
材料力学笔记(第五章)

材料力学(土)笔记第五章 梁弯曲时的位移1.梁的位移——挠度及转角为研究等直梁在对称弯曲时的位移取梁在变形前的轴线为x 轴,梁横截面的铅垂对称轴为y 轴而xy 平面即为梁上荷载作用的纵向对称平面梁发生对称弯曲变形后,其轴线将变成在xy 平面内的曲线1AC B度量梁变形后横截面位移的两个基本量是挠度:横截面形心(即轴线上的点)在垂直于x 轴方向的线位移ω转角:横截面对其原来位置的角位移θ 梁变形后的轴线是一条光滑的连续曲线,且横截面仍与该曲线保持垂直因此横截面的转角θ也就是曲线在该点处的切线与x 轴之间的夹角度量等直梁弯曲变形程度的是曲线的曲率梁的变形还受到支座约束的影响通常就用这两个位移量来反映梁的变形情况梁轴线弯曲成曲线后,在x 轴方向也将发生线位移 但在小变形情况下,梁的挠度远小于跨长,梁变形后的轴线是一条平坦的曲线横截面形心沿x 轴方向的线位移与挠度相比属于高阶微量,可略去不记因此在选定坐标后,梁变形后的轴线可表达为()f x ω=式中,x 为梁在变形前轴线上任一点的横坐标;ω为该点的挠度梁变形后的轴线称为挠曲线,在线弹性范围内,也称为弹性曲线上述表达式则称为挠曲线(或弹性曲线)方程由于挠曲线为一平坦曲线,故转角θ可表达为''tan ()f x θθω≈== 称为转角方程即挠曲线上任一点处的切线斜率'ω可足够精确地代表该点处横截面的转角θ 由此可见,求得挠曲线方程后,就能确定梁任一横截面挠度的大小,指向及转角的数值 正值的挠度向下,负值的挠度向上正值的转角为逆时针转向,负值的转角为顺时针方向2.梁的挠曲线近似微分方程及其积分为求得梁的挠曲线方程,利用曲率κ与弯矩M 间的物理关系,即 1M EIκρ== 式中曲率κ为度量挠曲线弯曲程度的量,是非负的这是梁在线弹性范围内纯弯曲情况下的曲率表达式在横力弯曲时,梁横截面上除弯矩M 外尚有剪力S F 但工程用梁,其跨长l 一般均大于横截面高度的10倍剪力S F 对于梁位移的影响很小,可略去不计,故该式子依然适用式中的M 和ρ均为x 的函数,即1()()()M x x x EIκρ== 在数学中,平面曲线的曲率与曲线方程导数间的关系有'''23/21()(1)x ωρω=±+ 取x 轴向右为正,y 轴向下为正时曲线凸向上时''ω为正,凸向下时为负而按弯矩的正、负号规定,梁弯曲后凸向下时为正,凸向上为负,符号相反于是得到 '''23/2()(1)M x EIωω=-+ 由于梁的挠曲线为一平坦曲线,因此,'2ω与1相比十分微小可以略去不计故上式可近似的写为 ''()M x EIω=-上式略去了剪力S F 的影响,并略去了'2ω项 故称为梁的挠曲线近似微分方程若为等截面直梁,其弯曲刚度EI 为一常量,上式可改写为''()EI M x ω=-对于等直梁,上式进行积分,并通过由梁的变形相容条件给出的边界条件确定积分常数 即可求得梁的挠曲线方程当全梁各横截面上的弯矩可用单一的弯矩方程表示时,梁的挠曲线近似微分方程仅有一个 将上式的两端各乘以dx ,经积分一次,得'1()EI M x dx C ω=-+⎰再积分一次,即得12[()]EI M x dx dx C x C ω=-++⎰两式子中积分常数1C 、2C 可通过挠曲线的边界条件确定例如在简支梁中,左右铰支座处的挠度均等于零在悬臂梁中,固定端处的挠度和转角均等于零确定积分常数1C 、2C 后,就分别得到梁的转角方程和挠曲线方程从而可以确定任一横截面的转角和挠度1C 和2C 的几何意义 由于以x 为自变量,在坐标原点即0x =处的定积分恒等于零因此,积分常数'100x C EI EI ωθ===,20C EI ω=式中,0θ和0ω分别表示坐标原点处截面的转角和挠度若梁上的荷载不连续即分布荷载在跨度中间的某点处开始或结束,以及集中荷载或集中力偶作用处梁的弯矩需分段写出,各段梁的挠曲线近似微分方程也随之不同在对各段梁的近似微分方程积分时,均将出现两个积分常数为确定这些积分常数,除需利用支座处的约束条件外还需利用相邻两段梁在交界处位移的连续条件例如左、右两段梁在交界处的截面应具有相等的挠度和转角不论是约束条件和连续条件,均发生在各段挠曲线的边界处故均成为边界条件,即弯曲位移中的变形相容条件遵循两个原则①对各段梁,都是从同一坐标原点到截面之间的梁段上的外力列出弯矩方程所以后一段梁的弯矩方程包括前一段的弯矩方程的新增的()x a -项②对()x a -项的积分,以()x a -作为自变量于是由x a =处的连续条件,就能得到两段梁上相应的积分常数分别相等的结果 对于弯矩方程需分为任意几段的情况,只要遵循上述规则同样可以得到各梁段上相应的积分常数分别相等的结果从而简化确定积分常数的运算3.按叠加原理计算梁的挠度和转角梁在微小变形条件下,其弯矩与荷载成线性关系 在线弹性范围内,挠曲线的曲率与弯矩成正比当挠度很小时,曲率与挠度间呈线性关系梁的挠度和转角均与作用在梁上的荷载成线性关系在这种情况下梁在几项荷载(如集中力、集中力偶或分布力)同时作用下某一横截面的挠度或转角 就分别等于每项荷载单独作用下该截面的挠度或转角的叠加,即为叠加原理 已知梁在每项荷载单独作用下的挠度和转角表则按叠加原理来计算梁的最大挠度和最大转角将较为方便4.奇异函数·梁挠曲线的初参数方程5.梁的刚度校核·提高梁的刚度的措施5.1 梁的刚度校核对于梁的挠度,其许可值通常用许可挠度与跨长之比值[]l ω作为标准 梁的刚度条件可表达为 max[]ll ωω≤ max []θθ≤ 一般土建工程中的构件,强度要求是主要的刚度要求一般处于从属地位但当对构件的位移限制很严,或按强度条件所选用的构件截面过于单薄时刚度条件也可能起控制作用5.2 提高梁的刚度的措施由梁的位移表可见梁的位移(挠度和转角)除了与梁的支承和荷载情况有关还与其弯曲刚度EI 成反比,与跨长l 的n 次幂成正比减小梁的位移,可采取下列措施①增大梁的弯曲刚度EI②调整跨长和改变结构5.梁内的弯曲应变能当梁弯曲时,梁内将积蓄应变能梁在线弹性变形过程中弯曲应变能V ε在数值上等于作用在梁上的外力所作的功W梁在纯弯曲时各横截面上的弯矩M 为常数,并等于外力偶矩e M当梁处于线弹性范围内e EI EI θρ=== θ与e M 呈线性关系直线下的三角形面积就代表外力偶所作的功W ,即12e W M θ=从而得纯弯曲时梁的弯曲应变能 12e V M εθ=即得2222e M l M l V EI EIε== 横力弯曲时,梁内应变能包含两个部分:与弯曲变形相应的弯曲应变能和与切应变形相应的剪切应变能对于弯曲应变能,取长为dx 的梁段,其相邻两横截面的弯矩应分别为()M x 和()()M x dM x +在计算微段的应变能时,弯矩的增量为一阶无穷小,可略去不计 计算器弯曲应变能为2()2M x dV dx EIε= 全梁的弯曲应变能则可通过积分求得为2()2l M x V dx EIε=⎰ 式中,()M x 为梁任一横截面上的弯矩表达式 当各段梁的弯矩表达式不同时,积分需分段进行梁的剪切应变能远小于弯曲应变能,可略去不计。
材料力学计算器

重点结果,部分数据需点击弯曲变形填写变量后自动计算
扭转变形 极惯性矩 抗扭截面系数
Ip
Wp
0
0
许用应力
脆性材料 强度校核
0 扭转刚度
G*Iz 0
计算应力
(面1)拉应力
(面2)拉应力
拉应力合力
0
压应力
扭转切应力
0
弯扭合应力
0
校核
安全 安全 安全
图&弯矩图,最后通过叠加求出弯矩,挠度,转角
均布载荷q作用
弯曲计算
集中载荷F作用
杆长 x (m)
2.5
0
0
0
0
图层法求挠度&转角
0
均 剪力Fq(N)
凹 0
0Байду номын сангаас
0
0
1
结果
0
0
0
0
0
0
0
0
扭转计算
集中载荷F作用 杆长 x (m)
0 0
0
均 剪力Fq(N)
凹 0
0
0
0
挠度 转角
轴向拉力 杆上作用单位的分力
杆长 截面面积
挠度 轴向应力
结果
0
0
0
0
轴力变形计算
0 0 0
弯曲刚度
μ
E*Iz
E*Iy
0
0
以下计算方法为图层法,需要自行画剪力图&弯矩图,最
弯矩Mz 应力σz1 应力σz2 应力σy
剪力 F(N)
弯矩与坐标轴面积 单位力下的剪力 单位力作用下的弯矩 单位力下形心处弯矩 单位力偶形心处弯矩
挠度z 挠度y 转角z 转角y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 0 0
0 计算结果 0 0 挠度 转角 0 0
计算结果 挠度 轴向应力 0 0
均
凹 0
0
扭转计算
剪力 F(N) 扭矩Mx 扭转切应力τ 扭矩与坐标轴的面积 单位力作用下的剪力 单位力作用下的扭矩 集中载荷F作用 杆长 x (m) 0 0 0 0 剪力Fq(N)
均
凹 0
单位力下形心处扭矩 挠度 转角
0 结果 0 0
0 0 0
轴力变形计算
轴向拉力 杆上作用单位的分力 杆长 截面面积 挠度 轴向应力
以下计算方法为图层法,需要自行画剪力图&弯矩图,最
弯曲计算
剪力 F(N) 弯矩Mz 应力σ z1 应力σ z2 应力σ y 弯矩与坐标轴面积 单位力下的剪力 单位力作用下的弯矩 单位力下形心处弯矩 单位力偶形心处弯矩 挠度z 挠度y 转角z 转角y 集中载荷F作用 杆长 x (m) 2.5 0 0 0 0 图层法求挠度&转角 0 0 0 1 结果 0 0 0 0 0 0 0 0 剪力Fq(N)
凹 0
均布载荷q作用 杆长 x(m) 0 0 0 0 凸 0 0
计算结果 弯矩Mz σ z1 σ z2 σy 0 0 0 0
0 1
0 计算结果
0 0 0 0
0 0 0 0
挠度z 挠度y 转角z 转角) 0 0 凹 0 0 凸 0
计算结果 扭矩Mx 切应力τ 0 0
只填写蓝色部分,其他区域自动计算,黄色区域为重点结果,部
弯曲变形 面积 截面参数 A 0 屈服极限应力 σs 材料参数 材料 备注 弹性模量 E 切变模量 G 0 σ -1 Iz 0 惯性矩 Iy 0 弯曲极限应力 σb Wz1 0 安全系数 抗弯截面系数 Wz=Iz/e Wz2 0
Wy 0
许用应力 塑性材料 备注 强度校核 疲劳校核 0 0 弯曲刚度 泊松比 μ E*Iz E*Iy 0 0
0 0 0
重点结果,部分数据需点击弯曲变形填写变量后自动计算
扭转变形 极惯性矩 抗扭截面系数 Ip 0 许用应力 脆性材料 强度校核 0 扭转刚度 G*Iz 0 Wp 0 计算应力 (面1)拉应力 (面2)拉应力 拉应力合力 压应力 扭转切应力 弯扭合应力 校核
0 0 0
安全 安全 安全
图&弯矩图,最后通过叠加求出弯矩,挠度,转角
