初中的数学九大几何模型
初中数学几何模型

全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型:说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是°、°、°、°及有一个角是°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇度旋度,造等边三角形遇度旋度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋度,造中心对称说明:IS 8模型变形BEFcEB说明:说明:nnnnnnnnnnnnnnnnnnnnnnn nnnnn口叩皿皿皿皿皿中点模型 边构诗中{fflt 逢阳点闵iS 中幽城 几何最值模型 VH *h 轴对称模型 对称最值 线mi 差模型 fflftffw 同侧"异侧两蜒段之利罐短视它 同侧、异删芮线投之羞媪小槐型 四边形周怏垠小根地 三角形眉长 必小檢哩三线穀之和 她知爬制过桥模取旋转最值说明:找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值。
简拼模型三角形j四边形E 面积等分说明:说明:3045602说明:ACOCOAA 模型一:手拉手模型-旋转型全等<2)等濮的AA Mfr=血°拟述°均为等媵直甬M 册A 结险(DA (UCtAO^l>j 超乙他»③。
E 平分£忖了儿(1)―况> Sfr :LDW 牛底皿力能转至右囲检置A 皓论:> 右图中①bOCWMe\QAC AOSD 』 >⑨延氏M 交购于点G 必肖5氏-LBOA⑵特燥惜况>条件m 3MB ,厶伽■剜,将AXD 龍讳至右團位蛊a gife :右gcp fflAfJCD^iOJ^AC?JCiM£33②延长M 交加于点瓦愁有3EC -LUGA f BD 000B (5)-—--——=—-=tan ZlfX D®ACOCOA 3f^SDLAC.灘接也JC >临加*†g ・a+o>s ⑥矢"訐c&J 冊哒相垂直的四嬷)<3)任翦腰三角晤†辭,。
初中几何48个模型作业帮

初中几何是数学中的一个重要部分,它涉及到许多基本的几何概念和定理。
在学习初中几何时,了解和掌握一些常见的几何模型是非常有帮助的。
以下是48个初中几何模型:1. 等边三角形模型2. 等腰三角形模型3. 直角三角形模型4. 平行四边形模型5. 菱形模型6. 矩形模型7. 正方形模型8. 梯形模型9. 圆模型10. 扇形模型11. 弓形模型12. 切线模型13. 抛物线模型14. 双曲线模型15. 椭圆模型16. 角平分线定理模型17. 中线定理模型18. 弦长定理模型19. 勾股定理模型21. 外角和定理模型22. 线段比例定理模型23. 相似三角形判定定理模型24. 三角形内心定理模型25. 三角形外心定理模型26. 三角形重心定理模型27. 三角形垂心定理模型28. 四边形对角线性质定理模型29. 四边形面积公式模型30. 圆的周长公式模型31. 圆的面积公式模型32. 扇形面积公式模型33. 弓形面积公式模型34. 点到直线距离公式模型35. 两点间距离公式模型36. 角平分线性质定理模型37. 中位线定理模型38. 切线的性质定理模型39. 切线的判定定理模型40. 抛物线性质定理模型41. 双曲线性质定理模型43. 角的平分线性质定理的逆定理模型44. 三线合一的逆定理模型45. 线段垂直平分线的逆定理模型46. 余角、补角定理的逆定理模型47. 同位角、内错角、同旁内角定理的逆定理模型48. 正弦、余弦、正切的应用(三角函数的应用)这些几何模型可以帮助你更好地理解和掌握初中几何的知识点,并且能够让你更加熟练地解决各种几何问题。
希望这些信息对你有所帮助!。
初中数学几何公式大全和九大几何模型

初中数学几何公式和九大几何模型1过两点有且只有一条直线2两点之间线段最短3同角或等角的补角相等4同角或等角的余角相等5过一点有且只有一条直线和已知直线垂直6直线外一点与直线上各点连接的所有线段中,垂线段最短7平行公理经过直线外一点,有且只有一条直线与这条直线平行8如果两条直线都和第三条直线平行,这两条直线也互相平行9同位角相等,两直线平行10内错角相等,两直线平行11同旁内角互补,两直线平行12两直线平行,同位角相等13两直线平行,内错角相等14两直线平行,同旁内角互补15定理三角形两边的和大于第三边16推论三角形两边的差小于第三边17三角形内角和定理三角形三个内角的和等于180°18推论1直角三角形的两个锐角互余19推论2三角形的一个外角等于和它不相邻的两个内角的和20推论3三角形的一个外角大于任何一个和它不相邻的内角21全等三角形的对应边、对应角相等22边角边公理(SAS)有两边和它们的夹角对应相等的两个三角形全等23角边角公理(ASA)有两角和它们的夹边对应相等的两个三角形全等24推论(AAS)有两角和其中一角的对边对应相等的两个三角形全等25边边边公理(SSS)有三边对应相等的两个三角形全等26斜边、直角边公理(HL)有斜边和一条直角边对应相等的两个直角三角形全等27定理1在角的平分线上的点到这个角的两边的距离相等28定理2到一个角的两边的距离相同的点,在这个角的平分线上29角的平分线是到角的两边距离相等的所有点的集合30等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)31推论1等腰三角形顶角的平分线平分底边并且垂直于底边32等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33推论3等边三角形的各角都相等,并且每一个角都等于60°34等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35推论1三个角都相等的三角形是等边三角形36推论2有一个角等于60°的等腰三角形是等边三角形37在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38直角三角形斜边上的中线等于斜边上的一半39定理线段垂直平分线上的点和这条线段两个端点的距离相等40逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42定理1关于某条直线对称的两个图形是全等形43定理2如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^247勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1平行四边形的对角相等53平行四边形性质定理2平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3平行四边形的对角线互相平分56平行四边形判定定理1两组对角分别相等的四边形是平行四边形57平行四边形判定定理2两组对边分别相等的四边形是平行四边形58平行四边形判定定理3对角线互相平分的四边形是平行四边形59平行四边形判定定理4一组对边平行相等的四边形是平行四边形60矩形性质定理1矩形的四个角都是直角61矩形性质定理2矩形的对角线相等62矩形判定定理1有三个角是直角的四边形是矩形63矩形判定定理2对角线相等的平行四边形是矩形64菱形性质定理1菱形的四条边都相等65菱形性质定理2菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1四边都相等的四边形是菱形68菱形判定定理2对角线互相垂直的平行四边形是菱形69正方形性质定理1正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1关于中心对称的两个图形是全等的72定理2关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79推论1经过梯形一腰的中点与底平行的直线,必平分另一腰80推论2经过三角形一边的中点与另一边平行的直线,必平分第三边81三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2S=L×h83(1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84(2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85(3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91相似三角形判定定理1两角对应相等,两三角形相似(ASA)92直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93判定定理2两边对应成比例且夹角相等,两三角形相似(SAS)94判定定理3三边对应成比例,两三角形相似(SSS)95定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96性质定理1相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97性质定理2相似三角形周长的比等于相似比98性质定理3相似三角形面积的比等于相似比的平方99任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三点确定一个圆。
初中数学九大几何模型
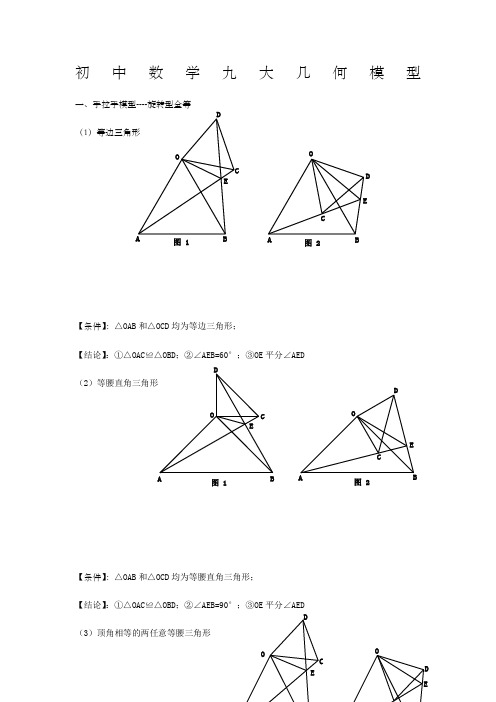
初中数学九大几何模型一、手拉手模型----旋转型全等 (1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED(2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED(3)顶角相等的两任意等腰三角形OB C DE图 1OABCD E图 2OABCDE图 1OACDE图 2OCDEOD E【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ;OAB COBCDEOB CDEOA CD③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ;③2△OCD △OCE OC 21S S =-(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=AOBCDE 图 1A OBCDEM N图 2A OBCDEF图 3A O BCDEMN 图 4证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
初中数学九大几何模型-初中几何九大模型-初中九大几何模型
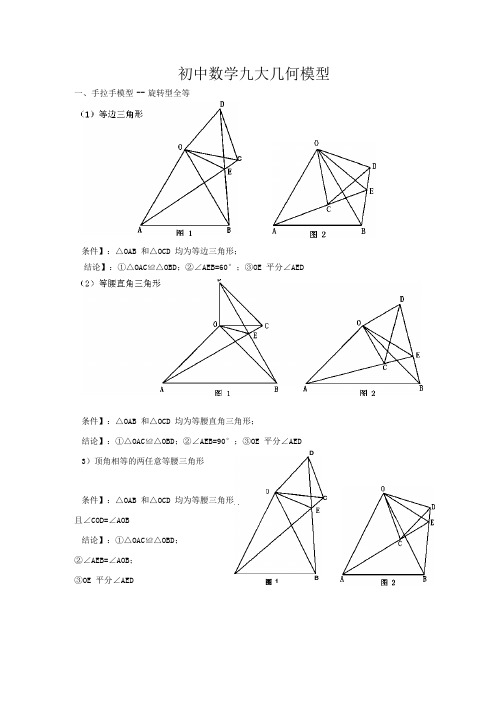
初中数学九大几何模型结论】:①△OAC≌△OBD;②∠AEB=60°;③OE 平分∠AED条件】:△OAB 和△OCD 均为等腰直角三角形;结论】:①△OAC≌△OBD;②∠AEB=90°;③OE 平分∠AED 3)顶角相等的两任意等腰三角形条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB结论】:①△OAC≌△OBD; ②∠AEB=∠AOB; ③OE 平分∠AEDC条件】:△OAB 和△OCD 均为等边三角形;一、手拉手模型 -- 旋转型全等B图 1DC二、模型二:手拉手模型--- 旋转型相似(1)一般情况【条件】:CD∥AB,将△OCD 旋转至右图的位置②延长 AC交 BD 于点E,必有∠BEC=∠BOA;③BD= OD= OB=tan∠OCD;④BD⊥AC;AC OC OA2⑤连接AD、BC,必有AD2+ BC2= AB2+CD2;⑥S三、模型三、对角互补模型1)全等型-90°结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;O O△BCD条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOBB2)全等型-120°条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB结论】:①CD=CE;②OD+OE=OC;③S△DCE = S△OCD + S△OCE = 3OC2证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB上取一点F,使OF=OC,证明△OCF为等边三角形。
3)全等型-任意角ɑ条件】:①∠AOB=2ɑ,∠DCE=180-2ɑ;②CD=CE;结论】:①OC 平分∠AOB;②OD+OE=2OC·cosɑ;③S△DCE = S△OCD + S△OCE =OC2sinαcosα※当∠DCE 的一边交 AO的延长线于 D 时(如右下图):原结论变成:①可参考上述第②种方法进行证明。
初中数学九大几何模型
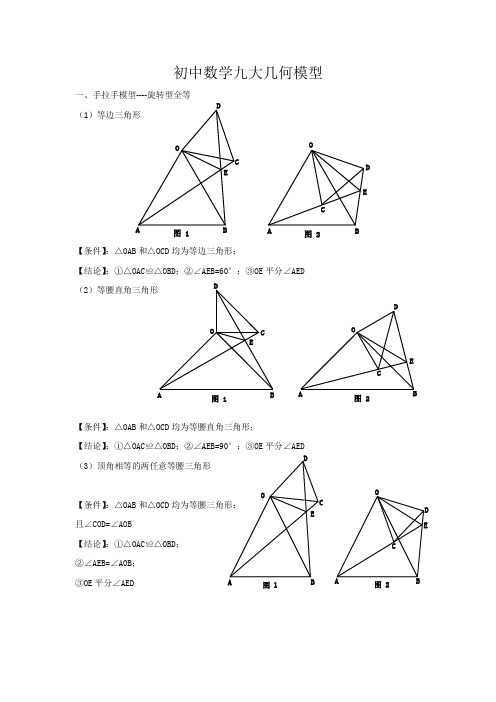
初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
(完整版)初中数学九大几何模型

初中数学九大几何模型OD ECABAED DOECBABOC ECAEDD图2图 2、手拉手模型 - 旋转型全等D E③OE 平分∠ AED图 2图 1 OABD OAO ②∠ AEB=∠AOB ; 且∠ COD=∠AOB1)等边三角形3)顶角相等的两任意等腰三角形 2)等腰直角三角形图 1图 1C结论】:①△ OAC ≌△ OBD ;C条件】:△ OAB 和△ OCD 均为等边三角形条件】:△ OAB 和△ OCD 均为等腰直角三角形条件】:△ OAB 和△ OCD 均为等腰三角形 结论】:①△ OAC ≌△ OBD ;②∠ AEB=60°;③ OE 平分∠ 结论】:①△ OAC ≌△ OBD ;②∠ AEB=90°;③ OE 平分∠、模型二:手拉手模型 -- 旋转型相似(1)一般情况 【条件】:CD ∥AB , 将△ OCD 旋转至右图的位置 O OD EA A结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ;②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA2)特殊情况 条件】:CD ∥ AB ,∠ AOB=90°将△ OCD 旋转至右图的位置 A 结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ; ②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA ; ③ A BD C O O C D O O A B tan ∠OCD ;④BD ⊥AC ; ⑤连接 AD 、BC ,必有 AD 2 BC 2 AB 2三、模型三、对角互补模型1)全等型 -90 ° 条件】:①∠ AOB=∠ DCE=90°;② OC 平分∠ AOB结论】:① CD=CE ;② OD+OE= 2 OC ;③ S △DCE CD ;⑥S△BCD证明提示: ①作垂直,如图 2,证明△ CDM ≌△ CEN ②过点 C 作 CF ⊥ OC , 如图 3,证明△ ODC ≌△ FEC ※当∠ DCE 的一边交 AO 的延长线于 D 时(如图 4): S△OCDS以上三个结论:① CD=CE ;② OE-OD= 2 OC ; ③ S △ OCE S △ OCD2)全等型 -120 °条件】:①∠ AOB=2∠ DCE=120°;② OC 平分∠ AOB32 结论】:① CD=CE ;② OD+OE=O ;C ③ S △DCES △OCDS △OCEOC 2 4证明提示:①可参考“全等型 -90 °”证法一;②如右下图:在 OB 上取一点 F ,使 OF=OC ,证明△ OCF 为等边三角形。
初中几何九大模型汇总

初中几何九大模型汇总1. 点(Point):点是几何中最基本的对象,它没有长度、宽度或高度,只有位置。
点通常用大写字母标记,例如A、B、C等。
2. 线段(Line Segment):线段是由两个点确定的,它是一条有限长度的直线。
线段通常用两个字母标记,如AB。
线段具有长度和方向。
3. 直线(Line):直线是无限延伸的线段,它由无数个点组成,没有起点和终点。
直线通常用一条小箭头标记,如AB。
直线上的任意两点可以确定一条直线。
4. 角(Angle):角是由两条射线共享一个起点而形成的,它是两边之间的夹角。
角可以分为锐角、直角和钝角。
角通常用大写字母标记,如∠ABC。
5. 三角形(Triangle):三角形是由三条线段组成的一个闭合图形。
三角形的内部有三个顶点和三条边。
三角形可以根据边长和角度分为不同的类型,如等边三角形、等腰三角形等。
6. 四边形(Quadrilateral):四边形是由四条线段组成的一个闭合图形。
四边形的内部有四个顶点和四条边。
四边形可以根据边长和角度分为不同的类型,如矩形、正方形、菱形等。
7. 五边形(Pentagon):五边形是由五条线段组成的一个闭合图形。
五边形的内部有五个顶点和五条边。
五边形可以分为凹五边形和凸五边形。
8. 六边形(Hexagon):六边形是由六条线段组成一个闭合图形。
六边形的内部有六个顶点和六条边。
六边形可以分为凹六边形和凸六边形。
9. 圆形(Circle):圆形是由一个中心点和一个半径确定的,它由无数个点组成的闭合曲线。
圆形的内部为圆的内部,外部为圆的外部。
通过研究这九大基本模型,我们可以深入了解几何形状的特征和性质。
学生们可通过观察和比较不同形状的特点,理解几何变换、相似性、对称性等概念。
此外,还可以通过实际生活中的例子,将几何知识应用于实际问题中,提高学生的应用能力。
总之,初中几何九大模型是学习几何必不可少的基础,通过对它们的认识和掌握,可以帮助学生更好地理解和应用几何知识。
初中所有几何模型

初中所有几何模型
初中几何中常见的模型包括但不限于以下几种:
1. 手拉手模型:这种模型通常涉及到两个三角形,其中一个三角形的顶点与另一个三角形的对应顶点相连。
根据角度和边的关系,可以证明这两个三角形是相似的或全等的。
2. 倍长中线模型:如果一个中线长度超过另一边的一半,则可以通过倍长中线来构造新的三角形,从而利用中线性质进行证明。
3. 平行线模型:通过平行线的性质,可以证明一些角的关系,或者利用平行线的传递性来证明一些线段的比例关系。
4. 角平分线模型:利用角平分线的性质,可以证明一些角或者线段的比例关系。
5. 直角三角形模型:通过直角三角形的性质,可以证明一些角或者线段的关系。
6. 对角线模型:利用对角线的性质,可以证明一些线段的比例关系,或者通过构造新的三角形来证明一些结论。
7. 旋转模型:通过旋转图形,可以证明一些结论或者找到一些新的等量关系。
8. 相似三角形模型:通过相似三角形的性质,可以证明一些角或者线段的比例关系。
9. 特殊四边形模型:对于一些特殊的四边形,如平行四边形、矩形、菱形等,可以利用它们的性质来证明一些结论。
以上是一些常见的初中几何模型,它们都是基于几何的基本性质和定理构建的。
掌握这些模型可以帮助学生在解决几何问题时更加高效和准确。
初中数学九大几何模型
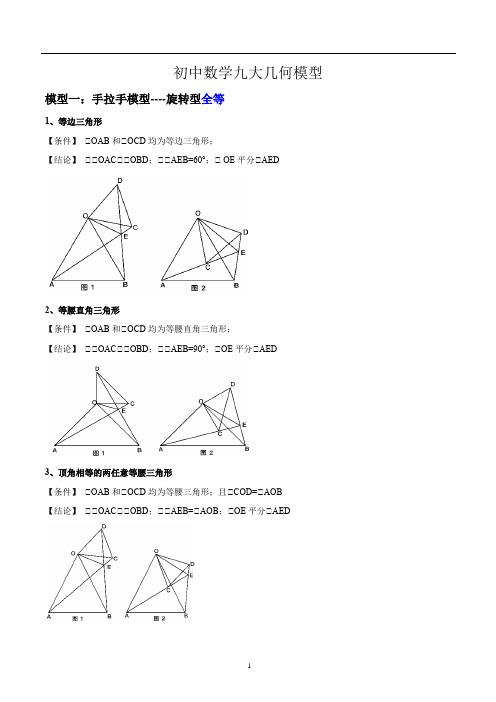
初中数学九大几何模型模型一:手拉手模型----旋转型全等1、等边三角形【条件】△OAB和△OCD均为等边三角形;【结论】△△OAC△△OBD;△△AEB=60°;△ OE平分△AED2、等腰直角三角形【条件】△OAB和△OCD均为等腰直角三角形;【结论】△△OAC△△OBD;△△AEB=90°;△OE平分△AED3、顶角相等的两任意等腰三角形【条件】△OAB和△OCD均为等腰三角形;且△COD=△AOB【结论】△△OAC△△OBD;△△AEB=△AOB;△OE平分△AED模型二:手拉手模型----旋转型相似1、一般情况【条件】 CD△AB ,将△OCD 旋转至右图的位置【结论】 △右图中△OCD△△OAB→→→△OAC△△OBD ;△延长AC 交BD 于点E ,必有△BEC=△BOA2、特殊情况【条件】 CD△AB ,△AOB=90° 将△OCD 旋转至右图的位置【结论】 △右图中△OCD△△OAB→→→△OAC△△OBD ; △延长AC 交BD 于点E ,必有△BEC =△BOA ; △BD AC=OD OC=OB OA=tan∠OCD ;△BD△AC ;△连接AD 、BC ,必有AD 2+BC 2=AB 2+CD 2 ; △BD AC S ABCD •=21模型三:对角互补模型1、全等型-90°【条件】 △△AOB=△DCE=90°;△OC 平分△AOB【结论】 △CD=CE ;△OD+OE=2OC ;△2ODCE OCD OCE 12S S S OC ∆∆=+= 证明提示:△作垂直,如图2,证明△CDM△△CEN△过点C 作CF△OC ,如图3,证明△ODC△△FEC ※当△DCE 的一边交AO 的延长线于D 时(如图4):以上三个结论:△CD=CE ;△OE -OD=2OC ;△2△OCD △OCE OC 21S S =-2、全等型-120°【条件】 △△AOB=2△FCE=120°;△OC 平分△AOB【结论】 △CF=CE ;△OF+OE=OC ;△2OFCE OCF OCE 4S S S ∆∆=+=证明提示:△可参考“全等型-90°”证法一;△如图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
(完整版)初中数学九大几何模型

初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
初中数学几何公式大全和九大几何模型

初中数学几何公式和九大几何模型1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12 两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22 边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理(SSS) 有三边对应相等的两个三角形全等26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^247勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2 S=L×h83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84 (2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85 (3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三点确定一个圆。
初中数学几何模型归纳

初中数学几何模型归纳1. 直线模型:直线是最基本的几何图形,可以用直线方程y = kx + b 来表示。
其中,k 是斜率,b 是截距。
2. 点模型:点是几何图形中的基本元素,可以用坐标(x, y) 来表示。
3. 线段模型:线段是由两个端点确定的有限长度的直线部分。
线段可以用起点和终点的坐标来表示。
4. 射线模型:射线是由一个端点和一个方向确定的无限延伸的直线部分。
射线可以用起点和方向向量来表示。
5. 角模型:角是由两条射线的公共端点和这两条射线之间的夹角组成的。
角可以用顶点、始边和终边来表示。
6. 三角形模型:三角形是由三条边和三个内角组成的多边形。
三角形可以用三边的长度和三个内角的大小来表示。
7. 四边形模型:四边形是由四条边和四个内角组成的多边形。
四边形可以用四边的长度和四个内角的大小来表示。
8. 圆模型:圆是由一个圆心和一个半径确定的平面上的所有点到圆心的距离都等于半径的图形。
圆可以用圆心和半径来表示。
9. 椭圆模型:椭圆是由两个焦点和一个长轴、短轴确定的平面上的所有点到两个焦点的距离之和等于常数的图形。
椭圆可以用两个焦点和长轴、短轴的长度来表示。
10. 双曲线模型:双曲线是由两个焦点和一个实轴、虚轴确定的平面上的所有点到两个焦点的距离之差等于常数的图形。
双曲线可以用两个焦点和实轴、虚轴的长度来表示。
11. 正多边形模型:正多边形是由相等的边和相等的内角组成的多边形。
正多边形可以用边数和内角度数来表示。
12. 梯形模型:梯形是由一对平行边和一对非平行边组成的四边形。
梯形可以用两对边的长度和夹角来表示。
13. 矩形模型:矩形是由四个直角和两对相等的边组成的四边形。
矩形可以用两对边的长度和夹角来表示。
14. 正方形模型:正方形是特殊的矩形,它的四个边都相等且四个角都是直角。
正方形可以用边长来表示。
15. 三角形面积模型:三角形的面积可以通过底边长度和高来计算,公式为S = (底边长度×高) / 2。
初中几何46种模型大全

初中几何46种模型大全篇一:在初中几何学习中,学生需要掌握各种几何模型的性质和应用。
下面是46种常见的初中几何模型的介绍和拓展。
1. 点:几何学中最基本的对象,没有大小和形状。
2. 线段:由两个点确定的一段连续直线。
3. 直线:无限延伸的、由无数个点组成的连续直线。
4. 射线:起点固定,无限延伸的直线段。
5. 平行线:在同一平面上,永不相交的两条直线。
6. 垂直线:两条直线相交时,相互间的角度为90度。
7. 角:由两条线段或射线共享一个端点所夹成的图形。
8. 直角:角度为90度的角。
9. 锐角:角度小于90度的角。
10. 钝角:角度大于90度但小于180度的角。
11. 三角形:由三条线段连接的图形。
12. 等腰三角形:两边相等的三角形。
13. 等边三角形:三边相等的三角形。
14. 直角三角形:一条边与另外两条边成90度角的三角形。
15. 斜边:直角三角形的最长边。
16. 等腰梯形:有两对平行边,且一对边相等的梯形。
17. 长方形:有四个直角的四边形。
18. 正方形:四边相等且有四个直角的四边形。
19. 平行四边形:有两对平行边的四边形。
20. 五边形:有五条边的多边形。
21. 六边形:有六条边的多边形。
22. 正多边形:所有边相等且所有角相等的多边形。
23. 圆:平面上所有到圆心距离相等的点的集合。
24. 弧:圆上的一段连续曲线。
25. 弦:圆上连接两个非相邻点的线段。
26. 切线:与圆只有一个交点的直线。
27. 弓形:圆上的一段弧和与之相连的两条半径所围成的图形。
28. 圆心角:以圆心为顶点的角。
29. 多边形:有多个边和角的图形。
30. 正多边形:所有边相等且所有角相等的多边形。
31. 直角梯形:有一对直角且有两对平行边的梯形。
32. 正弦:在直角三角形中,对于一个角,其对边与斜边的比值。
33. 余弦:在直角三角形中,对于一个角,其邻边与斜边的比值。
34. 正切:在直角三角形中,对于一个角,其对边与邻边的比值。
初中数学54个几何模型

初中数学54个几何模型初中数学中的几何模型是指在几何学中用来描述和表示几何概念的模型。
下面将介绍54个常见的几何模型。
1. 点:几何中最基本的概念,没有大小和形状。
2. 直线:由无数个点连成的路径,无限延伸,没有宽度。
3. 射线:由一个起点出发,无限延伸的路径。
4. 线段:两个点之间的路径,有特定的长度。
5. 面:由无数个点连成的平面,有长度和宽度,没有厚度。
6. 圆:由同一平面上距离圆心相等的点组成的闭合曲线。
7. 椭圆:平面上到两个焦点的距离之和恒定的点的轨迹。
8. 椭圆弧:椭圆上的一段曲线。
9. 双曲线:平面上到两个焦点的距离之差恒定的点的轨迹。
10. 双曲线弧:双曲线上的一段曲线。
11. 抛物线:平面上到一个焦点的距离等于到直线的距离的点的轨迹。
12. 抛物线弧:抛物线上的一段曲线。
13. 球:由空间中到一个固定点的距离恒定的点组成的集合。
14. 圆锥:由平面和母线(与平面交于一点的直线)构成的几何体。
15. 圆柱:由平面和平行于平面的两个母线构成的几何体。
16. 圆台:由平面和平行于平面的两个母线及它们之间的曲面构成的几何体。
17. 球台:由平面和球的一部分构成的几何体。
18. 球梯:由平面和球的一部分及它们之间的曲面构成的几何体。
19. 直角三角形:有一个内角为90度的三角形。
20. 等腰三角形:有两边相等的三角形。
21. 等边三角形:三边长度均相等的三角形。
22. 直角梯形:有一个内角为90度的梯形。
23. 等腰梯形:有两边平行且相等的梯形。
24. 矩形:四个内角均为90度的四边形。
25. 正方形:四边长度均相等且内角均为90度的四边形。
26. 平行四边形:有两组对边平行的四边形。
27. 菱形:有四个边相等的四边形。
28. 六边形:有六个边的多边形。
29. 正六边形:六边形的六个内角均为120度。
30. 五边形:有五个边的多边形。
31. 正五边形:五边形的五个内角均为108度。
32. 正多边形:所有边和内角均相等的多边形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学九大几何模型一、手拉手模型----旋转型全等 (1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED(2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED(3)顶角相等的两任意等腰三角形OAB C DE图 1OABCD E图 2OABCDE图 1OABCDE图 2OCDEOCD E【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型OCOCDEOB CDEOA CDAOBCDE 图 1(1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
A OBCDE M N 图 2A OBCDE F 图 3A O BCDEMN 图 4A OBCEFAOBCEFF(3)全等型-任意角ɑ【条件】:①∠AOB=2ɑ,∠DCE=180-2ɑ;②CD=CE ;【结论】:①OC 平分∠AOB ;②OD+OE=2OC ·cos ɑ; ③αcos αsin OC S S S 2△OCE △OCD △DCE ⋅⋅=+=※当∠DCE 的一边交AO 的延长线于D 时(如右下图):原结论变成:① ; ② ; ③ 。
可参考上述第②种方法进行证明。
请思考初始条件的变化对模型的影响。
对角互补模型总结:①常见初始条件:四边形对角互补,注意两点:四点共圆有直角三角形斜边中线;②初始条件“角平分线”与“两边相等”的区别;A OBEDCAOBECDAO BCDE③注意OC 平分∠AOB 时,∠CDE=∠CED=∠COA=∠COB 如何引导?四、模型四:角含半角模型90° (1)角含半角模型90°---1【条件】:①正方形ABCD ;②∠EAF=45°;【结论】:①EF=DF+BE ;②△CEF 的周长为正方形ABCD 周长的一半; 也可以这样:【条件】:①正方形ABCD ;②EF=DF+BE ;【结论】:①∠EAF=45°;(2)角含半角模型90°---2【条件】:①正方形ABCD ;②∠EAF=45°;【结论】:①EF=DF-BE ;ABDEF AB CDFG AB CDEF ABCDE F ABCDE F(3)角含半角模型90°---3【条件】:①Rt △ABC ;②∠DAE=45°;【结论】:222DE CE BD =+(如图1)若∠DAE 旋转到△ABC 外部时,结论222DE CE BD =+仍然成立(如图2)(4)角含半角模型90°变形【条件】:①正方形ABCD ;②∠EAF=45°;【结论】:△AHE 为等腰直角三角形; 证明:连接AC (方法不唯一)A B ABCFABCDEABCDEFABC D GHFEABCDGHF E∵∠DAC=∠EAF=45°,∴∠DAH=∠CAE ,又∵∠ACB=∠ADB=45°; ∴△DAH ∽△CAE ,∴AEACAH DA∴△AHE ∽△ADC ,∴△AHE 为等腰直角三角形模型五:倍长中线类模型 (1)倍长中线类模型---1【条件】:①矩形ABCD ;②BD=BE ;③DF=EF ; 【结论】:AF ⊥CF模型提取:①有平行线AD ∥BE ;②平行线间线段有中点DF=EF ; 可以构造“8”字全等△ADF ≌△HEF 。
(2)倍长中线类模型---2【条件】:①平行四边形ABCD ;②BC=2AB ;③AM=DM ;④CE ⊥AB ; 【结论】:∠EMD=3∠MEA辅助线:有平行AB ∥CD ,有中点AM=DM ,延长EM ,构造△AME ≌△DMF ,连接CM 构造等腰△EMC ,等腰△MCF 。
(通过构造8字全等线段数量及位置关系,角的大小转化)ABCEF DH ABFDHABCDME ADME F模型六:相似三角形360°旋转模型(1)相似三角形(等腰直角)360°旋转模型---倍长中线法【条件】:①△ADE、△ABC均为等腰直角三角形;②EF=CF;【结论】:①DF=BF;②DF⊥BF辅助线:延长DF到点G,使FG=DF,连接CG、BG、BD,证明△BDG为等腰直角三角形;突破点:△ABD≌△CBG;难点:证明∠BAO=∠BCG(2)相似三角形(等腰直角)360°旋转模型---补全法【条件】:①△ADE、△ABC均为等腰直角三角形;②EF=CF;【结论】:①DF=BF;②DF⊥BF辅助线:构造等腰直角△AEG、△AHC;辅助线思路:将DF与BF转化到CG与EF。
AE BD FCAEBDFCHGAE BD FCA BDFCG(3)任意相似直角三角形360°旋转模型---补全法【条件】:①△OAB ∽△ODC ;②∠OAB=∠ODC=90°;③BE=CE ; 【结论】:①AE=DE ;②∠AED=2∠ABO辅助线:延长BA 到G ,使AG=AB ,延长CD 到点H 使DH=CD ,补全△OGB 、△OCH 构造旋转模型。
转化AE 与DE 到CG 与BH ,难点在转化∠AED 。
(4)任意相似直角三角形360°旋转模型---倍长法【条件】:①△OAB ∽△ODC ;②∠OAB=∠ODC=90°;③BE=CE ; 【结论】:①AE=DE ;②∠AED=2∠ABO辅助线:延长DE 至M ,使ME=DE ,将结论的两个条件转化为证明△AMD ∽△ABO ,此为难点,将△AMD ∽△ABC 继续转化为证明△ABM ∽△AOD ,使用两边成比例且夹角相等,此处难点在证明∠ABM=∠AODOABDCEOABDCEG HOAB DCEOA BDCEM模型七:最短路程模型(1)最短路程模型一(将军饮马类)总结:右四图为常见的轴对称类最短路程问题, 最后都转化到:“两点之间,线段最短:解决; 特点:①动点在直线上;②起点,终点固定(2)最短路程模型二(点到直线类1)【条件】:①OC 平分∠AOB ;②M 为OB 上一定点;③P 为OC 上一动点;④Q 为OB 上一动点;【问题】:求MP+PQ 最小时,P 、Q 的位置?辅助线:将作Q 关于OC 对称点Q ’,转化PQ ’=PQ ,过点M 作MH ⊥OA , 则MP+PQ=MP+PQ ’ MH(垂线段最短)ll 2AA'PQBB'lAl 1l 2PA+PQ+BQAPOQ MBQ'HPA(3)最短路程模型二(点到直线类2) 【条件】:A(0,4),B(-2,0),P(0,n ) 【问题】:n 为何值时,PA 55PB最小? 求解方法:①x 轴上取C(2,0),使sin ∠OAC=55;②过B 作BD ⊥AC ,交y 轴于点E ,即为所求;③tan ∠EBO=tan ∠OAC=21,即E (0,1)(4)最短路程模型三(旋转类最值模型)【条件】:①线段OA=4,OB=2;②OB 绕点O 在平面内360°旋转; 【问题】:AB 的最大值,最小值分别为多少?【结论】:以点O 为圆心,OB 为半径作圆,如图所示,将问题转化为“三角形两边之和大于第三边,两边之差小于第三边”。
最大值:OA+OB ;最小值:OA-OBOAB最小值位置最大值位置【条件】:①线段OA=4,OB=2;②以点O 为圆心,OB ,OC 为半径作圆; ③点P 是两圆所组成圆环内部(含边界)一点;【结论】:若PA 的最大值为10,则OC= 6 ;若PA若PA 的最小值为2,则PC 的取值范围是 0<PC<2【条件】:①Rt △OBC ,∠OBC=30°;②OC=2;③OA=1;④点P 为BC上动点(可与端点重合); ⑤△OBC 绕点O 旋转【结论】:PA 最大值为OA+OB=321+;PA 的最小值为13OA OB 21-==如下图,圆的最小半径为O 到BC 垂线段长。
BC模型八:二倍角模型【条件】:在△ABC 中,∠B=2∠C ;辅助线:以BC 的垂直平分线为对称轴,作点A 的对称点A ’,连接AA ’、BA ’、CA ’、 则BA=AA ’=CA ’(注意这个结论)此种辅助线作法是二倍角三角形常见的辅助线作法之一,不是唯一作法。
模型九:相似三角形模型 (1)相似三角形模型--基本型 平行类:DE ∥BC ;A 字型 8字型 A 字型 结论:BCDEAC AE AB AD ==(注意对应边要对应)(2)相似三角形模型---斜交型【条件】:如右图,∠AED=∠ACB=90°;AB C AB CA'AB C DEAD EC ADECAB CDEABCDE斜交型斜交型【结论】:AE ×AB=AC ×AD【条件】:如右图,∠ACE=∠ABC ;【结论】:AC 2=AE ×AB第四个图还存在射影定理:AE ×EC=BC ×AC ;BC 2=BE ×BA ;CE 2=AE ×BE ; (3)相似三角形模型---一线三等角型【条件】:(1)图:∠ABC=∠ACE=∠CDE=90°; (2)图:∠ABC=∠ACE=∠CDE=60°; (3)图:∠ABC=∠ACE=∠CDE=45°; 【结论】:①△ABC ∽△CDE ;②AB ×DE=BC ×CD ; 一线三等角模型也经常用来建立方程或函数关系。
