抛掷一枚硬币试验报告表
北师版数学七年级下册 抛硬币试验

500 1000
优等品数 m m
优等品率 n
7 16 43 81 164 414 825
0.7 0.8 0.86 0.81 0.82 0.828 0.825
(1)完成上表;
(2)根据上表,在这批乒乓球中任取一个,它为 优等品的概率大约是多少? 0.83
(3)如果重新再抽取 1000 个乒乓球进行质量检查, 对比上表记录下数据,两表的结果会一样吗? 为什么?
0.962
(2) 观察上表,可以发现,当抽取的瓷砖数 n≥400 时,合
格品率
m n
稳定在
0.962
的附近,
所以我们可取 p = 0.96 作为该型号瓷砖的合格品率的估计.
(3) 500000×96% = 480000 (块),可以估计该型号合格品
数为 480000 块.
频率与概率的关系
联系: 频率
个常数.
典例精析 例1 王老师将 1 个黑球和若干个白球放 入一个不透明的口袋并搅匀,让若干学生进行摸球实
验,每次摸出一个球(有放回),下表是活动进行中的 一组统计数据(结果保留两位小数):
摸球的次数n 100 150 200 500 800 1000
摸到黑球的 次数 m
摸到黑球m 的频率 n
23 31 60 130 0.23 0.21 0.30 0.26
里却用了 15 分钟 C. 今天是星期天,昨天必定是星期六 D. 小明步行的速度是每小时 40 千米
2. 口袋中有 9 个球,其中 4 个红球,3 个蓝球,2 个 白球,在下列事件中,发生的可能性为 1 的是 ( C ) A. 从口袋中拿一个球恰为红球 B. 从口袋中拿出 2 个球都是白球 C. 拿出 6 个球中至少有一个球是红球 D. 从口袋中拿出的 5 个球中恰为 3 红 2 白
抛硬币试验1

抛硬币试验“抛”出了什么此题设计目的是使学生理解随机抛掷一枚硬币时“出现正面和出现反面的可能性是相同的”,从而说明在比赛前用抛硬币的方法来决定谁先开球对比赛双方都是公平的。
问题的关键是:怎样才能让学生明白“出现正面和出现反面的可能性是相同的”即“它们的可能性都是1/2”呢?问了几个同事,大家都说“一看就知道,硬币只有两面,抛一次不是正面就是反面,出现正面和反面的可能性都是1/2”。
我也是这样想的。
不过,“一看就知道”的东西,为什么历史上那么多著名的数学家还要通过做成千上万次的试验来证明呢?这里面究竟隐藏着什么?在配套的《教师教学用书》第173页,有这样一段话:掷一枚硬币时,既可能出现正面,也可以出现反面,预先作出确定的判断是不可能的,但如果硬币均匀,直观上会感到出现正面与出现反面的机会应该相等,即在大量重复试验中正面朝上的频率,应该接近50%。
为了验证这点,在概率论的发展历史上,曾有许多著名的数学家也做过这个实验。
难道说我们的判断靠的就是“直观”,是一种感觉?这种感觉对不对,还得靠“验证”?可新的问题又来了,就算科学家做了成千上万次的试验不是也没有证明正面和反面的可能性都是1/2吗?何况,课堂上我们让孩子做得有限的数十,上百次试验。
说白了,做实验不但得不到结果,还会推翻最初的“直观”感觉。
问题越来越多,需要继续查资料:通过试验来确定概率是有风险的。
增加试验次数,可以降低这种风险,却不能消除风险本身,只有在试验次数无穷大的时候,才不存在这种风险。
试验次数越多,结果越逼近理论值。
当大量重复抛掷一枚硬币时,二者出现的频率在0.5附近摆动,我们就认为正面朝上和反面朝上的概率是1/2。
虽然,最后那句“二者出现的频率在0.5附近摆动,我们就认为正面朝上和反面朝上的概率是1/2”这种解释我认为非常牵强。
不过,心中的疑虑还是打消了不少。
我敢在课堂上大胆尝试:一、观察独立的20组数据1、学生两人合作,每人抛10次,做好记录。
抛硬币试验记录表(精选参考模板)
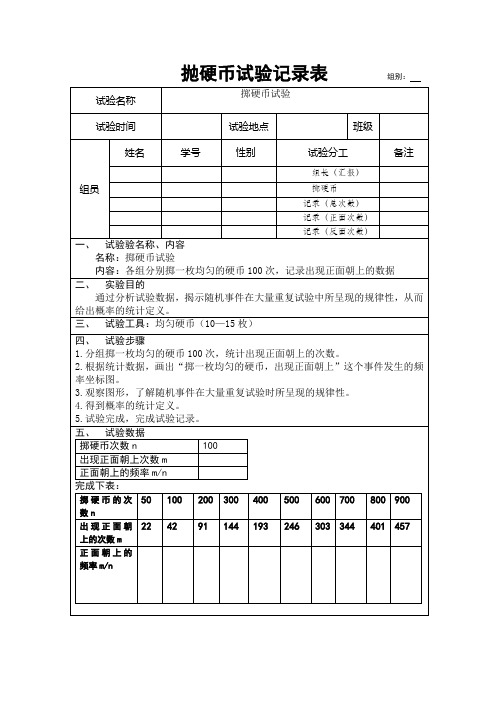
组别:
试验名称
掷硬币试验
试验时间
试验地点
班级
姓名
学号
性别
试验分工
备注
组长(汇报)
组员
掷硬币 记录(总次数)
记录(正面次数)
记录(反面次数)
一、 试验验名称、内容 名称:掷硬币试验 内容:各组分别掷一枚均匀的硬币 100 次,记录出现正面朝上的数据
二、 实验目的 通过分析试验数据,揭示随机事件在大量重复试验中所呈现的规律性,从而
5.试验完成,完成试验记录。
五、 试验数据
掷硬币次数 n
100
出现正面朝上次数 m
正面朝上的频率 m/n
完成下表:
掷 硬 币 的 次 50 100 200 300 400 500 600 700 800 900
数n
出 现 正 面 朝 22 42 91 144 193 246 303 344 401 457
给出概率的统计定义。 三、 试验工具:均匀硬币(10—15 枚)
四、 试验步骤
1.分组掷一枚均匀的硬币 100 次,统计出现正面朝上的次数。
2.根据统计数据,画出“掷一枚均匀的硬币,出现正面朝上”这个事件发生的频
率坐标图。
3.观察图形,了解随机事件在大量重复试验时所呈现的规律性。
4.得到概率的统计定义。
上的次数 m
正面朝上的
频率 m/n
六、画出“掷一枚均匀 的频率坐标图
的硬币,出现正面朝上”这个事件发生
0.6
0.5
0.4
0
100 200 300 400 500 600
七、 概率的统计定义:
。
八、
讨论问题(小组讨论) (1) 随机事件发生的频率在试验前能确定吗? (2) 随着试验次数的增加,随机事件发生的频率有何变化? (3) 概率与试验次数有关吗?
抛掷硬币结果分析探究

硬币实验结果报告摘要:总共N个人投掷一枚硬币169次,记正面为1,反面为0,得到N份抛硬币实验原始数据。
分析该数据,是否有规律性可循?关键字:抛硬币1.数学模型一.统计零项目(1)分类统计:对每份数据进行统计,以零的连环数作为分类依据,统计各类出现的次数记入表A(Xi,Xj)(2)累加对N份A表进行相应项的累加,结果记入表B中,即B(Xi,Xj)=A(xi,Xj)(3)计算对应项的概率先累计B表,再用各项除以该累计值得P(Xi,Xj)=B(Xi,Xj)/B(xi,Xj)二.统计一项目过程同上。
2.相关算法:一份原始数据是一个13*13的表格,每项取值只能为0,1以行为主序,将各行串接起来形成一个比较长的01串。
在该串中依次统计连环Xi个零出现的次数,过程如下:依次令Xi=1~169,在01串中寻找如下的子串:(10..01),(串首0..01),(10..0串尾), (串首0..0串尾),中间0..0表示Xi个零。
出现则令计数器Xj增加1(开始Xj为零),统计到了串尾后令A(Xi,Xj)=1。
所有Xi统计毕,未统计到的项则自动零。
待169个Xi统计毕,所有Xi个连环零出现j次的情况在A(Xi,Xj)中表现为1,其余不出现者为零。
统计所有N份数据,在每一份数据统计毕后立即累加到B(Xi,Xj)上,所有N份完后B(Xi,Xj)也完成了累加。
最后计算P(Xi,Xj)=B(Xi,Xj)/B(xi,Xj)3.图表:1234567出现次数连环零的个数10000000 2000.001721000.0051640.01204830.0017210.0068850.0137690.0223750.0430290.0344230.0361450.015 40.0550770.0516350.0430290.0240960.0086060.0017210.00344250.0808950.0275390.0154910.00344200060.0361450.0172120000070.020*********80.013769000000进行分析后,得出以下数据:E(Xi)=E(Xj)=E(Yi)=E(Yj)=这说明一般情况下出现最多的情况是连环3或4个零出现8或9次4.结束语。
硬币跳高实验报告册

硬币跳高实验报告册实验目的通过观察和记录,探究硬币在不同高度下的反弹高度与初始高度的关系,以及硬币跳高过程中的能量转化。
实验材料和设备1. 一枚硬币2. 一把直尺3. 一个测量高度的计量器实验原理硬币跳高过程中涉及到动能和势能的转化。
当硬币从高处自由落下时,由于地球引力的作用,它会具有一定的下落速度和势能。
当硬币撞击地面时,一部分势能转化为动能,使硬币产生反弹,弹起的高度则取决于初始高度和地面反弹后的势能。
实验步骤1. 使用直尺测量初始时的高度,记录下来,并作为初始高度。
2. 将硬币放在初始高度上方,让其自由落下,并记录下反弹的高度。
3. 将硬币从不同高度释放,重复步骤2,记录不同初始高度下的反弹高度。
4. 根据实验记录数据分析得出结论。
实验记录和结果初始高度(cm)反弹高度1(cm)反弹高度2(cm)反弹高度3(cm)平均反弹高度(cm)50 20 18 19 19 100 35 32 34 33.67 150 45 42 44 43.67 200 55 52 54 53.67 250 70 65 68 67.67 根据上表中的实验记录可以得出以下结论:1. 初始高度和反弹高度之间存在着一定的线性关系,即初始高度越高,反弹高度也越高。
2. 从数值上看,初始高度和平均反弹高度的比值约为1:0.4左右。
也就是说,平均反弹高度约为初始高度的40%左右。
这进一步验证了硬币跳高过程中存在着能量转化。
实验分析和讨论1. 通过实验可以看出,硬币落地后的反弹高度与初始高度之间具有一定的线性关系。
这是因为地球引力所产生的势能转化为动能,再转化为反弹高度时,符合牛顿运动定律的规律。
2. 虽然实验结果存在一定的误差,但可以通过多次重复实验来减小误差。
同时,可以使用更加精确的测量工具来提高测量结果的准确度。
3. 实验中没有考虑空气阻力对硬币运动的影响。
在实际情况下,空气阻力会对硬币的运动产生一定的影响,因此在实验设计中可以考虑使用真空环境来减小阻力的影响。
北师大版七年级数学下册《抛硬币试验》PPT课件

2 频率的稳定性
第2课时 抛硬币试验
问题引入 掷一枚质地均匀的硬币,硬币落下后,会出现两种
情况:
正面朝上
正面朝下
你认为正面朝上和正面朝下的可能性相同吗?
频率与概率 做一做 (1) 同桌两人做 20 次掷硬币的游戏,并将记录
记载在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
里却用了 15 分钟 C. 今天是星期天,昨天必定是星期六 D. 小明步行的速度是每小时 40 千米
2. 口袋中有 9 个球,其中 4 个红球,3 个蓝球,2 个 白球,在下列事件中,发生的可能性为 1 的是 ( C ) A. 从口袋中拿一个球恰为红球 B. 从口袋中拿出 2 个球都是白球 C. 拿出 6 个球中至少有一个球是红球 D. 从口袋中拿出的 5 个球中恰为 3 红 2 白
(4) 观察上面的折线统计图,你发现了什么规律? 当实验的次数较少时,折线在“0.5 水平直线” 的上下摆动的幅度较大,随着实验的次数的增 加,折线在“0.5 水平直线”的上下摆动的幅度 会逐渐变小.
当试验次数很多时, 正面朝上的频率折线 差不多稳定在“ 0.5 水平线” 上.
(5) 下表列出了一些历史上的数学家所需所做的掷硬 币试验的数据:
正面朝下的频率
(2)累计全班同学的试验结果,并将数据汇总填入下表:
实验总次数 20 40 60 80 100 120 140 160 180 200 正面朝上
的次数
正面朝上 的频率
正面朝下 的次数
正面朝下 的频率
(3) 根据上表,完成下面的折线统计图. 频率
1.0 0.7 0.5 0.2
0 20 40 60 80 100 120 140 160 180 200 实验总次数
投掷硬币实验

题目:投掷一个硬币,直到|Heads-Tails|==N,统计总投掷次数,写一个函数,Gap(N),它返回总投掷次数,并对一系列的N,比如N=1:30,做100次实验,统计总投掷次数的平均值,估计Gap(N)的期望值。
文件名建为:gaping.m%Gap(N)的期望实现算法function z=gaping(N)%赋初值Heads=0;Tails=0;%正面、反面次数为0s=0;%期望初值为0%投掷硬币实现算法while abs(Heads-Tails)~=N%当正面与反面的绝对值之差不等于N时r=rand();%投掷硬币,即产生(0,1)的随机数if r>0.5%表示正面Heads=Heads+1;%记录出现正面的次数else %表示反面Tails=Tails+1;%记录出现反面的次数ends=s+r;endz=s;%返回期望值文件名建为:gap.m%Gap(N)的总投掷次数的平均值实现算法function y=gap(N)%赋初值Heads=0;Tails=0;%正面、反面次数为0%投掷硬币实现算法while abs(Heads-Tails)~=N%当正面与反面的绝对值之差不等于N时r=rand();%投掷硬币,即产生(0,1)的随机数if r>0.5%表示正面Heads=Heads+1;%记录出现正面的次数else %表示反面Tails=Tails+1;%记录出现反面的次数endendy=Heads+Tails;%当N为一定值时,记录所需要投掷的总次数文件名随便建,比如aa1.mx=input('请输入投掷硬币试验次数(1=<x<=1000):');%设置实验次数A=[];B=[];%建立空矩阵m=0;n=0;%总投掷次数之和、期望初值为0for N=1:30%绝对值之差设置值for i=1:xy=gap(N);%调用y=gap(N)的函数z=gaping(N);%调用y=gaping(N)的函数A=[A,y];%将调用函数得出的独立数据用矩阵拼装起来B=[B,z];%将调用函数得出的独立数据用矩阵拼装起来endend%计算总投掷次数的平均值for N=1:30for j=x*(N-1)+1:x*Nm=m+A(j);%求当N为一定值时的总投掷次数的的平均值n=n+B(j);%求当N为一定值时的期望值endfprintf('做%5d次试验所得Gap(%2d)总投掷次数的平均值是:%10.8f,期望值是:%10.8f\n',x,N,m/x,n/x)end。
2023-2024学年度北师七下数学6.2 第2课时 抛硬币试验【课件】

想一想 事件A发生的概率P(A)的取值范围是什么?必
然事件发生的概率是多少?不可能事件发生的概 率又是多少?
必然事件发生的概率为1;不可能事件发 生的概率为0;随机事件A发生的概率P(A)是0 与1之间的一个常数.
典例精析 例 王老师将1个黑球和若干个白球放入一个不
2.口袋中有9个球,其中4个红球,3个蓝球, 2个白球,在下列事件中,发生的可能性为1 的是( C ) A.从口袋中拿一个球恰为红球 B.从口袋中拿出2个球都是白球 C.拿出6个球中至少有一个球是红球 D.从口袋中拿出的球恰为3红2白
3.小凡做了5次抛掷均匀硬币的实验,其中有
3次正面朝上,2次正面朝下,他认为正面朝
(1)补全上表中的有关数据,根据上表数据估计 从袋中摸出一个球是黑球的概率是多少;
(2)估算袋中白球的个数. 解:(1)251÷1000≈0.25.∵大量重复试验事 件发生的频率逐渐稳定到0.25附近,∴估计从 袋中摸出一个球是黑球的概率是0.25; (2)设袋中白球为x个,1=0.25(1+x),x=3.
概率
事件发生的 可能性大小
在实际问题中,若事件的概率未知,常用频率作 为它的估计值.
区别:频率本身是随机的,在试验前不能确定,做同
样次数或不同次数的重复试验得到的事件的频率都可能 不同,而概率是一个确定数,是客观 存在的,与每次试 验无关.
当堂练习
1.下列事件发生的可能性为0的是( D ) A.掷两枚骰子,同时出现数字“6”朝上 B.小明从家里到学校用了10分钟, 从学校回到家里却用了15分钟 C.今天是星期天,昨天必定是星期六 D.小明步行的速度是每小时40千米
抛硬币统计表
抛硬币的次数
正面向上的次数
反面向上的次数
抛硬币次
数的一半
正面向上的次数是否接近抛硬币总次数的一半
抛硬币试验数据表一
抛硬币的次数
正面向上的次数
反面向上的次数
抛硬币次
数的一半
正面向上的次数是否接近抛硬币总次数的一半
抛硬币试验数据表一
抛硬币的次数
正面向上的次数
反面向上的次数
抛硬币次
数的一半
组别
抛硬币的总次数
正面向上的总次数
反面向上的总次数
抛硬币总次数的一半
正面向上的次数是否接近抛硬币总次数的一半
第()组
抛硬币试验数据表二
组别
抛硬币的总次数
正面向上的总次数
反面向上的总次数
抛硬币总次数的一半
正面向上的次数是否接近抛硬币总次数的一半
第()组抛硬币试验数据表二组别抛硬币的总次数
正面向上的总次数
反面向上的总次数
抛硬币总次数的一半
正面向上的次数是否接近抛硬币总次数的一半
第()组
正面向上的次数是否接近抛硬币总次数的一半
抛硬币试验数据表一
抛硬币的次数
正面向上的次数
反面向上的次数
抛硬币次
数的一半
正面向上的次数是否接近抛硬币总次数的一半
抛硬币试验数据表二
组别
抛硬币的总次数
正面向上的总次数
反面向上的总次数
抛硬币总次数的一半
正面向上的次数是否接近抛硬币总次数的一半
第()组
抛硬币试验数据表二
概率匹配实验报告

概率匹配实验报告概率匹配实验报告概率是数学中一个非常重要的概念,它在各个领域中都有广泛的应用。
而概率匹配实验则是一种通过实际操作来验证概率理论的方法。
在本次实验中,我们通过一系列的实验操作,来验证概率匹配的准确性和可靠性。
实验一:硬币抛掷实验首先,我们进行了一组硬币抛掷实验。
我们选择了一枚普通的硬币,然后进行了100次连续的抛掷。
通过记录正面朝上和反面朝上的次数,我们得到了一组数据。
经过统计分析,我们发现正面朝上和反面朝上的次数非常接近,符合概率匹配的预期结果。
实验二:骰子实验接下来,我们进行了一组骰子实验。
我们选择了一个六面骰子,然后进行了100次连续的掷骰子操作。
同样地,通过记录每个面出现的次数,我们得到了一组数据。
再次进行统计分析后,我们发现每个面出现的频率非常接近1/6,也符合概率匹配的预期结果。
实验三:扑克牌实验最后,我们进行了一组扑克牌实验。
我们选择了一副标准的52张扑克牌,然后进行了100次连续的抽牌操作。
通过记录每个花色和每个点数的出现次数,我们得到了一组数据。
再次进行统计分析后,我们发现每个花色和每个点数的出现频率非常接近1/4和1/13,也符合概率匹配的预期结果。
通过以上三组实验,我们可以得出一个结论:概率匹配是一种可靠的方法,可以用来验证概率理论的准确性。
在实验中,我们通过大量的实际操作和统计分析,得到了与理论预期相符合的结果。
这表明概率匹配是一种有效的实验方法,可以用来验证概率理论的可靠性。
然而,我们也要注意到实验结果中的一些偏差。
虽然我们的实验结果与理论预期非常接近,但并不意味着概率匹配是完全准确的。
实际上,由于实验中的随机性和个体差异,我们无法完全消除偏差的可能性。
因此,在进行概率匹配实验时,我们应该保持谨慎,并结合统计分析来评估实验结果的可靠性。
综上所述,概率匹配实验是一种验证概率理论的有效方法。
通过实际操作和统计分析,我们可以得到与理论预期相符合的结果。
然而,我们也要注意实验结果中的偏差,并结合统计分析来评估实验结果的可靠性。
条件概率的实验报告(3篇)

第1篇一、实验目的本次实验旨在通过实际操作,验证条件概率的概念,并探究不同条件下条件概率的变化规律。
二、实验原理条件概率是指在某一条件下,事件A发生的概率。
设事件A和事件B同时发生的概率为P(A∩B),事件B发生的概率为P(B),则事件A在事件B发生的条件下发生的概率为P(A|B)。
P(A|B) = P(A∩B) / P(B)三、实验器材1. 硬币一枚2. 50张写有数字1到50的纸牌3. 计算器4. 实验记录表四、实验步骤1. 抛硬币实验(1)将硬币抛掷10次,记录正面朝上的次数。
(2)计算正面朝上的概率P(正面)。
(3)在正面朝上的条件下,再抛掷硬币5次,记录正面朝上的次数。
(4)计算在正面朝上的条件下,正面朝上的概率P(正面|正面)。
2. 纸牌实验(1)将50张纸牌洗匀,随机抽取一张,记录其数字。
(2)计算抽到数字1的概率P(1)。
(3)在抽到数字1的条件下,再随机抽取一张纸牌,记录其数字。
(4)计算在抽到数字1的条件下,抽到数字2的概率P(2|1)。
五、实验结果与分析1. 抛硬币实验(1)正面朝上的次数:7次(2)正面朝上的概率P(正面) = 7 / 10 = 0.7(3)在正面朝上的条件下,正面朝上的次数:3次(4)在正面朝上的条件下,正面朝上的概率P(正面|正面) = 3 / 5 = 0.62. 纸牌实验(1)抽到数字1的概率P(1) = 1 / 50 = 0.02(2)在抽到数字1的条件下,抽到数字2的概率P(2|1) = 1 / 49 ≈ 0.02六、实验结论1. 通过抛硬币实验和纸牌实验,验证了条件概率的概念。
2. 在抛硬币实验中,正面朝上的条件下,正面朝上的概率略低于总体概率,这可能是由于随机性导致的。
3. 在纸牌实验中,抽到数字1的条件下,抽到数字2的概率与总体概率相同,说明在特定条件下,事件发生的概率不会改变。
4. 本次实验结果表明,条件概率在现实生活中的应用具有广泛性,对理解和解决实际问题具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试验次数( )
正面朝上的次数( )
正面朝上的比例( )
第三步:观察、分析各组试验结果,并对结果进讨论分析。
(黑板附表2)
第四步:计算机模拟抛掷一枚硬币试验。
试验次数( )
正面朝上的频数( )
正面朝上的频率( )
第五步:历史上一些抛掷硬币的试验结果。
“抛掷硬币”试验
一、试验条件
二、试验步骤
第一步:每人做10次抛掷一枚硬币试验,完成试验要求,并对结果进行分析。
试验记录表格:
试验次数
正面向上次数
正面向上比例
10
条形图:(横轴为试验结果,仅取两个值,1(正面)和0(反面),纵轴为:正面向上出现的比例)
(黑板附表1)
第二步:分小组统计试验结果,并上报黑板附表2,并对结果进行分析。
