行星齿轮传动比计算
行星轮系传动比计算

1 行星轮系的传动比
CONTENTS
目
2 行星轮系传动比计算
录
行星轮系的传动比
iGHK
nGH nKH
nG nK
nH nH
(1)m
从齿轮G到K所有从动齿数积 从齿轮G到K所有主动齿数积
式中:G、K——周转齿轮系中的两个轮 m——从G到K齿轮间外啮合齿轮的对数
行星轮系的传动比
应用上式应注意:
1)G轮与K轮的轴线平行或重合,才能用上式;
2)齿数比前的符号按定轴齿轮系的方法确定, 且必须有正、负号。
3)将 nG、nK、nH
三个量代入公式时,必须带有转向的“+、-”号,将其中一 个转向设为正,相反的要连同负号一起代入上式。
4) iGHK iGK
iGHK
nG nKG
nH nH
谢谢观计算
例1 图示的差动齿轮系中,已知 z1 =20,z2 =30,z3 =80,
n1 =100 r/min,n3 =20 r/min。试问: 1)n1 与 n3 转向相同时,nH =? 2)n1 与 n3 转向相反时,nH =?
总结
1.行星轮系的传动比 2.行星轮系传动比的计算
行星减速箱传动比计算公式

行星减速箱传动比计算公式行星减速箱是一种常用的传动装置,它由太阳轮、行星轮、内齿轮和外齿轮等部件组成,通过这些部件的组合和运动来实现传动的目的。
在实际应用中,我们经常需要计算行星减速箱的传动比,以便选择合适的传动方案。
本文将介绍行星减速箱传动比的计算公式及其应用。
行星减速箱的传动比是指输入轴和输出轴的转速之比,它可以用来描述行星减速箱的传动效果。
在计算传动比时,我们需要考虑太阳轮、行星轮和内齿轮的齿数,以及它们之间的传动关系。
下面是行星减速箱传动比的计算公式:传动比 = (1 + ZS/ZP) (1 + ZI/ZP)。
其中,ZS为太阳轮的齿数,ZP为行星轮的齿数,ZI为内齿轮的齿数。
这个公式的推导过程比较复杂,我们可以简单地理解为,传动比等于太阳轮和行星轮之间的传动比与行星轮和内齿轮之间的传动比的乘积。
这个公式可以帮助我们快速准确地计算行星减速箱的传动比,为传动方案的选择提供依据。
在实际应用中,我们可以通过这个公式来计算不同传动比下的输出转速,从而选择合适的行星减速箱。
例如,如果我们需要将输入轴的转速降低10倍,那么我们就可以通过这个公式来计算出需要的行星减速箱传动比,然后选择合适的齿轮组合。
除了计算传动比,行星减速箱的设计还需要考虑到传动效率、扭矩传递和结构强度等因素。
在实际应用中,我们还需要综合考虑这些因素,选择合适的行星减速箱型号和参数,以满足实际的传动需求。
除了上面介绍的基本行星减速箱传动比计算公式外,还有一些特殊情况下的计算方法。
例如,当行星减速箱的内齿轮和外齿轮的齿数相等时,传动比可以简化为:传动比 = 1 + ZS/ZP。
这个简化的公式可以帮助我们快速计算出内齿轮和外齿轮齿数相等时的传动比,为一些特殊情况下的传动方案选择提供便利。
总之,行星减速箱传动比的计算是行星减速箱设计和应用中的重要内容,它可以帮助我们选择合适的传动方案,满足不同的传动需求。
通过上面介绍的计算公式,我们可以快速准确地计算出行星减速箱的传动比,为传动方案的选择提供依据。
齿轮系传动比计算
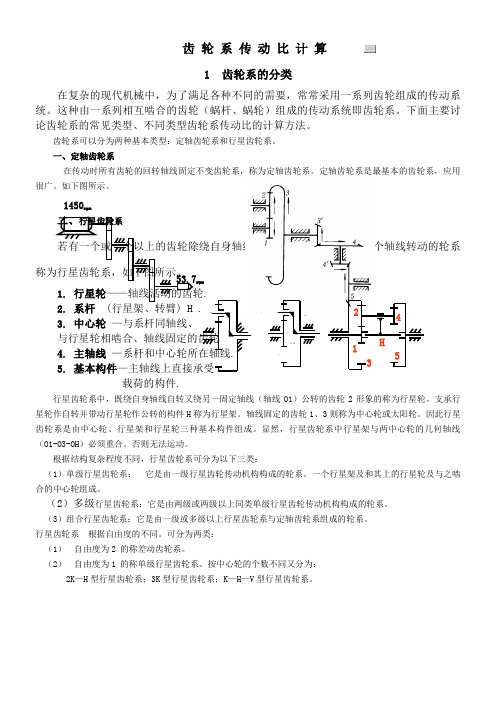
齿 轮 系 传 动 比 计 算1 齿轮系的分类在复杂的现代机械中,为了满足各种不同的需要,常常采用一系列齿轮组成的传动系统。
这种由一系列相互啮合的齿轮(蜗杆、蜗轮)组成的传动系统即齿轮系。
下面主要讨论齿轮系的常见类型、不同类型齿轮系传动比的计算方法。
齿轮系可以分为两种基本类型:定轴齿轮系和行星齿轮系。
一、定轴齿轮系在传动时所有齿轮的回转轴线固定不变齿轮系,称为定轴齿轮系。
定轴齿轮系是最基本的齿轮系,应用很广。
如下图所示。
二、行星齿轮系若有一个或一个以上的齿轮除绕自身轴线自转外,其轴线又绕另一个轴线转动的轮系称为行星齿轮系,如下图所示。
1. 行星轮——轴线活动的齿轮2. 系杆 (行星架、转臂3. 中心轮 —与系杆同轴线、4. 主轴线 5. 基本构件载荷的构件.行星齿轮系中,既绕自身轴线自转又绕另一固定轴线(轴线O1)公转的齿轮2形象的称为行星轮。
支承行星轮作自转并带动行星轮作公转的构件H 称为行星架。
轴线固定的齿轮1、3则称为中心轮或太阳轮。
因此行星齿轮系是由中心轮、行星架和行星轮三种基本构件组成。
显然,行星齿轮系中行星架与两中心轮的几何轴线(O1-O3-OH )必须重合。
否则无法运动。
根据结构复杂程度不同,行星齿轮系可分为以下三类:(1)单级行星齿轮系: 它是由一级行星齿轮传动机构构成的轮系。
一个行星架及和其上的行星轮及与之啮合的中心轮组成。
(2)多级行星齿轮系:它是由两级或两级以上同类单级行星齿轮传动机构构成的轮系。
(3)组合行星齿轮系:它是由一级或多级以上行星齿轮系与定轴齿轮系组成的轮系。
行星齿轮系根据自由度的不同。
可分为两类: (1) 自由度为2 的称差动齿轮系。
(2) 自由度为1 的称单级行星齿轮系。
按中心轮的个数不同又分为:2K —H 型行星齿轮系;3K 型行星齿轮系;K —H —V 型行星齿轮系。
1450rpm53.7rpm2 定轴齿轮系传动比的计算一、齿轮系的传动比齿轮系传动比即齿轮系中首轮与末轮角速度或转速之比。
行星齿轮传动比最简计算方法--公式法

在《机械原理》上,行星齿轮求解是通过列一系列方程式求解,其求解过程繁琐容易出错,其实用不着如此,只要理解了传动比eab i 的含义,就可以很快地直接写出行星齿轮的传动比,其关键是掌握几个根据e ab i 的含义推导出来公式,随便多复杂的行星齿轮传动机构,根据这几个公式都能从头写到尾直接把其传动比写出来,而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。
一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1 a cx a bxa bc i i i = ―――――――――――――――――――――――――2a cb a bc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后,不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。
关键是要善于选择中间的一些部件作为参照,使其最后形成都是定轴传动,所以这些参照基本都是一些行星架等例如象论坛中“大模王”兄弟所举的例子:在此例中,要求出e ab i =,如果行星架固定不动的话,这道题目就简单多了,就是一定轴传动。
所以我们要想办法把e ab i 变成一定轴传动,所以可以根据公式a cx a bx a bci i i =将x 加进去, 所以可以得出:e bx e ax eab i i i =要想变成定轴传动,就要把x 放到上面去,所以这里就要运用第一个公式1=+c ba abc i i 了,所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。
定轴传动的传动比就好办了,直接写出来就可以了。
即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构:已知其各轮的齿数为z 1=100,z 2=101,z 2’ =100 ,z 3=99。
双联行星齿轮的传动比

双联行星传动比计算通常需要考虑多个因素,包括太阳轮和行星架的转速、齿圈的齿数、以及太阳轮和齿圈之间的传动比等。
根据您提供的信息,可以使用以下公式计算双联行星齿轮传动的合理传动比:
传动比= 太阳轮转速/ 齿圈转速
其中,太阳轮转速是输入端的转速,齿圈转速是输出端的转速,传动比表示太阳轮转速与齿圈转速之比。
需要注意的是,双联行星齿轮系统的传动比受到多种因素的影响,如行星架的选择、齿圈的大小、太阳轮的大小、行星齿轮的材料和制造工艺等。
因此,在实际应用中,需要根据具体情况进行详细的计算和设计,以确保传动比的准确性和可靠性。
行星齿轮传动比分析与计算

行星齿轮传动比分析与计算一、行星轮系传动比的计算 (一)行星轮系的分类若轮系中,至少有一个齿轮的几何轴线不固定,而绕其它齿轮的固定几何轴线回转,则称为行星轮系。
行星轮系的组成:行星轮、行星架(系杆)、太阳轮 (二)行星轮系传动比的计算以差动轮系为例(反转法) 转化机构(定轴轮系) T 的机构1234差动轮系:2个运动行星轮系:,对于行量轮系:H H W W W -=111W H H W W W -=222W H H W W W -=333W 0=-=H H H H W W W H W 13313113)1(Z Z W W W W W W i H HH H H⋅'-=--==03=W 1310Z Z W W W H H-=--11311+==Z Z W W i H H )(z f W W W W W W iH B H A H BH A HAB=--==0=B W∴∴例12.2:图示为一大传动比的减速器,Z 1=100,Z 2=101,Z 2'=100,Z 3=99。
求:输入件H 对输出件1的传动比i H1解:1,3中心轮;2,2'行星轮;H 行星架 给整个机构(-W H )绕OO 轴转动∵W 3=0∴∴若Z 1=99行星轮系传动比是计算出来的,而不是判断出来的。
AHHA H H A H AB i W WW W W i -=-=--=110HAB AH i i -=1213223113)1('⋅⋅⋅-=--=Z Z Z Z W W W W i H HHH H Hi Z Z Z Z W W W 13213210'=--H H i Z Z Z Z W W 13213211'=+-HH i i 131100100991011⨯⨯-=100001001009910111111=⨯⨯-==HH i i 1001-=H i(三)复合轮系传动比的计算复合轮系:轮系中既含有定轴轮系又含有行星轮系,或是包含由几个基本行星轮系的复合轮系。
行星齿轮传动比计算公式

行星齿轮传动比计算公式
行星齿轮传动是一种广泛应用于机械传动系统中的一种机构。
它由太阳齿轮、行星齿轮和内齿圈组成,通过太阳齿轮的输入,实现输出转矩和速度的变换。
行星齿轮传动的传动比计算公式如下:
传动比 = (1 + N) / N
其中,N为行星齿轮的齿数。
其中太阳齿轮和内齿圈的齿数可以通过齿轮的模数、齿数比和齿数关系计算得到。
行星齿轮的齿数决定了传动比的大小。
需要注意的是,在实际传动中,行星齿轮传动常常采用多级的组合形式,以实现更大范围的传动比。
在多级行星齿轮传动中,每个级别的传动比都可以使用上述的传动比计算公式进行计算,最终的传动比等于各级传动比之积。
总之,行星齿轮传动的传动比计算公式为(1 + N) / N,其中N为行星齿轮的齿数。
行星齿轮机构传动比计算方法

行星齿轮机构传动比计算方法Key words: epicyclic gear train; speed ratio; compute way.随着行星齿轮减速器以及行星齿轮传动在变速箱中的广泛应用,对行星齿轮传动的了解和掌握已成为工程技术人员的必要技能。
但是,对于刚接触行星齿轮传动的工程技术人员来说,行星齿轮传动的速比计算比较不容易理解和掌握。
本文通过对各类参考资料及教科书中的行星齿轮传动速比计算方法进行总结归纳,并针对常用的最具代表性的2K-H型行星齿轮传动,分别用不同方法对其传动特性方程进行了推导论证。
行星齿轮传动或称周转轮系。
根据《机械原理》[1]上的定义,我们可把周转轮系分为差动轮系和行星轮系。
为理解方便,本论文所讨论限于2K-H型周转轮系。
关于行星齿轮传动(周转轮系)的速比计算方法,归纳起来有两大类四种方法,分别为由行星架固定法和力矩法组成的分析法;由速度图解法和矢量法组成的图解法[2]。
矢量图解法一般适用于圆锥齿轮组成的行星齿轮传动,在此不作介绍;下面分别运用其它三种计算方法对2K-H型周转轮系的传动特性方程(1)进行推导。
1-太阳轮 2-行星轮 3-内齿圈 H -行星架 图1 行星齿轮传动Fig 1 Epicyclic gear train0)1(31=++-αωωαωH (1) 结合图1,式中1ω为太阳轮1的转速、Hω为行星架H 转速、3ω为内齿圈3转速、α为内齿圈3与太阳轮1的齿数比即13Z Z =α。
1 行星架固定法机械专业教科书上一般介绍的都是此种方法,也可叫转化机构法。
其理论是一位名叫Wlies 的科学家于1841年提出的,即“一个机构整体的绝对运动并不影响其内部各构件间的相对运动” [3],就像手表的时针、分针、秒针的相对运动不会因带表人的行动而变化。
如图2所示,其中太阳轮1、行星轮2、内齿圈3、行星架H 的转速分别为Hωωωω、、、321。
我们假定整个行星轮系放在一个绕支点O 旋转的圆盘上,此圆盘的转速为 H ω-。
行星齿轮传动比最简计算方法公式法

行星齿轮传动比计算在《机械原理》上,行星齿轮求解是通过列一系列方程式求解,其求解过程繁琐容易出错,其实用不着如此,只要理解了传动比eab i 的含义,就可以很快地直接写出行星齿轮的传动比,其关键是掌握几个根据e ab i 的含义推导出来公式,随便多复杂的行星齿轮传动机构,根据这几个公式都能从头写到尾直接把其传动比写出来,而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。
一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1a cxa bxa bcii i =―――――――――――――――――――――――――2 acba bci i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后,不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。
关键是要善于选择中间的一些部件作为参照,使其最后形成都是定轴传动,所以这些参照基本都是一些行星架等例如象论坛中“大模王”兄弟所举的例子:在此例中,要求出eab i =,如果行星架固定不动的话,这道题目就简单多了,就是一定轴传动。
所以我们要想办法把e ab i 变成一定轴传动,所以可以根据公式a cxabxa bci i i =将x 加进去,所以可以得出:e bxe axe abi i i =要想变成定轴传动,就要把x 放到上面去,所以这里就要运用第一个公式1=+c ba abc i i 了,所以)1()1(xbe xae e bxe axe abi i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。
定轴传动的传动比就好办了,直接写出来就可以了。
即)1()1())1(1())1(1()1()1(01ce b d a ec e b dc e a c xbe xae e bx e ax eab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构:已知其各轮的齿数为z 1=100,z 2=101,z 2’ =100 ,z 3=99。
行星齿轮传动比8个公式

行星齿轮传动比8个公式
1.齿轮比计算公式:
齿轮比=-(R+2)/(R+1),其中R为行星轮的齿数。
2.行星轮直径公式:
行星轮的直径可以通过行星轮齿数来计算。
行星轮直径=齿数*模数。
3.太阳轮直径公式:
太阳轮的直径可以通过太阳轮齿数来计算。
太阳轮直径=齿数*模数。
4.行星轮轮齿厚度公式:
行星轮的轮齿厚度可以通过行星轮直径和模数来计算。
行星轮轮齿厚度=2*模数。
5.太阳轮轮齿厚度公式:
太阳轮的轮齿厚度可以通过太阳轮直径和模数来计算。
太阳轮轮齿厚度=2*模数。
6.行星齿轮传动的速度比公式:
速度比=齿数A/齿数B,其中齿数A为太阳轮齿数,齿数B为行星轮齿数。
7.行星齿轮传动的扭矩比公式:
扭矩比=(半径A/半径B)^2,其中半径A为太阳轮半径,半径B为行星轮半径。
8.行星齿轮传动的传动效率公式:
传动效率=输出功率/输入功率。
综上所述,行星齿轮传动的8个常用公式分别是齿轮比计算公式、行星轮直径公式、太阳轮直径公式、行星轮轮齿厚度公式、太阳轮轮齿厚度公式、行星齿轮传动的速度比公式、行星齿轮传动的扭矩比公式和行星齿轮传动的传动效率公式。
这些公式帮助工程师在设计和计算行星齿轮传动时能够准确地确定齿轮比、轮齿尺寸和传动性能等参数,从而提高传动系统的可靠性和效率。
行星轮系传动比的计算

行星轮系传动比的计算
回忆上节内容:定轴轮系传动比的计算公式为:i1k=n1/nk=i1*i2*i3* (i)
定轴轮系的特点是:每个齿轮都是围绕固定的周线旋转,没有自身的公转.
今天我们看以下行星轮系,请同学们思考:行星的运动特点?
对,行星一方面不仅围绕固定的轴线旋转,而且会围绕太阳公转.
下面这张图就是行星轮系,结构和特点我们看一下:
结构:齿圈,太阳轮,行星轮,行星齿轮架
原理:行星齿轮不仅自转,还有围绕太阳轮的公转.
计算传动比:转化法:化行星轮系为定轴轮系
简化结构如下:
太阳轮:n1 z1
行星轮:n2 z2
齿圈:n3 z3
行星架:nh Zh
则传动比计算公式为:ng-nh/nk-nh=(-1)m齿轮G,K之间所有从动轮齿数的连乘积/齿轮G,K之间所有主动轮齿数的连乘积
例题:如图所示为圆锥齿轮组成的差动轮系,Z1=Z2=Z3,求齿轮1,3和行星架H三者转速的关系
解:该轮系为差动轮系,其中齿轮1,3及行星架H的轴线均互相平行或重合,将齿轮1看作主动轮,齿轮3看作从动轮,并设齿轮1的转向为正,通过画箭头,齿轮3的箭头与齿轮1 的相反,故为负,由公式计算:
N1-nh/n3-nh=-z2z3/z1z2=-z3/z1=-1
所以三者转速关系为:
2nh=n1+n3
分析:行星轮系在汽车上的应用:1.汽车后桥差速器
2.行星齿轮机构变速器。
行星齿轮齿比计算

行星齿轮齿比计算行星齿轮齿比是指行星齿轮传动中太阳轮、行星轮和内齿圈之间的齿数比值。
它在机械传动中起着重要的作用,决定了传动的速比和扭矩分配。
下面将从行星齿轮齿比的定义、计算公式、应用以及优缺点等方面进行阐述。
一、行星齿轮齿比的定义行星齿轮传动是一种复杂的机械传动形式,由太阳轮、行星轮和内齿圈组成。
其中,太阳轮位于中间,行星轮围绕太阳轮旋转,内齿圈固定不动。
行星齿轮齿比就是指太阳轮和内齿圈之间的齿数比值,用来描述行星齿轮传动的速比。
二、行星齿轮齿比的计算行星齿轮齿比的计算可以通过以下公式得到:齿比 = (太阳轮齿数 + 内齿圈齿数)/ 太阳轮齿数三、行星齿轮齿比的应用行星齿轮传动由于其结构紧凑、传动效率高等特点,在工业生产中得到了广泛应用。
它常用于汽车变速器、风力发电机、机床等领域。
其中,汽车变速器是行星齿轮传动最常见的应用之一。
通过调整行星齿轮齿比,可以实现不同的速比,从而满足不同速度和扭矩要求。
四、行星齿轮齿比的优缺点行星齿轮传动具有以下优点:1. 结构紧凑,体积小,重量轻,承载能力强;2. 传动效率高,能够实现高速比传动;3. 扭矩分配均匀,能够平稳传动;4. 可以实现多级传动,提高传动比。
然而,行星齿轮传动也存在一些缺点:1. 制造和安装难度较大,加工精度要求高;2. 齿轮接触应力大,耐久性较差;3. 成本较高。
行星齿轮齿比作为行星齿轮传动中的重要参数,对传动性能和应用范围有着重要影响。
通过合理选择和设计行星齿轮齿比,可以满足不同的传动要求。
在实际应用中,需要根据具体情况进行齿轮参数的选择,以实现最佳的传动效果。
齿轮传动比范围

齿轮传动比范围
齿轮传动比是指两个相邻齿轮之间的旋转速度比值。
其计算公式为:传动比 = 驱动齿轮的齿数÷被驱动齿轮的齿数。
齿轮传动比的范围取决于所使用的齿轮类型和数量。
在常见的齿轮传动系统中,一般可以通过组合不同的齿轮来实现各种不同的传动比。
以下是一些常见的齿轮传动比范围:
1. 直齿轮传动:传动比通常在1:1到6:1之间。
2. 锥齿轮传动:传动比通常在1:1到5:1之间。
3. 行星齿轮传动:传动比通常在3:1到10:1之间。
4. 变速箱传动:传动比范围很大,通常可达到20:1或更高。
需要注意的是,齿轮传动比的范围还受到齿轮的尺寸、材料、精度等因素的影响。
在设计齿轮传动系统时,应根据具体情况选择合适的齿轮类型和数量,并进行详细的计算和分析。
行星齿轮传动比的计算公式

行星齿轮传动比计算在《机械原理》上,行星齿轮求解是通过列一系列方程式求解,其求解过程繁琐容易出错,其实用不着如此,只要理解了传动比eab i 的含义,就可以很快地直接写出行星齿轮的传动比,其关键是掌握几个根据e ab i 的含义推导出来公式,随便多复杂的行星齿轮传动机构,根据这几个公式都能从头写到尾直接把其传动比写出来,而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。
一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1 acx a bx abci i i = ―――――――――――――――――――――――――2 a cb abc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后,不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。
关键是要善于选择中间的一些部件作为参照,使其最后形成都是定轴传动,所以这些参照基本都是一些行星架等例如:在此例中,要求出e ab i =,如果行星架固定不动的话,这道题目就简单多了,就是一定轴传动。
所以我们要想办法把e ab i 变成一定轴传动,所以可以根据公式a cx a bx a bci i i =将x 加进去, 所以可以得出:e bx e ax eab i i i =要想变成定轴传动,就要把x 放到上面去,所以这里就要运用第一个公式1=+c ba abc i i 了,所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。
定轴传动的传动比就好办了,直接写出来就可以了。
即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构:已知其各轮的齿数为z 1=100,z 2=101,z 2’ =100 ,z 3=99。
行星齿轮传动比最简计算方法公式法

行星齿轮传动比计算在《机械原理》上,行星齿轮求解就是通过列一系列方程式求解,其求解过程繁琐容易出错,其实用不着如此,只要理解了传动比eab i 的含义,就可以很快地直接写出行星齿轮的传动比,其关键就是掌握几个根据e ab i 的含义推导出来公式,随便多复杂的行星齿轮传动机构,根据这几个公式都能从头写到尾直接把其传动比写出来,而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。
一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1 a cx a bx abci i i = ―――――――――――――――――――――――――2 a cb abc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后,不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。
关键就是要善于选择中间的一些部件作为参照,使其最后形成都就是定轴传动,所以这些参照基本都就是一些行星架等例如象论坛中“大模王”兄弟所举的例子:在此例中,要求出e ab i =?,如果行星架固定不动的话,这道题目就简单多了,就就是一定轴传动。
所以我们要想办法把e ab i 变成一定轴传动,所以可以根据公式a cx a bx a bci i i =将x 加进去, 所以可以得出:e bx e ax eab i i i =要想变成定轴传动,就要把x 放到上面去,所以这里就要运用第一个公式1=+c ba abc i i 了,所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。
定轴传动的传动比就好办了,直接写出来就可以了。
即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构:已知其各轮的齿数为z 1=100,z 2=101,z 2’ =100 ,z 3=99。
行星齿轮机构传动比计算方法

行星齿轮机构传动比计算方法Key words: epicyclic gear train; speed ratio; compute way.随着行星齿轮减速器以及行星齿轮传动在变速箱中的广泛应用,对行星齿轮传动的了解和掌握已成为工程技术人员的必要技能。
但是,对于刚接触行星齿轮传动的工程技术人员来说,行星齿轮传动的速比计算比较不容易理解和掌握。
本文通过对各类参考资料及教科书中的行星齿轮传动速比计算方法进行总结归纳,并针对常用的最具代表性的2K-H型行星齿轮传动,分别用不同方法对其传动特性方程进行了推导论证。
行星齿轮传动或称周转轮系。
根据《机械原理》[1]上的定义,我们可把周转轮系分为差动轮系和行星轮系。
为理解方便,本论文所讨论限于2K-H型周转轮系。
关于行星齿轮传动(周转轮系)的速比计算方法,归纳起来有两大类四种方法,分别为由行星架固定法和力矩法组成的分析法;由速度图解法和矢量法组成的图解法[2]。
矢量图解法一般适用于圆锥齿轮组成的行星齿轮传动,在此不作介绍;下面分别运用其它三种计算方法对2K-H型周转轮系的传动特性方程(1)进行推导。
1-太阳轮 2-行星轮 3-内齿圈 H -行星架 图1 行星齿轮传动Fig 1 Epicyclic gear train0)1(31=++-αωωαωH (1) 结合图1,式中1ω为太阳轮1的转速、Hω为行星架H 转速、3ω为内齿圈3转速、α为内齿圈3与太阳轮1的齿数比即13Z Z =α。
1 行星架固定法机械专业教科书上一般介绍的都是此种方法,也可叫转化机构法。
其理论是一位名叫Wlies 的科学家于1841年提出的,即“一个机构整体的绝对运动并不影响其内部各构件间的相对运动” [3],就像手表的时针、分针、秒针的相对运动不会因带表人的行动而变化。
如图2所示,其中太阳轮1、行星轮2、内齿圈3、行星架H 的转速分别为Hωωωω、、、321。
我们假定整个行星轮系放在一个绕支点O 旋转的圆盘上,此圆盘的转速为 H ω-。
行星齿轮传动比计算

行星齿轮传动比计算在《机械原理》上,行星齿轮求解是通过列一系列方程式求解,其求解过程繁琐容易出错,其实用不着如此,只要理解了传动比e ab i 的含义,就可以很快地直接写出行星齿轮的传动比,其关键是掌握几个根据e ab i =ab i (E 是指固定件,即是固定的太阳轮,A 为主动件,B 为被动件)说明:H abi =(Na-NH)/(Nb-NH),那么如果H 一开始是E ,那么e ab i =(Na-NE)/(Nb-NE)=Na/Nb=ab i NE 的转速为0........由于的含义推导出来公式,随便多复杂的行星齿轮传动机构,根据这几个公式都能从头写到尾直接把其传动比写出来,而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。
一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1a cx a bxa bc i i i = ―――――――――――――――――――――――――2a cb a bc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后,不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。
关键是要善于选择中间的一些部件作为参照,使其最后形成都是定轴传动,所以这些参照基本都是一些行星架等在此例中,要求出e ab i =?,如果行星架固定不动的话,这道题目就简单多了,就是一定轴传动。
所以我们要想办法把e ab i 变成一定轴传动,所以可以根据公式a cx a bx a bci i i =将x 加进去, 所以可以得出:e bx e ax eab i i i =要想变成定轴传动,就要把x 放到上面去,所以这里就要运用第一个公式1=+c ba abc i i 了,所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在e ab i 就变成了两个定轴传动之间的关系式了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
创作编号:BG7531400019813488897SX创作者:别如克*行星轮系传动比的计算【一】能力目标1.能正确计算行星轮系和复合轮系的传动比。
2.熟悉轮系的应用。
【二】知识目标1.掌握转化机构法求行星轮系的传动比。
2.掌握混合轮系传动比的计算。
3.熟悉轮系的应用。
【三】教学的重点与难点重点:行星轮系、混合轮系传动比的计算。
难点:转化机构法求轮系的传动比。
【四】教学方法与手段采用多媒体教学,联系实际讲授,提高学生的学习兴趣。
【五】教学任务及内容一、行星轮系传动比的计算(一)行星轮系的分类若轮系中,至少有一个齿轮的几何轴线不固定,而绕其它齿轮的固定几何轴线回转,则称为行星轮系。
行星轮系的组成:行星轮、行星架(系杆)、太阳轮 (二)行星轮系传动比的计算以差动轮系为例(反转法) 转化机构(定轴轮系) T 的机构1H H W W W -=111W 2H H W W W -=222W 3H H W W W -=333W40=-=H H H H W W W H W 13313113)1(Z Z W W W W W W i H HH H H⋅'-=--== 差动轮系:2个运动行星轮系:3=W ,1310Z Z W W W H H-=--11311+==Z Z W W i H H)(z f W W W W W W iH B H A H BH A HAB=--==对于行量轮系:0=B W∴AHHA H H A H AB i W WW W W i -=-=--=110∴HAB AH i i -=1例12.2:图示为一大传动比的减速器,Z 1=100,Z 2=101,Z 2'=100,Z 3=99。
求:输入件H 对输出件1的传动比i H1解:1,3中心轮;2,2'行星轮;H 行星架 给整个机构(-W H )绕OO 轴转动213223113)1('⋅⋅⋅-=--=Z Z Z Z W W W W i H HH创作编号:BG7531400019813488897SX创作者: 别如克*∵W 3=0∴H H Hi Z Z Z Z W W W 13213210'=--H H i Z Z Z Z W W 13213211'=+-∴HH i i 131100100991011⨯⨯-=100001001009910111111=⨯⨯-==HH i i若Z 1=991001-=H i行星轮系传动比是计算出来的,而不是判断出来的。
(三)复合轮系传动比的计算复合轮系:轮系中既含有定轴轮系又含有行星轮系,或是包含由几个基本行星轮系的复合轮系。
复合轮系传动比的计算:先将混合轮系分解成行星轮系和定轴轮系,然后分别列出传动比计算式,最后联立求解。
1、分析轮系的组成1、2、2'、3——定轴轮系; 1'、4、3'、H ——周转轮系 2、分别写出各轮系的传动比定:213223113)1('-==Z Z Z Z W W i周:311313)1(''''''-=--=Z ZW W W W i H H H3、找出轮系之间的运动关系⎭⎬⎫==''3311W W W W联立求解:32321131111Z Z Z Z Z Z Z Z W W i HH'''''++==(H ,5这一整体)例12.3 电动卷扬机减速器, Z 1=24,Z 2=48,Z 2'=30,Z 3=90 Z 3'=20,Z 4=30,Z 5=80,求i 1H123H42'1232H 14565H 2(a)(b)2H54132'3'解:(1)1,2-2',3,H ——周转轮系;3',4,5——定轴轮系(2)21323113)1(''-=--=Z Z Z Z W W W W i H HH355353'''-==Z ZW W i(3)⎭⎬⎫=='533W W W W H(4)联立 311=H i 若m in /14501r n =min /77.4631145011r i n n H H ≈==二、齿轮系的应用 (一)定轴轮系的应用1、实现大传动比传动2、实现较远距离的传动(减小机构的尺寸和重量)3、实现换向传动4、实现变速传动(汽车齿轮变速箱)5、实现多分路传动(机械式钟表机构) (二)行星轮系和复合轮系的应用1、实现大传动比2、实现运动的合成3、实现运动的分解。
(汽车后桥差减速器)4、实现变速、换向传动5、结构紧凑的大功率传动6、利用行星轮输出的复杂运动满足某些特殊要求。
三、其他新型齿轮传动装置简介 (一)摆线针轮行星传动摆线针轮行星传动的工作原理、输出机构与渐开线少齿差行星传动基本相同,其结构上的差别在于行星轮2改为延长外摆线的等距曲线作齿廓称为摆线轮;用针棒代替中心轮1的轮齿,称为针轮。
摆线针轮行星传动机构具有减速比大(一般可达iHV=9~115,多级可获得更大的减速比),结构紧凑、传动效率高(一般可达90%~94% 左右)、传动平稳等优点。
此外,还有无齿顶相碰和齿廓重叠干涉等问题。
创作编号:BG7531400019813488897SX创作者:别如克*(二)谐波齿轮传动这种传动是借助波发生器迫使相当于行星轮的柔轮产生弹性变形,来实现与钢轮的啮合。
谐波齿轮传动由三个基本构件组成:谐波发生器、刚轮、柔轮。
四、减速器减速器的种类很多。
常用的齿轮及蜗杆减速器按其传动及结构特点,大致可分为三类:(1)齿轮减速器:主要有圆柱齿轮减速器、圆锥齿轮减速器和圆锥—圆柱齿轮减速器三种。
(2)蜗杆减速器:主要有圆柱蜗杆减速器、圆弧齿蜗杆减速器、锥蜗杆减速器和蜗杆—齿轮减速器等。
(3)行星减速器:主要有渐开线行星齿轮减速器、摆线针轮减速器和谐波齿轮减速器等。
(一)常用减速器的主要类型、特点和应用1、齿轮减速器齿轮减速器按减速齿轮的级数可分为单级、二级、三级和多级减速器几种;按轴在空间的相互配置方式可分为立式和卧式减速器两种;按运动简图的特点可分为展开式、同轴式和分流式减速器等。
单级圆柱齿轮减速器的最大传动比一般为8——10,作此限制主要为避免外廓尺寸过大。
若要求i>10时,就应采用二级圆柱齿轮减速器。
二级圆柱齿轮减速器应用于i:8—50及高、低速级的中心距总和为250—400mmm的情况下。
三级圆柱齿轮减速器,用于要求传动比较大的场合。
圆锥齿轮减速器和二级圆锥—圆柱齿轮减速器,用于需要输入轴与输出轴成90~配置的传动中。
因大尺寸的圆锥齿轮较难精确制造,所以圆锥—圆柱齿轮减速器的高速级总是采用圆锥齿轮传动以减小其尺寸,提高制造精度。
齿轮减速器的特点是效率高、寿命长、维护简便,因而应用极为广泛。
2、蜗杆减速器蜗杆减速器的特点是在外廓尺寸不大的情况下可以获得很大的传动比,同时工作平稳、噪声较小,但缺点是传动效率较低。
蜗杆减速器中应用最广的是单级蜗杆减速器。
单级蜗杆减速器根据蜗杆的位置可分为上置蜗杆、下置蜗杆及侧蜗杆三种,其传动比范围一般为i:10—70。
设计时应尽可能选用下置蜗杆的结构,以便于解决润滑和冷却问题。
3、蜗杆—齿轮减速器这种减速器通常将蜗杆传动作为高速级,因为高速时蜗杆的传动效率较高。
它适用的传动比范围为50—130。
(二)减速器传动比的分配由于单级齿轮减速器的传动比最大不超过10,当总传动比要求超过此值时,应采用二级或多级减速器。
此时就应考虑各级传动比的合理分配问题,否则将影响到减速器外形尺寸的大小、承载能力能否充分发挥等。
根据使用要求的不同,可按下列原则分配传动比:(1)使各级传动的承载能力接近于相等;(2)使减速器的外廓尺寸和质量最小;(3)使传动具有最小的转动惯量;(4)使各级传动中大齿轮的浸油深度大致相等。
(三)减速器的结构图示为单级直齿圆柱齿轮减速器的结构,它主要由齿轮(或蜗杆)、轴、轴承、箱体等组成。
箱体必须有足够的刚度,为保证箱体的刚度及散热,常在箱体外壁上制有加强肋。
为方便减速器的制造、装配及使用,还在减速器上设置一系列附件,如检查孔、透气孔、油标尺或油面指示器、吊钩及起盖螺钉等。
小结:1、行星轮系传动比的计算。
2、混合轮系传动比的计算。
3、轮系的应用。
作业与思考:1、“转化机构法”的根据何在?2、摆线针轮行星传动中,针轮与摆线轮的齿数差为多少?3、谐波齿轮减速器与摆线针轮减速器相比有何特点?创作编号:BG7531400019813488897SX创作者:别如克*。
