三次函数的单调区间和极值课件
三次函数

第28关:三次函数专题—全解全析一、定义:定义1、形如的函数,称为“三次函数”(从函数解析式的结构上命名)定义2、三次函数的导数,把叫做三次函数导函数的判别式二、三次函数图象与性质的探究:1、单调性一般地,当时,三次函数在上是单调函数;当时,三次函数在上有三个单调区间(根据两种不同情况进行分类讨论)2、对称中心三次函数是关于点对称,且对称中心为点,此点的横坐标是其导函数极值点的横坐标。
证明:设函数的对称中心为(m,n)。
按向量将函数的图象平移,则所得函数是奇函数,所以化简得:上式对恒成立,故,得,。
所以,函数的对称中心是()。
可见,y=f(x)图象的对称中心在导函数y=的对称轴上,且又是两个极值点的中点,同时也是二阶导为零的点。
3、三次方程根的问题(1)当△=时,由于不等式恒成立,函数是单调递增的,所以原方程仅有一个实根。
(2)当△=时,由于方程有两个不同的实根,不妨设,可知,为函数的极大值点,为极小值点,且函数在和上单调递增,在上单调递减。
此时:①若,即函数极大值点和极小值点在轴同侧,图象均与轴只有一个交点,所以原方程有且只有一个实根。
②若,即函数极大值点与极小值点在轴异侧,图象与轴必有三个交点,所以原方程有三个不等实根。
③若,即与中有且只有一个值为0,所以,原方程有三个实根,其中两个相等。
4、极值点问题若函数f(x)在点x0的附近恒有f(x)≥f(x) (或f(x)≤f(x)),则称函数f(x)在点x0处取得极大值(或极小值),称点x为极大值点(或极小值点)。
当时,三次函数在上的极值点要么有两个。
当时,三次函数在上不存在极值点。
5、最值问题函数若,且,则:;三、三次函数与导数专题:1. 三次函数与导数例题例1. 函数.(1)讨论函数的单调性;(2)若函数在区间(1,2)是增函数,求的取值范围.解:(Ⅰ),的判别式△=36(1-a).(ⅰ)当a≥1时,△≤0,则恒成立,且当且仅当,故此时在R上是增函数.来自QQ群3(ⅱ)当且,时,有两个根:,若,则, 当或时,,故在上是增函数;当时,,故在上是减函数;若,则当或时,,故在和上是减函数;当时,,故在上是增函数;(Ⅱ)当且时,,所以当时,在区间(1,2)是增函数.当时,在区间(1,2)是增函数,当且仅当且,解得.综上,的取值范围是.例 2. 设函数,其中。
三次函数的图象与性质

解:(1)由原式,得 = 3 − 2 − 4 + 4,
∴ ′ = 3 2 − 2 − 4.
1
1
(2)由′ −1 = 0,得 = 2.此时有 = ( 2 − 4)( − 2),
′ = 3 2 − − 4.
4
令′ = 0,得 = 3或 = −1
= −
求导:’ = 3 2 − 3 = 3( + 1)( − 1)
令’ = 0,则 = ±1.
列表:
−∞, −
−
−,
, +∞
’
+
0
−
0
+
增
极大
减
极小
增
y
y
o
−1
x
1
′ 图象
x
o
−1
1
图象
探究二:三次函数 = 3 + 2 + + ( ≠ 0)在R上
2 + 12 ≤ + 6,
由题意可知,1 ≥ −2, 2 ≤ 2,即൝
2 + 12 ≤ 6 − .
解不等式组,得−2 ≤ ≤ 2.
优解:因为′ = 3 2 − 2 − 4的图象是开口向上且过点(0,4)
的抛物线,
4 + 8 ≥ 0,
由条件,得′ −2 ≥ 0, ′ 2 ≥ 0,即ቊ
解:(1) ′ = 3 2 − 3 = 3( 2 − )
当 < 0时,对,有′ > 0,所以 的单调增区间为(−∞, +∞);
当 > 0时,由′ > 0,解得 < − 或 > ;由′ < 0,解得− < <
11三次函数的性质及其简单应用

所以 1 2 c 3c 或 1 2 c 3c 解之得 0 c 7 4 3或c 7 4 3 7 4 3 ) 故所求c的范围是(0, ( 7 4 3, )
例5 设
a为实数,函数 f ( ) 的极值; 在什么范围内取值时,曲线 y f ( x)与 x 轴仅有一个交点 (2)当 2 解:(1) f ( x ) 3 x 2 x 1 1 5 f ( x ) f ( ) a , 极小值是 f (1) a 1 ∴ 的极大值是 3 27 (2)函数
南京一中
孔凡海
由二次函数类比三次函数的图象和性质
二次函数
y ax2 bx c
三次函数
y ax3 bx2 cx d
图象特征 单调性 对称性
a 0 开口向上 a 0 开口向下
单调区间2个 对称轴 x
b 2a
a 0 朝向右上 a 0 朝向右下
单调区间1个或3个
所以
y ax3 bx2 cx d (a ≠0),函数的对称中心是(
b b ,f ( ) )。 3a 3a
3 2 f ( x ) ax bx cx d (a ≠0是中心对 ) 性质3:函数 b b , f ( ) )。 称图形,其对称中心是( 3a 3a
尽管如此,我们还要进一步加强对三次函数 的单调性、极值、对称性、图象变化规律、切线 方程等性质的研究,这也有助于提高知识的系统 性以及对三次函数的理解水平,拓宽解题思路。
解:(I)(b 1) 4c 3 2 2 (II)因为 F ( x) f ( x) g( x) x 2bx (b c) x bc ,2 3 x 4bx b 2 c 0 所以F(x)的导方程为:
2024版《函数的单调性》全市一等奖完整版PPT课件

利用单调性证明不等式
1 2
构造函数 根据不等式的特点,构造一个与不等式相关的函 数。
判断函数单调性 通过求导或差分等方法判断所构造函数的单调性。
3
利用单调性证明不等式 根据函数的单调性,结合不等式的性质,证明不 等式成立。
2024/1/29
18
利用单调性解决实际应用问题
要点一
建立数学模型
要点二
判断函数单调性
2024/1/29
21
导数与微分在函数单调性研究中的应用
导数大于零的区间内函数单调 增加,导数小于零的区间内函 数单调减少。
2024/1/29
导数等于零的点为函数的驻点, 需要进一步判断其左右两侧导 数的符号来确定该点的单调性。
微分的概念可以应用于函数单 调性的研究,通过微分可以分 析函数的局部变化率,进而判 断函数的单调性。
14
指数函数与对数函数
对数函数 $y = log_a x$($a > 0, a neq 1$)的单调 性
当 $0 < a < 1$ 时,函数在 $(0, +infty)$ 上单调递减。
当 $a > 1$ 时,函数在 $(0, +infty)$ 上单调递增。
指数函数与对数函数的图像关于直线 $y = x$ 对称,即 互为反函数。
2024/1/29
19
05
函数单调性与其他知识点关联
2024/1/29
20
函数奇偶性与周期性对单调性影响
奇函数在对称区间上的单调性相 同,偶函数在对称区间上的单调
性相反。
周期函数在一个周期内的单调性 与整体单调性一致,可以通过研 究一个周期内的单调性推断整体
的单调性。
第37讲 三次函数的图像与性质(学生版)

第37讲三次函数的图像与性质三次函数f(x)=ax3+bx2+cx+d(a≠0)具有丰富的性质,利用导数研究这些性质,其研究的过程与方法具有普遍性,一般性和有效性,可以迁移到其他函数的研究中.本专题主要研究三次函数的单调性,极值,最值,对称性等,并在研究的过程中体会数形结合,分类与整合,化归与转化等思想方法.1.已知函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R),设直线l1,l2分别是曲线y=f(x)的两条不同的切线,若函数f(x)为奇函数,且当x=1时f(x)有极小值为-4.①求a,b,c,d的值;②若直线l3亦与y=f(x)相切,且三条不同的直线l1,l2,l3交于点G(m,4),求实数m的取值范围.2.已知函数f(x)=x3-tx2+1,求证:对任意实数t,函数f(x)的图像总存在两条切线相互平行.3.已知函数32()3f x x x ax =-+()a ∈R ,()|()|g x f x =.(1)求以(2,(2))P f 为切点的切线方程,并证明此切线恒过一个定点;(2)若()g x kx ≤对一切[0,2]x ∈恒成立,求k 的最小值()h a 的表达式;(3)设0a >,求()y g x =的单调增区间.4.已知函数f(x)=2x3-ax2+b.(1)讨论f(x)的单调性;(2)是否存在a,b,使得f(x)在区间[0,1]的最小值为-1且最大值为1?若存在,求出a,b的所有值;若不存在,说明理由.5.已知函数32()1(0,)f x x ax bx a b =+++>∈R 有极值,且导函数'()f x 的极值点是()f x 的零点.(极值点是指函数取极值时对应的自变量的值)(1)求b 关于a 的函数关系式,并写出定义域;(2)证明:33b a >;(3)若(),'()f x f x 这两个函数的所有极值之和不小于72-,求a 的取值范围.。
新湘教版高中数学选择性必修第二册1.3.3三次函数的性质:单调区间和极值

题型探究·课堂解透
提醒1 求三次函数的最值 例1 已知函数f(x)=x3-x2+ax+b,若曲线y=f(x)在(0,f(0))处的切 线方程为y=-x+1. (1)求a,b的值; (2)求函数y=f(x)在[-2,2]上的最小值.
解析: (1)由已知可得f(0)=b=1. 又f′(x)=3x2-2x+a,所以f′(0)=a=-1. (2)由(1)可知f(x)=x3-x2-x+1,f′(x)=3x2-2x-1, 令f′(x)>0,解得x<-13或x>1, 所以f(x)在[-2,-13)和[1,2]上单调递增,在[13,1)上单调递减. 又因为f(-2)=-9,f(1)=0,所以函数y=f(x)在[-2,2]上的最小值为-9.
1.3.3 三次函数的性质:单调区间和极值
新知初探·课前预习
题型探究·课堂解透
新知初探·课前预习
教材要点 要点一 最值的概念❶ 一般地,如果在区间[a,b]上函数y=f(x)的图象是一条_连__续_不__断__的曲 线,那么它必有最大值和最小值.
批注❶ (1)给定的区间必须是闭区间,y=f(x)的图象在开区间上虽然连续不 断,但不能保证有最大值或最小值. (2)在闭区间上的每一点必须连续,即在闭区间上有间断点也不能保 证y=f(x)有最大值和最小值.
+
0
-
0+
f(x) 3
↗
16 3
↘
-16
3
↗
-3
∴f(x)min=f(2)=-136,f(x)max=f(-2)=136.
提醒2 由函数的最值确定参数的值
例2 设23<a<1,函数f(x)=x3-32ax2+b在区间[-1,1]上的最大值为1,最 小值为- 6,求函数的解析式.
《函数的单调性与极值》课件2 (北师大版选修2-2)

例3 (2)
讨论函数 f ( x) ( x 1) x 的单调性
2 3
解 (1)该函数的定义域为( , )
2 2 1 5x 2 / 3 3 f ( x ) x ( x 1) x 1 3 3x 3 2 / 令 f ( x ) 0得 x , 显然 x =0为f ( x )的不可导点, 5 2 于是 x 0, x 分定义区间为三个子区间 5 2 2 ( , 0), (0, ), ( , ) 5 5
/
( x 0)
所以f ( x)在区间[0, )内单调增加, 又f (0) 0 因此, 当x 0时, 恒有f ( x) f (0), x 即 ln(1 x) 1 x
二、函数的极值
定义: 在其中当 (1) 时,
则称
称
为
的极大点 ,
为函数的极大值 ;
(2)
则称 称
为
的极小点 , 为函数的极小值 .
中值定理条件, 因此应有
即
因为
故
x ln(1 x ) 证法 2 证明不等式 1 x
x 设函数f ( x) ln(1 x) , 1 x 因为f ( x)在[0, )上连续, 当x 0时, 1 1 x x x f ( x) 0, 2 2 1 x (1 x) (1 x)
x f/(x) f(x)
( , -
7 ) 6
7 6
7 7 ( , ) 6 10
7 10
7 ( , ) 10
+
不可导 极大值
-
0 极小值
+
从表中可知:
7 7 x1 是极大值点,极大值f ( ) 0 6 6 7 7 7 3 x2 是极小值点,极小值f ( ) 980 10 10 50 7 7 单调增加区间(-, ),( , ) 6 10 7 7 单调减少区间( , )。 6 10
三次函数图像与性质(解析版)

专题2-2三次函数图像与性质【题型1】求三次函数的解析式【题型2】三次函数的单调性问题【题型3】三次函数的图像【题型4】三次函数的最值、极值问题【题型5】三次函数的零点问题【题型6】三次函数图像,单调性,极值,最值综合问题【题型7】三次函数对称中心【题型8】三次函数的切线问题【题型9】三次函数根与系数的关系1/342/34【题型1】求三次函数的解析式(1)一般式:()³²f x ax bx cx d =+++(a ≠0)(2)交点式:()123()()()f x a x x x x x x =---(a ≠0)1.若三次函数()f x 满足()()()()00,11,03,19f f f f ''====,则()3f =()A .38B .171C .460D .965【解析】待定系数法,求函数解析式设()³²f x ax bx cx d =+++,则()232f x ax bx c '=++,由题意可得:()()()()0011031329f d f a b c d f c f a b c ⎧==⎪=+++=⎪⎨==⎪⎪=+'=⎩'+,解得101230a b c d =⎧⎪=-⎪⎨=⎪⎪=⎩,则()3210123f x x x x =-+,所以()32310312333171f =⨯-⨯+⨯=.【题型2】三次函数的单调性问题三次函数是高中数学中的一个重要内容,其考点广泛且深入,主要涉及函数的性质、图像、最值、零点以及与其他函数的综合应用等方面。
以下是对三次函数常见考点的详细分析:1.三次函数的定义与形式∙定义:形如f (x )=ax 3+bx 2+cx +d (其中a ≠=0)的函数称为三次函数。
∙形式:注意系数a ,b ,c ,d 的作用,特别是a 的正负决定了函数的开口方向(a >0开口向上,a <0开口向下)。
三次函数性质总结.
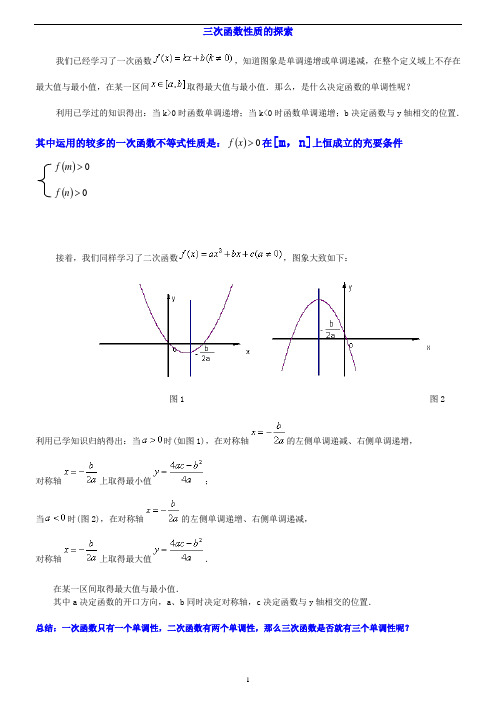
三次函数性质的探索我们已经学习了一次函数,知道图象是单调递增或单调递减,在整个定义域上不存在最大值与最小值,在某一区间取得最大值与最小值.那么,是什么决定函数的单调性呢?利用已学过的知识得出:当k>0时函数单调递增;当k<0时函数单调递增;b决定函数与y轴相交的位置.其中运用的较多的一次函数不等式性质是:()0>f在[m,n]上恒成立的充要条件x()0>fm()0>fn接着,我们同样学习了二次函数,图象大致如下:图1 图2利用已学知识归纳得出:当时(如图1),在对称轴的左侧单调递减、右侧单调递增,对称轴上取得最小值;当时(图2),在对称轴的左侧单调递增、右侧单调递减,对称轴上取得最大值.在某一区间取得最大值与最小值.其中a决定函数的开口方向,a、b同时决定对称轴,c决定函数与y轴相交的位置.总结:一次函数只有一个单调性,二次函数有两个单调性,那么三次函数是否就有三个单调性呢?三次函数专题一、定义:定义1、形如32(0)y ax bx cx d a =+++≠的函数,称为“三次函数”(从函数解析式的结构上命名)。
定义2、三次函数的导数232(0)y ax bx c a '=++≠,把2412b ac ∆=-叫做三次函数导函数的判别式。
由于三次函数的导函数是二次函数,而二次函数是高中数学中的重要内容,所以三次函数的问题,已经成为高考命题的一个新的热点和亮点。
特别是文科。
系列探究1:从最简单的三次函数3x y =开始反思1:三次函数31y x =+的相关性质呢? 反思2:三次函数31y x =-+的相关性质呢? 反思3:三次函数()311y x =-+的相关性质呢?(2012天津理)(4)函数22)(3-+=x x f x在区间(0,1)内的零点个数是 B (A )0 (B )1 (C )2 (D )3系列探究2:探究一般三次函数)0()(23>+++=a d cx bx ax x f 的性质:先求导2()32(0)f x ax bx c a '=++>1.单调性:(1)若22120b ac =-≤△(),此时函数()f x 在R 上是增函数;(2)若22120b ac =->△(),令2()320f x ax bx c '=++=两根为12,x x 且12x x <,则()f x 在12(,),()x x -∞+∞上单调递增,在12(,)x x 上单调递减。
三次函数及其简单性质

26.(12 浙江理 17)设 a R ,若 x 0 时,均有[(a 1)x 1](x2 ax 1) 0 ,则 a ___________.( 3 ) 2
27(. 17
江苏理
11)已知函数
f
(x)
x3
2x
ex
1 ex
,其中 e 是自然对数的底数.若
f
(a 1)
2x, x a
②若 f (x) 无最大值,则实数 a 的取值范围是_______________.( (,1) )
23.(15 安徽理 15)设 x3 ax b 0 ,其中 a , b 均为实数.下列条件中,使得该三次方程仅有一个实根
的是_________________.(写出所有正确条件的编号)(①③④⑤)
A. [2,10]
B. [1,8]
C. [2,2]
D. [0,9]
16.已知函数 f (x) (x a)3 3x a(a 0) 在[1, b] 上的值域为[2 2a,0] ,则 b 的取值范围是( )
A. [0,3]
B. [0,2]
C. [2,3]
D. (1,3]
17.(11 天津文 20)函数 f (x) ax3 3 x2 1(a 0) ,当 x [ 1 , 1 ] 时 f (x) 0 ,则 a 的范围是( )
不可能的是···········································································( )
A. S 1且 T 0
B. S 1且 T 1
C. S 2且 T 2
D. S 2且 T 3
三次函数的图象与性质课件-2025届高三数学一轮复习

THANK YOU
(
).
. > 0, < 0, > 0, > 0
√
. > 0, < 0, < 0, > 0
. < 0, < 0, > 0, > 0
. > 0, > 0, > 0, < 0
y
P
x2
O
x1
x
【点拨】当三次函数有两个极值点 Δ > 0 时,若a > 0,则三次函数曲线形状为
单减, x1, x2 单增
极小值 f (x1)
极大值 f (x2)
Байду номын сангаас
0
y
o
y
x o
在上单调递减
无极值
f ( x) 的图像
对称中心
b
3a
(− ,f −
b
3a
x
)(即拐点,其横坐标为二阶导函数零点)
总结:
1.三次函数的单调性由a来决定; Δ > 0
若a > 0,则三次函数曲线形状为“N字型”;
若a < 0,则三次函数曲线形状为“反N字型”
2 + =0
∆= 4 2 −
f ( x)的单调性
12
f ( x) 的极值
a0
a0
0
0
y
y
0
y
y
x1
x
o x1
x2
o x
−∞, x1 , x2,+∞
o
在上单调递增
单增, x1, x2 单减
极大值 f (x1)
极小值 f (x2)
湘教版高中数学选修1-1第3章 3.3.3 三次函数的性质:单调区间和极值

3.3.3三次函数的性质:单调区间和极值[读教材·填要点]设F(x)=ax3+bx2+cx+d(a≠0),则F′(x)=3ax2+2bx+c是二次函数,可能有以下三种情形:(1)函数F′(x)没有零点,F′(x)在(-∞,+∞)上不变号.①若a>0,则F′(x)恒正,F(x)在(-∞,+∞)上递增;②若a<0,则F′(x)恒负,F(x)在(-∞,+∞)上递减.(2)函数F′(x)有一个零点x=w.①若a>0,则F′(x)在(-∞,w)∪(w,+∞)上恒正,F(x)在(-∞,+∞)上递增;②若a<0,则F′(x)在(-∞,w)∪(w,+∞)上恒负,F(x)在(-∞,+∞)上递减.(3)函数F′(x)有两个零点x=u和x=v,设u<v.①若a>0,则F′(x)在(-∞,u)和(v,+∞)上为正,在(u,v)上为负;F(x)在(-∞,u)上递增,在(u,v)上递减,在(v,+∞)上递增.可见F(x)在x=u处取极大值,在x=v处取极小值.②若a<0,则F′(x)在(-∞,u)和(v,+∞)上为负,在(u,v)上为正;F(x)在(-∞,u)上递减,在(u,v)上递增,在(v,+∞)上递减.可见F(x)在x=u处取极小值,在x=v处取极大值.[小问题·大思维]1.在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,想一想,在[a,b]上一定存在最值和极值吗?在区间(a,b)上呢?提示:在区间[a,b]上一定有最值,但不一定有极值.如果函数f(x)在[a,b]上是单调的,此时f(x)在[a,b]上无极值;如果f(x)在[a,b]上不是单调函数,则f(x)在[a,b]上有极值;当f(x)在(a,b)上为单调函数时,它既没有最值也没有极值.2.若函数y=f(x)的图象是一条连续不断的曲线,且在区间[a,b]上有且只有一个极小值点,那么该极小值是否是函数的最小值?提示:借助图象可知,该极小值就是函数的最小值.求下列函数的单调区间和极值.(1)y=2x3+6x2-18x+3;(2)y=-x3+12x+6.[自主解答](1)函数的定义域为R.y′=6x2+12x-18=6(x+3)(x-1),令y′=0,得x=-3或x=1.当x变化时,y′,y的变化情况如下表:当x=-3时,函数有极大值,且y极大值=57;当x=1时,函数有极小值,且y极小值=-7.(2)y′=-3x2+12=-3(x+2)(x-2),令y′=0,则x1=-2,x2=2.当x变化时,y′,y的变化情况如下表:∴函数f(x)的单调减区间为(-∞,-2),(2,+∞);单调增区间为(-2,2).当x=-2时,y有极小值,且y极小值=f(-2)=-10;当x=2时,y有极大值,且y极大值=f(2)=22.(1)求多项式函数的单调区间,关键是求出f′(x)后,解不等式f′(x)>0和f′(x)<0.(2)单调区间可以是开区间,如果区间端点在定义域内,也可写成闭区间.1.求函数y=8x3-12x2+6x+1的极值.解:y′=24x2-24x+6=6(4x2-4x+1),令y′=6(4x2-4x+1)=0,解得x1=x2=1 2.当x变化时,y′,y的变化情况如表所示:所以此函数无极值.求下列各函数的最值.(1)f (x )=-x 3+x 2+x +1,x ∈[-3,2]; (2)f (x )=x 3-3x 2+6x -2,x ∈[-1,1]. [自主解答] (1)f ′(x )=-3x 2+2x +1, 令f ′(x )=-(3x +1)(x -1)=0,得 x =-13或x =1.当x 变化时f ′(x )及f (x )的变化情况如下表:∴当x =2时,f (x )取最小值-1; 当x =-3时,f (x )取最大值34.(2)f ′(x )=3x 2-6x +6=3(x 2-2x +2)=3(x -1)2+3, ∵f ′(x )在[-1,1]内恒大于0, ∴f (x )在[-1,1]上为增函数. 故x =-1时,f (x )最小值=-12; x =1时,f (x )最大值=2.即f (x )的最小值为-12,最大值为2.求函数f (x )在[a ,b ]上的最大值和最小值的步骤:(1)求函数的导数f ′(x );(2)求方程f ′(x )=0的全部实根x 0,且x 0∈[a ,b ];(3)求最值,有两种方式:①是将f (x 0)的值与f (a ),f (b )比较,确定f (x )的最大值与最小值;②是判断各分区间上的单调性,然后求出最值.2.求函数f (x )=4x 3+3x 2-36x +5在区间[-2,2]上的最大值和最小值. 解:f ′(x )=12x 2+6x -36=6(2x 2+x -6), 令f ′(x )=0,解得x 1=-2,x 2=32.又f (-2)=57,f ⎝⎛⎭⎫32=-1154,f (2)=-23, ∴函数f (x )的最大值为57,最小值为-1154.设f (x )=-13x 3+12x 2+2ax .(1)若f (x )在⎝⎛⎭⎫23,+∞上存在单调递增区间,求a 的取值范围; (2)当0<a <2时,f (x )在[1,4]上的最小值为-163,求f (x )在该区间上的最大值.[自主解答] (1)由f ′(x )=-x 2+x +2a =-⎝⎛⎭⎫x -122+14+2a , 当x ∈⎣⎡⎭⎫23,+∞时,f ′(x )的最大值为f ′⎝⎛⎭⎫23=29+2a ;令29+2a >0,得a >-19. 所以,当a ∈⎝⎛⎭⎫-19,+∞时,f (x )在⎝⎛⎭⎫23,+∞上存在单调递增区间. (2)令f ′(x )=0,得两根x 1=1-1+8a2, x 2=1+1+8a2.所以f (x )在(-∞,x 1),(x 2,+∞)上单调递减,在(x 1,x 2)上单调递增.当0<a <2时,有x 1<1<x 2<4,所以f (x )在[1,4]上的最大值为f (x 2),又f (4)-f (1)=-272+6a <0, 即f (4)<f (1).所以f (x )在[1,4]上的最小值为f (4)=8a -403=-163. 得a =1,x 2=2,从而f (x )在[1,4]上的最大值为f (2)=103.(1)f (x )在区间I 上为增函数⇒f ′(x )≥0在区间I 上恒成立,f (x )在区间I 上为减函数⇒f ′(x )≤0在区间I 上恒成立.(2)由函数的最值来确定参数的问题是利用导数求函数最值的逆向运用,解题时一般采用待定系数法,列出含参数的方程或方程组,从而求出参数的值,这也是方程思想的应用.3.已知函数f (x )=x 3+ax 2+bx +5,曲线y =f (x )在点P (1,f (1))处的切线方程为y =3x +1.(1)求a ,b 的值;(2)求y =f (x )在[-3,1]上的最大值.解:(1)依题意可知点P (1,f (1))为切点,代入切线方程y =3x +1可得,f (1)=3×1+1=4,∴f (1)=1+a +b +5=4,即a +b =-2, 又由f (x )=x 3+ax 2+bx +5得, 又f ′(x )=3x 2+2ax +b ,而由切线y =3x +1的斜率可知f ′(1)=3, ∴3+2a +b =3,即2a +b =0,由⎩⎪⎨⎪⎧ a +b =-2,2a +b =0.解得⎩⎪⎨⎪⎧a =2,b =-4,∴a =2,b =-4.(2)由(1)知f (x )=x 3+2x 2-4x +5, f ′(x )=3x 2+4x -4=(3x -2)(x +2), 令f ′(x )=0,得x =23或x =-2.当x 变化时,f (x ),f ′(x )的变化情况如下表:∴f (x )的极大值为f (-2)=13,极小值为f ⎝⎛⎭⎫23=9527, 又f (-3)=8,f (1)=4,∴f (x )在[-3,1]上的最大值为13.已知f (x )=x 3+ax 2+bx +c 在x =1与x =-2时都取得极值. (1)求a ,b 的值;(2)若x ∈[-3,2]时都有f (x )>2c -12恒成立,求c 的取值范围.[巧思] 解决不等式恒成立问题,大多可用函数的观点来审视,用函数的有关性质来处理,而导数是研究函数性质的有力工具,因而常将不等式f (x )>g (x )(f (x )<g (x ))恒成立问题转化为F (x )=f (x )-g (x )>0(F (x )=f (x )-g (x )<0)恒成立问题,再用导数方法探讨F (x )的单调性及最值.[妙解] (1)f ′(x )=3x 2+2ax +b ,由题意,得⎩⎪⎨⎪⎧ f ′(1)=0,f ′(-2)=0,即⎩⎪⎨⎪⎧3+2a +b =0,12-4a +b =0,解得⎩⎪⎨⎪⎧a =32,b =-6.(2)由(1)知f ′(x )=3x 2+3x -6. 令f ′(x )=0得x =-2或x =1.当x 变化时,f ′(x ),f (x )的变化情况如表所示:∴f (x )在[-3,2]上的最小值为c -72.即2c -12<c -72,∴c <-3,∴c 的取值范围为(-∞,-3).1.下面四幅图都是在同一坐标系中某三次函数及其导函数的图象,其中一定不.正确的序号是( )A .①③B .③④C .②③④D .②④解析:根据函数的单调性与其导函数函数值之间的关系,易得③④一定不正确. 答案:B2.函数f (x )=2x 3-9x 2+12x +1的单调递减区间为( ) A .(1,2) B .(2,+∞)C .(-∞,1)D .(-1,+∞),(2,+∞)解析:f ′(x )=6x 2-18x +12, 令f ′(x )<0,得1<x <2. 答案:A3.函数f (x )=x 3-3x (|x |<1)( ) A .有最大值,但无最小值 B .有最大值,也有最小值 C .无最大值,但有最小值 D .既无最大值,也无最小值解析:f ′(x )=3x 2-3=3(x +1)(x -1),当x ∈(-1,1)时,f ′(x )<0,所以f (x )在(-1,1)上是单调递减函数,无最大值和最小值.答案:D4.若函数y =-x 3+6x 2+m 的极大值等于13,则实数m 等于________.解析:y ′=-3x 2+12x ,由y ′=0,得x =0或x =4,容易得出当x =4时函数取得极大值,所以-43+6×42+m =13,解得m =-19.答案:-195.若f (x )=ax 3+bx 2+cx +d (a >0)是R 上的增函数,则a ,b ,c 的关系式为________.解析:f ′(x )=3ax 2+2bx +c ≥0在R 上恒成立,则⎩⎪⎨⎪⎧a >0,Δ=4b 2-12ac ≤0,从而解得a >0,且b 2≤3ac .答案:a>0且b2≤3ac6.已知函数f(x)=2x3-6x2+a在[-2,2]上有最小值-37,求a的值及f(x)在[-2,2]上的最大值.解:f′(x)=6x2-12x=6x(x-2),由f′(x)=0得x=0,或x=2.当x变化时,f′(x),f(x)变化情况如下:∴当x=-2时,f(x)min=-40+a=-37,得a=3.故x=0时,f(x)最大值是3.一、选择题1.函数y=f(x)在[a,b]上()A.极大值一定比极小值大B.极大值一定是最大值C.最大值一定是极大值D.最大值一定大于极小值解析:由最值与极值的概念可知,D选项正确.答案:D2.函数y=x3-3x+3在区间[-3,3]上的最小值为()A.1B.5C.12 D.-15解析:y′=3x2-3,令y′=0,得3x2-3=0,∴x=1或x=-1.当-1<x<1时,y′<0;当x>1或x<-1时,y′>0,∴y极小值=1,y极大值=5.又当x=-3时,y=-15;当x=3时,y=21,∴y min=-15.答案:D3.若x=-2与x=4是函数f(x)=x3+ax2+bx的两个极值点,则有()A .a =-2,b =4B .a =-3,b =-24C .a =1,b =3D .a =2,b =-4解析:f ′(x )=3x 2+2ax +b ,依题意有-2和4是方程3x 2+2ax +b =0的两个根,所以有-2a 3=-2+4,b3=-2×4,解得a =-3,b =-24.答案:B4.函数f (x )=x 3-3x 2-9x +k 在区间[-4,4]上的最大值为10,则其最小值为( ) A .-10 B .-71 C .-15D .-22解析:f ′(x )=3x 2-6x -9=3(x -3)(x +1). 由f ′(x )=0得x =3或x =-1. 又f (-4)=k -76,f (3)=k -27, f (-1)=k +5,f (4)=k -20. 由f (x )max =k +5=10,得k =5, ∴f (x )min =k -76=-71. 答案:B 二、填空题5.函数f (x )=x 3-15x 2-33x +6的单调递减区间为________. 解析:f ′(x )=3x 2-30x -33=3(x -11)(x +1), 令f ′(x )<0,得-1<x <11. ∴f (x )的单调递减区间为(-1,11). 答案:(-1,11)6.若函数f (x )=x 3+x 2+mx +1是R 上的单调函数,则实数m 的取值范围是________. 解析:f ′(x )=3x 2+2x +m ,∵f (x )在R 上是单调函数, ∴Δ=4-12m ≤0,即m ≥13.答案:⎣⎡⎭⎫13,+∞7.若a >0,b >0,且函数f (x )=4x 3-ax 2-2bx +2在x =1处有极值,则ab 的最大值等于________.解析:∵f ′(x )=12x 2-2ax -2b , ∴Δ=4a 2+96b >0,又x =1是极值点, ∴f ′(1)=12-2a -2b =0,即a +b =6.ab ≤(a +b )24=9,当且仅当a =b 时“=”成立,∴ab 的最大值为9.答案:98.函数f (x )=x 3-12x 2-2x +5,对任意x ∈[-1,2]都有f (x )>m ,则实数m 的取值范围是________.解析:由f ′(x )=3x 2-x -2=0,得x =-23或x =1,由题意知只要f (x )min >m 即可, 易知f (x )min =f (1)=72,所以m <72.答案:⎝⎛⎭⎫-∞,72 三、解答题9.求下列各函数的最值: (1)f (x )=-x 3+3x ,x ∈[-3,3]; (2)f (x )=x 2-54x (x <0).解:(1)f ′(x )=3-3x 2=3(1-x )(1+x ). 令f ′(x )=0,得x =1或x =-1,当x 变化时,f ′(x ),f (x )变化情况如下表:又因为f (x )在区间端点处的函数值为f (-3)=0, f (3)=-18,所以f (x )max =2,f (x )min =-18. (2)f ′(x )=2x +54x 2.令f ′(x )=0,得x =-3. 当x 变化时,f ′(x ),f (x )的变化情况如下表:所以x 故f (x )的最小值为f (-3)=27,无最大值.10.已知函数f (x )=x 3+ax 2+bx +c 在x =-23与x =1处都取得极值.(1)求a ,b 的值及函数f (x )的单调区间.(2)若x ∈[-1,2],不等式f (x )<c 2恒成立,求c 的取值范围. 解:(1)由f (x )=x 3+ax 2+bx +c ,得f ′(x )=3x 2+2ax +b ,因为f ′(1)=3+2a +b =0,f ′⎝⎛⎭⎫-23=43-43a +b =0,解得a =-12,b =-2, 所以f ′(x )=3x 2-x -2=(3x +2)(x -1),当x 变化时,f ′(x ),f (x )的变化情况如表: 单调递增 单调递减 单调递增所以函数f (x )的递增区间为⎝⎭⎫-∞,-23和(1,+∞); 递减区间为⎝⎛⎭⎫-23,1. (2)由(1)知,f (x )=x 3-12x 2-2x +c ,x ∈[-1,2],当x =-23时,f ⎝⎛⎭⎫-23=2227+c 为极大值,因为f (2)=2+c ,所以f (2)=2+c 为最大值.要使f (x )<c 2(x ∈[-1,2])恒成立,只需c 2>f (2)=2+c , 解得c <-1或c >2.故c 的取值范围为(-∞,-1)∪(2,+∞).。
三次函数的单调区间和极值课件

-6 -6
-8 -8
5
10
18
结论:
1. 三次函数没有极值或极大值小于零或 极小值大于零时图象与x轴交点只有一个;
2. 三次函数极大值等于零或极小值等于 零时图象与x轴交点有二个;
3. 三次函数极大值大于零且极小值小于 零时图象与x轴交点有三个.
19
例 2:已知函数 a R, f (x) 2x3 3(a 1)x2 6ax.
14
(3)当 a1时, x( ,a)(1, ),f'(x)0 x(a,1)f'(x)0 f(x)单调增(区 ,a)和 间 (1, ), f(x)单调减 (a,区 1)
注意:含参数三次函数单调区间分类的讨论标准 其导函数二次函数对应的方程是否有实根, 若有实根比较两实根的大小
分类整合, 转化与化归
9
三次函数与其导函数图象之间的关系
减区间:(-∞, x1), (x2, +∞)
增区间:(x1, x2)
减区间: (-∞, +∞)
减区间: (-∞, +∞)
10
思考根据上表三次函数的单调性与极值有哪 些重要的结论?
11
热身训练:已知函数 f (x) x3 3x2 ax 2 (1)函数 f(x)在 R 上单调函数,求实数 a 的取值范围
第4章 4.3.3 三次函数的性质: 单调区间和极值
莆田华侨中学数学组 何高萍 高二(6)班
1
引例:指出下列函数的单调区间和极值点, 并画出函数及对应导函数的草图 (1) f (x) 2x3 3x2; (2) f (x) 3x3 6x2 4x 5; (3) f (x) x3 2x2 2x 7; (4) f (x) x3 3x2 9x
三次函数的性质;单调区间和极值资料

变式训练:
1.讨论函数f(x)=x3 +ax+5的增减性。
2.已知f(x)=x3 +ax2 +(a+6)x+1有极大值和极小值,
则a的取值范围为( D)
A.-1<a<2 B.-3<a<6 C.a<-1或a>2 D.a<-3或a>6
3.已知函数f (x) x3 ax在R上递增, 则a的取值范围是 _______ .
9
三次函数图象与x轴交点问题
三次函数f(x)=ax3 +bx2 +cx+d(a 0)图象的性质揭示了 一元三次方程ax3 +bx2 +cx+d=0(a 0)根的实质. 由f(x)的图象的性质不难看出: 方程实数根的个数即f(x)图象与轴的交点个数.
三次函数f(x)的导数F '(x) 3ax2 2bx c(a 0)
1.若=4b2 -12ac 0即b2 3ac,则三次函数f(x)无极值, 图象在R上为单调函数,其图象与x轴有且有一个交点. 即方程ax3 +bx2 +cx+d=0(a 0)有且有一个实数根.
a>0
a<0
10
2.若=4b2 -12ac>0即b2>3ac,则三次函数f(x)有2个极值点x1x2 , 不妨设极大值为f(x1),极小值f(x2 ),其图象与x轴交点情况 取决于2个极值点与x轴的关系:
14
变式训练
1.方程x3-6x2+9x-4=0的实数根个数是( B ) A.3 B.2 C.1 D.0
2.设a为实数,函数f (x) x3 x2 x a. (1)求f (x)的极值;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三次函数与其导函数图象之间的关系
减区间:(-∞, x1), (x2, +∞)
增区间:(x1, x2)
减区间: (-∞, +∞)
减区间: (-∞, +∞)
10
思考根据上表三次函数的单调性与极值有哪 些重要的结论?
11
热身训练:已知函数 f (x) x3 3x2 ax 2 (1)函数 f(x)在 R 上单调函数,求实数 a 的取值范围
个不同的交点,求 m 的取值范围;
函数与方程, 数形结合
21
f(x)与g(x)的
图象有交点
f(x)=g(x) 有实数根
F(x)=f(x)g(x)有零点
22
课堂小结
知识技能
思想方法
成功体验
23
知识技能: 1、会利用导数求三次函数单调区间和极值 注:含参数三次函数单调性分类标准其导函数 二次函数对应的方程的实根是否存在,若存在 判断两根的大小
-6 -6
-8 -8
5
10
18
结论:
1. 三次函数没有极值或极大值小于零或 极小值大于零时图象与x轴交点只有一个;
2. 三次函数极大值等于零或极小值等于 零时图象与x轴交点有二个;
3. 三次函数极大值大于零且极小值小于 零时图象与x轴交点有三个.
19
例 2:已知函数 a R, f (x) 2x3 3(a 1)x2 6ax.
2. 方程 exx2=m 有且只有一根,求 m 的取值范围. 若 x<2 呢?
25
谢谢指导
26
第4章 4.3.3 三次函数的性质: 单调区间和极值
莆田华侨中学数值点, 并画出函数及对应导函数的草图 (1) f (x) 2x3 3x2; (2) f (x) 3x3 6x2 4x 5; (3) f (x) x3 2x2 2x 7; (4) f (x) x3 3x2 9x
(2)函数 f(x)有极值,求实数 a 的取
值范围
12
解f'(: x)3x26xa
令f '(x)0
(1)3 61a 20
解得 :a3
(2)3 6 1a 2 0
解得 :a3
13
例 2:已知函数 a R, f (x) 2x3 3(a 1)x2 6ax. (1)求函数 f (x) 的单调区间;
变式:当 a=-2 时, (1)若曲线 y=f(x)与 直线 y=m 有三个不同 的交点,求 m 的取值
范围; f(x)2x33x21x2
20
例 2:已知函数 a R, f (x) 2x3 3(a 1)x2 6ax.
当 a=-2 时, (2)若曲线 y=f(x)与直线 y=-12x+m 有两
思考2、系数a >0时, a, b,c 变化时,图像特 征会变化吗? 系数 a 和导函数(二次函数)判别式 决定图像特征变化
7
三次函数与其导函数图象之间的关系
增区间:(-∞, x1), (x2, +∞)
减区间:(x1, x2)
增区间: (-∞, +∞)
增区间: (-∞, +∞)
8
思考3、当系数 a <0 时,请同学们类比 a>0学习变化规律
14
(3)当 a1时, x( ,a)(1, ),f'(x)0 x(a,1)f'(x)0 f(x)单调增(区 ,a)和 间 (1, ), f(x)单调减 (a,区 1)
注意:含参数三次函数单调区间分类的讨论标准 其导函数二次函数对应的方程是否有实根, 若有实根比较两实根的大小
分类整合, 转化与化归
2、通过三次函数图象研究函数零点个数 思想方法: 数形结合,函数与方程,分类整合, 转化与化归等数学思想
24
1、设 a>0,函数 f(x)=axx2++1b(b 为常数). (1)证明:函数 f(x)的极大值点和极小值点各有一个; (2)若 b=0,函数 f(x)的极大值为 1, 试求 a 的值.此 时 f(x)=2 有几个根?
数学思想
15
例 2:已知函数 a R, f (x) 2x3 3(a 1)x2 6ax. (1)求函数 f (x) 的单调区间;
(2)若 a<0,讨论函数 f(x)图象与 x 轴的交 点个数;
(3)当 a 取何值时,函数 f(x)图象与 x 轴 有且只有一个交点;
数形结合数 学思想
16
探究:三次函数图像与x轴交点有哪几种可能性?
小结:利用导数求函数单调性步骤
2
f(x)2x33x2
f'(x)6x26x
3
f(x) 3x36x24x5
f'(x)9x21x24
4
f(x)x32x22x7
f'(x)3x24x2
5
f(x)x33x29x
f'(x)3x26x9
6
思考:三次函数与其导函数图象之间的关系 ?
思考1、哪个系数对单调性没影响?d
解: f ' ( x ) 6 x 2 6 x 12
f '(x) 6(xa)(x1) 令f '(x) 0解得x1 a或x2 1 (1)当a1时,f '(x)0f (x)单调增区间为 -, ( ) (2)当a1时,x(,1)(a,),f '(x) 0 x(1,a) f '(x) 0 f (x)单调增区(间,1)和(a,),f (x)单调减区(1间 ,a)
6 4 2
-15
-10
-5
-2
-4
-6
-8
5
10
15
6
4
2 C
-15
-10
-5 -2
-4
-6
-8
5
10
15
6 4 2
-15
-10
-5
C -2
-4
-6
-8
5
10
15
6 4 2
-15
-10
-5
C
-2
-4
-6
-8
5
10
15
17
6 6
4 4
2 2
-15
-10
-5
5
10
15
-15
-10
-5
-2
-2
-4 -4
