(完整)高中数学导数基础练习题

合集下载

高中数学导数练习题

高中数学导数练习题一、基础题1. 求函数 $f(x) = x^3 3x$ 的导数。

2. 求函数 $f(x) = \sqrt{1+x^2}$ 的导数。

3. 求函数 $f(x) = \frac{1}{x^2}$ 的导数。

4. 求函数 $f(x) = \ln(x^2 + 1)$ 的导数。

5. 求函数 $f(x) = e^{2x}$ 的导数。

二、应用题1. 已知函数 $f(x) = ax^2 + bx + c$，求 $f'(x)$ 并说明其几何意义。

2. 某物体做直线运动，其位移 $s$ 与时间 $t$ 的关系为 $s =t^2 2t + 1$，求物体在 $t=2$ 时的瞬时速度。

3. 已知函数 $f(x) = \frac{1}{\sqrt{x}}$，求曲线在$x=4$ 处的切线方程。

4. 求函数 $f(x) = \sin(x)$ 在区间 $[0, \pi]$ 上的最大值和最小值。

5. 已知函数 $f(x) = \ln(x 1)$，求 $f(x)$ 的单调区间。

三、综合题1. 设函数 $f(x) = (x^2 1)^3$，求 $f'(x)$。

2. 已知函数 $f(x) = \frac{2x + 3}{x 1}$，求 $f'(x)$。

3. 求函数 $f(x) = \sqrt{1 + \sqrt{1 + x^2}}$ 的导数。

4. 已知函数 $f(x) = e^{x^2}$，求曲线在 $x=0$ 处的切线方程。

5. 设函数 $f(x) = \ln(\sin^2 x)$，求 $f'(x)$。

四、拓展题1. 已知函数 $f(x) = \frac{1}{x^2 + 1}$，求 $f''(x)$。

2. 设函数 $f(x) = (x^3 + 1)^4$，求 $f'''(x)$。

3. 已知函数 $f(x) = \arctan(x)$，求 $f'(x)$。

高中数学导数练习题附答案

高中数学导数练习题附答案一、解答题 1．已知函数()1e -=xx f x . (1)求()f x 极值点；(2)若()()4g x f x =-，证明：2x >时，()()f x g x >成立.2．已知函数()ln f x x x x =-，()2ln 1g x a x x =-+.(1)求函数()f x 的最小值；(2)若()0g x ≤在()0,∞+上恒成立，求实数a 的值； (3)证明：1111232022e 2023+++⋅⋅⋅+>，e 是自然对数的底数. 3．已知函数2()cos sin e f x x x x -=--，[]0,x π∈． (1)求()f x 的最大值；(2)证明：2e sin e e cos 1x x x x x x x -+>+-；(3)若320()2e f x ax -++≥恒成立，求实数a 的取值范围.4．已知函数()32f x x ax bx =++的图象在点(0,(0))f 处的切线斜率为4-，且2x =-时，()y f x =有极值． (1)求()f x 的解析式；(2)求()f x 在3,2上的最大值和最小值．5．已知函数()()e sin x f x rx r *=⋅∈N ，其中e 为自然对数的底数.(1)若1r =，求函数()y f x =的单调区间；(2)证明：对于任意的正实数M ，总存在大于M 的实数a ，b ，使得当[,]x a b ∈时，|()|1f x ≤.6．已知函数2()ln (2)f x x a x a =+<． (1)若2a =-，求函数()f x 的极小值点；(2)当2(]0,x ∈时，讨论函数()f x 的图象与函数(2)22y a x a =+--的图象公共点的个数，并证明你的结论．7．设函数()()2()ln 1f x x a x x =++-，其中R a ∈.(1)1a =时，求曲线()y f x =在点()()1,1f 处的切线方程； (2)讨论函数()f x 极值点的个数，并说明理由； (3)若()0,0x f x ∀>成立，求a 的取值范围. 8．已知函数21()(1)ln 2f x x ax a x =-+-，(2) 2.f '= (1)求a 的值;(2)求函数()f x 的极小值.9．已知函数e ()(1)1xf x b x a=+-+(1)当114a b ==-，时，求曲线()y f x =在点（0，f （0））处的切线方程； (2)当1a =时，()2f x ≥恒成立，求b 的值． 10．已知函数()()()2e 1,e 2.718xf x m x m R =-+∈≈.(1)选择下列两个条件之一：①12m =；②1m =，判断()f x 在区间()0,∞+上是否存在极小值点，并说明理由；(2)已知0m >，设函数()()()1ln g x f x mx mx =-+.若()g x 在区间()0,∞+上存在零点，求实数m 的取值范围.【参考答案】一、解答题1．(1)极大值点为2x =，无极小值点； (2)证明见解析. 【解析】【分析】（1）利用导数求出函数的单调区间即得解；（2）令()()()()4e 31e exx x x F x f x g x --=-=-，利用导数求出函数()F x 的最小值即得证. (1)解：由题意，得()2e xxf x -'=，令()0f x '>，得2x <；()0f x '<，得2x >；列表如下：所以()f x 极大值点为2x =，无极小值点. (2)证明：()()()4e 34e x x g xf x -=-=，令()()()()4e 31e e xx x x F x f x g x --=-=-， ∴()()()()42442e e e 22e e ex xx x x x x F x +----'=-=. 当2x >时，20x -<，24x >，从而42e e 0x -<，∴()0F x '>，()F x 在()2,+∞上是增函数，∴()()221120e eF x F >=-=. ∴当2x >时，()()f x g x >成立. 2．(1)1- (2)2(3)证明见解析【解析】【分析】（1）求导求单调性即可求解；（2）()()220a x g x x x-'=>，分类讨论单调性得到()ln 1222max g x a a a =-+，要使()0g x ≤在()0,∞+恒成立，则()0max g x ≤，即ln 10222a a a -+≤，又由（1）可得到ln 10222a a a -+≥，所以ln 10222a a a -+=，即可求解；（3）由（2）知()22ln 1g x x x =≤-得到22ln 1x x ≤-，所以ln 1t t ≤-，所以e 1xx ≥+，即11e >nn n+，代入证明即可. (1)()f x 的定义域为()0,∞+，()ln f x x '=，当()0,1x ∈时，()0f x '<，当(1,)x ∈+∞时，()0,f x '>故()f x 在()01,上单调递减，在(1,)+∞上单调递增. 所以()()11min f x f ==-. (2)()()2220a a x g x x x x x-'=-=>，当0a ≤时，()0g x '<，()g x 在()0,∞+上单调递减，此时存在()00,1x ∈，使得()()010g x g >=，与题设矛盾.当0a >时，x ∈时，()0g x '>，)x ∈+∞时，()0g x '<，故()g x 在上单调递增，在)+∞上单调递减，所以()1ln 12222max a a a ag g x a ==+=-+，要使()0g x ≤在()0,∞+恒成立，则()0max g x ≤，即ln 10222a a a -+≤又由（1）知()ln 1f x x x x =-≥-，即ln 1x x x -≥-，（当且仅当1x =时，等号成立）.令2a x =有ln 10222a a a -+≥，故ln 10222a a a -+=且12a = 所以2a =. (3)证明：由（2）知()22ln 1g x x x =≤-得22ln 1x x ≤-（当且仅当1x =时等号成立），令)0x t =>，则ln 1t t ≤-（当且仅当1t =时等号成立），令e x t =，所以ln e e 1x x ≤-，即e 1x x ≥+（当且仅当0x =时等号成立），令()*10x n N n =>∈，则111e >1n n n n++=从而有11111320212022223420222023e e e ee>12320212022⋅⋅⋅⨯⨯⨯⨯⨯ 所以111112*********e2023.+++⋯++>【点睛】导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，对导数的应用的考查主要从以下几个角度进行：(1)考查导数的几何意义，往往与解析几何、微积分相联系．(2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数． (3)利用导数求函数的最值(极值)，解决生活中的优化问题． (4)考查数形结合思想的应用． 3．(1)2max ()e f x -=- (2)证明见解析 (3)1,6a ⎡⎫∈+∞⎪⎢⎣⎭【解析】【分析】（1）直接利用导数判断单调性，求出最大值；（2）利用分析法，转化为证明1e x x -＞f (x ). 令g (x )＝1e xx-，[]0,x π∈，利用导数求出g (x )≥g (2)＝-2e -，而2max ()(0)e f x f -==-，即可证明；（3）把问题转化为x cos x －sin x ＋2ax 3≥0恒成立，令h (x )＝x cos x －sin x ＋2ax 3，[]0,x π∈，二次求导后，令()6sin x ax x ϕ=-，对a 分类讨论：i. a ≤－16， ii. a ≥16，iii.－16＜a ＜16，分别利用导数计算即可求解. (1)∵2()cos sin e f x x x x -=--，[]0,x π∈，∴()cos sin cos sin 0f x x x x x x x '=--=-，∴f (x )在[0，π]上单调递减，∴2max ()(0)e f x f -==-．(2)要证2e sin e e cos 1x x x x x x x -+>+-，只要证21cos sin e e x x x x x -->--，即证1e xx -＞f (x )，令g (x )＝1e x x -，[]0,x π∈，则()2e xx g x -'=，故g (x )在（0，2）上单调递减；g (x )在（2，π）上单调递增，所以g (x )≥g (2)＝-2e -，又 f (x )≤-2e -，且等号不同时取到，所以2e sin e e cos 1x x x x x x x -+>+- (3)()3220f x ax -≥++e ，等价于x cos x －sin x ＋2ax 3≥0，令h (x )＝x cos x －sin x ＋2ax 3，[]0,x π∈，则()2sin 66sin h x x x ax x ax x '=-+=（-），令()6sin x ax x ϕ=-，则()6cos x a x ϕ=-'，i.当a ≤－16时，()0x ϕ'，所以()ϕx 在[0，π]上递减，所以()(0)0x ϕϕ=，所以()0h x '≤，所以h (x )在[0，π]上递减，所以h (x )≤h （0）＝0，不合题意． ii.当a ≥16时，()0x ϕ'，所以()ϕx 在[0，π]上递增，所以()(0)0x ϕϕ= 所以()0h x '≥，所以h (x )在[0，π]上递增，所以h (x )≥h （0）＝0，符合题意． iii.当－16＜a ＜16时，因为(0)610a ϕ=-<'，()160a ϕπ=+>'，且()x ϕ'在[0，π]上递增，所以0x ∃[]0,π∈，使得()00x ϕ'=，所以当0(0,)x x ∈时，()0x ϕ'<，此时()ϕx 在（0，x 0）上递减，所以()(0)0x ϕϕ<=，所以()0h x '<，所以h (x )在（0，x 0）上递减，所以h (x )＜h （0）＝0，不合题意．综上可得： 1,6a ⎡⎫∈+∞⎪⎢⎣⎭. 【点睛】导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，对导数的应用的考查主要从以下几个角度进行： (1)考查导数的几何意义，往往与解析几何、微积分相联系．(2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数． (3)利用导数求函数的最值(极值)，解决生活中的优化问题． (4)考查数形结合思想的应用． 4．(1)32()24f x x x x =+- (2)最大值为8，最小值为4027-．【解析】【分析】（1）由题意可得(0)4,(2)1240,f b f a b ==-⎧⎨-=-+=''⎩从而可求出,a b ，即可求出()f x 的解析式，（2）令()0f x '=，求出x 的值，列表可得(),()f x f x '的值随x 的变化情况，从而可求出函数的最值 (1)由题意可得，2()32f x x ax b '=++．由(0)4, (2)1240,f b f a b ==-⎧⎨-=-+=''⎩解得2,4.a b =⎧⎨=-⎩ 经检验得2x =-时，()y f x =有极大值．所以32()24f x x x x =+-． (2)由（1）知，2()344(2)(32)f x x x x x '=+-=+-．令()0f x '=，得12x =-，223x =，()'f x ，()f x 的值随x 的变化情况如下表：由表可知()f x 在[3,2]-上的最大值为8，最小值为27-． 5．(1)增区间为32,2,44k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ 减区间为52,2,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(2)证明过程见解析. 【解析】【分析】（1）对函数求导，利用辅助角公式合并为同名三角函数，利用单调增减区间代入公式求解即可.（2）将绝对值不等式转化为11sin e e xxrx ⎛⎫⎛⎫-≤≤ ⎪ ⎪⎝⎭⎝⎭，移向构造新函数，利用导数判定单调性，借助零点定理和隐零点证明新构造函数恒正，再结合三角函数的特有的周期特点寻找M 即可. (1)()e (sin cos )sin 4x x f x x x x π⎛⎫'=+=+ ⎪⎝⎭令22242k x k πππππ-≤+≤+，得32,244x k k ππππ⎡⎤∈-+⎢⎥⎣⎦令322242k x k ππππ+≤+≤π+，得24x k ππ⎡∈+⎢⎣,524k ππ⎤+⎥⎦当32,244x k k ππππ⎡⎤∈-+⎢⎥⎣⎦时, ()0f x '>,()f x 单调递增当24x k ππ⎡∈+⎢⎣,524k ππ⎤+⎥⎦时, ()0,()f x f x '< 单调递減综上() f x 单调递增区间为32,2,44k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦单调递减区间为 52,2,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(2)要证|()|1f x ≤，即证e sin 1xrx ⋅≤，即证11sin =e e xx rx ⎛⎫≤ ⎪⎝⎭即证 11sin e e xxrx ⎛⎫⎛⎫-≤≤ ⎪ ⎪⎝⎭⎝⎭在[,]x a b ∈时成立即可,[,]x a b ∈时,1sin 0e 1sin 0e xxrx rx ⎧⎛⎫-≤⎪ ⎪⎪⎝⎭⎨⎛⎫⎪+≥ ⎪⎪⎝⎭⎩. 令1()sin e x h x rx ⎛⎫=- ⎪⎝⎭, 1()cos e xh x r rx ⎛⎫'=+ ⎪⎝⎭当222,k k x rr πππ⎛⎫+ ⎪∈⎪ ⎪⎝⎭时, cos 0,r rx > 所以1()cos 0,e xh x r rx ⎛⎫'=+> ⎪⎝⎭所以()h x 单调递增，2210,e k rk h rππ⎛⎫⎛⎫=-< ⎪ ⎪⎝⎭⎝⎭2221210(0)e k r k h k r ππππ+⎛⎫⎛⎫+ ⎪⎪=±>> ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭0(2)22,k k x rrπππ+∴∃∈ , 满足()00h x =由单调性可知02,k x x r π⎛⎫∈⎪⎝⎭, 满足()0()0h x h x <= 又因为当021,,sin 0,0,xk x x rx r e π⎛⎫⎛⎫∈>≥ ⎪ ⎪⎝⎭⎝⎭ 1sin 0xrx e ⎛⎫∴+≥ ⎪⎝⎭，所以1sin 0e 1sin 0e xxrx rx ⎧⎛⎫-≤⎪ ⎪⎪⎝⎭⎨⎛⎫⎪+≥ ⎪⎪⎝⎭⎩能够同时满足，对于任意的正实数M ，总存在正整数k ，且满足2Mr k π>时, 使得 2k M r π>成立，所以不妨取 02,,2k Mr a k b x rππ⎛⎫=>= ⎪⎝⎭则,a b M >且[,]x a b ∈时，1sin 01sin 0xxrx e rx e ⎧⎛⎫-≤⎪ ⎪⎪⎝⎭⎨⎛⎫⎪+≥ ⎪⎪⎝⎭⎩，故对于任意的正实数M ，总存在大于M 的实数,a b ，使得当[,]x a b ∈ 时,|()|1f x ≤. 6．(1)详见解析； (2)详见解析；【解析】【分析】（1）由2a =-，得到2()2ln f x x x =-，然后求导2()2f x x x'=-求解；（2）令2()ln (2)22=+-+++g x x a x a x a ，求导()()21()--'=x a x g x x，分0a ≤，012a <<，12a =，122a<<讨论求解. (1)解：当2a =-时，2()2ln f x x x =-，所以2()2f x x x'=-，令()0f x '=，得1x =，当01x <<时，()0f x '<，当1x >时，()0f x '>，所以1x =是函数()f x 的极小值点； (2)当2(]0,x ∈时，令2()ln (2)22=+-+++g x x a x a x a ，则()()2212(2)()2(2)---++'=+-+==x a x a x a x a g x x a x x x，当0a ≤时，01x <<时，()0g x '<，12x <≤时，()0g x '>，所以当1x =时，()g x 取得极小值，且0x →，()g x ∞→+，当()110g a =+>，即10a -<≤，函数()f x 的图象与函数(2)22y a x a =+--的图象无公共点；当()110g a =+=，即1a =-时，函数()f x 的图象与函数(2)22y a x a =+--的图象有1个公共点；当()()11022ln 20g a g a ⎧=+<⎪⎨=+≥⎪⎩，即21ln 2-≤<-a 时，函数()f x 的图象与函数(2)22y a x a =+--的图象有2个公共点；当()()11022ln 20g a g a ⎧=+<⎪⎨=+<⎪⎩，即2ln 2a <-，函数()f x 的图象与函数(2)22y a x a =+--的图象有1个公共点；当012a <<，即02a <<时，02ax <<或1x >时，()0g x '>，12a x <<时，()0g x '<，所以当2ax =时，()g x 取得极大值，当1x =时，()g x 取得极小值，且0x →，()g x →-∞，因为()110g a =+>恒成立，所以函数()f x 的图象与函数(2)22y a x a =+--的图象只有1个公共点；当12a =，即2a =时，()0g x '≥恒成立，所以()g x 在(0,2]上递增，所以函数()f x 的图象与函数(2)22y a x a =+--的图象有1个公共点；当122a <<，即24a <<时，01x <<或22a x <<时，()0g x '>，12ax <<时，()0g x '<，所以当1x =时，()g x 取得极大值，当2ax =时，()g x 取得极小值，且0x →，()g x →-∞，因为()110g a =+>，()22ln 20=+<g a ，2ln 20242⎛⎫=-+++> ⎪⎝⎭a a a g a a 恒成立，所以()f x 的图象与函数(2)22y a x a =+--的图象只有1个公共点.综上：当10a -<≤时，函数()f x 的图象与函数(2)22y a x a =+--的图象无公共点；当1a =-或 2ln 2a <-或04a <<时，()f x 的图象与函数(2)22y a x a =+--的图象只有1个公共点；当21ln 2-≤<-a 时，函数()f x 的图象与函数(2)22y a x a =+--的图象有2个公共点.7．(1)322ln230x y -+-=(2)当0a <时，函数()f x 有一个极值点；当809a ≤≤时，函数()f x 无极值点；当89a >时，函数()f x 有两个极值点. (3)0,1【解析】【分析】（1）将1a =代入函数()f x 中，得出函数()f x 的解析式，进而可以求出切点坐标，再利用导数的几何意义及点斜式即可求解；（2）根据已知条件，对a 进行分类讨论，利用导数法求函数极值的步骤及函数极值的定义即可求解；（3）根据()0,0x f x ∀>成立，转化为()min 0,0x f x ∀>即可，再利用第（2）的结论即可求解.(1)当1a =时，()2()ln 1f x x x x =++-()()21ln 1111ln 2f =++-=，所以切点为()1,ln2，()()11321,12111112f x x k f x ''=+-∴==+⨯-=++，所以曲线()y f x =在点()()1,1f 处的切线的斜率为()312k f ='=，所以曲线()y f x =在点()1,ln2处的切线的斜率切线方程为()3ln212y x -=-，即322ln230x y -+-= (2)由题意知函数()f x 的定义域为()1,-+∞，()()21212111ax ax a f x a x x x +-+=+-='++，令()()221,1,g x ax ax a x =+-+∈-+∞，（i ）当0a =时，()10f x '=>，函数()f x 在()1,-+∞单调递增，无极值点（ii ）当0a >时，()Δ98a a =-，①当809a <≤时，()()Δ0,0,0g x f x '≤≥≥，所以函数()f x 在()1,-+∞单调递增，无极值点；②当89a >时，Δ0>，设方程2210ax ax a +-+=两根1212,,x x x x == 此时12x x <()121211111,,,110,12444x x x x g x +=-∴---=>-<<∴<-> ()()121,,,x x x ∴∈-+∞时，()()0,0g x f x '>>，函数()f x 单调递增；()12,x x x ∈时，()()0,0g x f x '<<，函数()f x 单调递减.∴函数有两个极值点；③当0a <时，()Δ980a a =->，设方程2210ax ax a +-+=两根1212,,x x x x ==此时12x x >()12110,1x g x -=>∴-<<()11,x x ∴∈-时，()()0,0g x f x '>>，函数()f x 单调递增；()1,x x ∈+∞时，()()0,0g x f x '<<，函数()f x 单调递减.∴函数有一个极值点；综上所述：当0a <时，函数()f x 有一个极值点；当809a ≤≤时，函数()f x 无极值点；当89a >时，函数()f x 有两个极值点.(3)由()0,0x f x ∀>成立等价于()min 0,0x f x ∀>≥即可.①当809a ≤≤时，函数()f x 在()0,+∞上单调递增，()()00,0,f x =∴∈+∞时，()0f x >，符合题意； ②当819a <≤时，由()00g >，得20x ≤，∴函数()f x 在()0,+∞上单调递增，又()()00,0,f x =∴∈+∞时，()0f x >，符合题意；③当1a >时，由()00<g ，得20x >()20,x x ∴∈时， ()f x 单调递减,()()200,0,f x x =∴∈时，()0f x <时，不合题意；④当0a <时，设()()ln 1h x x x =-+，()0,x ∈+∞，时，()()110,11x h x h x x x =-=>∴+'+在()0,+∞上单调递增. ∴当()0,x ∞∈+时，()()00h x h >=，即()ln 1x x +<，可得()()()221f x x a x x ax a x <+-=+-，当11x a>-时，()210ax a x +-<，此时()0f x <，不合题意.综上，a 的取值范围是0,1.【点睛】解决此题的关键是第一问利用导数的几何意义及点斜式即可，第二问主要是对参数进行分类讨论，再结合利用导数法求函数的极值的步骤即可，第三问主要将恒成立问题转化为最值问题再结合第二问的结论即可求解.8．(1)1-(2)极小值32【解析】【分析】（1）求导函数，结合(2)2f '=解方程即可；（2）令()0f x '=进而分析单调性，即可求出极值．(1)由题意可得()1a f x x a x '-=-+，故()12222a f a -'=-+=， 1.a ∴=- (2)由（1）得21()2ln 2f x x x x =+-，所以()()210f x x x x '=+->，令()210f x x x '=+-=，解得1x =，因为当(0,1)x ∈时，()0f x '<，当(1,)x ∈+∞时，()0f x '>，所以函数()y f x =在(0,1)上单调递减，在(1,)+∞上单调递增，所以当1x =时，函数()f x 取得极小值()312f =．9．(1)25y x =+(2)0b =【解析】【分析】（1）利用切点和斜率求得切线方程.（2）由()2f x ≥恒成立构造函数()()2g x f x =-，对b 进行分类讨论，结合()'g x 研究()g x 的最小值，由此求得b 的值.(1) 当114a b ==-，时，()4e 21x f x x =-+，则()4e 2x f x '=-又因为(0)5,(0)2f f '==所以曲线()y f x =在点（0，f （0））处的切线方程为()520y x -=-，即25y x =+．(2)当1a =时，令函数()()()2e 11x g x f x b x =-=+--，则()2f x ≥恒成立等价于()0g x ≥恒成立．又()e 1,x g x b '=+-．当1b ≥时，()e 10,x g x b '=+->，g (x )在R 上单调递增，显然不合题意；当1b <时，令()e 10,x g x b '=+-<，得ln(1)x b <-．令()e 10x g x b '=+->，得()ln 1x b >-，所以函数g (x )在(,ln(1))b -∞-上单调递减，在(ln(1),)b -+∞上单调递增，所以当ln(1)x b =-时，函数g (x )取得最小值．又因为()00g =，所以0x =为g (x )的最小值点．所以ln(1)0b -=，解得0b =．10．(1)选择①不存在，理由见解析；选择②存在，理由见解析(2)[)1,+∞【解析】【分析】（1）若选择①，则()1x f x e x '=--，令()1x q x e x =--，由于()q x '在R 上单调递增，且()00f '=，从而可求出求出()f x '的单调区间，进而可求出()f x '的最小值非负，则()f x 无极值；若选择②，则()22x f x e x '=--,令()22x n x e x =--，由()n x '在R 上单调递增，且()ln 20n '=，可得()f x '的单调区间，从而得其最小值小于0 ，进而可判断函数的极值，（2）令()0g x =，则可得()()()1ln 1ln ln 0x x mx e x mx e x mx mx----+=--=⎡⎤⎣⎦，令()ln t x mx =-，即转化为10t e t --=有解，构造函数()1t h t e t -=-，由导数可得()1t h t e t -=-由唯一零点1t =，从而将问题转化为()1ln x mx =-在()0,∞+有解，即1ln ln m x x +=-，再构造函数()ln l x x x =-，利用导数求出函数的值域可得1ln m +的范围，从而可求出实数m 的取值范围(1)若选择①12m =，则()()2112x f x e x =-+，则()1x f x e x '=--. 令()1x q x e x =--，则()1x q x e '=-，由()q x '单调递增，且()00q '=，得()0q x '>在()0,∞+上恒成立，所以()f x '在()0,∞+上单调递增，所以当()0,x ∈+∞时，()()00f x f ''>=，则()f x 在()0,∞+上单调递增，不存在极小值点.若选择②1m =，则()()21x f x e x =-+，则()22x f x e x '=--.令()22x n x e x =--，则()2x n x e '=-，()n x '单调递增，且()ln 20n '=，所以()f x '在()0,ln 2上单调递减，()ln 2,+∞上单调递增.又()ln 22ln 20f '=-<，()2260f e '=->，所以存在()0ln 2,2x ∈，满足()00f x '=.则()f x 在()00,x 上单调递减，在()0,x +∞上单调递增，所以()f x 存在极小值点0x .(2)令()0g x =，则()12ln 0x e mx mx mx --+=.又0mx >，所以()()()()()11ln 1ln ln ln ln 0x x x mx mx e e x mx x mx e x mx mx e-----+=-+=--=⎡⎤⎣⎦. 令()ln t x mx =-，即可转化为10t e t --=有解.设()1t h t e t -=-，则由()110t h t e -'=-<可得1t <，则()h t 在(),1t ∈-∞上单调递减，在()1,t ∈+∞上单调递增.又()10h =，所以()1t h t e t -=-有唯一的零点1t =.若()g x 在区间()0,∞+上存在零点，则()1ln x mx =-在()0,∞+有解.整理得. 设()ln l x x x =-，由()11l x x '=-，知()l x 在()0,1x ∈上单调递减，在()1,x ∈+∞上单调递增，又当0x +→时，()l x →+∞，则()()11l x l ≥=，所以1ln 1m +≥，得1m ≥.故实数m 的取值范围是[)1,+∞.【点睛】关键点点睛：此题考查导数的应用，考查利用导数解决零点问题，解题的关键是由()0g x =可得()()ln 1ln 0x mx e x mx ----=⎡⎤⎣⎦，令()ln t x mx =-，将问题转化为10t e t --=有解，构造()1t h t e t -=-利用导数讨论其解的情况即可，考查数学转化思想和计算能力，属于较难题。

高二导数练习题及答案文库

高二导数练习题及答案文库导数是高中数学中的重要知识点之一，掌握导数的概念和运算方法对学生的数学学习至关重要。

为了帮助高二学生更好地巩固导数知识，提高解题能力，本文整理了一些高二导数练习题及其详细答案，供学生参考和练习。

一、基础练习题1. 求函数f(x) = 3x² - 2x + 1的导数f'(x)。

解：根据导数的定义，可得：f'(x) = lim(Δx→0)⁡[f(x + Δx) - f(x)] / Δx代入函数f(x)的表达式，展开并化简：f'(x) = lim(Δx→0)⁡[(3(x + Δx)² - 2(x + Δx) + 1) - (3x² - 2x + 1)] / Δx= lim(Δx→0)⁡[3x² + 6xΔx + 3(Δx)² - 2x - 2Δx + 1 - 3x² + 2x - 1] /Δx= lim(Δx→0)⁡(6xΔx + 3(Δx)² - 2Δx) / Δx= lim(Δx→0)⁡(6x + 3Δx - 2) = 6x - 2所以，函数f(x) = 3x² - 2x + 1的导数f'(x)为6x - 2。

2. 已知函数g(x) = 4x³ + 2x² - x的导数g'(x)，求g'(1)的值。

解：根据导数的定义，g'(x) = lim(Δx→0)⁡[g(x + Δx) - g(x)] / Δx代入函数g(x)的表达式，展开并化简：g(x + Δx) = 4(x + Δx)³ + 2(x + Δx)² - (x + Δx)= 4x³ + 12x²Δx + 12xΔx² + 4(Δx)³ + 2x² + 4xΔx + 2(Δx)² - x - Δx= 4x³ + 2x² - x + 12x²Δx + 12xΔx² + 4(Δx)³ + 4xΔx + 2(Δx)² - Δx代入导数的定义：g'(x) = lim(Δx→0)⁡[(4x³ + 2x² - x + 12x²Δx + 12xΔx² + 4(Δx)³ + 4xΔx + 2(Δx)² - Δx) - (4x³ + 2x² - x)] / Δx= lim(Δx→0)⁡(12x²Δx + 12xΔx² + 4(Δx)³ + 4xΔx + 2(Δx)² - Δx) / Δx= lim(Δx→0)⁡(12x² + 12xΔx + 4(Δx)² + 4x + 2Δx - 1)= 12x² + 4x - 1将x = 1代入上述导数表达式，可得：g'(1) = 12(1)² + 4(1) - 1 = 15所以，g'(1)的值为15。

高中导数试题题型及答案

高中导数试题题型及答案1. 计算函数$ f(x) = x^3 - 3x^2 + 2 $在点$ x = 1 $处的导数。

答案：首先求导数$ f'(x) $，得到$ f'(x) = 3x^2 - 6x $。

然后将$ x = 1 $代入，得到$ f'(1) = 3(1)^2 - 6(1) = -3 $。

2. 已知函数$ g(x) = \sin(x) + \cos(x) $，求其在$ x =\frac{\pi}{4} $处的导数。

答案：求导数$ g'(x) $，得到$ g'(x) = \cos(x) - \sin(x) $。

然后将$ x = \frac{\pi}{4} $代入，得到$ g'(\frac{\pi}{4}) = \cos(\frac{\pi}{4}) - \sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} = 0 $。

3. 判断函数$ h(x) = x^2e^x $在$ x = 0 $处的单调性。

答案：求导数$ h'(x) $，得到$ h'(x) = 2xe^x + x^2e^x $。

然后将$ x = 0 $代入，得到$ h'(0) = 2(0)e^0 + 0^2e^0 = 0 $。

由于导数为0，无法判断单调性，需要进一步分析。

4. 给定函数$ k(x) = \ln(x) $，求其在区间$ (1, 2) $上的单调区间。

答案：求导数$ k'(x) $，得到$ k'(x) = \frac{1}{x} $。

由于$ k'(x) > 0 $对于所有$ x > 0 $成立，因此函数$ k(x) $在区间$ (1, 2) $上单调递增。

(完整)高中数学导数基础练习题

导数基础练习题20170305一、选择题1．曲线y =2x 2−x 在点(0,0)处的切线方程为（）A. x +y +2=0B. x −y +2=0C. x −y =0D. x +y =0 2．“a ≤0”是“函数f(x)=ax +lnx 存在极值”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 3．设曲线2y x =上任一点(,)x y 处的切线的斜率为()g x ，则函数()()cos h x g x x =的部分图像可以为（）4．已知函数f(x)=(ex−1−1)(x −1)，则（）A. 当x <0，有极大值为2−4eB. 当x <0，有极小值为2−4eC. 当x >0，有极大值为0D. 当x >0，有极小值为05．已知函数()f x 是奇函数，当0x <时，()()ln 2f x x x x =-++，则曲线()y f x =在1x =处的切线方程为（）A ．23y x =+B ．23y x =-C ．23y x =-+D ．23y x =-- 6．如果函数()y f x =的图象如图，那么导函数()y f x '=的图象可能是（）7．已知()f x 是定义在()0,+∞上的函数，()()f x f x '是的导函数，且总有()()f x xf x '>，则不等式()()1f x xf >的解集为A. (),0-∞B. ()0,1C. ()0,+∞D.（1，+∞）8．已知函数()f x 是偶函数，当0x >时，()()21ln f x x x =-，则曲线()y f x =在点()()1,1f --处的切线的斜率为（）A.2-B.1-C.1D.2 9．在下面的四个图象中，其中一个图象是函f （x ）＝13x 3＋ax 2＋（a 2－1）x ＋1（a ∈R ）的导函数y ＝f ′（x ）的图象，则f （－1）等于（）．A二、填空题10．定义在R 上的偶函数f(x)满足：当x <0时，f(x)=xx−1，则曲线y =f(x)在点(2,f(2))处的切线的斜率为__________． 11，(0,3]x ∈，其图象上任意一点00(,)P x y 处的切线的斜恒成立，则实数a 的取值范围是． 12．设函数f(x)=x 3−3x +1,x ∈[−2,2]的最大值为M ，最小值为m ，则M +m =__________．13．在平面直角坐标系xoy 中，若曲线y =ax 2+bx （a,b 为常数）过点P(2,−5)，且该曲线在点P 处的切线与直线7x +2y +3=0平行，则a +b = .14．过函数 ()32325f x x x x =-++图像上一个动点作函数的切线，则切线倾斜角的取值范围是 __________. 15，若0'()1f x =，则 16．已知定义域为R 的奇函数()y f x =的导函数为()'y f x =，当0x ≠时，，则 a b c ，，的大小关系是．17，直线l 与函数()(),f x g x 的图像都相切于点（1,0）．（1）求直线l 的方程及函数()g x 的解析式；（2）若()()()h x f x g x '=-（其中()g x '是()g x 的导函数），求函数()h x 的极大值． 18．已知函数f(x)=x 2−2x ，g(x)=ax −1，若∀x 1∈[−1,2]，∃x 2∈[−1,2]，使得f(x 1)=g(x 219 （1）若3x =是()f x 的极值点，求()f x 的极大值；（2）求a 的范围，使得()1f x ≥恒成立．本卷由系统自动生成，请仔细校对后使用，答案仅供参考。

完整版)高等数学——导数练习题

完整版)高等数学——导数练习题高等数学——导数练题一．选择题1.若 $\lim\limits_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{f(x+2\Delta x)-f(x)}=k$，则$k=$（）。

A。

$2$ B。

$k$ C。

$k$ D。

以上都不是2.若 $f(x)=\sin\alpha-\cos x$，则 $f'(a)=$（）。

A。

$\sin\alpha$ B。

$\cos\alpha$ C。

$\sin\alpha+\cos\alpha$ D。

$2\sin\alpha$3.$f(x)=ax^3+3x^2+2$，若 $f'(-1)=4$，则 $a$ 的值等于（）。

A。

$4$ B。

$10$ C。

$13$ D。

$16$4.函数 $y=x\sin x$ 的导数为（）。

A。

$y'=2x\sin x+x\cos x$ B。

$y'=\dfrac{\sin x}{2x}+x\cosx$ C。

$y'=\dfrac{\sin x}{x}+\cos x$ D。

$y'=-x\cos x$5.函数 $y=x^2\cos x$ 的导数为（）。

A。

$y'=2x\cos x-x^2\sin x$ B。

$y'=2x\cos x+x^2\sin x$ C。

$y'=x^2\cos x-2x\sin x$ D。

$y'=x\cos x-x^2\sin x$6.函数 $y=\dfrac{1}{x^2+a}$ 的导数为 $-\dfrac{2x}{(x^2+a)^2}$，那么 $x$ 等于（）。

A。

$a$ B。

$-a$ C。

$\sin x$ D。

无法确定7.函数 $y=\dfrac{xcosx+\sin x}{2x}$ 的导数为（）。

A。

$y'=\dfrac{x\sin x-\cos x}{x^2}$ B。

$y'=\dfrac{2x\cosx-\sin x}{x^2}$ C。

(完整版)导数的几何意义(基础练习题)

导数的几何意义（1）1.设f(x)＝1x，则limx→af x－f ax－a等于( )A．－1aB.2aC．－1a2D.1a22．在曲线y＝x2上切线倾斜角为π4的点是( )A．(0,0) B．(2,4)C．(14，116) D．(12，14)3．设曲线y＝ax2在点(1，a)处的切线与直线2x－y－6＝0平行，则a＝( )A．1 B.1 2C．－12D．－14．若曲线y＝h(x)在点P(a，h(a))处切线方程为2x＋y＋1＝0，则( )A．h′(a)<0 B．h′(a)>0C．h′(a)＝0 D．h′(a)的符号不定5．一木块沿某一斜面自由下滑，测得下滑的水平距离s与时间t之间的函数关系为s＝18t2，则当t＝2时，此木块在水平方向的瞬时速度为( )A. 2B. 1C.12D.146．函数f (x )＝－2x 2＋3在点(0,3)处的导数是________．7．如图是函数f (x )及f (x )在点P 处切线的图像，则f (2)＋f ′(2)＝________.8．设曲线y ＝x 2在点P 处的切线斜率为3，则点P 的坐标为________．9．已知曲线y ＝2x 2上的点(1,2)，求过该点且与过该点的切线垂直的直线方程．10．求双曲线y ＝1x 在点(12，2)处的切线的斜率，并写出切线方程．导数的几何意义（2）1．如果曲线y ＝f (x )在点(x 0，f (x 0))处的切线方程为x ＋2y －3＝0，那么( )A ．f ′(x 0)＞0B ．f ′(x 0)＜0C ．f ′(x 0)＝0D ．f ′(x 0)不存在2．函数在处的切线斜率为（） A ．0 B 。

1 C 。

2 D 。

33．曲线y ＝12x 2－2在点⎝ ⎛⎭⎪⎫1，－32处切线的倾斜角为( )A ．1B.π4 C.54πD ．－π44．在曲线y ＝x 2上切线的倾斜角为π4的点是( ) A ．(0,0) B ．(2,4) C.⎝ ⎛⎭⎪⎫14，116D.⎝ ⎛⎭⎪⎫12，14 5．设f (x )为可导函数，且满足lim x →0 f (1)－f (1－2x )2x＝－1，则过曲线y ＝f (x )上点(1，f (1))处的切线斜率为( ) A ．2 B ．－1 C ．1D ．－26．设f ′(x 0)＝0，则曲线y ＝f (x )在点(x 0，f (x 0))处的切线( ) A ．不存在B ．与x 轴平行或重合C ．与x 轴垂直D ．与x轴斜交7．函数在点处的导数的几何意义是__________________________________________________;曲线在点P处的切线方程为是_____________________________________________.8．已知函数f(x)＝x2＋3，则f(x)在(2，f(2))处的切线方程为_________________________9．求过点P(-1,2)且与曲线y=3x2-4x+2在点M(1,1)处的切线平行的直线方程10．若曲线f(x)=ax3+3x2+2在x=-1处的切线斜率为4，求a的值。

高一数学导数试题及答案

高一数学导数试题及答案一、选择题（每题4分，共40分）1. 函数f(x)=x^3-3x^2+2的导数为（）。

A. f'(x)=3x^2-6xB. f'(x)=3x^2-6x+2C. f'(x)=3x^2-6x+1D. f'(x)=3x^2-6x-2答案：A2. 函数f(x)=sinx的导数为（）。

A. f'(x)=cosxB. f'(x)=-sinxC. f'(x)=sinxD. f'(x)=-cosx答案：A3. 函数f(x)=e^x的导数为（）。

A. f'(x)=e^xB. f'(x)=e^(-x)C. f'(x)=-e^xD. f'(x)=0答案：A4. 函数f(x)=lnx的导数为（）。

A. f'(x)=1/xB. f'(x)=lnxC. f'(x)=xD. f'(x)=1答案：A5. 函数f(x)=x^2的导数为（）。

A. f'(x)=2xC. f'(x)=2D. f'(x)=x答案：A6. 函数f(x)=1/x的导数为（）。

A. f'(x)=-1/x^2B. f'(x)=1/x^2C. f'(x)=-1/xD. f'(x)=1/x答案：A7. 函数f(x)=x^3的导数为（）。

A. f'(x)=3x^2B. f'(x)=3xC. f'(x)=3答案：A8. 函数f(x)=sinx+cosx的导数为（）。

A. f'(x)=cosx-sinxB. f'(x)=sinx+cosxC. f'(x)=sinx-cosxD. f'(x)=-cosx-cosx答案：A9. 函数f(x)=ln(x+1)的导数为（）。

A. f'(x)=1/(x+1)B. f'(x)=1/xC. f'(x)=ln(x+1)D. f'(x)=x+1答案：A10. 函数f(x)=e^(2x)的导数为（）。

高中数学导数精选题目(附答案)

高中数学导数精选题目（附答案）(1)函数的单调性与其导数正负的关系一般地，在区间(a，b)内函数的单调性与导数有如下关系：导数函数的单调性f′(x)>0单调递增f′(x)<0单调递减f′(x)＝0常数函数(2)函数图象的变化趋势与导数值大小的关系一般地，设函数y＝f(x)，在区间(a，b)上：导数的绝对值函数值变化函数的图象越大快比较“陡峭”(向上或向下)越小慢比较“平缓”(向上或向下)(3)极值点与极值①极小值点与极小值如图，函数f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0；且在点x＝a附近的左侧f′(x)＜0，右侧f′(x)＞0，则称点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．②极大值点与极大值函数f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0；且在点x＝b附近的左侧f′(x)＞0，右侧f′(x)＜0，则称点b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．③极值点与极值极小值点、极大值点统称为极值点，极大值和极小值统称为极值．(4)求可导函数y＝f(x)的极值的方法解方程f′(x)＝0，当f′(x0)＝0时：①如果在x0附近的左侧f′(x)>0，右侧f′(x)<0，那么f(x0)是极大值．②如果在x0附近的左侧f′(x)<0时，右侧f′(x)>0，那么f(x0)是极小值．(5)函数y＝f(x)在区间[a，b]上的最值一般地，如果在区间[a，b]上函数y＝f(x)的图象是一条连续不断的曲线，那么它必有最大值和最小值．(6)函数最值的求法求函数y＝f(x)在闭区间[a，b]上的最值的步骤如下：①求函数y＝f(x)在区间(a，b)内的极值；②将函数y＝f(x)的各极值与端点处的函数值f(a)，f(b)比较，其中最大的一个是最大值，最小的一个是最小值．(7)如果在区间(a，b)内恒有f′(x)＝0，则f(x)有什么特性？答：f(x)为常数函数，不具有单调性．(8)在区间(a，b)内，若f′(x)>0，则f(x)在此区间上单调递增，反之也成立吗？答：不一定成立．比如y＝x3在R上为增函数，但其在x＝0处的导数等于零．也就是说f′(x)>0是y＝f(x)在某个区间上单调递增的充分不必要条件．(9)下图为导函数y＝f′(x)的图象，则函数y＝f(x)的单调区间是什么？答：单调递增区间：(－∞，－3]，[－2,1]，[3，＋∞)；单调递减区间：[－3，－2]，[1,3]．(10):若函数f(x)为可导函数，且在区间(a，b)上是单调递增(或递减)函数，则f′(x)满足什么条件？答：f′(x)≥0(或f′(x)≤0)．(11):若函数f(x)在(a，b)上满足f′(x)>0(或f′(x)<0)，则f(x)在(a，b)上具备什么样的单调性？答：若f′(x)>0，则f(x)在(a，b)上为增函数；若f′(x)<0，则f(x)在(a，b)上为减函数．(12):f′(x)>0或f′(x)<0的解集与函数f(x)的单调区间有什么关系？答：f′(x)>0的解集对应函数f(x)的单调递增区间；f′(x)<0的解集对应函数f(x)的单调递减区间．(13):函数的极大值一定大于极小值吗？答：不一定，课本P27图1.3－11中c处的极小值大于f处的极大值．(14):函数f(x)的定义域为开区间(a，b)，导函数f′(x)在(a，b)内的图象如图所示，则函数f(x)在开区间(a，b)内有几个极小值点？答：一个．x1，x2，x3是极值点，其中x2是极小值点. x1、x3是极大值点．(15)：已知x0是函数f(x)定义域内的一点，当满足什么条件时，f(x0)是f(x)的极大值？当满足什么条件时，f(x0)是f(x)的极小值？答：当f′(x0)＝0，且在x0附近的左侧f′(x)>0，右侧f′(x)<0时，f(x0)是极大值；当f′(x0)＝0，且在x0附近的左侧f′(x)<0，右侧f′(x)>0时，f(x0)是极小值．(16):导数为0的点都是极值点吗？答：不一定，如f(x)＝x3，f′(0)＝0，但x＝0不是f(x)＝x3的极值点．所以，当f′(x0)＝0时，要判断x＝x0是否为f(x)的极值点，还要看f′(x)在x0两侧的符号是否相反．(17):函数y＝f(x)在给定区间(a，b)内一定有极值点吗？答：不一定，若函数y＝f(x)在区间(a，b)内是单调函数，就没有极值点．(18):若a≥f(x)恒成立，则a的取值范围是什么？若a≤f(x)恒成立，则a的取值范围是什么？答：(1)a≥f(x)恒成立⇔a≥f(x)ma x.(2)a≤f(x)恒成立⇔a≤f(x)mi n.1．(1)设函数f(x)在定义域内可导，y＝f(x)的图象如图所示，则导函数y＝f′(x)的图象可能为()(2)已知f′(x)是f(x)的导函数，f′(x)的图象如图所示，则f(x)的图象只可能是()2．(1)函数y＝f(x)的图象如图所示，则导函数的图象大致是()(2)函数y＝f(x)在定义域R上有导数，其导函数的图象如图所示，则函数y ＝f(x)的递增区间为____________；递减区间为________________．3．求证：函数f(x)＝e x－x－1在(0，＋∞)内是增函数，在(－∞，0)内是减函数．利用导数判断函数f(x)在(a，b)内的单调性的步骤(1)求f′(x)；(2)确定f′(x)在(a，b)内的符号；(3)得出结论．4．试证明：函数f(x)＝ln xx在区间(0,2)上是单调递增函数．5．求下列函数的单调区间：(1)f(x)＝x3－2x2＋x；(2)f(x)＝3x2－2l n x.利用导数求函数单调区间的步骤(1)求函数的定义域；(2)求f′(x)，解不等式f′(x)>0(或f′(x)<0)；(3)利用不等式的解集与定义域求交集得单调区间．注意事项：①求函数的单调区间，必须在函数的定义域内进行．②如果函数的单调区间有多个时，单调区间不能用“∪”符号连接，只能用“，”或“和”隔开．③导数法求得的单调区间一般用开区间表示．6．求函数f(x)＝e xx－2的单调区间．7．已知函数f(x)＝x3－a x－1.讨论f(x)的单调区间．提示：由题意，可先求f′(x)，然后根据a的取值情况，讨论f′(x)>0或f′(x)<0的解集即可．8．(1)本例中f(x)不变，若f(x)为单调递增函数，求实数a的取值范围；(2)本例中f(x)不变，若f(x)在区间(1，＋∞)内为增函数，求a的取值范围；(3)本例中f(x)不变，若f(x)在区间(－1,1)上为减函数，试求a的取值范围；(4)本例中f(x)不变，若f(x)的单调递减区间为(－1,1)，求a的取值范围；(5)本例中f(x)不变，若f(x)在区间(－1,1)上不单调，求a的取值范围．9．求下列函数的极值：(1)f(x)＝x2e－x; (2)y＝ln x x.10．求下列函数的极值：(1)f(x)＝13x3－x2－3x＋3；(2)f(x)＝2xx2＋1－2.11．已知f(x)＝x3＋3a x2＋b x＋a2在x＝－1时有极值0，求常数a，b的值．12．已知f(x)＝a x3＋b x2＋c x(a≠0)在x＝±1处取得极值，且f(1)＝－1.(1)试求常数a，b，c的值；(2)试判断x＝±1是函数的极大值点还是极小值点，并说明理由．13．求函数f(x)＝x3－3a x＋b(a≠0)的极值．提示：分类讨论a取不同值时，函数的单调性，进而求极值．14．设函数f(x)＝－13x3＋x2＋(m2－1)x(x∈R)，其中m>0.(1)当m＝1时，求曲线y＝f(x)在点(1，f(1))处的切线的斜率；(2)求函数f(x)的单调区间与极值15．求下列各函数的最值．(1)f(x)＝－x3＋3x，x∈[－3，3]；(2)f(x)＝x2－54x(x<0)．16．求下列各函数的最值．(1)f(x)＝x3－3x2＋6x－2，x∈[－1,1]；(2)f(x)＝12x＋S i n x，x∈[0,2π]．17．已知函数f(x)＝(4x2＋4a x＋a2)x，其中a<0.(1)当a＝－4时，求f(x)的单调递增区间；(2)若f(x)在区间[1,4]上的最小值为8，求a的值．18．已知函数f(x)＝a x3－6a x2＋b，x∈[－1,2]的最大值为3，最小值为－29，求a，b的值．19．已知f(x)＝x l n x，g(x)＝－x2＋a x－3.(1)求函数f(x)的最小值；(2)对一切x∈(0，＋∞)，2f(x)≥g(x)恒成立，求实数a的取值范围．提示：2f(x)≥g(x)恒成立，可转化为2f(x)－g(x)≥0恒成立，然后利用分离参数法求a的取值范围．(1)a≥f(x)(或≤f(x))恒成立⇔a≥f(x)ma x(或≤f(x)mi n);(2)a≥f(x)(或≤f(x))恒有解⇔a≥f(x)mi n(或≤f(x)ma x)；(3)f(x)≥g(x)恒成立⇔F(x)mi n≥0(其中F(x)＝f(x)－g(x));(4)f (x )≥g (x )恒有解⇔F (x )ma x ≥0(其中F (x )＝f (x )－g (x ))． 20．设函数f (x )＝x e x－x ⎝ ⎛⎭⎪⎫a 2x ＋1＋2.(1)若a ＝1，求f (x )的单调区间；(2)当x ≥0时，f (x )≥x 2－x ＋2恒成立，求a 的取值范围．参考答案：1.解： (1)由函数的图象可知：当x <0时，函数单调递增，导数始终为正；当x >0时，函数先增后减再增，即导数先正后负再正，对照选项，应选D.(2)从f ′(x )的图象可以看出，在区间⎝ ⎛⎭⎪⎫a ，a ＋b 2内，导数单调递增；在区间⎝ ⎛⎭⎪⎫a ＋b 2，b 内，导数单调递减．即函数f (x )的图象在⎝ ⎛⎭⎪⎫a ，a ＋b 2内越来越陡，在a ＋b 2，b 内越来越平缓，由此可知，只有选项D 符合．2.解析：选D 因为函数f (x )在(0，＋∞)和(－∞，0)上都是单调递减的，即f ′(x )<0.解析：由f ′(x )的图象可知，当x ∈(－2，－1)∪(1,3)∪(4，＋∞)时，f ′(x )>0；当x ∈(－∞，－2)∪(－1,1)∪(3,4)时，f ′(x )<0.故函数f (x )的增区间为(－2，－1)，(1,3)，(4，＋∞)；减区间为(－∞，－2)，(－1,1)，(3,4)．3.解：由于f (x )＝e x －x －1，所以f ′(x )＝e x －1，当x ∈(0，＋∞)时，e x ＞1，即f ′(x )＝e x －1>0. 故函数f (x )在(0，＋∞)内为增函数，当x ∈(－∞，0)时，e x <1，即f ′(x )＝e x －1<0. 故函数f (x )在(－∞，0)内为减函数．4.证明：由于f (x )＝ln xx ，所以f ′(x )＝1x ·x －ln x x 2＝1－ln x x 2. 由于0<x <2，所以l n x <l n 2<1，故f ′(x )＝1－ln xx 2>0，即函数f (x )＝ln xx 在区间(0,2)上是单调递增函数. 5.解： (1)函数的定义域为R ，∵f (x )＝x 3－2x 2＋x ，∴f ′(x )＝3x 2－4x ＋1. 令f ′(x )>0，解得x >1或x <13.因此f (x )的单调递增区间是⎝ ⎛⎭⎪⎫－∞，13，(1，＋∞)．令f ′(x )<0，解得13<x <1.因此f (x )的单调递减区间是⎝ ⎛⎭⎪⎫13，1.(2)函数的定义域为(0，＋∞)，f ′(x )＝6x －2x ＝2·3x 2－1x .令f ′(x )>0，即2·3x 2－1x >0，解得－33<x <0或x >33，又x >0，∴x >33；令f ′(x )<0，即2·3x 2－1x <0，解得x <－33或0<x <33，又x >0，∴0<x <33. ∴f (x )的单调递增区间为⎝ ⎛⎭⎪⎫33，＋∞；单调递减区间为⎝⎛⎭⎪⎫0，33.6.解：函数f (x )的定义域为(－∞，2)∪(2，＋∞)． f ′(x )＝e x (x －2)－e x (x －2)2＝e x (x －3)(x －2)2.因为x ∈(－∞，2)∪(2，＋∞)，所以e x >0，(x －2)2>0. 由f ′(x )>0得x >3，所以函数f (x )的单调递增区间为(3，＋∞)；由f ′(x )<0得x <3，又定义域为(－∞，2)∪(2，＋∞)，所以函数f (x )的单调递减区间为(－∞，2)和(2,3). 7.解： f ′(x )＝3x 2－a . (1)当a ≤0时，f ′(x )≥0，所以f (x )在(－∞，＋∞)上为增函数． (2)当a >0时，令3x 2－a ＝0，得x ＝±3a3.当x >3a 3或x <－3a3时，f ′(x )>0; 当－3a 3<x <3a 3时，f ′(x )<0. 因此f (x )在⎝ ⎛⎭⎪⎫－∞，－3a 3，⎝ ⎛⎭⎪⎫3a 3，＋∞上为增函数，f (x )在⎝ ⎛⎭⎪⎫－3a 3，3a 3上为减函数．综上可知，当a ≤0时，f (x )在R 上为增函数．当a >0时，f (x )在⎝ ⎛⎭⎪⎫－∞，－3a 3，⎝ ⎛⎭⎪⎫3a 3，＋∞上为增函数，在⎝ ⎛⎭⎪⎫－3a 3，3a 3上为减函数．8.解：(1)由已知得f ′(x )＝3x 2－a ，因为f (x )在(－∞，＋∞)上是单调增函数，所以f ′(x )＝3x 2－a ≥0在(－∞，＋∞)上恒成立，即a ≤3x 2对x ∈R 恒成立．因为3x 2≥0，所以只需a ≤0.又因为a ＝0时，f ′(x )＝3x 2≥0， f (x )＝x 3－1在R 上是增函数，所以a ≤0.即实数a 的取值范围为(－∞，0]．(2)因为f ′(x )＝3x 2－a ，且f (x )在区间(1，＋∞)上为增函数，所以f ′(x )≥0在(1，＋∞)恒成立，即3x 2－a ≥0在(1，＋∞)恒成立，所以a ≤3x 2在(1，＋∞)恒成立，即a的取值范围为(－∞，3]．(3)由f′(x)＝3x2－a≤0在(－1,1)上恒成立，得a≥3x2在x∈(－1,1)恒成立．因为－1<x<1，所以3x2<3，所以a≥3.即a的取值范围是[3，＋∞)．(4)由例题可知，f(x)的单调递减区间为－3a3，3a3，∴3a3＝1，即a＝3.(5)∵f(x)＝x3－a x－1，∴f′(x)＝3x2－a，由f′(x)＝0，得x＝±3a3(a≥0)，∵f(x)在区间(－1,1)上不单调，∴0<3a3<1，即0<a<3.故a的取值范围为(0,3)．9.解：(1)函数的定义域为R.f′(x)＝2x e－x－x2e－x＝x(2－x)e－x.令f′(x)＝0，得x＝0或x＝2.当x变化时，f′(x)，f(x)的变化情况如下表：由上表可以看出，当x＝0时，函数有极小值，且f(0)＝0.当x＝2时，函数有极大值，且f(2)＝4 e2.(2)函数y＝ln xx的定义域为(0，＋∞)，y′＝1－ln xx2.令y′＝0，即1－ln xx2＝0，得x＝e.当x变化时，y′，y的变化情况如下表：由表可知，当x＝e时，函数有极大值1 e.10.解：(1)函数的定义域为R，f′(x)＝x2－2x－3.令f′(x)＝0，得x＝3或x＝－1.当x变化时，f′(x)，f(x)的变化情况如下表：∴x＝－1是f(x)的极大值点，x＝3是f(x)的极小值点．∴f(x)极大值＝143，f(x)极小值＝－6.(2)函数的定义域为R，f′(x)＝2(x2＋1)－4x2 (x2＋1)2＝－2(x－1)(x＋1)(x2＋1)2.令f′(x)＝0，得x＝－1或x＝1.当x变化时，f′(x)，f(x)的变化情况如下表：由表可以看出：当x ＝－1时，函数f (x )有极小值，且f (－1)＝－22－2＝－3；当x ＝1时，函数f (x )有极大值，且f (1)＝22－2＝－1. 11.解： ∵y ＝f (x )在x ＝－1时有极值为0，且f ′(x )＝3x 2＋6a x ＋b ，∴⎩⎨⎧ f ′(－1)＝0，f (－1)＝0，即⎩⎨⎧3－6a ＋b ＝0，－1＋3a －b ＋a 2＝0. 解得⎩⎨⎧ a ＝1，b ＝3或⎩⎨⎧a ＝2，b ＝9.①当a ＝1，b ＝3时，f ′(x )＝3x 2＋6x ＋3＝3(x ＋1)2≥0， y ＝f (x )在R 上为增函数，无极值，故舍去． ②当a ＝2，b ＝9时，f ′(x )＝3x 2＋12x ＋9＝3(x ＋1)(x ＋3)．当x 变化时，f ′(x )，f (x )的变化情况如下表：由表可知，f (x )在x ＝－1处取极小值且f (－1)＝0. ∴a ＝2，b ＝9.12.解：f ′(x )＝3a x 2＋2b x ＋c ， (1)法一：∵x ＝±1是函数的极值点，∴x ＝±1是方程3a x 2＋2b x ＋c ＝0的两根．由根与系数的关系知⎩⎪⎨⎪⎧－2b 3a ＝0， ①c 3a ＝－1， ②又f (1)＝－1，∴a ＋b ＋c ＝－1，③ 由①②③解得a ＝12，b ＝0，c ＝－32.法二：由f ′(1)＝f ′(－1)＝0，得3a ＋2b ＋c ＝0，① 3a －2b ＋c ＝0，②又f (1)＝－1，∴a ＋b ＋c ＝－1，③ 由①②③解得a ＝12，b ＝0，c ＝－32.(2)f (x )＝12x 3－32x ，∴f ′(x )＝32x 2－32＝32(x －1)(x ＋1)．当x <－1或x >1时f ′(x )>0，当－1<x <1时，f ′(x )<0.∴函数f (x )在(－∞，－1)和(1，＋∞)上是增函数，在(－1,1)上是减函数．∴当x ＝－1时，函数取得极大值，x ＝－1为极大值点；当x ＝1时，函数取得极小值，x ＝1为极小值点.13.解： f ′(x )＝3(x 2－a )(a ≠0)，当a <0时，f ′(x )>0恒成立，即函数在(－∞，＋∞)上单调递增，此时函数没有极值；当a >0时，令f ′(x )＝0，得x ＝－a 或x ＝a .当x 变化时，f ′(x )与f (x )的变化情况如下表：∴f (x )的极大值为f (－a )＝2a a ＋b ，极小值为f (a )＝－2a a ＋b .14.解：(1)当m ＝1时，f (x )＝－13x 3＋x 2，f ′(x )＝－x 2＋2x ，故f ′(1)＝1.所以曲线y ＝f (x )在点(1，f (1))处的切线的斜率为1.(2)f ′(x )＝－x 2＋2x ＋m 2－1.令f ′(x )＝0，解得x ＝1－m 或x ＝1＋m .因为m >0，所以1＋m>1－m.当x变化时，f′(x)，f(x)的变化情况如下表：所以函数f(x)的单调递减区间为(－∞，1－m)，(1＋m，＋∞)，递增区间为(1－m,1＋m)．函数f(x)在x＝1－m处取得极小值f(1－m)，且f(1－m)＝－23m3＋m2－13.函数f(x)在x＝1＋m处取得极大值f(1＋m)，且f(1＋m)＝23m3＋m2－13.15.解：(1)f′(x)＝3－3x2＝3(1－x)(1＋x)．令f′(x)＝0，得x＝1或x＝－1，当x变化时，f′(x)，f(x)的变化情况如下表：所以x＝1和x＝－1是函数在[－3，3]上的两个极点，且f(1)＝2，f(－1)＝－2.又因为f(x)在区间端点处的取值为f(－3)＝0，f(3)＝－18.所以f(x)ma x＝2，f(x)mi n＝－18.(2)f′(x)＝2x＋54x2.令f′(x)＝0得x＝－3.当x变化时，f′(x)，f(x)的变化情况如下表：所以x ＝－3时，f (x )取得极小值，也就是最小值，故f (x )的最小值为f (－3)＝27，无最大值．16.解：(1)f ′(x )＝3x 2－6x ＋6＝3(x 2－2x ＋2)＝3(x －1)2＋3，因为f ′(x )在[－1,1]内恒大于0，所以f (x )在[－1,1]上为增函数．故x ＝－1时，f (x )取最小值为－12， x ＝1时，f (x )取最大值为2. (2)f ′(x )＝12＋co S x ，令f ′(x )＝0，又x ∈[0,2π]，解得x ＝2π3或x ＝4π3.计算得f (0)＝0，f (2π)＝π，f ⎝ ⎛⎭⎪⎫2π3＝π3＋32，f ⎝ ⎛⎭⎪⎫4π3＝2π3－32.所以当x ＝0时，f (x )有最小值f (0)＝0；当x ＝2π时，f (x )有最大值f (2π)＝π 17.解： (1)当a ＝－4时，f ′(x )＝2(5x －2)(x －2)x，令f ′(x )>0，得x ∈⎝ ⎛⎭⎪⎫0，25或x ∈(2，＋∞)，故函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0，25和(2，＋∞)． (2)f ′(x )＝(10x ＋a )(2x ＋a )2x ，a <0，由f ′(x )＝0得x ＝－a 10或x ＝－a2.当x ∈⎝ ⎛⎭⎪⎫0，－a 10时，f (x )单调递增；当x ∈－a 10，－a 2时，f (x )单调递减；当x∈⎝ ⎛⎭⎪⎫－a 2，＋∞时，f (x )单调递增．易知f (x )＝(2x ＋a )2x ≥0，且f ⎝ ⎛⎭⎪⎫－a 2＝0.①当－a2≤1，即－2≤a <0时，f (x )在[1,4]上的最小值为f (1)，由f (1)＝4＋4a＋a 2＝8，得a ＝±22－2，均不符合题意．②当1<－a 2≤4，即－8≤a <－2时，此时15<－a 10≤45，f (x )在[1,4]上的最小值为f ⎝ ⎛⎭⎪⎫－a 2＝0，不符合题意．③当－a2>4，即a <－8时，f (x )在[1,4]上的最小值可能在x ＝1或x ＝4处取得，而f (1)＝8时没有符合题意的a 值，由f (4)＝2(64＋16a ＋a 2)＝8得a ＝－10或a ＝－6(舍去)，当a ＝－10时，f (x )在(1,4)上单调递减，f (x )在[1,4]上的最小值为f (4)＝8，符合题意．综上知，a ＝－10.18.解：由题设知a ≠0，否则f (x )＝b 为常函数，与题设矛盾．f ′(x )＝3a x 2－12a x ＝3a x (x －4)，令f ′(x )＝0，得x 1＝0，x 2＝4(舍去)．(1)当a >0，且x 变化时，f ′(x )，f (x )的变化情况如下表：由表可知，当x ＝0时，f (x )取得极大值，也就是函数在[－1,2]上的最大值，∴f (0)＝3，即b ＝3.又f (－1)＝－7a ＋3，f (2)＝－16a ＋3<f (－1)， ∴f (2)＝－16a ＋3＝－29，解得a ＝2.(2)当a <0时，同理可得，当x ＝0时，f (x )取得极小值，也就是函数在[－1,2]上的最小值，∴f (0)＝－29，即b ＝－29.又f (－1)＝－7a －29，f (2)＝－16a －29>f (－1)， ∴f (2)＝－16a －29＝3，解得a ＝－2. 综上可得，a ＝2，b ＝3或a ＝－2，b ＝－29.19.解： (1)已知函数f (x )的定义域为(0，＋∞)，f ′(x )＝l n x ＋1，当x ∈⎝ ⎛⎭⎪⎫0，1e 时，f ′(x )<0，f (x )单调递减，当x ∈⎝ ⎛⎭⎪⎫1e ，＋∞时，f ′(x )>0，f (x )单调递增．所以f (x )mi n ＝f ⎝ ⎛⎭⎪⎫1e ＝－1e . (2)2x l n x ≥－x 2＋a x －3，则a ≤2l n x ＋x ＋3x ，设h (x )＝2l n x ＋x ＋3x (x >0)，则h ′(x )＝(x ＋3)(x －1)x 2， ①x ∈(0,1)，h ′(x )<0，h (x )单调递减； ②x ∈(1，＋∞)，h ′(x )>0，h (x )单调递增；所以h (x )mi n ＝h (1)＝4，对一切x ∈(0，＋∞)，2f (x )≥g (x )恒成立，所以a ≤h (x )mi n ＝4，即a 的取值范围是(－∞，4]． 20.解：(1)∵a ＝1， ∴f (x )＝x e x －x ⎝ ⎛⎭⎪⎫12x ＋1＋2＝x e x －12x 2－x ＋2， ∴f ′(x )＝(e x －1)(x ＋1)， ∴当－1<x <0时，f ′(x )<0; 当x <－1或x >0时，f ′(x )>0，∴f (x )在(－1,0)上单调递减，在(－∞，－1)，(0，＋∞)上单调递增． (2)由f (x )≥x 2－x ＋2，得x ⎝ ⎛⎭⎪⎫e x －a ＋22x ≥0，当x ＝0时，显然成立；当x >0时，即e x x ≥a ＋22恒成立．记g (x )＝e xx ，则g ′(x )＝e x (x －1)x 2，当0<x <1时，g ′(x )<0，g (x )是减函数，当x >1时，g ′(x )>0，g (x )是增函数．∴g(x)的最小值为g(1)＝e，∴a＋22≤e，得a≤2e－2.即a的取值范围是(－∞，2e－2]．。

高中数学导数训练题含答案

导数训练一、单选题（共33题；共66分）1.曲线在处的切线方程是（）A. B. C. D.2.若，则等于（）A. 0B. 1C. 3D.3.下列各式正确的是（）A. (a为常数)B.C.D.4.函数+e的导函数是（）A. B. C. D.5.曲线在点处的切线方程为（）A. B. C. D.6.曲线在点（1,1）处的切线方程为（）A. B. C. D.7.函数的导函数（）A. B. C. D.8.某运动物体的位移（单位：米）关于时间（单位：秒）的函数关系式为,则该物体在秒时的瞬时速度为（）A. 1米／秒B. 2米／秒C. 3米／秒D. 4米／秒9.f′(x)是函数f(x)＝x3＋2x＋1的导函数，则f′(－1)的值为（）A. 0B. 3C. 4D. －10.函数的导数为（）A. B. C. D.11.设函数，若，则等于（）A. B. C. D.12.已知曲线y＝2x2上一点A(2,8)，则在点A处的切线斜率为( )．A. 4B. 16C. 8D. 213.曲线在处的切线的斜率为（）A. -1B.C.D. 114.下列求导运算的正确是（）A. 为常数B.C.D.15.已知曲线的一条切线的斜率为2，则切点的横坐标为( )A. 1B. ln2C. 2D. e16.一物体做直线运动，其位移(单位: )与时间(单位: )的关系是，则该物体在时的瞬时速度是（）A. B. C. D.17.函数的单调增区间是（）A. B. C. D.18.已知函数的值为（）A. B. C. D.19.已知函数，则（）A. B. C. D.20.函数= 的极值点为( )A. B. C. 或 D.21.已知函数,直线过点且与曲线相切,则切点的横坐标为( )A. B. 1 C. 2 D.22.函数在点处切线方程为（）A. B. C. D.23.若有极大值和极小值，则的取值范围是（）A. B. C. D.24.函数的导数为（）A. ＝2B. ＝C. ＝2D. ＝25.设，若，则（）A. B. C. D.26.函数的单调递减区间为（）A. B. C. D.27.曲线在点处的切线方程是A. B. C. D.28.已知函数，则函数的图象在处的切线方程为（）A. B. C. D.29.一物体在力F(x)＝2x＋3(x的单位：m，F的单位：N)的作用下，沿着与力F相同的方向，从x＝1运动到x＝4处，求力F(x)所做的功．（）A. 24B. 25C. 26D. 2730.函数的单调递减区间是（）A. B. C. D.31.已知函数，则其导数（）A. B. C. D.32.曲线在处的切线倾斜角是（）A. B. C. D.33.已知函数，且，则的值为（）A. B. C. D.二、填空题（共10题；共11分）34.函数的单调递增区间是________.35.已知函数为的导函数,则的值为________.36.已知函数，则函数的图像在点处的切线方程为________.37.函数在处的切线方程是，则________.38.设函数可导，若，则________．39.已知函数的导函数为，若，则的值为________.40.若函数,则的值为________．41.已知，则________．42.已知函数( 为常数)，若为的一个极值点，则________.________.43.曲线在点处的切线方程为________．三、解答题（共7题；共55分）44.已知函数，当时，有极大值3.（1）求该函数的解析式；（2）求该函数的解析式；（3）求函数的单调区间.（4）求函数的单调区间.45.如果函数f(x)= (a＞0)在x=±1时有极值，极大值为4，极小值为0，试求函数f(x)的解析式.46.已知函数.(I)若曲线在点处的切线方程为,求的值；(II)若,求的单调区间.47.已知（1）判断单调性（2）判断单调性（3）当时，求的最大值和最小值（4）当时，求的最大值和最小值48.已知函数，求曲线在点处的切线方程；49.已知在与时都取得极值．（1）求的值；（2）求的值；（3）若，求的单调区间和极值。

(完整版)导数基础练习测试

导数基础练习（共2页，共17题）一．选择题（共14题）1．函数f（x）＝sin2x的导数f′（x）＝（）A．2sinx B．2sin2x C．2cosx D．sin2x2．曲线f（x）＝lnx+2x在点（1，f（1））处的切线方程是（）A．3x﹣y+1＝0 B．3x﹣y﹣1＝0 C．3x+y﹣1＝0 D．3x﹣y﹣5＝0 3．若函数f（x）＝sin2x，则f′（）的值为（）A．B．0 C．1 D．﹣4．函数f（x）＝xsinx+cosx的导数是（）A．xcosx+sinx B．xcosx C．xcosx﹣sinx D．cosx﹣sinx 5．的导数是（）A．B．C．D．6．y＝xlnx的导数是（）A．x B．lnx+1 C．3x D．17．函数y＝cose xA．﹣e x sine x B．cose x C．﹣e x D．sine x8．已知，则f′（）＝（）A．﹣1+ B．﹣1 C．1 D．09．函数的导数是（）A．B．C．e x﹣e﹣x D．e x+e﹣x10．函数y＝x2﹣2x在﹣2处的导数是（）A．﹣2 B．﹣4 C．﹣6 D．﹣811．设y＝ln（2x+3），则y′＝（）A．B．C．D．12．已知函数，则f′（x）等于（）A．B．C．0 D．13．曲线y＝x2+3x在点A（2，10）处的切线的斜率k是（）A．4 B．5 C．6 D．714．曲线y＝4x﹣x2上两点A（4，0），B（2，4），若曲线上一点P处的切线恰好平行于弦AB，则点P的坐标为（）A．（1，3）B．（3，3）C．（6，﹣12） D．（2，4）二．填空题（共2题）15．求导：（）′＝_________．16．函数y＝的导数是_________．三．解答题（共1题）17．求函数y＝e x5 +2的导数．导数基础练习（试题解析）一．选择题（共14题）1．函数f（x）＝sin2x的导数f′（x）＝（）A．2sinx B．2sin2x C．2cosx D．sin2x考点：简单复合函数的导数．考查学生对复合函数的认识，要求学生会对简单复合函数求导．分析：将f（x）＝sin2x看成外函数和内函数，分别求导即可．解答：将y＝sin2x写成，y＝u2，u＝sinx的形式．对外函数求导为y′＝2u，对内函数求导为u′＝cosx，∴可以得到y＝sin2x的导数为y′＝2ucosx＝2sinxcosx＝sin2x．∴选D．红色sin2x、蓝色sin2x2．曲线f（x）＝lnx+2x在点（1，f（1））处的切线方程是（）A．3x﹣y+1＝0 B．3x﹣y﹣1＝0 C．3x+y﹣1＝0 D．3x﹣y﹣5＝0考点：简单复合函数的导数；直线的点斜式方程．考查学生对切线方程的理解，要求写生能够熟练掌握．分析：先要求出在给定点的函数值，然后再求出给定点的导数值．将所求代入点斜式方程即可．解答：对f（x）＝lnx+2x求导，得f′（x）＝+2．∴在点（1，f（1））处可以得到f（1）＝ln1+2＝2，f′（1）＝1+2＝3．∴在点（1，f（1））处的切线方程是：y﹣f（1）＝f′（1）（x﹣1），代入化简可得，3x﹣y﹣1＝0．∴选B．3．若函数f（x）＝sin2x，则f′（）的值为（）A．B．0 C．1 D．﹣考点：简单复合函数的导数．计算题．求函数在某点处的导数值，应该先利用导数的运算法则及初等函数的导数公式求出导函数，再求导函数值．分析：先利用复合函数的导数运算法则求出f（x）的导函数，将x＝代入求出值．解答：解：f′（x）＝cos2x（2x）′＝2cos2x，∴f′（）＝2cos＝1，∴选C．红色sin2x、蓝色2cos2x4．函数f（x）＝xsinx+cosx的导数是（）A．xcosx+sinx B．xcosx C．x cosx﹣sinx D．c osx﹣sinx考点：导数的乘法与除法法则；导数的加法与减法法则．计算题．本题考查导数的运算法则、基本初等函数的导数公式．属于基础试题．分析：利用和及积的导数运算法则及基本初等函数的导数公式求出函数的导数．解答：解：∵f（x）＝xsinx+cosx，∴f′（x）＝（xsinx+cosx）′＝（xsinx）′+（cosx）′＝x′sinx+x（sinx）′﹣sinx＝sinx+xcosx﹣sinx＝xcosx，∴选B．红色xsinx+cosx、蓝色xcosx5．的导数是（）A．B．C．D．考点：导数的乘法与除法法则．计算题．本题考查导数的除法运算法则，解题时认真计算即可，属于基础题．分析：利用导数的四则运算法则，按规则认真求导即可解答：解：y′＝＝＝∴选A．红色、绿色y′＝6．y＝xlnx的导数是（）A．x B．lnx+1 C．3x D．1考点：导数的乘法与除法法则．导数的综合应用．本题考查导数的乘法法则，考查了基本初等函数的导数公式，属于基础题．分析：直接由导数的乘法法则结合基本初等函数的导数公式求解．解答：解：∵y＝xlnx，∴y′＝（xlnx）′＝x′lnx+x（lnx）′＝．∴选B．红色xlnx、绿色lnx+17．函数y＝cose x的导数是（）A．﹣e x sine x B．cose x C．﹣e x D．sine x考点：导数的乘法与除法法则．导数的概念及应用．本题主要考查导数的基本运算，要求熟练掌握常见函数的导数公式以及导数的运算法则．分析：根据导数的运算法则即可得到结论．解答：解：函数的导数为f′（x）＝﹣sine x（e x）′＝﹣e x sine x，∴选A．红色cose x、绿色﹣e x sine x8．已知，则f′（）＝（）A．﹣1+B．﹣1 C．1 D．0考点：导数的加法与减法法则．计算题．本题主要考查了导数的运算，以及求函数值，解题的关键是正确求解导函数，属于基础题．分析：本题先对已知函数进行求导，再将代入导函数解之即可．解答：解：∴选B．红色、绿色－sinx9．函数的导数是（）A．B．C．e x﹣e﹣x D．e x+e﹣x考点：导数的加法与减法法则．计算题．本题考查导数的运算，牢记求导公式是解本题的关键．分析：根据求导公式（u+v）′＝u′+v′及（e x）′＝e x即可求出函数的导数．解答：解：∵，∴y′＝＝．∴选A．红色、蓝色10．函数y＝x2﹣2x在﹣2处的导数是（）A．﹣2 B．﹣4 C．﹣6 D．﹣8考点：导数的加法与减法法则．计算题；导数的概念及应用．本题考查导数的加法与减法法则，考查基本初等函数的导数公式，是基础的计算题．分析：求出原函数的导函数，在导函数解析中取x＝﹣2计算即可得到答案．解答：解：由y＝x2﹣2x，得y′＝2x﹣2．∴y′|x＝﹣2＝2×（﹣2）﹣2＝﹣6．∴选C．红色y＝x2﹣2x、蓝色y′＝2x﹣211．设y＝ln（2x+3），则y′＝（）A．B．C．D．考点：导数的运算．导数的概念及应用．本题主要考查导数的计算，要求熟练掌握复合函数的导数公式，属于基础题．分析：根据复合函数的导数公式即可得到结论．解答：解：∵y＝ln（2x+3），∴，∴选：D红色ln（2x+3）、蓝色12．已知函数，则f′（x）等于（）A．B．C．0 D．考点：导数的运算．导数的概念及应用．本题考查了常数的导数，只要理解常数c′＝0即可解决此问题．分析：我们知道：若函数f（x）＝c为常数，则f′（x）＝0，∴可得出答案．解答：解：∵函数，∴f′（x）＝0．∴选C．13．曲线y＝x2+3x在点A（2，10）处的切线的斜率k是（）A．4 B．5 C．6 D．7考点：导数的几何意义．计算题．本题考查函数在某点导数的几何意义的应用．分析：曲线y＝x2+3x在点A（2，10）处的切线的斜率k就等于函数y＝x2+3x在点A（2，10）处的导数值．解答：解：曲线y＝x2+3x在点A（2，10）处的切线的斜率，k＝y′＝2x+3＝2×2+3＝7，∴答案为7．红色x2+3x、蓝色2x+314．曲线y＝4x﹣x2上两点A（4，0），B（2，4），若曲线上一点P处的切线恰好平行于弦AB，则点P的坐标为（）A．（1，3）B．（3，3）C．（6，﹣12）D．（2，4）考点：导数的几何意义．考核导数的几何意义及两条直线平行斜率的关系．分析：首先求出弦AB的斜率，再利用导数的几何意义求出P点坐标．解答：解：设点P（x0，y0），∵A（4，0），B（2，4），∴kAB＝＝﹣2．∵过点P的切线l平行于弦AB，∴kl＝﹣2，∴根据导数的几何意义得知，曲线在点P的导数y′＝4﹣2x＝4﹣2x＝﹣2，即x0＝3，∵点P（x0，y）在曲线y＝4x﹣x2上，∴y0＝4x0﹣x02＝3．∴选B．红色4x ﹣x 2、蓝色4﹣2x二．填空题（共2题）15．求导：（）′＝，．考点：简单复合函数的导数．导数的概念及应用．本题主要考查导数的计算，根据复合函数的导数公式是解决本题的关键．分析：根据复合函数的导数公式进行求解即可．解答：解：＝(x 2+1)21，则函数的导数为y′＝(x 2+1)21－（x 2+1）′＝(x 2+1)21－×2x ＝，∴答案为：红色、蓝色精心整理16．函数y＝的导数是．考点：简单复合函数的导数．导数的概念及应用．本题主要考查导数的计算，根据复合函数的导数公式进行计算是解决本题的关键．分析：根据复合函数的导数公式进行计算即可．解答：解：函数的导数为y′＝＝，∴答案为：红色、蓝色三．解答题（共1题）17．求函数y＝e x5-+2的导数．考点：简单复合函数的导数．导数的概念及应用．本题考查导数的运算，以及导数基本知识的考查．分析：直接利用复合函数的导数求解运算法则求解即可．解答：解：函数y＝e x5-+2的导数：y′＝﹣5e x5-．∴答案为：y′＝﹣5e x5-．红色e x5-+2、蓝色﹣5e x5-。

高中数学导数练习题附答案

高中数学导数练习题附答案一、解答题 1．已知函数()()2ln 0f x a x ax a =+-> (1)求()f x 的最大值(2)若()0f x ≤恒成立，求a 的值 2．已知函数()()1ln 0f x a x x a x=-+>．(1)当1≥x 时，()0f x ≤恒成立，求实数a 的取值范围；(2)当1a =时，()()21g x xf x x =+-，方程()g x m =的根为1x 、2x ，且21x x >，求证：211e x x m ->+．3．已知函数()21si cos n 2f x x x a x x =-++．(1)当1a =-时，求曲线()y f x =在点()()0,0f 处的切线方程； (2)若函数()f x 在3π0,4⎡⎤⎢⎥⎣⎦上单调递减，求a 的取值范围． 4．已知函数()1e x axf x a=-+，0a ≠. (1)当1a =时，①求曲线()y f x =在0x =处的切线方程； ②求证：()f x 在(0,)+∞上有唯一极大值点； (2)若()f x 没有零点，求a 的取值范围. 5．已知函数()()32131.3f x x a x x =-++ (1)若1a =，求函数()f x 的单调区间; (2)证明：函数()2y f x a =-至多有一个零点. 6．已知函数21()(1)ln 2f x x ax a x =-+-，(2) 2.f '= (1)求a 的值;(2)求函数()f x 的极小值.7．已知函数()()2231ln 2f x x a a x a a x =-+-+. (1)若1a =，求()f x 在[]1,2上的值域； (2)若20a a -≠，讨论()f x 的单调性. 8．已知函数()1ln xf x x +=.(1)求()f x 在1x =处的切线方程； (2)当e x ≥时，不等式()ekf x x ≥+恒成立，求实数k 的取值范围； 9．已知函数e ()(1)1xf x b x a=+-+(1)当114a b ==-，时，求曲线()y f x =在点（0，f （0））处的切线方程； (2)当1a =时，()2f x ≥恒成立，求b 的值．10．已知函数()()e 11xf x b x a=+-+(1)当114a b ==-，时，求曲线()y f x =在点（0，f （0））处的切线方程； (2)当20e <≤a ，且2x >时，()()ln 1f x b a x ⎡>-⎣]恒成立，求b 的取值范围.【参考答案】一、解答题1．(1)22ln 2ln 2a a --+ (2)2a = 【解析】【分析】（1）求导求解单调性即可求出最值；（2）要使()0f x ≤成立必须()22ln 2ln 20a a a ϕ=--+≤，求单调性求解即可. (1)因为()()2ln 0f x a x ax a =+->，所以()()20axf x a x-'=>，由()0f x '>得20x a <<；()0f x '<得2x a>；所以()f x 在20,a⎛⎫⎪⎝⎭上单调递增，在2,a ⎛⎫+∞ ⎪⎝⎭上单调递减，故()222ln 2ln 2max f x f a a a ⎛⎫==--+ ⎪⎝⎭，即()()22ln 2ln 20a a a a ϕ=--+>.(2)要使()0f x ≤成立必须()22ln 2ln 20a a a ϕ=--+≤，因为()2a a aϕ-'=，所以当02a <<，()0a ϕ'<；当2a >时，()0a ϕ'>.所以()a ϕ在()0,2上单调递减，在()2,+∞上单调递增. 所以()()20min a ϕϕ==，所以满足条件的a 只有2，即2a =. 【点睛】用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面： (1)在利用导数讨论函数的单调区间时，首先要确定函数的定义域； (2)不能随意将函数的2个独立的单调递增（或递减）区间写成并集形式； (3)利用导数解决含参函数的单调性问题时，一般将其转化为不等式恒成立问题，解题过程中要注意分类讨论和数形结合思想的应用. 2．(1)02a <≤ (2)证明见解析【解析】【分析】（1）分析可知1≥x ，()()01f x f ≤=，分02a <≤、2a >两种情况讨论，利用导数分析函数()f x 在[)1,+∞上的单调性，验证()()1f x f ≤对任意的1≥x 是否恒成立，由此可求得实数a 的取值范围；（2）利用导数分析函数()g x 的单调性，可得出12101x x e<<<<，证明出31x x >，证明出当1,1e x ⎛⎫∈ ⎪⎝⎭时，()()11e 1g x x <--，可得出()241e 1x x m >=+-，结合不等式的性质可证得结论成立. (1)解：因为()()1ln 0f x a x x a x =-+>，则()222111a x ax f x x x x -+-'=--=，且()10f =，由题意可知，对任意的1≥x ，()()01f x f ≤=，设21y x ax =-+-，则24a ∆=-，（ⅰ）当02a <≤时，0∆≤，()0f x '≤恒成立且()f x '不恒为零，()f x 在[)1,+∞上是减函数，又因为()10f =，所以()0f x ≤恒成立；（ⅱ）当2a >时，0∆>，方程210x ax -+-=的根为1x =，2x =又因为121=x x ，所以121x x ．由()0f x '>得1x ≤<()0f x '<，得x所以()f x 在⎡⎢⎢⎣⎭上是增函数，在⎫+∞⎪⎪⎝⎭上是减函数，因为()10f =，所以()0f x ≤不恒成立．综上所述，02a <≤． (2)证明：当1a =时，()()21ln g x xf x x x x =+-=，()1ln g x x '=+，由()0g x '<，可得10e x <<，由()0g x '>，可得1ex >，所以()g x 在10,e ⎛⎫⎪⎝⎭上是减函数，在1,e ⎛⎫+∞ ⎪⎝⎭上是增函数，则()min 11e e g x g ⎛⎫==- ⎪⎝⎭，当01x <<时，()ln 0g x x x =<，所以，12101x x e <<<<，且10em -<<，当10,ex ⎛⎫∈ ⎪⎝⎭时，ln 1x <-，所以ln x x x <-，即()g x x <-．设直线y x =-与y m =的交点的横坐标为3x ，则3111ln x m x x x =-=->，下面证明当1,1e x ⎛⎫∈ ⎪⎝⎭时，()()11e 1g x x <--，设()()()111ln 1ln e 1e 1e 1h x x x x x x x ⎡⎤=--=-+⎢⎥---⎣⎦，令()()11ln e 1e 1p x x x =-+--，则()()()()22e 1111e 1e 1x p x x x x --'=-=--，当11ee 1x <<-时，()0p x '<，当11e 1x <<-时，()0p x '>，所以()p x 在11,e e 1⎛⎫ ⎪-⎝⎭上是减函数，在1,1e 1⎛⎫⎪-⎝⎭上是增函数，又因为10e p ⎛⎫= ⎪⎝⎭，()10p =，所以当11ex <<时，()0p x <，()0h x <，故当1,1e x ⎛⎫∈ ⎪⎝⎭时，()()11e 1g x x <--．设直线()111e y x =--与y m =的交点的横坐标为4x ，则41e 1x m -=-，可得()41e 1x m =+-，如下图所示：则()241e 1x x m >=+-，所以21431e x x x x m ->-=+，得证．【点睛】方法点睛：利用导数证明不等式问题，方法如下：（1）直接构造函数法：证明不等式()()f x g x >（或()()f x g x <）转化为证明()()0f x g x ->（或()()0f x g x -<），进而构造辅助函数()()()h x f x g x =-；（2）适当放缩构造法：一是根据已知条件适当放缩；二是利用常见放缩结论；（3）构造“形似”函数，稍作变形再构造，对原不等式同解变形，根据相似结构构造辅助函数. 3．(1)10y +=； (2)[)1,+∞. 【解析】【分析】（1）将1a =-代入函数()f x 中，得出函数()f x 的解析式，进而可以求出切点坐标，再利用导数的几何意义及点斜式即可求解；（2）根据已知条件可以将问题转化为恒成立问题，进而转化为求函数的最值问题，利用导数法求函数的最值即可求解. (1)当1a =-时，()2cos 1sin 2f x x x x x =--+()2cos 10000sin 012f =⨯--+=-，所以切点为0,1，()1sin cos x f x x x '=-++，∴(0)01sin 0cos00f '=-++=，所以曲线()y f x =在点()()0,0f 处的切线的斜率为(0)0k f '==，所以曲线()y f x =在点0,1处的切线的斜率切线方程为()()100y x --=⨯-，即10y +=.(2)由()21si cos n 2f x x x a x x =-++，得()s 1co i s n f x x a x x '=--+因为函数()f x 在3π0,4⎡⎤⎢⎥⎣⎦上单调递减，可得()0f x '≤对任意3π0,4x ⎡⎤∈⎢⎥⎣⎦恒成立，设()()1c s os in g x f x x a x x '==--+，则()cos 1sin g x a x x '=--. 因为si (n 0)001cos00g a =--+=，所以使()0f x '≤对任意3π0,4x ⎡⎤∈⎢⎥⎣⎦恒成立，则至少满足()00g '≤，即10a -≤，解得1a ≥. 下证明当1a ≥时，()0f x '≤恒成立，因为3π0,4x ⎡⎤∈⎢⎥⎣⎦，所以sin 0x ≥，因为1a ≥，所以()sin 1cos f x x x x '≤--+.记s ()cos n 1i h x x x x =--+，则π()1sin 14cos h x x x x ⎛⎫'=-=+ ⎝-⎪⎭. 当π0,2x ⎛⎫∈ ⎪⎝⎭时，()0h x '<；当π3π,24x ⎛⎫∈ ⎪⎝⎭时，()0h x '>. 所以函数()h x 在π0,2⎡⎫⎪⎢⎣⎭上单调递减，在π3π,24⎛⎤ ⎥⎝⎦上单调递增.因为ππ(),h h ⎛⎫==- ⎪⎝⎭33001044，所以()h x 在3π0,4⎡⎤⎢⎥⎣⎦上的最大值为(0)0h =. 即()()1sin cos 0f x h x x x x '≤=--+≤在3π0,4⎡⎤⎢⎥⎣⎦上恒成立. 所以a 的取值范围为[)1,+∞. 4．(1)①112y x =-；②证明见解析 (2){}()210,e -⋃【解析】【分析】（1）①利用导数求出切线的斜率，直接求出切线方程；②令()e 1e x xg x x =+-，利用导数判断出()g x 在(0,)+∞上有唯一零点0x ，利用列表法证明出()f x 在(0,)+∞上有唯一极大值点；（2）令()e xh x a ax =+-.对a 分类讨论：①0a <，得到当1a =-时，()f x 无零点；②0a >，()f x 无零点，符合题意. (1)若1a =，则()1e 1x xf x =-+，()2e 1e (e 1)x x x x f x +-=+'.①在0x =处，()()21110211f '+==+，(0)1f =-. 所以曲线()y f x =在0x =处的切线方程为112y x =-.②令()e 1e x xg x x =+-，()e x g x x '=-，在区间(0,)+∞上，()0g x '<，则()g x 在区间(0,)+∞上是减函数.又(1)10,g =>()22e 10,g =-+<，所以()g x 在(0,)+∞上有唯一零点0x . 列表得：0(2)()e e x x ax af x a--=+，令()e x h x a ax =+-，则()e xh x a '=-.①若0a <，则()0h x '>，()h x 在R 上是增函数.因为11e 10a h a a ⎛⎫⎛⎫=-+< ⎪ ⎪⎝⎭⎝⎭，()1 e > 0h =，所以()h x 恰有一个零点0x . 令0e 0x a +=，得0ln()x a =-.代入0()0h x =，得()ln 0a a a a -+--=，解得1a =-.所以当1a =-时，()h x 的唯一零点为0，此时()f x 无零点，符合题意. ②若0a >，此时()f x 的定义域为R .当ln x a <时，()0h x '<，()h x 在区间(,ln )a -∞上是减函数；当ln x a >时，()0h x '>，()h x 在区间(ln ,+)a ∞上是增函数. 所以min ()(ln )2ln h x h a a a a ==-. 又()010h a =+>，由题意，当2ln 0a a a ->，即20e a <<时，()f x 无零点，符合题意. 综上，a 的取值范围是{}()210,e -⋃.【点睛】导数的应用主要有：（1）利用导函数几何意义求切线方程；（2）利用导数研究原函数的单调性，求极值（最值）；（3）利用导数求参数的取值范围.5．(1)()f x 在(,1)-∞-，(3,)+∞上单调递增，在(1,3)-上单调递减 (2)证明见解析【解析】【分析】（1）直接求导后判断单调性即可；（2）先变形得到323033x a x x -=++，构造函数，求导后说明单调性即可证明. (1)当1a =时，()()321313f x x x x =-++，2()23f x x x '=--. 令()0f x '=，解得1x =-或3x =，当()(),13,x ∞∞∈--⋃+时，()0f x '>；当(1,3)x ∈-时，()0f x '<，故()f x 在(,1)-∞-，(3,)+∞上单调递增，在(1,3)-上单调递减.(2)()321()2333y f x a x a x x =-=-++，由于2330x x ++>，所以()20f x a -=等价于3230.33x a x x -=++设()32333x g x a x x =-++，则()g x '()()222269033x x x xx ++=++，当且仅当0x =或3x =-时，()0g x '=，所以()g x 在(,)-∞+∞上单调递增，故()g x 至多有一个零点，从而()2y f x a =-至多有一个零点. 6．(1)1- (2)极小值32【解析】【分析】（1）求导函数，结合(2)2f '=解方程即可；（2）令()0f x '=进而分析单调性，即可求出极值． (1)由题意可得()1a f x x a x '-=-+，故()12222a f a -'=-+=， 1.a ∴=- (2)由（1）得21()2ln 2f x x x x =+-，所以()()210f x x x x'=+->，令()210f x x x'=+-=，解得1x =，因为当(0,1)x ∈时，()0f x '<，当(1,)x ∈+∞时，()0f x '>，所以函数()y f x =在(0,1)上单调递减，在(1,)+∞上单调递增，所以当1x =时，函数()f x 取得极小值()312f =．7．(1)5,3ln 22⎡⎤--+⎢⎥⎣⎦；(2)答案见解析. 【解析】【分析】(1)代入a ＝1，求f (x )导数，根据导数判断f (x )在[1，2]上的单调性即可求其值域；(2)根据a 的范围，分类讨论f (x )导数的正负即可求f (x )的单调性. (1)a ＝1，则()2121ln ,02f x x x x x =--+>，()22121(1)20x x x f x x x x x-+-=-+='=，∴()f x 在()0,∞+单调递增，∴f (x )在[]1,2单调递增，∴()()()51,2,3ln 22f x f f ⎡⎤⎡⎤∈=--+⎣⎦⎢⎥⎣⎦，即f (x )在[1，2]上值域为5,3ln 22⎡⎤--+⎢⎥⎣⎦；(2)()()()()()223232,0x a a x ax a x a a f x x a a x x x x'-++--=-++==>，()10f x x a '=⇒=，22x a =， 200a a a -≠⇒≠且1a ≠，①当1a >时，21a a >>，0x a <<或2x a >时，()0f x '>，()f x 单调递增，2a x a <<时，()0f x '<，()f x 单调递减；②当01a <<时，201a a <<<，20x a <<或x a >时，()0f x '>，()f x 单调递增，2a x a <<时，()0f x '<，()f x 单调递减；③当0a <时，20a a >>，20x a <<时，()0f x '<，()f x 单调递减，2x a >，()0f x '>，()f x 单调递增；综上，当0a <时，f (x )在()20,a 单调递减，在()2,a +∞单调递增；当01a <<时，f (x )在()20,a ，(),a +∞单调递增，在()2,a a 单调递减；当1a >时，f (x )在()0,a ，()2,a +∞单调递增，在()2,a a 单调递减.8．(1)1y = (2)(],4∞- 【解析】【分析】（1）利用导数的几何意义直接求解即可；（2）分离变量可得()()()e 1ln x x k g x x++≤=，利用导数可求得()()e 4g x g ≥=，由此可得k 的取值范围. (1)()2211ln ln x xf x x x--'==-，()10f '∴=，又()11f =， ()f x ∴在1x =处的切线方程为1y =；(2)当e x ≥时，由()e k f x x ≥+得：()()()()e 1ln e x x k x f x x++≤+=，令()()()e 1ln x x g x x++=，则()2eln x xg x x -'=，令()eln h x x x =-，则()ee1x h x xx-'=-=， ∴当e x ≥时，()0h x '≥，()h x ∴在[)e,+∞上单调递增，()()e e elne 0h x h ∴≥=-=，()0g x '∴≥，()g x ∴在[)e,+∞上单调递增，()()()2e 1ln e e 4eg x g +∴≥==， 4k ∴≤，即实数k 的取值范围为(],4∞-.【点睛】方法点睛：本题考查导数的几何意义、利用导数解决函数中的恒成立问题；解决恒成立问题的基本思路是采用分离变量的方式，将问题转化为变量与函数最值之间关系，即由()a f x ≥得()max a f x ≥；由()a f x ≤得()min a f x ≤.9．(1)25y x =+(2)0b =【解析】【分析】（1）利用切点和斜率求得切线方程.（2）由()2f x ≥恒成立构造函数()()2g x f x =-，对b 进行分类讨论，结合()'g x 研究()g x 的最小值，由此求得b 的值.(1) 当114a b ==-，时，()4e 21x f x x =-+，则()4e 2x f x '=-又因为(0)5,(0)2f f '==所以曲线()y f x =在点（0，f （0））处的切线方程为()520y x -=-，即25y x =+．(2)当1a =时，令函数()()()2e 11x g x f x b x =-=+--，则()2f x ≥恒成立等价于()0g x ≥恒成立．又()e 1,x g x b '=+-．当1b ≥时，()e 10,x g x b '=+->，g (x )在R 上单调递增，显然不合题意；当1b <时，令()e 10,x g x b '=+-<，得ln(1)x b <-．令()e 10x g x b '=+->，得()ln 1x b >-，所以函数g (x )在(,ln(1))b -∞-上单调递减，在(ln(1),)b -+∞上单调递增，所以当ln(1)x b =-时，函数g (x )取得最小值．又因为()00g =，所以0x =为g (x )的最小值点．所以ln(1)0b -=，解得0b =．10．(1)25y x =+(2)[1,)-+∞【解析】【分析】（1）求出()'f x ，然后算出(0),(0)f f '即可；（2）由条件可得e (ln )1ln(1)xb x a x b x a+->-+-恒成立，构造函数()ln (1)h x x b x x =+>，则原不等式等价于e ()x h a(1)h x >-在(2,)x ∈+∞上恒成立，然后可证明2e 1e 10xx x x a--+≥-+>，然后得()h x 在()1,+∞上单调递增，然后即可求解. (1) 当114a b ==-，时，()4e 21x f x x =-+，则()4e 2x f x '=-又因为(0)5,(0)2f f '==所以曲线()y f x =在点（0，f （0））处的切线方程为25y x =+.(2)()()ln 1f x b a x ⎡>-⎣恒成立，即e 1ln(1)ln x bx x b x b a a +-+>-+恒成立. 等价于e (ln )1ln(1)xb x a x b x a+->-+-恒成立. 构造函数()ln (1)h x x b x x =+>，则e e ln 1ln(1)x xb x b x a a+>-+-在(2,)x ∈+∞上恒成立等价于e ()x h a(1)h x >-在(2,)x ∈+∞上恒成立. 因为20e <≤a ，所以2e e ,xx a -≥ 令函数2()e 1(2)x H x x x -=-+>，则2()e 1x H x -'=-，显然()H x '是增函数，则()(2)0,()H x H H x ''>=在()2,+∞上单调递增，所以()()20H x H >=，故2e 1e 10xx x x a--+≥-+>，从而可得()h x 在()1,+∞上单调递增，所以当()1,x ∈+∞时，()10bh x x'=+≥恒成立. 所以b x ≥-，所以1b ≥-，即b 的取值范围是[-1，+∞）【点睛】关键点睛：解答本题第二问的关键是将原不等式变形，构造出函数()ln (1)h x x b x x =+>，属于函数的同构类型，解答的关键是观察不等式的特点，变成同一函数在两个变量处的取值.。

高中数学导数练习题含答案

高中数学导数练习题含答案一、解答题 1．已知函数()()2ln 0f x a x ax a =+-> (1)求()f x 的最大值(2)若()0f x ≤恒成立，求a 的值 2．求下列函数的导数： (1)221()(31)y x x =-+； (2)2321xy x -=+； (3)e cos x y x =3．设函数()()2()ln 1f x x a x x =++-，其中R a ∈.(1)1a =时，求曲线()y f x =在点()()1,1f 处的切线方程； (2)讨论函数()f x 极值点的个数，并说明理由； (3)若()0,0x f x ∀>成立，求a 的取值范围. 4．已知函数()e 1x f x ax =--，a ∈R ． (1)当2a =时，求()f x 的单调区间；(2)若()f x 在定义域R 内单调递增，求a 的取值范围． 5．已知函数2()ln f x x x ax =-．(1)若()0f x ≤恒成立，求实数a 的取值范围； (2)若()112212ln 2ln 200x ax x ax x x -=-=>>，证明：()1212ln ln 10ln 2x x x x ⋅<<．6．已知函数2()2ln f x x x =-+，()()ag x x a x =+∈R . (1)求函数()f x 的单调区间；(2)若函数()f x 与()g x 有相同的极值点，求函数()g x 在区间1[,3]2上的最值.7．已知函数()()()()e 0=+->xf x x b a b 在()()1,1f --处的切线方程为()e 1e e 10x y -++-=．(1)求a ，b 的值；(2)若方程()f x m =有两个实数根12,x x ， ①证明：12m >-；②当0m <时，2121x x m ->+是否成立？如果成立，请简要说明理由．8．已知函数2()e 1)(x f x ax x =-+.(1)求曲线()y f x =在点(0,(0))f 处的切线的方程； (2)若函数()f x 在0x =处取得极大值，求a 的取值范围； (3)若函数()f x 存在最小值，直接写出a 的取值范围. 9．已知函数2()ln (2)(R)f x a x x a x a =+-+∈. (1)若1a =，求()f x 在区间[]1,e 上的最大值； (2)求()f x 在区间[]1,e 上的最小值()g a .10．已知函数()321623f x x ax x =+-+在2x =处取得极值． (1)求()f x 的单调区间；(2)求()f x 在[]4,3-上的最小值和最大值．【参考答案】一、解答题1．(1)22ln 2ln 2a a --+ (2)2a = 【解析】【分析】（1）求导求解单调性即可求出最值；（2）要使()0f x ≤成立必须()22ln 2ln 20a a a ϕ=--+≤，求单调性求解即可. (1)因为()()2ln 0f x a x ax a =+->，所以()()20axf x a x-'=>，由()0f x '>得20x a <<；()0f x '<得2x a>；所以()f x 在20,a⎛⎫⎪⎝⎭上单调递增，在2,a ⎛⎫+∞ ⎪⎝⎭上单调递减，故()222ln 2ln 2max f x f a a a ⎛⎫==--+ ⎪⎝⎭，即()()22ln 2ln 20a a a a ϕ=--+>.(2)要使()0f x ≤成立必须()22ln 2ln 20a a a ϕ=--+≤，因为()2a a aϕ-'=，所以当02a <<，()0a ϕ'<；当2a >时，()0a ϕ'>.所以()a ϕ在()0,2上单调递减，在()2,+∞上单调递增. 所以()()20min a ϕϕ==，所以满足条件的a 只有2，即2a =. 【点睛】用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面： (1)在利用导数讨论函数的单调区间时，首先要确定函数的定义域； (2)不能随意将函数的2个独立的单调递增（或递减）区间写成并集形式； (3)利用导数解决含参函数的单调性问题时，一般将其转化为不等式恒成立问题，解题过程中要注意分类讨论和数形结合思想的应用. 2．(1)21843x x +-；(2)222262(1)x x x --+；(3)e (cos sin )x x x -. 【解析】【分析】（1）（2）（3）由基本初等函数的导数公式，结合求导的乘除法则求各函数的导函数. (1)2222(21)(31)(21)(31)4(31)3(21)1843y x x x x x x x x x '''=-++-+=++-=+-.(2)2222222222(32)(1)(32)(1)2(1)2(32)262(1)(1)(1)x x x x x x x x x y x x x ''-+--+-+----'===+++.(3)(e )cos e (cos )e (cos sin )x x x y x x x x '''=+=-.3．(1)322ln230x y -+-=(2)当0a <时，函数()f x 有一个极值点；当809a ≤≤时，函数()f x 无极值点；当89a >时，函数()f x 有两个极值点. (3)0,1 【解析】【分析】（1）将1a =代入函数()f x 中，得出函数()f x 的解析式，进而可以求出切点坐标，再利用导数的几何意义及点斜式即可求解；（2）根据已知条件，对a 进行分类讨论，利用导数法求函数极值的步骤及函数极值的定义即可求解；（3）根据()0,0x f x ∀>成立，转化为()min 0,0x f x ∀>即可，再利用第（2）的结论即可求解. (1)当1a =时，()2()ln 1f x x x x =++-()()21ln 1111ln 2f =++-=，所以切点为()1,ln2，()()11321,12111112f x x k f x ''=+-∴==+⨯-=++，所以曲线()y f x =在点()()1,1f 处的切线的斜率为()312k f ='=，所以曲线()y f x =在点()1,ln2处的切线的斜率切线方程为()3ln212y x -=-，即322ln230x y -+-= (2)由题意知函数()f x 的定义域为()1,-+∞，()()21212111ax ax a f x a x x x +-+=+-='++，令()()221,1,g x ax ax a x =+-+∈-+∞，（i ）当0a =时，()10f x '=>，函数()f x 在()1,-+∞单调递增，无极值点（ii ）当0a >时，()Δ98a a =-，①当809a <≤时，()()Δ0,0,0g x f x '≤≥≥，所以函数()f x 在()1,-+∞单调递增，无极值点； ②当89a >时，Δ0>，设方程2210ax ax a +-+=两根1212,,x x x x ==此时12x x <()121211111,,,110,12444x x x x g x +=-∴---=>-<<∴<->()()121,,,x x x ∴∈-+∞时，()()0,0g x f x '>>，函数()f x 单调递增；()12,x x x ∈时，()()0,0g x f x '<<，函数()f x 单调递减. ∴函数有两个极值点；③当0a <时，()Δ980a a =->，设方程2210ax ax a +-+=两根1212,,x x x x ==此时12x x >()12110,1x g x -=>∴-<<()11,x x ∴∈-时，()()0,0g x f x '>>，函数()f x 单调递增； ()1,x x ∈+∞时，()()0,0g x f x '<<，函数()f x 单调递减.∴函数有一个极值点；综上所述：当0a <时，函数()f x 有一个极值点；当809a ≤≤时，函数()f x 无极值点；当89a >时，函数()f x 有两个极值点. (3)由()0,0x f x ∀>成立等价于()min 0,0x f x ∀>≥即可. ①当809a ≤≤时，函数()f x 在()0,+∞上单调递增，()()00,0,f x =∴∈+∞时，()0f x >，符合题意；②当819a <≤时，由()00g >，得20x ≤，∴函数()f x 在()0,+∞上单调递增，又()()00,0,f x =∴∈+∞时，()0f x >，符合题意； ③当1a >时，由()00<g ，得20x >()20,x x ∴∈时， ()f x 单调递减,()()200,0,f x x =∴∈时，()0f x <时，不合题意；④当0a <时，设()()ln 1h x x x =-+，()0,x ∈+∞，时，()()110,11x h x h x x x =-=>∴+'+在()0,+∞上单调递增. ∴当()0,x ∞∈+时，()()00h x h >=，即()ln 1x x +<，可得()()()221f x x a x x ax a x <+-=+-，当11x a>-时，()210ax a x +-<，此时()0f x <，不合题意.综上，a 的取值范围是0,1. 【点睛】解决此题的关键是第一问利用导数的几何意义及点斜式即可，第二问主要是对参数进行分类讨论，再结合利用导数法求函数的极值的步骤即可，第三问主要将恒成立问题转化为最值问题再结合第二问的结论即可求解.4．(1)2a = 时，函数 () f x 的单调增区间是(ln2,)+∞ ，递减区间为 (,ln2)-∞ ; (2)a 的取值范围为 (], 0-∞ 【解析】【分析】（1）将2a =代入，对()f x 求导，根据导数正负，确定函数增减即可；（2）()x f x e a '=-，根据题意函数单调增，所以需要()0f x '≥在R 上恒成立，利用参变分离即可求解. (1)当2a = 时，()e 21x f x x =--，()e 2x f x '∴=-.令()0f x '> ，即e 20x -> ，解得 : ln 2x > ；令()0f x '< ，即e 20x -< ，解得 :ln 2x < ；()f x ∴ 在ln 2x =时取得极小值，亦为最小值，即(ln 2)12ln 2f =- .∴ 当2a = 时，函数()f x 的单调增区间是(ln2,)+∞，递减区间为(,ln2)-∞.(2)()e 1x f x ax =-- ()e .x f x a ∴-'=()f x 在R 上单调递增，()e 0x f x a ∴='-≥ 恒成立，即e x a ≤在x ∈R 恒成立，x ∈R时,e (0,)x ∈+∞，0a ∴≤.即 a 的取值范围为(],0∞-.5．(1)1,e∞⎡⎫+⎪⎢⎣⎭(2)证明见解析【解析】【分析】（1）()0f x ≤恒成立，等价于ln xa x ≥恒成立，即max ln x a x ⎛⎫≥ ⎪⎝⎭，令()ln x g x x=，利用导数求出函数()g x 的最大值，即可得出答案；（2）()112212ln 2ln 200x ax x ax x x -=-=>>，即()1212,0x x x x >>为函数ln 2y x ax =-的两个零点，即()1212,0x x x x >>为方程ln 2x a x =的两个根，由（1）知102ea <<，且1201x x <<<，则要证()1212ln ln 10ln 2x xx x ⋅<<，只需证()1212ln 2ln ln x xx x >⋅，即证2122112212ln x x x x x x ->，令12,1x t t x =>，则要证22n 1l t tt ->，令()()12ln 1t t t t t ϕ=-->，利用导数证明()min 0t ϕ>即可. (1)解：因为函数()f x 的定义域为()0,∞+，所以()0f x ≤恒成立，等价于ln xa x ≥恒成立，所以maxln x a x ⎛⎫≥ ⎪⎝⎭，令()ln x g x x =，则()21ln x g x x-'=，当()0,e x ∈时，()0g x '>，()g x 单调递增；当()e,x ∈+∞时，()0g x '<，()g x 单调递减，所以()()max 1e eg x g ==，故1ea ≥，即实数a 的取值范围是1,e∞⎡⎫+⎪⎢⎣⎭；(2)证明：()112212ln 2ln 200x ax x ax x x -=-=>>，即()1212,0x x x x >>为函数ln 2y x ax =-的两个零点，即()1212,0x x x x >>为方程ln 20x ax -=的两个根，即()1212,0x x x x >>为方程ln 2xa x=的两个根，由（1）知102ea <<，即102ea <<，且1201x x <<<，由11ln 2x ax =，22ln 2x ax =，得()1212ln ln 2x x a x x -=-，所以1212ln ln 2x x a x x -=-，要证()1212ln ln 10ln 2x x x x ⋅<<，只需证()1212ln 2ln ln x x x x >⋅，即证121212ln ln 112ln ln ln ln x x x x x x +=+>⋅，即1211222ax ax +>，即12114a x x +>，也就是121212ln ln 112x x x x x x -+>⨯-，整理得221211222ln x x x x x x ->，即证2122112212ln x x xx x x ->，令12,1x t t x =>，则要证2112ln t t t t t -=->，令()()12ln 1t t t t tϕ=-->，则()()222221122110t t t t t t t tϕ--+'=+-==>，所以()t ϕ在()1,+∞上单调递增，所以()()10t ϕϕ>=，所以当t >1时，12ln t t t->，故原结论成立，即()1212ln ln 10ln 2x x x x ⋅<<．【点睛】本题考查了不等式恒成立问题和不等式的证明问题，考查了利用导数求函数的最值，考查了分离参数法，考查了转化思想，考查了学生的数据分析能力和逻辑推理能力，难度较大.6．(1)单增区间为(0,1)，单减区间为(1,)+∞(2)min ()2g x =，max 10()3g x =【解析】【分析】（1）求导之后，分别令()0f x '>，()0f x '<即可求出()f x 的单调区间；（2）由有相同的极值点求出a 的值，再利用对勾函数的单调性求出()g x 在区间1,32⎡⎤⎢⎥⎣⎦上的最值. (1)()f x 的定义域：()0,∞+()()22122x f x x x x--'=-+=，由()0f x '>得01x <<，由()0f x '<得1x >， ∴()f x 的单增区间为()0,1，单减区间为()1,+∞. (2)()21ag x x ='-，由（1）知()f x 的极值点为1.∵函数()f x 与()g x 有相同的极值点， ∴()10g '=，即10a -=，∴1a =，从而()1g x x x =+，()g x 在1,12⎡⎤⎢⎥⎣⎦上单调递减，在(]1,3上递增,又1522g ⎛⎫= ⎪⎝⎭，()1033g =,∴在区间1,32⎡⎤⎢⎥⎣⎦上，()()min 12g x g ==，()max 103g x =.7．(1)1a =，1b =(2)①证明见解析，②成立，理由见解析【解析】【分析】（1）求出导函数，再根据导数的几何意义及切点即在切线上又再曲线上，解出方程，解之即可；（2）①，由（1）求得函数的解析式及导数，利用导数求出函数()f x 的单调区间，从而可求得函数()f x 的最值，再根据方程()f x m =有两个实数根12,x x ，可得函数()f x 的最值m 的关系，即可得证；②，分别求出当直线过()1,0-，()()00,x f x 时和直线过()0,0，()()00,x f x 时割线方程，从而得1243x x x x ->-结合①即可得出结论. (1)解：()()1e xf x x b a =++-'，因为函数()f x 在()()1,1f --处的切线方程为()e 1e e 10x y -++-=，所以()111e eb f a '-=-=-，()()1110ef b a ⎛⎫-=--= ⎪⎝⎭，∴1a =，1b =或1e=a ，2e b =-（舍），所以1a =，1b =； (2)①证明：由（1）可知()()()1e 1x f x x =+-，()()2e 1xf x x '=+-，令()()()2e 1xg x f x x '==+-，则()()3e xg x x '=+，令()0g x '=，得3x =-，所以函数()g x 在(),3-∞-上递减，在()3,-+∞上递增，所以()()min 3g x g =-，即()()3min 3e 10f x f -''=-=--<，又x →+∞，()f x '→+∞，3x <-，()0f x '<，且()010f '=>，()1110ef '-=-<，∴()01,0x ∃∈-，使得()00f x '=，即()002e 10xx +-=，即01e 2x x =+，当0x x <时，()0f x '<，当0x x >时，()0f x '>，所以函数()f x 在()0,x -∞上递减，在()0,x +∞上递增，所以()()()()()0000min011e 1112x f x f x x x x ⎛⎫==+-=+- ⎪+⎝⎭()()()()()22000000211122222x x x x x x +-⎡⎤+⎡⎤⎣⎦=-=-=-++-⎢⎥+++⎣⎦， ∵()01,0x ∈-，∴()021,2x +∈，令()()1,1,2h x x x x=+∈，则()()2110,1,2h x x x '=->∈ ，所以函数()h x 在()1,2上递增，故()001522,22x x ⎛⎫++∈ ⎪+⎝⎭，所以()001122,022x x ⎡⎤⎛⎫-++-∈-⎢⎥ ⎪+⎝⎭⎣⎦，即()min 12f x >-， ∴12m >-；②解：成立，理由如下：当直线过()1,0-，()()00,x f x 时割线方程为()()()00112x y x mx +=-+=+，得()()030211m x x x -+=-+，当直线过()0,0，()()00,x f x 时割线方程为()()200012x y x m x x -+==+，得()()0042021mx x x x -+=+，∴()()()0124320002112111222m x mx x x x m x x x +->-=+=+>++++-+.【点睛】本题考查了导数得几何意义，考查了利用导数解决方程的根的问题，考查了不等式的证明问题，，考查了数据分析和处理能力，考查了转化思想，计算量比较大，属于难题.8．(1)1y = (2)1(,)2-∞ (3)10,4⎛⎤⎥⎝⎦【解析】【分析】（1）先求导后求出切线的斜率'(0)0f =，然后求出直线上该点的坐标即可写出直线方程；（2）根据函数的单调性和最值分类讨论；（3）分情况讨论，根据函数的单调性和极限求解.(1)解：由题意得：22'e 121)e 2)()((x x ax x a f x ax x x ax =-++-=+-'(0)0f =，(0)1f = 故曲线()y f x =在点(0,(0))f 处的切线的方程1y =.(2)由（1）得要使得()f x 在0x =处取得极大值，'()f x 在0x <时应该'()0f x >，'()f x 在0x >时应该'()0f x <，'e 2(1)()x x x ax f a =+-故①0a <且120a a -<，解得0a < ②0a >且120a a->，解得102a << 当0a =时，'()e x f x x =-，满足题意；当12a =时，'21(e )2x f x x =，不满足题意；综上：a 的取值范围为1(,)2-∞.(3)可以分三种情况讨论：①0a ≤②102a <<③12a ≥若0a ≤，()f x 在12(,)a a --∞上单调递减，在12(,0)a a -单调递增，在(0,)+∞上单调递减，无最小值；若102a <<时，当0x <时，x 趋向-∞时，()f x 趋向于0；当0x > ，要使函数取得存在最小值121221212112()[(41)0e ()]e a a a a a a a f a a a a a a -----=-=-≤+，解得104a <≤，故 12a x a -=处取得最小值,故a 的取值范围10,4⎛⎤ ⎥⎝⎦. 若12a ≥时，()f x 在x 趋向-∞时，()f x 趋向于0，又(0)1f =故无最小值；综上所述函数()f x 存在最小值， a 的取值范围10,4⎛⎤⎥⎝⎦. 9．(1)2e 3e 1-+(2)()()221,2ln ,22e 241e e 2e,2e a a a a g a a a a a a --≤⎧⎪⎪=--<<⎨⎪-+-≥⎪⎩ 【解析】【分析】（1）利用导数求得()f x 在区间[]1,e 上的最大值.（2）由()'f x 对a 进行分类讨论，由此求得()f x 在区间[]1,e 上的最小值()g a .(1)当1a =时，()()2ln 31e f x x x x x =+-≤≤，()()()'123123x x f x x x x--=+-=，所以()f x 在区间()()'31,,0,2f x f x ⎛⎫< ⎪⎝⎭递减；在区间()()'3,e ,0,2f x f x ⎛⎫> ⎪⎝⎭递增. ()()212,e e 3e 10f f =-=-+>，所以()f x 在区间[]1,e 上的最大值为2e 3e 1-+.(2)2()ln (2)(R,1e)f x a x x a x a x =+-+∈≤≤，()()()()'1222x x a a f x x a x x --=+-+=，当1,22aa ≤≤时，()f x 在区间()()()'1,e ,0,f x f x >递增，所以()f x 在区间[]1,e 上的最小值为()()1121f a a =-+=--. 当1e,22e 2a a <<<<时，()f x 在区间()()'1,,0,2a f x f x ⎛⎫< ⎪⎝⎭递减；在区间()',e ,02af x ⎛⎫> ⎪⎝⎭，()f x 递增. 所以()f x 在区间[]1,e 上的最小值为()22ln 2ln 222224a a a a a a f a a a a ⎛⎫⎛⎫=+-+⋅=-- ⎪ ⎪⎝⎭⎝⎭. 当e,2e 2a a ≥≥时，()f x 在区间()()()'1,e ,0,f x f x <递减，所以()f x 在区间[]1,e 上的最小值为()()()22e e 2e 1e e 2e f a a a =+-+=-+-. 所以()()221,2ln ,22e 241e e 2e,2e a a a a g a a a a a a --≤⎧⎪⎪=--<<⎨⎪-+-≥⎪⎩. 【点睛】利用导数求解函数的单调性、最值，若导函数含有参数，则需要对参数进行分类讨论，分类讨论标准的制定，可以考虑利用导函数的零点分布来进行分类. 10．(1)增区间为(),3-∞-，()2,+∞，减区间为()3,2-(2)()max 312f x =，()min 163f x =- 【解析】【分析】（1）根据题意得()20f '=，进而得12a =，再根据导数与单调性的关系求解即可；（2）由（1）知[]4,3x ∈-时，()f x 的增区间为[)4,3--，(]2,3，减区间为()3,2-，进而求解()4f -，()3f -，()2f ，()3f 的值即可得答案.(1)解：（1）()226f x x ax '=+-，因为()f x 在2x =处取得极值，所以()24460f a '=+-=，解得12a =．检验得12a =时，()f x 在2x =处取得极小值，满足条件.所以()26f x x x '=+-，令()0f x '>，解得3x <-或2x >，令()0f x '<，解得32x -<<，所以()f x 的增区间为(),3-∞-，()2,+∞，减区间为()3,2-；(2)解：令()260f x x x '=+-=，解得3x =-或2x =，由（1）知()f x 的增区间为(),3-∞-，()2,+∞，减区间为()3,2-；当[]4,3x ∈-时，()f x 的增区间为[)4,3--，(]2,3，减区间为()3,2- 又()()()()321138444642323f -=⨯-+⨯--⨯-+=， ()()()()321131333632322f -=⨯-+⨯--⨯-+=， ()321116222622323f =⨯+⨯-⨯+=-， ()32115333632322f =⨯+⨯-⨯+=-，所以()max 312f x =，()min 163f x =-．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

导数基础练习题20170305
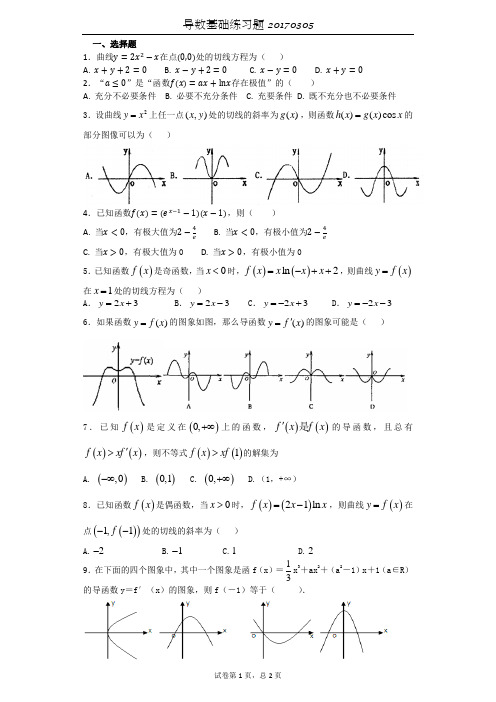
一、选择题
1．曲线y =2x 2−x 在点(0,0)处的切线方程为（）
A. x +y +2=0
B. x −y +2=0
C. x −y =0
D. x +y =0 2．“a ≤0”是“函数f(x)=ax +lnx 存在极值”的（）
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件 3．设曲线2
y x =上任一点(,)x y 处的切线的斜率为()g x ，则函数()()cos h x g x x =的部分图像可以为（）
4．已知函数f(x)=(e
x−1
−1)(x −1)，则（）
A. 当x <0，有极大值为2−4e
B. 当x <0，有极小值为2−4e
C. 当x >0，有极大值为0
D. 当x >0，有极小值为0
5．已知函数()f x 是奇函数，当0x <时，()()ln 2f x x x x =-++，则曲线()y f x =在1x =处的切线方程为（）
A ．23y x =+
B ．23y x =-
C ．23y x =-+
D ．23y x =-- 6．如果函数()y f x =的图象如图，那么导函数()y f x '=的图象可能是（）
7．已知()f x 是定义在()0,+∞上的函数，()()f x f x '是的导函数，且总有
()()f x xf x '>，则不等式()()1f x xf >的解集为
A. (),0-∞
B. ()0,1
C. ()0,+∞
D.（1，+∞）
8．已知函数()f x 是偶函数，当0x >时，()()21ln f x x x =-，则曲线()y f x =在点()()
1,1f --处的切线的斜率为（）
A.2-
B.1-
C.1
D.2 9．在下面的四个图象中，其中一个图象是函f （x ）＝
13
x 3＋ax 2＋（a 2
－1）x ＋1（a ∈R ）的导函数y ＝f ′（x ）的图象，则f （－1）等于（）．
A
二、填空题
10．定义在R 上的偶函数f(x)满足：当x <0时，f(x)=x
x−1，则曲线y =f(x)在点(2,f(2))处的切线的斜率为__________． 11，(0,3]x ∈，其图象上任意一点00(,)P x y 处的切线的斜恒成立，则实数a 的取值范围是． 12．设函数f(x)=x 3−3x +1,x ∈[−2,2]的最大值为M ，最小值为m ，则M +m =__________．
13．在平面直角坐标系xoy 中，若曲线y =ax 2+b
x （a,b 为常数）过点P(2,−5)，且该曲
线在点P 处的切线与直线7x +2y +3=0平行，则a +b = .
14．过函数 ()3
2
325f x x x x =-++图像上一个动点作函数的切线，则切线倾斜角的
取值范围是 __________. 15，若0'()1f x =，则 16．已知定义域为R 的奇函数()y f x =的导函数为()'y f x =，当0x ≠时，
，则 a b c ，，的大小关系是．
17，直线l 与函数()(),f x g x 的图像都相切于点（1,0）．
（1）求直线l 的方程及函数()g x 的解析式；
（2）若()()()h x f x g x '=-（其中()g x '是()g x 的导函数），求函数()h x 的极大值． 18．已知函数f(x)=x 2−2x ，g(x)=ax −1，若∀x 1∈[−1,2]，∃x 2∈[−1,2]，使得f(x 1)=g(x 2
19 （1）若3x =是()f x 的极值点，求()f x 的极大值；（2）求a 的范围，使得()1f x ≥恒成立．
本卷由系统自动生成，请仔细校对后使用，答案仅供参考。

答案第1页，总1页
参考答案
1．D 2．B 3．A 4．D 5．B 6．A 7．B 8．B 9．B 10．1
9 11
12．2 13．−3 143,4ππ⎫⎡⎫
⎪⎪⎢⎭⎣⎭
15．1 16．b c a << 17．（1）1y x =-，
g （2 18．(−∞,
−4]∪[2,+∞)【答案】（1）5-
；（2。