MATLAB环境下ISI信道仿真及自适应均衡器设计程序说明
自适应均衡论述与仿真

权值数不同时,均衡后眼图对比:
6 结语
仿真结果表明,随着均衡器权值 数的增加, 输出眼图汇聚程度也越高; 而且信道切换的瞬间均衡器的权值也 随之自适应调整并逐渐自适应调整。 从图中可以看出,均衡器输入信号由于 信道和噪声的影响,产生了严重的码间 干扰,接收机已经不能正常工作,而均 衡后信号眼图已经完全张开。可见使用 LMS 算法,均衡器能够正常收敛到最优 解并且能够跟踪住信道的变化。仿真源
图 12 权值数为3时,低通信道均衡器输出 Fig.12 The eye pattern of signal through low pass channel and 3-order adaptive filter
图 13 权值数为7时,低通信道均衡器输出 Fig.13 The eye pattern of signal through low pass channel and 7-order adaptive filter
如图2所示, 自适应滤波器其实是 FIR滤波器,且FIR滤波器的各权值由 LMS算法进行实时调整,最终使FIR滤 波器 的输出信号收敛到所需的信号 上。
3 LMS算法简述
从图2可以看出, 自适应均衡器的输 出为:
(9) 其中 为滤波器输出与期望信号的误 差函数。上式就是LMS 算法权值的更新 公式。 e( n ) 通过上面的讨论可以总结出LMS 算法的 具体步骤如下: 步骤l :初始化权值 步骤 2:当 n n 1 时,计算滤波器 的输出 y ( n) wHx ( n) , 计算误差函数 e ( n ) d ( n ) y ( n ), 更新滤波器的权值
J(n) 2X(n)D(n) 2X(n)X(n)TW(n) W(n 1) W(n) X(n)[D(n) XT (n) W(n)]
综合课程设计基于Matlab的自适应均衡器设计

电子信息系综合课程设计基于Matlab的自适应均衡器设计专业名称通信工程班级学号学生姓名指导教师设计时间2010.12.20~2011.1.7课程设计任务书专业:学号:学生姓名(签名):设计题目:基于Matlab的自适应均衡器设计一、设计实验条件实验室,Matlab软件二、设计任务及要求1. 课题要求系统学习时域均衡原理,掌握理论知识;2. 首先进行时域均衡原理和算法设计,再在所用的仿真软件Matlab上对设计进行仿真分析,最后写实验报告;3. 对整个系统设计进行回顾,总结心得。
三、设计报告的内容1.设计题目与设计任务(设计任务书)2.前言(绪论)(设计的目的、意义等)3.设计主体(各部分设计内容、分析、结论等)4.结束语(设计的收获、体会等)5.参考资料四、设计时间与安排1、设计时间:3周2、设计时间安排:熟悉实验设备、收集资料: 4天设计图纸、实验、计算、程序编写调试: 7天编写课程设计报告: 3天答辩: 1天基于Matlab的自适应均衡器设计一、设计目的及意义:通过本学期通信原理课程的学习,主要对数字信号系统的通信原理、传输机制等有了系统深入的了解。
而实践性的课程设计能够起到提高综合运用能力,加强理论知识的学习,提高实验技术,启发创造新思想的效果。
此次课程设计是自适应均衡器设计。
我们按照查找资料、软件选择、系统设计、仿真实现、结果优化这一流程进行。
不仅使我们进一步巩固了课程知识,也提高了我们分析问题、解决问题的能力。
二、设计主体:1 、设计原理数字信号经过这样的信道传输以后,由于受到了信道的非理想特性的影响,在接收端就会产生码间干扰(ISI),使系统误码率上升,严重情况下使系统无法继续正常工作。
理论和实践证明,在接收系统中插入一种滤波器,可以校正和补偿系统特性,减少码间干扰的影响。
这种起补偿作用的滤波器称为均衡器。
时域均衡是利用均衡器产生的时间波形去直接校正已畸变的波形,使包括均衡器在内的整个系统的冲击响应满无码间串扰条件。
MATLAB环境下ISI信道仿真及自适应均衡器设计程序说明书
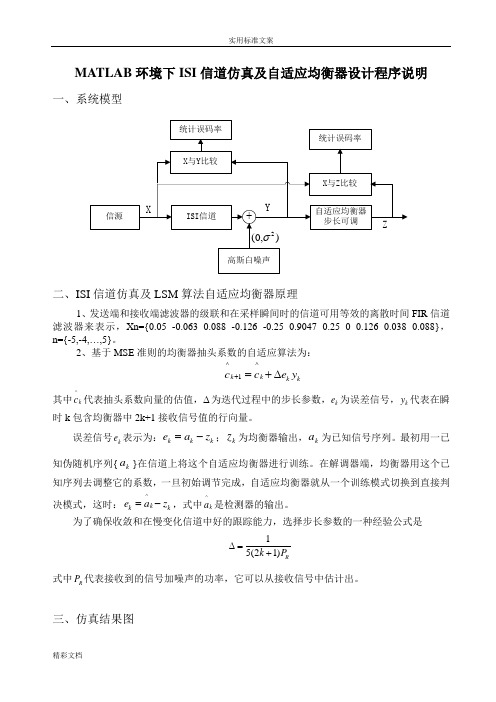
MATLAB 环境下ISI 信道仿真及自适应均衡器设计程序说明一、系统模型二、ISI 信道仿真及LSM 算法自适应均衡器原理1、发送端和接收端滤波器的级联和在采样瞬间时的信道可用等效的离散时间FIR 信道滤波器来表示,Xn={0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088},n={-5,-4,…,5}。
2、基于MSE 准则的均衡器抽头系数的自适应算法为:^^1k k k k c c e y +=+∆其中^k c 代表抽头系数向量的估值,∆为迭代过程中的步长参数,k e 为误差信号,k y 代表在瞬时k 包含均衡器中2k+1接收信号值的行向量。
误差信号k e 表示为:k k k e a z =-;k z 为均衡器输出,k a 为已知信号序列。
最初用一已知伪随机序列{k a }在信道上将这个自适应均衡器进行训练。
在解调器端,均衡器用这个已知序列去调整它的系数,一旦初始调节完成,自适应均衡器就从一个训练模式切换到直接判决模式,这时:^k k k e a z =-,式中^k a 是检测器的输出。
为了确保收敛和在慢变化信道中好的跟踪能力,选择步长参数的一种经验公式是15(21)R k P ∆=+ 式中R P 代表接收到的信号加噪声的功率,它可以从接收信号中估计出。
三、仿真结果图四、结论分析从结果图中我们可以看出,在信噪比逐渐增大的过程中,未经均衡器均衡的差错率没有明显改善,可知系统中始终存在码间干扰造成的误码;经均衡器均衡后的差错率则有明显改善。
但我们同时也可以看到在信噪比较低情况下,均衡器均衡之后的误码率并没有明显改善,甚至没有未均衡的差错率低,这主要是因为噪声为随机信号,功率大时对源信号影响较大,而且均衡器不易跟踪;当我们把均衡器的步长调低后,跟踪能力增强,差错率降低。
附源程序代码:main_plot.mclear;clc;echo off;close all;N=10000; %指定信号序列长度info=random_binary(N); %产生二进制信号序列SNR_in_dB=8:1:18; %AWGN信道信噪比for j=1:length(SNR_in_dB)[y,len]=channel(info,SNR_in_dB(j)); %通过既有码间干扰又有白噪声信道numoferr=0; %初始误码统计数for i=len+1:N+len, %从第len个码元开始为真实信号码元if (y(i)<0), %判决译码elsedecis=1;end;if (decis~=info(i-5)), %判断是否误码,统计误码码元个数numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 未经均衡器均衡,得到的误码率end;semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器,误码率结果图hold on;delta_1=0.11; %指定自适应均衡器的步长delta_2=0.09; %指定自适应均衡器的步长for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_1); %通过自适应均衡器,并设置步长为0.11 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率end;semilogy(SNR_in_dB,Pe,'blacko-'); %自适应均衡器均衡之后,误码率结果图hold on;for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_2); %通过自适应均衡器,并设置步长为0.09 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率end;semilogy(SNR_in_dB,Pe,'blue.-'); %自适应均衡器均衡之后,误码率结果图hold on;xlabel('SNR in dB');ylabel('Pe');title('ISI信道自适应均衡系统仿真');legend('未经均衡器均衡','经自适应均衡器均衡,步长detla=0.11',...'经自适应均衡器均衡,步长detla=0.09');random_binary.m%产生二进制信源随机序列function [info]=random_binary(N)if nargin == 0, %如果没有输入参数,则指定信息序列为10000个码元N=10000;end;for i=1:N,temp=rand;if (temp<0.5),info(i)=-1; % 1/2的概率输出为-1elseinfo(i)=1; % 1/2的概率输出为1endend;channel.m%模拟既有码间干扰又有高斯白噪声的信道function [y,len]=channel(x,snr_in_dB)SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换sigma=1/sqrt(2*SNR); %高斯白噪声的标准差%指定信道的ISI参数,可以看出此信道质量还是比较差的actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];len_actual_isi=(length(actual_isi)-1)/2;len=len_actual_isi;y=conv(actual_isi,x); %信号通过信道,相当于信号序列与信道模型序列作卷积%需要指出,此时码元序列长度变为N+len-1,译码时我们从第len个码元开始到N+len个结束for i=1:2:size(y,2),[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声end;y=y+noise; %叠加噪声gngauss.m%产生高斯白噪声function [gsrv1,gsrv2]=gngauss(m,sgma)if nargin == 0, %如果没有输入实参,则均方为0,标准差为1m=0; sgma=1;elseif nargin == 1, %如果输入实参为1个参数,则标准差为输入实参,均值为0 sgma=m; m=0;end;u=rand;z=sgma*(sqrt(2*log(1/(1-u))));u=rand;gsrv1=m+z*cos(2*pi*u);gsrv2=m+z*sin(2*pi*u);lms_equalizer.m%LSM算法自适应滤波器实现function [z]=lms_equalizer(y,info,delta)estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数K=5;for k=1:size(y,2)-2*K,y_k=y(k:k+2*K); %获取码元,一次11个z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和e_k=info(k)-z_k; %误差估计estimated_c=estimated_c+delta*e_k*y_k; %计算校正抽头系数z(k)=z_k; %均衡后输出的码元序列end;。
《信号与系统》课程设计-数字通信系统中ISI信道均衡器的设计和性能仿真

《信号与系统》课程设计——数字通信系统中ISI 信道均衡器的设计和性能仿真【设计题目】数字通信系统中ISI 信道均衡器的设计和性能仿真【设计要求】(1) 实现数字通信系统的误码率测试程序。
(2) 仿真码间串扰ISI 的影响。
(3) 讨论均衡器的性能。
【设计工具】MATLAB【设计原理】1、一个简单的二进制数字通信系统假设一个简单的二进制数字通信系统,接收机接收到的第n 个时间的信号Y n 可以描述为n n n N b Y +-=)12( (1)其中b n 是发射机发送的第n 个比特信息,b=0或b=1;N n 是接收机接收到信号的同时接收到的噪声,通常描述成均值为0,方差为2σ的高斯分布的随机噪声。
;1 ,0N Y b +-==.1 ,1N Y b ++==如果没有噪声存在,可以很容易地从接收到的信号Y 恢复出信息比特b 。
噪声较小时,若b=0,Y 更接近-1;若b=1,则Y 更接近+1,因此可以通过Y 的正负号恢复信息比特,即0~ ,0 if ;1~ ,0 if =<=>b Y b Y这个过程称为判决,b ~是恢复的比特信息。
但是由于噪声N 的随机性,总有一定的可能会出现较大的N 值,一旦噪声N 大到改变了接收信号Y 的正负号,就会出现判决的错误,导致误码的出现。
实际上,对于这种简单的系统,误码率(即误码出现的概率,Bit Error Rate ,BER )只与2/1σ有关。
定义信噪比(Signal-to-noise ratio ,SNR )2/1σ=SNR ,分子为信号功率,从(1)可知不考虑噪声时信号部分的功率恒等于1;分母为噪声的功率2σ。
下面的MATLAB 例程可以很容易仿真得到SNRdB=5dB()(log 1010SNR SNRdB ⨯=)时的BER 值。
MATLAB 例程:clear all; close all; % 将MATLAB 的变量清空SNRdB = 10; % 定义SNRdBSNR = 10^(SNRdB/10); % 获得SNRNoise_sigma = sqrt(1/SNR); % 从SNR 求出噪声的方差根NN = 1000000; % 仿真的比特总个数B_in = randint(1, NN); % randint()随机产生NN 个比特信号作为输入Y = (2*B_in - 1) + Noise_sigma*randn(1, NN); % randn()是产生高斯随机数的函数B_out = (Y > 0); % 判决N_error = sum(B_in ~= B_out) % 统计误码个数BER = N_error/NN % 计算BER对MATLAB 例程进行必要的修改,仿真SNRdB 从0dB 到10dB 时的BER ,MATLAB 的semilogy()绘图函数,请自己查阅MATLAB 帮助了解该函数的使用说明。
基于MATLAB的通信系统传输信道性能仿真研究毕业设计说明书

1 绪论通信就是把信息从一地有效地传递到另一地,及消息传递的全过程。
通信是由通信系统来实现的,通信系统是只完成信息传递的传输介质和全部设备的总称。
现代通信系统主要借助电磁波在自由空间的传播或在导引媒体中的传输机理来实现,前者称为无线通信系统,后者称为有线通信系统。
1.1 课题的研究背景及意义1.1.1 通信系统研究背景实际的通信系统是一个功能结构相当复杂的系统,对这个系统作出的任何改变(如改变某个参数的设置、改变系统的结构等)都可能影响到整个系统的性能和稳定。
因此,在对原有的通信系统作出改进或建立一个新系统之前,通常需要对这个系统进行建模和仿真,通过仿真结果衡量方案的可行性,从中选择最合理的系统配置和参数设置,然后再应用于实际系统中,这个过程就是通信系统仿真[1]。
在通信技术快速发展的今天,人们对通信系统的性能以及造价都提出了比较高的要求,于是通信仿真便应运而生。
仿真是衡量系统性能的工具,它通过仿真模型的仿真结果来推断原系统的性能,从而为新系统的建立或原系统的改造提供可靠的参考。
现代计算机科学技术快速发展,已经研发出了新一代的可视化的仿真软件。
这些功能强大的仿真软件,使得通信系统仿真的设计和分析过程变得相对直观和便捷,由此也使得通信系统仿真技术得到了更快的发展[2]。
通过仿真.可以降低新系统失败的可能性,消除系统中潜在的弊端,防止对系统中某些功能部件造成过量的负载,优化系统的整体性能,因此,仿真是科学研究和工程建设中不可缺少的方法。
计算机辅助分析和设计技术发展十分迅速,出现了大量实用仿真软件与工具,并应用于通信系统建模、分析和设计,使得通信系统仿真发展很快。
计算机辅助技术基本上有两大类,一是基于公式的方法,用计算机计算复杂的公式;二是用计算机仿真系统的信号波形,即波形级仿真。
现代计算机软硬件技术的快速发展,新一代的可视化的仿真软件的使用使得通信系统仿真的设计和分析过程变得相对直观和便捷,推动了通信系统仿真的快速发展。
MATLAB环境下ISI信道仿真及自适应均衡器设计程序说明书

MATLAB 环境下ISI 信道仿真及自适应均衡器设计程序说明一、系统模型二、ISI 信道仿真及LSM 算法自适应均衡器原理1、发送端和接收端滤波器的级联和在采样瞬间时的信道可用等效的离散时间FIR 信道滤波器来表示,Xn={0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088},n={-5,-4,…,5}。
2、基于MSE 准则的均衡器抽头系数的自适应算法为:^^1k k k k c c e y +=+∆其中^k c 代表抽头系数向量的估值,∆为迭代过程中的步长参数,k e 为误差信号,k y 代表在瞬时k 包含均衡器中2k+1接收信号值的行向量。
误差信号k e 表示为:k k k e a z =-;k z 为均衡器输出,k a 为已知信号序列。
最初用一已知伪随机序列{k a }在信道上将这个自适应均衡器进行训练。
在解调器端,均衡器用这个已知序列去调整它的系数,一旦初始调节完成,自适应均衡器就从一个训练模式切换到直接判决模式,这时:^k k k e a z =-,式中^k a 是检测器的输出。
为了确保收敛和在慢变化信道中好的跟踪能力,选择步长参数的一种经验公式是15(21)R k P ∆=+ 式中R P 代表接收到的信号加噪声的功率,它可以从接收信号中估计出。
三、仿真结果图四、结论分析从结果图中我们可以看出,在信噪比逐渐增大的过程中,未经均衡器均衡的差错率没有明显改善,可知系统中始终存在码间干扰造成的误码;经均衡器均衡后的差错率则有明显改善。
但我们同时也可以看到在信噪比较低情况下,均衡器均衡之后的误码率并没有明显改善,甚至没有未均衡的差错率低,这主要是因为噪声为随机信号,功率大时对源信号影响较大,而且均衡器不易跟踪;当我们把均衡器的步长调低后,跟踪能力增强,差错率降低。
附源程序代码:main_plot.mclear;clc;echo off;close all;N=10000; %指定信号序列长度info=random_binary(N); %产生二进制信号序列SNR_in_dB=8:1:18; %AWGN信道信噪比for j=1:length(SNR_in_dB)[y,len]=channel(info,SNR_in_dB(j)); %通过既有码间干扰又有白噪声信道numoferr=0; %初始误码统计数for i=len+1:N+len, %从第len个码元开始为真实信号码元if (y(i)<0), %判决译码elsedecis=1;end;if (decis~=info(i-5)), %判断是否误码,统计误码码元个数numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 未经均衡器均衡,得到的误码率end;semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器,误码率结果图hold on;delta_1=0.11; %指定自适应均衡器的步长delta_2=0.09; %指定自适应均衡器的步长for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_1); %通过自适应均衡器,并设置步长为0.11 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率end;semilogy(SNR_in_dB,Pe,'blacko-'); %自适应均衡器均衡之后,误码率结果图hold on;for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_2); %通过自适应均衡器,并设置步长为0.09 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率end;semilogy(SNR_in_dB,Pe,'blue.-'); %自适应均衡器均衡之后,误码率结果图hold on;xlabel('SNR in dB');ylabel('Pe');title('ISI信道自适应均衡系统仿真');legend('未经均衡器均衡','经自适应均衡器均衡,步长detla=0.11',...'经自适应均衡器均衡,步长detla=0.09');random_binary.m%产生二进制信源随机序列function [info]=random_binary(N)if nargin == 0, %如果没有输入参数,则指定信息序列为10000个码元N=10000;end;for i=1:N,temp=rand;if (temp<0.5),info(i)=-1; % 1/2的概率输出为-1elseinfo(i)=1; % 1/2的概率输出为1endend;channel.m%模拟既有码间干扰又有高斯白噪声的信道function [y,len]=channel(x,snr_in_dB)SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换sigma=1/sqrt(2*SNR); %高斯白噪声的标准差%指定信道的ISI参数,可以看出此信道质量还是比较差的actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];len_actual_isi=(length(actual_isi)-1)/2;len=len_actual_isi;y=conv(actual_isi,x); %信号通过信道,相当于信号序列与信道模型序列作卷积%需要指出,此时码元序列长度变为N+len-1,译码时我们从第len个码元开始到N+len个结束for i=1:2:size(y,2),[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声end;y=y+noise; %叠加噪声gngauss.m%产生高斯白噪声function [gsrv1,gsrv2]=gngauss(m,sgma)if nargin == 0, %如果没有输入实参,则均方为0,标准差为1m=0; sgma=1;elseif nargin == 1, %如果输入实参为1个参数,则标准差为输入实参,均值为0 sgma=m; m=0;end;u=rand;z=sgma*(sqrt(2*log(1/(1-u))));u=rand;gsrv1=m+z*cos(2*pi*u);gsrv2=m+z*sin(2*pi*u);lms_equalizer.m%LSM算法自适应滤波器实现function [z]=lms_equalizer(y,info,delta)estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数K=5;for k=1:size(y,2)-2*K,y_k=y(k:k+2*K); %获取码元,一次11个z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和e_k=info(k)-z_k; %误差估计estimated_c=estimated_c+delta*e_k*y_k; %计算校正抽头系数z(k)=z_k; %均衡后输出的码元序列end;。
simulink matlab仿真环境教程

simulink matlab仿真环境教程Simulink是面向框图的仿真软件。
演示一个Simulink的简单程序【例1.1】创建一个正弦信号的仿真模型。
步骤如下:(1) 在MATLAB的命令窗口运行simulink命令,或单击工具栏中的图标,就可以打开Simulink模块库浏览器(Simulink Library Browser) 窗口,如图1.1所示。
图7.1 Simulink界面(2) 单击工具栏上的图标或选择菜单“File”——“New”——“Model”,新建一个名为“untitled”的空白模型窗口。
(3) 在上图的右侧子模块窗口中,单击“Source”子模块库前的“+”(或双击Source),或者直接在左侧模块和工具箱栏单击Simulink下的Source子模块库,便可看到各种输入源模块。
(4) 用鼠标单击所需要的输入信号源模块“Sine Wave”(正弦信号),将其拖放到的空白模型窗口“untitled”,则“Sine Wave”模块就被添加到untitled窗口;也可以用鼠标选中“Sine Wave”模块,单击鼠标右键,在快捷菜单中选择“add to 'untitled'”命令,就可以将“Sine Wave”模块添加到untitled窗口,如图1.2所示。
(5) 用同样的方法打开接收模块库“Sinks”,选择其中的“Scope”模块(示波器)拖放到“untitled”窗口中。
(6) 在“untitled”窗口中,用鼠标指向“Sine Wave”右侧的输出端,当光标变为十字符时,按住鼠标拖向“Scope”模块的输入端,松开鼠标按键,就完成了两个模块间的信号线连接,一个简单模型已经建成。
如图1.3所示。
(7) 开始仿真,单击“untitled”模型窗口中“开始仿真”图标,或者选择菜单“Simulink”——“Start”,则仿真开始。
双击“Scope”模块出现示波器显示屏,可以看到黄色的正弦波形。
自适应均衡器的设计与仿真

2014届毕业设计(论文)摘要在移动通信领域中,码间干扰始终是影响通信质量的主要因素之一。
为了提高通信质量,减少码间干扰,在接收端通常采用均衡技术抵消信道的影响。
由于信道响应是随着时间变化的,通常采用自适应均衡器。
自适应均衡器能够自动的调节系数从而跟踪信道,成为通信系统中一项关键的技术。
本篇论文在对无线通信信道进行研究的基础上,阐述了信道产生码间干扰的原因以及无码间干扰的条件,介绍了奈奎斯特第一准则和时域均衡的原理。
深入研究了均衡器的结构和自适应算法,在均衡器的结构中主要介绍了4种自适应均衡器结构即线性横向均衡器、线性格型均衡器、判决反馈均衡器和分数间隔均衡器,并对这几种结构进行了比较。
对于系数调整算法主要介绍了常用的几种算法,包括LMS算法、RLS算法以及盲均衡常用的恒模算法(CMA),并讨论了它们各自的优缺点。
最后选用线性横向均衡器结构与上述3种系数调整算法,利用MATLAB进行仿真,并对结果进行分析与比较。
关键字:自适应均衡器,LMS,RLS,CMA ,MATLABAbstractIn the field of mobile communications, the inter-symbol interferences (ISI) is always one of the primary factor which effects transmission. Adaptive equalization is mainly solution of dealing with ISI. Equalizers are often used to combat the influence of channels for improving communication’s quality and decreasing ISI in receivers. Sometimes, channel response varies due to time, the adaptive equalizer is always necessary. Equalizer coefficients can be automatically adjusted to track the channel as a key communication system technology.On the basis of studying on wireless communication channel, this paper discusses the reasons of resulting inter-symbol interference (ISI) and without conditions, introduces Nyquist first rule and the theory of adaptive equalizers. The equalizer structures and the adaptive algorithm are particularly studied in this paper. Mainly introducing and comparing four adaptive equalizer structures, such as linear horizontal equalizer, line personality type equalizer, decision feedback equalizer, fractionally spaced equalizers. Then we research the algorithms of the adaptive equalizer which are often used, including LMS, RLS, CMA, and discuss their respective advantages and disadvantages. Finally, we choose different adaptive equalizer structures and algorithms, and use the MATALB tool to simulate, at the end of this paper we analyze and compare the results.Keywords: adaptive equalizer, LMS, RLS, CAM, MATLAB目录摘要 (I)ABSTRACT (II)目录 (III)第一章绪论 (1)1.1引言 (1)1.2国内(外)研究现状 (1)1.3论文研究的内容及主要工作 (2)第二章信道、码间干扰及均衡技术 (3)2.1信道 (3)2.1.1 恒参信道 (4)2.1.2 变参信道 (4)2.2通信信道模型 (6)2.3码间干扰 (7)2.4自适应均衡的原理与特点 (10)2.5本章小结 (11)第三章均衡器结构 (12)3.1自适应均衡简介 (12)3.2均衡器的分类 (12)3.3线性横向均衡器结构(LTE) (13)3.4线性格型均衡器(LLE) (14)3.5判决反馈均衡器(DFE) (15)3.6分数间隔均衡器(FSE) (17)3.7本章总结 (20)第四章自适应均衡算法的理论基础 (22)4.1最小均衡误差算法(LMS) (22)4.2递归最小二乘算法(RLS) (25)4.3盲均衡算法 (27)4.4本章小结 (30)第五章均衡器的仿真与实现 (31)5.1采用线性横向均衡器与LMS算法 (31)5.2采用线性横向均衡器与RLS算法 (31)5.3利用恒模算法和线性横向均衡器 (32)总结 (35)参考文献 (36)致谢 (37)附录 (38)第一章绪论1.1引言通常信道特性是一个复杂的函数,它可能包括各种线性失真、非线性失真、交调失真、衰落等。
LMMSE算法信道均衡MATLAB仿真
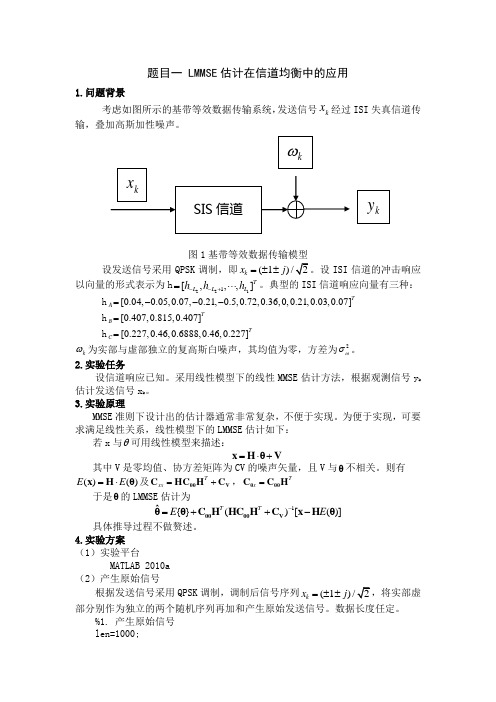
题目一 LMMSE 估计在信道均衡中的应用1.问题背景考虑如图所示的基带等效数据传输系统,发送信号k x 经过ISI 失真信道传输,叠加高斯加性噪声。
图1基带等效数据传输模型设发送信号采用QPSK调制,即(1)/k x j =±±ISI 信道的冲击响应以向量的形式表示为h 2211[,,,]T L L L h h h --+=⋅⋅⋅。
典型的ISI 信道响应向量有三种:h [0.04,0.05,0.07,0.21,0.5,0.72,0.36,0,0.21,0.03,0.07]T A =--- h [0.407,0.815,0.407]T B =h [0.227,0.46,0.6888,0.46,0.227]T C =k ω为实部与虚部独立的复高斯白噪声,其均值为零,方差为2ωσ。
2.实验任务设信道响应已知。
采用线性模型下的线性MMSE 估计方法,根据观测信号y k 估计发送信号x k 。
3.实验原理MMSE 准则下设计出的估计器通常非常复杂,不便于实现。
为便于实现,可要求满足线性关系,线性模型下的LMMSE 估计如下:若x 与θ可用线性模型来描述:=⋅+x H θV其中V 是零均值、协方差矩阵为CV 的噪声矢量,且V 与θ不相关。
则有()()E E =⋅x H θ及T xx =+θθV C HC H C ,T x =θθθC C H于是θ的LMMSE 估计为1ˆ{}()[()]T T E E -=++-θθθθV θθC H HC H C x H θ具体推导过程不做赘述。
4.实验方案 (1)实验平台MATLAB 2010a(2)产生原始信号根据发送信号采用QPSK调制,调制后信号序列(1)k x j =±±部分别作为独立的两个随机序列再加和产生原始发送信号。
数据长度任定。
%1. 产生原始信号 len=1000;xR=randint(1, len);xI=randint(1, len);for i=1:len;if xR(i)==0;xR(i)=-1;endif xI(i)==0;xI(i)=-1;endend % 用循环可能效率低,数据量大时要用矩阵运算xk_source=(xR+1j*xI)/sqrt(2);并绘出星座图。
基于matlab数字均衡器设计说明书

2.设计原理2.1数字滤波器2.1.1 数字滤波器的原理简介数字滤波器的功能是把输入序列通过一定的运算,变换成输出序列。
数字滤波器一般可用两种方法实现:一种是根据描述数字滤波器的数学模型或信号流程图,用数字硬件构成专用的数字信号处理机,即硬件方式;另一种是编写滤波器运算程序,在计算机上运行,即软件方式。
考虑到软件的灵活性及易于实现,本文采用软件方式实现数字滤波器。
数字滤波器有无限冲激响应(IIR)和有限冲激响应(FIR)两种。
下面分别介绍:(1) IIR滤波器IIR滤波器的特点是:单位冲激响应h(n)是无限长的;系统函数H(z)在有限长Z平面(0<|Z|<∞)有极点存在;结构上存在输出到输入的反馈,也即结构上是递归型的;因果稳定的IIR滤波器其全部极点一定在单位圆内。
其系统函数为(1)计算机上实现时则需要用到差分方程的形式,如下(2)IIR滤波器有四种基本的网络结构(具体参看文献[3]),直接I型、直接II 型、级联型与并联型。
其中直接I型需要2N个延迟单元,而直接II型只需要N个延迟单元。
因此,用软件实现时,直接II型少占用存储单元。
级联型则是将N阶IIR系统函数分解成二阶因式连乘积,并联型则是将系统函数化成部分分式之和,则可得到IIR数字滤波器的并联结构。
(2) FIR滤波器IIR滤波器的特点是:系统的单位冲激响应h(n)是个有限长序列;系统函数|H(z)|在|z|>0处收敛,极点全部在z=0处(即FIR一定为稳定系统);结构上主要是非递归结构,没有输出到输入反馈。
但有些结构中(例如频率抽样结构)也包含有反馈的递归部分。
其系统函数的一般形式为(3)对应的差分方程为(4)FIR系统的基本结构有直接型、级联型、快速卷积型、频率取样型等。
2.1.2 FIR与IIR滤波器的比较与选择IIR滤波器可以用比FIR滤波器少的阶数来满足相同的技术指标,这样,IIR滤波器所用的存储单元和所用的运算次数都比FIR滤波器少。
matlab信道仿真课程设计

matlab信道仿真课程设计一、课程目标知识目标:1. 掌握Matlab软件的基本操作,熟悉其在信道仿真中的应用;2. 理解并掌握信道模型的基本原理,包括信道冲激响应、信道衰落等;3. 学会使用Matlab进行信道仿真的编程与调试。
技能目标:1. 能够运用Matlab软件构建并实现不同类型的信道模型;2. 能够根据实际需求,调整信道参数,进行仿真实验;3. 能够对仿真结果进行分析和解释,提出优化方案。
情感态度价值观目标:1. 培养学生对通信工程领域的兴趣,激发其探索精神;2. 培养学生具备良好的团队合作意识,提高沟通与协作能力;3. 培养学生严谨的科学态度,注重实验数据的真实性。
本课程针对高年级通信工程及相关专业学生,结合学科特点,注重理论与实践相结合。
通过本课程的学习,使学生能够熟练运用Matlab软件进行信道仿真,提高其在通信领域的实际操作能力。
同时,培养学生具备良好的团队合作意识,提升其综合素质,为未来从事相关领域工作打下坚实基础。
教学要求包括但不限于:课堂讲解、上机实践、小组讨论、课后作业等,旨在使学生达到上述课程目标,实现具体学习成果。
二、教学内容1. Matlab软件入门:Matlab基本操作与常用命令,数据类型与结构,脚本与函数编写;2. 信道模型原理:介绍信道的基本概念,信道冲激响应,信道衰落类型(如瑞利衰落、对数正态衰落等);3. Matlab信道仿真编程:基于Matlab的信道仿真流程,编程技巧与调试方法;- 信道建模:构建不同类型的信道模型,如AWGN信道、多径信道等;- 参数设置:调整信道参数,如路径损耗、多径时延等;- 仿真实验:进行信道仿真实验,观察与分析仿真结果;4. 信道仿真结果分析:分析仿真结果,探讨信道特性对通信系统性能的影响;5. 优化方案设计:针对仿真过程中发现的问题,提出信道优化方案;6. 教学案例分析:结合教材中的实际案例,分析信道仿真的应用场景和实际意义。
MATLAB基本操作和Simulink信道仿真

实验报告课程名称:MATLAB程序设计实验项目:MATLAB基本操作和信道仿真班级:学号:姓名:成绩:教师签字:1.实验项目名称MATLAB 基本操作和信道仿真2.实验目的熟悉MATLAB 的运行环境,学习矩阵生成和计算、基本运算、基本函数、符号运算和绘图等操作;加性高斯白噪声信道仿真和衰落多径信道仿真。
3.实验内容与实验步骤 要完成的实验内容:常见离散信号的MATLAB 产生和图形显示;利用DFT 分析离散时间信号的频谱;离散系统的差分方程、冲激响应和卷积分析;基于MATLAB 的数字滤波器设计;信道仿真。
应用(或涉及)的原理: (1)单位抽样序列⎩⎨⎧=01)(n δ≠=n n 在MATLAB 中可以利用zeros()函数实现,;1)1();,1(==x N zeros x如果)(n δ在时间轴上延迟了k 个单位,得到)(k n -δ即:⎩⎨⎧=-01)(k n δ≠=n kn单位阶跃序列⎩⎨⎧01)(n u00<≥n n 在MATLAB 中可以利用ones()函数实现,);,1(N ones x =正弦序列)/2sin()(0ϕπ+=S f n f A n x在MATLAB 中1:0),/***2sin(*0-=+=N n fai f n f pi A x s复正弦序列n j e n x ϖ=)(在MATLAB 中1:0),**exp(-==N n n w j x指数序列n a n x =)((2)在MATLAB 中1:0,.^-==N n n a xN 点序列()x n 的DFT 定义:∑∑-=--===121N n kn NjN n knNen x Wn x k X π)(][)(在MATLAB 中,可以用函数X = fft(x,N)和x = ifft(X,N)计算N 点序列的DFT 正、反变换。
(3)于一个离散系统,其输入、输出关系可用以下差分方程描述:[][]NMkk k k dy n k p x n k ==-=-∑∑输入信号分解为冲激信号,[][][]m x n x m n m δ∞=-∞=-∑。
MATLAB环境下ISI信道仿真及自适应均衡器设计程序说明

MATLAB环境下ISI信道仿真及自适应均衡器设计程序说明MATLAB是一种广泛用于科学计算和工程领域的高级编程语言和环境。
在MATLAB环境下,可以进行ISI(Inter-Symbol Interference)信道仿真及自适应均衡器设计。
ISI是指传输过程中,当前符号对后续符号产生的干扰,会导致接收端的误码率增加。
自适应均衡器旨在消除ISI,提高信号的传输质量。
下面是一个示例程序,用于说明在MATLAB环境下进行ISI信道仿真及自适应均衡器设计的步骤和方法:1.生成发送信号:首先,定义发送信号的长度和发送符号序列。
可以使用随机数生成器或自定义发送符号序列。
例如,可以使用randi函数生成一个长度为N的随机二进制序列。
2.传输信号:将发送信号通过ISI信道传输。
可以使用MATLAB中的conv函数来模拟信号通过ISI信道,conv函数将发送信号与信道冲激响应进行卷积操作。
信道冲激响应可以根据具体的信道特性进行定义,例如,可以使用瑞利衰落信道或AWGN(Additive White Gaussian Noise)信道。
3.加入噪声:在传输信号的基础上添加噪声。
可以使用MATLAB中的awgn函数来添加高斯白噪声。
awgn函数通过指定信号的信噪比(SNR)来控制噪声的强度。
4.接收信号:接收被噪声污染的信号。
可以使用MATLAB中的corr函数来计算接收信号与发送信号之间的相关性,以便后续均衡器设计。
5.自适应均衡器设计:使用自适应均衡器算法来消除ISI。
在MATLAB环境中,有多种自适应均衡器算法可供选择,包括LMS(Least Mean Squares)、NLMS (Normalized Least Mean Squares)、RLS(Recursive Least Squares)等算法。
6.误码率评估:使用误码率作为性能指标来评估均衡器的性能。
可以通过比较接收信号与发送信号之间的误差来计算误码率。
信道均衡技术的MATLAB仿真开题报告.doc

[13]Godard,D,Self-Recovering Equalization and Carrier Trackingin Two-Dimensional Data
CommunicatioSystems,Communications[J],IEEETransactionson[legacy,pre-1988],vol.28,no.11,pp.1867-682,1975.
[5]吴伟陵.牛凯.移动通信原理[M].北京:电子工业出版社,2005.
[6]何振亚.自适应信号处理[M].北京:科学出版社,2002.
[7]沈福民.自适应信号处理[M].西安:西安电子科技大学出版社,2001.
[8]陈怀琛.MATLAB及其在理工课程中的应用指南[M].西安:西安电子科技大学出版社,2004.
CommunicatioSystems》中表示,最常用于均衡的线性滤波器是一个横向滤波器,称为线性均衡。有两种常用的方法确定均衡器的抽头系数:迫零(ZF)准则和最小均方误差(MMSE)准则。研究表明,线性均衡器对于像固定电话这样的信道来说性能良好,因此这种算法被广泛应用到各种码间干扰不是很严重的场合。然而随着移动通信技术的发展,这种均衡算法的弱点逐渐暴露出来。因此人们把研究的重点放在了实现简单、性能较好的非线性均衡器上。
RLS自适应滤波器的Matlab设计与仿真概要

1引言目前,自适应滤波器技术在通信和雷达技术的信道均衡、回波抵消、噪声消除或抑制、语音编码、自适应跳频、天线旁瓣抑制、谱线增强、雷达杂波处理、雷达运动目标显示、窄带干扰抑制以及生物医学中的微弱电信号的处理等方面均获得了广泛的应用. 自适应滤波器是这样的处理器, 它在输入信号特性未知或者输入信号特性变化时,能够调整自己的参数, 以满足某种最佳滤波准则的要求.在设计滤波器时应该根据输入信号的特性,设计出最佳的滤波器. 那么, 什么样的滤波效果才算是最佳呢? 必须有一个判断的标准. 至今已研究出很多最佳滤波准则. 常见的有最小均方误差准则、最小二乘准则等. 最佳滤波准则和自适应滤波器关系密切,最佳滤波准则规定了与某种特性的信号对应的最佳参数,而这个最佳参数指出了自适应滤波器调整参数的方向. 以下主要介绍这两个准则.(1 最小均方误差准则 LM S(Least M ean Squar e 就是要使输出信号和理想信号的误差的平方的均值最小. 设 d(n 为滤波器输出要逼近的信号, y(n 为滤波器输出信号, 则误差为 e(n =d(n -y(n , 最小均方误差准则就是要使 E {e 2(n }达到最小.(2 最小二乘准则 LS(Least Squar e 就是要使一定范围内(从 k 到 k+m - 误差的平方和达到最小, 也就是要使 k+m -1i =k Σ达到最小.2最小二乘法 (RLS最小二乘算法(LS, Least -squar es 是一种批处理方法, 通过一个数据块接一个数据块的重复计算来适应非平稳数据, 因此它的计算量大. 推广最小二乘法将得到一种应用更广泛的算法, 即递推最小二乘法(R LS . 一般说来, R LS 算法具有较好的收敛性能和跟踪能力, 但是要求较多的计算量, 目前最快的 R LS 算法要比 LM S 算法多 2-3倍的计算量, 因此, R LS 自适应滤波一般用于要求较高的场合. 2. 1R LS 算法原理由于 LM S 算法的收敛速度很慢,为了得到较快的收敛速度, 有必要设计包含附加参数的更复杂的算法. 在快速收敛算法的推导中, 我们将采用最小二乘法. 因此, 将直接处理接收数据, 使二次性能指数最小, 而 LM S 是使平方误差的期望值最小. 这就意味着用时间平均而不是统计平均来表示性能指数.基于时间平均的最小平方误差被定义如下:J(n =ni =1Σλe 2(i (1式中, λ是接近 1, 但是小于 1的加权因子, 且误差 e(i 为:e(i =d(i -X T W (n (2 且 X (i =[x(i , x(i -1 , … , x(i -M +1 ]T(3 式中, X (i 是 i时刻的输入数据向量, W (n 是 n 时刻的新的抽头增益向量. 因而 e(i 是用 n 时刻的抽头增益向量测试时刻的旧数据所得的误差, J(n 是在所有旧数据上用新抽头增益所得的累计平方误差.要完成 R LS 算法就要找到均衡器的抽头增益向量 W (n , 使得累计平方误差J(n 最小. 为了测试新的抽头增益向量, 会用到那些先前的数据. 而因子λ会在计算时更依赖于新近的数据, 也就是说, J(n 会丢掉非稳定环境中的较旧的数据. 如果信道是稳定的, 那么λ可以设为 1.为了获得 J(n 的最小值, 可使 J(n 的梯度为 0, 即坠 J(n =0通过运算可知:R (nW 赞 (n =P(n (4式中, W 赞 (n 是 R LS 均衡器的最佳抽头增益向量. 方阵 R (n 是输入数据向量X (i 的确定相关矩阵, 向量 P(n 是输入向量 X (i 和期望输出 d(i 之间的确定互相关矩阵, 即:R (n =ni =1Σλn-1X *(i X T (i (5 P(n =n i =1Σλn-1d *(i X (i(6要用式(4 均衡器的抽头增益向量W 赞 (n , 就需要计算 R -1(n . 从式(5 中 R (n 的定义式, 我们可以得到关于 R (n-1 的递归公式:R (n =λR (n-1 +X (n X T (n (7同理得到 P(n 的递推表示式为:P(n =λP(n-1 +X (n d(n (8根据矩阵求逆定理, 若 A , B 是 M ×M 的正定矩阵,C 是一个 M ×N 矩阵,D 是一个 N ×N 矩阵, 当 A =B -1+CD -1C T 时, 有 A -=B-BC (D +C T BC -1C TB.现令 A =R (n , B -1=λR (n-1 , C=XR LS 自适应滤波器的 M at l ab 设计与仿真张立萍(赤峰学院物理与电子信息工程系,内蒙古赤峰024000摘要:自适应滤波技术已经被广泛应用于数字通信、雷达、生物医学和工业控制等领域 . 本文介绍了 R LS 算法, 并以随机干扰噪声信号为研究对象, 在 Matlab 上设计了 R LS 自适应滤波器的 M 文件,进行了仿真, 为硬件实现提供了有力的参考 . 关键词:自适应滤波器; R LS 算法; Matlab ; M 文件中图分类号:TN 273. 2文献标识码:A 文章编号 :1673-260X (2011 04-0025-02Vol. 27No. 4Apr. 2011第 27卷第 4期 2011年 4月赤峰学院学报(自然科学版 Journal of Chifeng University (Natural Science Edition 25--(n , D =J, 可以得到 R -1(n 递归公式:R -1(n =1R -1(n-1 - R -1(n-1 X (n X T (n R -1(n-1! " (9 令:K (n =R -1(n-1 X (n (10则(9 变为:R -1(n =λ-1[R -1(n-1 -K (n X T (n R -1(n-1 ](11 将式(10 中 K (n 的表示式重新安排:K (n =λ-1R -1(n-1 X (n -λ-1K (n X T (n R -1(n-1 X (n=λ-1[R -1(n-1 -K (n X T (n R -1(n-1 ]X (n=R -1(n X (n (12 由式(4 、 (8 、 (11 和式(12 可得W 赞 (n 的递推公式:W 赞 (n =R -1(n P(n =R -1(n [λP(n-1 +X (n d(n=λR -1(n P(n-1 +R -1(n-1 X (n d(n=λλ-1[R -1(n-1 -K (n X T (n R -1(n-1 ]P(n-1 +R -1(n-1 X (n d(n =R -1(n-1 P(n-1 -K (n X T (n R -1(n-1 P(n-1 +K (n d(n =W 赞 (n-1 -K (n X T (n W 赞 (n-1 +K (n d(n=W 赞 (n-1 +K (n [d(n -X T (n W 赞 (n-1 ]=W 赞 (n-1 +K (n α(n式中:α(n =d(n -X T (n W 赞 (n-1内积 X T (n W 赞 (n-1 表示利用 n-1时刻滤波器权系数对期望响应 d(n 作的一个估计, 所以称为先验估计误差.2. 2R LS 算法实现①初始化:W 赞 (0 =0, R -1(0 =δ-1I , δ是一个正常数②对于每一个时刻n=1, 2, … , 进行如下计算:y(n =W T(n-1 X (ne(n =d(n -y(nK (n =R -1(n-1 X (nα(n =d(n -X T (n W 赞 (n-1R -1(n =λ-1[R -1(n-1 -K (n X T (n R -1(n-1 ]W 赞 (n =W 赞 (n-1 +K (n α(n这样, 就用 R -1(n 的递归运算来取代了矩阵反演运算[X T (n X (n ]-1. 其中, δ是正则化参数, δ的设定与信噪比有关, 正则化参数δ与信噪比的关系己由 M oust a-ki des (1997 给出详细说明.3RLS 自适应滤波器 M 文件的设计与仿真根据前面介绍的 R LS 算法, 用 M A TLA B 设计 R LS 自适应滤波器. 下面将在M A TLA B 环境中编写 M 文件对 R LS 算法进行设计和仿真, 验证算法的可行性.在 M A TLA B 中编写 M 文件 R LS. m , 其中, 各参数的意义如下:s:标准正弦信号, 最大峰值为 m axV p=1. 00.sn:标准信号叠加标准白噪声(最大峰值为 m axV p=3. 94 . st ep:滤波器指数加权因子λ, 取值为 0. 99.W (n :滤波器的权向量序列.en:s(i 信号减去滤波器输出信号后得到的误差信号. N :时域抽头 R LS 算法滤波器阶数, 取值为 128.dl en:输入信号抽样点数, 取值为 1024.del t a:正则化参数δ, 取值为 0. 001.R LS 算法中各向量的更新表达式在 M 文件中的实现代码为:f or n=N :dl en;u=sn((n :-1:(n-N +1 ;v=p*u' ;k=v/(st ep+u*v ;y(n =u*w;e(n =s(n -y(n ;w=w+k*conj (e(n ;p=(1/st ep *(eye(N -k*u *p;end仿真时, 原始信号选为 si n((0. 05*pi *t , 其中 t =1:dl en, 噪声信号采用标准白噪声, 在 M A TLA B 环境中运行 R LS. m 文件, 调用绘图函数, 得到 R LS 算法的仿真结果如图 1. R LS 算法的均方误差曲线如图 2所示.4结束语R LS 算法具有良好的收敛速度,除收敛速度快于 LM S 算法以及稳定性强外, 而且具有更高的起始收敛速度、更小的权噪声和更大的抑噪能力.———————————————————参考文献 :〔 1〕么晖 . 基于 FPGA 的自适应滤波器设计 [D]. 硕士学位论文 . 北京 :航天科工集团第三研究院 , 2005.〔 2〕黄埔堪 , 陈建文 , 楼生强 . 现代数字信号处理 [M]. 北京 :电子工业出版社 , 2003.〔 3〕龚耀寰 . 自适应滤波器 [M]. 北京 :电子工业出版社 , 1989. 〔 4〕韩利竹 . MATLAB 电子仿真与应用 [M]. 北京 :国防工业出版社 , 2001.〔 5〕王立宁 , 乐光新 . MATLAB 与通信仿真 [M]. 北京 :人民邮电出版社 , 2000.〔 6〕 Simon Haykin . Adaptive Filter Thearo[M]. 北京 :电子工业出版社 , 2006.图 2R LS算法的均方误差曲线图 1R LS 算法的输入和输出曲线26 --。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB 环境下ISI 信道仿真及自适应均衡器设计程序说明
一、系统模型
二、ISI 信道仿真及LSM 算法自适应均衡器原理
1、发送端和接收端滤波器的级联和在采样瞬间时的信道可用等效的离散时间FIR 信道滤波器来表示,Xn={0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088},n={-5,-4,…,5}。
2、基于MSE (均方准则)的均衡器抽头系数的自适应算法为:
^^1k k k k c c e y +=+∆
其中^
k c 代表抽头系数向量的估值,∆为迭代过程中的步长参数,k e 为误差信号,k y 代表在瞬时k 包含均衡器中2k+1接收信号值的行向量。
误差信号k e 表示为:k k k e a z =-;k z 为均衡器输出,k a 为已知信号序列。
最初用一已知伪随机序列{k a }在信道上将这个自适应均衡器进行训练。
在解调器端,均衡器用这个已知序列去调整它的系数,一旦初始调节完成,自适应均衡器就从一个训练模式切换到直接判决模式,这时:^k k k e a z =-,式中^k a 是检测器的输出。
为了确保收敛 和 在慢变化信道中好的跟踪能力,选择步长参数的一种经验公式是
15(21)R k P ∆=+ 式中R P 代表接收到的信号加噪声的功率,它可以从接收信号中估计出。
三、仿真结果图
四、结论分析
从结果图中我们可以看出,在信噪比逐渐增大的过程中,未经均衡器均衡的差错率没有明显改善,可知系统中始终存在码间干扰造成的误码;经均衡器均衡后的差错率则有明显改善。
但我们同时也可以看到在信噪比较低情况下,均衡器均衡之后的误码率并没有明显改善,甚至没有未均衡的差错率低,这主要是因为噪声为随机信号,功率大时对源信号影响较大,而且均衡器不易跟踪;当我们把均衡器的步长调低后,跟踪能力增强,差错率降低。
附源程序代码:
main_plot.m
clear;
clc;
echo off;
close all;
N=10000; %指定信号序列长度
info=random_binary(N); %产生二进制信号序列
SNR_ in _dB=8:1:18; %AWGN信道信噪比
for j=1:length(SNR _in_ dB)
[y, len ]=channel(info, SNR _in _dB(j)); %通过既有码间干扰又有白噪声信道
numoferr=0; %初始误码统计数
for i=len+1:N+len, %从第len个码元开始为真实信元
if (y(i)<0), %判决译码
decis=-1;
else
decis=1;
end;
if (decis~=info(i-5)), %判断是否误码,统计误码码元个数
numoferr=numoferr+1;
end;
end;
Pe(j)=numoferr/N; % 未经均衡器均衡,得到的误码率
end;
semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器,误码率结果图
hold on;
delta_1=0.11; %指定自适应均衡器的步长
delta_2=0.09; %指定自适应均衡器的步长
for j=1:length(SNR_in_dB)
y=channel(info,SNR_in_dB(j)); %通过信道
z=lms_equalizer(y,info,delta_1); %通过自适应均衡器,并设置步长为0.11 numoferr=0;
for i=1:N,
if (z(i)<0),
decis=-1;
else
decis=1;
end;
if (decis~=info(i)),
numoferr=numoferr+1;
end;
end;
Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率
end;
semilogy(SNR _in _ dB, Pe ,'blacko-'); %自适应均衡器均衡之后,误码率结果图 hold on;
for j=1:length(SNR_in_dB)
y=channel(info,SNR_in_dB(j)); %通过信道
z=lms_equalizer(y,info,delta_2); %通过自适应均衡器,并设置步长为0.09 numoferr=0;
for i=1:N,
if (z(i)<0),
decis=-1;
else
decis=1;
end;
if (decis~=info(i)),
numoferr=numoferr+1;
end;
end;
Pe(j)=numoferr/N; % 经自适应均衡器均衡后,得到的误码率
end;
semilogy(SNR_in_dB,Pe,'blue.-'); %自适应均衡器均衡之后,误码率结果图
hold on;
xlabel('SNR in dB');
ylabel('Pe');
title('ISI信道自适应均衡系统仿真');
legend('未经均衡器均衡','经自适应均衡器均衡,步长detla=0.11',...
'经自适应均衡器均衡,步长detla=0.09');
random_binary.m
%产生二进制信源随机序列
function [info]=random_binary(N)
if nargin == 0, %如果没有输入参数,则指定信息序列为10000个码元
N=10000;
end;
for i=1:N,
temp=rand;
if (temp<0.5),
info(i)=-1; % 1/2的概率输出为-1
else
info(i)=1; % 1/2的概率输出为1
end
end;
channel.m
%模拟既有码间干扰又有高斯白噪声的信道
function [y,len]=channel(x,snr_in_dB)
SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换
sigma=1/sqrt(2*SNR); %高斯白噪声的标准差
%指定信道的ISI参数,可以看出此信道质量还是比较差的
actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];
len_ actual _isi=(length(actual_isi)-1)/2;
len=len_actual_isi;
y=conv(actual_isi,x); %信号通过信道,相当于信号序列与信道模型序列作卷积
%需要指出,此时码元序列长度变为N+len-1,译码时我们从第len个码元开始到N+len个结束
for i=1:2:size(y,2),
[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声
end;
y=y+noise; %叠加噪声
gngauss . m
%产生高斯白噪声
function [gsrv1,gsrv2]=gngauss(m,sgma)
if nargin == 0, %如果没有输入实参,则均方为0,标准差为1
m=0; sgma=1;
elseif nargin == 1, %如果输入实参为1个参数,则标准差为输入实参,均值为0 sgma=m; m=0;
end;
u=rand;
z=sgma*(sqrt(2*log(1/(1-u))));
u=rand;
gsrv1=m+z*cos(2*pi*u);
gsrv2=m+z*sin(2*pi*u);
lm _equalizer .m
%LSM算法自适应滤波器实现
function [z]=lms_equalizer(y,info,delta)
estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数
K=5;
for k=1:size(y,2)-2*K,
y_k=y(k:k+2*K); %获取码元,一次11个
z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和
e_k=info(k)-z_k; %误差估计
estimated_c=estimated_c+delta*e_k*y_k; %计算校正抽头系数
z(k)=z_k; %均衡后输出的码元序列
end;。
