参数可变的多混沌映射加密系统

合集下载

基于混沌映射的加密技术研究

基于混沌映射的加密技术研究随着信息技术的不断进步，网络安全已经成为人们越来越关注的问题。

特别是随着数字货币、云计算、物联网等新兴技术的不断出现，将大量的数据信息在线上传、传输和存储，不可避免地会遭到各种攻击和窃取。

因此，保护网络信息安全变得至关重要。

在信息安全保障的方法中，密钥加密技术具有一定的优势。

日益成熟的混沌映射加密技术以其不可逆的特性和极高的随机性而成为了密码学领域新兴的研究方向。

一、混沌映射介绍混沌映射是指一类特殊的非线性离散映射，又称非线性动力学系统。

其特点是具有敏感依赖于初始值和参数值的特性，导致即使在非常微小的初始偏差下，其演化轨迹也会产生巨大差异。

因此，混沌映射在密码学中能够作为安全密钥或者伪随机数产生器使用。

目前，混沌映射已经被广泛应用于数据加密、信号处理、图像加密等领域。

二、基于混沌映射的加密方法由于混沌映射的不可逆特性以及随机性，各种基于混沌映射的加密方法逐渐被提出。

其中比较常见的是一次性密码本加密算法、分组密码算法、串行密码算法及其组合等。

1、一次性密码本加密算法一次性密码本是由完全随机的比特序列组成的。

使用一次性密码本可以实现绝对安全的加密，而且也不会受到任何攻击手段的破解。

但是，一次性密码本需要提前准备好密钥，而这个密钥也必须在传输时不能被窃取。

同时，一次性密码本还需要具备高质量的随机序列，此操作也较为困难。

因此，一次性密码本的使用也很少。

2、分组密码算法分组密码算法是目前应用最广泛的加密算法，其中使用最多的是DES、3DES、AES等算法。

在分组密码中，将明文按固定长度的分组处理，然后对每一组按照固定的规则生成一个密文输出。

其中最常使用的是基于Feistel结构的分组密码算法，其具有良好的性质，即使在密钥不同时，对于同一明文，加密出来的密文各不相同。

由于混沌映射具有随机性和不可逆特性，可以作为分组密码算法的加密子函数。

3、串行密码算法串行密码算法将混沌映射作为基本的流密码产生器，其输出随机序列作为密钥进行加解密。

基于多层参数扰动的混沌映射图像加密系统的设计与实现(精)

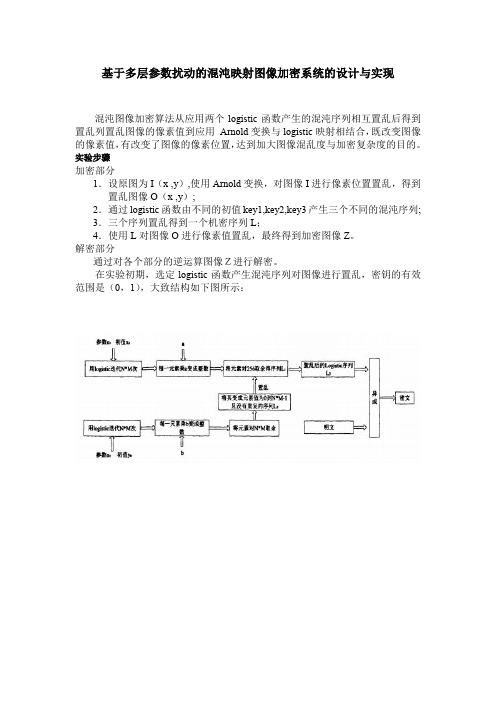
基于多层参数扰动的混沌映射图像加密系统的设计与实现混沌图像加密算法从应用两个logistic函数产生的混沌序列相互置乱后得到置乱列置乱图像的像素值到应用Arnold变换与logistic映射相结合，既改变图像的像素值，有改变了图像的像素位置，达到加大图像混乱度与加密复杂度的目的。

实验步骤加密部分1．设原图为I（x ,y）,使用Arnold变换，对图像I进行像素位置置乱，得到置乱图像O（x ,y）;2．通过logistic函数由不同的初值key1,key2,key3产生三个不同的混沌序列;3．三个序列置乱得到一个机密序列L；4．使用L对图像O进行像素值置乱，最终得到加密图像Z。

解密部分通过对各个部分的逆运算图像Ｚ进行解密。

在实验初期，选定logistic函数产生混沌序列对图像进行置乱，密钥的有效范围是（0，1），大致结构如下图所示：实验结果如下：经过logistic混沌序列置乱（密钥设置为0.123，0.124，0.1）后有：解密后得到考虑到单纯的logistic混沌系统加密抗破解不强，复杂度不够，所以需要再加入其他的置乱算法进一步置乱图像。

由此，本实验选用Arnold变换。

实验如下（迭代100次）：把两种加密结合起来，这样就加大了图像的复杂度，实验如下：经过Arnold变换后得到：接着进行logistic置乱，得到加密图像：通过逆运算最终还原由于采用了Arnold变换，所以加密图像就有了较大的局限性，不能够达到广泛加密的目的，而且目前图像复杂度还是不够高，还原效果也不是很好，所以实验下一步將针对这些不足决定采取分位平面并且对信息量最大的位平面进行分块加密的方法。

使用更准确的方法尽量减少误差，得到效果更好的还原图像。

对于一个256的灰度图像，位平面分离后如图所示：对这些平面分块（只分块含信息量多的位平面）后分别进行加密，具体步骤大致如下图：这样，不仅改变了图像的直方图，总的平均灰度值也改变了，而且采用可渐进式的解码算法，只要任一层的密钥不对都不可能把图像恢复。

可变区间混沌映射在图像加密中的应用研究

实验结果表明，该算法是一个具有较好的安全性能和抗攻击能力的混沌加密算法。
关键词：段线性混沌映射；标准映射；混沌密码；密码分析；序列密码分中图法分类号：Ｐ０＋７Ｔ３９．文献标识码：Ａ文章编号：００７２２１）４５７．３１０．０４（００２。１６０
０引言
传统加密技术通常把多媒体信息作为普通数据流进行加密，因此存在一定的局限性。目前，究人员已经提出了很多研基于离散混沌映射的加密系统，应地也出现了大量分析混相沌密码系统的方法 “ 。混沌具有如下的一些特征使之很适合捌
５７１６
２１，１（４００３２）
计算机工程与设计ＣｍｐｔｎｉｅｒｇＤｇ
Ｏ信息安全技术・
可变区间混沌映射在图像加密中的应用研究
李波（重庆教育学院计算机与现代教育技术系，重庆４０６）００７
１混沌映射的选择
１１伪随机序列的生成．
为了充分利用分段线性混沌映射的运算速度快的特点，
本文采用文献［］出的区间数目参数化的ＰＣ来产生拟混３提ＬＭ
沌伪随机序列。同分段区间ＰＣ相比较，混沌映射具有ＬＭ该更高的安全性。区间数目参数化ＰＣ的数学表达式为ＬＭ

基于多个一维混沌映射系统的多重加密算法

新的基于多个一维混沌映射的对称加密算法，算法利用了混沌系统的伪随机性｝本该在
加密或解密过程中，算法产生了在固定区间的混沌伪随机序列．对各种类型文件的信息进行了加密与解密该并
ｉｔｒａ．Ｕｓｎｈｓａｇｒｔｍ．ａｌｋｎｓｏｉｓ（ｕｈａｎｅｖ１ｉｇｔｉｌｏｉｈｌｉｄｆｆｅｌｓｃｓＴｘ．Ｂｔｍｐ，ＷａｎＯｏｙａｄＳｎ）ａｅｅｃｙｔｄａｄｒｎｒｐｅｎ
ｐｏｓｄｎｈｉｐａｅｒＴｈｉａｇｉｈｍｕｓｓｈｅｒｐｏｅｉｔｓｐ．ｓｌｏｒｔｅｔｐｓｕｄｒｎｄｅｏ— ａｏｍｏｆｈａｉｓｓｅｓＤｕｒｎｃｏｔｃｙｔｍ．ｉｇｔｅｈｐｒｃｓｏｆｏｅｓ
批注本地保存成功开通会员云端永久保存去开通
维普资讯
第２卷第２５期
２００８年５月
新疆大学学报（自然科学版）
ＪｕｎｌｆＸｉｊｎｏｒａｎｉｇＵｎｉｅｓｔＮａｕａｃｅｃｉｉｎｏａｖｒｉｙ（ｔｒｌｉｎｅＥｄｔ）Ｓｏ
ｄｃｙｅｅｒｐｔｄ．ＴｈｅｃｒｐｔｎａｙｉｆｔｓａｇｏｉｈａｓａｓｅｉｅｎｔｓｐａｅｒＳｉｕｌｉｅｕｌｓｓｏｗｈａｙａｌｓｓｏｈｉｌｒｔｍｈｌｏｂｅｎｇｖｎｉｈｉｐ．ｍａｔｏｎｒｓｔｈｔｔ

参数可变的离散混沌加密系统

Ｃｌｇ，ｉａｇＳｃｕｎ６５１Ｃｉ）ｏｌｅＸｃｎｉａ１０３，ｈｎｅｈｈａ
ＡｂｔａｃＴｈｉａｅｒｐｓｄａｎｗｈａｔｒｔｓｓｅｂｓｄｏｈｏｉｔｃｍａｉｈｎｅｒｍｅｅｓＳｓｅｐ — ｓｒｔ：ｓｐｐｒｐｏｏｅｅｃｏｉｃｙｐｏｙｔｍａｅｎｔｅｌｇｓｉｐｕｓｎｇｃａｇｄｐａａｔｒ．ｙｔｍａｃｒａｍｅｅｓａｄｔｅｏｄｅｆｓｂ— ｅｏｒｓｏｄｉｇｔｈｔｒｔｅｎｍｂｅｆｃｏｉｐｗｅｅｕｓｄｂｙｕｉｇｌｅｒｃｎｇｕｔｔｒｎｈｒｒｏｕｋｙｃｒｅｐｎｎｏｔｅｉｅａｉｕｖｒｏｈａｔｃｍａｒｅｓｎｉａｏｒｅｎｎ
＝
学、经济学和气象科学。混沌系统具有对初值和系统参数的敏
感性以及轨道的不确定性，些特性使得混沌系统对于构造密这码系统是一个很好的选择，且使离散混沌加密系统抵抗统计并分析攻击具有鲁棒性。目前提出了很多基于离散混沌映射的加密系统 “Ｊ相应地也出现了大量分析混沌密码系统的方，
钟黔川，清新一朱，张平莉
（．１电子科技大学计算机科学与工程学院，成都６０５；．１０４２西昌学院，四川西昌６５１）１０３
摘
要：提出一种参数动态可变的离散混沌加密算法，算法使用线性同余随机数发生器产生混沌映射的系统该

多混沌加密算法

多混沌加密算法引言随着互联网的快速发展，信息安全问题变得越来越重要。

在传输敏感信息时，我们需要使用加密算法来保护数据的安全性。

多混沌加密算法是一种基于混沌理论的加密方法，它具有高度的安全性和灵活性。

本文将介绍多混沌加密算法的原理、特点以及应用领域。

什么是混沌理论混沌理论是指描述非线性动力系统中复杂、随机和无序运动的一种数学方法。

混沌系统具有高度敏感性和不可预测性，即使微小的变化也可能导致系统的巨大差异。

混沌系统的运动是不可重复的，这使得它成为加密算法的理想选择。

多混沌加密算法原理多混沌加密算法基于多个混沌系统的运动来加密数据。

它利用混沌系统的不可预测性和敏感性，将明文数据转化为看似随机的密文。

多混沌加密算法的核心原理如下：1.混沌系统的选择：多混沌加密算法选择多个混沌系统作为加密器。

这些混沌系统的参数和初始条件可以通过密钥来确定，从而增加了加密的强度和随机性。

2.数据的转化：明文数据经过混沌系统的运动，转化为看似随机的密文。

混沌系统的运动是不可预测的，因此密文具有高度的安全性。

3.密钥的生成：多混沌加密算法通过混沌系统的运动生成密钥。

密钥的生成过程是不可逆的，只有知道初始条件和参数的人才能还原密钥。

4.密文的解密：接收方通过相同的密钥和混沌系统参数还原出明文数据。

由于混沌系统的运动是不可预测的，只有掌握正确的密钥才能成功解密。

多混沌加密算法的特点多混沌加密算法具有以下特点：1.高度的安全性：多混沌加密算法利用混沌系统的不可预测性和敏感性，使得密文具有高度的安全性。

即使攻击者获取了部分密文和加密器的参数，也很难还原出明文数据。

2.灵活性：多混沌加密算法可以根据需要选择不同的混沌系统和参数，从而提供不同级别的安全性。

这使得算法可以适应不同场景的需求。

3.抗干扰能力：多混沌加密算法具有很强的抗干扰能力。

由于混沌系统的运动是不可预测的，即使在信道传输过程中受到干扰，也不会对密文的安全性产生明显影响。

4.计算效率较低：由于多混沌加密算法涉及多个混沌系统的运动，其计算效率相对较低。

基于混沌映射的多媒体加密算法设计

基于混沌映射的多媒体加密算法设计随着大数据、人工智能、云计算等技术的快速发展，网络安全问题日益引起人们的关注。

多媒体数据在互联网上的传输和存储安全问题尤其引起了广泛的关注。

如何有效地保护多媒体数据的安全性是当前亟待解决的问题。

其中，利用混沌映射实现多媒体加密是一种热门的方法。

一、混沌及其应用混沌是指那些看似无规则的、复杂的、乱糟糟的运动形态，具有极度敏感的初值和参数依赖性，但又有其内在的规律性、统计性和自相似性。

混沌理论是现代非线性动力学中的重要分支之一，其内在的复杂性使其在很多领域都有广泛的应用。

混沌映射是混沌的一个典型应用之一。

混沌映射是指将一个状态映射到另一个状态的一种方法，其输入是一个初始状态，输出是一个新状态。

混沌映射具有非线性、随机性和灵敏度等特点，可以被广泛应用于密码学、通信、信息隐藏等领域中。

二、多媒体加密算法概述多媒体加密算法是指对音频、视频、图像等多媒体数据进行加密保护，防止非法访问和篡改。

多媒体加密算法通常包括加密和解密两个过程。

在加密过程中，先将多媒体数据转换为数字信号，然后采用某种加密算法对数字信号进行加密，使得被加密后的信号无法被窃听者解密得到原始信息。

在解密过程中，采用相应的解密算法将被加密的数字信号恢复为原始的多媒体数据。

三、基于混沌映射的多媒体加密算法设计基于混沌映射的多媒体加密算法是利用混沌映射对多媒体数据进行加密保护。

其主要步骤包括：1. 对多媒体数据进行数字化处理，将其转换为二进制数字信号。

2. 采用混沌映射算法生成一组密钥，用于对数字信号进行加密。

3. 设计加密算法，将数字信号与混沌密钥进行异或运算加密。

4. 将加密后得到的数字信号再次利用混沌密钥进行加密，以增强加密算法的安全性。

5. 将加密后的数字信号转换为多媒体数据，完成加密过程。

设计基于混沌映射的多媒体加密算法需要考虑以下几个方面：1. 混沌映射算法的选择混沌映射算法的选择对加密算法的安全性和性能有着重要影响。

基于多重混沌映射的加密技术研究

基于多重混沌映射的加密技术研究在信息时代的今天，网络安全问题显得越来越重要。

随着技术的不断进步和信息量的增大，网络攻击手段也不断翻新，而传统的加密方法已经不能满足当今信息安全的要求。

因此，基于多重混沌映射的加密技术逐渐成为一种新的选择，得到了广泛的关注和研究。

一、多重混沌映射的概念混沌是指一种高度敏感的动态系统，它的状态随时间而变化，即使系统的初值只有微小的变化，最终结果也会完全不同。

混沌系统常用来表示生物学、天文学、物理学、工程学等领域中的复杂现象。

多重混沌映射是利用多个混沌系统组合在一起，构建出更加复杂的动态系统来实现加密的一种技术。

混沌映射的本质是一种离散的非线性映射，在加密过程中，系统的状态被用作加密密钥进行信息的加密和解密。

二、多重混沌映射的特点1. 随机性强多重混沌映射技术的本质是依靠多个混沌系统的性质构建的一个新的混沌系统，这使得加密产生的密文与明文之间的关系变得极为复杂，密钥空间大大增加，随机性也就得到了增强，从而保证了加密的安全性。

2. 抗攻击能力强由于多重混沌映射技术具有非线性、敏感依赖于初始条件、混沌特性等多种特征，这些特性使它能够有效地抵御不同形式的攻击，包括差分攻击、线性攻击和频谱攻击等。

3. 实现简单多重混沌映射技术的实现相对简单，不需要复杂的数学方法和专门的软件包，只需要进行混沌系统的选择、构建和连接即可完成对信息的加密和解密，这大大提高了加密技术的可行性和实用性。

三、多重混沌映射的应用多重混沌映射技术在众多领域都有着广泛的应用，如通信系统、计算机网络、物联网、金融和安全监控等。

1. 通信系统多重混沌映射技术可以实现对通信信号的加密和解密，保证通讯内容不被窃取和篡改，保护信息安全。

同时，多重混沌映射还可以提高通讯的带宽和抗干扰能力，使得通讯质量更加稳定和高效。

2. 计算机网络多重混沌映射技术可以用于保护网络传输数据的隐私、保证其完整性和可用性，确保网络安全运行。

在分布式计算和高性能计算中，多重混沌映射技术也可以帮助实现任务分配、负载平衡和可靠性管理等重要的功能。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第38卷第2期电子科技大学学报 V ol.38 No.22009年3月 Journalof University of Electronic Science and Technology of China Mar. 2009 参数可变的多混沌映射加密系统钟黔川1,2，朱清新1，张平莉2(1. 电子科技大学计算机科学与工程学院成都 610054; 2. 西昌学院四川西昌 615013)【摘要】利用混沌映射具有对初值和系统参数的敏感性以及轨道的不确定性，提出一种基于多个一维混沌映射的加密算法。

该加密算法使用线性同余随机数发生器产生混沌映射的系统参数和3个一维混沌映射的使用顺序，同时通过输出反馈方式动态改变混沌映射初值、迭代次数以及线性同余随机数发生器参数。

实验结果和安全性分析表明，该算法密钥空间大，具有对明文和密钥的敏感性，能有效抵抗选择明文等穷举攻击和统计分析攻击。

关键词分组密码; 混沌加密系统; 混沌映射; 输出反馈中图分类号 TP309 文献标识码 A doi: 10. 3969/j. issn. 1001-0548. 2009. 02. 28Multiple Chaotic Maps Encryption SystemZHONG Qian-chuan 1,2, ZHU Qing-xin 1, and ZHANG Ping-li 2(1. School of Computer Science and Engineering, University of Electronic Science and Technology of China Chengdu 610054;2. Xichang College Xichang Sichuan 615013)Abstract A new cryptosystem based on multiple one-dimensional chaotic maps is proposed by utilizing theproperties of chaotic map such as sensitivity to initial conditions and system parameters, and orbit uncertainty. The system parameters of chaotic maps and the using order of three one-dimensional maps are generated by using linear congruent generators. The initial value and iterative number of chaotic map and linear congruence generator (LCG) parameters are dynamically changed by output feedback. Simulation results and security analyses show that the proposed cryptosystem has large key space and high sensitivity to key and plaintext, and can resist the brute attack and statistical attack.Key words block cipher; chaotic encryption system; chaotic map; output feedback收稿日期： 2007 − 12 − 05；修回日期：2008 − 06 − 25基金项目：国家自然科学基金(60671033)；国家教育部博士点基金(2006061405)作者简介：钟黔川(1970 − )，男，博士，主要从事信息安全、混沌密码、数字水印技术等方面的研究.在过去的许多年里，文献[1-4]提出了一些基于一维混沌映射的加密系统，也有一些混沌加密系统被成功攻击[6-10]，它的安全性已成为专家学者关注的一个热点。

由于混沌映射具有对初值和系统参数的敏感性以及轨道的不确定性，这些特性和分组密码的特点是相吻合的。

混沌密码系统一般使用混沌映射的初值、系统参数、迭代次数作为密钥进行加密/解密，本文算法试图使混沌映射每一步迭代都最大限度地保证上述3个参数的最大取值空间，并且利用输出反馈来动态改变这些参数，有力地保障了算法的安全性。

1 混沌加密算法算法的描述：(1) 在算法中，128位的密钥被分成多个8 bit 为单位的块，每块称作会话密钥，进一步将密钥划分成32 bit 为单位的子密钥,1,2,,4i K i µ="和64 bit 为单位的子密钥,1,2i K i =，它们都是以十六进制来表示的，其划分情况为：123416123412K k k k k k K K K K K K µµµµ===" (1) (2) 在加密/解密过程中明文/密文被分成多个 8 bit 为单位的块，其划分情况分别为：1234n P PP P P P =" (2)1234n C C C C C C =" (3)(3) 在加密/解密过程中选取3个一维混沌映射来进行加密/解密，它们分别是：Logistic 映射、帐篷映射、正弦映射，如表1所示。

表中第1列为混沌映射名称，第2列是3个混沌映射的编号，第3列是3个混沌映射对应的迭代表达式，第4列是混沌映射系统参数取值范围，该范围表示相应混沌映射处于混沌状态。

(4) 开始时由会话密钥和子密钥构造的初始值分别为：5212|()/2mod 1|b X K K =+ (4)第2期钟黔川等: 参数可变的多混沌映射加密系统 27512345678(b N k k k k k k k k =++++16910111213141516)mod 2k k k k k k k k +++ (5)随机数由线性同余随机数发生器(LCG)产生：31314()mod (21)i i Y K Y K µµ−=+− (6)式中 3102b Y X ⎢⎥=×⎣⎦。

由i Y 产生的混沌映射号M 、使用会话密钥的顺序号j 分别为：mod 3i M Y = (7)j =(mod 16)1i Y + (8)表1 混沌映射编号、表达式、系统参数取值范围混沌映射 M 迭代表达式系统参数 Logistic 映射 0 1(1)n n n X X X µ+=−3.57≤µ≤4.0 Tent 映射 1 10.5(1)0.5nn n n n X X X X X µµ+⎧=⎨−>⎩≤1.4≤µ≤2.0 Sine 映射21sin()n n X X µ+=0.87≤µ≤1.0(5) 混沌映射的迭代次数N 和初值X 分别为：N = N b + k i (9) 8((/2))mod 1b j X X k =+ (10) 根据混沌映射号M 的不同取值选择不同的混沌映射系统参数i µ产生式：525212525212525212((()mod 2)/2)0.43 3.570((()mod 2)/2)0.6 1.41((()mod 2)/2)0.130.872i i i i ii K Y K M K Y K M K Y K M µµµµµµµµµ⎧=+×⎪+=⎪⎪=+×⎪⎨+=⎪⎪=+×⎪⎪+=⎩ (11) (6) 明文/密文每一块被加密/解密，用初值X 和系统参数i µ使混沌映射迭代N 次。

新值()X X ′被用于构造明文/密文以及作为下一步迭代输出反馈的一部分，如下列等式所示：313(21)i K P X µ′′⎢⎥=+−⎣⎦ (12)52(2269)i T P X ′⎢⎥=+×−⎣⎦ (13)52(/2)mod 1b X T ′= (14)314mod (21)K T µ′=− (15) 3(10)mod 509bi N P X ′′=+× (16) 3mod 256i C K µ′= (17) 31(256((21)mod 256))mod 256i i P C X ′⎢⎥=+−−⎣⎦(18)对于加密/解密下一块明文/密文，上一次的b N ′和bX ′分别代替式(9)、式(10)中的b N 和b X ，3K µ′和4K µ′分别更新式(6)中的随机发生器参数3K µ和4K µ。

加密/解密过程基本相同，唯一不同之处在于加密过程用的是式(17)，解密过程用的是式(18)。

解密过程先用式(18)求i P ，再用式(12)~式(16)求3K µ′、T 、bX ′、4K µ′、b N ′。

在文献[11]中已论证了随机数发生器中乘法器和模的取值问题，由于在式(6)中乘法器是由密钥分离而来，可以不考虑它的取值问题。

在式(6)中模取1231−，这是根据文献[11]的建议来取的值，因为它是一个奇素数，产生的随机数具有比较大的周期。

由于双精度占64位，其中第1位是符号位，依次是指数位，占11位，剩余的52位是尾数，因此取522作为式(4)、式(11)的模是恰当的，充分保证了系统参数i µ的密钥取值空间，又不会引入小数的不确定位。

2 实验及结果分析采用以下试验环境：CPU 是Intel Celeron 处理器，主频为450 MHz ；内存为196 MB ；操作系统为Windows 2000；使用VC++编程实现本文的算法。

表2 实验过程中各参数列表映射号M明文字符迭代初值X系统参数λi迭代次数N 迭代后的值X new 明文P i 密文C i 0 c 0.133 403 297 840 231 970 0 3.683 713 007 864 660 500 053 601 0.394 756 240 339 066 140 0991890 h 0.633 037 490 339 064 530 0 3.871 761 393 019 213 400 0160 0.708 277 388 238 566 560 0 1041962 a 0.352 808 638 238 547 360 00.950 761 432 193 328 870 0269 0.567 398 850 620 930 100 0972341 o 0.708 023 850 620 917 770 0 1.703 204 690 709 347 900 0133 0.315 985 471 868 431 180 0 1111761 t 0.019 110 471 868 436 951 0 1.557 561 908 008 875 600 0291 0.669 446 086 867 080 850 0 11664 1 i 0.372 571 086 867 066 640 0 1.813 862 702 424 441 400 0296 0.417 392 040 562 097 170 0 1051580c0.710 360 790 562 095 450 03.859 613 384 402 577 300 01800.944 324 050 746 886 520 099171表2为使用密钥“12B4A54432FF4B7C4A923D 274C172437”对明文“chaotic ”进行加密的过程。