空间点线面之间位置关系知识点总结
(完整word版)空间点线面之间位置关系知识点总结,推荐文档

高中空间点线面之间位置关系知识点总结第一章 空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体.旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的结构特征1.1棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱.2.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
2.2圆锥——以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥。
3.1棱台——用一个平行于底面的平面去截棱锥,我们把截面与底面之间的部分称为棱台. 3.2圆台——用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.4.1球——以半圆的直径所在直线为旋转轴,半圆旋转一周形成的旋转体叫做球体,简称球. (二)空间几何体的三视图与直观图1.投影:区分中心投影与平行投影。
平行投影分为正投影和斜投影。
2.三视图——正视图;侧视图;俯视图;是观察者从三个不同位置观察同一个空间几何体而画出的图形;画三视图的原则: 长对齐、高对齐、宽相等3.直观图:直观图通常是在平行投影下画出的空间图形。
4.斜二测法:在坐标系'''x o y 中画直观图时,已知图形中平行于坐标轴的线段保持平行性不变,平行于x 轴(或在x 轴上)的线段保持长度不变,平行于y 轴(或在y 轴上)的线段长度减半。
重点记忆:直观图面积=原图形面积 (三)空间几何体的表面积与体积 1、空间几何体的表面积①棱柱、棱锥的表面积: 各个面面积之和②圆柱的表面积 ③圆锥的表面积2S rl r ππ=+④圆台的表面积22Srl r Rl R ππππ=+++ ⑤球的表面积24S R π=⑥扇形的面积公式213602n R S lr π==扇形(其中l 表示弧长,r 表示半径) 2、空间几何体的体积①柱体的体积 V S h =⨯底 ②锥体的体积 13V S h =⨯底③台体的体积 1)3V S S S S h =++⨯下下上上( ④球体的体积343V R π=第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系2.1.11 平面含义:平面是无限延展的2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
空间点、线、面之间的位置关系

空间点、线、面之间的位置关系1.线与线的位置关系:平行、相交、异面(特别注意一下:垂直只是相交与异面当中的特殊情况,我们说相交有相交垂直,异面有异面垂直)2.线与面的位置关系:线在面内(选择题时一定要考虑)、线面平行、线面相交3.如何确定一个平面?方法(1)三个不共线的点可以确定一个平面方法(2)两条相交线可以确定一个平面方法(3)两条平行线可以确定一个平面4.如何证明三点共线?具体的做法:就是把其中两点确定的直线作为两个面的交线,证明剩下这一点是这两个面的交点,那么交点必在交线上,则三点共线。
5.如何证明线线平行?方法(1)利用三角形或梯形的中位线方法(2)利用平行四边形方法(3)利用线段对应成比例(通常题目中会出现三等份点或四等份点)方法(4)垂直于同一个面的两条直线互相平行方法(5)借助一个性质:两个面相交,其中一个面内的一条直线平行于另一个面,则这条线平行于两个面的交线(利用这个性质来证明在以往的高考中出现过若干次,同学们需要注意一下)6.如何证明线面平行?方法(1)只需证明这条直线与平面内的一条直线平行即可,简称线线平行推出线面平行。
方法(2)只需把这条直线放入一个合适的平面内,然后证明这个平面与已知平面平行即可,简称面面平行推出线面平行。
特别注意:直线平行于平面,可以得出直线与平面内无数条直线平行,但得不出与平面内任意一条直线平行。
7.如何证明面面平行?只需证明其中一个面内的两条相交线分别平行于另一个面即可。
8.如何证明线面垂直?只需证明这条直线分别与平面内的两条相交线互相垂直即可。
特别注意:直线垂直于平面,可以得出直线与平面内任意一条直线都垂直。
9.如何证明面面垂直?只需证明其中一个面内的一条直线垂直与另一个面即可。
特别注意:面面垂直,既得不出两个面内的任意两条直线互相垂直,也得不出其中一个面内的任意一条直线都垂直于另一个面。
10.异面直线的夹角范围是多少?如何求出异面直线的夹角?夹角范围是:0°~ 90°在求异面直线的夹角时,要把两条异面直线平移使它们出现交点,有时只需平移一条,有时两条都需要平移,这个过程中用得比较多的是中位线,当平移后两条直线出现交点时,复杂些的在三角形中利用余弦定理来求。
1.空间点线面之间的位置关系

空间点线面之间的位置关系一.平面的基本性质:公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. 公理2:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线.公理3:经过不在同一条直线上的三点,有且只有一个平面.推论1:经过一条直线和直线外的一点有且只有一个平面.推论2:经过两条相交直线有且只有一个平面.推论3:经过两条平行直线有且只有一个平面.二.空间直线与平面之间的位置关系:1.直线与平面的位置关系可分为:直线在平面内;直线与平面平行;直线成平面相交;2.平面与平面之间位置关系分为:面面平行;面面相交;面面重合;3.空间直线之间的位置关系:相交,平行,异面;三.等角定理、平行公理:定理:如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补;推论:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等;平行公理:平行与同一条直线的两条直线平行;空间平行具有传递性,空间平行平面也具有传递性;四.证明方法:1.证明三点共线的常用方法:(1)首先找出两个平面,然后证明这三点都是这两个平面的公共点。
由公理三得证;(2)选择其中两点确定一条直线,然后证明另一点也在其上;2.证明直线共面通常的方法:()1先由其中两条直线确定一个平面,再证明其余的直线都在此平面内(纳入法);()2分别过某些点作多个平面,然后证明这些平面重合(重合法);()3也可利用共面向量定理来证明.3.证明三线共点的方法:先证两条直线交于一点,再证明第三条直线经过这点,转化为证明点在线上的问题;()1如果A、B是交点,那么AB是交线;()2如果两个不同平面有三个或者更多的交点,那么它们共面;()3如果lαβ=∈,点P是α、β的一个公共点,那么P l4.证明几点共面的问题可以先取三点(不共线的三点)确定一个平面,再证其余各点都在这个平面内;1.分别和两条异面直线平行的两条直线的位置关系是: A .一定平行 B.一定相交 C.一定异面 D.相交或异面2.如果在两个平面内分别各有一条直线,这两条直线互相平行,那么这两个平面的位置关系为: A .平行 B.相交 C.平行或相交 D.垂直或相交3.已知下列命题:其中真命题的个数为: ; (1)若直线l 平行于α内无数条直线,则 l α;(2)若直线l 在平面α外,则 l α; (3)若直线 a b ,直线⊂b α,则 a α; (4)若直线 a b ,⊂b α,那么直线a 平行于平面α内的无数条直线;4.空间三条直线互相平行,由每两条平行直线确定一个平面,则可确定平面的个数为:5.若三个平面两两相交,且三条交线互相平行,则这三个平面将空间分成 部分;6.如果两条异面直线称为一对,那么在正方体的十二条棱中,共有异面直线 对;7.空间中有四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的; .A 充分非必要条件;.B 必要非充分条件;.C 充要条件;.D 非充分非必要条件.8.不共面的四个定点到平面α的距离都相等,这样的平面α共有.A 3个 .B 4个 .C 6个 .D 7个9.已知两个不同的平面α、β和两条不重合的直线,m 、n ,有下列四个命题 ①若α⊥m n m ,//,则α⊥n ②若βαβα//,,则⊥⊥m m③若βαβα⊥⊂⊥则,,//,n n m m ④若n m n m //,,,//则=βαα其中正确命题的个数是 A .0个 B .1个 C .2个 D .3个 10.设m ,n 是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题: ①若m ⊥α,n ∥α,则m ⊥n ;②若α∥β,β∥γ,m ⊥α,则m ⊥γ; ③若m ∥α,n ∥α,则m ∥n ;④若α⊥γ,β⊥γ,则α∥β.其中正确命题的序号是 A .①和② B .②和③ C .③和④ D .①和④ 11.已知直线a 、b 、c 和平面M ,则可以得到a//b 的是 : ;A.a//M ,b//MB.a ⊥c ,b ⊥cC.a 、b 与平面M 成等角D.a ⊥M ,b ⊥M . 12.已知直线m 、n 平面βα,,下列命题中正确的是A.若直线m 、n 与平面α所成的角相等,则m//nB.若m ⊥α,n ⊥β,α⊥β,则m ⊥nC.若m ⊂α,β⊂n ,m//n ,则α//βD.若m//α,,//,//βαβn 则m//n13.已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是( )A .,,m n m n αα若则‖‖‖B .,,αγβγαβ⊥⊥若则‖C .,,m m αβαβ若则‖‖‖D .,,m n m n αα⊥⊥若则‖14.已知βα,是相异两平面,n m ,是相异两直线,则下列命题中不正确...的是 ( ) A.若m ∥α⊥m n ,,则α⊥n B.若⊥m βα⊥m ,,则α∥β C.若⊥m βα⊂m ,,则⊥αβ D.若m ∥n =⋂βαα,,则m ∥n 15.设有直线m 、n 和平面α、β.下列四个命题中,正确的是( )A.若m ∥α,n ∥α,则m ∥n ;B.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC.若α⊥β,m ⊂α,则m ⊥β;D.若α⊥β,m ⊥β,m ⊄α,则m ∥α 16.已知n m ,是两条不同的直线,βα,为两个不同的平面,有下列四个命题: ①若βα⊥⊥n m ,,m ⊥n ,则βα⊥;②若n m n m ⊥,//,//βα,则βα//; ③若n m n m ⊥⊥,//,βα,则βα//;④若βαβα//,//,n m ⊥,则n m ⊥. 其中正确的命题是(填上所有正确命题的序号)_______________.17.正方体1111ABCD A B C D -中,P 、Q 、R 分别是AB 、AD 、11B C 的中点. 那么,正方体的过P 、Q 、R 的截面图形是.A 三角形.B 四边形.C 五边形.D 六边形18.如图,l αβ= ,A 、B α∈,C β∈,且C l ∉,直线AB l M = ,过A 、B 、C 三点 的平面记作γ,则γ与β的交线必通过.A 点A ; .B 点B ; .C 点C 但不通过点M ; .D 点C 和点MAB CD 1A 1B 1C 1D PD RαβlM A B C题型二:证明点共线,线共点,点共面,线共面问题 例1.点共面:1.(07江苏)如图,已知1111ABCD A B C D -是棱长为3的正方体,点E 在1AA 上,点F 在1CC 上,且11AE FC ==.求证:1,,,E B F D 四点共面;2.(08四川)如图,平面ABEF ⊥平面ABCD ,四边形ABEF 与ABCD 都是直角梯形,90BAD FAB ∠=∠=︒,BC ∥12AD ,BE ∥12AF .证明:C 、D 、F 、E 四点共面;例3.线共面:1.已知:a ,b ,c ,d 是不共点且两两相交的四条直线,求证:a ,b ,c ,d 共面。
点线面间的位置关系知识点总结(含题)(

点线面间的位置关系知识点总结一、三个公理公理1如果一条直线上的两点在一个平面内,那么_________________________________________公理2:过________________________ 的三个点,有且只有一个平面公理3:如果两个不重合的平面有一个公共点,那么它们有且只有_____________________________二、空间两条直线间的位置关系分类为:______________ , ______________ ,_______________ ;其中__________ , _________ 合称为______________三、空间直线与平面间的位置关系分类为:__________________ ,____________ ,__________________ ;其中__________ , _________ 合称为______________四、空间平面与平面间的位置关系分类为:______________ ,当两个平面成90。
时,属于____________ 关系常用证明技巧一、线面平行列1 (2IH1年怀化楓蝌)如图所示*已知几0是单位止方WABCn-A^.C^的面A^BA和面』肮2>的中心*求证:卩总〃平面ncr^n.练习1. 正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q且AP = DQ. 求证:PQ//平面BCE.2・妇匿,四棱链/一乩噸一平面所裁*截面为平厅四边形吕他求证,m/zz面日捌3* (加10年彌考■陕丙雜)如图’在四棱饰P ABCD中.底血ABCD^矩形「只4 丄平SLUJC/h .lP-.Ltf, BP-IiC-1, E, F分别&l f B T PC 的中点.门)证明* EF//平血知";卩)求二棱锥E—.【号「的休枳匚(2)1/3二、线面垂直1、(2006年北京卷)如图,在底面为平行四边形的四棱锥P ABCD中,AB 点E是PD的中点•(I)求证:AC PB ; (n)求证:PB〃平面AEC ;2、( 2006年浙江卷)如图,在四棱锥P-ABCD中,底面为直角梯形BAD=90 ° ,PA丄底面ABCD,且PA= AD=AB=2BC,M、N 分别为PC、PB 求证:PB丄DM;3、(2006年福建卷)如图,四面体ABCD中,0、E分别是BD、BC的中点,CA(I)求证:AO 平面BCD;AC , PA 平面ABCD,且PA AB , CB CD BD 2, AB AD . 2.,AD // BC, /的中点•ADOE4、( 2006年重庆卷)如图,在四棱锥P—ABCD中,PA 底面ABCD, PC、DAB 为直角,AB II CD,AD=CD=24B,E、F 分另U为CD的中点.(I)试证:CD 平面BEF;5、(全国H ?理?9题)如图,在四棱锥SCS-ABCD中,底面ABCD为正方形,侧棱SD丄底面ABCD , E、F分别是AB、的中点。
(完整word版)点线面之间的位置关系的知识点总结,推荐文档

高中空间点线面之间位置关系知识点总结第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系2.1.11 平面含义:平面是无限延展的2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
3 三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内 符号表示为A ∈LB ∈L => L α A ∈α B ∈α公理1作用:判断直线是否在平面内(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理2作用:确定一个平面的依据。
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P ∈α∩β =>α∩β=L ,且P ∈L 公理3作用:判定两个平面是否相交的依据2.1.2 空间中直线与直线之间的位置关系1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点同一条直线的两条直线互相平行。
符号表示为:设a 、b 、c 是三条直线 a ∥b 。
2 公理4:平行于 c ∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补4 注意点:① a'与b'所成的角的大小只由a 、b 的相互位置来确定,与O 的选择无关,为简便,点O 一般取在两直线中的一条上; ② 两条异面直线所成的角θ∈(0, );③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a ⊥b ;④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;D CBAα LA ·α C ·B·A · α P· αLβ 共面直线=>a ∥c2⑤计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
空间中点线面的位置关系

空间中点、线、面的位置关系一、平面的基本性质(1)点和直线的基本性质:连接两点的线中,最短;过两点一条直线,并且一条直线。
(2)平面的基本性质:1如果一条直线的点在一个平面内,那么这条直线上的所有点在这个平面内。
这时我们就说或。
作用:判断直线在平面内。
2经过不在同一直线的三点,有且只有个平面。
也可以简单地说成:的三点确定一个平面。
过不共线的三点A、B、C的平面,通常记作:。
3如果不重合的两个平面有个公共点,那么它们有且只有条过这个点的公共直线。
如果两个平面有一条公共直线,则称这两个平面。
这条公共直线叫做这两个平面的(3)平面的基本性质的推论:1经过一条直线和直线的一点,有且只有个平面。
2经过两条直线,有且只有个平面。
3经过两条直线,有且只有个平面。
(4)共面与异面直线:共面:空间中的几个点或几条直线,如果都在,我们就说它们共面。
共面的两条直线的位置关系有和两种。
异面直线:既又的直线叫异面直线。
判断两条直线为异面直线的方法:与一平面相交于一点的直线与这个平面内任一不过该点的直线是异面直线。
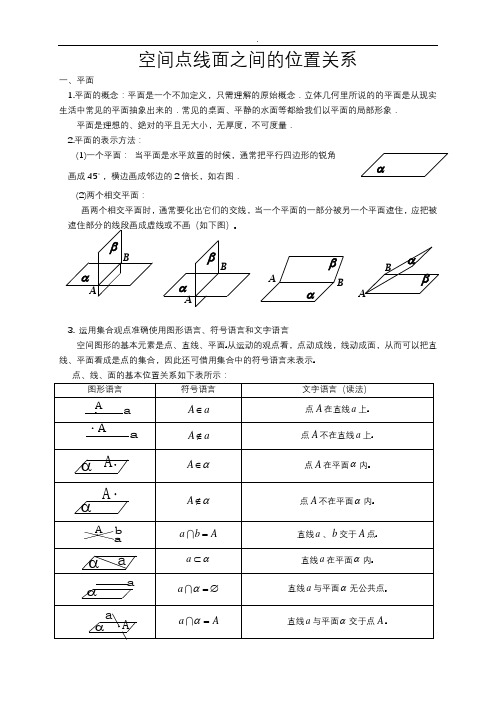
(5)符号语言:点A在平面α内,记作;点A不在平面α内,记作。
直线l在平面α内,记作;直线l不在平面α内,记作。
平面α与平面β相交于直线a, 记作 .直线l和直线m相交于点A,记作,简记作:。
基本性质01可以用集合语言描述为:如果点A α,点B α,那么直线AB α。
例1. 已知三条直线a、b、c两两相交但不共点,求证:a、b、c共面。
例2.已知三条平行线a 、b 、c 都与直线d 相交.求证:它们共面.例 3.正方体1111D C B A ABCD -中,对角线C A 1与平面1BDC 交于AC O ,、BD 交于点M . 求证:点1C 、O 、M 共线.例4.已知三个平面α、β、γ两两相交,且α⋂β=c ,β⋂γ=a ,γ⋂α=b , 且直线a 和b 不平行.求证: a 、b 、c 三条直线必相交于同一点._1_ B _二、空间中的平行关系1.空间平行直线的本性质(空间平行线的传递性): 平行于同一直线的两条直线 。
人教高中数学必修第二册8.4空间点线面之间的位置关系 知识点
位置关系
交点个数图形Βιβλιοθήκη 言符号语言直线在平面内
无数个
直线在平面外
直线与平面相交
只有一个
直线与平面平行
没有
2、直线和平面平行
1.定义:如果一条直线和一个平面没有公共点,那么这条直线与这个平面平行.
2.判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
推论3:经过两条平行直线,有且只有一个平面.
(1)以上是确定平面的四个不同的条件,是判断两个平面重合的依据,是证明点线共面的依据,也是作截面、辅助面的依据.
(2)“有且只有一个”的含义要准确理解.这里的“有”是说图形的存在,“只有一个”是说图形唯一.因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证.
(3)异面直线所成角的范围是 .
2.求异面直线所成角的步骤
(1)恰当选点,由平移构造出一个交角;
(2)证平行关系成立;
(3)把角放入三角形或其它平面图形中求出;
(4)作结论:若求出的角是锐角或直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角才是所求异面直线所成的角.
七、直线、平面的位置关系
5.直线与平面垂直的性质
(1)性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.
符号语言:a⊥α,b⊥α⇒a∥b,
如图:
(2)一条直线垂直于一个平面,它就和平面内的任意一条直线垂直.
符号语言:a⊥α,b⊂α⇒a⊥b,
如图:
6.设P是三角形ABC所在平面α外一点,O是P在α内的射影
(1)若PA=PB=PC,则O为△ABC的外心.特别地当∠C=90°时,O为斜边AB中点.
空间点线面之间位置关系知识点总结

高中空间点线面之间位置关系知识点总结第一章 空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体.旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的结构特征1.1棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱.2.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
2.2圆锥——以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥。
3.1棱台——用一个平行于底面的平面去截棱锥,我们把截面与底面之间的部分称为棱台.3.2圆台——用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.4.1球——以半圆的直径所在直线为旋转轴,半圆旋转一周形成的旋转体叫做球体,简称球.(二)空间几何体的三视图与直观图1.投影:区分中心投影与平行投影。
平行投影分为正投影和斜投影。
2.三视图——正视图;侧视图;俯视图;是观察者从三个不同位置观察同一个空间几何体而画出的图形;画三视图的原则: 长对齐、高对齐、宽相等3.直观图:直观图通常是在平行投影下画出的空间图形。
4.斜二测法:在坐标系'''x o y 中画直观图时,已知图形中平行于坐标轴的线段保持平行性不变,平行于x 轴(或在x 轴上)的线段保持长度不变,平行于y 轴(或在y 轴上)的线段长度减半。
重点记忆:直观图面积=原图形面积(三)空间几何体的表面积与体积1、空间几何体的表面积①棱柱、棱锥的表面积: 各个面面积之和②圆柱的表面积 ③圆锥的表面积2S rl r ππ=+④圆台的表面积22S rl r Rl R ππππ=+++ ⑤球的表面积24S R π=⑥扇形的面积公式213602n R S lr π==扇形(其中l 表示弧长,r 表示半径) 2、空间几何体的体积①柱体的体积 V S h =⨯底②锥体的体积 13V S h =⨯底 ③台体的体积 1)3V S S S S h =++⨯下下上上(④球体的体积343V R π= 2π2π2r rl S +=第二章 直线与平面的位置关系 2.1空间点、直线、平面之间的位置关系 2.1.1 1 平面含义:平面是无限延展的 2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
点线面之间的位置关系

空间点、线、面之间的位置关系一、空间点、直线、平面之间的位置关系 1、平面的基本性质公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内; 公理2:过不在一条直线上的三点,有且只有一个平面;公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
公理4(又称平行公理):平行于同一条直线的两条直线平行;等角定理:空间中如果两个角的两边分别对应平行,那么着两个角相等或互补. 2、空间中直线与直线之间的位置关系 (1)位置关系的分类⎧⎧⎪⎨⎨⎩⎪⎩相交直线共面直线平行直线异面直线:不同在任何一个平面内,没有公共点(2)异面直线所成的角①定义:设a,b 是两条异面直线,经过空间中任一点O 作直线a ’∥a,b ’∥b,把a ’与b ’所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角) ②范围:02π⎛⎤⎥⎝⎦,3、空间中直线与平面之间的位置关系 位置关系 直线a 在平面α内直线a 与平面α相交 直线a 与平面α平行公共点 有无数个公共点有且只有一个公共点没有公共点符号表示a α⊂a A α= //a α图形表示4、空间中平面与平面之间的位置关系 位置关系 图示表示法 公共点个数两平面平行//αβ两平面相交斜交aαβ=有无数个公共点在一条直线上垂直αβ⊥aαβ=有无数个公共点在一条直线上二、直线、平面平行的判定及其性质1、直线与平面平行的判定与性质(1)判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;(2)性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;2、平面与平面平行的判定与性质(1)判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行;(2)性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
注:能否由线线平行得到面面平行?(可以。
只要一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,这两个平面就平行)三、直线、平面垂直的判定及其性质1、直线与平面垂直(1)定义:如果直线l与平面α内的任意一条直线都垂直,则直线l与平面α垂直;(2)判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;2、平面与平面垂直(1)定义:如果两个平面所成的二面角是直二面角,就说这两个平面互相垂直;(2)判定定理:一个平面过另一个平面的垂线,则这两个平面垂直;(2)性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
空间点线面的位置关系知识点归纳

空间点、线、面之间的位置关系知识点归纳1. 平面的表示法概念几何里的平面是_________, 常用平行四边形表示平面。
表示法平面一般用一个希腊字母α、β、γ…来表示,也可以用平行四边形的对角线上两个点的字母来表示。
若A、B、C三点不共线,则可称平面ABC。
2.平面的基本性质公理1如果一条直线的_______在一个平面内,那么这条直线上的所有点都在这个平面内。
公理2 过______________________的三点,有且只有一个平面。
推论1过一条直线和______________一点,有且只有一个平面。
推论2 经过两条________直线,有且只有一个平面。
推论3经过两条________直线,有且只有一个平面。
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的_______________。
学法指导①公里1可证明直线在平面内,只要证明直线上有两个点在平面内即行。
②公里2体现了平面无限延展的性质。
利用公里2可证明两个平面相交(只需证明一个点同时在两个平面内),也可证明若干个点共线(证明若干个点同时在两个平面内,则这若干个点在两个平面的交线上,即共线)。
③公里3及三个推论是确定平面的条件,是将空间几何转化为平面几何的理论基础。
公里3中已知的三点不能在同一条直线上,推论1中已知的点不能在直线上,这些条件都不可以削弱,否则就有无数个平面。
3.异面直线__________________一个平面内的两条直线叫做异面直线。
即空间内既不平行又不相交的直线。
为了表示异面直线不共面的特点,作图时,通常用一个或两个平面衬托(如课本第45页的图)4.空间直线间、平面间的位置关系(1)两条直线的位置关系①相交直线:同一平面内,有且只有一个公共点;②平行直线:同一平面内,没有公共点;③异面直线:不同在任何一个平面内,没有公共点。
相交直线和平行直线也称共面直线(2)两个平面的位置关系①两个平行平面:没有公共点;②两个相交平面:有一条公共直线。
点线面之间的位置关系的知识点总结

高中空间点线面之间位置关系知识点总结第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系2.1.11 平面含义:平面是无限延展的2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
3 三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内 符号表示为A ∈LB ∈L => L α A ∈α B ∈α公理1作用:判断直线是否在平面内(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理2作用:确定一个平面的依据。
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P ∈α∩β =>α∩β=L ,且P ∈L 公理3作用:判定两个平面是否相交的依据2.1.2 空间中直线与直线之间的位置关系1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点同一条直线的两条直线互相平行。
符号表示为:设a 、b 、c 是三条直线 a ∥b 。
2 公理4:平行于 c ∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补4 注意点:① a'与b'所成的角的大小只由a 、b 的相互位置来确定,与O 的选择无关,为简便,点O 一般取在两直线中的一条上; ② 两条异面直线所成的角θ∈(0, );③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a ⊥b ;D CBAα LA·α C ·B·A · α P· αLβ 共面直线=>a ∥c2④两条直线互相垂直,有共面垂直与异面垂直两种情形;⑤计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
根据点线面之间的相对位置关系的知识点总结

根据点线面之间的相对位置关系的知识点
总结
在几何学中,点、线和面是最基本的几何概念。
它们之间的相对位置关系对于理解和解决几何问题至关重要。
以下是根据点线面之间的相对位置关系的一些重要知识点的总结:
1. 点和线的关系:
- 直线上的每个点都在同一条直线上;
- 直线外的点不存在于同一条直线上。
2. 点和平面的关系:
- 平面可以由无数个点组成;
- 平面上的每个点都在同一平面上;
- 平面外的点不存在于同一平面上。
3. 线和平面的关系:
- 一条直线在平面上可以有三种不同的相交情况:
- 直线和平面相交于一个点;
- 直线和平面平行,不相交;
- 直线包含在平面内。
4. 线和线的关系:
- 直线和直线可能相交于一个点,此时它们称为交线;
- 直线和直线可能平行,不相交。
5. 面和面的关系:
- 两个平面可以平行,不相交;
- 两个平面可以相交于一条直线;
- 两个平面可以相交于一点。
6. 直线、平面和点的关系:
- 一条直线可能与一个点相交;
- 一条直线可能与一个平面相交;
- 一个平面可能与一个点相交。
以上是根据点线面之间的相对位置关系的一些重要知识点的总结。
通过理解和掌握这些知识点,你将能够更好地解决几何问题和分析几何结构。
空间点线面之间位置关系知识点总结

高中空间点线面之间位置关系知识点总结第一章 空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体.旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的结构特征1.1棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱.2.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
2.2圆锥——以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥。
3.1棱台——用一个平行于底面的平面去截棱锥,我们把截面与底面之间的部分称为棱台. 3.2圆台——用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.4.1球——以半圆的直径所在直线为旋转轴,半圆旋转一周形成的旋转体叫做球体,简称球. (二)空间几何体的三视图与直观图1.投影:区分中心投影与平行投影。
平行投影分为正投影和斜投影。
2.三视图——正视图;侧视图;俯视图;是观察者从三个不同位置观察同一个空间几何体而画出的图形;画三视图的原则: 长对齐、高对齐、宽相等3.直观图:直观图通常是在平行投影下画出的空间图形。
4.斜二测法:在坐标系'''x o y 中画直观图时,已知图形中平行于坐标轴的线段保持平行性不变,平行于x 轴(或在x 轴上)的线段保持长度不变,平行于y 轴(或在y 轴上)的线段长度减半。
重点记忆:直观图面积=原图形面积 (三)空间几何体的表面积与体积 1、空间几何体的表面积①棱柱、棱锥的表面积: 各个面面积之和②圆柱的表面积 ③圆锥的表面积2S rl r ππ=+④圆台的表面积22Srl r Rl R ππππ=+++ ⑤球的表面积24S R π=⑥扇形的面积公式213602n R S lr π==扇形(其中l 表示弧长,r 表示半径) 2、空间几何体的体积①柱体的体积 V S h =⨯底 ②锥体的体积 13V S h =⨯底③台体的体积1)3V S S h =+⨯下上( ④球体的体积343V R π=第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系 2.1.11 平面含义:平面是无限延展的2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
高中数学空间点线面之间的位置关系的知识点总结

高中空间点线面之间位置关系知识点总结第二章直线与平面的位置关系2.1空间点、直线、平面之间的位置关系2.1.11平面含义:平面是无限延展的 2平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
3(1)公理符号表示为公理1(2)公理使A ∈α、公理2(3)公理公理32.1.212公理4强调:公理公理4作用:判断空间两条直线平行的依据。
3等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补 4注意点:①a'与b'所成的角的大小只由a 、b 的相互位置来确定,与O 的选择无关,为简便,点O 一般取在两直线中的一条上; ②两条异面直线所成的角θ∈(0,);③当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a ⊥b ;④两条直线互相垂直,有共面垂直与异面垂直两种情形;⑤计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
2.1.3—2.1.4空间中直线与平面、平面与平面之间的位置关系1、直线与平面有三种位置关系: (1)直线在平面内——有无数个公共点D CBAα 共面直线2(2)直线与平面相交——有且只有一个公共点(3)直线在平面平行——没有公共点指出:直线与平面相交或平行的情况统称为直线在平面外,可用aα来表示aαa∩α=Aa∥α2.2.直线、平面平行的判定及其性质2.2.1直线与平面平行的判定1、直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
简记为:线线平行,则线面平行。
符号表示:=>a∥α2.2.212(1(2(32.2.3—1、定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
(完整)空间点线面之间位置关系知识点总结,推荐文档

2.1.3 — 2.1.4 空间中直线与平面、平面与平面之间的位置关系
①柱体的体积 V S底 h
②锥体的体积
V
1 3 S底
h
③台体的体积
V 13(S上上 S S下下 S ) h
④球体的体积V 4 R3 3
1、直线与平面有三种位置关系: (1)直线在平面内 —— 有无数个公共点 (2)直线与平面相交 —— 有且只有一个公共点 (3)直线在平面平行 —— 没有公共点 指出:直线与平面相交或平行的情况统称为直线在平面外,可用 a
画三视图的原则: 长对齐、高对齐、宽相等
2.1.2 空间中直线与直线之间的位置关系 1 空间的两条直线有如下三种关系:
相交直线:同一平面内,有且只有一个公共点;
β
P
α ·L
3.直观图:直观图通常是在平行投影下画出的空间图形。
共面直 平行直线:同一平面内,没有公共点;
4.斜二测法:在坐标系 x 'o ' y ' 中画直观图时,已知图形中平行于坐标轴的线段保持平行性不变,平行于 x
的四个顶点或者相对的两个顶点的大写字母来表示,如平面 AC、平面 ABCD 等。
(1)多面体——由若干个平面多边形围成的几何体.
3 三个公理:
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。其中,这条定直 (1)公理 1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内
(1)若 A1B2 A2B1 0 ,两直线相交;
(2)若 A1B2 A2B1 0 ,两直线平行或重合;
(3)若 A1A2 B1B2 0 ,若两直线垂直。
10.点 (x1, y1)和(的x2中, y点2 ) 坐标是
空间点线面之间位置关系知识点总结

高中空间点线面之间位置关系知识点总结第一章 空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体.旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的结构特征棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱.棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
圆锥——以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥。
棱台——用一个平行于底面的平面去截棱锥,我们把截面与底面之间的部分称为棱台. 圆台——用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.球——以半圆的直径所在直线为旋转轴,半圆旋转一周形成的旋转体叫做球体,简称球. (二)空间几何体的三视图与直观图1.投影:区分中心投影与平行投影。
平行投影分为正投影和斜投影。
2.三视图——正视图;侧视图;俯视图;是观察者从三个不同位置观察同一个空间几何体而画出的图形;画三视图的原则: 长对齐、高对齐、宽相等3.直观图:直观图通常是在平行投影下画出的空间图形。
4.斜二测法:在坐标系'''x o y 中画直观图时,已知图形中平行于坐标轴的线段保持平行性不变,平行于x 轴(或在x 轴上)的线段保持长度不变,平行于y 轴(或在y 轴上)的线段长度减半。
重点记忆:直观图面积=原图形面积(三)空间几何体的表面积与体积 1、空间几何体的表面积①棱柱、棱锥的表面积: 各个面面积之和②圆柱的表面积 ③圆锥的表面积2S rl r ππ=+④圆台的表面积22Srl r Rl R ππππ=+++ ⑤球的表面积24S R π=⑥扇形的面积公式213602n R S lr π==扇形(其中l 表示弧长,r 表示半径) 2、空间几何体的体积①柱体的体积 V S h =⨯底 ②锥体的体积 13V S h =⨯底③台体的体积 1)3V S S S S h =++⨯下下上上( ④球体的体积343V R π=第二章 直线与平面的位置关系空间点、直线、平面之间的位置关系 2.1.11 平面含义:平面是无限延展的2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
高中数学空间点线面之间的位置关系的知识点总结

高中空间点线面之间位置关系知识点总结2.1空间点、直线、平面之间的位置关系 2.1.11 平面含义:平面是无限延展的2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
3 三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内 符号表示为A ∈LB ∈L => L α A ∈α B ∈α公理1作用:判断直线是否在平面内(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理2作用:确定一个平面的依据。
D CBAα LA·α C ·B· A· α(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P ∈α∩β =>α∩β=L ,且P ∈L 公理3作用:判定两个平面是否相交的依据 2.1.2 空间中直线与直线之间的位置关系 1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点; 异面直线: 不同在任何一个平面内,没有公共点。
2 公理4:平行于同一条直线的两条直线互相平行。
符号表示为:设a 、b 、c 是三条直线a ∥bc ∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补4 注意点:① a'与b'所成的角的大小只由a 、b 的相互位置来确定,与O 的选择无关,为简便,点O 一般取在两直线中的一条上;② 两条异面直线所成的角θ∈(0, );③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a ⊥b ;P· αLβ共面直线=>a ∥c2④两条直线互相垂直,有共面垂直与异面垂直两种情形;⑤计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
空间点线面位置关系整理(ppt)

在二维平面中,一个点可以确定一条 直线,但直线本身不能确定一个具体 的点。同样,在三维空间中,一个点 也可以确定一个平面,但平面本身不 能确定一个具体的点。
点与面之间的关系
总结词
点与面之间的关系是相对复杂的,一个点可以位于一个平面上,但不能确定一个平面。
详细描述
在二维平面中,一个点可以位于一个平面上,但这个平面本身不能被一个单独的点所确 定。在三维空间中,一个点也可以位于一个曲面上,但这个曲面本身不能被一个单独的
详细描述
线在面上的变换通常涉及到直线的平移、旋 转或倾斜等操作。这种变换可以用来描述一 个物体在平面上的运动或变化,例如桥梁的 伸缩、建筑物的旋转等。此外,这种变换还 可以用来研究几何图形在平面上的运动规律 和性质。
06
空间点线面位置关系的证明
点在线上的证明
定义法
根据点的定义,如果一个点在直线上 ,则该点满足直线的方程。通过验证 点的坐标是否满足直线的方程,可以 证明该点在线上。
3
线可以用来确定建筑物的空间形态和方向感。
点线面在建筑学中的应用
01
面在建筑学中的应用
02
面可以表示建筑物的立面、屋顶、地面等。
面可以用来确定建筑物的空间大小、形状和功能分区等。
03
点线面在计算机图形学中的应用
01
02
03
点在计算机图形学中的 应用
点可以表示像素的位置 和颜色信息。
点可以用来实现图像的 缩放、旋转和平移等变
点在面上的变换
总结词
点在面上的变换是指一个点在一个平面 上的位置变化。
VS
详细描述
与点在线上的变换类似,点在面上的变换 也可以通过平移、旋转或缩放等操作来实 现。这种变换可以用来描述一个物体在平 面上的运动或变化,例如飞行器在空中的 飞行轨迹。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a⊥b;
④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;
⑤ 计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
2.1.3 — 2.1.4 空间中直线与平面、平面与平面之间的位置关系
1、直线与平面有三种位置关系:
(1)直线在平面内 —— 有无数个公共点
(2)直线与平面相交 —— 有且只有一个公共点
高中空间点线面之间位置关系知识点总结
第一章 空间几何体
(一)空间几何体的结构特征
(1)多面体——由若干个平面多边形围成的几何体 .
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。其中,这条定直线
称为旋转体的轴。
(2)柱,锥,台,球的结构特征
1.1 棱柱——有两个面互相平行, 其余各面都是四边形, 并且每相邻两个四边形的公共边都互相平行, 由这
简记为:线线平行,则线面平行。
符号表示:
aα
b β =>a ∥ α
a∥b
2.2.2 平面与平面平行的判定
1、两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。
符号表示: aβ bβ a∩ b = P β∥α a∥ α b∥ α
2、判断两平面平行的方法有三种: (1)用定义; (2)判定定理; (3)垂直于同一条直线的两个平面平行。 2.2.3 — 2.2.4 直线与平面、平面与平面平行的性质 1、定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。 简记为:线面平行则线线平行。 符号表示:
A
B
α· C ·
·
公理 2 作用:确定一个平面的依据。
(3)公理 3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为: P∈ α∩β => α ∩β=L,且 P∈ L
公理 3 作用:判定两个平面是否相交的依据
β
2.1.2 空间中直线与直线之间的位置关系
1 空间的两条直线有如下三种关系:
x
轴(或在 x 轴上)的线段保持长度不变,平行于 y 轴(或在 y 轴上)的线段长度减半。 重点记忆:直
观图面积 = 原图形面积 ( 三 ) 空间几何体的表面积与体积 1、空间几何体的表面积 ①棱柱、棱锥的表面积: 各个面面积之和
②圆柱的表面积 S = 2 πrl + 2 πr 2
③圆锥的表面积 S rl
公理 4 作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补
4 注意点:
① a' 与 b' 所成的角的大小只由 a、b 的相互位置来确定,与 O 的选择无关,为简便,点 O 一般取在两直
线中的一条上;
② 两条异面直线所成的角 θ∈(02 , ) ; ③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作
圆锥。
3.1 棱台——用一个平行于底面的平面去截棱锥,我们把截面与底面之间的部分称为棱台
.
3.2 圆台——用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台 .
4.1 球——以半圆的直径所在直线为旋转轴,半圆旋转一周形成的旋转体叫做球体,简称球
.
(二与平行投影。平行投影分为正投影和斜投影。
2. 三视图——正视图;侧视图;俯视图;是观察者从三个不同位置观察同一个空间几何体而画出的图形;
画三视图的原则: 长对齐、高对齐、宽相等
3. 直观图:直观图通常是在平行投影下画出的空间图形。
4. 斜二测法:在坐标系 x 'o ' y' 中画直观图时,已知图形中平行于坐标轴的线段保持平行性不变,平行于
个顶点或者相对的两个顶点的大写字母来表示,如平面 AC、平面 ABCD等。
3 三个公理:
(1)公理 1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内
符号表示为
A∈L
B∈L => L
α
A∈α
A
α·
L
B∈α
公理 1 作用:判断直线是否在平面内 (2)公理 2:过不在一条直线上的三点,有且只有一个平面。 符号表示为: A、 B、C三点不共线 => 有且只有一个平面 α, 使 A∈α 、B∈α、C∈α 。
(3)直线在平面平行 —— 没有公共点
指出:直线与平面相交或平行的情况统称为直线在平面外,可用 a α来表示
L
p α
aα
a
∩α =A
a
∥α
2.2. 直线、平面平行的判定及其性质
2.2.1 直线与平面平行的判定
1、直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
a∥α a β a ∥b α∩β= b 作用:利用该定理可解决直线间的平行问题。 2、定理:如果两个平面同时与第三个平面相交,那么它们的交线平行。 符号表示: α∥β α∩γ= a a ∥b β∩γ= b
4 R3 3
第二章 直线与平面的位置关系
2.1 空间点、直线、平面之间的位置关系 2.1.1
D
α A
C B
1 平面含义:平面是无限延展的
2 平面的画法及表示 (1)平面的画法: 水平放置的平面通常画成一个平行四边形, 锐角画成 450,且横边画成邻边的 2 倍长(如
图)
(2)平面通常用希腊字母 α、β 、γ等表示,如平面 α 、平面 β等,也可以用表示平面的平行四边形的四
共面直线
相交直线:同一平面内,有且只有一个公共点; 平行直线:同一平面内,没有公共点;
α
P
·L
异面直线: 不同在任何一个平面内,没有公共点。
2 公理 4:平行于同一条直线的两条直线互相平行。
符号表示为:设 a、b、c 是三条直线
a∥b c∥b
=>a∥c
强调:公理 4 实质上是说平行具有传递性,在平面、空间这个性质都适用。
r2
④圆台的表面积 S rl
r 2 Rl
R2 ⑤球的表面积 S 4 R2
⑥扇形的面积公式 S扇形
n R2 360
1 lr (其中 l 表示弧长, r 表示半径)
2
2、空间几何体的体积
①柱体的体积 V S底 h
②锥体的体积 V
1 3 S底 h
③台体的体积
V
1( 3
S上
S上 S下
S下 ) h
④球体的体积 V
些面所围成的几何体叫做棱柱。
1.2 圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱
.
2.1 棱锥——有一个面是多边形, 其余各面是有一个公共顶点的三角形, 由这些面所围成的几何体叫做棱锥。
2.2 圆锥——以直角三角形的一直角边所在的直线为旋转轴, 其余各边旋转而形成的曲面所围成的几何体叫
