初二数学-八年级数学动点问题专项训练
初二数学动点问题练习含答案word文档良心出品
动态问题它们在线段、射线或弧线上运动的一类所谓“动点型问题”是指题设图形中存在一个或多个动点,..解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题开放性题目.关键:动中求静数形结合思想转化思想数学思想:分类思想从点P∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,1、如图1,梯形ABCD中,AD秒的速度移动,以2 cm/从C开始沿CB向点B边以A开始沿AD1cm/秒的速度移动,点Q t秒。
Q 分别从A,C同时出发,设移动时间为如果P,6 时,四边形是平行四边形;当t=. 8时,四边形是等腰梯形当t=上任上,且DM=1,N为对角线AC2、如图2,正方形ABCD的边长为4,点M在边DC5 意一点,则DN+MN的最小值为°90?ACB?AC?60°BC?2O Rt△ABC,?B中,.点、如图,在,是的中点,过3COOlACDAB作重合的位置开始,绕点.从与作逆时针旋转,交过点点边于点的直线?lABl ∥CEE于点的旋转角为,设直线交直线.??EDBCAD;的长为1()①当度时,四边形是等腰梯形,此时??EDBCAD;度时,四边形是直角梯形,此时的长为②当l?EDBC90°?)当(2是否为菱形,并说明理由.时,判断四边形CEO ;;②解:(1)①30,160,1.5?0 .是菱形时,四边形EDBC)当∠(2α=90BA 0DAB, 是平行四边形∴四边形EDBC∵∠α=∠ACB=90//,∴BCED. ∵CE// 000.在Rt△ABC,∠B=60,BC=2, ∴∠中,∠ACB=90A=30C1AC O3320=2.,∴=30中,∠. =2∴AOA=AD= .在Rt△AOD=4,∴ABACB A 又∵四边形EDBC是平行四边形,. BD∴=2. ∴BD=BC(备用图)EDBC是菱形∴四边形E.D于,BE⊥MN于ADMNACB=90°4、在△ABC中,∠,AC=BC,直线经过点C,且⊥MN M M M C D C C E N D EA B B B A AD E图1N 图3N 图21;DE=AD+BE绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②(1)当直线MN ;的位置时,求证:DE=AD-BE绕点(2)当直线MNC旋转到图2具有怎样的等量关系?请写出这个等量BEAD、当直线MN绕点C旋转到图3的位置时,试问DE、(3). 关系,并加以证明∠ACD=90°CAD+∠ACD=90°∴∠BCE+∠解:(1)①∵∠ACD=ACB=90°∴∠CEB ADC≌△CAD=∠BCE ∵AC=BC ∴△∴∠DE=CE+CD=AD+BE ∴CE=AD,CD=BE ∴②∵△ADC≌△CEBAC=BC ∴∠ACD=∠CBE 又∵(2) ∵∠ADC=∠CEB=∠ACB=90°DE=CE-CD=AD-BE∴∴CE=AD,CD=BE ∴△ACD≌△CBE) ,3的位置时,DE=BE-AD(或AD=BE-DEBE=AD+DE等(3) 当MN旋转到图∠CBE,又∵AC=BC,∵∠ADC=∠CEB=∠ACB=90°∴∠ACD= DE=CD-CE=BE-AD. CD=BE,∴∴△ACD≌△CBE,∴AD=CE,90??AEF BCABCDE,5、数学课上,张老师出示了问题:如图1,四边形是边是正方形,点的中点.DCG?EFCFEFFAE 交正方形外角=,求证:的平行线.且于点ECABMMEAM,易证,连接经过思考,小明展示了一种正确的解题思路:取=的中点,则ECF△AME≌△EFAE?,所以.在此基础上,同学们作了进一步的研究:CEBCEBCB外)的任意是边上(除的中点”改为“点,(1)小颖提出:如图2,如果把“点是边EFAE”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明一点”,其它条件不变,那么结论“= 过程;如果不正确,请说明理由;EFAEEBCC”是“的延长线上(除=点外)的任意一点,其他条件不变,结论(2)小华提出:如图3,点仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.D )正确.解:(1A EC?AMMEABM D ,连接证明:在,使上取一点.A F135???AME??BME?45BE??BM..,°°F M 135ECF?CF??DCF?45??,.是外角平分线,°°B C E G ECF????AME.B 1 图C E G90?AEB??CEFAEB??BAE??90?,,°°D A ?BAE??CEF?△AME≌△BCFEF??AE?(ASA...) F (2)正确.NAN?CENEBA..使的延长线上取一点证明:在,连接B E C G?BN?BE??N??PCE?45N ..°FF2图ABCDBE?AD D .是正方形,四边形∥A D ACEF????NAEBEA??DAE??..ECF≌△?△ANE)ASA(.EF??AE.B E C G B E C G 3图沿射线M从3,动点P且MB外一点,AB=5A到射线MB的距离为是射线射线6、如图, MB 上,MB=9,A 的运动时间为t. 秒的速度移动,设MB方向以1个单位/P 值;PAB为直角三角形的t)△t)△1 PAB为等腰三角形的值;(2 求(值为直角三角形的ABM=45 AB=5 3()若且∠°,其他条件不变,直接写出△PABt2BC∥ADCDABCDBCEF∥EABE于点,交中,是作7、如图1,在等腰梯形的中点,过点6BC?AB?4,BC60?∠B?EF到)求点的距离;求:.(,1.ADCBCMN∥ABPEFPM?PMMEF交折线过过作于点作,(2)点交为线段上的一个动点,PNxEP?N.,连结于点,设PMNP△NMN△AD的周长;若的形状是否发生改变?若不变,求出2)①当点在线段,上时(如图改变,请说明理由;PMN△NDCP为等腰三角形?若存在,请求出所有),是否存在点②当点在线段,使上时(如图3x满足要求的的值;若不存在,请说明理由N A A A D D DN PPF F F EE EBBBC C CM M3图1 图2图(第25题)AD A DF EF EBC BC5图(备用)图4(备用)1.?BE?2AB.GEG?BC2EEAB于点∵∴为11解()如图,过点的中点,作122.2EG1?BGBE?,??1?3.Rt△30?60,?∠BEG??B∠EBG2∴在中,∴3.3BC A D E即点到的距离为PMN△NAD的形状不发生改变.2)①当点上运动时,在线段(F E.∥EG?EGEF,PMPM?EF,∴∵.?3PM?EG.GM4?MNAB?EPEF∥BC,?同理,∴∵ BCG ,∥ABPH?MNMNPH如图2,过点于作,∵1图NA D 31.?PH?PM.??60?,∠PMH?30∠NMC?∠B∴∴22PFE533.???MN?MH?4MH?PM cos30??.NH∴则H222 BCMG?22.7?PN?NH?PH??PNH△Rt在中,????2图??22????.4PM?PN?MN?3?7?PMN△的周长∴=MNCNDC△PMN△在线段的形状发生改变,但上运动时,恒为等边三角形.②当点.?MNMR?NRPM?PNPRR于时,如图3当,作,则3?.MR.3MN?3.MN?2MR?△MNCMC?类似①,∵是等边三角形,∴∴2.?6?1?3?2?x?EPGM?BC?BG?MC此时,A DA D A DN P PP)F(EF EFE N RNBCBCBCGMGM GM 图54图3图x?EP?GM?6?1?3.?3?5?3.MPMC?MN?MNMP?此时,,这时时,如图当4NP?NM∠NPM?∠PMN?30?.∠MNC?60?,∠PMN?120?,则5,当又时,如图∠PNM?∠MNC?180?.△PMCPF为直角三角形.∴与重合,因此点MC?PM tan30??1.x?EP?GM?6?1?1?4.此时,∴??3?5PMN△x?2或时,或4综上所述,当为等腰三角形.8BC??△ABCAB?AC10ABD厘米,点为厘米,8、如图,已知中,的中点.点A点向上由在线段点点运动,点向的速度由上以在线段如果点(1)PBC3cm/sBC同时,QCAC 运动4△CQP BPD△是否全等,请说明理由;与的运动速度与点P的运动速度相等,经过1秒后,①若点Q△CQP BPD△与能够使P的运动速度不相等,当点Q的运动速度为多少时,②若点Q 的运动速度与点全等?△ABC都逆时针沿以原来的运动速度从点B同时出发,以②中的运动速度从点C出发,点P (2)若点Q△ABC的哪条边上相遇?第一次在三边运动,求经过多长时间点P与点Q A3??1BP?CQ?31?t)①∵∴厘米,秒,解:(15BD?AB?10ABD厘米.厘米,点∵为∴的中点DQBD?5PC?BC?8PC?8?3?PCBC?BP,厘米,又∵厘米,∴∴BCPCQP△BPD≌△C?B??AB?AC.∴又∵,∴,vv?5?CQ?BDBPCQP?PC?4,?BPCQ△BPD≌△C?B??QP,,,∴则②∵,,又∵155CQ?v??4BP Q4t4??t Q333P秒。
初中八年级下册数学动点问题试题附答案

初中八年级下册数学动点问题试题附答案问题一已知点A(-2, 5)和点B(4, -1),求线段AB的中点的坐标。
解答一根据坐标的定义,线段的中点坐标可以通过求两个端点的坐标的平均值得到。
因此,我们可以计算出线段AB的中点的坐标如下:中点坐标x = (x<sub>A</sub> + x<sub>B</sub>)/2 = (-2 + 4)/2 = 1中点坐标y = (y<sub>A</sub> + y<sub>B</sub>)/2 = (5 - 1)/2 = 2 所以线段AB的中点的坐标是(1, 2)。
问题二已知点C(3, -2)和点D(-5, 6),求线段CD的长度。
解答二根据坐标的定义,计算线段的长度可以使用两点之间的距离公式。
对于两点(x<sub>1</sub>, y<sub>1</sub>)和(x<sub>2</sub>,y<sub>2</sub>),它们之间的距离可以通过以下公式进行计算:距离= √((x<sub>2</sub> - x<sub>1</sub>)^2 + (y<sub>2</sub> - y<sub>1</sub>)^2)因此,我们可以计算出线段CD的长度如下:距离= √((-5 - 3)^2 + (6 - (-2))^2) = √(64 + 64) = √128 = 8√2所以线段CD的长度为8√2。
问题三已知点E(2, -3)和线段DE的长度为10,求点D的坐标。
解答三根据坐标的定义,求点D的坐标可以通过已知点E的坐标和线段DE的长度进行计算。
首先,我们将点D的坐标记为(x, y)。
然后,根据两点之间的距离公式,我们可以得到以下方程:10 = √((x - 2)^2 + (y - (-3))^2)对上述方程进行化简,我们可以得到以下方程:100 = (x - 2)^2 + (y + 3)^2这是一个关于x和y的二次方程。
初二数学动点练习题

初二数学动点练习题1. 直线上的动点问题- 题目:在直线AB上,点C是动点,当点C沿着直线AB移动时,求证∠ACB是一个恒定的角度。
2. 圆上的动点问题- 题目:圆O的半径为5,点P是圆上的动点。
求证:无论点P在圆上如何移动,OP的长度始终为5。
3. 动点与线段的关系- 题目:线段AB的长度为10,点C是线段AB上的动点。
当点C从A向B移动时,求线段AC的长度与线段BC的长度之和是否恒定。
4. 动点与三角形的面积- 题目:三角形ABC的面积为30平方单位,点D是边AB上的动点。
求证:无论点D在AB上如何移动,三角形ACD的面积始终是三角形ABC面积的一半。
5. 动点与平行四边形的对角线- 题目:平行四边形ABCD中,点E是边AB上的动点,点F是边CD 上的动点,且EF始终是平行四边形的对角线。
求证:无论点E和点F如何移动,EF的长度始终等于AB和CD的长度之和。
6. 动点与圆的切线- 题目:圆O的半径为6,点P是圆O外的一点,点Q是圆O上的动点。
当点Q沿着圆O移动时,求证:点P到圆O的切线长度始终等于点P到点Q的距离。
7. 动点与相似三角形- 题目:三角形ABC与三角形DEF相似,点G是三角形ABC的动点,点H是三角形DEF的动点,且GH始终是三角形ABC和三角形DEF的对应边的平行线。
求证:无论点G和点H如何移动,三角形AGH与三角形DEF始终相似。
8. 动点与坐标系- 题目:在平面直角坐标系中,点A的坐标为(2,3),点B的坐标为(5,6)。
点C是线段AB上的动点,其坐标为(x,y)。
求证:无论点C如何移动,x和y的和始终等于点A和点B坐标的和。
练习题答案提示:- 对于直线上的动点问题,可以利用角度的恒定性,结合直线的性质来证明。
- 对于圆上的动点问题,可以利用圆的半径性质来证明。
- 对于动点与线段的关系问题,可以利用线段长度的加法性质来证明。
- 对于动点与三角形的面积问题,可以利用三角形面积的计算公式来证明。
初中八年级上册数学动点问题试卷附答案

初中八年级上册数学动点问题试卷附答案
一、选择题
1. 一辆汽车以每小时60千米的速度向东行驶,经过2小时后改变方向,以每小时40千米的速度向北行驶,求其位移。
A. 40千米
B. 80千米
C. 100千米
D. 120千米
答案:D. 120千米
2. 一辆自行车向前行驶30分钟后,记下此时的位置。
然后车辆停下来,待30分钟后,以相同的时间和速度往后倒退,到达原点。
求此自行车的位移。
A. 0千米
B. 5千米
C. 10千米
D. 15千米
答案:A. 0千米
二、填空题
1. 一个物体从A点出发,以每秒2米的速度向东行驶10秒,
然后改变方向,以每秒3米的速度向南行驶15秒,最后以每秒4
米的速度向西行驶20秒。
求物体的位移为______米。
答案:-20
2. 一架飞机以每秒200米的速度向东飞行30秒,然后改变方向,以每秒300米的速度向南飞行40秒,最后以每秒400米的速
度向西飞行50秒。
求飞机的位移为______米。
答案:-4000
三、解答题
1. 一个人从原点出发,以每小时5千米的速度向西行驶1小时,然后改变方向,以每小时8千米的速度向南行驶2小时,最后以每
小时10千米的速度向东行驶3小时。
求此人的位移和位移方向。
答案:位移为-23千米,位移方向为东南方向。
2. 一个物体以每秒10米的速度向北行驶30秒,然后改变方向,以每秒15米的速度向东行驶40秒,最后以每秒20米的速度向南
行驶50秒。
求物体的位移和位移方向。
答案:位移为20米,位移方向为南方。
八年级数学动点问题专题

解决动点问题的主要步骤
认真审题作出图形, 如果涉及特定的时刻,
化动为静
就作出特定时刻的图形
利用题目中的几何条件, 建立几何等量关系
用s=vt表示所需要的线段长
列出方程或函数表达式
对号入座,代入 几何等量关系
17
4、△ABC中,∠B=90°,AB=5cm, BC=7cm,P从A沿AB向B以1cm/s的速度移 动,Q从B沿BC向C以2cm/s的速度移动。 (1)如果P、Q分别从A、B同时出发, 几秒后△PBQ的面积等于4cm2; C
当点P在CD上运动时,设运动时间为t, 求AP、DP和CP的长
B
C
P
A
D
3
如图:梯形ABCD中,AD//BC, AD=9cm,BC=6cm,点P从点A出发,沿 着AD的方向向终点D以每秒一个单位的速 度运动,当点P在AD上运动时,设运动时 间为t,求当t为何值时,四边形APCB为 平行四边形
B
C
A
A.10
B.12
C.14
D.16
D
C
P
A
B
练习2、如图已知 ABCD中,AB=7,BC=4, ∠A=30°
(1)点P从点A沿AB边向点B运动,速度为1cm/s。
若设运动时间为t(s),连接PC,当t为何值时, △PBC为等腰三角形?
D
A 30° 7P
若△PBC为等腰三角形
C
则PB=BC
4 B
∴7-t=4
5
变式1:如图:梯形ABCD中,AD//BC,
AD=9cm,BC=6cm,梯形的高为5cm.点P
从点A出发,沿着AD的方向向终点D以每
秒一个单位的速度运动,当点P在AD上运
(完整)八年级数学动点问题专题

(2)设四边形APQC的面积为y(cm2),求y与t的关系式.
10.如图1,在长方形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B运动,点Q从点B以2cm/s的速度沿BC边向点C运动,如果P、Q同时出发,设运动时间为ts.
(1)出发2秒后,求△ABP的周长。
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按 的路径运动,且速度为每秒2㎝,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
(备用图)
12.如图,在△ABC中,∠B=60°,AB=12㎝,BC=4㎝,现有一动点P从点A出发,以2㎝/秒的速度沿射线AB运动,试回答下列问题:
八年级数学动点问题专题
班级姓名
1.如图:已知正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,求DN+MN的最小值是。
2.等边三角形ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC上一点,若AE=2,则EM+CM最小值为。
第1题第2题第3题
3.如图,锐角三角形ABC中,∠C=45°,N为BC上一点,NC=5,BN=2,M为边AC上的一个动点,则BM+MN的最小值是。
4.如图,在直角梯形ABCD中,∠ABC=90°,DC//AB,BC=3,DC=4,AD=5.动点P从B点出发,由B→C→D→A沿边运动,则△ABP的最大面积为()
A.10 B.12 C.14 D.16
5.如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是( )
初二数学-八年级数学动点问题专项训练.doc

初二数学-八年级数学动点问题专项训练.docS ABC.1、当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证S DEF S CEF122、当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请赐予证明;若不可立,S DEF、S CEF、S ABC又有怎样的数量关系?请写出你的猜想,不需证明.例3、正方形四条边都相等,四个角都是90°.如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是直线MN上一点,以AE为边在直线MN的上方作正方形AEFG.(1)如图1,当点E在线段BC上(不与点B、C重合)时:①判断△ADG与△ABE是否全等,并说明原因:②过点F作FH⊥MN,垂足为点H,察看并猜测线段BE与线段CH的数量关系,并说明原因;(2)如图2,当点E在射线CN上(不与点C重合)时:①判断△ADG与△ABE是否全等,不需说明原因:②过点F作FH⊥MN,垂足为点H,已知GD=4,求△CFH的面积.例4,在△ABC中,∠CAB=70°。
在同一平面内,将△ABC绕点A旋转到△AB'C'的地点,使得CC'∥AB,则∠B'AB=练习1。
已知:如图,AB=16cm,动点P从点A出发,沿AB以2cm/s的速度向点B运动,设点P运动的时间为t秒,请解答下列问题:(1)用含t的式子表示线段AP,PB的长分别为()cm.A。
t;16-tB.2t: 16-2tC. 2t: 16—tD. t: 16-2t2.(上接第1题)(2)点P出发()秒抵达B点。
A. 4B.8C. 10D. 163.已知:如图,AB=18cm,动点P从点A出发,沿AB以2cm/s的速度向点B运动,动点QA运从点B出发,沿BA以1cm/s的速度向点动.P,Q两点同时出发,当点P抵达点B时,点P,Q同时停止运动,设点P运动的时间为t秒,请解答下列问题:(1)用含t的式子表示线段AP,QB长分别()cm.A. 18-2t: 2t为B. t: 18-t c. t: 2tD.2t: t。
八年级数学动点专题(人教版)(含答案)

动点专题(人教版)一、单选题(共10道,每道10分)1.已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=12,BC=24,动点P从点A出发沿AD向点D以每秒1个单位的速度运动,动点Q从点C出发沿CB向点B以每秒2个单位的速度运动,P,Q同时出发,当点P停止运动时,点Q也随之停止,连接PQ,DQ.设点P的运动时间为t秒,当t为( )秒时,△PDQ≌△CQD.A.6B.5C.4D.3答案:C解题思路:试题难度:三颗星知识点:动点问题2.已知:如图,在矩形ABCD中,AB=4,AD=10,点E为边AD上一点,且AE=7.动点P从点B出发,沿BC向点C以每秒2个单位的速度运动,连接AP,DP.设点P的运动时间为t 秒.当t为( )秒时,△DCP≌△CDE.A.7B.3C. D.答案:C解题思路:试题难度:三颗星知识点:动点问题3.已知:如图,在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.点P在线段BC上以每秒2cm的速度由点B向点C运动,同时点Q在线段CA上由点C向点A运动.设点P 的运动时间为t秒,当t为( )秒时,△BPD与△CQP可能全等.A. B.C.3D.3或4答案:B解题思路:试题难度:三颗星知识点:动点问题4.已知:如图,在矩形ABCD中,AB=4cm,BC=6cm,点E为AB的中点,如果点P在线段BC上以每秒1cm的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.设点P的运动时间为t秒,若某一时刻△BPE与△CQP全等,则点Q的运动速度是( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:动点问题5.已知:如图,在长方形ABCD中,AB=DC=4,AD=BC=5.延长BC到点E,使CE=2,连接DE.动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒.当t为( )秒时,△ABP和△DEC全等.A.2B.2或12C.1D.1或6答案:D解题思路:试题难度:三颗星知识点:动点问题6.如图,在长方形ABCD中,AB=20cm,BC=4cm,动点P以4cm/s的速度从B点出发,沿BA 方向向点A移动,同时动点Q以1cm/s的速度,沿CD方向向点D移动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t(s),则当t为( )秒时,线段PQ恰好平分长方形ABCD的面积.A.3B.4C.5D.6答案:B解题思路:试题难度:三颗星知识点:动点问题7.如图,在梯形ABCD中,AD∥BC,DC=4,BC=6,动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒2个单位长度的速度向终点D运动,当其中一个动点到达终点时,另一动点也随之停止运动.设运动时间为t秒,当t为( )时,△MNC是以MN为底的等腰三角形.A.1B.2C.3D.答案:D解题思路:试题难度:三颗星知识点:动点问题8.如图,在长方形ABCD中,∠B=90°,AB=6m,BC=8m,动点P以3m/s的速度从点A出发,沿AC方向向点C移动,同时动点Q以2m/s的速度从点C出发,沿CB方向向点B移动;当P,Q两点中其中一点到达终点时,则停止运动.设运动时间为t秒,则当t为( )秒时,△PQC是以PQ为底的等腰三角形.A.2B.5C. D.答案:A解题思路:试题难度:三颗星知识点:动点问题9.已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边线运动,运动路径为:G—C—D—E—F—H,相应的△ABP的面积y()关于运动时间t (s)的图象如图2.若AB=6cm,则下列四个结论中正确的个数有( )①图1中的BC长是4cm;②图2中的M点表示第4秒时y的值为24;③图1中的CD长是4cm;④图2中的N点表示第12秒时y的值为18.A.1个B.2个C.3个D.4个答案:C解题思路:试题难度:三颗星知识点:动点问题的函数图象10.如图1,在长方形ABCD中,动点P从B点出发,以2cm/s的速度沿BC-CD-DA运动到A 点停止,设点P的运动时间为x(s),△ABP的面积为y(),y关于x的函数图象如图2所示,则长方形ABCD的面积是( ).A.4B.8C.10D.16答案:D解题思路:试题难度:三颗星知识点:动点问题的函数图象。
人教版八年级上册数学期末动点问题训练题(含简单答案)

人教版八年级上册数学期末动点问题训练题(1)若点在线段上,如图所示,且,则______(2)若点在边上运动,如图所示,则、、之间的关系为(3)如图,若点在斜边的延长线上运动,请写出(1)求证:;(2)探究与的数量关系,并证明你的结论.(3)若,直接写出的值为__________P AB ①50α∠=︒12∠+∠=P AB ②α∠1∠2∠③P BA ()CE CD <α∠AF EF =AD CF 2AD CD =CF(1)求的面积;(2)如图1,若,,作交于,平分,平分交求出(用表示);(3)如图2.若,轴于,点从点出发,在射线(1)如图1,若,则_______°ABO V 60ACB ∠=︒180NFC FCN FNC ∠+∠+∠=︒GF AB ∥AC F FP GFC ∠FN AFP ∠BAC ∠α()36P ,PC x ⊥C M P 15α=︒CBA ∠'=(2)如图2,点P 在延长线上,且.①连接,试探究,,之间是否存在一定数量关系,猜想并说明理由.②连接,若,C ,P 三点共线,,,求的长.6.如图1,,,,.(1)求C 点的坐标;(2)如图2,P 为y 轴负半轴上一个动点,当P 点在y 轴负半轴上向下运动时,始终保持,,过D 作轴于E 点,求的值;(3)如图3,已知点F 坐标为,当G 在y 轴的负半轴上沿负方向运动时,作,始终保持,与y 轴负轴交于点,与x 轴正半轴交于点,当G 点在y 轴的负半轴上沿负方向运动时,求的值.7.如图,中,,,,,若动点从点开始,按的路径运动,且速度为每秒.设运动的时间为秒.(1)当点在上时,______时,把的周长分成相等的两部分?(2)当点在上时,______时,把的面积分成相等的两部分?(3)当点在所有运动过程中,连接或,求当为何值时,的面积为12?BD DAP DBC α∠=∠=CP AP BP CP CA 'A '10BP =1CP =CA '2OA =4OB =90BAC ∠=︒AB AC =PA PD =90APD ∠=︒DE x ⊥OP DE -(44)--,Rt FGH V 90GFH ∠=︒FG (0)G m ,FH (0)H n ,m n +ABC V 90C ∠=︒8cm AC =6cm BC =10cm AB =P C C A B C →→→2cm t P AB t =CP ABC V P AB t =CP ABC V P PC PB t BCP V(1)请直接写出,两点的坐标;(2)如图,分别以,为直角边向右侧作等腰交轴于点,连接,求证:;(3)如图,点为y 轴上一动点,点在直线侧作等腰,若连接E ,,三点按逆时针顺序排列B C 1AB BC Rt x M BM BM DE ⊥2F (),33G m m -+Rt BCE V F G ((1)如图1,当点D 在边上时.①求证:;②直接判断结论,,的关系 (2)如图2,当点D 在边的延长线上时,其他条件不变,请写出(1)求的度数;(2)当点运动到使时,求(3)当点运动时,与BC ABD ACE ≌△△BC DC CE BC CBD ∠P ACB ABD =∠∠P APB ∠ADB ∠(1)如图①,动点在轴负半轴上,且交于点、交于点,求证:.(2)如图,在(1)的条件下,连接,求证:.(3)如图③,E 为的中点,动点G 在轴上,,,连接,作交轴于F ,猜想,、之间的数量关系,并说明理由.13.已知中.(1)如图1、2,若点是上一点,且,点是上的动点,将沿对折,点的对应点为(点和点在直线的异侧),与交于点.①当时,求的度数.②当是等腰三角形时,求的度数.(2)如图3,若点是上一点,且,是线段上的动点,以为直角构造等腰直角(三点顺时针方向排列),在点的运动过程中,直接写出的最小值.14.在平面直角坐标系中,点B 、C 的坐标分别为、,点A 在第一象限,且是等边三角形.点D 的坐标为,E 是边上一动点,连接,以为边在右侧作等边,连接.(1)求出A 点坐标;(2)当点F 落在边上时,与全等吗?若全等,请给予证明;若不全等,请说明理由;(3)当以为腰的是等腰三角形时,的长为_________.C x AH BC ⊥BC H OB P △≌△AOP BOC ②OH 2OHP AHB ∠=∠AB y (0,)G n 0n <GE EF GE ⊥x GB OB AF Rt ABC △90930∠︒∠︒C BC B =,且=,=D CB 2CD =E AB DBE V DE B B'B'C AB 'DB AB H 20∠=︒'B EA EDB ∠B HE 'V DEB ∠D CB 2CD =M AC MDN ∠DMN V D M N ,,M CN NB +(0,0)(12,0)ABC V (4,0)AB DE DE DE DEF V CF AC CDF V BED V DF CDF V BE(1)若,① ,②判断线段,之间有怎样的位置关系并说明理由;(2)设,,则x ,y 之间的数量关系为(3)如图2,当时,若线段,90BAC ∠=︒BCA ∠=BC CE BAC x ∠=︒BCE y ∠=︒CE AB ∥3BC =ABC V______.17.已知:如图,在平面直角坐标系中,点B是x轴上的动点,点,点,轴于点D.(1)当点B坐标为时,求证:;(2)在(1)的条件下,探究并证明和的位置关系;(3)当的周长最小时,求点B的坐标.()0,2A()5,3CCD x⊥()3,0OAB DBC≌△△AB BCABCV参考答案:(4)17. (2),(3)CEP DBP BPB +∠∠=∠AB BC ⊥()2,0B。
八年级动点问题专题训练

八年级动点问题专题训练动点问题,听起来好像很复杂,其实就像我们生活中的小插曲。
想象一下,你在操场上跑步,突然发现朋友在另一边挥手,你心里那一激灵,立马转身去追他。
这时候,你就成了动点,简单吧?动点问题其实就是研究这些点在空间中如何移动的过程。
比如说,有个小球从一边滚到另一边,咕噜咕噜地,或是有人骑着单车飞驰而过,风驰电掣,想象一下这些场景,不是很有趣吗?再说说具体的情况,比如你和朋友在公园里玩捉迷藏。
你躲在一棵大树后面,心里想着,等他经过时我就跳出来。
你是个动点,对吧?你的位置在不断变化,等他走远了,你可能就想换个地方。
这个时候,你的移动速度、方向,都和你的策略息息相关。
如果你觉得他快要发现你,可能就会加快脚步,嘿嘿,动点问题就是这么灵活多变,简单易懂!再来点幽默的,我们常说“脚下生风”,那就是动点的真谛。
想象你在学校的跑道上,和同学比赛,耳边风呼呼地吹,心里想着“我一定要赢!”这时候,你的每一步都是一次动点的演绎。
跑步时的速度、步伐,甚至是呼吸,都是在帮助你走向终点。
就像是电视剧里的主角,跌宕起伏,紧张又刺激。
动点的变化,不光是我们在操场上,生活中无处不在。
比如说,你坐公交车,看着窗外的风景飞快而过,哎,那可真是瞬息万变。
车窗外的树木、电线杆,一眨眼就不见了,仿佛在提醒我们,生活就是一场旅程,动点的问题也在这个过程中不断展现。
想象一下,你在车里,听着歌,窗外的景色伴随着音乐的节奏,瞬间让你觉得自己像电影里的主角,真是个小动点啊。
我们的生活就像一场舞蹈。
每个人都是舞者,走动、旋转、停顿,各自的节奏都不一样。
你在舞池中晃动的时候,其实也是在体验动点的奥秘。
你的每一个动作、每一次转身,都是在与周围的环境互动。
正如古人所说,“步步生花”,每一步都充满了变化与魅力。
这种感觉,特别让人上瘾,仿佛自己是个主角,舞动着自己的故事。
而动点问题中,数学就是那个幕后推手。
它让我们能够分析、理解、预测我们的移动和变化。
最新初二数学八年级数学动点问题专项训练

动点问题专项训练1.如图,△ABC 是边长为6的等边三角形,P 是AC 边上一动点,由A 向C 运动(与A 、C 不重合),Q 是CB 延长线上一点,与点P 同时以相同的速度由B 向CB 延长线方向运动(Q 不与B 重合),过P 作PE ⊥AB 于E ,连接PQ 交AB 于D .(1)当∠BQD =30°时,求AP 的长;(2)当运动过程中线段ED 的长是否发生变化?如果不变,求出线段ED 的长;如果变化请说明理由.【答案】解:(1)∵△ABC 是边长为6的等边三角形,∴∠ACB =60°。
∵∠BQD =30°,∴∠QCP =90°。
设AP =x ,则PC =6﹣x ,QB =x ,∴QC =QB +C =6+x 。
∵在Rt △QCP 中,∠BQD =30°,∴PC =12QC ,即6﹣x =12(6+x ),解得x =2。
∴当∠BQD =30°时,AP =2。
(2)当点P 、Q 运动时,线段DE 的长度不会改变。
理由如下:作QF ⊥AB ,交直线AB 的延长线于点F ,连接QE ,PF 。
∵PE ⊥AB 于E ,∴∠DFQ =∠AEP =90°。
∵点P 、Q 做匀速运动且速度相同,∴AP =BQ 。
∵△ABC 是等边三角形,∴∠A =∠ABC =∠FBQ =60°。
∴在△APE 和△BQF 中,∵∠A =∠FBQ ,AP =BQ ,∠AEP =∠BFQ =90°,∴△APE ≌△BQF (AAS )。
∴AE =BF ,PE =QF 且PE ∥QF 。
∴四边形PEQF 是平行四边形。
∴DE =12EF 。
∵EB +AE =BE +BF =AB ,∴DE =12AB 。
又∵等边△ABC 的边长为6,∴DE =3。
∴当点P 、Q 运动时,线段DE 的长度不会改变。
2. 如图,已知一次函数1y kx b =+的图象与x 轴相交于点A ,与反比例函数2c y x =的图象相交于B (-1,5)、C (25,d )两点.点P (m ,n )是一次函数1y kx b =+的图象上的动点. (1)求k 、b 的值;(2)设31m 2-<<,过点P 作x 轴的平行线与函数2c y x=的图象相交于点D .试问△P AD 的面积是否存在最大值?若存在,请求出面积的最大值及此时点P 的坐标;若不存在,请说明理由;(3)设m 1a =-,如果在两个实数m 与n 之间(不包括m 和n )有且只有一个整数,求实数a 的取值范围.【答案】解:(1)将点B 的坐标代入2c y x =,得c 51=- ,解得c=5-。
初二动点问题的解题练习题

初二动点问题的解题练习题动点问题是初中数学中一个重要的概念,涉及了物体的运动与位置变化。
通过解动点问题的练习题,既可以提高学生对动点问题的理解,又能锻炼他们的数学思维和解题能力。
下面是几道初二动点问题的解题练习题,帮助学生巩固和拓展相关知识。
练习题一:小明和小刚在田径场上同时从同一地点出发沿着同一直线向前走,小明的速度是每小时5千米,小刚的速度是每小时4千米。
如果他们相距20千米,那么他们走了多久?解答:假设两人走了t小时后相遇,则小明走了5t千米,小刚走了4t千米。
由于他们相距20千米,可以得到以下方程:5t - 4t = 20t = 20所以,他们走了20小时后相遇。
练习题二:一架飞机从A地到B地,飞行了240千米,折返飞行了120千米后返回A地。
飞机以每小时300千米的速度飞行,这架飞机在折返飞行后返回A地用了多少时间?解答:假设折返飞行花费了t小时,则飞机从A地到折返点用了(240 + 120)千米 ÷ 300千米/小时 = 1小时。
又因为返回A地所用的时间等于从A地到折返点所用时间的两倍,所以可以写出以下方程:t + 1 + t = 2t + 1 = t + t + 1 = 3解方程可得,t = 1所以,这架飞机在折返飞行后返回A地用了1小时。
练习题三:小明和小红在一个长为600米的田径跑道上同时起跑,小明的速度是每秒2米,小红的速度是每秒3米。
小红比小明快了1圈时,他们相遇的位置距离起跑线多远?解答:小红比小明快了1圈,实际上就是小红比小明多跑了600米。
设他们相遇的位置距离起跑线x米。
由于小明和小红的速度比是2:3,所以可以得到以下方程:2x = 3(x + 600)解方程可得,x = 1800所以,他们相遇的位置距离起跑线1800米远。
练习题四:一个人从A地出发,每小时走8千米的速度,另一个人从B地出发,每小时走10千米的速度。
两人同时出发后,在2小时后相遇。
如果他们相距40千米,A地在B地的东南方向。
八年级数学动点问题专项训练(最新整理)
动点问题专项训练1.如图,在矩形中,AB=2,,动点P 从点B 出发,沿路线作匀速运动,那么的ABCD 1BC =B C D →→ABP △面积S 与点P 运动的路程之间的函数图象大致是( )xD C P BAA .B .C .D .2.如图1,在直角梯形ABCD 中,动点P 从点B 出发,沿BC ,CD 运动至点D 停止.设点P 运动的路程为,△ABP 的x 面积为y ,如果y 关于x 的函数图象如图2所示,则△BCD 的面积是( )A .3B .4C .5D .6图1ABCP D 图23.如图,△ABC 和的△DEF 是等腰直角三角形,∠C=∠F=90°,AB=2.DE=4.点B 与点D 重合,点A,B(D),E 在同一条直线上,将△ABC 沿方向平移,至点A 与点E 重合时停止.设点B,D 之间的距离为x ,△ABC 与△DEF重叠部分的D E →面积为y ,则准确反映y 与x 之间对应关系的图象是( )4.如图,点G 、D 、C 在直线a 上,点E 、F 、A 、B 在直线b 上,若从如图所示的位置出发,沿直线b a b Rt GEF ∥,△向右匀速运动,直到EG 与BC 重合.运动过程中与矩形重合部分的面积(S )随时间(t )变化的图象GEF △ABCD 大致是( )aABCD5.(2009年牡丹江)如图,平面直角坐标系中,在边长为1的正方形ABCD 的边上有一动点P 沿A B C D A →→→→运动一周,则P 的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是( )6.如图1,在矩形ABCD 中,动点P 从点B 出发,沿BC 、CD 、DA 运动至点A 停止,设点P 运动的路程为,△ABP 的x 面积为y ,如果y 关于的函数图象如图2所示,则矩形ABCD 的面积是( )x A .10 8.16 C. 20 D .367.如图,三个大小相同的正方形拼成六边形ABCDEF ,一动点P 从点A 出发沿着A →B →C →D →E 方向匀速运动,最后到达点E .运动过程中PEF ∆的面积(s )随时间(t )变化的图象大致是( )8.如图8,点A 、B 、C 、D 为圆O 的四等分点,动点P 从圆心O 出发,沿O-C-D-O 的路线作匀速运动.设运动时间为秒, t ∠APB 的度数为y 度,则下列图象中表示y 与t 之间函数关系最恰当的是9. 13.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图4所示,设小矩形的长和宽分别为x 、y ,剪去部分的面积为20,若2≤x ≤10,则y 与x 的函数图象是:ABCDA .。
初二数学动点问题专项试卷

一、选择题(每题3分,共30分)1. 在平面直角坐标系中,点P(a,b)在直线y=2x+1上运动,那么a与b的关系是:A. a+b=1B. a=2bC. a=2b+1D. a=2b-12. 已知点A(2,3),点B在x轴上,且AB=5,那么点B的坐标可能是:A. (7,0)B. (-3,0)C. (-7,0)D. (3,0)3. 在△ABC中,AB=AC,点D在BC上,且BD=CD,那么∠ADB与∠ADC的关系是:A. ∠ADB=∠ADCB. ∠ADB=∠BACC. ∠ADB=∠BAC/2D. ∠ADB=∠BAC/34. 在平面直角坐标系中,点M在直线y=x+1上运动,那么点M的坐标满足:A. x=y-1B. x=y+1C. y=x-1D. y=x+15. 已知直线l的方程为2x-3y+6=0,那么直线l与x轴的交点坐标是:A. (3,0)B. (-3,0)C. (0,2)D. (0,-2)6. 在△ABC中,AB=AC,点D在BC上,且BD=CD,那么∠ADB与∠ADC的关系是:A. ∠ADB=∠ADCB. ∠ADB=∠BACC. ∠ADB=∠BAC/2D. ∠ADB=∠BAC/37. 已知点P(a,b)在直线y=-2x+3上运动,那么a与b的关系是:A. a+b=3B. a=2bC. a=2b+3D. a=2b-38. 在平面直角坐标系中,点Q(m,n)在直线y=3/2x-2上运动,那么m与n的关系是:A. m=n+4B. m=2n-4C. m=n-4D. m=2n+49. 已知直线l的方程为x+4y-12=0,那么直线l与y轴的交点坐标是:A. (0,3)B. (0,-3)C. (4,0)D. (-4,0)10. 在△ABC中,AB=AC,点D在BC上,且BD=CD,那么∠ADB与∠ADC的关系是:A. ∠ADB=∠ADCB. ∠ADB=∠BACC. ∠ADB=∠BAC/2D. ∠ADB=∠BAC/3二、填空题(每题5分,共20分)11. 在平面直角坐标系中,点P(2,3)在直线y=mx+1上运动,那么m的取值范围是______。
人教版八年级上册数学期末动点问题压轴题专题训练(含解析)

人教版八年级上册数学期末动点问题压轴题专题训练(1)当时,点C 的坐标为 .(2)动点A 在运动的过程中,试判断发生变化,请说明理由.(3)当时,在坐标平面内是否存在一点若存在,请直接写出点P 的坐标;若不存在,请说明理由.(1)如图1,当点在边上时.①求证:;②求证:;(2)如图2,当点在边的延长线上时,其他条件不变,请写出2a =3a =D BC ABD ACE ≌△△BC DC CE =+D BC(1)请直接写出点A 和点B 的坐标;(2)请判断的形状并说明理由;(3)下列结论:①四边形为定值.请选择一个正确的结论并说明理由.(1)求证:;(2)求的面积;(3)点M ,N 分别是线段,上的动点,连接,求的最小值.DEF OEDF OEF DFE ∠+∠CD CE =CDE BC BD MN 12MN DN +(1)求出点的坐标.(2)求证:.(3)数学活动小组进行深入探究后发现变,你同意这个说法吗?请说明理由B OD BC =(1)如图①,请找出图中与相等的角,并说明理由;(2)如图②,交轴于点,过点作轴于点,求证:平分;(3)如图③,若,点在轴正半轴移动,且,取,连交轴OAB ∠BC x M C CD x ⊥,2D AM CD =AD BAC ∠()3,0A B y OB OA >()0,3P CP x边三角形,使其与点在直线的两侧,与直线相交于点(点与点A 不重合),连接.(1)如图,当时,①求证:;②在点A 运动的过程中,的度数是否会发生改变?如果会请说明理由,如果不会请求出的度数;(2)在点A 运动的过程中,试探究线段,,之间的数量关系.11.在平面直角坐标系中,点在轴的正半轴上,点在第一象限,,.(1)如图1,求证:是等边三角形;(2)如图1,若点M 为y 轴正半轴上一动点,以为边作等边三角形,连接并延长交轴于点,求证:;(3)如图2,若,,点为的中点,连接、交于,请问、与之间有何数量关系,并证明你的结论.12.在平面直角坐标系中,点A 为y 轴正半轴上一点,点B 为x 轴上一动点,连接ABD C AB DC l E E EB 120BAC ∠<︒ABE ACE =∠∠DCB ∠DCB ∠EA EB ED A y B OB AB =150BOP ∠=︒OAB BM BMN NA x P 2AP AO =BC BO ⊥BC BO =D CO AC DB E AE BE CE,以为腰作等腰,.(1)如图1,点B 在x 轴负半轴上,点C 的坐标是,直接写出点A 和点B 的坐标;(2)如图2,点B 在x 轴负半轴上,交x 轴于点D ,若平分.且点C 的纵坐标是,求线段的长;(3)如图3,点B 在x 轴正半轴上,以为边在左侧作等边,连接,,若,且,求的面积.13.等腰直角中,,,,点、分别是轴,轴上两个动点,直角边交轴于点,斜边交轴于点.(1)如图1,已知点的横坐标为,直接写出点的坐标;(2)如图2,若点为轴上的固定点,且,当点在轴正半轴运动时,分别以、为直角边在第一、二象限作等腰直角和等腰直角,连接交轴于点,问当点在轴的正半轴上运动时,的长度是否变化?若变化请说明理由;若不变化,请求出的长度.14.在平面直角坐标系中,点为坐标原点,点、分别位于轴和轴AB AB Rt ABC △90BAC ∠=︒(2,2)-AC BD ABC ∠3-BD BC BC BCE EO CO 60COE ∠=︒8CO =AOC ABC 90BAC ∠=︒AB AC =ABC C ∠=∠B A x y AC x D BC y E C 2-A A x ()6,0A -B y OB AB BOD ABC CD y P B y BP BP O ()6,0B -()0,6A x y上,连接,交轴于点.(1)求点的坐标;(2)动点从出发以个单位/秒的速度沿轴向终点运动,连接,将线段绕着点逆时针旋转后得到线段,与为对应点.连接、,为的面积,用含的式子表示;(3)在()的条件下,连接,过点作于,交轴于,交于,若,求点的坐标.15.如图①,在中,,现有一动点,从点出发,沿着三角形的边运动,回到点停止,速度为,设运动时间为秒.(1)如图①,当的面积等于面积的一半时,求的值:(2)如图②,点在边上,点在边上,在的边上,若另外有一个动点与点同时从点出发,沿着边运动,回到点停止.在两点运动过程中的某一时刻,以为顶点的三角形恰好与全等,求点的运动速度.16.如图,在平面直角坐标系中,,点在轴正半轴上,.AB CA AB ⊥x C C P B 2x C AP AP A 90︒AQ P Q PQ CQ S PCQ △t S 2BQ A AH BQ ⊥G x H PQ AC M :2:1APM AQM S S = H Rt ABC △90,12cm,16cm,20cm B AB BC AC ∠=︒===P A AB BC CA →→A 2cm /s t ABP ABC t D BC 4cm CD =E AC 5cm,,3cm CE ED BC ED =⊥=ABC Q P A AC CB BA →→A ,,A P Q EDC △Q ()0,9A B x 45OAB ∠=︒(1)求出点坐标;(2)动点从点出发,以每秒个单位长度的速度沿轴正半轴运动,同时点从点出发,以相同速度沿轴向左运动,连接,过点作交直线于点,连接,设点的运动时间为,请用含的式子表示的面积;(3)在(2)的条件下,直线与直线交于点,当时,求点坐标.17.已知中,,过点的直线交轴于,其中是方程组的解,(1)求的值(2)动点从点出发,沿线段以每秒1个单位的速度运动,运动时间为秒;请用含的式子表示线段的长度;并直接写出此时的取值范围;(3)在(2)的条件下,当为何值时,直线与直线互相垂直.18.在平面直角坐标系中,O 为坐标原点,直线交x 轴的正半轴于点A ,交y 轴的B P O 1y Q B x PQ O OG PQ ⊥AB G PG P t t OPG PQ AB H 72OPG S =△H AOB OA OB a ==A AM x (),0M b ,a b 3830a b a b +=⎧⎨+=⎩,a b P A AO t t OP t t BP AM AB(1)如图1求的长;(2)如图2动点E 在第二象限,点E 的坐标为,连接,,请写出面积s 与t 的关系;(3)在(2)的条件下,如图3点F 在第一象限,连接、、,,连接,当,求的值.OD (,)t m DE OE ODE FE FD FA 30ADF ∠=FE FA =EB 12,4EBO ODA ODA EFA EOB ∠=∠∠+∠=∠t m +参考答案:1.(1)(2)动点A 在运动的过程中,的值不变,(3)或或【分析】本题考查全等三角形判定及性质.(1)根据题意过点C 作轴于点,证明出,利用全等性质即可得到本题答案;(2)由(1)得,利用全等性质及点坐标表示线段长即可得到本题答案;(3)根据题意分3种情况讨论P 点位置,利用全等三角形性质及判定即可得到本题答案.【详解】(1)解:如下图,过点C 作轴于点E ,则,,∵是等腰直角三角形,∴,∴,∴.在和中,∴(AAS ),∵,∴,∴,∴;(2)解:动点A 在运动的过程中,的值不变.理由如下:(2,3)-+c d (4,)1-(3,2)--(2,1)-CE y ⊥E ACE BAO ≌ACE BAO ≌CE y ⊥CEA AOB ∠=∠ABC ,90AC BA BAC =∠︒=90ACE CAE BAO CAE ∠+∠=︒=∠+∠ACE BAO ∠=∠ACE △BAO CEA AOB ACE BAOAC BA ∠=∠⎧⎪∠=∠⎨⎪=⎩ACE BAO ≌(0,1),(0,2)B A -12BO AE AO CE ====,123OE =+=2,3C -()+c d由(1)知,,∵,,∴,∴,∴,又∵点C 的坐标为,∴,即的值不变;(3)解:存在一点P ,使与全等,符合条件的点P 的坐标是或或,分为三种情况讨论:①如下图,过点P 作轴于点E ,则,∴,∴,在和中,,∴(AAS ),∴,∴,即点P 的坐标是,②如下图,过点C 作轴于点M ,过点P 作轴于点E ,ACE BAO ≌(0,1)B (0,)A a -1,BO AE AO CE a ====1OE a =+(,1)C a a --(,)c d 11c d a a +=--=-+c d PAB ABC (4,)1-(3,2)--(2,1)-PE x ⊥90PBA AOB PEB ∠=∠=∠=︒90,90EPB PBE PBE ABO ∠+∠=︒∠+∠=︒EPB ABO ∠=∠PEB △BOA △EPB OBA PEB BOA PB BA ∠=∠⎧⎪∠=∠⎨⎪=⎩PEB BOA △≌△1,3PE BO EB AO ====314OE =+=(4,)1-CM x ⊥PE x ⊥则.∵,∴,∴,∴,∴,在和中,,∴(AAS ),∴.∵,∴,即点P 的坐标是;③如下图,过点P 作轴于点E ,则.∵,∴,∴,90CMB PEB ∠=∠=︒CAB PAB △≌△45,PBA CBA BC BP ∠=∠=︒=90CBP ∠=︒90,90MCB CBM CBM PBE ∠+∠=︒∠+∠=︒MCB PBE ∠=∠CMB BEP △MCB EBP CMB BEP BC PB ∠=∠⎧⎪∠=∠⎨⎪=⎩CMB BEP △≌△,PE BM CM BE ==3,4),10C B -((,)2,413PE OE BE BO ==-=-=(3,2)--PE x ⊥90BEP BOA ∠=∠=︒CAB PBA △≌△,90AB BP CAB ABP =∠=∠=︒90,90ABO PBE PBE BPE ∠+∠=︒∠+∠=︒∴.在和中,,∴(AAS ),∴,∴,即点P 的坐标是,综上所述,符合条件的点P 的坐标是或或.2.(1)①见解析;②见解析;(2),见解析【分析】本题主要考查了等边三角形,全等三角形.(1)①根据等边三角形的性质得出,,,根据得出,从而说明三角形全等;②根据全等的性质得出,然后根据即得;(2)根据等边三角形的性质得出,,,根据得出,从而说明,根据全等的性质得出,然后根据即得.【详解】(1)证明:①∵和是等边三角形,∴,,.∴,∴.在和中,,∴;②∵,ABO BPE ∠=∠BOA △PEB △ABO BPE BOA PEB BA PB ∠=∠⎧⎪∠=∠⎨⎪=⎩BOA PEB △≌△1,3PE BO BE OA ====312OE BE BO =-=-=(2,1)-(4,)1-(3,2)--(2,1)-BC CD CE +=AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠-∠=∠-∠BAD EAC ∠=∠BD CE =BC BD CD =+AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠+∠=∠+∠BAD EAC ∠=∠ABD ACE ≌△△BD CE =+=BC CD BD ABC ADE V 60BAC DAE ∠=∠=︒AB BC AC ==AD DE AE ==BAC DAC DAE DAC ∠-∠=∠-∠BAD CAE ∠=∠ABD △ACE △AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()SAS ABD ACE △≌△ABD ACE ≌△△∵,,∴,∴是等腰直角三角形,即∵点D 是线段中点,∴,,(0,6)A (6,0)B 6O A O B ==AOB ∠AB OD AB ⊥12OD AD AB ==∠∵,,∴在中,∵在(1)中已求出根据翻折可知:、∴N 点关于的对称点H 在根据对称性有:∴,∴是等边三角形,∵N 点关于的对称点是点H ,3BD =30CBD ∠=︒DG Rt BDG △12DG BD =CE CD =11BDC BKC △BE BK DBC KBC ∠=∠60BDK DBC KBC ∠=∠+∠=︒BDK BE NH如图,,即:,在中,PNC DNC∠=∠24PNC αβ∠==2αβ=MCN DCM DCN x β∠=∠+∠=+MCN △180MCN DCN NMC ∠+∠+∠=2180x βαα+++=︒3180x βα++=︒解得:,.II.当点在线段上时,如图,,,即:,在中,,,即:联立得:,解得:,此时:,不合题意舍去;III .当点在线段上时,如图,,52550x βα=︒⎧⎪=︒⎨⎪=︒⎩∴5DCM ∠=︒N PD 180PNC DNC ∠+∠=︒∴24180αβ+=︒290αβ+=︒∴MCN DCM DCN x β∠=∠+∠=+ CMN PCN MCN CMN x βα∠=∠+∠=++∴4180PCN NDC x βαβ∠+∠=+++=︒5180x βα++=︒2602905180x x ααββα+=︒⎧⎪+=︒⎨⎪++=︒⎩11.2526.2537.5x βα=︒⎧⎪=︒⎨⎪=︒⎩11.2526.5PCN DCN ∠=︒<∠=︒N DM PNC DNC ∠=∠【详解】(1)解:过点B 作轴于点D ,∵,∴,∵轴,∴,∵,∴,∴,在和中,,∴,∴,∵,∴;(2)解:∵,∴,∴,∵轴,∴,∴,∴,在和中,BD y ⊥()()6,0,0,3A C -6,3OA OC ==BD y ⊥90BCD CBD ∠+∠=︒90ACB ∠=︒90BCD ACO ∠+∠=︒ACO CBD ∠=∠ACO △CBD △90AOC CDB ACO CBDAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩≌ACO CBD 6,3OA CD OC BD ====()0,3C ()3,3B -90ACB ∠=︒90BCF ∠=︒90CBF F ∠+∠=︒BE y ∥90AEF ∠=︒90CAD F ∠+∠=︒CAD CBF ∠=∠CAD CBF V∴,∴,∵,∴∴.【点睛】本题主要考查了三角形综合,折叠的性质,全等三角形的判定和性质,角平分线的性质,解题的关键是掌握全等三角形的判定方法,全等三角形对应边相等,对应角相等;折叠前后对应角相等;角平分线上的点到两边距离相等.7.(1)(2)见解析(3)的度数总是保持不变,理由见解析【分析】本题考查了全等三角形的性质与判定,等腰三角形的性质,坐标与图形;(1)根据等腰三角形的性质解答即可;(2)根据等式的性质得出,进而利用证明与全等,进而解答即可;(3)根据全等三角形的性质得出,进而利用平角的定义解答即可.【详解】(1)解:如图所示,过作轴于,()Rt Rt HL EFO EFN ≌FN FO =(),0F t FO t=-2FG HG t +=-()2,0-COD ∠BAC OAD ∠=∠SAS BAC OAD AOD ABO ∠=∠A AE x ⊥E),点C 是的中点,,D 作轴于点F ,,,4=AB 114222AB ==⨯=DF x ⊥90DFO =︒90FDO DOF +∠=︒),的坐标为,关于x 轴的对称点,则的坐标为,交x 轴于点,则为定值,此时的周长最小.作轴于点Q ,114222AB '==⨯=M '()0,2M '''M ''M AM ''P PAM C AM AP ''=+ AM 'PAM '△()4,4A -AQ y ⊥对于(3),作轴,先证明,可得,再得出,进而得出,根据等腰直角三角形的性质和判定即可得出答案.【详解】(1).理由:,;(2)证明:如图②中,延长交的延长线于点..∵,,,.,即.垂直平分,平分.(3)的长度不变,.理由:如图③中,过点作轴于点...CH y ⊥≌CHB BOA △△,3===CH BO BH OA 3==OA OP ==OB PH CH OAB OBC ∠=∠90,90OAB OBA OBC OBA ∠+∠=∠+∠=︒︒ OAB OBC ∴∠=∠AB CD T ,90,90,AD CD ADT T BAM BCT BAM ⊥∴∠=∴∠+∠=∴∠=∠︒︒ BC BA ===90CB T A B M ∠∠︒()CBT ABM ASA ∴≌△△CT AM ∴=2,2AM CD CT CD =∴= CD DT =,AD CT AD ⊥∴ CT ,AC AT AD ∴=∴BAC ∠OQ 3OQ =C CH y ⊥H 90,90CHB BOA HBC HCB ∴∠=∠=∴∠+∠=︒︒90,90,ABC OBA HBC HCB OBA ∠=∴∠+∠=︒︒∴∠=∠..,..,.【点睛】本题主要考查了全等三角形的性质和判定,同角的余角相等,线段垂直平分线的性质,等腰直角三角形的性质和判定等,构造辅助线是解题的关键.10.(1)①见解析;②不变,(2)或【分析】(1)①根据垂直平分线的性质得出,再由等边对等角及各角之间的数量关系求解即可;②设与交于点M ,根据等边三角形的性质及各角之间的关系得出,即可求解;(2)分两种情况进行分析:当时,当时,分别利用全等三角形的判定和性质及等边三角形的判定和性质分析求解即可.【详解】(1)证明:①点A 、E 在线段的垂直平分线l 上,∴,∴,∴,即;②在点A 运动的过程中,的度数不变,理由如下:如图,设与交于点M ,(),CB AB CHB BOA AAS =∴ ≌△△,3∴===CH BO BH OA ()()3,0,0,3,3A P OA OP ∴== ,BH OP OB PH CH ∴=∴==90,45CHP CPH OPQ ∠=∴∠=∠=︒︒ 90,45∠=∴∠=︒=︒∠ POQ OQP OPQ 3OQ OP ∴==30DCB ∠=︒ED EB EA =+EB ED EA=+AC AB EC EB ==,AB CD 260ECB ∠=︒120BAC ∠<︒120BAC ∠>︒BC ,AC AB EC EB ==,ABC ACB EBC ECB ∠∠∠∠==ABC EBC ACB EBC ∠∠∠∠-=-ABE ACE ∠∠=DCB ∠AB CD∵是等边三角形,∴ ,∴,∴,∴,∴,∴,∵,∴,即;(2)当时,在上截取,连接,∵,∴,由(1)得直线,,∴,∴是等边三角形,∴ ,∴,即,ABD ,60AB AD BAD ∠==︒AD AC =ADC ACE ∠∠=,ABE ADC EBC ECB ∠∠∠∠==,180,180AMD EMB BED ABE EMB BAD ADC AMD ∠∠∠∠∠∠∠∠==︒--=︒--60BED BAD ∠∠==︒,EBC ECB BED EBC ECB ∠∠∠∠∠+==260ECB ∠=︒30DCB ∠=︒120BAC ∠<︒ED EF EA =AF ED DF EF =+ED DF EA =+l BC ⊥30DCB ∠=︒903060AED ∠=︒-︒=︒AEF 60,EAF BAD AE AF ∠∠==︒=–EAF BAF BAD BAF ∠∠∠∠=-BAE DAF ∠∠=∴,∴,∵,∴;当时,如图所示在上截取,连接,∵,∴,由(1)得直线,,,∴,∴F 是等边三角形,∴,∴,∴,∴,∴,∵,∴;综上可得:或.【点睛】题目主要考查线段垂直平分线的性质,全等三角形的判定和性质,等边三角形的判定和性质等,理解题意,作出相应辅助线是解题关键,同时注意进行分类讨论.11.(1)见解析(2)见解析(3),证明见解析【分析】(1)根据有一个角是的等腰三角形是等边三角形可得结论;(SAS)BAE DAF ≌ EB DF =ED DF EA =+ED EB EA =+120BAC ∠>︒EB EF EA =AF EB BF EF =+EB BF EA =+l BC ⊥30DCB ∠=︒BE BC =903060AEB AEC ∠∠==︒-︒=︒AE 60,EAF BAD AE AF ∠∠==︒=–EAF DAF BAD DAF ∠∠∠∠-=EAD BAF ∠∠=(SAS)BAF DAE ≌ BF ED =EB BF EA =+EB ED EA =+ED EB EA =+EB ED EA =+AE BE CE =+60︒(2)根据证明,得,由8字形可得,最后由含角的直角三角形的性质可得结论;(3)如图2,在上截取,先证,方法是根据题意得到三角形为等边三角形,三角形为等腰直角三角形,确定出度数,根据,且,得到度数,进而确定出为,再由,得到,再由,且夹角,利用得到三角形与三角形全等,利用全等三角形的对应边相等得到,得到三角形为等边三角形,得到,由,等量代换即可得证.【详解】(1)解:证明:,,,,是等边三角形;(2)证明:由(1)知:是等边三角形,,是等边三角形,,,,,,,,,,,,SAS MBO NBA ≌OMB ANB ∠∠=60FAM FBN ∠∠==︒30︒AC AG CE =60AEB ∠=︒ABO BOC ABD ∠AB BC =150ABC ∠=︒BAE ∠AEB ∠60︒AG CE =AE CG =AB CB =BAC BCA ∠=∠SAS BCG BAE BG BE =BEG BE EG =AE EG AG =+150BOP ∠=︒ 90AOP ︒=∠60AOB ∴∠=︒OB AB = OAB ∴ OAB 60ABO ∴∠=︒BMN BM BN ∴=60MBN ∠=︒MBO NBA ∴∠=∠AB OB = (SAS)MBO NBA ∴△≌△OMB ANB ∴∠=∠AFM BFN ∠=∠ 60FAM FBN ∴∠=∠=︒60OAP FAM ∠=∠=︒ 90AOP ︒=∠30APO ∴∠=︒;(3),理由如下:如图2,在上截取,连接,,即,,,,为的中点,平分,即,,,,,,,在和中,,,,为等边三角形,,.【点睛】本题是三角形综合题,考查了等腰直角三角形的性质和判定,等边三角形的性质和判定,全等三角形的判定和性质,以及含角的直角三角形的性质,添加辅助线.12.(1),2AP AO ∴=AE BE CE =+AC AG EC =BG AG EG CE EG +=+AE CG =BC BO ⊥ BC BO =90OBC ∴∠=︒D CO BD ∴OBC ∠45CBD OBD ∠=∠=︒60ABO ∠=︒ 105ABD ∴∠=︒150ABC ∠=︒AB OB BC == 15BAC BCA ∴∠=∠=︒154560AEB ∴∠=︒+︒=︒ABE CBG AB CB BAE BCG AE CG =⎧⎪∠=∠⎨⎪=⎩(SAS)ABE CBG ∴△≌△BG BE ∴=BEG ∴△BE EG ∴=AE AG EG CE BE ∴=+=+30︒()02A ,()40B -,∴,∵∴,∵,∴,,90ADC BOA ∠=︒=∠90CAD BAO ABO ∠+∠=︒=∠CAD ABO ∠=∠(2,2)C -2CD =2OD =∴,,∴,;(2)解:如图2,作轴,交轴于,交的延长线于,∴,∵平分,∴,,,∴,∴,∵,∴,∵,∴,∴,∵,,∴,∴,∴的长为6;(3)解:∵为等边三角形,∴,,如图3,在上截取,使,连接,2AO CD ==4BO AD AO OD ==+=()02A ,()40B -,CM x ⊥x N BA M 90BNM BNC ∠=︒=∠BD ABC ∠MBN CBN ∠=∠BN BN =90BNM BNC ∠=︒=∠()ASA MBN CBN ≌3MN CN ==∥CM AO ACM CAO ∠=∠90CAO BAO ABD BAO ∠+∠=︒=∠+∠CAO ABD ∠=∠ACM ABD ∠=∠AC AB =90MAC DAB ∠=︒=∠()ASA ACM ABD ≌6BD CM CN MN ==+=BD BCE BE CE =60BEC EBC ECB ∠=∠=∠=︒OC OF OF OE =EF∴是等边三角形,∴,∴∵,∴,∴,OEF OE EF =60OEF ∠=︒=∠OEF BEF BEC ∠-∠=∠-∠OE EF =BEO CEF ∠=∠()SAS BEO CEF ≌OBE FCE ∠=∠13.(1)(2)【分析】(1)如图①,过作 轴于, 证明可得从而可得答案;(2)如图①,过点作 轴于点.证明 ,可得 ,再证明,从而可得: .【详解】(1)解: 如图①,过作 轴于,∴,∵,∴,∴,∵,∴.∴,,∴,∴,故答案为 : .(2)的长度不变,理由如下:如图②, 过点作 轴于点.()0,23BP =C CF y ⊥F ,ACF BAO ≌CF AO =C CE y ⊥E CBE BAO ≌,6CE BO BE AO ===CPE DPB ≌3BP EP ==C CF y ⊥F 90,90CFA AOB ACF CAF ∠=∠=︒∠+∠=︒90BAC ∠=︒90CAF OAB ∠+∠=︒ACF OAB ∠=∠AC AB =()AAS ACF BAO ≌CF AO =2c x =- 2CF AO ==()0,2A ()0,2BP C CE y ⊥E∵ ,∴∵∴ .∵90ABC ∠=︒90CBE ABO ∠+∠=︒90BAO ABO ∠+∠=︒CBE BAO ∠=∠90CEB AOB ∠=∠=∵,∴,在和中,90BAC PAQ ∠=∠=︒BAP CAQ ∠=∠BAP △CAQ AB AQ =⎧∴四边形为正方形,∴,过作于点,∵AOCN 6OA CN OC ===T TL CN ⊥L AH BQ⊥AOH TLQ ≌∴,解得;②当点在上,点∴,解得;3AP DE cm AQ EC ===,352x =103x =cm/s P AB 5AP EC cm AQ ==,532x =65x =cm/s∴点P 的路程为∴点P 的路程为3AP ED AQ EC ===,AB +1216205AQ =++-=4543x =5AP EC cm AQ ==,AB +1216203AQ =++-=4345x =从出发,以每小时从出发,以相同速度沿,①当在线段上时,P O Q B OQ ∴=AP =t P AO,等腰,,设,,为的一个外角,RO PO ∴=∴POR 45R BAO ∴∠=∠=︒QPO α∠=45RPQ α∴∠=︒-QON BOG α∠==∠ABO ∠ OBG,,,,90HTA ∴∠=︒45HAT OAB ∠=∠=︒45HAT AHT ∴∠=∠=︒HT AT ∴=由(1)知,,则,∵直线与直线互相垂直,∴,()1.0M -1OM =BP AM 90MNB ∠=︒。
初中八年级下册数学动点问题试题附答案

初中八年级下册数学动点问题试题附答案
本文档为初中八年级下册数学动点问题试题及其答案附录。
以下为试题内容:
试题一
1. 一辆汽车每小时行驶60千米。
已知一条道路上两个小车相距120千米,两车同时从两端开始开过。
在2小时后两车相遇,求另一辆小车时速是多少?
答案:另一辆小车的时速是40千米/小时。
试题二
2. 一架直升机从A地出发,向东飞行100千米后转向南飞行,飞行速度为60千米/小时。
飞行2小时后,在B地降落。
求直升机从A地到B地的飞行距离及飞行时间。
答案:直升机从A地到B地的飞行距离为140千米,飞行时间为3小时。
试题三
3. 一列火车以每小时80千米的速度从A地开往B地,一辆汽
车以每小时60千米的速度同时从B地向A地开。
若两车从相距
200千米的时候开始计时,火车到达B地后返回A地的时候,两车
相距250千米。
求两地的距离。
答案:A地和B地的距离为450千米。
试题四
4. 一条有笔直通道,两边都是田地。
东边的直边上有一棵高度
为2米的树,西边的直边上有一棵高度为3米的树。
直道的宽度为
4米,人从田地一头走到另一头的时间为2分钟。
求人的步行速度。
答案:人的步行速度为60米/分钟。
希望上述试题及答案能帮助到您。
如有其他问题或需要进一步帮助,请随时告知。
八年级数学动点问题专项训练

八年级数学动点问题专项训练Revised on July 13, 2021 at 16:25 pm动点问题专项训练1.如图;在矩形ABCD 中;AB=2;1BC =;动点P 从点B 出发;沿路线B C D →→作匀速运动;那么ABP △的面积S 与点P 运动的路程x 之间的函数图象大致是2.如图1;在直角梯形ABCD 中;动点P 从点B 出发;沿BC;CD 运动至点D 停止.设点P 运动的路程为x ;△ABP 的面积为y ;如果y 关于x 的函数图象如图2所示;则△BCD 的面积是 A .3 B .4 C .5 D .63.如图;△ABC 和的△DEF 是等腰直角三角形;∠C=∠F=90°;AB=2.DE=4.点B 与点D 重合;点A;BD;E 在同一条直线上;将△ABC 沿D E →方向平移;至点A 与点E 重合时停止.设点B;D 之间的距离为x ;△ABC 与△DEF 重叠部分的面积为y;则准确反映y 与x 之间对应关系的图象是4.如图;点G 、D 、C 在直线a 上;点E 、F 、A 、B 在直线b 上;若a b Rt GEF ∥,△从如图所示的位置出发;沿直线b 向右匀速运动;直到EG 与BC 重合.运动过程中GEF △与矩形ABCD 重合部分....的面积S 随时间变化的图象大致是5.2009年牡丹江如图;平面直角坐标系中;在边长为1的正方形ABCD 的边上有一动点P 沿A B C D A →→→→运动一周;则P 的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是6.如图1;在矩形ABCD 中;动点P 从点B 出发;沿BC 、CD 、DA 运动至点A 停止;设点P 运动的路程为x ;△ABP 的面积为y;如果y 关于x 的函数图象如图2所示;则矩形ABCD 的面积是图12O5 xAB P D 图2O31 1 3 Sx A . O 113 Sx O 3 Sx 3O 11 3 Sx B . C . D . 2D C P BA G D C EF A B a第4题图s t O A s t O B C s t O Ds tO 1 2 3 4 12 y s O 1 234 1 2 y s O s 1 2 3 4 1 2 y sO 1 2 3 4 1 2 y O A BC DA .10 8.16 C. 20 D .367.如图;三个大小相同的正方形拼成六边形ABCDEF ;一动点P 从点A 出发沿着A →B →C →D →E 方向匀速运动;最后到达点E .运动过程中PEF ∆的面积s 随时间t 变化的图象大致是 8.如图8;点A 、B 、C 、D 为圆O 的四等分点;动点P 从圆心O 出发;沿O-C-D-O 的路线作匀速运动.设运动时间为t 秒; ∠APB 的度数为y 度;则下列图象中表示y 与t 之间函数关系最恰当的是 9. 13.一张正方形的纸片;剪去两个一样的小矩形得到一个“E ”图案;如图4所示;设小矩形的长和宽分别为x 、y;剪去部分的面积为20;若2≤x ≤10;则y 与x 的函数图象是: 10.如图;AB 是半圆O 的直径;点P 从点O 出发;沿OA AB BO --的路径运动一周.设OP 为s ;运动时间为t ;则下列图形能大致地刻画s 与t 之间关系的是11.锐角△ABC 中;BC =6;,12=∆ABC S 两动点M 、N 分别在边AB 、AC 上滑动;且MN ∥BC;以MN 为边向下作正方形MPQN;设其边长为x ;正方形MPQN 与△ABC 公共部分的面积为yy >0;当x = ;公共部分面积y 最大;y 最大值 = ; 6. 2012贵州遵义12分如图;△ABC 是边长为6的等边三角形;P 是AC 边上一动点;由A 向C 运动与A 、C 不重合;Q 是CB 延长线上一点;与点P 同时以相同的速度由B 向CB 延长线方向运动Q 不与B 重合;过P 作PE ⊥AB 于E ;连接PQ 交AB 于D .1当∠BQD =30°时;求AP 的长;2当运动过程中线段ED 的长是否发生变化 如果不变;求出线段ED 的长;如果变化请说明理由. 答案解:1∵△ABC 是边长为6的等边三角形;∴∠ACB =60°..∵∠BQD =30°;∴∠QCP =90°..设AP =x ;则PC =6﹣x ;QB =x ;∴QC =QB +C =6+x .. ∵在Rt △QCP 中;∠BQD =30°;∴PC =12QC ;即6﹣x =126+x ;解得x =2.. ∴当∠BQD =30°时;AP =2..2当点P 、Q 运动时;线段DE 的长度不会改变..理由如下:作QF ⊥AB ;交直线AB 的延长线于点F ;连接QE ;PF .. ∵PE ⊥AB 于E ;∴∠DFQ =∠AEP =90°.. ∵点P 、Q 做匀速运动且速度相同;∴AP =BQ .. ∵△ABC 是等边三角形;∴∠A =∠ABC =∠FBQ =60°.. ∴在△APE 和△BQF 中;∵∠A =∠FBQ ;AP =BQ ;∠AEP =∠BFQ =90°;∴△APE ≌△BQFAAS .. ∴AE =BF ;PE =QF 且PE ∥QF ..∴四边形PEQF 是平行四边形..A .B DC 第6题图 E . F . P. · PA OB s t O s O t O s tO s tA B C D∴DE =12EF .. ∵EB +AE =BE +BF =AB ;∴DE =12AB .. 又∵等边△ABC 的边长为6;∴DE =3..∴当点P 、Q 运动时;线段DE 的长度不会改变..12. 2012江苏泰州12分 如图;已知一次函数1y kx b =+的图象与x 轴相交于点A ;与反比例函数2c y x=的图象相交于B -1;5、C 25;d 两点.点Pm ;n 是一次函数1y kx b =+的图象上的动点. 1求k 、b 的值;2设31m 2-<<;过点P 作x 轴的平行线与函数2cy x=的图象相交于点D .试问△PAD 的面积是否存在最大值 若存在;请求出面积的最大值及此时点P 的坐标;若不存在;请说明理由;3设m 1a =-;如果在两个实数m 与n 之间不包括m 和n 有且只有一个整数;求实数a的取值范围.答案解:1将点B 的坐标代入2c y x=;得c51=- ;解得c=5-.. ∴反比例函数解析式为25y x=-..将点C 52;d 的坐标代入25y x =-;得5d =252=--..∴C 52;-2..∵一次函数1y kx b =+的图象经过B -1;5、C 52;-2两点;∴5k b52k b 2=-+⎧⎪⎨-=+⎪⎩;解得k=2b=3-⎧⎨⎩.. 2存在..令1y 0=;即2x 30-+=;解得3x 2=..∴A 32;0..由题意;点Pm ;n 是一次函数1y 2x 3=-+的图象上的动点;且31m 2-<<∴点P 在线段AB 上运动不含A 、B ..设P3nn 2-,.. ∵DP ∥x 轴;且点D 在25y x=-的图象上;∴D P D 5y y n x =n ==-,;即D 5n n-,..∴△PAD的面积为2113n 51349S PD OP=+n=n +222n 4216-⎛⎫⎛⎫=⋅⋅⋅-- ⎪ ⎪⎝⎭⎝⎭.. ∴S 关于n 的二次函数的图象开口向下;有最大值.. 又∵n =2m 3-+;31m 2-<<;得0n 5<<;而30n=52<<.. ∴当3n=2时;即P 3342,时;△PAD 的面积S 最大;为4916.. 3由已知;P 1a,2a+1- ..易知m ≠n ;即1a 2a+1-≠;即a 0≠.. 若a 0>;则m 1n <<..由题设;m 0n 2>≤,;解出不等式组的解为10a 2<≤.. 若a 0<;则n 1m <<..由题设;n 0m 2<≥,;解出不等式组的解为1a 02<-≤..综上所述;数a 的取值范围为1a 02<-≤;10a 2<≤..考点反比例函数和一次函数综合问题;曲线上点的坐标与方程的关系;平行的性质;二次函数的性质;不等式组的应用..分析1根据曲线上点的坐标与方程的关系;由B 的坐标求得c=5-;从而得到25y x=-;由点C 在25y x=-上求得d 2=-;即得点C 的坐标;由点B 、C 在1y kx b =+上;得方程组;解出即可求得k 、b 的值..2求出△PAD 的面积S 关于n 的二次函数也可求出关于m ;应用二次函数的最值原理即可求得面积的最大值及此时点P 的坐标..3由m ≠n 得到a 0≠..分a 0>和a 0<两种情况求解..22. 2012山东济南9分如图;已知双曲线ky x=;经过点D 6;1;点C 是双曲线第三象限上的动点;过C 作CA ⊥x 轴;过D 作DB ⊥y 轴;垂足分别为A ;B ;连接AB ;BC . 1求k 的值;2若△BCD 的面积为12;求直线CD 的解析式; 3判断AB 与CD 的位置关系;并说明理由. 答案解:1∵双曲线k y x =经过点D 6;1;∴k16=;解得k =6.. 2设点C 到BD 的距离为h ;∵点D 的坐标为6;1;DB ⊥y 轴;∴BD =6;∴S △BCD =12×6 h =12;解得h =4..∵点C 是双曲线第三象限上的动点;点D 的纵坐标为1;∴点C 的纵坐标为1-4= -3..∴63x=;解得x = -2..∴点C 的坐标为-2;-3.. 设直线CD 的解析式为y =kx +b ;则2k b 36k b 1-+=-⎧⎨+=⎩;解得1k 2b 2⎧=⎪⎨⎪=-⎩.. ∴直线CD 的解析式为1y x 22=-.. 3AB ∥CD ..理由如下:∵CA ⊥x 轴;DB ⊥y 轴;点C 的坐标为-2;-3;点D 的坐标为6;1; ∴点A 、B 的坐标分别为A -2;0;B 0;1..设直线AB的解析式为y=mx+n;则2m n0n1-+=⎧⎨=⎩;解得1m2n1⎧=⎪⎨⎪=⎩..∴直线AB的解析式为1y x12=+..∵AB、CD的解析式k都等于12相等..∴AB与CD的位置关系是AB∥CD..考点反比例函数综合题;待定系数法;曲线上点的坐标与方程的关系;平行的判定..分析1把点D的坐标代入双曲线解析式;进行计算即可得解..2先根据点D的坐标求出BD的长度;再根据三角形的面积公式求出点C到BD 的距离;然后求出点C的纵坐标;再代入反比例函数解析式求出点C的坐标;然后利用待定系数法求一次函数解析式解答..3根据题意求出点A、B的坐标;然后利用待定系数法求出直线AB的解析式;可知与直线CD的解析式k值相等;所以AB、CD平行..。
专题. 反比例函数(动点问题)(巩固篇)(专项练习)八年级数学下册基础知识专项讲练(苏科版)

专题11.30反比例函数(动点问题)(巩固篇)(专项练习)一、单选题1.如图,点M 是反比例函数y =4x(x <0)图象上一点,MN ⊥y 轴于点N .若P 为x 轴上的一个动点,则△MNP 的面积为()A .2B .4C .6D .无法确定2.如图,点A 是双曲线3y x =在第一象限上的一个动点,连接AO 并延长交另一分支于点B ,以AB 为边作等边△ABC ,点C 在第四象限.下列结论:①连接OC ,则AB OC ⊥;②点C 在函数()90y x x =->上运动.则()A .①对②错B .①错②对C .①②都对D .①②都错3.如图,过双曲线(0)ky x x =>上的动点A 作AB x ⊥轴于点B ,P 是直线AB 上的点,且满足2AP AB =,过点P 作x 轴的平行线交此双曲线于点C .如果APC △的面积为8,则k 的值为()A .10B .8C .16D .124.如图,矩形OABC 的顶点О与坐标原点重合,边OA ,OC 分别落在x 轴和y 轴上,点B 的坐标为()42,,点D 是边BC 上一动点,函数()0ky x x=>的图像经过点D ,且与边AB 交于点E ,连接OB 、OD .若线段OB 平分AOD ∠,则点E 的纵坐标为()A .12B .34C .1D .325.如图,A 、B 是函数y =12x上两点,P 为一动点,作PB ∥y 轴,PA ∥x 轴.若S △BOP =3.6,则S △ABP =()A .3.6B .4.8C .5.4D .66.如图,在平面直角坐标系中,A (8,0),点B 为一次函数y x =图像上的动点,以OB 为边作正方形OBCD ,当AB 最小时,点D 恰好落在反比例函数k y x =的图像上,则k =()A .-9B .-12C .-16D .-257.如图,线段AB 是直线y =x +1的一部分,其中点A 在y 轴上,点B 横坐标为2,曲线BC 是双曲线k y x=(0k ≠)的一部分,由点C 开始不断重复“A−B−C”的过程,形成一组波浪线,点P(2019,m )与Q(2025,n )均在该波浪线上,G 为x 轴上一动点,则△PQG 周长的最小值为()A .16B .6+C .6+D .98.如图,将边长为10的正三角形OAB 放置于平面直角坐标系xOy 中,C 是AB 边上的动点(不与端点A ,B 重合),作CD ⊥OB 于点D ,若点C ,D 都在双曲线y =k x上(k >0,x >0),则k 的值为()A .B .C .9D .9.如图,已知点A 是直线y=x 与反比例函数y=(k >0,x >0)的交点,B 是y=图象上的另一点,BC ∥x 轴,交y 轴于点C .动点P 从坐标原点O 出发,沿O→A→B→C (图中“→”所示路线)匀速运动,终点为C ,过点P 作PM ⊥x 轴,PN ⊥y 轴,垂足分别为M ,N .设四边形OMPN 的面积为S ,P 点运动时间为t ,则S 关于t 的函数图象大致为()A .B .C .D .10.如图,反比例函数2y x =和正比例函数12y x =的图象交于点M ,N ,动点(),0P m 在x 轴上.若PMN 为直角三角形,则m 的值为()A .2m =5B .52m =52C .2m =±或52D .52m =±或5二、填空题11.如图,点()2,2A -在反比例函数k y x=的图象上,点M 在x 轴的正半轴上,点N 在y 轴的负半轴上,且5OM ON ==.点(),P x y 是线段MN 上一动点,过点A 和P 分别作x 轴的垂线,垂足为点D 和E ,连接OA 、OP .当OAD OPE S S < 时,x 的取值范围是________.12.如图,已知点A 是反比例函数3y x=-(0x <)的图像上的一个动点,连接OA ,若将线段OA 绕点O 顺时针旋转90°得到线段OB ,则点B 所在反比例图像的函数关系式是____.13.如图,点A 是双曲线4y x=在第一象限上的一动点,连接AO 并延长交另一分支于点B ,以AB 为斜边作等腰Rt △ABC ,点C 在第二象限,随着点A 的运动,点C 的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为_____.14.如图,A 、B 是函数y =12x图象上两点,P 为一动点.作PB ∥y 轴.PA ∥x 轴,下列说法中:①AOP BOP ≌△△;②AOP BOP S S =;③若OA =OB ,则OP 平分∠AOB ;④若4BOP S =,则16ABP S =.正确的序号是___.15.如图,点A 为反比例函数k y x=图象上的一点,过点A 作AB ⊥y 轴于B ,点C 为x 轴上的一个动点,△ABC 的面积为3,则k 的值为________.16.如图,点A 、B 是反比例函数y 12x =图象上的两个动点,过点A 、B 分别作AC ⊥x 轴、BD ⊥x 轴,分别交反比例函数y 3x=-图象于点C 、D ,得四边形ACBD 是平行四边形.当点A 、B 不断运动时,现有以,结论:①▱ACBD 可能是菱形;②▱ACBD 不可能是矩形;③▱ACBD 可能是正方形;④▱ACBD 不可能是正方形.其中正确的是_____.(写出所有正确结论的序号)17.如图,函数112y x =+与函数(0)k y x x =>图像的交于点P ,点P 的纵坐标为4,PB x ⊥轴,垂足为点B ,点M 是函数(0)ky x x =>图像上一动点(不与P 点重合),过点M 作MD AP⊥于点D ,若45PMD ∠=︒,点M 的坐标是________.18.如图,点A 是反比例函数()280y x x=>的图象上的一动点,过点A 分别作x 轴、y 轴的平行线,与反比例函数1k y x=(0k ≠,0x >)的图象交于点B 、点C ,连接OB ,OC .若四边形OBAC 的面积为5,则k =________.三、解答题19.如图,一次函数114y k x =+与反比例函数22k y x=的图象交于点()2,A m 和()6,2B --,与y 轴交于点C .(1)1k =,2k =;(2)过点A 作AD x ⊥轴于点D ,点P 是反比例函数在第一象限的图象上一点,设直线OP与线段AD 交于点E ,当:4:1ODE ODAC S S ∆=四边形时,求点P 的坐标.(3)点M 是坐标轴上的一个动点,点N 是平面内的任意一点,当四边形ABMN 是矩形时,求出点M 的坐标.20.如图,反比例函数1k y x=的图像与一次函数2y mx n =+的图像相交于(),1A a -,()1,3B -两点.(1)求反比例函数和一次函数的解析式;(2)点P 在线段AB 上,且:1:2AOP BOP S S = ,直接写出点P 的坐标;(3)设直线AB 交y 轴于点C ,点(),0N t 是x 轴正半轴上的一个动点,过点N 作NM x ⊥轴交反比例函数1k y x=的图像于点M ,连接CN ,OM .若S 四边形COMN >3,直接写出t 的取值范围.21.如图,在平面直角坐标系中,直线y x =与反比例函数图象交于点(),A a a ,点1,22B a a ⎛⎫ ⎪⎝⎭为反比例函数()0k y x x =>图象上的点,连接OB ,AB ,且AOB S ∆为3.(1)求反比例函数的解析式;(2)点P 为y 轴上一动点,当ABP 的周长最小时,直接写出点P 的坐标.22.一次函数2y x =--的图象与反比例函数k y x=的图象相交于()3,A m -,(),3B n -两点.(1)求这个反比例函数的解析式;(2)根据图象写出使一次函数值不大于反比例函数值的x 的取值范围.(3)若动点E 在y 轴上,且6EBA S =△,求动点E 的坐标.23.如图,一次函数()110y k x b k =+≠的图象与反比例函数()220k y k x=≠的图象交于点()14A ,,()4B n -,两点.(1)求一次函数和反比例函数的表达式;(2)连接AO 并延长交双曲线于点C ,点D 为y 轴上一动点,点E 为直线AB 上一动点,连接CD ,DE ,求当CD DE +最小时点D 的坐标;24.如图,点A 在反比例函数(00)m y m x x =>>,的图像上,点A 的纵坐标为3.过点A 作x 轴的平行线交反比例函数(0)n y n m x x=>>,的图像于点C .点P 为线段AC 上一动点,过点P 作AC 的垂线,分别交反比例函数m y x =和n y x =的图像于点B ,D .(1)当416m n ==,时,①若点P 的横坐标为4(如图1),求直线AB 的函数表达式;②若点P 是AC 的中点(如图2),试判断四边形ABCD 的形状,并说明理由;(2)四边形ABCD 能否成为正方形?若能,求此时m ,n 之间的数量关系;若不能,说明理由.参考答案1.A 【分析】根据1()2MNP P M S MN y y ∆=⋅-求解.解:设点M 坐标为(,)a b ,点M 在反比例函数图象上,4ab ∴=,111()()()2222MNP P M S MN y y a b ab ∆∴=⋅-=⨯--==.故选:A .【点拨】本题考查反比例函数系数k 的几何意义,解题关键是掌握xy k =,掌握坐标系内求图形面积的方法.2.C【分析】设点A 的坐标为(a ,3a),连接OC ,则OC ⊥AB ,表示出OC ,过点C 作CD ⊥x 轴于点D ,设出点C 坐标,在Rt △OCD 中,利用勾股定理可得出x 2的值,进而得出结论.解:如图,设A (a ,3a ),点C 始终在双曲线()0k y x x=->上运动,∵点A 与点B 关于原点对称,∴OA =OB ,∵△ABC 为等边三角形,∴AB ⊥OC ,OC,∵AO =∴CO 过点C 作CD ⊥x 轴于点D ,则可得∠AOD =∠OCD (都是∠COD 的余角),设点C 的坐标为(x ,y ),则tan ∠AOD =tan ∠OCD ,即3x a a y =-,解得23a y x =-.在Rt △COD 中,CD 2+OD 2=OC 2,即2222273y x a a +=+,将23a y x =-代入,可得:2227x a =,故23a x y x ==-=,则xy =-9,即k =-9,所以,点C 在函数()90y x x=->上运动.所以,①②都对,故选:C .【点拨】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.3.D【分析】设AB =a ,则PB =3a ,从而得到B kx a =,3C k x a =,根据矩形的性质,得到PC =AD =BE =B C x x -,利用三角形面积为载体建立等式计算即可.解:设AB =a ,则PB =3a ,过点C 作CE ⊥x 轴,垂足为E ,过点A 作AD ∥x 轴,交CE 于点D ,则四边形APCD 是矩形,四边形BPCE 是矩形,∴CE =PB =3a ,∵点A 、点C 都在函数(0)k y x x =>的图像上,∴A B k x x a==,3C k x a =,根据矩形的性质,得到PC =AD =BE =B C x x -=3kk a a -,∵APC △的面积为8,∴1(2823kk a a a-⨯=,解得k =12,故选D .【点拨】本题考查了反比例函数的图像及其性质,矩形的判定和性质,三角形面积计算,熟练掌握反比例函数的性质是解题的关键.4.B【分析】先根据矩形的性质,角平分线定义得出DBO DOB ∠=∠,然后根据等腰三角形的判定得出BD OD =,在Rt COD 中根据勾股定理可求出CD ,从而求出点D 的坐标,根据待定系数法求出反比例函数解析式,最后把4x =代入求解即可.解:解∶∵OB 平分AOD ∠,∴AOB DOB ∠=∠,∵四边形ABCD 是矩形,()42B ,,∴BC OA ∥,4BC AO ==,2==OC AB ,90BCO ∠=︒,∴DBO AOB ∠=∠,∴DBO DOB ∠=∠,∴BD OD =,设BD OD a ==,则4CD BC BD a =-=-,在Rt COD 中,222CO CD OD +=,∴()22242a a -+=,解得52a =,∴32CD =,∴3,22D ⎛⎫ ⎪⎝⎭,∴3232k =⨯=,∴3y x =,当4x =时,34y =,∴点E 的纵坐标为34.故选:B .【点拨】本题考查了矩形的性质,等腰三角形的判定,勾股定理,待定系数法等知识,正确求出点D 的坐标是解题的关键.5.C【分析】延长BP ,交x 轴于点C ,由题意可设点1212,,,A a B b a b ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,则有1212,,AP a b BP OC b b a=-=-=,然后由S △BOP =3.6可进行求解问题.解:延长BP ,交x 轴于点C ,如图所示:∵PB ∥y 轴,PA ∥x 轴,∴AP BP ⊥,BC x ⊥轴,由题意可设点1212,,,A a B b a b ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,则有1212,,AP a b BP OC b b a =-=-=,∵S △BOP =3.6,∴1 3.62BP OC ⋅=,即12127.2b b a ⎛⎫-= ⎪⎝⎭,解得:25b a =,∴()111212130123 5.42225APB S AP BP a b a b a a a ⎛⎫⎛⎫=⋅=--=⨯-⨯= ⎪ ⎪⎝⎭⎝⎭ ;故选C .【点拨】本题主要考查反比例函数与几何的综合,熟练掌握反比例函数的性质及几何意义是解题的关键.6.C【分析】根据垂线段最短可得,当AB 垂直直线y x =时AB 最短,此时△AOB 是等腰直角三角形,易求OB =42D 作DE ⊥x 轴于点E ,知△DEO 为等腰直角三角形,求出DE ,OE 的长即可得到结论.解:根据垂线段最短可得,当AB 垂直直线y x =时AB 最短,∵∠AOB =45°∴∠BAO =45°∴△AOB 是等腰直角三角形,∵点A 的坐标为(8,0)∴OA =8∴42BO BA ==∵四边形OBCD 是正方形,∴90DO BO DOB ==∠=︒∴45DOC BOC ∠=∠=︒过点D 作DE ⊥x 轴于点E ,∴45ODE DOE ∠=∠=︒∴△DEO 为等腰直角三角形,∴4DE OE ==∵点D 在第二象限,∴D (-4,4)又点D 在反比例函数k y x=的图像上∴(4)416k =-⨯=-故选:C .【点拨】本题考查了最短路径问题、待定系数法求函数解析式、正方形的性质等知识,解答此题的关键是正确求出点D 的坐标.7.B【分析】由点B 在直线y=x+1上,点B 横坐标为2,可求纵坐标,确定点B 的坐标,进而求出反比例函数的关系式,再确定点C 的坐标,由点C 开始不断重复“A-B-C”的过程,可以推断点P (2019,m )与Q (2025,n )具体所在的位置,再依据对称,求线段的和最小的方法求出答案.解:当x=2时,y=x+1=2+1=3,∴B (2,3)∵B (2,3)在双曲线k y x =上,∴k=6把x=6代入6y x=得:y=1,∴C (6,1)∵2019÷6=336……3,2025÷6=337……3,∴点P 落在第337个“A-B-C”的P 处,而点Q 落在第338个“A-B-C”的Q 处,示意如图:把3x =代入6,y x =2,y ∴=∴P (2019,2),Q (2025,2),PQG 周长的最小,PQ=6定值,∴只要GP+GQ 最小即可,过Q 作QH x ⊥轴,使Q,H 关于x 轴对称,连接HP 交x 轴于,G ()2025,2,H ∴-6,4,PQ QH ∴==由勾股定理得:PH =∴PQG 周长的最小值为PQ+GP+GQ=6PH PQ +=+故选B .【点拨】考查反比例函数、一次函数的图象和性质,轴对称性质的应用,根据规律推断出点P 、Q 的位置,找出点G 的位置,依据勾股定理求出线段的长,是解决问题的关键.8.D【分析】根据等边三角形的性质表示出D ,C 点坐标,进而利用反比例函数图象上点的坐标特征得出答案.解:过点D 作DE ⊥x 轴于点E ,过C 作CF ⊥x 轴于点F ,如图所示.可得:∠ODE =30°,∠BCD =30°,设OE =a ,则OD =2a ,DE a ,∴BD =OB ﹣OD =10﹣2a ,BC =2BD =20﹣4a ,AC =AB ﹣BC =4a ﹣10,∴AF =12AC =2a ﹣5,CF AF 2a ﹣5),OF =OA ﹣AF =15﹣2a ,∴点D (a a ),点C [15﹣2a 2a ﹣5)].∵点C 、D 都在双曲线y =k x 上(k >0,x >0),∴a a =(15﹣2a )2a ﹣5),解得:a =3或a =5.当a =5时,DO =OB ,AC =AB ,点C 、D 与点B 重合,不符合题意,∴a =5舍去.∴点D (3,∴k =故选D .【点拨】本题考查了反比例函数图象上点的坐标特征以及等边三角形的性质,解题的关键是找出点D 、C 的坐标.9.B解:设点P 的运动速度为v ,①由于点A 在直线y=x 上,故点P 在OA 上时,四边形OMPN 为正方形,四边形OMPN 的面积S=(vt )2,②点P 在反比例函数图象AB 时,由反比例函数系数几何意义,四边形OMPN 的面积S=k ;③点P 在BC 段时,设点P 到点C 的总路程为a ,则四边形OMPN 的面积=OC•(a ﹣vt )=﹣2OC v ⋅t+2OC a ⋅,只有B 选项图形符合.故选B .考点:动点问题的函数图象.10.D 【分析】联立方程组212y x y x ⎧=⎪⎪⎨⎪=⎪⎩并求解,得到(2,1),(2,1)M N --,由两点间距离公式求出,,PM PN MN 的长,再分90,90,90PMN PNM MPN ∠=︒∠=︒∠=︒三种情况依据勾股定理列出方程求解即可解:联立方程组得212y x y x ⎧=⎪⎪⎨⎪=⎪⎩,解得,21x y =-⎧⎨=-⎩或21x y =⎧⎨=⎩,(2,1),(2,1)M N ∴--∵(),0P m ∴[][]2222(2)0(1)45,PN m m m =--+--=++222(22)(11)20,MN =--+--=2222(2)(01)45,PM m m m =-+-=-+①若90PNM ∠=︒时,则有222PN MN PM +=,22452045m m m m ∴+++=-+,5,2m \=-②若90MPN ∠=︒时,则有222PM PN MN +=,22454520.m m m m ∴-++++=,m ∴=③若90PMN ∠=︒时,则有222PM MN PN +=,22452045m m m m ∴-++=++,52m ∴=;综上所述,m 的值为52±或故选:D .【点拨】本题考查了一次函数与反比例函数的交点问题,正确进行分类讨论是解题的关键.11.14x <<【分析】先求出反比例函数的解析式,再求出线段MN 的解析式,最后联立两个解析式求出B 和C 两个点的坐标,再根据k 的几何意义,确定P 点位置,即可得到相应的x 的取值范围.解:∵点()2,2A -∴()224k =⨯-=-,所以反比例函数的解析式为:4y x=-,因为5OM ON ==,∴()()5,0,0,5M N -,设线段MN 解析式为:()05y px q x =+≤≤,∴505p q q +=⎧⎨=-⎩,∴15p q =⎧⎨=-⎩,∴线段MN 解析式为:()505y x x =-≤≤,联立以上两个解析式得:54y x y x =-⎧⎪⎨=-⎪⎩,解得:14x y =⎧⎨=-⎩或41x y =⎧⎨=-⎩,经检验,符合题意;由图可知,两个函数的图像交点分别为点B 和点C ,∴()1,4B -,()4,1C -,∵OAD OPE S S < ,∴P 点应位于B 和C 两点之间,∴14x <<,故答案为:14x <<.【点拨】本题涉及到了动点问题,考查了反比例函数的图像与性质、k 的几何意义、待定系数法等内容,解决本题的关键是牢记反比例函数的图像与性质,理解k 的几何意义,以及能联立两个函数的解析式求交点坐标等,本题蕴含了数形结合的思想方法等.12.3y x=【分析】如图,设A (m ,n ),过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,得到AC =n ,OC =-m ,根据反比例函数图象上点的坐标特征可得3=-mn ,根据平角的定义及角的和差关系可得∠OAC =∠BOD ,根据旋转的性质可得OB =OA ,利用AAS 可证明△ACO ≌△ODB ,根据全等三角形的性质得到AC =OD =n ,CO =BD =-m ,可得点B 坐标,利用待定系数法即可得答案.解:如图,设A (m ,n ),过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,∵点A 是反比例函数3y x=-(0x <)的图像上的一个动点,∴3=-mn ,AC =n ,OC =-m ,∵将线段OA 绕点O 顺时针旋转90°得到线段OB ,∴∠AOB =90°,OA =OB ,∴∠OAC +∠AOC =∠BOD +∠AOC =90°,∴∠OAC =∠BOD ,在△ACO 和△ODB 中,ACO BDO OAC BOD OA OB ∠=⎧⎪∠=∠⎨⎪=⎩,∴△ACO ≌△ODB ,∴AC =OD =n ,CO =BD =-m ,∴B (n ,-m ),设过点B 的反比例函数的解析式为k y x=,∴3k mn =-=,∴点B 所在反比例图像的函数关系式为3y x =,故答案为:3y x=【点拨】本题考查了坐标与图形变化-旋转,反比例函数图形上点的坐标特征,待定系数法求反比例函数的解析式,全等三角形的判定和性质,正确的作出辅助线是解题的关键.13.y =-4x【分析】连结OC ,作CD ⊥x 轴于D ,AE ⊥x 轴于E ,如图,设A 点坐标为4,a a骣琪琪桫,再证明△COD ≌△OAE (AAS ),表示C 点坐标为4,a a骣琪-琪桫,从而可得答案.解:连结OC ,作CD ⊥x 轴于D ,AE ⊥x 轴于E ,如图,设A 点坐标为4,a a骣琪琪桫,∵A 点、B 点是正比例函数图象与双曲线4y x =的交点,∴点A 与点B 关于原点对称,∴OA =OB∵△ABC 为等腰直角三角形,∴OC =OA ,OC ⊥OA ,∴∠DOC +∠AOE =90°,∵∠DOC +∠DCO =90°,∴∠DCO =∠AOE ,∵在△COD 和△OAE 中CDO OEA DCO EOA CO OAìÐ=ÐïïÐ=Ðíï=ïî∴△COD ≌△OAE (AAS ),∴OD =AE =4a,CD =OE =a ,∴C 点坐标为4,a a骣琪-琪桫,∵44a a -=-g ,∴点C 在反比例函数4y x =-图象上.故答案为:4y x=-【点拨】本题考查的是等腰直角三角形的性质,三角形全等的判定与性质,反比例函数的图象与性质,利用三角形的全等确定C 的坐标是解本题的关键.14.②③##③②【分析】由点P 是动点,可判断出①错误,设出点P 的坐标,求出AP 、BP 的长,再利用三角形面积公式计算即可判断出②;利用角平分线定理的逆定理可判断③;先求出矩形OMPN 的面积为4,进而得出mn =4,最后用三角形的面积公式解答即可.解:∵点P 是动点,∴BP 与AP 不一定相等,∴BOP △与AOP 不一定全等,故①不正确;设P (m ,n ),∵BP ∥y 轴,∴B (m ,12m ),A (12n ,n )∴AP =|12n-m |∴S △AOP =12·|12n-m |n =12|12-mn |同理:S △BOP =12·|12m -n |m =12|12-mn |∴S △AOP =S △BOP ;故②正确;如图1,过点P 作PF ⊥OA 于F ,PE ⊥OB 于E ,∴BOP S =12OB ·PE ,AOP S =12OA ·PF∵BOP AOP S S = ,∴OB ·PE =OA ·PF∵OA =OB ,∴PE =PF ,∵PE ⊥OB ,PF ⊥OA∴OP 是∠AOB 的平分线,故③正确;如图2,延长BP 交x 轴于N ,延长AP 交轴于M ,∵AM ⊥y 轴,BN ⊥x 轴,∴四边形OMPN 是矩形,∵点A ,B 在双曲线y =12x 上,∴6AMO ONB S S == ,∵4BOP S = ,∴2PMO PNO S S == ,∴S 矩形OMPN =4,∴mn =4,∴m =4n ∴12|3|2||BP n n n n m=-=-=,8||12AP m n n =-=∴1182||822||APBS AP BP n n ∆=⨯=⨯⨯=故④不正确;故答案为②③.【点拨】本题属于反比例函数与几何综合题,主要考查了反比例函数的性质、三角形面积公式、角平分线定理逆定理、矩形的判定和性质等知识点,正确作出辅助线并灵活应用所学知识是解答本题的关键.15.6【分析】连接OA ,可得S △ABO =S △ABC =3,根据反比例函数k 的几何意义,可求出k 的值.解:连接OA ,∵AB ⊥y 轴,∴AB ∥x 轴,∴S △ABO =S △ABC =3,即:12|k |=3,∴k =6或k =-6,∵在第二象限,∴k =-6,故答案为:-6.【点拨】考查反比例函数的图象和性质,理解反比例函数k 的几何意义以及同底等高的三角形的面积相等,是解决问题的前提.16.①②④【分析】设A(a,12a),B(b,12b),则C(a,-3a),D(b,-3b),由平行四边形的性质AC=BD列出方程求得a、b的关系,进而得B、C的坐标,根据坐标可以判断BC不与x轴平行,从而判断AC与BD垂直,进而判断③错误;②④正确;根据随着|a|不断变小,AC越来越大,BC越来越小,可以判断AC有可能与BC相等,进而判断①的正误.解:设A(a,12a),B(b,12b),则C(a,-3a),D(b,-3b),∵AC=BD,∴-15a=15b,∴a=-b,∴yC=-3a=3b≠yB=12b,∴BC不与x轴平行,∴AC与BC不可能垂直,∴▱ACBD不可能是矩形,▱ACBD不可能是正方形.故③错误;②④正确;∵随着|a|不断变小,AC越来越大,BC越来越小,∴AC有可能与BC相等,故①正确;故答案为①②④.【点拨】本题主要考查了反比例函数的图象与性质,平行四边形的性质,菱形的判定,矩形、正方形的判定,解题的关键是由平行四边形的对边相等,得出a、b的关系.17.(12,2)【分析】过点D作GH⊥PB,交BP的延长线于G,作MH⊥HG于H,证得△PGD≅△DHM(AAS),得PG=DH,DG=MH,设D(m,112m ),表示出点M的坐标,从而得出m的方程,解方程即可.解:过点D作GH⊥PB,交BP的延长线于G,作MH⊥HG于H,如图所示,∵△PMD 是等腰直角三角形,∴PD =DM ,∵∠PDG +∠MDH =90°,∠PDG +∠DPG =90°,∴∠DPG =∠MDH ,∵∠G =∠H ,∴△PGD ≅△DHM (AAS),∴PG =DH ,DG =MH ,∵点P 的纵坐标为4,∴将y =4代入112y x =+,得x =6,∴P 点坐标为(6,4),将P (6,4),代入(0)k y x x =>,得:k =24,∴反比例函数解析式为:24(0)y x x=>设D (m ,112m +),∴DG =m -6,PG =132m -,∴MH =m -6,DH =132m -,∴M (332m -,172m -),∵点M 在反比例24y x=的图象上,∴31372422m m ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭ ,解得16m =,210m =,当m =6时,M (6,4)(舍去),当m =10时,M (12,2),故答案为:(12,2).【点拨】本题是反比例函数与一次函数图象的交点问题,主要考查了函数图象上点的坐标的特征,等腰直角三角形的性质,全等三角形的判定与性质,构造全等三角形表示出点M 的坐标是解题的关键.18.3【分析】延长,AB AC 分别交y 轴,x 轴于点,E D ,易得四边形OBAC 的面积等于8k -,即可得解.解:延长,AB AC 分别交y 轴,x 轴于点,E D ,∵AB x 轴,AC y 轴,则:四边形AEOD 为矩形,,OBE ODC 为直角三角形,∵点A 在反比例函数()280y x x=>的图象上,点B 、点C 在反比例函数1k y x =(0k ≠,0x >)上,∴8AEOD S =矩形,2OBE ODC k S S ==,∴四边形OBAC 的面积85OBE ODC AEOD S S S k =--=-= 矩形,∴3k =;故答案为:3.【点拨】本题考查一直图形面积求k 值.熟练掌握k 值的几何意义,是解题的关键.19.(1)1,12;(2)⎝;(3)()0,8-或()8,0-.【分析】(1)根据点B 的坐标,利用待定系数法即可求出1k 、2k 的值;(2)根据一次函数图象上点的坐标特征求出点A 、C 的坐标,根据梯形的面积公式求出ODAC S 四边形的值,进而即可得出ODE S ∆的值,结合三角形的面积公式即可得出点E 的坐标,利用待定系数法即可求出直线OP 的解析式,再联立直线OP 与双曲线的解析式成方程组,通过解方程组求出点P 的坐标;(3)过点B 作直线12M M AB ⊥交x 轴于点2M 交y 轴于点1M ,作出符合题意的图形,利用待定系数法求出直线12M M 的解析式,再求出1M 、2M 的坐标即可.(1)解:将点()6,2B --代入114y k x =+,1264k -=-+,解得:11k =,故一次函数的解析式为;14y x =+,将点()6,2B --代入22k y x =,226k -=-,解得:212k =,故反比例函数的解析式为12y x =;故答案为:1,12(2)解:依照题意,画出图形,如图所示.当2x =时,246m =+=,∴点A 的坐标为()2,6;当0x =时,14044y x =+=+=,∴点C 的坐标为()0,4,∵()114621022()ODAC S OC AD OD =+⋅=⨯+⨯=四边形,:4:1ODE ODAC S S ∆=四边形,∴111210224ODE S OD DE DE =⋅=⨯=⨯ ,∴52DE =,即点E 的坐标为52,2⎛⎫ ⎪⎝⎭,设直线OP 的解析式为y kx =,将点52,2E ⎛⎫ ⎪⎝⎭代入y kx =,得522k =,解得:54k =,∴直线OP 的解析式为54y x =,联立得1254y x y x ⎧=⎪⎪⎨⎪=⎪⎩,解得:11x y ⎧⎪⎨⎪⎩22x y ⎧=⎪⎨⎪=⎩,∵点P 在第一象限,∴点P的坐标为⎝;(3)解:过点B 作直线12M M AB ⊥交x 轴于点2M 交y 轴于点1M ,依照题意画出图形,如图所示.则1290CBM CBM ∠=∠=︒时,四边形11ABM N 与22ABM N 是满足题意的矩形,∵直线AB 的解析式为4y x =+,∴可设直线12M M 的解析式为y x b =-+,把点()6,2B --代入y x b =-+得到26b -=+,解得8b =-,直线12M M 的解析式为8y x =--,当0x =时,8088y x =--=-=-,当0y =时,08x =--,解得8x =-,∴()10,8M -,()28,0M -,故点M 的坐标为()0,8-或()8,0-.【点拨】本题考查了待定系数法求出一次函数及反比例函数解析式、一次函数图象上点的坐标特征、梯形(三角形)的面积公式、矩形的性质,解题的关键是根据题意画出图形,作出辅助线.20.(1)反比例函数的解析式为3y x-=,一次函数解析式为2y x =-+;(2)点P 的坐标为(53,13);(3)t >32【分析】(1)将点B ,点A 坐标代入反比例函数的解析式,可求a 和k 的值,利用待定系数法可求一次函数解析式;(2)连接OA ,OB ,OP ,求得OC 的长,根据AOB AOC BOC S S S =+ ,:1:2AOP BOP S S = ,求得BOP BOC POC S S S =+ 进而求得点P 的坐标;(3)先求出点C 坐标,由面积关系可求解.解:(1)∵反比例函数k y x=的图像与一次函数y mx n =+的图像相交于(),1A a -,()1,3B -两点,∴()131k a =-⨯=⨯-,∴3,3k a =-=,∴点()3,1A -,∴反比例函数的解析式为3y x-=,由题意可得:313m n m n =-+⎧⎨-=+⎩,解得:12m n =-⎧⎨=⎩,∴一次函数解析式为2y x =-+;(2)连接OA ,OB ,OP ,令0x =代入22y x =-+,解得22y =,∴一次函数与y 轴的交点C 坐标为()0,2,∴2OC =,∵点P 在线段AB 上,∴设点P 为(),2m m -+,∵点A ()3,1-,点B ()1,3-,∴4AOB AOC BOC S S S =+= ,∵:1:2AOP BOP S S = ,∴2833BOP AOB S S == ,∵1BOP BOC POC S S S m =+=+ ,∴813m +=,解得53m =,∴123m -+=,∴点P 的坐标为51,33⎛⎫ ⎪⎝⎭;(3)∵直线AB 交y 轴于点C ,∴点C ()0,2,∴31222OMN OCN COMN S S S t =+=+⨯⨯ 四边形,∵3COMN S >四边形,∴312322t +⨯⨯>,∴32t >.【点评】本题考查了反比例函数与一次函数的交点问题,利用待定系数法求解析式,反比例函数的性质等知识,求出两个解析式是解题的关键.21.(1)4y x =;(2)100,3P ⎛⎫ ⎪⎝⎭.【分析】(1)先求出直线OA 的解析式为y x =,直线OB 的解析式为4y x =,过点A作AC x ∥轴,交OB 于C ,在求出1,4C a a ⎛⎫ ⎪⎝⎭,进而得出1344AC a a a =-=,根据21313324244AOB AOC ABC S S S a a a a a =+=⨯⨯+⨯⨯= ,再根据面积即可得出a 的值,求出()2,2A ,即可得出答案;(2)根据(1)可得:()2,2A ,()1,4B ,由于点D 与点A 关于y 轴对称,可知当PA PB +的值最小,即B ,P ,D 三点在同一直线上时ABP 的周长最小,求出直线BD 的解析式为21033y x =+,即可得出答案.(1)解:∵设直线OA 的解析式为1y k x =,将(),A a a 代入,得出:11k =,∴直线OA 的解析式为y x =,设直线OB 的解析式为2y k x =,将1,22B a a ⎛⎫ ⎪⎝⎭代入,得出:24k =,∴直线OB 的解析式为4y x =,过点A 作AC x ∥轴,交OB 于C ,∵(),A a a ,∴点C 的纵坐标为a ,∵点C 在直线OB 上,∴点c 的横坐标为:14a ,∴1,4C a a ⎛⎫ ⎪⎝⎭,∴1344AC a a a =-=,∴21313324244AOB AOC ABC S S S a a a a a =+=⨯⨯+⨯⨯= ,∴2334a =,解得:12a =,22a =-(舍去),∴()2,2A ,∴224k =⨯=,∴反比例函数的解析式为:4y x=;(2)解:根据(1)可得:()2,2A ,()1,4B ,∵点D 与点A 关于y 轴对称,∴PA PD =,∴AB PA PB AB PD PB ++=++,∵AB 为定值,∴当PA PB +的值最小,即B ,P ,D 三点在同一直线上时ABP 的周长最小,∴()2,2D -,设直线BD 的解析式为y ax b =+,将()1,4B ,()2,2D -,代入得:422a b a b +=⎧⎨-+=⎩,解得:23103a b ⎧=⎪⎪⎨⎪=⎪⎩,∴直线BD 的解析式为21033y x =+,当0x =时,103y =,∴100,3P ⎛⎫ ⎪⎝⎭.【点拨】本题考查反比例函数与一次函数,轴对称的性质,正确得出反比例函数解析式是解题的关键.22.(1)3y x=-;(2)-<3≤0x 或1x ≥;(3)()0,5-或()0,1【分析】(1)将点A 坐标代入直线表达式,求出m ,得到具体坐标,再将点A 坐标代入反比例函数表达式,求出k 值可;(2)求出点B 坐标,结合图像可得结果;(3)设点E 坐标为()0,a ,求出直线AB 与y 轴交点F 的坐标,再根据6EBA S =△,列出方程,解之可得.(1)解:将()3,A m -代入2y x =--得:()321m =---=,∴()3,1A -,代入k y x=中,得:()313k =-⨯=-,∴3y x=-;(2)将(),3B n -代入2y x =--中,得32n -=--,解得:1n =,∴()1,3B -,由图像可知:当一次函数图像在反比例函数图像下方时,对应的x 为-<3≤0x 或1x >,∴使一次函数值不大于反比例函数值的x 的取值范围是-<3≤0x 或1x ≥.(3)设点E 坐标为()0,a ,直线AB 与y 轴交于点F ,在2y x =--中,令0x =,则=2y -,∴()0,2F -,∵6EBA S =△,∴()162B A EF x x ⨯⨯-=,即12462a ⨯--⨯=,解得:5a =-或1a =,∴点E 的坐标为()0,5-或()0,1.【点拨】本题考查了一次函数与反比例函数交点问题,用待定系数法确定反比例函数的解析式;要能够熟练掌握待定系数法,学会表示交点形成的三角形面积是解题的关键.23.(1)一次函数解析式为3y x =+,反比例函数解析式为4y x=;(2)()03D -,【分析】(1)先把点A 坐标代入反比例函数解析式中求出反比例函数解析式,进而求出点B 的坐标,再把A 、B 的坐标代入一次函数解析式中求出一次函数解析式即可;(2)设直线AB 与x 轴,y 轴分别交于N ,M ,作点C 关于y 轴的对称点H ,连接CH 交y 轴于G ,连接HD ,推出当H D E 、、三点共线且HD AB ⊥时,HD DE +最小,即CD DE +最小;求出()()3003N M -,,,,进而证明45OMN ONM ∠=∠=︒,即可退出45GHD GDH =︒=∠∠,得到DG HG =;由对称性可知()14C --,,则()14H -,,由此求出3OD =,则()03D -,.(1)解:把()14A ,代入到反比例函数()220k y k x=≠中得:241k =,∴24k =,∴反比例函数解析式为4y x =,把()4B n -,代入到()4B n -,4y x=中得:414n ==--,∴()41B --,;把()14A ,,()41B --,代入到一次函数()110y k x b k =+≠中得:11441k b k b +=⎧⎨-+=-⎩,∴113k b =⎧⎨=⎩,∴一次函数解析式为3y x =+;(2)解:设直线AB 与x 轴,y 轴分别交于N ,M ,作点C 关于y 轴的对称点H ,连接CH 交y 轴于G ,连接HD ,∴CD HD =,∴CD DE HD DE +=+,∴当H D E 、、三点共线且HD AB ⊥时,HD DE +最小,即CD DE +最小;在3y x =+中,令0x =,则3y =,令0y =,则3x =-,∴()()3003N M -,,,,∴3OM ON ==,∴45OMN ONM ∠=∠=︒,∴45GDH EDM ==︒∠∠,∴45GHD GDH =︒=∠∠,∴DG HG =;由对称性可知()14C --,,∴()14H -,,∴41OG DG HG ===,,∴3OD =,∴()03D -,.【点拨】本题主要考查了一次函数与反比例函数综合,轴对称最短路径问题,等腰直角三角形的性质与判定,正确作出辅助线确定当H D E 、、三点共线且HD AB ⊥时,HD DE+最小,即CD DE +最小是解题的关键.24.(1)①直线AB 的解析式为344y x =-+;②四边形ABCD 是菱形,理由见分析;(2)四边形ABCD 能成为正方形,9m n +=.【分析】(1)①先确定出点A ,B 坐标,再利用待定系数法即可得出结论;②先确定出点D 坐标,进而确定出点P 坐标,进而求出PD PB ,,即可得出结论;(2)先确定出33m A ⎛⎫ ⎪⎝⎭,,33n C ⎛⎫ ⎪⎝⎭,进而求出点P 的坐标,再求出B ,D 坐标,最后用BD AC =,即可得出结论.(1)解:①∵4m =,∴反比例函数为4y x=,当4x =时,1y =,∴()41B ,,当3y =时,∴43x =,∴43x =,∴433A ⎛⎫ ⎪⎝⎭,设直线AB 的解析式为y kx b =+,∴43341k b k b ⎧+=⎪⎨⎪+=⎩,解得344k b ⎧=-⎪⎨⎪=⎩,∴直线AB 的解析式为344y x =-+;②四边形ABCD 是菱形,理由如下:由①知,433A ⎛⎫ ⎪⎝⎭,∵AC x ∥轴,∴1633C ⎛⎫ ⎪⎝⎭,,∵点P 是线段AC 的中点,∴1033P ⎛⎫ ⎪⎝⎭,,当103x =时,由4y x =得,65y =,由16y x =得,245y =,∴56359PB =-=,355249PD =-=,∴PB PD =,∵PA PC =,∴四边形ABCD 为平行四边形,∵BD AC ⊥,∴四边形ABCD 是菱形;(2)解:四边形ABCD 能是正方形,理由:当四边形ABCD 是正方形,记AC BD ,的交点为P ,P 为AC 的中点,∴BD AC =,当3y =时,由m y x =得,3m x =,由n y x=得,3n x =,∴33m A ⎛⎫ ⎪⎝⎭,,33n C ⎛⎫ ⎪⎝⎭,∴36m n P +⎛⎫ ⎪⎝⎭,∴66m n m B m n +⎛⎫ +⎝⎭,,66m n n D m n +⎛⎫ ⎪+⎝⎭,,∵BD AC =,∴6633n m n m m n m n -=-++,∴18m n +=.【点拨】此题是反比例函数综合题,主要考查了待定系数法,平行四边形的判定,菱形的判定和性质,正方形的性质,判断出四边形ABCD 是平行四边形是解本题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
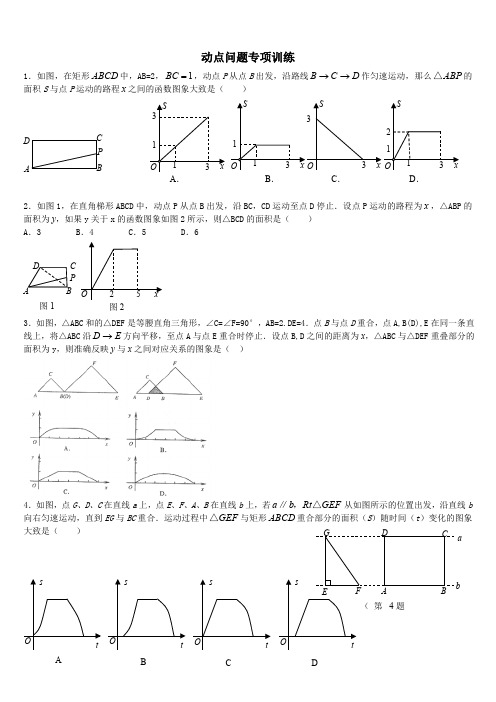
b 向右匀速运动,直到 EG 与 BC 重合.运动过程中 △GEF 与矩形 ABCD 重合部分的面积(S )随时间(t )变化的图动点问题专项训练1.如图,在矩形 ABCD 中,AB=2, BC = 1 ,动点 P 从点 B 出发,沿路线 B → C → D 作匀速运动,那么 △ A BP 的 面积 S 与点 P 运动的路程 x 之间的函数图象大致是( )SSS S33DAC P B1O 113 x O 13 xO213 x O 13 xA .B .C .D .2.如图 1,在直角梯形 ABCD 中,动点 P 从点 B 出发,沿 BC ,CD 运动至点 D 停止.设点 P 运动的路程为 x ,△ABP 的 面积为 y ,如果 y 关于 x 的函数图象如图 2 所示,则△BCD 的面积是( ) A .3 B .4 C .5 D .6DC PAB O 25 x图 1图 2△3.如图, ABC 和的△DEF 是等腰直角三角形,∠C=∠F=90°,AB=2.DE=4.点 B 与点 D 重合,点 A,B(D),E 在同一条直 线上,将△ABC 沿 D → E 方向平移,至点 A 与点 E 重合时停止.设点 B,D 之间的距离为 △x , ABC 与△DEF 重叠部分的面积为 y ,则准确反映 y 与 x 之间对应关系的图象是()4.如图,点 G 、D 、C 在直线 a 上,点 E 、F 、A 、B 在直线 b 上,若 a ∥b ,Rt △GEF 从如图所示的位置出发,沿直线....象大致是()G DC as s s sEFAB b(第 4 题Ot O t O t O tA B C D5.(20XX 年牡丹江)如图,平面直角坐标系中,在边长为 1 的正方形 ABCD 的边上有一 动s stOt .(第 6 题图).O C 8。
点 P 沿 A → B → C → D → A 运动一周,则 P 的纵坐标 y 与点 P 走过的路程 s 之间的函数关系用图象表示大致是()yy2 2 11 y2 1 y2 1O 1 2 3 4sO 1 2 3 4s O 1 2 3 4 s O 1 2 3 4sABC D6.如图 1,在矩形 ABCD 中,动点 P 从点 B 出发,沿 BC 、CD 、DA 运动至点 A 停止,设点 P 运动的路程为 x ,△ABP 的 面积为 y ,如果 y 关于 x 的函数图象如图 2 所示,则矩形 ABCD 的面积是( )A .10 8.16 C. 20 D .367.如图,三个大小相同的正方形拼成六边形 ABCDEF ,一动点 P 从点 A 出发沿着 A → B → C → D → E 方向匀速 运动,最后到达点 E .运动过程中 ∆PEF 的面积( s )随时间(t )变化的图象大致是( )s sPA · B.C DO8.如图.,点 A 、B 、C 、D 为圆 O 的四等分点,动点 P 从圆心 O 出发,沿 O-C-D-O 的路线作匀速运动.设运动时间为 t 秒,∠APB 的度数为 y 度,则下列图象中表示 y 与 t 之间函数关系最恰当的是9. 13.一张正方形的纸片,剪去两个一样的小矩形得到一个“E ”图案,如图4 所示,设小矩形的长和宽分别为x 、y ,剪去部分的面积为 20,若 2≤x ≤10,则 y 与 x 的函数图象是:10.如图,AB 是半圆 O 的直径,点 P 从点 O 出发,沿 O A - AB - BO 的路径运动一周.设OP 为 s ,运动时间为t ,则QC ,即 6﹣x = (6+x ),解得 x =2。
下列图形能大致地刻画 s 与 t 之间关系的是()PssssAO B OA . t OB . tOC . tOD . t11.锐角△ABC 中,BC =6, S∆ABC= 12, 两动点 M 、N 分别在边 AB 、AC 上滑动,且 MN ∥BC ,以 MN 为边向下作正方形 MPQN ,设其边长为 x ,正方形 MPQN 与△ABC 公共部分的面积为 y (y >0),当 x = ,公共部分面积 y 最大,y 最大值= ,6. (2012 贵州遵义 12 △分)如图,ABC 是边长为 6 的等边三角形,P 是 AC 边上一动点,由 A 向 C 运动(与 A 、C 不重合),Q 是 CB 延长线上一点,与点 P 同时以相同的速度由 B 向 CB 延长线方向运动(Q 不与 B 重合),过 P 作 PE ⊥AB于 E ,连接 PQ 交 AB 于 D .(1)当∠BQD =30°时,求 AP 的长;(2)当运动过程中线段 ED 的长是否发生变化?如果不变,求出线段 ED 的长;如果变化请说明理由.【答案】解:(△1)∵ABC 是边长为 6 的等边三角形,∴∠ACB =60°。
∵∠BQD =30°,∴∠QCP =90°。
设 AP =x ,则 PC =6﹣x ,QB =x ,∴QC =QB +C =6+x 。
∵在 △R t QCP 中,∠BQD =30°,∴PC = 1 12 2∴当∠BQD =30°时,AP =2。
(2)当点 P 、Q 运动时,线段 DE 的长度不会改变。
理由如下:作 QF ⊥AB ,交直线 AB 的延长线于点 F ,连接 QE ,PF 。
∵PE ⊥AB 于 E ,∴∠DFQ =∠AEP =90°。
∵点 P 、Q 做匀速运动且速度相同,∴AP =BQ 。
∵△ABC 是等边三角形,∴∠A =∠ABC =∠FBQ =60°。
∴在△APE 和△BQF 中,∵∠A =∠FBQ ,AP =BQ ,∠AEP =∠BFQ =90°,∴△APE ≌△BQF (AAS )。
∴AE =BF ,PE =QF 且 PE ∥QF 。
∴四边形 PEQF 是平行四边形。
12.(2012江苏泰州12分)如图,已知一次函数y=kx+b的图象与x轴相交于点A,与反比例函数y=,d)两点.点P(m,n)是一次函数y=kx+b的图象上的动点.2xx将点C(,d)的坐标代入y=-,得d=-=-2。
∴C(,-2)。
52x2∵一次函数y=kx+b的图象经过B(-1,5)、C(,-2)两点,2⎧5=-k+b-2=k+b⎩⎪⎩令y=0,即-2x+3=0,解得x=3。
∴A(,0)。
22∴DE=1EF。
2∵EB+AE=BE+BF=AB,∴DE=12学习必备欢迎下载AB。
又∵等边△ABC的边长为6,∴DE=3。
∴当点P、Q运动时,线段DE的长度不会改变。
12cx 的图象相交于B(-1,5)、C((1)求k、b的值;521(2)设-1<m<3c,过点P作x轴的平行线与函数y=的图象相交于点D.试问△P AD的面积是2否存在最大值?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由;(3)设m=1-a,如果在两个实数m与n之间(不包括m和n)有且只有一个整数,求实数a的取值范围.【答案】解:(1)将点B的坐标代入y=2c c,得5=,解得c=-5。
x-15∴反比例函数解析式为y=-。
255552251⎪⎧k=-2∴⎨5,解得⎨。
b=32(2)存在。
31由题意,点P(m,n)是一次函数y=-2x+3的图象上的动点,且-1<m<1∴点P在线段AB上运动(不含A、B)。
设P(3-n,n)。
232∴ y = y = n ,x = - ,即 D ( - ,n )。
n n∴△PAD 的面积为 S = PD ⋅ OP= ⋅ + ⎪ ⋅ n= - n - ⎪ + 。
∴当 n= 时,即 P ( , )时,△PAD 的面积 S 最大,为 【分析】(1)根据曲线上点的坐标与方程的关系,由 B 的坐标求得 c= - 5 ,从而得到 y = - 5;由点 C 在 y = - 上x x求得 d = -2 ,即得点 C 的坐标;由点 B 、C 在 y = kx + b 上,得方程组,解出即可求得 k 、b 的值。
∵DP ∥x 轴,且点 D 在 y = -25x学习必备 欢迎下载的图象上,5 5D P D1 1 ⎛ 3 - n 5 ⎫ 1 ⎛ 3 ⎫2 492 2 ⎝ 2 n ⎭ 4 ⎝ 2 ⎭ 16∴S 关于 n 的二次函数的图象开口向下,有最大值。
又∵n = -2m + 3 , -1 < m < 3 3,得 0 < n < 5 ,而 0 < n= < 5 。
2 23 3 3 492 4 2 16(3)由已知,P (1 - a, 2a+1)。
易知 m ≠n ,即1 - a ≠ 2a+1 ,即 a ≠ 0 。
若 a > 0 ,则 m <1 < n 。
由题设, m > 0,n ≤ 2 ,解出不等式组的解为 0 < a ≤若 a < 0 ,则 n <1 < m 。
1 2。
由题设, n ≥ 0,m < 2 ,解出不等式组的解为 - 1 2≤ a < 0 。
1 1综上所述,数 a 的取值范围为 - ≤ a < 0 , 0 < a ≤ 。
2 2【考点】反比例函数和一次函数综合问题,曲线上点的坐标与方程的关系,平行的性质,二次函数的性质,不等式组的应用。
5 2 21(△2)求出 PAD 的面积 S 关于 n 的二次函数(也可求出关于 m ),应用二次函数的最值原理即可求得面积的最大值及此时点 P 的坐标。
(3)由 m ≠n 得到 a ≠ 0 。
分 a > 0 和 a < 0 两种情况求解。
22. (2012 山东济南 9 分)如图,已知双曲线 y =kx,经过点 D (6,1),点 C 是双曲线第三象限上的动点,过 C 作CA ⊥x 轴,过 D 作 DB ⊥y 轴,垂足分别为 A ,B ,连接 AB ,BC .(1)求 k 的值;(2△)若 BCD 的面积为 12,求直线 CD 的解析式;(3)判断 AB 与 CD 的位置关系,并说明理由.【答案】解:(1)∵双曲线 y = k。
⎪⎩b = -2 ⎪⎩n = 1 学习必备欢迎下载k经过点 D (6,1),∴ = 1 ,解得 k =6。
x 6(2)设点 C 到 BD 的距离为 h ,∵点 D 的坐标为(6,1),DB ⊥y 轴,∴BD =6,∴△S BCD =1 2×6h=12,解得 h =4。
∵点 C 是双曲线第三象限上的动点,点 D 的纵坐标为 1,∴点 C 的纵坐标为 1-4= -3。
∴ 6x= 3 ,解得 x = -2。
∴点 C 的坐标为(-2,-3)设直线 CD 的解析式为 y =kx +b ,⎧1 ⎧-2k + b = -3 ⎪k = 则 ⎨ ,解得 ⎨2 。
