实验2 Matlab的基本运算
第二讲 MATLAB基本运算

矩阵下标的用途
访问超出矩阵范围时,产生 Index exceeds matrix dimentions 存储超出矩阵范围时,矩阵自动调节 大小,将指定位置元素置入,其他没 指定数的位置默认为零。
2010-12-25
21
矩阵下标的用途
(2)矩阵连接 例:a=[1 2;3 4] b=[a a+5; a-5 zeros(size(a)] 将小矩阵嵌套入大矩阵,实现矩阵连接。
将矩阵按创建原则写入一个M文件, 在MATLAB的命令窗口或程序中直接执 行该M文件,即将矩阵调入工组空间。
2010-12-25
15
利用MATLAB函数创建矩阵 利用MATLAB函数创建矩阵 MATLAB
ones( m, n) - m行n列的1阵产生 zeros(m, n) -产生m行n列的全0阵 rand(m, n) -产生m行n列均匀分布全列的在 [0,1]区间的随机阵 randn(m, n) -产生m行n列的正态分布矩阵 eye(n) -产生n维单位阵
2010-12-25 18
2.2.3 矩阵的下标 .2.3
子矩阵提取A(v1, v2)
v1表示子矩阵包含的行标构成的向量 v2表示子矩阵包含的列标构成的向量 B1=A(:, [1, 3]) 为:时表示要提取所有行(列) B2=A(1:2:end, :) end表示最后一行(列) B3=A([3,2,1],[2,3,4]) 例: B4=A(:, end:-1:1) 提取A矩阵所有行、1,3列 提取A矩阵 3,2,1 行、2,3,4 列构成子矩阵 提取A矩阵全部奇数行,所有列 将A矩阵左右翻转
2010-12-25
13
直接输入法创建矩阵
例:创建矩阵
matlab实验二

北京工业大学Matlab实验报告**: ***学号: ************: **实验二、Matlab 的基本计算(一)实验目的1.掌握建立矩阵的方法。
2.掌握Matlab 各种表达式的书写规则以及常用函数的使用。
3.能用Matlab 进行基本的数组、矩阵运算。
4.掌握矩阵分析的方法以及能用矩阵运算或求逆法解线性方程组。
5.掌握Matlab 中的关系运算与逻辑运算。
(二)实验环境1.计算机2.MATLAB7.0集成环境(三)实验内容及要求1、熟练操作MATLAB7.0运行环境;2、自主编写程序,必要时参考相关资料;3、实验前应写出程序大致框架或完整的程序代码;4、完成实验报告。
(四)实验程序设计1.利用diag 等函数产生下列矩阵。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=032570800a ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=804050702b2.利用reshape 函数将1题中的a 和b 变换成行向量。
3.产生一个均匀分布在(-5,5)之间的随机矩阵(10×2),要求精确到小数点后一位。
4.已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=76538773443412A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=731203321B求下列表达式的值:(1) B A K *611+=和I B A K +-=12(其中I 为单位矩阵)(2) B A K *21=和B A K *.22=(3) 331^A K =和3.32^A K =(4) B A K /41=和A B K \42=(5) ],[51B A K =和]2:);],3,1([[52^B A K = 5.下面是一个线性方程组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.03216/15/14/15/14/13/14/13/12/1x x x(1)求方程的解(矩阵除法和求逆法)(2)将方程右边向量元素3b 改为0.53,再求解,并比较3b 的变化和解的相对变化。
高等数学:MATLAB实验

MATLAB实验
2.fplot绘图命令 fplot绘图命令专门用于绘制一元函数曲线,格式为:
fplot('fun',[a,b]) 用于绘制区间[a,b]上的函数y=fun的图像.
MATLAB实验 【实验内容】
MATLAB实验
由此可知,函数在点x=3处的二阶导数为6,所以f(3)=3为 极小值;函数在点x= 1处的二阶导数为-6,所以f(1)=7为极大值.
MATLAB实验
例12-10 假设某种商品的需求量q 是单价p(单位:元)的函 数q=12000-80p,商 品的总成本C 是需求量q 的函数 C=25000+50q.每单位商品需要纳税2元,试求使销售 利润达 到最大的商品单价和最大利润额.
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验 实验九 用 MATLAB求解二重积分
【实验目的】 熟悉LAB中的int命令,会用int命令求解简单的二重积分.
MATLAB实验
【实验M步A骤T】 由于二重积分可以化成二次积分来进行计算,因此只要
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
实验七 应用 MATLAB绘制三维曲线图
【实验目的】 (1)熟悉 MATLAB软件的绘图功能; (2)熟悉常见空间曲线的作图方法.
【实验要求】 (1)掌握 MATLAB中绘图命令plot3和 mesh的使用; (2)会用plot3和 mesh函数绘制出某区间的三维曲线,线型
Matlab实验

MATLAB实验报告学校:湖北文理学院学院:物理与电子工程学院专业:电子信息工程学号: 2013128182 姓名:张冲指导教师:宋立新实验一 MATLAB环境的熟悉与基本运算一、实验目的:1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验内容1、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye(其它不会用的指令,依照此方法类推)2、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
3、初步程序的编写练习,新建M-file,保存(自己设定文件名,例如exerc1、exerc2、exerc3……),学习使用MATLAB的基本运算符。
三、练习1)help rand,然后随机生成一个2×6的数组,观察command window、command history和workspace等窗口的变化结果。
2)学习使用clc、clear,了解其功能和作用。
3)用逻辑表达式求下列分段函数的值4)求[100,999]之间能被21整除的数的个数。
(提示:rem,sum的用法)四、实验结果1)2)clc:清除命令窗口所有内容,数值不变;clear:初始化变量的值。
3)4)实验二 MATLAB数值运算一、实验目的1、掌握矩阵的基本运算2、掌握矩阵的数组运算二、实验内容1)输入C=1:2:20,则C(i)表示什么?其中i=1,2,3, (10)2)输入A=[7 1 5;2 5 6;3 1 5],B=[1 1 1; 2 2 2; 3 3 3],在命令窗口中执行下列表达式,掌握其含义:A(2, 3) A(:,2) A(3,:) A(:,1:2:3) A(:,3).*B(:,2)A(:,3)*B(2,:) A*B A.*B A^2 A.^2 B/A B./A3)二维数组的创建和寻访,创建一个二维数组(4×8)A,查询数组A第2行、第3列的元素,查询数组A第2行的所有元素,查询数组A第6列的所有元素。
二MATLAB基本操作

10
§2.4 逻辑和关系运算
二. 关系操作符 MATLAB提供了六种关系操作符,这些
操作符与逻辑运算配合使用,可使程序 设计更加灵活。 例如:if and(a==1,b>5)
……
end 则当a=1且b>5时执行指定的语句。
例如:a=[1 2 3; 4 5 6; 7 8 9] 又如:b=[1:3; 4:6; 7:9]
c=[1: 6 : 0.5] 注意:关于:的使用相当灵活,大家可随
着学习的不断深入对:的使用逐步加深 灵活。
§2.2 矩阵基础
(2)从外部数据文件读取 load score.dat
(3) 利用matlab内部函数产生矩阵 例如:b=eye(3); 单位阵 c= ones(2,5); 全一阵 d=zeros(3,2); 全零阵 e=rand(2,3); 随机阵
这样很容易产生元素等值的矩阵: c3=8×ones(8,9);
§2.3 矩阵产生和操作
MATLAB提供的rand和randn可分别产 生均匀分布和正态分布的随机数。 例如要产生[0,1]之间均匀分布的随机向 量R(100×1),可输入R=rand(100,1) 如果要产生[-a,a](a为正数)之间均匀分 布的随机数则应输入
§2.5操作符和特殊字符
7. xor 功能:异或操作。 格式:C=xor(A,B) C=xor(A,B)完成阵列A和B对应元素的 异或操作。 如: A=[0 0 pi eps]
B=[0 -2 4 1.2] C=xor(A,B) C=0 1 0 1
§2.7 基本数学函数
一.三角函数
Matlab基本运算

2.1 变量和数据操作2.1.1 变量与赋值1.变量命名在MA TLA B 6.5中,变量名是以字母开头,后接字母、数字或下划线的字符序列,最多63个字符。
在MA TLA B中,变量名区分字母的大小写。
2.赋值语句(1) 变量=表达式(2) 表达式其中表达式是用运算符将有关运算量连接起来的式子,其结果是一个矩阵。
2.1.2 预定义变量在MA TLA B工作空间中,还驻留几个由系统本身定义的变量。
例如,用pi表示圆周率π的近似值,用i,j表示虚数单位。
预定义变量有特定的含义,在使用时,应尽量避免对这些变量重新赋值。
2.1.3 内存变量的管理1.内存变量的删除与修改MATLAB工作空间窗口专门用于内存变量的管理。
在工作空间窗口中可以显示所有内存变量的属性。
当选中某些变量后,再单击Delete 按钮,就能删除这些变量。
当选中某些变量后,再单击Ope n按钮,将进入变量编辑器。
通过变量编辑器可以直接观察变量中的具体元素,也可修改变量中的具体元素。
clear命令用于删除M A TLA B工作空间中的变量。
w ho和wh os这两个命令用于显示在MAT LAB工作空间中已经驻留的变量名清单。
who 命令只显示出驻留变量的名称,whos在给出变量名的同时,还给出它们的大小、所占字节数及数据类型等信息。
2.内存变量文件利用MA T文件可以把当前MA TL AB工作空间中的一些有用变量长久地保留下来,扩展名是.mat。
MA T文件的生成和装入由save和load 命令来完成。
常用格式为:save 文件名[变量名表] [-append][-ascii]load 文件名[变量名表] [-ascii]其中,文件名可以带路径,但不需带扩展名.mat,命令隐含一定对.mat文件进行操作。
MATLAB实验

MATLAB实验一:MATLAB语言基本概念实验实验目的:1. 熟悉MATLAB语言及使用环境;2.掌握MATLAB的常用命令;3.掌握MATLAB的工作空间的使用;4.掌握MATLAB的获得帮助的途径。
5.掌握科学计算的有关方法,熟悉MATLAB语言及其在科学计算中的运用;6.掌握MATLAB的命令运行方式和M文件运行方式;7.掌握矩阵在MATLAB中的运用。
实验方案分析及设计:本次实验主要目的是了解MATLAB的使用环境,以及常用的一些命令的使用;了解矩阵在MATLAB实验中的具体运用,以及相关的一些符号命令的使用。
实验器材:电脑一台,MATLAB软件实验步骤:打开MATLAB程序,将实验内容中的题目依次输入MATLAB中,运行得到并记录结果,最后再对所得结果进行验证。
实验内容及要求:1.熟悉MATLAB的菜单和快捷键的功能2.熟悉MATLAB的命令窗口的使用3.熟悉常用指令的使用format clc clear help lookfor who whos 4.熟悉命令历史窗口的使用5. 熟悉MATLAB工作空间的功能将工作空间中的变量保存为M文件,并提取该文件中的变量6.熟悉MATLAB获取帮助的途径将所有plot开头的函数列出来,并详细给出plotfis函数的使用方法1. 输入 A=[7 1 5;2 5 6;3 1 5],B=[1 1 1; 2 2 2;3 3 3],在命令窗口中执行下列表达式,掌握其含义:A(2, 3) A(:,2) A(3,:) A(:,1:2:3)A(:,3).*B(:,2) A(:,3)*B(2,:) A*BA.*BA^2 A.^2 B/A B./AA=[7 1 5;2 5 6;3 1 5]7 1 52 5 63 1 5>> B=[1 1 1; 2 2 2;3 3 3]1 1 12 2 23 3 3>> A(2, 3)6>> A(:,2)151>> A(3,:)3 1 5>> A(:,1:2:3)7 52 63 5>> A(:,3).*B(:,2)51215>> A(:,3)*B(2,:)10 10 1012 12 1210 10 10>> A*B24 24 2430 30 3020 20 20>> A.*B7 1 54 10 129 3 15>> A^266 17 6642 33 7038 13 46>> A.^249 1 254 25 369 1 25>> B/A0.1842 0.2105 -0.23680.3684 0.4211 -0.47370.5526 0.6316 -0.7105>> B./A0.1429 1.0000 0.20001.0000 0.4000 0.33331.0000 3.0000 0.60002.输入 C=1:2:20,则 C (i )表示什么?其中 i=1,2,3, (10)1到19差为2,i 代表公差3. 试用 help 命令理解下面程序各指令的含义:cleart =0:0.001:2*pi;subplot(2,2,1);polar(t, 1+cos(t))subplot(2,2,2);plot(cos(t).^3,sin(t).^3)subplot(2,2,3);polar(t,abs(sin(t).*cos(t)))subplot(2,2,4);polar(t,(cos(2*t)).^0.5)4计算矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242之和。
电气专业MATLAB仿真实验

电气专业MATLAB仿真实验实验一、二 MATLAB 基础实验一.实验目的1. 熟悉MATLAB 的运行环境极其基本操作。
2. 掌握MATLAB 的基本运算。
二.实验内容1.了解MATLAB 语言环境。
(1) MATLAB 的变量精度。
键入: a=pi ;b=exp(1);使用命令format 改变显示变量精度,观察变量a 、b 的显示值。
(2) 变量查询。
变量查询命令有who 、whos ,用于查询变量并作记录。
(3) 联机帮助。
使用help 命令,查找sqrt()函数和abs()函数的使用方法。
2. 掌握矩阵和数组的基本运算。
(1)在MATLAB 命令窗口中生成矩阵A ,⎥⎦⎤⎢⎣⎡=194375A 。
①将矩阵A 的第2行第3列元素的值修改为8;②将矩阵A 的第1行的前2个元素的值修改为1、2。
程序:A=[5 7 3;4 9 1]①A(2,3)=8②A([1],[1,2])=[1 2](2)计算矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242之和。
程序:B=[5 3 5;3 7 4;7 9 8]+[2 4 2;6 7 9;8 3 6](3)求⎥⎦⎤⎢⎣⎡+-+-+-+-++=i i i i i i i i i i x 44934967235741725384的共轭转置。
程序:x=[4+8i,3+5i,2-7i,1+4i,7-5i;3+2i,7-6i,9+4i,3-9i,4+4i]y=x ’(4)计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
程序:a=[6 9 3;2 7 5]b=[2 4 1;4 6 8]; a.*b实验三、四 矩阵和数组的基本运算一.实验目的1. 掌握MATLAB 的基本运算。
2. 掌握MATLAB 的关系运算和逻辑运算。
二.实验内容(1)对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
matlab实验报告

matlab实验报告实验1 熟悉matlab 的开发环境及矩阵操作⼀、实验的教学⽬标通过本次实验使学⽣熟悉MATLAB7.0的开发环境,熟悉MA TLAB ⼯作界⾯的多个常⽤窗⼝包括命令窗⼝、历史命令窗⼝、当前⼯作⽬录窗⼝、⼯作空间浏览器窗⼝等。
掌握建⽴表达式书写规则及常⽤函数的使⽤,建⽴矩阵的⼏种⽅法。
⼆、实验环境计算机、MATLAB7.0集成环境三、实验内容1、熟悉命令窗⼝的使⽤,⼯作空间窗⼝的使⽤,⼯作⽬录、搜索路径的设置。
命令历史记录窗⼝的使⽤,帮助系统的使⽤。
2、在当前命令窗⼝中输⼊以下命令:x=0:2:10 y=sqrt(x),并理解其含义。
3、求下列表达式的值(1)w=)1034245.01(26-?+?(2)x=ac b e abc cb a ++-+++)tan(22ππ,其中a=3.5,b=5,c=-9.8 四、实验总结1、熟悉了命令窗⼝的使⽤,⼯作空间窗⼝的使⽤。
2、了解了⼯作⽬录、搜索路径的设置⽅法。
---5317383399351542实验2 MATLAB 基本运算⼀、实验的教学⽬标通过本次实验使学⽣掌握向量和矩阵的创建⽅法;掌握矩阵和数组的算术运算、逻辑运算和关系运算;掌握字符数组的创建和运算;了解创建元胞数组和结构体的⽅法。
⼆、实验环境计算机、MATLAB7.0集成环境三、实验内容1、要求在闭区间]2,0[π上产⽣具有10个等距采样点的⼀维数组。
试⽤两种不同的指令实现。
(提⽰:冒号⽣成法,定点⽣成法)2、由指令rng('default'),A=rand(3,5)⽣成⼆维数组A ,试求该数组中所有⼤于0.5的元素的位置,分别求出它们的“全下标”和“单下标”。
(提⽰:find 和sub2ind )3、创建3阶魔⽅矩阵a 和3阶对⾓阵b ,c=a(1:3,1:3)(1)计算矩阵a,b 和c 的⾏列式、逆矩阵并进⾏最⼤值的统计。
(2)⽐较矩阵和数组的算术运算:b 和c 的*、/、^和.*、./、.^。
实验2Matlab的基本运算281313

实验1 Matlab 的基本运算(2)实验目的:1、 掌握建立矩阵的方法;2、 掌握Matlab 各种表达式的书写规则以及常用函数的使用。
实验内容:1. 设有矩阵A 和BA ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦12345678910111213141516171819202122232425 B ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦30161769023497041311(1)求它们的乘积C (2)将矩阵C 的右下角⨯32子矩阵赋给D(3)查看Matlab 工作空间的使用情况2. 已知:矩阵...A -⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥-⎣⎦2310077804145655325032695454314 完成下列操作:(1)取出A 的前3行构成矩阵B ,前两列构成矩阵C ,左下角⨯22子矩阵构成矩阵D ,B 与C 的乘积构成矩阵E 。
(2)分别求E<D ,E&D ,E|D ,~E|~D 和find(A>=10&A<25)3. 完成下列操作:(1)求[100,999]之间能被21整除的数的个数。
提示:先利用冒号表达式,再利用find 和length 函数。
(2)建立一个字符串向量,删除其中的大写字母。
提示:利用find 函数和空矩阵。
3. 建立元胞矩阵B 并回答有关问题。
B{1,1}=1;B{1,2}=’Brenden ’;B{2,1}=reshape(1:9,3,3);B{2,2}={12,34,2;54,21,3;4,23,67};(1)size(B)的值是多少?(2)B(2)和B(4)的值分别是多少?(3)B(3)=[]和B{3}=[]执行后,B 的值分别是多少?4. 设A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦310121342,B ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦102111211,求满足关系A X B -=32的X 。
5. 用结构数组来存储3名学生的基本情况数据,每名学生的数据包括学号、姓名、班级和某学期三门必修课的编号和名称。
实验二MATLAB的矩阵操作_参考答案

1
5
>> A(k)
ans =
23
10
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
>> B=A([1,2,3],:)
B =
23.0000 10.0000 -0.7780 0
41.0000 -45.0000 65.0000 5.0000
32.0000 5.0000 0 32.0000
y =
-128.4271
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
A=[-1,5,-4;0,7,8;3,61,7]
B=[8,3,-1;2,5,3;-3,2,0]
>> A+6*B
ans =
47 23 -10
12 37 26
-15 73 7
&
ans =
-1.2768 -0.4743 0.2411
2.1229 1.3173 -0.2924
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14]
>> k=find(A>=10&A<=25)
(2)
(3)
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
(2)A*B、A.*B和B*A
(3)A/B及B/A
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
matlab实验报告总结精选

matlab实验报告总结电气工程学院自动化102班 2012年12月21日实验一 MATLAB环境的熟悉与基本运算一、实验目的1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识1.熟悉MATLAB环境MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。
2.掌握MATLAB常用命令变量与运算符变量命名规则如下:变量名可以由英语字母、数字和下划线组成变量名应以英文字母开头长度不大于31个区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
MATLAB运算符,通过下面几个表来说明MATLAB的各种常用运算符表2 MATLAB算术运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式的基本运算表7 两种运算指令形式和实质内涵的异同表的常用函数表8 标准数组生成函数表9 数组操作函数三、实验内容1、新建一个文件夹2、启动,将该文件夹添加到MATLAB路径管理器中。
3、保存,关闭对话框4、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye5、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
6、初步程序的编写练习,新建M-file,保存,学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
注意:每一次M-file的修改后,都要存盘。
练习A:help rand,然后随机生成一个2×6的数组,观察command window、command history和workspace等窗口的变化结果。
学习使用clc、clear,了解其功能和作用。
答:clc是清除命令窗体内容 clear是清除工作区间输入C=1:2:20,则C表示什么?其中i=1,2,3,?,10。
MATLAB运算基础(第2章)答案

实验01讲评、参考答案讲评未交实验报告的同学名单数学:6人(11、12级)信科:12-04, 12-22, 13-47批改情况:问题1:不仔细,式子中出错。
问题2:提交的过程不完整。
问题3:使用语句尾分号(;)不当,提交的过程中不该显示的结果显示。
问题4:截屏窗口没有调整大小。
附参考答案:《MATLAB软件》课内实验王平实验01 MATLAB运算基础(第2章MATLAB数据及其运算)一、实验目的1. 熟悉启动和退出MATLAB 的方法。
2. 熟悉MATLAB 命令窗口的组成。
3. 掌握建立矩阵的方法。
4. 掌握MATLAB 各种表达式的书写规则以及常用函数的使用。
二、实验内容1. 数学表达式计算先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
1.1 计算三角函数122sin 851z e=+(注意:度要转换成弧度,e 2如何给出) 示例:点击Command Window 窗口右上角的,将命令窗口提出来成悬浮窗口,适当调整窗口大小。
命令窗口中的执行过程:1.2 计算自然对数221ln(1)2z x x =++,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦(提示:clc 命令擦除命令窗口,clear 则清除工作空间中的所有变量,使用时注意区别,慎用clear 命令。
应用点乘方) 命令窗口中的执行过程:1.3 求数学表达式的一组值0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--提示:利用冒号表达式生成a 向量,求各点的函数值时用点乘运算。
命令窗口中的执行过程:1.4 求分段函数的一组值2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.5提示:用逻辑表达式求分段函数值。
命令窗口中的执行过程:1.5 对工作空间的操作接着显示MATLAB当前工作空间的使用情况并保存全部变量提示:用到命令who, whos, save, clear, load,请参考教材相关内容。
MATLAB实验报告

实验二MATLAB语言基础一、实验目的基本掌握MA TLAB向量矩阵数组的生成及基本运算(区分数组运算和矩阵预算)、常用的数学函数。
了解字符串的操作。
二、实验内容(1)向量的生成和运算。
(2)矩阵的创建、引用和运算。
(3)多维数组的创建和运算。
(4)字符创的操作。
三、实验步骤1.向量的生成和运算1)向量的生成<1>、直接输入法<2> 冒号表达式法<3> 函数法:Linspace()是线性等分函数,logspace()是对数等分函数。
2)向量的运算1>维数相同的行、列向量之间可以相加减,标量可以与向量直接相乘除。
2>向量的点积与叉积运算E1和E2虽然表达式相同,但E1是标量,E2是矩阵。
2.矩阵的创建、引用和运算1)矩阵的创建和引用矩阵是由m*n元素构成的矩形结构,行向量和列向量是矩阵的特殊形式。
1>直接输入法:2>抽取法:包括单下标抽取和全下表抽取两种方式,且两种方式抽取的元素都必须以小括号括起来。
3>函数法:利用ones(m;n)创建全1矩阵,zeros()创建全0矩阵,eyes()创建单位矩阵等等。
4>拼接法:纵向拼接横向拼接5>利用拼接函数cat()repmat()和变形函数reshape()>> A1=[1 2 3;9 8 7 ;4 5 6];A2=A1.';>> cat(1,A1,A2) 沿行向拼接ans =1 2 39 8 74 5 61 9 42 8 53 7 6>> cat(2,A1,A2) 沿列向拼接ans =1 2 3 1 9 49 8 7 2 8 54 5 6 3 7 6>> repmat(A1,2,2)ans =1 2 3 1 2 39 8 7 9 8 74 5 6 4 5 61 2 3 1 2 39 8 7 9 8 74 5 6 4 5 6> A=linspace(2,18,9)A =2 4 6 8 10 12 14 16 18 >> reshape(A,3,3)ans =2 8 144 10 166 12 182)矩阵的运算练习(1)用矩阵除法求下列方程组的解x=[x1;x2;x3]>> A=[6 3 4;-2 5 7;8 -1 -3];B=[3;-4;-7];X=A\BX =1.0200-14.00009.7200(2)求矩阵的秩A=[6 3 4;-2 5 7;8 -1 -3];>> rank(A)ans =3[X,lamda]=eig(A)X =0.8013 -0.1094 -0.16060.3638 -0.6564 0.86690.4749 0.7464 -0.4719lamda =9.7326 0 00 -3.2928 00 0 1.5602(3)矩阵的开方>> B=sqrtm(A)B =2.2447 + 0.2706i 0.6974 - 0.1400i 0.9422 - 0.3494i -0.5815 + 1.6244i 2.1005 - 0.8405i 1.7620 - 2.0970i1.9719 - 1.8471i -0.3017 + 0.9557i 0.0236 +2.3845i (4)矩阵的指数与对数:> C=expm(A)C =1.0e+004 *1.0653 0.5415 0.63230.4830 0.2465 0.28760.6316 0.3206 0.3745>> logm(C)ans =6.0000 3.0000 4.0000-2.0000 5.0000 7.00008.0000 -1.0000 -3.0000(6)矩阵的转置D=A'D =6 -2 83 5 -14 7 -3(7)矩阵的提取与翻转:通过各种特定函数如triu(A)、tril(A),diag(A)、flipud (A)、fliplr(A)等等。
matlab实验报告

实验一:MATLAB基本操作一、实验目的1、学习掌握MA TLAB语言的基本操作方法2、掌握命令窗口的使用3、熟悉MA TLAB的数据表示、基本运算和程序控制语句4、熟悉MA TLAB程序设计的基本方法二、实验内容和要求2.b.帮助命令的使用,查找SQRT函数的使用方法按Start-help-search,输入sqrtc.矩阵运算(1)已知A=[1 2;3 4];B=[5 5;7 8];求A^2*B输入A=[1 2;3 4];B=[5 5;7 8];A^2*B结果为:ans =105 115229 251(2)矩阵除法已知A=[1 2 3 ;4 5 6;7 8 9];B=[1 0 0;0 2 0;0 0 3];求A/B,A\BA/B=1.0000 1.0000 1.00004.0000 2.5000 2.00007.0000 4.0000 3.0000A\B=1.0e+016 *0.3152 -1.2609 0.9457-0.6304 2.5218 -1.89130.3152 -1.2609 0.9457(3)矩阵的转置及共轭转置已知A=[15+i,2-i,1;6*i,4,9-i];求A.',A'A=15.0000 + 1.0000i 2.0000 - 1.0000i 1.00000 + 6.0000i 4.0000 9.0000 - 1.0000iA.'=15.0000 + 1.0000i 0 + 6.0000i2.0000 - 1.0000i 4.00001.0000 9.0000 - 1.0000iA'=15.0000 - 1.0000i 0 - 6.0000i2.0000 + 1.0000i 4.00001.0000 9.0000 + 1.0000i(4)使用冒号选出指定元素已知A=[1 2 3;4 5 6;7 8 9];求A中第三列前两个元素;A中所有第二行的元素A =1 2 34 5 67 8 9求A中第三列前两个元素:A([1,2],3)ans =36求A中所有第二行的元素:A(2,1:1:end)ans =4 5 6(5)方括号[]用magic函数生成一个4阶魔方矩阵,删除该矩阵的第四列magic(4)ans =16 2 3 135 11 10 89 7 6 124 14 15 1a=ans;a(:,[1,2,3])ans =16 2 35 11 109 7 64 14 153..多项式(1)求多项式p(X)=x^3-2x-4的根(2)已知A=[1.2 3 5 0.9;5 1.7 5 6;3 9 0 1;1 2 3 4]求矩阵A的特征多项式;求矩阵多项式中未知数为20时的值;把矩阵A作为未知数代入到多项式中;(1)a=[1,0,-2,-4]x=roots(a)x =2.0000-1.0000 + 1.0000i-1.0000 - 1.0000i(2)求特征多项式系数:A=[1.2 3 5 0.9;5 1.7 5 6;3 9 0 1;1 2 3 4]p=poly(A)p =1.0000 -6.9000 -77.2600 -86.1300 604.5500求矩阵多项式中未知数为20时的值:c=polyval(p,20)c =7.2778e+004把矩阵A作为未知数代入到多项式中:c=polyval(p,A)c =1.0e+003 *0.3801 -0.4545 -1.9951 0.4601-1.9951 0.2093 -1.9951 -2.8880-0.4545 -4.8978 0.6046 0.43530.4353 0.0840 -0.4545 -1.16174、基本程序设计(1)编写命令文件:计算1+2+3+……+n<2000;n=0;s=0;while s<2000n=n+1;s=s+n;endn=n-1n =62(2)编写函数文件:分别用for和while循环结构编写程序,求2的0到n次幂的和。
信号与系统信号基本运算的MATLAB实现实验报告

信号与系统实验报告实验一、信号基本运算的MATLAB 实现一、实验目的学习如何利用Matlab 实现信号的基本运算,掌握信号的基本运算的原理,加深对书本知识的理解。
二、实验材料PC 机一台三、实验内容1、(1)编写如图Exercise1.1所示波形的MATLAB 函数。
(2)试画出f(t),f(0.5t),f(1-2t)的波形。
解:程序如下: 实验结果: function yt = f2(t)yt=tripuls(t,4,0.5); t=-3:0.01:5; subplot(311) plot(t,tx(t)) title('f£¨t£©') subplot(312) plot(t,tx(0.5*t)) title('f(0.5t)') subplot(313) plot(t,tx(-2*t)) title('f(-2t)') 2、画出如图exercise1.2所示序列f[2k]、f[-k]和f[k+2],f[k-2]的波形。
并求f[k]的和。
解:程序如下:function f=ls(k)f=3.*(k==-2)+1.*(k==-1)+(-2).*(k==0)+(-1).*(k==1)+2.*(k==2)+(-3).*(k==3);Exercise 1.1-3f[k] kExercise1.2k=-5:0.01:10;subplot(321)stem(k,ls(k)) 实验结果:title('f[k]')subplot(322)stem(k,ls(2*k))title('f[2k]')subplot(323)stem(k,ls(-1*k))title('f[-k]')subplot(324)stem(k,ls(k+2))title('f[k+2]')subplot(325)stem(k,ls(k-2))title('f[k-2]')subplot(326)plot(k,sum(ls(-2:3)))title('Sum f[k]')3、解:程序如下:function y=tx(t)y=0.*(t>=2|t<-1)+(2-t).*(t>=1&t<2)+1.*(t>=-1&t<1); t=-5:0.01:5; 实验结果:ft1=tripuls(t-3,2,0.5);subplot(311)plot(t,ft1)title('f(t)')ft1=tripuls(-t-3,2,0.5);subplot(312)plot(t,ft1)title('f(-t)')ft1=tripuls(-2*t-2,2,0.5);subplot(313)plot(t,ft1)title('f(1-2t)')。
实验2_连续时间信号的Matlab表示与计算
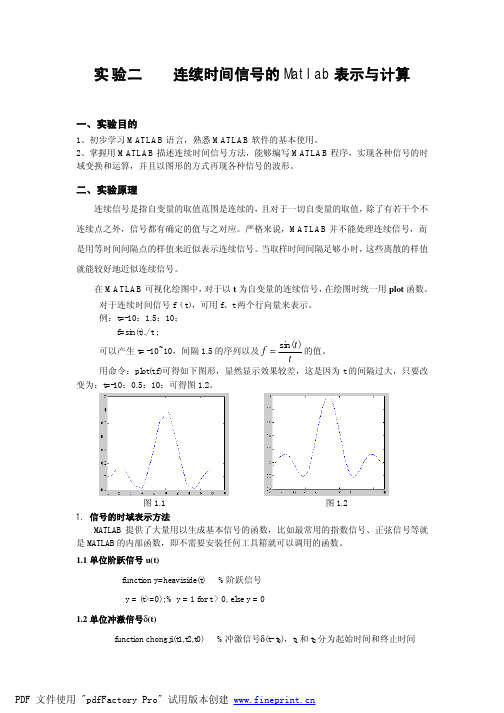
y=A*exp(a*t) 例如图 1-3 所示指数衰减信号的 MATLAB 源程序如下(取 A=1,a=-0.4): %program7_1 Decaying expponential signal A=1;a=-0.4; t=0:0.01:10; ft=A*exp(a*t); plot(t,ft);grid on; 1.4正弦信号
例如图 1-10 所示周期性矩形脉冲信号和周期性三角波脉冲信号的 MATLAB 源程序如 下:
%program7_8 Periodic pulse generator T=0:1/1E3:1;% 1kHz sample freq for 1 sec D=0:1/3:1;% 3Hz repetition freq Y=pulstran(T,D,'rectpuls',0.1); figure(1);plot(T,Y);grid on;axis([0,1,-0.1,1.1]); T=0:1/1E3:1; % 1kHz sample freq for 1sec D=0:1/3:1;% 3Hz repetition freq Y=pulstran(T,D,'tripuls',0.1,-1); figure(2);plot(T,Y);grid on;axis([0,1,-0.1,1.]);
到-1 线性递减的;在其他周期内依次类推。例如图 1-9 所示的周期性三角波信号的 MATLAB 源程序如下:
%program1-9 Periodic triangular pulse signal
t=-5*pi:pi/10:5*pi;
x=sawtooth(t,0.5);
实验2 MATLAB数值及符号运算

MATLAB 实验报告学生姓名:王朝 学号:1314080213 专业班级:电子信息科学与技术二班实验类型:□ 验证 □√ 综合 □ 设计 □ 创新 实验日期: 实验成绩: 一.实验名称实验2 MATLAB 数值及符号运算二 实验目的:1、了解伴随矩阵、稀疏矩阵、魔方矩阵、对角矩阵、范德蒙等矩阵的创建,掌握矩阵的基本运算2、掌握矩阵的数组运算3、掌握多项式的基本运算4、会求解代数方程5、掌握创建符号表达式和矩阵的方法6、掌握符号表达式三、实验内容:1、生成一个3行3列的随机矩阵,并逆时针旋转90°,左右翻转,上下翻转。
2、已知a=[1 2 3],b=[4 5 6], 求a.\b 和a./ b3、数组和矩阵有何不同?4、已知a=[1 2 3;4 5 6;7 8 0],求其特征多项式并求其根。
5、已知多项式a(x)=x 2+2x+3,b(x)=4x 2+5x+6,求a ,b 的积并微分。
6、求解方程1)⎩⎨⎧=+=+ 133x 2822121x x x 2)⎪⎩⎪⎨⎧=+=+=+343 23x 212212121x x x x x3)⎩⎨⎧=++=++ 243x 2132321321x x x x x 7、用两种方法创建符号矩阵,A =[ a, 2*b][3*a, 0]并把其中的a 改为c 。
8、计算二重不定积分 9、对符号方程f = ax2+bx+c 求解1)对x 求解2)对a 求解。
10、求解微分方程0)0(,1)0(,02222===++dx dy y y dx dy dxy d 。
四.实验环境PC 微机MATLAB 系统五、实验内容和步骤1、生成一个3行3列的随机矩阵,并逆时针旋转90°,左右翻转,上下翻转。
>> a=magic(3)a =8 1 63 5 74 9 2>> b=rot90(a) 逆时针旋转90°b =6 7 21 5 98 3 4>> c=fliplr(b) 左右翻转c =dxdyxe xy ⎰⎰-2 7 69 5 14 3 8>> d=flipud(c) 上下翻转d =4 3 89 5 12 7 62、已知a=[1 2 3],b=[4 5 6],求a.\b和a./ ba.\bans =4.0000 2.5000 2.0000a./ bans =0.2500 0.4000 0.50003、数组和矩阵有何不同?数组中的元素可以是字符等,矩阵中的只能是数,这是二者最直观的区别。
matlab入门 实验报告

matlab入门实验报告Matlab入门实验报告一、引言Matlab是一种功能强大的数学软件,广泛应用于科学计算、数据分析和工程设计等领域。
本实验报告将介绍Matlab的基本使用方法和一些常见的数学计算实例。
二、Matlab的基本操作1. Matlab的安装和启动Matlab可以从官方网站下载并安装在计算机上。
安装完成后,双击桌面上的Matlab图标即可启动软件。
2. Matlab的界面和基本操作Matlab的界面由主窗口、命令窗口和编辑器等组成。
在命令窗口中可以输入和执行Matlab命令,编辑器可以编写和保存Matlab脚本。
3. Matlab的数据类型和变量Matlab支持多种数据类型,包括数值型、字符型、逻辑型等。
可以使用赋值语句将值存储在变量中,例如:x = 5。
4. Matlab的基本数学运算Matlab可以进行基本的数学运算,如加减乘除、幂运算等。
例如,输入命令:y = 2*x + 3,即可计算出变量y的值。
三、Matlab的数学函数1. Matlab的数学函数库Matlab内置了大量的数学函数,可以进行各种复杂的数学运算和数据处理。
例如,sin函数用于计算正弦值,sqrt函数用于计算平方根。
2. Matlab的矩阵运算Matlab是一个强大的矩阵计算工具,可以进行矩阵的加减乘除、转置、求逆等运算。
例如,输入命令:A = [1 2; 3 4],即可创建一个2x2的矩阵。
3. Matlab的符号计算Matlab还支持符号计算,可以进行代数运算和求解方程等。
例如,输入命令:syms x; solve(x^2 - 2*x - 3 = 0, x),即可求解方程的根。
四、Matlab的数据可视化1. Matlab的绘图功能Matlab提供了丰富的绘图函数,可以绘制各种类型的图形,如曲线图、散点图、柱状图等。
例如,输入命令:plot(x, y),即可绘制x和y的曲线图。
2. Matlab的图像处理Matlab还可以进行图像处理,如读取、显示和编辑图像。
序列的基本运算时域变换离散信号的卷积和实验二

序列的基本运算时域变换离散信号的卷积和实验一、实验目的1、熟悉用MATLAB描绘二维图像的方法。
2、掌握用MATLAB对序列进行基本的运算和时域变换的方法。
二、实验器材MATLAB软件。
三、实验原理1、加法:x1(n)+x2(n)序列的加法运算为对应位置处量值的相加,在MATLAB中可用运算符“+”实现,但要求参与运算的序列的长度必须相等。
如果长度不等或者长度相等但采样位置不同,则不能直接应用该运算符,此时需要先给定参数使序列具有相同的位置向量和长度。
2、乘法:x1(n)·x2(n)序列的乘法运算为对应位置处量值的相乘,在MATLAB中由数组运算符“.*”实现,也受到“+”运算符同样的限制。
3、反折:x(n)→x(-n)序列的反折指序列的每个量值都对n=0做一个对称操作,从而得到一个新序列。
在MATLAB中可由fliplr(x)函数实现,此时序列位置的反折则由-fliplr(n)实现。
4、平移:x(n)→x(n-m)平移操作是将序列的每个量值都移动m个位置,在得到的新序列中,量值和原序列相同,只是位置向量n发生变化,当m>0时,表示序列向右平移,此时新序列的位置向量为n+m;当m<0时,表示序列向左平移,此时新序列的位置向量为n-m。
四、实验内容对x(n)={2,1,2,1,1}和x(n)={1,1,1,1,1}两个序列进行加法、乘法、卷积的运算。
1. 序列1()[2,1,2,1,1],22x n n =-≤≤ 与序列2()[1,1,1,1,1],04x n n =≤≤ 相加,并绘制出图形。
程序代码:主程序:clearclcx1=[2 1 2 1 1];n1=[-2:2];x2=[1 1 1 1 1];n2=[0:4];[y,n] = sigadd(x1,n1,x2,n2);stem(n,y);axis([-3,5,-1,4]);xlabel('时间序列n');ylabel('y(n)');title('y=x1(n)+x2(n)');调用程序:function [y,n] = sigadd(x1,n1,x2,n2)n = min(min(n1),min(n2)):max(max(n1),max(n2));y1 = zeros(1,length(n)); y2 = y1;y1(find((n>=min(n1))&(n<=max(n1))==1))=x1;y2(find((n>=min(n2))&(n<=max(n2))==1))=x2;y = y1+y2;仿真结果:图2.1 序列12x x + 仿真图2. 序列1()[2,1,2,1,1],22x n n =-≤≤ 与序列2()[1,1,1,1,1],04x n n =≤≤ 相乘法,并绘制出图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验1 Matlab 的基本运算(2)实验目的:1、 掌握建立矩阵的方法;2、 掌握Matlab 各种表达式的书写规则以及常用函数的使用。
实验内容:1. 设有矩阵A 和BA ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦12345678910111213141516171819202122232425 B ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦30161769023497041311(1)求它们的乘积C>> A=1:25;A=reshape(A,5,5);A=A';B=[3,0,16;17,-6,9;0,23,-4;9,7,0;4,13,11];C=A*BC =93 150 77258 335 237423 520 397588 705 557753 890 717(2)将矩阵C 的右下角⨯32子矩阵赋给D>> D=C(3:5,2:3)D =520 397705 557890 717(3)查看Matlab 工作空间的使用情况2. 已知:矩阵...A -⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥-⎣⎦2310077804145655325032695454314 完成下列操作:(1)取出A 的前3行构成矩阵B ,前两列构成矩阵C ,左下角3*2子矩阵构成矩阵D ,B 与C 的乘积构成矩阵E 。
A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14];B=A(1:3,:)C=A(1:4,1:2)D=A(2:4,1:2)E=B*CB =23.0000 10.0000 -0.7780 041.0000 -45.0000 65.0000 5.000032.0000 5.0000 0 32.0000C =23.0000 10.000041.0000 -45.000032.0000 5.00006.0000 -9.5400D =41.0000 -45.000032.0000 5.00006.0000 -9.5400E =1.0e+003 *0.9141 -0.22391.20802.71231.1330 -0.2103(2)分别求E<D,E&D,E|D,~E|~D和find(A>=10&A<25) >> E<Dans =0 10 00 1>> E&Dans =1 11 11 1>> E|Dans =1 11 11 1>> ~E|~Dans =0 00 00 0>> find(A>=10&A<25)ans =153. 完成下列操作:(1)求[100,999]之间能被21整除的数的个数。
q=100:999;w=rem(q,21);e=find(w==0);r=length(e)r =143提示:先利用冒号表达式,再利用find和length函数。
(2)建立一个字符串向量,删除其中的大写字母。
提示:利用find函数和空矩阵。
A=['kjkfEFTDFDhjkfdj'];e=find(A>'A'&A<'Z');A(e)=[]A =kjkfhjkfdj3. 建立元胞矩阵B并回答有关问题。
B{1,1}=1;B{1,2}=’Brenden’;B{2,1}=reshape(1:9,3,3);B{2,2}={12,34,2;54,21,3;4,23,67};(1)size(B)的值是多少?(2)B(2)和B(4)的值分别是多少?(3)B(3)=[]和B{3}=[]执行后,B的值分别是多少?>> clear B;B{1,1}=1;B{1,2}='Brenden';B{2,1}=reshape(1:9,3,3);B{2,2}={12,34,2;54,21,3;4,23,67};>> size(B)ans =2 2>> B(2)B(4)ans =[3x3 double]ans ={3x3 cell}>> B(3)=[]B =[1] [3x3 double] {3x3 cell}>> B{3}=[]B =[1] [3x3 double] []4. 设A⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦310121342,B⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦102111211,求满足关系A X B-=32的X。
A=[3,1,0;-1,2,1;3,4,2];B=[1,0,2;-1,1,1;2,1,1];X=(3.*A-B)./2X =4.0000 1.5000 -1.0000-1.0000 2.5000 1.00003.5000 5.5000 2.50005. 用结构数组来存储3名学生的基本情况数据,每名学生的数据包括学号、姓名、班级和某学期三门必修课的编号和名称。
> clear studentstudent=struct('no','20','name', '张听说', 'bj', 'j1','b1','001','m1','sx','b2','002','m2','yy','b3','003','m3','hx');>> student=struct('no','22','name', '张月', 'bj', 'j2','b1','001','m1','sx','b2','002','m2','yy','b3','003','m3','hx');>> student(2)=struct('no','20','name', '张听说', 'bj', 'j1','b1','001','m1','sx','b2','002','m2','yy','b3','003','m3','hx'); >> student(3)=struct('no','23','name', '里说', 'bj', 'j1','b1','001','m1','sx','b2','002','m2','yy','b3','003','m3','hx'); >> student(1), student(2),student(3)ans =no: '22'name: '张月'bj: 'j2'b1: '001'm1: 'sx'b2: '002'm2: 'yy'b3: '003'm3: 'hx'ans =no: '20'name: '张听说'bj: 'j1'b1: '001'm1: 'sx'b2: '002'm2: 'yy'b3: '003'm3: 'hx'ans =no: '23'name: '里说'bj: 'j1'b1: '001'm1: 'sx'b2: '002'm2: 'yy'b3: '003'6、求矩阵...A -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦2310077841456532954314的最大值、最小值、中值和平均值。
A=[23,10,-0.778;41,-45,65;32,-9.54,3.14];q=max(max(A))q=min(min(A))q =65q =-45> A=reshape(A,1,9); >> q=(median(A)) q =10>> q=mean(A)q =13.2024>>。
