圆中三角函数综合例题及练习
圆与相似三角形、三角函数专题(含答案)

圆与相像三角形、解直角三角形及二次函数的综合种类一:圆与相像三角形的综合1.如图, BC 是⊙ A 的直径,△ DBE的各个极点均在⊙ A 上, BF⊥ DE于点 F.求证: BD·BE= BC·BF.2.如图,在 Rt△ ABC中,∠ ACB= 90°,以 AC为直径的⊙ O 与 AB 边交于点 D,过点 D 作⊙O 的切线,交 BC 于点 E.(1)求证:点 E 是边 BC的中点;求证:2=BD·BA;(2)BC(3)当以点 O, D, E,C 为极点的四边形是正方形时,求证:△ABC是等腰直角三角形.解:(1) 连接 OD,∵ DE为切线,∴∠ EDC+∠ ODC=90° .∵∠ ACB=90°,∴∠ ECD+∠ OCD= 90° .又∵ OD= OC,∴∠ ODC=∠ OCD,∴∠ EDC=∠ ECD,∴ ED= EC.∵AC 为直径,∴∠ADC= 90°,∴∠ BDE+∠ EDC= 90°,∠ B+∠ECD= 90°,∴∠ B=∠ BDE,∴ ED= EB,∴ EB=EC,即点 E 为边 BC的中点(2)∵ AC为直径,∴∠ ADC=∠ ACB=90° .又∵∠ B=∠ B,∴△ ABC∽△ CBD,∴ABBC= BCBD,∴B C2= BDBA(3)当四边形 ODEC为正方形时,∠ OCD= 45° .∵AC 为直径,∴∠ ADC= 90°,∴∠ CAD=90°-∠ OCD= 90°- 45°= 45°,∴ Rt△ ABC 为等腰直角三角形种类二:圆与解直角三角形的综合3.如图,在△ ABC中,以 AC 为直径作⊙ O 交 BC 于点 D,交 AB 于点 G,且 D 是 BC 的中点,DE⊥ AB,垂足为点 E,交 AC 的延伸线于点 F.(1)求证:直线EF是⊙ O 的切线;(2)已知 CF= 5, cosA=25,求 BE 的长.解: (1)连接 OD.∵ CD=DB,CO= OA,∴ OD 是△ ABC的中位线,∴OD∥ AB, AB=2OD.∵ DE⊥ AB,∴ DE⊥OD,即 OD⊥ EF,∴直线 EF是⊙ O 的切线(2)∵ OD∥ AB,∴∠ COD=∠ A,∴ cos∠ COD= cosA= 25.在 Rt△ DOF中,∵∠ ODF= 90°,∴ cos∠ FOD= ODOF= 25.设⊙ O 的半径为 r,则 rr + 5= 25,解得 r= 103,∴ AB= 2OD= AC= 203.在 Rt△ AEF中,∵∠ AEF= 90°,∴ cosA= AEAF=AE5+ 203=25,∴ AE= 143,∴ BE=AB- AE=203- 143= 24.(2015 ·资阳 )如图,在△ ABC中, BC是以 AB 为直径的⊙ O 的切线,且⊙ O 与 AC 订交于点D, E 为 BC 的中点,连接 DE.(1)求证: DE 是⊙ O 的切线;(2)连接 AE,若∠ C= 45°,求 sin∠ CAE的值.解: (1)连接 OD,BD,∵ OD= OB,∴∠ ODB=∠ OBD.∵ AB 是直径,∴∠ ADB= 90°,∴∠ CDB= 90° .∵ E为 BC的中点,∴ DE=BE,∴∠ EDB=∠ EBD,∴∠ ODB+∠ EDB=∠ OBD+∠ EBD,即∠ EDO=∠ EBO.∵ BC 是以 AB 为直径的⊙ O 的切线,∴ AB⊥ BC,∴∠ EBO=90°,∴∠ ODE= 90°,∴ DE 是⊙ O 的切线(2)过点 E 作 EF⊥ CD于点 F,设 EF= x,∵∠ C=45°,∴△ CEF,△ABC 都是等腰直角三角形,∴CF= EF= x,∴ BE= CE= 2x,∴AB= BC= 22x.在 Rt△ ABE中, AE= AB2+ BE2= 10x,∴ sin∠ CAE= EFAE= 10105.如图,△ ABC 内接于⊙ O,直径 BD 交 AC 于点 E,过点 O 作 FG⊥ AB,交 AC 于点 F,交 AB 于点 H,交⊙ O 于点 G.(1)求证: OF·DE= OE·2OH;(2)若⊙ O 的半径为12,且 OE∶OF∶ OD= 2∶3∶ 6,求暗影部分的面积. (结果保存根号 )解: (1)∵ BD 是直径,∴∠ DAB= 90° .∵ FG⊥ AB,∴ DA∥ FO,∴△FOE∽△ADE,∴FOAD=OEDE,即OFDE=OEAD.∵O 是BD 的中点, DA∥ OH,∴ AD= 2OH,∴ OFDE= OE2OH(2)∵⊙ O 的半径为12,且 OE∶ OF∶ OD=2∶ 3∶ 6,∴ OE= 4, ED=8,OF= 6,∴ OH= 6.在 Rt△OBH 中,OB= 2OH,∴∠ OBH= 30°,∴∠ BOH= 60°,∴ BH= BOsin60°= 12× 32= 63,∴ S 暗影= S 扇形 GOB-S△OHB=60×π× 122360- 12× 6×63= 24π- 183种类三:圆与二次函数的综合6.如图,在平面直角坐标系中,已知 A(- 4,0), B(1,0),且以 AB 为直径的圆交 y 轴的正半轴于点 C(0,2),过点 C作圆的切线交 x 轴于点 D.(1)求过 A,B, C 三点的抛物线的分析式;(2)求点 D 的坐标;(3)设平行于 x 轴的直线交抛物线于E,F 两点,问:能否存在以线段EF为直径的圆,恰巧与x轴相切若存在,求出该圆的半径,若不存在,请说明原因.解: (1)y=- 12x2- 32x+2(2)以 AB 为直径的圆的圆心坐标为O′ (-32,0),∴O′ C= 52, O′ O= 32.∵ CD为圆 O′的切线,∴O′ C⊥ CD,∴∠ O′CO+∠ DCO= 90° .又∵∠CO′ O+∠ O′ CO=90°,∴∠ CO′ O=∠DCO,∴△ O′ CO∽△ CDO,∴ O′ OOC= OCOD,∴322= 2OD,∴ OD= 83,∴点 D 的坐标为 (83,0)(3)存在.抛物线的对称轴为直线x=- 32,设满足条件的圆的半径为|r| ,则点 E 的坐标为 (- 32+ r, r)或 F(- 32-r , r),而点 E 在抛物线y =- 12x2- 32x+2 上,∴ r=- 12(- 32+ |r|)2 - 32(- 32+ |r|) + 2,∴ r1=- 1+ 292, r2=-1- 292(舍去 ).故存在以线段EF 为直径的圆,恰巧与x 轴相切,该圆的半径为-1+ 2927.如图,抛物线y=ax2+ bx- 3 与 x 轴交于 A, B 两点,与y 轴交于点C,经过 A,B, C 三点的圆的圆心抛物线的极点为M(1 ,m)恰幸亏此抛物线的对称轴上,E.⊙ M的半径为.设⊙ M与y 轴交于点D,(1)求 m 的值及抛物线的分析式;(2)设∠ DBC=α,∠ CBE=β,求 sin( α-β)的值;(3)研究坐标轴上能否存在点 P,使得以 P, A, C 为极点的三角形与△ BCE相像若存在,请指出点 P 的地点,并直接写出点 P 的坐标;若不存在,请说明原因.解: (1)由题意,可知 C(0,- 3),- b2a=1,∴抛物线的分析式为 y= ax2- 2ax- 3(a> 0).过点 M 作 MN ⊥y 轴于点 N,连接 CM,则 MN = 1, CM= 5,∴ CN= 2,于是 m=- 1.同理,可求得 B(3,0),∴ a× 32- 2a× 3- 3=0,解得 a= 1. ∴抛物线的分析式为 y= x2- 2x-3(2)由 (1)得, A(-1 ,0), E(1,- 4), D(0, 1),∴△ BCE为直角三角形, BC=32, CE= 2,∴OBOD=31= 3, BCCE= 322=3,∴ OBOD= BCCE,即 OBBC= ODCE,∴ Rt△BOD∽ Rt△BCE,得∠ CBE=∠ OBD=β,所以 sin(α-β )=sin(∠ DBC-∠ OBD)= sin∠ OBC= COBC= 22(3)明显 Rt△ COA∽ Rt△ BCE,此时点 O(0, 0).过点 A 作 AP2⊥ AC 交 y 轴的正半轴于点 P2,由 Rt△ CAP2∽Rt△ BCE,得 P2(0,13).过点 C 作 CP3⊥ AC交 x 轴的正半轴于点 P3,由 Rt△P3CA∽ Rt△ BCE,得 P3(9,0).故在座标轴上存在三个点 P1(0, 0),P2(0, 13),P3(9, 0),使得以 P, A, C为极点的三角形与△ BCE相像。
高中数学-单位圆与三角函数线练习题

高中数学-单位圆与三角函数线练习题5分钟训练(预习类训练,可用于课前) 1.若单位圆的圆心与坐标原点重合,有下列结论:①单位圆上任意一点到原点的距离都是1;②单位圆与x 轴的交点为(1,0);③过点(1,0)的单位圆的切线方程为x=1;④与x 轴平行的单位圆的切线方程为y=1.以上结论正确的个数为( )A.1B.2C.3D.4 解析:单位圆与x 轴的交点为(1,0)和(-1,0);与x 轴平行的单位圆的切线方程为y=±1,所以②④错误.显然①③正确. 答案:B2.对角α的正弦线叙述错误的是( ) A.正弦线的起点为坐标原点 B.正弦线为有向线段C.正弦线的长度为不大于1的正数D.当角α的终边不在坐标轴上时,正弦线所在直线平行于y轴 解析:正弦线的长度有可能为0,所以C 答案错误. 答案:C3.如图1-1-2,PM⊥x 轴,AT⊥x 轴,则α的正弦线、余弦线、正切线分别是____________、____________、____________,其中OM=___________,MP=____________,AT=____________.图1-1-2 图1-1-3解析:根据正弦线、余弦线、正切线的定义作出. 答案:MP OM AT cosα sinα tanα4.如图1-1-3,分别作出角β的正弦线、余弦线、正切线,并比较角β的正弦值、余弦值、正切值的大小.解:根据正弦线、余弦线、正切线的定义作出下图.正弦线、余弦线、正切线分别是''P M 、'OM 、'AT ,并且sinβ>cosβ>tanβ. 10分钟训练(强化类训练,可用于课中) 1.若-43π<α<2π-,从单位圆中的三角函数线观察sinα、cosα、tanα的大小是( )图1-1-4A.sinα<tanα<cosαB.tanα<sinα<cosαC.cosα<sinα<tanαD.sinα<cosα<tanα 解析:在单位圆中,作出43π-<α<2π-内的一个角及其正弦线、余弦线、正切线,|OM |<|MP |<|AT |,考虑方向可得MP <OM <AT .答案:D2.若角α的正切线位于第一象限,则角α属于( )A.第一象限B.第一、二象限C.第三象限D.第一、三象限解析:由正切线的定义知,当角α是第一、三象限角时,正切线都在第一象限. 答案:D3.在(0,2π)内,使sinx >cosx 成立的x 的取值范围为( )A.(4π,2π)∪(π,45π) B.(4π,π)C.(4π,45π)D.(4π,π)∪(45π,23π)解析:在单位圆中画三角函数线,如图所示,要使在(0,2π)内sinx >cosx ,则x∈(4π,45π).答案:C4.如果cosα=cosβ,则角α与β的终边除可能重合外,还有可能( ) A.关于x 轴对称 B.关于y 轴对称 C.关于直线y=x 对称 D.关于原点对称 解析:利用单位圆中的余弦线即得,如图.答案:A5.利用三角函数线证明|sinα|+|cosα|≥1.证明:当角α的终边在坐标轴上时,正弦线(余弦线)变成一个点,而余弦线(正弦线)的长等于r (r=1),所以|sinα|+|cosα|=1,当角α的终边落在四个象限时,如图,利用三角形两边之和大于第三边有|sinα|+|cosα|=|MP|+|OM|>1,综上有|sinα|+|cosα|≥1.6.设43π<α<π,角α的正弦线、余弦线、正切线的数量分别为a 、b 、c ,由图比较a 、b 、c 的大小.解:如图所示,|MP|<|OM|<|AT|,而a=|MP|,b=-|OM|,c=-|AT|,∴a>b >c.30分钟训练(巩固类训练,可用于课后)1.(安徽合肥统考,1)sin4·tan7的值( )A.大于0B.小于0C.等于0D.不大于0解析:4弧度的角是第三象限角,7弧度的角是第一象限角,由单位圆中的正弦线和正切线知sin4<0,tan7>0,所以sin4·tan7<0. 答案:B 2.若θ∈(0,2π),则sinθ+cosθ的一个可能值是( ) A.32 B.72πC.224-D.1解析:由θ∈(0,2π)知sinθ+cosθ>1,A 、B 、C 、D 四个选项中仅有224->1,故选C.答案:C3.适合cosα≥21的角α的集合是( ) A.[2kπ+3π,2kπ+35π](k∈Z ) B.[2kπ+3π,2kπ+32π](k∈Z )C.[2kπ-3π,2kπ+3π](k∈Z )D.[2kπ+3π,2kπ-3π](k∈Z )解析:在单位圆中作图,如图,α的范围是2kπ-3π≤α≤2kπ+3π.答案:C4.若sinα=sinβ,则角α与β的终边除可能重合外,还有可能( ) A.关于x 轴对称 B.关于y 轴对称 C.关于直线y=x 对称 D.关于原点对称 解析:利用单位圆中的正弦线即得,如图.答案:B5.分别作出下列各角的正弦线、余弦线、正切线:(1)4π;(2)32π-.解:如图,正弦线:MP ,余弦线:OM ,正切线:AT .(1) (2)6.利用三角线,求满足sinx≤21的角x 的集合. 解:由图可知,值为21的正弦线11P M 和22P M ,易得出∠M 1OP 1=6π,∠M 2OP 2=65π,故满足sinx≤21的x 的集合为{x|2kπ+65π≤x≤2kπ+613π,k∈Z }.7.求函数y=x cos 21-的定义域. 解:如图,因为1-2cosx≥0,所以cosx≤21,所以x∈[2kπ+3π,2kπ+35π](k∈Z ).8.已知关于x 的方程(2sinα-1)x 2-4x+4sinα+2=0有两个不相等的正根,试求角α的取值范围.解:设方程的两根为x 1、x 2,这个方程有两个不相等正根必满足的条件为⎪⎩⎪⎨⎧>•>+>∆,0,0,02121x x x x 即 ⎪⎪⎪⎩⎪⎪⎪⎨⎧>-+>->+---.01sin 22sin 4,01sin 24,0)2sin 4)(1sin 2(4)4(2ααααα 化简得⎪⎪⎪⎩⎪⎪⎪⎨⎧>-<><<-.21sin 121sin ,21sin ,23sin 23αααα或故21<sinα<23.利用三角函数线,在单位圆中标出满足条件的角α的终边位置,即图中两阴影部分的交集,故2kπ+6π<α<2kπ+3π或2kπ+32π<α<2kπ+65π,k∈Z ,即α的取值范围是{α|2kπ+6π<α<2kπ+3π,k∈Z }∪{α|2kπ+32π<α<2kπ+65π,k∈Z }.9.设α是第二象限的角,作α的正弦线、余弦线、正切线,由图证明cos 2α+sin 2α=1. 证明:如图,OM =cosα,MP =sinα,在Rt△MOP 中,|OM|2+|MP|2=|OP |2=1,所以cos 2α+sin 2α=1.10.设α为任意角,求|sinα|+|cosα|的取值范围.解:由正弦线、余弦线及三角形三边关系,可知|sinα|+|cosα|的取值范围为[1,2]. 11.已知α∈(0,2),求证:sinα<α<tanα. 证明:在单位圆中,利用三角函数线的定义,有MP =sinα,AT =tanα.又由α=,显然S △OAP <S扇形OAP<S △OAT ,即21·OA ·MP <21·OA ·<21··AT .化简得<α<,所以sinα<α<tanα.。
中考热点:(一)构造三角形外接圆解四类难题;(二)圆+三角函数综合题型

中考热点:构造三角形外接圆解四类难题一、问题导读在解证几何题时,四点共圆已经被一些学生所了解或重视,然而作三角形的外接圆还没有被学生重视,使对许多几何题的证明难于入手.下面介绍作三角形外接圆这个辅助圆的思路和方法,以期待对你的学习有所帮助。
二、典例精析类型1 作三角形外接圆,求含有乘积式问题例1.已知AD是△ABC的角平分线,求证:ABAC=AD+BDCD.【分析】作辅助圆,根据同弧所对的圆周角相等和角平分线证明相似得出比例式,再证△BAD∽△ECD,根据相似三角形的性质得出ADED=BDDC,即可得出答案.【解答】证明:作△ABC的外接圆O,延长AD交⊙O于E,连接CE,∵AE平分∠BAC,∴∠BAD=∠EAC,∵∠B=∠E,∴△ABD∽△AEC,∴AB/AE=AD/AC,∴ABAC=ADAE=AD(AD+DE)=AD2+ADED,∵∠B=∠E,∠BAD=∠DCE,∴△BAD∽△ECD,∴AD/CD=BD/ED,∴ADED=BDDC,∴ABAC=ADAE=AD+BDDC.【点评】本题考查了相似三角形的性质和判定,圆周角定理的应用,解此题的关键是推出△ABD∽△AEC 和△BAD∽△ECD,主要考查学生的推理能力.例2.如图,ABCD是圆内接四边形,AB、DC的延长线交于E,AD、BC的延长线交于F,EP、FQ切圆于P、Q两点,求证:EP+FQ=EF.【分析】作辅助圆,构建四点共圆的四边形,利用切割线定理列式:EP2=ECED,FQ2=FCFB,得出结论.【解答】证明:作△BCE的外接圆,交EF于G,连接CG,∵A、B、C、D四点共圆,∴∠FDC=∠ABC,∵B、C、G、E四点共圆,∴∠ABC=∠CGE,∴∠FDC=∠ABC=∠CGE,∴F、D、C、G四点共圆,由切割线定理得:EP=ECED,FQ=FCFB,EF=(EG+GF)EF=EGEF+GFEF=ECED+FCFB,∴EP+FQ=EF.【点评】本题考查了切割线定理和圆内接四边形的性质,本题运用了圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角);反之也成立;在证明线段的平方和时,一方面考虑利用勾股定理来求,另一方面考虑利用切割线定理列式得出.类型2 作三角形外接圆,利用圆中的角证明线段的和差倍半问题例3.四边形ABCD内接于圆,另一圆的圆心在边AB上且与其余三边相切,求证:AD+BC=AB.【分析】先画图,设AB上的圆心为P,由等腰三角形的性质得,∠CMB=∠PDC,则M,P,C,D四点共圆,从而得出∠AMD=∠ADM,最后证得AD+BC=AB.【解答】证明:设AB上的圆心为P,在AB上取一点M,使MB=BC,连接MC,MD,PD,PC 等腰△CMB中,∠CMB=∠MCB,∴∠CMB=1/2(∠MCB+∠CMB)=1/2(180°﹣∠B),=1/2∠ADC (圆内接四边形ABCD的对角相加为180°),=∠PDC (设圆P切AD于E,切DC于F,有PE=PF,Rt△PDE和Rt△PDF中,一对儿直角边相等,且斜边是公共的,∴两Rt△全等,可得PD平分∠CDA),∴M,P,C,D四点共圆,∴∠AMD=∠DCP=1/2∠DCB (同理,可证PC平分∠DCB),=1/2(180°﹣∠A)(ABCD的另一对儿对角和为180°,=1/2(∠ADM+∠AMD),∴∠AMD=∠ADM∴AD=AM,∴AD+BC=AM+MB=AB.例4.如图,在△ABC中,AB=AC,D是底边BC上一点,E是线段AD上一点且∠BED=2∠CED=∠A.求证:BD=2CD.【分析】首先作DO∥AB交AC于O,得出O为△EDC的外心,进而得出△ACE∽△ADF,即有AD/AC=AF/AE,即可得出△ADO∽△BAE,即可得出BD=2CD.【解答】证明:作DO∥AB交AC于O.则由AB=AC易知OD=OC,且∠DOC=∠BAC=2∠CED,所以O为△EDC的外心,取F为△EDC的外接圆与AC的交点,连接DF,则OF=OC=OD,∠ACE=∠ADF.所以△ACE∽△ADF,即有AD/AC=AF/AE.再由DO∥AB,∠ADO=∠BAE,∠AOD=180﹣∠DOC=180°﹣∠A=180°﹣∠BED=∠AEB,所以△ADO∽△BAE,即得OD/AE=AD/AB=AF/AE.故AF=OD=OC=1/2CF,从而AO=2OC.由DO∥AB,得:BD=2CD.类型3 作三角形的外接圆,利用圆中的角判断三角形的形状例5.已知:AD是△ABC的中线,若∠ABC+∠CAD=90.试判断△ABC的形状.分析:作△ABC的外接圆.使分散的∠ABC.∠CAD集中在一起,从而知道中线AD在外接圆的直径上.根据圆中弦的定理,可判断△ABC的形状.解:作△ABC的外接圆.延长AD交外接圆于E.连结BE.∵∠EBC=∠CAD,又∠ABC+∠CAD=90°,∴∠ABC+∠EBC=90°,即∠ABE=90°.AE是△ABC的外接圆的直径.又AD是BC边上的中线.(1)当BC不是外接圆的直径时,即BC为弦,则 AD⊥BC,AD是BC边的中垂线.△ABC为等腰三角形.(2)当BC是外接圆的直径时,∠CAB=90°,△ABC为直角三角形.例6. 设P、Q为线段BC 上两定点,且BP=CQ.A为BC外一动点.当点A运动到使∠BAP=∠CAQ时,△ABC是什么三角形?分析:作△ABC的外接圆,能把角等转化为弦等,构造全等三角形.证明:作△ABC的外接圆,延长AP、AQ分别交外接圆于E、F.连结BE、CF.∵∠BAP=∠CAQ,即∠BAE=∠CAF,∴BE=FC, 弧BE=弧CF,∴弧BF=弧CE, ∴∠EBP=∠FCQ,又BP=CQ,∴△BEP≌△CFQ.∠E=∠F,在△ABE和△ACF中,∠E=∠F,∠BAE=∠CAF,BE=CF.∴△ABE≌△ACF,AB=AC, ∴△ABC是等腰三角形.类型4 作三角形的外接圆,解几何综合题例7.已知:A、B、C三点不在同一直线上.(1)若点A、B、C均在半径为R的⊙O上,i)如图①,当∠A=45°,R=1时,求∠BOC的度数和BC的长;ii)如图②,当∠A为锐角时,求证:sinA=BC/2R;(2)若定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动,如图③,当∠MAN=60°,BC=2时,分别作BP⊥AM,CP⊥AN,交点为P,试探索在整个滑动过程中,P、A两点间的距离是否保持不变?请说明理由.【分析】(1)i)根据圆周角定理得出∠BOC=2∠A=90°,再利用勾股定理得出BC的长;ii)作直径CE,则∠E=∠A,CE=2R,利用sinA=sinE=BC/2R,得出即可;(2)首先证明点A、B、P、C都在⊙K上,再利用sin60°=BC/AP,得出AP=2/ sin60°=4√3/3(定值).【解答】(1)i)∵A、B、C均在⊙O上,∴∠BOC=2∠A=2×45°=90°,∵OB=OC=1,∴BC=√2,注:也可延长BO或过O点作BC的垂线构造直角三角形求得BC.ii)证法一:如图②,连接EB,作直径CE,则∠E=∠A,CE=2R,∴∠EBC=90°∴sinA=sinE=BC/2R,证法二:如图③.连接OB、OC,作OH⊥BC于点H,则∠A=1/2∠BOC=∠BOH,BH=1/2BC∴sinA=sin∠BOH=BH/OB=1/2BC/R=BC/2R,(2)如图④,连接AP,取AP的中点K,连接BK、CK,在Rt△APC中,CK=1/2AP=AK=PK,同理得:BK=AK=PK,∴CK=BK=AK=PK,∴点A、B、P、C都在⊙K上,∴由(1)ii)可知sin60°=BC/AP∴AP=2/ sin60°=4√3/3(定值),故在整个滑动过程中,P、A两点间的距离不变.【点评】此题主要考查了圆周角定理以及解直角三角形和四点共圆等知识,根据已知得出点A、B、P、C 都在⊙K上以及sin60°=BC/AP是解题关键.中考热点:圆+三角函数综合题型一、问题导读“圆”这一部分知识,多年来都是中考的重点,锐角三角函数大家也不算陌生,那么当圆遇上三角函数又会出现什么呢?下面就和大家分享一下圆偶遇三角函数之后所发生的一个小片段吧!当然如果想了解具体发生了什么,首先得记住他们的暗号喔,通过下面问题的探讨,不难发现它们携手并进暗号呢。
(完整版)人教版九年级下册:圆和三角函数综合练习(含答案)

圆与三角函数1 •已知,如图,AB是。
O的直径,点C为。
O上一点,OF丄BC于点F,交。
O于点E, AE 与BC交于点H,点D为OE的延长线上一点,且/ ODBN AEC(1)求证:BD是O O的切线;(2)求证:CE二EH?EA(3)若。
O的半径为5,sinA^L,求BH的长.2•如图,已知AB是。
O的直径,C是。
O上任一点(不与A,B重合),AB丄CD于E,BF为O O的切线,OF// AC,连结AF, FC, AF与CD交于点G,与。
O交于点H,连结CH.(1)求证:FC是O O的切线;(2)求证:GC=GE(3)若cos/ AOC=-, O O的半径为r,求CH的长.3•已知。
O是以AB为直径的厶ABC的外接圆,OD// BC交。
O于点D,交AC于点E,连接AD、BD, BD 交AC于点F.(1)求证:BD平分/ ABC;(2)延长AC到点P,使PF=PB求证:PB是。
O的切线;(3)如果AB=10, cos/ ABC」,求AD.54.如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且/ ACBd DCE(1 )判断直线CE与。
O的位置关系,并证明你的结论;(2)若上&门/ACB据,BC=2求O O的半径.5 •如图,AB是。
O的直径,D、E为。
O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD连接AC交。
O于点F,连接AE、DE、DF.(1 )证明:/ E=Z C;(2) 若/ E=55,求/ BDF的度数;(3) 设DE交AB于点G,若DF=4, cosB二,E是・,的中点,求EG?ED的值.E6. AB, CD是。
O的两条弦,直线AB, CD互相垂直,垂足为点E,连接AD,过点B作BF丄AD,垂足为点F,直线BF交直线CD于点G.(1) 如图1,当点E在。
O外时,连接BC,求证:BE平分/ GBC(2) 如图2,当点E在。
圆中三角函数综合例题及练习

圆中的三角函数解决几何图形的三角函数求值问题,关键在于,找到相关的直角三角形.若没有现成的直角三角形,则需根据所给的条件,合理构造直角三角形,或把角进行转化。
圆中有关此类问题的解决也不例外,现就解题策略分析如下:一、用圆周角的性质把角转化到直角三角形中例1(成都市)如图1,已知AB 是⊙O 的直径,弦CD ⊥AB , AC =BC =1,那么sin ∠ABD 的值是 .解析:在⊙O 中,∠ACD =∠ABD ;又由于AB 为⊙O 的直径,CD ⊥AB ,则∠ACD =∠ABC . Rt △ABC 中,AB =22BC AC +=221)22(+=3,从而sin ∠ABD =ABAC =322.评注:借用“同弧所对圆周角相等”,把要求函数值的角予以转化,充分本现了转化思想的巧妙运用。
二、用直径与所对圆周角构造直角三角形例2(烟台市)已知AB是半圆O 的直径,弦AD 、BC 相交于点P ,若∠DPB =α,等于A .sinαB .COSαC .tanαD .1tan α解析: 连结BD ,由于AB 为直径,则∠ADB =90°, 于是,在Rt △PBD 中,有COSα=PBPD, 而点C 和点A 在圆周上,所以∠A =∠C , 又∠APB =∠CPD ,则△APB ∽△CPD, 从而CD AB =PB PD ,所以CDAB=COSα,故选B 。
评注:直径所对的圆周角是直角。
由此,可以得到一个直角三角形,从而为使用三角函数创造条件,因此,在解题中,要倍加关注直径所对圆周角。
三、转化条件中的垂直关系构造直角三角形例3(武汉市)如图4,等腰三角形ABC 中,AC =BC =10,AB =12。
以BC 为直径作⊙O 交A B 于点D ,交AC 于点G ,DF ⊥AC ,垂足为F ,交CB 的延长线于点E 。
(1)求证:直线EF 是⊙O 的切线; (2)求sin ∠E 的值。
解析:(1)证明:如图5,连结OD 、CD ,因为BC 是直径,所以CD ⊥AB , 而AC =BC ,则D 是AB 的中点 又因为O 是CB 的中点,所以OD //AC由于DF ⊥AC ,则OD ⊥EF ,于是EF 是⊙O 的切线.(2)连结BG ,因为BC 是直径,所以∠BGC =90° 图 图4 B 图1BCD在Rt △BCD 中,CD =22AD AC -=22610-=8而AB ·CD =2ABC S ∆= AC ·BG , 则有BG =AC CD AB ⋅=10812⨯=548. 在Rt △BCG 中,CG =22BG BC -=22)548(10-=514; 又因为BG ⊥AC , DF ⊥AC ,所以BG //EF ,则∠E =∠CBG ,从而sin ∠E =sin ∠CBG =BC CG =10514=257评注:挖掘图形中的隐含关系,把已知条件中的垂直关系进行转化,从而构造直角三角形,为求角的函数值提供便利.例4.如图,Rt △ABC 中, ∠ACB=90°,AC=4, BC=2,以AB 上的一点0为圆心作⊙O 分别与AC .BC 相切于点D ,E 。
圆与相似及三角函数综合问题--2023年中考数学压轴题(解析版)

圆与相似及三角函数综合问题1典例剖析1(2022·四川·巴中市教育科学研究所中考真题)四边形ABCD内接于⊙O,直径AC与弦BD交于点E,直线PB与⊙O相切于点B.(1)如图1,若∠PBA=30°,且EO=EA,求证:BA平分∠PBD;(2)如图2,连接OB,若∠DBA=2∠PBA,求证:△OAB∽△CDE.【答案】(1)见解析(2)见解析【解析】(1)证明:连接OB,∵直线PB与⊙O相切于点B,∴∠PBO=90°,∴∠PBA+∠ABO=90°,∵∠PBA=30°,∴∠ABO=60°,又∵OA=OB,∴△AOB为等边三角形,又∵OE=AE,∴BE平分∠ABO,∴∠ABE=1∠ABO=30°,2∴BA平分∠PBD;(2)证明:∵直线PB与⊙O相切于点B,∴∠PBO=90°,∴∠PBA+∠ABO=90°,∵AC为直径,∴∠ABC=90°,∴∠OBC+∠ABO=90°,∴∠OBC=∠PBA,∵OB=OC,∴∠PBA=∠OBC=∠OCB,∴∠AOB=2∠OCB=2∠PBA,∵∠ACD=∠ABD=2∠PBA,∴∠AOB=∠ACD,又∵∠BAO=∠BDC,∴△OAB∽△CDE.2(2022·广东深圳·中考真题)一个玻璃球体近似半圆O,AB为直径,半圆O上点C处有个吊灯EF, EF⎳AB, CO⊥AB,EF的中点为D,OA=4.(1)如图①,CM为一条拉线,M在OB上,OM=1.6,DF=0.8,求CD的长度.(2)如图②,一个玻璃镜与圆O相切,H为切点,M为OB上一点,MH为入射光线,NH为反射光线,,求ON的长度.∠OHM=∠OHN=45°,tan∠COH=34(3)如图③,M是线段OB上的动点,MH为入射光线,∠HOM=50°,HN为反射光线交圆O于点N,在M从O运动到B的过程中,求N点的运动路径长.【答案】(1)2(2)ON=207π(3)4+169【解析】(1)∵DF=0.8,OM=1.6,DF∥OB∴DF为△COM的中位线∴D为CO的中点∵CO=AO=4∴CD=2(2)过N 点作ND ⊥OH ,交OH 于点D ,∵∠OHN =45°,∴△NHD 为等腰直角三角形,即ND =DH ,又∵tan ∠COH =34,∴tan ∠NOD =34,∴tan ∠NOD =ND OD=34,∴ND :OD =3:4,设ND =3x =DH ,则OD =4x ,∵OD +DH =OH ,∴3x +4x =4,解得x =47,∴ND =127,OD =167,∴在Rt △NOD 中,ON =ND 2+OD 2=127 2+167 2=207;(3)如图,当点M 与点O 重合时,点N 也与点O 重合.当点M 运动至点A 时,点N 运动至点T ,故点N 路径长为:OB +l BT .∵∠NHO =∠MHO ,∠THO =∠MHO ,∠HOM =50°.∴∠OHA =∠OAH =65°.∴∠THO =65°,∠TOH =50°.∴∠BOT =80°,∴l BT =2π×4×80°360°=169π,∴N 点的运动路径长为:OB +l BT =4+169π,故答案为:4+169π.3(2022·黑龙江哈尔滨·中考真题)已知CH 是⊙O 的直径,点A ,点B 是⊙O 上的两个点,连接OA ,OB ,点D ,点E 分别是半径OA ,OB 的中点,连接CD ,CE ,BH ,且∠AOC =2∠CHB .(1)如图1,求证:∠ODC =∠OEC ;(2)如图2,延长CE 交BH 于点F ,若CD ⊥OA ,求证:FC =FH ;(3)如图3,在(2)的条件下,点G 是BH 上一点,连接AG ,BG ,HG ,OF ,若AG :BG =5:3,HG =2,求OF 的长.【答案】(1)见解析(2)见解析(3)OF =193【解析】(1)如图1.∵点D ,点E 分别是半径OA ,OB 的中点∴OD =12OA ,OE =12OB ∵OA =OB ,∴OD =OE∵∠BOC =2∠CHB ,∠AOC =2∠CHB∴∠AOC =∠BOC∵OC =OC∴△COD ≅△COE ,∴∠CDO =∠CEO ;(2)如图2.∵CD ⊥OA ,∴∠CDO =90°由(1)得∠CEO =∠CDO =90°,∴sin ∠OCE =OE OC=12∴∠OCE =30°,∴∠COE =90°-∠OCE =60°∵∠H =12∠BOC =12×60°=30°∴∠H =∠ECO ,∴FC =FH(3)如图3.∵CO =OH ,FC =FH∴OF ⊥CH∴∠FOH =90°连接AH.∵∠AOC=∠BOC=60°∴∠AOH=∠BOH=120°,∴AH=BH,∠AGH=60°∵AG:BG=5:3设AG=5x,∴BG=3x在AG上取点M,使得AM=BG,连接MH ∵∠HAM=∠HBG,∴△HAM≌△HBG∴MH=GH,∴△MHG为等边三角形∴MG=HG=2∵AG=AM+MG,∴5x=3x+2∴x=1,∴AG=5∴BG=AM=3,过点H作HN⊥MG于点NMN=12GM=12×2=1,HN=HG⋅sin60°=3∴AN=MN+AM=4,∴HB=HA=NA2+HN2=19∵∠FOH=90°,∠OHF=30°,∴∠OFH=60°∵OB=OH,∴∠BHO=∠OBH=30°,∴∠FOB=∠OBF=30°∴OF=BF,在Rt△OFH中,∠OHF=30°,∴HF=2OF∴HB=BF+HF=3OF=19,∴OF=193.【点睛】本题主要考查了圆周角定理,等边三角形的判定和性质,全等三角形的判定与性质,等腰三角形的性质,勾股定理以及解直角三角形等知识,正确作出辅助线构造全等三角形是解答本题的关键.4(2022·黑龙江绥化·中考真题)如图所示,在⊙O的内接△AMN中,∠MAN=90°,AM=2AN,作AB ⊥MN于点P,交⊙O于另一点B,C是AM上的一个动点(不与A,M重合),射线MC交线段BA的延长线于点D,分别连接AC和BC,BC交MN于点E.(1)求证:△CMA∽△CBD.(2)若MN=10,MC=NC,求BC的长.(3)在点C运动过程中,当tan∠MDB=34时,求MENE的值.【答案】【答案】(1)证明见解析(2)310(3)32【解析】(1)解:∵AB⊥MN,∴∠APM=90°,∴∠D+∠DMP=90°,又∵∠DMP+∠NAC=180°,∠MAN=90°,∴∠DMP+∠CAM=90°,∴∠CAM=∠D,∵∠CMA=∠ABC,∴△CMA∽△CBD.(2)连接OC,∵∠MAN=90°,∴MN是直径,∵MN=10,∴OM=ON=OC=5,∵AM=2AN,且AM2+AN2=MN2,∴AN=25,AM=45,∵S△AMN=12AM⋅AN=12MN⋅AP,∴AP=4,∴BP=AP=4,∴NP=AN2-AP2=2,∴OP=5-2=3,∵MC =NC ,∴OC ⊥MN ,∴∠COE =90°,∵AB ⊥MN ,∴∠BPE =90°,∴∠BPE =∠COE ,又∵∠BEP =∠CEO ,∴△COE ∽△BPE∴CO BP =OE PE =CE BE ,即54=OE PE =CE BE由OE +PE =OP =3,∴OE =53,PE =43,∴CE =OC 2+OE 2=52+53 2=5310,BE =BP 2+PE 2=42+43 2=4310,∴BC =5310+4310=310.(3)过C 点作CG ⊥MN ,垂足为G ,连接CN ,则∠CGM =90°,∴∠CMG +∠GCM =90°,∵MN 是直径,∴∠MCN =90°,∴∠CNM +∠DMP =90°,∵∠D +∠DMP =90°,∴∠D =∠CNM =∠GCM ,∵tan ∠MDB =34,∴tan ∠CNM =tan ∠GCM =34,∵tan ∠GCM =GM CG∴设GM =3x ,CG =4x ,∴CM =5x ,∴CN =20x 3,NG =16x 3,∴NM =25x 3,∴OM =ON =25x 6,∵AM =2AN ,且AM 2+AN 2=MN 2,∴AN =553x ,AM =1053x ,∵S△AMN=12AM⋅AN=12MN⋅AP,∴AP=103x=PB,∴NP=53x,∴PG=163x-53x=113x,∵∠CGE=∠BPE=90°,∠CEG=∠BEP,∴△CGE∽△BPE,∴CG BP =GEPE=CEBE,即4x103x=GEPE=CEBE∴GE=2x,PE=53x∴ME=5x,NE=10x3,∴ME:NE=3:2,∴MENE的值为3 2.【点睛】本题考查了圆的相关知识、相似三角形的判定与性质、三角函数、勾股定理等知识,涉及到了动点问题,解题关键是构造相似三角形,正确表示出各线段并找出它们的关系,本题综合性较强,属于压轴题.2满分训练一、解答题【共20题】1(2022·内蒙古内蒙古·中考真题)如图,⊙O是△ABC的外接圆,EF与⊙O相切于点D,EF∥BC 分别交AB,AC的延长线于点E和F,连接AD交BC于点N,∠ABC的平分线BM交AD于点M.(1)求证:AD平分∠BAC;(2)若AB:BE=5:2,AD=14,求线段DM的长.【答案】(1)见解析(2)DM=2【解析】(1)证明:连接OD交BC于点H.∵EF与⊙O相切于点D∴OD⊥EF,∴∠ODF=90°,∵BC∥EF,∴∠OHC=∠ODF=90°,∴OD⊥BC,∴BD=CD,∴∠BAD=∠CAD 即AD平分∠BAC;(2)解:∵BC∥EF,∴BE AE =ND AD,∵AB:BE=5:2,AD=14,∴DN=2147,∵∠BAD=∠CAD,∠CAD=∠CBD,∴∠BAD=∠CBD,∵BM平分∠ABC,∴∠ABM=∠CBM,∴∠BAD+∠ABM=∠CBD+∠CBM,∴∠BMD=∠MBD,∴BD=DM,∵∠NBD=∠BAD,∠BDM=∠ADB,∴△BDN∽△ADB,∴ND BD =DB AD∴BD2=ND⋅AD=2147×14=4,∴BD=2(负值舍去),∴DM=BD=2【点睛】本题主要考查圆的基本性质,切线的性质、相似三角形的判定和性质,平行线分线段成比例定理,等腰三角形的判定和性质;找出相似三角形,列相似比求解是解决本题的关键.2(2022·湖北黄石·中考真题)如图CD是⊙O直径,A是⊙O上异于C,D的一点,点B是DC延长线上一点,连接AB、AC、AD,且∠BAC=∠ADB.(1)求证:直线AB是⊙O的切线;(2)若BC=2OC,求tan∠ADB的值;(3)在(2)的条件下,作∠CAD的平分线AP交⊙O于P,交CD于E,连接PC、PD,若AB=26,求AE ⋅AP的值.【答案】(1)见解析(2)22(3)42【解析】(1)解:如图所示,连接OA ,∵CD 是⊙O 直径,∴∠CAD =90°,∴∠OAC +∠OAD =90°,又∵OA =OD ,∴∠OAD =∠ODA ,∵∠BAC =∠ADB ,∴∠OAD =∠BAC ,∴∠BAC +∠OAC =90°,即∠BAO =90°,∴AB ⊥OA ,又∵OA 为半径,∴直线AB 是⊙O 的切线;(2)解:∵∠BAC =∠ADB ,∠B =∠B ,∴△BCA ∽△BAD ,∴ACAD =BC BA,由BC =2OC 知,令半径OC =OA =r ,则BC =2r ,OB =3r ,在Rt △BAO 中,AB =OB 2-OA 2=22r ,在Rt △CAD 中,tan ∠ADC =AC AD =BC BA =2r 22r=22,即tan ∠ADB =22;(3)解:在(2)的条件下,AB =22r =26,∴r =3,∴CD =23,在Rt △CAD 中,AC AD=22,AC 2+AD 2=CD 2,解得AC =2,AD =22,∵AP 平分∠CAD ,∴∠CAP =∠EAD ,又∵∠APC =∠ADE ,∴△CAP ∽△EAD ,∴AC AE =AP AD,∴AE ⋅AP =AC ⋅AD =2×22=42.【点睛】本题主要考查了圆切线的判定,直径所对的圆周角是直角,相似三角形的性质与判定,解直角三角形,勾股定理,等腰三角形的性质等等,熟知相关知识是解题的关键.3(2022·湖北襄阳·中考真题)如图,AB 是半圆O 的直径,点C 在半圆O 上,点D 为BC 的中点,连接AC ,BC ,AD ,AD 与BC 相交于点G ,过点D 作直线DE ∥BC ,交AC 的延长线于点E .(1)求证:DE 是⊙O 的切线;(2)若AC =BD ,CG =23,求阴影部分的面积.【答案】(1)见解析(2)1532【解析】(1)证明:连接OD ,如图所示,∵点D 为BC 的中点,∴OD ⊥BC∵DE ∥BC ,∴OD ⊥DE .∴DE 是⊙O 的切线.(2)连接BD ,如图所示,∵AC =BD∴BD =AC∵点D 为BC 的中点,∴CD =BD ,∴AC =CD =BD ,∴∠CAD =∠BAD =30°.∵AB 是半圆O 的直径,∴∠ACB =∠ADB =90°,在Rt △ACG 中,tan ∠CAD =CG CA ,sin ∠CAD =CG AG,∴CA =CG tan30°,AG =CG sin30°,∵CG =23,∴CA =23×3=6,AG =43,∴BD =CA =6,∴S △ACG =12CG ⋅AC =63,在Rt △ABD 中,tan ∠BAD =BD AD ,∴AD =BDtan30°=633=6 3.∵DE ∥BC ,∴S △CAG S △EAD =AG AD 2,即63S ΔEAD =49,∴S △EAD =2732.∴S 阴影部分=S △EAD -S △ACG =1532.【点睛】本题主要考查了切线的判定定理、垂径定理、圆周角定理以及相似三角形的性质,解直角三角形,掌握以上知识是解题的关键.4(2022·辽宁鞍山·中考真题)如图,⊙O 是△ABC 的外接圆,AB 为⊙O 的直径,点E 为⊙O 上一点,EF ∥AC 交AB 的延长线于点F ,CE 与AB 交于点D ,连接BE ,若∠BCE =12∠ABC .(1)求证:EF 是⊙O 的切线.(2)若BF =2,sin ∠BEC =35,求⊙O 的半径.【答案】(1)过程见解析(2)3【解析】(1)证明:连接OE .∵∠BCE =12∠ABC ,∠BCE =12∠BOE ,∴∠ABC =∠BOE ,∴OE ∥BC ,∴∠OED =∠BCD .∵EF ∥CA ,∴∠FEC =∠ACE ,∴∠OED +∠FEC =∠BCD +∠ACE ,即∠FEO =∠ACB .∵AB 是直径,∴∠ACB =90°,∴∠FEO =90°,∴FE ⊥EO .∵EO 是⊙O 的半径,∴EF 是⊙O 的切线.(2)∵EF ∥AC ,∵BF =2,sin ∠BEC =35.设⊙O 的半径为r ,∴FO =2+r ,AB =2r ,BC =65r .∵EO BC =FO AB ,∴r 65r =2+r 2r ,解得r =3,∴⊙O 的半径是3.【点睛】本题主要考查了切线的性质和判定,解直角三角形,熟练掌握相关定理是解题的关键.5(2022·辽宁朝阳·中考真题)如图,AC 是⊙O 的直径,弦BD 交AC 于点E ,点F 为BD 延长线上一点,∠DAF =∠B .(1)求证:AF 是⊙O 的切线;(2)若⊙O 的半径为5,AD 是△AEF 的中线,且AD =6,求AE 的长.【答案】(1)见解析(2)365【解析】(1)证明:∵AC 是直径,∴∠ADC =90°,∴∠ACD +∠DAC =90°,∵∠ACD =∠B ,∠B =∠DAF ,∴∠DAF =∠ACD ,∴∠DAF +∠DAC =90°,∴OA ⊥AF ,∵AC 是直径,∴AF 是⊙O 的切线;(2)解:作DH ⊥AC 于点H ,∵⊙O 的半径为5,∴AC =10,∵∠AHD =∠ADC =90°,∠DAH =∠CAD ,∴△ADH ~△ACD ,∴AD AC =AH AD,∴AD 2=AH ⋅AC ,∵AD =6,∴AH =3610=185,∵AD 是△AEF 的中线,∠EAF =90°,∴AD =ED ,AE=2AH=365.【点睛】本题主要考查了圆周角定理,切线的判定定理,相似三角形的判定与性质,等腰三角形的性质等知识,根据相似三角形的判定与性质求出AH的长是解题的关键.6(2022·山东菏泽·中考真题)如图,在△ABC中,以AB为直径作⊙O交AC、BC于点D、E,且D是AC的中点,过点D作DG⊥BC于点G,交BA的延长线于点H.(1)求证:直线HG是⊙O的切线;(2)若HA=3,cos B=25,求CG的长.【答案】(1)见解析(2)65【解析】(1)连接OD,∵DG⊥BC,∴∠BGH=90°,∵D是AC的中点,AB为直径,∴OD∥BC,∴∠BGH=∠ODH=90°,∴直线HG是⊙O的切线;(2)由(1)得OD∥BC,∴∠HBG=∠HOD,∵cos∠HBG=25,∴cos∠HOD=25,设OD=OA=OB=r,∵HA=3,∴OH=3+r,在Rt△HOD中,∠HDO=90°,∴cos∠HOD=ODOH =r3+r=25,解得r=2,∴OD=OA=OB=2,OH=5,BH=7,∵D是AC的中点,AB为直径,∴BC=2OD=4,∵∠BGH=∠ODH=90°,∴△ODH∼△BGH,∴OH BH =ODBG,即57=2BG,∴BG=145,∴CG=BC-BG=4-145=65.【点睛】本题考查了切线的判定,三角形中位线的性质,平行线的判定和性质,相似三角形的判定和性质及解直角三角形,熟练掌握知识点是解题的关键.7(2022·贵州黔西·中考真题)如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交AC于点E,DH⊥AC,垂足为H,连接DE并延长交BA的延长线于点F.(1)求证:DH是⊙O的切线;(2)若E为AH的中点,求EFFD的值.【答案】(1)见解析(2)23【解析】(1)连接OD,则OD=OB.∴∠ODB=∠ABC.∵AB=AC,∴∠ABC=∠C.∴∠ODB=∠C.∴OD∥AC.∴∠DHC=∠HDO.∵DH⊥AC,∴∠DHC=∠HDO=90°.∴DH⊥OD.∴DH是⊙O的切线.(2)连接AD和BE.∵AB是⊙O的直径,∴OA=OB,∠ADB=∠AEB=90°.∵OD∥AC∴OB OA =BD CD=1∴CD=BD.∴OD⎳AC且OD=12AC.∵OD∥AE,∴∠AEF=∠ODF.∵∠F=∠F,∴△FAE∽△FOD.∴FE FD =AE OD.∵∠DHA=∠BEA=90°∴DH∥BE∴CH HE =CD BD=1∴CH=HE.∵E为AH的中点,∴AE=EH=CH.∴AE=13AC∴FE FD =AEOD=13AC12AC=23.【点睛】本题考查了切线的判定和性质,圆周角定律,平行线分线段成比例,三角形相似的判定与性质等知识,熟练掌握以上判定和性质是本题解题的关键.8(2022·贵州安顺·中考真题)如图,AB是⊙O的直径,点E是劣弧BD上一点,∠PAD=∠AED,且DE=2,AE平分∠BAD,AE与BD交于点F.(1)求证:PA是⊙O的切线;(2)若tan∠DAE=22,求EF的长;(3)延长DE,AB交于点C,若OB=BC,求⊙O的半径.【答案】(1)见解析(2)1(3)2【解析】(1)证明:∵AB 是⊙O 的直径,∴∠ADB =90°,∴∠DAB +∠DBA =90°,∵AD =AD ,∴∠AED =∠ABD ,∵∠PAD =∠AED ,∴∠PAD =∠ABD ,∴∠BAD +∠PAD =∠BAD +∠ABD =90°,即∠PAB =90°,∴PA 是⊙O 的切线,(2)如图,连接OE ,EB ,∵AE 平分∠BAD ,∴∠DAE =∠BAE ,∴DE =BE =2∴OE ⊥BD∵OA =OE ,∴∠OEA =∠OAE ,∴∠DAE =∠AEO ,∴AD ∥OE ,∵AB 是⊙O 的直径,∴AD ⊥DB ,AE ⊥EB ,即∠ADF =∠BEF =90°,∵DE ⏜=DE⏜∴∠DAE =∠DBE ,∴tan ∠EBF =tan ∠DAE =22,∴EF EB =22,∴EF =22EB =1;(3)如图,过点B 作BG ∥AD ,由(2)可知AD ∥OE ,∴OE ∥BG ,∵AO =OB =BC ,∴DE =EG =GC ,设⊙O 的半径为x ,则GB =12OE =12x ,∵AD ∥BG ,∴△CGB ∽△CDA ,∴CG CD =GB AD ,∴AD =3GB =32x ,∵OE⊥DB,∴DB⊥GB,∵DE=2,∴DG=2DE=22,在Rt△DBG中,DB2=DG2-GB2=8-12x 2,在Rt△ADB中,AD2+DB2=AB2,即32x2+8-12x2=2x 2,解得:x=2(负值舍去),∴⊙O的半径为2.【点睛】本题考查了切线的判定,圆周角定理的推论,平行线分线段成比例,相似三角形的性质与判定,解直角三角形,综合运用以上知识是解题的关键.9(2022·山东枣庄·中考真题)如图,在半径为10cm的⊙O中,AB是⊙O的直径,CD是过⊙O上一点C的直线,且AD⊥DC于点D,AC平分∠BAD,点E是BC的中点,OE=6cm.(1)求证:CD是⊙O的切线;(2)求AD的长.【答案】(1)见解析(2)AD=365【解析】(1)证明:连接OC,如图:∵AC平分∠BAD,∴∠DAC=∠CAO,∵OA=OC,∴∠CAO=∠OCA,∴∠DAC=∠OCA,∴AD∥OC,∵AD⊥DC,∴CO⊥DC,∵OC是⊙O的半径,∴CD是⊙O的切线;(2)解:∵E是BC的中点,且OA=OB,∴OE是△ABC的中位线,AC=2OE,∵OE=6,∴AC=12,∵AB是⊙O的直径,∴∠ACB=90°=∠ADC,又∠DAC=∠CAB,∴△DAC∽△CAB,∴ADAC =ACAB,即AD12=1220,∴AD=365.【点睛】本题考查圆的切线的判定定理,相似三角形的判定及性质等知识,解题的关键是熟练应用圆的相关性质,转化圆中的角和线段.10(2022·山东济宁·中考真题)如图,在矩形ABCD中,以AB的中点O为圆心,以OA为半径作半圆,连接OD交半圆于点E,在BE上取点F,使AE=EF,连接BF,DF.(1)求证:DF与半圆相切;(2)如果AB=10,BF=6,求矩形ABCD的面积.【答案】(1)见解析(2)2003【解析】(1)证明:连接OF.∵AE=EF,∴∠DOA=∠FOD.∵AO=FO,DO=DO,∴△DAO≅△DFO(SAS)∴∠DAO=∠DFO.∵四边形ABCD是矩形,∴∠DAO=90°∴∠DFO=90°.∴DF与半圆相切.(2)解:连接AF,∵AO=FO,∠DOA=∠DOF,∴DO⊥AF,∵AB为半圆的直径,∴∠AFB=90°,∴BF⊥AF,∴DO∥BF.∴∠AOD=∠ABF.∵∠OAD=∠AFB=90°,∴△AOD∽△FBA∴AO BF =DO AB,∴56 BF =DO10,∴DO=253,在RtΔAOD中,AD=DO2-AO2=2532-52=203.∴矩形ABCD的面积为203×10=2003.【点睛】本题考查了切线的性质,相似三角形的性质与判定,勾股定理,矩形的性质,掌握以上知识是解题的关键.11(2022·青海西宁·中考真题)如图,在Rt△ABC中,∠C=90°,点D在AB上,以BD为直径的⊙O 与AC相切于点E,交BC于点F,连接DF,OE交于点M.(1)求证:四边形EMFC是矩形;(2)若AE=5,⊙O的半径为2,求FM的长.【答案】(1)详见解析(2)253【解析】(1)∵BD是⊙O的直径,∴∠BFD=90°,∴∠CFD=90°,∴⊙O与AC相切于点E,∴OE⊥AC,∴∠OEC=∠AEO=90°,又∴∠C=90°,∴∠C=∠CFD=∠OEC=90°,∴四边形EMFC是矩形.(2)解:在Rt△AOE中∠AEO=90°AE=5OE=OB=2,∴OA2=AE2+OE2,∴OA=AE2+OE2=52+22=3,∴AB=OA+OB=3+2=5,∴∠AEO=∠C=90°,∴OE⎳BC,∴△AEO∼△ACB,∴AE AC =AOAB,即5AC=35,∴AC =553,∴CE =AC -AE =553-5=253,∴四边形EMFC 是矩形,∴FM =CE =253.【点睛】本题考查了矩形的判定,相切,勾股定理,平行线的判定与性质以及相似三角形的判定与性质,解题的关键是:(1)根据各角之间的关系,找出四边形EMFC 的三个角均为直角.(2)利用勾股定理及相似三角形的性质,求出AC 的长度.12(2022·辽宁大连·中考真题)AB 是⊙O 的直径,C 是⊙O 上一点,OD ⊥BC ,垂足为D ,过点A 作⊙O 的切线,与DO 的延长线相交于点E .(1)如图1,求证∠B =∠E ;(2)如图2,连接AD ,若⊙O 的半径为2,OE =3,求AD 的长.【答案】(1)见解析(2)2213【解析】(1)解:∵OD ⊥BC ,∴∠ODB =90°,∵AE 是⊙O 的切线,∴∠OAE =90°,在ΔODB 和ΔOAE 中,∠ODB =∠OAE =90°,∠DOB =∠AOE ,∴∠B =∠E ;(2)解:如图,连接AC .∵⊙O 的半径为2,∴OA =OB =2,AB =4,∵在ΔODB 和ΔOAE 中,∠ODB =∠OAE =90°,∠DOB =∠AOE ,∴ΔODB ∼ΔOAE ,∴OD OA =OB OE ,即OD 2=23,∴OD =43,在RtΔODB中,由勾股定理得:OD2+DB2=OB2,∴DB=OB2-OD2=22-43 2=253.∵OD⊥BC,OD经过⊙O的圆心,∴CD=DB=253,∴BC=2DB=453.∵AB是⊙O的直径,C是⊙O上一点,∴∠ACB=90°,在RtΔACB中,由勾股定理得:AC2+BC2=AB2,2=83.∴AC=AB2-BC2=42-453在RtΔACD中,由勾股定理得:AC2+CD2=AD2,∴AD=AC2+CD2=83 2+253 2=2213.【点睛】本题考查切线的定义、圆周角定理、垂径定理、勾股定理、相似三角形的判定与性质等,综合性较强,熟练掌握上述知识点,通过证明ΔODB∼ΔOAE求出OD的长度是解题的关键.13(2022·青海·中考真题)如图,AB是⊙O的直径,AC是⊙O的弦,AD平分∠CAB交⊙O于点D,过点D作⊙O的切线EF,交AB的延长线于点E,交AC的延长线于点F.(1)求证:AF⊥EF;(2)若CF=1,AC=2,AB=4,求BE的长.【答案】(1)见解析(2)2【解析】(1)证明:连接OD,∵AD平分∠CAB,∴∠CAD=∠OAD,∵OA=OD,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴OD∥AF,∵EF为⊙O的切线,∴OD⊥EF,∴AF⊥EF.(2)解:由(1)得:OD∥AF,∴△ODE∽△AFE,∵AC=2,CF=1,∴AF=3,∵AB=4,∴OD=2,OB=2,∴OE:AE=OD:AF,设BE为x,∴OE=OB+BE=2+x,∴2+x 4+x =23,解得:x=2,即BE的长为2.【点睛】本题主要考查了切线的性质,相似三角形的判定和性质,熟练掌握切线的性质,相似三角形的判定和性质是解题的关键.14(2022·广西柳州·中考真题)如图,已知AB是⊙O的直径,点E是⊙O上异于A,B的点,点F是EB的中点,连接AE,AF,BF,过点F作FC⊥AE交AE的延长线于点C,交AB的延长线于点D,∠ADC的平分线DG交AF于点G,交FB于点H.(1)求证:CD是⊙O的切线;(2)求sin∠FHG的值;(3)若GH=42,HB=2,求⊙O的直径.【答案】(1)见解析(2)22(3)⊙O的直径为65【解析】(1)证明:连接OF.∵OA=OF,∴∠OAF=∠OFA,∵EF=FB,∴∠CAF=∠FAB,∴∠CAF=∠AFO,∴OF∥AC,∵AC⊥CD,∴OF ⊥CD ,∵OF 是半径,∴CD 是⊙O 的切线.(2)∵AB 是直径,∴∠AFB =90°,∵OF ⊥CD ,∴∠OFD =∠AFB =90°,∴∠AFO =∠DFB ,∵∠OAF =∠OFA ,∴∠DFB =∠OAF ,∵GD 平分∠ADF ,∴∠ADG =∠FDG ,∵∠FGH =∠OAF +∠ADG ,∠FHG =∠DFB +∠FDG ,∴∠FGH =∠FHG =45°,∴sin ∠FHG =sin45°=22(3)解:过点H 作HM ⊥DF 于点M ,HN ⊥AD 于点N .∵HD 平分∠ADF ,∴HM =HN ,S △DHF ∶S △DHB =FH ∶HB =DF ∶DB∵△FGH 是等腰直角三角形,GH =42∴FH =FG =4,∴DFDB=42=2设DB =k ,DF =2k ,∵∠FDB =∠ADF ,∠DFB =∠DAF ,∴△DFB ∽△DAF ,∴DF 2=DB •DA ,∴AD =4k ,∵GD 平分∠ADF∴FG AG =DF AD =12∴AG =8,∵∠AFB =90°,AF =12,FB =6,∴AB =AF 2+BF 2=122+622=65∴⊙O 的直径为65【点睛】本题是一道综合性题目,考查了圆的相关性质、切线的判定、相似三角形的判定和性质、角平分线性、勾股定理等知识,熟练掌握以上知识是解题的关键.15(2022·广西河池·中考真题)如图,AB 是⊙O 的直径,E 为⊙O 上的一点,∠ABE 的平分线交⊙O 于点C ,过点C 的直线交BA 的延长线于点P ,交BE 的延长线于点D .且∠PCA =∠CBD .(1)求证:PC为⊙O的切线;(2)若PC=22BO,PB=12,求⊙O的半径及BE的长.【答案】(1)见解析(2)⊙O的半径为3,BE的长为2【解析】(1)证明:连接OC,∵BC平分∠ABE,∴∠ABC=∠CBD,∵OC=OB,∴∠ABC=∠OCB,∵∠PCA=∠CBD,∴∠PCA=∠OCB,∵AB是直径,∴∠ACB=90°,∴∠ACO+∠OCB=90°,∴∠PCA+∠ACO=90°,∴∠PCO=90°,∴OC⊥PC,∵OC是半径,∴PC是OO的切线;(2)连接AE,设OB=OC=r,∵PC=22OB,∴PC=22r,∴OP=OC2+PC2=r2+(22r)2=3r,∵PB=12,∴4r=12,∴r=3,由(1)可知,∠OCB=∠CBD,∴OC=BD,△PCO∽△PDB∴OC BD =OPPB,∠D=∠PCO=90°,∴3 BD =9 12,∴BD=4,∵AB是直径,∴∠AEB=90°,∴∠AEB=∠D=90°,∴AE⎳PD,∴BE BD =BA BP,∴BE4=6 12,∴BE=2.【点睛】本题考查了切线的判定,勾股定理,等腰三角形的性质、相似三角形的性质与判定,平行线分线段成比例,解题的关键是学会添加常用辅助线,构造平行线解决问题.16(2022·山东聊城·中考真题)如图,点O是△ABC的边AC上一点,以点O为圆心,OA为半径作⊙O,与BC相切于点E,交AB于点D,连接OE,连接OD并延长交CB的延长线于点F,∠AOD=∠EOD.(1)连接AF,求证:AF是⊙O的切线;(2)若FC=10,AC=6,求FD的长.【答案】(1)见解析(2)FD的长为8310-83【解析】(1)根据SAS证△AOF≌△EOF,得出∠OAF=∠OEF=90°,即可得出结论;(2)根据勾股定理求出AF,证△OEC∽△FAC,设圆O的半径为r,根据线段比例关系列方程求出r,利用勾股定理求出OF,最后根据FD=OF-OD求出即可.(1)证明:在△AOF和△EOF中,OA=OE∠AOD=∠EOD OF=OF,∴△AOF≌△EOF(SAS),∴∠OAF=∠OEF,∵BC与⊙O相切,∴OE⊥FC,∴∠OAF=∠OEF=90°,即OA⊥AF,∵OA是⊙O的半径,∴AF是⊙O的切线;(2)解:在Rt△CAF中,∠CAF=90°,FC=10,AC=6,∴AF=FC2-AC2=8,∵BC与⊙O相切,AF是⊙O的切线∴∠OEC=∠FAC=∠90°,∵∠OCE=∠FCA,∴△OEC∽△FAC,∴EO AF =CO CF,设⊙O的半径为r,则r8=6-r10,解得r=8 3,在Rt△FAO中,∠FAO=90°,AF=8,AO=8 3,∴OF=AF2+AO2=8310,∴FD=OF-OD=8310-83,即FD的长为8310-83.【点睛】本题主要考查切线的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识,熟练掌握切线的判定和性质是解题的关键.17(2022·湖南湘西·中考真题)如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M.(1)求证:BC是⊙O的切线.(2)若CF=2,sin C=35,求AE的长.【答案】(1)见解析(2)1255【解析】(1)连接OE,方法一:∵AE平分∠BAC交BC于点E,∴∠BAC=2∠OAE,∵∠FOE=2∠OAE,∴∠FOE=∠BAC,∴OE∥AB,∵∠B=90°,∴OE ⊥BC ,又∵OE 是⊙O 的半径,∴BC 是⊙O 的切线;方法二:∵AE 平分∠BAC 交BC 于点E ,∴∠OAE =∠BAE ,∵OA =OE ,∴∠OAE =∠OEA ,∴∠BAE =∠OEA ,∴OE ∥AB ,∵∠B =90°,∴OE ⊥BC ,又∵OE 是⊙O 的半径,∴BC 是⊙O 的切线;(2)连接EF ,∵CF =2,sin C =35,∴OE OF +CF=35,∵OE =OF ,∴OE =OF =3,∵OA =OF =3,∴AC =OA +OF +CF =8,∴AB =AC •sin C =8×35=245,∵∠OAE =∠BAE ,∴cos ∠OAE =cos ∠BAE ,即AB AE =AE AF ,∴245AE=AE 3+3,解得AE =1255(舍去负数),∴AE 的长为1255.【点睛】本题主要考查切线的判定和三角函数的应用,熟练掌握切线的判定定理和三角函数是解题的关键.18(2022·甘肃兰州·中考真题)如图,⊙O 是△ABC 的外接圆,AB 是直径,OD ⊥OC ,连接AD ,∠ADO =∠BOC ,AC 与OD 相交于点E .(1)求证:AD 是⊙O 的切线;(2)若tan ∠OAC =12,AD =32,求⊙O 的半径.【答案】(1)见解析(2)2【解析】(1)证明:∵OD⊥OC,∴∠COD=90°,∵∠BOC+∠COD+∠AOD=180°,∴∠BOC+∠AOD=90°,∵∠ADO=∠BOC,∴∠ADO+∠AOD=90°,∵∠ADO+∠AOD+∠OAD=180°,∴∠OAD=90°,∵OA是⊙O的半径,∴AD是⊙O的切线;(2)解:∵AB是⊙O的直径,∴∠ACB=90°,∴∠B+∠BAC=90°,∵∠BAC+∠CAD=∠OAD=90°,∴∠B=∠CAD,∵∠B+∠BOC+∠OCB=∠ADO+∠CAD+∠AED=180°,∠ADO=∠BOC,∴∠AED=∠OCB,∵OB=OC,∴∠B=∠OCB,∴∠AED=∠CAD,∴DE=AD=32,∵OC=OA,∴∠OAC=∠OCA,∵OC⊥OD,∴∠COE=90°,∴tan∠OAC=tan∠OCA=OEOC =12,设OC=OA=R,则OE=12 R,在Rt△OAD中,∠OAD=90°,由勾股定理,得OD2=OA2+AD2,即12R+322=R2+32 2,解得:R=2或R=0(不符合题意,舍去),∴⊙O的半径为2.【点睛】本题考查切线的判定,解直角三角形,勾股定理,等腰三角形的判定,圆周角定理的推论,本题属圆的综合题目,熟练掌握相关性质与判定是解题的关键.19(2022·广东广州·中考真题)如图,AB是⊙O的直径,点C在⊙O上,且AC=8,BC=6.(1)尺规作图:过点O作AC的垂线,交劣弧AC于点D,连接CD(保留作图痕迹,不写作法);(2)在(1)所作的图形中,求点O到AC的距离及sin∠ACD的值.【答案】(1)作图见解析;(2)点O到AC的距离为3,sin∠ACD的值是55【解析】(1)解:①分别以A,C为圆心,适当长(大于AC长度的一半)为半径作弧,记两弧的交点为E;②作直线OE,记OE与AC交点为D;③连结CD,则线段AC的垂线DE、线段CD为所求图形,如下图所示;(2)解:记OD与AC的交点为F,如下图所示:∵OD⊥AC,∴F为AC中点,∴OF是△ABC的中位线,∴OF=12BC=3,∵OF⊥AC,∴OF的长就是点O到AC的距离;Rt△ABC中,∵AC=8,BC=6,∴AB=10,∴OD=OA=12AB=5,∴DF=OD-OF=5-3=2,∵F为AC中点,∴CF=12AC=4,Rt△CDF中,∵DF=2,CF=4,∴CD=25,则sin∠ACD=DFCD=225=55,∴点O到AC的距离为3,sin∠ACD的值是55.【点睛】本题考查了圆的基本性质、垂径定理及其推论、勾股定理、线段垂直平分线的尺规作图、锐角三角函数等,属于综合题,欲求某角的某三角函数值,首先想到的应该是能否在直角三角形中进行,如果没有现成的直角三角形,则需要设法构造(作辅助图形).20(2022·山东淄博·中考真题)已知△ABC是⊙O的内接三角形,∠BAC的平分线与⊙O相交于点D,连接DB.(1)如图1,设∠ABC的平分线与AD相交于点I,求证:BD=DI; 图1(2)如图2,过点D作直线DE∥BC,求证:DE是⊙O的切线; 图2(3)如图3,设弦BD,AC延长后交⊙O外一点F,过F作AD的平行线交BC的延长线于点G,过G作⊙O的切线GH(切点为H),求证:GF=GH. 图3【答案】(1)见解析(2)见解析(3)见解析【解析】(1)证明:∵AD是∠BAC的平分线,BI是∠ABC的平分线,∴∠BAD=∠DAC=∠CBD,∠ABI=∠IBC,∵∠BID=∠ABI+∠BAD,∠DBI=∠IBC+∠CBD,∴∠BID=∠DBI,∴BD=DI;(2)证明:连接OD,∵AD是∠BAC的平分线,∴BD=CD,∴OD⊥BC,∵DE∥BC,∴OD⊥DE,∵OD是⊙O的半径,∴DE是⊙O的切线;(3)证明:过点H作⊙O的直径HI,连接BH,HC,IC,∵HI是⊙O的直径,GH是⊙O的切线,∴∠HCI =∠IHG =90°,∴∠IHC +∠I =90°=∠IHC +∠GHC ,∴∠I =∠GHC ,∵∠HBG =∠I ,∴∠HBG =∠GHC ,∴△HBG ∽△CHG ,∴HG CG =GB HG,∴GH 2=GC ×GB ,∵AD ∥FG ,∴∠DAF =∠GFC ,∵∠DAF =∠DBC ,∴∠GFC =∠DBC ,∴△GFC ∽△GBF ,∴GF GB =GC GF,∴GF 2=GC ×GB ,∴GF 2=GH 2,∴GF =GH .【点睛】本题考查了切线的判定和性质,相似三角形的判定和性质,圆周角定理,垂径定理,解题的关键是正确寻找相似三角形解决问题,学会用转化的思想思考问题.。
(完整版)锐角三角函数与圆综合训练题(含答案)

数学锐角三角函数与圆综合训练题1、如图,D 为。
O 上一点,点 C 在直径BA 的延长线上, /CDA=/CBD. (1)求证:CD 2=CA?CB; (2)求证:CD 是。
O 的切线; (3)过点B 作。
O 的切线交 CD 的延长线于点 E,若BC=12 , tan/CDA=W,求BE 的长. 3 解答: (1)证明:/ CDA= / CBD , /C=/C, AADC ^ADBC ,—=—,即 CD 2=CA ?CB ;DC BC(2)证明:如图,连接 OD.. AB 是。
的直径,Z ADB=90 °, Z1 + Z3=90°. • •• OA=OD ,,/2=/3, . . / 1 + /2=90°.又/CDA=/CBD,即 /4=/1, Z4+ Z 2=90 °,即 / CDO=90 °,• •• ODXOA.又・••OA 是。
的半径,,CD 是。
的切线; (3)解:如图,连接 OE.• •• EB 、CD 均为 OO 的切线,ED=EB , OE± DB / ABD+ / DBE=90 Z OEB+ Z DBE=90 °, . . / ABD= / OEB, • . / CDA= / OEB .而 tan/CDA=W,「tan/OEB =J25J,3 BE 3• •• RtACDO^RtACBE, ...旦旦!* j:8=8, CB BE BE 3在 RtACBE 中,设 BE=x ,「.(x+8) 2=x 2+122解得 x=5.即 BE 的长为2、如图,AD 是^ABC 的角平分线,以点 C 为圆心,CD 为半径作圆交 BC 的延长线于点E,交AD 于点F,交 AE 于点 M ,且 / B= / CAE , EF : FD=4 : 3. (1)求证:点F 是AD 的中点; (2)求 cos/ AED 的值;(3)如果BD=10 ,求半径 CD 的长.解 (1)证明:.「AD 是△ ABC 的角平分线,,/1 = /2,答: ・• / ADE= / 1 + /B, /DAE=/2+ /3,且/B= / 3, . . / ADE= / DAE . . ED=EA ,.「ED 为。
数学《圆与相似三角形、三角函数综合题》专题训练(含答案)

2020-2021学年中考数学培优训练讲义(七)《圆与相似三角形、三角函数综合题》专题训练班级姓名座号成绩1.如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接PF.若tan∠FBC=,DF=,则PF的长为.2.如图AB是⊙O的直径,点C是的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且=,CE的延长线交DB的延长线于F,AF交⊙O于点H,当OB=2时,则BH的长为.(第1题图)(第2题图)(第3题图)3.如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC、PB,若cos∠PAB=,BC=1,则PO的长.4.已知:在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,交BC于点E.(1)如下左图,过点D作弦DF⊥AB垂足为H,连接EF交AB于G,求证:EF∥AC;(2)如下右图,在(1)的条件下,过点G作GN⊥BC垂足为N,若OG=3,EN=4,求线段DH的长.5.如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.(1)求证:EF是⊙O的切线;(2)连接DG,若AC∥EF时.①求证:KG2=KD•KE;②若cos C=,AK=,求BF的长.作业思考:1. 如图,四边形ABCD内接于⊙O,且对角线AC⊥BD,垂足为点E,过点C作CF⊥AB于点F,交BD于点G.(1)如图①,连接EF,若EF平分∠AFG,求证:AE=GE;(2)如图②,连接CO并延长交AB于点H,若CH为∠ACF的平分线,AD=3,且tan∠FBG=,求线段AH长.参考答案:1.如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.(1)求证:PF平分∠BFD.(2)若tan∠FBC=,DF=,求EF的长.【分析】(1)根据切线的性质得到OE⊥AD,由四边形ABCD的正方形,得到CD⊥AD,推出OE∥CD,根据平行线的性质得到∠EFD=∠OEF,由等腰三角形的性质得到∠OEF=∠OFE,根据角平分线的定义即可得到结论;(2)连接PF,由BF是⊙O的直径,得到∠BPF=90°,推出四边形BCFP是矩形,根据tan∠FBC =,设CF=3x,BC=4x,于是得到3x+=4x,x=,求得AD=BC=4,推出DF∥OE ∥AB于是得到DE:AE=OF:OB=1:1即可得到结论.【解答】解:(1)连接OE,BF,PF,∵∠C=90°,∴BF是⊙O的直径,∵⊙O与AD相切于点E,∴OE⊥AD,∵四边形ABCD的正方形,∴CD⊥AD,∴OE∥CD,∴∠EFD=∠OEF,∵OE=OF,∴∠OEF=∠OFE,∴∠OFE=∠EFD,∴EF平分∠BFD;(2)连接PF,∵BF是⊙O的直径,∴∠BPF=90°,∴四边形BCFP是矩形,∴PF=BC,∵tan∠FBC=,设CF=3x,BC=4x,∴3x+=4x,x=,∴AD=BC=4,∵点E是切点,∴OE⊥AD∴DF∥OE∥AB∴DE:AE=OF:OB=1:1∴DE=AD=2,∴EF==10.【点评】本题考查了切线的性质,正方形的性质,圆周角定理,等腰三角形的性质,平行线的性质,切割线定理,正确的作出辅助线是解题的关键.2.如图,AB是⊙O的直径,点C是的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且=,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.【分析】(1)先判断出∠AOC=90°,再判断出OC∥BD,即可得出结论;(2)先利用相似三角形求出BF,进而利用勾股定理求出AF,最后利用面积即可得出结论.【解答】证明:(1)连接OC,∵AB是⊙O的直径,点C是的中点,∴∠AOC=90°,∵OA=OB,CD=AC,∴OC是△ABD是中位线,∴OC∥BD,∴∠ABD=∠AOC=90°,∴AB⊥BD,∵点B在⊙O上,∴BD是⊙O的切线;解:(2)由(1)知,OC∥BD,∴△OCE∽△BFE,∴,∵OB=2,∴OC=OB=2,AB=4,,∴,∴BF=3,在Rt△ABF中,∠ABF=90°,根据勾股定理得,AF=5,∵S△ABF=AB•BF=AF•BH,∴AB•BF=AF•BH,∴4×3=5BH,∴BH=.【点评】此题主要考查了切线的判定和性质,三角形中位线的判定和性质,相似三角形的判定和性质,求出BF=3是解本题的关键.3.如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.(1)求证:PB是⊙O的切线;(2)求证:E为△PAB的内心;(3)若cos∠PAB=,BC=1,求PO的长.【分析】(1)连接OB,根据圆周角定理得到∠ABC=90°,证明△AOP≌△BOP,得到∠OBP=∠OAP,根据切线的判定定理证明;(2)连接AE,根据切线的性质定理得到∠PAE+∠OAE=90°,证明EA平分∠PAD,根据三角形的内心的概念证明即可;(3)根据余弦的定义求出OA,证明△PAO∽△ABC,根据相似三角形的性质列出比例式,计算即可.【解答】(1)证明:连接OB,∵AC为⊙O的直径,∴∠ABC=90°,∵AB⊥PO,∴PO∥BC∴∠AOP=∠C,∠POB=∠OBC,OB=OC,∴∠OBC=∠C,∴∠AOP=∠POB,在△AOP和△BOP中,,∴△AOP≌△BOP(SAS),∴∠OBP=∠OAP,∵PA为⊙O的切线,∴∠OAP=90°,∴∠OBP=90°,∴PB是⊙O的切线;(2)证明:连接AE,∵PA为⊙O的切线,∴∠PAE+∠OAE=90°,∵AD⊥ED,∴∠EAD+∠AED=90°,∵OE=OA,∴∠OAE=∠AED,∴∠PAE=∠DAE,即EA平分∠PAD,∵PA、PB为⊙O的切线,∴PD平分∠APB∴E为△PAB的内心;(3)解:∵∠PAB+∠BAC=90°,∠C+∠BAC=90°,∴∠PAB=∠C,∴cos∠C=cos∠PAB=,在Rt△ABC中,cos∠C===,∴AC=,AO=,∵△PAO∽△ABC,∴,∴PO===5.【点评】本题考查的是三角形的内切圆和内心、相似三角形的判定和性质、切线的判定,掌握切线的判定定理、相似三角形的判定定理和性质定理是解题的关键.4.已知:在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,交BC于点E.(1)如图1,求证:AD=CD;(2)如图2,过点D作弦DF⊥AB垂足为H,连接EF交AB于G,求证:EF∥AC;(3)如图3,在(2)的条件下,过点G作GN⊥BC垂足为N,若OG=3,EN=4,求线段DH的长.【分析】(1)如图1中,连接BD,利用等腰三角形的三线合一的性质证明即可.(2)如图2中,连接BD,想办法证明∠ADF=∠DFE即可.(3)连接AE.设OA=OB=r,则AB=BC=2r,BG=3+r,利用平行线分线段成比例定理,构建方程求出r,即可解决问题.【解答】(1)证明:如图1中,连接BD.∵AB是直径,∴∠ADB=90°,∴BD⊥AC,∵BA=BC,∴AD=CD.(2)证明:如图2中,连接BD.∵AB⊥DF,∴=,∴∠ADF=∠ABD,∵∠DFE=∠ABD,∴∠ADF=∠DFE,∴EF∥AC.(3)解:如图3中,连接AE.设OA=OB=r,则AB=BC=2r,BG=3+r,∵EG∥AC,∴=,∵BC=BA,∴BE=BG=3+r,∴BN=3+r﹣4=r﹣1,∵AB是直径,GN⊥BC∴∠AEB=∠GNB=90°,∴GN∥AE,∴=,∴=,解得r=9或﹣1(舍弃),∴BG=12,BN=8,∴NG===4,∴EG===2,∵GN∥AE,∴=,∴=,∴AE=6,∵∠C=∠DAH,∠AEC=∠AHD=90°,∴△AEC∽△DHA,∴==2,∴DH=3.【点评】本题属于圆综合题,考查了垂径定理,解直角三角形,平行线分线段成比例定理,等腰三角形的判定和性质等知识,教育的关键是学会添加常用辅助线,属于中考压轴题.5.如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.(1)求证:EF是⊙O的切线;(2)连接DG,若AC∥EF时.①求证:△KGD∽△KEG;②若cos C=,AK=,求BF的长.【分析】(1)连接OG,由EG=EK知∠KGE=∠GKE=∠AKH,结合OA=OG知∠OGA=∠OAG,根据CD⊥AB得∠AKH+∠OAG=90°,从而得出∠KGE+∠OGA=90°,据此即可得证;(2)①由AC∥EF知∠E=∠C=∠AGD,结合∠DKG=∠CKE即可证得△KGD∽△KGE;②连接OG,由设CH=4k,AC=5k,可得AH=3k,CK=AC=5k,HK=CK﹣CH=k.利用AH2+HK2=AK2得k=1,即可知CH=4,AC=5,AH=3,再设⊙O半径为R,由OH2+CH2=OC2可求得,根据知,从而得出答案.【解答】解:(1)如图,连接OG.∵EG=EK,∴∠KGE=∠GKE=∠AKH,又OA=OG,∴∠OGA=∠OAG,∵CD⊥AB,∴∠AKH+∠OAG=90°,∴∠KGE+∠OGA=90°,∴EF是⊙O的切线.(2)①∵AC∥EF,∴∠E=∠C,又∠C=∠AGD,∴∠E=∠AGD,又∠DKG=∠GKE,∴△KGD∽△KEG;②连接OG,∵,AK=,设,∴CH=4k,AC=5k,则AH=3k∵KE=GE,AC∥EF,∴CK=AC=5k,∴HK=CK﹣CH=k.在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即,解得k=1,∴CH=4,AC=5,则AH=3,设⊙O半径为R,在Rt△OCH中,OC=R,OH=R﹣3k,CH=4k,由勾股定理得:OH2+CH2=OC2,即(R﹣3)2+42=R2,∴,在Rt△OGF中,,∴,∴.【点评】本题是圆的综合问题,解题的关键是掌握等腰三角形的性质、平行线的性质,圆周角定理、相似三角形的判定与性质及切线的判定等知识点.作业思考:1.如图,四边形ABCD内接于⊙O,且对角线AC⊥BD,垂足为点E,过点C作CF⊥AB于点F,交BD于点G.(1)如图①,连接EF,若EF平分∠AFG,求证:AE=GE;(2)如图②,连接CO并延长交AB于点H,若CH为∠ACF的平分线,AD=3,且tan∠FBG=,求线段AH长.【分析】(1)由垂直的定义,角平分线的定义,角的和差证明EF=EI,同角的余角相等得∠AEF=∠GEI,四边形的内角和,邻补角的性质得∠FAE=∠IGE,最后根据角角边证明△AEF≌△GEI,其性质得AE=GE;(2)由圆周角定理,等角的三角函数值相等求出⊙O的半径为,根据平行线的性质,勾股定理,角平分线的性质定理,三角形相似的判定与性质,一元二次方程求出t的值为,最后求线段AH的长为.【解答】证明:(1)过点E作EI⊥EF交CF于点I,如图①所示:∵CF⊥AB,∴∠AFG=90°,又∵EF平分∠AFG,∴∠EFA=∠EFI=45°,又∵EF⊥EI,∴∠FEI=90°,又∵∠EFI+∠EIF=90°,∴∠EIF=45°,∴EF=EI,又∵∠EAF+∠AFG+∠FGE+∠GEA=360°,∠AFG=∠AEG=90°,∴∠EGF+∠FAE=180°,又∵∠EGF+∠EGI=180°,∴∠EGI=∠FAE,又∵∠AEB=∠AEF+∠FEG,∠FEI=∠GEI+∠FEG,∴∠AEF=∠GEI,在△AEF和△GEI中,,∴△AEF≌△GEI(AAS),∴AE=GE;(2)连接DO并延长,交⊙O于点P,连接AP,如图②甲所示:∵∠ABD与∠P是⊙O上弧AD所对的圆周角,∴∠ABD=∠P,又∵DP为⊙O的直径,∴∠PAD=90°,又∵tan∠FBG=,∴tan∠P==,又∵AD=3,∴AP=4,PD=5,∴OD=,过点H作HJ⊥AC于点J,过点O作OK⊥AC于点K,设AJ=3t,CF=x,如图②乙所示,∵HJ⊥AC,BD⊥AC,∴HJ∥BD,∴∠ABD=∠AHJ,又∵tan∠ABD=∴tan∠AHJ=,又∵AJ=3t,∴HJ=4t,在Rt△AHJ中,由勾股定理得:AH===5t,又∵CH是∠ACF的平分线,且HF⊥CF,HJ⊥AC,∴HF=HJ=4t,∴AF=AH+HF=9t,又∵CF=x,∴CJ=x,又∵∠BFG=∠GEC,∠FGB=∠EGC,∴△FBG∽△ECG,∴∠FBG=∠ECG,∴tan∠FCJ===,解得:x=12t,∴CF=CJ=12t,∴AC=15t,∴CK=t,又∵OK∥HJ,∴=,∴OK===t,∴在Rt△OCK中,由勾股定理得:OK2+KC2=OC2,即(t)2+(t)2=()2,解得:t=,或t=﹣(舍去),∴AH=5t=.【点评】本题综合考查了垂线的定义,平行线的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,解直角三角形,一元二次方程等相关知识,重点掌握相似三角形的判定与性质,难点是辅助线构建全等三角形,圆周角和相似三角形.。
专题 三角函数与圆-圆中三角形函数的综合运用
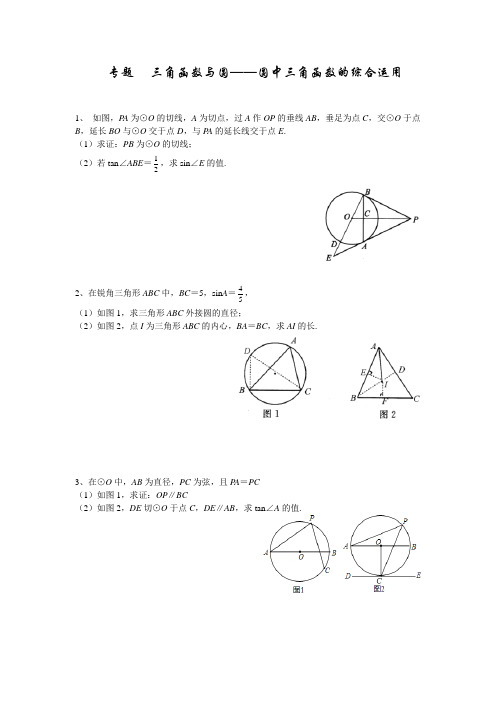
专题三角函数与圆——圆中三角函数的综合运用
1、如图,P A为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B,延长BO与⊙O交于点D,与P A的延长线交于点E.
(1)求证:PB为⊙O的切线;
(2)若tan∠ABE=1
2
,求sin∠E的值.
2、在锐角三角形ABC中,BC=5,sin A=4
5
,
(1)如图1,求三角形ABC外接圆的直径;
(2)如图2,点I为三角形ABC的内心,BA=BC,求AI的长.
3、在⊙O中,AB为直径,PC为弦,且P A=PC
(1)如图1,求证:OP∥BC
(2)如图2,DE切⊙O于点C,DE∥AB,求tan∠A的值.
4、如图,已知CD为⊙O的直径,点A为DC延长线上一点,B为⊙O上一点,且∠ABC =∠D.
(1)求证:AB为⊙O的切线;
(2)若tan D=1
2
,求sin A的值.
5、已知:如图PT是⊙O的切线,T为切点,P AB是经过圆心O的割线. (1)求证:∠PTA=∠BTO;
(2)若PT=4,P A=2,求sin B的值.
6、如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠AB C.(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC=2
3
,tan∠AEC=
5
3
,求圆的直径.
7、如图,AB为⊙O的直径,CE⊥AD于E,连BE,CD CB
. (1)求证:CE为⊙O的切线;
(2)若AE=6,⊙O的半径为5,求tan∠BEC的值.。
圆和三角函数结合经典例题

圆和三角函数结合经典例题很多朋友在学习数学课程时,都会遇到圆和三角函数,它们有很多共同之处,也能互相结合起来,被广泛应用在物理、化学、生物等科学方面,这篇文章将通过一些经典例题,阐述圆和三角函数之间的联系。
首先,让我们来介绍一下什么是圆和三角函数,圆是一种几何图形,由一个圆心和一个固定的半径构成,而三角函数则是一种数学模型,包括正弦、余弦和正切函数等。
而圆和三角函数之间的结合,主要体现在图形方面,例如:<b>例题1:在半径为1的圆上,求圆周上一点A的正弦函数值?</b>解:这里的点A的极坐标形式为(1,),其中α代表该点A与圆心构成的直线与正半轴之间的夹角,那么A点的正弦函数就是:sin α = y/1 = 1/1 = 1可以看出,圆的半径就是正弦函数的分母,其他情况也类似,比如:<b>例题2:在半径为2的圆上,求圆周上一点B的余弦函数值?</b>解:这里的点B的极坐标形式为(2,),其中β代表该点B与圆心构成的直线与正半轴之间的夹角,那么B点的余弦函数就是:cos β = x/2 = 2/2 = 1从上面的例题可以看出,圆与三角函数之间的结合,可以把圆周上的每一点看成是一个正弦、余弦和正切函数,由此可以用这些函数来表示和求解圆上的点与特定角度之间的距离。
此外,圆与三角函数结合还可以用来描述圆上椭圆的长短轴,其中长轴是圆周长,短轴是半径,因此椭圆的长短轴可以用圆的半径和圆周长来近似表示:2πR(R为半径)。
最后,圆也可以用三角函数的方法来绘制,比如,要想在极坐标系中绘制一个半径为2的圆,只需要将极坐标系中的点(x,y)替换成(2cosα,2sinα),即可把圆表示为三角函数,这样,圆就可以用三角函数的方式绘制出来。
综上所述,圆和三角函数之间的结合,可以应用在几何、物理、化学、生物等诸多学科中,它们的结合还可以用来描述圆上椭圆的长轴和短轴,也可以用来表示圆周上点与某个角度之间的距离,并且可以把圆绘制成三角函数的形式。
1-2-1 单位圆中的三角函数线

基 础 巩 固一、选择题1.(江苏苏州五中期中)角α的正弦线、余弦线和正切线的数量分别为a ,b ,c ,如果5π4<α<3π2,那么a ,b ,c 的大小关系为( )A .a >b >cB .b >c >aC .c >b >aD .a >c >b[答案] C2.已知角α的余弦线是长度为单位长度的有向线段,那么角α的终边在( )A .x 轴上B .y 轴上C .直线y =-x 上D .直线y =x 上 [答案] A3.下列各式正确的是( ) A .sin1>sin π3 B .sin1<sin π3 C .sin1=sin π3 D .sin1≥sin π3 [答案] B[解析] 1和π3的终边均在第一象限,且π3的正弦线大于1的正弦线,则sin1<sin π3.4.下列判断中错误的是( ) A .α一定时,单位圆中的正弦线一定B .单位圆中有相同正弦线的角相等C .α和α+π有相同的正切线D .有相同正切线的两个角的终边在同一直线上 [答案] B[解析] 有相同正弦线的角相差2π的整数倍,不一定相等,故选B.5.若MP 和OM 分别是角α=7π8的正弦线和余弦线,那么下列结论中正确的是( )A .MP <OM <0B .OM >0>MPC .OM <MP <0D .MP >0>OM[答案] D[解析] 作出单位圆中的正弦线、余弦线,比较知D 正确. 6.如图所示,角α的终边与单位圆交于点P ,过点P 作PM ⊥x 轴于点M ,过点A 作单位圆的切线AT 交OP 的反向延长线至点T ,则有( )A .sin α=OM ,cos α=PMB .sin α=MP ,tan α=OTC .cos α=OM ,tan α=ATD .sin α=MP ,tan α=AT[答案] D 二、填空题7.若角α的余弦线长度为0,则它的正弦线的长度为________. [答案] 18.若角α的正弦线的长度为12,且方向与y 轴的正方向相反,则sin α的值为________.[答案] -12 三、解答题9.解不等式组⎩⎪⎨⎪⎧sin x ≥0,2cos x -1>0.[解析] 由⎩⎪⎨⎪⎧sin x ≥0,2cos x -1>0,得⎩⎨⎧sin x ≥0,cos x >12,在直角坐标系中作单位圆,如图所示,由三角函数线可得⎩⎨⎧2k π≤x ≤2k π+π(k ∈Z ),2k π-π3<x <2k π+π3(k ∈Z ).解集恰好为图中阴影重叠的部分,故原不等式组的解集为{x |2k π≤x <2k π+π3,k ∈Z }.10.在单位圆中画出满足cos α=12的角α的终边,并写出α组成的集合.[解析] 如图所示,作直线x =12交单位圆于M 、N ,连接OM 、ON ,则OM 、ON 为α的终边.由于cos π3=12,cos 5π3=12,则M 在π3的终边上,N 在5π3的终边上,则α=π3+2k π或α=5π3+2k π,k ∈Z .所以α组成的集合为S ={α|α=π3+2k π或α=5π3+2k π,k ∈Z }.。
高中数学-单位圆与三角函数线练习

高中数学-单位圆与三角函数线练习(限时:10分钟)1.已知α(0<α<2π)的正弦线和余弦线相等,且符号相同,那么α的值为( ) A.3π4或π4 B.5π4或7π4 C.π4或5π4 D.π4或7π4答案:C2.已知角α的正弦线和余弦线是符号相反、长度相等的有向线段,则α的终边在( ) A .第一象限的角平分线上 B .第四象限的角平分线上 C .第二、四象限的角平分线上 D .第一、三象限的角平分线上解析:由条件知sin α=-cos α,α的终边应在第二、四象限的角平分线上. 答案:C3.若α是第一象限角,则sin α+cos α的值与1的大小关系是( ) A .sin α+cos α>1 B .sin α+cos α=1 C .sin α+cos α<1 D .不能确定解析:作出α的正弦线和余弦线,由三角形“任意两边之和大于第三边”的性质可知sin α+cos α>1.答案:A4.若π4<θ<π2,则下列不等式成立的是( )A .sin θ>cos θ>tan θB .cos θ>tan θ>sin θC .sin θ>tan θ>cos θD .tan θ>sin θ>cos θ解析:如图,由三角函数线可知,AT >PM >OP ,即tan θ>sin θ>cos θ答案:D5.已知π4<x <π2,a =21-sin x ,b =2cos x ,c =2tan x,试比较a 、b 、c 的大小.解析:如图所示,在单位圆中MP 、OM 、AT 分别是x 的正弦线、余弦线、正切线.在△OMP 中,OM >OP -MP 即cos x >1-sin x 又∵AT >OA ,∴tan x >1 ∴tan x >cos x >1-sin x , ∴2tan x>2cos x>21-sin x∴c >b >a(限时:30分钟)1.在[0,2π]上满足sin x ≥12的x 的取值范围是( )A.⎣⎢⎡⎦⎥⎤0,π6B.⎣⎢⎡⎦⎥⎤π6,5π6C.⎣⎢⎡⎦⎥⎤π6,2π3D.⎣⎢⎡⎦⎥⎤5π6,π解析:可以直接用特殊角来验证.取x =π6,则sin x =12≥12成立,故排除D ;再取x =π2,则sin x =1≥12成立,排除A ;再取x =5π6,则sin x =sin 5π6=12≥12成立,故选B.答案:B2.设a =sin(-1),b =cos(-1),c =tan(-1),则有( ) A .a <b <c B .b <a <c C .c <a <b D .a <c <b解析:如图作出角α=-1 rad 的正弦线、余弦线及正切线,显然b =cos(-1)=OM >0,c =tan(-1)<a =sin(-1)<0,即c <a <b .答案:C3.在(0,2π)内,使sin x >cos x 成立的x 的取值范围是( ) A.⎝⎛⎭⎪⎫π4,π2∪⎝ ⎛⎭⎪⎫π,54π B.⎝ ⎛⎭⎪⎫π4,π C.⎝ ⎛⎭⎪⎫π4,54π D.⎝ ⎛⎭⎪⎫π4,π∪⎝⎛⎭⎪⎫54π,32π解析:如图,当π4<α<5π4时,sin α>cos α,故选C.答案:C4.cos1,sin1,tan1的大小关系是( ) A .sin1<cos1<tan1 B .tan1<sin1<cos1 C .cos1<tan1<sin1 D .cos1<sin1<tan1解析:如图,有OM <MP <AT ,即cos1<sin1<tan1. 答案:D5.下列关系中正确的是( ) A .sin11°<cos10°<sin12° B .sin12°<sin11°<cos10° C .sin11°<sin 12°<cos10°D .sin12°<cos10°<sin11°解析:在单位圆中画出角12°,11°的相应正弦线,10°的相应余弦线,直接观察可知选C.答案:C6.在(0,2π)内使cos x >sin x >tan x 成立的x 的取值范围是( ) A.⎝⎛⎭⎪⎫π4,3π4 B.⎝ ⎛⎭⎪⎫5π4,3π2 C.⎝ ⎛⎭⎪⎫3π2,2π D.⎣⎢⎡⎦⎥⎤3π2,7π4解析:在同一个单位圆中分别作出正弦线、余弦线、正切线,即可看出. 答案:C7.若α、β为第二象限角,且sin α>sin β,则cos α与cos β的大小关系为__________. 解析:如图,显然有cos α>cos β. 答案:cos α>cos β 8.若θ∈⎝⎛⎭⎪⎫3π4,π,则下列各式错误的是________.①sin θ+cos θ<0; ②sin θ-cos θ>0; ③|sin θ|<|cos θ|; ④sin θ+cos θ>0.解析:若θ∈⎝ ⎛⎭⎪⎫3π4,π,则sin θ>0,cos θ<0,sin θ<|cos θ|,所以sin θ+cos θ<0.答案:④9.函数y =sin x +cos x -12的定义域是________.解析:由题意得⎩⎪⎨⎪⎧sin x ≥0,cos x ≥12,利用单位圆中的三角函数线得⎩⎪⎨⎪⎧2k π≤x ≤2k π+πk ∈Z ,2k π-π3≤x ≤2k π+π3k ∈Z .解得⎩⎨⎧x ⎪⎪⎪⎭⎬⎫2k π≤x ≤2k π+π3,k ∈Z .答案:⎩⎨⎧x ⎪⎪⎪⎭⎬⎫2k π≤x ≤2k π+π3,k ∈Z10.求函数y =log 2sin x 的定义域.解析:要使函数有意义,x 的取值满足sin x >0. 如图所示,MP →是角x 的正弦线,则有sin x =MP >0, ∴MP 的方向向上,∴角x 的终边在x 轴的上方, ∴2k π<x <2k π+π(k ∈Z ),即函数y =log 2sin x 的定义域是(2k π,2k π+π),k ∈Z .11.利用单位圆中的三角函数线,求满足⎩⎪⎨⎪⎧sin x ≥0,2cos x -1>0的x 的取值范围.解析:由⎩⎪⎨⎪⎧sin x ≥0,2cos x -1>0,得⎩⎪⎨⎪⎧sin x ≥0,cos x >12.如图所示,由三角函数线可得⎩⎪⎨⎪⎧2k π≤x ≤2k π+πk ∈Z ,2k π-π3<x <2k π+π3k ∈Z .此交集为图形中的阴影重叠部分, 即2k π≤x <2k π+π3(k ∈Z ).故x 的取值范围为{x |2k π≤x <2k π+π3,k ∈Z }.12.已知α∈⎝⎛⎭⎪⎫0,π2,求证:1<sin α+cos α<π2.证明:如图所示,设角α的终边与单位圆交于点P (x ,y ),过P 作PM ⊥Ox 、PN ⊥Oy ,M 、N 分别为垂足.∴|MP |=y =sin α,|OM |=x =cos α, 在△OMP 中,|OM |+|MP |>|OP |, ∴sin α+cos α>1.∵S △OAP =12|OA |·|MP |=12y =12sin α,S △OBP =12|OB |·|NP |=12x =12cos α, S 扇形OAB =14π×12=π4,又∵S △OAP +S △OBP <S 扇形OAB ,∴12sin α+12cos α<π4,即sin α+cos α<π2,∴1<sin α+cos α<π2.。
中考数学专题复习——锐角三角函数与圆的综合

2023年中考数学专题——锐角三角函数与圆的综合一、综合题1.如图,△ABC内接于⊙O,直径DE⊥AB于点F,交BC于点 M,DE的延长线与AC的延长线交于点N,连接AM.(1)求证:AM=BM;(2)若AM⊥BM,DE=8,∠N=15°,求BC的长.2.如图,D、E是以AB为直径的⊙O上两点,且∠AED=45°.(1)过点D作DC∥AB,求证:直线CD与⊙O相切;(2)若⊙O的半径为12,sin∠ADE=34,求AE的长.3.如图,四边形ABCD内接于⊙O,BD是⊙O的直径,点A为BD的中点,切线AE交CB的延长线于点E。
(1)求证:AE∥BD。
(2)若⊙O的半径为2.5,CD=4,求AE的长。
4.如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作CE⊥AC交AD的延长线于点E,F 为CE的中点,连结DB,DF.(1)求∠CDE的度数.(2)求证:DF是⊙O的切线.(3)若tan∠ABD=3时,求ACDE的值.5.如图,在⊙O中,C,D分别为半径OB,弦AB的中点,连接CD并延长,交过点A的切线于点E.(1)求证:AE⊥CE.(2)若AE=2,sin∠ADE=13,求⊙O半径的长.6.如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接BD、DE.(1)求DE是⊙O的切线;(2)设△CDE的面积为S1,四边形ABED的面积为S2,若S2=5S1,求tan∠BAC的值;(3)在(2)的条件下,连接AE,若⊙O的半径为2,求AE的长.7.如图,O是ABC∆的外接圆,连接OC,过点A作AD OC交BC的延长线于点D,45ABC∠= .(1)求证:AD是O的切线;(2)若3sin5CAB∠=,O的半径为,求AB的长.8.如图,AB是⊙O的直径, BC交⊙O于点D,E是BD的中点,连接AE交BC于点F,∠ACB =2∠EAB.(1)判断直线AC与⊙O的位置关系,并说明理由;(2)若3cos4C=,8AC=,求BF的长.9.如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.(1)求证:BA=BC;(2)若AG=2,cosB=35,求DE的长.10.如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于E,过点A作AF⊥AC于F交⊙O于D,连接DE,BE,BD(1)求证:∠C=∠BED;(2)若AB=12,tan∠BED=34,求CF的长.11.如图,AB为O的直径,BC为O的切线,AD OC‖,交O于点D,E为弧AB的中点,连接DE,交AB于点F.(1)求证:CD为O的切线;(2)求证:22AD OC OA⋅=;(3)若3cos5A=,求tan E .12.如图,在△ABC中,AB=AC,以AC边为直径作 O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.(1)求证:EF是 O的切线;(2)若EB=6,且sin∠CFD= 35,求 O的半径.13.如图,在Rt△ABC中,点在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD。
圆与相似三角形、三角函数专题(含答案)

圆与相似三角形、解直角三角形及二次函数的综合类型一:圆与相似三角形的综合1.如图,BC是⊙A的直径,△DBE的各个顶点均在⊙A上,BF⊥DE于点F.求证:BD·BE=BC·BF.2.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.(1)求证:点E是边BC的中点;(2)求证:BC2=BD·BA;(3)当以点O,D,E,C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.解:(1)连结OD,∵DE为切线,∴∠EDC+∠ODC=90°.∵∠ACB=90°,∴∠ECD+∠OCD=90°.又∵OD=OC,∴∠ODC=∠OCD,∴∠EDC=∠ECD,∴ED=EC.∵AC为直径,∴∠ADC=90°,∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,∴∠B=∠BDE,∴ED=EB,∴EB=EC,即点E为边BC的中点(2)∵AC为直径,∴∠ADC=∠ACB=90°.又∵∠B=∠B,∴△ABC∽△CBD,∴ABBC=BCBD,∴BC2=BD•BA(3)当四边形ODEC为正方形时,∠OCD=45°.∵AC为直径,∴∠ADC=90°,∴∠CAD=90°-∠OCD=90°-45°=45°,∴Rt△ABC为等腰直角三角形类型二:圆与解直角三角形的综合3.如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC的中点,DE⊥AB,垂足为点E,交AC的延长线于点F.(1)求证:直线EF是⊙O的切线;(2)已知CF=5,cosA=25,求BE的长.解:(1)连结OD.∵CD=DB,CO=OA,∴OD是△ABC的中位线,∴OD∥AB,AB=2OD.∵DE⊥AB,∴DE⊥OD,即OD⊥EF,∴直线EF是⊙O的切线(2)∵OD∥AB,∴∠COD=∠A,∴cos∠COD=cosA=25.在Rt△DOF中,∵∠ODF=90°,∴cos∠FOD=ODOF=25.设⊙O的半径为r,则rr+5=25,解得r=103,∴AB=2OD=AC =203.在Rt△AEF中,∵∠AEF=90°,∴cosA=AEAF=AE5+203=25,∴AE=143,∴BE =AB-AE=203-143=24.(2015·资阳)如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连结DE.(1)求证:DE是⊙O的切线;(2)连结AE,若∠C=45°,求sin∠CAE的值.解:(1)连结OD,BD,∵OD=OB,∴∠ODB=∠OBD.∵AB是直径,∴∠ADB=90°,∴∠CDB =90°.∵E为BC的中点,∴DE=BE,∴∠EDB=∠EBD,∴∠ODB+∠EDB=∠OBD+∠EBD,即∠EDO=∠EBO.∵BC是以AB为直径的⊙O的切线,∴AB⊥BC,∴∠EBO=90°,∴∠ODE =90°,∴DE是⊙O的切线(2)过点E作EF⊥CD于点F,设EF=x,∵∠C=45°,∴△CEF,△ABC都是等腰直角三角形,∴CF=EF=x,∴BE=CE=2x,∴AB=BC=22x.在Rt△ABE中,AE=AB2+BE2=10x,∴sin∠CAE=EFAE=10105.如图,△ABC内接于⊙O,直径BD交AC于点E,过点O作FG⊥AB,交AC于点F,交AB于点H,交⊙O于点G.(1)求证:OF·DE=OE·2OH;(2)若⊙O的半径为12,且OE∶OF∶OD=2∶3∶6,求阴影部分的面积.(结果保留根号)解:(1)∵BD是直径,∴∠DAB=90°.∵FG⊥AB,∴DA∥FO,∴△FOE∽△ADE,∴FOAD=OEDE,即OF•DE=OE•AD.∵O是BD的中点,DA∥OH,∴AD=2OH,∴OF•DE=OE•2OH (2)∵⊙O的半径为12,且OE∶OF∶OD=2∶3∶6,∴OE=4,ED=8,OF=6,∴OH=6.在Rt△OBH中,OB=2OH,∴∠OBH=30°,∴∠BOH=60°,∴BH=BO•sin60°=12×32=63,∴S阴影=S扇形GOB-S△OHB=60×π×122360-12×6×63=24π-183类型三:圆与二次函数的综合6.如图,在平面直角坐标系中,已知A(-4,0),B(1,0),且以AB为直径的圆交y轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.(1)求过A,B,C三点的抛物线的解析式;(2)求点D的坐标;(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.解:(1)y=-12x2-32x+2(2)以AB为直径的圆的圆心坐标为O′(-32,0),∴O′C=52,O′O=32.∵CD为圆O′的切线,∴O′C⊥CD,∴∠O′CO+∠DCO=90°.又∵∠CO′O+∠O′CO=90°,∴∠CO′O=∠DCO,∴△O′CO∽△CDO,∴O′OOC=OCOD,∴322=2OD,∴OD=83,∴点D的坐标为(83,0) (3)存在.抛物线的对称轴为直线x=-32,设满足条件的圆的半径为|r|,则点E的坐标为(-32+r,r)或F(-32-r,r),而点E在抛物线y=-12x2-32x+2上,∴r=-12(-32+|r|)2-32(-32+|r|)+2,∴r1=-1+292,r2=-1-292(舍去).故存在以线段EF为直径的圆,恰好与x轴相切,该圆的半径为-1+2927.如图,抛物线y=ax2+bx-3与x轴交于A,B两点,与y轴交于点C,经过A,B,C 三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为.设⊙M与y轴交于点D,抛物线的顶点为E.(1)求m的值及抛物线的解析式;(2)设∠DBC=α,∠CBE=β,求sin(α-β)的值;(3)探究坐标轴上是否存在点P,使得以P,A,C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.解:(1)由题意,可知C(0,-3),-b2a=1,∴抛物线的解析式为y=ax2-2ax-3(a>0).过点M作MN⊥y轴于点N,连结CM,则MN=1,CM=5,∴CN=2,于是m=-1.同理,可求得B(3,0),∴a×32-2a×3-3=0,解得a=1.∴抛物线的解析式为y=x2-2x-3 (2)由(1)得,A(-1,0),E(1,-4),D(0,1),∴△BCE为直角三角形,BC=32,CE=2,∴OBOD=31=3,BCCE=322=3,∴OBOD=BCCE,即OBBC=ODCE,∴Rt△BOD∽Rt △BCE,得∠CBE=∠OBD=β,因此sin(α-β)=sin(∠DBC-∠OBD)=sin∠OBC=COBC=22(3)显然Rt△COA∽Rt△BCE,此时点O(0,0).过点A作AP2⊥AC交y轴的正半轴于点P2,由Rt△CAP2∽Rt△BCE,得P2(0,13).过点C作CP3⊥AC交x轴的正半轴于点P3,由Rt△P3CA∽Rt△BCE,得P3(9,0).故在坐标轴上存在三个点P1(0,0),P2(0,13),P3(9,0),使得以P,A,C为顶点的三角形与△BCE相似。
最新圆中三角函数综合例题及练习

圆中的三角函数解决几何图形的三角函数求值问题,关键在于,找到相关的直角三角形.若没有现成的直角三角形,则需根据所给的条件,合理构造直角三角形,或把角进行转化。
圆中有关此类问题的解决也不例外,现就解题策略分析如下:一、用圆周角的性质把角转化到直角三角形中例1(成都市)如图1,已知AB 是⊙O 的直径,弦CD ⊥AB , 22AC =,BC =1,那么sin ∠ABD 的值是 .解析:在⊙O 中,∠ACD =∠ABD ;又由于AB 为⊙O 的直径,CD ⊥AB ,则∠ACD =∠ABC . Rt △ABC 中,AB =22BC AC +=221)22(+=3,从而sin ∠ABD =ABAC =322.评注:借用“同弧所对圆周角相等”,把要求函数值的角予以转化,充分本现了转化思想的巧妙运用。
二、用直径与所对圆周角构造直角三角形例2(烟台市)已知AB是半圆O 的直径,弦AD 、BC 相交于点P ,若∠DPB =α,那么CDAB等于A .sinαB .COSαC .tanαD .1tan α解析: 连结BD ,由于AB 为直径,则∠ADB =90°, 于是,在Rt △PBD 中,有COSα=PBPD, 而点C 和点A 在圆周上,所以∠A =∠C , 又∠APB =∠CPD ,则△APB ∽△CPD , 从而CD AB =PB PD ,所以CDAB=COSα,故选B 。
评注:直径所对的圆周角是直角。
由此,可以得到一个直角三角形,从而为使用三角函数创造条件,因此,在解题中,要倍加关注直径所对圆周角。
三、转化条件中的垂直关系构造直角三角形例3(武汉市)如图4,等腰三角形ABC 中,AC =BC =10,AB =12。
以BC 为直径作⊙O 交A B 于点D ,交AC 于点G ,DF ⊥AC ,垂足为F ,交CB 的延长线于点E 。
(1)求证:直线EF 是⊙O 的切线; (2)求sin ∠E 的值。
专题31 圆中的角与锐角三角函数(解析版)

专题31 圆中的角与锐角三角函数1、如图,△ABC内接于⊙O.(Ⅰ)如图①,连接OA,OC,若∠B=28°,求∠OAC的度数;(Ⅱ)如图②,直径CD的延长线与过点A的切线相交于点P.若∠B=60°,⊙O的半径为2,求AD,PD的长.解:(Ⅰ)∵∠AOC=2∠ABC,∠B=28°,∴∠AOC=56°,∵OA=OC,∴∠OAC=∠OCA,∴;(Ⅱ)如图②,连接OA.∵PA与⊙O相切于点A,∴PA⊥OA,∵∠AOC=2∠ABC,∠B=60°,∴∠AOC=120°.又OA=OD,∴△AOD是等边三角形,∴AD=OA=2,∵∠PAO=90°,∴∠P=30°.在Rt△PAO中,PO=2OA=4,∴PD=PO﹣OD=2.2、如图,在⊙O中,AB为⊙O的直径,C为⊙O上一点,P是的中点,过点P作AC的垂线,交AC的延长线于点D.(1)求证:DP是⊙O的切线;(2)若AC=5,sin∠APC=,求AP的长.(1)证明:∵P是的中点,∴=,∴∠PAD=∠PAB,∵OA=OP,∴∠APO=∠PAO,∴∠DAP=∠APO,∴AD∥OP,∵PD⊥AD,∴PD⊥OP,∴DP是⊙O的切线;(2)解:连接BC交OP于E,∵AB为⊙O的直径,∵P是的中点,∴OP⊥BC,CE=BE,∴四边形CDPE是矩形,∴CD=PE,PD=CE,∵∠APC=∠B,∴sin∠APC=sin∠APC==,∵AC=5,∴AB=13,∴BC=12,∴PD=CE=BE=6,∵OE=AC=,OP=,∴CD=PE=﹣=4,∴AD=9,∴AP===3.3、如图1所示,以点M(﹣1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,与⊙M相切于点H的直线EF交x轴于点E(﹣5,0),交y轴于点F(0,).(1)求⊙M的半径r;(2)如图2所示,连接CH,弦HQ交x轴于点P,若cos∠QHC=,求的值;(3)如图3所示,点P为⊙M上的一个动点,连接PE,PF,求PF+PE的最小值.解:(1)如图1,连接MH,∵E(﹣5,0),F(0,﹣),M(﹣1,0),∴OE=5,OF=,EM=4,∴在Rt△OEF中,tan∠OEF==,∴∠OEF=30°,∵EF是⊙M的切线,∴∠EHM=90°,∴sin∠MEH=sin30°=,∴MH=ME=2,即r=2;(2)如图2,连接DQ、CQ,MH.∵∠QHC=∠QDC,∠CPH=∠QPD,∴△PCH∽△PQD,∴,由(1)可知,∠HEM=30°,∴∠EMH=60°,∵MC=MH=2,∴△CMH为等边三角形,∴CH=2,∵CD是⊙M的直径,∴∠CQD=90°,CD=4,∴在Rt△CDQ中,cos∠QHC=cos∠QDC=,∴QD=CD=3,∴;(3)连MP,取CM的点G,连接PG,则MP=2,G(﹣2,0),∴MG=CM=1,∴,又∵∠PMG=∠EMP,∴△MPG∽△MEP,∴,∴PG=PE,∴PF+PE=PF+PG,当F,P,G三点共线时,PF+PG最小,连接FG,即PF+PE有最小值=FG,在Rt△OGF中,OG=2,OF=,∴FG===.∴PF+PE的最小值为.4、如图,⊙O的直径AB=10,弦BC=,点P是⊙O上的一动点(不与点A、B重合,且与点C分别位于直径AB的异侧),连接PA,PC,过点C作PC的垂线交PB的延长线于点D.(1)求tan∠BPC的值;(2)随着点P的运动,的值是否会发生变化?若变化,请说明理由,若不变,则求出它的值;(3)运动过程中,AP+2BP的最大值是多少?请你直接写出它来.解:(1)连接AC,∵AB是⊙O的直径,∴∠ACB=90°,在Rt△ABC中,AB=10,BC=2,∴AC==4,∴tan∠BPC=tan∠BAC==;(2)的值不会发生变化,理由如下:∵∠PCD=∠ACB=90°,∴∠1+∠PCB=∠2+∠PCB,∴∠1=∠2,∵∠3是圆内接四边形APBC的一个外角,∴∠3=∠PAC,∴△CBD∽△CAP,∴=,在Rt△PCD中,=tan∠BPC=,∴==;(3)由(2)知BD=AP,=2(AP+BP)=2(BD+BP)=2PD=,由tan∠BPC=,得:cos∠BPC=,∴AP+2BP=PC≤AB=10,∴AP+2BP的最大值为10.5、在图1至图3中,⊙O的直径BC=30,AC切⊙O于点C,AC=40,连接AB交⊙O于点D,连接CD,P是线段CD上一点,连接PB.(1)如图1,当点P,O的距离最小时,求PD的长;(2)如图2,若射线AP过圆心O,交⊙O于点E,F,求tan F的值;(3)如图3,作DH⊥PB于点H,连接CH,直接写出CH的最小值.解:(1)如图1,连接OP,∵AC切⊙O于点C,∵BC=30,AC=40,∴AB=50.由,即,解得CD=24,当OP⊥CD时,点P,O的距离最小,此时.(2)如图2,连接CE,∵EF为⊙O的直径,∴∠ECF=90°.由(1)知,∠ACB=90°,由AO2=AC2+OC2,得(AE+15)2=402+152,解得.∵∠ACB=∠ECF=90°,∴∠ACE=∠BCF=∠AFC.又∠CAE=∠FAC,∴△ACE∽△AFC,∴.∴.(3)CH的最小值为.解:如图3,以BD为直径作⊙G,则G为BD的中点,DG=9,∴点H总在⊙G上,GH=9,∴当点C,H,G在一条直线上时,CH最小,此时,,,即CH的最小值为.6、如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.(1)求证:BC是⊙O的切线;(2)求证:AD2=AB•AF;(3)若BE=8,sin B=,求AD的长,解:(1)如图1,连接OD,则OA=OD,∴∠ODA=∠OAD,∵AD是∠BAC的平分线,∴∠OAD=∠CAD,∴∠ODA=∠CAD,∴OD∥AC,∴∠ODB=∠C=90°,∵点D在⊙O上,∴BC是⊙O的切线;(2)如图2,连接OD,DF,EF,∵AE是⊙O的直径,∴∠AFE=90°=∠C,∴EF∥BC,∴∠B=∠AEF,∵∠AEF=∠ADF,∴∠B=∠ADF,由(1)知,∠BAD=∠DAF,∴△ABD∽△ADF,∴,∴AD2=AB•AF;(3)如图3,连接OD,由(1)知,OD⊥BC,∴∠BDO=90°,设⊙O的半径为R,则OA=OD=OE=R,∵BE=8,∴OB=BE+OE=8+R,在Rt△BDO中,sin B=,∴sin B==,∴R=5,∴AE=2OE=10,AB=BE+2OE=18,连接EF,由(2)知,∠AEF=∠B,∠AFE=∠C=90°,∴sin∠AEF=sin B=,在Rt△AFE中,sin∠AEF===,∴AF=由(2)知,AD2=AB•AF=18×=,∴AD==.7、如图,AB为圆O的直径,C为圆O上一点,D为BC延长线一点,且BC=CD,CE⊥AD于点E.(1)求证:直线EC为圆O的切线;(2)设BE与圆O交于点F,AF的延长线与CE交于点P,①求证:PC2=PF•PA②若PC=5,PF=4,求sin∠PEF的值.证明:(1)∵CE⊥AD于点E,∴∠DEC=90°,∵BC=CD,∴C是BD的中点,又∵O是AB的中点,∴OC是△BDA的中位线,∴OC∥AD,∴∠OCE=∠CED=90°,∴OC⊥CE,又∵点C在圆上,∴CE是圆O的切线;(2)①连接AC,∵OC⊥CE,∴∠ECO=90°,∵AB是直径,∴∠ACB=90°=∠ECO,∴∠ECA=∠OCB,∵OC=OB,∴∠OCB=∠OBC=∠ACE,∵∠ABF=∠ACF,∴∠OBC﹣∠ABF=∠ACE﹣∠ACF,∴∠EBC=∠ECF,且∠EBC=∠CAP,∴∠ECF=∠CAP,且∠CPF=∠CPA,∴△PCF∽△PAC,∴∴PC2=PF•PA②∵AB是直径,点F在圆上,∴∠AFB=∠PFE=90°=∠CEA,∵∠EPF=∠EPA,∴△PEF∽△PAE,∴∴PE2=PF•PA∴PE=PC在直角△PEF中,sin∠PEF=.8、如图,AB为⊙O的直径,CD⊥AB于点G,E是CD上一点,且BE=DE,延长EB至点P,连接CP,使PC=PE,延长BE与⊙O交于点F,连结BD,FD.(1)连结BC,求证:△BCD≌△DFB;(2)求证:PC是⊙O的切线;(3)若tan F=,AG﹣BG=,求ED的值.解:(1)证明:因为BE=DE,所以∠FBD=∠CDB,在△BCD和△DFB中:∠BCD=∠DFB∠CDB=∠FBDBD=DB所以△BCD≌△DFB(AAS).(2)证明:连接OC.因为∠PEC=∠EDB+∠EBD=2∠EDB,∠COB=2∠EDB,所以∠COB=∠PEC,因为PE=PC,所以∠PEC=∠PCE,所以∠PCE=∠COB,因为AB⊥CD于G,所以∠COB+∠OCG=90°,所以∠OCG+∠PEC=90°,即∠OCP=90°,所以OC⊥PC,所以PC是圆O的切线.(3)因为直径AB⊥弦CD于G,所以BC=BD,CG=DG,所以∠BCD=∠BDC,因为∠F=∠BCD,tan F=,所以∠tan∠BCD==,设BG=2x,则CG=3x.连接AC,则∠ACB=90°,由射影定理可知:CG2=AG•BG,所以AG=,因为AG﹣BG=,所以,解得x=,所以BG=2x=,CG=3x=2,所以BC=,所以BD=BC=,因为∠EBD=∠EDB=∠BCD,所以△DEB∼△DBC,所以,因为CD=2CG=4,所以DE=.9、如图1,在直角坐标系中,直线l与x、y轴分别交于点A(2,0)、B(0,)两点,∠BAO的角平分线交y轴于点D.点C为直线l上一点,以AC为直径的⊙G经过点D,且与x轴交于另一点E.(1)求出⊙G的半径r,并直接写出点C的坐标;(2)如图2,若点F为⊙G上的一点,连接AF,且满足∠FEA=45°,请求出EF的长?解:(1)连接GD,EC.∵∠OAB的角平分线交y轴于点D,∴∠GAD=∠DAO,∵GD=GA,∴∠GDA=∠GAD,∴∠GDA=∠DAO,∴GD∥OA,∴∠BDG=∠BOA=90°,∵GD为半径,∴y轴是⊙G的切线;∵A(2,0),B(0,),∴OA=2,OB=,在Rt△AOB中,由勾股定理可得:AB===设半径GD=r,则BG=﹣r,∵GD∥OA,∴△BDG∽△BOA,∴=,∴r=2(﹣r),∴r=,∵AC是直径,∴∠AEC=∠AOB=90°,∴EC∥OB,∴==,∴==,∴EC=2,AE=,∴OE=2﹣=,∴C的坐标为(,2);(2)过点A作AH⊥EF于H,连接CE、CF,∵AC是直径,∴AC=2×=∴∠AEC=∠AFC=90°∵∠FEA=45°∴∠FCA=45°∴在Rt△AEH中,由勾股定理可知:AF=CF=,设OE=a∴AE=2﹣a∵CE∥OB∴△ACE∽△ABO∴=,∴CE=2,∵CE2+AE2=AC2,∴22+(2﹣a)2=∴a=或a=(不合题意,舍去)∴AE=∴在Rt△AEH中,由勾股定理可得,AH=EH=,∴在Rt△AEH中,由勾股定理可知:FH2=AF2﹣AH2=()2﹣()2=2,∴FH=,∴EF=EH+FH=.10、如图,在平面直角坐标系中,A(0,4),B(3,4),P为线段OA上一动点,过O,P,B三点的圆交x轴正半轴于点C,连结AB,PC,BC,设OP=m.(1)求证:当P与A重合时,四边形POCB是矩形.(2)连结PB,求tan∠BPC的值.(3)记该圆的圆心为M,连结OM,BM,当四边形POMB中有一组对边平行时,求所有满足条件的m 的值.(4)作点O关于PC的对称点O',在点P的整个运动过程中,当点O'落在△APB的内部(含边界)时,请写出m的取值范围.解:(1)∵∠COA=90°∴PC是直径,∴∠PBC=90°∵A(0,4)B(3,4)∴AB⊥y轴∴当A与P重合时,∠OPB=90°∴四边形POCB是矩形(2)连结OB,(如图1)∴∠BPC=∠BOC∵AB∥OC∴∠ABO=∠BOC∴∠BPC=∠BOC=∠ABO∴tan∠BPC=tan∠ABO=(3)∵PC为直径∴M为PC中点①如图2,当OP∥BM时,延长BM交x轴于点N ∵OP∥BM∴BN⊥OC于N∴ON=NC,四边形OABN是矩形∴NC=ON=AB=3,BN=OA=4设⊙M半径为r,则BM=CM=PM=r∴MN=BN﹣BM=4﹣r∵MN2+NC2=CM2∴(4﹣r)2+32=r2解得:r=∴MN=4﹣∵M、N分别为PC、OC中点∴m=OP=2MN=②如图3,当OM∥PB时,∠BOM=∠PBO∵∠PBO=∠PCO,∠PCO=∠MOC∴∠OBM=∠BOM=∠MOC=∠MCO在△BOM与△COM中∴△BOM≌△COM(AAS)∴OC=OB==5∵AP=4﹣m∴BP2=AP2+AB2=(4﹣m)2+32∵∠ABO=∠BOC=∠BPC,∠BAO=∠PBC=90°∴△ABO∽△BPC∴∴PC=∴PC2=BP2=[(4﹣m)2+32]又PC2=OP2+OC2=m2+52∴[(4﹣m)2+32]=m2+52解得:m=或m=10(舍去)综上所述,m=或m=(4)∵点O与点O'关于直线对称∴∠PO'C=∠POC=90°,即点O'在圆上当O'与O重合时,得m=0当O'落在AB上时,则m2=4+(4﹣m)2,得m=当O'与点B重合时,得m=∴0≤m≤或m=11、如图F为⊙O上的一点,过点F作⊙O的切线与直径AC的延长线交于点D,过圆上的另一点B作AO的垂线,交DF的延长线于点M,交⊙O于点E,垂足为H,连接AF,交BM于点G.(1)求证:△MFG为等腰三角形.(2)若AB∥MD,求证:FG2=EG•MF.(3)在(2)的条件下,若DF=6,tan∠M=,求AG的长.(1)证明:连接OF.∵DM是⊙O的切线,∴DM⊥OF,∴∠MFG+∠OFA=90°,∵BM⊥AD,∴∠AHG=90°,∴∠OAF+∠AGH=90°,∵OF=OA,∴∠OFA=∠OAF,∵∠MGF=∠AGH,∴∠MFG=∠AGF,∴MF=MG,∴△MFG是等腰三角形.(2)证明:连接EF.∵AB∥DM,∴∠MFA=∠FAB,∵∠FAB=∠FEG,∠MFG=∠MGF,∴∠FEG=∠MFG,∵∠EGF=∠MGF,∴△EGF∽△FGM,∴=,∴FG2=EG•GM,∵MF=MG,∴FG2=EG•MF.(3)解:连接OB.∵∠M+∠D=90°,∠FOD+∠D=90°,∴∠M=∠FOD,∴tan M=tan∠FOD==,∵DF=6,∴OF=8,∵DM∥AB,∴∠M=∠ABH,∴tan M=tan∠ABH==,∴可以假设AH=3k,BH=4k,则AB=BG=5k,GH=k,AG=k,在Rt△OHB中,∵OH2+BH2=OB2,∴(8﹣3k)2+(4k)2=82,解得k=,∴AG=.12、如图,AB是⊙O的直径,弦CD⊥AB于点H,连接AC,过弧BD上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE.(1)求证:△ECF∽△GCE;(2)求证:EG是⊙O的切线;(3)延长AB交GE的延长线于点M,若,求EM的值.(1)证明:如图1中,∵AC∥EG,∴∠G=∠ACG,∵AB⊥CD,∴=,∴∠CEF=∠ACD,∴∠G=∠CEF,∵∠ECF=∠ECG,∴△ECF∽△GCE;(2)证明:如图2中,连接OE,∵GF=GE,∴∠GFE=∠GEF=∠AFH,∵OA=OE,∴∠OAE=∠OEA,∵∠AFH+∠FAH=90°,∴∠GEF+∠AEO=90°,∴∠GEO=90°,∴GE⊥OE,∴EG是⊙O的切线.(3)解:如图3中,连接OC.设⊙O的半径为r.在Rt△AHC中,tan∠ACH=tan∠G=,∵AH=3,∴HC=4,在Rt△HOC中,∵OC=r,OH=r﹣3,HC=4,∴(r﹣3)2+(4)2=r2,∴r=,∵GM∥AC,∴∠CAH=∠M,∵∠OEM=∠AHC,∴△AHC∽△MEO,∴=,∴=,∴EM=.13、如图,AB为⊙O的直径,CD⊥AB于点E,F是CD上一点,且BF=DF,延长FB至点P,连接CP,使PC=PF,延长BF与⊙O交于点G,连结BD,GD.(1)连结BC,求证:CD=GB;(2)求证:PC是⊙O的切线;(3)若tan G=,且AE﹣BE=,求FD的值.解:(1)∵BF=DF,∴∠BDF=∠DBF,在△BCD与△DGB中,,∴△BCD≌△DGB(AAS),∴CD=GB;(2)如图1,连接OC,∵∠COB=2∠CDB,∠CFB=∠CDB+∠DBF=2∠CDB,∴∠COB=∠CFB,∵PC=PF,∴∠COB=∠CFB=∠PCF,∵AB⊥CD,∴∠COB+∠OCE=90°,∴∠PCF+∠OCE=∠PCO=90°,∴OC⊥CP,∵OC是半径,∴PC是⊙O的切线;(3)如图2,连接AD,∵AB是⊙O的直径,∴∠ADB=90°,∵AB⊥CD,∴=,∴∠BDE=∠A=∠G,∵tan G=,∴tan A=,即AE=3DE,同理可得:DE=3BE,∴AE﹣BE=3DE﹣DE=,解得:DE=,∴CD=2DE=2,∴BE==,∴BD==,∵∠BCD=∠FDB,∠BDC=∠FBD,∴△BCD∽△FDB,∴,∵BC=BD,∴FD===.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆中的三角函数
解决几何图形的三角函数求值问题,关键在于,找到相关的直角三角形.若没有现成的直角三角形,则需根据所给的条件,合理构造直角三角形,或把角进行转化。
圆中有关此类问题的解决也不例外,现就解题策略分析如下:
一、用圆周角的性质把角转化到直角三角形中
例1(成都市)如图1,已知AB 是⊙O 的直径,弦CD ⊥AB,
22AC =,BC =1,那么sin ∠AB D的值是 .
解析:在⊙O 中,∠ACD =∠AB D;
又由于AB 为⊙O 的直径,CD ⊥AB ,则∠ACD =∠AB C. Rt △ABC 中,A B=
22BC AC +=221)22(+=3,
从而sin ∠ABD =AB
AC =32
2.
评注:借用“同弧所对圆周角相等”,把要求函数值的角予以转化,充分本现了转化思想
的巧妙运用。
二、用直径与所对圆周角构造直角三角形
例2(烟台市)已知A B是半圆O 的直径,弦AD 、BC 相交于点P ,若∠DPB =α,那么CD
AB
等于
A .sinα
B .
C OSα C.t anα D.1
tan α
解析: 连结BD ,由于AB 为直径,则∠ADB =90°, 于是,在Rt △PBD 中,有C OSα=
PB
PD
, 而点C 和点A 在圆周上,所以∠A =∠C , 又∠APB =∠CPD ,则△APB ∽△CPD , 从而
CD AB =PB PD ,所以CD
AB
=CO Sα,故选B。
评注:直径所对的圆周角是直角。
由此,可以得到一个直角三角形,从而为使用三角函数创造条件,因此,在解题中,要倍加关注直径所对圆周角。
三、转化条件中的垂直关系构造直角三角形
例3(武汉市)如图4,等腰三角形ABC 中,AC =BC =10,AB =12。
以B C为直径作⊙O 交AB 于点D ,交AC 于点G ,DF ⊥A C,垂足为F ,交CB 的延长线于点E 。
(1)求证:直线EF 是⊙O 的切线; (2)求sin ∠E的值。
解析:(1)证明:如图5,连结O D、CD ,
因为BC 是直径,所以CD ⊥AB , 而A C=BC ,则D 是AB 的中点 又因为O 是CB 的中点,所以O D//AC
由于DF ⊥AC,则OD ⊥E F,于是EF 是⊙O 的切线.
(2)连结BG ,因为B C是直径,所以∠BGC =90° 图 B D
E F G O
C B D
O
图1
E D
O
A
B
C
D
O B 在Rt △BCD 中,CD =
22AD AC -=22610-=8
而A B·CD =2ABC S ∆= A C·BG , 则有BG =
AC CD AB ⋅=10812⨯=5
48
. 在Rt △BCG 中,CG =22BG BC -=22
)548(
10-=5
14
; 又因为BG ⊥AC , DF ⊥AC ,所以B G//EF,
则∠E =∠CBG ,从而sin ∠E =sin ∠CBG =BC CG =10514
=25
7
评注:挖掘图形中的隐含关系,把已知条件中的垂直关系进行转化,从而构造直角三角形,为求角的函数值提供便利.
例4.如图,Rt △ABC 中, ∠AC B=90°,A C=4, B C=2, 以A B上的一点0为圆心作⊙O分别与AC .BC 相切于点D,E 。
(1)求⊙O 的半径。
(2)求sin ∠BOC 的值。
证:(1):连OE ,OD ,证四边形OECD 为正方形,设半径为R,
2R =44R -, R=3
4; (2)
10
10
3,作CM ⊥AB 于M ,易求AB=25.AB · CM=BC ·A C, ∴CM=
554,易求OC =R 2=324,∴sin ∠BOC=OC
CM =1010
3
例5.如图,等腰△ABC 中,AB=A C,以AB 为直径作⊙O, 交BC 于点D,D E⊥AC 于点E。
(1)求证:DE 为⊙O 的切线:
(2)若B C=45,A E=1,求co s ∠AEO 的值。
图5
E
B
解:(1)连OD, ∠C=∠ABC =∠O DB. OD//A C,∴ ∠O DE=∠D EC =90° (2) ∠AEO=∠D OE, co s∠AE O= co s∠D OE=OE
OD
,连DA.证C D=BD =25, 证△CDE∽△CDA,CD 2
=C E·CA=CE · (CE+1) ∴CE =4, DE=22CE CD -=2, OD=
21AC=2
5
,OE=22OD DE +=241,
∴cos ∠AEO== cos ∠DOE=
OE
OD =4141
5
●专练
1.如图,已知Rt△ABC 和Rt△EBC ,∠B =90°.以边AC 上的点D为圆心, OA 为半径的⊙O 与EC 相切于点D ,AD∥BC.
(l)求证: ∠E=∠AC B:
(2)若AD =1, tan ∠DAC=2
2
,求B C的长.
2.如图,已知点0是Rt△ABC的直角边AC 上一动点,以D为圆心,OA 为半径的⊙O 交AB于D 点, DB 的垂直平分线交BC 于F,交BD 于E 。
(l )连结DF,请你判断直线DF 与⊙O的位置关系,并证明你的结论 (2)当点D 运动到OA =2O C时,恰好有点D 是AE 的中点,求tan ∠B 。
A
F
D D
A B 3.如图,在△ABC 中.AB=BC ,以AB 为直径的⊙O 交AC 于点D .过D 作DF⊥BC,交AB 的延长线于点E,垂足为F . (1)求证;直线DE 是⊙O的切线;
(2) 当A B=5,AC=8时,求cos ∠E 的值.
4.如图,Rt△ABC 中, ∠C=90°,B D平分 ∠AB C,以AB 上一点0为圆心, 过B 、D 两点作⊙O,⊙O 交AB 于点E E F⊥AC (1)求证:⊙O 与AC 相切:
(2)若EF=2,BC =4,求ta n∠A 的值。
5.如图, △ABP 中,∠ABP=90°,以AB 为直径作⊙O 交AP 于点C,在弧AC 上取一点F,使弧C F=弧CB,过C 作AF 的垂线,垂足为M,MC 的延长线交BP 于D。
(1)求证:C D为⊙O 的切线。
(2)连BF 交AP 于B若BE =6,EF=2.求tan ∠FAE 。
6.如图,A B是⊙O的直径,AC 是弦,点D是BC 的中点,DP AC ⊥,垂足为点P .
(1)求证:P D是⊙O 的切线.
(2)若AC =6, cosA =3
5
,求PD 的长.
7.如图,⊙O的直径AB 交弦CD 于点M,且M 是CD 的中点.过点B作BE ∥ CD ,交A C的延长线于点E .连接B C.
(1)求证:BE 为⊙O 的切线;
(2)如果C D=6,tan ∠BC D=2
1
,求⊙O 的直径的长.
8.如图,△DEC 内接于⊙O ,AC 经过圆心O 交
O 于点B,且AC ⊥DE,垂足为F ,
连结AD、B E,若1
sin 2
A =
,∠BED =30°. (1)求证:AD 是⊙O 的切线;
(2)DCE △是否是等边三角形?请说明理由; (3)若O 的半径2R =,试求CE 的长.
B
A
B
A
C
9.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=,求的值.。
