正12面体画法
2024年中考数学一轮复习考点精讲课件—几何图形的初步

.
【详解】解:∵正方形厚纸板的边长为4 2,∴ = = 4 2,
∴ = 2 + 2 = 8,又∵ = = = ,∴ = = 2, = 4,
∴ = + = 6,故答案为:6.
考点二 直线、射线、线段的相关概念
一、直线、射线、线段的相关概念
2024年中考数学一轮复习考点精讲课件—几何图形的初步
主讲人:XXX
考点一 认识几何图形
几何图形的概念: 我们把实物中抽象出来的各种图形叫做几何图形,几何图形分为平面图形和立体图形.
立体图形的概念:有些几何图形的各个部分不都在同一平面内,这个图形叫做立体图形.
平面图形的概念:有些几何图形的各个部分在同一平面内的图形,这个图形叫做平面图形.
体体积分别记为:甲 和乙 .下列说法正确的是:
(
)
【详解】解:由图可知,设甲方案中长方体箱子的正方形底面的边
长为,长方体的高为
则
4 = 8
=2
解得
∴甲 = 2 × 2 × 10 = 40
2 + = 14
= 10
设乙方案中长方体箱子的正方形底面的边长为,长方体的高为
则
A.甲 > 乙
线段的性质:两点的所有连线中,线段最短. 简称:两点之间,线段最短.
线段的长度比较方法:1)度量法:分别用刻度尺测量线段AB、线段CD的长度,再进行比较
2)叠加法:让线段某一段端点重合,比较另一边两端点的位置.
线段中点的概念:把一条线段分成两条相等的线段的点叫线段中点.
考点二 直线、射线、线段的相关概念
为4cm的正方形纸片制作了如图所示的七巧板(如图 1)
,并设计了一幅作品“我跑步,我快乐”创作画(如图 2)
素描几何体——十二面体

素描几何体——十二面体教学目标:要求学生掌握物体的基本造型个性、理解物体的结构与基本透视。
教学重点:物体的形状个性、结构、透视教学难点:物体的分面、透视教学过程:一、石膏十二面体就是隶属于石膏几何形体训练的其中一个内容,它的特点为:块面齐整、造型简练、明暗表现清楚的几大特点,所以在素描练习中具有重要的地位,下面就它的结构特点与素描画法做一个简单的介绍。
二、结构特点这节课所介绍的多面体的基本形为五边形,而多面体则由十二个五边形所组成,每个五边形的各条边均与其她的五边形相连,形成一个完整的多面体,结构清楚、明暗效果直接明了,让画者很容易的区分黑白灰的层次感觉,便于绘画练习。
三、素描画法十二面体的素描画法具体分为一下几个步骤:第一步,考虑画面的构图,也就就是说把十二面体在纸上画多大,画在什么位置上。
第二步,用直线画出大的形状。
这个步骤画的时候用线不要太重,以便于后边几个步骤中能够进行修理。
第三步画出具体形状。
在进行这个步骤的绘画练习时,要把您所能瞧到的五边形全部绘画出来,但同时要注意,由于角度的不同,所瞧到的五边形也发生了很大的变化,既各边的长短在视觉上有了很大的差异。
第四步就是画出明暗效果,在十二面体的明暗表现时,由于它的块面特点,所以较为容易区分,不必要再先铺设大的色块,直接表现即可。
但就是再画的时候要注意每一个五边形,由于距离光线的远近不同,五边形本身也就会出现明暗的深浅变化,一般离光近的一边重,其它边要逐渐变浅。
第五步就是进行画面上的调整,在这个环节,要求画者要根据画面应有的效果去对画面进行修正,也就就是说要添加一些细节部分,去除掉一些繁琐的内容。
这样一幅十二面体的素描就画了出来。
四、作业石膏几何体——十二面体临摹五、作品欣赏。
素描第十二课ppt十二面体

几何特征与结构分析
二面角
相邻两个面之间的夹角在正则十 二面体中是相等的。
应用领域
在建筑设计、化学分子结构、游 戏设计等领域中,十二面体的形 态经常被采用。
01
02
对称性
正则十二面体具有很高的对称性 ,属于正多面体的一种。
03
结构稳定性
由于其高度对称和均匀分布的质 量,正则十二面体在几何结构上 是相对稳定的。
2024/1/25
16
明暗交界线确定和过渡自然
1
确定明暗交界线
明暗交界线是素描中表现物体立体感的 关键,它位于亮部与暗部的交界处。在 十二面体的素描中,要准确找出明暗交 界线的位置。
2
过渡自然
为了使画面看起来更加自然,需要在明 暗交界线两侧进行适当的过渡处理。可 以使用渐变的手法,使亮部逐渐过渡到 暗部,暗部逐渐过渡到亮部。
混乱。
2024/1/25
对比与统一
在画面布局中,要注意左右、上下的平衡, 避免画面倾斜或失重。
审美观念培养
通过欣赏优秀素描作品,学习构图、线条、 明暗等处理技巧,提高审美能力和创作水平 。
24
背景元素选择和搭配建议
背景元素选择
根据十二面体的特点和创作意图,选择合适的背景元素,如几何图形、抽象线 条、自然元素等。
立体感。
14
04
光影处理技巧在十二面体素描中应 用
2024/1/25
15
光源判断及投影规律掌握
确定光源方向
判断阴影形状
在素描十二面体时,首先要确定光源 的方向,这决定了阴影的落点和形状 。
根据光源方向和十二面体的结构,判 断阴影的形状和分布,注意阴影的虚 实变化。
理解投影规律
平面立体轴测投影图的画法

平面立体及其轴测投影
表3-1 轴间角和轴向伸缩系数
第7 页
平面立体及其轴测投影
第8 页
(二)轴测图的性质
由于轴测图是用平行投影法绘制的, 因此它具有平行投影的基本性质,即平 行性和等比性。 ➢ 平行性:形体上相互平行的线段,其
轴测投影也相互平行;与坐标轴平行 的线段,其轴测投影必与相应的轴测 轴平行,如图3-32所示。 ➢ 等比性:形体上两平行线段的长度之 比在投影图上保持不变。
(a)
(b)
(c) 图3-33 绘制三棱锥的正等轴测图
平面立体及其轴测投影
第 11 页
2.端面法
对于棱柱类和棱锥类形体,其轴测图通常可 先画出能反映其特征的一个端面或底面,然后以 此为基础画出可见侧棱和底边棱线,这种画法称 为端面法。利用端面法绘制棱台类形体的轴测图 时,通常先画出其上底面或下底面,然后以此为 基础画出可见侧棱,最后连接各侧棱的顶点,即 可完成形体的轴测图。
将空间物体连同确定其位置的直角坐标系,沿不平行 于任何一个坐标平面的方向,用平行投影法投射在某一选 定的单一投影面上所得到的具有立体感的图形,称为轴测 投影图,简称轴测图,如图3-31所示。
第3 页
图3-31 轴测图的形成
平面立体及其轴测投影
在轴测投影中,我们把选定的投影面P
称 为 轴 测 投 影 面 ; 把 空 间 直 角 坐 标 轴 OX ,
三棱锥的正等轴测图。
作图步骤: (1)在图3-33(a)中建立三棱锥的 坐标系O-XYZ,从而可确定三棱锥上S,A, B,C顶点的坐标值。为作图方便起见, 可使XOY坐标面与锥底面重合,OX轴通 过B点,OY轴通过C点。 (2)按轴间角120°画出正等轴测图 的轴测轴,然后沿各轴测轴上量取每个顶 点的坐标,以确定各顶点在轴测图中的位 置,如图3-33(b)所示。 (3)连接各顶点,擦去不可见棱线, 然后描深可见棱线,结果如图3-33(c) 所示。
立体几何知识点

高一上学期立体几何知识点一、点、线(直线、射线、线段)、平面1平面的表示方法平行四边形(平面a平面ABCD,平面AC)或三角形二、立体图形的画法斜二测1、x不变、y一半、夹角45度2、斜二测和原图形的面积比为f42直观图2-1直观图的定义:是观察者站在某一点观察一个空间几何体而画出的图形,直观图通常是在平行投影下画出的空间图形。
2-2斜二测法做空间几何体的直观图⑴在已知图形中取互相垂直的轴Ox、Oy,即取/xOy=90°;⑵画直观图时,把它画成对应的轴O‘x‘、O'y,取/x‘O‘y'=45°或135°,它们确定的平面表示水平平面;⑶在坐标系x‘o'y‘中画直观图时,已知图形中平行于数轴的线段保持平行性不变;平行于x轴的线段保持长度不变;平行于y轴的线段长度减半。
结论:采用2斜二测法作出的直观图的面积是原平面图形的—4看不到的线用虚线(或者不画)需要有立体感。
(想垂直就垂直,想在里就在里,想在外就在外。
)三、立体图形之间的关系。
1点和线的位置关系(点在线上,点在线外)2点和面的位置关系(点在面上,点在面外)3线和线的位置关系(平行、相交、异面)4线和面的位置关系(线在面上,线面平行,线面相交(线面垂直))5面和面的位置关系(平行、相交(重合))四、各种角的范围1、异面直线所成的角的取值范围是2、直线与平面所成的角的取值范围是3、斜线与平面所成的角的取值范围4、二面角的大小用它的平面角来度量;取值范围是五、射影定理㈠空间几何体的类型1多面体:由若干个平面多边形围成的几何体。
围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。
2旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。
其中,这条直线称为旋转体的轴。
棱柱多面体由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点;连接不在同一个面上的两个顶点的线段叫做多面体的对角线.按多面体的面数可把多面体分为四面体、五面体、六面体.其中,四个面均为全等的正三六、角形的四面体叫做正四面体.旋转体由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体.这条定直线叫做旋转体的轴.棱柱的结构特征一般地,有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱(prism).棱柱中,两个互相平行的面叫做底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的顶点.底面是三角形、四边形、五边形的棱柱分别叫做三棱柱、四棱柱、五棱柱,可以用表示底面各顶点的字母或一条对角线端点的字母表示棱柱,如下图的六棱柱可以表示为棱柱ABCDEF-A'B‘C‘D‘E'F‘或棱柱A’D.侧棱与底面不垂直的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱;底面是正多边形的直棱柱叫做正棱柱;底面是平行四边形的棱柱叫做平行六面体;侧棱与底面垂直的平行六面体叫做直平行六面体.斜棱柱直棱称正棱柱平行六面体七、直平行六面体1棱柱的结构特征1.1棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
9.9 棱柱与棱锥 第三课时 棱锥与它的性质、直棱柱和正棱锥的直观图的画法、正多面体

上一页
下一页
末页
瞻前顾后
要点突破
典例精析
演练广场
5.正棱锥的性质 (1)各侧棱相等,各侧面都是全等的等腰三角形.各等腰三角形底边上的高相等. (2)正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形;正棱锥的高、侧棱和 侧棱在底面内的射影也组成一个直角三角形. 6.直棱柱和正棱锥的直观图的画法 画直观图有四个步骤:①画轴(即建立三维空间直角坐标系);②画底面;③画侧棱(正棱 锥画高);④成图. 7.正多面体的概念 每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正 多面体,正多面体的各个面是全等的正多边形,各条棱是相等的线段.
解析:由于正棱锥的各侧棱长、斜高均相等,故对应的二面角、侧棱与底面所成的角也 相等,故①②正确.根据正棱锥的定义知④正确,对于③,其中的对角面有多种情况,如五 棱锥、六棱锥等,故③末页
瞻前顾后
要点突破
典例精析
演练广场
2.若正四棱锥的高为 6,侧棱长为 8,则棱锥的底面边长为( (A)2 7 (B)4 7 (C) 14 (D)2 14
2.棱锥的分类 棱锥的底面可以是三角形、四边形、五边形„„我们把这样的棱锥分别叫做三棱锥、四 棱锥、五棱锥„„ 3.棱锥的性质 定理:如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底 面面积的比等于顶点到截面距离与棱锥高的平方比. 4.正棱锥的概念 如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫 做正棱锥.
本题以四棱锥为载体,考查立体几何中的线面关系及空间角的概念和计算.
首页
上一页
下一页
末页
瞻前顾后
要点突破
典例精析
演练广场
正方体的12种画法

正方体的12种画法正方体是几何中最为常见的图形,它包含6个面,每一个面都相等。
画正方体有许多种方法,本文将探讨其中的十二种画法。
首先,我们以基本的正方形开始,这是基本的正方体的最基本的画法。
它只需要用户绘制四个平行的边和四个相交的角。
它看起来很简单,但千万不要低估它的实用性。
用这种方法画出来的正方体仍旧是完整的,而且画出来非常精确。
其次,有折线图法。
这种方法画出来的正方体更容易看清楚,即使是最复杂的正方体都可以用这种方法表达出来。
折线图法使用折线来表示正方体的面,这样可以清楚地看到其各个面的构造,而用线条和数学计算也可以确定出正方体的体积。
第三,有正多边形图法。
这种方法可以使用正多边形来表示正方体,比如正六边形、正十边形等等。
用正多边形表达出正方体可以更清楚地展示出正方体的六个面以及它们之间的联系,并且正多边形也可以有效地表达出正方体的体积。
第四,有立方体图法。
这种方法可以使用立方体的形状来画出正方体,根据立方体的三维面和每一个面的距离可以准确地表示出正方体的形状。
而且,立方体图法也可以准确地表达出正方体的面积和体积。
第五,有格子画法。
这种方法使用多个小格子来表示正方体,这种方法可以在很多不同的地方被应用,比如以视频游戏中经典的方块游戏来模拟正方体,或者以带有像素的3D图像来表示正方体等等。
第六,有立方图法。
这种方法可以使用立方图来表示正方体,立方图由六个面和八个顶点组成,无论是在空间还是在二维平面上,立方图都可以用来表示正方体的形状。
第七,有多边形画法。
这种方法可以使用多边形来表示正方体,大部分的情况下,多边形是正六边形或者正十二边形,这样可以清楚地表现出正方体的六个面和它们之间的相互联系。
对于多边形画法,关键在于如何控制多边形的形状和大小来表示出正方体,这样可以表示出正方体的体积。
第八,有连接图法。
这种方法可以使用连线或者箭头来表示正方体,关键在于如何把正方体的六个面和它们之间的联系表示出来。
陕西省榆林市横山区横山中学高中美术教案:正十二面体结构画法

单元(章节)课题结构素描本节课题十二面体结构画法三维目标知识与技能:要求学生掌握物体的基本造型个性、理解物体的结构和基本透视过程与方法:通过示范与讲解,在听讲中理解其结构与画法,在实践中进一步掌握画法。
情感、态度价值观:在学习中提升绘画技能,在实践中树立信心。
提炼的课题十二面体由于块面较多,结构复杂,对学生来说比较难,特别是在造型与观察中存在形体不准,观察方法单一。
教学重难点教学重点:物体的形状个性、结构、透视。
教学难点:物体的分面、透视。
教学过程导入示范与讲解一、十二面体的特点石膏十二面体是隶属于石膏几何形体训练的其中一个内容,它的特点为:块面齐整、造型简练、明暗表现清楚的几大特点,所以在素描练习中具有重要的地位,下面就它的结构特点和素描画法做一个简单的介绍二、结构特点这节课所介绍的多面体的基本形为五边形,而多面体则由十二个五边形所组成,每个五边形的各条边均与其他的五边形相连,形成一个完整的多面体,结构清楚、明暗效果直接明了,让画者很容易的区分黑白灰的层次感觉,便于绘画练习。
(如图)三、结构画法(示范与讲解)十二面体的素描画法具体分为一下几个步骤:第一步,考虑画面的构图,也就是说把十二面体在纸上画多大,画在什么位置上。
第二步,用直线画出大的形状。
这个步骤画的时候用线不要太重,以便于后边几个步骤中能够进行修理。
(如图)第三步画出具体形状。
在进行这个步骤的绘画练习时,要把你所能看到的五边形全部绘画出来,但同时要注意,由于角度的不同,所看到的五边形也发生了很大的变化,既各边的长短在视觉上有了很大的差异。
组织学生开展实践操作。
多孔材料建模
2、正12面体空间排布
利用草图工具栏,绘制如右图所示的正12面体,他 的12个面都是由5边形组成,每个边之间的夹角为 108°与正4面体的夹角109 °十分接近。
利用扫掠按钮将每个边进行扫掠并且填充成实体,如下左图所示。再 以左图为基本元素用对称与平移按钮将,绘制下右图所示的模型,作 为多孔材料的一个基本单元。
再利用布尔操作以及矩形阵列完成下面右图的模型创建。左图是文献中多孔 材 料的模型。
结论:由于正12面体在空间不能紧密排布(它的中间总有一定的夹角
使其不能紧密排布),也就是说不能满足分析中的一个顶点4个方向的 思路,因此几何模型仍不完美,对后续的网格划分有很大的影响。
3、六面体的球切
以长方体为例,将长方体分为4个部分每个部分为一个正方体,并在个4 个部分中画球使其恰好多出每个面一部分而又不完全切透,如下图(左) 所示。同理画出4个球体并对其进行布尔操作得到下图(右)所示的结果。
4、14面体的空间排布
上面的方法2中正12面体在空间不能密排,通过资料的查询了解到14面体在 空间是可以密排的,也就是说14面体能够满足分析中的1个顶点4个方向的 条件。14面体是由4个大5边形的面(A)、 8个小5边形的面(B)和2个6边 形的面(C)组成的。
A
B
C
14面体的3个不同面的顶点空间坐标是由以下的公式确定的(α=
通过上述的顶点坐标确定14面体三个基本面的位置,并利用草图工具栏绘 制出14面体,如下左图。再利用对称以及草图工具栏完成14面体的空间排 布,如下右图。
从上右图中可以发现14面体在空间排布的时候 是有规律的,通过分析得出规律单元是由6个 14面体及两个5边形A组成的的12面体和两个5 边形B组成的12面体构成;其中6个14面体的中 两两一组他们的6边形面分别向着X、Y、Z3个 方向4个12面体填充他们之间的空隙。
2023年人教版高考数学总复习第一部分考点指导第八章立体几何第一节基本立体图形

3π 27
·x3,
V球 V圆锥
4 =
273π·x3
=75m.06
,解得 m=33.36 克.
33π·x3
5.(求几何体的体积)某校开展社会实践活动,学生到工厂制作一批景观
灯箱(如图,在直四棱柱上加工,所有顶点都在棱上),灯箱最上面是正
方形,与之相邻的四个面都是全等的正三角形,灯箱底部是边长为 a 的
【解析】选 D.如图,过 C′作 C′M′∥y′轴,交 x′轴于 M′,
在△C′M′B′中,因为 B′C′与 x′轴垂直且 B′C′=2 2 ,
∠C′M′B′=45°,所以 C′M′=siBn′C45′ ° =2
2 2
=4.由斜二测
2
画法知 CM=2C′M′=8,所以△ABC 的边 AB 上的高为 8.
棱柱、棱锥、棱台的侧面分别是平行四边形、三角形、梯形. 判断棱台的方法:侧棱延长后是否交于一点.
2.旋转体的结构特征
(1)圆柱:矩形绕其__任__一__边__所在的直线旋转一周形成的轨迹围成的几何体. (2)圆锥:直角三角形绕其_直__角__边__所在的直线旋转一周形成的轨迹围成的几何体. (3)圆台:直角梯形绕其_垂__直__于__底___边__的__腰__所在的直线旋转一周形成的轨迹围成的
表面积 S 表面积=S 侧+2S 底
锥体(棱锥和圆锥)
S 表面积=S 侧+S 底
台体(棱台和圆台) S 表面积=S 侧+S 上+S 下
球
S=_4_π_R_2_
体积
V=_S_h_ V=13 _S_h_
V=13 (S 上+S 下
+ S上S下 )h
4 R3
V=__3_______
1.必修二 P106T8
正五棱锥直观图的简易画法
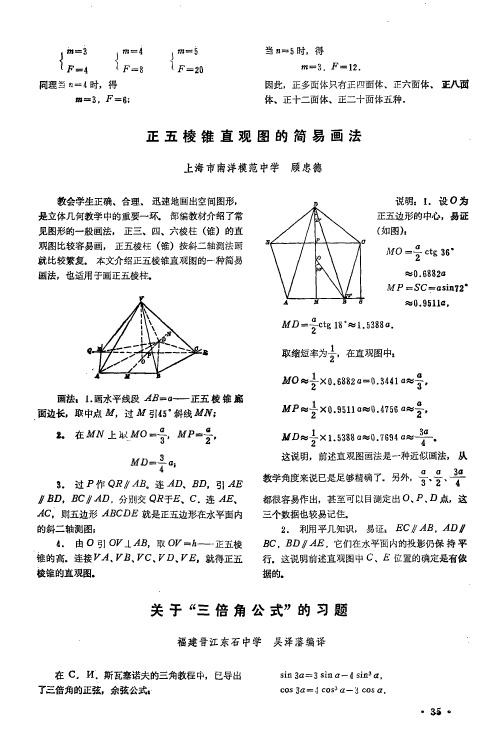
O 引 O犷 I A B
,
取 O犷 = h
、
— 就 得正 五
,
正 五棱
B D
它们在水平 面 内的投 影仍 保 持 平
、
行
.
这说明前述 直 观 图 中 C
。
百 位 置 的确 定是有依
棱 锥的 直 观图
。
据的
关 于
“
三 倍 角公 式
”
的 习 题
福 建 晋江 东 石 中 学
`
吴 泽 藩编 译
在 C
、
连 AE
都很 容 易作 出
2
.
,
甚 至 可 以 目测 定 出 O
. ,
D
点
,
,
这
I
则五边 形 A B C 刀 E 就是 正 五边形在 水 平面 内
.
三 个数据也较易 记 住
BC
,
的 斜二 轴 测 图 ,
4
利用平 几 知识 泌A E
,
`
易证
:
E C 产A B
A刀
锥的 高
。
由 连接 犷 A 犷刀 犷 C 犷 D 犷 E
。
MO
=
本 文介 绍 正 五棱 锥直 观 图 的一 种简 易
要 2
.
。
一
t g 36
。
, ,
’
也适 用 于 画 正五 棱柱
岛 0 6 88 2 a
盯P 二 S C =
透 皿
。
a s
in 7 2
,
.
岛 0 9 5 1 1。
c`g
M
D 一
昔
“
,
’
“ ` 5 3 88 a
基本体的三视图

五棱柱旳三视图
9
正五边形作图措施:
10
正五边形作图措施:
11
二、棱锥
S
A
C
B
12
注意:
三棱锥旳三视图
三棱锥左视图不
是一种等腰三角形。
s'
s"
a’ b' c' a"(c") b"
a
c
s
b
13
三、圆柱
转向(侧影)轮廓线旳投影。
转向(侧影) 转向(侧影)
轮廓线
轮廓线
14
孔转向(侧影)轮廓线旳投影
截交线为圆 截交线为矩形 截交线为椭圆 截交线为部分椭
圆
截交线为部分椭 圆
41
[例题一] 求侧平面与圆柱旳截交线
y
截平面平行圆柱轴线 截交线为矩形
42
y
[例题二]圆柱体被切片
y1 y
侧平面R 水平面Q 立体旋装90˚ 怎么体现?
43
y y1
[例题三]圆柱体开槽
y1 y
侧平面R
y y1
水平面Q
44
空心圆柱开圆孔
70
空心圆柱开马蹄槽
空心圆柱开键槽
71
60
[例题一] 完毕正方体与半圆柱相交旳主视图
61
[例题二] 求三棱柱穿孔后旳投影
c' b'
c" b"
a' a"
a c
b
62
[例题三] 完毕两圆柱旳相贯线
清除!
a'
b'
1'
2'
c'Leabharlann a" b" 1"
