【原创】R语言股票时间序列分析报告代码
【原创】R语言k-Shape时间序列聚类方法对股票价格时间序列聚类数据分析报告论文(含代码数据)

咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablogR语言k-Shape时间序列聚类方法对股票价格时间序列聚类数据分析报告来源:大数据部落| 有问题百度一下“”就可以了这次,我们将使用k-Shape时间序列聚类方法检查与我们有业务关系的公司的股票收益率的时间序列。
企业对企业交易和股票价格在本研究中,我们将研究具有交易关系的公司的价格变化率的时间序列的相似性,而不是网络结构的分析。
由于特定客户的销售额与供应商公司的销售额之比较大,当客户公司的股票价格发生变化时,对供应商公司股票价格的反应被认为更大。
k-Shapek-Shape [Paparrizos和Gravano,2015]是一种关注时间序列形状的时间序列聚类方法。
在我们进入k-Shape之前,让我们谈谈时间序列的不变性和常用时间序列之间的距离。
时间序列距离测度欧几里德距离(ED)和动态时间扭曲(DTW)通常用作距离测量值,用于时间序列之间的比较。
咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog两个时间序列x =(x1,...,xm)和y =(y1,...,ym)的ED,其中m是系列的长度如下。
DTW是ED的扩展,允许局部和非线性对齐。
k-Shape提出称为基于形状的距离(SBD)的距离。
k-Shape算法k-Shape聚类侧重于缩放和移位的不变性。
k-Shape有两个主要特征:基于形状的距离(SBD)和时间序列形状提取。
SBD互相关是在信号处理领域中经常使用的度量。
使用FFT(+α)代替DFT来提高计算效率。
归一化互相关(系数归一化)NCCc是互相关系列除以单个系列自相关的几何平均值。
检测NCCc最大的位置ω。
咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablogSBD取0到2之间的值,两个时间序列越接近0就越相似。
形状提取通过SBD找到时间序列聚类的质心向量有关详细的表示法,请参阅文章。
时间序列分析R语言代码

时间序列分析R语言代码时间序列分析是统计学中的一个重要分支,主要用于研究随时间变化的数据。
它可以帮助我们了解数据的趋势、周期性和季节性等特征,从而为预测和决策提供依据。
R语言是一种功能强大的统计分析工具,提供了丰富的时间序列分析函数和包,以下是一个简单的时间序列分析R语言代码示例。
首先,我们需要加载需要用到的包,如`ggplot2`和`forecast`。
```Rlibrary(ggplot2)library(forecast)```接下来,我们可以导入时间序列数据,并将其转换为时间序列对象。
假设我们有一个名为`data.csv`的数据文件,其中包含每个月份的销售额数据。
```Rdata <- read.csv("data.csv")ts_data <- ts(data$Sales, start = c(2000, 1), frequency = 12) ```通过绘制时间序列图,我们可以直观地观察数据的趋势和季节性。
```Rggplot(data, aes(x = Month, y = Sales)) +geom_line( +xlab("Month") +ylab("Sales") +theme_minimal``````R```接下来,我们可以通过绘制分解后的趋势、季节性和随机成分图来进一步研究数据的特征。
```Rtheme_minimal```我们还可以使用自回归移动平均模型(ARIMA)对时间序列数据进行建模和预测。
首先,我们需要估计ARIMA模型的参数。
```Rarima_model <- auto.arima(ts_data)```通过`auto.arima(`函数,R会自动选择最佳的ARIMA模型。
然后,我们可以使用这个模型来进行预测。
假设我们希望对未来12个月的销售额进行预测。
```Rforecast_data <- forecast(arima_model, h = 12)```最后,我们可以绘制预测结果和置信区间的图表。
【原创】R语言时间序列arima和随机森林模型预测分析报告(附代码数据)
##
## Model df: 4. Total lags used: 8
checkresiduals(lm_mod)
##
## Breusch-Godfrey test for serial correlation of order up to 10
## Q* = 2.2891, df = 5, p-value = 0.8079
##
## Model df: 3. Total lags used: 8
checkresiduals(arireg)
##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(2,2,1) errors
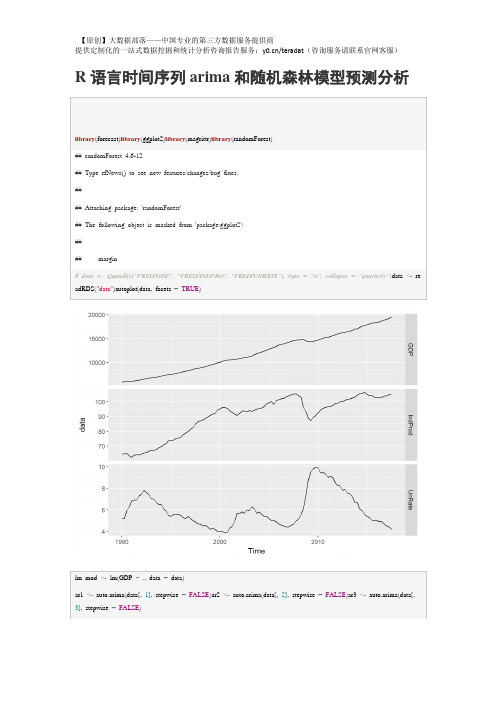
lm_mod<-lm(GDP~.,data=data)
ar1<-auto.arima(data[,1],stepwise=FALSE)ar2<-auto.arima(data[,2],stepwise=FALSE)ar3<-auto.arima(data[,3],stepwise=FALSE)
GDP<-forecast(ar1)$meanIndProd<-forecast(ar2)$meanUnRate<-forecast(ar3)$meanf3<-cbind(IndProd,UnRate)arireg<-auto.arima(data[,1],stepwise=FALSE,xreg=data[,-1])
summary(lm_mod)
##
## Call:
## lm(formula = GDபைடு நூலகம் ~ ., data = data)
时间序列分析R语言程序

#例2.1 绘制1964——1999年中国年纱产量序列时序图(数据见附录1.2)Data1.2=read.csv("C:\\Users\\Administrator\\De sktop\\附录1.2.csv",header=T)#如果有标题,用T;没有标题用Fplot(Data1.2,type='o')#例2.1续tdat1.2=Data1.2[,2]a1.2=acf(tdat1.2)#例2.2绘制1962年1月至1975年12月平均每头奶牛产奶量序列时序图(数据见附录1.3)Data1.3=read.csv("C:\\Users\\Administrator\\De sktop\\附录1.3.csv",header=F)tdat1.3=as.vector(t(as.matrix(Data1.3)))[1:168 ]#矩阵转置转向量plot(tdat1.3,type='l')#例2.2续acf(tdat1.3) #把字去掉pacf(tdat1.3)#例2.3绘制1949——1998年北京市每年最高气温序列时序图Data1.4=read.csv("C:\\Users\\Administrator\\De sktop\\附录1.4.csv",header=T)plot(Data1.4,type='o')##不会定义坐标轴#例2.3续tdat1.4=Data1.4[,2]a1.4=acf(tdat1.4)#例2.3续Box.test(tdat1.4,type="Ljung-Box",lag=6) Box.test(tdat1.4,type="Ljung-Box",lag=12)#例2.4随机产生1000个服从标准正态分布的白噪声序列观察值,并绘制时序图Data2.4=rnorm(1000,0,1)Data2.4plot(Data2.4,type='l')#例2.4续a2.4=acf(Data2.4)#例2.4续Box.test(Data2.4,type="Ljung-Box",lag=6) Box.test(Data2.4,type="Ljung-Box",lag=12) #例2.5对1950——1998年北京市城乡居民定期储蓄所占比例序列的平稳性与纯随机性进行检验Data1.5=read.csv("C:\\Users\\Administrator\\De sktop\\附录1.5.csv",header=T)plot(Data1.5,type='o',xlim=c(1950,2010),ylim=c (60,100))tdat1.5=Data1.5[,2]a1.5=acf(tdat1.5)#白噪声检验Box.test(tdat1.5,type="Ljung-Box",lag=6) Box.test(tdat1.5,type="Ljung-Box",lag=12)#例2.5续选择合适的ARMA模型拟合序列acf(tdat1.5)pacf(tdat1.5)#根据自相关系数图和偏自相关系数图可以判断为AR (1)模型#例2.5续 P81 口径的求法在文档上#P83arima(tdat1.5,order=c(1,0,0),method="ML")#极大似然估计ar1=arima(tdat1.5,order=c(1,0,0),method="ML") summary(ar1)ev=ar1$residualsacf(ev)pacf(ev)#参数的显著性检验t1=0.6914/0.0989p1=pt(t1,df=48,lower.tail=F)*2#ar1的显著性检验t2=81.5509/ 1.7453p2=pt(t2,df=48,lower.tail=F)*2#残差白噪声检验Box.test(ev,type="Ljung-Box",lag=6,fitdf=1) Box.test(ev,type="Ljung-Box",lag=12,fitdf=1) #例2.5续P94预测及置信区间predict(arima(tdat1.5,order=c(1,0,0)),n.ahead= 5)tdat1.5.fore=predict(arima(tdat1.5,order=c(1,0 ,0)),n.ahead=5)U=tdat1.5.fore$pred+1.96*tdat1.5.fore$seL=tdat1.5.fore$pred-1.96*tdat1.5.fore$seplot(c(tdat1.5,tdat1.5.fore$pred),type="l",col =1:2)lines(U,col="blue",lty="dashed")lines(L,col="blue",lty="dashed")#例3.1.1 例3.5 例3.5续#方法一plot.ts(arima.sim(n=100,list(ar=0.8))) #方法二x0=runif(1)x=rep(0,1500)x[1]=0.8*x0+rnorm(1)for(i in 2:length(x)){x[i]=0.8*x[i-1]+rnorm(1)}plot(x[1:100],type="l")acf(x)pacf(x)##拟合图没有画出来#例3.1.2x0=runif(1)x=rep(0,1500)x[1]=-1.1*x0+rnorm(1)for(i in 2:length(x)){x[i]=-1.1*x[i-1]+rnorm(1)}plot(x[1:100],type="l")acf(x)pacf(x)#例3.1.3方法一plot.ts(arima.sim(n=100,list(ar=c(1,-0.5)))) #方法二x0=runif(1)x1=runif(1)x=rep(0,1500)x[1]=x1x[2]=x1-0.5*x0+rnorm(1)for(i in 3:length(x)){x[i]=x[i-1]-0.5*x[i-2]+rnorm(1)}plot(x[1:100],type="l")acf(x)pacf(x)#例3.1.4x0=runif(1)x1=runif(1)x=rep(0,1500)x[1]=x1 x[2]=x1+0.5*x0+rnorm(1)for(i in 3:length(x)){x[i]=x[i-1]+0.5*x[i-2]+rnorm(1)}plot(x[1:100],type="l")acf(x)pacf(x)又一个式子x0=runif(1)x1=runif(1)x=rep(0,1500)x[1]=x1x[2]=-x1-0.5*x0+rnorm(1)for(i in 3:length(x)){x[i]=-x[i-1]-0.5*x[i-2]+rnorm(1)}plot(x[1:100],type="l")acf(x)pacf(x)#均值和方差smu=mean(x)svar=var(x)#例3.2求平稳AR(1)模型的方差例3.3mu=0mvar=1/(1-0.8^2) #书上51页#总体均值方差cat("population mean and var are",c(mu,mvar),"\n")#样本均值方差cat("sample mean and var are",c(mu,mvar),"\n")#例题3.4svar=(1+0.5)/((1-0.5)*(1-1-0.5)*(1+1-0.5))#例题3.6 MA模型自相关系数图截尾和偏自相关系数图拖尾#3.6.1法一:x=arima.sim(n=1000,list(ma=-2))plot.ts(x,type='l')acf(x)pacf(x)法二x=rep(0:1000)for(i in 1:1000){x[i]=rnorm[i]-2*rnorm[i-1]}plot(x,type='l')acf(x)pacf(x)#3.6.2法一:x=arima.sim(n=1000,list(ma=-0.5))plot.ts(x,type='l')acf(x)pacf(x)法二x=rep(0:1000)for(i in 1:1000){x[i]=rnorm[i]-0.5*rnorm[i-1]}plot(x,type='l')acf(x)pacf(x)##错误于rnorm[i] : 类别为'closure'的对象不可以取子集#3.6.3法一:x=arima.sim(n=1000,list(ma=c(-4/5,16/25))) plot.ts(x,type='l')acf(x)pacf(x)法二:x=rep(0:1000)for(i in 1:1000){x[i]=rnorm[i]-4/5*rnorm[i-1]+16/25*rnorm[i-2] }plot(x,type='l')acf(x)pacf(x)##错误于x[i] = rnorm[i] - 4/5 * rnorm[i - 1] + 16/25 * rnorm[i - 2] :##更换参数长度为零#例3.6续根据书上64页来判断#例 3.7拟合ARMA(1,1)模型,x(t)-0.5x(t-1)=u(t)-0.8*(u-1),并直观观察该模型自相关系数和偏自相关系数的拖尾性。
r语言时间序列预测代码

r语言时间序列预测代码一、引言R语言是一种广泛使用的统计软件,在做时间序列预测中有着非常重要的作用。
本文将介绍其在时间序列预测中的基本原理和应用例子,并提供R语言时间序列预测代码。
二、R语言时间序列预测原理时间序列预测就是根据历史数据预测未来数据发展的趋势。
它有三种主要的类型:趋势分析、季节性分析和平稳性分析。
趋势分析就是预测从过去到将来的趋势变化。
季节性分析就是预测一些带有明显季节性变动的变量,例如气温变化,季节性分析可以用来减少预测中的不确定性并预测出可能出现的短期变化。
平稳性分析就是预测在某一时间点之后,变量会围绕某一水平进行摆动的变化,这就是ARIMA模型。
R语言有三种常用的时间序列预测模型:ARIMA模型、自回归模型和移动平均模型。
三、R语言时间序列预测示例下面的示例使用R语言的ARIMA模型来预测一个出行指数的变化: # 导入模块library(forecast)# 读取数据data <- read.csv('travel_index.csv')# 将数据转换成时间序列data_ts <- ts(data, frequency =12,start=c(2015,1),end=c(2020,10))# 训练模型arima_model <- auto.arima(data_ts)# 预测forecast <- forecast(arima_model, h = 24)# 结果可视化plot(forecast)四、结论本文介绍了R语言在时间序列预测中的基本原理和应用,并提供了一个实例的R语言时间序列预测代码。
R语言在时间序列预测中有着广泛的应用,使用起来很方便,可以快速得到准确结果。
【原创】R语言股票时间序列分析报告代码

有问题到淘宝找“大数据部落”就可以了library(quantmod)# library(neuralnet)library(quantmod)library(plyr)library(TTR)library(ggplot2)library(scales)library(tseries)data=read.csv("600119.csv")a=data$收盘价a=diff(a)/a[-length(a)]a[a=="NaN"]=0a[a=="Inf"]=0##浏览数据data[,2]=data$日期data[,4]=c(0, a)##绘制时间序列图## 收集历史资料,加以整理,编成时间序列,并根据时间序列绘成统计图。
时间序列分析通常是把各种可能发生作用的因素进行分类,传统的分类方法是按各种因素的特点或影响效果分为四大类:(1)长期趋势;(2)季节变动;(3)循环变动;(4)不规则变动。
data=data[nrow(data):1,]plot(data[,2],data[,4])##技术指标lines( data[,2], DEMA(data[,4]) ,col="green")lines( data[,2], SMA(data[,4]) ,col="red")legend("bottomright",col=c("green","red"),legend =c("DEMA","SMA"),lty= 1,pch=1)有问题到淘宝找“大数据部落”就可以了## 从时间序列图形来看,序列有明显趋势,所以该序列一定不是平稳序列。
因为原序列为非平稳序列,所以选择一阶差分继续分析birthstimeseries=data[,4]birthstimeseries <-ts(birthstimeseries, frequency=300, start=c(1998,1 5))birthstimeseries=na.omit(birthstimeseries)## 2)Decompose the time series data into trend, seasonality and error components. (10 points)## 开始分解季节性时间序列。
R语言常用上机命令分功能整理——时间序列分析为主

R语言常用上机命令分功能整理——时间序列分析为主第一讲应用实例•R的基本界面是一个交互式命令窗口,命令提示符是一个大于号,命令的结果马上显示在命令下面。
•S命令主要有两种形式:表达式或赋值运算(用’<-’或者’=’表示)。
在命令提示符后键入一个表达式表示计算此表达式并显示结果。
赋值运算把赋值号右边的值计算出来赋给左边的变量。
•可以用向上光标键来找回以前运行的命令再次运行或修改后再运行。
•S是区分大小写的,所以x和X是不同的名字。
我们用一些例子来看R软件的特点。
假设我们已经进入了R的交互式窗口。
如果没有打开的图形窗口,在R中,用:> x11() 可以打开一个作图窗口。
然后,输入以下语句:x1 = 0:100x2 = x1*2*pi/100y = sin(x2)plot(x2,y,type="l")这些语句可以绘制正弦曲线图。
其中,“=”是赋值运算符。
0:100表示一个从0到100 的等差数列向量。
第二个语句可以看出,我们可以对向量直接进行四则运算,计算得到的x2 是向量x1的所有元素乘以常数2*pi/100的结果。
从第三个语句可看到函数可以以向量为输入,并可以输出一个向量,结果向量y的每一个分量是自变量x2的每一个分量的正弦函数值。
plot(x2,y, type="l",main="画图练习",sub="好好练", xlab="x轴",ylab='y轴')有关作图命令plot的详细介绍可以在R中输入help(plot)数学函数abs,sqrt:绝对值,平方根 log, log10, log2 , exp:对数与指数函数 sin,cos,tan,asin,acos,atan,atan2:三角函数 sinh,cosh,tanh,asinh,acosh,atanh:双曲函数简单统计量sum, mean, var, sd, min, max, range, median, IQR(四分位间距)等为统计量,sort,order,rank与排序有关,其它还有ave,fivenum,mad,quantile,stem等。
【原创】R语言数据挖掘预测模型的股票交易系统

4基于数据挖掘预测模型的股票交易系统根据上市保险公司的业务分析和财务分析来看,对投资者来投资中国平安的价值最高,由于实验运行时间较长,数据挖掘分析的方法相同,与选择哪家上市保险公司历史交易数据无关。
本文选择了中国人寿历史交易数据进行了数据挖掘与分析。
4.1数据来源本文所用数据为中国人寿(601628)历史交易数据,数据来源于雅虎财经网站(网址:https:// )。
获取方法为如下R 代码:library(tseries)CLI_Web_1 <- as.xts(get.hist.quote("601628.ss",start="2007-01-09",quote=c("Open", "High", "Low", "Close","V olume","AdjClose")))head(CLI_Web_1)并将所下载数据转换为R 中的时间序列对象(xts 对象),本实验的数据开始时间为2007年1月9日,结束时间为2016年6月4日。
4.2建模过程4.2.1数据处理用R 函数colnames 将下载数据整理成如下统一格式:Open High Low Close V olume Adjusted2007-01-09 37.00 40.20 37.00 38.93 319018900 34.162007-01-10 39.80 40.30 38.72 39.46 68610200 34.632007-01-11 38.80 39.60 37.01 38.29 43902500 33.602007-01-12 37.79 39.74 37.50 39.50 42177400 34.662007-01-15 39.82 43.45 38.95 43.45 56131900 38.132007-01-16 45.28 46.88 44.06 45.05 44567700 39.534.2.2 定义数据挖掘任务本模型所要解决的数据挖掘任务为预测任务。
R语言时间序列分析

2397.53 7600.60 5198.24 12600.08 5702.63 15151.84 5814.58 17914.66 6470.23 0.71 19756.21 7225.14 28541.72 9957.58 34061.01 12421.25 30114.41 9638.77 45060.69
同样的,这个文件(/tsdldata/data/fancy.dat )包含着一家位于昆士兰海滨度假圣地 的纪念品商店从 1987 年 1 月到 1987 年 12 月的每月销售数据(原始数据源于 Wheelwright and Hyndman, 1998)。我们将数据读入 R 使用以下代码:
1987 5021.82 1988 5496.43 1989 8573.17 1990 8093.06 1991 11637.39 1992 23933.38 1993 30505.41
1664.81 6423.48 2499.81 5835.10 4717.02 9690.50 5921.10 8476.70 4826.64 13606.89 7615.03 25391.35 10243.24 30821.33
使用 R 进行实现序列分析
o o o o
时间序列分析 读取时间序列数据 绘制时间曲线图 分解时间序列
分解非季节性数据 分解季节性数据 季节性的修正
o
使用指数平滑法进行预测
简单指数平滑法 Holt 指数平滑法 Holt-Winters 指数平滑法
o
ARIMA 模型
时间序列的差分 选择一个合适的 ARIMA 模型
o
使用 ARIMA 模型进行预测
链接与拓展阅读
时间序列分析
使用R语言进行时间序列(arima,指数平滑)分析

使用R语言进行时间序列(arima,指数平滑)分析读时间序列数据您要分析时间序列数据的第一件事就是将其读入R,并绘制时间序列。
您可以使用scan()函数将数据读入R,该函数假定连续时间点的数据位于包含一列的简单文本文件中。
数据集如下所示:••••••••••••••••Age of Death of Successive Kings of England#starting with William the Conqueror#Source: McNeill, "Interactive Data Analysis"604367505642506568436534...仅显示了文件的前几行。
前三行包含对数据的一些注释,当我们将数据读入R时我们想要忽略它。
我们可以通过使用scan()函数的“skip”参数来使用它,它指定了多少行。
要忽略的文件顶部。
要将文件读入R,忽略前三行,我们键入:•••> kings[1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48[26] 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56在这种情况下,英国42位连续国王的死亡年龄已被读入变量“国王”。
一旦将时间序列数据读入R,下一步就是将数据存储在R中的时间序列对象中,这样就可以使用R的许多函数来分析时间序列数据。
要将数据存储在时间序列对象中,我们使用R中的ts()函数。
例如,要将数据存储在变量'kings'中作为R中的时间序列对象,我们键入:••••••Time Series:Start = 1End = 42Frequency = 1[1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48[26] 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56有时,您所拥有的时间序列数据集可能是以不到一年的固定间隔收集的,例如,每月或每季度。
【原创】R语言案例数据分析可视化报告 (附代码数据)

R语言案例数据分析可视化报告这个问题集的目标是让你参与到R中的一些活动中,并且在欣赏数据可视化的重要性的同时进行一个深思熟虑的练习。
对于每个问题,创建一个代码块或文本响应,完成/回答所请求的活动或问题。
Questions计算每列的均值,方差和每对之间的相关性library(ggplot2)library(GGally)library(fBasics)## Loading required package: timeDate## Loading required package: timeSeries#### Rmetrics Package fBasics## Analysing Markets and calculating Basic Statistics## Copyright (C) 2005-2014 Rmetrics Association Zurich## Educational Software for Financial Engineering and Computational Science## Rmetrics is free software and comes with ABSOLUTELY NO WARRANTY.basicStats(data, ci = 0.95)## x1 x2 x3 x4 y1 y2## nobs 11.000000 11.000000 11.000000 11.000000 11.000000 11.000000## NAs 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000## Minimum 4.000000 4.000000 4.000000 8.000000 4.260000 3.100000## Maximum 14.000000 14.000000 14.000000 19.000000 10.840000 9.260000## 1. Quartile 6.500000 6.500000 6.500000 8.000000 6.315000 6.695000## 3. Quartile 11.500000 11.500000 11.500000 8.000000 8.570000 8.950000## Mean 9.000000 9.000000 9.000000 9.000000 7.500909 7.500909## Median 9.000000 9.000000 9.000000 8.000000 7.580000 8.140000## Sum 99.000000 99.000000 99.000000 99.000000 82.510000 82.510000## SE Mean 1.000000 1.000000 1.000000 1.000000 0.612541 0.612568## LCL Mean 6.771861 6.771861 6.771861 6.771861 6.136083 6.136024## UCL Mean 11.228139 11.228139 11.228139 11.228139 8.865735 8.865795## Variance 11.000000 11.000000 11.000000 11.000000 4.127269 4.127629 ## Stdev 3.316625 3.316625 3.316625 3.316625 2.031568 2.031657## Skewness 0.000000 0.000000 0.000000 2.466911 -0.048374 -0.978693## Kurtosis -1.528926 -1.528926 -1.528926 4.520661 -1.199123 -0.514319 ## y3 y4## nobs 11.000000 11.000000## NAs 0.000000 0.000000## Minimum 5.390000 5.250000## Maximum 12.740000 12.500000## 1. Quartile 6.250000 6.170000## 3. Quartile 7.980000 8.190000## Mean 7.500000 7.500909## Median 7.110000 7.040000## Sum 82.500000 82.510000## SE Mean 0.612196 0.612242## LCL Mean 6.135943 6.136748## UCL Mean 8.864057 8.865070## Variance 4.122620 4.123249## Stdev 2.030424 2.030579## Skewness 1.380120 1.120774## Kurtosis 1.240044 0.628751cor(data, use="complete.obs", method="kendall")## x1 x2 x3 x4 y1 y2## x1 1.00000000 1.00000000 1.00000000 -0.4264014 0.6363636 0.56363636 ## x2 1.00000000 1.00000000 1.00000000 -0.4264014 0.6363636 0.56363636 ## x3 1.00000000 1.00000000 1.00000000 -0.4264014 0.6363636 0.56363636 ## x4 -0.42640143 -0.42640143 -0.42640143 1.0000000 -0.4264014 -0.42640143 ## y1 0.63636364 0.63636364 0.63636364 -0.4264014 1.0000000 0.56363636 ## y2 0.56363636 0.56363636 0.56363636 -0.4264014 0.5636364 1.00000000 ## y3 0.96363636 0.96363636 0.96363636 -0.4264014 0.6000000 0.60000000 ## y4 -0.09090909 -0.09090909 -0.09090909 0.4264014 -0.1636364 -0.01818182 ## y3 y4## x1 0.96363636 -0.09090909## x2 0.96363636 -0.09090909## x3 0.96363636 -0.09090909## x4 -0.42640143 0.42640143## y1 0.60000000 -0.16363636## y2 0.60000000 -0.01818182## y3 1.00000000 -0.05454545## y4 -0.05454545 1.00000000ggcorr(data, geom = "blank", nbreaks = 5, label = TRUE,palette = "RdYlBu", hjust = .75)+geom_point(size = 10, aes(color = coefficient > 0, alpha = abs(coefficient) > 0.4)) +scale_alpha_manual(values = c("TRUE" = 0.25, "FALSE" = 0)) +guides(color = FALSE, alpha = FALSE)3.为每个x,yx,y数据对创建散点图。
【原创】R语言对股票数据进行LDA判别分析预测(附代码数据)

得到模型的结果 其中,第一个参数是判别式的形式,第二个参数是用 来训练的样本数据。lda 命令执行后, 会输出构成判别 式的各个系数。
## Call: ## lda(Direction ~ Lag1 + Lag2, data = Smarket, subset = train) ##
【原创】附代码数据 有问题到淘宝找“大数据部落”就可以了
## 3rd Qu.:2004 ## Max. ## ## Min. :2005
3rd Qu.: 0.596750 Max. : 5.733000 Lag4 Min.
3rd Qu.: 0.596750 Max. : 5.733000 Lag5 Min. :-4.92200
Lag3 :-4.922000
3rd Qu.: 0.596750 Max. : 5.733000
数据相关性
cor(Smarket[-9])
## ## Year ## Lag1 ## Lag2 ## Lag3 ## Lag4 ## Lag5
Year
Lag1
Lag2
Lag3
Lag4
1.00000000 0.029699649 0.030596422 0.033194581 0.035688718 -0.026294328 -0.010803402 -0.002985911 0.03059642 -0.026294328 1.000000000 -0.025896670 -0.010853533 0.03319458 -0.010803402 -0.025896670 1.000000000 -0.024051036 0.03568872 -0.002985911 -0.010853533 -0.024051036 1.000000000 0.02978799 -0.005674606 -0.003557949 -0.018808338 -0.027083641
【原创】R语言股票回归、时间序列分析报告论文附代码数据

【原创】R语言股票回归、时间序列分析报告论文附代码数据论文题目:股票价格回归分析报告摘要:主要思路为了准确的估计股票价格,了解股票的一般规律,更好的为资本市场提供参考意见和帮助股民进行投资股票作出正确的决策,本文从股票价格指数与整个经济环境角度出发,采用多元回归分析方法,应用月度时间序列数据,通过选取综合反映股票市场上所有公司股票价格整体水平的指标建立了线性回归模型,得出了股票价格趋势变动的影响因素.关键词:回归模型;指数模型;股票价格;预测一、引言主要思路为了准确的估计股票价格,本文从股票价格指数与整个经济环境角度出发,采用多元回归分析方法,应用月度时间序列数据建立了线性回归模型,具体分析步骤:1.关系分析基于以上原理,为大致了解股票价格与诸因素之间的关系,先分别绘制股票价格与各个因素之间的散点图,并分析它们之间的关系.股价用上证A股指数来表示,这样可以减少人为因素对股票价格的影响,尽量将注意力集中在我们假设选用的自变量上.我们采用的数据是2012年和2015年上半年的月度数据,分析影响我国股市趋势的因素。
之所以选取2012年和2015年7月的统计资料是基于以下两点考虑:中国股市发展时间较短,采用年度数据会因为样本量太小而使得回归分析失去意义;数据取得的存在较大难度,因季度数据不全而只能选取月度数据.因此选取2012年和2015年7月份月度数据作为样本.2.指数光滑时间序列展望模子3.挑选多项式回来模子3.1变量选取通过向前向后逐步迭代回归模型筛选出显著性较强的变量进行回归建模。
3.2明显性检修根据F值和p值统计量来判别模子是不是具有明显的统计意义。
3.3拟合预测使用得到的模型对实际数据进行拟合和预测。
4.分析得出结论得出各个自变量之间的关系,和它们对因变量的影响极端经济意义。
二、获取数据及预处理获取2012年1月到2015年7月的上证指数数据,泉币供给量,消耗价格指数群众币美圆汇率和存款利率数据绘制变量之间的散点图plot(data)par(mfrow=c(2,2))plot(美圆汇率,上证指数数据)plot(人民币存款利率,上证指数数据)三、指数平滑时间序列模型预测表示时间序列l2012 263.670 19.925 240.655 131.620 245.665 368. -51.615 -156.545 69.235 -46.705 -329.040 -181.635 -2. -65.535 87.565 79.200 37.740 -157.900 -118.655 59. -50.230 142.300 -11.580 -25.710 47.830 -92.995 -115.865Aug Sep Oct Nov Dec2012 -130.350 -216.610 125.145 163.415 44.4802013 145.310 5.895 236.405 97.135 -142.5552014 -176.755 -108.775 -71.055 32.655 -149.3202015Jan Feb Mar Apr May Jun Ju利用HoltWinters函数展望:p.hw<-XXX,h=24)h=24透露表现展望24个值四、进行多元回归模型并进行分析summary(lmmod)显示回来成效Call:lm(formula = y ~ x1 + x2 + x3 + x4, data = data)Residuals:Min 1Q Median 3Q Max-543.94 -90.09 1.69 113.01 500.68Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) -3.457e+04 9.319e+03 -3.710 0. ***x1 3.325e-03 1.369e-03 2.430 0. *x2 1.341e+01 2.663e+01 0.503 0.x3 4.787e+01 1.400e+01 3.420 0. **x4 7.870e+02 3.380e+02 2.328 0. *---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 246.5 on 38 degrees of freedomMultiple R-squared: 0.4804, Adjusted R-squared: 0.4257F-statistic: 8.783 on 4 and 38 DF, p-value: 4.012e-05回来成效分析从输出成效能够看出,回来方程为,变量和的统计量的估量值分别为-3.457e+04, 3.325e-03, 1.341e+01,4.787e+01和7.870e+02,除x2以外由对应的值都比显著性水平0.05小,可得两个偏回归系p数在显著性水平0.05下均显著不为零。
R语言实现时间序列分析

R语言-时间序列时间序列:可以用来预测未来的参数,1.生成时间序列对象1 sales <- c(18, 33, 41, 7, 34, 35, 24, 25, 24, 21, 25, 20,2 22, 31, 40, 29, 25, 21, 22, 54, 31, 25, 26, 35)3# 1.生成时序对象4 tsales <- ts(sales,start = c(2003,1),frequency = 12)5 plot(tsales)6# 2.获得对象信息7 start(tsales)8 end(tsales)9 frequency(tsales)10# 3.对相同取子集11 tsales.subset <- window(tsales,start=c(2003,5),end=c(2004,6))12 tsales.subset 结论:手动生成的时序图2.简单移动平均案例:尼罗河流量和年份的关系1 library(forecast)2 opar <- par(no.readonly = T)3 par(mfrow=c(2,2))4 ylim <- c(min(Nile),max(Nile))5 plot(Nile,main='Raw time series')6 plot(ma(Nile,3),main = 'Simple Moving Averages (k=3)',ylim = ylim)7 plot(ma(Nile,7),main = 'Simple Moving Averages (k=3)',ylim = ylim)8 plot(ma(Nile,15),main = 'Simple Moving Averages (k=3)',ylim = ylim)9 par(opar) 结论:随着K值的增大,图像越来越平滑我们需要找到最能反映规律的K值3.使用stl做季节性分解案例:Arirpassengers年份和乘客的关系1# 1.画出时间序列2 plot(AirPassengers)3 lAirpassengers <- log(AirPassengers)4 plot(lAirpassengers,ylab = 'log(Airpassengers)')5# 2.分解时间序列6 fit <- stl(lAirpassengers,s.window = 'period')7 plot(fit)8 fit$time.series9 par(mfrow=c(2,1))10# 3.月度图可视化11 monthplot(AirPassengers,xlab='',ylab='')12# 4.季度图可视化13 seasonplot(AirPassengers,bels = T,main = '') 原始图 对数变换 总体趋势图 月度季度图4.指数预测模型 4.1单指数平滑 案例:预测康涅狄格州的气温变化# 1.拟合模型fit2 <- ets(nhtemp,model = 'ANN')fit2# 2.向前预测forecast(fit2,1)plot(forecast(fit2,1),xlab = 'Year',ylab = expression(paste("Temperature (",degree*F,")",)),main="New Haven Annual Mean Temperature")# 3.得到准确的度量accuracy(fit2) 结论:浅灰色是80%的置信区间,深灰色是95%的置信区间 4.2有水平项,斜率和季节项的指数模型 案例:预测5个月的乘客流量1# 1.光滑参数2 fit3 <- ets(log(AirPassengers),model = 'AAA')3 accuracy(fit3)4# 2.未来值预测5 pred <- forecast(fit3,5)6 pred7 plot(pred,main='Forecast for air Travel',ylab = 'Log(Airpassengers)',xlab = 'Time') 8# 3.使用原始尺度预测9 pred$mean <- exp(pred$mean)10 pred$lower <- exp(pred$lower)11 pred$upper <- exp(pred$upper)12 p <- cbind(pred$mean,pred$lower,pred$upper)13 dimnames(p)[[2]] <- c('mean','Lo 80','Lo 95','Hi 80','Hi 95')14 p 结论:从表格中可知3月份的将会有509200乘客,95%的置信区间是[454900,570000] 4.3ets自动预测 案例:自动预测JohnsonJohnson股票的趋势1 fit4 <- ets(JohnsonJohnson)2 fit43 plot(forecast(fit4),main='Johnson and Johnson Forecasts',4 ylab="Quarterly Earnings (Dollars)", xlab="Time") 结论:预测值使用蓝色线表示,浅灰色表示80%置信空间,深灰色表示95%置信空间5.ARIMA预测步骤: 1.确保时序是平稳的 2.找出合理的模型(选定可能的p值或者q值) 3.拟合模型 4.从统计假设和预测准确性等角度评估模型 5.预测library(tseries)plot(Nile)# 1.原始序列差分一次ndiffs(Nile)dNile <- diff(Nile)# 2.差分后的图形plot(dNile)adf.test(dNile)Acf(dNile)Pacf(dNile)# 3.拟合模型fit5 <- arima(Nile,order = c(0,1,1))fit5accuracy(fit5)# 4.评价模型qqnorm(fit5$residuals)qqline(fit5$residuals)Box.test(fit5$residuals,type = 'Ljung-Box')# 5.预测模型forecast(fit5,3)plot(forecast(fit5,3),xlab = 'Year',ylab = 'Annual Flow') 原始图 一次差分图形1 fit6 <- auto.arima(sunspots)2 fit63 forecast(fit6,3)4 accuracy(fit6)5 plot(forecast(fit6,3), xlab = "Year",6 ylab = "Monthly sunspot numbers")。
【原创】R语言多元Copula GARCH 模型时间序列预测数据分析报告论文(含代码数据)

咨询QQ:3025393450欢迎登陆官网:/datablogR语言多元Copula GARCH 模型时间序列预测数据分析报告来源:和宏观经济数据不同,金融市场上多为高频数据,比如股票收益率序列直观的来说,后者要比前者“抖动”多了有漂移且随机波动的序列,在一元或多元的情况下,构建Copula函数模型和GARCH模型是最好的选择。
多元GARCH家族中,种类非常多,需要自己多推导理解,选择最优模型。
本文使用R软件对3家上市公司近十年的每周回报率为例建立模型。
首先我们可以绘制这三个时间序列。
在这里使用多变量的ARMA-GARCH模型。
咨询QQ:3025393450欢迎登陆官网:/datablog本文考虑了两种模型1 ARMA模型残差的多变量GARCH过程2 ARMA-GARCH过程残差的多变量模型(基于Copula)1 ARMA-GARCH模型> fit1 = garchFit(formula = ~arma(2,1)+ garch(1,1),data = dat [,1],cond.dist =“std”)可视化波动隐含的相关性> emwa_series_cor = function(i = 1,j = 2){+ if((min(i,j)== 1)&(max(i,j)== 2)){+ a = 1; B = 5; AB = 2}+}咨询QQ:3025393450欢迎登陆官网:/datablog2 BEKK(1,1)模型:BEKK11(dat_arma)隐含的相关性对单变量GARCH模型残差建模咨询QQ:3025393450欢迎登陆官网:/datablog第一步可能是考虑残差的静态(联合)分布。
单变量边际分布是而联合密度为可视化密度。
【原创】r语言arima预测时间序列Google trend Data附代码数据

Nowcasting of financial consumer complaint using Google trend Data 读取数据library(tseries)data=read.csv("需要改的.csv")data1=read.csv("原数据.csv",skip=1)查看部分数据读取客户反馈数据head(data)Date.received Product Sub.product1 07/29/2013 Consumer Loan Vehicle loan2 07/29/2013 Bank account or service Checking account3 07/29/2013 Bank account or service Checking account4 07/29/2013 Bank account or service Checking account5 07/29/2013 Mortgage Conventional fixed mortgage6 07/29/2013 Bank account or service Checking account Issue Sub.issue1 Managing the loan or lease2 Using a debit or ATM card3 Account opening, closing, or management4 Deposits and withdrawals5 Loan servicing, payments, escrow account6 Deposits and withdrawalsCompany State ZIP.code Tags1 Wells Fargo & Company VA 245402 Wells Fargo & Company CA 95992 Older American3 Santander Bank US NY 100654 Wells Fargo & Company GA 300845 Franklin Credit Management CT 061066 Bank of America TX 75025Consumer.consent.provided. Submitted.via pany1 N/A Phone 07/30/20132 N/A Web 07/31/20133 N/A Fax 07/31/20134 N/A Web 07/30/20135 N/A Web 07/30/20136 N/A Web 07/30/2013Company.response.to.consumer Timely.response. Consumer.disputed.1 Closed with explanation Yes No2 Closed with explanation Yes No3 Closed Yes No4 Closed with explanation Yes No5 Closed with explanation Yes No6 Closed with explanation Yes NoComplaint.ID1 4688822 4688893 4688794 4689495 4758236 468981读取谷歌trend的数据head(data1)Week plaint...United.States.1 2012-12-02 412 2012-12-09 503 2012-12-16 394 2012-12-23 295 2012-12-30 316 2013-01-06 53将要改编的数据里日期单位变成week 和原数据一样然后把Q栏客户反馈一周的加起来:Consumer disputed?dataall=merge(data1,data2 )Week plaint...United.States. data21 2012.48 41 116742 2012.49 50 138173 2012.50 39 139754 2012.51 29 140185 2012.52 31 10344然后放到原数据里(原数据里所有数据都不能动等于就是把改编数据里的客户反馈统计一下以周的单位加到原数据里)测试数据之间的关联correlation,cor(dataall[,3],dataall[,2])[1] 0.2878895从相关检测的结果,由于相关系数大于零,因此可以认为两者之间存在一定的正相关关系。
【原创】r语言基于逻辑回归模型的ST股票分析附代码数据

基于逻辑回归模型的ST股票分析研究问题通过对某股票数据分析,了解经营活动产生的现金流量净额净资产收益率... 每股收益和每股净资产对股票是否ST的影响。
数据介绍随机抽取的股票。
因变量是否为ST股票(0=非ST,1=ST)。
为了能够预测是否为ST,我们采集了下面这些来自当年的指标。
该数据存放在 csv 文件上市公司数据 (1).csv 中。
做完整的逻辑回归分析,包括参数估计、假设检验,以及预测评估和模型评价;因变量(是否为ST)STindex[1] 1 0数据描述绘制变量之间的散点图经营活动产生的现金流量净额净资产收益率...经营活动产生的现金流量净额 1.00000000 -0.06822659净资产收益率... -0.06822659 1.00000000每股收益 0.14347066 0.46849026每股净资产 0.39543001 -0.10833833ST -0.11777849 0.11277458每股收益每股净资产 ST经营活动产生的现金流量净额 0.1434707 0.3954300 -0.1177785净资产收益率... 0.4684903 -0.1083383 0.1127746每股收益 1.0000000 0.3101421 -0.1607072每股净资产 0.3101421 1.0000000 -0.4064833ST -0.1607072 -0.4064833 1.0000000从上面的图中,我们可以看到各个变量之间的相关关系,其中每股收益和每股净资产呈正相关关系。
绘制箱线图可以看到ST股票和非ST股票的4个变量具有显著差异。
非ST股票的各项指标要高于ST股票的变量值。
建立逻辑回归模型因此进行逻辑回归模型的分析。
随机抽取2/3作为训练集summary(fit)data = data_train)Deviance Residuals:Min 1Q Median 3Q Max-1.5105 -0.9038 -0.3875 0.9781 1.9334Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) 7.272e-01 4.283e-01 1.698 0.08950 .经营活动产生的现金流量净额 3.803e-10 4.233e-10 0.899 0.36888 净资产收益率... 2.198e-01 2.808e-01 0.783 0.43365每股收益 -2.121e+00 8.805e-01 -2.409 0.01600 *每股净资产 -4.901e-01 1.641e-01 -2.986 0.00282 **---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1(Dispersion parameter for binomial family taken to be 1)Null deviance: 96.716 on 70 degrees of freedomResidual deviance: 74.795 on 66 degrees of freedomAIC: 84.795Number of Fisher Scoring iterations: 6从输出结果可以看出,回归方程为ST= 1.285e+1.532e-10经营活动产生的现金流量净额 +3.023e-01 净资产收益率-2.078e+00每股收益-4.586e-01 股净资产,变量和的统计量的估计值分别为1.285e+00、1.532e-10、3.023e-01、-2.078e+00和-4.586e-01 ,每股收益和每股净资产对应的值都比显著性水平0.05小,可得2个偏回归系p数在显著性水平0.05下均显著不为零。
【原创】R语言时间序列图与地图绘制案例 附代码数据

plotly_POST(;public")
)
绘制锂产量地区图
s<-plot_geo(lithium)%>%
add_trace(
z=~Production1,color=~Production1,colors='Blues',
text=~COUNTRY,locations=~CODE,marker=list(line=l)
)%>%
colorbar(title='Lithium Production In Metric Tons')%>%
xaxis=list(zeroline=FALSE,
rangeslider=list(type="date"),
title="Number of Employees in the Automotive Industry"
))
plotly_POST(p,filename="Employee Number",sharing="public")
layout(
title='2016 Lithium Production<br>Source:<a href="https:///wiki/List_of_countries_by_lithium_production">Wikipedia Data</a>',
geo=g
xaxis=list(zeroline=FALSE,
rangeslider=list(type="date")
))
plotly_POST(p2,filename="Oil Excise",sharing="public")
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有问题到淘宝找“大数据部落”就可以了library(quantmod)# library(neuralnet)library(quantmod)library(plyr)library(TTR)library(ggplot2)library(scales)library(tseries)data=read.csv("600119.csv")a=data$收盘价a=diff(a)/a[-length(a)]a[a=="NaN"]=0a[a=="Inf"]=0##浏览数据data[,2]=data$日期data[,4]=c(0, a)##绘制时间序列图## 收集历史资料,加以整理,编成时间序列,并根据时间序列绘成统计图。
时间序列分析通常是把各种可能发生作用的因素进行分类,传统的分类方法是按各种因素的特点或影响效果分为四大类:(1)长期趋势;(2)季节变动;(3)循环变动;(4)不规则变动。
data=data[nrow(data):1,]plot(data[,2],data[,4])##技术指标lines( data[,2], DEMA(data[,4]) ,col="green")lines( data[,2], SMA(data[,4]) ,col="red")legend("bottomright",col=c("green","red"),legend =c("DEMA","SMA"),lty= 1,pch=1)有问题到淘宝找“大数据部落”就可以了## 从时间序列图形来看,序列有明显趋势,所以该序列一定不是平稳序列。
因为原序列为非平稳序列,所以选择一阶差分继续分析birthstimeseries=data[,4]birthstimeseries <-ts(birthstimeseries, frequency=300, start=c(1998,1 5))birthstimeseries=na.omit(birthstimeseries)## 2)Decompose the time series data into trend, seasonality and error components. (10 points)## 开始分解季节性时间序列。
## 一个季节性时间序列中会包含三部分,趋势部分、季节性部分和无规则部分。
分解时间序列就是要把时间序列分解成这三部分,然后进行估计。
## 对于可以使用相加模型进行描述的时间序列中的趋势部分和季节性部分,我们可以使用 R中的“decompose()” 函数来估计。
这个函数可以估计出时间序列中趋势的、季节性的和不规则的部分,而此时间序列须是可以用相加模型描述的。
## “decompose()” 这个函数返回的结果是一个列表对象,里面包含了估计出的季节性部分,趋势部分和不规则部分,他们分别对应的列表对象元素名为“seasonal” 、“trend” 、和“random” 。
有问题到淘宝找“大数据部落”就可以了birthcomponents <-decompose(birthstimeseries)plot(birthcomponents)## 要剔除某个趋势时(我们就去掉季节因素),我们可以运用减法去掉该因素,下图就是去掉季节性因素后的修正序列。
birthstimeseriesseasonallyadjusted<-birthstimeseries-birthcomponents$s easonalplot(birthstimeseriesseasonallyadjusted)有问题到淘宝找“大数据部落”就可以了acf(birthstimeseriesseasonallyadjusted)有问题到淘宝找“大数据部落”就可以了##看图中的横轴lag表示滞后阶数,纵轴表示对应各阶的相关系数,0阶滞后表示对自己的自相关系数,所以一般对应的相关系数值为1,再看图中上下的蓝色虚线内为95%置信区间,若lag>0对应的相关系数均在该区间内则表示该变量自相性问题不严重pacf(birthstimeseriesseasonallyadjusted)有问题到淘宝找“大数据部落”就可以了##看图中的横轴lag表示滞后阶数,纵轴表示对应各阶的相关系数,0阶滞后表示对自己的自相关系数,所以一般对应的相关系数值为1,再看图中上下的蓝色虚线内为95%置信区间,若lag>0对应的相关系数均在该区间内则表示该变量自相性问题不严重datad=diff(birthstimeseriesseasonallyadjusted)## 3)Use Holt’s exponential smoothing to make short-term forecasts. ## 指数平滑法(Exponential Smoothing,ES)是布朗(Robert G..Brown)所提出,布朗认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续到未来,所以将较大的权数放在最近的资料。
## 指数平滑法是生产预测中常用的一种方法。
也用于中短期经济发展趋势预测,所有预测方法中,指数## 一次指数平滑法## 平滑是用得最多的一种。
简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用;移动平均法则不考虑较远期的数据,并在加权移动平均法中给予近期资料更大的权重;而指数平滑法则兼容了全期平均和移动平均所长,不舍弃过去的数据,但是有问题到淘宝找“大数据部落”就可以了仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。
## 也就是说指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法,它是通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测。
其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。
## 简单指数平滑法。
简单指数平滑适用于可用相加模型描述,并且处于恒定水平和没有季节变动的时间序列地短期预测。
## 简单指数平滑法提供了一种方法估计当前时间点上的水平。
为了更加准确的估计当前时间的水平,我们使用alpha参数来控制平滑,alpha的取值在0-1之间。
当alpha越接近0,临近预测的观测值在预测中的权重就越小。
plot(datad)## 从该图中可以看出整个曲线处于大致不变的水平,且随机变动在整个时间序列范围内也可以认为是大致不变的,所以该序列可以大致被描述为一个相加模型,因此我们可以使用简单指数平滑法进行预测。
我们采用R中的HoltWinters()函数,为了能够使用Holt Winters中的指数平滑,我们需要进行参数设置:beta=FALSE和gamma=FALSE,预测结果如下图:有问题到淘宝找“大数据部落”就可以了## 此外我们可以画出预测值和实际值,看看预测效果:hm=HoltWinters(datad,beta=F,gamma = F)hm## Holt-Winters exponential smoothing without trend and without seasona l component.#### Call:## HoltWinters(x = datad, beta = F, gamma = F)#### Smoothing parameters:## alpha: 0.0009575354## beta : FALSE## gamma: FALSE#### Coefficients:## [,1]## a -0.0001333355cat("HoltWinters()告诉我们alpha参数的估计值约为",hm$alpha,",非常接近0,说明该序列比较平稳,默认情况下HoltWInters仅会给出原始时间序列所覆盖时期内的预测,预测值存在房子名为为fitted的变量中,我们可以通过rainseriesforecasts $fitted来获取这些值。
")## HoltWinters()告诉我们alpha参数的估计值约为 0.0009575354 ,非常接近0,说明该序列比较平稳,默认情况下HoltWInters仅会给出原始时间序列所覆盖时期内的预测,预测值存在房子名为为fitted的变量中,我们可以通过rainseriesforecasts $fitted来获取这些值。
plot(hm)有问题到淘宝找“大数据部落”就可以了## 从之前的alpha和上图,可见我们预测的过于平滑,R提供了样本预测误差平方和(SSE)来衡量预测效果。
可以通过rainseriesforecasts$SSE来获取该值。
hm$SSE## [1] 91.00893## 4)Fit the data with appropriate ARIMA Models.z=datad## 然后我们绘制自相关图和偏自相关图对序列进行进一步的检测acf(z)有问题到淘宝找“大数据部落”就可以了## 从上面的图中我们可以发现自相关系数在滞后一期之后,很快录入到置信区间之内,因此可以认为该序列平稳pacf(z)有问题到淘宝找“大数据部落”就可以了## 从偏相关系数的置信区间来看,由于相关系数都在置信区间之内,因此可以认为该序列平稳## Predictive model: ARIMA models predict## 然后检测序列的平稳性和独立性,这里我们使用的是Box-Ljung testBox.test(z,lag=10,type="Ljung")#### Box-Ljung test#### data: z## X-squared = 1128.9, df = 10, p-value < 2.2e-16## 由于p值大于0.05,因此我们接受原假设认为该数列独立,即原数列为白噪声序列 ## 然后我们对序列进行单位根检测,如果序列不存在单位根,那么该数列是平稳序列adf.test(z )## Warning in adf.test(z): p-value smaller than printed p-value#### Augmented Dickey-Fuller Test有问题到淘宝找“大数据部落”就可以了#### data: z## Dickey-Fuller = -28.804, Lag order = 16, p-value = 0.01## alternative hypothesis: stationary## 由于p值大于0.05,因此我们接受原假设认为该数列平稳## 从上面的自相关图和偏相关图,我们可以看到该模型为arima( 1,0,0 )library("forecast")## Warning: package 'forecast' was built under R version 3.3.3x<-arima(z,c(1,0,0))## 因此建立模型之后对该序列进行预测r1 <-predict(x,n.ahead=12)plot(forecast(x,h=12))## 在预测之后,我们可以得到该序列的预测置信区间,深蓝色的区域是95%的置信区间,而且蓝色的区域代表90%的置信区间。
