数据结构实验3
数据结构实验报告三

数据结构实验报告三数据结构实验报告三引言:数据结构是计算机科学中的重要内容之一,它研究的是如何组织和存储数据以便高效地访问和操作。
本实验报告将介绍我在数据结构实验三中的实验过程和结果。
实验目的:本次实验的主要目的是熟悉并掌握树这种数据结构的基本概念和操作方法,包括二叉树、二叉搜索树和平衡二叉树等。
实验内容:1. 实现二叉树的创建和遍历在本次实验中,我首先实现了二叉树的创建和遍历。
通过递归的方式,我能够方便地创建一个二叉树,并且可以使用前序、中序和后序遍历方法对二叉树进行遍历。
这些遍历方法的实现过程相对简单,但能够帮助我们更好地理解树这种数据结构的特点。
2. 实现二叉搜索树的插入和查找接下来,我实现了二叉搜索树的插入和查找操作。
二叉搜索树是一种特殊的二叉树,它的左子树上的节点的值都小于根节点的值,右子树上的节点的值都大于根节点的值。
通过这种特性,我们可以很方便地进行插入和查找操作。
在实现过程中,我使用了递归的方法,通过比较节点的值来确定插入的位置或者进行查找操作。
3. 实现平衡二叉树的插入和查找平衡二叉树是为了解决二叉搜索树在某些情况下可能会退化成链表的问题而提出的。
它通过在插入节点的过程中对树进行旋转操作来保持树的平衡。
在本次实验中,我实现了平衡二叉树的插入和查找操作。
通过对树进行左旋、右旋等操作,我能够保持树的平衡,并且能够在O(log n)的时间复杂度内进行插入和查找操作。
实验结果:通过本次实验,我成功地实现了二叉树、二叉搜索树和平衡二叉树的相关操作。
我编写了测试代码,并对代码进行了测试,结果表明我的实现是正确的。
我能够正确地创建二叉树,并且能够使用前序、中序和后序遍历方法进行遍历。
对于二叉搜索树和平衡二叉树,我能够正确地进行插入和查找操作,并且能够保持树的平衡。
实验总结:通过本次实验,我深入了解了树这种数据结构的特点和操作方法。
二叉树、二叉搜索树和平衡二叉树是树的重要应用,它们在实际开发中有着广泛的应用。
数据结构 实验三

实验三实验名称线性表综合练习实验性质设计性实验学时数6学时一、实验目的1.根据实际问题,应用线性表的顺序存储结构。
2.根据实际问题,深入理解线性表的链式存储结构。
3.通过线性表结构解决现实中的一些问题。
二、实验内容1. 线性表的两种存储结构。
2. 不同存储结构上进行插入、删除等操作的算法。
3. 通过线性表结构解决现实中的一些问题。
三、实验过程1、实验题目[问题描述]设计一个学生信息系统,要求:(1)每条信息包含学号,姓名,性别,院系,宿舍等项。
(2)能够对数据信息进行查找,插入,删除等。
(3)选择合适的存储结构,在主程序上运行,验证其正确性,并写出程序执行结果。
[基本要求](1)按实验内容编写完整的程序,并上机验证。
(2)实验完成后,提交电子档教师验收程序,并提交填写好的实验报告。
[测试数据]由学生依据软件工程的测试技术自己确定。
注意测试边界数据。
2、源程序#include<stdio.h>#include<malloc.h>#define MAXSIZE 200#define ElemType int#define OK 1#define ERROR 0typedef struct Node{char number[50];char name[50];char sex[50];char department[50];char dormitory[50];struct Node *next;}Node,*LinkList;void InitList(LinkList *L) //初始化线性表{*L=(LinkList)malloc(sizeof(Node));(*L)->next=NULL;}void CreateFromTail(LinkList L) //尾插法建表{int x,i;printf("请输入学生人数:");scanf("%d",&x);char number[50];char name[50];char sex[50];char department[50];char dormitory[50];Node *s,*r;r=L;printf("输入学生信息\n");for(i=0;i<x;i++){s=(Node*)malloc(sizeof(Node));printf("输入学生学号:");scanf("%s",s->number);printf("输入学生姓名:");scanf("%s",s->name);printf("输入学生性别:");scanf("%s",s->sex);printf("输入学生院系:");scanf("%s",s->department);printf("输入学生宿舍号:");scanf("%s",s->dormitory);r->next=s;r=s;}r->next=NULL;}Node *Get (LinkList L,int i) //按序号查找{char number[50];char name[50];char sex[50];char department[50];char dormitory[50];int j;Node *p;if(i<=0)return NULL;p=L;j=0;while((p->next!=NULL)&&(j<i)){p=p->next;j++;}if(i==j){printf("该学生信息为:\n");printf("学号:%s",p->number);printf("姓名:%s",p->name);printf("性别:%s",p->sex);printf("院系:%s",p->department);printf("宿舍号:%s",p->dormitory);printf("\n");}elsereturn NULL;}int InsList(LinkList L,int i) //插入操作{char number[50],name[50],sex[50],department[50],dormitory[50];Node *pre,*s;int k;if(i<=0) return ERROR;pre=L;k=0;while((pre!=NULL)&&(k<i-1)){pre=pre->next;k=k+1;}if(!pre){printf("插入位置不合理");return ERROR;}s=(Node *)malloc(sizeof(Node));printf("输入学生学号:");scanf("%s",s->number);printf("输入学生姓名:");scanf("%s",s->name);printf("输入学生性别:");scanf("%s",s->sex);printf("输入学生院系:");scanf("%s",s->department);printf("输入学生宿舍号:");scanf("%s",s->dormitory);s->next=pre->next;pre->next=s;return OK;}int DelList(LinkList L,int i) //删除{Node *pre,*r;int k;pre=L;k=0;while((pre->next!=NULL)&&(k<i-1)){pre=pre->next;k=k+1;}if(!(pre->next)){printf("删除结点的位置i不合理");return ERROR;}r=pre->next;pre->next=r->next;free(r);return OK;}void print(LinkList L) //打印{LinkList p;p=L->next;while(p){printf("该学生信息为:\n");printf("学号:%s",p->number);printf("姓名:%s",p->name);printf("性别:%s",p->sex);printf("院系:%s",p->department);printf("宿舍号:%s",p->dormitory);printf("\n");p=p->next;}}int main(){LinkList L;int i,choice,x,j;InitList(&L);CreateFromTail(L);do{printf("请选择对线性表的操作:1.插入 2.删除 3.查找 4.打印 0.退出\n");scanf("%d",&choice);switch(choice){case 1:printf("请输入插入位置");scanf("%d",&i);InsList(L,i);print(L);break;case 2:printf("请输入要删除的位置" );scanf("%d",&j);DelList(L,j);printf("删除后信息为:");print(L);break;case 3:int n;printf("输入要查找的学生的位置:");scanf("%d",&n);Get(L,n);break;case 4:print(L);case 0:break;default:printf("请您输入正确的操作!");break;}printf("*******谢谢使用*******\n");}while(choice!=0);return 0;}。
数据结构实验三栈和队列的应用

数据结构实验三栈和队列的应用数据结构实验三:栈和队列的应用在计算机科学领域中,数据结构是组织和存储数据的重要方式,而栈和队列作为两种常见的数据结构,具有广泛的应用场景。
本次实验旨在深入探讨栈和队列在实际问题中的应用,加深对它们特性和操作的理解。
一、栈的应用栈是一种“后进先出”(Last In First Out,LIFO)的数据结构。
这意味着最后进入栈的元素将首先被取出。
1、表达式求值在算术表达式的求值过程中,栈发挥着重要作用。
例如,对于表达式“2 + 3 4”,我们可以通过将操作数压入栈,操作符按照优先级进行处理,实现表达式的正确求值。
当遇到数字时,将其压入操作数栈;遇到操作符时,从操作数栈中弹出相应数量的操作数进行计算,将结果压回操作数栈。
最终,操作数栈中的唯一值就是表达式的结果。
2、括号匹配在程序代码中,检查括号是否匹配是常见的任务。
可以使用栈来实现。
遍历输入的字符串,当遇到左括号时,将其压入栈;当遇到右括号时,弹出栈顶元素,如果弹出的左括号与当前右括号类型匹配,则继续,否则表示括号不匹配。
3、函数调用和递归在程序执行过程中,函数的调用和递归都依赖于栈。
当调用一个函数时,当前的执行环境(包括局部变量、返回地址等)被压入栈中。
当函数返回时,从栈中弹出之前保存的环境,继续之前的执行。
递归函数的执行也是通过栈来实现的,每次递归调用都会在栈中保存当前的状态,直到递归结束,依次从栈中恢复状态。
二、队列的应用队列是一种“先进先出”(First In First Out,FIFO)的数据结构。
1、排队系统在现实生活中的各种排队场景,如银行排队、餐厅叫号等,可以用队列来模拟。
新到达的顾客加入队列尾部,服务完成的顾客从队列头部离开。
通过这种方式,保证了先来的顾客先得到服务,体现了公平性。
2、广度优先搜索在图的遍历算法中,广度优先搜索(BreadthFirst Search,BFS)常使用队列。
从起始节点开始,将其放入队列。
数据结构实验三实验报告

数据结构实验三实验报告数据结构实验三实验报告一、实验目的本次实验的目的是通过实践掌握树的基本操作和应用。
具体来说,我们需要实现一个树的数据结构,并对其进行插入、删除、查找等操作,同时还需要实现树的遍历算法,包括先序、中序和后序遍历。
二、实验原理树是一种非线性的数据结构,由结点和边组成。
树的每个结点都可以有多个子结点,但是每个结点只有一个父结点,除了根结点外。
树的基本操作包括插入、删除和查找。
在本次实验中,我们采用二叉树作为实现树的数据结构。
二叉树是一种特殊的树,每个结点最多只有两个子结点。
根据二叉树的特点,我们可以使用递归的方式实现树的插入、删除和查找操作。
三、实验过程1. 实现树的数据结构首先,我们需要定义树的结点类,包括结点值、左子结点和右子结点。
然后,我们可以定义树的类,包括根结点和相应的操作方法,如插入、删除和查找。
2. 实现插入操作插入操作是将一个新的结点添加到树中的过程。
我们可以通过递归的方式实现插入操作。
具体来说,如果要插入的值小于当前结点的值,则将其插入到左子树中;如果要插入的值大于当前结点的值,则将其插入到右子树中。
如果当前结点为空,则将新的结点作为当前结点。
3. 实现删除操作删除操作是将指定的结点从树中移除的过程。
我们同样可以通过递归的方式实现删除操作。
具体来说,如果要删除的值小于当前结点的值,则在左子树中继续查找;如果要删除的值大于当前结点的值,则在右子树中继续查找。
如果要删除的值等于当前结点的值,则有三种情况:- 当前结点没有子结点:直接将当前结点置为空。
- 当前结点只有一个子结点:将当前结点的子结点替代当前结点。
- 当前结点有两个子结点:找到当前结点右子树中的最小值,将其替代当前结点,并在右子树中删除该最小值。
4. 实现查找操作查找操作是在树中寻找指定值的过程。
同样可以通过递归的方式实现查找操作。
具体来说,如果要查找的值小于当前结点的值,则在左子树中继续查找;如果要查找的值大于当前结点的值,则在右子树中继续查找。
数据结构实验报告三

L->r[j+1]=L->r[0];
}
}
main()
{
SortList *L;
int i;
L->r[0].key=0;
L->r[1].key=49;
L->r[2].key=38;
L->r[3].key=65;
L->r[4].key=97;
L->r[5].key=76;
}SortList;
void InsertSort(SortList *L)
{
int i,j;
for(i=2;i<=L->length;i++)
if(L->r[i].key<L->r[i-1].key){
L->r[0]=L->r[i];
for(j=i-1;L->r[0].key<L->r[j].key;j--)
L->r[6].key=13;
L->r[7].key=27;
L->r[8].key=52;
L->length=8;
SelectSort(L);
printf("\n\n");
for(i=1;i<=L->length;i++)
printf("%d\n",L->r[i].key);
}
附2:原程序
#define SORT_LIST_MAXSIZE 20
typedef int KeyType;
typedef int InfoType;
typedef struct{
国家开放大学《数据结构》课程实验报告(实验3 ——栈、队列、递归设计)参考答案

x=Pop(s); /*出栈*/
printf("%d ",x);
InQueue(sq,x); /*入队*/
}
printf("\n");
printf("(10)栈为%s,",(StackEmpty(s)?"空":"非空"));
printf("队列为%s\n",(QueueEmpty(sq)?"空":"非空"));
ElemType Pop(SeqStack *s); /*出栈*/
ElemType GetTop(SeqStack *s); /*取栈顶元素*/
void DispStack(SeqStack *s); /*依次输出从栈顶到栈底的元素*/
void DispBottom(SeqStack *s); /*输出栈底元素*/
} SeqQueue; /*定义顺序队列*/
void InitStack(SeqStack *s); /*初始化栈*/
int StackEmpty(SeqStack *s); /*判栈空*/
int StackFull(SeqStack *s); /*判栈满*/
void Push(SeqStack *s,ElemType x); /*进栈*/
sq=(SeqQueue *)malloc(sizeof(SeqQueue));
InitQueue(sq);
printf("(8)队列为%s\n",(QueueEmpty(sq)?"空":"非空"));
printf("(9)出栈/入队的元素依次为:");
数据结构实验报告3

数据结构实验报告3数据结构实验报告3引言:数据结构是计算机科学中的一个重要概念,它涉及到数据的组织、存储和管理。
在本次实验中,我们将探索一些常见的数据结构,并通过实验来验证它们的性能和效果。
一、线性表线性表是最基本的数据结构之一,它是一种由一组数据元素组成的有序序列。
在本次实验中,我们使用了顺序表和链表来实现线性表。
顺序表是一种连续存储的数据结构,它可以通过下标来访问元素。
我们通过实验比较了顺序表的插入和删除操作的时间复杂度,发现在插入和删除元素较多的情况下,顺序表的性能较差。
链表是一种非连续存储的数据结构,它通过指针来连接各个元素。
我们通过实验比较了链表的插入和删除操作的时间复杂度,发现链表在插入和删除元素时具有较好的性能。
二、栈栈是一种特殊的线性表,它只允许在表的一端进行插入和删除操作。
在本次实验中,我们实现了栈的顺序存储和链式存储两种方式。
顺序存储的栈使用数组来存储元素,我们通过实验比较了顺序存储栈和链式存储栈的性能差异。
结果表明,在元素数量较少的情况下,顺序存储栈具有较好的性能,而在元素数量较多时,链式存储栈更具优势。
三、队列队列是一种特殊的线性表,它只允许在表的一端进行插入操作,在另一端进行删除操作。
在本次实验中,我们实现了队列的顺序存储和链式存储两种方式。
顺序存储的队列使用数组来存储元素,我们通过实验比较了顺序存储队列和链式存储队列的性能差异。
结果表明,顺序存储队列在插入和删除元素时具有较好的性能,而链式存储队列在元素数量较多时更具优势。
四、树树是一种非线性的数据结构,它由一组称为节点的元素组成,通过节点之间的连接来表示数据之间的层次关系。
在本次实验中,我们实现了二叉树和二叉搜索树。
二叉树是一种每个节点最多有两个子节点的树结构,我们通过实验验证了二叉树的遍历算法的正确性。
二叉搜索树是一种特殊的二叉树,它的左子树的所有节点都小于根节点,右子树的所有节点都大于根节点。
我们通过实验比较了二叉搜索树的插入和查找操作的时间复杂度,发现二叉搜索树在查找元素时具有较好的性能。
北京理工大学数据结构实验报告3

《数据结构与算法统计》实验报告——实验三学院:班级:学号:姓名:一、实验目的1 熟悉VC环境,学会使用C++解决关于二叉树的问题。
2 在上机、调试的过程中,加强对二叉树的理解和运用。
3 锻炼动手编程和独立思考的能力。
二、实验内容遍历二叉树。
请输入一棵二叉树的扩展的前序序列,经过处理后生成一棵二叉树,然后对于该二叉树输出前序、中序和后序遍历序列。
三、程序设计1、概要设计为实现上述程序功能,首先需要二叉树的抽象数据结构。
⑴二叉树的抽象数据类型定义为:ADT BinaryTree {数据对象D:D是具有相同特性的数据元素的集合。
数据关系R:若D=Φ,则R=Φ,称BinaryTree为空二叉树;若D≠Φ,则R={H},H是如下二元关系;(1)在D中存在惟一的称为根的数据元素root,它在关系H下无前驱;(2)若D-{root}≠Φ,则存在D-{root}={D1,Dr},且D1∩Dr =Φ;(3)若D1≠Φ,则D1中存在惟一的元素x1,<root,x1>∈H,且存在D1上的关系H1 ⊆H;若Dr≠Φ,则Dr中存在惟一的元素xr,<root,xr>∈H,且存在上的关系Hr ⊆H;H={<root,x1>,<root,xr>,H1,Hr};(4)(D1,{H1})是一棵符合本定义的二叉树,称为根的左子树;(Dr,{Hr})是一棵符合本定义的二叉树,称为根的右子树。
基本操作:CreatBiTree(BiTree &T)操作结果:按先序次序建立二叉链表表示的二叉树TPreOrderTraverse(BiTree T,int (*visit)(char e))初始条件:二叉树T已经存在,visit是对结点操作的应用函数操作结果:先序遍历二叉树T ,对每个结点调用visit函数仅一次;一旦visit()失败,则操作失败。
InOrderTraverse(BiTree T,int (*visit)(char e))初始条件:二叉树T已经存在,visit是对结点操作的应用函数操作结果:中序遍历二叉树T ,对每个结点调用visit函数仅一次;一旦visit()失败,则操作失败。
数据结构_实验三_报告

实验报告实验三二叉树的基本操作实现及其应用一、实验目的1.熟悉二叉树结点的结构和对二叉树的基本操作。
2.掌握对二叉树每一种操作的具体实现。
3.学会利用递归方法编写对二叉树这种递归数据结构进行处理的算法。
4.会用二叉树解决简单的实际问题。
二、实验内容题目一设计程序实现二叉树结点的类型定义和对二叉树的基本操作。
该程序包括二叉树结构类型以及每一种操作的具体的函数定义和主函数。
1 按先序次序建立一个二叉树,2按(A:先序 B:中序 C:后序 D:层序)遍历输出二叉树的所有结点3求二叉树中所有结点数4求二叉树的深度5 判断二叉树是否为空**************************************************************** 三、实验步骤㈠、数据结构与核心算法的设计描述/* 定义DataType为char类型 */typedef char DataType;/* 二叉树的结点类型 */typedef struct BitNode{DataType data;struct BitNode *lchild,*rchild;}*BiTree;相关函数声明:1、/* 初始化二叉树,即把树根指针置空 */void BinTreeInit(BiTree &BT)2、/* 按先序次序建立一个二叉树*/void BinTreeCreat(BiTree &BT)3、/* 检查二叉树是否为空 */int BinTreeEmpty(BiTree &BT)4、/*按任一种遍历次序(包括按先序、中序、后序、按层次)输出二叉树中的所有结点 */void PreOrderBinTraverse(BiTree &T)//先序void InOrderBinTraverse(BiTree &T)//中序void PostOrderBinTraverse(BiTree &T)//后序void LevelOrderTraverse(BiTree &T)//层序5、/* 求二叉树的深度 */int BinTreeDepth(BiTree BT)6、/* 求二叉树中所有结点数 */void BinTreeCount(BiTree T,int &count)㈢程序调试及运行结果分析在调试过程中,开始时按先序次序建立二叉树时,其中一句if(ch=='')T=NULL;调试中发现此句无法是函数结束,经分析知道输入的空格不会被读入,导致函数无法结束,最终将起改为:if(ch=='@')T=NULL;运行正确。
《数据结构》实验3链表

三、源代码以及实验结果为
四、源代码以及实验结果为
五、源代码以及实验结果为
六、源代码以及实验结果为
七、附加题以及实验体会:
{
NODE *s; /*定义指向结点类型的指针*/
s=(NODE *)malloc(sizeof(NODE));
/*生成新结点*/
3
4
5
return 1;
}
/*删除P所指向的结点的后继结点*/
void DelLinkList(NODE *p)
{ NODE *q;
if(p->next!=0)
{ q=p->next; /* q指向p的后继结点*/
ch=getchar();
while(ch!='$')
{ p=(NODE *)malloc(sizeof(NODE));
p->data=ch;
1
2
ch=getchar();
}
return (head);
}
/*在链表的P指定结点之后插入值为x的结点*/
int InsLinkList(NODE *p, char x)
四、设有两个单链表A、B,其中元素递增有序,编写算法将A、B归并成一个按元素值递减(允许有相同值)有序的链表C,要求用A、B中的原结点形成,不能重新申请结点。
五、已知单链表表示的线性表中含有两类的数据元素(字母字符,数字字符)。试设计算法,按结点的值将单链表拆分成两个循环链表,分别只含有数字或字母。要求:利用原表中的结点空间作为这两个表的结点空间,头结点可另开辟空间。
附加题:如果换成循环单链表该如何实现?
即题目变成:已知单循环链表表示的线性表中含有两类的数据元素(字母字符,数字字符)。试设计算法,按结点的值将单链表拆分成两个循环链表,分别只含有数字或字母。
数据结构实验三——二叉树基本操作及运算实验报告

《数据结构与数据库》实验报告实验题目二叉树的基本操作及运算一、需要分析问题描述:实现二叉树(包括二叉排序树)的建立,并实现先序、中序、后序和按层次遍历,计算叶子结点数、树的深度、树的宽度,求树的非空子孙结点个数、度为2的结点数目、度为2的结点数目,以及二叉树常用运算。
问题分析:二叉树树型结构是一类重要的非线性数据结构,对它的熟练掌握是学习数据结构的基本要求。
由于二叉树的定义本身就是一种递归定义,所以二叉树的一些基本操作也可采用递归调用的方法。
处理本问题,我觉得应该:1、建立二叉树;2、通过递归方法来遍历(先序、中序和后序)二叉树;3、通过队列应用来实现对二叉树的层次遍历;4、借用递归方法对二叉树进行一些基本操作,如:求叶子数、树的深度宽度等;5、运用广义表对二叉树进行广义表形式的打印。
算法规定:输入形式:为了方便操作,规定二叉树的元素类型都为字符型,允许各种字符类型的输入,没有元素的结点以空格输入表示,并且本实验是以先序顺序输入的。
输出形式:通过先序、中序和后序遍历的方法对树的各字符型元素进行遍历打印,再以广义表形式进行打印。
对二叉树的一些运算结果以整型输出。
程序功能:实现对二叉树的先序、中序和后序遍历,层次遍历。
计算叶子结点数、树的深度、树的宽度,求树的非空子孙结点个数、度为2的结点数目、度为2的结点数目。
对二叉树的某个元素进行查找,对二叉树的某个结点进行删除。
测试数据:输入一:ABC□□DE□G□□F□□□(以□表示空格),查找5,删除E预测结果:先序遍历ABCDEGF中序遍历CBEGDFA后序遍历CGEFDBA层次遍历ABCDEFG广义表打印A(B(C,D(E(,G),F)))叶子数3 深度5 宽度2 非空子孙数6 度为2的数目2 度为1的数目2查找5,成功,查找的元素为E删除E后,以广义表形式打印A(B(C,D(,F)))输入二:ABD□□EH□□□CF□G□□□(以□表示空格),查找10,删除B预测结果:先序遍历ABDEHCFG中序遍历DBHEAGFC后序遍历DHEBGFCA层次遍历ABCDEFHG广义表打印A(B(D,E(H)),C(F(,G)))叶子数3 深度4 宽度3 非空子孙数7 度为2的数目2 度为1的数目3查找10,失败。
数据结构实验三实验报告

数据结构实验三实验报告篇一:数据结构实验报告3计算机科学与技术系实验报告专业名称网络系统管理课程名称数据结构与算法项目名称顺序表的排序实验班级 13网管班学号130405XX姓名汪康实验题目:顺序表的排序实验1、问题分析本次试验要求使用直接插入排序算法给顺序表中的元素进行排序,那么在设计算法时,需考虑以下4点:(1)建立一个顺序表;(2)在顺序表中插入元素;(3)给表中元素进行排序(4)设计主函数,完成以上功能2、概要设计1)为了实现上述程序功能,需要:(1)建立一个自定义函数SqList;(2)建立函数InitSqList,用来申请地址空间和插入表中元素;(3)建立函数InsertSort,将顺序表中的元素排序;(4)建立函数print,用来输出排好序的元素;(5)最后,设计主函数main,调用以上函数。
2)本程序包含5个函数:(1)主函数main()(2)自定义函数SqList()(3)初始化顺序表函数InitSqList()(4)排序函数InsertSort()(5)输出函数print()各函数间关系如下: SqListInitSqListInsertSortprint3、详细设计#include "stdio.h"//因程序中存在输入和输出函数,设计头文件用来存储 #include "stdlib.h"//stdlib.h里定义了五种类型、一些宏和通用工具函数#include "malloc.h" //程序中含有申请地址空间#define MAXSIZE 10 //自定义一个常量MAXSIZE,其最大值为10typedef struct{ //定义数据类型为结构型int r[MAXSIZE];//定义一个整型数组r,也就是将数组r中的元素放入顺序表L中,之后用来比较最大和最小值int last; //定义一个整型变量last,也就是分量last,用来记录顺序表L中最后一个数据元素的下标}SqList;SqList*L;//将顺序表L定义成SqListvoid InitSqList()//向系统申请一个存储空间给顺序表L,并输入表中的元素 {L->last=-1;//将表L置空scanf("%d",&i);//输入表长if(i>0){printf("请输入需排序元素()");for(L->last=1;L->lastlast++)} } scanf("%d",&(L->r[L->last]));//在表L最后一个元素的下标不超过i的情况下,向顺序表L中输入元素 int i;//定义一个整型变量i,作为表长变量 L = (SqList *)malloc(sizeof(SqList)); //通过函数malloc给顺序表L分配一个大小为10的分配空间void InsertSort(){ //对顺序表L中的元素做直接插入排序int i,j; //定义整型变量i和j,i作为循环控制变量for(i = 1; i last; i++){L->r[0] = L->r[i];//将待插入的元素存到监视哨r[0]中j=i-1; //j指向i的下一元素while(L->r[0] r[j]){ //寻找插入位置L->r[j+1] = L->r[j];j=j-1;}}} L->r[j+1]=L->r[0]; //将待插入的元素插入到已排序的序列中void print(){//将排好序的顺序表L输出int i; //定义一个整型变量i,作为循环控制变量for(i = 2; i last; i++)}printf("%d ",L->r[i]); //输出已排序的数据元素int main(){ //用主函数调用子函数} InitSqList(); //调用函数InitSqList InsertSort(); //调用函数InsertSort print();//调用函数print return 0;4、调试分析在此次实验中,运行后发现很多错误,有的是括号少了,有的是标点符号忘记加了,导致一直运行错误,经过仔细检查,排除了错误,最后运行成功,得到了结果。
《数据结构》实验报告三:几种查找算法的实现和比较

第三次实验报告:几种查找算法的实现和比较//2019-12-4//1.随机生成5万个整数,存入一个文件;//2.算法实现:(1)顺序查找:读入文件中的数据,查找一个key,统计时间;// (2)二分查找:读入文件,排序,二分查找key,统计时间;// (3)分块查找:读入文件,分100块,每块300+数字,查找key,统计时间// (4)二分查找树:读入文件,形成BST,查找key,统计时间//二叉排序树:建立,查找#include "stdio.h"#include "time.h"#include "stdlib.h"struct JD{//定义分块查找的链表结点结构int data;JD *next;};struct INDEX_T{//定义分块查找中,索引表结构int max;//这一块中最大的数字,<maxJD *block;//每一块都是一个单向链表,这是指向块的头指针};INDEX_T myBlock[100];//这是索引表的100项struct NODE{//定义的二分查找树结点结构int data;NODE *left;NODE *right;};const int COUNT=50000;//结点个数int key=666;//待查找的关键字int m=1;//int *array2;void createData(char strFileName[]){//产生随机整数,存入文件srand((unsigned int)time(0));FILE *fp=fopen(strFileName,"w");for(int i=1;i<=COUNT;i++)fprintf(fp,"%d,",rand());fclose(fp);}void createBST(NODE* &bst){//产生5万个随机整数,创建二叉排序树FILE *fp=fopen("data.txt","r");for(int i=1;i<=COUNT;i++){int num;fscanf(fp,"%d,",&num);//从文件中读取一个随机整数//若bst是空子树,第一个结点就是根结点//若bst不是空子树,从根结点开始左小右大,查找这个数字,找到了直接返回,//找不到,就插入到正确位置//创建一个结点NODE* p=new NODE;p->data=num;p->left=0;p->right=0;if(0==bst)//空子树{bst=p;continue;}//非空子树,//在bst中,查找给结点,NODE *q=bst;//总是从根结点开始查找while(1){if(p->data == q->data)//找到了,直接退出break;if(p->data < q->data && q->left==0){//小,往左找,且左边为空,直接挂在q之左q->left=p;break;}if(p->data < q->data && q->left!=0){//小,往左找,且左边非空,继续往左边找q=q->left;continue;}if(p->data > q->data && q->right==0){//大,往右找,且右边为空,直接挂在q之右q->right=p;break;}if(p->data > q->data && q->right!=0){//大,往右找,且右边非空,继续往右边找q=q->right;continue;}}}}int BST_Search(NODE *bst,int key){//在bst中找key,if(0==bst)return -1;//非空子树,//在bst中,查找给结点,NODE *q=bst;//总是从根结点开始查找while(1){if(key == q->data)//找到了,直接退出return 1;if(key < q->data && q->left==0)//小,往左找,且左边为空,找不到return -1;if(key < q->data && q->left!=0)//小,往左找,且左边非空,继续往左边找{q=q->left;continue;}if(key > q->data && q->right==0)//大,往右找,且右边为空,找不到return -1;if(key > q->data && q->right!=0){//大,往右找,且右边非空,继续往右边找q=q->right;continue;}}}void inOrder(NODE *bst){if(bst!=0){inOrder(bst->left);array2[m]=bst->data;//反写回array数组,使数组有序// printf("%7d",array2[m]);m++;inOrder(bst->right);}}int getBSTHeight(NODE *bst){if(bst==0)return 0;else{int hl=getBSTHeight(bst->left);int hr=getBSTHeight(bst->right);int h=hl>hr?hl:hr;return h+1;}}void makeArray(int array[],char strFileName[]) {//生成5万个随机整数FILE *fp=fopen(strFileName,"r");int i=1;while(!feof(fp)){fscanf(fp,"%d,",&array[i]);// printf("%6d",array[i]);i++;}}int Seq_Search(int array[],int key){//在无序顺序数组中,找data是否存在,-1=不存在,存在返回位置下标//监视哨:把要找的那个数放到首部array[0]=key;//for(int i=COUNT;array[i]!=key;i--);if(i>0)//找到了,返回下标return i;return -1;//查找不成功,返回-1}int Bin_Search(int array[],int key){//在有序存储的数组中查找key,找到返回位置,找不到返回-1 int low=1,high=COUNT,mid;while(1){if(low>high)//找不到return -1;mid=(low+high)/2;if(key == array[mid])return mid;else if(key<array[mid])high=mid-1;elselow=mid+1;}}void makeBlock(INDEX_T myBlock[],char strFileName[]) {//从文件中读取整数,分配到块中去//1.初始化块索引表,分100块,400,800,1200,for(int i=0;i<=99;i++){myBlock[i].max=400+400*i;//400,800,1200, (40000)myBlock[i].block=0;}//2.打开文件,读取整数,把每一个整数分配到相应的块中去FILE *fp=fopen(strFileName,"r");while(!feof(fp)){int num=0;fscanf(fp,"%d,",&num);//把num分配到num/400块中,挂到该块链表第一个int blockID=num/400;//求出应该挂在的块号//生成一个新节点,把num放进去,挂上JD *p=new JD;p->data=num;p->next=myBlock[blockID].block;myBlock[blockID].block=p;}fclose(fp);}int Block_Search(INDEX_T myBlock[],int key){int blockID=key/400;//找到块号JD* p=myBlock[blockID].block;while(p!=0){if(p->data==key)return blockID;//能找到p=p->next;}return -1;//找不到}void main(){clock_t begin,end;int pos=-1;//1.生成文件,存入5万个随机整数createData("data.txt");//2.顺序查找int *array=new int[COUNT+1];makeArray(array,"data.txt");//从文件中读取数据begin=clock();for(int k=1;k<=10000;k++)pos=Seq_Search(array,key);end=clock();printf("顺序查找:%d所在的位置=%d.时间=%d毫秒\n",key,pos,end-begin);//3.二分查找树NODE *bst=0;createBST(bst);//产生5万个随机数字,建立一个二叉排序树begin=clock();for(k=1;k<=10000;k++)pos=BST_Search(bst,key);//在bst中找key,找到返回1,找不到返回-1end=clock();printf("二叉排序树查找:%d所在的位置=%d.时间=%d毫秒\n",key,pos,end-begin);array2=new int[COUNT+1];inOrder(bst);//中序输出bst// int height=getBSTHeight(bst);//求出bst的高度// printf("BST高度=%d.\n\n",height);//4.二分查找,利用前面二叉排序树产生的array2,查找key begin=clock();for(k=1;k<=10000;k++)pos=Bin_Search(array2,key);end=clock();printf("二分查找:%d所在的位置=%d.时间=%d毫秒\n",key,pos,end-begin);//5.分块查找,关键字范围[0,32767],分配到100块中去,每一块中存400个数字makeBlock(myBlock,"data.txt");//从文件中读取数据,产生块begin=clock();for(k=1;k<=10000;k++)pos=Block_Search(myBlock,key);//在block中查找key,找到返回块号,找不到返回-1end=clock();printf("分块查找:%d所在的块=%d.时间=%d毫秒\n",key,pos,end-begin);/*for(k=0;k<=99;k++){printf("\n\n\n第%d块<%d:\n",k,myBlock[k].max);JD *q=myBlock[k].block;//让q指向第k块的第一个结点while(q!=0){//输出第k块中所有数字printf("%7d ",q->data);q=q->next;}}*/}。
(中央电大)数据结构实验报告3

中央广播电视大学实验报告(学科:数据结构)姓名班级学号实验日期成绩评定教师签名批改日期实验名称:实验三二叉树3.1 二叉树的顺序存储结构和链式存储结构【问题描述】设一棵完全二叉树用顺序存储方法存储于数组tree中,编写程序:(1)根据数组tree,建立与该二叉树对应的链式存储结构。
(2)对该二叉树采用中序遍历法显示遍历结果。
【基本要求】(1)在主函数中,通过键盘输入建立设定的完全二叉树的顺序存储结构。
(2)设计子函数,其功能为将顺序结构的二叉树转化为链式结构。
(3)设计子函数,其功能为对给定二叉树进行中序遍历,显示遍历结果。
(4)通过实例判断算法和相应程序的正确性。
【实验步骤】(1)运行PC中的Microsoft Visual C++ 6.0程序,(2)点击“文件”→“新建”→对话窗口中“文件”→“c++ Source File”→在“文件名”中输入“X1.cpp”→在“位置”中选择储存路径为“桌面”→“确定”,(3)输入程序代码,程序代码如下:#include<stdio.h>#include<malloc.h>#include<string.h>#include<stdlib.h>#include<memory.h>#define MaxSize 10typedef struct node{char data。
struct node *left,*right。
}NODE。
void Creab(char *tree,int n,int i,NODE *p)。
void Inorder(NODE *p)。
void main(){NODE *p。
char tree[MaxSize]。
int n=1。
int i=1。
printf("请输入完全二叉数的节点值(连续输入字符,以回车结束输入。
):")。
while((tree[n] = getchar( )) != '\n') n++。
数据结构-实验3

《数据结构》实验报告年级_2012级__ 学号_ 姓名 _ 成绩______专业_计算机科学与技术实验地点__指导教师_实验项目:实验三队列实验性质设计性实验日期:一、实验目的:1、掌握队列及其基本操作的实现。
2、进一步掌握实现数据结构的编程方法。
二、实验内容与要求:1、实验题目一:队列的定义及其相关操作算法的实现要求:编程实现队列的类型定义及其初始化操作、入队操作、出队操作、取队头操作、输出操作等,并对其进行验证。
2、实验题目二:病人看病模拟要求:利用题目一所定义的队列(顺序队或链队)实现病人看病模拟程序,并进行验证给出结果。
三、实验问题描述编写一个程序,反映病人到医院看病,排队看医生的情况。
在病人排队过程中,主要重复两件事:(1)病人到达诊室,将病历本交给护士,拍到等待队列中候诊。
(2)护士从等待队列中取出下一位病人的兵力,该病人进入诊室就诊。
要求模拟病人等待就诊这一过程,程序采用菜单方式,其选项及功能说明如下:(1)排队————输入排队病人的病历号,加入到病人排队队列中。
(2)就诊————病人排队队列中最前面的病人就诊,并将其从队列中删除。
(3)查看排队————从队首到队尾列出所有的排队病人的病历号。
(4)不再排队,余下依次就诊————从队首到队尾列出所有的排队病人的病历号,并退出运行。
(5)下班————退出运行。
四、实验步骤1.实验问题分析此程序采用队列数据结构,存储结构为单链表,采用此种结构一方面可以减少数据复杂程度,增加系统稳定性也利用动态分配内存的方法,便于内存管理,充分利用内存空间2.功能(函数)设计void SeeDoctor(){ int sel,flag=1,find,no;QuType *qu;QNode *p;qu=(QuType *)malloc(sizeof(QuType));qu->front=qu->rear=NULL;}五、实验结果(程序)及分析#include<stdio.h>#include<malloc.h>typedef struct qnode{int data;struct qnode *next;}QNode;typedef struct {QNode *front,*rear;}QuType;void SeeDoctor(){int sel,flag=1,find,no;QuType *qu;QNode *p;qu=(QuType *)malloc(sizeof(QuType));qu->front=qu->rear=NULL;while(flag==1){printf("1:排队 2:就诊 3:查看排队 4:不再排队,余下依次就诊 5:下班请选择:");scanf("%d",&sel);switch(sel){case 1:printf(" >>输入病历号:");do{scanf("%d",&no);find=0;p=qu->front;while(p!=NULL && !find)if(p->data==no)find=1;elsep=p->next;if(find)printf(" >> 输入的病历号重复,重新输入:");}while(find==1);p=(QNode *)malloc(sizeof(QNode));p->data=no;p->next=NULL;if(qu->rear==NULL)qu->front=qu->rear=p;else{qu->rear->next=p;qu->rear=p;}break;case 2:if(qu->front==NULL)printf(" >>没有排队的病人!\n");else{p=qu->front;printf(" >>病人%d就诊\n",p->data);if(qu->rear==p)qu->front=qu->rear=NULL;elsequ->front=p->next;free(p);}break;case 3:if(qu->front == NULL)printf(" >>没有排队的病人!\n");else{p=qu->front;printf(" >>排队病人:");while(p!=NULL){printf("%d",p->data);p=p->next;}printf("\n");}break;case 4:if(qu->front==NULL)printf(" >>没有排队的病人!\n");else{p=qu->front;printf(" >>病人按以下顺序就诊:");while(p!=NULL){printf("%d",p->data);p=p->next;}printf("\n");}flag=0;break;case 5:if(qu->front!=NULL)printf(" >>请排队的病人明天就医!\n"); flag=0;break;}}}int main(){SeeDoctor();return 0;}六、结论与分析在本次试验中进一步理解队列的基本运算的实现,掌握队列的定义及其基本操作,掌握队列的存储结构及基本运算的实现和掌握队列的操作和应用,差不多也提高使用理论知识指导解决实际问题的能力。
数据结构实验三
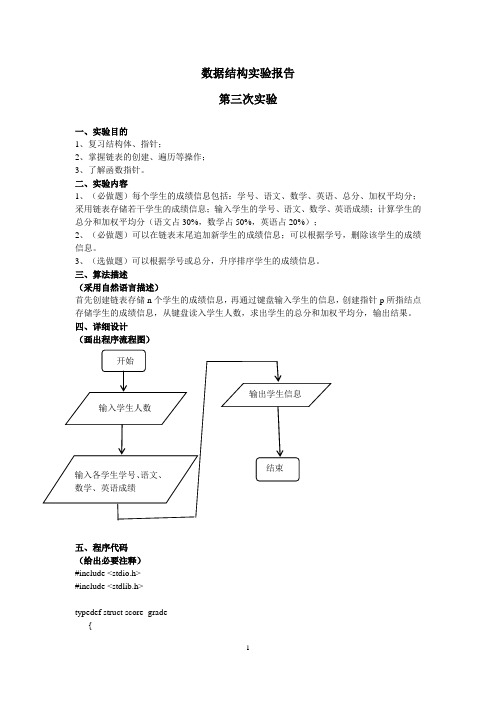
数据结构实验报告第三次实验一、实验目的1、复习结构体、指针;2、掌握链表的创建、遍历等操作;3、了解函数指针。
二、实验内容1、(必做题)每个学生的成绩信息包括:学号、语文、数学、英语、总分、加权平均分;采用链表存储若干学生的成绩信息;输入学生的学号、语文、数学、英语成绩;计算学生的总分和加权平均分(语文占30%,数学占50%,英语占20%);2、(必做题)可以在链表末尾追加新学生的成绩信息;可以根据学号,删除该学生的成绩信息。
3、(选做题)可以根据学号或总分,升序排序学生的成绩信息。
三、算法描述(采用自然语言描述)首先创建链表存储n个学生的成绩信息,再通过键盘输入学生的信息,创建指针p所指结点存储学生的成绩信息,从键盘读入学生人数,求出学生的总分和加权平均分,输出结果。
四、详细设计(画出程序流程图)五、程序代码(给出必要注释)#include <stdio.h>#include <stdlib.h>typedef struct score_grade{long number;int Chinese;int Math;int English;int sum;double average;struct score_grade *next;}student;student* Input_Score(int n){int i;student *stu,*p,*q;p=(student*)malloc(sizeof(student));stu=p;q=p;printf("请输入第1个考生的信息\n");scanf("%ld",&p->number);scanf("%d",&p->Chinese);scanf("%d",&p->Math);scanf("%d",&p->English);p->sum=(p->Chinese)+(p->Math)+(p->English);p->average=(p->Chinese)*0.3+(p->Math)*0.5+(p->English)*0.2;for(i=2;i<=n;i++){p=(student*)malloc(sizeof(student));p->next=NULL;printf("请输入第%d个考生的信息\n",i);scanf("%ld",&p->number);scanf("%d",&p->Chinese);scanf("%d",&p->Math);scanf("%d",&p->English);p->sum=(p->Chinese)+(p->Math)+(p->English);p->average=(p->Chinese)*0.3+(p->Math)*0.5+(p->English)*0.2;q->next=p;q=p;}return stu;}void Output(student *stu,int n){int i;student *p;printf("学生考试信息\n");while(p->next!=NULL){printf("学生学号:%ld\n",p->number);printf("语文成绩:%d\n",p->Chinese);printf("数学成绩:%d\n",p->Math);printf("英语成绩:%d\n",p->English);printf("总分:%d\n",p->sum);printf("平均分:%.1f\n",p->average);printf("\n");p=p->next;}printf("学生学号:%ld\n",p->number);printf("语文成绩:%d\n",p->Chinese);printf("数学成绩:%d\n",p->Math);printf("英语成绩:%d\n",p->English);printf("总分:%d\n",p->sum);printf("平均分:%.1f\n",p->average);printf("\n");}void Delete(student *stu){long number;printf("请输入需要删除的考生学号\n");scanf("%ld",&number);student *a,*b;a=stu;b=stu->next;while(b){if((b->number)==number){a->next=b->next;free(b);break;}a=a->next;b=b->next;}}{int n,a,i;printf("请输入考生人数:\n");scanf("%d",&n);student *stu;stu=Input_Score(n);Output(stu,n);Delete(stu);Output(stu,n);}六、测试和结果(给出测试用例以及测试结果)七、用户手册(告诉用户如何使用程序)输入考生人数和考生信息便可以运行程序。
国家开放大学《数据结构》课程实验报告(实验3 ——栈、队列、递归设计)参考答案

/*判队空*/
int QueueEmpty(SeqQueue *sq)
{
if(sq->rear==sq->front)
return 1;
else
return 0;
}
/*循环队列入队*/
void InQueue(SeqQueue *sq,ElemType x)
{
if ((sq->rear+1)%MaxSize==sq->front) /*队满*/
InitStack(s);
printf("(2)栈为%s\n",(StackEmpty(s)?"空":"非空"));
printf("(3)输入要进栈的数据个数:");
scanf("%d",&n);
printf("依次输入进栈的%d个整数:",n);
/*数据依次进栈*/
for(i=0; i<n; i++)
{
printf("循环队列已空,不能进行出队操作!\n");
exit(1);
}
else{
x=sq->data[sq->front];
sq->front=(sq->front+1)%MaxSize;
return x;
}
}
/*取队头元素*/
ElemType GetQueue(SeqQueue *sq)
{
void InitQueue(SeqQueue *sq); /*初始化队列*/
int QueueEmpty(SeqQueue *sq); /*判队空*/
数据结构实验报告三

<1>初始化一个队列。
循环队列:
链队列:
<2>判断是否队空。
循环队列:
链队列:
<3>判断是否队满。
循环队列:
第一组数据:入队n个元素,判断队满
第二组数据:用循环方式将1到99,99个元素入队,判队满
入队
第一组数据:4,7,8,12,20,50
第二组数据:a,b,c,d,f,g
出队
取队头元素
3.数据结构设计
循环队列
4.算法设计
(除书上给出的基本运算(这部分不必给出设计思想),其它实验内容要给出算法设计思想)
求当前队列中的元素个数:书写函数配合出队函数和判对空函数,定义一个整型变量i计数,在一个循环中每出对一次,计数器加一,直到对空,返回i即为队列元素个数。
第二题:首先判断队列是否队满,如果队满打印队满,结束程序,如果队列不满则进行下一步操作,定义一个变量x,从键盘输入其值,判断如果x的值为0,结束程序,如果不为0进入循环,如果x的模运算不等于0,将x入队,反之出队,直到x的模运算等于0,最后通过循环输出队列。
实现:从列不空,删除Q的队头元素用e返回其值,并返回OK,则返回ERROR
Status EnQueue (LinkQueue *Q, QE1emType e) {
QueuePtr p
if (Q->front==Q- >rear)
三、循环队列与链队列性能分析
1.循环队列与链队列基本操作时间复杂度均为0(1);
2.队列的抽象数据队列Data同线性表。元素具有相同的类型,相邻元素具有前驱和后继关系。Operation InitQueue(*Q):初始化操作,建立一个空队列Q. DestoryQueue(*Q):若队列Q存在,则销毁它。ClearQueue(*Q):将队列Q清空 GetHead(Q,*e):若队列Q存在且非空,用e返回队列Q的队头元素。EnQueue(*Q,e):若队列Q存在且非空, 插入新元素e到队列Q中并称为队元素。DeQueue(*Q,*e):删除队列Q中队头元素,并用e返回其值QueueL ength(Q)。
北京理工大学数据结构实验三报告

} top++; stack[top]=ch; } else if(ch=='^'||ch=='%') { while(stack[top]=='^'||stack[top]=='%') { exp[t]=stack[top]; top--; t++; } top++; stack[top]=ch; } else if(ch=='*'||ch=='/') { while(stack[top]=='*'||stack[top]=='/') { exp[t]=stack[top]; top--; t++; } top++; stack[top]=ch; } else { // printf("第%d 个数开始出错!\n",i+1); judge=1; flag=0; break; } i++; ch=str[i]; } if(k!=l) { printf("括号不匹配!\n"); judge=1; flag=0; } else if (str[zs-1]=='+'||str[zs-1]=='-'||str[zs-1]=='*'||str[zs-1]== '/')
二叉树中不存在度大于 2 的结点) ,并且,二叉树的子树有左右之分, 其次序不能任意颠倒。 4. 二叉树的性质 (1)在二叉树的第 i 层上至多有 个结点(i≥1) 。
(2)深度为 k 的二ቤተ መጻሕፍቲ ባይዱ树至多有
个结点(k≥1) 。
数据结构实验报告三

数据结构实验报告三数据结构实验报告三引言:数据结构作为计算机科学的重要基础,对于计算机程序的设计和性能优化起着至关重要的作用。
在本次实验中,我们将深入研究和实践数据结构的应用,通过实验来验证和巩固我们在课堂上所学到的知识。
一、实验目的本次实验的主要目的是通过实践操作,进一步掌握和理解数据结构的基本概念和操作。
具体来说,我们将学习并实现以下几个数据结构:栈、队列、链表和二叉树。
通过对这些数据结构的实现和应用,我们将更好地理解它们的特点和优势,并能够灵活运用于实际问题的解决中。
二、实验内容1. 栈的实现与应用栈是一种后进先出(LIFO)的数据结构,我们将学习如何使用数组和链表两种方式来实现栈,并通过实例来演示栈的应用场景,如括号匹配、表达式求值等。
2. 队列的实现与应用队列是一种先进先出(FIFO)的数据结构,我们将学习如何使用数组和链表两种方式来实现队列,并通过实例来演示队列的应用场景,如任务调度、消息传递等。
3. 链表的实现与应用链表是一种动态数据结构,相比数组具有更好的灵活性和扩展性。
我们将学习如何使用指针来实现链表,并通过实例来演示链表的应用场景,如链表的插入、删除、反转等操作。
4. 二叉树的实现与应用二叉树是一种常见的树形结构,我们将学习如何使用指针来实现二叉树,并通过实例来演示二叉树的应用场景,如二叉树的遍历、搜索等操作。
三、实验过程1. 栈的实现与应用我们首先使用数组来实现栈,并编写相关的入栈、出栈、判空、获取栈顶元素等操作。
然后,我们通过括号匹配和表达式求值两个实例来验证栈的正确性和应用性。
2. 队列的实现与应用我们使用数组来实现队列,并编写相关的入队、出队、判空、获取队头元素等操作。
然后,我们通过任务调度和消息传递两个实例来验证队列的正确性和应用性。
3. 链表的实现与应用我们使用指针来实现链表,并编写相关的插入、删除、反转等操作。
然后,我们通过链表的插入和删除操作来验证链表的正确性和应用性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
if(T)
{
for(int i=0;i<lay;i++)
printf(" ");
printf("%c\n",T->data);
DisplayPrint(T->lchild,lay+1);
DisplayPrint(T->rchild,lay+1);
}
}
//求结点的个数
int Node(BinTree T)
{
int static N=0;
if(T)
{
Node(T->lchild);
N++;
Node(T->rchild);
}
return N;
}
//求叶子的个数
int Leaf(BinTree T)
{
int static L=0;
if(T)
{
Leaf(T->lchild);
if(!(T->lchild||T->rchild))//没有左子树和右子树,就是叶子
有语法错误和打程序时的拼写错误,主要就是根据出错的地方进行单方面的调试。
六、对算法的程序的讨论、分析,改进设想,其它经验教训:
在算法实现上,从算法的效率看,非递归方法具有较好的时间效率,递归方法书写形式较为简捷,更为直观,一般具有较好的空间效率。
在按要求访问树中某些结点的数据元素时,选择一种合适的访问顺序是有必要的。
#include <string.h>
#include <malloc.h>
#include <stdlib.h>
#define NULL 0
typedef char DataType;
typedef struct BinTNode
{
DataType data;
struct BinTNode *rchild,*lchild;
PostOrder(T->rchild);
printf("%c",T->data);
}
}
//用广义表表示二叉树
void ListPrint(BinTree T)
{
if(T)
{
printf("%c",T->data);
if(T->lchild != NULL || T->rchild != NULL)
}BinTNode,*BinTree;
//创建二叉数
void Create(BinTree *T)
{
char ch;
if((ch = getchar()) == '*')//输入'*'时该节点为空
*T = NULL;
else
{
*T = (BinTree)malloc(sizeof(BinTNode));
}
}
//中序遍历二叉树
void InOrder(BinTree T)
{
if(T)
{
InOrder(T->lchild);
printf("%c",T->data);
InOrder(T->rchild);
}
}
//后序遍历二叉树
void PostOrder(BinTree T)
{
if(T)
{
PostOrder(T->lchild);
L++;
Leaf(T->rchild);
}
return L;
}
//交换左子树和右子树
void Change(BinTree *T)
{
if(*T)
{
BinTNode *temp;
Change(&(*T)->lchild);
Change(&(*Tgt;lchild;
{
printf("(");
ListPrint(T->lchild);
if(T->lchild != NULL)
printf(",");
ListPrint(T->rchild);
printf(")");
}
}
}
//用凹入表表示二叉树
/*对于凹入表表示二叉树,其实就是把二叉树结点的深度表示出来*/
void DisplayPrint(BinTree T,int lay)
二、程序设计的基本思想,原理和算法描述:
(包括程序的结构,数据结构,输入/输出设计,符号名说明等)
基本思想:对任意一棵二叉树,试将其所有节点的左、右子树交换。并将交换前、后不同的二叉树分别用前序、中序、和后序三种不同的方法进行遍历。
基本原理:同基本线性表、特殊线性表相似,二叉树也有顺序和链式两种基本的存储结构。因此针对不同的存储结构,在实现左右子树交换的过程中方法会有不同。在程序实现过程中要求不同功能分别用单个的函数实现,其中按层遍历二叉树的函数用顺序方法实现,其他函数用链式方法实现。
利用树对不同数据元素进行组合,在排序和某些特殊应用情景下是一种不错的选择。
七、对实验方式、组织、设备、题目的意见和建议:
对题目可以更加综合一下,与后面学到的图结合起来,那么它的作用会更大。
printf("结点的个数:nodes = %d\n",Node(T));
printf("叶子的个数:leaves = %d\n",Leaf(T));
Change(&T);
printf("交换左右子树,并用广义表表示法:");
ListPrint(T);
printf("\n");
}
四、运行输出结果:
InOrder(T);
printf("\n");
printf("输出后序遍历:");
PostOrder(T);
printf("\n");
printf("输出广义表表示法:");
ListPrint(T);
printf("\n");
printf("输出凹入表表示法:\n");
DisplayPrint(T,1);
叶结点的值为3
只有左孩子或右孩子的结点则其值分别等于左孩子或右孩子的值
左、右孩子均有的结点,则其值等于左、右孩子结点的值之和
用广义表表示法显示所建二叉树
阅读理解建立Huffman树的算法,对该算法进行运行及调试。具体实现要求:
1.调试并运行Huffman算法,验算《回家作业六》的第3题。
2.(★)求Huffman树的带权路径长度WPL。
(*T)->data = ch;
Create(&(*T)->lchild);
Create(&(*T)->rchild);
}
}
//先序遍历二叉树
void PreOrder(BinTree T)
{
if(T)
{
printf("%c",T->data);
PreOrder(T->lchild);
PreOrder(T->rchild);
(*T)->lchild=(*T)->rchild;
(*T)->rchild=temp;
}
}
void main()
{
BinTree T;
printf("输入先序序列:");
Create(&T);
printf("输出先序遍历:");
PreOrder(T);
printf("\n");
printf("输出中序遍历:");
3.用凹入表表示所建二叉树。
4.分别利用前序遍历、中序遍历、后序遍历所建二叉树。
5.求二叉树结点总数,观察输出结果。
6.求二叉树叶子总数,观察输出结果。
7.交换各结点的左右子树,用广义表表示法显示新的二叉树。
8.(★)二叉树采用链接存储结构,其根结点指针为T,设计一个算法对这棵二叉树的每个结点赋值:(注意要修改DataType类型)
《数据结构》实验报告三
一、上机实验的问题和要求:
要求采用二叉链表作为存储结构,完成二叉树的建立,前序、中序和后序遍历的操作,求所有叶子及结点总数的操作等。具体实现要求:
1.基于先序遍历的构造算法:输入是二叉树的先序序列,但必须在其中加入虚结点以示空指针的位置。假设虚结点输入时用空格字符表示。
2.用广义表表示所建二叉树。
基本原理:(1)创建二叉树。(2)用三种不同的方法遍历交换左右子树前的二叉树。(3)交换二叉树中所有结点的左右子树。(4)用三种不同的方法遍历交换左右子树后的二叉树。
三、源程序及注释:
//要求采用二叉链表作为存储结构,完成二叉树的建立,前序、中序和后序遍历的操作,求所有叶子及结点总数的操作等
#include <stdio.h>
