《风险理论与非寿险精算》期末复习
保险精算学-笔记-涵盖(利息,生命表,寿险精算及实务,非寿险,风险理论,内容丰富)

保险精算学-笔记-涵盖(利息,⽣命表,寿险精算及实务,⾮寿险,风险理论,内容丰富)第⼀章:利息理论基础第⼀节:利息的度量⼀、利息的定义利息产⽣在资⾦的所有者和使⽤者不统⼀的场合,它的实质是资⾦的使⽤者付给资⾦所有者的租⾦,⽤以补偿所有者在资⾦租借期内不能⽀配该笔资⾦⽽蒙受的损失。
⼆、利息的度量利息可以按照不同的标准来度量,主要的度量⽅式有1、按照计息时刻划分:期末计息:利率期初计息:贴现率2、按照积累⽅式划分:(1)线性积累:单利计息单贴现计息(2)指数积累:复利计息复贴现计息(3)单复利/贴现计息之间的相关关系单利的实质利率逐期递减,复利的实质利率保持恒定。
单贴现的实质利率逐期递增,复贴现的实质利率保持恒定。
时,相同单复利场合,复利计息⽐单利计息产⽣更⼤的积累值。
所以长期业务⼀般复利计息。
时,相同单复利场合,单利计息⽐复利计息产⽣更⼤的积累值。
所以短期业务⼀般单利计息。
3、按照利息转换频率划分:(1)⼀年转换⼀次:实质利率(实质贴现率)(2)⼀年转换次:名义利率(名义贴现率)(3)连续计息(⼀年转换⽆穷次):利息效⼒特别,恒定利息效⼒场合有三、变利息1、什么是变利息2、常见的变利息情况(1)连续变化场合(2)离散变化场合第⼆节:利息问题求解原则⼀、利息问题求解四要素1、原始投资本⾦2、投资时期的长度3、利率及计息⽅式4、本⾦在投资期末的积累值⼆、利息问题求解的原则1、本质任何⼀个有关利息问题的求解本质都是对四要素知三求⼀的问题。
2、⼯具现⾦流图:⼀维坐标图,记录资⾦按时间顺序投⼊或抽出的⽰意图。
3、⽅法建⽴现⾦流分析⽅程(求值⽅程)4、原则在任意时间参照点,求值⽅程等号两边现时值相等。
第三节:年⾦⼀、年⾦的定义与分类1、年⾦的定义:按⼀定的时间间隔⽀付的⼀系列付款称为年⾦。
原始含义是限于⼀年⽀付⼀次的付款,现已推⼴到任意间隔长度的系列付款。
2、年⾦的分类:(1)基本年⾦约束条件:等时间间隔付款付款频率与利息转换频率⼀致每次付款⾦额恒定(2)⼀般年⾦不满⾜基本年⾦三个约束条件的年⾦即为⼀般年⾦。
中国精算师考试《非寿险精算》试题网友回忆版一

中国精算师考试《非寿险精算》试题(网友回忆版)一[单选题]1.根据保险公司风险资本比率所在的不同范围,监管部门会采取相应的措施。
(江南博哥)当风险资本比率()时,属于授权控管水准,监管部门可以对保险公司采取重整或清算的行动。
A.大于200%B.介于150%至200%之间C.介于100%至150%之间D,介于70%至100%之间E低于70%参考答案:D参考解析:风险资本比率=总调整资本/最低风险资本XIOo除比率越大,则风险越小。
200%以上——无行动水准150%-200%——公司行动水准100%-150%——监管行动水准70%-100%——授权控管水准70%以下——强制控管水准[单选题]2.某公司承保业务如下表所示:()OA.0.148B.0.168C.0.188D.0.208E.0.228参考答案:B参考解析:财务稳定性系数K是保险赔付随机变量的标准差Q与所收保费P的比值,即K=Q∕P°K越小,财务越稳定。
设n个独立的危险单位,每个保额a元,损失概率为p,损失变量服从二项分布B(n,p),则保险赔付的标准差Q=Tnp(1-p),纯保费p=em q,则财务稳定系数n=Q= ------------------- - --------= ------Pαnq√⅞α设有n类业务,第i类有ni个独立的危险单位,每个保额ai元,损失概率pi,则赔付的方差DXi=a⅛Mi-PJ,则所有业务的财务稳定系数为QJD,Ei1D)-JXg E1DXiJ比J4n<Pι(i-P。
】-F-Σ{1ιi n i p i^∑11⅝n i p j^∑1ι⅜∏iPi因此,业务一和业务三合并的财务稳定系数为_Q_√M∏1p1(i-PJ+申a p aα-p・)3nd>,+a√⅛¾⅛____________κ_√5000z×6000×003×0.97÷1000001×300×0.03×0.97二SOOOX6000×0J3+100000×300×0.03=0.168[单选题]3.一组样本数据满足以下条件:(1)均值=35,000(2)标准差=75,000(3)中值二10,000(4)90%分位数=Io0,000(5)样本服从WeibUI1分布用分位数估计法估计WeibU11分布的参数丫,估计结果0。
非寿险精算记忆部分

风险资本比率大于200%时,属于无行动水准;风险比率介于150%至200%时,属于公司行动水准;风险资本比率介于100%至150%时,属于监管行动水准;风险资本比率介于70%至100%时,属于授权监控水准;风险资本低于70%,属于强制控管水准。
VaR的优点:1、VaR技术可以在事前计算投资组合的风险;2、VaR方法可以涵盖影响金融资产的各种不同市场因素,同时该方法也可以测度非线性的风险问题。
VaR的缺点:1、VaR并没有给出最坏情形下的损失;2、VaR并没有给出损失的尾部分布的描述;3、VaR的度量结果存在误差;4、V aR方法不满足次可加性,不符合一致性风险度量的要求。
条件尾部期望CTE的优点:1、它代表了超额损失的平均水平,反映了损失VaR时平均损失的大小,更体现潜在的风险价值;2、CTE的计算通过构造功能函数而化为一个凸性优化问题,必定存在最优解;3、求CTE的同时,VaR也可同时获得,因此可以对风险实行双重监控;4、CTE具有次可加性。
常用来作为损失次数的理论分布有:泊松分布、二项分布、负二项分布。
常用的损失额理论分布:对数正态分布、帕累托分布、伽马分布、对数伽马分布、韦伯分布和塔方分布。
保险人在费率厘定的过程中需要满足以下几个目标:1、费率应足够保险人支付期望赔付和费用。
2、费率中还应包括风险附加部分,以应付不可预期的事件的发生。
3、费率系统应鼓励保险人进行损失控制。
4、费率水平要合理稳定。
5、费率要满足监管部门的要求。
6、制定出来的费率要简单易懂。
纯保费法是建立在每个危险单位的损失基础上的,它需要严格定义的危险单位。
若危险单位不知道或各危险单位间有差异,比如,火灾险的情形,则纯保费法不适用。
损失率法得到的是当前费率的变化,所以它需要当前的费率和保费的历史记录。
而新业务的费率厘定,只能利用相关公司或相关险种的损失数据,没有历史记录,那么只能用纯保费法。
损失率法不适用于新业务的费率厘定。
非寿险精算考试复习资料

非寿险精算哈尔滨商业大学王磊概论论述风险与保险的基本关系(考试论述)寿险与非寿险的关系(统一用A4纸答号,随试卷上交500字以上)一、非寿险和非寿险精算非寿险是与寿险相对而言的,是指寿险以外的其它保险业务,主要包括财产保险、责任保险、健康保险和意外伤害保险等。
(一)财产保险财产保险是以有形的物质财富及相关利益为保险标的的一种保险。
主要包括火灾保险、运输保险和工程保险等。
1、火灾保险●特点:首先,火灾保险的保险标的只能存放于固定场所并处于相对静止状态下的各种财产物资;其次,火灾保险承报财产的地址不能随意变动,如果被保险人确实需要变动保险财产的存放地点,必须征得保险人的同意。
●费率:影响火灾保险费率的因素有建筑结构及等级、占用性质、承保风险的种类、地理位置、被保险人防灾设备和措施等。
●类别:火灾保险可分为团体火灾保险和普通家庭财产保险两种。
团体火灾保险以企业及其它法人团体为保险对象,普通家庭财产保险则面向居民区家庭或个人。
2、运输保险运输保险包括运输工具保险和和运输货物保险,其中运输工具保险又可分为汽车保险、船舶保险和航空保险。
●汽车保险包括车身损失险和第三者责任保险(承保被保险人在汽车使用过程中对第三者造成的财产损失和人身伤亡依法应付的赔偿责任,在许多国家、包括我国属于强制险)。
影响汽车保险的因素大体为两类:从人因素和从车因素。
●船舶保险包括碰撞责任(与其它物体碰撞造成对方损失)和非碰撞责任(船舶本身)保险。
影响船舶保费的因素为航行环境和船舶本身条件。
●航空保险包括机身险、第三者责任险和旅客意外伤害险。
3、工程保险工程保险主要包括建筑工程、安装工程、和科技工程保险三大类。
保险责任主要包括物质损失和第三者责任。
(二)责任保险1、普通责任保险:承保被保险人在公共活动场所的过错行为致使他人财产损失或人身伤害所造成的损失。
2、产品责任保险:指以产品制造者、销售者、维修者的产品责任为承保责任的险种。
3、职业责任保险:承保各种职业技术人员在本职工作中因疏忽和过失造成的财产损失和人身伤亡依法应付的赔偿责任。
风险模型与非寿险精算学 (16)

var(X2) = E(X22) − [E(X2)]2 = 71, 135, 800 − (6, 557)2 = (5304)2
风险模型与非寿险精算学
0 导论 1 分保协议 2 特定分布 3 通货膨胀 4 估计 5 超额保单2.1 6对真数题正态分布 2.2 正态分布
logU − µ Uk = σ − kσ
风险模型与非寿险精算学
0 导论 1 分保协议 2 特定分布 3 通货膨胀 4 估计 5 超额保单2.1 6对真数题正态分布 2.2 正态分布
代码
LN<-function(mu,sigma,L,U,k){ Lk<-(log(L)-mu)/sigma-k*sigma Uk<-(log(U)-mu)/sigma-k*sigma exp(k*mu+k^2*sigma^2/2)*(pnorm(Uk)-pnorm(Lk)) } LN(7.5,0.85,1000,5000,0) #分布 LN(7.5,0.85,0,1000,1) #均值 LN(7.5,0.85,5000,1e15,2) #方差
Example 2.2 计算与前一个例子中描述的分保协议相同的情况下保险人支付的 净索赔金额的方差:
(a)无任何协议 (b)仅使用协议1 (c)仅使用协议2
风险模型与非寿险精算学
0 导论 1 分保协议 2 特定分布 3 通货膨胀 4 估计 5 超额保单2.1 6对真数题正态分布 2.2 正态分布
解
如果没有这两项协议,保险人将全额赔偿每项损失. 所以方差 是:
var(X) = e2µ+σ2 (eσ2 − 1) = e2(8.5)+0.64(e0.64 − 1) = (6408)2
协议1,保险人支付每笔损失X的 75%. 因此,净数额 为X1 = 0.75X,方差为:
《非寿险精算》试题及答案

《非寿险精算》试题及答案(解答仅供参考)第一套一、名词解释1. 非寿险精算:非寿险精算是研究非寿险业务中风险评估、保费定价、准备金评估、损失分布分析等领域的数学和统计方法。
2. 损失概率:损失概率是指在一定时间内,某一特定风险事件发生的可能性。
3. 纯保费:纯保费是指保险公司为了覆盖预期的损失成本而收取的保费。
4. 保险准备金:保险准备金是保险公司为应对未来可能发生的索赔而储备的资金。
5. 责任年限法:责任年限法是一种计算未决赔款准备金的方法,基于假设所有未决赔款将在一定年限内结案。
二、填空题1. 非寿险精算的主要内容包括风险评估、______、准备金评估和损失分布分析。
答案:保费定价2. 在非寿险业务中,______是决定保费水平的重要因素。
答案:损失概率和损失程度3. 如果实际赔付金额超过已收取的保费和投资收益之和,就需要动用______来支付。
答案:保险准备金4. 在非寿险精算中,______是一种常用的损失分布模型。
答案:泊松分布或帕累托分布5. 在责任年限法中,如果假设所有未决赔款将在一年内结案,那么这就是______责任年限法。
答案:一年三、单项选择题1. 非寿险精算主要应用于哪种类型的保险业务?A. 寿险B. 健康险C. 财产险D. 意外险答案:C. 财产险2. 下列哪一项不属于非寿险精算的内容?A. 风险评估B. 保费定价C. 投资管理D. 准备金评估答案:C. 投资管理3. 在非寿险精算中,用来衡量风险大小的指标是?A. 损失概率B. 损失程度C. 风险暴露D. 风险溢价答案:A. 损失概率4. 下列哪种方法可以用来计算非寿险业务的未决赔款准备金?A. 综合比例法B. 平均估算法C. 责任年限法D. 追溯法答案:C. 责任年限法5. 在非寿险精算中,如果某风险事件的发生概率为0.1,且每次发生时的平均损失为1000元,则该风险的期望损失为?A. 10元B. 100元C. 1000元D. 10000元答案:B. 100元四、多项选择题1. 非寿险精算的主要内容包括:A. 风险评估B. 保费定价C. 准备金评估D. 损失分布分析E. 投资管理答案:ABCD2. 下列哪些因素会影响非寿险业务的保费定价?A. 损失概率B. 损失程度C. 营运费用D. 目标利润E. 法律法规答案:ABCD3. 下列哪些方法可以用来计算非寿险业务的未决赔款准备金?A. 综合比例法B. 平均估算法C. 责任年限法D. 追溯法E. 预测法答案:ABCD4. 在非寿险精算中,以下哪些是常用的损失分布模型?A. 正态分布B. 泊松分布C. 帕累托分布D. 对数正态分布E. 卡方分布答案:BC5. 下列关于非寿险精算的陈述中,哪些是正确的?A. 非寿险精算是研究非寿险业务中的风险评估和管理的学科。
非寿险精算课后习题答案(中精-主编 韩天雄)

第一章 1T0.09811S ==2T5.6569σ== 3T[]{}()14%,25%, 1.1,()12.5%,20.2%, 2.6%()0.1036()0.456()()0.0051p p p m m F p Fp p Fpp F p m F E R E R R E R R Treynor E R R Sharpe Jensen s alpha E R R E R R σβσβσβ======-==-=='=-+-=度量值度量值度量值4T[]{}()0.099()0.4091()()()()0m Fm m Fmm F m m F m m E R R Treynor E R R Sharpe Jensen s alpha E R R E R R E R E R βσβ-==-=='=-+-=-=度量值度量值度量值5T[]{}()() 1.2%p F p m F Jensen s alpha E R R E R R β'=-+-=-度量值 6T0.950.90.810,10,0ξξξ===7T0.990.990.990.990.99()0.9933330.99109109330.99109332.326109286.53P X X P ξξξξξ≤=--⎛⎫≤= ⎪⎝⎭-⎛⎫Φ= ⎪⎝⎭-== 8T222()331()109(1)(2)39.65992.2018E X r r Var X r r r θθθ⎧==⎪-⎪⎨⎪==⎪--⎩=⎧⎨=⎩ 0.950.950.990.99()110.95114.9510.99281.48rrrF x x Q Q Q Q θθθθθθ⎛⎫=- ⎪+⎝⎭⎛⎫-= ⎪+⎝⎭=⎛⎫-= ⎪+⎝⎭=9T()[]011()11pprQ Q p r pE X QF x dx dx x r Q θθθθθ-⎛⎫∧=-= ⎪+⎝⎭⎡⎤⎛⎫⎢⎥=-⎪ ⎪-+⎢⎥⎝⎭⎣⎦⎰⎰111()()111111111p p p r p pr p pCTE Q E X E X Q p Q p r r Q Q p r Q θθθθθθθ--⎡⎤=+-∧⎣⎦-⎧⎫⎡⎤⎛⎫⎪⎪⎢⎥=+-- ⎪⎨⎬ ⎪---+⎢⎥⎪⎪⎝⎭⎣⎦⎩⎭⎛⎫=+∙∙⎪ ⎪--+⎝⎭0.950.990.950.9939.66, 2.20,114.95,281.48243.60548.70r Q Q CTE CTE θ====∴==15T()222212112212|111111p p p p p p x Q x x Q Q Q CTE E X X Q dxp dx dx p p pμσμμσσμσμ-⎛⎫-+∞⎪⎝⎭--⎛⎫⎛⎫--+∞+∞ ⎪ ⎪⎝⎭⎝⎭-⎛⎫- ⎪ ⎪⎝⎭⎡⎤=>⎣⎦=-⎡⎤⎢⎥=+-⎢⎥⎣⎦=+--⎰⎰⎰ 0.950.950.950.950.95()0.95330.9510933 1.645109212.29257.89P X Q Q Q Q CTE ≤=-⎛⎫Φ= ⎪⎝⎭-==∴=第二章 2T(1)从表中可以得出索赔额组中值i i f X 和索赔频率1841600121610122101====∑∑=-=i i i i i i f x X f x X由题知)(~2σ,u LN X ,对数正态分布的期望和方差如下:()()()122222-==++σσσeeX Var X E u u根据矩估计法可知:()2222248.605)(111216222=--=-=++X X n ne e eu u σσσ由此可以求得:47.099.6==∧∧σu(2)()()%27.0748.214000ln 4000ln =-=⎪⎪⎭⎫⎝⎛->-=>φσσu u P P x x3T每份保单赔款次数X 服从泊松分布,X 的概率密度函数为: ())32,10(!,,==-k k ex f kλλ由极大似然估计可以得到:X nXni ==∑=∧1iλ而且1965.01==∑=ni i i f x X所以1965.0=∧λ 5T韦伯分布的分布函数为:()rcx e X F --=1令7.012.01=-=---rrcx cx ee解得韦伯分布的20%和70%分位数:()()rrc x c x 17.012.03.0ln 8.0ln ⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-=根据观测数据可以知道 :8.02.07.02.0==x x令()()8.03.0ln 2.08.0ln 11=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-rrc c 解得12.135.1==r c7T指数分布的概率密度函数为()xex f λλ-=,由极大似然估计得到220011==∧Xλ 2x 分布检验的检验假设:0H :赔款额分布服从参数22001=λ的指数分布 1H :赔款额分布不服从参数22001=λ的指数分布显著水平005.0=α,查自由度为41161=--=--k n 的2x 分布表, 得到分位数14.86,所以拒绝域为86.142≥x 赔款额落在0~100的理论概论为:()3653.0220011000022001000==≤≤-⎰dx e X P x同理可得8.2312=E 2.1473=E 4.934=E 3.595=E 1036=E()86.1489.3316122≥=-=∑=i ii i E E Q x在拒绝域范围内,所以拒绝原假设0H ,不能用指数分布模拟个别理赔分布。
风险模型与非寿险精算学 (36)
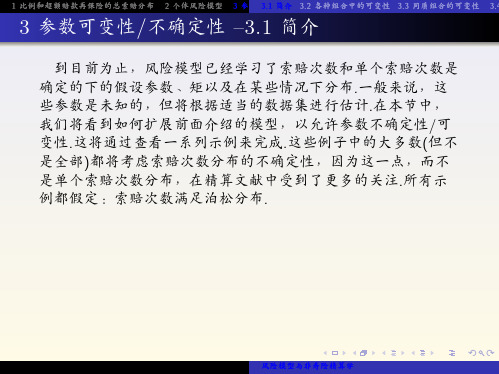
n
(ii) E[ Si] = nE[S1] = 0.2nm1 (因为{Si}ni=1具有相同分
i=1
布)
n
n
n
var[ Si] = E[var( Si|λ)]+varE( Si|λ) = E[nλm2]+var[nλ
i=1
i=1
i=1
风险模型与非寿险精算学
1 比例和超额赔款再保险的总索赔分布 2 个体风险模型 3 参数可3.变1 性简/介不确3.定2 性各种4组真合题中的可变性 3.3 同质组合的可变性 3.4
n
E Si =nE [Si] = 0.2nm1
i=1 n
var Si =nvar [Si] = 0.2nm2 + 0.01nm21.
i=1
风险模型与非寿险精算学
1 比例和超额赔款再保险的总索赔分布 2 个体风险模型 3 参数可3.变1 性简/介不确3.定2 性各种4组真合题中的可变性 3.3 同质组合的可变性 3.4
风险模型与非寿险精算学
1 比例和超额赔款再保险的总索赔分布 2 个体风险模型 3 参数可3.变1 性简/介不确3.定2 性各种4组真合题中的可变性 3.3 同质组合的可变性 3.4
答案 I
令Si表示组合中第i个保单的总索赔. 随机变量{Si|λ}ni=1独立同分布,每个变量都有一个参数为λ的 复合泊松分布F (x).随机变量λ满足以下分布: P (λ = 0.1) = 0.5 P (λ = 0.3) = 0.5.
1 比例和超额赔款再保 性各种4组真合题中的可变性 3.3 同质组合的可变性 3.4
解I
令组合中第i个保单的泊松参数为λi, i = 1, 2, ..., n, {λi}ni=1看作 是一组独立同分布的随机变量,每一个都有以下分布
精算模型期末试题及答案

精算模型期末试题及答案一、单选题1. 在精算模型中,风险管理的核心是:A. 保险公司的利润最大化B. 保险公司的偿付能力保持稳定C. 保险公司的市场份额提高D. 保险公司的资产负债表达到平衡答案:B. 保险公司的偿付能力保持稳定2. 下列哪项是精算模型中的风险类型:A. 技术风险B. 战略风险C. 信用风险D. 所有选项答案:D. 所有选项3. 承保准备金的计算方法主要有以下几种:A. 静态法和动态法B. 单纯保守法和单纯激进法C. 固定百分点法和利率曲线法D. 所有选项答案:D. 所有选项二、填空题1. 在精算模型中,经济风险可以通过________方法进行测量。
答案:风险价值2. 风险控制的核心是_____________。
答案:风险管理3. 在风险投资决策中,收益与风险之间存在_________关系。
答案:正相关三、简答题1. 简述保险公司经营风险管理的重要性及方法。
答案:保险公司经营风险管理的重要性在于确保保险公司的偿付能力和稳定性。
方法包括但不限于:建立合理的资本管理制度、制定适当的投资策略、合理估计和控制保险责任准备金、建立完善的内部控制系统、及时响应市场变化等。
2. 请解释什么是风险价值(Value at Risk,VaR)。
答案:风险价值是一种用来衡量金融机构面临的风险的指标。
它代表了在一定的置信水平下,资产价值可能发生的最大损失。
VaR可通过统计方法计算,从而帮助机构进行风险管理和金融决策。
四、综合题某保险公司在进行新产品定价时,需要考虑产品的风险,并进行资本管理,以保证公司的偿付能力。
请根据以下信息完成下列任务。
1. 假设该新产品的预期未来现金流入为100,000元,预期未来现金流出为80,000元。
计算该产品的净现值。
答案:100,000 - 80,000 = 20,000元2. 根据风险管理的原则,该保险公司希望在90%的置信水平下,最大的损失不超过3%。
请计算风险价值(VaR)。
风险模型与非寿险精算学 (23)

证明 我们希望计算积分的值:
∞
x
1 √
e−
1 2
(
log
x−µ σ
)2
dx
xσ 2π
α
换元,
u
=
log x−µ σ
−σ
.
所以积分变成:
∞
√1
e−
1 2
(u+σ)2
σeµ+uσ+σ2
du
σ 2π
log
a−µ σ
−σ
指数项部分进行合并,我们得到:
第二个积分就是我们在第(ii)(a)部分计算出的概率.所以:
E(R) = 2.26164 − 25 × 0.05745 = 0.8253
风险模型与非寿险精算学
0 导论 1 分保协议 2 特定分布 3 通货膨胀 4 估计 5 超额保单 6 真题
同样,第二个分保协议(其中R是再保险人支付的超过30的金 额),我们得到:
Y = 0, if X ≤ L Y = X − L, if X > L
风险模型与非寿险精算学
0 导论 1 分保协议 2 特定分布 3 通货膨胀 4 估计 5 超额保单 6 真题
显然,任何超额保单的到期保费将低于无超额保单的保费. 超额保单的保险人情况与超额损失再保险的再保险人相同.投 保人在损失方面的情况与超额损失再保险合同的保险人完全相 同.
自留额 25 30
保费 48.5 38.2
根据每个再保险安排,计算发生索赔涉及再保险人的概率. 通过调查分出给再保险人的每项索赔的平均金额,计算出哪一个 自留额最有价值(忽略保险人对风险的态度) 第2年,假设所有其他条件相同,保险公司认为通货膨胀将使其 组合中索赔的均值和标准偏差增加8%.如果再保险人收取与以前 相同的保险费,那么下一年哪一个自留额将是最有价值的.
保险精算期末复习题

死亡人数为( B ) 。 A.2073.92 【 s ( x) e
0 t dt
x
100 x 2 1 100 x 2 ) 】 ( ) , lx l0 s( x) ( 10000 x 1 x 1
6. 已知 20 岁的生存人数为 1 000 人,21 岁的生存人数为 998 人,22 岁的生存人数为 992 人, 则 1 | q20 为( C ) 。 A. 0.008 B. 0.007 C. 0.006
1 dax Ax
x
(2)终身寿险和期末付终身年金:1 ia (3)定期寿险和定期年金:1
iAx Ax
Ax ;1 ax:n Ax:n
dax:n Ax:n
x
(4)死亡时赔付寿险和连续年金:1 a (5)其它关系式: 三、选择题
Ax vax ax ; A1 vax:n ax:n x:n
二、简答题:
1
1. 人寿保险精算的原理的内容【Cf:教材 P3】 保险的基本原理是将众多投保人的保费集中到承保人处, 当风险发生后, 由承保人承担损 失。它的理论基础是概率论和大数定律。 投保人通过付出少量且固定的保费, 将大量的不确定的损失转移到承保人或保险公司身上; 承保人利用保费收入一方面保证赔偿的正常进行, 另一方面, 通过分析与计算来合理调配 资金, 提高保险基金的投资效益, 最终使投保人和承保人都有所收获。 2.债劵定价原理的内容及四种常用债劵价格计算公式。 【Cf:教材 P38-39】 债劵定价原理:债券的理论价格就是债劵未来息票收入的现值与到期偿还值的现值之和。 债券定价的基本公式: P rFan Cv
非寿险第二章-复习

0, 2 1的正态分布称为标准正态分布,记为N(0,1).
标准正态分布的密度函数为:
x
( x)
分布函数为: ( x) ( x)dx
1 e 2
x2 2
任意一个正态分布随机变量X, 都可以通过线性变换化为标准 正态分布随机变量,即:
X 若 X ~ N ( , ) , 则 Z = ~ N (0,1) .
§2.1 研究损失分布的数学工具
2.1.1 随机变量及其分布
随机变量及其分布 : 用X、Y、Z等大写字母表示随机变量;随机变 量X的分布函数,记作F(x)= P (X ,x . x) R
2.1.2 离散型随机变量和连续型随机变量
保险期限内,保险标的发生保险事故的次数N 的取值只能是0、1、2、…,这种只能取有限个 值或可列个值的随机变量,我们称之为离散型随 机变量。离散型随机变量除了用分布函数刻划其 规律以外,还可以用分布列来反映其分布规律。 离散型随机变量的分布列和分布函数的关系 可用下式表示:F ( x) pi
S X1 X 2 X N X i
假设诸 X i独立同分布,且与N独立。
由条件期望和条件方差的性质以及独立性假设可以得到:
i1
N
ES ( EN )( EX1 ) ;
VarS ( EX 1 ) 2 (VarN ) ( EN )(VarX 1 )
2.3.2 复合泊松分布
2
2
如果在条件期望和条件方差中Y不取定,那么 E( X Y )和Var ( X Y ) 都是随机变量Y的函数,因而也是随机变量。关于这两个随 机变量有如下重要性质:
EX E E ( X Y ) VarX Var E ( X Y ) E Var ( X Y )
中国精算师《非寿险精算》过关必做500题(含历年真题)(第5章 非寿险准备金评估)【圣才出品】

圣才电子书 十万种考研考证电子书、题库视频学习平台
12 月 31 日,利用七十八法则计算未到期责任准备金,结果为( )。[2011 年秋季真题]
A.小于 200
B.大于等于 200,小于 250
C.大于等于 250,小于 300
D.大于等于 300,小于 350
7
i 1
pˆ3
13 i 78
63 ,未到期责准备金的比例为:1 78
63 78
15 。因此未到期责任准备金为: 78
15 1000 192 。 78
5.某保险公司的直接理赔费用和已付赔款如表 5-4 和表 5-5 所示。 表 5-4 累积直接理赔费用 单位:元
4 / 66
圣才电子书 十万种考研考证电子书、题库视频学习平台
表 5-6
5 / 66
圣才电子书 十万种考研考证电子书、题库视频学习平台
由此可得最终进展因子(表 5-7): 表 5-7
因此可估计各事故年的最终赔款:
2008 年发生的赔案最终赔款为: 521101.37186 71487.63 ; 2009 年发生的赔案最终赔款为: 398761.753874 69937.49 ; 2010 年发生的赔案最终赔款为: 341253.358322 114602.7 。
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 5 章 非寿险准备金评估
一、单项选择题(以下各小题所给出的 5 个选项中,只有一项最符合题目要求,请将 正确选项的代码填入括号内)
1.某财产保险公司在一年内的保费收入如表 5-1 所示(单位:千元)。 表 5-1
假设保单期限为一年,且保费收入在季度内是均匀的,到年末按季提取未到期责任准备
非寿险精算答案整理

一:假设某保单的损失服从指数分布,概率密度函数为)0();(>=-x e x f x λλ其中,λ为未知参数,如果该保单过去各年的损失观测值为),(21n x x x ,求参数λ的极大似然估解:利用极大似然估计的方法,可以得到xxnni i1ˆ1==∑=λ二:假设某保险业务的累积损失S 服从复合泊松分布,泊松参数为20,而每次损失的金额服从均值为100的指数分布,用正态近似求累积损失的99%的分位数。
解:[]400000)100100(20)()()()()(200010020)()(222=+=+==⨯==X E N VAR N E X VAR S VAR X E S E λ分位数=3471)(326.2)(=⨯+S VAR S E加二、某保单规定的免赔额为20,该保单的损失服从参数为0.2的指数分布,求该保险人对该保险保单的期望赔款。
解: 令⎩⎨⎧≥-≤=2020200X X X Y ,,为保险人的赔款随机变量4202.052.0)20()2020()(-∞-=-=>-=⎰e dx e x X X E Y E x三、假设某公司承保的所有汽车每年发生交通事故的次数都服从泊松分布,而不同汽车的泊松分布参数不同,假设只取两个值(1或2),进一步假设λ的先验分布为4.0)2(,6.0)1(====λλp p ,如果汽车一年内发生4次事故,求该汽车索赔频率λ的后验分布。
解:λλλ-==e x P !4)4(41241)14(-===e x P λ 22416)24(-===e x P λ 2031.04.024166.0246.024)41(211=⨯+⨯⨯===---e e e x P λ7969.04.024166.0246.02416)42(212=⨯+⨯⨯===---e e e x P λ=)(λE 1)41(⨯==x P λ+2)42(⨯==x P λ=1.7969四:假设某险种的损失次数服从参数为0.2的泊松分布,对于一次保险事故,损失为5000元的概率是80%,损失为10000元的概率是20%,请计算保险公司的累积损失的分布 解:为简化计算,假设一个货币单位为5000元,解:818731.0)0(2.0===--e e f s λ ,130997.08.02.0)0()1()1(2.0=⨯⨯==-e f f f S X s λ043229.0))0()2(2)1()1((2)2(=+=S X S X s f f f f f λ五:假设某保险人签发了两份保单六:假设保险业务在一年内是均匀分布,保险期限为1年,各日历年的已赚保费如下,2000解:如果把1998年生效的相对费率看做是1,则1999年生效的相对费率为1.08,2001年生效的相对费率为1772.19.01*8.01=,2000年的相对费率为7.01.5%87*8.01.5%12*1=+,2001年的相对费率为1.08*12.5%+1.1772*12.5%=1.09215,2002年的相对费率为1.08*12.5%+1.1772*87.5%=1.16505,将所有年费的已赚保费调整到2002年的水平,可得等水平已赚保费为3100*1.1772/1.07+3200*1.1772/1.09215+3500*1.1772/1.16505=10396.28 八:某险种当年的相对费率和保费收入、过去三年的等水平已赚保费和经验损失数据如下表所示,假设A 为基础类别,经验数据的可信度为40%,如果整体保费需要上调15%,请计算调整后的相对费率。
保险学期末考试复习重点

保险学期末复习重点第一章1、什么是风险,风险具有哪些特征?风险:是人们在从事某种活动或决策的过程中,预期未来结果的随机不确定性。
风险特征:(一)客观性(二)损失性(三)不确定性(四)普遍性(五)可测性(六)可变性(发展性)(七)社会性2、风险的构成要素有哪些?(一)风险因素:(二)风险事故(三)风险损失(从保险的角度研究)(四)风险载体3、风险有哪几种分类方式?(2班了解)一、按风险发生的原因分类(一)自然风险(二)社会风险(三)政治风险(四)经济风险二、按风险性质(导致结果)分类:(一)纯粹风险(二)投机风险(三)收益风险三、依风险发生的形态分类:(一)静态风险(二)动态风险四、依风险涉及和影响的范围分类:(一)基本风险(二)特定风险五、依风险指向的标的分类(一)财产风险(二)责任风险(三)信用风险(四)人身风险六、按风险的损失程度分类:(一)高度风险(二)中度风险(三)低度风险4、简述风险管理的程序(企业)风险管理的过程:(一)风险管理目标的确定(二)风险识别—风险管理的基础(三)风险衡量(估价或评价)(四)风险处理(五)风险管理评估5.简述可保风险的条件一、可保风险的存在(一)风险必须是纯粹风险1、只有损失,没有收益的风险;2、个人受损时,社会也会受损(二)经济上具有可行性1、损失的程度不要偏大或偏小;2、损失的发生必须具有偶然性(三)存在大量具有同质风险的标的1、同质风险:风险单位在种类、品质、性能、价值等方面大体相近。
2、同质风险发生的概率相同。
(四)风险必须具有现实的可测性1、风险具有确定的概率分布;2、损失可以用货币进行确定和计量。
*6、保险和风险管理的关系如何?(2班了解)(一)风险是保险与风险管理产生和发展的前提和客观依据,保险与风险管理同以风险为管理对象。
(二)保险是风险管理的一个传统有效手段,是社会化风险管理的重要组成部分;是最能够适应风险不确定性与不平衡性发生规律的合理机制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常用分布 二项分布、泊松分布、均匀分布、指数分布、 正态分布、伽玛分布、贝塔分布 期望、方差
第三章 损失分布的贝叶斯方法
3.1 贝叶斯方法的基本过程 3.2 先验概率的估计 3.3 先验概率与后验概率 3.4 损失函数与贝叶斯估计量 3.5 贝叶斯方法的理论基础-主观概率
5.5 中心极限定理与正态分布逼近
令 s (1 )E(S) ,称θE(S)为保单组合的安全
附加保费,称θ为相对附加安全系数(或安全附 加保费率)。
第六章 短期聚合风险模型
6.1 引 言 6.2 理赔次数和理赔额的分布 6.3 理赔总量模型 6.4 复合泊松分布及其性质 6.5 聚合理赔量的近似模型
保费计算与实际相差较大; 准备金的提取不充分; 赔付过早发生; 营运成本扩大; 佣金的提高; 投资失利; 巨灾事故频繁发生; 风险聚合估计不周;
意外责任事故的赔付; 市场条件发生不利的变化; 保单责任文字界定不清晰; 宏观经济环境的不利变化; 法律法规的改变; 公司管理人员的贪污渎职行
第四章 随机模拟
4.1 引 言 4.2 均匀分布的随机数与伪随机数 4.3 服从各种分布的随机数 4.4 模拟应用举例 4.5 模拟样本的容量
4.2 均匀分布的随机数与伪随机数
产生均匀分布随机数的方法: 1、检表法 2、物理方法(可获得真正的随机数) 3、数学方法(伪随机数)
自然取中法(平方取中法) 倍积取中法 乘同余法(Skellam一阶线性同余法)
e n
fS (x)
n0
n!
p*n (x)
E(S) p1
Var(S ) p2
S的矩母函数:
M S (t) M N [ln M C (t)] e[MC (t)1]
6.4 复合泊松分布及其性质
1、求和的封闭性
定理6.4.1 若S1,S2,…,Sm是相互独立的随机变量,且
Si是服从参数为λi的复合泊松分布,理赔额的分布
风险理论与非寿险精算
期末复习
主要内容
第一章 风险与精算
第七章 长期聚合风险模型
第二章 损失分布
第八章 效用理论与保险决
第三章 损失分布的贝叶斯 策
方法
第九章 费率厘定
第四章 随机模拟
第十章 经验费率
第五章 短期个体风险模型 第十一章 准备金
第六章 短期聚合风险模型 第十二章 再保险
t
第八章 效用理论与保险决策问题
8.1 引言 8.2 效用与期望效用原理 8.3 效用函数与风险态度 8.4 效用原理与保险定价问题 8.5 期望效用的计算 8.6 效用理论的应用
8.2 效用与期望效用原理
最大期望效用原理:在具有风险和不确定的条 件下,个人进行决策的行为动机和准则是获得 最大的期望效用值,而不是为了获得最大期望 金额值。
风险和不确定情形下的一般决策准则:人们将 追求效用的期望值尽可能地达到最大。
8.3 效用函数与风险态度
决策者的三类风险态度: 1、u(w)为线性函数,即u’’(w)=0,
称决策者为风险中立型。 2、u(w)为凸函数(上凸),即
第一章 风险与精算
1.1 风险的含义 1.2 保险经营中的风险和风险因素 1.3 保险精算问题 1.4 本书的基本内容
1.2 保险经营中的风险和风险因素
保险公司的收支
收入
支出
保费收入 投资收入 分保和再保险佣金 新投入资本 其他收入
赔付 营运费用 再保险费 红利、税务 其他杂费
保险公司面临的不确定因素 (非寿险公司经营中的风险因素)
从先验概率到后验概率的过程是直接应用贝叶斯公
式,即
f (x ) f ( ) f ( x)
f (x ) f ( )d
其中 f (x ) f ( )d 是与θ无关的常数。
可以把贝叶斯公式简化为 f ( x) ∝ f (x ) f ()
∝表示“成比例关系”。
3.4 损失函数与贝叶斯估计量
常用的三种损失函数形式及其贝叶斯估计
1、利用个体理赔的分布计算总理赔S的均值
n
n
E(S) E( X k ) 和方差Var(S) Var(X k ) 。
k 1
k 1
2、对S的分布进行标准化处理:
P{S s} P{S E(S) s E(S) } Var(S) Var(S)
3、利用中心极限定理近似计算:
P{S s} ( s E(S) ) Var (S )
一般地,对估计值的精确度要求越高,对样 本容量的要求就越大。
第五章 短期个体风险模型
5.1 引 言 5.2 个别保单的理赔分布 5.3 独立和分布的卷积 5.4 求理赔分布的矩母函数法 5.5 中心极限定理与正态分布逼近 5.6 应用举例
5.1 引 言
假定第i 张保单可能的理赔为Xi,则Xi为非负随机变 量(i=1,2,…,n)。进而保险人在这个时间段内的理赔或 赔付总量为:
M S (t) M X1 (t)M X2 (t)L M Xn (t), t 0 (5.4.1)
若X1,X2,…,Xn同分布,设其共同的矩母函数为MX(t) ,
则有:
M S (t) [M X (t)]n , t 0
(5.4.2)
5.5 中心极限定理与正态分布逼近
利用中心极限定理求保单数很多时保单组合的总理 赔分布,基本步骤为:
命题6.3 设若短期聚合风险模型中的N和C的数 学期望和方差都存在,则有
E(S) E(N)E(C)
Var(S) E2 (C)Var(N ) E(N )Var(C)
6.4 复合泊松分布及其性质
复合泊松分布S的分布函数和密度函数:
FS (x)
n0
e n
n!
P*n (x)
S的均值和方差:
Var( X ) Var(E(B | I )) E(Var(B | I )) E2 (B)Var(I ) E(I )Var(B) q(1 q)E2 (B) qVar(B)
5.3 独立和分布的卷积
两项卷积 离散型随机变量的两项卷积
5.4 求理赔分布的矩母函数法
对于独立的随机变量和 S X1 X 2 L X n,由于 X1,X2,…,Xn相互独立,因此有:
6.1 引 言
用N表示某类保单在单位时间内的理赔次数,用Ci 表示该类保单第i次理赔金额,则理赔总量S为:
S
C1
C2
L
CN
N
Ci ,
i 1
0,
N 0 N 0
称为短期聚合风险模型,其中:
N取值为非负整数,称为理赔数变量。 Ci是取值于正数(连续或离散)称为理赔额变量。
6.3 理赔总量模型
函数为Pi(x), i=,1,2,…,m,则S= S1+S2+…+Sm服从参 m
数为 i 的复合泊松分布, S的理赔额的分布 i 1
函数为:
P(x)
m i 1
i
Pi
(
x)
6.4 复合泊松分布及其性质
2、可分解性
定理6.4.2 假设S服从复合泊松分布,参数λ>0,个别理 赔额为离散型概率分布,记πi=P(C=xi),其中x1,x2,…,xm 表示个别理赔额的取值;记Ni为S中取值为xi的次数, i=1,2,…,m,则有 N N1 N2 L Nm , N 0 ,且 S x1N1 x2 N2 L xm Nm , N 0 则以下结论成立: a) N1,N2,…,Nm相互独立; b) Ni服从参数λi =λπi的泊松分布, i=1,2,…,m 。
4.3 服从各种分布的随机数
随机数生成方法:
1) 反函数法
2) 取舍法
3) Box-Muller法
4) 极方法 标准正态分布:
标准正态分布随机数生成方法
1) 检表法
2) 中心极限定理法
标准正态分布→ 正态分布N(μ,σ2) →对数正态分布
u
→ v =μ+σu → exp(v)
泊松分布的随机数
泊松分布随机数生成方法:
6.4 复合泊松分布及其性质
3、分布计算的递推性
推论6.4.1 假设S服从复合泊松分布,若理赔额C仅取值 为正整数,则有如下迭代公式:
f (0) e
f
(x)
x i 1
i x
i
f
(x i)
x i p(i) f (x i), i1 x
x 1, 2,L
第七章 长期聚合风险模型 (破产理论)
为; ……
1.3 保险精算问题
保险精算的四个问题: (1)厘订费率 (2)准备金计提及其分配 (3)再保险形式的选择及自留额的确定问题 (4)资产负债配比与偿付能力问题
第二章 损失分布
2.1 引言 2.2 获得损失分布的一般过程 2.3 损失分布的数学工具 2.4 拟合损失分布
2.1 引言
损失与赔付 损失:承保标的的可能发生的实际损失大小。 赔付:保险人按承保合同规定的保险责任所 支付的实际费用。 赔付≤实际损失
2.2 获得损失分布的一般过程
获得随机变量概率分布的方法: 数理统计方法 又称为频率学派方法,主要依靠样本信息来估计未 知参数,从而获得概率分布。 贝叶斯方法 又称为主观贝叶斯方法,通过采用“先验概率”、 “损失函数”等主观信息,在不具备样本信息的情 况下估计未知参数,获得损失分布。 随机模拟方法 利用现代计算机技术,用机器的高速运算结果来模 拟实际过程,以获得对实际过程的了解。
n
S X1 X 2 L X n X i i 1
称之为短期个体风险模型。
短期个体风险模型的四个假设条件
假设1 每张保单是否发生理赔以及理赔额大小是相互独
立的,即Xi是相互独立的随机变量。
假设2 每张保单至多发生一次理赔。若用随机变量I表示
