2018年清华大学自主招生及领军计划试题和解析
清华2018自主招生试题及答案

2018清华自主招生试题与答案(2018清华自主招生)1、如图所示的电路,闭合开关S ,当滑动变阻器滑片P 向右移动时,下列说法正确的是 CA.电流表读数变小,电压表读数变大B.小电泡L 变暗C.电容器C 上电荷量减小D.电源的总功率变小(2018清华自主招生)2、如图所示,固定的倾斜光滑杆上套有一个质量为m的圆环,圆环与竖直放置的轻质弹簧一端相连,弹簧的另一端固定在地面上的A点,弹簧处于原长h。
让圆环沿杆滑下,滑到杆的底端时速度为零.则在圆环下滑过程中 C A.圆环机械能守恒B.弹簧的弹性势能先增大后减小C.弹簧的弹性势能变化了mgh D.弹簧的弹性势能最大时圆环的动能最大3、(2018清华自主招生)4、如图所示,有三个斜面a,b,c,底边的长分别为L、L 、2L高度分别为2h、h、h ,某物体与三个斜面间的动摩擦因数都相同,这个物体分别沿三个斜面从顶端由静止下滑到底端,忽略空气阻力,三种情况相比较,下列说法正确的是BDA.物体克服摩擦力做的功W c= 2W b= 4W aB.物体克服摩擦力做的功W c= 2W b= 2W aC.物体到达底端的动能E ka= 2E kb= 2E kcD .物体到达底端的动能E ka >2E kb >2E kc解:克服摩擦力做的功 cos W mg x mgx =μθ=μ斜底则有 ::W 2:1:1c b a W W =动能定理 k mgx mgx E -μ=高底则有 E ka >2E kb >2E kc(2018清华自主招生)10、2013 年 12 月 6 日,“嫦娥三号”携带月球车“玉兔号”运动到地月转移轨道的P 点时做近月制动后被月球俘获,成功进入环月圆形轨道Ⅰ上运行,如图所示。
在“嫦娥三号”沿轨道Ⅰ经过 P 点时,通过调整速度使其进入椭圆轨道Ⅱ,在沿轨道Ⅱ经过Q 点时,再次调整速度后又经过一系列辅助动作,成功实现了其在月球上的“软着陆”。
14-18年北清自招博雅领军数学真题-数论基础与整除

北大博雅15.1.已知n为不超过2015的正整数,且1234n n n n+++的个位数字为0,则满足条件的正整数n的个数为()A.1511B.1512C.1513D.前三个答案都不对清华领军2015.18.已知存在实数r,使得圆周222x y r+=上恰好有n个整点,则n可以等于()A.4B.6C.8D.12分类存疑北大博雅2016.4.函数1,,(,)1,,(),0,qx p q p q NP pf xQ+⎧==∈⎪=⎨⎪∉⎩则满足(0,1)x∈且1()7f x>的x的个数为()A.12B.13C.14D.前三个答案都不对4.【解答】D满足(0,1)x∈,且1()7f x>的x的个数为11,分别为1121312341523344555566,,,,,,,,,,。
【评析】这个函数是非常有名的黎曼函数的一部分,但是对于学生的要求很低,只需要准确理解题意即可,问题本身并不困难。
北大博雅2016.14.已知正整数,,,a b c d满足ab cd=,则a b c d+++有可能等于()A.101B.301C.401D.前三个答案都不对14.【解答】B考虑a=mn,b=pq,c=mp,d=nq则a+b+c+d=mn+pq+mp+nq=(m+q)(n+p),于是a+b+c+d不是质数即可。
如301=7×43=(1+6)×(1+42),于是a=1,b=252,c=42,d=6即得正确答案是B。
【评析】数论不定方程问题,其中的换元方法是数论中的经典。
北大博雅2017.1.若正整数,,a b c满足402a b c++=,则使得10n| abc的最大正整数n是()A.5B.6C.7D.以上答案均不正确【1】Da=25,b=25,c=352时,n 可取4,下面我们将说明n 不可能大于4:若n ≥5,先考虑5n |abc :由于a+b+4=402,而402并不是5的倍数,所以abc 不可能均为5的倍数。
清华、北大2018-2019学年自主招生面试真题汇总

清华、北大2018-2019学年自主招生面试真题汇总2016年自主招生即将来临,考生和家长需要着手准备了。
除了报名申请材料之外,自主招生最重要的环节就是笔试和面试部分。
下面中国自主招生网小编汇总了清华大学、北京大学2011-2015年部分面试题,供报考2016自主招生的考生们参考。
清华大学清华大学2015年自主招生面试部分真题1.假设给你一次穿越的机会,你最希望穿越到什么时候?做什么人?干什么?2.清华大学的校训是什么?你是如何理解的?如果你被清华大学录取,你如何去践行这一校训?3.如果你是班长,如何组织一次关于雷锋精神的班级活动?活动内容,请向班里同学发表一段两分钟的“学雷锋”活动动员演讲。
4.“是休学创业,还是毕业后创业。
”5.要不要休学当老板?清华大学2014年自主招生面试部分真题一、领军计划:1、怎么看待单独二孩政策?2、谈谈对节假日安排的看法,有什么建议?3、怎么看待社会公平?二、自强计划:1、请讲一个你的经历中体现你“自强”的故事。
2、你对自己的大学生活有何规划?将来想从事何种职业?3、你认为自己的家乡至今仍然贫困的原因有哪些?应该如何解决?4、你曾经遇到过的最大困难是什么?你是如何面对和解决的?5、谈谈“如何看待春运一票难求的现象,怎么解决这个问题?6、如何看待社会公平?7、结合考生的申请材料,提出一些与考生自身经历有关的问题,如问考生家乡的特产是什么。
清华大学2013年自主招生面试部分真题【综合面试】分上午与下午两场进行:每场考生都有三道相同的必答题目,面试时间为10分钟左右,三位考官对一位考生。
另根据面试时间的剩余情况,考官也会根据考生的特点增加其他题目。
据考生回忆,必答题有:1.“人类一思考,上帝就发笑。
请在90秒内作答?基于你的评价,你打算在当下、在未来做些什么?”2.请以“我和诺贝尔奖的距离”为题发表一段2 分钟的演讲,可准备1 分钟。
3.近期上海、南京、杭州等地接连出现H7N9型禽流感的感染病例,并且造成数名感染者死亡,世界卫生组织和中国政府都高度关注这一病情,并且采取了积极的救治措施,但是公众依然非常想要知道和这个事件相关的各种信息。
2018年清华大学领军计划测试物理学科解析

2018年清华大学领军计划测试物理学科解析注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考点名称填写在答题卡上,并在规定位置粘贴考试用条形码。
2.客观题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
主观题用黑色墨水的钢笔或签字笔将答案写在答题卡相应位置上。
答在试卷上的无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试题为考生回忆版,有部分缺题一.选择题1.在粗糙地面上,某时刻乒乓球的运动状态如图所示,水平向右运动且逆时针旋转,则一段时间后乒乓球的可能运动状况:A、静止B、可能向前无滑滚动C、原地向左滚动D、原地向右滚动1.【参考答案】ABCD。
【名师解析】注意到角速度方向和平动速度造成的效果是相反的,所以在从初态到稳定过程中,以上过程都有可能出现。
2.杨氏双缝干涉实验中,双缝距光屏8cm,现将光屏靠近双缝,屏上原来3级亮纹处依旧为亮纹,则移动的距离可能为()A.4.8B.4C.3.4D.3【参考答案】ABCD【名师解析】杨氏双缝干涉亮条纹的位置为k Dx dλ=,k =0,±1,±2,···, 其中,d 为双缝间距,D 为双缝到光屏的距离,λ为光的波长。
依题意有03D k Dd dλλ=,0D D <,D 0=8cm ,其中,k 为正整数。
所以03D D k=,k =4,5,6,···, 所以k =4,D =6cm ;k =5,D =4.8cm ; k =6,D =4cm ; k =7,D =3.4cm ; k =8,D =3cm ;···。
所以选项ABCD 正确。
3.有一辆汽车以恒定功率由静止开始沿直线行驶,不计阻力,一定时间t 内走过的路程为s ,则A .s 与t 成正比。
B .s 与t 的二次方成正比 C. s 与t 的二分之一次方成正比 D. s 与t 的二分之三次方成正比 【参考答案】D【名师解析】汽车功率恒定,即P F v =⋅恒定,F 是牵引力,v 是瞬时速度,根据动能定理,有Pt= 212mv ,而v=ds dt,可得dsdt12t ,积分得32x t =, 所以s 与t 的32次方从成正比。
2018年清华北大自招真题

值为( )
A. 63
B. 1009
C. 2018
D. 前三个答案都不
对
【解答】D
【考点】数列问题以及基本不等式的应用
【解析】令 x = k + r(k Z且0 k n −1, 0 r 1) ,当 k = 0 时 x[x] = 0 ; k 1时,则
k2 x[x] = (k + r)k k 2 + k , x[x] 有 k 个取值;
x2 − 2a x − a − 2ax +1 = 0 (x − a)2 − 2a x − a +1− a2 = 0 ( x − a − a)2 = 2a2 −1
,
2a2
−1
0
x − a = a
2a2 −1 0
2a2
−1
,要使原方程有三个互不相等实根,则
a
2019 2018
−1=
2018
,
−a1
+
a2
−
a3
+
... −
a2017
+
a2018
=
(1−
1)(1− 1
1 )(1 − 2
1)...(1− 3
1) 2018
−1
=
−1
,
两式相加即得
a2
+
a4
+ ... +
a2018
=
2018 −1 2
=
2017 2
.
6. 已知实数 A,b,c 成公差非 0 的等差数列,在平面直角坐标系中,点 P 的坐标为(-3, 2),点 N 的坐标为(2,3),过点 P 作直线 Ax+by+c=0 的垂线,垂足为点 M,则 M,N 间的 距离的最大值与最小值的乘积是( )
清华大学2018自主招生、领军计划笔试真题.doc

清华大学2018自主招生、领军计划笔试真
自主招生频道为大家提供清华大学2018自主招生、领军计划笔试真题,一起来看看吧!更多高考资讯请关注我们网站的更新!
清华大学2018自主招生、领军计划笔试真题
清华大学2018年自主招生及领军计划笔试真题,供2019及2020届考生参考学习。
6月10日,清华大学2018年自主招生考试全面启动,2018年清华大学自主招生、领军计划依然在全国设置多个考点,考生可就近选择。
自主招生测试为初试和复试。
一、笔试时间
初试时间为6月10日上午9:00-12:00,共3个小时。
二、笔试模式
初试采用笔试形式,理科类:数学、物理、化学;文科类:数学、语文、历史。
清华理科笔试都是选择,共75题,数学35道题,物理20道,化学20道。
时间是数学90分钟,理化90分钟。
三、笔试难度
题目比高考难多了,这是真正看“水平”的。
基本是对学竞赛的有优势。
尤其理化有大学内容,没学竞赛的,有很多题可
能“看不懂”!
数学尚可,物理很难,全是大学知识,化学有些简单题。
四、笔试真题
化学:涉及空气污染的比较多,还有大学的有机化学,如:哪些气体会导致空气污染,测出其中含量?地球的臭氧含量以及造成大气污染的元素?化学有一道是高考原题。
物理:涉及热力学知识点是“理想气体”,难度偏大。
清华大学领军计划暨自主招生数学2018+解析

2018清华大学领军计划暨自主招生测试数学与逻辑1.,,p q r 均为素数,且pqrp q r为整数,则()A.,,p q r 中一定有一个是2B.,,p q r 中一定有一个是3C.,,p q r 中一定有两个数相等D.pqrp q r也为素数【答案】DA 项:举反例:3,5,7p q r ,此时7pqrp q r ;B 项:举反例:2,5,7p q r ,此时5pqrp q r;C 项:由A 、B 知C 项不对;D 项:由题意p q r 为pqr 的因子,而pqr 的因子只有1,,,,,,,p q r pq pr qr pqr ,结合大小关系,可知///p q r pq pr qr pqr ,不妨设p q r ,若p q r pqr ,则3pqr p q r r ,从而3pq ,这是不可能的,故只能//p q r pq pr qr 这意味着//pqrp q r p q r,均为素数,则D 正确。
2.,,,,a b c d e 均为素数,且平均数为13,则()A.中位数最大为17B.中位数最大为19C.中位数最小为5D.中位数最小为7【答案】B平均数为13的五个数之和为65,设中位数的最大值为x ,则有365x ,从而知x 最大为19,又3,5,19,19,19满足要求,故最大值为19;对于最小值,可构造出3,3,3,3,53使得中位数为3,而易证中位数为2不成立,因此最小值为3。
3.整数,,x y z 满足5x y z ,问这样的 ,,x y z 有几组()A.100 B.101C.102D.103【答案】C解法一:若,,x y z 中有两个零,共2326C 组解;若,,x y z 中只有一个零,共11234248C C 组解;若,,x y z 均非零,共234248C 组解。
综上,所求解的组数=6+48+48=102组。
解法二:若||0x :此时x 只能取0,而012345,,,,,543210y y y y y y z z z z z z ,共20组;若||1x :此时x 可取1 ,而01234,,,,43210y y y y y z z z z z,共21632 组;若||2x :此时x 可取2 ,而0123,,,3210y y y y z z z z ,共21224 组;若||3x :此时x 可取3 ,而012,,210y y y z z z ,共2816 组;若||4x :此时x 可取4 ,而01,10y y z z ,共248 组;若||5x :此时x 可取5 ,而y ,z 只能都等于0,共2组.综上,所求总组数2032241682102 。
【2018-2019】清华自主招生试题-范文word版 (24页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==清华自主招生试题篇一:自主招生清华大学历届面试题201X-201X年清华大学自主招生面试题【201X年面试题】201X年清华大学在沪自主招生暨保送生冬令营面试在华东师范大学第二附属中学举行,共有180多位沪上高三生参加。
上午9时30分左右,第一批面试学生走出考场。
来自七宝中学的高三学生朱易说,感到有些意外的是个人面试题:老子和孔子有一天打架,你会帮助谁?一根火柴在不能折断的前提下,如何摆成一个三角形?“这些题都非常有意思,我当时灵机一动,说将火柴放在墙角,不就构成了一个三角形吗?”小朱说,但是他感觉面试官明显不满足一个答案,继续追问还有别的方法吗,小朱并没有想出好的办法,“我想,这样的题目主要是考查学生思维的广度和宽度。
1,如何看待高考加分政策?2,《阿凡达》很火,欧美大片、日本动漫也很受欢迎。
如何在这种环境下发展中国文化?3,用一个成语形容你眼中的哥本哈根气候会议。
4,用关键词概括201X年中国现状。
5,中国是否已步入高房价时代,你的观点是?6,一根火柴在不能折断的前提下,如何摆成一个三角形?7,就张磊向耶鲁大学捐款8888888美元发表观点。
8,第一次和第二次世界大战期间,有什么重大的化学发明?9,为什么要把清华大学作为第一志愿填报?10.老子和孔子有一天打架,你会帮助谁?远程面试题目:1,谈古论今:任选中国古代和当代人物各一位作对比阐释。
2,为什么要上大学,是否每个人都应该上大学?3,假设你是清华校长,说说明年怎么举办清华百年校庆?【201X年面试题】部分面试题:●你如何看待我国四万亿救市计划?●如果你采访温总理,你将如何提问?要求:所提问题不能太大众化。
●如何看待情怀的含义。
●怎样做一名精英。
●你认为当大法官应具备怎样的素质?●谈谈对陈水扁家族弊案的看法。
2018年___自主招生数学试卷(含答案解析)

2018年___自主招生数学试卷(含答案解析)2018年___自主招生数学试卷一、选择题(本大题共6小题,共24.0分)1.√16的平方根是()A.4B.±4C.22.若√(1−x)2=x−1成立,则x满足()A.x≥1B.x≥C.x≤1D.±23.已知x=√5−1,则x2+2x的值是()A.2B.3C.4D.54.如图所示的四条直线a、b、c、d,直线a、b与水平线平行,以其中一条为x轴,d与水平线垂直,取向右为正方向;直线c、以其中一条为y轴,取向上为正方向.某同学在此坐标平面上画了二次函数x=xx2+2xx+2(x≠0)的图象如图,则下面结论正确的是()A.a为x轴,c为y轴B.a为x轴,d为y轴C.b为x轴,c 为y轴D.b为x轴,d为y轴5.如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,xx⊥xx,垂足为H,HM平分∠xxx,HM交AB于x.若xx=3,xx=1,则MH长为()A.1B.1.5C.0.5D.0.76.如图,△xxx中,∠x=90°,D是BC边上一点,∠xxx=3∠xxx,xx=8,xx=7.则AB的值为()A.15B.20C.2√2+7D.2√2+√7二、填空题(本大题共10小题,共40.0分)7.已知实数x、y满足x+2x=5,则x−x=3.8.分解因式:x2+4xx+4x2+x+2x−2=(x+2x+1)2−3.9.在平面直角坐标系中,点A,B的坐标分别为(x,3),(3x−1,3),若线段AB与直线x=2x+1相交,则m的取值范围为(0,1)。
10.若一个圆锥的侧面展开图是半径为18cm,圆心角为240°的扇形,则这个圆锥的底面半径长是9cm。
11.如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D、N处,B在同一直线上,分别落在M、F与BE交于点G.设AB=√3,那么△xxx的周长为4+4√3.12.如图,已知点x1,x2,…,xx均在直线x=x−1上,点x1,x2,…,xx均在双曲线x=−x上,x1x1⊥x并且满足:x1x2⊥x轴,x2x2⊥x轴,…,xx−1xx⊥x轴,xxxx⊥x轴,且x1x2=x2x3=…=xx−1xx,则n的最小值为2.1.由题意可知,点B在x轴负半轴,点A在x轴正半轴,且AB垂直于x轴,因此AB的斜率为0,即AB为x轴,所以B的纵坐标为0.又因为B在x轴负半轴,所以其横坐标为负数,设为-a。
清华大学自主招生试题含答案
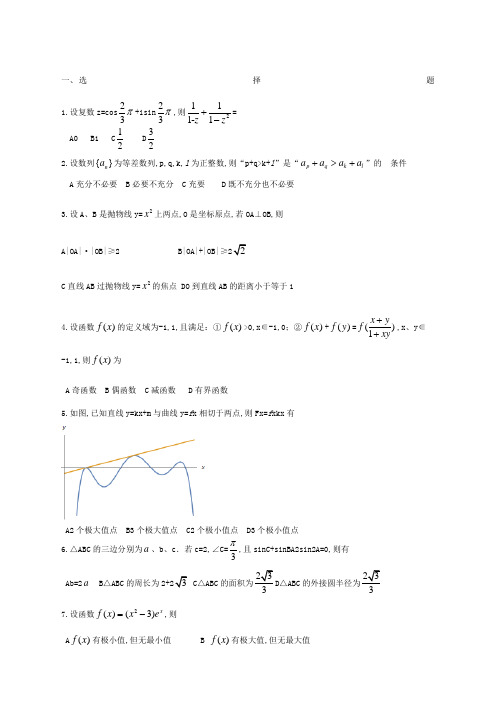
一、 选择题1.设复数z=cos23π+isin 23π,则2111-1z z +-= A0 B1 C 12 D 322.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的 条件 A 充分不必要 B 必要不充分 C 充要 D 既不充分也不必要3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则A|OA|·|OB|≥2 B|OA|+|OB|≥22C 直线AB 过抛物线y=2x 的焦点 DO 到直线AB 的距离小于等于14.设函数()f x 的定义域为-1,1,且满足:①()f x >0,x ∈-1,0;②()f x +()f y =()1x yf xy++,x 、y ∈-1,1,则()f x 为A 奇函数B 偶函数C 减函数D 有界函数5.如图,已知直线y=kx+m 与曲线y=f x 相切于两点,则Fx=f xkx 有A2个极大值点 B3个极大值点 C2个极小值点 D3个极小值点 6.△ABC 的三边分别为a 、b 、c .若c=2,∠C=3π,且sinC+sinBA2sin2A=0,则有 Ab=2a B △ABC 的周长为3 C △ABC 23D △ABC 的外接圆半径为237.设函数2()(3)xf x x e =-,则A ()f x 有极小值,但无最小值B ()f x 有极大值,但无最大值C 若方程()f x =b 恰有一个实根,则b>36e D 若方程()f x =b 恰有三个不同实根,则0<b<36e8.已知A={x,y ∣222x y r +=},B={x,y ∣222()()x a y b r -+-=,已知A∩B={11,x y ,22,x y },则 A0<22ab +<22r B 1212()(y )0a x x b y -+-=C 12x x +=a ,12y y +=bD 22ab +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为 A1 B2 C3 D410.设数列{n a }的前n 项和为n S ,若对任意正整数n,总存在正整数m,使得n S =m a ,则 A{n a }可能为等差数列 B{n a }可能为等比数列C{n a }的任意一项均可写成{n a }的两项之差D 对任意正整数n,总存在正整数m,使得n a =m S11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测:3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是 A 甲 B 乙 C 丙 D 丁12.长方体ABCD 1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为A13 B 2313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D,其面积为S,则A 若S=4,则k 的值唯一B 若S=12,则k 的值有2个 C 若D 为三角形,则0<k ≤23D 若D 为五边形,则k>4 14.△ABC 的三边长是2,3,4,其外心为O,则OA AB OB BC OC CA ⋅+⋅+⋅= A0 B15 C212 D 29215.设随机事件A 与B 互相独立,且PB=,PA B=,则 APA= BPB A=0.3 CPAB= DPA+B=16.过△ABC 的重心作直线将△ABC 分成两部分,则这两部分的面积之比的 A 最小值为34 B 最小值为45 C 最大值为43 D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形,则不同的选法有 A105种 B225种 C315种 D420种18.已知存在实数r,使得圆周222x y r +=上恰好有n 个整点,则n 可以等于 A4 B6 C8 D1219.设复数z 满足2|z|≤|z1|,则 A|z|的最大值为1 B|z|的最小值为13 Cz 的虚部的最大值为23 Dz 的实部的最大值为1320.设m,n 是大于零的实数,a =mcosα,msinα,b =ncosβ,nsinβ,其中α,β∈0,2πα,β∈0,2π.定义向量12a =2α2α,12b =2β2β,记θ=αβ,则A 12a ·12a =aB 1122ab ⋅=2θC 112222||44a b mn θ-≥ D 112222||44a b mn θ+≥21.设数列{n a }满足:1a =6,13n n n a a n++=,则 An ∈N,n a <3(1)n + Bn ∈N,n a ≠2015 Cn ∈N,n a 为完全平方数 Dn ∈N, n a 为完全立方数 22.在极坐标系中,下列方程表示的图形是椭圆的有Aρ=1cos sin θθ+ Bρ=12sin θ+ Cρ=12cos θ- Dρ=112sin θ+23.设函数2sin ()1xf x x x π=-+,则A ()f x ≤43B|()f x |≤5|x| C 曲线y=()f x 存在对称轴 D 曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c,若△ABC 为锐角三角形,则AsinA>cosB BtanA>cotB C 222a b c +> D 333a b c +> 25.设函数()f x 的定义域是1,1,若(0)f =(0)f '=1,则存在实数δ∈0,1,使得 A ()f x >0,x ∈ δ,δ B ()f x 在 δ,δ上单调递增C ()f x >1,x ∈0,δD ()f x >1,x ∈ δ,026.在直角坐标系中,已知A1,0,B1,0.若对于y 轴上的任意n 个不同的点k P k=1,2,…,n,总存在两个不同的点i P ,j P ,使得|sin ∠A i P B sin ∠A j P B|≤13,则n 的最小值为A3 B4 C5 D627.设非负实数x,y 满足2x+y=1,则A 最小值为45 B 最小值为25C 最大值为1 D最大值为1328.对于50个黑球和49个白球的任意排列从左到右排成一行,则A 存在一个黑球,它右侧的白球和黑球一样多B 存在一个白球,它右侧的白球和黑球一样多C 存在一个黑球,它右侧的白球比黑球少一个D 存在一个白球,它右侧的白球比黑球少一个29.从1,2,3,4,5中挑出三个不同数字组成五位数,其中有两个数字各用两次,例如12231,则能得到的不同的五位数有A300个 B450个 C900个 D1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0,则 AL 是轴对称图形 BL 是中心对称图形 CL{x,y ∣22x y +≤1} DL{x,y ∣12≤y ≤12} Answer1.解析 2111-1z z +-=211-zz z zz z +-=11-z z z z +-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+-- =212sin 2sincos333i πππ-⋅-22cos()sin()33sin )22i i ππππ-+-+ =cos 0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]66i ππ-+-1sin )662i i ππ+-=1,选B2.简解 ()p q k l a a a a +-+=p+q-k+ld,与公差d 的符号有关,选D3.解析设A 211,x x ,B 222,x x ,OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案A,||||OA OB ⋅=2,正确;答案B,|OA|+|OB|≥,正确;答案C,直线AB 的斜率为222121x x x x --=21x x +=111x x -方程为y-21x =111x x -x-1x ,焦点0,14不满足方程,错误;答案D,原点到直线AB :111x x -x-y+1=0的距离1,正确;选ABD4.解析x=y=0⇒(0)f =0,y=-x ⇒()()f x f x -=-,()f x 为奇函数,A 正确;()f x ≡0,B 错误;12x x <,1()f x -2()f x =1()f x +2()f x -=12121x x f x x ⎛⎫- ⎪-⎝⎭>0⇒1()f x >2()f x ⇒()f x ↓,C 正确;()f x =-tan2x π满足已知条件,但无界,D 错误;选A,C 5.简解将直线平移知:斜率为k 的直线,与曲线y=()f x 至多有五个公共点,其中在此直线先下方后上方的两个区间,先上方后下方的三个区间,故()F x 有三个极大值点,两个极小值点;选BC6.解析2R=sin c C⇒正确; 又sinC+sinB-A=sinB+A+sinB-A=2sinBcosA=2sin2A=4sinAcosA ⇒cosA=0或sinB=2sinA ⇒A=2π或b=2a ; A=2π时a周长为b=2a时,2c =222cos a b ab C +-⇒a2π,同样有周长为,选BCD7.简解()f x '=x+3x-1xe ,36)(3)f x f e =-=极大(, )(1)-2f x f e ==极小(,作出其大致图象,如图 选BD8.解析已知即半径相等的两圆⊙O:222x y r +=与⊙C:222()()x a y b r -+-=交于相异的两点111(,)P x y 、222(,)P x y ;0<|OC|<2|r|⇔0<22a b +<42r ,A 错;四边形O 1P C 2P 是菱形⇒对角线OC 与12P P 垂直且平分,BC 正确;22a b +=1122ax by +⇔22221111()()a x b y x y -+-=+⇔11||||CP OP =,D 正确;总之,选BCD9.解析关于z 的方程22224430z z x y +++-=有非负实数解0⇒2234x y +≤,-3,设x=rcos θ,y=rsin θ,θ∈0,2π,r ∈0,2d=r5cos θ+4sin θsin θ+arctan54-3≥设a =2,3,bd ≥2a b ⋅-3=2||||a b cos ,a b ,a b -3,作图知,a b 最大值是b 与OY 夹角,此时d ≥-3=3;选C 10.解析答案A,常数列0,0,0,...满足要求;答案B,公比q=1时因n 1a ≠1a ,结论假,q ≠1时,111(1)1n m a q a q q --=-⇔111n m q q q--=-常数,也不可能;答案C,1n n n a S S -=-=m t a a -,满足要求;答案D,n a =m S =t a ,并非对所有数列成立;选AC 11.简解答案甲乙丙不能保证只有一个正确,故选D 12.等体积法,选B13.解析如图:不等式组表示过点P-1,-2的直线的下方与正方形ABCD 围成的面积图形 k>0时,S 单调增,梯形2P ABC 面积为285>4,故S=4只有一解,A 正确;△1P AB 、△34P P D 的面积分别为45、1,都比12大,故再两个三角形内各存在一个围成面积为12的直线,B 正确;k<0时,围成的仍然是三角形,C 错误;围成五边形,斜率大于直线PC 的斜率4,D 正确;选ABD14.简解取AB 的中点D,则OA AB ⋅=OA ×AB ×cos π-∠OAB=-AB ×OA ×cos ∠OAB=-212AB ,同理OB BC ⋅ =212BC -,212OC CA CA ⋅=-,原式=222129()22AB BC CA -++=- .选D15.简解设PAB=x,则PA=+x,根据PAB=PAPB 有x=+x ×⇒=;PA=,A 正确;PB-A=正确;PAB=,C 正确;PA+B=PA+PB-PAB=,D 错误;选ABC16.解析设△ABC 的重心为G,面积为1,过点G 的直线与三角形边AB 、AC 分别相交于D 、E,AD=xAB,AE=yAC,则有12AB ×ACsinA=1,如图 特别的x,y ∈{0,1}时,DE 为三角形的中线,此时分成两部分面积比值为1 当x,y ∈0,1时,△ADE 面积S=12AD ×AEsinA=12xAB ×yACsinA=xy,D 、G 、E 三点共线⇒存在实数λ,使得DG DEλ=⇒AG AD -=λAE AD -⇒AG =1-λAD +λAE =1-λx AB +λy AC ,又AG =13AB +13AC ⇒1(1)313x y λλ⎧-=⎪⎪⎨⎪=⎪⎩,消去λ得到11x y +=3,因11x y +≥⇔23⇔S ≥49,等号成立当且仅当x=y=23⇔DE ∥BC,故S 最小值为49,1-S 的最大值为59;故两面积比值有最小值45,最大值54;选BD17.解析先看一个顶点处构成钝角的三角形个数,加设此点为A,从A 逆时针方向的点依次记为k A k=1,2,3,…,7,顺时针方向的顶点依次记为k A -k=1,2,3,…,7,△n m A AA -要构成以A 为钝角的钝角三角形,则n+m ≤7,有1+2+3+…+6=21个;于是共可构成15×21=315个钝角三角形;选C 18.简解正数点关于x 轴、y 轴对称,故一定是4的倍数;选ACD 19.简解设x=x+yix,y ∈R,代入化简得到2214()39x y ++≤,表示以-13,0为圆心,以23为半径的圆及其内部,根据图形,选ACD20. 解析12a ·12a 是一个数值,不是向量,A 错;1122a b⋅cos22αβsin22αβ2αβ-2θ,B 正确;11222||a b -=2)22αβ+2)22αβ2αβ-=2θ≥22θ=24θ,C 正确; 同理D 正确 选BCD 21.简解13n n a n a n++=,迭乘得到n a =n+2n+1n ;3(1)n a n <+⇔nn+2<2(1)n +,A 正确;2015=5×13×31,不可能是三个连续整数之积,B 正确;三个连续整数积不可能为完全平方数和立方数,CD 错误;选AB22.简解A 去分母,化成直角坐标方程为x+y=1,表示直线;B 为ρ=1211cos()22πθ-+表示椭圆;C 为ρ=1211cos 2θ-表示椭圆;D 为ρ=112cos()2πθ-+表示双曲线;选BC23.解析()f x ≤43⇔gx=24443sin x x x π-+-≥0,1()=g()2g x 极小值=0,A 正确;|()|f x ≤5|x|⇔|sin πx|≤|32x x x -+|.作图象知成立,B 正确;x=12是其一条对称轴,C 正确;()()f a x f a x -++不可能为常数,故D 错误;选ABC24.简解A+B>2π⇒A>2π-B ⇒sinA>sin 2π-B=cosB,tanA>tan 2π-B=cotB,AB 正确;锐角三角形,一定有222a b c +>,C 正确;三角形三边长为,,1时,满足锐角三角形条件,但330.50.90.854+=<1,D 错误;总之,选ABC25.解析根据导数定义,对任意ε>0,存在δ>0,当|x|<δ时,|()(0)f x f x--1|<ε⇔x1-ε+1<()f x <x1+ε+1,对ε取值可知AC 正确;(0)f '=1>0,知在0附近存在区间,()f x '>0,B 正确;对于函数y=x+1,D 不正确;总之,选ABC26.解析将所有的|sin ∠A i P B sin ∠A j P B|,按从小到大排序,共有2n C 个,其中最小者不大于13,最大为2,于是213n C ≥2,n 的最小值为4.选B 27.解析设x=rcos θ,y=rsin θ,θ∈0,2π.2x+y=1⇔r=12cos sin θθ+=rcos θ+r=cos 12cos sin θθθ++,记作T ;去分母得到Tsin θ+2T-1cos θθ+arctan 21T T-=1解得T ≥45,等号成立当且仅当θ+arctan 21T T -=θ+arctan 34=2π,A 正确;当θ=0时T=2,θ=2π时T=1,最大值为2,C 正确;选AC28.简解黑球先放好,放白球,选A29.解析先从五个数字中,将这三个数字中选出来,有35C 种方法,如选了123;在确定不重复用的数字,有13C 种方法,如选3;对数字3安排有15A 种方法,余下的对数字1安排有24C 种方法,剩下的两位安排2;有35C 13C 15A 24C =900.选C30.简解解方程得到221y x =--易知它关于两坐标轴及原点都对称,AB 正确;22x y +1-≤1有-2≤x ≤2条件,但已知中无此条件,故C 错误;设2x=tan θ,θ∈-2π , 2π,2y =-21sec 4θ+sec θ-34,当sec θ=2时,2max y =14,-12≤y ≤12,D 正确;选ABD。
2018年清华大学自主招生笔试面试指导

2018年清华大学自主招生考试笔试、面试综合素质测试指导攻略第一部分:清华大学2018年自主招生实施办法第二部分:清华大学自主招生笔试特点及备考第三部分:清华大学自主招生面试特点及备考第四部分:清华大学自主招生面试历年真题第一篇清华大学自主招生实施办法根据《国务院关于深化考试招生制度改革的实施意见》、《教育部关于进一步完善和规范高校自主招生试点工作的意见》的要求,我校将全面贯彻落实党的教育方针,围绕“综合评价、多元择优、因材施招、促进公平”的人才选拔理念,开展2018年自主招生工作。
一、机构与原则我校自主招生工作在清华大学招生工作领导小组的领导下,由清华大学招生办公室负责具体工作的组织和实施。
自主招生认定及录取工作按照综合评价、公平公正、宁缺毋滥的原则择优确定认定、录取名单,学校纪委、监察部门全程监督,并接受社会监督。
二、招收类型及申请条件具有各类特长及创新潜质的优秀高中毕业生均可申请。
申请学生应至少具备以下方面特质之一,并提供相关证明材料:1.研究创作方面:在科技发明、研究实践、文学创作等方面具有突出表现的学生。
2.突出才能方面:在人文与社会、创新与设计等方面具有突出才能或在相关学习实践中取得优异成绩的学生。
3.学科奥赛方面:在数学、物理、化学、生物、信息学等学科具有学科特长,且在学科奥林匹克竞赛中表现突出的学生。
三、招生专业2018年我校自主招生录取人数不超过教育部核准的自主招生计划。
各学科类型及对应的初试测试科目如下:学科类型测试科目包含专业类(方向)理科类数学与逻辑理科综合(物化)建筑类土木类环境、化工与新材料类机械、航空与动力类能源类电子信息类计算机类自动化与工业工程类数理类化生类临床医学类经济、金融与管理类法学类文理通识类文科类数学与逻辑文科综合(文史)人文与社会类人文与社会类(经学方向) 人文与社会类(出土文献方向) 经济、金融与管理类法学类文理通识类说明:1、“人文与社会类(经学方向)”专业方向申请条件:1)热爱中国文化,品行端正,以学习与研究儒家经典为终身职志;2)受过较系统的蒙学教育,能背诵《三字经》、《百家姓》、《千字文》、《笠翁对韵》、《龙文鞭影》;3)有较好的经学基础,能背诵“四书”(《大学》、《中庸》、《论语》、《孟子》),以及《周易》、《诗经》中的一种;4)有初步的文字学基础,学习过《说文解字》,能用篆书默写540部首,能简单讲解“六书”。
2018年北京清华大学自主招生暨领军计划数学试题Word版含解析

2018年清华大学自主招生暨领军计划试题1.已知函数x e a x x f )()(2+=有最小值,则函数a x x x g ++=2)(2的零点个数为( ) A .0 B .1 C .2 D .取决于a 的值 【答案】C【解析】注意)()(/x g e x f x=,答案C .2. 已知ABC ∆的三个内角C B A ,,所对的边为c b a ,,.下列条件中,能使得ABC ∆的形状唯一确定的有( )A .Z c b a ∈==,2,1B .B bC a C c A a A sin sin 2sin sin ,1500=+=C .060,0sin cos )cos(cos sin cos ==++C C B C B C B A D .060,1,3===A b a【答案】AD .3.已知函数x x g x x f ln )(,1)(2=-=,下列说法中正确的有( ) A .)(),(x g x f 在点)0,1(处有公切线B .存在)(x f 的某条切线与)(x g 的某条切线平行C .)(),(x g x f 有且只有一个交点D .)(),(x g x f 有且只有两个交点【答案】BD【解析】注意到1-=x y 为函数)(x g 在)0,1(处的切线,如图,因此答案BD .4.过抛物线x y 42=的焦点F 作直线交抛物线于B A ,两点,M 为线段AB 的中点.下列说法中正确的有( )A .以线段AB 为直径的圆与直线23-=x 一定相离 B .||AB 的最小值为4 C .||AB 的最小值为2D .以线段BM 为直径的圆与y 轴一定相切 【答案】AB【解析】对于选项A ,点M 到准线1-=x 的距离为||21|)||(|21AB BF AF =+,于是以线段AB 为直径的圆与直线1-=x 一定相切,进而与直线23-=x 一定相离;对于选项B ,C ,设)4,4(2a a A ,则)1,41(2a a B -,于是2414||22++=a a AB ,最小值为4.也可将||AB 转化为AB 中点到准线的距离的2倍去得到最小值;对于选项D ,显然BD 中点的横坐标与||21BM 不一定相等,因此命题错误. 5.已知21,F F 是椭圆)0(1:2222>>=+b a by a x C 的左、右焦点,P 是椭圆C 上一点.下列说法中正确的有( ) A .b a 2=时,满足02190=∠PF F 的点P 有两个 B .b a 2>时,满足02190=∠PF F 的点P 有四个C .21F PF ∆的周长小于a 4D .21F PF ∆的面积小于等于22a【答案】ABCD .【解析】对于选项A ,B ,椭圆中使得21PF F ∠最大的点P 位于短轴的两个端点;对于选项C ,21PF F ∆的周长为a c a 422<+;选项D ,21PF F ∆的面积为22212121212||||21sin ||||21a PF PF PF F PF PF =⎪⎭⎫ ⎝⎛+≤∠⋅. 6.甲、乙、丙、丁四个人参加比赛,有两花获奖.比赛结果揭晓之前,四个人作了如下猜测: 甲:两名获奖者在乙、丙、丁中; 乙:我没有获奖,丙获奖了; 丙:甲、丁中有且只有一个获奖; 丁:乙说得对.已知四个人中有且只有两个人的猜测是正确的,那么两个获奖者是( ) A .甲B .乙C .丙D .丁【答案】BD【解析】乙和丁同时正确或者同时错误,分类即可,答案:BD .7.已知AB 为圆O 的一条弦(非直径),AB OC ⊥于C ,P 为圆O 上任意一点,直线PA 与直线OC 相交于点M ,直线PB 与直线OC 相交于点N .以下说法正确的有( ) A .P B M O ,,,四点共圆 B .N B M A ,,,四点共圆 C .N P O A ,,,四点共圆D .以上三个说法均不对【答案】AC【解析】对于选项A ,OPM OAM OBM ∠=∠=∠即得;对于选项B ,若命题成立,则MN 为直径,必然有MAN ∠为直角,不符合题意;对于选项C ,MAN MOP MBN ∠=∠=∠即得.答案:AC .8.C B A C B A cos cos cos sin sin sin ++>++是ABC ∆为锐角三角形的( ) A .充分非必要条件 B .必要非充分条件 C .充分必要条件D .既不充分也不必要条件【答案】B【解析】必要性:由于1cos sin )2sin(sin sin sin >+=-+>+B B B B C B π,类似地,有1sin sin ,1sin sin >+>+A B A C ,于是C B A C B A cos cos cos sin sin sin ++>++.不充分性:当4,2ππ===C B A 时,不等式成立,但ABC ∆不是锐角三角形.9.已知z y x ,,为正整数,且z y x ≤≤,那么方程21111=++z y x 的解的组数为( ) A .8B .10C .11D .12【答案】B 【解析】由于xz y x 311121≤++=,故63≤≤x . 若3=x ,则36)6)(6(=--z y ,可得)12,12(),15,10(),18,9(),24,8(),42,7(),(=z y ; 若4=x ,则16)4)(4(=--z y ,可得)8,8(),12,6(),20,5(),(=z y ; 若5=x ,则6,5,320,211103=≤≤+=y y y z y ,进而解得)10,5,5(),,(=z y x ; 若6=x ,则9)3)(3(=--z y ,可得))6,6(),(=z y . 答案:B .10.集合},,,{21n a a a A Λ=,任取A a a A a a A a a n k j i i k k j j i ∈+∈+∈+≤<<≤,,,1这三个式子中至少有一个成立,则n 的最大值为( ) A .6B .7C .8D .9【答案】B11.已知000121,61,1===γβα,则下列各式中成立的有( ) A .3tan tan tan tan tan tan =++αγγββα B .3tan tan tan tan tan tan -=++αγγββαC .3tan tan tan tan tan tan =++γβαγβαD .3tan tan tan tan tan tan -=++γβαγβα【答案】BD【解析】令γβαtan ,tan ,tan ===z y x ,则3111=+-=+-=+-zxzx yz y z xy x y ,所以)1(3),1(3),1(3zx z x yz y z xy z y +=-+=-+=-,以上三式相加,即有3-=++zx yz xy .类似地,有)11(311),11(311),11(311+=-+=-+=-zxx z yz z y xy y x ,以上三式相加,即有3111-=++=++xyzz y x zx yz xy .答案BD . 12.已知实数c b a ,,满足1=++c b a ,则141414+++++c b a 的最大值也最小值乘积属于区间( )A .)12,11(B .)13,12(C .)14,13(D .)15,14(【答案】B【解析】设函数14)(+=x x f ,则其导函数142)(/+=x x f ,作出)(x f 的图象,函数)(x f 的图象在31=x 处的切线321)31(7212+-=x y ,以及函数)(x f 的图象过点)0,41(-和)7,23(的割线7174+=x y ,如图,于是可得321)31(7212147174+-≤+≤+x x x ,左侧等号当41-=x 或23=x 时取得; 右侧等号当31=x 时取得.因此原式的最大值为21,当31===c b a 时取得;最小值为7,当23,41=-==c b a 时取得,从而原式的最大值与最小值的乘积为)169,144(37∈.答案B .13.已知1,1,,,222=++=++∈z y x z y x R z y x ,则下列结论正确的有( ) A .xyz 的最大值为0 B .xyz 的最大值为274- C .z 的最大值为32D .z 的最小值为31-【答案】ABD14.数列}{n a 满足)(6,2,1*1221N n a a a a a n n n ∈-===++,对任意正整数n ,以下说法中正确的有( )A .n n n a a a 221++-为定值 B .)9(mod 1≡n a 或)9(mod 2≡n aC .741-+n n a a 为完全平方数D .781-+n n a a 为完全平方数 【答案】ACD 【解析】因为2112221122213226)6(++++++++++++-=--=-n n n n n n n n n n n a a a a a a a a a a a n n n n n n n a a a a a a a 22121122)6(++++++-=+-=,选项A 正确;由于113=a ,故76)6(2121121221-=+-=--=-++++++n n n n n n n n n n n a a a a a a a a a a a ,又对任意正整数恒成立,所以211211)(78,)(74n n n n n n n n a a a a a a a a +=--=-++++,故选项C 、D 正确.计算前几个数可判断选项B 错误.说明:若数列}{n a 满足n n n a pa a -=++12,则n n n a a a 221++-为定值.15.若复数z 满足11=+zz ,则z 可以取到的值有( ) A .21B .21-C .215- D .215+ 【答案】CD 【解析】因为11||1||=+≤-zz z z ,故215||215+≤≤-z ,等号分别当i z 215+=和i z 215-=时取得.答案CD . 16. 从正2016边形的顶点中任取若干个,顺次相连构成多边形,若正多边形的个数为( ) A .6552 B .4536 C .3528 D .2016 【答案】C【解析】从2016的约数中去掉1,2,其余的约数均可作为正多边形的边数.设从2016个顶点中选出k 个构成正多边形,这样的正多边形有k2016个,因此所求的正多边形的个数就是2016的所有约数之和减去2016和1008.考虑到732201625⨯⨯=,因此所求正多边形的个数为352810082016)71)(931)(32168421(=--++++++++.答案C .17.已知椭圆)0(12222>>=+b a b y a x 与直线x y l x y l 21:,21:21-==,过椭圆上一点P 作21,l l 的平行线,分别交21,l l 于N M ,两点.若||MN 为定值,则=ba( ) A .2B .3C .2D .5【答案】C【解析】设点),(00y x P ,可得)2141,21(),2141,21(00000000y x y x N y x y x M +--++,故意2020441||y x MN +=为定值,所以2,1641422===b a b a ,答案:C .说明:(1)若将两条直线的方程改为kx y ±=,则kb a 1=;(2)两条相交直线上各取一点N M ,,使得||MN 为定值,则线段MN 中点Q 的轨迹为圆或椭圆.18. 关于y x ,的不定方程y x 21652=+的正整数解的组数为( ) A .0B .1C .2D .3【答案】B19.因为实数的乘法满足交换律与结合律,所以若干个实数相乘的时候,可以有不同的次序.例如,三个实数c b a ,,相乘的时候,可以有Λ),(),(,)(,)(ca b ab c c ba c ab 等等不同的次序.记n 个实数相乘时不同的次序有n I 种,则( )A .22=IB .123=IC .964=ID .1205=I 【答案】B【解析】根据卡特兰数的定义,可得1121221)!1(!1------=⋅==n n n n nn n n C n n C nA C I .答案:AB . 关于卡特兰数的相关知识见《卡特兰数——计数映射方法的伟大胜利》.20.甲乙丙丁4个人进行网球淘汰赛,规定首先甲乙一组、丙丁一组进行比赛,两组的胜者争夺冠军.4个人相互比赛的胜率如表所示:表中的每个数字表示其所在的选手击败其所在列的选手的概率,例如甲击败乙的概率是0.3,乙击败丁的概率是0.4.那么甲刻冠军的概率是 . 【答案】0.165【解析】根据概率的乘法公式 ,所示概率为165.0)8.05.03.05.0(3.0=⨯+⨯.21.在正三棱锥ABC P -中,ABC ∆的边长为1.设点P 到平面ABC 的距离为x ,异面直线CP AB ,的距离为y .则=∞→y x lim .【答案】23【解析】当∞→x 时,CP 趋于与平面ABC 垂直,所求极限为ABC ∆中AB 边上的高,为23. 22.如图,正方体1111D C B A ABCD -的棱长为1,中心为A A E A BC BF O 1141,21,==,则四面体OEBF 的体积为 .【答案】196【解析】如图,EBF G EBF O OEBF V V V --==21961161212111=⋅==--B BCC E GBF E V V .23.=+-⎰-dx x x n n )sin 1()(22012ππ .【答案】0【解析】根据题意,有0)sin 1()sin 1()(21222012=+=+-⎰⎰---dx x x dx x x n n n n ππππ.24.实数y x ,满足223224)(y x y x =+,则22y x +的最大值为 . 【答案】1【解析】根据题意,有22222322)(4)(y x y x y x +≤=+,于是122≤+y x ,等号当2122==y x 时取得,因此所求最大值为1.25.z y x ,,均为非负实数,满足427)23()1()21(222=+++++z t x ,则z y x ++的最大值与最小值分别为 . 【答案】2322- 【解析】由柯西不等式可知,当且仅当)0,21,1(),,(=z y x 时,z y x ++取到最大值23.根据题意,有41332222=+++++z y x z y x ,于是,)(3)(4132y z y x z y x +++++≤解得2322-≥++z y x .于是z y x ++的最小值当)2322,0,0(),(-=yz x 时取得,为2322-. 26.若O 为ABC ∆内一点,满足2:3:4::=∆∆∆COA BOC AOB S S S ,设AC AB AO μλ+=,则=+μλ .【答案】23【解析】根据奔驰定理,有329492=+=+μλ.27.已知复数32sin32cosππiz+=,则=+++2223zzzz.【答案】132i-【解析】根据题意,有iizzzzzz232135sin35cos122223-=+=-=+=+++ππ.28.已知z为非零复数,zz40,10的实部与虚部均为不小于1的正数,则在复平面中,z所对应的向量OP的端点P运动所形成的图形的面积为.【答案】20010033003π+-【解析】设),(Ryxyixz∈+=,由于2||4040zzz=,于是⎪⎪⎩⎪⎪⎨⎧≥+≥+≥≥,140,140,110,1102222yxyyxxyx如图,弓形面积为1003100)6sin6(20212-=-⋅⋅πππ,四边形ABCD的面积为100310010)10310(212-=⋅-⋅.于是所示求面积为30031003200)1003100()1003100(2-+=-+-ππ.29.若334tan=x,则=+++xxxxxxxxxxxcossincos2cossin2cos4cos2sin4cos8cos4sin.3【解析】根据题意,有xxxxxxxxxxxcossincos2cossin2cos4cos2sin4cos8cos4sin+++38tantan)tan2(tan)2tan4(tan)4tan8(tan==+-+-+-=xxxxxxxx.30.将16个数:4个1,4个2,4个3,4个4填入一个44⨯的数表中,要求每行、每列都恰好有两个偶数,共有种填法.【答案】44100031.设A 是集合}14,,3,2,1{Λ的子集,从A 中任取3个元素,由小到大排列之后都不能构成等差数列,则A 中元素个数的最大值为 .【答案】8【解析】一方面,设},,,{21k a a a A Λ=,其中141,*≤≤∈k N k .不妨假设k a a a <<<Λ21. 若9≥k ,由题意,7,33513≥-≥-a a a a ,且1335a a a a -≠-,故715≥-a a .同理759≥-a a .又因为1559a a a a -≠-,所以1519≥-a a ,矛盾!故8≤k .另一方面,取}14,13,11,10,5,4,2,1{=A ,满足题意.综上所述,A 中元素个数的最大值为8.。
2018年清华大学自主招生物理试题

4.假设房间向环境传递热量的速率正比于房间和环境之间的温度差,暖气片向房间传递热 量的速度也正比于暖气片与房间之间的温度差。暖气片温度恒为00,当环境温度为−5∘C时 ,房间温度保持在22∘C。当环境温度为−15∘C时,房间温度保持为16.5∘C。 (1)求暖气片的温度00; (2)给房子加一层保温材料,使得温差一定时房间散热的速率下降20%,求环境温度为−
2R 2gT 2
)
地球自转的速度为 u 2R T
则最小的发射速度为 u0 v0 u =
2gR(1 3 2R ) 2R 2gT 2 T
3.在磁场中,一静核衰变成为,,两两核,开始分别做圆周运动。已知和和两两核圆周运动的 半径和周期之比分别为�::�==45:1,�::�==90:117。此裂变反应质量亏损为�。。 (1)求和和两两核的电荷数之比�//�;; (2)求和和两两核的质量数之比�//�;; (3)求静核的质量数和电荷数; (4)求核核的动能��。。 3【解答】
mg
G
Mm R2
---------①
1
对于同步卫星:
G
Mm r2
m( 2 T
)2 r------②联立解得: v 3 2gR2 ----------------③ T
(2) 由机械能守恒:
1 2
mv02
G
Mm R
1 mv2 2
G
Mm r
----------④
联立②③④解得: v0
2gR(1 3
1 【解答】
(1)如图做受力分析。垂直斜面方向受力平衡: ==�����==4�//5 则摩擦力11为:11=�==5/4×4�//5=� 平行斜面方向做匀加速运动:�==11−�����==�−−3�//5=2�//5 则==25==4m/s2,且方向沿传送带向上 运动到物块速度与传送带速度相同时经过的时间为:11=//==1s 运动的距离为:11=�22/2=2m。 剩下的距离为22=−−11=18m,之后物块与传送带一起作匀速运动,则22=22/==4.5s 故==11+22=5.5s (2)法一:由第一问可知,在物块加速过程中摩擦力为11=�==40N 此时摩擦力对物块做功11 = 1111112/2 = 80J 匀速过程中摩擦力满足:22 = ����� = 35 � = 24N 则传送带做功22 = 2222 = 432J 则总做功 = 11 + 22 = 512J (注:若是求传送带做功,则需考虑内能的变化,此时11 = 111111 = 160J,22不变,总功为 = 11 + 22 = 592J) 法二:用功能原理,传送带对物块所做的功为物块获得的机械能(动能与重力势能) 则: =�22/2+ ������ = 512J
清华大学自招领军试题.docx

2016年清华大学自主招生暨领军计划试题1.已知函数f X X2 a eX有最小值,则函数g X X2 2x a的零点个数为( )A.0 B・1 C・2 D・取决于a的值2.已知ABC的三个角A, B , C所对的边分别为a, b , C・下列条件中,能使得ABC的形状唯一确定的有( )A. a 1 , b 2 , c ZB. A150 , a sinACSin C V 2asin C b sin BC.COS ASirl BCOSCCOS B C COS BSinC 0 , C 60D. a , b 1, A 603.已知函数f X X2 1, gx In X・下列说法中正确的有( )A. f X与gx在点(1,0)处有公切线B.存在fx的某条切线与g X的某条切线互相平行C. f X与gx有且只有一个交点D. f X与gx有且只有两个交点4.过抛物线y2 4x的焦点F作直线交抛物线于A, B两点,M为线段AB的中点.下列说法中正确的有( )3A.以线段AB为直径的圆与直线X —一定相离2B.IABl的最小值为4C・AB∣的最小值为2D.以线段BM为直径的圆与y轴一定相切X 2 25・已知Fl ,F2是椭圆C:= yn 1 a b 0的左、右焦点,P是椭圆C上一点・下a b列说法中正确的有( )A. a °2b时,满足FiPF2 90的点P有2个C. PFiF 2的周长小于4a2D. PFiF 2的面积小于等于 J26. 甲、乙、丙、丁四个人参加比赛,有两人获奖.比赛结果揭晓之前,四个人作了如下猜测.甲:两名获奖者在乙、丙、丁中; 乙:我没有获奖,丙获奖了; 丙:甲、丁中有且只有一人获奖; T :乙说得对.已知四个人中有且只有两个人的猜测是正确的,那么两名获奖者是( ) A •甲 B •乙 C •丙 D. T 7. 已知AB 为圆O 的一条弦(非直径),OC AB 于C ・P 为圆O 上任意一点, 直线PA 与直线OC 相交于点M ,直线PB 与直线OC 相交于点N ・以下说法正 确的有( )A ・O , M,B , P 四点共圆 B ・A,M,B, N 四点共圆 C. A,O,P, N 四点共圆 D. 前三个选项都不对8. SinA SinB SinC COS A COS B COSC 是 ABC 为锐角三角形的( )A. 充分非必要条件B. 必要非充分条件C. 充分必要条件D. 既不充分也不必要条件C ・ ^ant∑mt∑τπ-3tan tan tanA. 8B ・10,an ,任取C ・11D ・1210. 已知集合A aι 42 , 1i j k n , ai a j A, a j ak这三个式子中至少有一个成立,则 n的最大值为()A. 6 B ・ 7C ・8D ・911. 已知 1 ,61 , 121 , 则下列各式中成立的有()A. tan tan tan tan tan tan 3B. tan tantan tantan tan3A, akA9. 已知X , y , z 为正整数,Xy Z,那么方程丄X2的解的组数为2D∙--- t<m -- r∑m~ 3 tan tan tan12.已知实数a , b , c 满足a b c 1,贝IJ 4a√' 1√ 4b 1 √4c 1的最大值与A. &18・关于X, y 的不定方程好615 2 丫的正整数解的组数为( )A. 0B ・1C ・2D ・319・因为实数的乘法满足交换律与结合律,所以若干个实数相乘的时候,可以有 不同的次序.例如,三个实数a , b , C 相乘的时候,可以有ab C , ba c , c ab13. 已知X , y , z R ,满足X y Z1 ,X 2y 2Z 21 ,则下列结论正确的有( )A. XyZ 的最大值为0B. XyZ 的最小值为・427C. Z 的最大值为23D ・Z 的最小值为・1314. 数列 a n 满足 aι 1, a2 2 , a n 26a n ι a n n N*・对任意正整数n ,以下说法中正确的有()A. a n 2ι a n 2 a n 为定值B ・ a n 1 mod 9 或 a∏ 2 mod 9 C. 4a n a n I 7为完全平方数D ・8a∏am 7为完全平方数C ・(13,14)D ・(14,15)1)B ・(12,13)最小值乘积属于区间(A. (11,12),则丿可以取到的值有(15.若复数Z 满足ζ16.从正2016边形的顶点中任取若干个,顺次相连构成多边形,其中正多边形 的个数为( ) A. 6552B. 4536C. 3528 D ・ 2016217・已知椭圆Iab 0与直线Ii : y—χ, 12:y — χ,过椭圆上一点P 2 2作Ii ,12的平行线,分别交Ii ,12于M, N 两点. 若MN 为定值, C. 2A. 12 2B. I3 12C. I4 96D. B 120220.甲乙丙丁 4个人进行网球淘汰赛,规定首先甲乙一组、丙丁一组进行比赛, 两组的胜者争夺冠军.4个人相互比赛时的胜率如下表所示:甲乙丙T甲 — 0.3 0.3 0.8 乙 0.7 — 0.6 0.4 丙0.7 0.4 — 0.5 T0.20.60.5—表中的每个数字表示其所在行的选手击败其所在列的选手的概率,例如甲击败乙的 概率是0.3 ,乙击败丁的概率是0.4・那么甲赢得冠军的概率是 ____________ ・21・在正三棱锥P ABC 中,ABC 的边长为1・设点P 到平面ABC 的距离为x ,异面 直线AB与CP 的距离为y ,则Iim y ___________________ ・实数X , y 满足X 2y 2 34X 2 y 2 ,则X 2 y 2的最大值为 X , y , Z 均为非负实数,满足X最大值为22・如图,正方体ABCDAl BlCIDl 的棱长为1 ,中心为O ,AlE 17⅛A ,则四面体4OEBF 的体积为XdX =23.X1 Sin 2n26. ° 为AB C 内一点,满足SAoB : S BoCS COA2无解;题意.3. BD.27・已知复数Z COS_28∙已知Z 为非零复数,isin ——,贝IJ z 3 - E ________ ・3z 2z 2Z 40J —的实部和虚部均为不小于1的正数,则在复平10 Z面中,Z 所对应的向量OP 的端点P 运动所形成的图形面积为29. 若 tan 4x —,贝——sin 4 *—— ----- sin 2 *—— --- &⅛-^一 Sin X _______3 cos8x cos4x COS 4x COS 2x COS 2xcos X COS X30. 将16个数:4个1, 4个2, 4个3, 4个4填入一个4X4的数表中,要求每行、每列都恰好有两个偶数,共有 __________ 种填法.31・A 是集合{1,2,3, ? ,14}的子集,从A 中任取3个元素,由小到大排列之后 都不能构成等差数列,则A 中元素个数的最大值为 答案及解析1. C ∙注意 f ,X e xg X •2. AD-对于选项A, 由于* b 卜b,于是C 有唯一取值2,符合题意;对于选项B, 根据正弦定理,a 2c 2 J∑ac b 2,于是可得 COS BP, B2对于选项C, 符合题意;条件即COS ASinBC °Λ^A ,B ,C90 ,30 ,60,60 ,60 ,60对于选项D, 根据正弦定理,有 Sin B 丄,又 A 60,于是 B 30 , C 90 ,2符合处的切线,如图.(J(I) =Inx4. AB.对于选项A,点M 到准线X1的距离为IlAFl2为直径的圆与直线X 1 一定相切,进而与直线2,于* 4a 24-,最小4值为4;对于选项D,显然BD 中点的横坐标与IJfM 圧一定相等,因此命题错误.25・ABCD ・对于选项A 和B,椭圆中使得FiPF 2最大的点P 位于短轴的两个端点; 对于选项C, Fl PF 2的周长为2a 2c 4a ; 6. BD ・乙和丁同时正确或者同时错误,分类即可. 7. AC.对于选项A, OBM OAM OPM 即得;对于选项B,若命题成立,则 MN 为直径,必然有 对于选项C, MBN MOP MAN 即得.8. B.必要性: 由于 SinB SinC SinB Sin — B SinB COSB2'BF∣ -JlABI ,于是以线段AB2X E —定相离;2对于选项B 和C,设A4a 2,4a ,则B 对于选项D,Fl PF 2的面积为LSin2FiPF 2 I PFI I PF,-I I P FlI 丨 P f⅜ 丄a 2MAN 为直角,不符合题意;SinA SinB 1,于是Sin A Sin B Sin C SinB C Sin C ASinA B Sin B Sin C COS ACOS A COS B COSC不充分性:当A B C —时,不等式成立,而厶ABC并非锐角三角形.2 49. B.由于1 1 1 1 3 故3 X 6・2 X y Z X情形一若X 3,则1丄1 Hn_,艮卩丫 6 z 6 36 ,解得X, y, Z3,7,42,y Z 6X, y, Z 3,8,24, x, y, Z 3,9,18 , x, y, z 3,10,15, x, y, Z 3,12,12.情形二若X 4 丄即y 4 z 4 16 ,解得X, y, Z 4,5,20 ,y Z 4X, y, Z4,6,12,X, y,Z4,&8 ■I 1 3 2 口20情形三若X 5 ,则_ 丄此时有6 丄丄,于是y ,从Ift y5,6y Z 10 10 y Z y 3进而解得X, y, Z 5,5,10 ■πl 1 1情形四若X 6 ,则_ 丄即y 3 Z 3 9 ,解得X, y, Z 6,6,6 •y Z 310・ B.不妨假设aι a2S.若集合A中的正数的个数大于等于4,由于心阴和ai a4均大于a2 ,于是有a2 as a2 a4 aι,所以a3 a—矛盾.所以集合A中至多有3个正数.同理可知集合A 中至多有3个负数.取A 3,2,1,0, 1, 2, 3 , 满足题意,所以n的最大值为7・11 ・ BD.y L,rIXylyZlZX所以y X 1 Xy , Z y (3 1 yz , x z P3 1 zx ,以上三式相加,即有Xy yz ZX 3.12∙ B ∙时取得;右侧等号当X 1时取得・因此原式的最大值为Qf ,当a31取得;最小值为JT , a b —4乘积为 7 √7 V147 厂打*=9 12,13 .加,即有Xy√3丄 ZX1 丄 1 — Xy yX y 7XyZ1丁 3— 1 ,以上三式相ZX设函数f √ 4x 1的图象,则其导函数「2 V4x 1•作出函数f X 的图象,函数f X 的图象在X1.处的切线y _XZl3r24P ,以及函数f X 的图象3√ 7,如图•,左侧等号当X丄或X43 2丄时3 从而原式最大值与最小值的由 Xy Z 1 , X 2y 2 z 21,可知 Xy yz ZX 0・ 设XyZ C ,则X , y , z 是关 于t 的方程2 t 2C 0的三个实根.令ft3t 2C ,利用导数可得时取得•丄3f →* C3 27所以—C XyZ0, 27,等号显然可以取到•故选项A, B所以A 正确. 由于H3 11 ,D 正确.计算前几个数即可判断B 错误.15・ CD.时取得. 16. C.从2016的约数中去掉1,2,其余的约数均可作为正多边形的边数.设从 2016个顶 点中选出k 个构成正多边形,这样的正多边形有 2016 k 个,因此所求的正多边形的 个数就是2016的所有约数之和减去2016和1008.考虑到201625327 ,因此所求正多边形的个数为(l÷2+4+8+16÷32)? (1+3+9) ? (1+7) - 2016- 1008=3528.17. C.--XO 24y°2为定值,所以r都对.因为X1 Z2 2 x I 2Y 22 1 Z 2,所以」Z 1,等号显然可以3取到.故选项 14. ACD ・ 因为 23∏ 2∏n 3 Un 1 C 错, 选项D 对∙ 2a 1√ 2 a∏2 26a n 2 6a∏ 2a∏ 1CIn 1 a2 a 1Γ 1a∏ 2a n2 1CIn Cln 26a∏1 Cln2I2 a∏6a∏ a n21 a* 1 6a∏ Ian1 Cln Cln2对任意正整数恒成立,所以4an a∏ 17Hn 1 Hn 8a∏ Hn 1 7 Hn 1 ∏n2故C,注若数列a n 满足 a∏ 2 Pan ι a n nN* ,则 a n 21 a∏ 2a∏ 为定值.C 1I ZI Z _ 1,古 一 IZZ 2二?,等号分别当Z JTi 和Z2 2-Ll2设P 点坐标为Xo , yo1 yθ- 4 Xo1 -yθ21N-Xo 21y°,因为収IMN注(1)若将两条直线的方程改为y kx ,则I J a-丄;Vb k(2)两条相交直线上各取一点M 9N ,使得呷为声值,则线段MN 中点Q 的 轨迹为圆或者椭圆.18. B.方程两边同时模3,可得χ2 2 ∙v mod 3 •因为3? 2『,故3? X 2,所以x? 1 mod 3 , 故ImOCI 3,所以y 是偶数・设y 2,nX21X 615 3 5 41 ,解得19・ AB.根据卡特兰数的定义,可得In C20・ 0.165 ・根据概率的乘法公式,所求概率为22.二如图.222mX 5即 X 59• 2m X 123y 12An n+ C 2n nl2n!n 1 !C 2n nl2.n2m m N * ,则0.3 ? (0∙ 5 ? 0∙3+0∙ 5 ?223. 0・9 2n 根据题意,有"X 1 1—VE GBF —[ 一VE BCC B —1・2 2 16 1' 961 Sin 2n X dx χ2∩ ι 1 sin2 n x dx965 CIVOEBF VO EBF 一VG EBF24・ 1.2 23 2 2 根据题意,有X y 4x y 取得,因此所求的最大值为1. 25・?,√22 3 . 22 2,于是X2 2 11,等号当X y ;时由柯西不等式可知,当且仅当X,y ,Z 1 1,-2,o 时, y Z 取到最大値F .2根据题意,2 y 3z丄3, 4于是4当X, y, Z的最小值26. 23.O O 22 32时取得,为根据奔驰定理,有-2 9 4- 927・ COS i Sin —33根据题意,Wx 3Z 2Z 2z 2z 2COSSi n20028. ____3设ZX yi ,其中X, y R 由于空ZZX于是πyy1,—10 402 2X y.sin — J-QQ- 100,四边形ABCD 的面积为 6 6 329・©・根据题意,有COS2X COS X COS X tan 2x tan X tan X ∙tan8x 30. 441000.首先确定偶数的位置有多少种选择.第一行两个偶数有C 种选择,下面考虑这两个偶数所在的列,每列还需再填一 个偶数,设为a,b.情形一 若a, b 位于同一行,它们的位置有3种选择,此时剩下的四个偶数所 填的位置唯一确定.情形二 若a, b 位于不同的两行,它们的位置有6种选择,此时剩下的四个偶 数所填的位置有2种选择. 所以偶数的不同 I 位置数为C 42 3 6 290 , 因此总的填法数 位 90 C 84 C 84441000 ・ 31. 8・一方面,设A a1,a2, ak , 其中k N% 1 k14・ 不妨假设 a 1 a2 a*・右 k 9 ,由题意, a3 aι 3 , a5 a3 3 ,且 a5 a3 a3 aι , 故 a5 aι 7 ,同理,a a 7 ,又因为 a5 a5 aι ,所以 aa , 矛盾.故k 8. 9 5 ∏9 9 1 15另一方面,取A 1,2,4,5,10,11,13,14 ,满足题意.2 - 10√~3 102 10 100√^3 100,于是所求面积为 2 ICQ- 1003 ιoo√^3 100 200- 10Q∕3^ 300 .3 弓形面积为12sin 4 X Sin 2xSin X Sin X cos8x COS 4x tan 8xcos4x cos2 Xtan 4x tan 4x tan 2 X综上所述,A中元素个数的最大值为8.I Ω 2V 4 b。
