高考自主招生数学试题及答案
2023年漳州一中高中自主招生考试数学试卷参考答案

漳州一中高中自主招生考试 数学参照答案及评分意见11. 且 12. (或 )13.4016 14. 15. 16. 三、解答题(本大题共有7小题, 共86分)17. (8分)原式 …………………………………………6分1-=………………………………………………………………8分 18. (10分)原式 ………………………………2分x x --=4162)4()4)(4(---+=x x x 4--=x ………………………7分∴当 时, 原式 ……………………10分19. (10分)(1)(4分) ………………………………………4分 (2)①(4分)树状图为:或列表法为:(画出树状图或列出表格得4分) ……………………………………………4分 ②(2分)因此411234==的倍数p …………………………………………2分 20. (12分)解法一:设参与 处公共场所旳义务劳动, 则学校派出 名学生^…………………………………………………………………………………2分依题意得: ………………………6分 由(1)得: , 由(2)得: ∴434433≤<x ………………………………………………………………8分 又 为整数, ∴ ……………………………………………………10分∴当 时, ………………………………………………11分答: 这所学校派出55名学生, 参与4处公共场所旳义务劳动 …………12分解法二:设这所学校派出 名学生, 参与 处公共场所旳义务劳动……1分 依题意得: ……………………………6分解得: …………………………………………………………8分 为整数, ∴ ………………………………………………………10分∴当 时, ………………………………………11分答: 这所学校派出55名学生, 参与4处公共场所旳义务劳动 …………12分 21. (14分)证法一:如图, 分别延长 、 相交于点 ………………1分 设 , ∵ ,∴ ,得 ………3分∴322=-=AM BM AB …………4分∵ , ∴ , 且 ,在 中, ………………………………6分 又∵ 、 ,∴)(ASA ECN MDN ∆≅∆……………………………………………………9分 ∴ 、 , ………………………………………11分 ∴ 、 , ∴ …………13分∴MBC NMB ∠=∠…………………………………………………………14分 证法二: 设 , 同证法一 ………………6分如图, 将 绕点 顺时针旋转 得到 , 连结 , ∵ , ∴ 是平角, 即点 三点共线,………………………………………………………………………………… 7分 ∴BEC BMA ∠=∠……………………………8分1==AM CE 、BM BE = …………………9分∴BEM BME ∠=∠…………………………10分 ∵MN CE CN NE ==+=+=25123 ……11分 ∴NEM NME ∠=∠…………………………12分 ∴NEM BEM NME BME ∠+∠=∠+∠ ∴AMB BEC BMN ∠=∠=∠………………13分 又∵MBC AMB ∠=∠∴MBC BMN ∠=∠…………………………14分 22. (16分)(1)(4分)设抛物线旳解析式为89252-⎪⎭⎫ ⎝⎛-=x a y ………………………1分∵抛物线通过 , ∴ , 解得: …………3分∴8925212-⎪⎭⎫ ⎝⎛-=x y (或225212+-=x x y ) …………………………4分(2)(4分)令 得 , ∴ ……………………………………1分 令 得 , 解得 、 ………………………3分∴)0 , 1(C 、) 0, 4(D …………………………………………………………4分(3)(8分)结论: …………………………………1分理由是: ①当点重叠时, 有………………………………2分②当 , ∵直线 通过点 、 , ∴直线 旳解析式为………3分设直线 与 轴相交于点 , 令 , 得 , ∴ ,则)2,0()2,0(B E 与点-有关x 轴对称………………4分 ∴ , 连结 , 则 ,∴ , …………………5分∵在 中, 有 …………………………………………6分∴BC AC AE PE PA PB PA +=>+=+…………………………………7分 综上所得BC AC BP AP +≥+………………………………………………8分 23. (16分)(1)(6分)解法一: 当点 在⊙ 上时, 设 与⊙交于点 ,∵ , ∴ ………………………1分 ∵ ∥ , ∴ ………………2分∴PD AP =…………………………………………3分又 , …………………4分………………………………………5分∴︒︒=⨯⨯=∠⨯=∠3018031213121AOB APE …6分 解法二: 设点 在⊙ 上时, 由已知有 , ……………………1分 ∴△ △ , ……………………………………………2分 ∴ , …………………………………………3分 在 △ 中, ……5分∴︒=∠30APC ……………………………………………………6分(2)(10分)k 值不随点P 旳移动而变化.理由是:∵ 是⊙ 右半圆上旳任意一点, 且 ∥ ,∴ ……………………………1分∵ 是⊙ 旳切线, ∴ ,⌒ ⌒又∵ , ∴ ,∴ABQ ACP ∠=∠ ……………………………2分 ∴ACP ∆∽OBQ ∆ ……………………………3分 ∴QBPCOB AC =……………………………………4分 又∵ 、 ,∴ACF ∆∽ABQ ∆……………………………………………………………6分 ∴BQCFAB AC = …………………………………………………………………7分 又∵ , ∴ 即 …………………………8分∴CF PC 2= 即CF PF = …………………………………………………9分 ∴ ,即 值不随点 旳移动而变化. ………………………10分。
高校自招数学试题及答案

高校自招数学试题及答案一、选择题(每题4分,共40分)1. 下列哪个数是无理数?A. 0.33333…(循环)B. πC. √2D. 1答案:B、C2. 已知函数f(x) = 2x - 3,求f(5)的值。
A. 7B. 4C. 1D. 2答案:A3. 若a > b > 0,下列不等式中正确的是:A. a^2 > b^2B. a + b > 2√(ab)C. a/b > b/aD. a^3 > b^3答案:D4. 已知等差数列的首项为1,公差为2,求第10项的值。
A. 19C. 17D. 16答案:A5. 圆的半径为5,求圆的面积。
A. 25πB. 50πC. 75πD. 100π答案:B6. 已知三角形ABC,∠A = 90°,AB = 3,AC = 4,求BC的长度。
A. 5B. 6C. 7D. 8答案:A7. 函数y = x^2 - 4x + 4的顶点坐标是什么?A. (2, 0)B. (-2, 0)C. (2, 4)D. (-2, 4)答案:A8. 已知正弦函数sin(x)的周期为2π,求余弦函数cos(x)的周期。
B. 2πC. 4πD. 8π答案:B9. 根据勾股定理,直角三角形的斜边长度是两直角边长度的平方和的平方根。
设a和b是直角边,c是斜边,下列哪个表达式是正确的?A. c = √(a^2 + b^2)B. a = √(c^2 + b^2)C. b = √(c^2 - a^2)D. c = √(b^2 - a^2)答案:A10. 已知一个数列的前三项为1, 1, 2,且每一项都是前两项的和,求第5项的值。
A. 4B. 5C. 6D. 7答案:C二、填空题(每题4分,共20分)11. 根据二项式定理,展开式(a + b)^3的通项公式是________。
答案:T_{r+1} = C_{3}^{r}a^{3-r}b^{r}12. 如果一个函数是奇函数,那么f(-x)等于________。
芜湖一中2022年高一自主招生考试数学试题及参考答案

芜湖一中2022年高一自主招生考试数学试卷(满分:150分)一、选择题(本大题共7小题,每小题6分,共42分,每小题只有一个选项正确,把正确的选项填在答题卡答题栏中)1.方程xΙxΙ-5ΙxΙ+4=0的实数根的个数是()A1B2C3D42.依次将正整数1,2,3,……的平方数排成一串:149162536496481100121144……,排在第1个位置的数字是1,排在第5个位置的数字是6,排在第10个位置的数字是4,排在第898个位置的数字是()A1B4C5D93.设抛物线y=x2+x-4与x轴的两个交点的坐标为(x1,0)和(x2,0),则x13-5x22+10=()A-19B-9C16D-274.若直角坐标系内两点M、N满足条件①M、N都在函数y的图象上②M、N关于原点对称,则称点对(M,N)是函数y的一个“共生点对”(点对(M,N)与(N,M)看作同一个”共生点对”),已知函数,则函数y的“共生点对”有()个A0B1C2D35.如图(1),E,F 是正方形ABCD 的边AD 上两个动点,满足AE=DF.连接CF 交BD 于点G,连接BE 交AG 于点H.若正方形的边长为4,则线段DH 长度的最小值是().A252-B5C 3D 3.56.如图(2),一个边长分别是6,8,10的直角三角形的一个顶点与正方形的点A 重合,另两个顶点在正方形的两边BC,CD 上,则正方形的面积是()图(1)图(2)图(3)7.如图(3)O 是正方形ABCD 对角线AC 上一点,OE ⟂OD,∠OED=45°,E 在AB 上,结论:①∠AOD=∠AED;②AD:OD=AF:EF;③OA OF OE ⋅=2;④若AB=6,BE=4,则OD=52,其中正确结论的个数是()A 1B 2C 3D 4二、填空题(本大题共7小题,每小题7分,共49分).9.若有四个不同的正整数a,b,c,d,满足(2022-a)(2022-b)(2022-c)(2022-d)=6,则a+b+c+d=.10.已知实数m≠n 且满足(m+2)2=3-3(m+2),(n+2)2=3-3(n+2),则.=+nm m n11.如图4,∠C =90°,BC =6,tanB =,点M 从点B 出发以每秒3个单位长度的速度在BA 上向点A 运动,点N 同时从点A 出发向点C 运动,其速度是每秒2个单位长度,当一点到达终点时,另一点也停止运动.当t 为秒时,△MNA 为等腰三角形.12.如图(5),点P 为函数xy 36=(x >0)的图象上一点,且到两坐标轴距离相等,⊙P 半径为2,A (4,0),B (8,0),点Q 是⊙P 上的动点,点C 是QB 的中点,则AC 的最小值是.13.如图图6,在∆ABC 中,AB=AC,以AB 为直径的圆交BC 于点D,连接AD ,点P 是AD 上一点,过点C 作CF ∥AB,延长BP 交AC 于E,交CF 于F,若PE=4,EF=5则BP=图(4)图(5)图(6)14.设自然数m,n,m>n,且(m+n)+(m-n)+mn+n m=75,则m+n=三、解答题(本大题共4小题,共59分,解答应写出必要的文字说明,演算或推演步骤)15.(1)(本题6分)解方程82)1()344=+++x x ((2)(本题7分)对于函数f (x )=ax 2+(b +1)x +b ﹣2(a ≠0),若存在实数x 0,使f (x 0)=x 0成立,则称x 0为f (x )的固定点.①当a =2,b =﹣4时,求f (x )的固定点;②若对于任意实数b ,函数f (x )恒有两个不相同的固定点,求a 的取值范围.16.(本题12分)某校开展研学旅行活动,决定租几辆客车,要求每辆车乘坐相同的人数,每辆车至多乘坐32人。
2023年温州中学自主招生数学试题含答案

2023年温州中学自主招生数学试题2023.4一试一、选择题:本大题共8题,每题4分,共32分.在每题给出旳旳四个选项中,只有一项是符合题目规定旳.1.已知b a >,则下列结论对旳旳是 ( ) A. 22b a > B. 33a b > C.b a 11< D. 1>ba2.用黑白两种颜色旳正六边形地面砖拼成若干个图案,规律如下图所示,则第2010个图案中,白色地面砖旳块数是A .8042ﻩB .8038ﻩﻩC .4024 ﻩﻩD.60333.有关x 旳整系数一元二次方程20(0)ax bx c a ++=≠中,若a b +是偶数,c 是奇数,则( )A.方程没有整数根 B .方程有两个相等旳整数根 C .方程有两个不相等旳整数根 D .不能鉴定方程整数根旳状况 4.如图所示,一种33⨯旳方格中,每一行,每一列,及每一对角线上旳三个数之和都相等,则x 旳值是( )A.6 B.7 C.8 D.95.若10010321⨯+⨯+=a a a x ,10010654⨯+⨯+=a a a y 且736=+y x ,其中正整数79 x6i a 满足71≤≤i a ,)6,5,4,3,2,1(=i ,则在坐标平面上),(y x 表达不一样旳点旳个数为( )ﻩﻩA.60ﻩ B.90ﻩ C.110ﻩ D.1206.气象台预报:“本市明天降水概率是80%”,但据经验,气象台预报旳精确率仅为80%,则在此经验下,本市明天降水旳概率为( )A.84% B.80% C.68% D.64% 7.设nnM 1723⨯+=,其中n 为正整数,则下列结论对旳旳是( ) A .有且仅有一种n ,使得M 为完全平方数 B.存在多于一种旳有限个n ,使得M 为完全平方数 C.存在无数个n ,使得M 为完全平方数 D.不存在n ,使得M 为完全平方数8.已知点A 、B 分别在x 轴正半轴、y 轴正半轴上移动,4AB =,则认为AB 直径旳圆.周.所扫过旳区域面积为( ) A.π4 B. π8 C. 42+π D . 46+π 二、填空题:本大题共6小题,每题5分,共30分. 9.若有关x 旳方程51122m x x ++=--无解,则______m =10.在Rt △ABC 中,C 为直角顶点,过点C 作AB 旳垂线,垂足为D,若A C、B C为方程0262=+-x x 旳两根,则AD ·BD 旳值等于11.我们规定[]x 表达不超过x 旳最大整数,如:[ 2.1]3-=-,[3]3-=-,[2.2]2=。
2024年浙江省温州市重点高中自主招生数学试卷+答案解析

2024年浙江省温州市重点高中自主招生数学试卷一、选择题:本题共8小题,每小题4分,共32分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.对正整数n,记n!…,则1!!!…!的末尾数为()A.0B.1C.3D.52.在分别标有号码2、3、4、…10的9个球中,随机取出两个球,记下它们的标号,则较大标号被较小标号整除的概率是()A. B. C. D.3.已知关于x的方程恰有一个实根,则满足条件的实数a的值的个数为()A.1B.2C.3D.44.函数与的图象可能是()A. B.C. D.5.十进制数278,记作,其实,二进制数有一个为整数进制数,把它的三个数字顺序颠倒得到的k进制数是原数的3倍,则()A.10B.9C.8D.76.正方形ABCD,正方形BEFG和正方形PKRF的位置如图所示,点G在线段DK上,正方形BEFG的边长为2,则的面积为()A.4B.2C.3D.7.两个等腰直角、如图放置,,,,DE与AC交于点H,连接BH,若,下列结论错误的是()A.≌B.为等边三角形C.D.8.如图,在圆内接四边形ABCD中,,,为圆心,,,,,则此四边形的面积为用含a、b、c、d表示四边形ABCD的面积A.B.C.D.二、填空题:本题共8小题,每小题4分,共32分。
9.已知a是64的立方根,是a的平方根,则的算术平方根为______.10.关于x的函数符合以下条件:函数在处无意义;当x取非零实数时都有如当时,有,可以求得则的函数表达式是______.11.如图,在“镖形”ABCD中,,,,则点D到AB的距离为______.12.已知正整数a,b,c满足,,则abc的最大值为______.13.AB为半圆O的直径,C为半圆弧的一个三等分点,过B,C两点的半圆O的切线交于点P,则______.14.矩形ABCD的边长,,E为AB的中点,F在线段BC上,F在线段BC上,且BF::2,AF分别与DE,DB交于点M,N,则______.15.实数a,b,c,d满足:一元二次方程的两根为a,b,一元二次方程的两根为c,d,则所有满足条件的数组为______.16.小明某天在文具店做志愿者卖笔,铅笔每支售4元,圆珠笔每支售7元.开始时他有铅笔和圆珠笔共350支,当天虽然笔没有全部卖完,但是他的销售收入恰好是2013元.则他至少卖出了______支圆珠笔.三、解答题:本题共4小题,共56分。
2023年广东省深圳中学自主招生数学试卷+答案解析

一、填空题:本题共15小题,共702023-2024学年广东省深圳中学自主招生数学试卷分。
1.计算:______.2.计算:______.3.已知,且,设,其中m 和n 是两个互质的正整数,则______.4.已知实数x ,y 满足,则______.5.如图,已知中,,D 是AB 的中点,,则______.6.若反比例函数的图象与一次函数的图象交于点和,则______.7.定义新运算:,例如:已知实数x 满足,则x 的最大值是______.8.如图,已知直线RS ,ST ,TR 都与相切,且,,,,的直径为,其中a 和b 都是有理数,则______.9.在平面直角坐标系中,由抛物线与x 轴所围出的区域内有______个整点横纵坐标都是整数的点边界上的点不计10.满足的全部实数x 的乘积等于______.11.如图所示为地板所铺瓷砖的一小部分.所有的瓷砖都是正方形,最小的正方形瓷砖是,次小的则是若以线段XY 为边长作正方形,则该正方形的面积为______12.已知三个非零实数x、y、z满足,则的值等于______.13.如图,在矩形ABCD中,,,若在AC,AB上各取一点M,N使的值最小,则这个最小值等于______.14.若正整数a、b、m满足且,则m的所有值之和等于______.15.一个的矩形ABCD,点P、Q、R、S分别为在AB、BC、CD、DA边上的点,如图所示.已知AP、PB、BQ、QC、CR、RD、DS、SA的长度都是正整数单位长,且PQRS为矩形,则矩形PQRS的面积的最大值是______.答案和解析1.【答案】308【解析】解:原式故答案为:分子、分母同时乘上和,再计算即可求解.本题考查了分母有理化,灵活运用二次根式的性质、掌握分母有理化的方法是解答本题的关键.2.【答案】972【解析】解:原式故答案为:根据特殊角的三角函数值、积的乘方法则计算即可.本题考查了实数的运算和特殊角的三角函数值,熟练掌握运算法则是关键.3.【答案】196【解析】解:解方程组,得,则,和n是两个互质的正整数,,,,故答案为:解方程组用含z的代数式表示出x、y,代入计算求出,根据质数的概念分别求出m、n,计算即可.本题考查的是质数和合数的概念、三元一次方程组的解法,正确由z表示出x、y是解题的关键.4.【答案】【解析】解:设,,原方程组可化为,由①可得:③,把③代入②可得:,解得:,把代入③得:,,,,,经检验,都是原方程的解.故答案为:根据换元法求出与的值,然后求出x和y的值,最后代入代数式求值.本题主要考查了分式方程的知识、换元法的知识、代数式求值的知识、二元一次方程的知识,难度不大,认真计算即可.5.【答案】40【解析】解:过B点作交AC的延长线于点E,,,,,为等腰直角三角形,AC::DB,,,为AB的中点,,在中,,,,解得,故答案为:过B点作交AC的延长线于点E,可证明为等腰直角三角形,,再利用勾股定理可得,结合平行线分线段成比例定理可得,根据勾股定理可求解,进而可求解本题主要考查等腰直角三角形,勾股定理,平行线分线段成比例定理等知识的综合运用,利用更改的求解是解题的关键.6.【答案】625【解析】解:将点和分别代入,得:,再将点和分别代入,得:,,,,故答案为:首先将点A,B代入反比例函数的解析式得,再将点A,b代入一次函数的解析式得,,据此可得,然后再将代入求值的代数式即可得出代数式的值.此题主要考查了的反比例函数与一次函数的交点,解答此题的关键是理解函数图象上的点都满足函数的解析式,满足函数解析式的点都在函数的图象上.7.【答案】4【解析】解:,,,,,,的最大值是故答案为:由新定义列出算式解方程即可.本题考查了解一元二次方程,新定义,解题的关键是由新定义列出算式.8.【答案】330【解析】解:如图,设直线RS,ST,TR都与相切于点A、点B、点C,则,,在中,,,,,连接OA、OB,则,,,,四边形OASB是正方形,,设,则,,,即,,,直径为,的直径为,即,,,故答案为:根据切线的性质,切线长定理以及正方形的性质进行计算即可.本题考查切线的性质,正方形的性质,掌握切线长定理以及正方形的性质是正确解答的前提9.【答案】14【解析】解:抛物线,令,即,解得从图中可以看出,抛物线与x轴所围出的区域内的整点有,,,,,,,,,,,,,故答案为:根据抛物线求出与x轴的交点,再利用图象找到整点即可.本题考查了二次函数的图象与性质,解题的关键是掌握二次函数图象上点的坐标特征.10.【答案】594【解析】解:当时,原式化简为:,,算式不成立;当时,原式化简为:,,;当时,原式化简为:,,;当时,原式化简为:,,;当时,原式化简为:,,算式不成立,故答案为:分情况计利用方程解出x的值,再将x的值相乘即可.本题考查了方程的解答,绝对值的性质的应用是解题关键.11.【答案】400【解析】解:如图:图中的四边形均为正方形,且最小正方形的边长为1cm,次小正方形的边长为3cm,,则,,,,,,,在中,,,由勾股定理得:,以线段XY为边长作正方形,则该正方形的面积为故答案为:依题意得,则,,进而得,,,由此得,,然后在中由勾股定理得,据此可得出答案.此题主要考查了正方形的性质,勾股定理,解答此题的关键是准确识图,根据正方形的性质求出相关线段的长.12.【答案】600【解析】解:,,,,,,,故答案为:先化简得到,代入得到结论即可.本题考查了分式的化简求值,实数的运算,正确地求得是解题的关键.13.【答案】16【解析】解:如图,作点B关于直线AC的对称点,交AC与E,连接,过作于G,交AC于F,由对称性可知,,,的最小值为的长;在中,,,由勾股定理,得,点B与点关于AC对称,,,,,,,又,∽,,,的最小值是故答案为:作点B关于直线AC的对称点,交AC与E,连接,过作于G于点F,再由对称性可知,因此求出的长即可.本题考查轴对称-最短路线问题,矩形的性质,勾股定理,相似三角形的判定与性质,面积法,根据题意作出辅助线是解题的关键.14.【答案】27【解析】解:①,②,①②,得,因式分解,得,,b均为正整数,且或,,或,,,或,或,或,的所有值之和等于第11页,共11页故答案为:根据已知条件①,②得到,因式分解得到,由于a ,b 均为正整数,于是得到或,求得,或,根据求得或,即可求得m 的所有值之和等于本题考查了因式分解的应用,正确的理解题意得到是解题的关键.15.【答案】150【解析】解:根据题意:设,,,,由∽,则,,又因为a ,b 是正整数,故,24,33,40,45,48,49,得,15,则或9,即有,,,,,,150,150,102,即:故答案为:如图,根据矩形的性质,可知∽,得到a ,b 的关系式,再由题意a ,b 是正整数,得到的的整数解,从而求出矩形PQRS 的面积,取最大值.本题主要考查了矩形的基本性质,相似三角形的判定和性质,求二元方程组的整数解及三角形的面积等知识的运用,是一个综合性较强的题目,在图形中找出相似三角形是解题的关键.。
省级重点高中自主招生数学真题8套(含答案)

省重点高中自主招生数学真题8套(含答案)第1套一、选择题(每小题5分,满分30分。
以下每小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填得0分。
)1、已知实数a 、b 、c 满足0254=-+-+++a b c b a ,那么bc ab +的值为( ) A 、0B 、16C 、-16D 、-32 2、设βα、是方程02322=--x x 的两个实数根,则βααβ+的值是( )A 、-1B 、1C 、32-D 、32 3、a 、b 、c 均不为0,若0<=-=-=-abc cxz b z y a y x ,则),(bc ab p 不可能在( ) A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限4、在ABC ∆中,C B ∠=∠2,下列结论成立的是( ) A 、AB AC 2= B 、AB AC 2< C 、AB AC 2> D 、AC 与AB 2大小关系不确定5、已知关于x 的不等式7<a x 的解也是不等式12572->-aa x 的解,则a 的取值范围 是( )A 、910-≥aB 、910->a C 、0910<≤-a D 、0910<<-a 6、如图,□ DEFG 内接于ABC ∆,已知ADE ∆、EFC ∆、DBG ∆的面积为1、3、1,那么□ DEFG 的面积为( ) A 、32B 、2C 、3D 、4 第6题图二、填空题(每小题5分,共30分)1、已知质数x 、y 、z 满足5719=-yz x ,则z y x ++= 。
2、已知点A (1,3),B (4,-1),在x 轴上找一点P ,使得AP -BP 最大,那么P 点的坐标是 。
3、已知AB 是⊙O 上一点,过点C 作⊙O 的切线交直线AB 于点D ,则当△ACD 为等腰三解形时,∠ACD 的度数为 。
自主招生考试数学卷(答案) (6)

A、第一象限 B、第二象限
C、第三象限 D、第四象限
24、函数 y 4sin x 3cos x 的最小值为 (
)
A .0
B .-3
C .-5
D . 13
25、已知角 的终边上有一点 P- 3, 4,则 cos (
A、0
3
B、 5
C、0.1
二、填空题:(共 30 分.)
) D、0.2
1.双曲线
D、 y sin x cos x
sin
21、若
5 13
,且
为第四象限角,则 tan
的值等于(
)
12
A、 5
12
B、 5
5
C、 12
5
D、 12
22、下列命题中正确的是(
)
A、第一象限角必是锐角
B、终边相同的角相等
C、相等的角终边必相同
D、不相等的角其终边必不相同
23、-870°角的终边所在的象限是( )
7、【答案】 C
【考点】复数的基本概念,复数代数形式的混合运算 【解析】【解答】解:z z + i = 2 − i 2 + 2i = 4 + 4i − 2i − 2i2 = 6 + 2i
故答案为:C
【分析】根据复数的运算,结合共轭复数的定义求解即可.
8、【答案】 B
【考点】旋转体(圆柱、圆锥、圆台)
自考本科数学卷
(满分 150 分,考试时间 120 分钟)
一、选择题:(本题共 25 小题,共 50 分)
1.对 2×2 数表定义平方运算如下:( )
a
c
b d
2
a
c
b d
a c
2024年广东省深圳中学自主招生数学试卷+答案

2024年广东省深圳中学自主招生数学试卷1.202420252024202363030301030×+=−×____________.2x +=的正数解为____________.3.等腰ABC △的底边AC 长为30,腰上的高为24,则ABC △的腰长为____________.4.已知实数m ,n 满足2202410m m ++=,224200n n ++=且1mn ≠,则601n mn=+____________. 5.若x 为全体实数,则函数223y x x =−+与2243y x x =−+的交点有____________个. 6.若0abc ≠,1a b c b c c a a b++=+++,则222a b c b c c a a b ++=+++____________. 7.K 为ABC △内一点,过点K 作三边的垂线KM ,KN ,KP ,若3AM =,5BM =,4BN =,2CN =,4CP =,则2AP =____________.8.记a ,b ,c 的最小值为{}min ,,a b c ,若{}()min 41,2,24fx x x x =++−+的最大值为M ,则6M =____________.9.已知正方形OBAC ,以OB 为半径作圆,过A 的直线交O 于M ,Q ,交BC 与P ,R 为PQ 中点,若18AP =,7PR =,则BC =____________.10.若a ,b ,c ,d ,e 为两两不同的整数,则22222()()()()()a b b c c d d e e f −+−+−+−+−的最小值为____________.11.PA ,PB 分别为1O 和2O 的切线,连接AB 交1O 于C 交2O 于D ,且AC BD =,已知1O 和2O 的半径分别为20和24,则2180PA PB = ____________.12.已知a ,b ,c 正整数,且只要1111a b c ++<,则111m a b c ++≤,设m 的最小值为r s (r s 为最简分数),则r s +=____________. 13.对于任意实数x ,y ,定义运算符号*,且*x y 有唯一解,满足()()()***a b c a c b c +=+,0*()(0*)(0*)a b a b +=+,则20*24=____________. 14.已知正整数A ,B ,C 且A C >,满足222879897ABC BCA CAB ++=,则ABC =____________.15.等腰三角形边长均为整数,其的面积在数值上是周长的12倍,则所有可能的等腰三角形的腰长之和为____________.2024深圳中学自招答案一、填空题.1.【解析】原式20242025220242023630306303018090054301030301020×+×++===−×−.2.x +=,x =, ∴218232x x x =−, ∵0x >,∴223218x −=,解得:5x =,∴该方程的正数解为5x =.3.【解析】①若ABC △为锐角三角形,如图所示:设ABC △的腰长为x ,在ACD △中,18AD =,在BCD △中,222(18)24x x −+=,解得:25x =,∴ABC △的腰长为25;②若ABC △为钝角三角形,如图所示:在BCD △中,222(18)24x x −+=,解得:25x =(舍), 综上所述:ABC △的腰长为25.4.【解析】由224200n n ++=得21120()2410n n+⋅+=,∵1m n ≠,∴m ,1n可以视为方程2202410x x ++=的两个实数根, ∴165m n +=−,∴60605011n mn m n ==++. 5.【解析】问题等价于方程2223243x x x x −+=−+的解的个数问题; ∴2240x x x +−=, 当0x ≥时,220x x −=,∴0x =或2x =;当0x <时,260x x −=,∴0x =或6x =(舍); 综上所述:函数223y x x =−+与2243y x x =−+的交点有2个. 6.【解析】222()()a b c a b c a b c a b c b c a c a b b c a c a b++++=+++++++++++, ∴222a b c a b c a b c b c a c a b++=++++++++, ∴2220a b c b c a c a b++=+++. 7.【解析】22222222()()KA KB KM AM KM BM AM BM −=−+=−, 同理可得:2222KB KC BN CN −=−,2222KC KA CP AP −=−,三式相加得:222222AM BN CP BM CN AP ++=++,∴222222.34452AP ++=++,解得212AP =.8.【解析】由题意作出以下图形:考虑24y x =−+与2y x =+的交点即可;联立242y x y x =−+ =+ ,解得2383x y = = ,∴83M =,∴616M =. 9.【解析】连接OP ,设AM x =,ACOC a ==, ∴18PM x =−,32QM x =−,由正方形的对称性:18OP AP ==,由圆幂定理:2AC AM AQ =⋅,22PM PQ OC OP ⋅=−,∴232a x =,2214(18)18x a −=−,∴214(18)3218x x −=−,解得:28823x =,∴BC ==.10.【解析】记1a b x −=,2b c x −=,3c d x −=,4d e x −=,5e a x −=,则1x 、2x 、3x 、4x 、5x 均为整数且不等于0,同时满足123450x x x x x ++++=,∴1x 、2x 、3x 、4x 、5x 中存在偶数个奇数,若存在2个1,2个1−,1个2,则对于1x 、2x 、3x 、4x 、5x 构成的数环而言必有一个1与1−相邻,这是不符合要求的,否则存在两数相等;所以至少存在两个数的绝对值为1,3个数的绝对值为2,∴222221234514x x x x x ++++≥,对于(,,,,)(1,3,5,4,2)a b c d e =而言可以取到14,故其最小值为14.11.【解析】过1O 、2O 、P 分别作AB 的垂线,垂足依次为E 、F 、G , ∴1190PAG O AE AO E ∠=°−∠=∠,2290PBG O BF BO F ∠=°−∠=∠,1122AE AG BD BF ===, ∴1APG O AE △∽△,2BPG O BF △∽△,∴1PA AO PG AE =,2PB BO PG BF =, ∴1122205246AO PA AO AE BO PB AO BF====,∴225180()180()1256PA PB =×=.12.【解析】不妨设a b c ≤≤,则2a ≥,当3a ≥时,1111111133412a b c ++≤++=; 当2a =时,11111112a b c b c ++=++<,∴1112b c +<,∴3b ≥, 当4b ≥时,1111111924520a b c ++≤++=, 当3b =时,1111114123742a b c ++≤++=, 即当(,,)(2,3,7)a b c =时,4142m =,83r s +=. 13.【解析】由(*)(*)(*)a b c a c b c +=+得*(*)(*)a b a c b c c =+−, ∴*(*)(*)*b a b c a c c a b =+−=,取0c =,则*(*0)(*0)(0*)(0*)0*()a b a b a b a b =+=+=+,对于0*()(0*)(0*)a b a b +=+,取0a b ==,得0*00=, 同时0*0(0*)(0*)0c c c =+−=,∴0*2c c =, ∴20*240*(2024)0*4422=+==.14.【解析】首先22228798971000ABC BCA CAB ++=<,∴A 、B 、C 均为一位数,且不为0,即从1到9,其次考虑末尾特点,222A B C ++的末尾为7,而完全平方数的末尾为014569,不考虑0,剩下14569,想要使得末尾为7,可以有1157++=或44917++=或56617++=或99927++=,由于A B C >>,故99927++=舍去(末尾为9的只有3、7两个),若满足1157++=,则对应的数为9、5、1,显然222951519195879897++>,舍去; 若满足56617++=,则对应的数为6、5、4,显然222654546465942057879897++=>,舍去; 若满足44917++=,则对应的数为8、3、2或8、7、2,计算222832328283879897++=符合题意;计算222872728287879897++>,舍去; 综上所述:832ABC =.15.【解析】设该等腰ABC △的腰为a ,底为b .由题意:112(2)2b a b ×+,∴48(2)b a b +,∴b 2322304(2)ab b a b −=+, ∴33223042304246082(48)(48)b b b b a b b b ++=−+−,∴3230446082(48)(48)(48)(48)b b b a b b b b b +==++−+−, 记4608(48)(48)b k b b =+−,k 为正整数,∴222248480kb b k −×−=,∴2∆==×为完全平方数,m =(m 为正整数),∴22248m k −=,即2()()48m k m k +−=, 由于2824823=×,有(81)(21)27++=个因子,应该存在(271)2114−÷+=组,考虑到()m k +与()m k −应该同奇偶,故存在14311−=组,列举如下: ∴(,)(1152,2)m k m k +−=或(576,4)或(384,6)或(288,8)或(192,12)或(144,16)或(128,18)或(96,24)或(72,32)或(64,36)或(48,48),∴(,)(577,575)m k =或)290,286(或)195,189(或)148,140(或(102,90)或(80,64)或(73,55)或(60,36)或(52,20)或(50,14)或(48,0), 根据求根公式,224824848(48)2m m b k k ×+×+=, 代入检验可得:当(,)(102,90)m k =或(80,64)或(60,36)或(52,20)或(50,14), 依次解得:80b =或96或144或240或336, ∵2a b k =+,∴2b k a +=,解得85a =或80或90或130或175, 综上所述:所有可能的等腰三角形的腰长之和为858090130175560++++=.。
2025年重点高中自主招生考试数学模拟试卷试题(含答案)

2025重点高中自主招生数学针对性模拟试卷(本试卷满分150分,时间2小时)一、选择题(每小题6分,共60分)1.若“14人中至少有2人在同一个月过生日”这一事件发生的概率为P ,则()A.P=0B.0<P<1C.P=1P>12.下列命题中,真命题的个数是()①一组对边平行且对角线相等的四边形是矩形②对角线互相垂直且相等的四边形是菱形③两组对角分别相等的四边形是平行四边形④一组对边平行,另一组对边相等的四边形是平行四边形A.0个 B.1个 C.2个 D.3个3.方程()1112=--x x 的根共有()A.1个B.2个C.3个D.4个4.设{}d c b a ,,,max 表示d c b a ,,,中最大的数,则⎭⎫⎩⎨⎧-210,2,260tan 2,45cos 2max 0π=()A.045cos 2 B.260tan 20- C.2π D.2105.若关于x 的方程012)14(2=-+++m x m x 的两根分别为1x 、2x ,且321=+x x ,则m =()A.-1或21 B.-1或1C.21-或21 D.21-或16.如图,在△ABC 中,点D 在线段AC 上,点F 在线段BC 延长线上,BF=5CF,且四边形CDEF 是平行四边形,△BDE 与△ADE 的面积之和为7,则△ABC 面积为()A.28 B.29 C.30 D.327.用数字0,1,2,3,4可以组成没有重复数字的四位数共有()A.64个 B.72个 C.96个 D.不同于以上答案8.已知y x ,是整数,则满足方程03432=---y x xy 的数对),(y x 共有()A.4对B.6对C.8对D.12对9.如图,在△ABC 中,AC=BC=4,D 是BC 的中点,过A,C,D 三点的圆O 与AB 边相切于点A,则圆O 的半径为()A.2B.5C.214D.714410.若关于x 的方程x k x =-23有三个不同解321,,x x x ,设,321x x x m ++=则m 的取值范围为()A.2<m B.23->m C.20<<m D.223<<-m 二、填空题(每小题6分共36分)11.已知△ABC 中,BC=1,AC=2,AB=3,则△ABC 的内切圆半径为.12.若y x 、满足⎪⎪⎩⎪⎪⎨⎧=+=+2454545yx xy y x xy ,则=+y x .13.如图,在平面直角坐标系中,抛物线22--=x x y 与x 轴交于A、B 两点(点A 在点B 左边),点E 在对称轴MN 上,点F 在以点C(-1,-4)为圆心,21为半径的圆上,则AE+EF 的最小值为.14.已知直线)0(1>+=k kx y 与双曲线xy 2=交于A、B 两点,设A、B 两点的坐标分别为),(11y x A 、),(22y x B ,则=-+-)1()1(1221y x y x .15.若21≤---a x x 对任意实数x 都成立,则实数a 的取值范围是.16.已知互不相等的正整数20321,,,,a a a a 满足202420321=+++a a a a ,设d 是20321,,,,a a a a 的最大公约数,则d 的最大值为.三、解答题(共54分)17.(12分)已知实数215-=a .(1)求a a +2的值;(2)求3223111aa a a a a +++++的值.18.(12分)已知一次函数)0(1)2(<+-=k x k y 的图象与y x 、轴分别交于点A、B.(1)若2-=k ,试在第一象限内直接写出点),(y x M 的坐标,使得A、B、M 三点构成一个等腰直角三角形;(2)设O 为坐标原点,求△OAB 的面积的最小值.19.(14分)如图,已知0120=∠AOB ,PT 切圆O 于T,A、B、P 三点共线,∠APT 的平分线依次交AT、BT 于C、D,连接BC、AD.(1)求证:△CDT 为等边三角形;(2)若AC=8,BD=2,求PC 的长.20.(16分)已知函数a x a x y -+-+=3)4(2.(1)若此函数的图象与x 轴交于点)0,()0,(21x B x A 、,且2021≤<≤x x ,求a 的取值范围;(2)若20≤≤x ,求y 的最大值;(3)记a x a x x f -+-+=3)4()(2,若对于任意的40<<a ,都能找到200≤≤x ,使t x f ≥)(0,求t 的取值范围参考答案:一、选择题:1-5CBBDC6-10ACBDD 二、填空题:11、2321-+12、913、2914、-415、31≤≤-a 16、817.(1)∵215-=a ,512=+∴a ,5)12(2=+∴a .4442=+∴a a ,12=+∴a a .(3)a a -=12,12)1()1(23-=--=-=-=∴a a a a a a a a .∴原式==++++-3321112aa a a a 122222112333-+=+=++a a a a a a a .当215-=a 时,原式=353)25(2152521511522152+=++-=-+-=--+-⨯.18.(1)当2-=k 时,52+-=x y ,满足题意的M 点有3个,分别为415,415(),215,5(),25,215(321M M M .(2)易求得)21,0(),0,12(k B kA --.k kk k OB OA S OAB 2212)2112(2121--=--=⋅=∴∆,0<k ,021>-∴k ,02>-k .有均值不等式得4)2(2122=-⋅-+≥∆k kS OAB ,当且仅当k k 221-=-,即21-=k 时,等号成立.∴△ABC 的面积的最小值为4.19.(1)证明:0120=∠AOB ,06021=∠=∠∴AOB ATB .∵PT 切⊙O 于T,∴∠BTP=∠TAP.∵PC 平分∠APT,∴∠APC=∠CPT.∵∠TCD=∠TAP+∠APC,∠CDT=∠BTP+∠CPT.∴∠TCD=∠CDT=00060260180=-.∴△CDT 为等边三角形.(3)解:设CT=DT=x ,∵∠TCD=∠CDT=∠BDP,∠BPD=∠CPT,∴△PCT∽△PDB.∴BDCTPD PC =①,∵∠DTP=∠PAC,∠APC=DPT,∴△ACP∽△TDP.∴PD PC TD AC =,∴TD AC BD CT =.∴xx 82=.∴4=x (负值舍去).∴CD=DT=CT=4.由①得244=-PC PC ,解得PC=8.20.解:(1)∵0)2()3(4)4(22>-=---=∆a a a ,2≠∴a .①当a x x -==3,121时,则231≤-<a ,∴21<≤a ;②当1,321=-=x a x 时,则130<-≤a .32≤<∴a .综上所述,a 的取值范围为31≤≤a 且2≠a .(2)对称轴为直线24a x -=.分三种情况讨论:①当024<-a,即4>a 时,当2=x 时,1-=a y 为最大值.②当2240≤-≤a,即40≤≤a 时,此时y 最大值在0=x 或2=x 处取得.(ⅰ)当242024a a --≥--时,则20≤≤a .此时,当0=x 时,a y -=3为最大值;(ⅱ)当242024aa --<--时,则42≤<a ,此时,当2=x 时,1-=a y 为最大值.③当224>-a,即0<a 时,当0=x 时,a y -=3为最大值.综上所述,当2<a 时,y 的最大值为a -3;当2>a 时,y 的最大值为1-a .(3)对称轴为直线24a x -=.∵40<<a ,∴2240<-<a.∴函数a x a x x f -+-+=3)4()(21在区间⎥⎦⎤⎢⎣⎡-24,0a 上是减函数,在区间⎥⎦⎤⎢⎣⎡-2,24a 上是增函数.∴对任意的)4,0(∈a ,存在]2,0[0∈x 使得t x f ≥|)(|0可化为对任意的)4,0(∈a ,t f ≥|)0(|或t f ≥|)2(|或t af ≥-)24(有一个成立即可.即t a f f f ≥⎭⎬⎫⎩⎨⎧-max 24(||,)2(||,)0(|即可.①当242024a a --≥--时,则20≤≤a ,|)2(||)0(|f f ≥.∴a a a a f f t -=⎭⎬⎫⎩⎨⎧---=⎭⎬⎫⎩⎨⎧-≤3|2)2(||,3||24(||,)0(|max2max ,∴1)3(min =-≤a t .②当242024aa --<--时,则42≤<a ,此时,|)0(||)2(|f f >.1|4)2(||,1||24(),2(|max2-=⎭⎬⎫⎩⎨⎧---=⎭⎬⎫⎩⎨⎧-≤∴a a a a f f t .∴1)1(min =-≤a t .综上所述,t 的取值范围为1≤t .。
自主招生考试数学卷(答案) (1)

自考本科数学卷(满分120分,考试时间120分钟)一、选择题:(本题共20小题,每小题5分,共50分)1.等比数列}{n a 的公比为q ,则“01>a ,且1>q ”是“对于任意正自然数n ,都有n n a a >+1”的()(A )充分非必要条件(B )必要非充分条件(C )充要条件(D )既非充分又非必要条件2.已知函数)(x f 是定义在R 上的奇函数,当0<x 时,x x f )31()(=,那么)9(1--f 的值为()(A )2(B )-2(C )3(D )-33.已知数列}{n a 中,31=a ,62=a ,n n n a a a -=++12,则2003a 等于()(A )6(B )-6(C )3(D )-34、0=b 是直线b kx y +=过原点的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5、方程43)22(log =x 的解为()A .4=x B .2=x C .2=x D .21=x 6.表中数据是我国各种能源消费量占当年能源消费总量的百分率,由表可知,从2011年到2014年,消费量占比增长率最大的能源是()A.天然气B.核能C.水利发电D.再生能源表我国各种能源消费的百分率原油(%)天然气(%)原煤(%)核能(%)水利发电(%)再生能源(%)2011年17.7 4.570.40.7 6.00.72014年17.55.666.01.08.11.87.若角α的终边过点()6,8P -,则角α的终边与圆221x y +=的交点坐标是()A.34,55⎛⎫- ⎪⎝⎭ B.43,55⎛⎫- ⎪⎝⎭ C.34,55⎛⎫- ⎪⎝⎭ D.43,55⎛⎫- ⎪⎝⎭8.关于x,y 的方程y mx n =+和221x y m n +=在同一坐标系中的图象大致是()12349.已知()2nx -的二项展开式有7项,则展开式中二项式系数最大的项的系数是()A.-280B.-160C.160D.56010.若有7名同学排成一排照相,恰好甲、乙两名同学相邻,并且丙、丁两名同学不相邻的概率是()A.421B.121C.114D.2711、已知定义在R 上的函数12)(-=-mx x f (m 为实数)为偶函数,记)3(log 5.0f a =,)5(log 2f b =,)2(m f c =,则c b a ,,的大小关系为()A 、c b a <<B 、b a c <<C 、b c a <<D 、ab c <<12、不等式152x x ---<的解集是()A 、(,4)-∞B 、(,1)-∞C 、(1,4)D 、(1,5)13、函数x x y 2cos sin =是()A 、偶函数B 、奇函数C 、非奇非偶函数C 、既是奇函数,也是偶函数14、若(12)a +1<(12)4-2a ,则实数a 的取值范围是()A 、(1,+∞)B 、(12,+∞)C 、(-∞,1)D 、(-∞,12)15、化简3a a 的结果是()A 、aB 、12aC 、41aD 、83a16、下列计算正确的是()A 、(a3)2=a9B 、log36-log32=1C 、12a -·12a =0D 、log3(-4)2=2log3(-4)17、三个数a =0.62,b =log20.3,c =30.2之间的大小关系是()A 、a<c<bB 、a<b<cC 、b<a<cD 、b<c<a18、8log 15.021+-⎪⎭⎫ ⎝⎛的值为()A 、6B 、72C 、16D 、3719、下列各式成立的是()A 、()52522n m n m +=+B 、(ba)2=12a 12bC 、()()316255-=-D 、31339=20、设2a =5b =m ,且1a +1b=3,则m 等于()A 、310B 、10C 、20D 、100二、填空题:(共20分)1.sin15°.cos15°=___2.在△ABC 中,AB=1,AC=2,A=60°,则S ∆ABC=___3.若1.3.x 成等比数列,则实数x=_______.三、解答题:(本题共3小题,共50分)1.计算:34cos49()15(4log 212π+--+.2.设c b a ,,分别是ABC ∆的三个内角A 、B 、C 所对的边,S 是ABC ∆的面积,已知4,5,a b S ===(1)求角C ;(2)求c 边的长度.3.已知函数)1,0()(≠>+=b b b a x f x的图象过点)4,1(和点)16,2(.(1)求)(x f 的表达式;(2)解不等式23)21()(x x f ->;(3)当]4,3(-∈x 时,求函数6)(log )(22-+=x x f x g 的值域.参考答案:一、选择题1-5题答案:AABCA 6-10题答案:DADBA 11-15题答案:BABAB;16-20题答案:BBCDA.部分选择题解析:6、【答案】D 【解析】根据表1可知,从2011年到2014年,天然气:5.6 4.5100%24.4%4.5-⨯≈,核能:1.00.7100%42.9%0.7-⨯≈,水力发电:8.1 6.0100%35%6.0-⨯=,再生能源:1.80.7100%157.1%0.7-⨯≈,则消费量占比增长率最大的能源是再生能源.7、【答案】A 【解析】因为()6,8P -,10=,设交点为()11,x y ,又因为圆的半径为1,因此有11141085y y =⇒=,1131065x ==,又因为终边在第二象限,所以选A.8、【答案】D 【解析】当221x y m n +=的图象为椭圆时,00m n >>,,则y mx n =+的图象单调递增,且与y 轴的截距大于0,A 、B 均不符;当221x y m n +=的图象为双曲线时,○1当00m n <>,时,双曲线的焦点在y 轴上,y mx n =+的图象单调递减,且与y 轴的截距大于0;○2当00m n ><,时,双曲线的焦点在x 轴上,y mx n =+的图象单调递增,且与y 轴的截距小于0,综上所述,选项D 正确.9、【答案】B 【解析】()2nx - 的二项展开式有7项,6n ∴=,()616C 2kk kk T x -+=-,又展开式中二项式系数最大的项为第4项,则()3363346C 2160T x x -=-=-,则其系数为160-.10、【答案】A 【解析】先利用捆绑法将甲乙进行捆绑并全排列,有22A 种排列方法,将甲乙作为一个整体,除去丙丁将其他人进行全排列,有44A 种排列方法,再利用插空法将丙丁进行插空,有25A 种排列方法;总共有77A 种排列方法,所以概率为24224577A A A 4A 21⋅⋅=.二、填空题1.答案:0.252.答案:解析:由三角形的面积公式,得3.答案:9三、解答题解:原式=)3cos(23(121ππ++-+=3cos 233π--=21233--=12.解:(1)由题知5,4,35===b a SC ab S sin 21=Csin 542135⨯⨯=∴23sin =∴C 又 C 是ABC ∆的内角3π=∴C 或32π=C (2)当3π=C 时,3cos2222πab b a c -+=215422516⨯⨯⨯-+=21=21=∴c当32π=C 时,22222cos3c a b ab π=+-215422516⨯⨯⨯++=61=61=∴c xx f 4)(=∴(2)23)21(4x x-> 32222->∴xx 322->∴x x 0322<--∴x x 31<<-∴x ∴不等式的解集为)3,1(-(3)64log )(22-+=x x g x 62log 222-+=x x 622-+=x x 7)1(2-+=x 1(3,4]-∈- 7)(min -=∴x g 当4=x 时,max ()18g x =∴值域为]18,7[-。
高校自招数学试题及答案

高校自招数学试题及答案一、选择题(每题5分,共20分)1. 若函数f(x) = ax^2 + bx + c(a ≠ 0)的图像经过点(1, 2)和(2,3),则下列哪个选项是正确的?A. a + b + c = 2B. 4a + 2b + c = 3C. a + 2b + c = 3D. 4a + b + c = 5答案:C2. 已知数列{an}是等差数列,且a1 + a2 + a3 = 12,a2 + a3 + a4 = 18,则a1 + a5的值是多少?A. 18B. 20C. 24D. 26答案:B3. 若复数z满足|z - 1| = |z + i|,则z对应的点在复平面上位于哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:B4. 已知函数f(x) = ln(x) + 1/x,若f(x)在区间(0, +∞)上单调递增,则实数k的取值范围是?A. k > 0B. k ≥ 1C. k ≤ -1D. k ≤ 0答案:B二、填空题(每题5分,共20分)5. 若一个圆的直径为10,则该圆的面积为_______。
答案:25π6. 已知向量a = (3, -1),b = (2, 4),则向量a与向量b的数量积为_______。
答案:57. 若函数f(x) = x^3 - 3x^2 + 2在区间[1, 2]上单调递增,则实数k的取值范围是_______。
答案:k ≤ -18. 已知等比数列{an}的前三项分别为1,2,4,则该数列的通项公式为an = _______。
答案:2^(n-1)三、解答题(每题15分,共40分)9. 已知函数f(x) = x^2 - 4x + 3,求f(x)的单调区间,并说明理由。
答案:函数f(x)的单调递增区间为[2, +∞),单调递减区间为(-∞, 2)。
理由是f(x)的导数为f'(x) = 2x - 4,令f'(x) > 0得x > 2,令f'(x) < 0得x < 2。
自主招生考试数学试卷及参考答案

自主招生考试数学试卷及参考答案(总9页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--22第2自主招生考试 数学试题卷亲爱的同学:欢迎你参加考试!考试中请注意以下几点:1.全卷共三大题,满分120分,考试时间为100分钟。
2.全卷由试题卷和答题卷两部分组成。
试题的答案必须做在答题卷的相应位置上。
做在试题卷上无效。
3.请用钢笔或圆珠笔在答题卷密封区上填写学校、姓名、试场号和准考证号,请勿遗漏。
4.答题过程不准使用计算器。
祝你成功!一、选择题(本题共6小题,每小题5分,共30分.在每小题的四个选项中,只有一个符合题目要求)1.如果一直角三角形的三边为a 、b 、c ,∠B=90°,那么关于x 的方程a(x 2-1)-2cx+b(x 2+1)=0的根的情况为A 有两个相等的实数根B 有两个不相等的实数根C 没有实数根D 无法确定根的情况2.如图,P P P 123、、是双曲线上的三点,过这三点分别作y 轴的垂线,得三个三角形P A O P A O P A O 112233、、,设它们的面积分别是S S S 123、、,则 A S S S 123<< B S S S 213<< C S S S 132<<D S S S 123==3.如图,以BC 为直径,在半径为2圆心角为900的扇形内作半圆,交弦AB 于点D ,连接CD ,则阴影部分的面积是33第5A π-1B π-2C 121-πD 221-π4.由325x y a x y a x y a m-=+⎧⎪+=⎪⎨>⎪⎪>⎩得a>-3,则m 的取值范围是A m>-3B m ≥-3C m ≤-3D m<-3 5.如图,矩形ABCG (AB <BC )与矩形CDEF 全等,点B 、C 、D 在同一条直线上,APE ∠的顶点P 在线段BD 上移动,使APE ∠为直角的点P 的个数是 A 0 B 1 C 2 D 36.已知抛物线y=ax 2+2ax+4(0<a<3),A (x 1,y 1)B(x 2,y 2)是抛物线上两点,若x 1<x 2,且x 1+x 2=1-a,则A y 1< y 2B y 1= y 2C y 1> y 2D y 1与y 2的大小不能确定二、填空题(本题共6小题,每小题5分,共30分.把答案填写在题中横线上)7. 二次函数y =ax 2+(a -b )x —b 的图象如图所示,44那么化简222||a ab b b -+-的结果是______▲________.8. 如图所示,在正方形 ABCD 中,AO ⊥BD 、OE 、FG 、HI 都垂直于 AD ,EF 、GH 、IJ 都垂直于AO ,若已知 S ΔA JI =1, 则S 正方形ABCD = ▲9.将一个棱长为8、各个面上均涂有颜色的正方体,锯成64个同样大小的小正方体,其中所有恰有2面涂有颜色的小正方体表面积之和为 ▲ 10.用黑白两种颜色正方形的纸片按黑色纸片数逐渐加l 的规律拼成一列图案:(1)第4个图案中有白色纸片 ▲ 张 (2)第n 个图案中有白色纸片 ▲ 张(3)从第1个图案到第100个图案,总共有白色纸片 ▲ 张第10题 第7题第8题5511.如图所示,线段AB 与CD 都是⊙O 中的弦,其中108,,36,O O AB AB a CD CD b ====,则⊙O 的半径R= ▲12.阅读下列证明过程: 已知,如图四边形ABCD 中,AB =DC ,AC =BD ,AD ≠BC ,求证:四边形ABCD 是等腰梯形.读后完成下列各小题.(1)证明过程是否有错误?如有,错在第几步上,答: ▲ . (2)作DE ∥AB 的目的是: ▲ .(3) 判断四边形ABED 为平行四边形的依据是: ▲ . (4)判断四边形ABCD 是等腰梯形的依据是 ▲ .(5)若题设中没有AD ≠BC ,那么四边形ABCD 一定是等腰梯形吗为什么 答 ▲ .自主招生考试第11题第12题66数学标准答案一、选择题(本题共6小题,每小题5分,共30分.在每小题的四个选项中,只有一个符合题目要求)二、填空题(本题共6小题,每小题5分,共30分.把答案填写在题中横线上)7. ______-1__________ 8. 256 9. 57610.(1) 13 (2) 3n+1 (3) 15250 11. a b12.(1)没有错误 (2)为了证明AD ∥BC(3) 一组对边平行且相等的四边形是平行四边形(4)梯形及等腰梯形的定义 (5) 不一定,因为当AD =BC 时,四边形ABCD 是矩形 三、解答题(本题共5小题,共60分.解答应写出必要的计算过程、推演步骤或文字说明)13.(本小题10分)某公园门票每张10元,只供一次使用,考虑到人们的不同需求,也为了吸引更多游客,该公园除保留原有的售票方法外,还推出一种“购个人年票”的售票方法(个人年票从购买之日起,可供持票者使用一年)。
高考单招试卷数学试卷答案

一、选择题(本大题共10小题,每小题5分,共50分)1. 若函数f(x) = ax^2 + bx + c的图象开口向上,且顶点坐标为(1,-2),则a的取值范围是()A. a > 0B. a < 0C. a = 0D. 无法确定答案:A解析:函数f(x) = ax^2 + bx + c的图象开口向上,说明a > 0。
顶点坐标为(1,-2),代入函数得f(1) = a1^2 + b1 + c = -2,即a + b + c = -2。
由于a > 0,故选A。
2. 下列命题中正确的是()A. 若a > b,则a^2 > b^2B. 若a > b,则a^3 > b^3C. 若a > b,则a^4 > b^4 D. 若a > b,则a^5 > b^5答案:B解析:对于选项A,当a = -1,b = -2时,a > b但a^2 < b^2,故A错误。
对于选项B,由于a > b,则a^3 > a^2 b > b^3,故B正确。
对于选项C,当a = -1,b = -2时,a > b但a^4 < b^4,故C错误。
对于选项D,当a = -1,b = -2时,a > b但a^5 < b^5,故D错误。
3. 已知等差数列{an}的前n项和为Sn,若a1 = 3,公差d = 2,则S10 = ()A. 90B. 100C. 110D. 120答案:A解析:等差数列的前n项和公式为Sn = n/2 (a1 + an),其中an = a1 + (n-1)d。
代入已知条件得S10 = 10/2 (3 + 3 + 92) = 90。
4. 下列函数中,在定义域内单调递增的是()A. f(x) = x^2B. f(x) = 2^xC. f(x) = log2xD. f(x) = √x答案:B解析:函数f(x) = x^2在x < 0时单调递减,在x > 0时单调递增,故A错误。
北大自主招生数学试题

北大自主招生数学试题一、下列哪个数列不是等差数列?A. 1, 3, 5, 7, ...B. 2, 4, 8, 16, ...C. 10, 8, 6, 4, ...D. -1, 0, 1, 2, ...(答案:B)二、若复数z满足(1+i)z=2i,则z等于?A. 1-iB. 1+iC. -1+i(答案)D. -1-i三、设函数f(x) = x3 - 3x2 + 2,则f(x)的极小值点为?A. x = 0B. x = 1C. x = 2(答案)D. x = 3四、在三角形ABC中,若sinA:sinB = 3:4:5,则cosC的值为?A. 1/5B. -1/5(答案)C. 3/5D. 4/5五、已知向量a = (1, 2),b = (2, 1),则向量a与b的夹角θ的余弦值为?A. √5/5B. 2√5/5(答案)C. 1/√5D. -1/√5六、设集合A = {x | x2 - 5x + 6 = 0},B = {x | x2 - ax + a - 2 = 0},若B是A的子集,则a的取值范围是?A. a = 2或a = 3或a = 5B. a = 3或a = 5(答案)C. a = 2或a = 5D. a = 2或a = 3七、已知圆C的方程为x2 + y2 - 2x - 5 = 0,直线l的方程为2x - y - 1 = 0,则圆心C到直线l的距离为?A. √5B. 2√5/5C. √5/5(答案)D. 3√5/5八、若实数x, y满足约束条件x + y ≤ 2, x - y ≤ 1, x ≥ 0,则z = 2x + y的最大值为?A. 2B. 3C. 4D. 5(答案)九、设函数f(x) = ex - e(-x),则不等式f(x + 2) < f(1 - x)的解集为?A. (-∞, 3/2)B. (-3/2, +∞)(答案)C. (-∞, -1/2)D. (1/2, +∞)十、已知矩阵A = [1 2; 3 4],向量β = [5; 6],若向量α满足Aα = β,则α为?A. [-1; 2]B. [2; -1](答案)C. [1; 1]D. [-2; 1]。
高三自主招生试卷数学答案

一、选择题(每题5分,共25分)1. 下列各数中,属于有理数的是()A. √2B. πC. 0.1010010001…D. 1/3答案:D解析:有理数是可以表示为两个整数之比的数,即形如a/b(a和b为整数,b不为0)的数。
选项D可以表示为1/3,因此是有理数。
2. 已知函数f(x) = 2x - 3,若f(x) + f(-x) = 0,则x的值为()A. 1B. -1C. 0D. 2答案:B解析:根据题意,f(x) + f(-x) = 2x - 3 + 2(-x) - 3 = 0,化简得4x - 6 = 0,解得x = 1.5,即x = -1。
3. 若等差数列{an}的首项为a1,公差为d,且a1 + a2 + a3 = 12,a1 + a4 +a5 = 30,则该数列的通项公式为()A. an = 3n - 1B. an = 4n - 3C. an = 6n - 5D. an = 5n - 4答案:B解析:由等差数列的性质,a2 = a1 + d,a3 = a1 + 2d,代入a1 + a2 + a3 =12得3a1 + 3d = 12,化简得a1 + d = 4。
同理,a4 = a1 + 3d,a5 = a1 + 4d,代入a1 + a4 + a5 = 30得3a1 + 12d = 30,化简得a1 + 4d = 10。
解得d = 3,a1 = 1。
因此,通项公式为an = 4n - 3。
4. 已知复数z满足|z - 1| = |z + 1|,则z在复平面上的轨迹为()A. 直线B. 圆C. 双曲线D. 抛物线答案:A解析:由复数的模长性质,|z - 1| = |z + 1|表示复数z到点1和点-1的距离相等,即z位于直线y = 0上。
5. 下列各函数中,为奇函数的是()A. y = x^2B. y = x^3C. y = x^4D. y = |x|答案:B解析:奇函数满足f(-x) = -f(x)。
高中自招试题数学答案及解析

高中自招试题数学答案及解析试题一:已知函数\( f(x) = 3x^2 - 2x + 1 \),求其导数\( f'(x) \)。
答案:首先,根据导数的定义,我们对函数\( f(x) \)进行求导。
对于\( f(x) = 3x^2 - 2x + 1 \),其导数\( f'(x) \)为:\[ f'(x) = 6x - 2 \]解析:求导的过程涉及到幂函数的导数规则,即\( (x^n)' = n \cdot x^{n-1} \)。
对于常数项1,其导数为0。
将各项的导数相加,得到最终的导数表达式。
试题二:设集合A={1, 2, 3},集合B={2, 3, 4},求集合A和集合B 的交集A∩B。
答案:集合A和集合B的交集A∩B为{2, 3}。
解析:交集是指两个集合中共有的元素。
在这个例子中,我们可以看到元素2和3同时出现在集合A和集合B中,因此它们构成了这两个集合的交集。
试题三:若\( \sin(2x) = 2\sin(x) \),求\( x \)的值。
答案:根据二倍角公式,我们知道\( \sin(2x) = 2\sin(x)\cos(x) \)。
将题目中的等式代入,得到:\[ 2\sin(x)\cos(x) = 2\sin(x) \]由于\( \sin(x) \neq 0 \),我们可以除以\( 2\sin(x) \)得到:\[ \cos(x) = 1 \]这意味着\( x \)的值是\( 2k\pi \),其中\( k \)是整数。
解析:这个问题的关键在于识别并应用二倍角公式。
通过将等式转换为已知的三角恒等式,我们可以简化问题并找到\( x \)的解。
试题四:解不等式\( |x - 3| < 2 \)。
答案:不等式\( |x - 3| < 2 \)可以分解为两个不等式:\[ -2 < x - 3 < 2 \]解得:\[ 1 < x < 5 \]解析:绝对值不等式可以通过将其分解为两个不等式来解决。
高中自主招生考试数学试题(含答案详解)
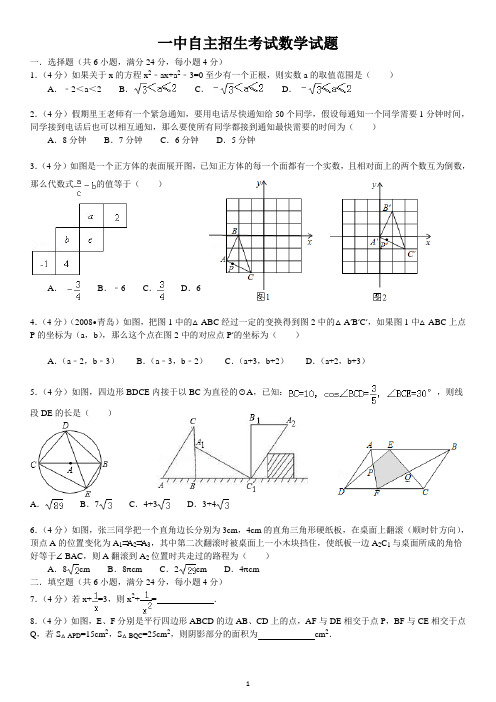
一中自主招生考试数学试题一.选择题(共6小题,满分24分,每小题4分)1.(4分)如果关于x的方程x2﹣ax+a2﹣3=0至少有一个正根,则实数a的取值范围是()A.﹣2<a<2B.C.D.2.(4分)假期里王老师有一个紧急通知,要用电话尽快通知给50个同学,假设每通知一个同学需要1分钟时间,同学接到电话后也可以相互通知,那么要使所有同学都接到通知最快需要的时间为()A.8分钟B.7分钟C.6分钟D.5分钟3.(4分)如图是一个正方体的表面展开图,已知正方体的每一个面都有一个实数,且相对面上的两个数互为倒数,那么代数式的值等于()A.B.﹣6C.D.64.(4分)(2008•青岛)如图,把图1中的△ABC经过一定的变换得到图2中的△A′B′C′,如果图1中△ABC上点P的坐标为(a,b),那么这个点在图2中的对应点P′的坐标为()A.(a﹣2,b﹣3)B.(a﹣3,b﹣2)C.(a+3,b+2)D.(a+2,b+3)5.(4分)如图,四边形BDCE内接于以BC为直径的⊙A,已知:,则线段DE的长是()A.B.7C.4+3D.3+46.(4分)如图,张三同学把一个直角边长分别为3cm,4cm的直角三角形硬纸板,在桌面上翻滚(顺时针方向),顶点A的位置变化为A1⇒A2⇒A3,其中第二次翻滚时被桌面上一小木块挡住,使纸板一边A2C1与桌面所成的角恰好等于∠BAC,则A翻滚到A2位置时共走过的路程为()A.8cm B.8πcm C.2cm D.4πcm二.填空题(共6小题,满分24分,每小题4分)7.(4分)若x+=3,则x2+=_________.8.(4分)如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=15cm2,S△BQC=25cm2,则阴影部分的面积为_________cm2.9.(4分)如图,正方形ABCD的边长为4cm,正方形AEFG的边长为1cm.如果正方形AEFG绕点A旋转,那么C、F两点之间的最小距离为_________cm.10.(4分)对于正数x,规定f(x)=,计算f()+f()+f()+…+f()+f()+f(1)+f(2)+f(3)+…+f(98)+f(99)+f(100)=_________.11.(4分)甲,乙,丙3人用擂台赛形式进行训练,每局2人进行单打比赛,另1人当裁判,每﹣局的输方去当下﹣局的裁判,而由原来的裁判向胜者挑战.半天训练结束时发现甲共打了12局,乙共打了21局,而丙共当裁判8局.那么,整个比赛的第10局的输方一定是_________.12.(4分)(2002•广州)如图所示,在正方形ABCD中,AO⊥BD,OE,FG,HI都垂直于AD,EF,GH,IJ都垂直于AO,若已知S△AIJ=1,则正方形ABCD的面积为_________.三.解答题(共6小题,满分52分)13.(6分)把几个数用大括号围起来,中间用逗号断开,如:{1,2,3},{2,7,8,19},我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当实数a是集合的元素时,实数8﹣a也必是这个集合的元素,这样的集合我们称为好的集合.(1)请你判断集合{1,2},{1,4,7}是不是好的集合;(2)请你写出满足条件的两个好的集合的例子.14.(8分)(2007•丽水)在课外活动时间,小王、小丽、小华做“互相踢踺子”游戏,踺子从一人传到另一人就记为踢一次.(1)若从小丽开始,经过两次踢踺后,踺子踢到小华处的概率是多少?(用树状图或列表法说明)(2)若经过三次踢踺后,踺子踢到小王处的可能性最小,应确定从谁开始踢,并说明理由.15.(8分)某中学为了进一步改善办学条件,决定计划拆除一部分旧校舍,建造新校舍.拆除旧校舍每平方米需80元,建造新校舍每平方米需要800元,计划在年内拆除旧校舍与建造新校舍共9000平方米,在实施中为扩大绿化面积,新建校舍只完成了计划的90%而拆除旧校舍则超过了计划的10%,结果恰好完成了原计划的拆、建总面积.(1)求原计划拆、建面积各是多少平方米?(2)若绿化1平方米需要200元,那么把在实际的拆、建工程中节余的资金全部用来绿化,可绿化多少平方米?16.(10分)如图,⊙O的直径EF=cm,Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=cm.E、F、A、B 四点共线.Rt△ABC以1cm/s的速度沿EF所在直线由右向左匀速运动,设运动时间为t(s),当t=0s时,点B与点F重合.(1)当t为何值时,Rt△ABC的直角边与⊙O相切?(2)当Rt△ABC的直角边与⊙O相切时,请求出重叠部分的面积(精确到0.01).17.(10分)(2008•广东)(1)如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;(2)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.18.(10分)(2008•益阳)我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,﹣3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.(1)请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;(2)你能求出经过点C的“蛋圆”切线的解析式吗?试试看;(3)开动脑筋想一想,相信你能求出经过点D的“蛋圆”切线的解析式.答案与评分标准一.C ,C ,A ,C ,D ,D甲,256,二.7,40,3,,三.解:(1)集合{1,2}不是好的集合,这是因为8﹣1=7,而7不是{1,2}中的数,所以{1,2}不是好的集合,{1,4,7}是好的集合,这是因为8﹣1=7,7是{1,4,7}中的数,8﹣4=4,4也是{1,4,7}中的数,8﹣7=1,1又是{1,4,7}中的数.所以{1,4,7}是好的集合;(2)答案不唯一.集合{4}、{3,4,5}、{2,6}、{1,2,4,6,7}、{0,8}等都是好的集合.解:(1)踺子踢到小华处的概率是.树状图如下:列表法如下:小丽小王小华小王(小丽,小王)(小王,小华)小华(小华,小丽)(小华,小王)(2)小王.树状图如下:理由:若从小王开始踢,三次踢踺后,踺子踢到小王处的概率是,踢到其它两人处的概率都是,因此,踺子踢到小王处的可能性是最小.解:(1)由题意可设拆旧舍x平方米,建新舍y平方米,则答:原计划拆建各4500平方米.(2)计划资金y1=4500×80+4500×800=3960000元实用资金y2=1.1×4500×80+0.9×4500×800=4950×80+4050×800=396000+3240000=3636000∴节余资金:3960000﹣3636000=324000∴可建绿化面积=平方米答:可绿化面积1620平方米.解:(1)∵∠BAC=30°,AB=,∴BC=又∵⊙O的直径EF=,即半径为,∠ACB=90°,∴当点B运动到圆心O时,AC边与⊙O相切.(如图1所示)(1分)此时运动距离为FO=,∴t=s.(2分)当BC边与⊙O相切时(如图2所示),设切点为G.连接OG,则OG⊥BC.(3分)由已知,∠BOG=∠BAC=30°,OG=,∴BO=2.(4分)又FO=,∴BF=.(此步亦可利用相似求解,请参照给分)∴此时s.(5分)由上所述,当秒时,Rt△ABC的直角边与⊙O相切.(6分)(2)由图1,此时⊙O与Rt△ABC的重叠部分为扇形COF.(7分)由已知,∠COF=60°,∴.(8分)由图2,设AC与⊙O交于点M,此时⊙O与Rt△ABC的重叠部分为扇形OMGE加上△OAM.(9分)过点M作MN⊥OG于N,则MN=GC.由(1)可知BG=1则MN=GC=.(10分)∴,∴∠MON=25°,即∠MOE=55°.(11分)∴.(12分)又∵OM=,∴点M到AB的距离h=OM•sin∠MOE≈1.419,(13分)∴S△AOM =•OA•h≈1.229cm2此时⊙O与Rt△ABC的重叠部分的面积为S扇形OMEF+S△AOM≈2.67cm2.(14分)解:(1)如图3,∵△DOC和△ABO都是等边三角形,且点O是线段AD的中点,∴OD=OC=OB=OA,∠1=∠2=60°,∴∠4=∠5.又∵∠4+∠5=∠2=60°,∴∠4=30°.同理∠6=30°.∵∠AEB=∠4+∠6,∴∠AEB=60°.(2)如图4,∵△DOC和△ABO都是等边三角形,∴OD=OC,OB=OA,∠1=∠2=60°.又∵OD=OA,∴OD=OB,OA=OC,∴∠4=∠5,∠6=∠7.∵∠DOB=∠1+∠3,∠AOC=∠2+∠3,∴∠DOB=∠AOC.∵∠4+∠5+∠DOB=180°,∠6+∠7+∠AOC=180°,∴2∠5=2∠6,∴∠5=∠6.又∵∠AEB=∠8﹣∠5,∠8=∠2+∠6,∴∠AEB=∠2+∠6﹣∠5=∠2+∠5﹣∠5=∠2,∴∠AEB=60°.解:(1)根据题意可得:A(﹣1,0),B(3,0);则设抛物线的解析式为y=a(x+1)(x﹣3)(a≠0),又∵点D(0,﹣3)在抛物线上,∴a(0+1)(0﹣3)=﹣3,解之得:a=1∴y=x2﹣2x﹣3(3分)自变量范围:﹣1≤x≤3(4分)(2)设经过点C“蛋圆”的切线CE交x轴于点E,连接CM,在Rt△MOC中,∵OM=1,CM=2,∴∠CMO=60°,OC=在Rt△MCE中,∵MC=2,∠CMO=60°,∴ME=4∴点C、E的坐标分别为(0,),(﹣3,0)(6分)∴切线CE 的解析式为(8分)(3)设过点D(0,﹣3),“蛋圆”切线的解析式为:y=kx ﹣3(k≠0)(9分)由题意可知方程组只有一组解即kx﹣3=x2﹣2x﹣3有两个相等实根,∴k=﹣2(11分)∴过点D“蛋圆”切线的解析式y=﹣2x﹣3.(12分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
卓越联盟自主招生数学试题(1)向量a ,b 均为非零向量,(a -2b )⊥a ,(b -2a )⊥b ,则a ,b 的夹角为 (A )6π(B )3π(C )23π (D )56π (2)已知sin2(α+γ)=n sin2β,则tan()tan()αβγαβγ++-+22等于(A )11n n -+(B )1n n +(C )1n n - (D )11n n +- (3)在正方体ABCD —A 1B 1C 1D 1中,E 为棱AA 1的中点,F 是棱A 1B 1上的点,且A 1F :FB 1=1:3,则异面直线EF 与BC 1所成角的正弦值为 (A )153(B )155(C )53(D )55(4)i 为虚数单位,设复数z 满足|z |=1,则2221z z z i-+-+的最大值为(A )2-1(B )2-2(C )2+1 (D )2+2(5)已知抛物线的顶点在原点,焦点在x 轴上,△ABC 三个顶点都在抛物线上,且△ABC 的重心为抛物线的焦点,若BC 边所在直线的方程为4x +y -20=0,则抛物线方程为(A )y 2=16x(B )y 2=8x(C )y 2=-16x (D )y 2=-8x(6)在三棱锥ABC —A 1B 1C 1中,底面边长与侧棱长均等于2,且E 为CC 1的中点,则点C 1到平面AB 1E 的距离为(A )3(B )2(C )32(D )22(7)若关于x 的方程||4x x +=kx 2有四个不同的实数解,则k 的取值范围为( ) (A )(0,1)(B )(14,1)(C )(14,+∞) (D )(1,+∞)(8)如图,△ABC 内接于⊙O ,过BC 中点D 作平行于AC 的直线l ,l 交AB 于E ,交⊙O 于G 、F ,交⊙O 在A 点的切线于P ,若PE =3,ED =2,EF =3,则PA 的长为(A )5(B )6 (C )7(D )22(9)数列{a n }共有11项,a 1=0,a 11=4,且|a k +1-a k |=1,k =1,2,…,10.满足这种条件的不同数列的个数为( ) (A )100(B )120(C )140 (D )160(10)设σ是坐标平面按顺时针方向绕原点做角度为27π的旋转,τ表示坐标平面关于y 轴的镜面反射.用τσ表示变换的复合,先做τ,再做σ,用σk表示连续k 次的变换,则στσ2τσ3τσ4是( ) (A )σ4(B )σ5(C )σ2τ(D )τσ2(11)设数列{a n }满足a 1=a ,a 2=b ,2a n +2=a n +1+a n . (Ⅰ)设b n =a n +1-a n ,证明:若a ≠b ,则{b n }是等比数列; (Ⅱ)若lim n →∞(a 1+a 2+…+a n )=4,求a ,b 的值.(12)在△ABC 中,AB =2AC ,AD 是A 的角平分线,且AD =kAC . (Ⅰ)求k 的取值范围;(Ⅱ)若S △ABC =1,问k 为何值时,BC 最短?(13)已知椭圆的两个焦点为F 1(-1,0),F 2(1,0),且椭圆与直线y =x相切. (Ⅰ)求椭圆的方程;(Ⅱ)过F 1作两条互相垂直的直线l 1,l 2,与椭圆分别交于P ,Q 及M ,N ,求四边形PMQN 面积的最大值与最小值.(14)一袋中有a 个白球和b 个黑球.从中任取一球,如果取出白球,则把它放回袋中;如果取出黑球,则该黑球不再放回,另补一个白球放到袋中.在重复n 次这样的操作后,记袋中白球的个数为X n . (Ⅰ)求EX 1;(Ⅱ)设P (X n =a +k )=p k ,求P (X n +1=a +k ),k =0,1,…,b ; (Ⅲ)证明:EX n +1=(1-1a b+)EX n +1. (15)(Ⅰ)设f (x )=x ln x ,求f ′(x );(Ⅱ)设0<a <b ,求常数C ,使得1|ln |bax C dx b a --⎰取得最小值;(Ⅲ)记(Ⅱ)中的最小值为m a ,b ,证明:m a ,b <ln2.一.选择题1. 2. 3. 4. 5. 6.7.8.9.10.B D B C A D C B B D二.解答题11.【解】(1)证:由1221,,2n n n a a a b a a a ++===+,得2112()().n n n n a a a a +++-=--令1,nn n b a a +=-则112n n b b +=-,所以{}n b 是以b a -为首项,以12-为公比的等比数列;(2)由(1) 可知1*11()()()2n n n n b a a b a n N -+=-=--∈,所以由累加法得1111()2(),11()2nn a a b a +---=---即121()[1()],32n n a a b a +=+---也所以有121()[1()](2),132n na ab a n n -=+---≥=时,1a a =也适合该式;所以1*21()[1()]()32n n a a b a n N -=+---∈1211()224412()[]()()()()13399212nn n a a a na b a n na b a n b a b a --+++=+--=+---+--+ 由于12lim()4,n n a a a →∞+++=所以24()0,()4,39a b a b a +-=--=解得6,3a b ==-.12.【解】(1)过B 作直线BE AC ,交AD 延长线于E ,如图右.所以,2,BD AB CD AC==也所以有2DE BE BDAD AC DC===,即2,3.BE AC AE BD == 在ABE ∆中,有2222cos .AE AB BE AB BE EBA =+-⋅∠即222(3)(2)(2)2(22)cos AD AC AC AC AC A =++⋅⋅所以,2229()88cos ,kAC AC AC A =+⋅即2816(1cos )(0,)99k A =+∈所以403k<<. (2)因为21sin sin 12ABC S AB AC A AC A ∆=⋅⋅==在ABC ∆中,有2222254cos 2cos 54cos sin ABC AB AC AB AC A AC AC A A-=+-⋅=-=记54cos sin A y A-=,则sin 4cos )5y A A A ϕ+=+=当sin()1A ϕ+=时,53y ⇒=此时y 取最小值,此时3cos 5A =.故当15k=时,BC 取最小值13.【解】设椭圆方程为22221(0)x y a b a b+=>>,因为它与直线y x =只有一个公共点,所以方程组22221,x y a b y x⎧+=⎪⎨⎪=⎩只有一解,整理得2222222()30a b x x a a b +-+-=.所以2222222(23)4((3)0,a a b a a b =--+-=得223a b +=.又因为焦点为12(1,0),(1,0)F F -,所以221,ab -=联立上式解得222,1a b ==所以椭圆方程为2212x y +=.(2)若PQ 斜率不存在(或为0)时,则||||22PMQN PQ MN S ⋅===四边形.若PQ 斜率存在时,设为(0)k k ≠,则MN 为1k-.所以直线PQ 方程为y kx k =+.设PQ 与椭圆交点坐标为1122(,),(,)P x y Q x y联立方程221,2.x y y kx k ⎧+=⎪⎨⎪=+⎩化简得2222(21)4220k x k x k +++-=.则22121222422,2121k k x x x x k k --+==++所以12|||PQ x x =-==同理可得||MN =所以222422242421||||(1)21124444()2(2)(21)2522252PMQNkPQ MN k k k S k k k k k k ⋅+++====-++++++四边形 242221114()4()12410424410k k k k k =-=-++++因为22144101018kk ++≥=(当且仅当21k =时取等号) 所以,2211(0,],1184410k k ∈++也所以2211164()[,2]1294410k k-∈++所以综上所述,PMQN S 四边形的面积的最小值为169,最大值为2.14.【解】(1)1n =时,袋中的白球的个数可能为a 个(即取出的是白球),概率为aa b+;也可能为1a +个(即取出的是黑球),概率为ba b+,故21(1)a b a ab b EX a a a b a b a b ++=⋅++⋅=+++. (2)首先,10(0);n aP X a P a b+=+=⋅+1k ≥时,第1n +次取出来有a k +个白球的可能性有两种; 第n 次袋中有a k +个白球,显然每次取出球后,球的总数保持不变,即a b +个白球(故此时黑球有b k-个),第1n +次取出来的也是白球,这种情况发生的概率为;ka kP a b+⋅+ 第n 次袋中有1a k +-个白球,第1n +次取出来的是黑球,由于每次球的总数为a b +个,故此时黑球的个数为1b k -+.这种情况发生的概率为11(1)k b k P k a b--+⋅≥+.故111()(1).n k k a k b k P X a k P P k a b a b+-+-+=+=⋅+⋅≥++ (3)第1n +次白球的个数的数学期望分为两类:第n 次白球个数的数学期望,即n EX .由于白球和黑球的总个数为a b +,第1n +次取出来的是白球,这种情况发生的概率是n EX a b +;第1n +次取出来的是黑球,这种情况发生的概率是na b EX a b+-+,此时白球的个数是 1.nEX +故21()(1)(1)(1)n n n nn n n n EX a b EX EX EX EX EX EX EX a b a b a b a b++-=+⋅+=+-+++++22()())11(1)1n n n n n EX EX EX EX EX a b a b a b a b=+-+-=-+++++15.(1)1()ln ln 1f x x x x x'=+⋅=+;(2)若ln ,c a ≤则|ln |ln ,x c x c -=-显然,当ln ,ln c a x c =-取最小; 若ln ,c b ≤则|ln |ln ,x c c x -=-当ln ,ln c b c x =-取最小.故ln ln .a c b ≤≤11|ln |[(ln )(ln )]c c b e b a ae x c dx x c dx c x dx b a b a -=-+---⎰⎰⎰1{[(ln 1)(1)][(1)(ln 1)]}c c e b ae x c dx c x dx b a =+-+++-+-⎰⎰由(1)知[(ln 1)(1)]ln |(1)()cce e ca ax c dx x x c e a +-+=-+-⎰[(1)(ln 1)](1)()ln |ccbc b e ec x dx c e a x x +-+=+--⎰所以,11|ln |(ln ln 2)()b c a x c dx a a b b e a b ac bc b a b a-=---+++-*--⎰记()2()ln ln ,cg c e a b c a a b b a b =-++--++则令()20cg c e a b '=-++=,得2a bc +=即2a b c +=时,1|ln |ba x C dxb a --⎰取最小值. (3)将2a bc +=代入()*式右边,1,[ln ln ()ln ]ln 22a bMa b a a b b a b b a +=--++<-等价于()ln ln ln ()ln 2()ln()ln ln 2ln 22a ba b a a b b b a a b a b a a b b b ++--<-⇔+⋅+<++ln()ln ln()ln 2ln 2ln(1)ln(1)2ln 2.b aa ab a a b a b b b b a b b a b⇔+-++-<⇔+++<由于0,12a a b b <<+<时,ln(1)ln 2.a b b b +<所以下面只须证明ln(1)ln 2ba b a+<即可.又ln(1)ln 2ln(1)ln 2.b a b a b a b a +<⇔+<令(0,1)at b =∈, 则11ln(1)ln(1)ln(1)t a b t b a t t +=+=+,注意到函数1ln(1)tt+是单调递增的,且 1.t < 所以111ln(1)ln(1)ln 21t t +<+=.得证.2012年卓越联盟自主招生数学试题2013年卓越联盟自主招生数学试题一、选择题:(本大题共4小题,每小题5分.在每小题给出的4个结论中,只有一项是符合题目要求的.) (1)已知()f x 是定义在实数集上的偶函数,且在(0,)+∞上递增,则(A )0.72(2)(log 5)(3)f f f <-<- (B) 0.72(3)(2)(log 5)f f f -<<- (C) 0.72(3)(log 5)(2)f f f -<-< (D) 0.72(2)(3)(log 5)f f f <-<-(2)已知函数()sin()(0,0)2f x x πωϕωϕ=+><<的图象经过点(,0)6B π-,且()f x 的相邻两个零点的距离为2π,为得到()y f x =的图象,可将sin y x =图象上所有点(A )先向右平移3π个单位长度,再将所得点的横坐标变为原来的12倍,纵坐标不变 (B) 先向左平移3π个单位长度,再将所得点的横坐标变为原来的12倍,纵坐标不变(C) 先向左平移3π个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变(D) 先向右平移3π个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变(3)如图,在,,,,A B C D E 五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为 (A )21 (B)24 (C)30 ( D)48 (4)设函数()f x 在R 上存在导数()f x ',对任意的x R ∈,有2()()f x f x x -+=,且在(0,)+∞上()f x x '>.若(2)()22f a f a a --≥-,则实数a 的取值范围为(A )[1,)+∞ (B) (,1]-∞ (C) (,2]-∞ (D) [2,)+∞ 二、填空题:(本大题共4小题,每小题6分,共24分)(5)已知抛物线22(0)y px p =>的焦点是双曲线2218x y p-=的一个焦点,则双曲线的渐 近线方程为 .(6)设点O 在ABC ∆的内部,点D ,E 分别为边AC ,BC 的中点,且21OD DE +=, 则23OA OB OC ++= .(7)设曲线22y x x -与x 轴所围成的区域为D ,向区域D 内随机投一点,则该点落 入区域22{(,)2}x y D x y ∈+<内的概率为 . (8)如图,AE 是圆O 的切线,A 是切点,AD 与OE 垂直,垂足是D ,割线EC 交圆O 于,B C ,且,ODC DBC αβ∠=∠=,则OEC ∠=(用,αβ表示)三、解答题(本大题共4小题,共56分.解答应写出文字说明,证明过程或演算步骤)(9)(本小题满分13分)在ABC ∆中,三个内角A 、B 、C 所对边分别为a 、b 、c .已知()(sin sin )()sin a c A C a b B -+=-.(1)求角C 的大小; (2)求sin sin A B ⋅的最大值. (10)(本题满分13分)设椭圆2221(2)4x y a a +=>的离心率为,斜率为k 的直线l 过点(0,1)E 且与椭圆交于,C D 两点.(1)求椭圆方程;(2)若直线l 与x 轴相交于点G ,且GC DE =,求k 的值; (3)设A 为椭圆的下顶点,AC k 、AD k 分别为直线AC 、AD 的斜率,证明对任意的k 恒 有2AC AD k k ⋅=-. (11)(本题满分15分)设0x >,(1)证明:2112xe x x >++; (2)若2112xye x x e =++,证明:0y x <<. (12)(本题满分15分)已知数列{}n a 中,13a =,2*1,,n n n a a na n N R αα+=-+∈∈.(1)若2n a n ≥对*n N ∀∈都成立,求α的取值范围;(2)当2α=-时,证明*121112()222n n N a a a +++<∈---.答案:(1)A ; (2)B ; (3)C ; (4)B . (5)y x =±; (6)2; (7)11π-; (8)βα-.2013大学自主招生模拟试题一一.选择题1. 把圆x 2+(y -1)2=1与椭圆9x 2+(y +1)2=9的公共点,用线段连接起来所得到的图形为( ) (A )线段 (B )不等边三角形 (C )等边三角形 (D )四边形2. 等比数列{a n }的首项a 1=1536,公比q=-12,用πn 表示它的前n 项之积。
