混凝土结构设计原理课件(共11)9
合集下载
混凝土结构设计原理全套课件完整版电子教案最新板

破坏有预兆;
➢ Fmax≈36kN
下一章 帮助
混凝土结构设计原理
绪论
由此可见,素混凝土结构中加入少量钢筋以后:
➢ 承载力有很大提高; ➢ 受力性能和破坏特征有明显改善。
❖ 注意:钢筋的主要作用是抗拉和抗剪,也可以抗
压。不同结构构件的配筋情况见教科书上 第2页各图。
主页 目录 上一章 下一章 帮助
混凝土结构设计原理
➢ 优点多,缺点少;缺点可克服。
帮助
混凝土结构设计原理
绪论
§0.5 混凝土结构的发展简况如何?
❖ 1824年,英国人J.Aspdin发明水泥;
主页
❖ 1850年,法国人mbot制成铁丝网水泥船;
目录
❖ 1859年,转炉炼钢成功;
上一章
❖ 1861年,法国人J.Monier取得钢筋混凝土板、管道、
普通钢筋
HPB300 10.0
HRB335、HRBF335、 HRB400、HRBF400、 HRB500、HRBF500
7.5
预应力钢筋 RRB400
5.0
3.5
钢筋的弹性模量
牌号或种类
HPB300 HRB335、HRB400、HRB500、HRBF335、 HRBF400、HRBF500、RRB400、预应力螺
绪论
混凝土结构设计原理
绪论
§0.1 什么是混凝土结构?
结 构:指各种工程实体的承重骨架。
主页
混凝土结构:以混凝土为主要材料制作的结构。如: 目 录
➢ 素混凝土结构:无筋或不配置受力钢筋的混凝土结构。 ➢ 钢筋混凝土结构:配置受力普通钢筋的混凝土结构。 上一章
➢ 预应力混凝土结构:配置受力的预应力钢筋,通过张 下一章 拉或其他方法建立预加应力的混凝土结构。
➢ Fmax≈36kN
下一章 帮助
混凝土结构设计原理
绪论
由此可见,素混凝土结构中加入少量钢筋以后:
➢ 承载力有很大提高; ➢ 受力性能和破坏特征有明显改善。
❖ 注意:钢筋的主要作用是抗拉和抗剪,也可以抗
压。不同结构构件的配筋情况见教科书上 第2页各图。
主页 目录 上一章 下一章 帮助
混凝土结构设计原理
➢ 优点多,缺点少;缺点可克服。
帮助
混凝土结构设计原理
绪论
§0.5 混凝土结构的发展简况如何?
❖ 1824年,英国人J.Aspdin发明水泥;
主页
❖ 1850年,法国人mbot制成铁丝网水泥船;
目录
❖ 1859年,转炉炼钢成功;
上一章
❖ 1861年,法国人J.Monier取得钢筋混凝土板、管道、
普通钢筋
HPB300 10.0
HRB335、HRBF335、 HRB400、HRBF400、 HRB500、HRBF500
7.5
预应力钢筋 RRB400
5.0
3.5
钢筋的弹性模量
牌号或种类
HPB300 HRB335、HRB400、HRB500、HRBF335、 HRBF400、HRBF500、RRB400、预应力螺
绪论
混凝土结构设计原理
绪论
§0.1 什么是混凝土结构?
结 构:指各种工程实体的承重骨架。
主页
混凝土结构:以混凝土为主要材料制作的结构。如: 目 录
➢ 素混凝土结构:无筋或不配置受力钢筋的混凝土结构。 ➢ 钢筋混凝土结构:配置受力普通钢筋的混凝土结构。 上一章
➢ 预应力混凝土结构:配置受力的预应力钢筋,通过张 下一章 拉或其他方法建立预加应力的混凝土结构。
混凝土结构设计原理-课件-第1章-材性资料
建规
s e p
sA
Ec
105 2.2 34.7
(N/mm2 )
fcu,k
sA=(0.4~0.5)fc
桥规
5~10次 ▲混凝土剪变模量Gc
Ec
105 2.2 34.74
(N
/
mm2 )
fcu,k
Gc=0.4 Ec
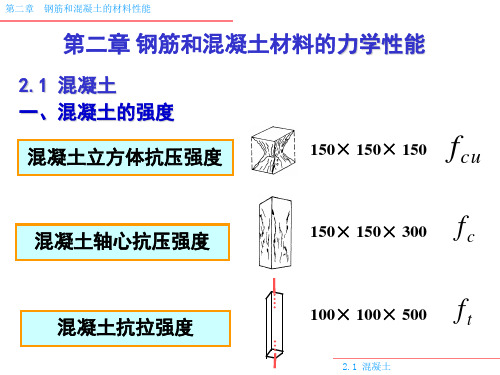
2.1 混凝土
第二章 钢筋和混凝土的材料性能
2、荷载长期作用下混凝土的变形性能--徐变
2.1 混凝土
第二章 钢筋和混凝土的材料性能
3 三轴应力状态
fcc fc (4.5 ~ 7)s 2
s 150
100
50
s Mpa
s
s
s
s
s
0 5 10 15 20 25 000
2.1 混凝土
第二章 钢筋和混凝土的材料性能
三、混凝土的变形
一次短期荷载下
受力变形 长期荷载下
砼变形
多次重复荷载下
收缩变形
比,这种徐变称为线性徐变。产生线性徐变的主要原因是凝胶体 的塑性流动。
当初应力si 在(0.5~0.8) fc 范围时,徐变最终虽仍收敛,但最 终徐变与初应力si不成比例,这种徐变称为非线性徐变。产生非
线性徐变的主要原因是裂缝的出现与发展。
当初应力si >0.8fc 时,混凝土内部微裂缝的发展已处于不稳
fcu
≤C50
n
2
0
0.002
u
0.0033
C80 1.5 0.00215 0.003
2.1 混凝土
第二章 钢筋和混凝土的材料性能
(4)三向受压时的变形性能
混凝土在横向受约束力作用时,不但可提高其强度,还可提高 其延性。
s e p
sA
Ec
105 2.2 34.7
(N/mm2 )
fcu,k
sA=(0.4~0.5)fc
桥规
5~10次 ▲混凝土剪变模量Gc
Ec
105 2.2 34.74
(N
/
mm2 )
fcu,k
Gc=0.4 Ec
2.1 混凝土
第二章 钢筋和混凝土的材料性能
2、荷载长期作用下混凝土的变形性能--徐变
2.1 混凝土
第二章 钢筋和混凝土的材料性能
3 三轴应力状态
fcc fc (4.5 ~ 7)s 2
s 150
100
50
s Mpa
s
s
s
s
s
0 5 10 15 20 25 000
2.1 混凝土
第二章 钢筋和混凝土的材料性能
三、混凝土的变形
一次短期荷载下
受力变形 长期荷载下
砼变形
多次重复荷载下
收缩变形
比,这种徐变称为线性徐变。产生线性徐变的主要原因是凝胶体 的塑性流动。
当初应力si 在(0.5~0.8) fc 范围时,徐变最终虽仍收敛,但最 终徐变与初应力si不成比例,这种徐变称为非线性徐变。产生非
线性徐变的主要原因是裂缝的出现与发展。
当初应力si >0.8fc 时,混凝土内部微裂缝的发展已处于不稳
fcu
≤C50
n
2
0
0.002
u
0.0033
C80 1.5 0.00215 0.003
2.1 混凝土
第二章 钢筋和混凝土的材料性能
(4)三向受压时的变形性能
混凝土在横向受约束力作用时,不但可提高其强度,还可提高 其延性。
混凝土结构设计原理课件

2. 钢筋混凝土材料的力学性能和构件的计算方 法都是建立在实验研究基础上的,许多计算公 式都是在大量试验资料的基础上用统计分析方 法得出的半理论半经验公式。
3.学习本课程是为了在工程建设中进行混凝土结 构的设计,它包括方案、材料选择、截面形式、 配筋、构造措施等。
4.学习本课程时,要学会运用现行的《混凝土结 构设计规范(GB50010—2002)》等。
高强混凝土和高强钢筋的发展、计算机的采用和先 进施工机械设备的发明,建造了一大批超高层建筑、 大跨度桥梁、特长跨海隧道、高耸结构等大型工程, 成为现代土木工程的标志。
设计计算理论:发展了以概率理论为基础的极限状 态设计法,基础理论问题大都得到解决,而新型混 凝土材料及其复合结构形式的出现又不断提出新的 课题,并不断促进混凝土结构的发展。
3. 呈碱性的混凝土可以保护钢筋,使钢筋混凝土结 构具有较好的耐久性。
4 钢筋混凝土结构的主要优缺点
优点: 1. 就地取材,节约钢筋;
2. 耐久性好,耐火性好;
3. 可模性好,便于结构型式的实现;
4. 现浇或装配整体式结构的整体性好, 刚度大。
缺点: 1. 自重大 γ=25kN/m3 轻骨料砼
2. 抗裂性差
混凝土结构的发展
第一阶段: 从钢筋混凝土的发明至上世纪初。 钢筋和混凝土的强度都比较低。 主要用于建造中小型楼板、梁、柱、拱和基础等 构件。 计算理论:结构内力和构件截面计算均套用弹性 理论,采用容许应力设计方法。
第二阶段:
从上世纪20年代到第二次世界大战前后。 混凝土和钢筋强度的不断提高。
1928年法国杰出的土木工程师E.Freyssnet发明了预应 力混凝土,使得混凝土结构可以用来建造大跨度
P
P
钢筋
3.学习本课程是为了在工程建设中进行混凝土结 构的设计,它包括方案、材料选择、截面形式、 配筋、构造措施等。
4.学习本课程时,要学会运用现行的《混凝土结 构设计规范(GB50010—2002)》等。
高强混凝土和高强钢筋的发展、计算机的采用和先 进施工机械设备的发明,建造了一大批超高层建筑、 大跨度桥梁、特长跨海隧道、高耸结构等大型工程, 成为现代土木工程的标志。
设计计算理论:发展了以概率理论为基础的极限状 态设计法,基础理论问题大都得到解决,而新型混 凝土材料及其复合结构形式的出现又不断提出新的 课题,并不断促进混凝土结构的发展。
3. 呈碱性的混凝土可以保护钢筋,使钢筋混凝土结 构具有较好的耐久性。
4 钢筋混凝土结构的主要优缺点
优点: 1. 就地取材,节约钢筋;
2. 耐久性好,耐火性好;
3. 可模性好,便于结构型式的实现;
4. 现浇或装配整体式结构的整体性好, 刚度大。
缺点: 1. 自重大 γ=25kN/m3 轻骨料砼
2. 抗裂性差
混凝土结构的发展
第一阶段: 从钢筋混凝土的发明至上世纪初。 钢筋和混凝土的强度都比较低。 主要用于建造中小型楼板、梁、柱、拱和基础等 构件。 计算理论:结构内力和构件截面计算均套用弹性 理论,采用容许应力设计方法。
第二阶段:
从上世纪20年代到第二次世界大战前后。 混凝土和钢筋强度的不断提高。
1928年法国杰出的土木工程师E.Freyssnet发明了预应 力混凝土,使得混凝土结构可以用来建造大跨度
P
P
钢筋
混凝土结构设计完整的ppt课件

要一个方向受力的板。 重要概念:荷载按构件刚度分配,按短跨方向传递。
《规范》规定:混凝土板应按下列原则进行计算:
1.两对边支承的板和单边嵌固的悬臂板,应按单向板计算;
2.四边支承的板(或邻边支承或三边支承)应按下列规定计 算:
(1)当长边与短边长度之比大于或等于3时,可按沿短边方向受 力的单向板计算;
(梁净长)1/3
(梁净长)1/4
(梁净长)1/3 (梁净长)1/4
6900 6 22 2/4
250 6 22 4/2
1800 150 150 6 22 4/2
2 20
250 6 22 4/2
内力重分布的过程
三个阶段: (1)弹性体系; (2)支座和跨中截面先后出现裂缝; (3)支座塑性铰形成。
超静定钢筋砼结构内力重分布的两个过程: 第一:受拉砼开裂至第一个塑性铰形成; 第二:第一个塑性铰形成直到结构破坏。
连续梁的设计弯矩按弹性计算,截面配筋按极限状态计算, 两者不一致?
超静定结构塑性内力重分布的概念
3.跨中弹性最不利弯矩和
M 跨中
1.02M0
1 2
(M
l
M
r
)
4.调幅后支座和跨中截面弯矩均不小于1/3Mo;
5.各控制截面的剪力设计值按荷载最不利布置和调 幅后支座弯矩由静力平衡条件计算确定。
例:按弯矩调幅法计算如图所示双 跨连续梁的支座及跨中弯矩。(图 中给出的是用线弹性方法计算出的 最不利支座及跨中弯矩,调幅系数 β=0.2,F=100kN,l=6m)
结构; (2)处于严重侵蚀性环境中的混凝土结构; (3)直接承受动力和重复荷载的混凝土结构 (4)要求有较高承载力储备的混凝土结构; (5)配置延性较差的受力钢筋的混凝土结构。
《规范》规定:混凝土板应按下列原则进行计算:
1.两对边支承的板和单边嵌固的悬臂板,应按单向板计算;
2.四边支承的板(或邻边支承或三边支承)应按下列规定计 算:
(1)当长边与短边长度之比大于或等于3时,可按沿短边方向受 力的单向板计算;
(梁净长)1/3
(梁净长)1/4
(梁净长)1/3 (梁净长)1/4
6900 6 22 2/4
250 6 22 4/2
1800 150 150 6 22 4/2
2 20
250 6 22 4/2
内力重分布的过程
三个阶段: (1)弹性体系; (2)支座和跨中截面先后出现裂缝; (3)支座塑性铰形成。
超静定钢筋砼结构内力重分布的两个过程: 第一:受拉砼开裂至第一个塑性铰形成; 第二:第一个塑性铰形成直到结构破坏。
连续梁的设计弯矩按弹性计算,截面配筋按极限状态计算, 两者不一致?
超静定结构塑性内力重分布的概念
3.跨中弹性最不利弯矩和
M 跨中
1.02M0
1 2
(M
l
M
r
)
4.调幅后支座和跨中截面弯矩均不小于1/3Mo;
5.各控制截面的剪力设计值按荷载最不利布置和调 幅后支座弯矩由静力平衡条件计算确定。
例:按弯矩调幅法计算如图所示双 跨连续梁的支座及跨中弯矩。(图 中给出的是用线弹性方法计算出的 最不利支座及跨中弯矩,调幅系数 β=0.2,F=100kN,l=6m)
结构; (2)处于严重侵蚀性环境中的混凝土结构; (3)直接承受动力和重复荷载的混凝土结构 (4)要求有较高承载力储备的混凝土结构; (5)配置延性较差的受力钢筋的混凝土结构。
混凝土结构设计原理(课件)

高性能混凝土的研究和应用,使得混凝土 结构的性能更加优异,满足了更加复杂和 多样化的工程需求。
02 混凝土结构设计基本原则
结构设计原则
01
02
03
04
Hale Waihona Puke 结构完整性确保混凝土结构在各种工况下 的整体性,避免出现裂缝、断
裂等损伤。
承载能力
根据预期的载荷和应力要求, 设计混凝土结构的承载能力。
耐久性
考虑环境因素和预期使用寿命 ,确保混凝土结构在使用期间
工现场进行搅拌、浇注和养护的混凝土构件。
按受力特点分类
混凝土结构可以分为框架结构、剪力墙结构、框架-剪力墙结构等。框架结构的受力特 点是主要承受横向和纵向的荷载,通过梁和柱的连接实现;剪力墙结构的受力特点是主 要承受横向荷载,通过剪力墙的连接实现;框架-剪力墙结构的受力特点是结合了框架
和剪力墙的特点,形成了一种混合结构形式。
05 混凝土结构设计中的问题 及解决措施
混凝土裂缝问题及解决措施
总结词
混凝土裂缝是混凝土结构设计中 常见的问题,会导致结构承载能
力下降和耐久性降低。
原因分析
混凝土裂缝产生的原因包括施工过 程控制不当、结构设计不合理、材 料质量不合格等。
解决措施
针对不同原因采取相应的解决措施, 如加强施工过程控制、优化结构设 计、选用优质材料等。
混凝土结构发展历程
19世纪中叶
20世纪初
随着水泥和混凝土技术的发展,混凝土开 始被应用于建筑和桥梁工程中。
钢筋混凝土的发明和应用,使得混凝土结 构的强度和稳定性得到了显著提高。
20世纪50年代
21世纪初
预应力混凝土的出现,进一步提高了混凝 土结构的承载能力和耐久性,为现代大型 混凝土结构的建造奠定了基础。
第一章-《混凝土结构设计原理》绪论PPT课件

11
(二)设计依据
1、国家标准
相关结构荷载、抗震设计、桩基技术、地基基 础设计规范
2、地质勘察报告
相关气象条件、工程地质条件、结构设计参数
12
结构设计参数
技术指标 结构类型 建筑结构安全等级 设计使用年限 抗震设防烈度 建筑抗震设防类别 设计基本地震加速度 设计地震分组 场地类别 房屋抗震等级 湿陷性黄土地基湿陷类型 湿陷等级 建筑物分类 地基处理方式 地基基础设计等级
2、水平地震作用计算
• 该建筑群主体质量和刚度沿高度分布比较均匀,故可用底 部剪力法计算水平地震作用。
• 本设计中结构的设防烈度为8度,查规范可知: 8度设防 烈度条件下,多遇地震结构的水平地震影响系数最大值 ,罕遇地震结构水平地震影响系数最大值 。
23
四、结构水平位移计算
• 本设计中,风荷载值远小于水平地震作用,故 只需进行水平地震作用下的位移验算。水平地震 作用下的位移为倒三角形分布荷载和顶点集中荷 载产生的位移之和。
2015年
建筑结构
2013级工程造价专业
2015.3.9
1
2015年
课程简介
学时: 64学时 时间:1~16周 考核要求:平时成绩 30% 期末成绩 70% 平时成绩:1.平时作业成绩
2.点名 3.课程展示
2
青海大学 结构设计原理
课程章节比例分配
重点章节:
第四章 钢筋混凝土结构轴心受力构件承载力 第五章 钢筋混凝土受弯构件正截面承载力 第六章 钢筋混凝土受弯构件斜截面承载力 第七章 钢筋混凝土受扭构件承载力 第八章 钢筋混凝土偏心受力构件承载力 第十二章 多层框架结构
• 受扭构件——空间受力
35
建筑结构
第1 章
(二)设计依据
1、国家标准
相关结构荷载、抗震设计、桩基技术、地基基 础设计规范
2、地质勘察报告
相关气象条件、工程地质条件、结构设计参数
12
结构设计参数
技术指标 结构类型 建筑结构安全等级 设计使用年限 抗震设防烈度 建筑抗震设防类别 设计基本地震加速度 设计地震分组 场地类别 房屋抗震等级 湿陷性黄土地基湿陷类型 湿陷等级 建筑物分类 地基处理方式 地基基础设计等级
2、水平地震作用计算
• 该建筑群主体质量和刚度沿高度分布比较均匀,故可用底 部剪力法计算水平地震作用。
• 本设计中结构的设防烈度为8度,查规范可知: 8度设防 烈度条件下,多遇地震结构的水平地震影响系数最大值 ,罕遇地震结构水平地震影响系数最大值 。
23
四、结构水平位移计算
• 本设计中,风荷载值远小于水平地震作用,故 只需进行水平地震作用下的位移验算。水平地震 作用下的位移为倒三角形分布荷载和顶点集中荷 载产生的位移之和。
2015年
建筑结构
2013级工程造价专业
2015.3.9
1
2015年
课程简介
学时: 64学时 时间:1~16周 考核要求:平时成绩 30% 期末成绩 70% 平时成绩:1.平时作业成绩
2.点名 3.课程展示
2
青海大学 结构设计原理
课程章节比例分配
重点章节:
第四章 钢筋混凝土结构轴心受力构件承载力 第五章 钢筋混凝土受弯构件正截面承载力 第六章 钢筋混凝土受弯构件斜截面承载力 第七章 钢筋混凝土受扭构件承载力 第八章 钢筋混凝土偏心受力构件承载力 第十二章 多层框架结构
• 受扭构件——空间受力
35
建筑结构
第1 章
混凝土结构设计原理课件(共)

混凝土结构设计原理
混凝土结构设计原理的课件,详细介绍了设计原理的定义与作用、混凝土的 组成与性质、混凝土结构设计的基本步骤等内容。
设计原理的定义与作用
设计原理是指在混凝土结构设计中,遵循的基本原则和规范,以确保结构的稳定性、安全性和可靠性。
混凝土的组成与性质
混凝土由水泥、砂、石子等材料按一定比例混合而成,具有较高的抗压强度、 耐久性和耐火性。
模板设计
为混凝土构件设计适当的模板, 以确保结构的准确性和美观性。
浇筑与养护
在浇筑后进行适当的养护,以提 高混凝土的强度和耐久性。
混凝土结构设计的常见问题及解决方 案
裂缝问题
通过加强混凝土的配筋和控制温度变化来解决。
荷载超限
检查结构设计的合理性,必要时进行荷载重新计算和构件加固。
使用寿命受限
使用防水、防霉和防腐等材料,增加结构的使用寿命。
压力
混凝土结构中的柱和墙受到 压力的作用。
剪力
混凝土结构中的梁和板受到 剪力的作用。
混凝土结构设计中的荷载计算
1 自重荷载
结构本身与构件的重力所 产生的荷载。
2 活载
3 风荷载
来自使用人员、家具设备 和其他可移动物体的荷载。
建筑物在风力作用下受到 的荷载。
混凝土结构的构造与施工要求
施工材料
选用高质量的混凝土材料,并确 保施工环境符合要求。
混凝土结构设计的基本步骤
1
结构需求分析
确定结构的用途、设计要求和荷载条件。
2
构件选择与布置
选择适合的构件类型和尺寸,并进行布置。
3
受力分析与设计
根据荷载作用下的受力情况,进行结构的承载能力计算和设计。
4
细部构造设计
混凝土结构设计原理的课件,详细介绍了设计原理的定义与作用、混凝土的 组成与性质、混凝土结构设计的基本步骤等内容。
设计原理的定义与作用
设计原理是指在混凝土结构设计中,遵循的基本原则和规范,以确保结构的稳定性、安全性和可靠性。
混凝土的组成与性质
混凝土由水泥、砂、石子等材料按一定比例混合而成,具有较高的抗压强度、 耐久性和耐火性。
模板设计
为混凝土构件设计适当的模板, 以确保结构的准确性和美观性。
浇筑与养护
在浇筑后进行适当的养护,以提 高混凝土的强度和耐久性。
混凝土结构设计的常见问题及解决方 案
裂缝问题
通过加强混凝土的配筋和控制温度变化来解决。
荷载超限
检查结构设计的合理性,必要时进行荷载重新计算和构件加固。
使用寿命受限
使用防水、防霉和防腐等材料,增加结构的使用寿命。
压力
混凝土结构中的柱和墙受到 压力的作用。
剪力
混凝土结构中的梁和板受到 剪力的作用。
混凝土结构设计中的荷载计算
1 自重荷载
结构本身与构件的重力所 产生的荷载。
2 活载
3 风荷载
来自使用人员、家具设备 和其他可移动物体的荷载。
建筑物在风力作用下受到 的荷载。
混凝土结构的构造与施工要求
施工材料
选用高质量的混凝土材料,并确 保施工环境符合要求。
混凝土结构设计的基本步骤
1
结构需求分析
确定结构的用途、设计要求和荷载条件。
2
构件选择与布置
选择适合的构件类型和尺寸,并进行布置。
3
受力分析与设计
根据荷载作用下的受力情况,进行结构的承载能力计算和设计。
4
细部构造设计
混凝土结构设计原理课件

斜截面剪切破坏的主要形态有斜压、剪压和斜拉三 种。斜截面受剪承截力计算公式是以剪压破坏特征为基 础建立的,其他两种破坏形态则是通过构造要求来防止 出现。
钢筋混凝土柱、剪力墙等偏心受力构件的斜截面受 剪承截力计算与受弯构件的主要区别,在于应考虑轴向 力的影响。在一定范围内,轴向压力可使构件的受剪承 载力提高,而轴向拉力则使受剪承载力降低。
箍筋对有腹筋梁受剪承载力的影响
受弯构件受剪性能的试验研究
构件斜截面承载力
1 建筑工程中受弯构件斜截面设计方法 2 .不配腹筋的板
V 0.7h ftbh0
1
βh——截面高度影响系数, 当h0<800mm时,取h0 =800mm; 当h0>2000mm时, 取h0=2000mm;
ft —8 f y sin
受弯构件斜截面受剪承载力的设计计算
构件斜截面承载力
也可以根据受弯承载力的要求,先选定弯起钢筋再 按下式计算所需箍筋:
nAsv1 V 0.7 ftbh0 0.8 f y Asb sin
s
1.25 f yvh0
nAsv1
V
1.75
1.0
ft bh0
0.8 f y Asb
受弯构件受剪性能的试验研究
构件斜截面承载力
纵向钢筋配筋率
试验表明,梁的受 剪承载力随纵向钢筋 配筋率ρ的提高而增 大 。这主要是纵向受 拉钢筋约束了斜裂缝 长度的延伸,从而增 大了剪压区面积的作 用。
纵向钢筋配筋率对有腹筋梁受剪承载力的影响
受弯构件受剪性能的试验研究
构件斜截面承载力
配箍率和箍筋强度
V 0.7 f tbh0
…7
集中荷载F的独立梁:
1.75
V 1 f tbh0
钢筋混凝土柱、剪力墙等偏心受力构件的斜截面受 剪承截力计算与受弯构件的主要区别,在于应考虑轴向 力的影响。在一定范围内,轴向压力可使构件的受剪承 载力提高,而轴向拉力则使受剪承载力降低。
箍筋对有腹筋梁受剪承载力的影响
受弯构件受剪性能的试验研究
构件斜截面承载力
1 建筑工程中受弯构件斜截面设计方法 2 .不配腹筋的板
V 0.7h ftbh0
1
βh——截面高度影响系数, 当h0<800mm时,取h0 =800mm; 当h0>2000mm时, 取h0=2000mm;
ft —8 f y sin
受弯构件斜截面受剪承载力的设计计算
构件斜截面承载力
也可以根据受弯承载力的要求,先选定弯起钢筋再 按下式计算所需箍筋:
nAsv1 V 0.7 ftbh0 0.8 f y Asb sin
s
1.25 f yvh0
nAsv1
V
1.75
1.0
ft bh0
0.8 f y Asb
受弯构件受剪性能的试验研究
构件斜截面承载力
纵向钢筋配筋率
试验表明,梁的受 剪承载力随纵向钢筋 配筋率ρ的提高而增 大 。这主要是纵向受 拉钢筋约束了斜裂缝 长度的延伸,从而增 大了剪压区面积的作 用。
纵向钢筋配筋率对有腹筋梁受剪承载力的影响
受弯构件受剪性能的试验研究
构件斜截面承载力
配箍率和箍筋强度
V 0.7 f tbh0
…7
集中荷载F的独立梁:
1.75
V 1 f tbh0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E ——钢筋的弹性模量Es和混凝土Ec弹性模量的比值;
ρ ——纵向受拉钢筋的配筋率,
=
As bh0
;
ψ ——钢筋应变不均匀系数,是裂缝之间钢筋的平均应
变与裂缝截面钢筋应变之比,它反映了裂缝间混凝土受
拉对纵向钢筋应变的影响程度。ψ愈小,裂缝间混凝土
协助钢筋抗拉作用愈强。该系数按下列公式计算
= 1.1 0.65 ftk te sk
= u y
= cu y
(1 k )h0 xa
9.3.3 受弯构件延性的因素和提高截面延性的措施
影响因素主要包括:纵向钢筋配筋率、混凝土极限
压应变、钢筋屈服强度及混凝土强度等。即极限压应变 cu
以及受压区高度 kh0 和 xa 两个综合因素。
提高截面延性的措施有:限制纵向受拉钢筋的配筋率; 规定受压钢筋和受拉钢筋的最小比例;在弯矩较大区段 适当加密箍筋。
各种构件正截面最大裂缝宽度计算公式为 :
max
= cr
sk
Es
(1.9c 0.08 deq )
te
式中 , te , sk 符号意义同前,当裂缝宽度演算时
te <0.01时,取te =0.01;
cr ——构件受力特征系数;
轴心受拉构件: cr = 2.7
偏心受拉构件: cr = 2.4 受弯构件和偏心受压构件: cr = 2.1
(l0
/ h)2
γf′意义同前。
裂缝宽度的验算是在满足构件承载力前提下进行的, 因而截面尺寸、配筋率等均已确定,验算中可能会出现 裂缝宽度不能满足《规范》要求的情况,此时可采取的 措施是选择直径较小的钢筋,或宜采用变形钢筋,必要 时还可适当增加配筋率。
由公式可知,Wmax主要与钢筋应力σsk,有效配筋 率ρte及钢筋直径有关,根据σsk,ρte及d三者的关系,
9.2 混凝土构件裂缝宽度计算
9.2.1 裂缝产生的原因
裂缝是工程结构中常见的一种作用效应,裂缝按其 形成的原因可分为两大类:一类是由荷载作用引起的裂 缝;另一类是由变形因素引起的裂缝,如温度变化、材 料收缩以及地基不均匀沉降引起的裂缝,由于变形因素 引起的裂缝计算因素很多,不易准确把握,故此处裂缝 宽度计算的裂缝主要是指荷载原因引起的裂缝。
度验算均采用荷载标准值和材料强度的标准值。
②由于可变荷载作用时间的长短对变形和裂缝宽度的大 小有影响,故验算变形和裂缝宽度时应按荷载短期效应 组合值并考虑荷载长期效应的影响进行。
9.1.5 受弯构件变形计算方法
为了简化计算,《规范》在挠度计算时采用了“最 小刚度原则”,即:在同号弯矩区段采用最大弯矩处的 截面抗弯刚度(即最小刚度)作为该区段的抗弯刚度, 对不同号的弯矩区段,分别取最大正弯矩和最大负弯矩 截面的刚度作为正负弯矩区段的刚度。
9.1.4 受弯构件变形验算
(1)变形验算目的与要求 受弯构件变形验算目的主要是用以满足适用性。
其主要从以下几个方面考虑:
1)保证结构的使用功能要求;
2)防止对结构构件产生不良影响;
3)防止对非结构构件产生不良影响;
4)保证使用者的感觉在可接受的程度之内。
因此,对受弯构件在使用阶段产生的最大变形值f必须
寸偏差等因素的影响,裂缝的出现、分布和开展宽度具 有很大的随机性。但它们又具有一定的规律,从平均意 义上讲,裂缝间距和宽度具有以下特性:
①裂缝宽度与裂缝间距密切相关。裂缝间距大裂缝宽 度也大。裂缝间距小,裂缝宽度也小。而裂缝间距与钢 筋表面特征有关,变形钢筋裂缝密而窄,光圆钢筋裂缝 疏而宽。在钢筋面积相同的情况下,钢筋直径细根数多, 则裂缝密而窄,反之裂缝疏而宽;
加以限制,即
f ≤[f]
其中 [ f ] —为挠 度变形限值。
混凝土结构构件变形和裂缝宽度验算属于正常使用 极限状态的验算,与承载能力极限状态计算相比,正常 使用极限状态验算具有以下二个特点:
①考虑到结构超过正常使用极限状态对生命财产的危 害远比超过承载能力极限状态的要小,因此其目标可
靠指标β值要小一些,故《规范》规定变形及裂缝宽
并规定0.4≤ ψ ≤1.0
式中 te ——按有效受拉混凝土面积计算的纵向受拉
钢筋配筋率, te
=
As Ate
。
Ate ——有效受拉混凝土面积。对受弯构件,近似取
Ate = 0.5bh (b f b)h f
sk ——按荷载短期效应组合计算的裂缝截面处纵向
受拉钢筋的应力,根据使用阶段(Ⅱ阶段)的应力状态 及受力特征计算:
《规范》给出了钢筋混凝土构件不需作裂缝宽度验算的 最大钢筋直径图表,通常裂缝宽度的控制在实际工程中 是用控制钢筋最大直径来满足。
9.3 混凝土构件的延性
9.3.1 延性概念 结构、构件或截面延性是指从屈服开始到达到最大
承载力或达到以后而承载力还没有显著下降期间的变形 能力。即延性是反映构件的后期变形能力。
③计算长期刚度Bl按式:
Bl
=
M q (
Mk 1) M k
Bs
④用Bl代替材料力学位移公式
f
=
S
Ml
2 0Leabharlann EI中的EI,计算出构件的最大挠度,并按式 f ≤ [ f ] 进行验算。
若验算结果 f > [ f ],从短期刚度计算公式可知, 增大截面高度是提高截面抗弯刚度、减小构件挠度的最 有效措施;若构件截面受到限制不能加大时,可考虑增 大纵向受拉钢筋的配筋率或提高混凝土强度等级,但作 用并不显著,对某些构件还可以充分利用纵向受压钢筋 对长期刚度的有利影响,在受压区配置一定数量的受压 钢筋,另外,采用预应力混凝土构件也是提高受弯构件 刚度的有效措施。实际工程中,往往采用控制跨高比的 方法来满足变形条件的要求。
“后期”是指从钢筋开始屈服进入破坏阶段直到最 大承载能力(或下降到最大承载能力的 85%)时的整个 过程。 延性要求的目的:
I. 满足抗震方面的要求;
II. 防止脆性破坏;
III.在超静定结构中,适应外界的变化;
IV. 使超静定结构能充分的进行内力重分布。
9.3.2 截面的延性的计算及影响因素
截面的延性用延性系数来表达,计算时采用平截面假 设。延性系数表达式:
③偏心受拉构件。大小偏心受拉构件σsk按下式计算:
sk
=
N ss e As (h as )
式中 e′——轴向拉力作用点至受压区或受拉较小边
纵筋合力点的距离,e = e0 yc as
yc′ ——截面重心至受压或较小受拉边缘的距离。
④偏心受压构件。偏心受压构件σsk按下式计算 :
sk
=
Ns (e h0 ) h0 As
第九章 混凝土构件的变 形及裂缝宽度验算
9.1 钢筋混凝土受弯构件的挠度验算
9.1.1截面弯曲刚度的概念及其定义
材料力学中,匀质弹性材料梁的跨中挠度为
f
=S
Ml
2 0
EI
式中 S ——与荷载类型和支承条件有关的系数;
EI——梁截面的抗弯刚度。
由于是匀质弹性材料,所以当梁截面的尺寸确定 后,其抗弯刚度即可确定且为常量,挠度f与M成线性 关系。
9.2.2 裂缝宽度验算的目的和要求
构件裂缝控制等级共分为三级:一级为严格要求不 出现裂缝,二级为一般要求不出现裂缝,三级为允许出 现裂缝。
一级和二级抗裂要求的构件,一般要采用预应力; 而普通的钢筋混凝土构件抗裂要求为三级,阶段都是 带裂缝工作的。当裂缝宽度较大时,一是会引起钢筋 锈蚀,二是使结构刚度减少、变形增加,在使用从而 影响结构的耐久性和正常使用,同时给人不安全感。 因此,对允许出现裂缝的钢筋混凝土构件,裂缝宽度 必须加以限制,要求使用阶段最大裂缝宽度小于允许
对钢筋混凝土构件,由于材料的非弹性性质和受拉 区裂缝的开展,梁的抗弯刚度不是常数而是变化的,其 主要特点如下:
①随荷载的增加而减少,即M越大,抗弯刚度越 小。验算变形时,截面抗弯刚度选择在曲线第Ⅱ阶段 (带裂缝工作阶段)确定;
②随配筋率ρ 的降低而减少。对于截面尺寸和材
料都相问的适筋梁,ρ小,变形大些;截面抗弯刚度
式中 , ——分别为受压及受拉钢筋的配筋率。
= 2.0 0.4
此处反映了在受压区配置受压钢筋对混凝土受压徐 变和收缩起到一定约束作用,能够减少构件在长期荷载 作用下的变形。上述θ适用于一般情况下的矩形、T形、 工字形截面梁,θ值与温湿度有关,对干燥地区,θ值应 酌情增加15%~25%。对翼缘位于受拉区的T形截面,θ 值应增加20%。
理论上讲,按Bmin计算会使挠度值偏大,但实际情况 并不是这样。因为在剪跨区段还存在着剪切变形,甚至 出现斜裂缝,它们都会使梁的挠度增大,而这是在计算 中没有考虑到的,这两方面的影响大致可以相互抵消, 亦即在梁的挠度计算中除了弯曲变形的影响外,还包含 了剪切变形的影响。
受弯构件变形验算按下列步骤进行:
小些;
③沿构件跨度,弯矩在变化,截面刚度也在变化, 即使在纯弯段刚度也不尽相同,裂缝截面处的小些, 裂缝间截面的大些;
④随加载时间的增长而减小。构件在长期荷载作 用下,变形会加大,在变形验算中,除了要考虑短期 效应组合,还应考虑荷载的长期效应的影响,故有长
期刚度Bs 和短期刚度Bl 。
9.1.2 短期刚度Bs
对受弯构件
sk
=
Ms 0.87 Ash0
式中 M s——按荷载短期效应组合计算的弯矩值,即 按全部永久荷载及可变荷载标准值求得的弯矩标准值。
9.1.3 长期刚度Bl
长期刚度Bl 是指考虑荷载长期效应组合时的刚度值。 在荷载的长期作用下,由于受压区混凝土的徐变以及受
拉区混凝土不断退出工作,即钢筋与混凝土间粘结滑移
c——混凝土保护层厚度,当c<20mm时,取c=20mm
deq——纵向受拉钢筋的等效直径(mm)。
