资料分析公式及例题
资料分析常考题型及相关公式

资料分析常考题型及相关公式
一、基期量(A)与现期量(B)
1. 基期量(A):常用公式:A=
常用速算技巧:①若选项首尾不同:截位直除法
②若选项首位相同:r或1+r用特殊分数替代
③若r很小:化除为乘
基期量的和或差:放缩法
间隔基期量:①求混合增长率;②求基期量
2.现期量(B):常用公式:B=A(1+r)
间隔现期量:①求混合增长率;②求现期量
特殊题型:若增长率与去年保持一致,预测今年的量:
方法一:利用增长量估算去年+去年的增长量
方法二:直接用公式=
二、增长量(△x)
1.计算型
常用公式:△x=B
常用速算技巧:r用特殊分数替代。
2.比较型
①“大大则大”
②看倍数关系
三、增长率(r)相关
1.常用公式 r=
常用速算技巧:截位直除法、插值法、分母用特殊分数替代。
2.两期混合增长率:(常用速算技巧:r用特殊分数替代)
3.拉动增长率=
4.合成增长率:大小居中,但不中,偏向基期基数较大的。
5.年均增长率:常用公式:末期值=初期值(1+年均增长率)n
常用速算技巧:
四、比重
1.现期比重=
2.基期比重=
3.比重的比较:①若部分r总体r,则比重上升;反之下降。
②比重上升或下降的百分点一般小于(部分r —总体r)的绝对值。
=50% 33.3% =25% =20% 16.7%
14.3% =12.5% 11.1% =10% 9.1%
8.3% 7.7% 66.7% 28.6% 22.2%。
资料分析常用万能公式模版

资料解析常用公式一,已知 2005 的量为 a,2006 年的量比 2005 年的量增加 r%,求 2006年的量 b。
b=(1+r%)二,已知 2006 的量为 b,2006 年的量比 2005 的量增加 r%,求 2005年的量 a。
a= b÷(1+r%)三,已知 2006 的量为 b,2006 年的量比 2005 的量增加 r%,求 2006年比 2005 年增加多少。
b÷(1+r%) ×r%四,已知 2005 的量为 a,2006 年的量比 2005 的量减少 r%,求 2006年的量 b。
b= a×(1-r%)五,已知 2006 的量为 b,2006 年的量比 2005 的量减少 r%,求 2005年的量 a。
a= b÷(1-r%)六,已知 2006 的量为 b,2006 年的量比 2005 的量减少 r%,求 2006年比 2005 年减少多少。
b÷(1-r%)×r%七,已知 2006 年的量为 b,年平均增加率为 r%,求 n 年后的量 a 是多少 ?a= (1+r%)n.八,别的,增加率的增加,只要考虑增加率自己相加减,比方已知2004 年的量为 b,2005 年比 2004 年增加 5%,2006 年增加率比 2005年提高了 5 个百分点,请问 2006 年的增加率为多少 ?5%+5%=10%九,“占计划百分之几”用完成数除以计划数乘100%,比方计划为100,完成 80,占计划就是80%;十,“超计划的百分之几”要扣除基数,比方计划100,完成 120,超计划的就是:(120-100)÷100×100%=20%;十一,“为昨年的百分之几”就是等于也许相当于昨年的百分之几,比方今年完成256 个单位,昨年为 100 个单位,今年为昨年的百分之几就是:(256÷100)×100%=256%;十二,“比昨年增加百分之几”应扣除原有基数,比方昨年100,今年 256;算法就是:(256-100)÷100×100%=156%。
公务员考试资料分析公式大全

公务员考试资料分析公式大全2.百分点表示相对指标的变化幅度,可直接相加减。
例如,从10%增长到20%,增长了10个百分点,而不是10%。
基期、现期、增长量、增长率基期量是对比参照时期的具体数值,现期量是相对于基期量的数值,增长量是现期量相对于基期量的变化量。
平均增长量是一段时间内平均每期的变化量,而增长率是现期量相对于基期量的变化指标。
年均增长率和间隔增长率年均增长率是基期量经过n个周期变为末期量B的情况下,计算出的平均增长率。
但当|x|>10%时,利用公式计算存在一定误差。
间隔增长率是已知第二期和第三期的增长率,求第三期相对于第一期的增长率。
混合增长率混合增长率是已知部分的增长率,求整体的增长率。
例如,A的增长率是a,B的增长率是b,而“A+B”的增长率是r,其中r介于a、b之间,且偏向于基数较大一方的增长率。
同比增长和环比增长同比增长是与历史同期相比的增长情况,而环比增长是与相邻上一个统计周期相比的增长情况。
平均数、比重、倍数、翻番和指数平均数包括现期平均数和基期平均数,其中A为现期总量,a为对应增长率,B为现期份数,b为对应增长率。
比重指部分在整体中所占的百分比,用个百分数或者“几成”表示。
倍数是A是B的多少倍,A÷B;而翻番是翻几番变为原来数值的倍。
指数是描述某种事物相对变化的指标值,假设基数为100,其他值与基期相比得到的数值。
删除有问题的段落。
1.修改每段话:算法可以帮助我们计算各种数值的变化。
例如,如果现在比过去增长了20%,那么我们可以用算法100×(1+20%)=120来计算。
同样地,如果现在比过去降低了20%,那么我们可以用算法100×(1-20%)=80来计算。
如果我们想知道某个数是原来的多少倍,我们可以用倍数进行计算。
例如,某城市2000年的人均住房使用面积达到14.8平方米,比1978年的3.8平方米高出3.9倍。
另外,我们也可以用翻番来计算数量加倍的情况。
2015年国考资料分析(公式)

(1)隔年增长率例1: 2010年为20万元, 2009年同比增长25.2%, 2008年同比增加12.2%, 则2010年比2008年增加了多少?25.2%+12.2%+25.2%*12.2%(2)倍数=m/n(m,n是两个单位相同的量) 多几倍=倍数-1例子1: 我有300元, 你有100元, 我是你的几倍?多几倍?我是你的300/100=3倍, 多几倍=3-1, 所以多1倍(3)部分增长率>整体增长率比重上升, 反之减少(4)年均增长量=(b-a)/n (b为增长后的量, a为增长前的量, n为增长次数)例子1:2010年的粮食产量为200万屯, 2014年为1000万屯, 求年均增长量?(1000-200)/4=200(5)年均增长率a*(1-x%)^n=b (a是增长前的量, b是增长后的量, n是增长次数, x%是增长率)(6)去年比重=今年比重*(1+整体增长率)/(1+部分增长率)例子1:2009年, 苹果产量为20万, 同比增长12%, 水果产量为100万, 同比增长20%, 求2008年苹果占水果的比重?20/100*(1+20%)/(1+12)(7)上期产量=本期产量/(1+增长率)例子1: 2002年苹果产量为20万屯, 增长率为20%, 求2001年产量?2001年产量=20/(1+20%)(8)同比: 与过去的大数比, 环比是与过去的小数比例子1:2001年7月苹果产量为100万屯, 同比增长20%, 环比增长12%, 求2000年7月苹果产量?2001年6月产量2000年7月苹果产量=100/(1+20%)2001年6月产量=100/(1+12%)(9)增长量=本期增长量*增长率/(1+增长率)例子1:2001年苹果产量为20万屯, 增长率为20%,比2000增长量?20*(1+20%)*20%(10)增长量=增长后的量-增长前的量例子1:2002年苹果产量为100万屯, 2001年为80万屯, 求增长量?100-80=80(11)增长率=增长量/增长前的量*100%例子1:2003年苹果产量为100万屯,2004年比2003年增长了20万屯, 求增长率?20/100*100%注: “比”字后面的量做分母(12)增长率(多几倍)=倍数-1(增长率=多几倍)。
资料分析计算公式整理

资料分析计算公式整理在进行资料分析时,掌握一些关键的计算公式是至关重要的。
这些公式能够帮助我们快速、准确地从大量的数据中提取有价值的信息,做出合理的判断和决策。
下面,我将为大家整理一些常见且实用的资料分析计算公式。
一、增长率相关公式1、增长率=(现期量基期量)÷基期量× 100%这是最基本的增长率计算公式。
例如,某公司去年的销售额为 100 万元,今年为 120 万元,那么今年的销售额增长率为(120 100)÷ 100 × 100% = 20%。
2、间隔增长率= r1 + r2 + r1×r2当涉及到间隔年份的增长率计算时,就需要用到这个公式。
假设第一年的增长率为 r1,第二年的增长率为 r2,那么从第一年到第二年的间隔增长率就是 r1 + r2 + r1×r2。
3、年均增长率=\(\sqrtn{\frac{现期量}{基期量}} 1 \)(n 为年份差)如果要计算一段时间内的平均增长率,就用这个公式。
比如,某地区 2010 年的 GDP 为 100 亿元,2020 年为 200 亿元,年份差为 10 年,那么年均增长率=\(\sqrt10{\frac{200}{100}} 1 \)。
1、比重=部分量÷整体量× 100%比如,某班级共有 50 名学生,其中男生 25 人,那么男生在班级中的比重就是 25÷50× 100% = 50%。
2、整体量=部分量÷比重已知部分量和比重,求整体量时使用。
假设某企业某产品的销售额占总销售额的 30%,该产品销售额为 100 万元,那么企业总销售额=100÷30% 。
3、部分量=整体量×比重当已知整体量和比重,求部分量时运用。
比如一个城市总人口为100 万人,其中老年人占比 20%,那么老年人的数量= 100×20% = 20 万人。
资料分析计算公式整理

资料分析计算公式整理在资料分析的过程中,计算公式的整理是非常重要的一步。
通过对数据的系统整理、统计和运算,可以得到准确的结果,进而为决策提供支持。
在这篇文章中,我将介绍一些常用的资料分析计算公式,并给出示例,以便读者更好地理解和应用。
一、平均值计算平均值是资料分析中最基本的计算方式之一,它可以帮助我们了解数据的集中趋势。
在进行平均值计算时,需要先将所有观测值相加,再除以观测值的个数。
示例:假设我们有一组数据:10, 12, 15, 18, 20那么平均值的计算公式为:(10 + 12 + 15 + 18 + 20) / 5 = 75 / 5 = 15二、中位数计算中位数是将一组数据按照大小顺序排列后,处于中间位置的观测值。
它对数据的极值不敏感,可以较好地反映数据的集中趋势。
示例:假设我们有一组数据:10, 12, 15, 18, 20首先将数据从小到大排列:10, 12, 15, 18, 20中位数即为中间位置的观测值,即15。
三、标准差计算标准差是度量数据离散程度的一种指标,它可以帮助我们判断一组数据是否分散或集中。
标准差的计算公式包括多个步骤,首先需要计算出各观测值与平均数的差值,然后求其平方,并对所有平方结果求和,最后将和值除以观测值的个数再开方。
示例:假设我们有一组数据:10, 12, 15, 18, 20首先计算平均值:(10 + 12 + 15 + 18 + 20) / 5 = 75 / 5 = 15然后计算差值的平方并求和:(10-15)^2 + (12-15)^2 + (15-15)^2 + (18-15)^2 + (20-15)^2 = 25 + 9 + 0 + 9 + 25 = 68最后将和值除以观测值的个数再开方:√(68/5) ≈ 3.28四、相关系数计算相关系数可以衡量两组变量之间的线性关系强弱。
它的取值范围在-1到1之间,接近-1表示强负相关,接近1表示强正相关,接近0表示无相关。
资料分析常用公式

资料分析常用公式1. 平均数公式平均数(Mean)是表示一组数据集中趋势的量数,计算公式为:$$\text{平均数} = \frac{\sum_{i=1}^{n} x_i}{n}$$其中,$ x_i $ 表示第 $ i $ 个数据,$ n $ 表示数据总数。
平均数适用于描述一组数据的总体水平,常用于市场调研、人口统计等领域。
2. 中位数公式中位数(Median)是将一组数据按大小顺序排列后位于中间位置的数,计算公式为:$$\text{中位数} =\begin{cases}\frac{x_{\frac{n+1}{2}} + x_{\frac{n}{2}}}{2} & \text{当 } n \text{ 为偶数时} \\x_{\frac{n+1}{2}} & \text{当 } n \text{ 为奇数时}\end{cases}$$其中,$ x_i $ 表示第 $ i $ 个数据,$ n $ 表示数据总数。
中位数适用于描述一组数据的中间水平,常用于描述收入、房价等分布不均的数据。
3. 标准差公式标准差(Standard Deviation)是衡量一组数据离散程度的量数,计算公式为:$$\sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i \mu)^2}{n}}$$其中,$ x_i $ 表示第 $ i $ 个数据,$ \mu $ 表示平均数,$ n $ 表示数据总数。
标准差适用于描述一组数据的波动程度,常用于质量控制、风险评估等领域。
4. 相关系数公式相关系数(Correlation Coefficient)用于衡量两个变量之间的线性关系程度,计算公式为:$$r = \frac{\sum_{i=1}^{n} (x_i \bar{x})(y_i\bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i \bar{x})^2}\sqrt{\sum_{i=1}^{n} (y_i \bar{y})^2}}$$其中,$ x_i $ 和 $ y_i $ 分别表示两个变量中的第 $ i $ 个数据,$ \bar{x} $ 和 $ \bar{y} $ 分别表示两个变量的平均数,$ n $ 表示数据总数。
资料分析公式

资料分析公式◆基期、现期基期(基础时期)、现期(现在时期)如果研究“和2006年相⽐较,2007年的某量发⽣某种变化”,则2006年为基期,2007年为现期;如果研究“和⽇本相⽐较,英国的某量发⽣某种变化”,则⽇本的数据为基期,英国的数据为现期。
◆增长率、增速(增长速度)、增幅;减少率、减少速度、减少幅度:增长率:=(现期量-基期量)÷基期量 = 增长量÷基期量增速、增幅:⼀般情况下,均与增长率相同。
(但在特殊语境下,增幅是指具体数值的增加,例如:某企业6⽉份的出⼝额和上⽉相⽐,有了800万美元的增幅,这⾥增幅就是指具体数值的增加。
)【例】某校去年招⽣⼈数2000⼈,今年招⽣⼈数为2120⼈,则今年的增长量为120⼈,增长率为 6% 。
(2120-2000=120,120÷2000×100%=6%)减少率:=(基期量-现期量)÷基期量 = 减少量÷基期量减少速度、减少幅度:与减少率相同【例】某校去年毕业⼈数1600⼈,今年毕业⼈数为1400⼈,则今年的减少量为200⼈,减少幅度为 12.5% 。
(1600-1400=200,200÷1600×100%=12.5%)【注】很明显,“减少率”本质上就是⼀种未带负号的“增长率”,所谓减少量为200⼈,就是增加量为(-200)⼈,减少幅度为12.5%,就是增加幅度为(-12.5%)。
◆百分数与百分点百分数:n% 即100n。
【例】某城市有30万⼈⼝,其中⽼年⼈有6万,则⽼年⼈占总⼈⼝的 20% 。
(6÷30×100%)百分点:n 个百分点即100n(注意百分点不带百分号),⼀般在考试中,单位为“个百分点”。
【例】某国今年粮⾷增产20%,去年增产了12%,则粮⾷的增长率提⾼了 8 个百分点(20%-12%=8%)【例】某地去年汽车销售总额⽐前年增加了8%,今年汽车销售总额⽐去年增加了13% 则今年汽车销售总额增幅提⾼了 5 个百分点。
资料分析常用公式

在学习前复习常用的公式: 1.同比增加量 Aa/1+a 2.隔年求增长率 r1+r2+r1r2 3.比重公式模型 A/B *(1+b)/(1+a) 4.乘除转换A/(1+a)=A*(1-a),a的绝对值<10% 5.比重变化量:A/B* (a-b)/(1+a) 6.比重变化率 (a-b)/(1+b) 问题分类击破 一、资料分析抓年份 去年今年和明年 年份问题是个小问题,但是,千里之堤毁于蚁穴,小细节上更容易出大问题,首先用笔画出年份,务必不要搞错,费了精力和时间,最后由于年份而功亏一篑,实不应该,公考的1分可能决定太多。
二、选项差距看难易 该放弃时就放弃 这是山东2013题目,较之往年,简单很多,一般用选项差距来衡量难易程度。
因为说到怎么算,大家都知道步骤,重要的还是如何很快的选出答案。
选项差距: 1 和2 差距很大,其实1.1和1.2,选项差距也接近10%呢,所以遇到这样的选项是很容易选出的。
比如101题,属于秒杀的题目。
而当遇到161 163 这样的恶心选项是,有时间就算,没时间就选一个走人。
比重问题:求比重、比重变化率、比重变化趋势、 比重变化趋势常考:口诀: 部分>整体,比重上升。
部分<整体,比重下降。
(这里的部分和整体分别指的部分和整体的增长率) 推导过程: 去年:部分A/(1+a) 整体:B/(1+b) 今年:部分A 整体B 去年比重:A(1+b)/B(1+a) 今年比重:A/B ---》到这里就很明显啦解题妙招 1、比较大小: 常规通分 例题:11793/1.302 9848/1.053比较大小 1053----1302 250 9848+250*9=2XXXX>11793 所以右边大于左边 差分法:(应用前提:分子分母都比另一个数小) 3.3 3.8 0.5 --------- ------- -------- (口诀:大就大值大 小就大值小) 1.092 1.163 0.7多 截位法、倍数法不赘述 补充:资料分析中的经典比较大小问题: 1150.9*7.8%/(1+7.8%) 1067.12*15%/(1+15%) 1246.97*10.9%/(1+10.9%) 1067.67*13%/(1+13%) 典型的A*a/(1+a)的形式,首先考虑A*a 2、乘除转换的应用: a=b/(1+X)=b*(1-x) x的绝对值要小于10%才适用 a=b*(1+x)=b/(1-x) 应用乘除转化时,绝对误差和选项误差比较,如果小于选项误差,则可以使用,绝对误差可以以-b*x2来近似估算(x的平方) 举例: 3772÷(1+3.4%)=( )。
事业单位自学资料-职测-资料分析常考公式大全

资料分析常考公式大全一、增长和百分点(Q 表示增长率,下同)1.基本概念⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧=⇒⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧≥≤⨯=⎩⎨⎧≥≤+=⇒⎪⎩⎪⎨⎧=+=⇒⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧≥≤+=+⨯=+=⇒⎪⎪⎩⎪⎪⎨⎧-=-=-=⇒⎪⎪⎩⎪⎪⎨⎧-=-=-=⇒)()6(3232)1()5()()()4(321)932(11)(1)3()(11)()()2()1()(1)()()1(首数法率量基量、率位错位加减法:精度位有效数字法:精度率基量位错位加减法:精度位有效数字法:精度率基现基、率首数法基量率尾数法量基现基、量位精度直接算不需要乘除系数,可以错位加减法:位有效数字法:精度现时,结果为,,特征数字法:率为率率现量首数法率现基现、率比较大小量现计算,首数法量现量率尾数法量现基现、量度拿到选项中然后判断精将计算,首数法基现比较大小基基现率尾数法基现量现、基a a a 2.隔年增长⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧≥≤++=⨯++=⎪⎩⎪⎨⎧⎩⎨⎧≥≤++=位精度直接算不需要乘除系数,可以错位加减法:位有效数字法:精度隔年倍数简单估算隔年增长率位精度直接算不需要乘除系数,可以错位加减法:位有效数字法:精度现期隔年基期32)1)(1()3()()2(32)1)(1()1(21212121Q Q Q Q Q Q Q Q 3.年均增长⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⨯+≈+=⨯+⨯≈+=⇒-≈=⎩⎨⎧⨯-=⨯+=⇒-=)(1)1())(1()1()(1)2()()1(估算偏大,选小年份差率现率现基估算偏小,选大年份差率基率基现估算偏大,选小年份差基现基现年均增长率年份差量现基年份差量基现尾数法年份差基现年均增长量年份差年份差年份差 4.百分点:百分数作差,结果读作百分点。
例如15%比10%多了5个百分点。
5.已知各个部分(部分和整体)的增长率,求整体(其他部分)的增长率。
资料分析公式及例题(最全)

A B 一、增长增长量 = 现期量 — 基期量增长率 = 增幅 = 增速 = 增长量 ÷ 基期量 = (现期量 — 基期量) ÷基期量 年均增长量、年均增长率:如果初值为 A ,第 n+1 年增长为 B ,年均增长量为 M ,年均增长率为 %,则:M=B −A = A( +x %)nn 增长量 = A × m , 当 m>0B 时, m 越大, m% 越大。
%现期量高,增长率高,则增长量高。
同比增长、环比增长同比增长:与上一年的同一时期相比的增长速度。
环比增长:与紧紧相邻的上一期相比的增长速度。
乘除法转化法: 当0 <x < 5%时, = ≈ × (1 ∓ x)B【例 1】2011 年全国农民工总量达到 25278 万人,比上年增加 1055 万人,增长 4.4%。
农民工从业仍以制造业、 建筑业和服务业为主, 从事建筑业的比重明显提 高。
从农民工的就业地区来看, 2011 年在东部地区务工的农民工 16537 万人, 比上年增加 324 万人;在中部地区务工的农民工 4438 万人,比上年增加 334 万 人, 增长 8.1%;在西部地区务工的农民工 4215 万人, 比上年增加 370 万人, 增 长 9.6%。
问题: 与上一年相比, 2011 年在东部地区务工的农民工人数增长率约为( )A . 2.0%B . 4.4%C . 5.2%D . 8.1%【例 2】2010 年,我国进出口贸易总额为 29727.6 亿美元,同比增长 34.7%。
其 中,出口额 15779.3 亿美元,同比增长 31.3%;进口额 13948.3 亿美元,同比增 1+m% 1+m%1±x 1长 38.7%。
问题: 2009 年我国进出口贸易总额约为( )万亿美元。
A.1.6B.2.2C.2.6D.3.0二、比重比重 = 分量÷总体量× 100%已知本期分量为 A,增长率为 a%,总量为 B,增长率为 b%,则:基期分量占总量的比重:A ÷ (1 + a%) A 1 + b%= ×B ÷ (1 + b%) B 1 + a%如果 a%>b%,则本期 A 占 B 的比重(B A)相较基期(B A× )有所上升。
资料分析计算公式整理

资料分析计算公式整理在进行资料分析时,掌握一些关键的计算公式是至关重要的。
这些公式能够帮助我们快速、准确地从大量的数据中提取有价值的信息,并得出有效的结论。
接下来,让我们一起对常见的资料分析计算公式进行梳理。
一、增长率相关公式增长率是资料分析中常见的一个指标,用于衡量数据的增长情况。
1、增长率=(现期量基期量)÷基期量 × 100%例如,某公司去年的销售额为 100 万元,今年的销售额为 120 万元,那么今年销售额的增长率为:(120 100)÷ 100 × 100% = 20%2、间隔增长率如果已知第二期相对于第一期的增长率为 r1,第三期相对于第二期的增长率为 r2,那么第三期相对于第一期的间隔增长率为:R = r1 +r2 + r1×r23、年均增长率假设初期值为A,末期值为B,经过n 年,年均增长率为r,则有:B = A ×(1 + r)^n二、比重相关公式比重用于反映部分在整体中所占的比例。
1、比重=部分值÷整体值 × 100%比如,某班级总人数为 50 人,其中男生有 25 人,那么男生在班级中的比重为:25÷50×100% = 50%2、整体值=部分值÷比重若已知部分值为 30,比重为 60%,则整体值为:30÷60% = 503、部分值=整体值×比重假如整体值为 80,比重为 25%,则部分值为:80×25% = 20三、平均数相关公式平均数是表示一组数据集中趋势的量数。
1、平均数=总数÷个数例如,一组数据 10、20、30、40、50,总数为 150,个数为 5,则平均数为:150÷5 = 302、总数=平均数×个数若平均数为 40,个数为 8,则总数为:40×8 = 320四、倍数相关公式倍数用于比较两个量之间的关系。
(完整版)资料分析公式汇总
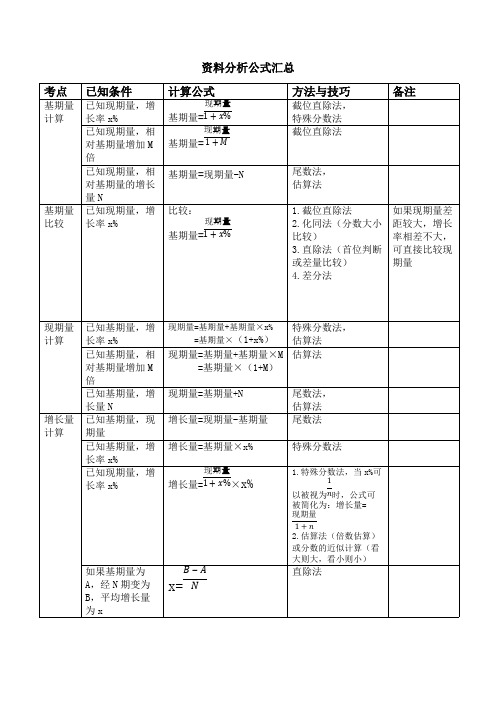
资料分析公式汇总考点已知条件计算公式方法与技巧备注已知现期量,增长率x%基期量=现期量1+x%截位直除法,特殊分数法已知现期量,相对基期量增加M 倍基期量=现期量1+M截位直除法基期量计算已知现期量,相对基期量的增长量N基期量=现期量-N尾数法,估算法基期量比较已知现期量,增长率x%比较:基期量=现期量1+x%1.截位直除法2.化同法(分数大小比较)3.直除法(首位判断或差量比较)4.差分法如果现期量差距较大,增长率相差不大,可直接比较现期量已知基期量,增长率x%现期量=基期量+基期量×x%=基期量×(1+x%)特殊分数法,估算法已知基期量,相对基期量增加M 倍现期量=基期量+基期量×M =基期量×(1+M )估算法现期量计算已知基期量,增长量N现期量=基期量+N 尾数法,估算法已知基期量,现期量增长量=现期量-基期量尾数法已知基期量,增长率x%增长量=基期量×x%特殊分数法已知现期量,增长率x%增长量=×x%现期量1+x% 1.特殊分数法,当x%可以被视为时,公式可1n 被简化为:增长量=现期量1+n2.估算法(倍数估算)或分数的近似计算(看大则大,看小则小)增长量计算如果基期量为A ,经N 期变为B ,平均增长量为xx=B ‒A N直除法增长量比较已知现期量,增长率x%增长量=×x%现期量1+x%1.特殊分数法,当x%可以被视为时,公式可1n被简化为:增长量=现期量1+n2.公式可变换为:增长量=现期量×,其中为x%1+x%x%1+x%增函数,所以现期量大,增长率大的情况下,增长量一定大已知基期量,增长量增长率=增长量基期量截位直除法,插值法已知现期量,基期量增长率=现期量‒基期量基期量截位直除法求平均增长率:如果基期量为A,第n+1期(或经n期)变为B,平均增长率为x%x%=-1nBA代入法,公式法B=A(1+X%)n当x%较小时可简化为B=A(1+nx%)求两期混合增长率:如果第一期和第二期增长率分别为r1和r2,那么第三期相对第一期增长率为r3r3= r1+r2+r1r2简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和(正负号带进公式计算)求总体增长率:整体分为A,B两个部分,分别增长a%与b%,整体增长率x%x%=A×a%+B×b%A+B x%=a%+B(b%-a%)A+B已知总体增长率和其中一个部分的增长率,求另一部分的增长率增长率计算求混合增长率:整体为A,增长率为a%,分为两个部分B,C,增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增现期量基期量长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率现期量基期量截位直除法,插值法已知部分增长量与整体增长量增长贡献量=部分增长量整体增长量截位直除法,插值法增长贡献率贡献率贡献率%=贡献量(产出量,所得量)投入量(消耗量,占用量)贡献率是指有效或有用成果数量与资源消耗及占用量之比,即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分,B拉动A增长x%x%=B的增长量A的基期量截位直除法,插值法某部分现期量为A,整体现期量为为B现期比重=AB截位直除法,插值法某部分基期量为A,增长率a%,整体基期量为B,增长率b%现期比重=AB×1+a%1+b%一般先计算,然后AB根据a和b的大小判断大小某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%一般先计算,然后AB根据a和b的大小判断大小比重计算求基期比重-现期比重:某部分现期量为A增长率a%,整体现期量为B,增长率b%两期比重差值计算:现期比重-基期比重=-×ABAB1+b%1+a%=×(1-)AB1+b%1+a%=×ABa%‒b%1+a%1.先根据a与b的大小判断差值计算结果是正数还是负数;2.答案小于|a-b|3.估算法(近似取整估算)4.直除法某部分现期量为A,整体现期量为B 现期比重=AB相当于分数大小比较,同上述做法比重比较基期比重与现期比重比较:某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%直除法,当部分增长率大于整体增长率,则现期比重大于基期比重。
数量关系与资料分析公式背诵及答案

数量关系与资料分析公式背诵及答案一、数量关系公式1.等差数列 d: ,a1,an。
通项公式:等差中项:前n项和:或2.等比数列q:通项公式:前n项和:3.加速度①v末= ; ② v= ; ③S= ; ④t=4.幂函数a n*a m=5.全错位排列(n把钥匙对应n把锁,每个锁和不能打开它的钥匙一起的排列方法数)D 1= ; D2= ; D3= ; D4= ; D5=行程问题1.等距离平均速度:适用于:直线往返、等距离两段、上下坡往返。
A B CA B C A B2.相对行程直线追击:①两人同时相向而行(面对面行走)S( )=②两人同时同向而行 S( )=环形相遇:①同点、反向 S( )=相遇时路程关系:相遇1次,S( )= 圈; 相遇n次,S( )= 圈②同点、同向 S( )=追及时路程关系:追上1次,S( )= 圈; 追上n次,S( )= 圈直线两端同时出发多次往返相遇S( )= =车头、车尾、车身问题①相向而行,两车从车头相遇到车尾相离S( )= =②同向而行,两车从相遇到相离S( )= =容斥原理问题容斥原理本质:去重补漏(不重不漏,每部分只加一次)1.两集合容斥:2.三集合容斥:3.非标准型:函数最值题型特征:单价或单利和销量此消彼长,问何时总价/总利润最高?计算法(两点式):设提价或降价的为X(注:无论问谁,设的都是的次数)①列方程:总价或总利润=()*()令总价/总利润为,解得X1,X2②当X=时,取最值。
二、资料分析公式1、基期量 = = (r代表增长率)增长量 = = = (r=1n)增长量比较:现期量和r都,那么增长量大年均增长量 =2、混合增长率口诀:,r混合偏向较大的。
3、间隔增长率公式:r间隔=;间隔倍数= ;间隔基期量=4、年均增长率:5、基期比重=6、基期比重比较=7、平均数增长率=256= 2 ;289= 2 ;324= 2 ;361= 2 ; 441= 2 ;484= 2 ;529= 2 ;576= 2 ; 676= 2 ;729= 2 ;784= 2 ;841= 2 ;一、数量关系公式1、等差数列 d:公差,a1首项,a n尾项。
资料分析计算公式整理

资料分析计算公式整理在进行资料分析时,掌握一些常用的计算公式能够帮助我们更高效、准确地处理数据和得出结论。
以下是对一些重要的资料分析计算公式的整理。
一、增长类计算公式1、增长量=现期量基期量例如,2022 年某公司的销售额为 100 万元,2021 年为 80 万元,那么增长量就是 100 80 = 20 万元。
2、增长率=增长量 ÷基期量 × 100%用上例的数据,增长率为(20 ÷ 80)× 100% = 25% 。
3、基期量=现期量 ÷(1 +增长率)假设 2023 年某产品的销量为 120 万件,同比增长 20%,则 2022 年的销量(基期量)为 120 ÷(1 + 20%)= 100 万件。
4、现期量=基期量 ×(1 +增长率)如果已知 2021 年某地区的人口为 50 万人,预计每年以 5%的速度增长,那么 2025 年的人口(现期量)为 50 ×(1 + 5%)^4 万人。
二、比重类计算公式1、比重=部分量 ÷整体量 × 100%比如,某班级男生有 20 人,全班共有 50 人,那么男生所占比重为(20 ÷ 50)× 100% = 40% 。
2、部分量=整体量 ×比重若已知某公司总利润为 1000 万元,其中 A 产品的利润占比为 30%,则 A 产品的利润为 1000 × 30% = 300 万元。
3、整体量=部分量 ÷比重比如某企业中研发部门的人数为 50 人,占总人数的 20%,则该企业总人数为 50 ÷ 20% = 250 人。
三、平均数类计算公式1、平均数=总数 ÷个数例如,某班级5 名学生的数学成绩分别为80、90、85、95、75 分,那么平均成绩为(80 + 90 + 85 + 95 + 75)÷ 5 = 85 分。
资料分析基本概念及常用公式

资料分析基本概念及常用公式(一)增长(下降)量、增长率公式本期量b/上时期量a例:13年水稻产量为b,12年产量为a,则13年比12年增长了多少?增长了=b-a增长率公式增长量/上时期量例:13年水稻产量为b,12年产量为a,则13年增长率为多少?增长率=(b-a)/a(二)同比和环比1.定义同比:指某一相同时期进行比较发生的量的增加或者的百分比的增加。
例:10年8月比09年8月增长了a环比:指本期与上一期进行比较发生的量的增加或者的百分比的增加。
例:10年8月比10年7月增长了b2.公式同比增长率=(本期量-去年同期量)/去年同期量×100%环比增长率=(本期量-上期量)/上期量×100%(三)年均增长量、年均增长率年均增长量:用来说明某种现象在一定时期内平均每期增长的数量。
公式:平均增长量=总增长量÷时间段例:10年水稻生产量为a,13年水稻生产量为b,则年均增长量为?增长量=(b-a)/3平均增长率:一段时间内某一数据指标平均每段时期的增长幅度。
例:10年水稻生产量为a,13年水稻生产量为b,则年均增长率为?增长率=a(1+x)n次方=b x为年增长率(四)百分比百分数(百分比):表示数量的增加和减少例:去年的产量为a,今年比去年增长20%,则今年为多少?今年产量=a×(1+20%)=1.2a。
例题:今年的产量为b,今年比去年增长20%,则去年为多少?去年产量=b÷(1+20%)=5/6b。
例题:去年的产量为a,今年的产量为b,今年比去年增长的百分比为多少?今年比去年增长量=b-a。
今年比去年增长的百分比=(b-a)a×100%(和谁比,谁就在分母位置)。
例题:今年的产量为b,只完成了(只占)计划的80%,则计划为多少?计划产量=b÷80%=54b。
例题:今年的产量为b,超额完成计划的20%,则计划为多少?计划产量=b÷(1+20%)=56b。
资料分析公式推导过程

资料分析公式推导过程1、平均数增长率平均数识别:均/每/单位,如人均收入=收入/人数。
平均数的增长率识别:平均+增长+%。
公式:(a-b)/(1+b)推导:平均数后除前,因此用收入/人数。
增长率r=现期/基期-1=现期平均数/基期平均数-1=A/B÷[A/B*(1+b)/(1+a)]-1=[1÷(1+b)/(1+a)]-1 =(1+a)/(1+b)-(1+b)/(1+b)= (a-b)/(1+b)。
例子:2020 年粉笔员工人数同比增长了20%,总收入同比增长了50%,问2020 年平均每名粉笔员工收入增长了______%答:平均+增长+%,因此是平均数的增长率。
平均数一般是后除前,因此用收入/人数,分子是收入,其增长率为a=50%,分母是人数,其增长率为b=20%,则r=(50%-20%)/(1+20%)。
2、平均数的增长量:(1)判定:平均数+增长+具体单位(如万元/家/个),即求某个主体的增长量,但这个主体是一个平均数,如平均每家企业的收入增长多少万元。
(2)推导过程:现期平均数- 基期平均数。
(3)公式:A/B*[(a-b)/(1+a)](同两期比重)。
3、基期比重计算公式:A/B*[(1+b)/(1+a)]。
4、两期比重比较(比较值大小)识别:两个时间+比重(上升/下降)了多少。
两期比重差:A/B*[(a-b)/(1+a)]。
推导:现期比重- 基期比重=A/B-A/B[(1+b)/(1+a)]=A/B[(a-b)/(1+a)]=(A/B[1/(1+a)](a-b))例子:已知,A: 现期部分量(例如:今年班级男生人数) a%: 部分量增长率(例如:今年班级男生的同比增长率)B: 现期整体量(例如:今年班级总人数) b%: 整体量增长率(例如:今年班级人数的同比增长率)求男学生站班级总数的比重变化了多少?5、两期平均数【知识点】两期平均数的比较:和两期比重的比较是完全一致的。
资料分析公式汇总【范本模板】

资料分析公式汇总考点已知条件计算公式方法与技巧备注基期量计算已知现期量,增长率x%基期量=截位直除法,特殊分数法已知现期量,相对基期量增加M倍基期量=截位直除法已知现期量,相对基期量的增长量N基期量=现期量-N 尾数法,估算法基期量比较已知现期量,增长率x%比较:基期量=1。
截位直除法2。
化同法(分数大小比较)3。
直除法(首位判断或差量比较)4。
差分法如果现期量差距较大,增长率相差不大,可直接比较现期量现期量计算已知基期量,增长率x%现期量=基期量+基期量×x%=基期量×(1+x%)特殊分数法,估算法已知基期量,相对基期量增加M倍现期量=基期量+基期量×M=基期量×(1+M)估算法已知基期量,增长量N现期量=基期量+N 尾数法,估算法增长量计算已知基期量,现期量增长量=现期量—基期量尾数法已知基期量,增长率x%增长量=基期量×x% 特殊分数法已知现期量,增长率x% 增长量=×x%1.特殊分数法,当x%可以被视为时,公式可被简化为:增长量=2。
估算法(倍数估算)或分数的近似计算(看大则大,看小则小)如果基期量为A,经N期变为B,平均增长量为xx=直除法增长量比较已知现期量,增长率x%增长量=×x%1.特殊分数法,当x%可以被视为时,公式可被简化为:增长量=2。
公式可变换为:增长量=现期量×,其中为增函数,所以现期量大,增长率大的情况下,增长量一定大增长率计算已知基期量,增长量增长率=截位直除法,插值法已知现期量,基期量增长率=截位直除法求平均增长率:如果基期量为A,第n+1期(或经n期)变为B,平均增长率为x%x%=—1代入法,公式法B=A(1+X%)n当x%较小时可简化为B=A(1+nx%)求两期混合增长率:如果第一期和第二期增长率分别为r1和r2,那么第三期相对第一期增长率为r3r3= r1+r2+r1r2 简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和(正负号带进公式计算)求总体增长率:整体分为A,B两个部分,分别增长a%与b%,整体增长率x%x%=x%=a%+已知总体增长率和其中一个部分的增长率,求另一部分的增长率求混合增长率:整体为A,增长率为a%,分为两个部分B,C,增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率截位直除法,插值法增长贡献率已知部分增长量与整体增长量增长贡献量=截位直除法,插值法贡献率贡献率%=贡献率是指有效或有用成果数量与资源消耗及占用量之比,即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分,B拉动A增长x%x%=截位直除法,插值法比重计算某部分现期量为A,整体现期量为为B现期比重=截位直除法,插值法某部分基期量为A,增长率a%,整体基期量为B,增长率b%现期比重=一般先计算,然后根据a和b的大小判断大小某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×一般先计算,然后根据a和b的大小判断大小求基期比重—现期比重:某部分现期量为A增长率a%,整体现期量为B,增长率b%两期比重差值计算:现期比重-基期比重=-×=×(1—)=×1.先根据a与b的大小判断差值计算结果是正数还是负数;2.答案小于|a—b|3.估算法(近似取整估算)4.直除法比重比较某部分现期量为A,整体现期量为B现期比重=相当于分数大小比较,同上述做法基期比重与现期比重比较:某部分现期量为A,基期比重=×直除法,当部分增长率大于整体增长率,则现期比增长率a%,整体现期量为B,增长率b% 重大于基期比重。
资料分析常用公式

资料分析常用公式1. 平均数公式平均数(Mean)是表示一组数据集中趋势的量数,计算公式为:$$\text{平均数} = \frac{\sum_{i=1}^{n} x_i}{n}$$其中,$ x_i $ 表示第 $ i $ 个数据,$ n $ 表示数据的总数。
平均数适用于描述数据的中心位置,常用于市场调查、产品评价等领域。
2. 中位数公式中位数(Median)是将一组数据从小到大(或从大到小)排列,位于中间位置的数值。
计算公式为:$$\text{中位数} = \begin{cases}x_{\frac{n+1}{2}} & \text{当 } n \text{ 为奇数时} \\\frac{x_{\frac{n}{2}} + x_{\frac{n}{2}+1}}{2} & \text{当 } n \text{ 为偶数时}\end{cases}$$中位数适用于描述数据的中心位置,特别适用于数据分布不均匀或存在异常值的情况。
3. 标准差公式标准差(Standard Deviation)是衡量一组数据离散程度的量数,计算公式为:$$\sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i \mu)^2}{n}}$$其中,$ \sigma $ 表示标准差,$ x_i $ 表示第 $ i $ 个数据,$ \mu $ 表示平均数,$ n $ 表示数据的总数。
标准差越大,表示数据的离散程度越大,反之越小。
4. 相关系数公式相关系数(Correlation Coefficient)用于衡量两个变量之间的线性关系程度,计算公式为:$$r = \frac{n(\sum xy) (\sum x)(\sum y)}{\sqrt{[n\sum x^2 (\sum x)^2][n\sum y^2 (\sum y)^2]}}$$其中,$ r $ 表示相关系数,$ x $ 和 $ y $ 分别表示两个变量,$ n $ 表示数据的总数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、增长
增长量= 现期量—基期量
增长率= 增幅= 增速= 增长量÷基期量 =(现期量—基期量)÷基期量年均增长量、年均增长率:
如果初值为A,第n+1年增长为B,年均增长量为M,年均增长率为,则:M=
增长量= ,当m0 时,m越大,越大。
现期量高,增长率高,则增长量高。
同比增长、环比增长
同比增长:与上一年的同一时期相比的增长速度。
环比增长:与紧紧相邻的上一期相比的增长速度。
乘除法转化法:
当x
【例1】2011年全国农民工总量达到25278万人,比上年增加1055万人,增长%。
农民工从业仍以制造业、建筑业和服务业为主,从事建筑业的比重明显提高。
从农民工的就业地区来看,2011年在东部地区务工的农民工16537万人,比上年增加324万人;在中部地区务工的农民工4438万人,比上年增加334万人,增长%;在西部地区务工的农民工4215万人,比上年增加370万人,增长%。
问题:与上一年相比,2011年在东部地区务工的农民工人数增长率约为()A.% B.% C.% D.%
【例2】2010年,我国进出口贸易总额为亿美元,同比增长%。
其中,出口额亿美元,同比增长%;进口额亿美元,同比增长%。
问题:2009年我国进出口贸易总额约为()万亿美元。
二、比重
比重= 分量÷总体量×100%
已知本期分量为A,增长率为a%,总量为B,增长率为b%,则:
基期分量占总量的比重:
如果a%b%,则本期A占B的比重()相较基期()有所上升。
如果a%b%,则本期A占B的比重()相较基期()有所下降。
本期比重较基期变化:
百分数、百分点
百分数,是形容比例或者增长率等常用的数值形式。
百分点,是指不带百分号的百分数,如:n个百分点,代表n%。
当我们进行实际量之间的比较时,一般使用“百分数”来表示,需要除以参考值。
当我们进行比例或者增长率之间的比较时,一般使用“百分点”来表示,偶尔也可以用百分数来表示,比较时直接相减即可,不需要除以参考值。
翻番
即变为原来的2倍。
翻n番:即变为原来的倍。
【例3】2010年,某省广电实际总收入为亿元,同比增长%。
其中,广告收入为亿元,同比增长%;有线网络收入为亿元,同比增长%;其他收入为亿元,同比增长%。
问题:2009年,该省广告收入占广电总收入的比重约为:()
% % % %
【例4】中国汽车工业协会发布的2009年4月份中国汽车产销数据显示,在其他国家汽车销售进一步疲软的情况下,国内乘用车销量却持续上升,当月销售已达万辆,比3月份增长%,同比增长%。
?
乘用车细分为基本型乘用车(轿车)、多功能车(MPV)、运动型多用途车(SUV)和交叉乘用车。
其中,轿车销量比3月份增长%,同比增长%;MPV销量比3月份下降%,同比下降%;SUV销量比3月份增长%,同比增长%;交叉型乘用车销量比3月份增长%,同比增长%。
轿车、MPV、SUV和交叉型乘用车销量占4月份乘用车总销量的比重分别为71%、2%、6%和21%。
问题:关于2009年3月份各种车型销量在总销量中所占比重的描述,以下正确的是:
A.MPV超过2% B.交叉型乘用车低于21%
C.SUV超过6% D.轿车超过71%
【例5】2011年,全国房地产开发企业房屋施工面积亿平方米,比上年增长%,增速比上年回落个百分点;其中,住宅施工面积亿平方米,增长%。
房屋新开工面积亿平方米,增长%增速比上年回落个百分点;其中,住宅新开工面积亿平方米,增长%,房屋竣工面积亿平方米,增长%,增速比上年提高5个百分点;其中,住宅竣工面积亿平方米,增长%。
问题:2011年,我国房地产开发企业住宅新开工面积占房屋新开工面积的比重比上年:()
A.上升了个百分点
B.上升了个百分点
C.下降了个百分点
D.下降了个百分点
三、平均数
平均量= 总量÷总数
平均数与增长
已知本期某事物的总量为A、总数为B,分别增长a%、b%,则基期平均数为:
已知本期某事物的总量为A、总数为B,分别增长a%、b%,则本期平均数的增长量为:
已知本期某事物的总量为A、总数为B,分别增长a%、b%,则本期平均数的增长率为:
【例6】2011年25家已公布一季报的房地产公司一季度实现营业收入亿元,同比增长9%;实现净利润亿元,同比增长31%;存货亿元,同比增长10%。
问题:已公布2011年一季报的房地产公司中,平均每家公司的存货比上年同期增长了约多少亿元?
一、根据以下资料,回答131~135题。
2008—2012年国家电网公司机组并网容量
2008年2009年2010年2011年2012年
并网总容量61300 67100 74400 81800 88000
其中:清洁能源机组并网容量13524 15357 17585 20260 24004 其中:水电并网容量12214 13419 14458 15617 16816 核电并网容量507 507 574 640 640
新能源发电机组并网容量803 1431 2553 4003 6548
2008—2012年国家电网公司机组上网电量
2008年2009年2010年2011年2012年
总上网电量22800 24300 28800 32400 33900
其中:清洁能源机组上网电量4161 4321 4903 5943 7177 其中:水电上网电量3662 3692 4103 4373 5518 核电上网电量353 355 308 416 475
新能源发电机组上网电量146 724 492 1154 1184
A.2010年 B.2009年 C.2012年 D.2011年
132.2012年清洁能源机组并网容量占当年并网机组总容量的比重比上年:A.上升了个百分占 B.上升了个百分点
C.下降了个百分点 D.下降了个百分点
133.下列年份中,清洁能源机组上网电量占当年并网机组总上网电量比重最高的是:
A.2009年 B.2008年 C.2012年 D.2011年134.下列哪一张图能反映2012年清洁能源机组并网容量中水电、核电和新能源发电的构成?
A B C D
135.关于2008~2012年间国家电网公司清洁能源的发展,能够从资料中推出的是:A.新能源发电机组上网电量从2011年开始超过核电上网电量
B.水电上网电量年均增长率超过同期水电并网容量
C.新能源发电机组并网容量翻了8番
D.核电上网电量保持持续增长
二、根据以下资料,回答116-120题。
某市2010年全年实现农业增加值亿元,比上年下降%。
粮食播种面积万公顷,比上年减少万公顷;粮食产量万吨,比上年下降%。
全市农业观光园1303个,比上年增加9个;观光园总收入亿元,比上年增长%。
民俗旅游实际经营户7979户,比上年减少726户;民俗旅游总收入亿元,增长%。
种业收入亿元,比上年增长%。
已利用设施农业占地面积18323公顷,比上年下降%;实现收入亿元,增长%。
2010年主要农副产品产量
116.该市2009年全年实现农业增加值约:
亿元亿元亿元亿元
117.该市2010年粮食平均产量约为每公顷:
吨吨吨吨
118.该市主要农副产品与上年相比,产量变化绝对值最小是:
A.肉类
B.禽蛋
C.水产品
D.牛奶
119.该市种业收入增长速度:
A.高于观光园总收入增长速度
B.高于设施农业收入增长速度
C.低于民俗旅游总收入增长速度
D.低于设施农业占地面积增长速度120.下列说法与资料相符的是:
年该市粮食产量不到蔬菜产量的1/3
年该市主要农副产品产量均有所下降
年该观光园数量为1312个
年该市单位面积粮食产量比上年有所下降
三、根据所给图表、文字资料回答问题。
2011年上年年,我国软件产业实现软件业务收入8065亿元,同比增长%,增速比去年同期高个百分点;实现利润103亿元,同比增长%。
其中,6月份完成软件业务收入1828亿元,同比增长,增速比5月份回升个百分点。
上半年,信息技术咨询服务、数据处理和营运服务实现收入761和1073亿元,同比增长%和%,分别高出全行业和个百分点;嵌入式系统软件实现收入1443亿元,同比增长%,增速比去年同期高个百分点。
软件产品和信息系统集成服务发展较为稳定,分别实现收入2867和1673亿元,同比增长%和%。
IC设计增长放缓,上半年实现收入248亿元,同比增长%,低于去年同期20个百分点以上。
年6月份我国软件业务收入占上半年的总值比重约为()
A、%
B、%
C、%
D、%
112.与2011年一季度相比,二季度软件业务收入增长了约()
A、%
B、%
C、%
D、
年上半年嵌入式系统软件收入同比增长了()
A、307亿元
B、365亿元
C、424亿元
D、488亿元
年上半年收入占整个软件产业的比重高于上半年同期水平的是()
A、信息系统集成
B、嵌入式系统集成
C、IC设计
D、软件产品
115.以下说法与资料相符的是()
A、2011年5月份我国软件产业实现软件业务收入同比增长%
B、2011年3月份我国软件产业实现软件业务收入高于4月份
C、2011年上半年信息技术服务实现收入超过1800亿元
D、2010年上半年IC设计实现收入同比增速为%。
