工程光学习题一答案
工程光学课后答案完整版_机械工业出版社_第二版_郁道银

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
第三版工程光学答案[1]
![第三版工程光学答案[1]](https://img.taocdn.com/s3/m/a7b6190ba7c30c22590102020740be1e650ecce7.png)
第一章3、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离. 解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm 即屏到针孔的初始距离为300mm。
4、一厚度为200mm的平行平板玻璃(设n=1。
5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?n0sinI1=n2sinI2(1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2) 由(1)式和(2)式联立得到n0。
16、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
如果在凸面镀反射膜,其会聚点应在何处?如果在凹面镀反射膜,则反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后,会聚点又在何处?说明各会聚点的虚实。
解:该题可以应用单个折射面的高斯公式来解决,设凸面为第一面,凹面为第二面. (1)首先考虑光束射入玻璃球第一面时的状态,使用高斯公式:会聚点位于第二面后15mm处.(2)将第一面镀膜,就相当于凸面镜像位于第一面的右侧,只是延长线的交点,因此是虚像。
还可以用β正负判断:(3)光线经过第一面折射:, 虚像第二面镀膜,则:得到:(4)在经过第一面折射物像相反为虚像。
18、一直径为400mm,折射率为1.5的玻璃球中有两个小气泡,一个位于球心,另一个位于1/2半径处。
沿两气泡连线方向在球两边观察,问看到的气泡在何处?如果在水中观察,看到的气泡又在何处?解:设一个气泡在中心处,另一个在第二面和中心之间。
(1)从第一面向第二面看(2)从第二面向第一面看(3)在水中19、.有一平凸透镜r=100mm,r,d=300mm,n=1。
5,当物体在时,求高斯像的位置。
工程光学-第一章-习题及解答

l
B
200mm
●● ●
A’ A B
2. 一束平行细光束入射到一半径r=30mm、 折射率n=1.5的玻璃球上,求其会聚点的位 置。如果在凸面镀反射膜,其会聚点应在何 处?如果在凹面镀反射膜,则折射光束在玻 璃中的会聚点又在何处?反射光束经前表面 折射后,会聚点又在何处?说明各会聚点的 虚实。
1
r5 30mm
代入①式,得:l5' 75mm (虚像)
距 1 面右侧75mm处
1
2
.
C
3. 有平凸透镜r=100mm,r=∞,d=300mm, n=1.5,当物体在-∞时,求高斯像的位置l’。 在第二面上刻一十字丝,
问: 其通过球面的共轭像处? 当入射高度h=10mm时,实际光线的像方 截距为多少?与高斯像面的距离为多少?
l,l ' , r
dl r l r l'
d
l
l'
0
112
l' l r
Q
C
l
ON
M
h
Q’ N O
l' r
6. 两薄透镜的焦距为 f1' 5.0cm
和
f
' 2
10.0cm
,相距5.0cm。若
一高为2.50cm的物体位于第一透镜前15.0cm处,求最后所成像
4. 一球面镜半径r=-100mm,求β=0,-0.1, -0.2, -1,1,5,10,∞时的物距和像距。
解:
1 12
l
l l r
l
5. 试从费马原理出发,导出凹球面反射镜 近轴成像公式: 1 1 2 ,做出示意图。
工程光学第一章练习参考答案

l 2 ' 15 mm
第一章 16
(2)凸面镀反射膜 r1
l , r 30 , n 1 , n ' 1 n' l' l' n l n' n ' n n ' n r r 1 11 30 15 mm
第一章 16
(3)凹面镀反射膜 (a)在左球面折射
l 2 ' 10 mm
第一章 16
(4)凹面镀反射膜 (a)在左球面折射 (b)在右球面第二次反射
r1
r2
l 2 ' 10 mm
(c)再左球面第三次折射
l 50 mm , r 30 , n 1 . 5 , n ' 1 n' l' 1 l' n l 1 .5 50 n ' n r 1 1 .5 30
n1
I2’
n 1 sin I 1 n 1 sin I 2 ' I1 I 2'
第一章 8
I1’ I1 n 0 sin I 1 n 1 sin I 1 ' n 1 sin I 2 n 2 sin 90 n 2 I 1 ' 90 I 2 I2
n0 n2 n1
3 10 1 . 526
8
1 . 966 10 m / s
8 8
3 10 2 . 417
1 . 241 10 m / s
第一章 4
D=?
h=200mm
全反射问题. (1)
n sin I 1 sin 90 sin I 1 I 41 . 81 n
I
1
工程光学课后答案-第二版-郁道银

工程光学第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学第一章习题及解答

解题技巧总结
建立清晰的解题思路
根据题目要求,建立清晰的解 题思路,明确解题方向和步骤。
提高计算能力
通过练习和总结,提高自己的 计算能力和准确性,避免因计 算失误导致错误。
仔细审题
在开始解题之前,务必仔细阅 读题目,明确题目要求和给定 条件。
准确应用公式和定理
在解题过程中,准确应用相关 的公式和定理,确保适用条件 和范围正确。
注意细节和隐含条件
在解题过程中,注意细节和隐 含条件,确保解题思路和结果 完整准确。
05 习题拓展
相关知识点拓展
01
光的干涉
光的干涉是光波动性的重要表现之一,它涉及到光的相干性、干涉条件、
干涉图样等知识点。可以进一步了解干涉现象在日常生活和科技领域中
的应用,如光学干涉仪、薄膜干涉等。
02
光的衍射
光的衍射描述了光在传播过程中遇到障碍物时发生的偏离直线传播的现
象。可以深入了解衍射与干涉的区别和联系,以及衍射在光学仪器设计、
光谱分析等领域的应用。
03
光学仪器
了解各种光学仪器的基本原理和应用,如显微镜、望远镜、照相机等。
探究这些仪器中光的干涉、衍射等现象的应用,以及如何提高光学仪器
的性能。
类似题目推荐
题目
什么是光的偏振现象?请举例说明。
答案
光的偏振现象是指光波的电矢量或磁矢量在某一特定方向 上振动。例如,自然光通过偏振片后,只能沿特定方向振 动的光波通过,形成线偏振光。
题目
简述光的色散现象。
答案
光的色散现象是指不同波长的光在传播速度上存在差异, 导致白光通过棱镜后分解成不同颜色的光谱。这是因为不 同波长的光在介质中的折射率不同。
取为无穷大。
工程光学第3版第一章习题答案

• 光学元件的特性与选择:不同光学元件具有不同的特性,如透镜的焦距、折射 率,反射镜的反射率、角度等。在选择和使用光学元件时,需要考虑系统的需 求和限制,如成像质量、光束直径、光谱范围等。
习题1.6
什么是光的衍射?衍射现象有哪些应用?
答案
光的衍射是指光波在遇到障碍物时,绕过障碍物的边缘继 续传播的现象。衍射现象在许多领域都有应用,如全息摄 影、光学仪器制造和光学信息处理等。
习题1.3答案
习题1.7
什么是光谱线及其分类?光谱分析的原理是什么?
答案
光谱线是指物质在特定温度和压力下发射或吸收的特定波长的光。根据产生机理 ,光谱线可分为发射光谱和吸收光谱。光谱分析的原理是利用物质对光的吸收、 发射或散射特性来分析物质的组成和结构。
习题1.2
简述光学显微镜的基本组成部分。
习题1.1答案
习题1.3
如何正确使用光学显微镜?
答案
使用光学显微镜时,应先调节光源亮度,然后调节聚光镜和物镜的焦距,确保 样品清晰可见。接着,通过调节载物台和调焦装置,使样品在显微镜视场中居 中。最后,通过目镜观察并记录观察结果。
习题1.2答案
习题1.4
什么是光的折射?折射率与题考察了光学显微镜的分辨本领与照 明方式、物镜的数值孔径和照明光的波长的 关系。光学显微镜的分辨本领主要取决于物 镜的数值孔径和照明光的波长。数值孔径越 大,照明光的波长越短,则显微镜的分辨本 领越高。同时,照明方式也会影响显微镜的 分辨本领,暗视场显微镜具有较高的对比度
练习题3
工程光学练习答案(带样题).doc

工程光学练习答案(带样题)期末,东北石油大学审查了09级工程光学的测量和控制材料。
第一章练习1,假设真空中的光速为3米/秒,则计算水中(n=1.333)、皇冠玻璃(n=1.51)、燧石玻璃(n=1.65)、加拿大树胶(n=1.526)、钻石(n=2.417)和其他介质中的光速。
解决方案:当灯在水中时,n=1.333,v=2.25m米/秒,当灯在皇冠玻璃中时,n=1.51,v=1.99m米/秒,当灯在燧石玻璃中时,n=1.65,v=1.82m米/秒,当灯在加拿大树胶中时,n=1.526,v=1.97m米/秒,当灯在钻石中时,n=2.417,v=1.24米/秒。
2.一个物体穿过针孔照相机,在屏幕上形成一个60毫米大小的图像。
如果屏幕被拉开50毫米,图像的尺寸变成70毫米,计算出从屏幕到针孔的初始距离。
解决方案:在同一个均匀的介质空间中,光直线传播。
如果选择通过节点的光,方向不会改变,从屏幕到针孔的初始距离为x,则可以根据三角形的相似性得到:因此,x=300mm毫米意味着从屏幕到针孔的初始距离是300毫米。
3、一块厚度为200毫米的平行平板玻璃(n=1.5),下面放一块直径为1毫米的金属板。
如果玻璃板上覆盖有圆形纸片,则要求玻璃板上方的任何方向都不能看到纸片。
这张纸的最小直径是多少?解决方案:如果纸片的最小半径是x,那么根据全反射原理,当光束从玻璃发射到空气中的入射角大于或等于全反射临界角时,就会发生全反射,正是由于这个原因,在玻璃板上方看不到金属片。
全反射的临界角由下式确定:(1)其中N2=1,n1=1.5,根据几何关系,利用平板的厚度和纸张与金属片的半径计算全反射临界角的方法如下:(2)纸张的最小直径x=179.385mm毫米可以通过组合等式(1)和(2)来获得,因此纸张的最小直径为358.77毫米4.光纤芯的折射率是n1.包层的折射率为n2,光纤所在介质的折射率为n0。
计算光纤的数值孔径(即n0sinI1,其中I1是光在光纤中以全反射模式传播时,光在入射端面的最大入射角)。
工程光学习题答案

⼯程光学习题答案⼯程光学习题答案第⼀章习题及答案1、已知真空中的光速c=3*108m/s,求光在⽔(n=1.333)、冕牌玻璃(n=1.51)、⽕⽯玻璃(n=1.65)、加拿⼤树胶(n=1.526)、⾦刚⽯(n=2.417)等介质中的光速。
解:则当光在⽔中, n=1.333 时,v=2.25*108m/s,当光在冕牌玻璃中,n=1.51 时,v=1.99*108m/s,当光在⽕⽯玻璃中,n=1.65 时,v=1.82*108m/s,当光在加拿⼤树胶中,n=1.526 时,v=1.97*108m/s,当光在⾦刚⽯中,n=2.417 时,v=1.24*108m/s。
2、⼀物体经针孔相机在屏上成⼀60mm ⼤⼩的像,若将屏拉远50mm,则像的⼤⼩变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则⽅向不变,令屏到针孔的初始距离为x,则可以根据三⾓形相似得出:所以x=300mm 即屏到针孔的初始距离为300mm。
3、⼀厚度为200mm 的平⾏平板玻璃(设n=1.5),下⾯放⼀直径为1mm 的⾦属⽚。
若在玻璃板上盖⼀圆形纸⽚,要求在玻璃板上⽅任何⽅向上都看不到该⾦属⽚,问纸⽚最⼩直径应为多少?解:令纸⽚最⼩半径为x,则根据全反射原理,光束由玻璃射向空⽓中时满⾜⼊射⾓度⼤于或等于全反射临界⾓时均会发⽣全反射,⽽这⾥正是由于这个原因导致在玻璃板上⽅看不到⾦属⽚。
⽽全反射临界⾓求取⽅法为:(1)其中n2=1, n1=1.5,同时根据⼏何关系,利⽤平板厚度和纸⽚以及⾦属⽚的半径得到全反射临界⾓的计算⽅法为:(2)联⽴(1)式和(2)式可以求出纸⽚最⼩直径x=179.385mm,所以纸⽚最⼩直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1 为光在光纤内能以全反射⽅式传播时在⼊射端⾯的最⼤⼊射⾓)。
工程光学习题解答(第1章)

第一章1.举例说明符合光传播基本定律的生活现象及各定律的应用.答:(1)光的直线传播定律影子的形成;日蚀;月蚀;均可证明此定律。
应用:许多精密的测量,如大地测量(地形地貌测量),光学测量,天文测量。
(2)光的独立传播定律定律:不同光源发出的光在空间某点相遇时,彼此互不影响,各光束独立传播.说明:各光束在一点交会,光的强度是各光束强度的简单叠加,离开交会点后,各光束仍按各自原来的方向传播。
2.已知真空中的光速c≈3×108m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1。
65)、加拿大树胶(n=1.526)、金刚石(n=2。
417)等介质中的光速。
解:v=c/n(1)光在水中的速度:v=3×108/1。
333=2。
25×108 m/s(2)光在冕牌玻璃中的速度:v=3×108/1。
51=1。
99×108 m/s(3)光在火石玻璃中的速度:v=3×108/1。
65=1.82×108 m/s(4)光在加拿大树胶中的速度:v=3×108/1。
526=1。
97×108 m/s(5)光在金刚石中的速度:v=3×108/2。
417=1。
24×108 m/s*背景资料:最初用于制造镜头的玻璃,就是普通窗户玻璃或酒瓶上的疙瘩,形状类似“冠”,皇冠玻璃或冕牌玻璃的名称由此而来。
那时候的玻璃极不均匀,多泡沫。
除了冕牌玻璃外还有另一种含铅量较多的燧石玻璃(也称火石玻璃)。
3.一物体经针孔相机在屏上成像的大小为60mm,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离.解:⇒l=300mm4.一厚度为200mm的平行平板玻璃(设n=1。
5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:本题是关于全反射条件的问题。
工程光学第一章习题答案

光学习题解答 CH11、 生活中有很多光学现象,例如,两个手电筒的发出的光在空气中相遇后又独自的直线转播,平面镜成像,水底的鱼看起来比实际浅等都符合光学基本定律。
2、 根据公式v=c/n 可得:光在水中的传播速度为:v=2.25×108m/s 光在冕牌玻璃中的传播速度为:v=1.987×108m/s 光在火石玻璃中的传播速度为:v=1.82×108m/s 光在加拿大树胶中的传播速度为:v=1.96×108m/s 光在金刚石中的传播速度为:v=1.241×108m/s3、 根据题意可得,可以设x 为屏到孔的距离,根据几何关系有如下式子成立:=+50x x 7060,可以解得x=300mm 4、 见图,本题涉及到全反射现象。
金属片边缘点发出光线照射到玻璃另一面是光密介质传入光疏介质,符合全反射条件,=θ∠ACB,有公式:,15.1sin 90sin =θ32sin =θ, D=2L CD +1=358.77mm图1.1习题45、①光从光密介质射到它与光疏介质的界面上,②入射角等于或大于临界角.这两个条件都是必要条件,两个条件都满足就组成了发生全反射的充要条件。
6、只要证明入射角和出射角相等就可以。
7、见下图,可知,光后偏角为:δ=αθ-,有1s i n s i n n=∂θ,由于∂,θ都很小,可知,∂=∂=sin ,sin θθ,得δ=αθ-=)1(-∂n图1.2 题78、见课本图1.6所示,数值孔径一般代表光纤传播光的能力。
记为NA 。
根据三角函数关系及其全反射临界条件有:=Im sin 90sin 21n n ,,01Im)90sin(1sin n n I =-解得NA=n 0sin I 1=2221n n -.9、光在冕牌玻璃中的折射率为n=1.51,由全反射临界条件:∂sin 90sin =n,由图可以知道,β=45o -∂,将n=1.51代人,可以解得θ=5o 40'。
工程光学第3版第一篇习题答案
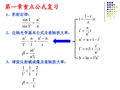
1 2 0
物像虚实相同,为实像.
[习题16解答]
(2)若凸面镀上反射膜, 光束经左侧球面反射成像.
1 1 2 l l r
求得:
l 15 l 0 l
物像虚实相反,成虚像。
[习题17]一折射球面r=150mm,n=1,n’=1.5, 问当物距分别为-、-1000mm、-100mm、0、 100mm、150mm和200mm时,垂轴放大率各 为多少?
解:根据近轴光学基本公式及垂轴放大率公式
n n n n l l r nl nl
先求l’ ,再求β .
为实像. 它又 物像虚实相同,故 A2 是左侧球面的物A3 ,为实物。根据光 路可逆性,可将A3看成左侧球面折射 形成的像。
[习题16解答]
(3)光束先经左侧球面折射形成 , 像 A1 ,再经右侧球面反射形成像 A2 。 最后经左侧球面折射形成像 A3
60 10 50 l3 n n n n 根据 l l r nl3 求得 l3 =75,3 = 0 nl3 物像虚实相反,成虚像。 即
前表面 后表面
1 n 1 n 2 R R n2
[习题15]一直径为20mm的玻璃球,其折射率 为 3 ,今有一光线以60入射角入射到该玻璃 球上,试分析光线经过玻璃球的传播情况。
解:在入射点A处,同时发生折 射和反射现象。 sin I1 n sin I 2
sin 60 ) 30 3 在A点处光线以60°的反射角返 回原介质,同时以30 °的折射角 进入玻璃球。折射光线到达B点, 并发生折射反射现象。由图得: I3 =I 2 =30, I5 =I3 =30 I 2 arcsin(
工程光学第三版课后答案1

第一章2、已知真空中的光速c =3*108m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的 光速。
解:则当光在水中,n=1.333 时,v=2.25*108m/s, 当光在冕牌玻璃中,n=1.51 时,v=1.99*108m/s, 当光在火石玻璃中,n =1.65 时,v=1.82*108m/s , 当光在加拿大树胶中,n=1.526 时,v=1.97*108m/s , 当光在金刚石中,n=2.417 时,v=1.24*108m/s 。
3、一物体经针孔相机在屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向 不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm 。
4、一厚度为200mm 的平行平板玻璃(设n=1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少? 解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1) 其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm , 所以纸片最小直径为358.77mm 。
8、.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
工程光学习题参考答案第一章几何光学基本定律
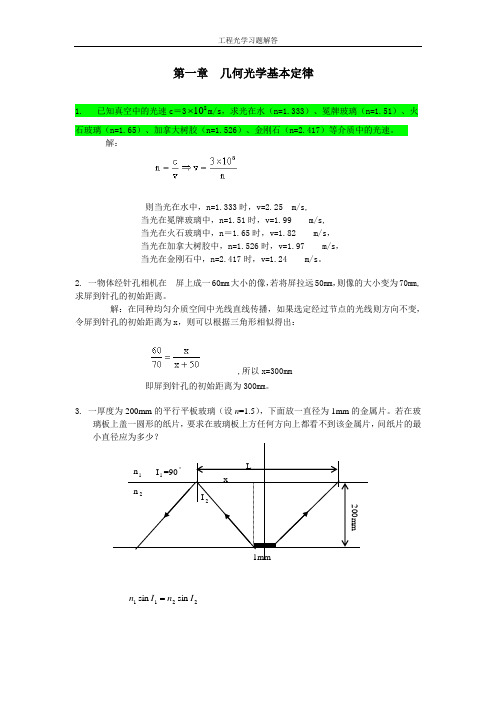
第一章 几何光学基本定律1. 已知真空中的光速c =3810⨯m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s ,当光在金刚石中,n=2.417时,v=1.24 m/s 。
2. 一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. 一厚度为200mm 的平行平板玻璃(设n =1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?2211sin sin I n I n =1mm I 1=90︒n 1 n 2200mmL I 2 x66666.01sin 22==n I745356.066666.01cos 22=-=I88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学答案_课后答案_郁道银_第二版_完整

10.长 60 mm,折射率为 1.5 的玻璃棒,在其两端磨成曲率半径为 10 mm 的凸 球面,试求其焦距。 解:
11.一束平行光垂直入射到平凸透镜上,会聚于透镜后 480 mm 处,如在此透镜 凸面上镀银,则平行光会聚于透镜前 80 mm 处,求透镜折射率和凸面曲率半径。 解 :
8
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
7
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
8.已知一透镜 度。 解:
求其焦距、光焦
9.一薄透镜组焦距为 100 mm,和另一焦距为 50 mm 的薄透镜组合,其组合焦 距仍为 100 mm,问两薄透镜的相对位置。 解:
6.希望得到一个对无限远成像的长焦距物镜,焦距
=1200mm,由物镜顶点到
像 面 的 距 离 L=700 mm , 由 系 统 最 后 一 面 到 像 平 面 的 距 离 ( 工 作 距 ) 为 ,按最简单结构的薄透镜系统考虑,求系统结构,并画出光路图。 解:
7.一短焦距物镜,已知其焦距为 35 mm,筒长 L=65 mm,工作距,按最简单结构 的薄透镜系统考虑,求系统结构。 解:
此为平板平移后的像。
5.棱镜折射角 材料的折射率。 解:
,C 光的最小偏向角
,试求棱镜光学
10
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
6.白光经过顶角
(2) 由(1)式和(2)式联立得到 n0 sinI1 . 5、一束平行细光束入射到一半径 r=30mm、折射率 n=1.5 的玻璃球上,求其会聚 点的位置。如果在凸面镀反射膜,其会聚点应在何处?如果在凹面镀反射膜,则 反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后, 会聚点又在何 处?说明各会聚点的虚实。 解:该题可以应用单个折射面的高斯公式来解决,
工程光学习题答案(附试题样本)

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学基础教程_习题参考答案

工程光学基础教程_习题参考答案工程光学基础教程_习题参考答案第一章光学基本知识与技术1.1 什么是光学?光学在人类生活中有哪些应用?答:光学是研究光的行为和性质的物理学科。
它涉及到光的产生、传播、变换、干涉、衍射、偏振以及光在介质中的行为等问题。
光学在人类生活中有着广泛的应用,如眼镜、镜头、显示器、照明、医疗器械、天文望远镜等。
1.2 光的波动性是如何描述的?答:光的波动性是指光是一种电磁波,具有振幅、频率、波长等特征。
它可以在空间中传播,并且可以表现出干涉、衍射等波动性质。
光的波动性可以通过波长、频率、振幅等参数进行描述。
1.3 什么是光的干涉?举例说明其应用。
答:光的干涉是指两列或两列以上的光波在空间中叠加时,由于光波的叠加产生明暗相间的干涉条纹的现象。
光的干涉在很多领域都有应用,例如光学干涉仪、双缝干涉实验、全息照相、光学通信等。
1.4 什么是光的衍射?举例说明其应用。
答:光的衍射是指光在遇到障碍物或孔径时,会绕过障碍物或孔径边缘,产生明暗相间的衍射图案的现象。
光的衍射在很多领域也有应用,例如光学透镜、衍射光学器件、全息照相、光学存储等。
1.5 什么是光的偏振?举例说明其应用。
答:光的偏振是指光波的电矢量在振动时,只在某个方向上振动,而在其他方向上振动为零的现象。
光的偏振在很多领域也有应用,例如偏振眼镜、偏振片、偏振光学器件等。
第二章光学透镜与成像2.1 什么是透镜?列举几种常见的透镜及其特点。
答:透镜是一种光学器件,它由一块透明材料制成,可以聚焦或发散光线。
常见的透镜包括凸透镜、凹透镜、平凸透镜、平凹透镜等。
2.2 凸透镜的成像原理是什么?如何计算凸透镜的焦距?答:凸透镜的成像原理是光线经过凸透镜后,平行于主轴的光线会聚于一点,这个点称为焦点。
焦距是指从透镜中心到焦点的距离。
凸透镜的焦距可以通过公式 f=1/v+1/u 进行计算,其中f为焦距,u为物距,v为像距。
2.3 凹透镜的成像原理是什么?如何计算凹透镜的焦距?答:凹透镜的成像原理是光线经过凹透镜后,平行于主轴的光线会朝透镜中心方向会聚于一点,这个点称为虚焦点。
工程光学,郁道银,第一章习题及答案

学习必备欢迎下载第一章习题及答案1、已知真空中的光速c=3*108m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333 时,v=2.25*108m/s, 当光在冕牌玻璃中,n=1.51 时,v=1.99*108m/s, 当光在火石玻璃中,n=1.65 时,v=1.82*108m/s,当光在加拿大树胶中,n=1.526 时,v=1.97*108m/s,当光在金刚石中,n=2.417 时,v=1.24*108m/s。
2、一物体经针孔相机在屏上成一60mm 大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm 的平行平板玻璃(设n=1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x, 则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为 n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即 n0sinI1,其中 I1 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 习题答案
4. 一厚度为200mm 的平行平板玻璃(设n=1.5),下面放一直径为1mm 的金属薄片。
若在玻璃板上盖一圆形的纸片,使得在玻璃板上方任何方向上都看不到该金属薄片,问纸片的最小直径应为多少?
解:如图所示,设纸片的最小直径为L ,考虑边缘光线满足全反射条件时
6667.090sin sin 02
12==n n I
74536.06667.01cos 22=-=I
L=(2x+1)mm=358.77mm
16. 一束平行细光束入射到一半径mm r 30=、折射率n=1.5的玻璃球上,求经玻璃球折射后会聚点的位置。
如果在凸面(第一面)镀反射膜,其会聚点应爱何处?如果在凹面(第二面)镀反射膜,则反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后,会聚点又在何处?说明各个会聚点的虚实。
解:(1)此时的成像过程如图(4)所示,平行细光束入射到玻璃球上,经左侧球面折射后形成中间像'1A ,它又是右侧球面的物2A ,经右侧球面再次成像于'2A 。
将-∞=1l ,11=n ,5.1'
1=n ,mm r 301=代入单个折射球面
成像公式
r n n l n l
n -=-''
'得 mm mm n n r n l 905.0305.11
'1'
1'1=⨯=-=
由于1l 和'1l 异号,01
'1'
111<=l n l n β,故无限远物与像'1A 虚实相同,即'1A 为实像。
但由于右侧球面的存在,实际光线不可能到达此处,故对于右侧球面2A 为虚物。
将
mm r n n mm mm r l l 30,1,5.1,30)6090(22'
22'12-====-=-=
再次代入单个折射球面成像公式得
151305.1305.01'
2
=+--=l 所以mm l 15'2=,此时02
'21'
222>=l n l n β,物2A 与像'2A 虚实相反,即'2A 为实像。
(2)当凸面镀反射膜时,平行细光束入射到玻璃球上,经左侧球面反射后成像,如图(5)所示。
将-∞=l 代入公式r
l l 2
11'=+得
mm r
l 152
'
==,为虚像。
(3)当凹面镀反射膜时,成像过程如图(6)所示:平行细光束入射到玻璃球上,经左侧球面折射后形成中间像'1A ,它又是右侧反射球面的物2A ,经右侧反射球面再次成像于'2A ,再经过前表面折射,最后成像于'3A 。
由(1)知mm l 302=,代入公式r
l l 2
11'=+得
30230
11'
2-=+l 所以mm l 10'
2-=,为实像。
(4)再继续经前表面折射时,光线由右向左传播成像,需根据光路的可逆性原理,将物看成像,将像看成物,即将
mm l 50'3=代入单个折射球面成像公式得
mm l 75)30
15.1505.1(1
3=--=-,为虚像。
mm r 302-=
图(4)
图(6)
18.一直径为400mm,折射率为1.5的玻璃球中有两个小气泡,一个位于球心,另一个位于1/2半径处,如图1(a)和(b)所示。
沿两气泡连线方向在球的两边观察,问看到的气泡在何处?如果在水中观察,看到的气泡又在何处?
解:依题意A点有两种情况如图1(a)和(b):
图1(a)
条件图1(a):
从右测观察时,将mm r 200-=,n=1.5,1'
=n 和物距
mm l A 300-=,mm l B 200-=,分别代入公式
r n n l n l
n -=-''
' 得 mm l A 400'-=,mm l B 200'
-=,物像位置如图(2)所示。
mm
图1(b )
从左侧观察时:
认为A 、B 均为像点,求其物。
此时,将mm r 200=,n=1,5.1'
=n 和mm l A 100'
=,
mm l B 200'
=,分别代入公式r n n l n l
n -=
-'
''解得 mm l A 80=,mm l B 200=,物像位置如图(3)。
mm
A 图(2)
在水中观察:
从右测观察时,将mm r 200-=,n=1.5,33.1'=n 和物距
mm l A 300-=,mm l B 200-=,分别代入公式
r n
n l n l
n -=-''
' 得 mm l A 320'-=,mm l B 200'-=
从左侧观察时:
认为A 、B 均为像点,求其物。
此时,将mm r 200=,n=1.33,5.1'
=n 和mm l A 100'=,
mm l B 200'
=,分别代入公式r n n l n l
n -=
-'
''解得 mm l A 99.93=,mm l B 200=。
mm
B B 图(3)
条件图1(b ):
从右测观察时,将mm r 200-=,n=1.5,1'
=n 和物距
mm l A 100-=,mm l B 200-=,分别代入公式
r n n l n l
n -=-''
' 得 mm l A 80'-=,mm l B 200'-=
从左侧观察时:
认为A 、B 均为像点,求其物。
此时,将mm r 200=,n=1,5.1'
=n 和mm l A 300'
=,
mm l B 200'
=,分别代入公式r n n l n l
n -=
-'
''解得 mm l A 400=,mm l B 200=,
在水中观察:
从右测观察时,将mm r 200-=,n=1.5,33.1'
=n 和物距
mm l A 100-=,mm l B 200-=,分别代入公式
r n n l n l
n -=-''
' 得 mm l A 99.93'-=,mm l B 200'-=
从左侧观察时:
认为A 、B 均为像点,求其物。
此时,将mm r 200=,n=1.33,5.1'
=n 和mm l A 300'=,
mm l B 200'
=,分别代入公式r n n l n l
n -=
-'''解得 mm l A 320=,mm l B 200=。
19 有平凸透镜5.1,300,,10021==∞==n mm d r mm r ,当物体在
∞-时,求高斯像的位置。
在第二面上刻一个十字丝,问其通
过球面的共轭像在何处?当入射高度mm h 10=时,实际光线的像方截距为多少?与高斯像面的距离为多少?
解:(1)根据近轴光的光线光路计算公式可求高斯像位置。
将mm r n n l 100,1,5.1,11'11===-∞=代入单个折射球面成像公式
r n n l n l
n -=-''',得mm l 300'1= d l l -='
1
2=(300-300)mm=0mm ,所以mm l 0'
2=
即:物体位于∞-时,其高斯像点在第二面的中心处。
(2)由光路的可逆性可知:第二面上的十字丝,其共轭像在物方∞-处。
(3)当mm h 101=时,如图(7)所示。
利用课本公式(1-9)~(1-12)求解得
光线经第1面折射,1.010010
sin 1
11===r h I ,
0667.01.05.11sin sin 1'1
1'1=⨯==I n n I 所以0'1822.30667.0arcsin ==I
00'111'19172.1)822.3739.50(=-+=-+=I I U U
mm mm U I r L 374.299)0334.00667.01(100)sin sin 1('1'11'1
=+⨯=+⨯=。
光线再经第2面折射,0'12'129172.1,626.0==--=-=U I mm d L L , 则0'202'2
2'28765.2,05018.09172.1sin 5.1sin sin -=-=-==I I n n I 0000'222'28765.28765.29172.19172.1=+-=-+=I I U U 由三角关系可得
mm U L x 0210.09172.1tan 626.0tan 0'12-=-==,
mm L 4169.08765.2tan 0210.00'
2
-=-=。
即它与高斯像面的距离为-0.4169mm 。
图(7)。
