悬臂梁模态分析实验报告.doc

合集下载

悬臂梁的振动模态实验报告

实验等截面悬臂梁模态测试实验一、实验目的1. 熟悉模态分析原理；2. 掌握悬臂梁的测试过程。

二、实验原理1. 模态分析基本原理理论上，连续弹性体梁有无限多个自由度，因此需要无限多个连续模型才能描述，但是在实际操作中可以将连续弹性体梁分为n 个集中质量来研究。

简化之后的模型中有n 个集中质量，一般就有n 个自由度，系统的运动方程是n 个二阶互相耦合（联立）的常微分方程。

这就是说梁可以用一种“模态模型”来描述其动态响应。

模态分析的实质，是一种坐标转换。

其目的在于把原在物理坐标系统中描述的响应向量，放到所谓“模态坐标系统”中来描述。

这一坐标系统的每一个基向量恰是振动系统的一个特征向量。

也就是说在这个坐标下，振动方程是一组互无耦合的方程，分别描述振动系统的各阶振动形式，每个坐标均可单独求解，得到系统的某阶结构参数。

多次锤击各点，通过仪器记录传感器与力锤的信号，计算得到第ｉ个激励点与定响应点（例如点2）之间的传递函数H i (ω)，从而得到频率响应函数矩阵中的一行频响函数的任一行包含所有模态参数，而该行的r 阶模态的频响函数的比值，即为r 阶模态的振型。

2. 激励方法为进行模态分析，首先要测得激振力及相应的响应信号，进行传递函数分析。

传递函数分析实质上就是机械导纳，i 和j 两点之间的传递函数表示在[]∑==Nr iN ri ri r H H H 121...[]Nr r r Nr rr r irk c j m ϕϕϕωωϕ (2112)∑=++-=[]{}[]Tr ir Nr r iN i i Y H H H ϕϕ∑==121...j点作用单位力时，在i点所引起的响应。

要得到i和j点之间的传递导纳，只要在j点加一个频率为ω的正弦的力信号激振，而在i点测量其引起的响应，就可得到计算传递函数曲线上的一个点。

如果ω是连续变化的，分别测得其相应的响应，就可以得到传递函数曲线。

根据模态分析的原理，我们要测得传递函数矩阵中的任一行或任一列，由此可采用不同的测试方法。

模态分析实验报告

《机械工程测试技术》综合实验报告实验项目名称：机械结构固有模态实验班级：机械32实验小组成员姓名（学号）：张豪47 张唯48赵亮49 景世钊33王汝之42 朱金格28实验小组组长：张豪实验报告日期： 15/12/12实验目的：针对机械结构（简支梁、悬臂梁、圆盘）的固有模态进行分析，了解几种常用的结构动态特性激励方法，掌握机械结构固有模态的测试系统设计、测试系统搭建、数据采集及信号分析方法和技术。

实验原理：模态分析方法及其应用：模态分析方法是把复杂的实际结构简化成模态模型，来进行系统的参数识别（系统识别），从而大大地简化了系统的数学运算。

通过实验测得实际响应来寻示相应的模型或调整预想的模型参数，使其成为实际结构的最佳描述。

主要应用有：用于振动测量和结构动力学分析。

可测得比较精确的固有频率、模态振型、模态阻尼、模态质量和模态刚度。

可用模态实验结果去指导有限元理论模型的修正，使计算模型更趋完善和合理。

用来进行结构动力学修改、灵敏度分析和反问题的计算。

用来进行响应计算和载荷识别。

模态分析基本原理：工程实际中的振动系统都是连续弹性体，其质量与刚度具有分布的性质，只有掌握无限多个点，在每瞬时的运动情况，才能全面描述系统的振动。

因此，理论上它们都属于无限多自由度的系统，需要用连续模型才能加以描述。

但实际上不可能这样做，通常采用简化的方法，归结为有限个自由度的模型来进行分析，即将系统抽象为由一些集中质块和弹性元件组成的模型。

模态分析是在承认实际结构可以运用所谓“模态模型”来描述其动态响应的条件下，通过实验数据的处理和分析，寻求其“模态参数”，是一种参数识别的方法。

模态分析的实质，是一种坐标转换。

其目的在于把原在物理坐标系统中描述的响应向量，放到所谓“模态坐标系统”中来描述。

这一坐标系统的每一个基向量恰是振动系统的一个特征向量。

也就是说在这个坐标下，振动方程是一组互无耦合的方程，分别描述振动系统的各阶振动形式，每个坐标均可单独求解，得到系统的某阶结构参数。

悬臂梁模态分析实验报告

悬臂梁模态分析实验报告一、实验目的通过对悬臂梁进行模态分析实验，了解悬臂梁在不同振动模态下的固有频率和振型，并验证计算模态分析结果的准确性。

二、实验原理悬臂梁是一种常见的结构形式，其在振动过程中会出现不同的振动模态，每个振动模态对应一个固有频率和振型。

模态分析是通过实验或计算的方法，确定一个结构在振动中的固有频率和振型的过程。

在本实验中，我们选择一根长度为L的悬臂梁，将其固定在一个支撑架上。

在悬臂梁上施加一个外力，使梁发生振动。

利用振动传感器测量悬臂梁不同位置处的振动加速度，并通过信号处理来得到悬臂梁的模态信息。

三、实验器材和仪器1.悬臂梁：长度为L、直径为d的悬臂梁2.支撑架：用来支撑悬臂梁的架子3.外力施加装置：用来在悬臂梁上施加外力的装置4.振动传感器：用来测量悬臂梁不同位置的振动加速度5.信号处理器：用来对振动信号进行处理和分析的设备四、实验步骤1.将悬臂梁固定在支撑架上，并调整支撑架的角度和高度，使悬臂梁处于水平状态。

2.在悬臂梁上选择一个合适的位置，安装振动传感器，并将传感器连接到信号处理器上。

3.利用外力施加装置，在悬臂梁上施加一个单一方向的外力。

4.启动信号处理器，并进行振动信号的采集和处理。

5.分析处理后的振动信号数据，得到悬臂梁的固有频率和振型。

五、实验结果及讨论根据实验数据，我们得到了悬臂梁的固有频率和振型，并与理论计算值进行比较。

整个实验过程中，我们进行了多次实验，分别在不同的外力大小下进行了振动测试。

通过对比实验数据和计算结果，验证了模态分析方法的准确性。

六、实验结论通过模态分析实验，我们成功地确定了悬臂梁在不同振动模态下的固有频率和振型，并验证了计算模态分析结果的准确性。

这对于进一步研究和应用悬臂梁的振动特性具有重要的意义。

七、实验心得通过本次实验，我深刻了解了悬臂梁的振动特性和模态分析的原理和方法。

实验过程中，我学会了如何正确选择和安装振动传感器，以及如何对振动信号进行分析处理。

悬臂梁实验报告

悬臂梁实验报告实验目的本实验旨在通过对悬臂梁的实验研究，探究其在不同条件下的变形和破坏情况，了解悬臂梁的受力特性以及工程中的应用。

实验原理悬臂梁是一种常见的结构形式，其上部只有一个端点支撑，另一端悬挑出来。

在实验中，我们通过在悬臂梁上加载，观察悬臂梁的变形和破坏情况，从而探究其受力特性。

悬臂梁的受力分析可以基于弹性力学的理论进行，根据悬臂梁的几何形状和材料特性，可以通过静力学的原理计算出悬臂梁在不同位置的应力和位移。

在实验中，我们使用悬臂梁测力传感器，可以实时监测悬臂梁上的应力和变形情况。

实验装置与步骤实验装置包括悬臂梁、加载装置和测量仪器等。

具体的实验步骤如下：1.调整加载装置使其稳固地连接到悬臂梁上；2.使用测力传感器测量悬臂梁的初始载荷；3.逐步增加载荷，记录悬臂梁的变形情况；4.当载荷接近悬臂梁的破坏载荷时，停止加载，并记录破坏载荷；5.对实验数据进行处理和分析。

结果与讨论在实验中，我们记录了不同载荷下悬臂梁的变形情况，得出如下结果：载荷（N）变形（mm）100 0.2200 0.6300 1.2400 2.0500 3.0600 4.5从实验数据可以看出，随着载荷的增加，悬臂梁的变形也逐渐增大。

在低载荷下，悬臂梁的变形比较小，呈线性关系。

随着载荷的增加到一定程度，悬臂梁的变形开始非线性增加，并且出现明显的弯曲变形。

当载荷达到约600N时，悬臂梁发生破坏。

在破坏前，悬臂梁表现出明显的弯曲变形，并且载荷与变形呈现非线性关系。

破坏时，悬臂梁发生断裂，载荷突然下降。

通过对实验数据的分析，我们可以得出悬臂梁的一些特性。

首先，悬臂梁的承载能力随着载荷的增加而增加。

其次，随着载荷的增大，悬臂梁的变形逐渐增大，并呈现出非线性的关系。

最后，悬臂梁在破坏前会发生明显的弯曲变形，载荷与变形呈现非线性关系。

结论本实验通过对悬臂梁的实验研究，得出了一系列结论。

悬臂梁在受力时会发生变形，随着载荷的增加，悬臂梁的变形逐渐增大。

悬臂梁实验报告

实验报告悬臂梁的模态实验姓名： xxx学号： xxx专业： xxx系别： xxx一、试验装置二、实验原理本实验采用锤击法测定悬臂梁的频响函数，将第S 点沿坐标X S 方向作用的锤击力和第r 点沿X r 方向的响应分别由相应的传感器转换为电信号，在由动态分析仪，按照随机振动理论，运算得出r,s 两点间的频响函数rs H ~，∑=+-==ni i i i k i s i r s r rs i k F X H 12)()()(0)21(~~λζλϕϕ （1）又由于响应信号是加速度，同时圆频率为ω，位移函数,sin t X x ω=其加速度为,sin 22x t X a ωωω-=-=用复数表示后，参照（1）可得到加速度频响函数为：∑=+--=-=ni i i i k i s i r s r a rs i kF X H 12)()()(202)21(~~λζλϕϕωω （2）由公式（2）可知，当k ωω=时，1=k λ，此时式（2）可近似写为：,22)(~)()()()()()(2kk k s k r k k k sk r k k a rs m i k i H ζϕϕζϕϕωωω-=-== （3）它对应频响函数a rs H ~的幅频曲线的第k 个峰值，其中在上面（3），k m kk k 2()(ω）式中=为各阶主质量．．．n k ,3,2,1=。

改变s 点的位置，在不同点激振，可以得到不同点与点r之间的频响函数，当s=r 时，就可得到点r 处的原点频响函数，表示为：∑=+--=ni i i i i i r i r a rr i k H 12)()()(2)21(~λζλϕϕω （4）它的第k 个峰值为：,2)(~)()()(2kk k r k r k k a rr k i H ζϕϕωωω-== （5）由（3）/（5）得到：（6）若另1)(=k rϕ，就可得到：（7）由（7）式，另s=1,2,3，．．．．．．ｎ，就可得到第k 阶主振型的各个元素。

悬臂梁实验报告

实验报告
实验名称：悬臂梁固有频率测试
实验目的：
1)熟悉基于Labview的数据采集过程
2)掌握时频域的信号分析
实验仪器设备：
1)悬臂梁实验模型：钢尺（宽：mm，厚：mm）；涡流传感器；前置放大电路及电源
2)数据采集卡，计算机，示波器，改锥等
3)基于Labview的数据采集程序及分析程序
实验过程：
1)准备工作：接好涡流传感器，加合适激励观察示波器输出波形；连接采样系统的硬件部分后，应用计算机中的采集程序观测输出波形是否正常。

2)调节悬臂梁实验模型即钢尺的长度（20cm，24cm，28cm），三个不同长度上加入两种激励方式（冲激、阶跃），应用采集系统采集两种激励方式下的涡流传感器输出数据，存储。

冲激：应用改锥敲击实现；阶跃：应用手按动实现。

3)应用数据分析软件进行数据分析。

实验结果及分析：
1)不同长度不同激励方式下采集的数据如下：
图a1钢尺长度：20cm，改锥敲击
图a2钢尺长度：20cm，手按动
图b1钢尺长度：24cm，改锥敲击
图b2钢尺长度：24cm，手按动
图c1钢尺长度：28cm，改锥敲击
图c2钢尺长度：28cm，手按动
2)数据分析及思考
思考题：
1)总结在实验和数据处理操作时需要注意的问题？
2)不同激励方式造成测试结果的误差有多大？哪种最好？
3)在上面实验中，最高能够找到第几阶固有频率？
4)比较悬臂梁频率测量的理论值和实验值，分析误差及来源？
5)查找一篇相关文献，该文献的测试对象以悬臂梁为原型，简要总结它的测试方案。

梁模态分析实验报告

一、实验目的1. 通过实验了解梁的模态特性，包括固有频率和振型；2. 掌握梁模态分析的基本方法，包括激振、信号采集、数据处理等；3. 熟悉实验设备的操作和调试，提高实验技能。

二、实验原理梁的模态分析是研究结构振动特性的重要手段。

本实验采用共振法进行梁的模态分析，即通过激振使梁产生振动，通过信号采集和数据处理得到梁的固有频率和振型。

三、实验设备与材料1. 实验设备：激振器、加速度传感器、信号采集系统、数据采集卡、计算机等；2. 实验材料：一根等截面简支梁。

四、实验步骤1. 将梁固定在实验台上，确保梁的支承条件符合简支梁的要求；2. 将加速度传感器粘贴在梁上，用于采集梁的振动信号；3. 连接信号采集系统和数据采集卡，确保信号采集系统与计算机正常连接；4. 开启激振器，进行激振实验；5. 采集梁的振动信号，并对信号进行预处理，如滤波、去噪等；6. 利用信号处理软件对采集到的信号进行频谱分析，得到梁的固有频率和振型。

五、实验结果与分析1. 实验数据（1）梁的几何参数：长度L=1000mm，宽度b=50mm，高度h=100mm；（2）材料参数：弹性模量E=2.06×10^5 MPa，密度ρ=7850 kg/m^3；（3）实验得到的固有频率和振型。

2. 实验结果分析（1）固有频率：根据实验数据，得到梁的前三阶固有频率分别为f1=50Hz、f2=120Hz、f3=180Hz；（2）振型：通过频谱分析，得到梁的前三阶振型如图1所示。

图1 梁的前三阶振型从实验结果可以看出，梁的固有频率和振型与理论计算值基本吻合，说明本实验所采用的模态分析方法具有较高的精度。

六、实验总结1. 通过本次实验，掌握了梁的模态分析基本方法，提高了实验技能；2. 熟悉了实验设备的操作和调试，为今后进行类似实验奠定了基础；3. 实验结果表明，本实验所采用的模态分析方法具有较高的精度，为工程实际提供了参考。

七、实验建议1. 在实验过程中，注意激振器的激振频率应与梁的固有频率接近，以提高实验精度；2. 信号采集时，应确保传感器粘贴牢固，避免信号干扰；3. 在数据处理过程中，注意滤波、去噪等预处理步骤，以提高数据质量；4. 实验过程中，应仔细观察梁的振动现象，以便及时发现问题并进行调整。

悬臂梁模态分析实验报告

梁几何尺寸
梁长 L=1m
梁直径D=12mm
固有频率（Hz）
实验值
8.491
54.216
154.607
304.354
494.691
理论值
8.687
54.445
152.270
298.774
547.260
有限元仿真值
8.475
53.089
148.54
290.74
479.92
误差原因：
（1）实验试件在并非是十分标准，5阶实验计算模态存在误差；
悬臂梁各阶固有频率及主振形的测定试验
一、实验目的
1、用共振法确定悬臂梁横向振动时的前五阶固有频率；
2、熟悉和了解悬臂梁振动的规律和特点；
3、观察和测试悬臂梁振动的各阶主振型，分析各阶固有频率及其主振型的实测值与理论计算值的误差。
二、仪器和设备
悬臂梁固定支座；脉冲锤1个；圆形截面悬臂钢梁标准件一个；加速度传感器一个；LMS振动噪声测试系统。
（2）有限元法分析一般包括四个步骤：物理模型的简化、数学模型的程序化、计算模型的数值化和计算结果的分析。每一个步骤在操作过程中都或多或少地引入了误差，这些误差的累积最终可能会对计算结果造成误差；
（3）实验基座刚度有限：Z方向上刚度基本上满足，但水平方向上即使两边夹紧也只能靠一根螺栓提供切向刚度，刚度有限。
199255?????ff?六ansys有限元模拟仿真结果61前五阶固有频率仿真数据62振型仿真图1阶振型仿真图2阶振型仿真图3阶振型仿真图4阶振型仿真图5阶振型仿真图七结果误差分析悬臂梁理论计算固有频率理论值有限元仿真值与实测值表梁几何尺寸梁长l1m梁直径d12mm固有频率hz1f2f3f4f5f实验值849154216154607304354494691理论值868754445152270298774547260有限元仿真值847553089148542907447992误差原因

悬臂梁的模态分析

悬臂梁的模态分析如图所示为一根长度为L 的等截面直杆，一端固定，一端自由。

己知杆材料的弹性模量211102.2m N E ⨯=，密度37800m kg =ρ，杆长m L 15.0=.对悬臂梁进行模态分析。

分析步骤1定义单元类型拾取菜单Main M--Preprocessor-Element Type-Add/Edit/Delete,弹出对话框，单击Add 按钮:弹出对话框，在左侧列表中选择Structural Solid ，在右侧列表中选择Brick 20node 186,单击OK 按钮:单击对话框的Close 按钮。

2定义材料性能参数拾取菜单Main Menu-Preprocessor--Material Props-Material Models.弹出对话框，在右侧列表中依次双击Structural - Linear – Elastic - Isotropic ，弹出对话框，在EX 文本框中输入2.2e11(弹性模量).在PRXY 文本框中输入0.3(泊松比).单击"OK"按钮:再双击右侧列表中Structural 下Density,弹出对话框，在DENS 文本框中输入7800(密度)，单击OK 按钮。

然后对话框。

3创建有限元模型、划分网格拾取菜单Main Menu - Preprocessor – Modeling-Create- Volumes - Block – By Dimension 。

弹出对话框，在X1,X2文本框中输入0,0.01，在Y1,Y2文本框中输入0，0.01，在Z1,Z2文本框中输入0，0.15,单击OK 按钮。

拾取菜单Main Menu-Preprocessor-Meshing-MeshTool。

弹出对话框，单击Size Controls，区域中Lines后Set，按钮，弹出拾取窗口，任意拾取块x轴和y轴方向的边各一条(短边)，单击OK按钮，弹出对话框, 在NDIV文本框中输入5，单击Apply按钮:再次弹出拾取窗口，拾取块z轴方向的边(长边)，单击OK按钮。

悬臂梁模态分析范文

悬臂梁模态分析范文悬臂梁是一种常见的结构形式，广泛应用于建筑、机械、航空航天等领域。

悬臂梁的模态分析是对其自由振动特性进行研究的一种方法。

通过模态分析，可以确定悬臂梁的固有频率和模态形态，为设计和优化悬臂梁结构提供依据。

悬臂梁的自由振动方程可以表示为：$$(EI \frac{d^4u(x)}{dx^4} + \rho A \frac{d^2u(x)}{dt^2}) =0$$其中，u(x)是悬臂梁的振动位移，x是悬臂梁上的坐标，E是弹性模量，I是惯性矩，$\rho$是材料密度，A是悬臂梁的截面面积。

为了求解悬臂梁的自由振动方程，需要确定边界条件。

通常情况下，悬臂梁一端固定，另一端自由。

边界条件可以表示为：$$u(0)=0$$$$M(0)=0$$$$\frac{d^2u(x)}{dx^2}，_{x=0} = 0$$其中，u(0)表示悬臂梁一端的振动位移，M(0)表示悬臂梁一端的弯矩。

对于悬臂梁的模态分析，通常采用有限元分析的方法。

有限元分析将悬臂梁离散为多个小单元，每个单元的振动位移可以近似为一个简单的函数。

通过将每个小单元的振动位移组合起来，可以得到整个悬臂梁的振动位移。

然后，通过将振动位移代入自由振动方程，可以得到一个特征值问题，即求解固有频率和模态形态。

在实际应用中，可以使用计算软件进行悬臂梁的模态分析。

常用的计算软件包括ANSYS、ABAQUS等。

这些软件提供了丰富的模态分析功能，可以快速、准确地求解悬臂梁的固有频率和模态形态。

模态分析结果可以用于评估悬臂梁结构的稳定性和安全性。

通过分析不同模态的振动形态，可以判断悬臂梁的潜在共振点和结构弱点。

在设计和优化悬臂梁结构时，可以根据模态分析结果进行结构改进，以提高悬臂梁的抗风、抗震能力。

总之，悬臂梁模态分析是对悬臂梁自由振动特性进行研究的重要方法。

通过模态分析，可以确定悬臂梁的固有频率和模态形态，为结构设计和优化提供依据。

利用计算软件进行模态分析可以提高分析效率和精确度，为工程实践提供技术支持。

悬臂梁模态实验测试与分析

安装调试等原因
外由于 ansys 是基于有限元理论编制的工程软件有似方法单元的节点数形函数的选网格的划等等
似计算的结果悬臂梁模态的试验值和 ansys 可作似值理论值是较吻合的能够
映悬臂梁的真实模态
悬臂梁设计的参考
将 βi L
入式 14
整理可得到 C3 和 C 4 的比值
15
ξi =
接着将式 11 除
C3 shβ i L − sin β i L =− C4 chβ i L + cos β i L
得到的即悬臂梁各的振型函数
C4
结合式 13
Y ( x ) = ξ i (sh β i x − sin β i x ) + ch β i x − cos β i x
悬臂梁模态试验案例
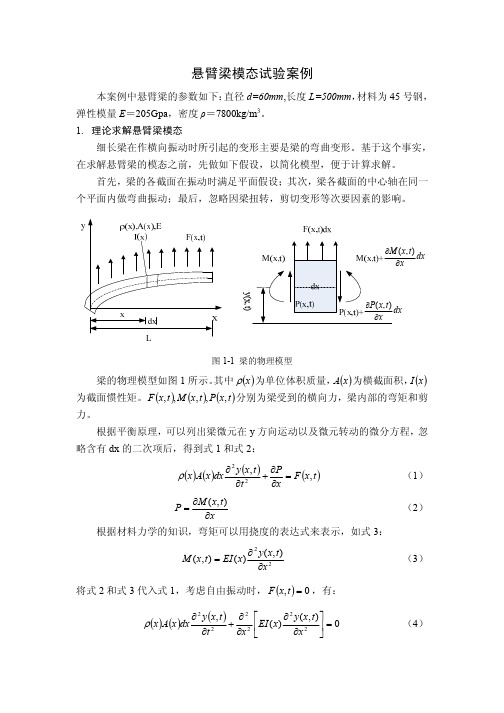
本案例中悬臂梁的参数如弹性模量 E＝205Gpa 直径 d=60mm,长度 L=500mm 材料 45 钢密度 ρ＝7800kg/m3
1. 理论求解悬臂梁模态细长梁在作横向振动时所引起的在求解悬臂梁的模态之前先做如形假设面假设剪要是梁的弯曲简化模型形基于这个实
测试结构的频响函数需对结构激振结构常用的激振方法有脉冲锤本文采用脉冲锤激振法
使
产生振动对于一般的工程境随机激振法
弦稳态激振法和
激振法通过用固定测量点(
度计) 移动激励点(锤
点)
或者固定激励点
移动测量点的方法系统的模态
测得频响函数矩
的某一行
然后
通过参数识
(3) 信
和曲线拟合得
采集和度传感器响应信放大路行接入 AZ804-A 信调理
单梁

悬臂梁实验报告范文

悬臂梁实验报告范文实验报告：悬臂梁实验1.引言悬臂梁是一种常见的结构，广泛应用于建筑、航空、机械等领域。

在工程设计、结构分析和实验研究中，了解悬臂梁的力学特性对于保证结构稳定性和可靠性有着重要意义。

本实验旨在通过对悬臂梁的实验研究，深入理解悬臂梁的受力分析、挠度计算以及变形规律，并将实验结果与理论计算进行对比，验证理论计算结果的准确性。

2.实验原理2.1悬臂梁的力学模型悬臂梁通常由一根直杆(悬臂)和迎接作用力的端杆组成。

在实验中，本实验选取了一根长度为L的悬臂梁，在其一端沿垂直方向施加一作用力，并在悬臂的自由端进行力学参数测量。

2.2悬臂梁的挠度计算悬臂梁在受力作用下会发生弯曲，产生挠度。

根据悬臂梁的挠度计算公式，可以得到悬臂梁的最大挠度和挠度分布情况。

3.实验步骤3.1实验器材准备（1）悬臂梁：本实验使用了一根长度为L的悬臂梁，悬臂梁的材料和截面尺寸在实验前确定。

（2）测力计：选择合适的测力计，将其连接到悬臂梁的一端，用于测量作用力的大小。

（3）位移传感器：选择合适的位移传感器，将其放置在悬臂梁的自由端，用于测量悬臂梁的挠度。

3.2实验操作（1）固定悬臂梁：将悬臂梁固定在实验台上，保持其水平和稳定。

（2）施加作用力：在悬臂梁的一端施加作用力，记录作用力的大小。

（3）测量挠度：使用位移传感器测量悬臂梁在不同位置的挠度，记录测量结果。

（4）重复实验：重复以上实验操作，至少进行3次实验，在不同作用力下测量悬臂梁的挠度。

4.实验结果4.1悬臂梁的挠度分布情况根据实验测量的数据，可以绘制悬臂梁的挠度分布曲线，分析挠度随悬臂长度的变化规律。

4.2实验结果与理论计算结果的对比将实验测得的挠度数据与理论计算的挠度进行对比，计算其误差并分析可能的原因。

5.结论通过对悬臂梁的实验研究，得到了悬臂梁的挠度分布情况，并将实验结果与理论计算进行了对比。

根据实验结果和对比分析，可以得出以下结论：（1）悬臂梁在受力作用下会发生弯曲，产生挠度，挠度随悬臂长度呈指数衰减。

结构模态分析实验报告

结构模态分析实验报告结构模态分析实验报告引言：结构模态分析是工程领域中一种重要的试验方法，通过对结构的自由振动特性进行测试和分析，可以了解结构的固有频率、振型及其与外部激励的响应。

本实验旨在通过实验测试和数据分析，对一根悬臂梁进行结构模态分析，以深入理解结构的振动特性。

实验装置与步骤：实验采用了一根长约1米的悬臂梁，悬臂梁的一端固定在实验台上，另一端悬空。

实验中使用了激励器和传感器，激励器通过施加动态载荷激励悬臂梁的振动，传感器则用于测量悬臂梁的振动响应。

首先，我们将悬臂梁固定在实验台上，并将激励器放置在悬臂梁的一侧。

接下来，我们通过激励器施加一系列不同频率的动态载荷，以激发悬臂梁的自由振动。

同时，传感器将记录悬臂梁在不同频率下的振动响应。

数据采集与分析：实验中，我们使用了振动传感器采集了悬臂梁在不同频率下的振动响应数据。

通过对这些数据的处理与分析，我们可以得到悬臂梁的固有频率、振型等信息。

首先，我们对采集到的数据进行预处理，去除噪声和干扰，以提取出悬臂梁的振动信号。

接下来，我们将振动信号进行傅里叶变换，得到频域上的振动谱。

通过分析振动谱，我们可以确定悬臂梁的固有频率。

在得到固有频率后，我们可以进一步分析悬臂梁的振型。

通过对悬臂梁在不同频率下的振动响应进行比较，我们可以观察到不同频率下悬臂梁的振动模态。

振动模态可以描述结构在振动时不同部位的相对位移和变形情况，对于结构的设计和分析具有重要意义。

结果与讨论：通过实验测试和数据分析，我们得到了悬臂梁的固有频率和振型信息。

根据我们的实验结果，悬臂梁的固有频率分别为f1、f2、f3等。

同时，我们观察到在不同频率下悬臂梁的振动模态呈现出不同的形态，这些形态可以用于分析结构的振动特性。

结构模态分析在工程领域中具有广泛的应用。

通过了解结构的固有频率和振型，我们可以评估结构的稳定性和动态响应特性，为结构的设计和改进提供依据。

此外，结构模态分析还可以用于故障诊断和结构健康监测等方面。

悬臂梁实验实验报告概述及报告范文

悬臂梁实验实验报告概述及报告范文1. 引言1.1 概述悬臂梁实验是力学实验中的一种常见实验，通过对悬臂梁在不同负载下的应变和挠度进行测量，探究材料在受力情况下的变形特性。

本实验旨在了解和分析悬臂梁的弯曲应力与挠度关系，并评估负载测试结果。

通过这次实验，我们可以获得有关材料力学性能以及结构设计优化的有用信息。

1.2 文章结构本文将按照以下结构展开讨论：引言、实验设置、数据分析与结果讨论、结果和讨论以及结论。

其中，引言部分将对实验目的和整体内容作简要介绍；实验设置部分将详细描述所使用的材料、设备和具体的实验步骤；数据分析与结果讨论部分将从数据收集与处理、弯曲应力与挠度关系以及负载测试结果等方面进行深入探讨；结果和讨论部分将总结并对比分析实验结果，并提出其意义和启示；最后，在结论部分将总结整个实验过程，并给出研究建议和展望，同时分享个人对此次实验的心得与体会。

1.3 目的本实验的主要目的是研究悬臂梁在受力情况下的弯曲应力与挠度关系，并评估负载测试结果。

通过实测数据的收集和处理，我们将分析不同负载条件下材料的变形特性，并探讨悬臂梁结构设计中可能存在的问题和优化方向。

此外，这次实验也将加深我们对力学理论与实际应用的理解，并提供一个综合运用知识和技能的机会。

2. 实验设置2.1 材料和设备:本实验所使用的材料包括悬臂梁、各类测力传感器、支撑架和负载施加装置等。

悬臂梁选用了具有一定强度和刚性的金属材料，以保证在负载作用下能够稳定承受力量，同时要求表面光滑均匀，以减小摩擦力的影响。

实验中我们选择了一种常见的钢材作为主要材料，其具有良好的机械性能和易于加工的特点。

测力传感器是实现对悬臂梁上各点产生应力及变形进行监测与记录的核心设备。

在本次实验中我们采用了高精度的压电式测力传感器，该传感器能够将受到的压力转换成相应的电信号输出，并且具有较小的非线性误差和较高的灵敏度。

支撑架主要用来固定悬臂梁并提供稳定支撑，在本次实验中我们采用了两个底座分别用螺栓固定在工作台上，并通过调节螺丝使其与水平面垂直。

悬臂梁实验报告(EMA)

夹紧也只能靠一根螺栓提供切向刚度，刚度有限。实验数据中可以看到出现了多余模态。即便如此，由实验结果可得出各阶的振型还是很准确的，频率误差也在可接受的范围内。
2、单元划分：如下图：
图2
3.3 单元属性设置六面体单元
3.4 求解类型选中 NORMAL MODES；求解阶数选择 20 个。
三、实验过程（略）
见实验数据
图 3 实验建模
四、结果分析表 1 1000Hz 内的模态频率及振型描述（按实验模型定义的方向）
阶次
1 2 3 4 5 6 7 8 9
计算 11.725 38.689 73.405 205.33 241.14 365.13 401.89 663.5 664.28
五、振型对比
图 4 第一阶图 5 第二阶
图 6 第三阶图 7 第四阶
图 8 第五阶图 9 计算第六阶，实验第七阶
图 10 计算第七阶，实验第六阶图 11 第八阶
图 12 第九阶
六、结果分析
实验结果与计算结果存在误差（6、7 阶模态颠倒）的原因可能如下：（1）实验试件在 5 阶后并非是标准件，所以 5 阶后计算模态并不可信；（2）实验件上有钻孔，且厚度不一，所以建模不能做到精确；（3）实验基座刚度有限：Z 方向上刚度基本上满足，但水平方向.26 223.88 404.44 408.39 666.63 696.23
误差（%） 0.043 -9 0.51 0.94 -7.1 --0.47 4.8
振型描述
Z 向一弯 Y 向一弯 Z 向二弯 Z 向三弯 Y 向二弯计算一扭，实验 Z 向四弯计算 Z 向四弯，实验一扭 Z 向五弯 Y 向三弯
悬臂梁模态测试实验报告
一、项目描述

悬臂梁实验报告

悬臂梁实验报告悬臂梁实验报告引言：悬臂梁是工程力学中常见的结构之一，广泛应用于桥梁、建筑和机械工程等领域。

本实验旨在通过悬臂梁的静力学实验，研究其受力特性和变形规律。

通过实验数据的采集和分析，可以进一步了解悬臂梁的力学性能，为工程实践提供参考。

实验装置：本次实验使用的悬臂梁实验装置由一根长而细的横梁固定在一端，另一端悬空，形成一个悬臂结构。

实验中使用了称重传感器、测力计、测量仪器等设备，用于测量悬臂梁的受力情况。

实验过程：1. 在实验开始前，首先将悬臂梁装置固定在实验台上，并保证其水平。

2. 将称重传感器安装在悬臂梁上，用于测量悬臂梁的受力。

3. 使用测力计测量悬臂梁上的外力，包括静力和动力。

4. 通过测量仪器记录悬臂梁的变形情况，包括挠度和角度。

5. 逐步增加悬臂梁上的外力，记录相应的受力和变形数据。

实验结果：通过实验数据的采集和分析，我们得到了以下结果：1. 受力特性：随着外力的增加，悬臂梁上的受力呈线性增长。

在小负荷情况下，悬臂梁的受力主要集中在固定端，随着外力的增加，受力逐渐向悬臂端转移。

当外力达到一定阈值时，悬臂梁会发生破坏。

2. 变形规律：悬臂梁在受力过程中会发生挠度和角度变化。

挠度是指悬臂梁在受力下产生的弯曲变形，随着外力的增加，挠度逐渐增大。

角度变化则是指悬臂梁在受力下产生的转动变形，同样随着外力的增加，角度变化逐渐增大。

3. 影响因素：悬臂梁的受力和变形受多种因素影响，包括外力的大小、悬臂梁的材料性质、悬臂梁的几何形状等。

在实验中，我们可以通过改变这些因素来研究其对悬臂梁性能的影响。

结论：通过本次实验，我们深入了解了悬臂梁的受力特性和变形规律。

悬臂梁在受力过程中呈现出线性增长的受力特性，同时产生挠度和角度变化。

这些实验结果对于工程实践具有重要意义，可以为桥梁、建筑和机械工程等领域的设计和施工提供参考。

未来研究方向：本实验只是对悬臂梁的基本受力特性和变形规律进行了研究，还有许多方面有待深入探索。

悬臂梁的振动模态实验报告

悬臂梁的振动模态实验报告悬臂梁是一种常见的结构，广泛应用于工程中。

在实际应用中，悬臂梁的振动特性是非常重要的，因为它会对悬臂梁结构的稳定性和安全性产生影响。

因此，了解悬臂梁的振动模态是一项必要的研究任务。

本次实验旨在通过实验方法测量和分析悬臂梁的振动模态，并探究不同参数对振动模态的影响。

实验过程中使用的设备和仪器包括悬挂系统、激励源、传感器、数据采集系统等。

实验步骤如下：1.悬挂梁结构：将悬挂系统固定在实验室的支架上，确保悬臂梁能够在完全自由的情况下自由振动。

2.激励源：将激励源与悬挂梁连接，通过激励源提供外力。

3.传感器：在悬臂梁上选择合适的位置安装传感器，用于测量悬臂梁的振动信号。

4.数据采集系统：将传感器与数据采集系统相连，用于实时采集和记录振动信号。

5.实施实验：通过激励源提供激励力，使悬臂梁产生振动，并同时记录悬挂梁的振动信号。

6.数据处理：通过数据采集系统获得的数据，使用相应的信号处理技术对振动信号进行处理，得到振动模态的相关参数。

7.结果分析：根据实验结果，分析悬臂梁的振动特性和模态，并探究不同参数对振动模态的影响。

通过以上实验步骤，我们可以获得悬臂梁的振动模态，并了解不同参数对振动模态的影响。

实验结果有助于工程设计中的结构设计和改进。

在实验过程中，我们还需要注意以下几个方面的问题：1.悬挂系统的稳定性和刚度：确保悬挂系统能够提供稳定的支撑，并且具有足够的刚度，以保证悬臂梁在振动过程中不会产生偏差。

2.激励源的选取：根据实际需求和悬臂梁的特性，选择合适的激励源，以提供适当的激励力。

3.传感器的准确性：选择合适的传感器，并保证传感器的准确性和灵敏度，以获得准确的振动信号。

4.数据采集和处理的准确性：使用合适的数据采集系统和信号处理技术，以保证数据采集和处理的准确性。

总之，通过本次实验，我们可以深入了解悬臂梁的振动模态，并探究不同参数对振动模态的影响。

这对于工程设计和结构改进具有重要意义，可以提高悬臂梁结构的稳定性和安全性。

悬臂梁模态分析实验报告.doc

悬臂梁的振动模态实验报告

模态分析实验报告

悬臂梁模态分析实验报告

悬臂梁实验报告

悬臂梁实验报告

悬臂梁实验报告

梁模态分析实验报告

悬臂梁模态分析实验报告

悬臂梁的模态分析

悬臂梁模态分析范文

悬臂梁模态实验测试与分析

悬臂梁实验报告范文

结构模态分析实验报告

悬臂梁实验实验报告 概述及报告范文

悬臂梁实验报告(EMA)

悬臂梁实验报告

悬臂梁的振动模态实验报告

悬臂梁实验实验报告概述及报告范文