计算机仿真习题及答案
武汉理工大学-计算机仿真实验作业答案

五、(10分)已知系统的传递函数为6168682)(232+++++=s s s s s s G 。
语言建立系统传递函数模型,并求:⑴ 该系统的单位阶跃响应;(2分)⑵ 输入函数为u(t)时的响应;(3分)(u(t)正弦信号,周期2秒,仿真时间8秒,采样周期0.1);(3) 输入函数为u(t)时的响应;(3分)(u(t)方波输入信号,周期10秒,仿真时间20秒,采样周期0.05)(4) 绘出系统的波德图(Bode )。
(2分)解答:num=[2 8 6];den=[1 8 16 6];sys=tf(num,den);t=0:0.1:8;y1=step(sys,t);u=sin(t*pi);y2=lsim(sys,u,t);subplot(2,2,1);plot(t,y1);grid;title('阶跃响应曲线');xlabel('响应时间');ylabel('响应值');hold on;subplot(2,2,2);plot(t,y2);grid on ;title('对sin(t)的响应曲线');xlabel('响应时间');ylabel('响应值');t=0:0.05:20u=square(pi/5*t)y3=lsim(sys,u,t);subplot(2,2,3);plot(t,y3)grid on ;title('对方波信号的响应曲线');xlabel('响应时间');ylabel('响应值');subplot(2,2,4);bode(sys);grid ;title('bode 图');运行结果:六、(10分)设二阶动力学系统的传递函数如下,假设将无阻尼固有频率固定为ωn =1 rad/s ,将阻尼比的值分别设置成ζ=0,0.1,0.2,0.3,…,MATLAB 语言编程,分析在这些阻尼比ζ的取值下该系统的阶跃响应。
计算机仿真习题及答案
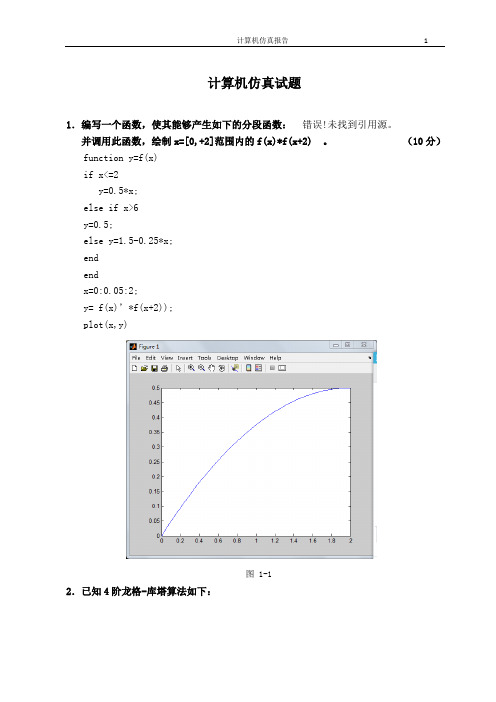
计算机仿真试题1.编写一个函数,使其能够产生如下的分段函数:错误!未找到引用源。
并调用此函数,绘制x=[0,+2]范围内的f(x)*f(x+2) 。
(10分)function y=f(x)if x<=2y=0.5*x;else if x>6y=0.5;else y=1.5-0.25*x;endendx=0:0.05:2;y= f(x)’*f(x+2));plot(x,y)图 1-12.已知4阶龙格-库塔算法如下:试利用该算法求解以下微分方程:(15分)本题可以调用MATLAB函数中龙格-库塔算法函数ode45,首先编写m文件:function dy=func(x,y)dy=-y+1;end再在主窗口调用此文件:[x,y]=ode45('func',[0,5],0)%这里的[0,5]为任取区间,表示方程在此范围的解。
运行结果如下:x =0.00010.00010.00020.00020.00050.00070.00100.00120.00250.00370.00500.00620.01250.01880.02510.0313 0.06270.09410.12550.15690.28190.40690.53190.65690.78190.90691.03191.15691.28191.40691.53191.65691.78191.90692.03192.15692.28192.40692.53192.65692.78192.90693.03193.15693.28193.40693.53193.65693.78193.90694.03194.15694.28194.40694.53194.65694.74274.82854.91425.0000y =0.00010.00010.00020.00020.00050.00070.00100.00120.0025 0.0037 0.0050 0.0062 0.0124 0.0186 0.0248 0.0309 0.0608 0.0898 0.1180 0.1452 0.2457 0.33430.41250.48160.54250.59630.64370.68550.72250.75510.78390.80930.83170.85150.86890.88430.89790.90990.92050.92980.93810.94540.95180.95740.96240.96690.97080.97420.97720.97990.98230.98430.98620.98780.98920.99050.99130.99200.99270.9933为只管起见,我们使用函数命令画出x-y(plot(x,y))的关系如下图:图1-23.用matlab语言求下列系统的状态方程、传递函数、零极点增益、和部分分式形式的模型参数,并分别写出其相应的数学模型表达式:(15分)(1)G(s)=324327242410355024s s ss s s s+++++++(2).X=2.25 -5 -1.25 -0.542.25 -4.25 -1.25 -0.2520.25 -0.5 -1.25 -121.25 -1.75 -0.25 -0.75 0X⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦uy= [0 2 0 2] X解:(1)a)求对应状态方程参数:num=[1 07 24 24]; den=[1 10 35 50 24]; [A,B,C,D]=tf2ss(num,den) 运行结果:A =-10 -35 -50 -241 0 0 00 1 0 00 0 1 0B =1C =1 7 24 24D =故,状态方程为:.X = x+ uY=[1 7 24 24]xb)求对应零极点增益模型参数:num=[1 07 24 24]; den=[1 10 35 50 24]; [Z,P,K]=tf2zp(num,den) 运行结果如下: Z =-2.7306 + 2.8531i -2.7306 - 2.8531i -1.5388P = -4.0000 -3.0000 -2.0000 -1.0000K = 1故变换后的零极点模型为: G(s)=c)求对应部分分式型:num=[1 07 24 24]; den=[1 10 35 50 24]; [R,P,H]=residue(num,den) 运行结果如下: R =4.0000 -6.0000 2.0000 1.0000P =-4.0000 -3.0000 -2.0000 -1.0000H = []故变换后的部分分式模型为:11223644)(+++++-+=s s s s s G(2)由题给条件,知:A=[2.25 -5 -1.25 -0.5; 2.25 -4.25 -1.25 -0.25;0.25 -0.5 -1.25 -1;1.25 -1.75-10 -35 -50 -24 1 0 0 0 0 1 0 0 0 0 1 010 0 0-0.25 -0.75] B=[4;2;2;0] C=[0 2 0 2],D=0 a)求传递函数矩阵: [num,den]=ss2tf(A,B,C,D) 运行结果为: num =0 4.0000 14.0000 22.0000 15.0000 den =1.0000 4.0000 6.2500 5.25002.2500 故,所对应传递函数模型为:25.225.525.641522144)(23423+++++++=s s s s s s s s Gb)求零极点模型:num=[0 4 14 22 15];en=[1 4 6.25 5.25 2.25]; [Z,P,K]=tf2zp(num,den) 运行结果为: Z =-1.0000 + 1.2247i -1.0000 - 1.2247i -1.5000 P =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iK =4.0000故,零极点模型为:)866.05.0()5.1()2247.11)(5.1(4)(2i s s i s s s G ±++±++=c)求对应部分分式模型: [R,P,H]=residue(num,den) 运行结果为: R =4.0000 -0.0000-0.0000 - 2.3094i -0.0000 + 2.3094iP =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iH = []故变换后的部分分式模型为:i s ii s i s s G 866.05.03094.2866.05.03094.25.14)(+++-+-++=4.已知一单位反馈系统开环传递函数为:,试绘制系统Nyquist图,判断闭环系统的稳定性,并求其单位阶跃响应。
计算机仿真试题A 答案

计算机仿真试题A 参考答案四、程序设计与算法题1. (只要是完成题目要求的程序都可以得分)(a)I=imread('flowers.jpg');J=imadd(I,50);K=immultiply(J,0.7);subplot(1,2,1), subimage(I);subplot(1,2,2),subimage(K);(b)I=imread(‘flowers.jpg’);J=imresize(I,1.2);K=imrotate(J,-45,’bilinear’,’crop’);subplot(131),subimage(I);subplot(132),subimage(J);subplot(133),subimage(K);(c)I=imread('flowers.jpg');[x,y,z]=cylinder;warp(x,y,z,I);J=rgb2gray(I);figure,imshow(J);2.主要算法流程如下:程序代码:%Example of PCA analysisclear all, close all;N=1000;fs=500;w=(1:N)*2*pi/fs;t=1:N;x=0.75*sin(w*5);y=sawtooth(w*7,0.5);D(1,:)=.5*y+.5*x+.1*rand(1,N);D(2,:)=.2*y+.7*x+.1*rand(1,N);D(3,:)=.7*y+.2*x+.1*rand(1,N);D(4,:)=-.6*y+-.24*x+.2*rand(1,N);D(5,:)=.6*rand(1,N);plot(t,D(1,:)+0,t,D(2,:)+2,t,D(3,:)+4,t,D(4,:)+6,t,D(5,:)+8);figure;for i=1:5D(i,:)=D(i,:)-mean(D(i,:));end[U,S,pc]=svd(D,0);pc=pc(:,1:5);for i=1:5pc(:,i)=pc(:,i)*sqrt(eigen(i));endfigure;plot(t,pc(:,1)-2,t,pc(:,2)+2);3(a)(注意这里n=4), As x =得:x As 1-= (b )流程图类似于上题,但注意这里已经有了混合信号,所以无需产生;并且是用ICA 进行分析。
智慧树答案计算机仿真技术知到课后答案章节测试2022年

第一章1.计算机仿真系统的三要素()答案:计算机、模型、系统2.系统研究一般有哪些方法()答案:仿真实验法;理论解析法;直接实验法3.哪些是以硬件为基础的仿真软件( )答案:Proteus4.欠实时仿真,仿真时钟比实际时钟慢。
例如烟火爆炸的仿真分析。
答案:对5.计算机仿真算法的误差主要有()答案:截断误差;舍入误差第二章1.MATLAB软件中,下面哪个命令是用来显示当前文件夹中文件名字的()答案:what2.下面这些哪个是属于元素群运算(点运算)()答案:exp(x)3.哪个是以硬件为基础的仿真软件( )答案:Proteus4.MATLAB是(矩阵实验室),其基本变量是矩阵,其数值元素的格式只有双精度(double)这种形式存在于MATLAB的workpace空间中。
答案:错5.在MATLAB中,运行以下代码,b的结果是()a=[1,0;1,0];b=all(a)答案:[1,0]第三章1.MATLAB中代码文件中边表明文件为函数文件的关键字是()答案:function2.在MATLAB的命令窗口中,运行以下代码,b的结果是()a=[1,0,1,0];forn=ax=n(1)&n(2);end答案:出现错误提示3.在MATLAB的fig窗口中,可以直接打开以下()格式的图形文件答案:fig4.在MATLAB中,对于m函数文件,下面的描述不正确的是()答案:m函数文件是不能够被simulink来调用的5.全局变量是共有变量,在函数文件中不能够直接访问,需要设置一个输入参数才能访问。
答案:错第四章1.以下说法不正确的是()答案:不同幂次的两个多项式不能进行乘法运算2.当实验或测试所获得的样本数据有误差时,适合用来估算数据的方法是()答案:曲线拟合3.若在MATLAB中已有语句a=sym(1); b=1; x=sym('b'),则以下叙述正确的是()答案:a是符号常量,x是符号变量4.若使用命令taylor(f,x,1,'Order',6)对f进行泰勒展开,则展开式的最高阶为()答案:55.在命令行窗口输入下列命令,则命令执行后的输出结果是()>>f=sym(1);>> eval(int(f,1,4))答案:3第五章1.启动Simulink的方法有()答案:在命令行窗口中输入simulink命令;在“主页”选项卡中单击“文件”命令组中的“新建”命令按钮;在“主页”选项卡中单击SIMULINK命令组中的“Simulink”命令按钮2.在一个模型窗口上按住一个模块并同时按Shift键移动到另一个模型窗口,则()答案:在两个模型窗口都有这个模块3.为子系统定制参数设置对话框和图标,使子系统本身有一个独立的操作界面,这种操作称为子系统的()答案:封装4.已知仿真模型如图所示,各模块参数均采用默认设置,则示波器的输出波形是()答案:5.以下关于S函数的描述中,正确的有()答案:S函数有现成的模板程序;S函数模块能够被封装;利用S函数可以对Simulink模块库进行扩充第六章1.下列对象中,哪一个不属于MATLAB控制系统工具箱中规定的LTI对象?()答案:极点留数对象2.tf2zpk函数的作用是?()答案:零极点增益模型转换为状态空间模型3.在MATLAB命令窗口运行如下代码,返回结果为:()>>sys = drss(3,4);isct(sys)答案:14.求系统sys的阶跃相应,返回系统的输出和状态,step函数的调用格式为:()答案:[y,t,x]=step(sys)5.给定开环系统模型作波特图,频率向量w自动给出,作波特图,并在图上标注幅值裕度Gm和对应的频率wg,相位裕度Pm和对应的频率wp,所用函数及调用格式为:()答案:margin(sys)第七章1.在MATLAB的m文件中,可以将滞后环节转化为有理数形式的函数是?()答案:pade2.在simulink中,有多种PID模块,其中下面哪一个是离散的PID模块()答案:;3.在MATLAB的m文件中,LTI对象中属于滞后特征的属性是( )答案:Outputdelay;IOdelay;Inputdelay4.simulink中,PID模块中的只有Kp,Ki,Kd三个参数可以设置。
仿真模拟考试题及答案

仿真模拟考试题及答案一、选择题(每题2分,共20分)1. 下列哪个选项是计算机的基本组成部分?A. 显示器B. 键盘C. 鼠标D. 中央处理器(CPU)答案:D2. 互联网的缩写是:A. WWWB. TCP/IPC. HTTPD. Internet答案:D3. 在Excel中,以下哪个函数用于计算一组数据的平均值?A. SUM()B. AVERAGE()C. COUNT()D. MAX()答案:B4. 下列哪个是操作系统的常见功能?A. 网页浏览B. 程序管理C. 文档编辑D. 邮件发送答案:B5. 以下哪个选项是HTML语言的标签?A. <body>B. <paragraph>C. <text>D. <section>答案:A6. 在Word中,以下哪个功能可以调整文档的页边距?A. 插入B. 格式C. 视图D. 工具答案:B7. 下列哪个选项是数据库管理系统(DBMS)的特点?A. 数据共享B. 数据独立性C. 数据安全性D. 所有选项答案:D8. 在PowerPoint中,以下哪个功能可以插入图片?A. 插入B. 格式C. 动画D. 幻灯片放映答案:A9. 下列哪个选项是计算机病毒的特征?A. 自我复制B. 易于识别C. 有益健康D. 需要用户授权答案:A10. 以下哪个选项是网络协议?A. HTTPB. FTPC. SMTPD. 所有选项答案:D二、填空题(每空1分,共10分)1. 计算机的存储设备分为______和外部存储设备。
答案:内部存储设备2. 在网络中,IP地址由______位二进制数组成。
答案:323. 一个完整的电子邮件地址包括用户名和______。
答案:域名4. 在Windows操作系统中,______键可以快速切换应用程序窗口。
答案:Alt + Tab5. 计算机的硬件系统由输入设备、______、输出设备、存储设备和通信设备组成。
《计算机仿真技术》试题(含完整答案)

一、数值计算,编程完成以下各题〔共20分,每题5分〕1、脉冲宽度为d ,周期为T 的矩形脉冲的傅里叶级数如下式描述:)2cos(/)/sin(21[)(1τπππτn T d n T d n T d f n ∑∞=+=当150=n ,41=T d ,2/12/1<<-τ,绘制出函数)(τf 的图形。
解: syms n t;f=((sin(n*pi/4))/(n*pi/4))*cos(2*pi*n*t); s=symsum(f,n,1,150); y=(1+2*s)/4; x=-0.5:0.01:0.5; Y=subs(y,'t',x); plot(x,Y)2、画出函数5505.025.55.15.1cos 5)5(sin )(2x x x x ex x f x +++-=在区间[3,5]的图形,求出该函数在区间[3, 5]中的最小值点m in x 和函数的最小值m in f .解:程序如下 x=3:0.05:5;y=(sin(5*x).^2).*exp(0.05*x.^2)-5*(x.^5).*cos(1.5*x)+1.5*abs(x+5.5)+x.^2.5; mix_where=find(y==min(y)); xmin=x(mix_where); hold on; plot(x,y);plot(xmin,min(y),'go','linewidth',5);str=strcat('(',num2str(xmin),',',num2str(min(y)),')'); text(xmin,min(y),str); Xlabel('x')Ylabel('f(x)')经过运行后得到的图像截图如下:运行后的最小值点m in x =4.6,m in f = -8337.86253、画出函数xe x xf x 5.2cos )(3.02-⋅=-在[1,3]区间的图形,并用编程求解该非线性方程0)(=x f 的一个根,设初始点为20=x .解: x=1:0.02:3; x0=2;y=@(x)(cos(x).^2).*exp(-0.3*x)-2.5*abs(x); fplot(y,[1,3]); Xlabel('x') Ylabel('f(x)')X1=fzero('(cos(x).^2).*exp(-0.3*x)-2.5*abs(x)',x0)运行后求得该方程的一个根为z=0.3256。
计算机仿真技术 试卷及答案 共2套 AB卷

《计算机仿真技术》考试试卷(A卷)班级姓名学号一.填空题。
(每空1分,共20分)1、计算机仿真中系统由_________________、_________________、________________等三个要素组成。
2、常见的系统实验建模法有________________、________________、________________、________________等几种方法。
3、叙述simulink中常见的可变步长的仿真算法有:________________、________________、________________、________________。
(任举四种)4、MA TALB的Comand windows窗口中可以显示workspace中的全部变量的命令是_________________、_________________。
5、计算机仿真算法的算法引起的误差是________________、________________。
6、三维立体绘图中,________________ 是三维曲线绘图命令,________________是三维网格线绘图命令,________________着色表面图绘图命令。
7、符号运算中,泰勒级数计算的函数是________________傅里叶变换的函数________________二.简答题。
(本题5小题,每题8分,共40分)1、计算机仿真的目的和作用2、列举几种计算机仿真软件,并简要介绍一下(要求4种以上)3、matlab主界面主要包括那些窗口,分别有什么样的功能4、局部变量和全局变量之间的区别5、计算机仿真技术中相似性主要包含那几个方面三.编程题 (本题6小题、共40分)根据下面要求,写出程序代码。
1、(5分)设(2E-C-1B)A T=C-1,其中E是4阶单位矩阵,A T是4阶矩阵A的转置。
求矩阵A2、(5分)输入下面的矩阵,求出特征多项式和特征根,并求出特征多项式的微分。
《计算机仿真技术》试卷B(含答案)

《计算机仿真技术》考试试卷(B 卷)班级 姓名 学号一.填空题。
(每空1分,共20分)1、计算机仿真技术三要素是_______________、_________________、________________。
2、计算机仿真中模型能够代表系统来进行研究,模型主要有________________、________________、________________、________________等几类模型。
3、叙述simulink 中常见的固定步长的仿真算法有:________________、________________、________________、________________。
(任举四种)4、MATALB 主要相似性主要包含以下几种相似_________________、________________、___________________。
5、Simulink 中主要包含_________________、________________、_______________等几种模块。
6、符号运算中,泰勒级数计算的函数是________________,拉普拉斯变换的函数________________,傅里叶级数的计算函数是________________。
二.简答题。
(本题5小题,每题8分,共40分)1、简述根据信号类型分类,计算机仿真主要包含哪几种类型。
2、简述蒙特卡洛法建模的步骤。
3、m 函数文件和m 文本文件之间的区别。
4、叙述三维立体绘图常用的几个绘图指令及其功能。
5、简述matlab 软件的基本组成三.编程题 (本题6小题、共40分)根据下面要求,只需写出程序代码,不需计算结果和图形。
1、(5分)写出右面的矩阵D ,求出其大于4的元素有几个,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=059123107D并通过变量列出其在矩阵的位置和序号2、(5分)求解下面矩阵A 的行列式和逆矩阵,并利用命令取出系数矩阵的逆矩阵的第二行的数据,以小数点后面两位数值的形式显示出来。
《自动控制系统计算机仿真》习题参考答案

《自动控制系统计算机仿真》习题参考答案1-1 什么是仿真? 它的主要优点是什么?它所遵循的基本原则是什么?答:所谓仿真,就是使用其它相似的系统来模仿真实的需要研究的系统。
计算机仿真是指以数字计算机为主要工具,编写并且运行反映真实系统运行状况的程序。
对计算机输出的信息进行分析和研究,从而对实际系统运行状态和演化规律进行综合评估与预测。
它是非常重要的设计自动控制系统或者评价系统性能和功能的一种技术手段。
仿真的主要优点是:方便快捷、成本低廉、工作效率和计算精度都很高。
它所遵循的基本原则是相似性原理。
1-2 你认为计算机仿真的发展方向是什么?答:向模型更加准确的方向发展,向虚拟现实技术,以及高技术智能化、一体化方向发展。
向更加广阔的时空发展。
1-3 计算机数字仿真包括哪些要素?它们的关系如何?答:计算机仿真的三要素是:系统——研究的对象、模型——系统的抽象、计算机——仿真的工具和手段。
它们的关系是相互依存。
2-1 控制算法的步长应该如何选择?答:控制算法步长的选择应该恰当。
如果步长太小,就会增加迭代次数,增加计算量;如果步长太大,计算误差将显著增加,甚至造成计算结果失真。
2-2 通常控制系统的建模有哪几种方法?答:1)机理建模法;2)实验建模法;3)综合建模法。
2-3 用欧拉法求以下系统的输出响应()y t 在0≤t ≤1上,0.1h =时的数值解。
0y y +=, (0)0.8y =解:输入以下语句 绘制的曲线图2-4 用二阶龙格-库塔法对2-3题求数值解,并且比较两种方法的结果。
解:输入以下语句绘制的曲线图经过比较两种方法的结果,发现它们几乎没有什么差别。
3-1 编写两个m文件,分别使用for和while循环语句计算20031kk=∑。
解:第1个m文件,第2个m文件运行结果都是3-2 求解以下线性代数方程:123102211313121xxx⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦解:输入语句计算结果3-3 已知矩阵013=121542⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦A,218=414332⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦B试分别求出A阵和B阵的秩、转置、行列式、逆矩阵以及特征值。
计算机仿真技术操作试题
《计算机仿真》操作类试题及答案
一. 采用Simulink 模块仿真,将两个正弦源的频率设置为1Hz 和10Hz ,信号幅度均为1V ;要求示波器显示两个正弦波以及相乘后的波形。
(满分20分) 仿真参数设置:
仿真时间设置:0 到 2s 。
仿真步长设置:定步长(Fixed--Step ),最大步长0.001s 。
仿真算法设置:龙格--库塔法的 5 阶算法(ode5)。
二. 在Simulink 集成环境下建立如下图冲击响应控制模型,给定信号为0s 输入单位的阶跃信号,0.3秒后在扰动信号点输入单位阶跃信号。
仿真时间10秒,绘制相应的响应曲线。
(满分30分)
三. 已知R1=40Ω,R2=60Ω,C1=1μF ,L1=0.1mH ,t t u 3
s 102cos 40)(⨯⨯=π V,采用Simulink 建模,
仿真时间2s ,求:流过电阻R1的电流,电阻R2两端的电压,各测量采用display 模块显示输出。
(满分20分)
四、一台他励直流电动机电枢回路串接电阻起动,试用MATLAB/Simulink 对其起动过程进行仿真。
采用ode15s 算法,可变步长,仿真时间2s ,直流电源240V ,励磁电源300V ,其它参数如图。
(满分30分)
可以设置这台直流电机的各种参数:
起动器子系统,连接端口1、2采用connection port封装:
答案:
一. 仿真模型:
仿真结果:
二. 仿真模型:
仿真结果:
三.仿真结果:
四.仿真模型:
仿真结果:。
计算机仿真课后答案

第二章2.1x=[15 22 33 94 85 77 60]x(6)x([1 3 5])x(4:end)x(find(x>70))2.2T=[1 -2 3 -4 2 -3] ;n=length(T);TT=T';for k=n-1:-1:0B(:,n-k)=TT.^k;endBtest=vander(T)2.3A=zeros(2,5);A(:)=-4:5L=abs(A)>3islogical(L)X=A(L)2.4A=[4,15,-45,10,6;56,0,17,-45,0]find(A>=10&A<=20)2.5p1=conv([1,0,2],conv([1,4],[1,1]));p2=[1 0 1 1];[q,r]=deconv(p1,p2);cq='商多项式为'; cr='余多项式为';disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')])2.6A=[11 12 13;14 15 16;17 18 19];PA=poly(A)PPA=poly2str(PA,'s')第三章3.1n=(-10:10)';y=abs(n);plot(n,y,'r.','MarkerSize',20)axis equalgrid onxlabel('n')3.2x=0:pi/100:2*pi;y=2*exp(-0.5*x).*sin(2*pi*x);plot(x,y),grid on;3.3t=0:pi/50:2*pi;x=8*cos(t);y=4*sqrt(2)*sin(t);z=-4*sqrt(2)*sin(t);plot3(x,y,z,'p');title('Line in 3-D Space');text(0,0,0,'origin');xlabel('X'),ylable('Y'),zlable('Z');grid;3.4theta=0:0.01:2*pi;rho=sin(2*theta).*cos(2*theta); polar(theta,rho,'k');3.5[x,y,z]=sphere(20);z1=z;z1(:,1:4)=NaN;c1=ones(size(z1));surf(3*x,3*y,3*z1,c1);hold onz2=z;c2=2*ones(size(z2));c2(:,1:4)=3*ones(size(c2(:,1:4))); surf(1.5*x,1.5*y,1.5*z2,c2); colormap([0,1,0;0.5,0,0;1,0,0]);grid onhold off第四章4.1for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)endend4.2function[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;4.3y=0;n=100;for i=1:ny=y+1/i/i;endy4.4s=0;for i=1:5s=s+factor(i);ends4.5sum=0;i=1;while sum<2000sum=sum+i;i=i+1;end;n=i-24.6function k=jcsum(n)k=0;for i=0:nk=k+2^i;end或function k=jcsum1(n)k=0;i=0;while i<=nk=k+2^i;i=i+1;end第五章5.1A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';x=A\b5.2[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5])function f=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;5.3X=linspace(0,2*pi,50);Y=sin(X);P=polyfit(X,Y,3)AX=linspace(0,2*pi,50);Y=sin(X);Y1=polyval(P,X)plot(X,Y,':O',X,Y1,'-*')5.4x=0:2.5:10;h=[0:30:60]';T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41];xi=[0:0.5:10];hi=[0:10:60]';temps=interp2(x,h,T,xi,hi,'cubic');mesh(xi,hi,temps);第六章6.1syms xy=finverse(1/tan(x))6.2syms x yf=1/(1+x^2); g=sin(y);fg=compose(f,g)6.3syms xg=(exp(x)+x*sin(x))^(1/2);dg=diff(g)6.4F=int(int('x*exp(-x*y)','x'),'y')6.5syms xF=ztrans(x*exp(-x*10))6.6a=[0 1;-2 -3];syms sinv(s*eye(2)-a);6.7f=solve('a*x^2+b*x+c')6.8f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')6.9y=dsolve('D2y+2*Dy+2*y=0','y(0)=1','Dy(0)=0') ezplot(y),grid on6.10a=maple('simplify(sin(x)^2+cos(x)^2);')6.11f=maple('laplace(exp(-3*t)*sin(t),t,s);')6.12syms t xF=sin(x*t+2*t);L=laplace(F)第七章7.17.27.37.47.57.67.7第八章8.1(1)num=[5]; den=[1,2,2];sys=tf(num,den)(2)s = tf('s');H = [5/(s^2+2*s+2) ];H.inputdelay =2(3)h=tf([0.5,0],[1,-0.5,0.5],0.1)8.2num=2*[1,0.5];den=[1,0.2,1.01];sys=tf(num,den)[z,p,k]=tf2zp(num,den);zpk(z,p,k)[A,B,C,D]=tf2ss(num,den);ss(A,B,C,D)8.3num=[1,5]; den=[1,6,5,1]; ts=0.1;sysc=tf(num,den);sysd=c2d(sysc,ts,'tustin')8.4r1=1;r2=2;c1=3;c2=4;[A,B,C,D]=linmod('x84');[num,den]=ss2tf(A,B,C,D);sys=tf(num,den)8.5A=[1,1,0;0,1,0;0,0,2];B=[0,0;1,0;0,-2];n=size(A)Tc=ctrb(A,B);if n==rank(Tc)disp('系统完全能控');elsedisp('系统不完全能控');end第九章9.1num=[2,5,1];den=[1,2,3];bode(num,den);grid on ;figure;nyquist(num,den);9.2num=5*[1,5,6];den=[1,6,10,8];step(num,den);grid on ;figure;impulse(num,den);grid on ;9.3kosi=0.7;wn=6;num=wn^2;den=[1,2*kosi*wn,wn^2];step(num,den);grid on ;figure;impulse(num,den);grid on ;9.4den=[1,2,8,12,20,16,16];[rtab,info]=routh(den)a=rtab(:,1)if all(a>0)disp('系统是稳定的');elsedisp('系统是不稳定的');end9.5num=7*[1,5];den=conv([1,0,0],conv([1,10],[1,1]));[gm,pm,wg,wc]=margin(num,den)第十章10.1ng0=[1]; dg0=10000*[1 0 -1.1772];g0=tf(ng0,dg0); %满足开环增益的为校正系统的传递函数s=kw2s(0.7,0.5) %期望的闭环主导极点ngc=rg_lead(ng0,dg0,s);gc=tf(ngc,1)g0c=tf(g0*gc);rlocus(g0,g0c);b1=feedback(g0,1); %未校正系统的闭环传递函数b2=feedback(g0c,1); %校正后系统的闭环传递函数figure,step(b1,'r--',b2,'b'); grid on %绘制校正前后系统的单位阶跃响应曲线10.2KK=20;s1=-2+i*sqrt(6);a=1ng0=[10];dg0=conv([1,0],[1,4]);g0=tf(ng0,dg0);[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);gc=tf(ngc,dgc)g0c=tf(KK*g0*gc);b1=feedback(k*g0,1);b2=feedback(g0c,1);step(b1,'r--',b2,'b');grid on10.3KK=128;s1=-2+i*2*sqrt(3);a=2ng0=[10];dg0=conv([1,0],conv([1,2],[1,8]));g0=tf(ng0,dg0);[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);gc=tf(ngc,dgc)g0c=tf(KK*g0*gc);rlocus(g0,g0c);b1=feedback(k*g0,1);b2=feedback(g0c,1);figure,step(b1,'r--',b2,'b');grid on10.4ng0=[1];dg0=conv([1,0,0],[1,5]);g0=tf(ng0,dg0);w=logspace(-3,3);KK=1;Pm=50;[ngc,dgc]=lead4(ng0,dg0,KK,Pm,w);gc=tf(ngc,dgc);g0c=tf(KK*g0*gc);bode(KK*g0,w);hold on,bode(g0c,w);grid on,hold off [gm,pm,wcg,wcp]=margin(g0c)Kg=20*log10(gm)g1=feedback(g0c,1);bode(g1),grid on,[mag,phase,w]=bode(g1);a=find(mag<=0.707*mag(1));wb=w(a(1))max(mag)b=find(mag==max(mag))wr=w(b)10.5KK=40; Pm=50;ng0= KK *[1]; dg0=conv([1,0],conv([1,1],[1,4]));g0=tf(ng0,dg0) ;w=logspace(-2,4);[ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)gc=tf(ngc,dgc),g0c=tf(g0*gc);b1=feedback(g0,1); b2=feedback(g0c,1);step(b1,'r--', b2,'b'); grid onfigure, bode(g0,'r--',g0c,'b',w), grid on,[gm,pm,wcg,wcp]=margin(g0c), Km=20*log10(gm)10.6KK=200; bp=0.3; ts=0.7; delta=0.05;ng0=[1];dg0=conv([1,0],conv([0.1,1],conv([0.02 1],conv([0.01,1],[0.005 1]))));g0=tf(ng0,dg0);w=logspace(-4,3);t=[0:0.1:3];[mag,phase]=bode(KK*g0,w);[gm0,pm0,wg0,wc0]=margin(mag,phase,w),gm0=20*log10(gm0)%gm0 = -15.6769%2、确定期望的开环传递函数mr=0.6+2.5*bp;wc=ceil((2+1.5*(mr-1)+2.5*(mr-1)^2)*pi/ts), h=(mr+1)/(mr-1)w1=2*wc/(h+1), w2=h*w1w1=wc/10; w2=25;ng1=[1/w1,1]; dg1=conv([1/w2,1],conv([1,0],[1,0]));g1=tf(ng1,dg1);g=polyval(ng1,j*wc)/polyval(dg1,j*wc); K=abs(1/g); %剪切频率处幅值为1,求K值g1=tf(K*g1)%3、确定反馈环节传递函数h=tf(dg1,ng1); Kh=1/K;h=tf(Kh*h) %期望频率特性的倒特性%4、验算性能指标g2=feedback(KK*g0,h); %校正后,系统的开环传递函数b1=feedback(KK*g0,1); b2=feedback(g2,1);bode(KK*g0,'r--',g2,'b',h,'g',w);grid onfigure,step(b1, 'r--',b2, 'b',t); grid on,[pos,tr,ts,tp]=stepchar(b2,delta)。
计算机仿真技术试题含完整答案

一、数值计算,编程完成以下各题(共20分,每小题5分) 1、脉冲宽度为d ,周期为T 的矩形脉冲的傅里叶级数如下式描述:)2cos(/)/sin(21[)(1τπππτn T d n T d n T d f n ∑∞=+=当150=n ,41=T d ,2/12/1<<-τ,绘制出函数)(τf 的图形。
解: syms n t;f=((sin(n*pi/4))/(n*pi/4))*cos(2*pi*n*t); s=symsum(f,n,1,150); y=(1+2*s)/4; x=-0.5:0.01:0.5; Y=subs(y,'t',x); plot(x,Y)2、画出函数5505.025.55.15.1cos 5)5(sin )(2x x x x ex x f x +++-=在区间[3,5]的图形,求出该函数在区间[3, 5]中的最小值点m in x 和函数的最小值m in f .解:程序如下 x=3:0.05:5;y=(sin(5*x).^2).*exp(0.05*x.^2)-5*(x.^5).*cos(1.5*x)+1.5*abs(x+5.5)+x.^2.5; mix_where=find(y==min(y)); xmin=x(mix_where); hold on; plot(x,y);plot(xmin,min(y),'go','linewidth',5);str=strcat('(',num2str(xmin),',',num2str(min(y)),')'); text(xmin,min(y),str); Xlabel('x')Ylabel('f(x)')经过运行后得到的图像截图如下:运行后的最小值点m in x =4.6,m in f = -8337.86253、画出函数xe x xf x 5.2cos )(3.02-⋅=-在[1,3]区间的图形,并用编程求解该非线性方程0)(=x f 的一个根,设初始点为20=x .解: x=1:0.02:3; x0=2;y=@(x)(cos(x).^2).*exp(-0.3*x)-2.5*abs(x); fplot(y,[1,3]); Xlabel('x') Ylabel('f(x)')X1=fzero('(cos(x).^2).*exp(-0.3*x)-2.5*abs(x)',x0)运行后求得该方程的一个根为z=0.3256。
自动化专业计算机仿真练习题包含答案(适合本科函授用)666

[R,P,H]=residue(A,B,C,D);(5%)
计算机仿真习题
一、填空题
1.Matlab的程序文件和simulink的模型文件的扩展名分别是_.m_____、_.mdl___。
2.四阶龙格-库塔法的局部截断误差为___Oh(5)____________。(注:步长用h表示)
3.已知A=[1 2 1;2 3 0;1 0 1];B=[1 2 0;3 5 0;0 1 4],写出下列指令运行的结果:
用 ,
答:
5.设系统的微分方程为 ,y为系统输出量,u为系统输入量,试导出系统的标准状态方程。
答:
令 , (4%)
则有 (8%)
(10%)
三、简答题
1.在连续系统的数字仿真中,有哪几种常用的数值积分法?分别有哪些特点
答:欧拉法和龙格-库塔法.
欧拉法:是显示一步算法,可以自启动,但是精度较低
龙格-库塔法:也是显示一步算法,也可以自启动,四阶龙格-库塔法的精度较高,能满足大多数工程的精度要求。
[A,B,C,D]=tf2ss(num,den); (3%)
[Z,P,K]=tf2zp(num,den); (4%)
[R,P,H]=residue(num,den);(5%)
(2)(5%)
2. , , ,D=0
sys=ss(A,B,C,D);(2%)
[num,den]=ss2tf(A,B,C,D);(3%)
6.计算机仿真的三要素为系统、模型与计算机。
7.matlab中最基本的绘图函数是___plot__________。
二、综合计算题
1.系统结构如下图所示,写出该系统的连接矩阵W和W0.并写出连接矩阵非零元素阵WIJ,其中Gi表示传递函数, 表示反馈系数
计算机仿真 习题3 课后答案

习题3
1、已知系统响应函数为)sin(11)(θ+-=-bt e b
t y bt ,其中21l b -=,)1arctan(2
l
l -=θ,要求用不同的线型或颜色,在同一张图上绘制l 取值为0.2,、0.4、0.6、0.8时,系统在[]18,0∈t 区间内的响应曲线,并要求用2.0=l 和8.0=l 对它们相应的两条曲线进行文字标志。
答:刚开始因为没有考虑到相乘或相除矩阵的维度而总出错,后来理解清楚之后就简单多了。
编写程序如下:
得到结果:
2、用plot
3、mesh 、surf 指令,绘制2222)1()1(1y x y x z ++++-=
三维图(x 、y 范围自定)。
答:用plot3时,我定义]100,0[∈x ,]100,0[∈y ;并分别令22)1(y x a +-=,22)1(y x b ++=。
同时需注意将1变换成与a 、b 同维的矩阵。
得到结果:
在利用mesh、surf绘图时,为了图形美观取]
x,x=y.
[-
∈
100
,
100
程序如下:
得到结果:
3、对向量t进行以下运算可以构成3个坐标的值向量:)
y=,
cos(t
x=,)
sin(t
z=。
利用plot3指令,并选用绿色的实线绘制相应的三维曲线。
t
答:取pi
:0(
:1.0
=。
注意绿色是‘g’。
编写程序如下:
t*
)
10
得到结果:。
计算机仿真技术与cad第三版课后练习题含答案

计算机仿真技术与CAD第三版课后练习题含答案前言计算机仿真技术与CAD第三版是近年来广受欢迎的CAD教材。
本书涵盖了CAD 的基础知识、CAD的应用、计算机仿真技术等内容,适合CAD初学者和高级用户使用。
本文主要介绍本书的课后练习题及答案,希望对大家有所帮助。
第一章课后练习题及答案1.1 选择题1.以下哪项不是CAD应用的领域?A. 工程学B. 数学C. 植物学D. 医学答案:C2.CAD是什么的缩写?A. Computer-ded Design(计算机辅助设计)B. Computer-ded Distance(计算机辅助距离)C. Capsule-med Destruction(胶囊定向破坏)D. Capability-Assisted Driving(能力协助驾驶)答案:A1.2 填空题1.CAD软件主要分为三种类型,分别是2D __________ 、3D__________ 、仿真软件。
答案:制图软件、制造软件2.AutoCAD是一款 __________ 系统。
答案:二维制图3.CAD软件通常可以完成______________ 、___________ 、____________ 等操作。
答案:制图、设计、分析1.3 综合应用题设计一件简单的图形,包括设备名称、设备布局图、视图图和详细图。
并在AutoCAD中实现。
答:见图。
简单图形简单图形图中的简单图形包括了设备名称、设备布局图、视图图和详细图。
其中,设备名称为“简单图形”,设备布局图包含了该设备的位置、大小和方向信息,视图图包含了设备的3D视角,详细图则针对设备内部的结构进行了细节描绘。
使用AutoCAD可以方便地实现这件图形的设计和制图。
第二章课后练习题及答案……第三章课后练习题及答案……第四章课后练习题及答案……结语以上是《计算机仿真技术与CAD第三版》的部分课后练习题及答案,希望对大家有所帮助。
本书内容丰富、简明易懂,是一本非常优秀的CAD教材。
计算机仿真与建模考试试题

计算机仿真与建模考试试题一、单项选择题1. 在计算机仿真与建模中,以下哪个软件是用于创建和模拟三维计算机图形的?A. MATLABB. AutoCADC. SolidWorksD. 3ds Max2. 计算机仿真与建模常用的数学建模方法有哪些?A. 微分方程建模B. 蒙特卡洛模拟C. 神经网络模型D. 遗传算法优化3. 下面哪个软件是用于分析流体和气体流动的计算机仿真工具?A. ANSYSB. CATIAC. Pro/ENGINEERD. PTC Creo4. 在计算机仿真中,有哪些常见的物理模型?A. 质点模型B. 弹簧-质点模型C. 流体模型D. 电路模型5. 计算机仿真与建模的主要应用领域是什么?A. 机械工程B. 航空航天C. 生物医学D. 所有以上领域二、简答题1. 什么是计算机仿真与建模?计算机仿真与建模是指使用计算机技术和数学方法对现实世界的问题或系统进行建模和模拟实验的过程。
通过对系统各个组成部分的特性进行数学描述和计算机编程实现,可以模拟真实系统的行为,并进行虚拟实验和预测。
2. 计算机仿真与建模的主要步骤是什么?计算机仿真与建模的主要步骤包括:问题建模与分析、数学建模、软件工具选择与开发、模型验证与调试、模拟实验与结果分析等。
3. 计算机仿真与建模的优势有哪些?计算机仿真与建模具有以下优势:- 可以对复杂系统进行全面、高效的分析和研究,避免了大量实际实验和浪费资源;- 提供了研究系统性能、优化设计和决策支持的基础;- 可以预测系统行为并进行虚拟实验,帮助解决实际问题和提高生产效率;- 提供了客观、可重复的实验环境,方便对结果进行验证和比较。
4. 计算机仿真与建模的应用范围有哪些?计算机仿真与建模广泛应用于工程领域,包括机械工程、电气工程、航空航天、建筑工程等。
此外,它还在生物医学、交通运输、环境科学等领域有重要应用。
三、综合题某工程团队需要设计一种新型的风力发电机,用于发电和供电给一个小型城市。
计算机仿真测试题及答案

计算机仿真测试题及答案1. 选择题1.1 下列关于计算机仿真的定义,哪个是正确的?A. 计算机仿真是通过使用计算机来模拟现实世界的过程和现象B. 计算机仿真是通过使用计算机来生成虚拟的3D图像C. 计算机仿真是通过使用计算机来进行数据分析和统计D. 计算机仿真是通过使用计算机进行编程和软件开发答案:A1.2 计算机仿真的主要应用领域是:A. 电影和游戏制作B. 数据分析和统计C. 空气动力学和流体力学D. 软件开发和编程答案:C1.3 以下哪个是计算机仿真的一个重要优点?A. 精确模拟现实世界的过程和现象B. 速度快,可以实时进行模拟C. 不需要消耗大量的计算资源D. 可以替代真实的实验和测试答案:D2. 填空题2.1 计算机仿真可以帮助工程师在设计阶段进行 __________ 和__________。
答案:分析,优化2.2 计算机仿真可以用于预测产品在不同环境条件下的 __________和 __________。
答案:性能,行为2.3 在计算机仿真中,模型是对现实世界中的对象或系统进行的一个 __________ 描述。
答案:数学3. 简答题3.1 请简要解释计算机仿真的工作原理。
答案:计算机仿真的工作原理是基于数学模型和计算机算法。
首先,根据需要模拟的对象或系统的特性,工程师会构建一个数学模型,用来描述该对象或系统的行为。
然后,使用计算机算法对这个数学模型进行求解和模拟。
算法会根据初始条件和输入参数,计算出模拟过程中的各个时间点上的状态和输出结果。
最后,通过可视化等方式,将仿真结果呈现给使用者。
3.2 计算机仿真的主要应用领域有哪些?请举例说明。
答案:计算机仿真的主要应用领域包括航空航天、汽车工程、建筑设计、电子电路设计等。
例如,在航空航天领域,工程师可以使用计算机仿真来模拟飞机或火箭在不同高度、速度和气候条件下的飞行行为,以评估其性能和安全性。
在建筑设计领域,可以使用计算机仿真来模拟建筑物在地震或风暴等自然灾害中的响应,以提前预防和减少损失。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机仿真试题1.编写一个函数,使其能够产生如下的分段函数:错误!未找到引用源。
并调用此函数,绘制x=[0,+2]范围内的f(x)*f(x+2) 。
(10分)function y=f(x)if x<=2y=0.5*x;else if x>6y=0.5;else y=1.5-0.25*x;endendx=0:0.05:2;y= f(x)’*f(x+2));plot(x,y)图 1-12.已知4阶龙格-库塔算法如下:试利用该算法求解以下微分方程:(15分)本题可以调用MATLAB函数中龙格-库塔算法函数ode45,首先编写m文件:function dy=func(x,y)dy=-y+1;end再在主窗口调用此文件:[x,y]=ode45('func',[0,5],0)%这里的[0,5]为任取区间,表示方程在此范围的解。
运行结果如下:x =0.00010.00010.00020.00020.00050.00070.00100.00120.00250.00370.00500.00620.01250.01880.02510.0313 0.06270.09410.12550.15690.28190.40690.53190.65690.78190.90691.03191.15691.28191.40691.53191.65691.78191.90692.03192.15692.28192.40692.53192.65692.78192.90693.03193.15693.28193.40693.53193.65693.78193.90694.03194.15694.28194.40694.53194.65694.74274.82854.91425.0000y =0.00010.00010.00020.00020.00050.00070.00100.00120.0025 0.0037 0.0050 0.0062 0.0124 0.0186 0.0248 0.0309 0.0608 0.0898 0.1180 0.1452 0.2457 0.33430.41250.48160.54250.59630.64370.68550.72250.75510.78390.80930.83170.85150.86890.88430.89790.90990.92050.92980.93810.94540.95180.95740.96240.96690.97080.97420.97720.97990.98230.98430.98620.98780.98920.99050.99130.99200.99270.9933为只管起见,我们使用函数命令画出x-y(plot(x,y))的关系如下图:图1-23.用matlab语言求下列系统的状态方程、传递函数、零极点增益、和部分分式形式的模型参数,并分别写出其相应的数学模型表达式:(15分)(1)G(s)=324327242410355024s s ss s s s+++++++(2).X=2.25 -5 -1.25 -0.542.25 -4.25 -1.25 -0.2520.25 -0.5 -1.25 -121.25 -1.75 -0.25 -0.75 0X⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦uy= [0 2 0 2] X解:(1)a)求对应状态方程参数:num=[1 07 24 24]; den=[1 10 35 50 24]; [A,B,C,D]=tf2ss(num,den) 运行结果:A =-10 -35 -50 -241 0 0 00 1 0 00 0 1 0B =1C =1 7 24 24D =故,状态方程为:.X = x+ uY=[1 7 24 24]xb)求对应零极点增益模型参数:num=[1 07 24 24]; den=[1 10 35 50 24]; [Z,P,K]=tf2zp(num,den) 运行结果如下: Z =-2.7306 + 2.8531i -2.7306 - 2.8531i -1.5388P = -4.0000 -3.0000 -2.0000 -1.0000K = 1故变换后的零极点模型为: G(s)=c)求对应部分分式型:num=[1 07 24 24]; den=[1 10 35 50 24]; [R,P,H]=residue(num,den) 运行结果如下: R =4.0000 -6.0000 2.0000 1.0000P =-4.0000 -3.0000 -2.0000 -1.0000H = []故变换后的部分分式模型为:11223644)(+++++-+=s s s s s G(2)由题给条件,知:A=[2.25 -5 -1.25 -0.5; 2.25 -4.25 -1.25 -0.25;0.25 -0.5 -1.25 -1;1.25 -1.75-10 -35 -50 -24 1 0 0 0 0 1 0 0 0 0 1 010 0 0-0.25 -0.75] B=[4;2;2;0] C=[0 2 0 2],D=0 a)求传递函数矩阵: [num,den]=ss2tf(A,B,C,D) 运行结果为: num =0 4.0000 14.0000 22.0000 15.0000 den =1.0000 4.0000 6.2500 5.25002.2500 故,所对应传递函数模型为:25.225.525.641522144)(23423+++++++=s s s s s s s s Gb)求零极点模型:num=[0 4 14 22 15];en=[1 4 6.25 5.25 2.25]; [Z,P,K]=tf2zp(num,den) 运行结果为: Z =-1.0000 + 1.2247i -1.0000 - 1.2247i -1.5000 P =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iK =4.0000故,零极点模型为:)866.05.0()5.1()2247.11)(5.1(4)(2i s s i s s s G ±++±++=c)求对应部分分式模型: [R,P,H]=residue(num,den) 运行结果为: R =4.0000 -0.0000-0.0000 - 2.3094i -0.0000 + 2.3094iP =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iH = []故变换后的部分分式模型为:i s ii s i s s G 866.05.03094.2866.05.03094.25.14)(+++-+-++=4.已知一单位反馈系统开环传递函数为:,试绘制系统Nyquist图,判断闭环系统的稳定性,并求其单位阶跃响应。
(15分)k=10; z=[]; p=[0 -0.5];[num,den]=zp2tf(z,p,k); figure(1)nyquist(num,den,’k ’) title(‘Nyquist Plot ’) figure(2)[num1,den1]=cloop(num,den); step(num1,den1,’k ’) title (‘Step Response ’) num=[10];den=[2,2,2.5,1,0]; nyquist(num,den)下图1为奈奎斯特图,由图知,奈奎斯特曲线不包围(-1,0j )点,故而系统稳定。
图2为闭环系统的单位阶跃响应曲线。
图1-3图1-45.某单位负反馈系统的开环控制系统的传递函数为2k (0.80.64)()(0.05)(5)(40)K s s G s s s s s ++=+++ (1)绘制系统的根轨迹;(2) 当K=10时,绘制系统的Bode 图,判断系统稳定性,并且求出幅值裕度和相角裕度。
(15分) (1) num=[1 0.8 0.64];den=[1,45.05,202.25,10,0];rlocus(num,den)图1-5(2) num=[10 8 6.4];den=[1,45.05,202.25,10,0];[mag,phse,w]=bode(num,den);Margin(mag,phase,w)图1-6由图可知,相角裕度为26.9度,幅值裕度为116dB。
6.按照下图1所示采用Simulink建立系统的结构图文件。
(1)K=50,纪录图示三处的波形,分析系统的稳态性并给出稳态误差。
(2) K=200,纪录图示三处的波形,根据曲线分析系统的稳定性。
(3)编写程序求取K=200时的闭环传递函数,求出系统的闭环极点(特征根),说明系统的稳定性,分析与(2)得出的结论是否一致。
图1-7 simulink建模结构图图1-8 K=50时Scope响应图图1-9 K=50时Scop1 响应图图1-10 K=50时Scope2响应图(2)图1-11 K=200时系统结构图图1-12 K=200时Scope响应图图1-13 K=200时Scope1响应图图1-14 K=200时Scope2响应图(3)>>s=tf('s');>>G1=200;G2=1/s;G3=1/(s+5);G4=3/(s+2);>> G=feedback(feedback(G4,1)*G1*G2*G3,1)Transfer function:600-------------------------s^3 + 10 s^2 + 25 s + 600>>pole(G)ans =-12.05491.0275 + 6.9797i1.0275 - 6.9797i右半部有两个极点,系统不稳定,和(2)所得结果一致7.采用Simulink建立下列系统的模型,观察其响应,并设计一个PID控制器,使系统稳定。
图1-15 系统结构图图1-16 系统响应图由图16知系统不稳定、加入PID调节图1-17 加入PTD时系统结构图图1-18 加入PID时系统响应图。
