多元统计分析案例分析.doc
多元统计分析(1)

社会科学研究中的应用
1 2
社会现象分析
通过多元统计分析,研究人员可以分析社会现象 的多个方面,揭示其内在规律和影响因素。
政策效果评估
利用多元统计分析方法,政策制定者可以评估政 策实施的效果,以便调整和完善政策。
3
人口统计研究
分析人口数据的多个维度,如年龄、性别、教育 水平等,以揭示人口结构和社会发展的关系。
处理非结构化数据
深度学习在处理图像、 文本等非结构化数据方 面具有优势,可以扩展 多元统计分析的应用范 围。
统计计算与可视化技术的创新发展
01
高性能计算技术
利用高性能计算技术,可以加速多元统计分析的计算过程,提高分析效
率。
02
可视化技术
可视化技术可以帮助人们更直观地理解多元统计分析的结果,揭示数据
模型拟合与评估
利用样本数据对模型进行拟合,并通过相关指标评估模型的拟合优 度和预测能力。
假设检验与P值计算
根据研究假设进行假设检验,并计算相应的P值以判断假设是否成立 。
结果解释与评估
结果解释
对分析结果进行解释和说明,包括统计量的意义 、模型的预测能力等。
结果评估
根据专业知识、经验等对分析结果进行评估和判 断,以验证结果的合理性和可靠性。
目录
CONTENTS
01
引言
BIG DATA EMPOWERS TO CREATE A NEW
ERA
多元统计分析的定义
01
多元统计分析是一种研究多个变 量之间相互关系以及这些变量对 整体影响的统计方法。
02
它通过对多个变量的观测数据进 行综合分析,揭示变量之间的内 在规律和联系。
多元统计分析的应用领域
多元统计报告-王天豪-1201620203

中国地质大学研究生课程论文封面课程名称多元统计分析教师姓名陈兴荣研究生姓名王天豪研究生学号 1201620203 研究生专业安全工程所在院系工程学院类别: 硕士日期: 2016年12月1日评语注:1、无评阅人签名成绩无效;2、必须用钢笔或圆珠笔批阅,用铅笔阅卷无效;3、如有平时成绩,必须在上面评分表中标出,并计算入总成绩。
回归分析在油气储量密度影响因素分析中的应用摘要:在石油地质学和石油安全领域中,油气得以保存至今,是受油气的生、储、盖、运、聚五大作用共同控制的。
本文运用多元线性回归的方法,研究油气藏储量密度与生油条件参数的关系。
关键词:多元线性回归,储量密度1、回归分析模型原理回归分析法是一种处理变量间相关关系的数理统计方法,它不仅可以提供变量间相关关系的数学表达式,而且可以利用概率统计知识对此关系进行分析,以判别其有效性;还可以利用关系式,由一个或多个变量值,预测和控制另一个因变量的取值,进一步可以知道这种预测和控制达到了何种程度,并进行因素分析。
回归分析法就是以统计回归概念为基础,采用多种类型的回归方法建立预测方程,包括一元线性回归方程、多元线性回归方程、非线性回归方程等。
多元线性回归时要确定因变量与多个自变量之间的定量关系,它的数学模型为:y=β0+β1x1+…+βm x m+ε。
其中,β0,β1,βm为待定参数;ε为随机变量,是除x以外其他随机因素对y影响的总和。
其中,称E(y)=β0+β1x1+…+βm x m为理论回归方程。
在实际问题的研究中,事先并不能断定随机变量y与变量x1,x2,…,x m之间是否有线性关系,在进行回归参数的估计前,用多元线性回归方程去拟合随机变量y与变量x1,x2,…,x m之间的关系,只是根据一些定性分析所作的一种假设。
因此,当求出线性回归方程后,还需对回归方程进行显著性检验,一般采用两种统计方法对回归方程进行检验,一种是回归方程显著性的F检验;另一种是回归系数显著性的t检验。
多元统计分析方法在白酒香型识别中的应用

白酒是世界主要蒸馏酒品种之一,中国白酒历史悠久,是宝贵的民族遗产[1]。
白酒分析手段目前进入新的发展阶段,获得了令人瞩目的成果,包括常规检测技术、色谱技术等在内的众多分析检测手段,以揭示白酒的风味与白酒中微量成分及其量比的联系。
白酒风味物质研究已成为行业研究的大趋势[2]。
经研究证明,白酒风味组成极其复杂,组分种类很多,迄今为止从白酒中检测到的微量风味化合物有1 000余种[3]。
白酒中的微量成分十分丰富,不同产品中的香气种类和含量差异很大,这也是决定白酒香气、口感和风格的关键所在[4],但受研究条件的限制,对全部微量成分进行准确的定量或定性尚有一定困难。
多变量统计分析作为一种数理统计分析手段,已经越来越多的应用于酒类风味特征的研究中[5]。
目前,所涉及的统计分析软件最为广泛的是SPSS软件。
该软件在酒类风味特征研究中的应用方法主要有:主成分分析、聚类分析和判别分析等。
1 分析方法1.1 主成分分析主成分分析是在空间数据中找出几个能够控制所有变量的主成分,将数据从高维空间降至低维,从而使数据处理更为简便[6]。
一般提取特征值大于1或累计方差贡献率大于80%的因子为主成分,故提取出来的主成分包含了原始数据的大部分信息[7]。
在对数据进行主成分分析后,以主成分的得分做图即可得到所有样本的二维或三维PCA投影图,样本间的关系即可较好的表现出来,进而实现样本的分类[7]。
1.2 聚类分析简便且直观,广泛应用于指纹图谱研究。
其基本原理是按照一定准则将具有相同或相似性的物质聚为一类,例如采用欧式距离计算相似度后,通过ward最小方差法进行系统聚类等;聚类分析在白酒香型、风格等的归类和区分上有很好的应用[8]。
1.3 判别分析是根据事物特点的特征值及其所属的类按照一定的准则求出判别函数,根据判别函数对事物进行分类的一种分析方法[9]。
2 研究内容本文以酱香型白酒、浓香型白酒及清香型白酒为研究对象,采用气相色谱分析技术对白酒微量风味组分进行有效检测,色谱数据以多元统计学为基础,通过主成分分析(PCA)、聚类分析、判别分析等方法对三种不同香型白酒成分间的复杂量比关系进行分析,建立了一种主流白酒香型评判模型。
多元统计分析课程设报告计参考Word

XXXX课程设计任务书课程名称多元统计分析课题判别分析与因子分析专业班级学生姓名学号指导老师审批任务书下达日期任务完成日期目录课题一判别分析摘要 (1)一、指标和数据 (1)二、聚类分析的实施 (1)三、判别分析的实施 (2)四、结果分析 (5)课题二因子分析摘要 (6)一、数据 (6)二、因子分析的实施 (6)三、结果分析 (10)总结 (11)参考文献 (11)评分标准 (12)附表 (13)课题一判别分析摘要聚类分析(cluster analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术。
而判别分析是根据表明事物特点的变量值和它们所属的类,求出判别函数。
根据判别函数对未知所属类别的事物进行分类的一种分析方法。
核心是考察类别之间的差异。
本课题正是基于多元统计分析中聚类分析和判别分析的方法,以《各地区按行业分城镇单位就业人员平均工资》的调查数据为对象(预留出待判样本),借助Spss统计软件用聚类分析进行分类,并以分好的类别为依据对待判样本进行判别分类以及对已分类样本进行回判分析。
一、指标和数据按要求于国家统计局网站查找变量数大于等于10,样本数大于等于20的合适数据并整理。
得到整理后的《各地区按行业分城镇单位就业人员平均工资》(见附表一)。
其体系共有31个地区,19项指标。
具体指标x1:农、林、牧、渔业就业人员平均工资,简写“农、林、牧、渔业”(以下具以简写形式省略“就业人员平均工资”);x2:采矿业;x3:制造业;x4:电力、燃气及水的生产和供应;x5:建筑业;x6:交通运输、仓储和邮政业;x7:信息传输、计算机服务和软件业;x8:批发和零售业;x9:住宿和餐饮业;x10:金融业;x11:房地产业;x12:租赁和商务服务业;x13:科学研究、技术服务和地质勘查业;x14:水利、环境和公共设施管理业;x15:居民服务和其他服务业;x16:教育;x17:卫生、社会保障和社会福利业;x18:文化、体育和娱乐业;x19:公共管理和社会组织。
多元统计分析实例

多元统计分析实例院系: 商学院学号: 姓名:多兀统计分析实例本文收集了 2012年31个省市自治区的农林牧渔和相关农业数据,通过对对 收集的数据进行比较分析对31个省市自治区进行分类•选取了 6个指标农业产值 林业产值.牧业总产值,渔业总产值,农村居民家庭拥有生产性固定资产原值,农 村居民家庭经营耕地面积. 数据如下表: 江 区 京津北H 蒙宁林龙海苏江徽建西东南北南东西南庆川州南藏西肃海夏牘地北天河山内辽吉黒上江浙安福江山河湖湖广广海重四贵77西陕甘青宁新农业总产值 林业驰产{牧业总产懾业总产侬村居民家庭拥有生产性[5166.2954.83 154.16 12 98 12767. 09 0・5195.^9 £ 79 105. 01 61, 66 17508. 57 1. 58 3095.29 77.88 1747. 66 1?7. 74 17904. S3 1789847-41 79, 07 298. 83 8. 42 ^808. 38 2.51171.-57 97. 7G U1S. 86 26. 08 293曲.旳 10. 4 1539.65128. 68 16ZL 23 618. 74 249^7. 92 3. 781166.ES90. 1 1130. 36 34. 14 24937. SB S. 272315. 64 134. 51350. 63 77. 92 31507. 91 13. 56171.48 9.5572. 59 57. 45 4146. 13 0. 262966.72 99. 75 1226,18 1235.4 14541. 03 L251229.36 142.14 549. 01 687. 05 22747. 33 6 541867.64 209. 5 1119.73 334. 43 15134. 35 1. 391263.71 256. 45 48L 28 p03. 36 11821. 38 731003.21 228. 91 752. 63 333. 06 gggg. 31 L 57 39&0.储 107.01 22S5. 92 1267. 07 19168.14 L &4 3958.^5 140. 85 2255. 61 SS.4 12980. 72 1. &2 2488. 06 100.05 1334, X 626, 23 10813. 13 1. 71 2651.69 259. 97 1488. 58 279. 94 3904. 32 1. 22 2229. 27222.74 1134.14 914. 05 8516. 72 0.53 1724 245. 56 1072. 77 331. 74 11851. 56 L 37 4S0. 72 137.85 214. 14 236.27 11387. 06 0. 83 341.51 43.48 453. 9 44. 99 122S5. 74 L 29 2764- 9 151. 52269. 86 163. 77 13759.17 1.14364. 54.19421. 55 28. 21 11957. 31 L 181398.17225. S3 912. 97 63.1 19020. 92 1.. 6 53.39 2” 56 59. 02 0. 22 52935. 07 L 891526.23 58. 44 598. 72 14. 61 12273. 06 L 52984,24 20. 07 231. 72 1,8 1$486. 44 2. 72 117-09 4.57 137. 08 0. 56 21919.甜 L 33 240, 4&9・77 105, 72 13. 36 24266.19 3・69 1675収04485. 37 15* 26 35Q70. 315 76.聚类法设定4个群聚,采用了系统聚类法.下表为spss分析之后的结果.C A S E 0 5 10 15 20 25 内蒙 5 -+吉林7 -+云南25 - + -+江西14 -+ +-+陕西27 - + -+ |新疆31 -+ +- +安徽12 -+-+ 11广西20 —+ + — + +——————— +辽宁 6 ---+ | |浙江11 -+—+ 1福建13 -+ 1重庆22 -+ + ............... ....... + 贵州24 -+ 1|山西 4 -+ -+ | |甘肃28 -+ | | |北京 1 -+ | | |青海29 + + + | 1天津 2 -+ 1|上海9 -+ 1|宁夏30 -+ - +|西藏26 -+ |海南21 -+ |河北 3 | 1四川23 - + | |黑龙江8 -+-+ + .......... + |湖南18 -+ + + | | |湖北17 - + -+ +-+ + -------------- ■...... + 广东19 -+ | |江苏10 --——+ |山东15 ...... + ....... +河南16 ...... +从SPSS分析结果可以得到,内蒙,吉林,黑龙江,新疆为第2族群,这一族群的特点是农业收入可能不高,但是农民的固定资产,和耕地面积非常高,农民的富余程度或者机械化程度较高;山东是第3族群,这一族群中六个指标都处于较高水平农林牧渔四项收入都处于较高水平而且农民富余;西藏处于第4族群,这是因为,西藏人员较少,自然条件恶劣,可使用耕地少,但是,由于国家的扶持,农民的固定资产较多,农民相对而言比较富足;大多数省份属于第1族群,这一族群的特点在于六项指标都没有较为突出的一项,或者农林牧渔收入的本来就少,或者是农民的虽然比较辛苦,总体的农业收入较高,但是农民的收入水平比较低,固定资产较少•三.判别法X1,X2,X3,X4,X5,X6分别代表农业产值,林业产值.牧业总产值,渔业总产值,农村居民家庭拥有生产性固定资产原值,农村居民家庭经营耕地面积实验结果分析:从表上可以看出,组均值之间差值很大.各个分组,在6项指标上均值有较明显的差异.由表中可以知道,13456指标之间的sig 值较小,2指标sig 值有0.561较大, 不过仍说明接受原假设,各指标族群间差异较大.从表中可以知道,检验结果p值>0.05,此时,说明协方差矩阵相等,可以进行bayes检验.Fisher 分析法协方差矩阵的均等性的箱式检验典型判别式函数摘要由表中看出,函数1,2的特征值达到0.911,0.822比较大,对判别的贡献大由表中可知,3个Fishe判别函数分别为y i 2.928 0.003X20.626X6y2 2.269 0.002X2 0.489X6y3 0.975 0.009X2 0.01X3 0.03X4 0.037X6农村居民家庭拥有生产性固定资产原值对判别数据所属群体无用该表是原始变量与典型变量(标准化的典型判别函数)的相关系数,相关系数的绝对值越大,说明原始变量与这个判别函数的相关性越强.从表中可以看出相关性较强.符合较好.由上表可知各类别重心的位置,通过计算观测值与各重心的距离,距离最小的即为该观测值的分类.贝叶斯分析法该表为贝叶斯函数判别函数的取值,从图中可以知道三类贝叶斯函数y1 0.03X1 0.029X2 0.03X3 0.002X4 0.001X5 0.153X1 8.418第一类:第二y2 0.06X10.42X2 0.009X3 0.004X40.004X5 4.286X6 38.18类;第三y3 0.02X-I0.010X20.002X30.010X40.001X5 1.X620.732类;第四类:『4 0.OO3X-I 0.051X20.004x30.006x40.002x5 1.675x661.646将各样品的自变量值代入上述4个BayeS判别函数,得到函数值。
多元统计分析案例分析
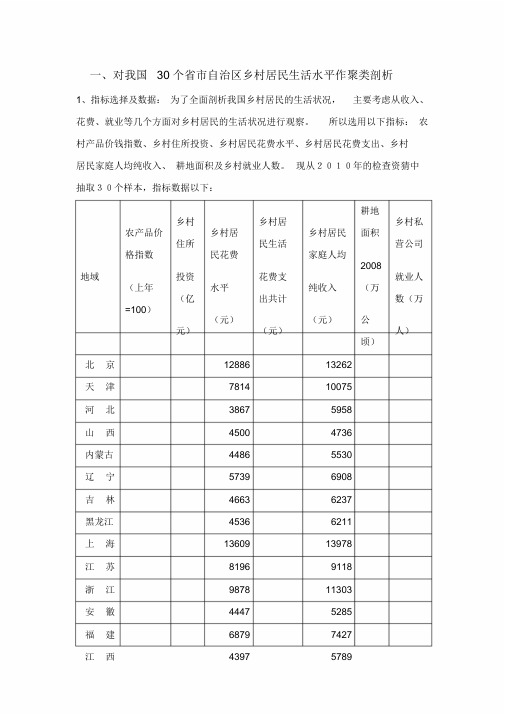
一、对我国30 个省市自治区乡村居民生活水平作聚类剖析1、指标选择及数据:为了全面剖析我国乡村居民的生活状况,主要考虑从收入、花费、就业等几个方面对乡村居民的生活状况进行观察。
所以选用以下指标:农村产品价钱指数、乡村住所投资、乡村居民花费水平、乡村居民花费支出、乡村居民家庭人均纯收入、耕地面积及乡村就业人数。
现从2010年的检查资猜中抽取30个样本,指标数据以下:耕地乡村乡村居乡村私农产品价乡村居乡村居民面积住所民生活营公司格指数民花费家庭人均2008地域投资花费支就业人(上年水平纯收入(万(亿出共计数(万=100)(元)(元)公元)(元)人)顷)北京12886 13262天津7814 10075河北3867 5958山西4500 4736内蒙古4486 5530辽宁5739 6908吉林4663 6237黑龙江4536 6211上海13609 13978江苏8196 9118浙江9878 11303安徽4447 5285福建6879 7427江西4397 5789山东5733 6990河南4061 5524湖北4758 5832湖南4513 5622广东5880 7890广西3561 4543海南3846 5275重庆3652 5277四川4748 5087贵州2926 3472云南3603 3952陕西3683 4105甘肃2975 3425青海3684 3863宁夏3894 4675新疆3590 4643数据根源:《中国统计年鉴2010》.2、将数据进行标准化变换:耕地乡村乡村居乡村私农产品价乡村居乡村居民面积住所民生活营公司格指数民花费家庭人均2008地域投资花费支就业人(上年水平纯收入(万(亿出共计数(万=100)(元)(元)公元)(元)人)顷)北京河北山西内蒙古辽宁吉林黑龙江上海江苏浙江安徽福建江西山东河南湖北湖南广东广西海南重庆四川贵州云南陕西甘肃宁夏新疆3、用K-均值聚类法对样本进行分类以下:聚类成员事例号地域聚类距离1 北京 12 天津 23 河北 34 山西 45 内蒙古 36 辽宁 27 吉林 38 黑龙江 39 上海 110 江苏 211 浙江 112 安徽 313 福建 214 江西 415 山东 316 河南 317 湖北 318 湖南 419 广东 220 广西 421 海南 422 重庆 423 四川 324 贵州 425 云南 326 陕西 427 甘肃 428 青海 429 宁夏 430 新疆 4分四类的状况下,最后分类结果以下:第一类:北京、上海、浙江。
多元统计分析(何晓群 中国人民大学) 第三章

2021/1/28
中国人民大学六西格玛质量管理研究中心
2021/1/28
中国人民大学六西格玛质量管理研究中心
23
目录 上页 下页 返回 结束
§3.2 相似性度量
2021/1/28
中国人民大学六西格玛质量管理研究中心
24
目录 上页 下页 返回 结束
§3.2 相似性度量
(2) 相关系数。这是大家最熟悉的统计量,它 是将数据标准化后的夹角余弦。
有时指标之间也可用距离来描述它们的接近程度。 实际上距离和相似系数之间可以互相转化,
• 与多元分析的其他方法相比,聚类分析的方法是 很粗糙的,理论上还不完善,但由于它能解决许 多实际问题,很受人们的重视,和回归分析、判 别分析一起被称为多元分析的三大方法。
2021/1/28
中国人民大学六西格玛质量管理研究中心
7
目录 上页 下页 返回 结束
§3.1 聚类分析的思想
• 3.1.2 聚类的目的
(2)一种改进的距离就是在前面曾讨论过 的马氏距离,它对一切线性变换是不变 的,不受指标量纲的影响。它对指标的 相关性也作了考虑,我们仅用一个例子 来说明。
2021/1/28
中国人民大学六西格玛质量管理研究中心
16
目录 上页 下页 返回 结束
§3.2 相似性度量
2021/1/28
中国人民大学六西格玛质量管理研究中心
2021/1/28
多元统计分析经典案例

29
Copyright CAE
当你看一张map时 .. 问你自己
• 它意味着什么? • 它对理解数据有什么附加的作用? • 它对我们所知道的市场/顾客的思考方式是否适 合?
– 如果不是 - 错在什么地方?
• 它是否帮助我更好地了解市场?
30
Copyright CAE
当你看一张map时 .. 问你自己
Bird
Dog
40% 40% 20% 20% 50%
Cat
10%
16
Copyright CAE
现在我们用颜色和动物名称两个变量 来做2-维的图表
努力来显示..
- 那些动物在颜色方面最相似,那些区别最大? - 那些颜色更倾向那类动物 - 那些动物和那些颜色有更强的相关性,那些相关性很弱
17
Copyright CAE
Copyright CAE
相关性分析 Correspondence Analysis
9
Copyright CAE
结构
• • • • • • 什么是相关性分析? 尝试通过练习了解它 输入的类型 设计录入的格式 执行分析 解释和表述分析的结果
10
Copyright CAE
什么是相关性分析?
• 经常也称作 Brand Mapping 或 CORAN Mapping
6
Copyright CAE
我们通常使用的多元分析技术…...
• • • • • • • • 相关性分析(Brand Mapping ) 主成分分析 因子分析 多元回归 聚类分析/市场细分 联合性分析/ 平衡(Trade off) 分析 判别分析 etc. etc. etc.
7
Copyright CAE
《多元统计分析》4

《多元统计分析》4.3 系统聚类法一、系统聚类法的概念系统聚类法(或层次聚类法)是通过一系列相继的合并或相继的分割来进行的,分为聚集的和分割的两种。
系统聚类法适用于样品数目n不是非常大的情形。
聚集系统法的基本思想是:开始时将n个样品各自作为一类,并规定样品之间的距离和类与类之间的距离,然后将距离最近的两类合并成一个新类,计算新类与其他类的距离;重复进行两个最近类的合并,每次减少一类,直至所有的样品合并为一类。
分割系统法的聚类步骤与聚集系统法正相反(略)。
聚集系统法最为常用,本讲着重介绍其中常用的五种方法。
聚集系统法的图示说明二、常用的系统聚类法1.最短距离法2.最长距离法3.类平均法4.重心法5.离差平方和法(Ward方法)所有这些聚类方法的区别在于类与类之间距离的定义不同。
1.最短距离法定义类与类之间的距离为两类最近样品间的距离,即,min K LKL iji G j G D d ∈∈=最短距离法的递推公式将类G K 和G L 合并成一个新类G M ,则G M 与任一类G J 之间距离的递推公式为{}min ,MJ KJ LJ D D D =例1(书中例6.3.1)设有五个样品,每个只测量了一个指标,分别是1,2,6,8,11,试用最短距离法将它们分类。
记G1={1},G2={2},G3={6},G4={8},G5={11},样品间采用绝对值距离。
G6=G1∪G2={1,2}。
G1G2G3G4G5G10G210G3540G47620G5109530G 7=G 3∪G 4={6,8}。
G 8=G 7∪G 5={6,8,11}。
G 6G 3G 4G 5G 60G 340G 4620G 5953G 6G 7G 5G 60G 740G 593G9=G6∪G8={1,2,6,8,11}。
最短距离法树形图G6G8G60G840最短距离法有一种挑选长链状聚类的倾向,称为链接倾向。
最短距离法不适合对分离得很差的群体进行聚类。
多元统计分析课程案例教学

多元统计分析课程案例教学研究摘要:多元统计分析是一门应用性很强的学科,本文从该课程的特点和案例教学的特点入手,分析研究了在该课程教学中应用案例教学的必要性,并结合教学内容探讨了实例分析在课程教学中的具体应用,从而说明案例教学是一种非常适合于该课程的教学方法。
关键词:多元统计分析案例教学教学方法一、多元统计分析课程的特点多元统计分析是近几十年来从经典统计学中迅速发展起来的一个分支,是一种综合分析方法,它能够在多个对象和多个指标互相关联的情况下分析它们的统计规律。
随着计算机的广泛应用及统计软件的普及,多元统计方法已被广泛应用于自然科学、工程技术、生命科学、经济管理和社会科学领域,同时也促进了理论的发展。
多元统计分析属于是概率统计的一部分,复杂的数学推导、论证,繁琐的矩阵、线代计算,深奥的概率知识、抽象的概念和理论是这门课程的特点。
如果有的学生学习在高等数学和概率统计的过程中没有打好基础,在最初看到该课程中大量的数学符号、公式推导时,就很容易产生畏难情绪。
因此,我们在教学过程中需要配合各种统计软件包如sas,spss的操作,通过简单的操作和计算,可以使学生利用多元统计分析方法解决实际问题更为简单方便,而适合的案例教学更能够将多元统计的理论和方法呈现于学生面前,加深学生对分析方法的认识和理解。
二、案例教学的特点案例教学是由美国哈佛法学院前院长克里斯托弗·哥伦布·朗代尔于1870年首创的教学方法,后经哈佛企管研究所所长郑汉姆推广,并从美国迅速传播到世界许多地方,被认为是代表未来教育方向的一种成功教育方法。
在20世纪80年代,案例教学引入我国,逐渐应用于教学过程中,并被广大教师认可。
案例教学是一种通过模拟或者重现现实生活中的一些场景,让学生把自己纳入案例场景中,通过讨论或者研讨的方式来进行学习的一种教学方法。
学生在教师的指导下,根据教学目的要求,对案例进行调查、阅读、思考、分析、讨论和交流等活动,通过实例学习分析问题和解决问题的方法或道理,进而提高分析问题和解决问题的能力。
多元统计分析第5章 案例分析 2020.5.6

1)建立Bayes判别准则 2)假设有一新样品 x0 满足 f1( x0 ) = 0.36
和 f2( x0 ) = 0.24, 判定 x0 的归属问题. 解 (1)
19
例3 设有两个正态总体 G1,G2,且
1
=
2 6
,2
=
4 2
,1
=
2
=
=
1 1
1 9
,
而其先验概率分布为 q1 = q2 = 0.5, 误判代价为
C(2 1) = e4 ,C(1 2) = e;试用Bayes判别法确定样本
X
3
=
5
应归属于哪一类?
解 由Bayes判别法知
W (x) =
f1( x) f2 ( x)
=
exp[(
x
−
)T
−1 ( 1
−
2
)]
exp( 4 x1
+
正常使用填空题需3.0以上版本雨课堂
作答
填空题 2分
Fisher判别法就是要找一个由p个变量组 成的 [填空1]使得各自组内点的 [填空2] 尽可能接近,而不同组间点的尽可能疏远
正常使用填空题需3.0以上版本雨课堂
作答
填空题 2分
判别分析中,若两个总体的协差阵相等,则 [填空1]判别与 [填空2]判别等价
• Bayes判别法 优点:错判率较小 不足之处: 需要获取总体的分布及参数值, 实现困难 实际问题中有时也没必要知道其分布
方法之优缺点
• Fisher判别 优点:可以分类,也可以分离 不足之处: 一般需假定各组的协方差阵相等 逐步判别 优点:对每个变量的地位进行评判 不足之处: 需结合Bayes判别一起使用
几种多元统计分析方法及其在生活中的应用

几种多元统计分析方法及其在生活中的应用一、本文概述随着大数据时代的到来,多元统计分析方法在各个领域中的应用日益广泛,其重要性和价值逐渐凸显。
本文旨在深入探讨几种主流的多元统计分析方法,包括主成分分析(PCA)、因子分析(FA)、聚类分析(CA)以及判别分析(DA)等,并阐述这些方法在生活实践中的具体应用。
我们将对每种多元统计分析方法进行详细介绍,包括其基本原理、实施步骤以及优缺点等方面。
通过这些基础知识的普及,为读者提供一个清晰的方法论框架,为后续的实际应用打下坚实基础。
我们将结合生活中的实际案例,详细阐述多元统计分析方法的应用场景。
这些案例可能涉及市场营销、医学诊断、社会调查、金融分析等多个领域,旨在展示多元统计分析方法在解决实际问题中的强大威力。
我们将对多元统计分析方法在生活中的应用前景进行展望,分析未来可能的发展趋势和挑战。
本文还将提出一些针对性的建议,以期推动多元统计分析方法在实践中的更广泛应用和发展。
通过本文的阐述,我们希望能够为读者提供一个全面、深入的多元统计分析方法及其在生活中的应用指南,为相关领域的研究和实践提供有益的参考。
二、多元统计分析方法介绍多元统计分析是一种在多个变量间寻找规律性的统计分析方法,其核心在于通过提取多个变量的信息,揭示出这些变量间的内在结构和相互关系。
以下是几种常见的多元统计分析方法及其特点。
多元回归分析:这种方法主要研究多个自变量对因变量的影响,旨在构建自变量与因变量之间的数学模型,并预测因变量的未来趋势。
多元回归分析可以帮助我们理解各个自变量对因变量的影响程度,以及这些影响是否显著。
主成分分析(PCA):PCA是一种降维技术,它通过正交变换将原始变量转换为线性无关的新变量,即主成分。
这些主成分按照其方差大小排序,前几个主成分通常可以代表原始数据的大部分信息。
PCA在数据压缩、特征提取和可视化等方面有广泛应用。
因子分析:因子分析通过提取公共因子来简化数据集,这些公共因子可以解释原始变量间的相关性。
《多元统计分析》第三章聚类分析

图像处理
聚类分析可用于图像分割、目 标检测等任务,提高图像处理 的效率和准确性。
社交网络
通过聚类分析,可以发现社交 网络中的社区结构,揭示用户 之间的关联和互动模式。
聚类分析的常用方法
K-均值聚类
一种迭代算法,通过最小化每个簇内对象与簇质 心的距离之和来实现聚类。需要预先指定簇的数 量K。
DBSCAN
感谢聆听
聚类结果的优化方法
层次聚类法
通过不断合并或分裂簇来优化聚类结果,可以灵活处理不同形状 和大小的簇,但计算复杂度较高。
基于密度的聚类法
通过寻找被低密度区域分隔的高密度区域来形成簇,可以发现任意 形状的簇,但对参数敏感。
基于网格的聚类法
将数据空间划分为网格单元,然后在网格单元上进行聚类,处理速 度较快,但聚类精度受网格粒度影响。
一种基于密度的聚类方法,通过寻找被低密度区 域分隔的高密度区域来实现聚类。可以识别任意 形状的簇,且对噪声数据具有较强的鲁棒性。
层次聚类
通过计算对象之间的距离,逐步将数据集构建成 一个层次结构的聚类树。可以分为凝聚法和分裂 法两种。
谱聚类
利用图论中的谱理论进行聚类分析,将数据集中 的对象表示为图中的节点,节点之间的相似度表 示为边的权重。通过求解图的拉普拉斯矩阵的特 征向量来实现聚类。
药物发现
通过对化合物库进行聚类分析,研究人员可以发现具有相 似化学结构和生物活性的化合物,从而加速新药的发现和 开发过程。
生物信息学
在基因表达谱、蛋白质互作网络等生物信息学研究中,聚 类分析可以帮助研究人员发现基因或蛋白质之间的功能模 块和调控网络。
在社交网络中的应用案例
社区发现
聚类分析可用于识别社交网络中的社区结构,即具有相似兴趣、行为或属性的用户群体。 这有助于社交网络运营商为用户提供更加个性化的推荐和服务。
多元统计分析--聚类分析

平,以便于对亚洲国家进行分类研究,这里我们 进行聚类分析(在World95.sav数据中筛选出亚洲 国家,使用Data→Select Cases→If condition is satisfied中选入region=3)。 详细步骤如下:
(1) 打开数据。使用菜单中File→Open命令,然后 选中要分析的数据World95.sav。
多元统计分析--聚类分析
2021/7/11
多元统计分析
何晓群
中国人民大学出版社
2021/7/11
中国人民大学六西格玛质量管理研究中心
2
第三章 聚类分析
• §3.1 • §3.2 • §3.3 • §3.4 • §3.5 • §3.6 • §3.7 • §3.8
聚类分析的思想 相似性度量 类和类的特征 系统聚类法 模糊聚类分析 K-均值聚类和有序样本聚类 计算步骤与上机实现 社会经济案例研究
38
目录 上页 下页 返回 结束
§3.7.3 计算步骤与上机实践 模糊聚类法
继续使用上面的例子,希望将亚洲国家或地区 分成3类进行分析研究。这里我们使用SPlus2000软件。
(略)
2021/7/11
中国人民大学六西格玛质量管理研究中心
39
目录 上页 下页 返回 结束
§3.8 社会经济案例研究
2021/7/11
2021/7/11
中国人民大学六西格玛质量管理研
§3.7 计算步骤与上机实践
本书以SPSS15.0软件来说明前面讲述的几种 聚类法的实现过程。具体步骤如下:
*分析所需要研究的问题,确定聚类分析所需 要的多元变量;
*选择对样品聚类还是对指标聚类; *选择合适的聚类方法; *选择所需的输出结果。 我们将实现过程用逻辑框图表示为图3.8。
多元统计分析第5章层次分析法

若取重量向量W= [W1,W2,… , Wn]T ,则有: AW=n•W W是判断矩阵A的特征向量,n是A的一个特征值。根据线性代数 知识可以证明,n是矩阵A的唯一非零的,也是最大的特征值。
上述事实告诉我们,如果有一组物体,需要知道它们的重量,而又 没有衡器,那么就可以通过两两比较它们的相互重量,得出每一对 物体重量比的判断,从而构成判断矩阵;然后通过求解判断矩阵的 最大特征值λ max和它所对应的特征向量,就可以得出这一组物体 的相对重量。
5.3 层次分析法的步骤
1 建立层次结构模型
将决策的目标、考虑的因素(决策准则)和决策 对象按它们之间的相互关系分为最高层、中间层 和最低层,绘出层次结构图。 最高层—目标层:决策的目的、要解决的问题。
中间层—准则层:考虑的因素、决策的准则。
最低层—方案层或措施层:决策时的备选方案。
n
归一化:
T
i
Wi W
T
W
i 1
n
i
(i 1,2,n)
则W W1,W2 ,,Wn 即为所求得特征向量
计算最大特征根
max
( AW ) i nWi i 1
n
( AW )i 表示向量AW的第i个分量
5.3 层次分析法的步骤
一致性检验
判断矩阵中的aij是根据资料数据、专家的意见和系统分析人 员的经验经过反复研究后确定。应用层次分析法保持判断思 维的一致性是非常重要的,只要矩阵中的aij满足三条关系式 (aii = 1;aji = 1/ aij;aij = aik/ ajk (i,j,k=1,2,….n) )时,就说 明判断矩阵具有完全的一致性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、对我国30个省市自治区农村居民生活水平作聚类分析
1、指标选择及数据:为了全面分析我国农村居民的生活状况,主要考虑从收入、消费、就业等几个方面对农村居民的生活状况进行考察。
因此选取以下指标:农
村产品价格指数、农村住宅投资、农村居民消费水平、农村居民消费支出、农村居民家庭人均纯
92.87 79.35 3590 3457.9 4643 4124.6 18.7 数据来源:《中国统计年鉴2010》
2、将数据进行标准化变换:
3、用K-均值聚类法对样本进行分类如下:
分四类的情况下,最终分类结果如下:
第一类:北京、上海、浙江。
第二类:天津、、辽宁、、福建、甘肃、江苏、广东。
第三类:浙江、河北、内蒙古、吉林、黑龙江、安徽、山东、河南、湖北、四川、云南。
第四类:山西、青海、宁夏、新疆、重庆、贵州、陕西、湖南、广西、江西、。
从分类结果上看,根据2 0 10年的调查数据,第一类地区的农民生活水平较高, 第二类属于中等水平,第三类、第四类属于较低水平。
二、判别分析
**.错误分类的案例
从上可知,只有一个地区判别组和原组不同,回代率为96%。
下面对新疆进行判别:
已知判别函数系数和组质心处函数如下:
判别函数分别为:Y1=0.18x1 +0.493x2 + 0.087x3 + 1.004x4 + 0.381x5 -0.041x6 -0.631x7
Y2=0.398x1+0.687x2 + 0.362x3 + 0.094x4 -0.282x5 + 1.019x6 -0.742x7
Y3=0.394x1-0.197x2 + 0.243x3-0.817x4 + 0.565x5-0.235x6 + 0.802x7 将西藏的指标数据代入函数得:丫1=-1.08671
Y2=-0.62213
Y3=-0.84188
计算丫值与不同类别均值之间的距离分别为:D1=138.5182756
D2=12.11433124
D3=7.027544292
D4=2.869979346
经过判别,D4最小,所以新疆应归于第四类,这与实际情况也比较相符。
三,因子分析:
分析数据在上表的基础上去掉两个耕地面积和农村固定资产投资两个指标。
经spss软件分析结果如下:
(1)各指标的相关系数阵:
从中可以看出,大部分指标的相关系数都比较高,各变量之间的线性关系较明确, 能够从中提取公共因子,适合因子分子。
(2)检验:
由上表可知:巴特利特球度检验统计量的观测值为 0.如果显著性水平a 为0.05,由于显著性水平小于
0.05,拒绝零假设,认为相关 系数矩阵与单位阵有显著差异,同时,KO 值为0.701,根据Kaiser 给出的度量标 准可知原有变量适合进行因子分析
(3)各指标的贡献率如下表:
从中可以看出,各个指标的贡献率都在百分之五十之上比较高。
从上表中可以看出,第一个因子的特征根为
3.449.解释原有五个变量总方差的
68%累积方差贡献率为68.973%。
第二个因子的特征根为0.863,解释原有变量
145.585.相应的概率p 接近为
(5)因子载荷阵如下:
Com ponent Matrix a
Component 1
2 农产品价格指数 .446 .88
3 农村居民消费 .967 -.052 消费支岀
.952 -.125 家庭人均纯收入 .936 -.039 就业人数
.729
-.258
Extracti on Method: Pri ncipal Component An alysis. a. 2 components extracted.
由上表可知,各指标在第一个因子上的载荷比较高,说明第一个因子很重要; 第二个因子与原有变量的相关性较小, 它对原有变量的解释作用不显著。
为便于 对各因子进行命名,对因子载荷阵实施正交旋转。
旋转之后的因子载荷阵:
总方差17.34%, (4)碎石图:
累计方差贡献率为86.313%。
Scree P lot
a
Rotati on Method: Varimax w ith Kaiser Normalizati on.
a. Rotati on con verged in 3 iterati ons.
(6)从上表可见,每个因子只有几个指标的因子载荷较大,因此可根据上表进行分类。
将五个指标按高载荷分成两类:
四,主成分分析:
(1)各指标间的相关系数矩阵如下表所示:
可以看到有些指标之间的相关性较强,如果直接进行综合分析会造成信息重叠, 所以用主成分分析将多个指标化成几个不相关的综合指标。
(2)求相关矩阵的特征值和特征向量:
从上表可知,前两个特征值累计贡献率已达86.313%。
说明前两个主成分基本包
含了全部指标具有的信息。
因此,取前两个特征值,并计算相应的特征向量: (3 )由上述因子分子的因子载荷阵计算主成分的特征向量阵为:
所以,前两个主成分为:
第一个主成分:F1=0.135112 X1+0.280371X2+ 0.276022X3+0.271383X4+0.211366X5
第二个主成分:F2=1.018454X1-0.059977X2-0.144175X3-0.044983X4-0.297578X5
在第一主成分中第二、三、四个指标的系数较大,这三个指标起主要作用,刻划了农居民的收入支出状况的综合指标。
在第二主成分中,第一个指标系数较大,是农产品价格水平指标。
(4)因子得分:
Extracti on Method: Pri ncipal Component An alysis. Rotati on Method: Varimax w ith Kaiser Normalizati on. Component Scores.
根据上表写出以下因子得分函数:
F1=-0.193农产品价格指数+0.285农村居民消费+0.307消费支出+0.272家庭人均纯收入+0.293就业人数
F2=1.009农产品价格指数+0.031农村居民消费-0.051消费支出+0.041家庭人均纯收入-0.218就业人数
(5)综合评价:以两个因子的方差贡献率为权数,综合评价模型为:
Z=0.63997F1+0.22315F2 (旋转之后的方差贡献率)
F1=0.135112 X1+0.280371X2+ 0.276022X3+0.271383X4+0.211366X5
F2=1.018454X1-0.059977X2-0.144175X3-0.044983X4-0.297578X5
将各地区指标值代入上式得到各地区农村生活水平的综合值及排名:
(6)对结果进行分析:
从中可以看出,各地区的农村居民生活水平存在差异。
其中,北京、上海、浙江、江苏地区 的综合评价值排名前列, 水平和消费水平两个方面。
于其他地区。
其次, 前十的地位。
青海、 水平发展比较落后。
说明这几个城市农村居民的生活水平比较高。
主要表现在农民收入
这几个城市属于沿海地区, 经济比较发达,工农业发展遥遥领先 山东、福建、辽宁、广东综合评价值相对较低。
不过也处于全国 天津 贵州、广西、重庆、新疆、甘肃、陕西、云南等几个地区农村居民生活
原因是这些地区大多位于中国中西部,地理位置不佳, 交通不便,经济 因此, 发展水平不高,进而影响到农村经济的发展。
农村居民收入水平和消费水平均比较低。
要提高这些地区农民的生活水平, 政府应该加大这些地区的基础设施建设, 村居民的收入水平。
提高这些地区农。
