【最新】人教版八年级数学下册第十七章《勾股定理(2)》公开课课件.ppt
合集下载
人教版 八年级下册数学 第17章勾股定理 17.1.2勾股定理的实际运用(课件)(共18张PPT)

人教版 数学八年级下册
17.1.2 勾股定理
(勾股定理的实际运用)
知识回顾 :
勾股定理:
如果直角三角形的两条直角边长分别为a,
B b,斜边长为c,那么 a2 b2 c2 .
c a
b
C
A
知识回忆 :
在△ABC中,∠C=90°.
(1)若b=8,c=10,则a= 6
;
(2)若a=5,b=10,则c = ������ ������ ;
B
c a
30°
C
b
A
(5)∵ ∠A=30°, ∴ c =2a
设a =x,则c = 2x ∵������������ + ������������ = ������������ ∴������������ + ������������ = (������������)������ 解得: ������ = ������ ������ ∴ ������ = ������ ������,������ = ������ ������
A
在Rt△ABC中,由勾股定理得:
AC= ������������������ + ������������������= ������������������ + ������������=13cm
答:吸管至少要做 13+4.6=17.6cm.
C
Hale Waihona Puke B练习提高6. 如图,甲船以16海里/时的速度离开码头向东北方向航行,乙船同 时由码头向西北方向航行,已知两船离开码头1.5小时后相距30海里, 问乙船每小时航行多少海里?
30 24
练习提高
7.如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米. (1)这个梯子的顶端距地面有多高? (2)如果梯子的底端B外移了2米,那么梯子的顶端A沿墙下滑了多少米?
17.1.2 勾股定理
(勾股定理的实际运用)
知识回顾 :
勾股定理:
如果直角三角形的两条直角边长分别为a,
B b,斜边长为c,那么 a2 b2 c2 .
c a
b
C
A
知识回忆 :
在△ABC中,∠C=90°.
(1)若b=8,c=10,则a= 6
;
(2)若a=5,b=10,则c = ������ ������ ;
B
c a
30°
C
b
A
(5)∵ ∠A=30°, ∴ c =2a
设a =x,则c = 2x ∵������������ + ������������ = ������������ ∴������������ + ������������ = (������������)������ 解得: ������ = ������ ������ ∴ ������ = ������ ������,������ = ������ ������
A
在Rt△ABC中,由勾股定理得:
AC= ������������������ + ������������������= ������������������ + ������������=13cm
答:吸管至少要做 13+4.6=17.6cm.
C
Hale Waihona Puke B练习提高6. 如图,甲船以16海里/时的速度离开码头向东北方向航行,乙船同 时由码头向西北方向航行,已知两船离开码头1.5小时后相距30海里, 问乙船每小时航行多少海里?
30 24
练习提高
7.如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米. (1)这个梯子的顶端距地面有多高? (2)如果梯子的底端B外移了2米,那么梯子的顶端A沿墙下滑了多少米?
八年级数学下册 第17章 勾股定理 17.1 勾股定理课件2 (新版)新人教版.pptx

17
【纠错园】 如图是一个长4 m,宽3 m,高2 m的有盖仓库,在其内壁 的A处(长的四等分点)有一只壁虎,B处(宽的三等分点) 有一只蚊子,求壁虎爬到蚊子处最短距离是多少.
18
19
【错因】本题考虑问题不全面,只考虑按长方体的高棱 展开,没考虑按长方体的长棱展开,漏掉其中一种情况.
20
13
【解析】把圆柱的侧面展开,得到如图所示的图形,
由题意知 1
AC=3,CE=205× =4, ∴AE= 32 4=2 5. ∴葛藤的最短长度为25尺.
答案:25
14
【备选例题】如图,长方体的底面边长分别为1cm和3cm, 高为6cm.如果用一根细线从点A开始经过4个侧面缠绕 一圈到达点B,那么所用细线最短需要( )
17.1 勾股定理 第2课时
1
【基础梳理】 1.勾股定理的应用 直角三角形中,根据勾股定理,已知两边可求第三边: Rt△ABC中,∠C=90°,a,b,c分别为内角A,B,C的对 边,(1)若已知边a,b,则c= a2 b2 ;(2)若已知边a,c,则 b= c2 a2 ;(3)若已知边b,c,则a= c2 b2.
10
11
知识点二 利用勾股定理解决立体图形中的最短路线 问题 【示范题2】(2017·东营中考)我国古代有这样一道数 学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤 自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意
12
是:如图所示,把枯木看作一个圆柱体,因一丈是十尺, 则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处 缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛 藤的最短长度是________尺.
2
2.立体图形中距离最短问题 (1)如图,圆柱的侧面展开图是_长__方__形__,点B的位置应 在长方形的边CD的_中__点__处,点A到点B的最短距离为线 段_A_B_的长度.
【纠错园】 如图是一个长4 m,宽3 m,高2 m的有盖仓库,在其内壁 的A处(长的四等分点)有一只壁虎,B处(宽的三等分点) 有一只蚊子,求壁虎爬到蚊子处最短距离是多少.
18
19
【错因】本题考虑问题不全面,只考虑按长方体的高棱 展开,没考虑按长方体的长棱展开,漏掉其中一种情况.
20
13
【解析】把圆柱的侧面展开,得到如图所示的图形,
由题意知 1
AC=3,CE=205× =4, ∴AE= 32 4=2 5. ∴葛藤的最短长度为25尺.
答案:25
14
【备选例题】如图,长方体的底面边长分别为1cm和3cm, 高为6cm.如果用一根细线从点A开始经过4个侧面缠绕 一圈到达点B,那么所用细线最短需要( )
17.1 勾股定理 第2课时
1
【基础梳理】 1.勾股定理的应用 直角三角形中,根据勾股定理,已知两边可求第三边: Rt△ABC中,∠C=90°,a,b,c分别为内角A,B,C的对 边,(1)若已知边a,b,则c= a2 b2 ;(2)若已知边a,c,则 b= c2 a2 ;(3)若已知边b,c,则a= c2 b2.
10
11
知识点二 利用勾股定理解决立体图形中的最短路线 问题 【示范题2】(2017·东营中考)我国古代有这样一道数 学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤 自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意
12
是:如图所示,把枯木看作一个圆柱体,因一丈是十尺, 则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处 缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛 藤的最短长度是________尺.
2
2.立体图形中距离最短问题 (1)如图,圆柱的侧面展开图是_长__方__形__,点B的位置应 在长方形的边CD的_中__点__处,点A到点B的最短距离为线 段_A_B_的长度.
人教版八年级数学下册第17章勾股定理PPT教学课件

二 利用勾股定理进行计算
例1 如图,在Rt△ABC中, ∠C=90°.
B
(1)若a=b=5,求c;
(2)若a=1,c=2,求b. 解:(1)据勾股定理得
C
A
c a2 b2 52 52 50 5 2;
(2)据勾股定理得
b c2 a2 22 12 3.
【变式题1】在Rt△ABC中, ∠C=90°. (1)若a:b=1:2 ,c=5,求a; (2)若b=15,∠A=30°,求a,c.
根据前面求出的C的面积直接填出下表:
C A B B A C
A的面积 B的面积 C的面积
左图 右图
4
9 9
13
25
16
思考 正方形A、B、C 所围成的直角三角形三条边之 间有怎样的特殊关系?
由上面的几个例子,我们猜想: 命题1 如果直角三角形的两条直角边长分别为a,b, 斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜 边的平方. c
B 4 C B 4 A A 3
3
图
图
C
归纳 当直角三角形中所给的两条边没有指明是斜边或 直角边时,其中一较长边可能是直角边,也可能是斜 边,这种情况下一定要进行分类讨论,否则容易丢解.
例2 已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
A D
AB2=AC2+BC2=25,
6 米
8米
解:根据题意可以构建一
直角三角形模型,如图.
在Rt△ABC中,
AC=6米,BC=8米,
A 6 米 B 由勾股定理得
AB AC 2 BC 2 6 2 82 10 米 .
【最新】人教版八年级数学下册第17章《勾股定理》优质公开课课件2.ppt
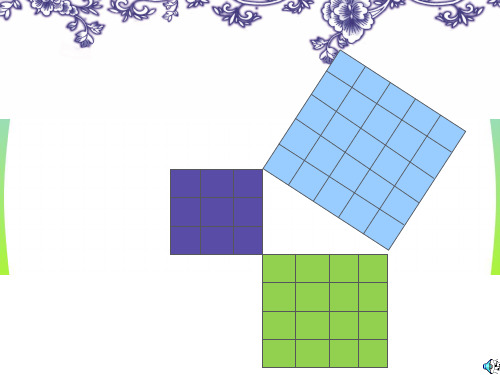
(图中每个小方格代表一个单位面积)
你是怎样得到正方形c 的面积。
C A
(2)在图1-2中,正方 形A,B,C中各含有多 少个小方格?它们的面 积各是多少?
B
图1-1
C A
B
图1-2
(3)你能发现图1-1中 三个正方形A,B,C的 面积之间有什么关系吗? 图1-2中呢?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b, 斜边为c,那么
a2 b2 c2 a c
b
即 直角三角形两直角边的平方和等 于斜边的平方。
结论变形 直角三角形中,两直角边的平方和等于斜边的平方;
c2=a2 + b2
cb
a
勾 股
在中国古代,人们把弯曲成直角的手臂的上半部分称为 "勾",下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”,较长的直角边称为“股”, 斜边称为“弦”.
C A
B
C
图1-1 A
(1)你能用三角 形的边长表示正方 形的面积吗?
(2)你能发现直 角三角形三边长度 之间存在什么关系 吗?与同伴进行交 流。
B
直角三角形两直角边的
图1-2
平方和等于斜边的平方
(3)分别以5厘米、12厘米为直角边作出一个直角
三角形,并测量斜边的长度。(2)中的规律对这
个三角形仍然成立吗?
13、志不立,天下无可成之事。2021/1/112021/1/112021/1/112021/1/111/11/2021
•
THE END 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other
2024八年级数学下册第十七章勾股定理17.1勾股定理第2课时应用勾股定理解实际问题课件新版新人教版

【解】(1)如图,过点A作AE⊥CD于点E,
则∠AEC=∠AED=90°.
∵∠ACD=60°,∴∠CAE=90°-60°=30°.
∴CE= AC=
DE=
km.∴AE=
km,
km.
∴AE=DE.∴△ADE是等腰直角三角形.∴AD=
+ = = AE= ×
度为x尺,则可列方程为( D )
A.x2-3=(10-x)2
B.x2-32=(10-x)2
C.x2+3=(10-x)2
D.x2+32=(10-x)2
【点拨】
如图,已知折断处离地面的高度为x尺,即AC=x尺,
则AB=(10-x)尺,BC=3尺.在Rt△ABC中,AC2+BC2=
AB2,即x2+32=(10-x)2.故选D.
2.[2023·岳阳 新考向·传承数学文化]我国古代数学名著《九章
算术》中有这样一道题:“今有圆材,径二尺五寸,欲为
方版,令厚七寸,问广几何?”结合如图,其大意是:今
有圆形材质,直径BD为25寸,要做成方形板材,使其厚
度CD达到7寸,则BC的长是( C )
A. 寸
B.25寸
C.24寸
D.7寸
选B.
4.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙
时,梯子底端到左墙脚的距离为0.7 m,顶端距离地面2.4
m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶
端距离地面2 m,那么小巷的宽度为( C )
A.0.7 m
B.1.5 m
C.2.2 m
D.2.4 m
【点拨】
如图,BC=2.4 m,AC=0.7 m,DE=
【最新】人教版八年级数学下册第十七章《勾股定理(二)》公开课课件

∵木板的宽2.2米大于1米,
∴ 横着不能从门框C通过;
∵木板的宽2.2米大于2米,
∴竖着也不能从门框通2过m.
∴ 只能试试斜着能否通过,
对 要角 求线 出AACC的 的A长 长1最 ,m大 怎, 样B因 求此呢需?
有一个边长为50dm 的正方形洞口,想用一 个圆盖去盖住这个洞口,圆的直径至少多 长?(结果保留整数)
第十八章 勾股定理 18.1 勾股定理(二)
zxxk
联系与区别
勾股定理的 应用
勾股定理的逆 定理
内容、表 示方法、 及由来
勾股定理
勾股定理与 勾股定理逆定理 的区别与联系
互逆命题的概念
勾
股
原命题与逆命题
定
理
活动1
勾股定理:直角三角形两直角边的平 方和等于斜边的平方.
如果在Rt△ ABC中,∠C=90°,
zxxk zxxk
2 .一直角三角形的一直角边长为7, 另两条 边长为两个连续整数,求这个直角三角形的 周长.
那么 a2 b2 c2 .
B
ac
C bA
结论变形
B
a
c
C
b
A
c2 = a2 + b2
练习
(1)求出下列直角三角形中未知的边.
B
6
C
回答:
10
A
2
30°
A
8 C
zxxk
45°
2
①在解决上述问题时,每个直角三角形需知道几个条件?
②直角三角形哪条边最长?
活动2
一个门框尺寸如下图所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过? ②若薄木板长3米,宽1.5米呢? ③若薄木板长3米,宽2.2米呢?为什么?
∴ 横着不能从门框C通过;
∵木板的宽2.2米大于2米,
∴竖着也不能从门框通2过m.
∴ 只能试试斜着能否通过,
对 要角 求线 出AACC的 的A长 长1最 ,m大 怎, 样B因 求此呢需?
有一个边长为50dm 的正方形洞口,想用一 个圆盖去盖住这个洞口,圆的直径至少多 长?(结果保留整数)
第十八章 勾股定理 18.1 勾股定理(二)
zxxk
联系与区别
勾股定理的 应用
勾股定理的逆 定理
内容、表 示方法、 及由来
勾股定理
勾股定理与 勾股定理逆定理 的区别与联系
互逆命题的概念
勾
股
原命题与逆命题
定
理
活动1
勾股定理:直角三角形两直角边的平 方和等于斜边的平方.
如果在Rt△ ABC中,∠C=90°,
zxxk zxxk
2 .一直角三角形的一直角边长为7, 另两条 边长为两个连续整数,求这个直角三角形的 周长.
那么 a2 b2 c2 .
B
ac
C bA
结论变形
B
a
c
C
b
A
c2 = a2 + b2
练习
(1)求出下列直角三角形中未知的边.
B
6
C
回答:
10
A
2
30°
A
8 C
zxxk
45°
2
①在解决上述问题时,每个直角三角形需知道几个条件?
②直角三角形哪条边最长?
活动2
一个门框尺寸如下图所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过? ②若薄木板长3米,宽1.5米呢? ③若薄木板长3米,宽2.2米呢?为什么?
2021年人教版八年级数学下册第17章《勾股定理》精品课件2

让我们一起再探究:等腰直角三角形三边关系
C
图1
A
图2
B C
图2-1
A
B 图2-2
(图中每个小方格代表一个单位面积)
A的面 B的面 C的面 积(单位 积(单位 积(单位
长度) 长度) 长度)
9
9 18
8
4
4
C A
S正方形c
B C
图2-1
A
413318 2
B
(单位面积)
图2-2
(图中每个小方格代表一个单位面积)
的发现,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,因此这个定理又有人叫做“百 牛定理”.)
勾股定理的证明方法(这里有六种)
证 法 一
走
证
进
法 二
数
学
证 法
史
三
(邹元治证明)
(赵爽证明) 赵爽:我国古代数学家
勾股定理的证明方法
证 法 四
走证
进
法 五
数
学
证 法
史六
(加菲尔德证明) 加菲尔德:第二十任总统
搞错了。你同意他的想法吗?你能解释这是 为什么吗?~
作业
教材第69页习题17.1第1、2、3题
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/2/42021/2/4Thursday, February 04, 2021
(梅文鼎证明) 梅文鼎:清代天文、数学家
(项明达证明) 项明达:清代数学家
做一做:
A
625
P
C
B
400
P的面积 =___2_2__5________ AB=_2__5_______ BC=__2_0_______
八年级数学下册第十七章勾股定理17.1勾股定理第2课时勾股定理的应用课件(新版)新人教版

例1 (教材P25例1)一个门框的尺寸如图所示,一块长3 m,宽2.2 m 的长方形木板能否从门框内通过?为什么?
名校讲 坛
【跟踪训练1】 (《名校课堂》17.1第2课时)八(2)班小明和小亮同学学 习了“勾股定理”之后,为了测得如图风筝的高度CE,他们进行了如 下操作: ①测得BD的长度为15米;(注:BD⊥CE) ②根据手中剩余线的长度计算出风筝线BC的长为25米; ③牵线放风筝的小明身高1.6米. 求风筝的高度CE.
第2课时 勾股定理的应用
学习目 标
1.能运用勾股定理及直角三角形的判定条件解决实际问题. 2.在运用勾股定理解决实际问题过程中,感受数学的“转化”思想, 体会数学的应用价值.
预习反 馈
阅读教材P25~26,体会例1、例2的解答过程,并完成下列预习内容:
1.如果一根木杆的底端离建筑物5米,13米长的木杆可以达到建筑物
的高度是( A )
A.12米
B.13米
C.14米
D.15米
预习反 馈
2.如图是我校的长方形水泥操场,如果一学生要从A角走到C角,至少
走( C ) A.140米
B.120米
C.100米
D.90米
第2题图
第3题图
3.如图,已知OA=OB,BC=1,则数轴上点A所表示的数为__ _1_0 .
名校讲 坛
端离墙6 m,如果梯子的顶端下滑了2 m,那么梯子底部
在水平方向滑动了
(A)
A.2 m
B.2.m
巩固训 练
2.如图所示(单位:mm)的长方形零件 上两孔中心A和B的距离为100mm. 3.小明的妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏 幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错 了.你能解释这是为什么吗? 解:582+462=5 480;742=5 476.荧屏对角线大约为74厘米.所以售 货员没有搞错.我们通常所说的29英寸或74厘米的电视机,是指其荧 屏对角线的长度.
名校讲 坛
【跟踪训练1】 (《名校课堂》17.1第2课时)八(2)班小明和小亮同学学 习了“勾股定理”之后,为了测得如图风筝的高度CE,他们进行了如 下操作: ①测得BD的长度为15米;(注:BD⊥CE) ②根据手中剩余线的长度计算出风筝线BC的长为25米; ③牵线放风筝的小明身高1.6米. 求风筝的高度CE.
第2课时 勾股定理的应用
学习目 标
1.能运用勾股定理及直角三角形的判定条件解决实际问题. 2.在运用勾股定理解决实际问题过程中,感受数学的“转化”思想, 体会数学的应用价值.
预习反 馈
阅读教材P25~26,体会例1、例2的解答过程,并完成下列预习内容:
1.如果一根木杆的底端离建筑物5米,13米长的木杆可以达到建筑物
的高度是( A )
A.12米
B.13米
C.14米
D.15米
预习反 馈
2.如图是我校的长方形水泥操场,如果一学生要从A角走到C角,至少
走( C ) A.140米
B.120米
C.100米
D.90米
第2题图
第3题图
3.如图,已知OA=OB,BC=1,则数轴上点A所表示的数为__ _1_0 .
名校讲 坛
端离墙6 m,如果梯子的顶端下滑了2 m,那么梯子底部
在水平方向滑动了
(A)
A.2 m
B.2.m
巩固训 练
2.如图所示(单位:mm)的长方形零件 上两孔中心A和B的距离为100mm. 3.小明的妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏 幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错 了.你能解释这是为什么吗? 解:582+462=5 480;742=5 476.荧屏对角线大约为74厘米.所以售 货员没有搞错.我们通常所说的29英寸或74厘米的电视机,是指其荧 屏对角线的长度.
人教版八年级数学下册第十七章《勾股定理》课件

(2)据勾股定理得
bA
b c2 a2 22 12 3.
巩固练习
设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
解:由勾股定理得62+b2=102, b=8;
a
(2)已知a=5,b=12,求c;
解:由勾股定理得52+122=c2 , c=13;
(3)已知c=25,b=15,求a. 解:由勾股定理得a2+152=252 , a=20.
x=10;
x
13
(2)由勾股定理得: ∵ x2+52=132 ∴ x2=132-52 =169-25 =144 x=12.
连接中考
1.在直角三角形中,若勾为3,股为4,则弦为( A )
A.5
B.6
C.7
D.8
2. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,
那么正方形ABCD的面积为( B )
1.求出下列直角三角形中未知的边.
B
B
AC=8 6
C
10
8
15
A
C
A
AB=17
C B
2
C
30° A
B
45° A 2
BC 1,AC 3
BC 2,AC 2
课堂检测
2.直角三角形中,以直角边为边长的两个正方形面积为7和8, 则以斜边为边长的正方形的面积为 15 .
3.如图,在平面直角坐标系中有两点A(5,0) 和B(0,4),求这两点间的距离.
想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离
是( C )
A.3 1π
B.3
2
C.3
4 π2 2
bA
b c2 a2 22 12 3.
巩固练习
设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
解:由勾股定理得62+b2=102, b=8;
a
(2)已知a=5,b=12,求c;
解:由勾股定理得52+122=c2 , c=13;
(3)已知c=25,b=15,求a. 解:由勾股定理得a2+152=252 , a=20.
x=10;
x
13
(2)由勾股定理得: ∵ x2+52=132 ∴ x2=132-52 =169-25 =144 x=12.
连接中考
1.在直角三角形中,若勾为3,股为4,则弦为( A )
A.5
B.6
C.7
D.8
2. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,
那么正方形ABCD的面积为( B )
1.求出下列直角三角形中未知的边.
B
B
AC=8 6
C
10
8
15
A
C
A
AB=17
C B
2
C
30° A
B
45° A 2
BC 1,AC 3
BC 2,AC 2
课堂检测
2.直角三角形中,以直角边为边长的两个正方形面积为7和8, 则以斜边为边长的正方形的面积为 15 .
3.如图,在平面直角坐标系中有两点A(5,0) 和B(0,4),求这两点间的距离.
想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离
是( C )
A.3 1π
B.3
2
C.3
4 π2 2
最新人教版八年级数学下册 17.1 勾股定理 ppt课件2 优质课件

勾股定理
外星人
在人类在寻找“外星人” 时,碰到个难题;一旦遇到“外星人” 该怎么与他们交谈?显然用人类的语言文字音乐是不行的。数学家华 罗庚建议,用一幅数形关系作为与“外星人”交谈的语言。这幅图中 有边长为3、4、5的正方形,它们又互相联结成一个三角形。三个正方 形都被分成了大小相等的一些小方格,并且每条边上的小方格的个数, 与这条边长度的数字相等。两个小方形的小方格数分别为9和16,其和 为25,恰好等于大方形的小方格数。整幅图反映;“在直角三角形中, 两条直角边的平方和等于斜边的平方。”
毕达哥拉斯出生于萨摩斯岛,自幼聪明好学,曾在名师门 下学习几何,自然学和哲学。后来来到巴比伦,印度和埃及, 吸收了阿拉伯文明和印度文明甚至中国文明的丰富营养。大约 在公元前530年,又返回萨摩斯岛,后来又迁居意大利的克罗通, 创建了自己的学术。毕达哥拉斯学术认为数最崇高,最神秘, 他们所讲的是整数。可惜,朝气蓬勃的毕达哥拉斯到了晚年不 仅学术保守,还反对新生事物,最后死与非命
思考题
生命的代价
有一位名叫商高(约公元前560年 ~公元前480年)的数学家,以他为代 表的一批学者组成了商高学派,既是 学习团体,又是政治、宗教团体,有 严格的清规戒律。比如,会员必须宣 誓“决不把知识传授给外人”,否则 要受到严重处分,甚至极刑——活埋。
在西方人们认为勾股定理是毕达哥拉斯先发现的,
并称之为“毕达哥拉斯定理”。不过早在公元前1120年 左右中国的商高就在对话中说到:“故折矩,此为勾广 三,股修四,经隅五。”你可能认为这是最早的勾股定 理,但是具调查在公元前1900年的一块巴比伦上午泥板 中,记载了15组勾股数。所以古巴比伦人才是勾股定理 最先的发现人。
证明方法
人教版八年级数学下册课件17.0勾股定理ppt

(1) ∠A=30°,求:BC、AC (2) ∠A=45°,求:BC、AC
练习2、一个3m
长的梯子AB,斜靠
在一竖直的墙AO 上,这时AO的距离 A
为2.5m,如果梯子 C 的顶端A沿墙下滑
0.5m,那么梯子底
端B也外移0.5m吗?
O
B
D
探究3、在数轴上画出表示 2, 3, 5 的点。
扩展
利用勾股定理作出长为 的线段.
面积各为多少?
SA+SB=S C C A
B 图甲
图甲 图乙 A的面积 4 9 B的面积 4 16 C的面积 8 25
A
图乙
B C
SA+SB=S C
2.观察图乙,小方格 的边长为1. ⑴ ⑵正方形A、B、C的 的面积有什么关系?
面积各为多少?
SA+SB=S C C Aa c
b B 图甲
图甲 图乙 A的面积 4 9 B的面积 4 16 C的面积 8 25
CD的长;
C
∵ ∠C=90° ∴AC2+BC2=AB2
BC AB 2 AC 2 132 52 12
S ABCLeabharlann 1 2ACBC
1 2
AB
CD
A
512 13 CD
CD 60 13
B D
勾股定理 如果直角三角形两直角边分别为a、b,
斜边为c,那么 a 2 b2 c2
互逆命题
勾股定理的逆定理 如果三角形的三边长a、b、c满足
AC=3,则BC的长为
.
B 4
C3 A
B 4 A3 C
3、如图,折叠长方形的一边,使点D 落在BC边上的点F处,若AB=8, AD=10. 求:EC的长.
练习2、一个3m
长的梯子AB,斜靠
在一竖直的墙AO 上,这时AO的距离 A
为2.5m,如果梯子 C 的顶端A沿墙下滑
0.5m,那么梯子底
端B也外移0.5m吗?
O
B
D
探究3、在数轴上画出表示 2, 3, 5 的点。
扩展
利用勾股定理作出长为 的线段.
面积各为多少?
SA+SB=S C C A
B 图甲
图甲 图乙 A的面积 4 9 B的面积 4 16 C的面积 8 25
A
图乙
B C
SA+SB=S C
2.观察图乙,小方格 的边长为1. ⑴ ⑵正方形A、B、C的 的面积有什么关系?
面积各为多少?
SA+SB=S C C Aa c
b B 图甲
图甲 图乙 A的面积 4 9 B的面积 4 16 C的面积 8 25
CD的长;
C
∵ ∠C=90° ∴AC2+BC2=AB2
BC AB 2 AC 2 132 52 12
S ABCLeabharlann 1 2ACBC
1 2
AB
CD
A
512 13 CD
CD 60 13
B D
勾股定理 如果直角三角形两直角边分别为a、b,
斜边为c,那么 a 2 b2 c2
互逆命题
勾股定理的逆定理 如果三角形的三边长a、b、c满足
AC=3,则BC的长为
.
B 4
C3 A
B 4 A3 C
3、如图,折叠长方形的一边,使点D 落在BC边上的点F处,若AB=8, AD=10. 求:EC的长.
人教版八年级数学下册《勾股定理(第2课时)》示范教学课件

世界上几个文明古国相继发现和研究过勾股定理,其证明方法有很多种,有兴趣的同学可以继续研究.
1876 年美国总统 Garfield 证明
刘徽证明
例1 作 8 个全等的直角三角形(2 条直角边长分别为 a,b, 斜边长为 c),再作 3 个边长分别为 a,b,c 的正方形,把它们拼成两个正方形(如图).你能利用这两个图形验证勾股定理吗?写出你的验证过程.
勾股定理(第2课时)
人教版八年级数学下册
命题如果直角三角形两直角边长分别为 a,b,斜边长为 c,那么_________.
a2+b2=c2
如何证明呢?
右图是我国古代证明该命题的“赵爽弦图”.
赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实.
你是如何理解的?你会证明吗?
解:由图可知大正方形的边长为:a+b,则面积为(a+b)2,由左图可得 (a+b)2=a2+b2+4× ,由右图可得 (a+b)2=c2+4× .根据面积相等,所以 a2 + b2=c2.
用分割拼接法证明勾股定理,其依据是“分割拼接前后图形的各部分的面积之和不变”.
例2 某同学提出了一种证明勾股定理的方法:如图 1,点 B 是正方形 ACDE 的边 CD 上一点,连接 AB,得到 Rt△ACB,三边分别为 a,b,c,将 △ACB 裁剪拼接至 △AEF 位置,如图 2,该同学用图 1、图 2 的面积不变证明了勾股定理.请你写出该方法证明勾股定理的过程.
解:如图2,连接 BF.在图1中,正方形 ACDE 的面积为 b2,在图2中,∠BAC=∠EAF,则 ∠EAF+∠BAE=90°,故 △BAF为等腰直角三角形.四边形 ABDF 的面积为: c2+ (b-a)(a+b)= c2+ (b2-a2).
1876 年美国总统 Garfield 证明
刘徽证明
例1 作 8 个全等的直角三角形(2 条直角边长分别为 a,b, 斜边长为 c),再作 3 个边长分别为 a,b,c 的正方形,把它们拼成两个正方形(如图).你能利用这两个图形验证勾股定理吗?写出你的验证过程.
勾股定理(第2课时)
人教版八年级数学下册
命题如果直角三角形两直角边长分别为 a,b,斜边长为 c,那么_________.
a2+b2=c2
如何证明呢?
右图是我国古代证明该命题的“赵爽弦图”.
赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实.
你是如何理解的?你会证明吗?
解:由图可知大正方形的边长为:a+b,则面积为(a+b)2,由左图可得 (a+b)2=a2+b2+4× ,由右图可得 (a+b)2=c2+4× .根据面积相等,所以 a2 + b2=c2.
用分割拼接法证明勾股定理,其依据是“分割拼接前后图形的各部分的面积之和不变”.
例2 某同学提出了一种证明勾股定理的方法:如图 1,点 B 是正方形 ACDE 的边 CD 上一点,连接 AB,得到 Rt△ACB,三边分别为 a,b,c,将 △ACB 裁剪拼接至 △AEF 位置,如图 2,该同学用图 1、图 2 的面积不变证明了勾股定理.请你写出该方法证明勾股定理的过程.
解:如图2,连接 BF.在图1中,正方形 ACDE 的面积为 b2,在图2中,∠BAC=∠EAF,则 ∠EAF+∠BAE=90°,故 △BAF为等腰直角三角形.四边形 ABDF 的面积为: c2+ (b-a)(a+b)= c2+ (b2-a2).
人教版八年级数学下册第十七章勾股定理课件

2.勾股定理的逆定理:如果三角形三边长a, b, c 满足a2+b2=c2,那么这个三角形是直角三角形.
勾股定理的逆定理是判定一个三角形是否是直角三 角形的一种重要方法,它通过“数转化为形”来确定三 角形的可能形状,在运用这一定理时应注意:
(1)首先确定最长边,不要理所当然认为c为最 长边;
(2)验证a2+b2与c2是否具有相等关系,若a2+b2 =c2,则△ABC是以∠C为直角的பைடு நூலகம்角三角形(若c2>a2 +b2,则△ABC是以∠C为钝角的钝角三角形;若c2<a2 +b2,则△ABC为锐角三角形).
3.勾股定理与勾股定理逆定理的区别与联系: 区别:勾股定理是直角三角形的性质定理,而其逆 定理是判定定理; 联系:勾股定理与其逆定理的题设和结论正好相 反,都与直角三角形有关. 4.常见的勾股定理三边的组合: ①3,4,5;②5,12,13;③6,8,10;④7, 24,25;⑤8,15,17.
5.经过证明被确认正确的命题叫做定理.我们把题 设、结论正好相反的两个命题叫做互逆命题.如果把其 中一个叫做原命题,那么另一个叫做它的逆命题. (例:勾股定理与勾股定理逆定理)
第十七章 勾股定理
1.勾股定理:如果直角三角形的两直角边长分别为 a,b,斜边长为c,那么a2+b2=c2.
勾股定理反映了直角三角形三边之间的关系,是直 角三角形的重要性质之一,其主要应用:
(1)已知直角三角形的两边求第三边; (2)已知直角三角形的一边与另两边的关系,求 直角三角形的另两边; (3)利用勾股定理可以证明线段平方关系的问题.
勾股定理(第2课时)(课件)-2022-2023学年八年级数学下册同步精品课堂(人教版)

勾股定理应用的常见类型
1.已知直角三角形的任意两边求第三边;
2.已知直角三角形的任意一边确定另两边的关系;
3.证明包含有平方(算术平方根)关系的几何问题;
4.求解几何体表面上的最短路径问题;
5.构造方程(或方程组)计算有关线段长度,解决生产、
生活中的实际问题.
课堂练习
1.一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯
三角形的面积公式可求BD,再利用
勾股定理便可求CD.
北东
A
C
D
Q
课堂练习
P
解:∵AC10,BC8,AB6,
B
∴AC2AB2BC2
北东
A
即△ABC是直角三角形,
C
D
Q
1
1
而S△ABC BC AB AC BD
2
2
24
解得:BD .
5
2
24
在Rt△BCD中,CD = BC 2 BD 2 82 6.4
路线最短?
B
A
B
A
方案①
B
A
方案②
方案③
针对练习
(2)如图,将圆柱侧面剪开展成一个长方形,点A到点B的最短路线是什么?
你画对了吗?
B
A
B
A
B
∵两点之间线段最短,
∴方案③的路线最短.
A
针对练习
(3)蚂蚁从点A出发,想吃到点B上的食物,它沿圆柱侧面爬行的最短路程是
多少?
解:在Rt△ABC中,
C
B
AC=12 cm,BC=18÷2=9(cm).
在Rt△A′DB中,由勾股定理得
2021年人教版八年级数学下册第17章《 勾股定理》公开课课件 (2).ppt

A
解:(1)∵△ABC是等边三角形,AD是高
BD 1BC3 2
在Rt△ABD中 , ∠ADB = 900
A2D A2B B2D B
D
C
A D 3 6 92 7 33 cm 1
若(2等)S边AB三C角2形B的CA边D长是a呢?
163 39 3(cm 2) 2
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/142020/12/14Monday, December 14, 2020
A
D
B
C
巩固
3.在等腰△ABC中,腰AB=10cm,底 BC=16cm,求底边BC上的高。
A
B
C
D
练习
3、△ABC中,AB=AC=20cm, BC=32cm.求△ABC面积.
先构造直角, A 再用勾股定理
B
D
C
巩固
5.如图,在△ABC中,AB=15,AC= 20, BC边上的高AD=12,求BC的长。
5米
3米
作业
1.如图,在Rt△ABC中,∠C=90°,点D 是BC边上的一点,且BD=AD=10, ∠ADC=60° ,求△ABC的面积.
A
C 60°
B
D
1、在一次地震中,一棵20米高的大树被 折断了,地震过后 ,测量了有关数据,测 得树梢着地点到树根的距离为6米.这棵 大树折断处离地面有多高?
∵ AB2=92+122=81+144=225= 152 ∴ AB=15(cm)
答:蚂蚁爬行的最短路程是15厘米.
巩固
2.如图,以A点环绕油罐建梯子,
人教版 八年级下册 17.1勾股定理(2)(12张PPT)

1.拼成的图1中有 两 个正方形,四___个直角三角形。
2.图中大正方形的边长为__a_+_b_,小正方形的边长为_c 。
3.你能请用两种不同方法表示图1中大正方形的面积, 列出一个等式,验证勾股定理吗? 分析:大正方形的面积= 边长的平方 =小正方形
的面积+ 四 个直角三角形的面积
得: ( a + b )2= c 2+ 4 ×2ab. (1) 化简 可得:
图2
活动三:用两个完全相同的直角三角形(直角边为a,b,斜 边为c)构成如图所示的梯形.填空: (1)梯形的面积= (上底+ 下底 ) 高
(2)如图ห้องสมุดไป่ตู้梯形的上底=a,下底= b ,高= a+b 。 (3)由“梯形面积等于三个直角三角形面积之和”可得:
1 (a b) (a b) 2 1 ab 1 c2
2
22
a2 b2 c2
【知识巩固】 1.一个直角三角形的三边分别为3,4,则
25 或 7
2.如右图,AD = 3,AB = 4,BC = 12,则求CD的长。
3.如图,从电线杆离地面6米处向地面拉一条长10米 的缆绳,这条缆绳在地面的固定点距离电线杆底部 有 8 米。
独学合作探究 帮扶交流 小组交流
17.1勾股定理(2)
温馨提示:
课本、双色笔、导学案
独学(前置)——1min
要求:组长交叉检查:独立完成导学案 【自主学习】中的问题完成情况。
【学习目标】
1.掌握勾股定理,理解利用拼图验证勾股定 理的方法。
2.会用勾股定理解答有关问题,树立数形结 合的思想。
【自主学习】 1.直角三角形的勾股定理: 直角三角形的 两条直角边的平方 等于斜边的平方 . 几何语言表述:和如图1.1-1,在RtΔABC中,∠C= 90°,
2.图中大正方形的边长为__a_+_b_,小正方形的边长为_c 。
3.你能请用两种不同方法表示图1中大正方形的面积, 列出一个等式,验证勾股定理吗? 分析:大正方形的面积= 边长的平方 =小正方形
的面积+ 四 个直角三角形的面积
得: ( a + b )2= c 2+ 4 ×2ab. (1) 化简 可得:
图2
活动三:用两个完全相同的直角三角形(直角边为a,b,斜 边为c)构成如图所示的梯形.填空: (1)梯形的面积= (上底+ 下底 ) 高
(2)如图ห้องสมุดไป่ตู้梯形的上底=a,下底= b ,高= a+b 。 (3)由“梯形面积等于三个直角三角形面积之和”可得:
1 (a b) (a b) 2 1 ab 1 c2
2
22
a2 b2 c2
【知识巩固】 1.一个直角三角形的三边分别为3,4,则
25 或 7
2.如右图,AD = 3,AB = 4,BC = 12,则求CD的长。
3.如图,从电线杆离地面6米处向地面拉一条长10米 的缆绳,这条缆绳在地面的固定点距离电线杆底部 有 8 米。
独学合作探究 帮扶交流 小组交流
17.1勾股定理(2)
温馨提示:
课本、双色笔、导学案
独学(前置)——1min
要求:组长交叉检查:独立完成导学案 【自主学习】中的问题完成情况。
【学习目标】
1.掌握勾股定理,理解利用拼图验证勾股定 理的方法。
2.会用勾股定理解答有关问题,树立数形结 合的思想。
【自主学习】 1.直角三角形的勾股定理: 直角三角形的 两条直角边的平方 等于斜边的平方 . 几何语言表述:和如图1.1-1,在RtΔABC中,∠C= 90°,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
。2021年1月11日星期一2021/1/112021/1/112021/1/11
• 15、会当凌绝顶,一览众山小。2021年1月2021/1/112021/1/112021/1/111/11/2021
• 16、如果一个人不知道他要驶向哪头,那么任何风都不是顺风。2021/1/112021/1/11January 11, 2021
• 学习重点: 运用勾股定理计算线段长度,解决实际问题.
说一说
勾股定理: 如果直角三角形的两条直角边长分别为a,b,斜边 长为c,那么a2+b2=c2.
已知一个直角三角形的两边,应用勾股定理可以求 出第三边,这在求距离时有重要作用.
想一想
例1 一个门框的尺寸如图所示,一块长3 m,宽 2.2 m的长方形薄木板能否从门框内通过?为什么?
(3)方程思想在本题中的运
用.
A
巩固练习
如图,一棵树被台风吹折断后,树顶端落在离底端 3米处,测得折断后长的一截比短的一截长1米,你能计 算树折断前的高度吗?
课堂小结
(1)利用勾股定理解决实际问题有哪些基本步骤? (2)你觉得解决实际问题的难点在哪里?你有什么
好的突破办法?利用勾股定理解决实际问题的 注意点是什么?请与大家交流. (3)本节课体现出哪些数学思想方法,都在什么情 况下运用?
有 AB2+BC2=AC2,
可列方程,得 x2+52=( x +1)2 ,
通过解方程可得.
A
拓展提高 形成技能
今有池方一丈,葭生其中央,出水一尺,引葭赴岸, 适与岸齐.问水深、葭长各几何?
利用勾股定理解决实际问题
的一般思路:
B
C
(1)重视对实际问题题意的
正确理解;
(2)建立对应的数学模型,
运用相应的数学知识;
八年级 下册
17.1 勾股定理(2)
课件说明
• 本课是在学习勾股定理的基础上,学习应用勾股定 理进行直角三角形的边长计算,解决一些简单的实 际问题.
课件说明
• 学习目标: 1.能运用勾股定理求线段长度,并解决一些简单的 实际问题; 2.在利用勾股定理解决实际生活问题的过程中,能 从实际问题中抽象出直角三角形这一几何模型, 利用勾股定理建立已知边与未知边长度之间的联 系,并进一步求出未知边长.
那么梯子底端B也外移0.5米吗?
跟踪练习:教科书第26页练习2.
想一想
问题 如果知道平面直角坐标系坐标轴上任意两点 的坐标为(x,0),(0,y),你能求这两点之间的距 离吗?
拓展提高 形成技能
今有池方一丈,葭生其中央,出水一尺,引葭赴岸, 适与岸齐.问水深、葭长各几何?
分析:
B
C
可设AB=x,则AC=x+1,
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
课后作业
作业:教科书第26页第1,2题.
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/1/112021/1/11Monday, January 11, 2021
• 10、人的志向通常和他们的能力成正比例。2021/1/112021/1/112021/1/111/11/2021 6:03:58 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/1/112021/1/112021/1/11Jan-2111-Jan-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。2021/1/112021/1/112021/1/11Monday, January 11, 2021 • 13、志不立,天下无可成之事。2021/1/112021/1/112021/1/112021/1/111/11/2021
解:在Rt△ABC中,根据勾股 定理,得 AC2=AB2+BC2=12+22=5.
AC= 5 ≈2.24. 因为 5 大于将实木际板问的题宽转2化.2为m数,学所问以 木板能题从,门建框立内几通何模过型.,画出图形,分
析已知量、待求量,让学生掌握解 决实际问题的一般套路.
D
C
A
Байду номын сангаас
B
1m
2m
做一做
例2 如图,一架2.6米长的梯子AB 斜靠在一竖直 的墙AO上,这时AO 为2.4米. (1)求梯子的底端B距墙角O多少米? (2)如果梯子的顶端A沿墙下滑0.5米,
•
THE END 17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2021/1/112021/1/112021/1/112021/1/11
谢谢观看
