matlab第二次实验
MATLAB - 第二次试验结果

一
第
7、8 节课 张皓
指导老师
2.从键盘输入 a, b, c 的值,输出一元二次方程 ax 2 + bx + c = 0 的根。
%Ex02_02 function Ex02_02() disp(['一元二次方程是: a*x^2+b*x+c=0,请输入 各系数']); a=input('a='); b=input('b='); c=input('c='); roots([a b c])
price=input('请输入商品的价格='); zk=0.*(price<200)+... 0.03.*((price<500)&(price>=200))+... 0.05.*((price>=500)&(price<1000))+... 0.08.*((price>=1000)&(price<2500))+... 0.1.*((price>=2500)&(price<5000))+... 0.14.*(price>=5000); p=price*(1-zk); disp(['折扣=',num2str(zk*100),'%']) disp(['实际销售价钱=',num2str(p),'元'])
将它们的值互换后输出。 %Ex02_01 function exchange(x,y) %用来实现数据交换 disp(['交换前:x=',num2str(x),',y=',num2str(y)]); z=x; x=y; y=z; disp(['交换后:x=',num2str(x),',y=',num2str(y)]);
Matlab第二次实验报告
Matlab第二次实验报告实验目的:1、了解plot函数和subplot函数的基本用法和matlab绘图的基本原理。
2、了解图形的属性设置。
比如画图的颜色,画图采用的线性标识符等。
二:实验基本知识1:1. 单窗口单曲线绘图;2. 单窗口多曲线绘图;3. 单窗口多曲线分图绘图;4. 多窗口绘图;5.可任意设置颜色与线型;6.图形加注功能;7.fplot——绘制函数图函数;8.ezplot——符号函数的简易绘图函数9:subplot—将画图区域分块函数。
实验内容:将高数课本后的18个图画出上机练习程序第1——6图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1);x=-50:1:50;y=a.*x.^3;subplot(3,2,1);plot(x,y,'r');title('y=a*x^3');xlabel('X');ylabel('Y');x=0:1:50;y=sqrt(a.*x.^3);subplot(3,2,2);plot(x,y,x,-y,'r');title('y^2=a*x^3');xlabel('X');ylabel('Y');x=-3:0.1:3;y=exp(-x.^2);subplot(3,2,3);plot(x,y,'r');title('y=e^x^2');xlabel('X');ylabel('Y');x=-3:0.1:3;y=8*a^3./(x.^2+4*a^2);subplot(3,2,4);plot(x,y,'r');title('y=8*a^3./(x.^2+4*a^2)'); xlabel('X');ylabel('Y');x=0:0.01:5;y=sqrt(x.^3./(a*2.-x)); subplot(3,2,5);plot(x,y,x,-y,'r');title('y^2*(2a-x)=x^3'); xlabel('X');ylabel('Y');%t=-1:0.01:5;%x=3*a.*t./(1+t.^3);%y=3*a*t.^2./(1+t.^3);subplot(3,2,6);ezplot('x.^3+y.^3-3*3*x.*y'); %plot(x,y);title('x^3+y^3-3axy=0'); xlabel('X');ylabel('Y');输入a=3:显示结果第7——10图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1)t=0:0.1:2*pi;x=a*cos(t).^3;y=a*sin(t).^3;subplot(2,2,1);plot(x,y,'b')title('x^1.5+y^1.5=a^1.5'); xlabel('X');ylabel('Y');t=-2*pi:0.1:2*pi;x=a.*(t-sin(t));y=a.*(1-cos(t));subplot(2,2,2);plot(x,y,'b')title('°ÚÏß');xlabel('X');ylabel('Y');t=0:0.01:2*pi;p=a.*(1-cos(t));subplot(2,2,3);plot(p.*cos(t),p.*sin(t),'b'); title('p=a(1-cos£¨t£©)'); xlabel('X');ylabel('Y');t=0:0.01:2*pi;p=a.*t;subplot(2,2,4);plot(p.*cos(t),p.*sin(t),'b'); title('p=at');xlabel('X');ylabel('Y');输入a=1,第11题图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º') figure(1);t=-2*pi:pi/100:2*pi;p=exp(a.*t);plot(p.*cos(t),p.*sin(t)); title('p=e^at');xlabel('X');ylabel('Y');输入a=0.1,显示结果:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1)t=0.2*pi:pi/100:100*pi;p=a./t;plot(p.*cos(t),p.*sin(t));title('p=at');xlabel('X');ylabel('Y');输入a=1,显示结果:第13——14题图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º');figure(1);t=0:pi/100:2*pi;p=(a^2.*sin(2*t)).^0.5;subplot(1,2,1);plot(p.*cos(t),p.*sin(t),-p.*cos(t),-p.*sin(t),'g'); title('p^2=a^2*sin(2t)');xlabel('X');p=(a^2.*cos(2*t)).^0.5;subplot(1,2,2);plot(p.*cos(t),p.*sin(t),-p.*cos(t),-p.*sin(t),'g'); title('p^2=a^2*cos(2t)');xlabel('X');ylabel('Y');输入a=1,显示结果:第15-16题图:clear;clc;a=input('ÇëÊäÈëa:');figure(1)t=0:pi/200:pi;p=a.*cos(3*t);subplot(1,2,1);plot(p.*cos(t),p.*sin(t),'r--');title('p=a*cos(3t)');xlabel('X');p=a.*sin(3*t);subplot(1,2,2);plot(p.*cos(t),p.*sin(t),'r--'); title('p=a*sin(3t)');xlabel('X');ylabel('Y');输入a=1,显示结果:第17——18题图:clear;clc;a=input('ÇëÊäÈëa:');figure(1);t=-pi:pi/200:pi;subplot(1,2,1);p=a.*sin(2*t);plot(p.*cos(t),p.*sin(t),'k-.'); title('p=a*sin(2t)');xlabel('X');ylabel('Y');p=a.*cos(2*t);subplot(1,2,2);plot(p.*cos(t),p.*sin(t),'k-.');title('p=a*cos(2t)');xlabel('X');ylabel('Y');输入a=1,显示结果:实验心得:这次实验主要是学习matlab软件的二维绘图功能:matlab软件还有丰富的图形修饰功能,如改变线条的形式和颜色;除此之外其还可以以多种形式如在一个图形中显示多个函数图形,一个figure中显示多个坐标系,还有一个程序中就可以用多个figure一起来表示不同的函数……在画图过程中你可能因为角度的区间取值不一样,画出来的图形可能跟书本上给出的图形有很大的差异,但没关系,只要你思路是对的,区间可以自己慢慢改动知道跟书本上给出的图形想接近。
MATLAB实验二

3. 三维图形
• 三、视点
➢view(az,el)-------------设置观察点方向
az为方位角,el为仰角。 • 方位角为视点位置在XY平面上的投影与X轴形成的角度,
正值表示逆时针,负值表示顺时针。 • 仰角为XY平面的上仰或下俯角,正值表示视点在XY平
面上方,负值表示视点在XY平面下方。
figure grid gtext hold subplot text title xlabel ylabel
创建图形窗口 放置坐标网格线 用鼠标放置文本 保持当前图形窗口内容 创建子图 放置文本 放置图形标题 放置X轴坐标标记 放置Y轴坐标标记
3. 三维图形 • 一、 plot3函数
• 将二维函数plot的功能扩展到三维空间,绘制三维图形。 • 函数格式:plot3(x1,y1,z1,c1,x2,y2,z2,c2,…)
theta=[0:0.01:2*pi];
rho=sin(2*theta).*cos(2*theta);
polar(theta,rho); 绘制极坐标图命令
title('polar plot');
例9、程序:
theta=linspace(0, 2*pi);
r=cos(4*theta);
polar(theta, r);
所组成的画面。
4. 动画设计
• 【例14】 播放一个不断变化的眼球程序段。
• m=moviein(20); 建立一个20个列向量组成的矩阵
• for j=1:20
•
plot(fft(eye(j+10))) %绘制出每一幅眼球图并保存到m矩阵中
• m(:,j)=getframe;
MatLAB第二次实验

自动控制理论实 验 报 告姓 名 班 级 成 绩_______________学 号 日 期 合作者________________________________________________________________________________________________一、实验题目:利用MATLAB 求系统的的瞬态性能指标 二、实验目的:1、熟悉并掌握MatlAB 软件在工程计算中的应用。
2、求系统的的瞬态性能指标。
三、实验仪器:电脑、MatlAB 软件; 四、实验内容用impulse 函数求单位脉冲响应,step 求求单位阶跃响应。
程序:%a_1.mt=[0:0.01:0.8] %num_G=[50];tao=0;den_G=[0.05 1+50*tao 50];G1=tf(num_G ,den_G);tao=0.0125;den_G=[0.05 50*tao tao 50];G2=tf(num_G ,den_G); tao=0.025;den_G=[0.05 1+50*tao 50];G3=tf(num_G ,den_G); %[y1,T]=impulse(G1,t);[y1a,T]=step(G1,t); [y2,T]=impulse(G2,t);[y2a,T]=step(G2,t); [y3,T]=impulse(G3,t);[y3a,T]=step(G3,t); %subplot(1,2,1)plot(T,y1,'r-',T,y2,'g-',T,y3,'b-')legend('tao=0','tao=0.0125','tao=0.025') xlabel('t(sec)') ylabel('x(t)'); grid on;subplot(1,2,2)plot(T,y1a,'r-',T,y2a,'g-',T,y3a,'b-')legend('tao=0','tao=0.0125','tao=0.025') grid on;xlabel('t(sec)') ylabel('x(t)');二、用lsim函数求任意输入响应程序:%3_2.mclc;t=[0:0.01:1];u=sin(2*pi*t);%tao=0.025;num_G=[50];den_G=[0.05 1+50*tao 50];G=tf(num_G,den_G);%y=lsim(G,u,t);%plot(t,u,'r-',t,y,'g-',t,u','b',t,y','r',t,u'-y,'b-','linewidth',1)legend('u(t)','xo(t)','u(t)','xo(t)','e(t)=u-y')grid;xlabel('t(sec)')ylabel('x(t)');三、利用MATLAB求系统的的瞬态性能指标程序:close all;%t=0:0.001:1;%yss=1;dta=0.02;%num_G=[50];tao=0;den_G=[0.05 1+50*tao 50];G1=tf(num_G,den_G);tao=0.0125;den_G=[0.05 1+50*tao 50];G2=tf(num_G,den_G);tao=0.025;den_G=[0.05 1+50*tao 50];G3=tf(num_G,den_G);y1=step(G1,t);y2=step(G2,t);y3=step(G3,t);%r=1;while y1(r)<yss;r=r+1;endtr1=(r-1)*0.001;%[ymax,tp]=max(y1);tp1=(tp-1)*0.001;%mp1=(ymax-yss)/yss;%s=1001;while y1(s)>1-dta & y1(s)<1+dta;s=s-1;endts1=(s-1)*0.001;%τ=0.0125r=1;while y2(r)<yss;r=r+1;endtr2=(r-1)*0.001;[ymax,tp]=max(y2);tp2=(tp-1)*0.001;mp2=(ymax-yss)/yss;s=1001;while y2(s)>1-dta &y2(s)<1+dta;s=s-1;endts2=(s-1)*0.001;%τ=0.025r=1;while y3(r)<yss;r=r+1;endtr3=(r-1)*0.001;[ymax,tp]=max(y3);tp3=(tp-1)*0.001;mp3=(ymax-yss)/yss;s=1001;while y3(s)>1-dta & y3(s)<1+dta;s=s-1;endts3=(s-1)*0.001;%[tr1 tp1 mp1 ts1;tr2 tp2 mp2 ts2;tr3 tp3 mp3 ts3]结果:ans =0.0640 0.1050 0.3509 0.3530 -------系统10.0780 0.1160 0.1523 0.2500 -------系统20.1070 0.1410 0.0415 0.1880 -------系统3任课教师:。
北科大matlab数学实验报告第二次

《数学实验》报告实验名称 MATLAB绘图学院材料科学与工程学院专业班级材料0801 姓名 xxxxxxx 学号 xxxxxxxxx2011年10月一、【实验目的】学会用MATLAB绘制二维曲线、三维曲线、三维曲面,掌握gtext, legend, title, xlabel, ylabel等指令用法。
二、【实验任务】第四章3、5、9题。
三、【实验程序】1.x1=-pi:pi/100:pi;y1=x1.*cos(x1);x2=pi:pi/100:4*pi;y2=x2.*tan(1./x2).*sin(x2.^3);x3=1:0.1:8;y3=exp(1./x3).*sin(x3);subplot(131),plot(x1,y1,'rp'),grid onaxis tighttitle('y1=x1cosx1')xlabel('x轴'),ylabel('y轴')gtext('y1=x1cosx1')legend('y1=x1cosx1')subplot(132),plot(x2,y2,'c-'),grid onaxis tighttitle('y2=x2tan(1/x2)sin(x2^3)')xlabel('x轴'),ylabel('y轴')gtext('y2=x2tan(1/x2)sin(x2^3)')legend('y2=x2tan(1/x2)sin(x2^3)')subplot(133);plot(x3,y3,'mx'),grid onaxis tighttitle('y3=e^(1/x3)sin(x3)')xlabel('x轴'),ylabel('y轴')gtext('y3=e^(1/x3)*sin(x3)')legend('y3=e^(1/x3)sin(x3)')2. t=0:pi/10:20*pi;x=t.*cos(pi/6.*t);uy=t.*sin(pi/6.*t);z=2*t;plot3(x,y,z),grid onxlabel('x轴 x=tcos(pi/6t)')ylabel('y轴 y=tsin(pi/6t)')zlabel('z轴 z=2t')title('圆锥螺线(0≤t≤20pi)')legend('圆锥螺线')3. %三维曲面t=-2:0.01:2;[x,y]=meshgrid(t);z1=5-x.^2-y.^2+eps;subplot(131),mesh(x,y,z1),title('三维曲面')%平面subplot(1,3,2)z2=3*ones(size(x))mesh(x,y,z2)title('平面')%交线r0=abs(z1-z2)<=1;zz=r0.*z2;yy=r0.*y;xx=r0.*x;subplot(1,3,3),plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'m-')title('交线')四、【实验结果】1.2.3.五、【实验总结】这次作业明显比第一次轻松了许多,在上课认真听讲后,又研读了书上的讲解和例题,起初是模仿,后来自己就能完全理解并做出题目来。
实验二MATLAB的矩阵操作_参考答案

1
5
>> A(k)
ans =
23
10
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
>> B=A([1,2,3],:)
B =
23.0000 10.0000 -0.7780 0
41.0000 -45.0000 65.0000 5.0000
32.0000 5.0000 0 32.0000
y =
-128.4271
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
A=[-1,5,-4;0,7,8;3,61,7]
B=[8,3,-1;2,5,3;-3,2,0]
>> A+6*B
ans =
47 23 -10
12 37 26
-15 73 7
&
ans =
-1.2768 -0.4743 0.2411
2.1229 1.3173 -0.2924
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14]
>> k=find(A>=10&A<=25)
(2)
(3)
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
(2)A*B、A.*B和B*A
(3)A/B及B/A
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
MATLAB第二次上机实验报告

电子科技大学电子工程学院标准实验报告(实验)课程名称MATLAB与数值分析学生姓名:学号:指导教师:一、实验名称实验二 线性方程组求解和函数的数值逼近二、实验目的通过上机实验,使学生对病态问题、线性方程组求解和函数的数值逼近方法有一个初步的理解。
实验涉及的核心知识点:病态方程求解、矩阵分解和方程组求解、Lagrange 插值。
实验重点与难点:算法设计和MATLAB 编程三、实验内容1. 对高阶多项式()()()()()2011220k p x x x x x k ==---=-∏编程求下面方程的解()190p x x ε+=并绘图演示方程的解与扰动量ε的关系。
2. 对220n =,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组()n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
3. 对函数()21125f x x =+ []1,1x ∈-的Chebyshev 点()()21cos 21k k x n π⎛⎫-= ⎪ ⎪+⎝⎭,1,2,,1k n =+编程进行Lagrange 插值,并分析插值结果。
四、实验数据及结果分析1. 对高阶多项式()()()()()2011220k p x x x x x k ==---=-∏编程求下面方程的解()190p x x ε+=并绘图演示方程的解与扰动量ε的关系。
p=[1,-1]; for i=2:20 n=[1,-i];p=conv(p,n); % 求多项式乘积 endm=zeros(1,21); % m 的最高次幂为20,有21项 hold on x=1:20;d=[-1,0,0.1,0.5,1]; for i=1:5delt=d(i); m(2)=delt;y=(roots(p+m))'; % 求多项式的根 plot(x,y,'-o','color',[i/5,i/20,i/10]); endtitle('方程p(x)=0的解与扰动量delt 的关系')legend('delt=-1','delt=0','delt=0.1','delt=0.5','delt=1')24681012141618200102030405060方程p(x)=0的解与扰动量delt 的关系delt=-1delt=0delt=0.1delt=0.5delt=12.对220n =,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组()n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
matlab数学实验报告

MATLAB数学实验报告指导老师:班级:小组成员:时间:201_/_/_Matlab第二次实验报告小组成员:1题目:实验四;MATLAB选择结构与应用实验目的:掌握if选择结构与程序流程控制;重点掌握break;return;pause语句的应用..问题:问题1:验证“哥德巴赫猜想”;即:任何一个正偶数n>=6均可表示为两个质数的和..要求编制一个函数程序;输入一个正偶数;返回两个质数的和..问题分析:由用户输入一个大于6的偶数;由input语句实现..由if判断语句判断是否输入的数据符合条件..再引用质数判断函数来找出两个质数;再向屏幕输出两个质数即可..编程:function z1;z2=geden;n=input'please input n'if n<6disp'data error';returnendif modn;2==0for i=2:n/2k=0;for j=2:sqrtiif modi;j==0k=k+1;endendfor j=2:sqrtn-iif modn-i;j==0k=k+1;endendif k==0fprintf'two numbers are'fprintf'%.0f;%.0f';i;n-ibreakendendend结果分析:如上图;用户输入了大于6的偶数返回两个质数5和31;通过不断试验;即可验证哥德巴赫猜想..纪录:if判断语句与for循环语句联合嵌套使用可使程序结构更加明晰;更快的解决问题..2题目:实验四;MATLAB选择结构与应用实验目的:用matlab联系生活实际;解决一些生活中常见的实际问题..问题:问题四:在一边长为1的四个顶点上各站有一个人;他们同时开始以等速顺时针沿跑道追逐下一人;在追击过程中;每个人时刻对准目标;试模拟追击路线;并讨论.. (1)四个人能否追到一起(2)若能追到一起;每个人跑过多少路程(3)追到一起所需要的时间设速率为1问题分析:由正方形的几何对称性和四个人运动的对称性可知;只需研究2个人的运动即可解决此问题..编程:hold onaxis0 1 0 1;a=0;0;b=0;1;k=0;dt=0.001;v=1;while k<10000d=norma-b;k=k+1;plota1;a2;'r.';'markersize';15;plotb1;b2;'b.';'markersize';15;fprintf'k=%.0f b%.3f;%.3f a%.3f;%.3f d=%.3f\n';k;b1;b2;a1;a2;da=a+b1-a1/d*dt;b2-a2/d*dt;b=b+b2-a2/d*dt;-b1-a1/d*dt;if d<=0.001breakendendfprintf'每个人所走的路程为:%.3f';k*v*dtfprintf'追到一起所需要的时间为%.3f';k*dt结果分析:上图为2人的模拟运动路线;有对称性可解决所提问题..-上图为运算过程和运算结果..四个人可以追到一起;走过的路程为1.003;时间也为1.003.纪录:此题利用正方形和运动的对称性可以简便运算..3题目:实验八;河流流量估计与数据插值目的:由一些测量数据经过计算处理;解决一些生活实际问题..问题:实验八上机练习题第三题:瑞士地图如图所示;为了算出他的国土面积;做以下测量;由西向东为x轴;由南向北为y轴;从西边界点到东边界点划分为若干区域;测出每个分点的南北边界点y1和y2;得到以下数据mm..已知比例尺1:2222;计算瑞士国土面积;精确值为41288平方公里..测量数据如下:x=7.0 10.5 13.0 17.5 34 40.5 44.5 48 56 61 68.5 76.5 80.5 91 96 101 104 106 111.5 118 123.5 136.5 142 146 150 157 158 ;y1=44 45 47 50 50 38 30 30 34 36 34 41 45 46 43 37 33 28 32 65 55 54 52 50 66 66 68;y2=44 59 70 72 93 100 110 110 110 117 118 116 118 118 121 124 121 121 121 122 116 83 81 82 86 85 68;问题分析:先由题目给定的数据作出瑞士地图的草图;再根据梯形法;使用trapz语句;来估算瑞士国土的面积..编程:x=7.0 10.5 13.0 17.5 34 40.5 44.5 48 56 61 68.5 76.5 80.5 91 96 101 104 106 111.5 118 123.5 136.5 142 146 150 157 158;y1=44 45 47 50 50 38 30 30 34 36 34 41 45 46 43 37 33 28 32 65 55 54 52 50 66 66 68;y2=44 59 70 72 93 100 110 110 110 117 118 116 118 118 121 124 121 121 121 122 116 83 81 82 86 85 68;plotx;y1;'r.';'markersize';15;plotx;y2;'r.';'markersize';15;axis0 160 0 135grid;hold ont=7:158;u1=splinex;y1;t;u2=splinex;y2;t;plott;u1plott;u2s1=trapzt;u1;s2=trapzt;u2;s=s2-s1*2222*22222/10000000;fprintf'S=%.0f';s结果分析:上图为由所给数据绘制出的瑞士地图..上图为运算结果;计算出瑞士的国土面积为42472平方公里;与准确值41288较为接近..纪录:使用梯形分割的方法;trapz语句可以方便计算不规则图形面积;但存在一定误差..4题目:实验七:圆周率的计算与数值积分目的:将数值积分最基本的原理应用于matlab之中;解决一些与积分有关的问题..问题:实验七上机练习题第一题:排洪量某河床的横断面如图7.3所示;为了计算最大排洪量;需要计算其断面积;试根据所给数据m用梯形法计算其断面积..问题分析:河床断面可近似分割成若干曲边梯形;近似处理把它们当做梯形来计算面积可使问题得到简化..编程:clc;clear;x=0 4 10 12 15 22 28 34 40;y=0 1 3 6 8 9 5 3 0;y1=10-y;plotx;y1;'k.';'markersize';15;axis0 40 0 10;grid;hold ont=0:40;u=splinex;y1;t;plott;u;s=40*10-trapzt;u;fprintf's=%.2f\n';s结果分析:上图为河床的断面图..上图为计算结果面积约为180.70平方米..纪录:使用梯形法计算不规则图形面积十分简便易行..5题目:实验七:圆周率的计算与数值积分目的:使用matlab计算解决一些有关积分的问题..问题:实验七上机练习题第三题:从地面发射一枚火箭;在最初100秒内记录其加速度如下;试求火箭在100秒时的速度..Ts=0 10 20 30 40 50 60 70 80 90 100;Am/s*s=30.00 31.63 33.44 35.47 37.75 40.33 43.29 46.69 50.67 54.01 57.23;问题分析:加速度为速度的微分;已知微分求积分;类似于面积问题;可使用梯形法来计算..编程:clc;clear;x=0 10 20 30 40 50 60 70 80 90 100;y=30.00 31.63 33.44 35.47 37.75 40.33 43.29 46.69 50.6754.01 57.23;plotx;y;'k.';'markersize';15;axis0 100 20 60;grid;hold ons=0:10:100;z=splinex;y;s;plots;y;v=trapzx;y;fprintf'v=%.2f\n';v结果分析:上图为加速度变化图..上图为计算结果;求得火箭在100秒时速度约为4168.95m/s..纪录:梯形法可以推广解决许多已知微分求积分的其他问题..6题目:实验七:圆周率的计算与数值积分目的:计算曲线弧长闭曲线周长可使用微元法;ds=sqrtdx^2+dy^2;在转化微积分问题;累加即可得到结果..问题:实验七上机练习题第三题:计算椭圆想x^2/4+y^2=1的周长;使结果具有五位有效数字..问题分析:编程:s=0;dx=0.001;for x=0:0.001:1.999dy=1.-x+0.001.^2/4-1.-x.^2/4;ds=sqrtdx.^2+dy.^2;s=s+ds;ends=4*s;fprintf'the length is'fprintf'%.4f';s结果分析:上图为计算结果;给定椭圆的周长约为9.1823五位有效数字纪录:计算不规则曲线弧长;可使用微元法;划分为若干小的看做直角三角形;利用勾股定理解决..7题目:实验九人口预测与数据拟合目的:掌握一些曲线拟合的方法;了解曲线拟合常用函数..问题:用电压U=10v的电池给电容器充电;t时刻的电压Vt=U-U-V0exp-t/τ;其中V0是电容器的初始电压;τ是充电常数;由所给数据确定V0和τ..t=0.5 1 2 3 4 5 7 9;V=3.64 3.52 2.74 1.78 1.34 1.01 0.57 0.37;问题分析:题中已给出函数关系式;为指数函数曲线拟合;将所给函数式整理可得标准的exp形函数曲线;从而便于解决..编程:t=0.5 1 2 3 4 5 7 9;V=3.64 3.52 2.74 1.78 1.34 1.01 0.57 0.37;plott;V;'k.';'markersize';20;axis0 10 0 4;grid;hold onpause0.5n=8;a=sumt1:n;b=sumt1:n.*t1:n;c=sumlogV1:n;d=sumt1:n.*logV1:n;A=n a;a b;B=c;d;p=invA*Bx=0:10;y=expp1+p2*x;plotx;y;'r-';'linewidth';2结果分析:上图为电压与时间关系图..上图为计算结果;即U-V0=1.4766;所以V0=8.5234;-1/τ=-0.2835;所以τ=3.5273纪录:曲线拟合的一个重难点是选择合适的曲线函数;才能提高拟合度..8题目:实验七圆周率的计算与数值积分目的:拓展圆周率的各种计算方法;掌握其他数值的近似计算方法..问题:实验七练习2:计算ln2的近似值精确到10的-5次方(1)利用级数展开的方法来计算(2)利用梯形法计算(3)利用抛物线法问题分析:级数展开;梯形法;抛物线法是常见的近似运算方法..编程:1级数展开的方法clc;clear;n=0;r=1;p=0;k=-1;while r>=0.1e-5n=n+1;k=k*-1;p1=p+k/n;r=absp1-p;fprintf'n=%.0f;p=%.10f\n';n;p1;p=p1;end2梯形法clc;clear;f=inline'1./x';x=1:0.1:2;y=fx;p=trapzx;y;fprintf'p=%.6f\n';p3抛物线法clc;clear;f=inline'1./x';a=1;b=2;n=1;z=quadf;a;b;fprintf'z=%.10f\n';z结果分析:(1)级数展开的方法(2)梯形法3抛物线法纪录:级数展开法;梯形法;抛物线法;计算近似值时应合理利用..梯形法和抛物线法不易提高精确度;级数展开法可以提高精确度..9题目:实验八河流流量估计与数据插值目的:掌握求插值多项式的方法;并利用此计算近似值..问题:已知y=fx的函数表如下x=0.40 0.55 0.65 0.80 0.90 1.05;y=0.41075 0.57815 0.69675 0.88811 1.02652 1.25382;求四次拉格朗日插值多项式;并由此求f0.596问题分析:利用所给函数表可计算拉格朗日插值多项式..编程:function p=lagrangex;yL=lengthx;a=onesL;for j=2:La:;j=a:;j-1.*x';endx=inva*y';for i=1:Lpi=xL-i+1;endx=0.40 0.55 0.65 0.80 0.90 1.05;y=0.41075 0.57815 0.69675 0.88811 1.02652 1.25382; plotx;y;'k.';'markersize';15axis0 2 0 2grid;hold on;p=lagrangex;y;t=0:0.1:1.5;u=polyvalp;t;plott;u;'r-'a=polyvalp;0.596结果分析:上图为所求结果;估算值和插值多项式..纪录:插值多项式是一项十分实用的方法..10题目:求正整数n的阶乘:p=1*2*3*…*n=n;并求出n=20时的结果目的:练习使用循环变量解决数学问题问题:对程序:Clear;clc;n=20;p=1;for i=1:np=p*i;fprintf’i=%.0f;p=%.0f\n’;i;pend进行修改使它:利用input命令对n惊醒赋值问题分析:题中给出程序中“n=20”修改;使用input命令;讲题中的输出命令放出循环之外..编程:clear;clc;n=input'n=';p=1;for i=1:np=p*i;endfprintf'i=%.0f;p=%.0f\n';i;p结果:n=20i=20;p=2432902008176640000>>结果分析:使用input命令可以实现人机对话;使用户自由赋值;输出语句在程序中的位置对输出的结果有很大的影响;在循环内部可以在计算过城中不断输出结果;在循环之外则可以控制只输出最后结果..11题目:对于数列{√2};n=1;2;…;求当其前n项和不超过1000时的n的值及合的大小..目的:运用条件循环解决文帝个项数的循环程序求解;问题:对程序:clear;clc;n=0;s=0;while s<=1000n=n+1;s=s+sqrtn;fprintf’n=%.0f;s=%.4f\n’;n;send问题分析:题中所给程序中的限制变量为上次循环之后的s;导致s超过上限后仍有一次的循环;若把循环变量改为这次的s;则可以避免这种情况的发生..编程:clear;clc;n=0;s=0;while s+sqrtn<=1000n=n+1;s=s+sqrtnfprintf'n=%.0f;s=%.4f\n';n;send结果:……s =970.8891n=128;s=970.8891s =982.2469n=129;s=982.2469s =993.6487n=130;s=993.6487>>结果分析:从结果中可以看出;最后一步为我们需要的答案;从这道题我们可以得出循环变量对一道编程的重要性..。
MATLABA第二次上机实验

实验二MATLAB矩阵分析与处理2.产生5阶希尔伯特矩阵H和5阶帕斯卡矩阵P,且求其行列式的值Hh和Hp以及他们的条件数Th和Tp,判断哪个矩阵性能更好。
为什么?程序代码及运算结果如下:> H=hilb(5)H =1.0000 0.5000 0.3333 0.2500 0.20000.5000 0.3333 0.2500 0.2000 0.16670.3333 0.2500 0.2000 0.1667 0.14290.2500 0.2000 0.1667 0.1429 0.12500.2000 0.1667 0.1429 0.1250 0.1111>> P=pascal(5)P =1 1 1 1 11 2 3 4 51 3 6 10 151 4 10 20 351 5 15 35 70>> Hh=det(H)Hh =3.7493e-012>> Hp=det(P)Hp =1>> Th=cond(H)Th =4.7661e+005>> Tp=cond(P)Tp =8.5175e+003由运算结果知Tp的值越接近1,故矩阵P的性能越好。
5.下面是一个线性方程组:A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6;](1)求方程的解。
(2)将方程右边向量元素b3改为0.53,在求解,并比较b3的变化和解的相对变化。
(3)计算系数矩阵A的条件数并分析结果。
程序代码及结果如下:>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6;]A =0.5000 0.3333 0.25000.3333 0.2500 0.20000.2500 0.2000 0.1667>> b=[0.95;0.67;0.52;]b =0.95000.67000.5200>> x=inv(A)*bx =1.20000.60000.6000>> b1=[0.95;0.67;0.53]b1 =0.95000.67000.5300>> x=inv(A)*b1x =3.0000-6.60006.6000>> B=cond(A)B =1.3533e+003由B的值知,B离1较远,故矩阵x的稳定性较差,改变b3的值为0.53,虽b3的值只增加了0.01,所得结果却发生的很大变化,这都是矩阵A的稳点性所决定的。
Matlab实验二
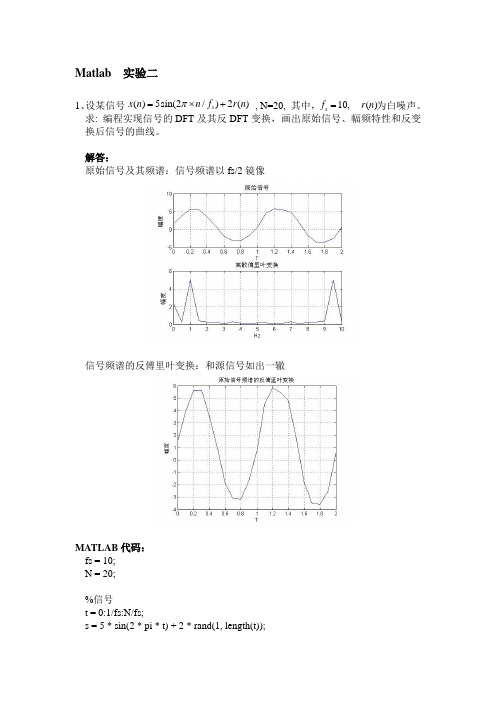
Matlab 实验二1、设某信号 , N=20, 其中, 为白噪声。
求: 编程实现信号的DFT 及其反DFT 变换,画出原始信号、幅频特性和反变换后信号的曲线。
解答:原始信号及其频谱:信号频谱以fs/2镜像信号频谱的反傅里叶变换:和源信号如出一辙MATLAB 代码: fs = 10; N = 20;%信号t = 0:1/fs:N/fs;s = 5 * sin(2 * pi * t) + 2 * rand(1, length(t));()5sin(2/)2()s x n n f r n π=⨯+10, () s f r n =%原始信号的幅频特性 s_fft = fft(s)/(N/2);f_label = linspace(0, fs, N+1); figure(1); subplot(211); plot(t, s);title('原始信号');xlabel('T');ylabel('幅度');grid on; subplot(212);plot(f_label, abs(s_fft));title('离散傅里叶变换');xlabel('Hz');ylabel('幅度');grid on;%反傅里叶变换 figure(2);s_ifft = ifft(s_fft)*(N/2); plot(t, s_ifft);title('原始信号频谱的反傅里叶变换');xlabel('T');ylabel('幅度');grid on; 2、一个线性是时不变系统差分方程为:1)计算并画出在 内的系统脉冲响应; 2)画出上面滤波器的幅频和相频图;3)产生信号 ,作为该系统的输入,计算并画出在 内的输出y (n)。
解答: 由系统的差分方程可得系统函数为:213125.05.0121)(----+-++=ZZZZz H则系统函数参数[b, a] = [[1, 2, 0, 1], [1, -0.5, 0.25]]。
matlab2022实验2参考答案

matlab2022实验2参考答案报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:MATLAB实验二MATLAB符号计算试验报告说明:1做试验前请先预习,并独立完成试验和试验报告。
2报告解答方式:将MATLAB执行命令和最后运行结果从命令窗口拷贝到每题的题目下面,请将报告解答部分的底纹设置为灰色,以便于批阅。
3在页眉上写清报告名称,学生姓名,学号,专业以及班级。
3报告以Word文档书写。
一目的和要求1熟练掌握MATLAB符号表达式的创建2熟练掌握符号表达式的代数运算3掌握符号表达式的化简和替换4熟练掌握符号微积分5熟练掌握符号方程的求解二试验内容1多项式运算(必做)1.1解方程:f(某)=某^4-10某某^3+34某某^2-50某某+25=0%采用数值方法:>>f=[1-1034-5025];>>root(f)%采用符号计算方法:f1=ym('某^4-10某某^3+34某某^2-50某某+25')olve(f1)1.2求有理分式R=(3某^3+某)(某^3+2)/((某^2+2某-2)(5某^3+2某^2+1))的商多项式和余多项式.a1=[3010];a2=[1002];a=conv(a1,a2);b1=[12-2];b2=[5201];b=conv(b1,b2);[p,r]=deconv(a,b);%注意:ab秩序不可颠倒。
%reidue用于实现多项式的部分分式展开,此处用deconv函数报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:%%此题,有同学程序如下:某1=[3010],某2=[1002],某3=[12-2],某4=[5201]某5=conv(某1,某2)[y6,r]=deconv(某5,某3)R=deconv(y6,某4)%%这种方法较第一种解法缺点:在除法运算中,会产生误差,故此题应先将分母的多项式相乘后,再与分子部分的多项式进行运算。
MATLAB实验二(修改)

实验二 信号的表示及其基本运算一、实验目的1、掌握连续信号及其MATLAB 实现方法;2、掌握离散信号及其MA TLAB 实现方法3、掌握离散信号的基本运算方法,以及MA TLAB 实现4 熟悉应用MATLAB 实现求解系统响应的方法4、了解离散傅里叶变换的MA TLAB 实现5、了解IIR 数字滤波器设计6、了解FIR 数字滤波器设计1二、实验设备计算机,Matlab 软件三、实验内容(一)、 连续信号及其MATLAB 实现1、 单位冲激信号()0,0()1,0t t t dt εεδδε-⎧=≠⎪⎨=∀>⎪⎩⎰ 例1.1:单位冲击信号的MATLAB 实现程序如下:t1=-4;t2=4;t0=0;dt=0.01;t=t1:dt:t2;n=length(t);x=zeros(1,n); x(1,(-t0-t1)/dt+1)=1/dt;stairs(t,x);axis([t1,t2,0,1.2/dt]);2、 任意函数()()()f t f t d τδττ+∞-∞=-⎰例1.2:用MA TLAB 画出如下表达式的脉冲序列()0.4(2)0.8(1) 1.2() 1.5(1) 1.0(2)0.7(3)f n n n n n n n δδδδδδ=-+-+++++++ 3 单位阶跃函数1,0()0,0t u t t ⎧≥⎪=⎨<⎪⎩例1.3:用MA TLAB 实现单位阶跃函数clear all;t=-0.5:0.001:1;t0=0;u=stepfun(t,t0);plot(t,u)axis([-0.5 1 -0.2 1.2])4 斜坡函数0()()g t B t t =-例1.4:用MA TLAB 实现g(t)=3(t-1)clear all;t=0:0.01:3;B=3;t0=1;u=stepfun(t,t0);n=length(t);for i=1:nu(i)=B*u(i)*(t(i)-t0);endplot(t,u)axis([-0.2 3.1 -0.2 6.2])5 抽样信号 抽样信号Sa(t)=sin(t)/t 在MATLAB 中用 sinc 函数表示。
matlab第二次实验报告

《数学建模实验》上机实验报告班级:计算机35班学号:2130505099姓名:田博文【实验一】一上底面半径2米、下底面半径4米、高4米的圆台形水池内盛满了水,由池底一横截面积为0.001平方米的小孔放水。
求在任意时刻的水面高度和将水放空所需的时间。
一、问题分析:在dt很小一段时间内,水的流速v可以看成是不变的与水面高度h有关的函数,即v=gh2;在dt时间内流出的水量,可以近似的为一圆柱,对应的圆柱高为dh;由于容器下降的水量与流出的水量相等,令小孔面积为b,即dV=π2r dh=bvdt;可得dh与dt的关系为:dh=bvdt/(π2r);根据相似三角形原理可得,r=4-h/2;初始条件有;h(0)=4;为表示方便,引入变量L=4-h故r=2+L/2二、代码:T=0;for L=0:0.001:4-0.001 %选取积分微元为0.001,即dhV=0.001*pi*(2+(1/2*L))^2; %水面处的dV,b=0.001t=V/(sqrt(2*(4-L)*9.8)*0.001) %dV与dt关系T=T+t;plot(T,(4-L),'red'); hold onend三、运行结果:四、结论:在任意时刻的水面高度和将水放空所需的时间如上图红线所示,横轴为时间,纵轴为水面高度。
【实验二】有A、B、C三个场地,每一个场地都出产一定数量的原料,同时也消耗一定数量的产品,具体数据如下表所示。
已知制成每吨产品需要消耗3吨原料,A、B两地,A、C两地和B、C两地之间的距离分别为150千米、100千米和200千米,假设每万吨原料运输1千米的运费为5000元,每万吨产品运输1千米的运费为6000元。
由于地区条件的差异,在不同地区设厂的费用不同,由于条件的限制,在B处建厂的规模不能超过5万吨,问:在这三地如何建厂、规模建多大才能使得总费用最小?地点年产原料(万吨)年销产品(万吨)生产费用(万元/万吨)A 20 7 150B 16 13 120C 24 0 100一、问题分析:设nij为i地运往j地的原料量,mij为i地运往j地的产品量,设A地为1地,B 为2地,C地为3地。
东南大学数字信号处理第二次MATLAB实验报告

原代码:
Fft函数:
在命令窗口输入:(手绘fft)
运行结果为:
在命令窗口输入:(原装fft)
运行后的结果为:
在命令窗口输入:(手绘dft)
运行结果为:
结果分析:
(1)由自己编写的my_fft函数与MATLAB自带的fft函数在cosk(k=0:511)的频谱图中结果相同,与之间的dft函数在运行结果上也表现出了一致性。
(2)运行时间的比较上从快到慢的顺序依次为fft(0.1152s)>my_fft (0.3157s)>my_dft(0.4038s), 结果符合预期,这说明my_fft函数在一定程度上能够简化计算,但是不及MATLAB底部的fft优秀,存在很大的改进空间(由于使用的是初等函数进行的循环迭代计算,运算速度较矩阵运算有一定的差距);(3)由于采用了蝶形算法使得计算的次数缩减,时间复杂度由N^2降为N*log2N,在理论上提高了效率。
当N=512时,DFT的复杂度为512^2=262144,FFT的复杂度为512*9=4608次,但由于空间的开销使得运行速度有一定的延缓。
matlab第二次实验

1、 产生5HZ ,15HZ ,30HZ 3个正弦信号,采样率100HZ ,3个信
号叠加之后,画出其频谱,ellip 产生3个带通滤波器,画出带同滤波器的频谱之后,分别从混合信号中过滤出3个正弦信号,并画出滤波器处理后的信号波形及其频谱。
2、 求N 点DFT 的幅度谱,假设:
()2sin(4)5cos(40)x t t t ππ=+N=40,60,80,100分别讨
论其频谱特点,找出不同。
如果加上正态噪声()2sin(4)5cos(40)0.8()x t t t w t ππ=++,同时令N=100,比较有噪声与没有噪声的频谱的区别。
3、 假设一源图像读取(imread ),显示(imshow ),卷和(conv2,二维信号卷
积和),格式转换(rgb2gray )采用下列2个高通和一个低通滤波器:
1010141010H -⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦ 2111181111H ---⎡⎤⎢⎥=--⎢⎥⎢⎥---⎣⎦ 311111119111H ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 分别对图像进行滤波,分析处理结果。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---101101101 prewwit 算子121000121⎡⎤⎢⎥⎢⎥⎢⎥---⎣⎦Robinson 算子,
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-0101014841085680148410101081,
拉普拉斯算子,分别使用上述3个算子与图像卷积和,分析结果。
matlab实验报告实验二

matlab实验报告实验二Matlab实验报告实验二引言Matlab是一种功能强大的数学软件,广泛应用于科学研究和工程实践中。
在实验二中,我们将探索Matlab的图像处理功能,并通过实际案例来展示其应用。
图像处理基础图像处理是指对图像进行数字化处理的过程,其目的是改善图像质量、提取有用信息或实现特定的应用需求。
在Matlab中,我们可以利用各种函数和工具箱来实现图像处理的各种任务,如图像增强、滤波、分割和特征提取等。
实验步骤1. 图像读取与显示在Matlab中,我们可以使用imread函数读取图像文件,并使用imshow函数将图像显示在屏幕上。
例如,我们可以读取一张名为"lena.jpg"的图像,并显示出来:```matlabimg = imread('lena.jpg');imshow(img);```2. 图像灰度化图像灰度化是将彩色图像转换为灰度图像的过程。
在Matlab中,我们可以使用rgb2gray函数将彩色图像转换为灰度图像。
例如,我们可以将上一步读取的图像转换为灰度图像:```matlabgray_img = rgb2gray(img);imshow(gray_img);```3. 图像二值化图像二值化是将灰度图像转换为二值图像的过程,其中只包含黑色和白色两种颜色。
在Matlab中,我们可以使用imbinarize函数将灰度图像二值化。
例如,我们可以将上一步得到的灰度图像二值化:```matlabbinary_img = imbinarize(gray_img);imshow(binary_img);```4. 图像平滑图像平滑是指去除图像中的噪声或细节,使得图像更加平滑和清晰。
在Matlab 中,我们可以使用imfilter函数对图像进行平滑处理。
例如,我们可以对上一步得到的二值图像进行平滑处理:```matlabsmooth_img = imfilter(binary_img, fspecial('average'));imshow(smooth_img);```5. 图像边缘检测图像边缘检测是指提取图像中物体边缘的过程,常用于目标检测和图像分割。
MATLAB实验二-绘图-参考答案-仅供参考

实验二:MATLAB 的绘图
实验目的:
1、掌握 MATLAB 的各种二维绘图; 2、掌握 MABLAB 的三维绘图; 3、了解 MABLAB 的 MATLAB 的绘图修饰。
实验内容
1、 2、 3、 1. 基本二维绘图函数 2. 颜色,线条的设置,绘制多图 3. 三维绘图 4. 图形标注,坐标,修饰等处理
0.1 x
sin(0.5 x) 和 y 0.2e 0.1x cos(0.5 x) 在区间
[0,2] 上的曲线图,添上图例、题头、坐标轴。
x=0:pi/20:2*pi; plot(x,0.2*exp(0.1*x)+sin(0.5*x),x,0.2*exp(0.1*x)+cos(0.5*x)) legend('0.2*exp(0.1*x)+sin(0.5*x)','0.2*exp(0.1*x)+cos(0.5*x)') xlabel('x'); ylabel('y'); title('两曲线示意图') 6、1)数据如下表所示: 数学系毕业学生去向 国家单位 私营企业 出国 读研 待业 比例(%) 10 40 5 20 25
实验要求
1、学生在实验操作过程中自己动手独立完成,1 人为 1 组。 2、完成实验报告:按照试验的每个题目的具体要求完成
实验数据记录及分析(命令与结果)
1、 运行该端程序,注释程序。 v=[‘-1’;’+1’]; t=[0:0.05:2*pi]; % t 的取值范围是 0 到 2pi,其步长为 0.05 plot(t,sin(t)); xlabel(‘time(0—2\pi)’); % 在坐标轴 x 上标注 time(0-2\pi) ylabel(‘value’); % 在坐标轴 y 标注 value text(pi/2,0.9,[‘\uparrowsin(\pi/2)=’,v(2,:)]); % 在 (pi/2, 0.9) 处用向上的箭头标注 sin(pi/2)=+1 text(pi*3/2,-0.9,[‘\downarrowsin(\pi*3/2)=’,v(1,:)]); text(0,0.6,[‘Date:’,date]); % 在(0,0.6)处显示 Date 当前日期 gtext( [‘Date:’,date]); % 通过鼠标箭头标注 Date 日期 2、运行该端程序(掌握 subplot,pause) ,注释程序 t=0:0.1:4*pi; y=exp(-0.1*t).*sin(t); clf % 清空绘图窗口 figure(1) % 新建一个绘图窗口, 标号为 1 subplot(2,2,1) % 将一个绘图窗口划分成一个 2*2 的子区域, 并按行从左至右 依次排号,1 表示第一个绘图子区域 stem(t,y) % 绘制火柴杆图 title('stem(t,y)') % 加标题为 stem(t,y) pause % 在当前完成的图像上停留,按任意键显示后面的命令 subplot(2,2,2) stairs(t,y) % 绘制阶梯图 title('stairs (t,y)') pause subplot(2,2,3)
信计01,郭巧真。10092002.第二次MATLAB数学实验报告

第二次MATLAB数学实验报告实验者:郭巧真系别:数学系班级:信计01学号:10092002 一:实验目的1:学会用MATLAB软件进行函数的数值运算。
如:求函数值、作函数图形、求数值函数的零点、求数值函数的最值、求数值函数的积分等;2:学会用MATLAB软件进行符号运算。
如:求极限、求导数、求积分、级数求和、泰勒展开、方程求根、微分方程组求解等符号运算;3:通过计算、画图等手段,加强对数学概念:极限、导数、积分的理解;4:了解数值积分理论,掌握几种计算复杂积分近似值的方法。
二:实验内容1:[1]题目:设 ,试在[-5,5]上求出函数的零点及极大、极小值。
[2]程序及其运行结果程序f=inline('exp(2*sin(x)).*cos(x)-exp(2*cos(x)).*sin(x)');c1=fzero(f,[-5,-4]) c2=fzero(f,[-4,-2]) c3=fzero(f,[-2,0.5]) c4=fzero(f,[0.5,0.8]) c5=fzero(f,[0.8,1.4])2sin 2cos ()cos sin x xf x e x e x =-c6=fzero(f,[2,4])[xmin1,fmim1]=fminbnd(f,-5,-4)[xmin2,fmim2]=fminbnd(f,0,1)[xmin3,fmim3]=fminbnd(f,2,3)ff=inline('-exp(2*sin(x)).*cos(x)+exp(2*cos(x) ).*sin(x)');[x1,y1]=fminbnd(ff,-1,0);xmax1=x1fmax1=-y1[x2,y2]=fminbnd(ff,1,2);xmax2=x2fmax2=-y2程序运行结果>>c1 =-4.9250c2 =-2.3562 c3 =0.2127 c4 =0.7854 c5 =1.3581 c6 =3.9270xmin1 =-4.0832 fmim1 =-3.2140 xmin2 =0.4737 fmim2 =-0.4885 xmin3 =2.2000 fmim3 =-3.2140 xmax1 =-0.6292 fmax1 =3.2140 xmax2 =1.0971fmax2 =0.4885>>(结合图像编程序)2: [1]题目:求方程 当 1、11、21时的根 [2]程序及其运行结果程序(1)s=1 程序f=inline('1/4*x^4+2*exp(x)-3*sin(x)-1'); x=fzero(f,[0,1])程序运行结果:结合下面的函数图形可以知道,此时没有零点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
disp(a);
n=input('请出入n=');
if n<=5&n>0
b=a(n,:);
disp(b);
else
c=a(end,:);
disp(c);
disp('输入超过行数!');
End
7、已知
(1)当 时,y的值是多少。
(2)当f(n)=1 2+2 3+3 4+…+n (n+1)时,y的值是多少。
y=((exp(0.3*a)-exp(-0.3*a))/2)*sin(a+0.3)+log((0.3+a)/2)
end
a=[-3.0:0.1:3.0]; %用顺序结构实现
y=((exp(0.3*a)-exp(-0.3*a))/2)*sin(a+0.3)+log((0.3+a)/2)
5、当n分别取100、1000、10000时,求下列各式的值;
b=fix((x-a*100)/10);
c=fix(x-a*100-b*10);
y=c*100+b*10+a;
Disp(y)
2、输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:
(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
答:degree=input('请输入成绩:');
请输入成绩:78
switch fix(degree/10)
case {0,1,2,3,4,5}
degree='E';
case {6}
degree='D';
case {7}
degree='C';
for i=1:4:x
m1=1/(i+4);
m=m+m1;
end
for j=3:4:x
n1=-1/(i+4);
n=n+n1;
end
sum =n+m;
disp(sum);
(2) ,要求用循环结构来实现。
n=input('请输入n=');
y=0;
for i=1:n
y=y+1/(4^i);
end
disp(y);
end
disp(b);
(2)1/2,1,3/2,2,5/2
_N=[1,2,3,4,5]; syms b
for i=1:5
b(1,i)=N(1,i)/2;
end
disp(b);
(3)1,1/2,1/3,1/4,1/5
N=[1,2,3,4,5]; syms b
for i=1:5
b(1,i)=1/N(1,i);
8、编写程序,建立向量N=[1,2,3,4,5],然后利用向量N产生下列向量:
(1)2,4,6,8,10
(2)1/2,1,3/2,2,5/2
(3)1,1/2,1/3,1/4,1/5
(4)1,1/4,1/6,1/9,1/25
(1)2,4,6,8,10
_N=[1,2,3,4,5];
for i=1:5
b(1,i)=2*N(1,i);
degree='E';
elseif 60<degree&°ree<69
degree='D';
elseif 70<degree&°ree<79
degree='C';
elseif 80<degree&°ree<89
degree='B';
else 90<degree&°ree<100
2.掌握利用for语句、while语句实现循环结构的方法;
3.熟悉利用向量运算来代替循环操作的方法并理解MATLAB程序设计的特点;
4.掌握定义和调用MATLAB函数的方法。
二、实验内容(ExperimentContent)
1、从键盘输入一个3位整数,将它反向输出。
x=input('请输入x:')
a=fix(x/100);
case {8}
degree='B';
case {9}
degree='A';
case {10}
degree='A';
otherwise
degree='error';
end
degree=degree
degree =
C
用if实现:
degree=input('请输入成绩:');
if 0<degree&°ree<59
degree='A';
end
degree
3、输入20个数,求其中最大数和最小数。要求分别用循环结构和调用MATLAB的max函数、min函数来实现。
答:(1)a=input('请输入二十个数');
max=a(1);
min=a(1);
for i=1:20;
if max<a(i);
max=a(i);
end
if min>a(i);
min=a(i);
end
end
max
min
(2)a=input('请输入二十个数');
max=max(a)
min=min(a)
4、 ,当a取-3.0、-2.9、-2.8、…、2.8、2.9、3.0时,求各点的函数值。要求分别用顺序结构和循环结构实现。
答:for a=-3.0:0.1:3.0 %用循环结构实现
答:function a=f1(n)
a=n+10*log(n^2+5)
y=f1(40)/(f1(30)+f1(20))
(2)当f(n)=1 2+2 3+3 4+…+n (n+1)时,y的值是多少。
function b=f2(n)
b=0;
for i=1:n
b=b+i*(i+1);
end
y=f2(40)/(f2(30)+f2(20))
end
disp(b);
(4)1,1/4,1/6,1/9,1/25
N=[1,2,3,4,5]; syms b
for i=1:5
b(1,i)=1/(N(1,i)^2);
end
disp(b);
9、当n分别取100、1000、10000时,求下列各式的值:
(1)
x=input('输入一个数字x:');
m=0;n=0;
(1)
n=input('请输入n=');
y=0;
for i=1:n
y=y+1/(i*i);
end
disp(y);
(2) ,要求用循环结构来实现。
n=input('请输入n=');
y=1;
for i=1:n
y=y*((2*i)*(2*i)/((2*i-1)*(2*i+1)));
end
disp(y);
6、建立5 6矩阵,要求输出矩阵第n行元素。当n值超过矩阵的行数时,自动转为输出矩阵最后一行元素,并给出出错信息。
三、个人心得(Personal Reflection)
通过这次上机,让我对matlab程序设计有了一个更深刻的认识,也让我发现了自己与其他同学在matlab虚席方面的差距。matlab像其他高级程序设计语言一样,算法灵活,功能强大。让我充分认识到算法的重要性。相信在今后的学习中,matlab一定会成为我的好帮手!
班级
Class
电信本二
姓名
Name
梅胜
学号
ID
1103050312
指导老师
Teacher
熊琼
课程名称
Course
MATLAB在信号处理的应用
编制日期
Date
实验名称
Title
实验三:MATLAB程序设计(1)
一、实验目的(Experiment Target)
1.掌握利用if语句、switch语句实现选择结构的方法;
