MATLAB第二次上机实验报告
MATLAB - 第二次试验结果

一
第
7、8 节课 张皓
指导老师
2.从键盘输入 a, b, c 的值,输出一元二次方程 ax 2 + bx + c = 0 的根。
%Ex02_02 function Ex02_02() disp(['一元二次方程是: a*x^2+b*x+c=0,请输入 各系数']); a=input('a='); b=input('b='); c=input('c='); roots([a b c])
price=input('请输入商品的价格='); zk=0.*(price<200)+... 0.03.*((price<500)&(price>=200))+... 0.05.*((price>=500)&(price<1000))+... 0.08.*((price>=1000)&(price<2500))+... 0.1.*((price>=2500)&(price<5000))+... 0.14.*(price>=5000); p=price*(1-zk); disp(['折扣=',num2str(zk*100),'%']) disp(['实际销售价钱=',num2str(p),'元'])
将它们的值互换后输出。 %Ex02_01 function exchange(x,y) %用来实现数据交换 disp(['交换前:x=',num2str(x),',y=',num2str(y)]); z=x; x=y; y=z; disp(['交换后:x=',num2str(x),',y=',num2str(y)]);
Matlab第二次实验报告
Matlab第二次实验报告实验目的:1、了解plot函数和subplot函数的基本用法和matlab绘图的基本原理。
2、了解图形的属性设置。
比如画图的颜色,画图采用的线性标识符等。
二:实验基本知识1:1. 单窗口单曲线绘图;2. 单窗口多曲线绘图;3. 单窗口多曲线分图绘图;4. 多窗口绘图;5.可任意设置颜色与线型;6.图形加注功能;7.fplot——绘制函数图函数;8.ezplot——符号函数的简易绘图函数9:subplot—将画图区域分块函数。
实验内容:将高数课本后的18个图画出上机练习程序第1——6图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1);x=-50:1:50;y=a.*x.^3;subplot(3,2,1);plot(x,y,'r');title('y=a*x^3');xlabel('X');ylabel('Y');x=0:1:50;y=sqrt(a.*x.^3);subplot(3,2,2);plot(x,y,x,-y,'r');title('y^2=a*x^3');xlabel('X');ylabel('Y');x=-3:0.1:3;y=exp(-x.^2);subplot(3,2,3);plot(x,y,'r');title('y=e^x^2');xlabel('X');ylabel('Y');x=-3:0.1:3;y=8*a^3./(x.^2+4*a^2);subplot(3,2,4);plot(x,y,'r');title('y=8*a^3./(x.^2+4*a^2)'); xlabel('X');ylabel('Y');x=0:0.01:5;y=sqrt(x.^3./(a*2.-x)); subplot(3,2,5);plot(x,y,x,-y,'r');title('y^2*(2a-x)=x^3'); xlabel('X');ylabel('Y');%t=-1:0.01:5;%x=3*a.*t./(1+t.^3);%y=3*a*t.^2./(1+t.^3);subplot(3,2,6);ezplot('x.^3+y.^3-3*3*x.*y'); %plot(x,y);title('x^3+y^3-3axy=0'); xlabel('X');ylabel('Y');输入a=3:显示结果第7——10图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1)t=0:0.1:2*pi;x=a*cos(t).^3;y=a*sin(t).^3;subplot(2,2,1);plot(x,y,'b')title('x^1.5+y^1.5=a^1.5'); xlabel('X');ylabel('Y');t=-2*pi:0.1:2*pi;x=a.*(t-sin(t));y=a.*(1-cos(t));subplot(2,2,2);plot(x,y,'b')title('°ÚÏß');xlabel('X');ylabel('Y');t=0:0.01:2*pi;p=a.*(1-cos(t));subplot(2,2,3);plot(p.*cos(t),p.*sin(t),'b'); title('p=a(1-cos£¨t£©)'); xlabel('X');ylabel('Y');t=0:0.01:2*pi;p=a.*t;subplot(2,2,4);plot(p.*cos(t),p.*sin(t),'b'); title('p=at');xlabel('X');ylabel('Y');输入a=1,第11题图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º') figure(1);t=-2*pi:pi/100:2*pi;p=exp(a.*t);plot(p.*cos(t),p.*sin(t)); title('p=e^at');xlabel('X');ylabel('Y');输入a=0.1,显示结果:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1)t=0.2*pi:pi/100:100*pi;p=a./t;plot(p.*cos(t),p.*sin(t));title('p=at');xlabel('X');ylabel('Y');输入a=1,显示结果:第13——14题图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º');figure(1);t=0:pi/100:2*pi;p=(a^2.*sin(2*t)).^0.5;subplot(1,2,1);plot(p.*cos(t),p.*sin(t),-p.*cos(t),-p.*sin(t),'g'); title('p^2=a^2*sin(2t)');xlabel('X');p=(a^2.*cos(2*t)).^0.5;subplot(1,2,2);plot(p.*cos(t),p.*sin(t),-p.*cos(t),-p.*sin(t),'g'); title('p^2=a^2*cos(2t)');xlabel('X');ylabel('Y');输入a=1,显示结果:第15-16题图:clear;clc;a=input('ÇëÊäÈëa:');figure(1)t=0:pi/200:pi;p=a.*cos(3*t);subplot(1,2,1);plot(p.*cos(t),p.*sin(t),'r--');title('p=a*cos(3t)');xlabel('X');p=a.*sin(3*t);subplot(1,2,2);plot(p.*cos(t),p.*sin(t),'r--'); title('p=a*sin(3t)');xlabel('X');ylabel('Y');输入a=1,显示结果:第17——18题图:clear;clc;a=input('ÇëÊäÈëa:');figure(1);t=-pi:pi/200:pi;subplot(1,2,1);p=a.*sin(2*t);plot(p.*cos(t),p.*sin(t),'k-.'); title('p=a*sin(2t)');xlabel('X');ylabel('Y');p=a.*cos(2*t);subplot(1,2,2);plot(p.*cos(t),p.*sin(t),'k-.');title('p=a*cos(2t)');xlabel('X');ylabel('Y');输入a=1,显示结果:实验心得:这次实验主要是学习matlab软件的二维绘图功能:matlab软件还有丰富的图形修饰功能,如改变线条的形式和颜色;除此之外其还可以以多种形式如在一个图形中显示多个函数图形,一个figure中显示多个坐标系,还有一个程序中就可以用多个figure一起来表示不同的函数……在画图过程中你可能因为角度的区间取值不一样,画出来的图形可能跟书本上给出的图形有很大的差异,但没关系,只要你思路是对的,区间可以自己慢慢改动知道跟书本上给出的图形想接近。
MATLAB上机实习报告

Matlab上机实习实习报告上周我们进行了本学期第二个实习部分-Matlab上机实习。
本次实习一星期,共做了四个部分。
分别是:一,Matlab基本操作;二,数值数组及其运算;三,Matlab图形绘制基础;四,SIMULINK仿真基础。
下面分别介绍个部分实习内容。
实习内容一Matlab基本操作1,实习目的:·掌握Matlab的启动和退出;·熟悉Matlab的命令窗口;·熟悉其他常用窗口和工具栏;2,对本软件有了初步认识后,接下来就开始指导书要求做一些训练了在指令窗中输入下面一段程序,功能是::画出衰减振荡曲线y=(e-t/3)sin3t及其他的包络线y0=(e-t/3)。
T的取值范围是[0,4 ]。
t=0:pi/50:4*pi;y0=exp(-t/3);y=exp(-t/3).*sin(3*t);plot(t,y,’-r’,t,y0,’:b’,t,-y0,’:b’)观察输出结果3,通过下拉菜单File:Preferences改变设置指令窗中的字体、颜色等。
如:数据显示格式的设置:Format short 小数点后四位(缺省情况),如显示p为3.1416。
Format long 小数点后十四位,如显示p为3.14159265358979。
Formant bank 小数点后两位,如显示p为3.14。
Format short e 小数点后四位科学记数法,如显示p为3.1416e+000。
Format long e 小数点后十四五位科学记数法,如显示p为3.141592653589793e+000。
在指令窗中键入y1=2*sin(0.3*pi)/(1+sqrt(5))然后利用回调指令计算y2=2*y1*cos(0.3*pi)/(1+sqrt(5))y1 =0.5000y2 =0.18164,了解软件中的一些功能和命令。
包括熟悉历史指令窗(Command History)、熟悉当前目录浏览器(Current Diretory)、熟悉工作空间浏览器(Workspace Browser),以及一些指令如: Clear 清除当前工作区中的所有变量Clc 清除指令窗中内容(未清除当前工作区中的变量)Clf 清除图形窗口Cd 设置当前工作目录Exit,quit 退出Matlab实习内容二数值数组及其运算1,实习目的·掌握一维数组的创建和寻访;·掌握二维数组的创建和寻访;·掌握的Matlab矩阵和数组的运算;·熟悉Matlab关系操作和逻辑操作;2,实习内容和步骤(1)常量与变量变量名区分字母大小写;变量名必须以字母打头,其后可以是任意字母,数字,或下划线的组合。
MATLAB上机实习报告

MATLAB上机实习报告Matlab上机实习实习报告十八周我们进行了本学期的第二次实习——Matlab上机实习。
本次实习一星期,共实习了五个部分。
分别是:一,Matlab基本操作;二,数值数组及其运算;三,Matlab图形绘制基础;四:SIMULINK仿真基础;五:句柄图形和图形用户界面制作。
下面分别介绍各部分内容:实习内容一Matlab基本操作1.实习目的:●掌握Matlab的启动和退出;●熟悉的命令窗口;●熟悉其它常用窗口和工具栏;2.输入一段程序:t=0:pi/50:4*pi;y0=exp(-t/3);y=exp(-t/3).*sin(3*t);plot(t,y,’-r’,t,y0,’:b’,t,-y0,’:b’)输出结果:3.了解文件中的一些功能和指令.例如:clear 清除当前工作区中所有变量clc 清除指令窗内容clf 清除图形窗口cd 设置当前工作目录exit,quit 退出MATLAB实习内容二数值数组及其运算1.实习目的●掌握一维数组的创建和寻访●掌握二维数组的创建和寻访●掌握MATLAB的矩阵和数组的运算●熟悉MATLAB关系操作和逻辑操作2.要求在闭区间[0,2pi]上产生50个等距采样的一维数组A,试用两种不同的指令实现。
要访问1到5元素如何实现;寻访7到最后一个元素如何实现;寻访第2.6.8个元素如何实现;寻访大于2的元素如何实现;给第3.5.9个元素赋值100如何实现:(1)>> A=linspace(0,2*pi,50);>> A=0:(50/49):50;>> AA =Columns 1 through 90 1.0204 2.0408 3.0612 4.0816 5.1020 6.1224 7.1429 8.1633Columns 10 through 189.1837 10.2041 11.2245 12.2449 13.2653 14.2857 15.3061 16.3265 17.3469Columns 19 through 2718.3673 19.3878 20.4082 21.4286 22.4490 23.4694 24.4898 25.5102 26.5306Columns 28 through 3627.5510 28.5714 29.5918 30.6122 31.6327 32.6531 33.6735 34.6939 35.7143Columns 37 through 4536.7347 37.7551 38.7755 39.7959 40.8163 41.8367 42.8571 43.8776 44.8980Columns 46 through 5045.9184 46.9388 47.9592 48.9796 50.0000(2)>> whos A>> A(1:5)ans =0 1.0204 2.0408 3.0612 4.0816(3)>> A(7:50)ans =Columns 1 through 86.12247.14298.16339.1837 10.2041 11.2245 12.2449 13.2653Columns 9 through 1614.2857 15.3061 16.3265 17.3469 18.3673 19.3878 20.4082 21.4286Columns 17 through 2422.4490 23.4694 24.4898 25.510226.5306 27.5510 28.5714 29.5918Columns 25 through 3230.6122 31.6327 32.6531 33.6735 34.6939 35.7143 36.7347 37.7551Columns 33 through 4038.7755 39.7959 40.8163 41.8367 42.8571 43.8776 44.8980 45.9184Columns 41 through 4446.9388 47.9592 48.9796 50.0000 (4)>> A([2 6 8])ans =1.0204 5.1020 7.1429(5)>> poison=find(A>2)poison =Columns 1 through 143 4 5 6 7 8 9 10 11 12 13 14 15 16Columns 15 through 2817 18 19 20 21 22 23 24 25 26 27 28 29 30Columns 29 through 4231 32 33 34 35 36 37 38 39 40 41 42 43 44Columns 43 through 4845 46 47 48 49 50 (6)>> A([3 5 9])=100(7)>> A=[1 2 3;4 5 6]A =1 2 34 5 63. 在指令窗口输入A=[1 2 3;4 5 6] 观察结果:分别用“全坐标”“单坐标”来寻访第2行第1列的元素,并说明二维数组元素的存储顺序。
MATLAB试验报告
实验二初试MATLAB一、实验目的1.熟悉视窗下的MATLAB环境;2.掌握MATLAB软件的基本使用方法;3.应用MATLAB命令建立系统数学模型;4.掌握利用MATLAB软件进行控制系统模型转换的方法。
二、实验属性(验证性)三、实验仪器设备及器材1.硬件要求基于IBM-PC或与之完全相兼容的带有中央处理器的奔腾及其以上机器至少64KB内存,推荐使用128KB以上内存。
2.软件要求安装有MATLAB,并且有Microsoft Word7.0(office95)以上支持的操作系统。
四、实验要求实验前要求熟悉相关MATLAB函数并预习实验的相关内容,写出预习报告。
实验时要按要求完成上机实验内容并且检验和调整程序,观察并记录仿真结果。
实验后写出实验报告,并对仿真实验结果进行分析、讨论。
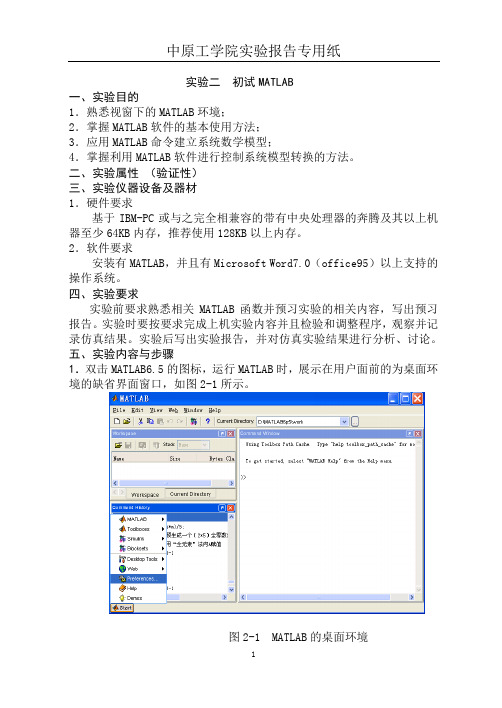
五、实验内容与步骤1.双击MATLAB6.5的图标,运行MATLAB时,展示在用户面前的为桌面环境的缺省界面窗口,如图2-1所示。
图2-1 MATLAB的桌面环境要求熟悉视窗下的MATLAB环境,分别观察和熟悉菜单项、工具栏、历史命令窗口、命令窗口、当前目录浏览器、工作空间浏览器、目录分类窗口、M文件编辑器/调试器、超文本帮助浏览器。
2.单击工具栏中帮助按钮(或者单击Help菜单中的MATLAB Help),打开MATLAB6.5的帮助系统,练习和熟悉MATLAB6.5的帮助系统的使用。
3.应用MATLAB命令编写相应M文件,建立图2-2系统的数学模型——闭环传递函数。
图2-2 调速系统g1=tf(1,[0.01,1]);g2=tf([0.17,1],[0.085,0]);g3=g1;g4=tf([0.15,1],[0.05,0]);g5=tf(70,[0.0067,1]);g6=tf(0.21,[0.15,1]);g7=tf(130,[1,0]);g11=feedback(g6,0.01*g4*g5*g1);g22=feedback(g1*g7,0.212);g33=feedback(g2*g3*g4*g5*g22,0.0044*g1);g=g1*g33Transfer function:2.321 s^3 + 261.2 s^2 + 3003 s + 9100--------------------------------------------------------------- 2.848e-013 s^8 + 1.564e-010 s^7 + 3.487e-008 s^6 + 4.042e-006 s^5 + 0.0002572 s^4 + 0.01876 s^3 + 1.266 s^2+ 13.21 s + 40.04实验三 基于MATLAB 的系统时域分析一、实验目的1.熟悉MATLAB 的各种绘图命令;2.掌握基于MATLAB 的控制系统时域分析方法。
MATLAB上机实验实验报告
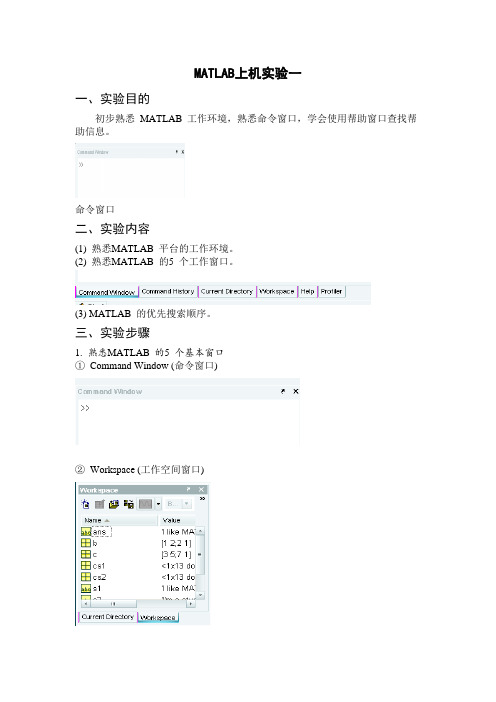
MATLAB上机实验一一、实验目的初步熟悉MATLAB 工作环境,熟悉命令窗口,学会使用帮助窗口查找帮助信息。
命令窗口二、实验内容(1) 熟悉MATLAB 平台的工作环境。
(2) 熟悉MATLAB 的5 个工作窗口。
(3) MATLAB 的优先搜索顺序。
三、实验步骤1. 熟悉MATLAB 的5 个基本窗口①Command Window (命令窗口)②Workspace (工作空间窗口)—③Command History (命令历史记录窗口)④Current Directory (当前目录窗口)⑤Help Window (帮助窗口)(1) 命令窗口(Command Window)。
在命令窗口中依次输入以下命令:>>x=1>> y=[1 2 34 5 67 8 9];>> z1=[1:10],z2=[1:2:5];>> w=linspace(1,10,10);>> t1=ones(3),t2=ones(1,3),t3=ones(3,1)>> t4=ones(3),t4=eye(4)x =1z1 =1 2 3 4 5 6 7 8 9 10 t1 =1 1 11 1 11 1t2 =1 1 1t3 =111t4 =1 1 11 1 11 1 1t4 =1 0 0 00 1 0 00 0 1 00 0 0 1思考题:①变量如何声明,变量名须遵守什么规则、是否区分大小写。
答:(1)变量声明1.局部变量每个函数都有自己的局部变量,这些变量只能在定义它的函数内部使用。
当函数运行时,局部变量保存在函数的工作空间中,一旦函数退出,这些局部变量将不复存在。
脚本(没有输入输出参数,由一系列MATLAB命令组成的M文件)没有单独的工作空间,只能共享调用者的工作空间。
当从命令行调用,脚本变量存在基本工作空间中;当从函数调用,脚本变量存在函数空间中。
2.全局变量在函数或基本工作空间内,用global声明的变量为全局变量。
MATLAB上机实验报告

Matlab上机实验报告实验二读入MATLAB下自带图像pout.tif1)利用亮度变换函数,调整图像亮度。
a)调整范围设定[0 1],[1 0],观测显示效果;b)调整范围设定[0.5 0.75],[1 0],观测显示效果。
解:a, I=imread('pout.tif');colormap;imshow(I);j=imadjust(I,[0 1],[1 0],1.5);figure;subimage(j);b, >> I=imread('pout.tif');colormap;imshow(I);j=imadjust(I,[0.5 0.75],[1 0],1.5);figure;subimage(j);2)利用对比度拉伸函数,压缩高值灰度(c值自行设定)。
解:I=imread('pout.tif');colormap;subplot(1,2,1);imshow(I);xlabel('a)原始图像');J=double(I);J=100*log(J+1);I=uint8(J);subplot(1,2,2);subimage(J);xlabel('b)非线性变换');3)利用直方图函数,生成并绘制图像直方图。
解:I=imread('pout.tif');subplot(1,2,1);imshow(I);title('原始图像');subplot(1,2,2);imhist(I);4)利用直方图修正函数,生成均衡化后的图像直方图(n值自定设定)。
解:I=imread('pout.tif');figure(1);subplot(1,2,1);imshow(I);xlabel('a)原始图像');J=histeq(I);figure(1);subplot(1,2,2);imshow(J);xlabel('b)直方图均衡');figure(2);imhist(I,100);figure(3);imhist(J,100);实验三1.运行例3、4,显示并分析输出结果,说明逆滤波和维纳滤波的区别。
第二次DSP上机实验报告 MATLAB实验报告

第二次DSP上机实验报告 MATLAB实验报告第二次DSP上机实验报告 MATLAB实验报告北京邮电大学信息与通信工程学院DSP--MATLAB实验报告实验名称:学生姓名:班级:班内序号:学号:日期:1.实验要求与目的要求:(1)用DFT分析频谱,得到高分辨率频谱清楚的谱线;(2)利用基2时间抽选的FFT算法,计算有限点的DFT,并与理论值相比较。
目的:掌握(a)用傅立叶变换进行信号分析时基本参数的选择。
(b)经过离散时间傅立叶变换(DTFT)和有限长度离散傅立叶变换(DFT)后信号频谱上的区别,前者DTFT时间域是离散信号,频率域还是连续的,而DFT在两个域中都是离散的。
(c)离散傅立叶变换的基本原理、特性,以及经典的快速算法(基2时间抽选法),体会快速算法的效率。
(d)获得一个高密度频谱和高分辨率频谱的概念和方法,建立频率分辨率和时间分辨率的概念,为将来进一步进行时频分析(例如小波)的学习和研究打下基础。
2关键算法分析第1页北京邮电大学信息与通信工程学院代码的重点是利用fft函数计算离散序列的DFT,难点是矩阵的加减乘除及乘方中所涉及的matlab语句的特点。
实验代码如下:(1)N=1000;n=(0:N-1);y=0.001*cos(0.45*n*pi)+sin(0.3*n*pi)-cos(0.302*n*pi-pi/4);y=0.001*cos(0.45*n*pi)+sin(0.3*n*pi)-cos(0.302*n*pi-pi/4);XK=fft(y,N);--fft函数两个参数分别是进行DFT变换的序列,及DFT 的长度subplot(3,1,1);stem(n,y);title("时域波形");xlabel("n");ylabel("y");subplot(3,1,2);stem(abs(XK),".");axis([0,500,0,600]);--限定x 轴与y轴的范围title("频域前500点波形");xlabel("k");ylabel("XK");subplot(3,1,3);stem(abs(XK),".");axis([800,900,0,600]);--x轴的范围很小,目的是能看到两条很近的谱线title("频域后500点部分波形");xlabel("k");ylabel("XK");(2)N=25;Q=0.9+j*0.3;n=(0:24);x=Q.^n;WN=exp(-j*2*pi/N);k=(0:24);WK=WN.^k;XK=(1-Q.^N)./(1-Q*WK);stem(XK);---理论值的计算XK1=fft(x,32);--32点基2时间抽选法的计算subplot(3,1,1);stem(n,x);title("时域波形");xlabel("n");ylabel("x");subplot(3,1,2);stem(XK);title("频域理论值");xlabel("k");ylabel("XK");subplot(3,1,3);stem(XK1);title("频域波形");xlabel("k");ylabel("XK1");第2页北京邮电大学信息与通信工程学院3.程序运行结果(1)(2)第3页北京邮电大学信息与通信工程学院4.问题分析这次实验的题目相对简单,编程过程中遇到的问题主要是矩阵的加减乘除及乘方运算所对应的matlab语句的规则和fft函数的使用,fft函数的使用方法通过help语句便可查得,其两个参数:第一个是指进行fft运算的序列,第二个值fft运算的长度。
MatLAB第二次实验

自动控制理论实 验 报 告姓 名 班 级 成 绩_______________学 号 日 期 合作者________________________________________________________________________________________________一、实验题目:利用MATLAB 求系统的的瞬态性能指标 二、实验目的:1、熟悉并掌握MatlAB 软件在工程计算中的应用。
2、求系统的的瞬态性能指标。
三、实验仪器:电脑、MatlAB 软件; 四、实验内容用impulse 函数求单位脉冲响应,step 求求单位阶跃响应。
程序:%a_1.mt=[0:0.01:0.8] %num_G=[50];tao=0;den_G=[0.05 1+50*tao 50];G1=tf(num_G ,den_G);tao=0.0125;den_G=[0.05 50*tao tao 50];G2=tf(num_G ,den_G); tao=0.025;den_G=[0.05 1+50*tao 50];G3=tf(num_G ,den_G); %[y1,T]=impulse(G1,t);[y1a,T]=step(G1,t); [y2,T]=impulse(G2,t);[y2a,T]=step(G2,t); [y3,T]=impulse(G3,t);[y3a,T]=step(G3,t); %subplot(1,2,1)plot(T,y1,'r-',T,y2,'g-',T,y3,'b-')legend('tao=0','tao=0.0125','tao=0.025') xlabel('t(sec)') ylabel('x(t)'); grid on;subplot(1,2,2)plot(T,y1a,'r-',T,y2a,'g-',T,y3a,'b-')legend('tao=0','tao=0.0125','tao=0.025') grid on;xlabel('t(sec)') ylabel('x(t)');二、用lsim函数求任意输入响应程序:%3_2.mclc;t=[0:0.01:1];u=sin(2*pi*t);%tao=0.025;num_G=[50];den_G=[0.05 1+50*tao 50];G=tf(num_G,den_G);%y=lsim(G,u,t);%plot(t,u,'r-',t,y,'g-',t,u','b',t,y','r',t,u'-y,'b-','linewidth',1)legend('u(t)','xo(t)','u(t)','xo(t)','e(t)=u-y')grid;xlabel('t(sec)')ylabel('x(t)');三、利用MATLAB求系统的的瞬态性能指标程序:close all;%t=0:0.001:1;%yss=1;dta=0.02;%num_G=[50];tao=0;den_G=[0.05 1+50*tao 50];G1=tf(num_G,den_G);tao=0.0125;den_G=[0.05 1+50*tao 50];G2=tf(num_G,den_G);tao=0.025;den_G=[0.05 1+50*tao 50];G3=tf(num_G,den_G);y1=step(G1,t);y2=step(G2,t);y3=step(G3,t);%r=1;while y1(r)<yss;r=r+1;endtr1=(r-1)*0.001;%[ymax,tp]=max(y1);tp1=(tp-1)*0.001;%mp1=(ymax-yss)/yss;%s=1001;while y1(s)>1-dta & y1(s)<1+dta;s=s-1;endts1=(s-1)*0.001;%τ=0.0125r=1;while y2(r)<yss;r=r+1;endtr2=(r-1)*0.001;[ymax,tp]=max(y2);tp2=(tp-1)*0.001;mp2=(ymax-yss)/yss;s=1001;while y2(s)>1-dta &y2(s)<1+dta;s=s-1;endts2=(s-1)*0.001;%τ=0.025r=1;while y3(r)<yss;r=r+1;endtr3=(r-1)*0.001;[ymax,tp]=max(y3);tp3=(tp-1)*0.001;mp3=(ymax-yss)/yss;s=1001;while y3(s)>1-dta & y3(s)<1+dta;s=s-1;endts3=(s-1)*0.001;%[tr1 tp1 mp1 ts1;tr2 tp2 mp2 ts2;tr3 tp3 mp3 ts3]结果:ans =0.0640 0.1050 0.3509 0.3530 -------系统10.0780 0.1160 0.1523 0.2500 -------系统20.1070 0.1410 0.0415 0.1880 -------系统3任课教师:。
MATLAB第二次上机实验报告

电子科技大学电子工程学院标准实验报告(实验)课程名称MATLAB与数值分析学生姓名:学号:指导教师:一、实验名称实验二 线性方程组求解和函数的数值逼近二、实验目的通过上机实验,使学生对病态问题、线性方程组求解和函数的数值逼近方法有一个初步的理解。
实验涉及的核心知识点:病态方程求解、矩阵分解和方程组求解、Lagrange 插值。
实验重点与难点:算法设计和MATLAB 编程三、实验内容1. 对高阶多项式()()()()()2011220k p x x x x x k ==---=-∏编程求下面方程的解()190p x x ε+=并绘图演示方程的解与扰动量ε的关系。
2. 对220n =,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组()n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
3. 对函数()21125f x x =+ []1,1x ∈-的Chebyshev 点()()21cos 21k k x n π⎛⎫-= ⎪ ⎪+⎝⎭,1,2,,1k n =+编程进行Lagrange 插值,并分析插值结果。
四、实验数据及结果分析1. 对高阶多项式()()()()()2011220k p x x x x x k ==---=-∏编程求下面方程的解()190p x x ε+=并绘图演示方程的解与扰动量ε的关系。
p=[1,-1]; for i=2:20 n=[1,-i];p=conv(p,n); % 求多项式乘积 endm=zeros(1,21); % m 的最高次幂为20,有21项 hold on x=1:20;d=[-1,0,0.1,0.5,1]; for i=1:5delt=d(i); m(2)=delt;y=(roots(p+m))'; % 求多项式的根 plot(x,y,'-o','color',[i/5,i/20,i/10]); endtitle('方程p(x)=0的解与扰动量delt 的关系')legend('delt=-1','delt=0','delt=0.1','delt=0.5','delt=1')24681012141618200102030405060方程p(x)=0的解与扰动量delt 的关系delt=-1delt=0delt=0.1delt=0.5delt=12.对220n =,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组()n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
同济大学Matlab实验报告(matlab应用实例)

实 验 报 告班级机械三班学号姓名- 1 -- 2 -画出衰减振荡曲线t ey t 3sin 3-=及其它的包络线30t e y -=,31t e y --=。
t 值的范围是');- 3 -4.通过M 脚本文件,画出下列分段函数所表示的曲面,用冷色调。
⎪⎪⎩⎪⎪⎨⎧-≤+≤+<->+=+-------15457.0117575.015457.0),(215.175.375.0216215.175.375.02112122212212122x x e x x ex x e x x p x x x x x x x x [X1,X2]=meshgrid(-1.5:0.1:1.5,-2:0.1:2);P=0.5457*exp(-0.75*X2.^2-3.75*X1.^2-1.5*X1).*(X1+X2>1)... + 0.7575*exp(-X2.^2-6*X1.^2).*(X1+X2>-1&X1+X2<=1)... + 0.5457*exp(-0.75*X2.^2-3.75*X1.^2+1.5*X1).*(X1+X2<=-1); surf(X1,X2,P);colormap(cool);colorbar('horiz'); shading flat;实验体会与总结通过此次实验,把课堂所学的理论知识运用到了实际中,了解了Matlab 的基本功能和用途。
经过4个实验基,本上掌握了Matlab 绘制曲线、曲面和构造分段函数的方法,相信此次实验会为以后Matlab 的学习奠定坚实的基础。
- 1 -实 验 报 告班级 机械三班 学号 姓名的值,输出一元二次方程2ax bx c ++=root方程形式:a*x^2+b*x+c=0 请输入各项系数: a=1 b=1 c=-1ans =-1.6180 0.6180exchange 请输入x :1 请输入y :0 x=0, y=1- 2 -',num2str(discount*100),'%']) 请输入商品价格:100折扣: 0%实际价格:100请输入商品价格:300 折扣: 3% 实际价格:291请输入商品价格:700 折扣: 5% 实际价格:665 请输入商品价格:1500 折扣: 8% 实际价格:1380请输入商品价格:3000折扣: 10% 实际价格:2700 请输入商品价格:6000 折扣: 14% 实际价格:5160- 3 -4.在.m 文件中编写程序实现,在同一坐标内,分别用不同线型和颜色绘制曲线0.510.2cos(4)y e x x π-=和0.522cos()y e x x π-=,标记两曲线交叉点,给出每条曲线的图注。
matlab上机实习报告

Matlab上机实习报告学院班级学号姓名指导老师:2011年12月25日第十六周我们进行了本学期第二个实习部分-Matlab上机实习。
时间过得很快,一周的时间转眼间就过去了。
通过实习我们对Matlab有了基本的了解。
本次实习一星期,共有五个部分。
分别是:一,Matlab基本操作;二,数值数组及其运算;三,Matlab图形绘制基础;四,SIMULINK仿真基础;五,句柄图形和图形用户界面制作。
实习内容一Matlab基本操作1,实习目的:·掌握Matlab的启动和退出;·熟悉Matlab的命令窗口;·熟悉其他常用窗口和工具栏;2,对本软件有了初步认识后,接下来就开始按照指导书要求做一些训练了在指令窗中输入下面一段程序,功能是::画出衰减振荡曲线y=(e-t/3)sin3t及其他的包络线y0=(e-t/3)。
T的取值范围是。
t=0:pi/50:4*pi;y0=exp(-t/3);y=exp(-t/3).*sin(3*t);plot(t,y,’-r’,t,y0,’:b’,t,-y0,’:b’)观察输出结果3,通过下拉菜单File:Preferences改变设置指令窗中的字体、颜色等。
如:数据显示格式的设置:Format short 小数点后四位(缺省情况),如显示p为3.1416。
Format long 小数点后十四位,如显示p为3.14159265358979。
Formant bank 小数点后两位,如显示p为3.14。
Format short e 小数点后四位科学记数法,如显示p为3.1416e+000。
Format long e 小数点后十四五位科学记数法,如显示p为3.141592653589793e+000。
在指令窗中键入y1=2*sin(0.3*pi)/(1+sqrt(5))然后利用回调指令计算y2=2*y1*cos(0.3*pi)/(1+sqrt(5))y1 =0.5000y2 =0.18164,了解软件中的一些功能和命令。
matlab实验报告2

第二次上机作业准备&要求:1、 运行课件第三章(课本第四章)讲过的例子,掌握Matlab 的流程控制语句、函数及脚本文件的编程、调试方法。
2、 本次作业(4~12题)要求全部写M 文件;3、 题目要求未明确要求写脚本文件还是函数文件的,学生自己决定是写脚本文件还是函数文件。
只要能够实现要求。
4、 列出第二章课堂上出现过的所有函数,知道它们的作用并试着调用这些函数。
作业:1. 继续完成第一次上机实验未完成的作业。
2. 分析脚本M 文件及函数M 文件的区别。
(1)脚本文件没有输入参数,也不返回输出参数,而函数文件可以带输入参数,也可以返回输出参数。
(2)脚本文件对MATLAB 工作空间中的变量进行操作,文件中所有命令的执行结果也完全返回到工作空间中,而函数文件中定义的变量为局部变量,当函数文件执行完毕时。
这些变量被清除。
(3)脚本文件可以直接运行。
在MATLAB 命令行窗口输入脚本文件的名字,就会顺序执行脚本文件中的命令。
而函数文件不能直接运行,要以函数调用的方式来调用。
3. 已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=7613870451A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=023352138B ,求下列表达式的值,并注意第(2)(3)小题表达式的结果有何特点:(1)B A 6+ 、I B A +-2(其中I 为单位阵);>> A+6*Bans =47 23 -1012 37 26-15 73 7>> A^2-B+Ians =-18 -217 1722 533 10921 867 526(2)A*B、A.*B、B*A、B.*A;>> A*Bans =14 14 16-10 51 21125 328 180>> A.*Bans =-8 15 40 35 24-9 122 0>> B*Aans =-11 0 -157 228 533 -1 28>> B.*Aans =-8 15 40 35 24-9 122 0(3)A/B、B\A、A./B、B.\A;A/Bans =1.2234 -0.92552.9787-0.9468 2.3511 -0.95744.6170 3.8723 13.8936>> B\Aans =-0.5106 -8.6170 -1.12770.7340 17.5745 1.8085-0.8830 -21.2128 0.4043>> A./Bans =-0.1250 1.6667 4.00000 1.4000 2.6667-1.0000 30.5000 Inf>> B.\Aans =-0.1250 1.6667 4.00000 1.4000 2.6667-1.0000 30.5000 Inf(4)[A, B]、[A([1 3],:);B^2]。
matlab数学实验报告

MATLAB数学实验报告指导老师:班级:小组成员:时间:201_/_/_Matlab第二次实验报告小组成员:1题目:实验四;MATLAB选择结构与应用实验目的:掌握if选择结构与程序流程控制;重点掌握break;return;pause语句的应用..问题:问题1:验证“哥德巴赫猜想”;即:任何一个正偶数n>=6均可表示为两个质数的和..要求编制一个函数程序;输入一个正偶数;返回两个质数的和..问题分析:由用户输入一个大于6的偶数;由input语句实现..由if判断语句判断是否输入的数据符合条件..再引用质数判断函数来找出两个质数;再向屏幕输出两个质数即可..编程:function z1;z2=geden;n=input'please input n'if n<6disp'data error';returnendif modn;2==0for i=2:n/2k=0;for j=2:sqrtiif modi;j==0k=k+1;endendfor j=2:sqrtn-iif modn-i;j==0k=k+1;endendif k==0fprintf'two numbers are'fprintf'%.0f;%.0f';i;n-ibreakendendend结果分析:如上图;用户输入了大于6的偶数返回两个质数5和31;通过不断试验;即可验证哥德巴赫猜想..纪录:if判断语句与for循环语句联合嵌套使用可使程序结构更加明晰;更快的解决问题..2题目:实验四;MATLAB选择结构与应用实验目的:用matlab联系生活实际;解决一些生活中常见的实际问题..问题:问题四:在一边长为1的四个顶点上各站有一个人;他们同时开始以等速顺时针沿跑道追逐下一人;在追击过程中;每个人时刻对准目标;试模拟追击路线;并讨论.. (1)四个人能否追到一起(2)若能追到一起;每个人跑过多少路程(3)追到一起所需要的时间设速率为1问题分析:由正方形的几何对称性和四个人运动的对称性可知;只需研究2个人的运动即可解决此问题..编程:hold onaxis0 1 0 1;a=0;0;b=0;1;k=0;dt=0.001;v=1;while k<10000d=norma-b;k=k+1;plota1;a2;'r.';'markersize';15;plotb1;b2;'b.';'markersize';15;fprintf'k=%.0f b%.3f;%.3f a%.3f;%.3f d=%.3f\n';k;b1;b2;a1;a2;da=a+b1-a1/d*dt;b2-a2/d*dt;b=b+b2-a2/d*dt;-b1-a1/d*dt;if d<=0.001breakendendfprintf'每个人所走的路程为:%.3f';k*v*dtfprintf'追到一起所需要的时间为%.3f';k*dt结果分析:上图为2人的模拟运动路线;有对称性可解决所提问题..-上图为运算过程和运算结果..四个人可以追到一起;走过的路程为1.003;时间也为1.003.纪录:此题利用正方形和运动的对称性可以简便运算..3题目:实验八;河流流量估计与数据插值目的:由一些测量数据经过计算处理;解决一些生活实际问题..问题:实验八上机练习题第三题:瑞士地图如图所示;为了算出他的国土面积;做以下测量;由西向东为x轴;由南向北为y轴;从西边界点到东边界点划分为若干区域;测出每个分点的南北边界点y1和y2;得到以下数据mm..已知比例尺1:2222;计算瑞士国土面积;精确值为41288平方公里..测量数据如下:x=7.0 10.5 13.0 17.5 34 40.5 44.5 48 56 61 68.5 76.5 80.5 91 96 101 104 106 111.5 118 123.5 136.5 142 146 150 157 158 ;y1=44 45 47 50 50 38 30 30 34 36 34 41 45 46 43 37 33 28 32 65 55 54 52 50 66 66 68;y2=44 59 70 72 93 100 110 110 110 117 118 116 118 118 121 124 121 121 121 122 116 83 81 82 86 85 68;问题分析:先由题目给定的数据作出瑞士地图的草图;再根据梯形法;使用trapz语句;来估算瑞士国土的面积..编程:x=7.0 10.5 13.0 17.5 34 40.5 44.5 48 56 61 68.5 76.5 80.5 91 96 101 104 106 111.5 118 123.5 136.5 142 146 150 157 158;y1=44 45 47 50 50 38 30 30 34 36 34 41 45 46 43 37 33 28 32 65 55 54 52 50 66 66 68;y2=44 59 70 72 93 100 110 110 110 117 118 116 118 118 121 124 121 121 121 122 116 83 81 82 86 85 68;plotx;y1;'r.';'markersize';15;plotx;y2;'r.';'markersize';15;axis0 160 0 135grid;hold ont=7:158;u1=splinex;y1;t;u2=splinex;y2;t;plott;u1plott;u2s1=trapzt;u1;s2=trapzt;u2;s=s2-s1*2222*22222/10000000;fprintf'S=%.0f';s结果分析:上图为由所给数据绘制出的瑞士地图..上图为运算结果;计算出瑞士的国土面积为42472平方公里;与准确值41288较为接近..纪录:使用梯形分割的方法;trapz语句可以方便计算不规则图形面积;但存在一定误差..4题目:实验七:圆周率的计算与数值积分目的:将数值积分最基本的原理应用于matlab之中;解决一些与积分有关的问题..问题:实验七上机练习题第一题:排洪量某河床的横断面如图7.3所示;为了计算最大排洪量;需要计算其断面积;试根据所给数据m用梯形法计算其断面积..问题分析:河床断面可近似分割成若干曲边梯形;近似处理把它们当做梯形来计算面积可使问题得到简化..编程:clc;clear;x=0 4 10 12 15 22 28 34 40;y=0 1 3 6 8 9 5 3 0;y1=10-y;plotx;y1;'k.';'markersize';15;axis0 40 0 10;grid;hold ont=0:40;u=splinex;y1;t;plott;u;s=40*10-trapzt;u;fprintf's=%.2f\n';s结果分析:上图为河床的断面图..上图为计算结果面积约为180.70平方米..纪录:使用梯形法计算不规则图形面积十分简便易行..5题目:实验七:圆周率的计算与数值积分目的:使用matlab计算解决一些有关积分的问题..问题:实验七上机练习题第三题:从地面发射一枚火箭;在最初100秒内记录其加速度如下;试求火箭在100秒时的速度..Ts=0 10 20 30 40 50 60 70 80 90 100;Am/s*s=30.00 31.63 33.44 35.47 37.75 40.33 43.29 46.69 50.67 54.01 57.23;问题分析:加速度为速度的微分;已知微分求积分;类似于面积问题;可使用梯形法来计算..编程:clc;clear;x=0 10 20 30 40 50 60 70 80 90 100;y=30.00 31.63 33.44 35.47 37.75 40.33 43.29 46.69 50.6754.01 57.23;plotx;y;'k.';'markersize';15;axis0 100 20 60;grid;hold ons=0:10:100;z=splinex;y;s;plots;y;v=trapzx;y;fprintf'v=%.2f\n';v结果分析:上图为加速度变化图..上图为计算结果;求得火箭在100秒时速度约为4168.95m/s..纪录:梯形法可以推广解决许多已知微分求积分的其他问题..6题目:实验七:圆周率的计算与数值积分目的:计算曲线弧长闭曲线周长可使用微元法;ds=sqrtdx^2+dy^2;在转化微积分问题;累加即可得到结果..问题:实验七上机练习题第三题:计算椭圆想x^2/4+y^2=1的周长;使结果具有五位有效数字..问题分析:编程:s=0;dx=0.001;for x=0:0.001:1.999dy=1.-x+0.001.^2/4-1.-x.^2/4;ds=sqrtdx.^2+dy.^2;s=s+ds;ends=4*s;fprintf'the length is'fprintf'%.4f';s结果分析:上图为计算结果;给定椭圆的周长约为9.1823五位有效数字纪录:计算不规则曲线弧长;可使用微元法;划分为若干小的看做直角三角形;利用勾股定理解决..7题目:实验九人口预测与数据拟合目的:掌握一些曲线拟合的方法;了解曲线拟合常用函数..问题:用电压U=10v的电池给电容器充电;t时刻的电压Vt=U-U-V0exp-t/τ;其中V0是电容器的初始电压;τ是充电常数;由所给数据确定V0和τ..t=0.5 1 2 3 4 5 7 9;V=3.64 3.52 2.74 1.78 1.34 1.01 0.57 0.37;问题分析:题中已给出函数关系式;为指数函数曲线拟合;将所给函数式整理可得标准的exp形函数曲线;从而便于解决..编程:t=0.5 1 2 3 4 5 7 9;V=3.64 3.52 2.74 1.78 1.34 1.01 0.57 0.37;plott;V;'k.';'markersize';20;axis0 10 0 4;grid;hold onpause0.5n=8;a=sumt1:n;b=sumt1:n.*t1:n;c=sumlogV1:n;d=sumt1:n.*logV1:n;A=n a;a b;B=c;d;p=invA*Bx=0:10;y=expp1+p2*x;plotx;y;'r-';'linewidth';2结果分析:上图为电压与时间关系图..上图为计算结果;即U-V0=1.4766;所以V0=8.5234;-1/τ=-0.2835;所以τ=3.5273纪录:曲线拟合的一个重难点是选择合适的曲线函数;才能提高拟合度..8题目:实验七圆周率的计算与数值积分目的:拓展圆周率的各种计算方法;掌握其他数值的近似计算方法..问题:实验七练习2:计算ln2的近似值精确到10的-5次方(1)利用级数展开的方法来计算(2)利用梯形法计算(3)利用抛物线法问题分析:级数展开;梯形法;抛物线法是常见的近似运算方法..编程:1级数展开的方法clc;clear;n=0;r=1;p=0;k=-1;while r>=0.1e-5n=n+1;k=k*-1;p1=p+k/n;r=absp1-p;fprintf'n=%.0f;p=%.10f\n';n;p1;p=p1;end2梯形法clc;clear;f=inline'1./x';x=1:0.1:2;y=fx;p=trapzx;y;fprintf'p=%.6f\n';p3抛物线法clc;clear;f=inline'1./x';a=1;b=2;n=1;z=quadf;a;b;fprintf'z=%.10f\n';z结果分析:(1)级数展开的方法(2)梯形法3抛物线法纪录:级数展开法;梯形法;抛物线法;计算近似值时应合理利用..梯形法和抛物线法不易提高精确度;级数展开法可以提高精确度..9题目:实验八河流流量估计与数据插值目的:掌握求插值多项式的方法;并利用此计算近似值..问题:已知y=fx的函数表如下x=0.40 0.55 0.65 0.80 0.90 1.05;y=0.41075 0.57815 0.69675 0.88811 1.02652 1.25382;求四次拉格朗日插值多项式;并由此求f0.596问题分析:利用所给函数表可计算拉格朗日插值多项式..编程:function p=lagrangex;yL=lengthx;a=onesL;for j=2:La:;j=a:;j-1.*x';endx=inva*y';for i=1:Lpi=xL-i+1;endx=0.40 0.55 0.65 0.80 0.90 1.05;y=0.41075 0.57815 0.69675 0.88811 1.02652 1.25382; plotx;y;'k.';'markersize';15axis0 2 0 2grid;hold on;p=lagrangex;y;t=0:0.1:1.5;u=polyvalp;t;plott;u;'r-'a=polyvalp;0.596结果分析:上图为所求结果;估算值和插值多项式..纪录:插值多项式是一项十分实用的方法..10题目:求正整数n的阶乘:p=1*2*3*…*n=n;并求出n=20时的结果目的:练习使用循环变量解决数学问题问题:对程序:Clear;clc;n=20;p=1;for i=1:np=p*i;fprintf’i=%.0f;p=%.0f\n’;i;pend进行修改使它:利用input命令对n惊醒赋值问题分析:题中给出程序中“n=20”修改;使用input命令;讲题中的输出命令放出循环之外..编程:clear;clc;n=input'n=';p=1;for i=1:np=p*i;endfprintf'i=%.0f;p=%.0f\n';i;p结果:n=20i=20;p=2432902008176640000>>结果分析:使用input命令可以实现人机对话;使用户自由赋值;输出语句在程序中的位置对输出的结果有很大的影响;在循环内部可以在计算过城中不断输出结果;在循环之外则可以控制只输出最后结果..11题目:对于数列{√2};n=1;2;…;求当其前n项和不超过1000时的n的值及合的大小..目的:运用条件循环解决文帝个项数的循环程序求解;问题:对程序:clear;clc;n=0;s=0;while s<=1000n=n+1;s=s+sqrtn;fprintf’n=%.0f;s=%.4f\n’;n;send问题分析:题中所给程序中的限制变量为上次循环之后的s;导致s超过上限后仍有一次的循环;若把循环变量改为这次的s;则可以避免这种情况的发生..编程:clear;clc;n=0;s=0;while s+sqrtn<=1000n=n+1;s=s+sqrtnfprintf'n=%.0f;s=%.4f\n';n;send结果:……s =970.8891n=128;s=970.8891s =982.2469n=129;s=982.2469s =993.6487n=130;s=993.6487>>结果分析:从结果中可以看出;最后一步为我们需要的答案;从这道题我们可以得出循环变量对一道编程的重要性..。
matlab第二次实验报告

《数学建模实验》上机实验报告班级:计算机35班学号:2130505099姓名:田博文【实验一】一上底面半径2米、下底面半径4米、高4米的圆台形水池内盛满了水,由池底一横截面积为0.001平方米的小孔放水。
求在任意时刻的水面高度和将水放空所需的时间。
一、问题分析:在dt很小一段时间内,水的流速v可以看成是不变的与水面高度h有关的函数,即v=gh2;在dt时间内流出的水量,可以近似的为一圆柱,对应的圆柱高为dh;由于容器下降的水量与流出的水量相等,令小孔面积为b,即dV=π2r dh=bvdt;可得dh与dt的关系为:dh=bvdt/(π2r);根据相似三角形原理可得,r=4-h/2;初始条件有;h(0)=4;为表示方便,引入变量L=4-h故r=2+L/2二、代码:T=0;for L=0:0.001:4-0.001 %选取积分微元为0.001,即dhV=0.001*pi*(2+(1/2*L))^2; %水面处的dV,b=0.001t=V/(sqrt(2*(4-L)*9.8)*0.001) %dV与dt关系T=T+t;plot(T,(4-L),'red'); hold onend三、运行结果:四、结论:在任意时刻的水面高度和将水放空所需的时间如上图红线所示,横轴为时间,纵轴为水面高度。
【实验二】有A、B、C三个场地,每一个场地都出产一定数量的原料,同时也消耗一定数量的产品,具体数据如下表所示。
已知制成每吨产品需要消耗3吨原料,A、B两地,A、C两地和B、C两地之间的距离分别为150千米、100千米和200千米,假设每万吨原料运输1千米的运费为5000元,每万吨产品运输1千米的运费为6000元。
由于地区条件的差异,在不同地区设厂的费用不同,由于条件的限制,在B处建厂的规模不能超过5万吨,问:在这三地如何建厂、规模建多大才能使得总费用最小?地点年产原料(万吨)年销产品(万吨)生产费用(万元/万吨)A 20 7 150B 16 13 120C 24 0 100一、问题分析:设nij为i地运往j地的原料量,mij为i地运往j地的产品量,设A地为1地,B 为2地,C地为3地。
MATLAB上机实习报告

Matlab上机实习实习报告十八周我们进行了本学期的第二次实习——Matlab上机实习。
本次实习一星期,共实习了五个部分。
分别是:一,Matlab基本操作;二,数值数组及其运算;三,Matlab图形绘制基础;四:SIMULINK仿真基础;五:句柄图形和图形用户界面制作。
下面分别介绍各部分内容:实习内容一Matlab基本操作1.实习目的:●掌握Matlab的启动和退出;●熟悉的命令窗口;●熟悉其它常用窗口和工具栏;2.输入一段程序:t=0:pi/50:4*pi;y0=exp(-t/3);y=exp(-t/3).*sin(3*t);plot(t,y,’-r’,t,y0,’:b’,t,-y0,’:b’)输出结果:3.了解文件中的一些功能和指令.例如:clear 清除当前工作区中所有变量clc 清除指令窗内容clf 清除图形窗口cd 设置当前工作目录exit,quit 退出MATLAB实习内容二数值数组及其运算1.实习目的●掌握一维数组的创建和寻访●掌握二维数组的创建和寻访●掌握MATLAB的矩阵和数组的运算●熟悉MATLAB关系操作和逻辑操作2.要求在闭区间[0,2pi]上产生50个等距采样的一维数组A,试用两种不同的指令实现。
要访问1到5元素如何实现;寻访7到最后一个元素如何实现;寻访第2.6.8个元素如何实现;寻访大于2的元素如何实现;给第3.5.9个元素赋值100如何实现:(1)>> A=linspace(0,2*pi,50);>> A=0:(50/49):50;>> AA =Columns 1 through 90 1.0204 2.0408 3.0612 4.0816 5.1020 6.1224 7.1429 8.1633Columns 10 through 189.1837 10.2041 11.2245 12.2449 13.2653 14.2857 15.3061 16.3265 17.3469Columns 19 through 2718.3673 19.3878 20.4082 21.4286 22.4490 23.4694 24.4898 25.5102 26.5306Columns 28 through 3627.5510 28.5714 29.5918 30.6122 31.6327 32.6531 33.6735 34.6939 35.7143Columns 37 through 4536.7347 37.7551 38.7755 39.7959 40.8163 41.8367 42.8571 43.8776 44.8980Columns 46 through 5045.9184 46.9388 47.9592 48.9796 50.0000(2)>> whos A>> A(1:5)ans =0 1.0204 2.0408 3.0612 4.0816(3)>> A(7:50)ans =Columns 1 through 86.12247.14298.16339.1837 10.2041 11.2245 12.2449 13.2653Columns 9 through 1614.2857 15.3061 16.3265 17.3469 18.3673 19.3878 20.4082 21.4286Columns 17 through 2422.4490 23.4694 24.4898 25.5102 26.5306 27.5510 28.5714 29.5918Columns 25 through 3230.6122 31.6327 32.6531 33.6735 34.6939 35.7143 36.7347 37.7551Columns 33 through 4038.7755 39.7959 40.8163 41.8367 42.8571 43.8776 44.8980 45.9184Columns 41 through 4446.9388 47.9592 48.9796 50.0000(4)>> A([2 6 8])ans =1.0204 5.1020 7.1429(5)>> poison=find(A>2)poison =Columns 1 through 143 4 5 6 7 8 9 10 11 12 13 14 15 16Columns 15 through 2817 18 19 20 21 22 23 24 25 26 27 28 29 30Columns 29 through 4231 32 33 34 35 36 37 38 39 40 41 42 43 44Columns 43 through 4845 46 47 48 49 50 (6)>> A([3 5 9])=100 (7)>> A=[1 2 3;4 5 6] A =1 2 3 4 5 63. 在指令窗口输入A=[1 2 3;4 5 6] 观察结果:分别用“全坐标”“单坐标”来寻访第2行第1列的元素,并说明二维数组元素的存储顺序。
matlab实验报告实验二

matlab实验报告实验二Matlab实验报告实验二引言Matlab是一种功能强大的数学软件,广泛应用于科学研究和工程实践中。
在实验二中,我们将探索Matlab的图像处理功能,并通过实际案例来展示其应用。
图像处理基础图像处理是指对图像进行数字化处理的过程,其目的是改善图像质量、提取有用信息或实现特定的应用需求。
在Matlab中,我们可以利用各种函数和工具箱来实现图像处理的各种任务,如图像增强、滤波、分割和特征提取等。
实验步骤1. 图像读取与显示在Matlab中,我们可以使用imread函数读取图像文件,并使用imshow函数将图像显示在屏幕上。
例如,我们可以读取一张名为"lena.jpg"的图像,并显示出来:```matlabimg = imread('lena.jpg');imshow(img);```2. 图像灰度化图像灰度化是将彩色图像转换为灰度图像的过程。
在Matlab中,我们可以使用rgb2gray函数将彩色图像转换为灰度图像。
例如,我们可以将上一步读取的图像转换为灰度图像:```matlabgray_img = rgb2gray(img);imshow(gray_img);```3. 图像二值化图像二值化是将灰度图像转换为二值图像的过程,其中只包含黑色和白色两种颜色。
在Matlab中,我们可以使用imbinarize函数将灰度图像二值化。
例如,我们可以将上一步得到的灰度图像二值化:```matlabbinary_img = imbinarize(gray_img);imshow(binary_img);```4. 图像平滑图像平滑是指去除图像中的噪声或细节,使得图像更加平滑和清晰。
在Matlab 中,我们可以使用imfilter函数对图像进行平滑处理。
例如,我们可以对上一步得到的二值图像进行平滑处理:```matlabsmooth_img = imfilter(binary_img, fspecial('average'));imshow(smooth_img);```5. 图像边缘检测图像边缘检测是指提取图像中物体边缘的过程,常用于目标检测和图像分割。
密码学 上机实验二报告(Matlab)

state = sub_bytes (state, inv_s_box);
% Display intermediate result if requested
ifverbose_mode
disp_hex ('After inv_sub_bytes : ', state)
end
% Extract the current round key (4 x 4 matrix) from the expanded key
程序清单:
程序代码如下所示:
functionplaintext = inv_cipher (ciphertext, w, inv_s_box, inv_poly_mat, vargin)
ifnargin > 0
% Switch the verbose mode flag on
verbose_mode = 1;
信息安全与密码学实验报告
序号
班级
姓名
学号
日期
时间
地点
1
信计1002
王志新
41064035
2012.12.10
18:00-21:00
实验楼102
指导教师:候书会
实验名称:
1、上机实验二
实验内容:
实验四现代对称密码学实验(验证性实验,4学时)
1、AES
A、实验内容:熟悉AES算法,并实现AES;
B、测试数据:任意,并验证加/解密结果。
else
% generate the column vector [16 13 10 7]'
col = (16 : -3 : 7)';
end
% Generate the row vector [0 4 8 12]
信计01,郭巧真。10092002.第二次MATLAB数学实验报告

第二次MATLAB数学实验报告实验者:郭巧真系别:数学系班级:信计01学号:10092002 一:实验目的1:学会用MATLAB软件进行函数的数值运算。
如:求函数值、作函数图形、求数值函数的零点、求数值函数的最值、求数值函数的积分等;2:学会用MATLAB软件进行符号运算。
如:求极限、求导数、求积分、级数求和、泰勒展开、方程求根、微分方程组求解等符号运算;3:通过计算、画图等手段,加强对数学概念:极限、导数、积分的理解;4:了解数值积分理论,掌握几种计算复杂积分近似值的方法。
二:实验内容1:[1]题目:设 ,试在[-5,5]上求出函数的零点及极大、极小值。
[2]程序及其运行结果程序f=inline('exp(2*sin(x)).*cos(x)-exp(2*cos(x)).*sin(x)');c1=fzero(f,[-5,-4]) c2=fzero(f,[-4,-2]) c3=fzero(f,[-2,0.5]) c4=fzero(f,[0.5,0.8]) c5=fzero(f,[0.8,1.4])2sin 2cos ()cos sin x xf x e x e x =-c6=fzero(f,[2,4])[xmin1,fmim1]=fminbnd(f,-5,-4)[xmin2,fmim2]=fminbnd(f,0,1)[xmin3,fmim3]=fminbnd(f,2,3)ff=inline('-exp(2*sin(x)).*cos(x)+exp(2*cos(x) ).*sin(x)');[x1,y1]=fminbnd(ff,-1,0);xmax1=x1fmax1=-y1[x2,y2]=fminbnd(ff,1,2);xmax2=x2fmax2=-y2程序运行结果>>c1 =-4.9250c2 =-2.3562 c3 =0.2127 c4 =0.7854 c5 =1.3581 c6 =3.9270xmin1 =-4.0832 fmim1 =-3.2140 xmin2 =0.4737 fmim2 =-0.4885 xmin3 =2.2000 fmim3 =-3.2140 xmax1 =-0.6292 fmax1 =3.2140 xmax2 =1.0971fmax2 =0.4885>>(结合图像编程序)2: [1]题目:求方程 当 1、11、21时的根 [2]程序及其运行结果程序(1)s=1 程序f=inline('1/4*x^4+2*exp(x)-3*sin(x)-1'); x=fzero(f,[0,1])程序运行结果:结合下面的函数图形可以知道,此时没有零点。
MATLAB上机实验实验报告

MATLAB上机实验实验报告实验名称:用MATLAB实现多项式拟合及插值一、实验目的:通过使用MATLAB实现多项式拟合及插值的方法,掌握MATLAB软件的基本操作和函数应用,进一步了解多项式拟合及插值的原理和实现过程。
二、实验原理:多项式拟合及插值是一种常见的数值分析方法,通过对已知数据点集合的拟合或插值,构造出一个多项式函数,用于近似表示原始数据。
1.多项式拟合:通过最小二乘法原理,选择一个合适的多项式函数,使得拟合出的多项式与已知数据点之间的误差最小。
拟合函数可以是一次、二次或高阶多项式。
2.多项式插值:通过已知数据点的横纵坐标值,构造一个满足这些点的多项式函数。
插值函数可以是一次、二次或高阶多项式。
插值函数经过每个已知数据点。
三、实验步骤:1.数据准备:选择一组已知数据,包含横纵坐标值。
数据点的个数可以根据具体情况自行确定。
2.多项式拟合:使用MATLAB中的polyfit函数,根据已知数据点进行多项式拟合。
根据拟合结果,获取拟合的多项式系数。
3.多项式插值:使用MATLAB中的polyfit函数,根据已知数据点进行多项式插值。
通过plot函数绘制原始数据点的散点图和插值多项式的曲线图。
可以尝试不同阶数的多项式插值。
4.结果分析:根据实验结果,分析拟合与插值的效果。
对比拟合结果与原始数据的误差大小,评估拟合的准确性。
对比插值结果与原始数据的差异,评估插值的精确度。
五、实验总结:通过这次实验,我熟练掌握了使用MATLAB实现多项式拟合及插值的方法。
在实验中,我了解了多项式拟合的原理,以及如何利用最小二乘法求取多项式拟合的系数。
同时,我也学会了如何使用MATLAB中的polyfit函数实现多项式拟合和插值。
通过实验结果的分析,我对拟合和插值的实际应用和效果有了更加深入的认识。
[1]MATLAB官方文档[2]高等数值分析教程以上为MATLAB上机实验实验报告,共计1200字。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子科技大学电子工程学院标准实验报告(实验)课程名称MATLAB与数值分析学生姓名:学号:指导教师:一、实验名称实验二 线性方程组求解和函数的数值逼近二、实验目的通过上机实验,使学生对病态问题、线性方程组求解和函数的数值逼近方法有一个初步的理解。
实验涉及的核心知识点:病态方程求解、矩阵分解和方程组求解、Lagrange 插值。
实验重点与难点:算法设计和MATLAB 编程三、实验内容1. 对高阶多项式()()()()()2011220k p x x x x x k ==---=-∏编程求下面方程的解()190p x x ε+=并绘图演示方程的解与扰动量ε的关系。
2. 对220n =,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组()n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
3. 对函数()21125f x x =+ []1,1x ∈-的Chebyshev 点()()21cos 21k k x n π⎛⎫-= ⎪ ⎪+⎝⎭,1,2,,1k n =+编程进行Lagrange 插值,并分析插值结果。
四、实验数据及结果分析1. 对高阶多项式()()()()()2011220k p x x x x x k ==---=-∏编程求下面方程的解()190p x x ε+=并绘图演示方程的解与扰动量ε的关系。
p=[1,-1]; for i=2:20 n=[1,-i];p=conv(p,n); % 求多项式乘积 endm=zeros(1,21); % m 的最高次幂为20,有21项 hold on x=1:20;d=[-1,0,0.1,0.5,1]; for i=1:5delt=d(i); m(2)=delt;y=(roots(p+m))'; % 求多项式的根 plot(x,y,'-o','color',[i/5,i/20,i/10]); endtitle('方程p(x)=0的解与扰动量delt 的关系')legend('delt=-1','delt=0','delt=0.1','delt=0.5','delt=1')24681012141618200102030405060方程p(x)=0的解与扰动量delt 的关系delt=-1delt=0delt=0.1delt=0.5delt=12.对220n =,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组()n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
for n=2:20 h=hilb(n);fprintf('\n\nn=%-10dcond(Hn)∞=%d',n,cond(h,'inf'))%cond :求矩阵范数X=1:n; b=h*X';[l u]=lu(h); %lu 分解x=u\(l\b); %利用lu 分解求线性其次方程组的根 x=x';fprintf('\n X ’=') for i=1:nfprintf('%-8.2f',X(i)) endfprintf('\n x ’=') for i=1:nfprintf('%-8.2f',x(i)) end end输出结果如下:n=2 cond(Hn)∞=2.700000e+001 X ’=1.00 2.00 x ’=1.00 2.00n=3 cond(Hn)∞=7.480000e+002 X ’=1.00 2.00 3.00 x ’=1.00 2.00 3.00n=4 cond(Hn)∞=2.837500e+004 X ’=1.00 2.00 3.00 4.00 x ’=1.00 2.00 3.00 4.00n=5 cond(Hn)∞=9.436560e+005X ’=1.00 2.00 3.00 4.00 5.00 x ’=1.00 2.00 3.00 4.00 5.00n=6 cond(Hn)∞=2.907028e+007X’=1.00 2.00 3.00 4.00 5.00 6.00x’=1.00 2.00 3.00 4.00 5.00 6.00n=7 cond(Hn)∞=9.851949e+008X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00x’=1.00 2.00 3.00 4.00 5.00 6.00 7.00n=8 cond(Hn)∞=3.387279e+010X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00x’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00n=9 cond(Hn)∞=1.099652e+012X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00x’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00n=10 cond(Hn)∞=3.535369e+013X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00x’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00n=11 cond(Hn)∞=1.229476e+015X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00x’=1.00 2.00 3.00 4.00 5.00 6.00 7.01 7.99 9.01 10.00 11.00 Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 2.692153e-017.> In cond at 48In Untitled7 at 3n=12 cond(Hn)∞=3.714499e+016X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00x’=1.00 2.00 3.00 4.00 5.03 5.87 7.34 7.38 9.72 9.48 11.22 11.96 Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 2.739612e-018.> In cond at 48In Untitled7 at 3n=13 cond(Hn)∞=3.650152e+017X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 13.00x’=1.00 2.00 3.00 4.06 4.50 8.73 -2.56 30.28 -25.84 46.13 -12.84 21.06 11.49 Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 2.448199e-019.> In cond at 48In Untitled7 at 3n=14 cond(Hn)∞=4.084635e+018Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 4.455948e-017.> In Untitled7 at 7X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 13.00 14.00x’=1.00 2.00 2.97 4.44 2.03 15.85 -1.01 -51.32 265.98-505.38 620.05 -421.65 185.67 -15.62 Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 1.024999e-018.> In cond at 48In Untitled7 at 3n=15 cond(Hn)∞=9.756108e+017X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 13.00 14.00 15.00x’=1.00 2.00 3.00 4.06 4.46 8.92 -2.48 25.12 0.44 -24.72 105.39 -105.03 95.41 -17.82 20.26 Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 9.721674e-019.> In cond at 48In Untitled7 at 3n=16 cond(Hn)∞=1.028629e+018Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 7.948463e-017.> In Untitled7 at 7X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 13.00 14.00 15.00 16.00x’=1.00 2.00 3.00 4.03 4.72 7.62 1.07 21.31 -5.46 0.61 73.43 -98.66 124.04 -53.40 38.17 12.52 Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 1.305919e-018.> In cond at 48In Untitled7 at 3n=17 cond(Hn)∞=1.038063e+018Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 1.798429e-016.> In Untitled7 at 7X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 13.00 14.00 15.00 16.00 17.00x’=1.00 2.00 2.99 4.10 4.13 10.17 -4.82 26.20 0.84 -8.49 39.86 6.13 2.66 5.80 41.30 -2.06 21.18 Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 1.076656e-019.> In cond at 48In Untitled7 at 3n=18 cond(Hn)∞=9.288018e+018Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 7.626119e-018.> In Untitled7 at 7X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 13.00 14.00 15.00 16.00 17.00 18.00x’=1.00 2.00 3.01 3.80 7.66 -12.72 83.21 -172.57 233.93-71.26 -41.44 -156.96 387.29 200.16 -1079.371233.14 -583.42 133.55 Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 1.592243e-019.> In cond at 48In Untitled7 at 3n=19 cond(Hn)∞=6.280448e+018Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 6.040620e-017.> In Untitled7 at 7X’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 13.00 14.00 15.00 16.00 17.00 18.00 19.00x’=1.00 2.00 3.00 3.87 6.72 -6.04 56.65 -114.38 178.86-96.36 43.65 -153.15 318.14 62.48 -704.50 954.66 -554.42 187.88 -0.06 Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 1.155429e-019. > In cond at 48 In Untitled7 at 3n=20 cond(Hn)∞=8.654794e+018Warning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 5.444860e-017. > In Untitled7 at 7X ’=1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 13.00 14.00 15.00 16.00 17.00 18.00 19.00 20.00x ’=1.00 2.00 2.98 4.33 2.17 19.67 -30.09 54.42 25.37 -114.26 123.00 54.10 -75.28 -8.20 77.82 -85.30 307.17 -360.30 236.32 -26.913. 对函数()21125f x x =+ []1,1x ∈-的Chebyshev 点()()21cos 21k k x n π⎛⎫-= ⎪ ⎪+⎝⎭,1,2,,1k n =+编程进行Lagrange 插值,并分析插值结果。
