c++课设报告《基于Dijkstra算法的最短路径问题求解》[1]
运筹学C语言实现Dijkstra算法求解图的最短路径

运筹学课程设计报告姓名:一、算法思想运用Dijkstra算法求解图的最短路径。
Dijkstra算法思想为:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S 表示,初始时S中只有一个源点,以后每求得一条最短路径, 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。
在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。
此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
二、算法流程或步骤Dijkstr算法具体步骤:(1)初始时,S只包含源点,即S=,v的距离为0。
U包含除v 外的其他顶点,U中顶点u距离为边上的权(若v与u有边)或)(若u不是v的出边邻接点)。
(2)从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
(3)以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u(u U)的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
(4)重复步骤(2)和(3)直到所有顶点都包含在S中。
三、算法源程序#include <iostream.h>int m;int n;float a[100][100];float dist[100];int prev[100];float MAX_V ALUE=10000;void dijkstra(){if(m<0||m>n) //当无顶点的情况return;bool *s=new bool[n+1];for(int i=0;i<n;i++){dist[i]=a[0][i]; //与源点相连的权值s[i]=false;if(dist[i]==MAX_V ALUE) //与源点无连接的顶点prev[i]=0; //设置对应权值为elseprev[i]=m; //与源点相连接的顶点设置为m }dist[m]=0;s[m]=true;for(int i1=0;i1<n;i1++){float temp=MAX_V ALUE;int u=m;for(int j=0;j<n;j++)if((!s[j])&&(dist[j]<temp))//与源点相连的顶点{u=j;temp=dist[j]; //设置temp成为与源点相连的顶点权值}s[u]=true;for(int j1=0;j1<n;j1++)if((!s[j1])&&(a[u][j1]<MAX_V ALUE)){float newdist=dist[u]+a[u][j1]; //算出与源点不直接相连的权值和if(newdist<dist[j1]){dist[j1]=newdist;prev[j1]=u;}}}}void path(){for(int i=0;i<n;i++)if(i!=m&&dist[i]<MAX_V ALUE){cout<<"由源到顶点"<<i<<"的最短路径为:(终点位置) "<<i;int temp=i;do{temp=prev[temp];cout<<" <-- "<<temp;}while(temp!=m);cout<<" (源位置)。
VC_实现基于Dijkstra算法的最短路径_部亚松

科技信息2008年第18期SCIENCE&TECHNOLOGYINFORMATION1.引言数据结构中图的运用极为广泛,通过图可以很好的分析交通及道路问题,利用图的最短路径可以计算两地间的最短距离,最小费用和最短时间。
由于最短路径问题在实际中常用于汽车导航系统以及各种应急系统等,这些系统要求在极短的时间内计算出最佳路线并且标示出来,这就决定了最短路径问题的实现应该是高效率的。
其实,无论是距离最短,时间最快还是费用最低,它们的核心算法都是最短路径算法。
[1-2]Dijkstra算法是求最短路径的经典算法,这里介绍用vc++实现Dijkstra算法,并提出图的另外一种存储结构,实现多条最短路径的查找。
2.数据结构定义为了方便查找最短路径,文中设计了如下数据结构来存储图中节点和边信息。
将图的节点作为对象,边作为节点的属性。
点对象Spoint的结构描述如下:classSPoint{public:CPointp;//该节点的坐标信息CArray<int,int>m_pre;//保存在最短路径中该节点的前一节点的ID号intnext;//在最短路径显示中起回溯作用CArray<double,double>m_cost;//保存点与点之间的关系};点的初始信息中m_pre为空,next为-1,在查找最短路径时修改其值方便输出最短路径;m_cost数组在编辑点间关系时修改,两个顶点之间有直接路径,点对象的m_cost数组中对应的权植为两个顶点的距离,否则,点对象的m_cost数组中对应的权植为无穷大。
无向图可以用一个Spoint数组来表示,如下:CArray<SPoint,SPoint>m_point;//保存点数组点标记从0开始。
3.Dijkstra算法3.1基本思想Dijkstra提出按路径长度递增顺序生成从源点ls到其他各顶点最短路径的算法,即:把图G中所有顶点分为两个顶点集,S为最短路径已确定的顶点集,V—S是最短路径尚未确定的顶点集,初始化时,只有源点ls的最短路径确定,故S中只含有源点ls,V—S包含除源点以外的其他顶点,在当前V—S顶点集中选择与源点ls距离最小的顶点加入S顶点集,直到S=V。
Dijkstra算法求最短路径

在交通网络中,常常会提出许多这样的问题:两地之间是否有路相通?在有多条通路的情况下,哪一条最近?哪一条花费最少等。
交通网络可以用带权图表示,图中顶点表示域镇,边表示两城之间的道路,边上权值可表示两城镇间的距离,交通费用或途中所需的时间等。
以上提出的问题就是带权图中求最短路径的问题,即求两个顶点间长度最短的路径。
最短路径问题的提法很多。
在这里仅讨论单源最短路径问题:即已知有向图(带权),我们希望找出从某个源点S∈V到G中其余各顶点的最短路径。
例如:下图(有向图G14),假定以v1为源点,则其它各顶点的最短路径如下表所示:图G14从有向图可看出,顶点v1到v4的路径有3条:(v1,v2,v4),(v1,v4),(v1,v3,v2,v4),其路径长度分别为:15,20和10。
因此v1到v4的最短路径为(v1,v3,v2,v4 )。
为了叙述方便,我们把路径上的开始点称为源点,路径的最后一个顶点为终点。
那么,如何求得给定有向图的单源最短路径呢?迪杰斯特拉(Dijkstra)提出按路径长度递增产生诸顶点的最短路径算法,称之为迪杰斯特拉算法。
迪杰斯特拉算法求最短路径的实现思想是:设有向图G=(V,E),其中,V={0,2,…,n-1},cost是表示G的邻接矩阵,G.arcs [i][j] .adj 表示有向边<i,j>的权。
若不存在有向边<i,j>,则G.arcs [i][j] .adj 的权为无穷大(这里取值为32767)。
设S是一个集合,其中的每个元素表示一个顶点,从源点到这些顶点的最短距离已经求出。
设顶点v0为源点,集合S的初态只包含顶点v0。
数组D记录从源点到其他各顶点当前的最短距离,其初值为D[i]= G.arcs[v0][i].adj ,i=1,…,n-1。
从S之外的顶点集合V-S 中选出一个顶点w,使D[w]的值最小。
于是从源点到达w只通过S 中的顶点,把w加入集合S中调整D中记录的从源点到V-S中每个顶点v的距离:从原来的D[v] 和D[w]+ G.arcs [w][v] .adj中选择较小的值作为新的D[v]。
毕业设计任务书-基于Dijkstra算法的最短路径搜索仿真

20年月日
系主任(签字):
20年月日
毕业设计任务书(理工)
学院
理学院
学生姓名
专业
软件技术
班级
0901
学号
指导教师
职称
讲师
课题名称
基于Dijkstra算法的最短路径搜索仿真
起止日期
自2012年02月20日起至20社会实际问题的课题
目的:通过课题设计的训练,使学生进一步复习、巩固和加深所学专业中的理论知识。从课题立项、理论研究、算法设计到程序编写和调试,使学生全面了解和掌握软件开发的基本方法和步骤。结合课题的设计,培养学生的自学能力,提高学生的动手能力、分析问题和解决问题的能力。
15周:整理打印各项文档;进行答辩前的准备,写出答辩提纲。
16周:论文答辩
五、主要参考文献资料:
[1]吕辉编著,由浅入深学C#:基础、进阶与必做300题,电子工业出版社,2011
[2]海杰尔斯伯格(Anders Hejlsberg),Mads Torgersen,Scott Wiltamuth等编著.C#程序设计语言.机械工业出版社2011
四、分阶段指导性进度计划:
1-2周:进行项目调研、搜集资料;熟悉开发工具;撰写开题报告。
3-5周:进行可行性分析、需求分析;确定系统的总体设计方案,完成总体设计报告书;开始文献翻译任务。
6-10周:完成系统详细设计、进行各模块的编码及单元测试;撰写论文,形成初稿。
11-14周:完成系统组装与各项测试;反复修改论文,形成论文定稿;完成文献翻译。
(1)采用图的邻接矩阵或邻接表实现最短路径问题中图的存储;
(2)采用Dijkstra算法求从某个源点到其余各顶点的最短路径;
基于最短路径优化问题Dijkstra算法程序的设计和实现

上式表示对某一个 j0 sn 1 , 有 Байду номын сангаас∞ < ∞ 这 ( 一 )若 , 意味着 '至 有一 条长度小于等于 3的路径且边权值之和 1 2 比长度小于等于 2的路径 的边权值之和小 , 于是我们选取边
设 c < ,> = E 是一 简单加权 图( 有向或无向图且 不合平行 边 )其 中 = , , { 。 … , , 并 约定 了所 有顶点 的一个 l , 次序 , 是起点 , 。 3 / 是终点. 用矩阵 A ( ) 将带权 图的权 = 值存放在矩 阵 A 中. 在加权 图中 , o(v, )r 0当且仅 权 J< > =>
个顶点 的最短路径权值之和; (的第 kk 0 l2…/ 从A・ ’ (= ,,, 1 , 一
收稿 日期 :0 7 1- 8 20 —0 0
作者简介 : 菊(97 )女 , 兰州人 , 岳秋 17一 , 甘肃 兰州城市学院计算机系教师 , 从事离散数学教学与研究.
引 言
求最短路径 以及最短距离 的问题在各个 领域都经 常用 到 ,九十年代公认 的求最短路径 的最好的算法是由 Ew.i . D— jsa提出的标 号算法 . kn 但是该算法采用手工求解 , 算量太 计 大, 尤其是规模较大 的问题 , 手工求解几乎是不可 能的. 随着 计算机科学技术的飞速发展 , 完全能够解决这类问题. 本文将 求解 EW.i s a . Dj t 算法的过程采用二维矩 阵存储数据 ,利用 kr
) 都不等于 0或 m,= , , , 一 . , s2 34 …n 1
其 中 a= , i r表示 至 有一条长度为 1 t 且边权值为 r 的 路 , m( = m是一个 比 r 大好 多倍 的数 , 这样就 不会影 响计算
Dijkstra最短路径算法实习报告

Dijkstra最短路径算法实习报告1.引言交通诱导系统的一个核心技术是最优路径的选择技术。
根据交通网络模型中各顶点和顶点之间的长度、时间或费用等属性权值,通过Dijkstra最短路径算法,解决有向图即交通网络模型中源点到其他顶点的最短路径问题。
2.建立交通道路网络模型交通道路网是路径诱导的基础和对象,首先需要建立交通道路网络模型。
交通道路网中的路段具有属性,且同一路段的两个方向其属性一般不完全相同,有向图能够很好地表达实际的交通网络,便于处理同路段两个方向的不同属性和单行线、交叉口转向限制等特殊交通属性。
综上,采用带权有向图来表达交通道路网。
其中,道路的终点和十字路口通常定义为一个顶点,两个顶点之间的道路定义为一条弧,每条弧根据其距离、途中所需时间或交通费用等定义为路段权值。
在有向图上,一条以i为起点,以j为终点的路径是一些顶点的序列,其中前一条弧的终点是后一条弧的起点,一条路线用一个有序的点集描述,而一条路线的长度、时间或者费用等属性为这条路径上的所有弧的权值之和。
这样便建立好了交通道路网络的模型。
3.最短路径算法迪杰斯特拉(Dijkstra)算法是经典路径诱导规划算法,Dijkstra算法是一个按路径长度递增的次序产生最短路径的算法,算法比较简单,容易实现,但计算量较大。
3.1算法分析:首先引进辅助向量D,它的每个分量D[i]表示当前所找到的从始点v0到每个终点vi的最短路径的长度。
为D[i]赋初值,若从v0到vi有弧,则D[i]为弧上的权值,否则置D[i]为∞。
则长度为D[j]=Min{D[i]|vi∈v}的路径就是从v0出发的长度最短的一条最短路径,此路径为v0—vj。
设下一条长度次短的路径的终点是vk,则这条路径或者是v0—vk,或者是v0—vj—vk。
它的长度是v0到vk弧上的权值或D[j]和vj到vk弧上权值之和。
3.2算法正确性证明:设s为为已切得最短路径的终点的集合,则有结论:下一条最短路径(设其终点为vx)或者是v0—vx,或者是中间只经过s中的顶点而最后到达顶点x的路径。
c语言基于_dijkstra_算法的最短路径求解_概述说明

c语言基于dijkstra 算法的最短路径求解概述说明1. 引言1.1 概述本篇长文将详细阐述基于Dijkstra算法的最短路径求解在C语言中的实现。
Dijkstra算法是一种用于求解图中最短路径问题的经典算法,通过计算从一个起始节点到其他所有节点的最短路径,并找出其中最短的一条路径。
该算法在交通网络、计算机网络、电力系统等领域有着广泛的应用。
1.2 文章结构本文共分为五个部分,每个部分都充分探讨了特定的主题。
以下是各部分内容概要:- 第一部分为引言,介绍了整篇文章的目标和结构。
- 第二部分将详细介绍Dijkstra算法的原理与应用,包括算法概述、最短路径问题定义与解决方法以及Dijkstra算法的核心思想与步骤。
- 第三部分着重介绍如何使用C语言实现Dijkstra算法来解决最短路径问题。
这包括程序设计思路和流程图、关键数据结构和变量说明以及算法关键代码实现解析与演示。
- 第四部分将通过具体案例进行实例分析,并展示程序运行结果,并对结果进行深入讨论与分析。
同时也会提供结果的可视化展示以及应用前景的展望。
- 最后一部分为结论与未来工作展望,总结回顾研究成果,并提出对相关研究方向与未来发展方向的建议。
1.3 目的本篇长文的主要目的在于全面介绍基于Dijkstra算法的最短路径求解在C语言中的实现方法,并通过实例分析来验证算法的准确性和有效性。
同时,本文还将探讨该算法在实际应用中可能面临的挑战,并提供进一步研究和发展方向上的建议。
希望读者能够通过本文更深入地了解Dijkstra算法以及其在最短路径求解中的应用,从而加深对该领域的理解并鼓励更多相关研究与创新。
2. Dijkstra算法的原理与应用2.1 Dijkstra算法概述Dijkstra算法是一种经典的图论算法,用于解决带权有向图中的最短路径问题。
该算法以一个起始节点作为出发点,通过不断更新节点间的最短路径长度和前驱节点,逐步确定到达其他节点的最短路径。
Dijkstra算法求最短路径C#版
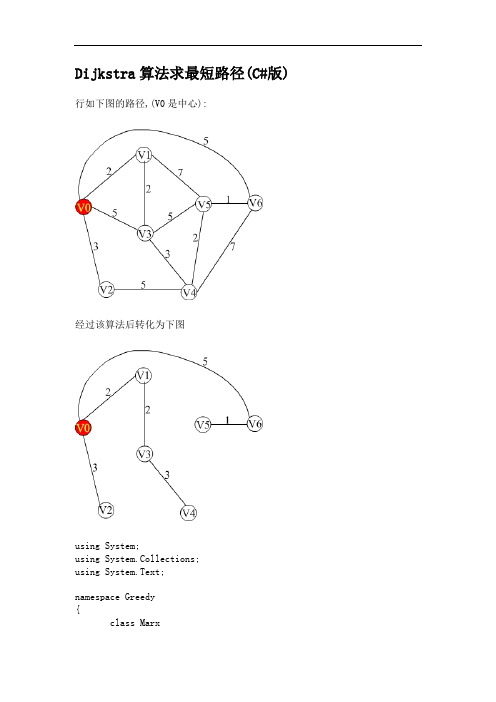
Dijkstra算法求最短路径(C#版) 行如下图的路径,(V0是中心):经过该算法后转化为下图using System;using System.Collections;using System.Text;namespace Greedy{class Marx{private int[] distance;private int row;private ArrayList ways = new ArrayList();public Marx(int n,params int[] d){this.row = n;distance = new int[row * row];for (int i = 0; i < row * row; i++){this.distance[i] =d[i];}for (int i = 0; i < this.row; i++) //有row 个点,则从中心到各点的路有row-1条{ArrayList w = new ArrayList();int j = 0;w.Add(j);ways.Add(w);}}//------------------------------public void Find_way(){ArrayList S = new ArrayList(1);ArrayList Sr = new ArrayList(1);int []Indexof_distance=new int[this.row];for(int i=0; i < row; i++){Indexof_distance[i]=i;}S.Add( Indexof_distance[0] );for (int i = 0; i < this.row; i++){Sr.Add( Indexof_distance[i] );}Sr.RemoveAt(0);int[] D = new int[this.row]; //存放中心点到每个点的距离//---------------以上已经初始化了,S和Sr(里边放的都是点的编号)------------------int Count = this.row - 1;while (Count>0){//假定中心点的编号是0的贪吃法求路径for (int i = 0; i < row; i++)D[i] = this.distance[i];int min_num = (int)Sr[0]; //距中心点的最小距离点编号foreach (int s in Sr){if (D[s] < D[min_num]) min_num = s;}//以上可以排序优化S.Add(min_num);Sr.Remove(min_num);//-----------把最新包含进来的点也加到路径中-------------((ArrayList)ways[min_num]).Add(min_num );//-----------------------------------------------foreach (int element in Sr){int position = element * (this.row) + min_num;bool exchange =false; //有交换标志if (D[element] < D[min_num] + this.distance[position])D[element] = D[element];else{D[element] =this.distance[position] + D[min_num];exchange = true;}//修改距离矩阵this.distance[element] =D[element];position = element *this.row;this.distance[position] =D[element];//修改路径---------------if (exchange == true){((ArrayList)ways[eleme nt]).Clear();foreach (int point in (ArrayList)ways[min_num])((ArrayList)wa ys[element]).Add(point);}}--Count;}}//----------------------------------------------------public void Display(){//------中心到各点的最短路径----------Console.WriteLine("中心到各点的最短路径如下: \n\n");int sum_d_index = 0;foreach(ArrayList mother in ways){foreach (int child in mother)Console.Write("V{0} -- ",child+1);Console.WriteLine(" 路径长{0}",distance[sum_d_index++]);}}}class MainEnterPoint{static void Main(string[] args){int r; //列数Console.Write("请输入点个数(含配送中心点): ");Int32.TryParse(Console.ReadLine(), out r);Console.WriteLine("各点分别为: \n");for (int i = 0; i < r; i++)Console.Write("V{0} ", i);Console.Write(" 假定第一个点是配送中心");Console.WriteLine("\n\n输入各点之间的距离(无通径的用个大整数表示)\n");int[] a = new int[r * r];int da;for (int i = 0; i < r; i++){for (int j = i + 1; j < r; j++){Console.Write("V{0} 到 V{1}的距离是: ",i,j);Int32.TryParse(Console.ReadLin e(), out da);a[i * r + j] = da;Console.WriteLine();}}//----完善距离矩阵(距离矩阵其实可以是个上三角矩阵,//----但为了处理方便,还是将其完整成一个对称阵)-----------for (int i = 0; i < r; i++){for (int j = 0; j < r; j++){if (i == j){a[i * r + j] = 0;}a[j * r + i] = a[i * r + j];}}Marx m=new Marx(r,a);Console.WriteLine();m.Find_way();m.Display();}}}//该程序不但能够算出从中心到各点的最短路径距离,而且把路径也保存了下来.车辆调度模型一、基于配送网络和调运优先准则的物流敏捷调动优先技术1. 支持物流敏捷调动优化的基础信息描述(1)配送中心货物库存信息配送中心(或调运中心,Depot)的货物库存信息由以下三元数组A 表示:A=( i, gi, qi )其中,i表示货物编码,i=1,2,3,…, 简记为i∈I;gi表示货物i的规格(单位重量、体积等),并假定所有货物换算为同一规格;qi货物i的库存数量。
C++用Dijkstra(迪杰斯特拉)算法求最短路径

C++⽤Dijkstra(迪杰斯特拉)算法求最短路径算法介绍迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此⼜叫狄克斯特拉算法。
是从⼀个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。
迪杰斯特拉算法主要特点是以起始点为中⼼向外层层扩展,直到扩展到终点为⽌。
Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
算法思想按路径长度递增次序产⽣算法: 把顶点集合V分成两组: (1)S:已求出的顶点的集合(初始时只含有源点V0) (2)V-S=T:尚未确定的顶点集合 将T中顶点按递增的次序加⼊到S中,保证: (1)从源点V0到S中其他各顶点的长度都不⼤于从V0到T中任何顶点的最短路径长度 (2)每个顶点对应⼀个距离值 S中顶点:从V0到此顶点的长度 T中顶点:从V0到此顶点的只包括S中顶点作中间顶点的最短路径长度 依据:可以证明V0到T中顶点Vk的,或是从V0到Vk的直接路径的权值;或是从V0经S中顶点到Vk的路径权值之和应⽤举例(1)题⽬:编写⼀个校园导游程序,为来访的客⼈提供各种信息查询服务。
主要功能:1.设计学校的校园平⾯图,所含景点不少于10个:顶点表⽰景点,边表⽰路径等; 2.为客⼈提供图中任意景点相关信息的查询; 3.为客⼈提供图中任意景点的问路查询,即查询⼈以景点间的⼀条最短路径。
要求:1.设计⼀个主界⾯; 2.设计功能菜单,供⽤户选择 3.有⼀定的实⽤性。
(2)设计思路: 1、该题主要有算法思路以及程序的逻辑思路,⾸先从逻辑思路讲,进⼊程序,⾸先设计⼀个主菜单,选项有景点信息查询,最短路径查询以及显⽰景点的平⾯视图三个⼦菜单,然后根据⽤户的输⼊选择的⼦菜单前的编号,分进⼊不同的⼦菜单;该功能是由if….else if…. 语句实现。
在景点信息查询和最短路径查询⼦菜单下还有⼆级⼦菜 单,都是列出所有景点并在前⾯编号,查询景点信息时,输⼊景点前⾯的编号即可,查询最短路径时,先输⼊起点的编号,再输⼊终点的编号。
c课设报告基于dijkstra算法的最短路径问题求解

c课设报告基于d i j k s t r a算法的最短路径问题求解Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#课程设计任务书1 需求分析Dijkstra 算法是由荷兰计算机科学家艾兹格·迪科斯彻发现的。
算法解决的是有向图中最短路径问题。
举例来说,如果图中的顶点表示城市,而边上的权重表示着城市间开车行经的距离。
Dijkstra 算法可以用来找到两个城市之间的最短路径。
Dijkstra 算法的输入包含了一个有权重的有向图G ,以及G 中的一个来源顶点S 。
我们以V 表示G 中所有顶点的集合。
图中的每一个边,都是两个顶点所形成的有序元素对。
(u ,v )表示从顶点u 到v 有路径相连。
假设E 为所有边的集合,而边的权重则由权重函数w :E → [0, ∞]定义。
因此,w (u ,v )就是从顶点u 到顶点v 的非负花费值(cost)。
边的花费可以想像成两个顶点之间的距离。
任两点间路径的花费值,就是该路径上所有边的花费值总和。
已知有V 中有顶点s 及t ,Dijkstra 算法可以找到s 到t 的最低花费路径. 最短路径)。
这个算法也可以在一个图中,找到从一个顶点s 到任何其他顶点的最短路径。
1.如果将交通网络化成带权图,假如用顶点表示城市,边表示公路段,则由这些顶点和边组成的图可表示沟通个城市的公路图,边的权用以表示两个城市之间的距离或者表示走过这段公路所需要的时间或通过这段路的难易程度等。
作为司机和乘汽车的人,自然会关心如下两个问题:(1)从甲地到乙地是否有公路(2)从甲地到乙地有几条公路,哪条公路最短或花费的代价最小 这就是我们要讨论的最短路径问题。
2.迪杰斯特拉提出的一个求最短路径的算法。
其基本思想是:按路径长度递增的顺序,逐个产生各最短路径。
3.首先引进辅助向量dist[],它的每一个分量dist[i]表示已经找到的且从源点0v 到每一个终点i v 的当前最短路径长度。
cc++图的最短路径Dijkstra(迪杰斯特拉)算法

cc++图的最短路径Dijkstra(迪杰斯特拉)算法c/c++ 图的最短路径 Dijkstra(迪杰斯特拉)算法图的最短路径的概念:⼀位旅客要从城市A到城市B,他希望选择⼀条途中中转次数最少的路线。
假设途中每⼀站都需要换车,则这个问题反映到图上就是要找⼀条从顶点A到B所含边的数量最少的路径。
我们只需从顶点A出发对图作⼴度优先遍历,⼀旦遇到顶点B就终⽌。
由此所得⼴度优先⽣成树上,从根顶点A到顶点B的路径就是中转次数最少的路径。
但是这只是⼀类最简单的图的最短路径问题。
有时,对于旅客来说,可能更关⼼的是节省交通费⽤;⽽对于司机来说,⾥程和速度则是他们感兴趣的的信息。
为了在图上表⽰相关信息,可对边赋以权值,权值可以表⽰两个城市之间的距离,或途中所需时间,或交通费⽤等等。
此时路径长度的度量就不再是路径上边的数⽬,⽽是路径上边权值之和。
实现思路:创建2个辅助int*数组dist path,1个bool数组sdist 存放⽬标顶点到每个顶点的最短距离path 存放⽬标顶点到每个顶点的路径s 被查找过的顶点设置为true,否则为false图为下图1,假设⽬标顶点为A,先从A开始找到各个顶点的权值,A B C D Edist010⽆穷⼤30100path-10000s true false false false falsepath含义:⽐如path[1]=0,就代表从下标为0的顶点(A顶点)到B顶点2,从dist⾥找到s为false的最⼩值,也就是dist[1]的值10,下标1说明是顶点B,再从B开始找到各个顶点的权值,更新dist和path,并设置B 为trueA B C D Edist010*******path-10100s true true false false false3,从dist⾥找到s为false最⼩值,也就是dist[3]的值30,下标3说明是顶点D,再从D开始找到各个顶点的权值,更新dist和path,并设置D为trueA B C D Edist010503090path-10303s true true false true false4,从dist⾥找到s为false最⼩值,也就是dist[2]的值50,下标2说明是顶点C,再从C开始找到各个顶点的权值,更新dist和path,并设置C为trueA B C D Edist010503060path-10302A B C D Es true true true true false5,从dist⾥找到s为false最⼩值,也就是dist[4]的值60,下标4说明是顶点E,再从E开始找到各个顶点的权值,更新dist和path,并设置E为trueA B C D Edist010503060path-10302s true true true true true下⾯两幅图可以帮助理解dijkstra.h#ifndef __mixspantree__#define __mixspantree__#include <stdio.h>#include <malloc.h>#include <assert.h>#include <memory.h>#include <stdlib.h>#include <stdbool.h>#define Default_vertex_size 20#define T char//dai biao ding dian de lei xing#define E int#define MAX_COST 0x7FFFFFFFtypedef struct GraphMtx{int MaxVertices;//zui da ding dian shu liang]int NumVertices;//shi ji ding dian shu liangint NumEdges;//bian de shu lianT* VerticesList;//ding dian listint** Edge;//bian de lian jie xin xi, bu shi 0 jiu shi 1}GraphMtx;//chu shi hua tuvoid init_graph(GraphMtx* gm);//打印⼆维数组void show_graph(GraphMtx* gm);//插⼊顶点void insert_vertex(GraphMtx* gm, T v);//添加顶点间的线void insert_edge(GraphMtx* gm, T v1, T v2, E cost);//最短路径void short_path(GraphMtx* g,T v,E* dist, int* path);#endifdijkstra.c#include "dijkstra.h"void init_graph(GraphMtx* gm){gm->MaxVertices = Default_vertex_size;gm->NumEdges = gm->NumVertices = 0;//kai pi ding dian de nei cun kong jiangm->VerticesList = (T*)malloc(sizeof(T) * (gm->MaxVertices));assert(NULL != gm->VerticesList);//创建⼆维数组//让⼀个int的⼆级指针,指向⼀个有8个int⼀级指针的数组//开辟⼀个能存放gm->MaxVertices个int⼀级指针的内存空间gm->Edge = (int**)malloc(sizeof(int*) * (gm->MaxVertices));assert(NULL != gm->Edge);//开辟gm->MaxVertices组,能存放gm->MaxVertices个int的内存空间 for(int i = 0; i < gm->MaxVertices; ++i){gm->Edge[i] = (int*)malloc(sizeof(int) * gm->MaxVertices);}//初始化⼆维数组//让每个顶点之间的边的关系都为不相连的for(int i = 0; i < gm->MaxVertices; ++i){for(int j = 0; j < gm->MaxVertices; ++j){if(i == j)gm->Edge[i][j] = 0;elsegm->Edge[i][j] = MAX_COST;}}}//打印⼆维数组void show_graph(GraphMtx* gm){printf(" ");for(int i = 0; i < gm->NumVertices; ++i){printf("%3c ", gm->VerticesList[i]);}printf("\n");for(int i = 0; i < gm->NumVertices; ++i){//在⾏⾸,打印出顶点的名字printf("%c:", gm->VerticesList[i]);for(int j = 0; j < gm->NumVertices; ++j){if(gm->Edge[i][j] == MAX_COST){printf("%3c ", '*');}else{printf("%3d ", gm->Edge[i][j]);}}printf("\n");}printf("\n");}//插⼊顶点void insert_vertex(GraphMtx* gm, T v){//顶点空间已满,不能再插⼊顶点了if(gm->NumVertices >= gm->MaxVertices){return;}gm->VerticesList[gm->NumVertices++] = v;}int getVertexIndex(GraphMtx* gm, T v){for(int i = 0; i < gm->NumVertices; ++i){if(gm->VerticesList[i] == v)return i;}return -1;}//添加顶点间的线void insert_edge(GraphMtx* gm, T v1, T v2, E cost){if(v1 == v2)return;//查找2个顶点的下标int j = getVertexIndex(gm, v1);int k = getVertexIndex(gm, v2);//说明找到顶点了,并且点之间还没有线if(j != -1 && k != -1 ){//因为是有⽅向,所以更新1个值gm->Edge[j][k] = cost;//边数加⼀gm->NumEdges++;}}//取得2个顶点之间的权值E getWeight(GraphMtx* g, int v1, int v2){if(v1 == -1 || v2 == -1) return MAX_COST;return g->Edge[v1][v2];}//最短路径void short_path(GraphMtx* g,T v,E* dist, int* path){int n = g->NumVertices;bool* s = (bool*)malloc(sizeof(bool) * n);assert(NULL != s);int vi = getVertexIndex(g, v);for(int i = 0; i < n; ++i){//获得各个顶点与⽬标顶点之间的权值dist[i] = getWeight(g, vi, i);s[i] = false;if(i != vi && dist[i] < MAX_COST){path[i] = vi;}else{path[i] = -1;}}s[vi] = true;int min;int w;for(int i = 0; i < n - 1; ++i){min = MAX_COST;//u为最短路径顶点的下标int u = vi;for(int j = 0; j < n; ++j){if(!s[j] && dist[j] < min){u = j;min = dist[j];}}//把u加⼊到s集合s[u] = true;//更新下⼀个点到所有点的权值for(int k = 0; k < n; ++k){w = getWeight(g, u, k);if(!s[k] && w < MAX_COST && dist[u] + w < dist[k]){ dist[k] = dist[u] + w;path[k] = u;}}}}dijkstramain.c#include "dijkstra.h"int main(){GraphMtx gm;//初始化图init_graph(&gm);//插⼊顶点insert_vertex(&gm, 'A');insert_vertex(&gm, 'B');insert_vertex(&gm, 'C');insert_vertex(&gm, 'D');insert_vertex(&gm, 'E');//添加连线insert_edge(&gm, 'A', 'B', 10);insert_edge(&gm, 'A', 'D', 30);insert_edge(&gm, 'A', 'E', 100);insert_edge(&gm, 'B', 'C', 50);insert_edge(&gm, 'C', 'E', 10);insert_edge(&gm, 'D', 'C', 20);insert_edge(&gm, 'D', 'E', 60);//打印图show_graph(&gm);int n = gm.NumVertices;E* dist = (E*)malloc(sizeof(E) * n);int* path = (int*)malloc(sizeof(int) * n);assert(NULL != dist && NULL != path);//最短路径short_path(&gm, 'A', dist, path);}编译⽅法:gcc -g dijkstra.c dijkstramain.c 执⾏结果如下图:。
数据结构课程设计报告Dijkstra算法求最短路径

3.5递归函数的应用---------------------------------------------------------------------------10
}MGrph;//邻接矩阵表示的图
3.1.1顶点的定义typedef char VertexType;//定义图的顶点为字符型 顶点的最大个数25
3.1.2ArcCell arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];二维数组用于存放邻接矩阵,每个位置代表的值为图中的权值,其余用无穷大3000表示。
}ArcCell;
typedef struct{
VertexType vexs[MAX_VERTEX_NUM];//一维数组,存储顶点
ArcCell arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];//邻接矩阵 :二维数组,存储边和弧
int vexnum,arcnum;//图的当前顶点数和弧数
2.原始数据的输入格式
2.1建图:2.1.1数字
2.2显示:2.2.1数字+逗号+数字+回车
2.2.2字母+回车
3.实现功能
3.1建立有向图
3.2显示存储的有向图
3.3显示从顶点到其他各个顶点的最短路径和是否存在路径
4.测试用例
4.1正确数据:输入顶点;边值信息
输出结果:最短路径是否存在,存在的情况最短路径是多少,其次是不存在。
第1章问题分析与任务定义
1、课程设计题目:
基于Dijkstra的最短路径改进算法

基于Dijkstra的最短路径改进算法
罗理;王锋
【期刊名称】《湖北汽车工业学院学报》
【年(卷),期】2007(021)002
【摘要】针对如何利用Diikstra算法来高效地查找图中任意两结点之间的最短路径这一问题,提出了2种优化方法:其一是应用图中各结点的出入度来简化查找任意两结点之间的最短路径;其二是利用已求出的两点之间的最短路径来快速获得其他结点之间的最短路径.
【总页数】4页(P22-25)
【作者】罗理;王锋
【作者单位】昆明理工大学,信息工程与自动化学院,云南,昆明,650051;昆明理工大学,信息工程与自动化学院,云南,昆明,650051
【正文语种】中文
【中图分类】TP301.6
【相关文献】
1.基于网络分级优化和Dijkstra算法的最短路径求解改进 [J], 尚文芳
2.基于一般Dijkstra的改进算法在最短路径问题中的应用 [J], 岳晓娟
3.一种基于Dijkstra最短路径算法的改进算法 [J], 王智广;王兴会;李妍
4.基于网络分级优化和Dijkstra算法的最短路径求解改进 [J], 尚文芳
5.基于改进Dijkstra的应急指挥车及时救援的最短路径算法的研究 [J], 王先全;周锡祥;余浩源;李浩;王向雨
因版权原因,仅展示原文概要,查看原文内容请购买。
Dijkstra算法求最短路径

/*利用邻接矩阵构造图,并求出某一顶点到其余顶点的最短路径并打印输出。
*/#include<stdio.h>#include<stdlib.h>#include <malloc.h>#define INFIN 65535#define MAX_VERTEX_NUM 20#define OK 1#define ERROR 0#define FALSE 0#define TRUE 1typedef int VRType;typedef int V ertexType;typedef int infoType;typedef int ShortPathTable;//最短路径长度数组typedef struct{VRType adj;infoType *info;}ArcCell,AdjMatrix [MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef struct{V ertexType vexs[MAX_VERTEX_NUM];AdjMatrix arcs;int vexnum,arcnum;//顶点数,弧数}MGtaph;int CreateUDN(MGtaph *G)//构造无向----图{int IncINfo,i,j,k,w,v1,v2;//0代表无弧信息printf(" 请依次输入顶点数弧数:");scanf("%d %d",&G->vexnum,&G->arcnum);//顶点数,弧数,弧信息/*printf("请输入顶点信息:\n");//顶点有权值时使用for(i=0;i<G->vexnum;i++)scanf("%d",&G->arcnum);*/for(i=0;i<G->vexnum;i++){for(j=0;j<G->vexnum;j++){G->arcs[i][j].adj=INFIN;G->arcs[i][j].info=NULL;}}printf("\n\n 请依次输入顶点1 顶点2 弧长:\n");for(k=0;k<G->arcnum;k++){printf(" (%d):",k+1);scanf("%d %d %d",&v1,&v2,&w);G->arcs[v1][v2].adj=w;}return OK;}int ShortestPath_DIJ(MGtaph *G,int *v0,int P[][MAX_VERTEX_NUM],ShortPathTable *D,int way[MAX_VERTEX_NUM])//P[v]最短路径,D[]带权长度{int v,w,i,j,min,final[MAX_VERTEX_NUM];way[0]=*v0;//路径第一个节点for(v=0;v<G->vexnum;++v){final[v]=FALSE;D[v]=G->arcs[*v0][v].adj;for(w=0;w<G->vexnum;++w)P[v][w]=FALSE;if(D[v]<INFIN){P[v][*v0]=TRUE;P[v][v]=TRUE;}}D[*v0]=0;final[*v0]=TRUE;for(i=1;i<G->vexnum;++i){min=INFIN;for(w=0;w<G->vexnum;++w){if(!final[w])if(D[w]<min){v=w;min=D[w];}}final[v]=TRUE;way[i]=v;//全路径for(w=0;w<G->vexnum;++w)if(!final[w]&&(min+G->arcs[v][w].adj<D[w])){D[w]=min+G->arcs[v][w].adj;for(j=0;j<G->vexnum;j++)P[w][j]=P[v][j];P[w][w]=TRUE;}}printf("\n");return OK;}int PrintfWay(MGtaph *G,int p[MAX_VERTEX_NUM][MAX_VERTEX_NUM],int D[MAX_VERTEX_NUM],int *v0,int *way){int i,j,temp;temp=INFIN;for(i=0;i<G->vexnum;i++){if(D[i]==INFIN||D[i]==0){if(*v0!=D[i])printf(" %d->%d 不通\n",*v0,i);continue;}printf(" %d",*v0);for(j=1;j<G->vexnum;j++){if(p[i][way[j]]==1){if(temp==way[j])continue;temp=way[j];printf("->%d",way[j]);}}printf(" 最短路径:%d\n",D[i]);}return OK;}int main(){MGtaph G;intv0,p[MAX_VERTEX_NUM][MAX_VERTEX_NUM],D[MAX_VERTEX_NUM],way[MAX_V ERTEX_NUM],temp,i,j;printf("********************************************************************* ***********");printf("* 有向图求最短路径*");printf("********************************************************************* ***********\n");printf(" 1、将所操作的图中各顶点编号,按0、1、2......方式一一对应。
基于Dijkstra算法最短路问题C语言实现

ZHANG Shumin1 WANG Yuanfen2 (1. Department of Mathematics, Qinghai Normal University, Xining 810008) (2. Hutai Middle School, Xining 810008)
总第322期 2016年第8 期
Compu计ter算&机• D与ig数ita字l 工En程gineering
Vol.44 No.8
1399
基 于 Dijkstra算 法 最 短 路 问 题 C 语言实现|
张淑敏1 王元芬2
(1 .青 海 师 范 大 学 数 学 系 西 宁 810008)(2.虎 台 中 学 西 宁 810008)
Key Words the shortest path problem, Dijkstra algorithm, C program Class Number TP301. 6
i 引言
在日常生活和工作中,为了取得最大的利益或 者节约更多的成本,人们都在试图用最简单的方法 找出尽可能短的路程到目的地,例如铺设管道中为 了节约成本而规划最合理的铺设方法,出门旅游选 择 合 适 的 出 游 路 线 和 出 游 方 式 等 。这 些 问 题 都 可 以划归为最短路径问题,尽可能快地计算最短路径 是 我 们 生 活 的 迫 切 需 求 。求 最 短 路 有 两 种 算 法 ,一 是求从某一点到其他各点之间最短距离的Dijkstra 算 法 ,二是求网络图上任意两点之间最短距离的矩 阵算法[2]。本 文 主 要 解 决 最 短 路 径 的 Dijkstra算 法的计算,利用其思想编写计算机程序,辅助完成 最 短 路 径 问 题 的 求 解 [4]。并 且 进 一 步 熟 悉 最 短 路 径 问 题 的 Dijkstra算 法 ,掌 握 其 思 想 ,并会利用其 算法解决一些优化问题。在 用 C 语言编程中,体会 利用简单语句就可以解决复杂问题的好处。
基于 dijsktra 算法的最短路径求解

基于dijsktra 算法的最短路径求解
Dijkstra 算法是一种贪心算法,用于解决带权重边的单源最短路径问题,可以用来求解任意两个节点之间的最短路径,它的时间复杂度为O(V^2),其中V 是节点数量。
以下是Dijkstra 算法的具体步骤:
1. 定义一个数组dist,表示每个节点到源节点的最短距离,初始时所有节点的距离设为无穷大,源节点的距离设为0。
2. 定义一个数组visited,表示每个节点的访问状态,初始时所有节点都未被访问。
3. 以源节点为起点,将dist[s] 设为0。
4. 对于每个未被访问的节点,找到到源节点距离最短的节点u,将其标记为已访问,并更新与u 相邻的节点的最短距离,具体方法为:对于所有与u 相邻的节点v,如果dist[v] > dist[u] + w(u, v)(其中w(u, v) 表示u 到v 的边权重),则更新dist[v] = dist[u] + w(u, v)。
5. 重复步骤4 直到所有节点都被访问。
最终,dist 数组中存储的即为源节点到其它所有节点的最短路径长度。
如果需要求源节点到目标节点的最短路径,可以使用回溯法,从目标节点开始,依次沿着dist 值不断递减的路径找到源节点。
最短路径_Dijkstra算法__实验报告

最短路径_Dijkstra算法__实验报告实验六:编程实现Dijkstra 算法求最短路问题.1.需求分析:首先让用户输入一个带权的有向图,输入时可通过一对一对输入存在弧的两个弧头与弧尾顶点以及弧上的权值从而输入整个有向图。
用户输入一对对弧后,我们可以采用数组的形式来进行存储每个顶点之间的权值,最后由用户输入该有向图的源点(即每个最短路径的起点),要求源点必须为刚才输入的各顶点中的某一个,如果用户输入错误,程序要给出错误信息提示并退出程序。
然后,我们可以设计一个Graph这样的类,将对关系的各种操作放入其中,然后我们在主函数中调运这个类就可以实现最短路问题的求解了。
2.概要设计:①.构造一个新的类Graph:class Graph{private: int arcs[MAX][MAX],Path[MAX][MAX],D[MAX];int arcnum,vexnum,weight,v0;Type a,b,vexs[MAX];public:void Creat_Graph();void Show_ShortestPath();void ShortestPath_DIJ();};②.结构化调用类中方法的主函数:int main(){Graph G;G.Creat_Graph();G.ShortestPath_DIJ();G.Show_ShortestPath();return 0;}3.代码实现:#include#define MAX 100#define INFINITY INT_MAXenum BOOL{FALSE,TRUE};using namespace std;templateclass Graph{private: int arcs[MAX][MAX],Path[MAX][MAX],D[MAX]; int arcnum,vexnum,weight,v0;Type a,b,vexs[MAX];public:void Creat_Graph();void Show_ShortestPath();void ShortestPath_DIJ();};templatevoid Graph::Creat_Graph(){int i,j,x,y;cout<<"请输入你要处理的有向图中包含弧的个数:"; cin>>arcnum;vexnum=0;for(i=1;i<=MAX;i++)for(j=1;j<=MAX;j++)arcs[i][j]=INT_MAX;for(i=1;i<=arcnum;i++){cout<<"请依次输入第"<<i<<"条弧的弧头与弧尾的顶点以及该弧上所附带的权值:"<<endl;< p="">cin>>a>>b>>weight;x=0; y=0;for(j=1;j<=vexnum;j++){if(vexs[j]==a){x=j; continue;}else if(vexs[j]==b){y=j; continue;}}if(x==0){vexs[++vexnum]=a; x=vexnum;}if(y==0){vexs[++vexnum]=b; y=vexnum;}arcs[x][y]=weight;}cout<<"请输入该有向图的源点(即各最短路径的起始顶点):";cin>>a;for(i=1;i<=vexnum;i++){if(vexs[i]==a){v0=i; break;}}}templatevoid Graph:: Show_ShortestPath(){int i,j,k;for(i=1;i<=vexnum;i++){if(i==v0) continue;if(D[i]!=INT_MAX){cout<<"从源点"<<vexs[v0]<<"到"<<vexs[i]<<"的最短路径为:"<<endl;< p="">for(k=1;k<=Path[i][0];k++){if(k!=1)cout<<"-->";for(j=1;j<=vexnum;j++)if(Path[i][j]==k)cout<<vexs[j];< p="">}cout<<" "<<"其最短的路径长度为:"<<d[i]<<endl;< p="">}else{cout<<"无法从源点"<<vexs[v0]<<"到达顶点"<<vexs[i]<<"."<<endl;< p="">}}cout<<endl;< p="">}templatevoid Graph::ShortestPath_DIJ(){int v,w,final[MAX],min,i,j;for(v=1;v<=vexnum;v++){final[v]=FALSE; D[v]=arcs[v0][v]; Path[v][0]=0;for(w=0;w<=vexnum;w++)Path[v][w]=FALSE;if(D[v]<int_max)< p="">{ Path[v][v0]=++Path[v][0]; Path[v][v]=++Path[v][0]; }}D[v0]=0; final[v0]=TRUE;for(i=1;i<=vexnum;i++){if(i==v0) continue;min=INT_MAX;for(w=1;w<=vexnum;w++)if(!final[w])if(D[w]<="">final[v]=TRUE;for(w=1;w<=vexnum;w++)if(!final[w]&&(min+arcs[v][w]<d[w])&&min<int_max&&arcs [v][w]<int_max)< p="">{D[w]=min+arcs[v][w];for(j=0;j<=vexnum;j++)Path[w][j]=Path[v][j];Path[w][w]=++Path[w][0];}}}int main(){Graph G;G.Creat_Graph();G.ShortestPath_DIJ();G.Show_ShortestPath();return 0;}4.调试分析:起先在主函数中调用类Graph时将类型参数T赋值为int从而导致用户输入的关系集合R中的元素必须为整数。
求解最短路径的Dijkstra算法

一、问题分析与任务定义本题主要是利用Dijkstra算法来求解顶点之间最短路径,其中包括如下几个待解决的问题:1 问题分析选择合适的结构表示图主要包括:用Dijkstra算法实现起来更要容易;时间复杂度小;自己可以熟练应用。
Dijstra算法的实现所应涉及到的各参数及变量:顶点的编号;各边权的初使化;如何求出从顶点到其他各点的最短距离;最短距离长度的求取等问题。
2 任务定义对任意图,选择合适的数据结构表示图,在此基础上实现求解最短路径的Dijkstra算法。
要求:对所设计的图的数据结构,提供必要的基本功能。
在带权的有向图中源点到终点的多条路径中寻找出一条各边权植之和最小的路径,即最短路径。
对任务的理解考虑设计的图结构是否具备必要的基本功能,具有实际的应用;图的邻接矩阵如何实现交互式;如何将输入的邻接矩阵溶入到dijstra 算法中去。
需要解决什么样的实际问题。
并且能够将程序与实际问题相结合,能够处理一般的最短路径问题。
二、概要设计和数据结构的选择按路径长度递增的顺序产生最短路径。
通过以上对问题的分析和任务的理解,设计出一个大体的模块和程序流程。
1程序中涉及到的结构体及子函数:1.1结构体:本程序设计使用了以下结构体:struct vertex{ int num; //顶点编号int data; //顶点信息}; //顶点类型typedef struct graph{int n; //图中顶点个数int e; //图中边的个数struct vertex vexs[MAXVEX]; //顶点集合int edges[MAXVEX][MAXVEX]; //边的集合}AdjMaxix; //图的邻接矩阵类型1.2子函数:设计本程序需分成几个模块,要用到以下几个子函数:AdjMaxix creatmgraph() //通过用户交互产生一个有向图的邻接矩阵;void dispmgraph(AdjMaxix adj)//用于输出一个有向图的邻接矩阵;void ppath(int path[],int i,int v0);//选择输出一条最短路径void DisPath(int dist[],int path[],int s[],int n,int v0)//用path计算最短路径void Dijkstra(AdjMaxix g,int v0) // Dijkstra算法void change(int num) //用于替换顶点编号1.3结构图与流程图1.3.1结构图 图1 结构图 1.3.2 流程图图2 程序流程图三、详细设计和编码ppathmainDisPaDijkstchangcreat dispm输入语句,cin>>n>>e; cin>>b>>t>>w;Dijkstra 算法dist[i]=g.edges[v0][i];s[i]=0;if(g.edges[v 0][i]<INF) path[i]=v0;else path[i]=-1; s[v0]=1;path[v0]=0;把源点放入s 中;for(i=0;i<n;i++)dist[j]=dist[u]+g.edges[u][j];得出最短路径;Do{} while(x!='n');if(i>=n);if(j>=n)结束开始yes noyes这里设计用邻接矩阵解决实际生活中城市间往返最短路径问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计任务书目录1 需求分析............................................................................................ - 1 -2 算法基本原理 ................................................................................... - 2 -3 类设计................................................................................................ - 3 -4 详细设计............................................................................................ - 5 -4.1类的接口设计 . (5)4.2类的实现 (5)4.3主函数设计 (7)5 DOS界面程序运行结果及分析 ....................................................... - 8 -5.1程序运行结果 . (8)5.2运行结果分析 (9)6 基于MFC的图形界面程序开发..................................................... - 9 -6.1基于MFC的图形界面程序设计.. (10)6.2程序测试 (13)6.3MFC程序编写总结 (14)7 参考文献.......................................................................................... - 15 -1 需求分析Dijkstra 算法是由荷兰计算机科学家艾兹格·迪科斯彻发现的。
算法解决的是有向图中最短路径问题。
举例来说,如果图中的顶点表示城市,而边上的权重表示著城市间开车行经的距离。
Dijkstra 算法可以用来找到两个城市之间的最短路径。
Dijkstra 算法的输入包含了一个有权重的有向图G ,以及G 中的一个来源顶点S 。
我们以V 表示G 中所有顶点的集合。
图中的每一个边,都是两个顶点所形成的有序元素对。
(u ,v )表示从顶点u 到v 有路径相连。
假设E 为所有边的集合,而边的权重则由权重函数w : E → [0, ∞]定义。
因此,w (u ,v )就是从顶点u 到顶点v 的非负花费值(cost)。
边的花费可以想像成两个顶点之间的距离。
任两点间路径的花费值,就是该路径上所有边的花费值总和。
已知有V 中有顶点s 及t ,Dijkstra 算法可以找到s 到t 的最低花费路径(i.e. 最短路径)。
这个算法也可以在一个图中,找到从一个顶点s 到任何其他顶点的最短路径。
1.如果将交通网络化成带权图,假如用顶点表示城市,边表示公路段,则由这些顶点和边组成的图可表示沟通个城市的公路图,边的权用以表示两个城市之间的距离或者表示走过这段公路所需要的时间或通过这段路的难易程度等。
作为司机和乘汽车的人,自然会关心如下两个问题:(1)从甲地到乙地是否有公路?(2)从甲地到乙地有几条公路,哪条公路最短或花费的代价最小? 这就是我们要讨论的最短路径问题。
2.迪杰斯特拉提出的一个求最短路径的算法。
其基本思想是:按路径长度递增的顺序,逐个产生各最短路径。
3.首先引进辅助向量dist[],它的每一个分量dist[i]表示已经找到的且从源点0v 到每一个终点i v 的当前最短路径长度。
它的初态为:如果从0v 到i v 有弧,则dist[i]为弧的权值;否则dist[i]为∞。
其中,长度为dist[j]=min{dist[i]|i v ∈V}的路径是从0v 出发的长度最短的一条最短路径,此路径为(0v ,i v )。
2 算法基本原理根据以上分析,可以得到如下描述的算法:①假设用带权的邻接矩阵arce[i][j]来表示带权有向图,arce[i][j]表示弧<i v ,j v >上的权值。
若<i v ,j v >不存在,则置arce[i][j]为∞(在计算机上可用允许的最大值代替)。
S 为已找到的从0v 出发的最短路径的终点的集合,它的初始状态为空集。
那么,从0v 出发到图上其余个顶点(终点)i v 可能达到的最短路径长度的初值为:dist[i]=arce[Locate Vex(G,0v )][i]i v ∈S ②选择j v 得dist[j]=min{dist[i]|i v ∈V-S}j v 就是当前求得的一条从0v 出发的最短路径的终点。
令S=S ∪{j}。
③修改从0v 出发到集合V-S 上任一顶点k v 可达的最短顶点长度。
如果 dist[j]+arce[j][k]<dist[k]则修改dist[k]为dist[k]=dist[j]+arce[j][k]④重复操作②、③共n-1次。
由此求得从0v 到图上其余各顶点的最短路径是依路径长度递增的序列。
用Dijkstra 算法求有向图G 的0v 顶点到其余顶点v 的最短路径P[v]及其带权长度D[v]。
这个算法是通过为每个顶点v 保留目前为止所找到的从s 到v 的最短路径来工作的。
初始时,源点s 的路径长度值被赋为0(d[s]=0), 同时把所有其他顶点的路径长度设为无穷大,即表示我们不知道任何通向这些顶点的路径(对于V 中所有顶点v 除s 外d[v]= ∞)。
当算法结束时,d[v]中储存的便是从s 到v 的最短路径,或者是无穷大(如果路径不存在的话)。
Dijstra算法的基础操作是边的拓展:如果存在一条从u到v的边,那么从s 到v的最短路径可以通过将边(u,v)添加到s到u的尾部来拓展。
这条路径的长度是d[u]+w(u,v)。
如果这个值比目前已知的d[v]的值要小,我们可以用新值来替代当前d[v]中的值。
拓展边的操作一直执行到所有的d[v]都代表从s到v最短路径的花费。
这个算法经过适当的组织因而当d[u]达到它最终的值的时候,每条边(u,v)都只被拓展一次。
算法维护两个顶点集S和Q。
集合S保留了我们已知的所有d[v]的值已经是最短路径的值顶点,而集合Q则保留其他所有顶点。
集合S初始状态为空,而后每一步都有一个顶点从Q移动到S。
这个被选择的顶点是Q中拥有最小的d[u]值的顶点。
当一个顶点u从Q中转移到了S中,算法对每条外接边(u,v)进行拓展。
Dijkstra(G,D,s){//用Dijkstra算法求有向网G的源点s到各顶点的最短路径长度//以下是初始化操作S={s};D[s]=0;//设置初始的红点集及最短距离for( all i∈V-S )do //对蓝点集中每个顶点iD[i]=G[s][i];//设置i初始的估计距离为w<s,i>//以下是扩充红点集for(i=0;i<n-1;i++)do{//最多扩充n-1个蓝点到红点集D[k]=min{D[i]:all i V-S};//在当前蓝点集中选估计距离最小的顶点kif(D[k]等于∞)return;//蓝点集中所有蓝点的估计距离均为∞时,//表示这些顶点的最短路径不存在。
S=S∪{k};//将蓝点k涂红后扩充到红点集for( all j∈V-S )do //调整剩余蓝点的估计距离if(D[j]>D[k]+G[k][j])//新红点k使原D[j]值变小时,用新路径的长度修改D[j],//使j离s更近。
D[j]=D[k]+G[k][j];}}3 类设计从上面的算法分析可以看到,根据算法设计了类class SPFA,public: intn;表示图里面的点数,public: int path[MAX][MAX];定义链接矩阵最多是1000个点,public: int dis[MAX];定义源点到其他点的距离,public: int src;定义源点,bool used[MAX]={false};定义点是否访问过了,初始化为未访问,初始化一下到各个点的距离,如果从k 点走到j 点的路很比原来的要短,那么更新,采用图的邻接矩阵或邻接表实现最短路径问题中图的存储,采用Dijkstra 算法求从某个源点到其余各顶点的最短路径。
第一步 先取()10W v =意即1v 到1v 的距离为0,而()j T v 是对()j T v 所赋的初值。
第二步 利用()1W v 已知,根据()(){}min ,j i ij T v W v w +对()j T v 进行修正。
第三步 对所有修正后的()j T v 求出其最小者()k T v 。
其对应的点k v 是1v 所能一步到达的点j v 中最近的一个,由于所有()0W u ≥。
因此任何从其它点j v 中转而到达k v 的通路上的距离都大于1v 直接到k v 的距离()k T v ,因此()k T v 就是1v 到k v 的最短距离,所以在算法中令()()k k W v T v =并从s 中删去k v ,若k=n 则()()k n W v W v =就是1v 到n v 的最短路线,计算结束。
否则令i k v v =回到第二步,继续运算,直到k=n 为止。
这样每一次迭代,得到1v 到一点k v 的最短距离,重复上述过程直到k n v v =。
Floyd 算法的基本原理和实现方法为:如果一个矩阵ij D d ⎡⎤=⎣⎦其中0ij d >表示i 与j 间的距离,若i 与j 间无路可通,则ij d 为无穷大。
i 与j 间的最短距离存在经过i 与j 间的k 和不经过k 两种情况,所以可以令1,2,3,,k n = ,n(n 为节点数)。
检查ij d 与ik kj d d +的值,在此,ik d 与kj d 分别为目前所知的i 到k 与k 到j 的最短距离,因此,ik kj d d +就是i 到j 经过k 的最短距离。
所以,若有ij ik kj d d d >+,就表示从i 出发经k 再到j 的距离要比原来的i 到j 距离短,自然把i 到j 的ij d 重写成ik kj d d +。
每当一个k 搜索完,ij d 就是目前i 到j 的最短距离。
重复这一过程,最后当查完所有k 时,ij d 就为i 到j 的最短距离。
4 详细设计首先,这个程序定义了一个类class SPFA,通过此类定义链接矩阵,采用图的邻接矩阵或邻接表实现最短路径问题中图的存储,然后通过主函数main调用class来实现,采用Dijkstra算法求从某个源点到其余各顶点的最短路径。
