Nernst 方程
能斯特方程计算电极电势

能斯特方程计算电极电势
能斯特方程(Nernst equation)是描述电化学反应中电极电势与物质浓度之间关系的方程。
它是由德国化学家沃尔弗冈·能斯特于19世纪末提出的,被认为是电化学基础理论的重要组成部分。
能斯特方程广泛应用于电化学实验和工业生产中,用于计算电极电势的变化。
E = E° - (RT/nF) ln(Q)
在这个方程中,E是电极电势,E°是标准电极电势,R是气体常数,T是温度,n是电子转移的摩尔数,F是法拉第常数,Q是反应物浓度的比值。
能斯特方程的应用范围很广。
它可以用来计算电池的电势差,以及电解过程中物质浓度对电极电势的影响。
在电池的设计和优化过程中,能斯特方程可以帮助确定最佳的反应条件,以提高电池的效能。
在环境监测和化学分析中,能斯特方程可以用来计算溶液中各种物质的浓度。
除了上述标准条件下的能斯特方程,还存在一些修正的能斯特方程,用于考虑非标准条件下的电极电势计算。
例如,考虑溶液的pH值、温度变化或电解质浓度差异等因素。
总之,能斯特方程是电化学领域中重要的计算公式,用于描述电极电势与物质浓度之间的关系。
通过能斯特方程,我们可以了解电化学反应的热力学特征,并为实验和工业应用提供指导。
恩斯特方程

能斯特方程(Nernst Equation)是电化学中的一个重要公式,它描述了在一定温度下,一个电极反应的标准电势与其实际可测量的电势之间的关系。
该方程用于计算平衡状态下氧化还原反应的电极电位以及在非标准条件下溶液中离子的电极电位。
能斯特方程的一般形式为:
其中:
E 是在给定条件下的实际电极电位(单位:伏特,V)。
E°是标准电极电位,在特定温度下、参与反应物质浓度均为1 mol/L时的电极电位。
R 是理想气体常数,大约为。
T 是绝对温度(单位:开尔文,K)。
n 是转移的电子数,即氧化还原反应的电子转移当量数。
F 是法拉第常数,大约为。
Q 是反应quotient,表示反应体系中各物种活度的比值,对于氧化还原反应来说,它是氧化态和还原态物质浓度的比值。
能斯特方程是理解电池电动势随温度和浓度变化的基础,并且在研究电化学电池、电解过程以及设计传感器等方面具有重要应用价值。
能斯特方程的应用

能斯特方程的应用一、什么是能斯特方程?能斯特方程,又称为能斯特-伯格方程或伯格-弗拉夫方程,是描述电化学反应动力学的一个重要数学公式。
该方程最初由德国化学家瓦尔特·能斯特(Walter Nernst)于1889年提出,后来被奥地利化学家汉斯·伯格(Hans Berger)和俄国物理化学家米哈伊尔·弗拉夫(Mikhail Fraday)分别推广和完善。
二、能斯特方程的公式能斯特方程的公式如下:E = E0 - (RT/nF)lnQ其中,E:电极电势E0:标准电极电势R:气体常数T:温度(开尔文)n:反应中电子转移数F:法拉第常数Q:反应物浓度比值三、能斯特方程的应用1. 计算标准电极电势标准电极电势是指在标准状态下,一个半反应中氧化剂和还原剂各处于1mol/L浓度时,该半反应对应的电极与标准氢电极之间的电位差。
通过能斯特方程可以计算出标准电极电势,具体步骤如下:(1)列出反应式和半反应式;(2)确定反应物和生成物的浓度;(3)代入能斯特方程计算标准电极电势。
2. 计算电极电势在非标准状态下,能斯特方程可以用来计算电极电势。
具体步骤如下:(1)列出半反应式;(2)确定反应物和生成物的浓度;(3)代入能斯特方程计算电极电势。
3. 计算化学平衡常数在一定条件下,一个化学反应达到平衡状态时,反应物和生成物的浓度比值称为化学平衡常数。
通过能斯特方程可以计算出化学平衡常数,具体步骤如下:(1)列出反应式和半反应式;(2)确定各组分的浓度;(3)代入能斯特方程求解。
4. 研究溶液中离子活度离子活度是指溶液中某种离子参与化学反应时所表现出的“真实”浓度。
通过能斯特方程可以研究溶液中离子活度的变化规律,从而探究溶液中离子的化学反应动力学。
5. 计算电解质的溶解度积电解质的溶解度积是指在某一温度下,电解质在水中达到平衡时,固体电解质与水中的离子浓度乘积等于一个定值。
通过能斯特方程可以计算出电解质的溶解度积,具体步骤如下:(1)列出反应式和半反应式;(2)确定各组分的浓度;(3)代入能斯特方程求解。
能斯特方程计算的详细解题步骤

能斯特方程计算的详细解题步骤能斯特方程,也称为Nernst方程,是描述化学电池内电动势与各种因素之间关系的方程。
它是由瑞士化学家沃尔特·能斯特于1889年提出的,并被广泛应用于电化学研究和工业生产中。
Nernst方程的一般形式如下:E = E° - (RT/nF) * ln(Q)其中,E代表电池的电动势,E°代表标准电动势,R代表理想气体常数,T代表温度,n代表电子转移的摩尔数,F代表法拉第常数,Q 代表电池中各种化学物质的活度积。
在实际应用中,Nernst方程可以用来计算电池的电动势随温度、浓度等因素的变化。
下面将详细介绍Nernst方程的计算步骤及应用。
步骤一:确定反应的半反应方程在应用Nernst方程之前,首先需要确定电池中发生的化学反应,并写出对应的半反应方程。
例如,对于铅-蓄电池(Pb/H2SO4/H2O2),其半反应方程可以写为:负极半反应:Pb + SO4²⁻ → PbSO4 + 2e⁻正极半反应:PbO2 + 4H⁺ + SO4²⁻ + 2e⁻ → PbSO4 + 2H2O步骤二:确定标准电动势标准电动势是指在标准状态下(浓度为1mol/L,压强为1atm,温度为25℃)的电池电动势。
可以通过标准电极电动势表或者其他方式获取。
以铅-蓄电池为例,其标准电动势可以查得为1.685V。
步骤三:确定温度和摩尔数在Nernst方程中,需要确定温度(单位为K)和电子转移的摩尔数。
通常情况下,温度可直接使用开尔文温标表示,而电子转移的摩尔数则可以从半反应中获得。
对于铅-蓄电池来说,电子转移的摩尔数为2。
步骤四:确定各种化学物质的活度积在Nernst方程中,化学物质的活度积是一个重要的参数。
它可以通过浓度或者其他方法来计算。
例如,在铅-蓄电池中,活度积可以表示为:Q = [PbSO4] / ([Pb][SO4²⁻])步骤五:代入Nernst方程进行计算将以上所得参数代入Nernst方程进行计算,就可以得到实际电池的电动势。
尼柯尔斯基方程表达式

尼柯尔斯基方程表达式尼柯尔斯基方程(Nernst equation),是描述电化学系统中电动势与各种物理化学参数之间关系的重要方程,由德国物理化学家沃尔弗冈·尼柯尔斯基于1889年提出。
该方程为了解电化学反应的动力学和平衡性质提供了理论基础,被广泛应用于电化学、生物化学、环境科学等领域。
尼柯尔斯基方程的一般形式为E = E° - (RT/nF)·lnQ,其中E表示电动势,E°表示标准电动势,R是理想气体常数,T表示温度,n 表示电子数,F表示法拉第常数,ln表示自然对数,Q表示反应物浓度或气体分压的乘积。
尼柯尔斯基方程的主要作用是用于计算电池或电解槽中的电动势。
在标准条件下,即温度为298K、物质浓度为1mol/L时,尼柯尔斯基方程简化为E = E° - (0.0592/n)·logQ。
这个简化形式常用于计算电池电势,其中E°是标准电动势,log是以10为底的对数运算。
尼柯尔斯基方程的应用非常广泛。
在电化学中,它可以用来计算电池的电势,帮助理解电池反应的趋势和速率。
在生物化学中,尼柯尔斯基方程常被用于描述细胞膜上离子通道的电位依赖性,从而解释细胞内外的离子平衡和传递过程。
在环境科学中,尼柯尔斯基方程用于计算水体中溶解氧的浓度,从而评估水体的氧化还原状态和生态健康程度。
尼柯尔斯基方程的应用需要注意一些限制条件。
首先,方程中的温度应以开尔文(K)为单位,因为理想气体常数R的单位是J/(mol·K)。
其次,方程中的浓度应以摩尔浓度表示,且浓度的单位应一致。
最后,尼柯尔斯基方程假设了电极界面处没有电势损失和电解液中离子活度无变化,这在实际情况下并不一定成立,因此在具体应用中需要考虑这些因素的影响。
尼柯尔斯基方程是电化学领域中的重要工具,能够帮助我们理解电化学系统中电动势和物理化学参数之间的关系。
通过对方程的应用,我们可以计算电池电势、解释细胞内外的离子平衡和评估水体的氧化还原状态,进而推动电化学、生物化学和环境科学等领域的研究和应用。
Nernst方程

Nernst方程
能斯特方程(Nernst equation)是热力学中的一个基本方程,它反映了可逆电池在一定条件下进行自发反应时,参与反应的各物质浓度的变化与反应进行的方向和程度之间的关系。
该方程由德国物理化学家能斯特于1889年提出,它包含了热力学基本原理中的许多重要概念,如熵、焓、自由能等,对于理解热力学和电化学的性质具有重要意义。
能斯特方程的现代形式如下:
ΔG°′ = ΔH°′ −TΔS°′
其中,ΔG°′表示可逆过程在一定温度下标准摩尔反应自由能的改变量,
ΔH°′表示标准摩尔反应焓,T表示绝对温度,ΔS°′表示标准摩尔反应熵。
这个方程反映了热力学第二定律的本质,即自然发生的宏观过程总是朝着熵增加的方向进行,而可逆过程的熵是不变的。
方程中的负号表示,随着反应的进行,系统总体的熵会增加,这是自然过程的基本特征。
对于化学反应,如果已知标准摩尔反应焓和标准摩尔反应熵,就可以通过能斯特方程计算出可逆过程在一定温度下标准摩尔反应自由能的改变量。
这对于理解化学反应的本质和预测化学过程的可能性具有重要意义。
此外,能斯特方程还可以扩展到其他领域,如电化学、半导体、催化剂等领域。
在这些领域中,能斯特方程可以帮助人们理解物质性质的变化规律和反应机制的本质,为科学研究和技术开发提供重要的理论依据。
总之,能斯特方程是热力学中的一个基本方程,它反映了自然过程的基本特征和可逆电池在一定条件下进行自发反应时的内在关系。
通过该方程的应用,我们可以更好地理解热力学和电化学的性质,预测化学过程的可能性,并为科学研究和技术开发提供重要的理论依据。
欧姆定律 nernst-planck 方程

欧姆定律 nernst-planck 方程
欧姆定律(Ohm's Law)是描述电路中电流与电压之间关系的基本定律。
它表明,当电路中的电阻恒定时,电流的大小与通过电路的电压成正比,即I=V/R,其中,I为电流强度,V为电压,R 为电阻。
欧姆定律可用于计算和控制电路中电流和电压的关系,是电学基础知识之一。
Nernst-Planck方程(Nernst-Planck Equation)是描述电解质物流动和扩散过程的方程,它是通过对离子传输问题的研究而得出的,可以应用于生物、化学、工程等多个领域。
该方程通过考虑每种离子在电场作用下的迁移,以及扩散和对流流动效应,来描述离子在液相中的传输情况。
Nernst-Planck方程可以用来模拟离子在不同条件下的运动和分布规律,从而可以为不同领域的理论研究、数值模拟和实验设计提供重要依据。
总之,欧姆定律和Nernst-Planck方程是两个重要的物理方程,一个描述了电路中电流与电压之间的关系,一个描述了离子在电扩散、流动等过程中的行为。
它们对于电学和生物、化学等领域的研究都具有重要意义。
浅谈nernst方程及其应用的教学

浅谈nernst方程及其应用的教学以《浅谈nernst方程及其应用的教学》为标题,写一篇3000字的中文文章一、引言Nernst方程又叫电势-活度方程,是电源电势理论的基础,是重要的化学方程。
Nernst方程是由德国化学家奥古斯特内恩斯特(Otto Nernst,1864-1941)发现的,主要用于解决电池和溶液反应之间的化学均衡。
它有助于理解电池反应的物理机理,可用于计算电池电势和电池操作温度。
Nernst方程的应用在许多方面,比如:从事电池设计和实验的化学家、材料科学家;电化学工程的研究工作和实际应用;结构生物学家和药理学家研究离子通道;医学生理学家研究电信号传导;以及材料表面处理的工程师等都需要使用Nernst方程。
为了更好地理解Nernst方程及其应用,教学者应注重学生思维能力的培养与加强,重视可操作性教学,让学生学习理解Nernst方程,自主分析应用其知识。
二、Nernst方程及其基本性质Nernst方程是一个化学平衡性状态下的电势方程,它建立在威廉柯尔(William C. Cole)提出的电势-活度理论基础之上,也被称为电势活度方程。
Nernst方程可以用来解释溶液中电离和电子移动间的关系,反映的便是电势的物理性质,尤其是溶液中的活度和温度。
Nernst方程可以写为:E = E0 - [RT/nF]lna其中,E表示电源电位,E0表示特定条件下的标准电位,R表示摩尔气体常数,T表示绝对温度,n表示电荷,F表示电容,a表示活度。
由Nernst方程可以看出,活度a和绝对温度T的变化会影响电势的变化。
当活度和温度变化时,电势也会发生变化,这正是化学平衡性及其相关性质的一个重要要素。
Nernst方程可以帮助我们准确的掌握活度和温度的数据,用这些数据来计算电池电势,从而知道活度和温度是如何影响电势的。
三、Nernst方程在教学中的应用(一)让学生思考Nernst方程及其应用Nernst方程及其应用是一个综合全面的学科,在教学和科学研究中都有着重要的应用价值。
能斯特方程 教学案例

能斯特方程教学案例能斯特方程(Nernst equation)是描述化学电池中电势和溶液浓度之间关系的方程。
它是由德国化学家沃尔夫冈·能斯特在19世纪末提出的,并在电化学领域作出了重要贡献。
能斯特方程的应用广泛,不仅在实验室中被用于测定电池的电势,也被用于工业生产和环境监测中。
在能斯特方程中,电势E和溶液中的化学物质浓度之间存在着一种数学关系。
方程的形式如下:E = E0 - (RT / nF) * ln([Ox] / [Red])其中,E表示电势,E0表示标准电势,在标准状态下反应的电势。
R是理想气体常数,T是温度,n是电子转移数,F是法拉第常数,[Ox]和[Red]分别表示氧化物和还原物的浓度。
举个实际的教学案例来说明能斯特方程的应用。
假设我们正在讲解关于电池原理和电势差的课程,我们可以通过一个实验案例来让学生更好地理解能斯特方程。
实验设备和材料:- 两个不同金属的片材(比如锌和铜)- 盐桥- 氯化铜溶液- 导线- 电压表实验步骤:1. 将锌片和铜片分别与导线连接,形成电池的两个电极。
2. 在化学实验室安全的条件下,将两个金属电极分别插入含有氯化铜溶液的两个杯子中,杯子之间用盐桥连接。
3. 使用电压表测量电池的电势。
4. 根据能斯特方程,根据溶液中铜离子和还原物的浓度以及标准电势的相关数据,计算电池的预测电势。
5. 比较实测电势和预测电势的差异,让学生思考差异产生的原因。
通过这个实验案例,学生可以更好地理解电池电势和溶液浓度之间的关系。
他们可以通过实验结果和能斯特方程的计算,理解电池中的化学反应是如何造成电势差的。
除了实验案例,能斯特方程在工业生产和环境监测中也有重要应用。
在电镀过程中,可以利用能斯特方程预测电解液浓度对电镀效果的影响。
在环境监测中,能斯特方程用于测定溶解氧浓度,从而判断水体的质量和氧气传输过程。
总结起来,能斯特方程在电化学领域具有重要的应用价值。
通过实验案例和实际应用的介绍,我们可以更全面、深刻和灵活地理解能斯特方程的原理和应用。
nernst方程
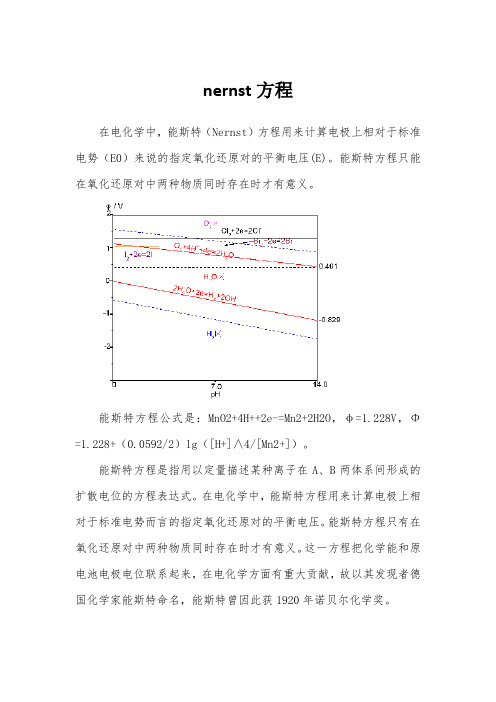
nernst
在电化学中,能斯特(Nernst)方程用来计算电极上相对于标准电势(E0)来说的指定氧化还原对的平衡电压(E)。能斯特方程只能在氧化还原对中两种物质同时存在时才有意义。
能斯特方程公式是:MnO2+4H++2e-=Mn2+2H2O,φ=1.228V,Φ=1.228+(0.0592/2)lg([H+]∧4/[Mn2+])。
fe3+ fe2+电极电势

fe3+ fe2+电极电势
铁的Fe3+和Fe2+离子在标准状态下的电极电势可以通过
Nernst方程来计算。
Nernst方程表示为:
E = E° (RT/nF)ln(Q)。
其中E是电极电势,E°是标准电极电势,R是气体常数,T是
温度(以开尔文度为单位),n是电子转移数,F是法拉第常数,Q
是电化学反应的反应商。
对于Fe3+和Fe2+之间的氧化还原反应,反
应为:
Fe3+ + e-> Fe2+。
在标准状态下,Fe3+和Fe2+的标准电极电势分别为
E°(Fe3+/Fe2+) = 0.77V。
根据Nernst方程,可以计算不同条件下
的电极电势。
例如,在25°C下,如果Fe3+和Fe2+的活度分别为
1M和0.1M,那么可以通过代入Nernst方程中计算出电极电势的值。
另外,需要注意的是,Fe3+和Fe2+的电极电势还受到溶液pH
值的影响。
在酸性条件下,Fe3+和Fe2+的电极电势会有所变化,因
此在实际应用中需要考虑溶液的酸碱性对电极电势的影响。
总之,Fe3+和Fe2+的电极电势是通过Nernst方程来计算的,
可以根据具体的反应条件和溶液性质来确定电极电势的数值。
同时,需要注意实际应用中可能存在的其他影响因素,如溶液的pH值等。
溶液ph与电极电势的关系式

溶液ph与电极电势的关系式
溶液的pH值与电极电势之间的关系可以用Nernst方程来表示:
E = E° - (RT/nF) ln[H+]
其中,E为电极电势,E°为标准电极电势,R为气体常数,T为绝对温度,n为电子的数量,F 为电子伏特,[H+]为溶液中的氢离子浓度。
由于溶液中的氢离子浓度与pH值之间存在着对数关系,因此可以将Nernst方程简化为:
E = E° - (RT/nF) pH
由此可以看出,溶液的pH值与电极电势之间存在着正比关系,即溶液的pH值越高,电极电势就越高。
另外,由于溶液中的氢离子浓度与pH值之间存在着对数关系,因此可以得出:
pH = -log[H+]
由此可以看出,溶液的pH值与氢离子浓度之间存在着反比关系,即溶液的pH值越高,氢离子浓度就越低。
总之,溶液的pH值与电极电势以及氢离子浓度之间存在着密切的关系,可以用Nernst方程来表示:E = E° - (RT/nF) ln[H+],也可以用简化的Nernst方程来表示:E = E° - (RT/nF) pH,以及pH = -log[H+]。
nernst方程及其有关的简单计算

nernst方程及其有关的简单计算Nernst方程是描述电化学系统中电势与浓度的关系的重要方程之一。
它是由德国化学家瓦尔特·尼尔斯特(Walther Nernst)在1889年提出的,因此得名为“尼尔斯特方程”或“Nernst方程”。
尼尔斯特方程的数学表达式为:E=E°-(0.0591/n)*log(Q)其中,E为电池的总电势,E°为标准电极电势(在标准条件下测量得到的电极电势),n为电子转移的电子数,Q为反应的反应物浓度比。
Nernst方程主要适用于涉及溶液中离子浓度的电化学反应。
它表明了电势与浓度之间的关系,从而可以用来计算电池电势随着浓度变化的情况。
这个方程在电化学实验和工业应用中具有广泛的应用。
为了更好地理解Nernst方程,我们来看一个简单的例子。
假设我们有一个锌-铜电池,其中锌溶液的浓度为0.1mol/L,铜溶液的浓度为0.01mol/L。
我们可以使用Nernst方程来计算此电池的电势。
在这个例子中,我们知道锌和铜之间的反应为:Zn(s) + Cu2+(aq) → Zn2+(aq) + Cu(s)根据这个反应,我们可以得到电子转移的电子数n=2(铜离子Cu2+接受两个电子)。
根据Nernst方程,我们可以将其改写为:E=E°-(0.0591/2)*log(Q)其中,E°为锌和铜电极的标准电势差。
对于此电池,E°可以从电化学数据手册中找到,假设为1.10V。
Q表示反应物(产品)浓度比。
在这个例子中,Q可以表示为[Zn2+]/[Cu2+],即锌离子浓度和铜离子浓度的比值。
根据题目提供的浓度值,我们可以计算得到Q=(0.1/1)/(0.01/1)=10。
将这些值代入Nernst方程中,我们可以计算出电池的电势E:E=1.10-(0.0591/2)*log10=1.10-(0.0591/2)*1=1.10-0.02955=1.07045V因此,该锌-铜电池的电势为1.07045V。
能斯特方程_高等教育-微积分

能斯特方程Nernst equation在电化学中,能斯特方程用来计算电极上相对于标准电势(E)来说的指定氧化还原对的平衡电压(E)电对的标准电极电势是在298K下,反应物的浓度为1mol·L-1(反应物为气态时,其分压为101kPa)时测得的,如果反应物的浓度和温度发生改变,则电对的电极电势也随着发生变化,它们之间的关系可以用能斯特方程表示.在常温下(25°C=298.15k),有以下关系式:假定反应为:氧化型+ne←———→还原型式中E──某一定浓度下的电极电势;E──标准电极电势;R──气体常数(8.314J·K -1mol-1);T──温度(K);n──电极反应中得到和失去的电子数;F──法拉第常数(96 485C·mol-1);[氧化型]或[还原型]──氧化型物质或还原型物质的浓度.应用这个方程时应注意:①方程式中的[氧化型]和[还原型]并不是专指氧化数有变化的物质,而是包括了参加电极反应的其他物质.②在电对中,如果氧化型或还原型物质的系数不是1,则[氧化型]或[还原型]要乘以与系数相同的方次.③如果电对中的某一物质是固体或液体,则它们的浓度均为常数,可认为是1.④如果电对中的某一物质是气体,它的浓度用气体分压来表示.⑤能斯特方程只能在氧化还原对中两种物质同时存在时才有意义。
能斯特方程式是表达电极电势跟浓度的关系式。
氧化还原电对的电极电势是半反应式中各物质浓度(或气体的压强)的函数。
设电对[氧化型]/[还原型]的半反应式是氧化型+ne还原型,则该电对的电极电势跟浓度的关系是式中E是该电对在非标准态下的电极电势,E是标准电极电势,n是半反应中得失电子数。
这就是能斯特方程式。
在半反应中,如果还有其他物质参与,则其浓度也应写在方程式中(固体和水除外)。
利用奈斯特方程,可以由改变物质的浓度(或气体压强)的方法来改变电对的电极电势,从而有可能改变氧化还原反应的方向。
静息电位的nernst方程

静息电位的nernst方程
静息电位是指神经元或肌细胞在静止状态下的负电荷内积累,使细胞内外形成电化学梯度的状态。
Nernst方程可以用来计算细胞内外离子的浓度差所产生的静息电位。
在神经系统中,钠、钾、氯等离子的质量浓度差决定了静息电位的大小和极性。
Nernst方程的公式为:
E = (RT/zF)ln([ion]out/[ion]in)
其中,E是静息电位,R是气体常数,T是绝对温度,z是离子电荷数,F是法拉第常数,[ion]out和[ion]in是离子在细胞外和内的浓度。
根据Nernst方程,当细胞外的钠离子浓度高于细胞内时,静息电位为正,细胞内外形成钠离子的梯度,使细胞保持充电状态。
反之,当细胞外的钾离子浓度高于细胞内时,静息电位为负,细胞内外形成钾离子的梯度,使细胞保持负电荷状态。
Nernst方程可以帮助科学家理解神经元和肌细胞的电生理学特性,也可用于诊断和治疗一些与离子失衡有关的疾病。
- 1 -。
静息电位的nernst方程

静息电位的nernst方程静息电位是指神经细胞或肌肉细胞在静息状态下的电位差。
在细胞膜内外分别维持正负离子浓度差的共同作用下,静息电位才能持续存在。
而这个离子浓度差的维持离不开一个理论基础:nernst方程。
Nernst方程是描述离子在膜上分布的数学公式,根据它可以预测任何给定离子的电化学激动子运动趋向。
它最初由荷兰科学家Nernst于1889年提出,并在阐释了细胞膜通透离子传输的机理后,成为理解细胞膜电位和离子稳定性的关键性原理之一。
因此,Nernst方程被用来测量和计算静息电位时,扮演了不可替代的角色。
那么,静息电位的Nernst方程如何应用于细胞膜内外的离子分布呢?以下是几个步骤:1. 根据离子选择Nernst方程的相应形式不同类型的离子在Nernst方程中有特定的形式,例如:$$E_K =\frac{RT}{z_iF}\ln\frac{[K^+]_{out}}{[K^+]_{in}}$$$$E_{Cl} = \frac{RT}{z_iF}\ln\frac{[Cl^-]_{in}}{[Cl^-]_{out}}$$其中,$E_K$代表钾离子的电位,$E_{Cl}$代表氯离子的电位,$T$代表绝对温度,$z_i$代表离子电荷,$F$代表法拉第常数(电荷转移数),$R$代表气体常数,$[K^+]_{in}$代表细胞膜内钾离子的浓度,$[K^+]_{out}$代表细胞膜外钾离子的浓度,$[Cl^-]_{in}$代表细胞膜内氯离子的浓度,$[Cl^-]_{out}$代表细胞膜外氯离子的浓度。
2. 确定细胞膜内外离子浓度差细胞膜内外的离子浓度差是静息电位的主要驱动力,它决定了细胞膜内外的离子向内外运动的趋势,从而影响了电位变化。
因此,准确测量和确定细胞膜内外离子浓度差非常重要。
此外,如果细胞膜内外离子浓度差发生变化,则Nernst方程需要重新应用以计算新的电位。
3. 计算静息电位计算静息电位的最简单方法是使用细胞膜内外离子浓度差和Nernst方程,这样就可以计算出特定离子(例如钾离子或氯离子)的电位。
氧化还原电位与ph换算公式

氧化还原电位与ph换算公式
氧化还原电位(E)与 pH 值之间的换算关系可以通过 Nernst
方程来描述。
Nernst 方程是描述电化学反应的电势变化与反应物浓
度之间关系的方程。
对于单电子氧化还原反应,Nernst 方程可以写作:
E = E° (0.0592/n) log([Red]/[Ox])。
其中,E 是氧化还原电位,E° 是标准氧化还原电位,n 是电
子转移数,[Red] 是还原物的浓度,[Ox] 是氧化物的浓度。
0.0592 是以 Volt 为单位的温度和 Faraday 常数的乘积。
另外,pH 与氧化还原电位之间的关系可以通过 Nernst 方程和pH 的定义来推导。
在标准状态下,将氢离子浓度([H+]) 代入Nernst 方程中,可以得到以下关系:
E = E° (0.0592/n) pH.
这个关系表明 pH 的变化会影响氧化还原电位。
当 pH 改变时,氢离子浓度的变化会导致氧化还原电位的变化。
因此,pH 值的变化
会对氧化还原反应的进行产生影响。
需要注意的是,这些公式都是在特定条件下成立的,例如在特定温度下,且需要考虑溶液中其他离子的影响。
在实际应用中,需要根据具体情况进行修正和适当的考虑。
氧化-还原滴定曲线计量点电极电位计算公式的推导

氧化-还原滴定曲线计量点电极电位计算公式的推导
答:
氧化-还原滴定曲线计量点电极电位计算公式的推导是基于Nernst方程的。
Nernst方程可以表示为:
E = E° + (RT/nF) ln[A]
其中,E代表电极电位,E°是标准电极电位,R是摩尔气体常数,T是系统的绝对温度,n是反应的电子数,F 是摩尔电荷,A代表化学反应的浓度比例。
将Nernst方程代入到滴定曲线计量点电极电位计算公式中,可以得到:
E = E° + (RT/nF) ln[(a + bx)/(c + dx)]
其中,x代表反应物浓度,a、b、c、d代表反应物的浓度系数。
此外,在滴定曲线计量点电极电位计算公式中,E°可以省略,因此最终的公式为:
E = (RT/nF) ln[(a + bx)/(c + dx)]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、离子浓度改变对氧化还原反应方向的影响
例 判断2Fe3++2I-=2Fe2++I2在标准状态下和 [Fe3+]=0.001mol·L-1 ,[I-]= 0.001 mol·L-1,[Fe2+]=1 mol·L-1
时反应方向如何? 解:(1) 标准状态:
—12 I2 + e = I-
0 =0.535 V
标准电极电势
为了实用方便,提出了标准电极电势的概念。 当电对处于标准状态(即物质皆为纯净物,组 成电对的有关物质浓度(活度)为1.0 mol·dm-3,涉 及气体的分压为1.0×105Pa时,该电对的电极电势为
标 准 电 极 电 势 , 用 符 号 φθ 表 示 。 通 常 温 度 为
298.15K。
Fe3+ + e = Fe2+ 0 =0.770 V
E0=0 (Fe3+/Fe2+)- 0 (I2/I-)=0.770-0.535=0.235 V>0
所以在标准状态下,上述反应能自发进行。
(2) 非标准状态: +=0.770+0.0592lg—0.1—00—1 = 0.0592 (V)
-=0.535+0.0592lg—0.1—00—1 = 0.718 (V) E=+--=0.592-0.718 =-0.121 (V)<0 所以在非标准状态下,上述反应向逆方向自发进行。
E(MnO4-/ Mn2+) = 1.512V+0—.05—92—Vlg(10-5) 8 5
= 1.04V
当 c (H+) = 2.0 mol.dm-3
E(MnO4-/
Mn2+)
=
1.512V+0—.05—92—Vlg(2 5
)8
= 1.541V
可知: c (H+) 浓度增加,电极电势增加, MnO4- 氧化性增强。
能斯特方程式
2.影响电极电势的因素
(1) 浓度对电极电势的影响
从能斯特方程式可看出,当体系的温度一定时,
对确定的电对来说,φ 主要取决于c(OX)/c(Red) 的
比值大小。
能斯特方程式
例 : 计 算 298.15K 下 , c(Zn2+) = 0.100mol·L-1 时 的
φ(Zn2+/Zn)值。
电极电势的测定
若干电对的标准电极电势(298.15K)
电对
氧化型+ne-
还原型
θ A
/V
K+/K Zn2+/Zn Fe2+/Fe H+/H2 Cu2+/Cu Ag+/Ag
F2/F-
K++e-
氧 Zn2+ +2e -
化 Fe2+ +2e-
能 2H+ +2e-
力 增
Cu2+
+2e-
强 Ag+ +e-
F2 +2e-
K
Zn 还
Fe 原
H2
能 力
Cu 增
Ag 强
F-
-2.925
-0.763 代 -0.44 数
0.000 值 +0.34 增 +0.7999 大
+2.87
能斯特方程式
能斯特方程式
1.能斯特方程(Nernst equation)
• 电极电势的大小,不仅取决于电对本身的性质, 还与反应温度、有关物质浓度、压力等有关。 • 能斯特从理论上推导出电极电势与浓度(或分 压)、温度之间的关系,对任一电对:
解:电极反应为 Zn2+ + 2e- Zn
(Zn2+/Zn)=φθ(Zn2+/Zn) +
0.0591V
{lgc(Zn2+)/cθ}
2
=-0.7626V + 0.0592V lg0.100
2
=-0.7922V
即当c(Zn2+)减少为cθ (Zn2+)十分之一时,
φ( Zn2+/Zn)值比φ θ(Zn2+/Zn)仅减少0.03V。
= + 1.36V +
0.0592V
1(10.0)14
lg
6
1
= + 1.50V
例题: 计算298K下 pH=5时,MnO4-/Mn2+ 的
电极电势(其他条件同标准态)。 解: 电极反应为:
MnO4-(aq)+8H+(aq)+5e- = Mn2+(aq)+4H2O 已知: c(MnO4-) = c(Mn2+) = 1mol.dm-3
作业:已知Cl2+2e- =2Cl- θ =1.358V MnO2+4H++2e- =Mn2+ + 2H2O θ =1.228V MnO4-+8H++5e- =Mn2+ + 4H2O θ =1.491V
通过计算,用MnO2制取氯气的时候盐酸的浓度最少为 多少?
电极反应: aOx + ne- ⇋ bRed
(OX/Red) (OX
/ Red ) RT nF
ln
[c (Ox) / c ]a [c (Red) / c ]b
能斯特方程式
•其中:F — 法拉第常数,F = 96485J·mol-1·V-1
•
n — 电极反应中转移的电子数
将 式 中 的 常 数 项 R = 8.314 J·K-1·mol-1, F = 96485 J·mol-1·V-1代入,并将自然对数改成常用对数, 在298.15K时,则有:
能斯特方程式
例 : 计 算 298.15K 下 , c(OH-) = 0.100mol·L-1 时 的
φ(O2/OH-)值。( 已知p(O2) =105 Pa)
解:电极反应为 O2 + 2H2O + 4e-
4OH-
φ(O2/OH-)=
φ
θ(O2/OH-)
+
0.0592V 4
lg
p(O 2 )/pθ
0.0591V lg [c (Ox) / c ]a
n
[c (Re d) / c ]b
能斯特方程式
• ◆应用能斯特方程时,应注 (意1):如果组成电对的物质是固体或液体,则它们的
浓度项不列入方程式中; 如果是气体,则要以气体物质的分压来表示。 (2)如果电极反应中,除了氧化态和还原态物质外, 还有参加电极反应的其他物质,如H+、OH-存在, 则应把这些物质也表示在能斯特方程中。 (3)半反应中的计量系数作为指数。
c(H+) = 1.0 10-5mol .dm-3, Z = 5 查表: E(MnO4-/ Mn2+)= +1.512V
E(MnO4-/ Mn2+) = E(MnO4-/ Mn2+)
+0—.0—59—2Vlg [—c(—M—nO—4-)—/c—][—c(—H+—) /—c—]8
Z
[c(Mn2+)/ c]
计算的φ (Cr2O72- /Cr3+ )值。
能斯特方程式
解:电极反应为
Cr2O
2 7
+
14H+
+
6e-
2Cr3+ + 7H2O
φ
2
(Cr2O7 /r3+ )
=φ
θ(Cr2O
2 7
/
Cr3+)
0.0592V lg n
[c(Cr2
O
2 7
-
)/c
θ
][c(H
)/c
θ
]14
[c(Cr 3 )/cθ ]2
{c (OH ) /cθ }4
=
+
0.401V
+
0.0592V 4
lg
1 (0.100 )4
= + 0.460 V
能斯特方程式
(2) 酸度对电极电势的影响
如果H+、OH-也参加电极反应,那么溶液酸度 的变化也会对电极电势产生影响。 例: 在298.15K下,将Pt片浸入c ( Cr2O72)- =c (Cr3+) =0.100 mol·L-1,c(H+) =10.0 mol·L-1溶液中。
