5第五次课—控制器的参数整定及其应用
PID控制器的参数整定及其应用

PID控制器未来的发展方向与应用前景
随着工业自动化技术的不断发展, PID控制器将朝着智能化、网络
化、集成化的方向发展。
新型的PID控制器将不断涌现, 如自适应PID控制器、模糊PID 控制器等,以满足更复杂、更高
要求的控制需求。
PID控制器在智能制造、机器人、 新能源等领域将得到更广泛的应 用,为工业自动化水平的提升做
PID控制器的改进与优化
积分分离PID
在积分作用较强的场合,通过将积分项进行分离,减小系统超调 量,提高系统稳定性。
抗积分饱和PID
在系统出现大幅度误差时,避免积分饱和导致系统失控,提高系 统的鲁棒性。
微分先行PID
将微分项放在偏差信号的前面,减小系统的超调量,提高系统的 动态性能。
PID控制器在物联网与人工智能时代的应用前景
02
PID控制器参数整定
比例系数(P)的作用与整定
总结词
比例系数是PID控制器中最重要的参数, 它决定了系统响应的增益和速度。
VS
详细描述
比例系数的作用是调节系统输出的增益, 当比例系数增大时,系统输出的响应速度 会加快,但过大会导致系统超调量增大, 甚至产生振荡;反之,过小则会使系统响 应速度变慢,甚至无法消除误差。在整定 时,需要根据系统的具体情况和要求,反 复调整比例系数,以达到理想的响应效果 。
pid控制器的参数整定及其 应用
目录
• PID控制器概述 • PID控制器参数整定 • PID控制器的应用 • PID控制器的发展趋势与展望 • 结论
01
PID控制器概述
PID控制器的定义
总结词
PID控制器是一种线性控制器,通过比例、积分和微分三个环节来调整系统输出 。
pid控制器参数整定方法及应用

pid控制器参数整定方法及应用1 绪论随着科技的发展,使用PID控制器参数及其应用已经成为当今时代中用于控制和调节机械系统的必需技术。
PID控制器的参数整定有助于更好地控制被控对象,提高控制性能。
本文述了PID控制器的参数整定方法,以及其在机械系统中的应用。
2 Pid控制器参数整定PID控制器参数整定通过选择适当的分子和分母系数来实现,这些系数实际上是控制器的“参数”,可以指导控制器对机械系统的控制行为。
下面通过实例来说明如何进行PID控制器参数整定: 假设我们正在使用PID控制一个汽车的控制系统,我们需要进行PID参数整定。
首先,我们需要通过试验来观察汽车的转弯能力以及汽车对转弯操作的响应,并记录读数。
然后,我们需要根据所获得的实验数据,确定PID控制器的Kp,Ki,Kd参数。
Kp:Kp参数可以定义为系统的放大系数,它可以保持系统的闭环响应更快。
Ki:Ki参数可以定义为系统的微调系数,它可以调整系统的稳定性。
Kd:Kd参数可以定义为系统的衰减系数,以防止系统产生过大的振荡。
根据实验数据,我们可以根据汽车的控制系统调节PID参数,使它能够更好地控制汽车的运动,并达到期望的控制效果。
3 Pid控制器的应用PID控制器的应用可以被广泛应用于机械系统,尤其是自动控制系统。
例如,它可以用于控制建筑电梯的运动,以达到轿厢精确控制的目的。
它还可以用于机器人控制,如翻转、移动或抓取物体。
此外,PID控制器可以被应用于各种控制系统中,如电力系统、工业系统、火车系统等。
在这些系统中,PID控制器可以用于控制速度,以达到预期的控制目标。
4 结论PID控制器参数整定是实现机械系统控制和调节的关键技术。
正确进行PID参数整定可以获得最佳的性能,而错误的参数设置可能会导致系统失控。
此外,PID控制器的应用可以被广泛应用于机械系统中以实现精确控制和调节。
PID控制器参数整定与应用

PID控制器参数整定与应用PID控制器由比例(P)、积分(I)和微分(D)三个部分组成。
比例控制器根据当前的偏差与参考值之间的差异给出一个输出。
积分控制器根据偏差随时间的累积计算输出,用于消除系统的稳态误差。
微分控制器根据偏差的变化率给出输出,用于稳定系统的动态响应。
PID控制器的输出是比例、积分和微分控制器的输出之和。
参数整定是指选择合适的PID控制器参数,使得控制系统能够稳定工作且具有良好的响应速度和抗干扰能力。
PID控制器的参数整定一般有以下几种方法:1.经验法:根据经验和实际控制系统的特点选择参数。
这种方法适用于控制系统较简单的情况,但不具有普适性。
2. Ziegler-Nichols方法:通过实验数据来确定参数。
首先将积分和微分参数设为零,逐渐增加比例参数,直到系统出现较小的超调(即超过参考值后回波的百分比),然后根据超调曲线确定比例和时间参数。
3. Chien-Hrones-Reswick方法:通过频域分析来确定参数。
首先将系统转化为频域传递函数,然后根据传递函数的特性来选择参数。
4.自整定方法:使用专门设计的算法来进行参数整定。
这些算法根据系统的频率响应和阶跃响应等特征进行参数的优化。
1.温度控制:PID控制器可以通过调节加热元件的功率来控制温度的稳定性和响应速度。
例如,在恒温恒湿箱中,通过测量温度偏差,计算出PID控制器的输出,来控制加热器的功率,使系统保持在设定温度下。
2.流量控制:PID控制器可以通过调节阀门的开度来控制液体或气体的流量。
例如,在一个水罐中,通过测量液位偏差,计算出PID控制器的输出,来控制阀门的开度,以维持设定的液位。
3.速度控制:PID控制器可以通过调节电机的输入电压或转矩来控制机械系统的速度。
例如,在一个电动机驱动的输送带系统中,PID控制器可以根据输送带的位置偏差,计算出对电机的控制信号,来控制输送带的速度。
4.位置控制:PID控制器可以通过调节电机的转矩或位置来控制机械系统的位置。
自动控制原理课程设计

自动控制原理课程设计一、课程目标知识目标:1. 理解自动控制原理的基本概念,掌握控制系统数学模型的建立方法;2. 掌握控制系统性能指标及其计算方法,了解各类控制器的设计原理;3. 学会分析控制系统的稳定性、快速性和准确性,并能够运用所学知识对实际控制系统进行优化。
技能目标:1. 能够运用数学软件(如MATLAB)进行控制系统建模、仿真和分析;2. 培养学生运用自动控制原理解决实际问题的能力,提高学生的工程素养;3. 培养学生团队协作、沟通表达和自主学习的能力。
情感态度价值观目标:1. 培养学生对自动控制原理的兴趣,激发学生探索科学技术的热情;2. 培养学生严谨、务实的学术态度,树立正确的价值观;3. 增强学生的国家使命感和社会责任感,认识到自动控制技术在国家经济建设和国防事业中的重要作用。
本课程针对高年级本科学生,结合学科特点和教学要求,将目标分解为具体的学习成果,为后续的教学设计和评估提供依据。
课程注重理论与实践相结合,提高学生的实际操作能力和解决实际问题的能力,为培养高素质的工程技术人才奠定基础。
二、教学内容本课程教学内容主要包括以下几部分:1. 自动控制原理基本概念:控制系统定义、分类及其基本组成;控制系统的性能指标;控制系统的数学模型。
2. 控制器设计:比例、积分、微分控制器的原理和设计方法;PID控制器的参数整定方法。
3. 控制系统稳定性分析:劳斯-赫尔维茨稳定性判据;奈奎斯特稳定性判据。
4. 控制系统性能分析:快速性、准确性分析;稳态误差计算。
5. 控制系统仿真与优化:利用MATLAB软件进行控制系统建模、仿真和分析;控制系统性能优化方法。
6. 实际控制系统案例分析:分析典型自动控制系统的设计原理及其在实际工程中的应用。
教学内容按照以下进度安排:第一周:自动控制原理基本概念及控制系统性能指标。
第二周:控制系统的数学模型及控制器设计。
第三周:PID控制器参数整定及稳定性分析。
第四周:控制系统性能分析及MATLAB仿真。
控制器参数整定的方法

控制器参数整定的方法控制器参数整定是指在控制系统中,通过调整控制器的参数使得系统具备所要求的稳定性、快速性、准确性等特性。
准确地整定控制器参数可以使得控制系统的动态性能最优化,从而提高系统的控制质量和稳定性。
通常来说,控制器参数整定可以从以下几个方面进行考虑:1. 稳定性要求:首先,需要确定系统的稳定性要求,即确定系统的闭环动态特性。
对于稳定性要求较高的系统,应该选择较小的控制器增益和较小的积分时间常数。
而对于容忍一定超调量和调整时间的系统,则可以调整控制器的参数,使得系统的动态特性更快速。
2. 模型准确性:控制器参数整定还要考虑系统的数学模型准确性。
如果系统的数学模型较精确,可以使用基于数学模型的整定方法,例如Ziegler-Nichols方法、极点配置法等。
但是实际系统的数学模型通常是未知的或者存在误差的,因此也可以采用试验法、经验法等基于试验数据的整定方法。
3. 考虑系统的性能指标:根据系统的实际需求,考虑系统的性能指标。
比如对于控制系统来说,通常会考虑超调量、调整时间、稳态误差等指标。
根据不同的性能指标,可以选取不同的参数整定方法。
例如,要求更快速的系统可以增大控制器的增益,降低积分和微分时间常数,来提高系统的响应速度。
4. 频域方法:频域方法是一种通过系统的频率响应来进行参数整定的方法。
这种方法主要基于控制系统的频率特性和频域响应,通过分析系统的相位裕度、增益裕度等性能指标,从而选取合适的控制器参数。
常用的频域方法有根轨迹法、小辛普森法等。
5. 自适应控制:自适应控制是一种能够根据系统实时变化状况调整参数的控制方法。
这种方法能够根据系统的反馈信号和预设目标信号之间的误差来调整控制器的参数,使得系统能够自动适应系统的变化。
自适应控制可以实现参数的在线整定,适用于系统的工作状态发生较大变化的情况。
总结起来,控制器参数整定应综合考虑稳定性要求、模型准确性、系统的性能指标等因素,选择合适的整定方法。
PID控制器参数整定方法及其应用研究

浙江大学硕士学位论文PID控制器参数整定方法及其应用研究姓名:曹刚申请学位级别:硕士专业:控制理论与控制工程指导教师:褚健;苏宏业20040301蛳江大学硕l:学位避文摘要随着工业生产的发展,于20世纪30年代,美国开始使用PID调节嚣,它比赢接作用式调节器具有更好的控制效果。
因而很快得到了工业界的认可。
至今,在所有生产过程控制中,大部分的回路仍采用结构简单、鲁棒性强的PID控制或改进型PID控制策略。
PID控制作为一种经典的控制方法,几乎遍及了整个工业自动化领域,是实际工业生产过程正常运行的基本保证;控制器的性能直接关系刘生产过程的平稳高教运行蛆及产品的最终质量,因此控制系统的设计主要体现在控制器参数的熬定上。
随着计算机技术的飞跃发展和人工智能技术渗透到自动控制领域,i醺年来出现了各种实用的PID控制器参数接定方法。
PID控制算法作为最通用的控制方法,对它的参数整定有许多方法;对于不同的控稍要求、不问的系统先验知识,考虑用不同的方法:这些算法既要考虑到收敛往、宣观、简荜易沼,还要综合负载干扰、过稷变化的影响,并能根据尽可能少盼信息和计算鬟,给密较好的络采。
论文在较为全面魏对PID控稍器参数自整定方法的现状分析研究的基础上,针对基予继电器菠镄鞠最小=乘的旮攘定方法戳及萁疯角的可行往进行了相关的矫究,主耍静工释帮结栗概括如下:为壳£琵一自由度PID控制器无法滚联舀称跟踪帮矫挠孪率箭的缺点,结合二自洳度控截器翡结梅帮蓥予辐毽最俊纯赫控制器参数整定方法,舞逶过分析得至《控制器参数求解公式,实现了二鸯出发PID控制器参数整定秘二螽出度PI控锖§器参数整定。
与豢授控割方法楣魄,该方法褥列静控粼器獒毒更好静潮环稚应褴能,劳且由于二鑫壹度系数鲍半爨定瞧,在整定PID控制器参数之蓠就霹激确定,因此,慰控制嚣参数的求鼹难度无影响。
针对~类一除大时涝不稳定姆魏慰象,普避鲶PID控制器缓鼹滤延要求,甚至不能实现系统的稳定。
PID控制器的参数整定(经验总结)

PID控制器的参数整定(1)PID是比例,积分,微分的缩写.比例调节作用:是按比例反应系统的偏差,系统一旦出现了偏差,比例调节立即产生调节作用用以减少偏差。
比例作用大,可以加快调节,减少误差,但是过大的比例,使系统的稳定性下降,甚至造成系统的不稳定。
积分调节作用:是使系统消除稳态误差,提高无差度。
因为有误差,积分调节就进行,直至无差,积分调节停止,积分调节输出一常值。
积分作用的强弱取决与积分时间常数Ti,Ti越小,积分作用就越强。
反之Ti大,则积分作用弱,加入积分调节可使系统稳定性下降,动态响应变慢。
积分作用常与另两种调节规律结合,组成PI调节器或PID调节器。
微分调节作用:微分作用反映系统偏差信号的变化率,具有预见性,能预见偏差变化的趋势,因此能产生超前的控制作用,在偏差还没有形成之前,已被微分调节作用消除。
因此,可以改善系统的动态性能。
在微分时间选择合适情况下,可以减少超调,减少调节时间。
微分作用对噪声干扰有放大作用,因此过强的加微分调节,对系统抗干扰不利。
此外,微分反应的是变化率,而当输入没有变化时,微分作用输出为零。
微分作用不能单独使用,需要与另外两种调节规律相结合,组成PD或PID控制器。
(2) PID具体调节方法①方法一确定控制器参数数字PID控制器控制参数的选择,可按连续-时间PID参数整定方法进行。
在选择数字PID参数之前,首先应该确定控制器结构。
对允许有静差(或稳态误差)的系统,可以适当选择P或PD控制器,使稳态误差在允许的范围内。
对必须消除稳态误差的系统,应选择包含积分控制的PI或PID控制器。
一般来说,PI、PID和P控制器应用较多。
对于有滞后的对象,往往都加入微分控制。
选择参数控制器结构确定后,即可开始选择参数。
参数的选择,要根据受控对象的具体特性和对控制系统的性能要求进行。
工程上,一般要求整个闭环系统是稳定的,对给定量的变化能迅速响应并平滑跟踪,超调量小;在不同干扰作用下,能保证被控量在给定值;当环境参数发生变化时,整个系统能保持稳定,等等。
控制器参数的理论整定法

因: 于是有:
Gc(ms , jω ) = S1=S1e j 0
代入
S1M p (m s , ω ) = 1
p (m s , ω ) = π
解得:
ω=ωs
1 S1 = M p (m , ω s )
控制器参数的理论整定法
例2 用衰减频率特性法整定比例调节器参数.已知被控对
象为纯迟延环节,其迟延时间为τ.
控制器参数的理论整定法
由稳定度判据
G c (ms , ω )G p (ms , ω ) = 1
得:
1 [m ssin p (m s , ω ) + cos p (m s , ω )] S1 = M p (m s , ω )
ω (1 + m ) S0 = sin p (m s , ω ) M p (m s , ω )
M c ( m s , j ω ) M p ( ms , j ω ) = 1 }
幅值条件 相角条件
c (ms , jω ) + p (ms , jω ) = π
求解时,先由相角条件计算出系统主导振荡分量的频 率,再代入幅值条件求出调节器的整定参数.
控制器参数的理论整定法
1.单参数调节器的整定
主要指比例调节器,其未定参数为比例增益S1.
解:因 于是有:
G (s) = e
τs
Gp (ms , jω) = e
=e
τ ( msω + jω)
τm sω jτω
=e
τm sω
e
jτω
M
p
p = τω
控制器参数的理论整定法
由相角条件得:
即:
τω = π π ωs = τ
或 δ =e
PID控制器参数整定与应用

PID控制器参数整定与应用PID控制器是一种常用的自动控制器,在工业自动化领域应用广泛。
它的主要作用是通过测量的偏差来调节执行器的控制量,从而使被控制对象的输出值与设定值之间达到最优的控制效果。
在实际中,PID控制器的参数整定是一个重要的环节,它直接影响控制系统的性能。
PID控制器由比例(P)、积分(I)和微分(D)三个控制部分组成,其中比例部分根据偏差的大小直接产生控制量,积分部分对偏差的积分产生控制量,微分部分对偏差的变化率产生控制量。
三个部分的输出量经过加权求和后作为最终的控制量。
整定PID控制器的参数需要根据被控制对象的特性进行调整,以达到快速、稳定、精确的控制效果。
常用的参数整定方法包括经验法、试验法和理论法。
经验法是根据工程师的经验和实际情况来调整PID控制器的参数。
比如,比例系数Kp的大小与偏差的关系可以通过试验来确定,当偏差增大时,可以逐渐增大Kp的值,直至产生足够的控制量来抵消偏差。
积分时间Ti和微分时间Td可以根据被控对象的时间常数和惯性大小来估计,通常由实验确定。
试验法是通过对控制系统进行一系列实验来获得最佳的参数值。
常见的试验方法有阶跃响应法、频率响应法和脉冲响应法。
阶跃响应法是将控制系统给定值变为一个阶跃信号,观察系统的响应情况,从而调整PID参数以使系统的超调量、稳定时间和上升时间等指标满足要求。
频率响应法是通过对控制系统施加不同频率的输入信号,测量系统的频率响应曲线来获得系统的增益和相位裕度,并根据理论模型进行参数整定。
脉冲响应法是通过给控制系统施加一系列脉冲信号,观察系统的响应特性,并在实验中逐步调整PID参数,直至达到最佳控制效果。
理论法是通过数学模型来推导PID控制器的参数,通常适用于被控对象的数学模型已知的情况。
这种方法可以根据被控对象的稳定裕度、相位裕度、动态响应等指标来推导PID参数的理论值,以实现最佳控制效果。
应用方面,PID控制器被广泛应用于各个领域,如工业过程控制、机械控制、电力系统控制等。
控制器的参数整定
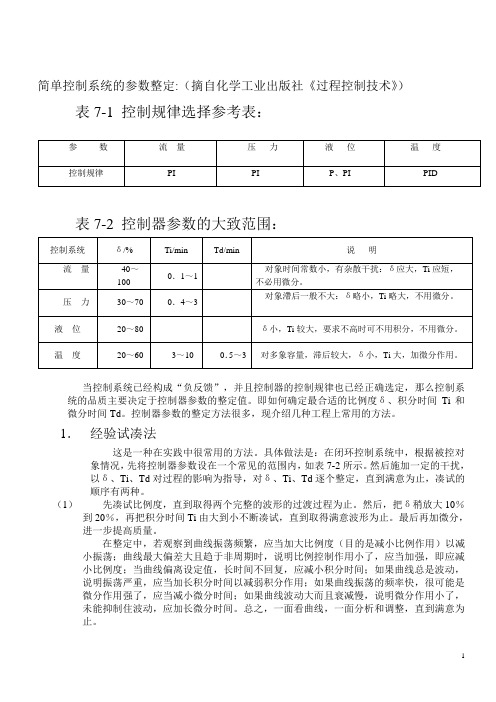
简单控制系统的参数整定:(摘自化学工业出版社《过程控制技术》)表7-1 控制规律选择参考表:表7-2 控制器参数的大致范围:当控制系统已经构成“负反馈”,并且控制器的控制规律也已经正确选定,那么控制系统的品质主要决定于控制器参数的整定值。
即如何确定最合适的比例度δ、积分时间Ti和微分时间Td。
控制器参数的整定方法很多,现介绍几种工程上常用的方法。
1.经验试凑法这是一种在实践中很常用的方法。
具体做法是:在闭环控制系统中,根据被控对象情况,先将控制器参数设在一个常见的范围内,如表7-2所示。
然后施加一定的干扰,以δ、Ti、Td对过程的影响为指导,对δ、Ti、Td逐个整定,直到满意为止,凑试的顺序有两种。
(1)先凑试比例度,直到取得两个完整的波形的过渡过程为止。
然后,把δ稍放大10%到20%,再把积分时间Ti由大到小不断凑试,直到取得满意波形为止。
最后再加微分,进一步提高质量。
在整定中,若观察到曲线振荡频繁,应当加大比例度(目的是减小比例作用)以减小振荡;曲线最大偏差大且趋于非周期时,说明比例控制作用小了,应当加强,即应减小比例度;当曲线偏离设定值,长时间不回复,应减小积分时间;如果曲线总是波动,说明振荡严重,应当加长积分时间以减弱积分作用;如果曲线振荡的频率快,很可能是微分作用强了,应当减小微分时间;如果曲线波动大而且衰减慢,说明微分作用小了,未能抑制住波动,应加长微分时间。
总之,一面看曲线,一面分析和调整,直到满意为止。
(2)是从表7-2中取Ti的某个值。
如果需要微分,则取Td=(1/3~1/4)Ti。
然后对δ进行凑试,也能较快达到要求。
实践证明,在一定范围内适当组合δ与Ti的数值,可以获得相同的衰减比曲线。
也就是说,δ的减小可用增加Ti的办法来补偿,而基本上不影响控制过程的质量。
所以,先确定Ti、Td再确定δ也是可以的。
2.衰减曲线法衰减曲线法比较简单,可分两种方法。
(1)4:1衰减曲线法当系统稳定时,在纯比例作用下,用改变设定值的办法加入阶跃扰动,观察记录曲线的衰减比。
PID控制器的参数整定及其应用[31]
![PID控制器的参数整定及其应用[31]](https://img.taocdn.com/s3/m/9a50e8b2fbb069dc5022aaea998fcc22bcd143d7.png)
将模糊逻辑与PID控制相结合,通过 模糊规则对PID参数进行自适应调整, 提高控制系统的鲁棒性和适应性。
采用遗传算法对PID参数进行优化, 通过模拟生物进化过程,寻找最优的 PID参数组合,提高控制系统的性能。
神经网络PID控制算法
利用神经网络的自学习、自组织能力, 对PID参数进行在线调整,以适应系 统参数的变化和不确定干扰。
PID在航空航天控制中的应用
在航空航天领域,PID控制器用于飞行器的导航、 姿态控制和推进器调节等,保证飞行器的安全和 稳定运行。
感谢您的观看
THANKS
实际工业系统参数整定
在实际工业系统中,PID控制器参数整定通常需要考虑系统的非线性、时变性和不确定性。
实际工业系统的控制过程往往比理论模型更为复杂,因此PID控制器参数整定需要更加细致和谨慎。常用的方法包括基于过 程的启发式调整、实验测试和在线自适应调整等。此外,为了保证系统的安全性和稳定性,通常还需要引入其他控制策略和 保护措施。
PID控制器与其他控制策略的结合
01
PID与模糊控制结合
将模糊逻辑控制与PID控制相结合,利用模糊逻辑处理不确定性和非线
性问题,提高控制系统的性能。
02
PID与预测控制结合
将预测控制与PID控制相结合,利用预测控制对系统未来行为的预测能
力,优化PID控制器的参数,提高系统的稳定性和鲁棒性。
03
PID与滑模控制结合
将滑模控制与PID控制相结合,利用滑模控制的快速响应和鲁棒性,提
高系统的动态性能和抗干扰能力。
PID控制器在智能控制领域的应用
1 2 3
PID在工业自动化中的应用
PID控制器广泛应用于工业自动化领域,如温度、 压力、流量等控制系统,提高生产过程的稳定性 和效率。
控制器参数整定方法及实例-zhm解读
PI控制器:
1 1 1 [0.9( / T ) 0.082] 0 K 0 2 [3.33( / T ) 0.3( / T ) ] T 0 0 I 1 2.2( T0 ) T0
§4.3控制器参数整定——三种常用工程整定方法的比
较
临界比例度法、衰减曲线法、反应曲线法都属于工程整定方法, 共同点是通过试验获取某些特征参数,然后再按照工程经验公式 计算控制器的整定参数; 不同点: 临界比例度法和衰减曲线法都是闭环整定方法,依赖系统在某种 运行状况下的特征参数都控制器参数进行整定,不需要掌握被控 过程的数学模型; 临界比例度法不适用于生产过程中不能反复振荡试验、对比例调 节是本质稳定的被控系统;在做衰减比较大的试验时,衰减曲线 法观测数据很难准确确定,不适用于过程变化快的系统;
PID控制器:
1 1 1 [1.35( / T ) 0.27] 0 K 0 TI [2.5( / T0 ) 0.5( / T0 ) 2 ] 1 0.6( / T0 ) T0 TD 0.37( / T0 ) T0 1 0.2( / T0 )
注意:准确地确定系统4:l(或l0:1)的衰减程度比较困难(±2/5%) 不适用于一些扰动比较频繁、过程变化比较快的系统
4、反应曲线法--开环整定方法
利用系统开环广义对象的阶跃响应曲线进行控制器参数整定。 齐格勒(Ziegler)-尼科尔斯(Nichols)在1942年提出的 步骤如下:
① 系统置于开环状态。 ② 在调节阀Gv(s)的输入端施加一个阶跃信号,记录下测量变 送环节Gm(s)的输出响应曲线y(t)。 ③ 根据阶跃响应曲线,得到广义对象的传递函数。
经验整定方法一:
先令PID成为纯P调节器(即令Ti=,Td=0) 按经验数据设置 整定控制系统,使之达到4:1衰减振荡的过渡过程曲线;
基于内模原理的PID控制器参数整定ppt课件

e G(s) 0.7 50s 290s 1
根据上式,分别按IMC法、ZN法、CC法整定PID参数如下: IMC法:取ε=40,相应有KC=4.32s,TI=302.5,TD=11.81s; ZN法:KC=9.94,TI=100s,TD=25s; CC法:KC=11.57,TI=117.2s,TD=17.88s.
简介
内模控制方法是Garcia和Morari于1982年首先正式提出,以其简 单、跟踪调节性能好、鲁棒性强、能消除不可测干扰等优点,为控 制理论界和工程界所重视。1989年Morari透彻研究了内模控制的鲁 棒性和稳定性,并且由其他学者推广到非线性系统,蓬勃发展中的 神经网络也引入到内模控制中。内模控制还和许多其它控制方式相 结合,如内模控制与模糊控制、内模控制和自适应控制、内模控制 和最优控制、预测控制的结合使内模控制不断得到改进并广泛应用 于工程实践中,取得了良好的效果。
Tps 1
(12)
就以上过程模型做两点说明:(1)对于最小相位系统,只需令 a=0即可;(2)对于像电站粉锅炉主蒸汽温度系统之类的多容高阶大 惯性环节,可以等效为上式,不过a=0,而且这种等效造成的误差可 以达到相当满意的程度。
根据内模控制器设计步骤,对Gm(s)作如(7)、(8)形式分解,
得到:
e Gm (s) (1 as) ps ,Gm (s) Kp Tps 1
知,采用 1 形式的一阶低通滤波器即可。至此可以给出对一大
s 1
类系统的内模PID整定步骤:
(1)对被控对象模型进行低阶等效,得到(12)式的形式; (2)按(13)式进行模型分解; (3)根据(14)式求出(13)式在s=0处的各阶导数值; (4)取r=1,选取滤波器时间常数ε,据(17)式求D(S)在s=0处 的各阶导数值; (5)据(18)式求f(s)在s=0处的各阶导数值; (6)据(15)式求取PID控制器参数; (7)仿真验证或现场观察控制效果,若满意,则结束;若不满 意,则返回(4)重新选择ε。
.PID控制器的参数整定及其应用

“广义对象”动态特性的 阶跃响应测试法*
典型自衡工业对象 的阶跃响应
u(t) u0
t 0
对象的近似模型:
y( s ) K e s u( s ) Ts 1
u1
对应参数见左图,而增益为:
y1 p
y(t)
y1 y 0 K y max y min
u1 u0 umax umin
y0 τ T0 T1 T
t
[ymin, ymax]为CV的测量范围; [umin, umax]为MV的变化范围,对于
T2 T3
阀位开度通常用0~100%表示。
Ziegler-Nichols参数整定法*
特点:适合于存在明显纯滞后的自衡对象,而且广义 对象的阶跃响应曲线可用“一阶+纯滞后”来近似。 整定公式:
单回路系统的“积分饱和”问题
d(t) ysp(t)
+ -
æ 1 ö K C ç1 ç T s÷ ÷ I ø è
u
v
广义 对象
+
+
y(t)
问题:当存在大的外部扰动时,很有可能出现控制阀调 节能力不够的情况,即使控制阀全开或全关,仍不能消 除被控输出y(t)与设定值ysp(t)之间的误差。此时,由于积 分作用的存在,使调节器输出u(t)无限制地增大或减少, 直至达到极限值。而当扰动恢复正常时,由于u(t)在可调 范围以外,不能马上起调节作用;等待一定时间后,系 统才能恢复正常。
工程整定法2-临界比例度法
步骤:
(1)先切除PID控制器中的积分与微分作用,取比例增益 KC为一较小值,并投入闭环运行; (2)将KC由小到大变化,对应于每一KC值作小幅度的设定 值阶跃响应,直至产生等幅振荡; (3)设等幅振荡时振荡周期为Tcr、控制器增益Kcmax ,再 根据控制器类型选择以下PID参数。 控制规律 P PI PID Kc 0.5Kcmax 0.45Kcmax 0.6Kcmax Ti 0.83Tcr 0.5Tcr Td
15 控制器参数的整定

① 将控制器的积分时间TI置于最大( TI =∞) ,微分时间TD 置零 (TD=0),比例带置为较大的数值, 把系统投入闭环运行。
② 系统稳定后,施加一个阶跃输入;减小比例度,直到出现衰减 振荡为止。记录比例带,及衰减振荡周期或上升时间。
华北电力大学 能源工程及自动化教研室
需要知道数学模型 理论计算整定方法
对数频率特性法 根轨迹法
工程整定法
不需要事先知道过程的数学模型, 可直接在系统中进行现场整定,比 较简单
经验法 衰减曲线法 临界比例度法 响应曲线法
华北电力大学 能源工程及自动化教研室
10
Click to edit Master title style 《化工仪表及过程控制》
Z (t )
K0
1
O
T0
t
G0' (s)
K0 es 1 T0s
1 es
1 T0s
T
dy
t
dt
y
t
Kxt
华北电力大学 能源工程及自动化教研室
D 0.8
TD (0.25 ~ 0.3)
20
Click to edit Master title style 《化工仪表及过程控制》
华北电力大学 能源工程及自动化教研室
8
Click to edit Master title style 《化工仪表及过程控制》
PID控制参数的整定方法---原则
被控过程的特点及其控制器参数范围
项目 时滞
流量 液体压力
无
气体压力 无
容量数 多容量 单容量
浙大工业过程控制-4.PID控制器的参数整定及其应用

2
pid控制器通过比较压力设定值与实际值之间的 误差,不断调整气瓶的阀门或泵的工作状态,从 而实现对压力的精确控制。
3
在压力控制系统中,pid控制器能够快速响应压 力的变化,并自动调整气瓶的阀门或泵的工作状 态,确保压力的稳定。
05 结论
pid控制器的发展趋势
智能化
随着人工智能和机器学习技术的发展,PID控制器将逐渐实现智能 化,能够自适应地调整参数,提高控制精度和稳定性。
详细描述
智能优化算法利用人工智能和优化算法,如遗传算法、粒子群算法等,自动确 定PID控制器的参数。这种方法能够处理高度非线性、不确定性和时变性的系统, 但需要较高的计算资源和较长的计算时间。
04 pid控制器的应用实例
液位控制系统
液位控制系统是pid控制器最常见的应 用之一。通过pid控制器,可以精确控 制液位的高度,使其保持在设定的范 围内。
浙大工业过程控制-4.pid控制器的 参数整定及其应用
目录
• 引言 • pid控制器的基本原理 • pid控制器的参数整定方法 • pid控制器的应用实例 • 结论Fra bibliotek01 引言
背景介绍
工业过程控制是实现工业自动化和智 能化的重要手段,而PID控制器作为 一种经典的控制算法,在工业过程控 制中得到了广泛应用。
PID控制器具有结构简单、易于实现、 鲁棒性强等优点,适用于各种线性或 非线性系统。
pid控制器的重要性
PID控制器在工业过程控制中发挥着至关重要的作用,能够提高系统的控制精度 、稳定性和响应速度,从而提高生产效率和产品质量。
PID控制器的参数整定是实现其优良性能的关键,需要根据不同的控制系统和工 况进行合理调整。
在液位控制系统中,pid控制器能够快 速响应液位的变化,并自动调整水泵 的工作状态,确保液位高度的稳定。
控制器参数整定方法及实例-zhm

y3 To Workspace
0
20
40
60
80
100
120
140
160
180
200
§4.3
控制器参数整定——举例
PID 1.8 1.6 9.4 Z-N C-C LINJIE
比例积分微分控制下,不同整定方法的响应曲线:
0.01 (s+0.2)(s+0.5)(s+0.1) Zero-Pole 1/s
0
20
40
60
80
100
120
140
160
180
200
§4.3控制器参数整定——举例
比例积分控制下,不同整定方法的响应曲线:
PI 1.6 1.4 Z-N C-C LINJIE
5.7 Step
1.2
0.01 (s+0.2)(s+0.5)(s+0.1) Zero-Pole 1/s
Scope
1/12.85
PI控制器:
1 1 1 [0.9( / T ) 0.082] 0 K 0 2 [3.33( / T ) 0.3( / T ) ] T 0 0 I 1 2.2( T0 ) T0
§4.3控制器参数整定——三种常用工程整定方法的比
较
临界比例度法、衰减曲线法、反应曲线法都属于工程整定方法, 共同点是通过试验获取某些特征参数,然后再按照工程经验公式 计算控制器的整定参数; 不同点: 临界比例度法和衰减曲线法都是闭环整定方法,依赖系统在某种 运行状况下的特征参数都控制器参数进行整定,不需要掌握被控 过程的数学模型; 临界比例度法不适用于生产过程中不能反复振荡试验、对比例调 节是本质稳定的被控系统;在做衰减比较大的试验时,衰减曲线 控制器参数整定——举例
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
手自动无扰动切换问题与实现
增量型 手操器 Man ysp(t) y(t)
+ -
+ u
e(t)
KC
TD s 1 AD TD s 1
+ +
Auto
1 TI s 1
实现方式: 在Auto (自动)状态,使手操器输出等于调节器的输出; 而在Man(手动)时,使调节器输出等于手操器的输出;
继电器型PID自整定器原理
[ymin, ymax]为CV的测量范围; [umin, umax]为MV的变化范围,对于
t
T2
T3
阀位开度通常用0~100%表示。
Ziegler-Nichols参数整定法*
特点:适合于存在明显纯滞后的自衡对象,而且广义 对象的阶跃响应曲线可用“一阶+纯滞后”来近似。 整定公式:
控制规律 P PI PID
工业PID控制器的选择
被控参数 控制器 备注 温度/成分 流量/压力 液位/料位 PID PI P *1
*1:当工业对象具 有较大的滞后时, 可引入微分作用; 但如果测量噪声较 大,则应先对测量 信号进行一阶或平 均滤波。
讨论:
选择原则分析。
PID工程整定法1-经验法
针对被控变量类型的不同,选择不同 的PID参数初始值,投运后再作调整。尽 管简单,但即使对于同一类型的被控变量, 如温度系统,其控制通道的动态特性差别 可能很大,因而经验法属最为“粗糙”的 整定法。
u
v
广义 对象
+
+
y(t)
问题:当存在大的外部扰动时,很有可能出现控制阀调 节能力不够的情况,即使控制阀全开或全关,仍不能消 除被控输出y(t)与设定值ysp(t)之间的误差。此时,由于积 分作用的存在,使调节器输出u(t)无限制地增大或减少, 直至达到极限值。而当扰动恢复正常时,由于u(t)在可调 范围以外,不能马上起调节作用;等待一定时间后,系 统才能恢复正常。
u
Rf 燃料
(2) 如何选择温度控制 器的正反作用,以 使闭环系统为负反 馈系统?
PID控制器的物理意义讨论
对于一般的自衡过程,当设定值或扰动发生阶 路变化时,为什么采用纯比例控制器会存在稳 态余差?(输入不为零,输出也不为零) 引入积分作用的目的是什么,为什么引入积分 作用会降低闭环控制系统的稳定性? 引入微分作用的目的是什么,为什么实际工业 过程中应用并不多?
响应曲线法举例(续)
对于无显著纯滞后的自衡对象 PID参数整定法(1/4准则)*
特点:适合于纯滞后不显著的自衡对象,而且广义对 象的阶跃响应为 “S” 型曲线。 初始整定参数: 1 1 1 K p *100 %, TI * Ts , TD * TI 4 4 4
Ts 为对象开环阶跃响应的过渡过程时间。
调节器 ysp + - 继电器 A T S 对象 D y
具有继电器型非线性控制系统
ysp + -
-d d -h h
G(s)
y
问题:如何分析上述非线性系统产生等幅振荡的条件 ?
继电器输入输出信号分析
结 论
讨论了PID控制规律的选取原则, 详细分析了单回路PID参数整定方法, 介绍了PID控制器的“防积分饱和”与 “无扰动切换”技术.
单回路系统积分饱和现象举例
单回路PID控制系统(无抗积分饱和措施)
单回路系统积分饱和仿真结果
单回路系统的防积分饱和原理
d(t) ysp(t)
+ -
e(s) KC
+ +
v
广义 对象
+
+
y(t)
1 TI s 1
讨论:正常情况为标准的PI控制算法;而当出现超限时, 自动切除积分作用。
单回路系统的抗积分饱和举例
参数调整:将上述PID控制器投入“Auto” (自动)方 式,并适当改变控制回路的设定值,观察控制系统跟 踪性能。若响应过慢且无超调,则适当加大KC,例如 增大到原来的两倍;反之,则减小KC值。
响应曲线1/4准则法举例
单回路系统的“积分饱和”问题
d(t) ysp(t)
+ -
æ 1 ö KC ç 1 ç T s÷ ÷ I ø è
KC
Tp 1 K p
0 .9 Tp 1 Kp
TI
TD
3 .3
ห้องสมุดไป่ตู้
Tp 1 1 .2 K p
2 .0
0 .5
响应曲线法举例
已知:假设温度测量 变送器的量程为200 ~ 400℃。 K = 1.75, T = 9 min, τ = 7 min. Kc = 0.8, Ti = 14 min, Td = 3.5 min.
本讲基本要求
了解PID控制规律的选取原则, 掌握单回路PID控制器的参数整定方法, 了解PID控制器的“防积分饱和”与 “无扰动切换”技术, 了解PID参数的自整定方法。
PID参数对控制性能的影响
控制器增益 Kc或比例度δ 增益 Kc 的增大(或比例度δ下降),使系统的调节作 用增强,但稳定性下降; 积分时间Ti 积分作用的增强(即Ti 下降),使系统消除余差的能 力加强,但会引起相角滞后,使控制系统的稳定性下 降; 微分时间Td 微分作用增强(即Td 增大),可使系统的超前作用增 强,稳定性得到加强,但对高频噪声起放大作用,主 要适合于特性滞后较大的广义对象,如温度对象等。
“广义对象”动态特性的 阶跃响应测试法*
典型自衡工业对象 的阶跃响应
u(t) u0
0 t
对象的近似模型:
u1
y(s) K s e u ( s) Ts 1
对应参数见左图,而增益为:
y(t) p y0 τ T0 T1 T
y1
y1 y0 K ymax ymin
u1 u0 umax umin
工程整定法2-临界比例度法
步骤:(1)先将切除PID控制器中的积分与微分作用,取 比例增益KC较小值,并投入闭环运行; (2)将KC由小到大变化,对应于某一KC值作小幅度的设 定值阶跃响应,直至产生等幅振荡; (3)设等幅振荡时振荡周期为Tcr、控制器增益Kcr ,再 根据控制器类型选择以下PID参数。 控制规律 P PI PID Kc Ti 0.83Tcr 0.5Tcr 0.12Tcr Td
0.5Kcr 0.45Kcr
0.6Kcr
单回路PID参数整定仿真举例
工程整定法3-响应曲线法*
临界比例度法的局限性:
生产过程有时不允许出现等幅振荡,或者无法产生正 常操作范围内的等幅振荡。
响应曲线法PID参数整定步骤:
(1)在手动状态下,改变控制器输出(通常采用阶跃 变化),记录被控变量的响应曲线; (2)由开环响应曲线获得单位阶跃响应曲线,并求取 “广义对象”的近似模型与模型参数; (3)根据控制器类型与对象模型,选择PID参数并投 入闭环运行。在运行过程中,可对增益作调整。
练习题
对于题图,所示的加热炉出口温度控制系统,假设变送器量程 为200 ~ 300℃。试回答以下问题并说明理由:
(1)燃料控制阀选用“气开”阀还是“气关阀”?
(2)温度控制器该选“正作用”还是“反作用”? (3)若在手动控制状态,燃料控制阀风压(或者说温度控 制器输出电流)减少3%,炉出口温度的变化过程如题5-8下 表格所示。请确定“广义对象”的特性参数K、T、τ。 (4)若温度控制器采用PID调节器,试确定PID参数,并给 出SimuLink仿真曲线(假设设定值从270℃上升至280℃ )。
PID控制器的 参数整定与应用问题
上一讲内容回顾
讨论仿真系统SimuLink的使用方法; 介绍了单回路控制器“正反作用”的选 择原则; 描述了单回路系统的常用性能指标; 通过仿真讨论了PID控制律的意义及与 控制性能的关系。
控制器的“正反作用”选择
Tsp Tm 进料 T
出料 TC
问题: (1) 如何选择控制阀的 “气开气关”?
