实验三.哈夫曼编码的贪心算法设计
实验四哈夫曼编码的贪心算法设计（ 4 学时）
［实验目的］
1. 根据算法设计需要，掌握哈夫曼编码的二叉树结构表示方法；
2. 编程实现哈夫曼编译码器；
3. 掌握贪心算法的一般设计方法。
实验目的和要求
（1）了解前缀编码的概念，理解数据压缩的基本方法；
（2）掌握最优子结构性质的证明方法；
（3）掌握贪心法的设计思想并能熟练运用
（4）证明哈夫曼树满足最优子结构性质；
（5）设计贪心算法求解哈夫曼编码方案；
（6）设计测试数据，写出程序文档。
实验内容j
设需要编码的字符集为{d1, d2, -dn }，它们出现的频率为k i a k{w1, w2, --wn}，应用哈夫曼树构ki 造最短的不等长编码方案。
核心源代码
#include
#include
#include
typedef struct
{
unsigned int weight；// 用来存放各个结点的权值
unsigned int parent，LChild，RChild；// 指向双亲、孩子结点的指针
} HTNode， *HuffmanTree；// 动态分配数组，存储哈夫曼树
typedef char *HuffmanCode；// 动态分配数组，存储哈夫曼编码
可编辑
// 选择两个 parent 为 0，且 weight 最小的结点 s1 和 s2 void Select(HuffmanTree *ht,int n,int *s1,int *s2) {
int i,min;
for(i=1; i<=n; i++)
{
if((*ht)[i].parent==0)
{
min=i;
break;
}
}
for(i=1; i<=n; i++)
{
if((*ht)[i].parent==0)
{
if((*ht)[i].weight<(*ht)[min].weight)
min=i;
}
}
*s1=min;
for(i=1; i<=n; i++)
if((*ht)[i].parent==0 && i!=(*s1))
中衡算法分析与【设计明细】-实验二-哈夫曼编码
昆明理工大学信息工程与自动化学院学生实验报告 （201 —201 学年第一学期） 课程名称：算法设计与分析开课实验室：年月日 一、上机目的及内容 1.上机内容 设需要编码的字符集为{d1, d2, …, dn}，它们出现的频率为{w1, w2, …, wn}，应用哈夫曼树构造最短的不等长编码方案。 2.上机目的 （1）了解前缀编码的概念，理解数据压缩的基本方法； （2）掌握最优子结构性质的证明方法； （3）掌握贪心法的设计思想并能熟练运用。 二、实验原理及基本技术路线图（方框原理图或程序流程图） （1）证明哈夫曼树满足最优子结构性质； （2）设计贪心算法求解哈夫曼编码方案； （3）设计测试数据，写出程序文档。 数据结构与算法: typedef char *HuffmanCode; //动态分配数组，存储哈夫曼编码 typedef struct { unsigned int weight; //用来存放各个结点的权值 unsigned int parent,LChild,RChild; //指向双亲、孩子结点的指针 } HTNode, *HuffmanTree; //动态分配数组，存储哈夫曼树 程序流程图：
三、所用仪器、材料（设备名称、型号、规格等或使用软件） 1台PC及VISUAL C++6.0软件
四、实验方法、步骤（或：程序代码或操作过程） 程序代码： #include
算法设计与分析实验报告贪心算法
算法设计与分析实验报告 贪心算法 班级：2013156 学号：201315614 姓名：张春阳哈夫曼编码 代码 #include printf("\n"); for(i=0;i 软件02 1311611006 张松彬利用贪心算法构造哈夫曼树及输出对应的哈夫曼编码 问题简述： 两路合并最佳模式的贪心算法主要思想如下： （1）设w={w0,w1,......wn-1}是一组权值，以每个权值作为根结点值，构造n棵只有根的二叉树 （2）选择两根结点权值最小的树，作为左右子树构造一棵新二叉树，新树根的权值是两棵子树根权值之和 （3）重复（2），直到合并成一颗二叉树为 一、实验目的 （1）了解贪心算法和哈夫曼树的定义（2）掌握贪心法的设计思想并能熟练运用（3）设计贪心算法求解哈夫曼树（4）设计测试数据，写出程序文档 二、实验内容 （1）设计二叉树结点数据结构，编程实现对用户输入的一组权值构造哈夫曼树（2）设计函数，先序遍历输出哈夫曼树各结点3)设计函数，按树形输出哈夫曼树 代码： #include 实验四 哈夫曼编码的贪心算法设计（4学时） [实验目的] １. 根据算法设计需要,掌握哈夫曼编码的二叉树结构表示方法; ２. 编程实现哈夫曼编译码器; ３. 掌握贪心算法的一般设计方法。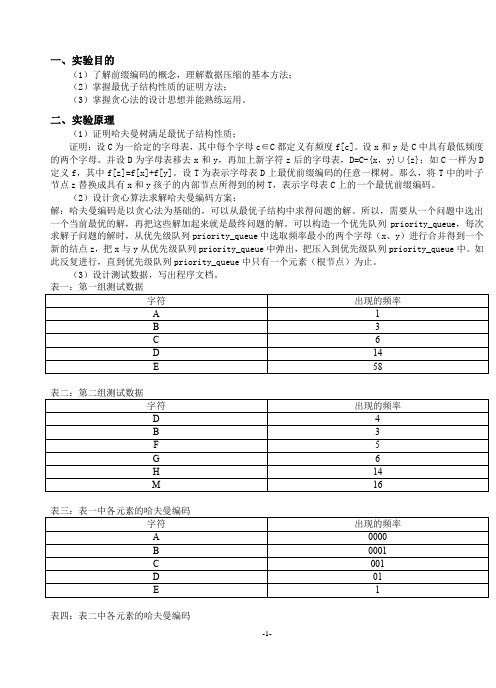 实验目的和要求 （1）了解前缀编码的概念，理解数据压缩的基本方法； （2）掌握最优子结构性质的证明方法； （3）掌握贪心法的设计思想并能熟练运用 （4）证明哈夫曼树满足最优子结构性质； （5）设计贪心算法求解哈夫曼编码方案； （6）设计测试数据，写出程序文档。 实验内容 设需要编码的字符集为{d 1, d 2, …, dn }，它们出现的频率为 {w 1, w 2, …, wn }，应用哈夫曼树构造最短的不等长编码方案。 核心源代码 #include //选择两个parent为0，且weight最小的结点s1和s2 void Select(HuffmanTree *ht,int n,int *s1,int *s2) { int i,min; for(i=1; i<=n; i++) { if((*ht)[i].parent==0) { min=i; break; } } for(i=1; i<=n; i++) { if((*ht)[i].parent==0) { if((*ht)[i].weight<(*ht)[min].weight) min=i; } } *s1=min; for(i=1; i<=n; i++) 《数据结构与算法设计》 实验报告 ——实验一 学院： 班级： 学号： 姓名： 一、实验目的 1.通过实验实践、巩固线性表的相关操作； 2.熟悉VC环境，加强编程、调试的练习； 3.用C语言编写函数，实现循环链表的建立、插入、删除、取数据等基本操作； 4.理论知识与实际问题相结合，利用上述基本操作实现约瑟夫环。 二、实验内容 1、采用单向环表实现约瑟夫环。 请按以下要求编程实现： ①从键盘输入整数m，通过create函数生成一个具有m个结点的单向环表。环表中的 结点编号依次为1，2，……，m。 ②从键盘输入整数s（1<=s<=m）和n，从环表的第s个结点开始计数为1，当计数到 第n个结点时，输出该第n结点对应的编号，将该结点从环表中消除，从输出结点 的下一个结点开始重新计数到n，这样，不断进行计数，不断进行输出，直到输出 了这个环表的全部结点为止。 三、程序设计 1、概要设计 为实现上述程序功能，应用单向环表寄存编号，为此需要建立一个抽象数据类型：单向环表。 （1）、单向环表的抽象数据类型定义为： ADT Joseph{ 数据对象：D={ai|ai∈ElemSet,i=1,2,3……,n,n≥0} 数据关系：R1={ 实验报告一 课程C++ 实验名称简单算法设计第 1 页专业_数学与应用数学_ __ 班级__ 双师一班学号105012011056 姓名陈萌 实验日期：2013 年 3 月9 日报告退发(订正、重做) 一、实验目的 1. 理解算法设计与分析的基本概念，理解解决问题的算法设计与实现过程； 2. 掌握简单问题的算法设计与分析，能设计比较高效的算法； 3. 熟悉C/C++语言等的集成开发环境，掌握简单程序设计与实现的能力。 二、实验内容 (一)相等元素问题 1.问题描述 元素唯一性问题：给出一个整数集合，假定这些整数存储在数组A[1…n]中，确定它们中是否存在两个相等的元素。请设计出一个有效算法来解决这个问题，你的算法的时间复杂性是多少？ 2. 具体要求（若在ACM平台上提交程序，必须按此要求）――平台上1767题 输入：输入的第一行是一个正整数m，表示测试例个数。接下来几行是m个测试例的数据，每个测试例的数据由两行组成，其中第一行为一个正整数n (n<=500)，表示整数序列的长度，第二行给出整数序列，整数之间用一个空格隔开。 输出：对于每个测试例输出一行，若该组测试例中存在两个相等的元素则输出”Yes”，否则，输出”No”。每个测试例的输出数据用一行表示。 3. 测试数据 输入：3 10 9 71 25 64 38 52 5 31 19 45 16 26 35 17 92 53 24 6 57 21 12 34 2 17 86 75 33 20 15 87 32 7 84 35 26 45 78 96 52 22 37 65 9 43 21 3 33 91 输出：No Yes No (二) 整数集合分解 1.问题描述 设计算法把一个n个元素的整数集合（n为偶数）分成两个子集S1和S2，使得：每个新的集合中含有n/2个元素，且S1中的所有元素的和与S2中的所有元素的和的差最大。 2. 具体要求（若在ACM平台上提交程序，必须按此要求）――平台上1768题 输入的第一行是一个正整数m，表示测试例个数。接下来几行是m个测试例的数据，每个测试例的数据由两行组成，其中第一行为一个正整数n (n为偶数，且n<=500)，表示原整数集合的长度，第二行给出这n个整数序列，整数之间用一个空格隔开。 输出：对于每个测试例输出两行，分别表示新生成的整数集合。其中，第一行是元素和比较小的整数集合，第二行是元素和比较大的整数集合，整数之间用一个空格隔开。两个测 实验三树的应用 一.实验题目： 树的应用——哈夫曼编码 二.实验内容： 利用哈夫曼编码进行通信可以大大提高信道的利用率，缩短信息传输的时间，降低传输成本。根据哈夫曼编码的原理，编写一个程序，在用户输入结点权值的基础上求哈夫曼编码。 要求：从键盘输入若干字符及每个字符出现的频率，将字符出现的频率作为结点的权值，建立哈夫曼树，然后对各个字符进行哈夫曼编码，最后打印输出字符及对应的哈夫曼编码。 三、程序源代码: #include 算法设计与分析实验报告 学院：信息学院 专业：物联网1101 姓名：黄振亮 学号：20113379 2013年11月 目录 作业1 0-1背包问题的动态规划算法 (7) 1.1算法应用背景 (3) 1.2算法原理 (3) 1.3算法描述 (4) 1.4程序实现及程序截图 (4) 1.4.1程序源码 (4) 1.4.2程序截图 (5) 1.5学习或程序调试心得 (6) 作业2 0-1背包问题的回溯算法 (7) 2.1算法应用背景 (3) 2.2算法原理 (3) 2.3算法描述 (4) 2.4程序实现及程序截图 (4) 2.4.1程序源码 (4) 2.4.2程序截图 (5) 2.5学习或程序调试心得 (6) 作业3循环赛日程表的分治算法 (7) 3.1算法应用背景 (3) 3.2算法原理 (3) 3.3算法描述 (4) 3.4程序实现及程序截图 (4) 3.4.1程序源码 (4) 3.4.2程序截图 (5) 3.5学习或程序调试心得 (6) 作业4活动安排的贪心算法 (7) 4.1算法应用背景 (3) 4.2算法原理 (3) 4.3算法描述 (4) 4.4程序实现及程序截图 (4) 4.4.1程序源码 (4) 4.4.2程序截图 (5) 4.5学习或程序调试心得 (6) 作业1 0-1背包问题的动态规划算法 1.1算法应用背景 从计算复杂性来看,背包问题是一个NP难解问题。半个世纪以来,该问题一直是算法与复杂性研究的热点之一。另外,背包问题在信息加密、预算控制、项目选择、材料切割、货物装载、网络信息安全等应用中具有重要的价值。如果能够解决这个问题那么则具有很高的经济价值和决策价值，在上述领域可以获得最大的价值。本文从动态规划角度给出一种解决背包问题的算法。 1.2算法原理 1.2.1、问题描述： 给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问:应如何选择装入背包的物品，使得装入背包中物品的总价值最大? 形式化描述：给定c >0, wi >0, vi >0 , 1≤i≤n.要求找一n元向量(x1,x2,…,xn,), xi ∈{0,1}, ?∑ wi xi≤c,且∑ vi xi达最大.即一个特殊的整数规划问题。 1.2.2、最优性原理： 设(y1,y2,…,yn)是 (3.4.1)的一个最优解.则(y2,…,yn)是下面相应子问题的一个最优解: 证明:使用反证法。若不然,设(z2,z3,…,zn)是上述子问题的一个最优解,而(y2,y3,…,yn)不是它的最优解。显然有 ∑vizi > ∑viyi (i=2,…,n) 且 w1y1+ ∑wizi<= c 因此 v1y1+ ∑vizi (i=2,…,n) > ∑ viyi, (i=1,…,n) 说明(y1,z2, z3,…,zn)是(3.4.1)0-1背包问题的一个更优解,导出(y1,y2,…,yn)不是背包问题的最优解,矛盾。 1.2.3、递推关系： 0023算法笔记——【贪心算法】哈夫曼编码问题 1、问题描述 哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%～90%之间。哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0，1串表示各字符的最优表示方式。一个包含100,000个字符的文件，各字符出现频率不同，如下表所示。 有多种方式表示文件中的信息，若用0,1码表示字符的方法，即每个字符用唯一的一个0,1串表示。若采用定长编码表示，则需要3位表示一个字符，整个文件编码需要300,000位；若采用变长编码表示，给频率高的字符较短的编码；频率低的字符较长的编码，达到整体编码减少的目的，则整个文件编码需要（45×1+13×3+12×3+16×3+9×4+5×4）×1000=224,000位，由此可见，变长码比定长码方案好，总码长减小约25%。 前缀码：对每一个字符规定一个0,1串作为其代码，并要求任一字符的代码都不是其他字符代码的前缀。这种编码称为前缀码。编码的前缀性质可以使译码方法非常简单；例如001011101可以唯一的分解为0,0,101,1101，因而其译码为aabe。 译码过程需要方便的取出编码的前缀，因此需要表示前缀码的合适的数据结构。为此，可以用二叉树作为前缀码的数据结构：树叶表示给定字符；从树根到树叶的路径当作该字符的前缀码；代码中每一位的0或1分别作为指示某节点到左儿子或右儿子的“路标”。 从上图可以看出，表示最优前缀码的二叉树总是一棵完全二叉树，即树中任意节点都有2个儿子。图a表示定长编码方案不是最优的，其编码的二叉树不是一棵完全二叉树。在一般情况下，若C是编码字符集，表示其最优前缀码的二叉树中恰有|C|个叶子。每个叶子对应于字符集中的一个字符，该二叉树有|C|-1个内部节点。 给定编码字符集C及频率分布f,即C中任一字符c以频率f(c)在数据文件中出现。C的一个前缀码编码方案对应于一棵二叉树T。字符c在树T中的深度记为d T(c)。d T(c)也是字符c的前缀码长。则平均码长定义为： 《算法设计》实习报告 班级 XXXX 名 XX 学号 XXXXXXX 1.给出Dijkstra算法的思想,并用C或C++实现，并分析该算法的复杂度。对下 图所示的有向网，试利用Dijkstra算法求出从源点1到其他顶点的最短路径。 实习报告的内容： <一>解决问题和算法思想 这个问题即为单源最短路问题。解决单源最短路径的基本思想是把图中所有结点分为两组，每一个结点对应一个距离值。设置两个结点的集合S和T，集合S中存放已找到最短路径的结点，集合T存放当前还未找到最短路径的结点。初始状态时，集合S只包含源点，设为V0，然后不断从集合T中选择到源点V0路径长度最短的结点u加入到集合S中，集合S每加入一个新的结点u都要修改从源点V0到集合T中剩余结点的当前最短路径长度值，集合T中各结点的新的当前路径最短路径，为原来的最短路径与从源点过结点u到达该结点的路径长度中的较小者。此过程不断重复，直到集合T中的结点全部加入到集合S中为止。 <二>调试通过的源程序 (1)顺序表打包文件:seqlist.h typedef struct { datatype list[maxsize]; int size; }seqlist; void listinitiate(seqlist *l) { l->size=0; } int listlength(seqlist l) { return l.size; } int listinsert(seqlist *l,int i,datatype x) { int j; if(l->size>=maxsize) { printf("it is too full!\n"); return 0; } else if(i<0||i>l->size) { printf("error!\n"); return 0; } else { for(j=l->size;j>i;j--) l->list[j]=l->list[j-1]; l->list[i]=x; l->size++; return 1; } } int listdelete(seqlist *l,int i,datatype *x) { int j; if(l->size<=0) { printf("it is empty!\n"); return 0; } else if(i<0||i>l->size-1) { printf("error!\n"); return 0; } else { *x=l->list[i]; for(j=i+1;j<=l->size-1;j++) l->list[j-1]=l->list[j]; l->size--; return 1; } } int listget(seqlist l,int i,datatype *x) { if(i<0||i>=l.size-1) { printf("error!\n"); return 0; } else { *x=l.list[i]; return 1; } } （2）邻接矩阵打包文件:adjmgraph.h #include if((*ht)[i].weight < (*ht)[min].weight) min = i; } } *s2 = min; } void CrtHuffmanTree(HuffmanTree *ht , int *w, int n) { /* w存放已知的n个权值，构造哈夫曼树ht */ int m,i; int s1,s2; m=2*n-1; *ht=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); /*0号单元未使用*/ for(i=1;i<=n;i++) {/*1-n号放叶子结点，初始化*/ (*ht)[i].weight = w[i]; (*ht)[i].LChild = 0; (*ht)[i].parent = 0; (*ht)[i].RChild = 0; } for(i=n+1;i<=m;i++) { (*ht)[i].weight = 0; (*ht)[i].LChild = 0; (*ht)[i].parent = 0; (*ht)[i].RChild = 0; } /*非叶子结点初始化*/ /* ------------初始化完毕！对应算法步骤1---------*/ for(i=n+1;i<=m;i++) /*创建非叶子结点,建哈夫曼树*/ { /*在(*ht)[1]~(*ht)[i-1]的范围内选择两个parent为0且weight最小的结点，其序号分别赋值给s1、s2返回*/ select(ht,i-1,&s1,&s2); (*ht)[s1].parent=i; (*ht)[s2].parent=i; (*ht)[i].LChild=s1; (*ht)[i].RChild=s2; (*ht)[i].weight=(*ht)[s1].weight+(*ht)[s2].weight; } }/*哈夫曼树建立完毕*/ void outputHuffman(HuffmanTree HT, int m) { if(m!=0) { 银行家算法设计实验报告 银行家算法设计实验报告 一．题目分析 1.银行家算法： 我们可以把操作系统看做是银行家，操作系统管理的资源相当于银行家管理的资金，进程向操作系统请求资源相当于客户向银行家贷款。操作系统按银行家制定的规则为进程分配资源，当进程首次申请资源时，要测试该进程尚需求的资源量，若是系统现存的资源可以满足它尚需求的资源量，则按当前的申请量来分配资源，否则就推迟分配。 当进程在执行中继续申请资源时，先测试该进程申请的资源量是否超过了它尚需的资源量。若超过则拒绝分配，若没有超过则再测试系统尚存的资源是否满足该进程尚需的资源量，若满足即可按当前的申请量来分配，若不满足亦推迟分配。 2.基本要求： （1）可以输入某系统的资源以及T0时刻进程对资源的占用及需求情况的表项，以及T0时刻系统的可利用资源数。 （2）对T0时刻的进行安全性检测，即检测在T0时刻该状态是否安全。 （3）进程申请资源，用银行家算法对其进行检测，分为以下三种情况： A. 所申请的资源大于其所需资源，提示分配不合理不予分配并返回 B. 所申请的资源未大于其所需资源， 但大于系统此时的可利用资源，提 示分配不合理不予分配并返回。 C. 所申请的资源未大于其所需资源， 亦未大于系统此时的可利用资源，预 分配并进行安全性检查： a. 预分配后系统是安全的，将该进 程所申请的资源予以实际分配并 打印后返回。 b. 与分配后系统进入不安全状态，提示系统不安全并返回。 （4）对输入进行检查，即若输入不符合条件，应当报错并返回重新输入。 3.目的： 根据设计题目的要求，充分地分析和理解题 目，叙述系统的要求，明确程序要求实现的功能以及限制条件。 明白自己需要用代码实现的功能，清楚编写每部分代码的目的，做到有的放矢，有条理不遗漏的用代码实现银行家算法。 淮海工学院计算机工程学院实验报告书 课程名：《算法分析与设计》 题目：实验3 贪心算法 哈夫曼编码 班级：软件102班 学号：11003215 姓名：鹿迅 实验3 贪心算法 实验目的和要求 （1）了解前缀编码的概念，理解数据压缩的基本方法； （2）掌握最优子结构性质的证明方法； （3）掌握贪心法的设计思想并能熟练运用 （4）证明哈夫曼树满足最优子结构性质； （5）设计贪心算法求解哈夫曼编码方案； （6）设计测试数据，写出程序文档。 实验内容 设需要编码的字符集为{d 1, d 2, …, dn }，它们出现的频率为 {w 1, w 2, …, wn }，应用哈夫曼树构造最短的不等长编码方案。 实验环境 Turbo C 或VC++ 实验学时 2学时，必做实验 数据结构与算法 struct huffman { double weight; //用来存放各个结点的权值 int lchild,rchild,parent; //指向双亲、孩子结点的指针 }; 核心源代码 #include int min=11000; int min1; for(int k=0;k 本科实验报告 课程名称：算法设计与分析 实验项目：递归与分治算法 实验地点：计算机系实验楼110 专业班级：物联网1601 学号：2016002105 学生：俞梦真 指导教师：郝晓丽 2018年05月04 日 实验一递归与分治算法 1.1 实验目的与要求 1．进一步熟悉C/C++语言的集成开发环境； 2．通过本实验加深对递归与分治策略的理解和运用。 1.2 实验课时 2学时 1.3 实验原理 分治（Divide-and-Conquer）的思想：一个规模为n的复杂问题的求解，可以划分成若干个规模小于n的子问题，再将子问题的解合并成原问题的解。 需要注意的是，分治法使用递归的思想。划分后的每一个子问题与原问题的性质相同，可用相同的求解方法。最后，当子问题规模足够小时，可以直接求解，然后逆求原问题的解。 1.4 实验题目 1．上机题目：格雷码构造问题 Gray码是一个长度为2n的序列。序列无相同元素，每个元素都是长度为n的串，相邻元素恰好只有一位不同。试设计一个算法对任意n构造相应的Gray码（分治、减治、变治皆可）。 对于给定的正整数n，格雷码为满足如下条件的一个编码序列。 （1）序列由2n个编码组成，每个编码都是长度为n的二进制位串。 （2）序列中无相同的编码。 （3）序列中位置相邻的两个编码恰有一位不同。 2．设计思想： 根据格雷码的性质，找到他的规律，可发现，1位是0 1。两位是00 01 11 10。三位是000 001 011 010 110 111 101 100。n位是前n-1位的2倍个。N-1个位前面加0，N-2为倒转再前面再加1。 3．代码设计： 实验报告 （2009/2010学年第一学期） 课程名称算法分析与设计A 实验名称动态规划法 实验时间2009 年11 月20 日指导单位计算机学院软件工程系 指导教师张怡婷 学生姓名丁力琪班级学号B07030907 学院(系) 计算机学院专业软件工程 实验报告 实验名称动态规划法指导教师张怡婷实验类型验证实验学时2×2实验时间2009-11-20一、实验目的和任务 目的：加深对动态规划法的算法原理及实现过程的理解，学习用动态规划法解决实际应用中的最长公共子序列问题。 任务：用动态规划法实现求两序列的最长公共子序列，其比较结果可用于基因比较、文章比较等多个领域。 要求：掌握动态规划法的思想，及动态规划法在实际中的应用；分析最长公共子序列的问题特征，选择算法策略并设计具体算法，编程实现两输入序列的比较，并输出它们的最长公共子序列。 二、实验环境(实验设备) 硬件：计算机 软件：Visual C++ 三、实验原理及内容（包括操作过程、结果分析等） 1、最长公共子序列（LCS）问题是：给定两个字符序列X={x1,x2,……,x m}和Y={y1,y2,……,y n}，要求找出X和Y的一个最长公共子序列。 例如：X={a,b,c,b,d,a,b},Y={b,d,c,a,b,a}。它们的最长公共子序列LSC={b,c,d,a}。 通过“穷举法”列出所有X的所有子序列，检查其是否为Y的子序列并记录最长公共子序列并记录最长公共子序列的长度这种方法，求解时间为指数级别的，因此不可取。 2、分析LCS问题特征可知，如果Z={z1,z2,……，z k}为它们的最长公共子序列，则它们一定具有以下性质： （1）若x m=y n，则z k=x m=y n，且Z k-1是X m-1和Y n-1的最长公共子序列； （2）若x m≠y n且x m≠z k，则Z是X m-1和Y的最长公共子序列； （3）若x m≠y n且z k≠y n，则Z是X和Y的最长公共子序列。 这样就将求X和Y的最长公共子序列问题，分解为求解较小规模的问题： 若x m=y m，则进一步分解为求解两个（前缀）子字符序列X m-1和Y n-1的最长公共子序列问题； 如果x m≠y n，则原问题转化为求解两个子问题，即找出X m-1和Y的最长公共子序列与找出X 和Y n-1的最长公共子序列，取两者中较长者作为X和Y的最长公共子序列。 由此可见，两个序列的最长公共子序列包含了这两个序列的前缀的最长公共子序列，具有最优子结构性质。 3、令c[i][j]保存字符序列X i={x1,x2,……,x i}和Y j={y1,y2,……,y j}的最长公共子序列的长度，由上述分析可得如下递推式： 0 i=0或j=0 c[i][j]= c[i-1][j-1]+1 i,j>0且x i=y j max{c[i][j-1],c[i-1][j]} i,j>0且x i≠y j 由此可见，最长公共子序列的求解具有重叠子问题性质，如果采用递归算法实现，会得到一个指数时间算法，因此需要采用动态规划法自底向上求解，并保存子问题的解，这样可以避免重复计算子问题，在多项式时间内完成计算。 4、为了能由最优解值进一步得到最优解（即最长公共子序列），还需要一个二维数组s[][]，数组中的元素s[i][j]记录c[i][j]的值是由三个子问题c[i-1][j-1]+1,c[i][j-1]和c[i-1][j]中的哪一个计算得到，从而可以得到最优解的当前解分量（即最长公共子序列中的当前字符），最终构造出最长公共子序列自身。 第四章作业 部分参考答案 1． 设有n 个顾客同时等待一项服务。顾客i 需要的服务时间为n i t i ≤≤1,。应该如何安排n 个顾客的服务次序才能使总的等待时间达到最小？总的等待时间是各顾客等待服务的时间的总和。试给出你的做法的理由（证明）。 策略： 对 1i t i n ≤≤进行排序，,21n i i i t t t ≤≤≤ 然后按照递增顺序依次服务12,,...,n i i i 即可。 解析：设得到服务的顾客的顺序为12,,...,n j j j ，则总等待时间为 ,2)2()1(1221--+++-+-=n n j j j j t t t n t n T 则在总等待时间T 中1j t 的权重最大，jn t 的权重最小。故让所需时间少的顾客先得到服务可以减少总等待时间。 证明：设,21n i i i t t t ≤≤≤ ，下证明当按照不减顺序依次服务时，为最优策略。 记按照n i i i 21次序服务时，等待时间为T ，下证明任意互换两者的次序，T 都不减。即假设互换j i ,)(j i <两位顾客的次序，互换后等待总时间为T ~ ，则有.~ T T ≥ 由于 ,2)2()1(1221--+++-+-=n n i i i i t t t n t n T ,2)()()2()1(1221--+++-++-++-+-=n n j i i i i i i i t t t j n t i n t n t n T ,2)()()2()1(~ 1221--+++-++-++-+-=n n i j i i i i i i t t t j n t i n t n t n T 则有 .0))((~ ≥--=-i j i i t t i j T T 同理可证其它次序，都可以由n i i i 21经过有限次两两调换顺序后得到，而每次交换，总时间不减，从而n i i i 21为最优策略。 算法设计与分析课程实验项目目录 学生：学号： *实验项目类型：演示性、验证性、综合性、设计性实验。 *此表由学生按顺序填写。 本科实验报告专用纸 课程名称算法设计与分析成绩评定 实验项目名称蛮力法指导教师 实验项目编号实验项目类型设计实验地点机房 学生学号 学院信息科学技术学院数学系信息与计算科学专业级 实验时间2012年3月1 日～6月30日温度24℃ 1.实验目的和要求： 熟悉蛮力法的设计思想。 2.实验原理和主要容： 实验原理：蛮力法常直接基于问题的描述和所涉及的概念解决问题。 实验容：以下题目任选其一 1).为蛮力字符串匹配写一段可视化程序。 2).写一个程序，实现凸包问题的蛮力算法。 3).最著名的算式谜题是由大名鼎鼎的英国谜人 H.E.Dudeney(1857-1930)给出的： S END +MORE MONEY . 这里有两个前提假设： 第一，字母和十进制数字之间一一对应，也就是每个字母只代表一个数字，而且不同的字母代表不同的数字；第二，数字0不出现在任何数的最左边。求解一个字母算术意味着找到每个字母代表的是哪个数字。请注意，解可能并不是唯一的，不同人的解可能并不相同。3.实验结果及分析： （将程序和实验结果粘贴，程序能够注释清楚更好。） 该算法程序代码如下： #include "stdafx.h" #include "time.h" int main(int argc, char* argv[]) { int x[100],y[100]; int a,b,c,i,j,k,l,m,n=0,p,t1[100],num; int xsat[100],ysat[100]; printf("请输入点的个数：\n"); scanf("%d",&num); getchar(); clock_t start,end; start=clock(); printf("请输入各点坐标:\n"); for(l=0;l 算法与分析实验报告软件工程专业 安徽工业大学 指导老师：许精明 实验内容 1：杨辉三角 2：背包问题 3：汉诺塔问题 一：实验目的 1：掌握动态规划算法的基本思想，学会用其解决实际问题。 2：通过几个基本的实验，提高算法分析与设计能力，提高动手操作能力和培养良好的编程习惯。 二：实验内容 1：杨辉三角 2：背包问题 3：汉诺塔问题 实验一：杨辉三角 问题分析： ①每行数字左右对称，由1开始逐渐变大，然后变小，回到1。 ②第n行数之和为2^n。 ③下一行每个数字等于上一行的左右两个数字之和。 算法设计及相关源代码： public void yanghui(int n) { int[] a = new int[n]; if(n==1){ System.out.println(1); }else if(n==2) { System.out.print(1 + " " +1); }else{ a[1]=1; System.out.println(a[1]); a[2]=1; System.out.println(a[1]+" "+a[2]); for(int i=3;i<=n;i++){ a[1]=a[i]=1; for(int j=i-1;j>1;j--){ a[j]=a[j]+a[j-1]; } for(int j=1;j<=i;j++){ System.out.print(a[j]+" "); } System.out.println(); } } } 实验结果：n=10 实验二：0-1背包问题 问题分析：：令V(i,j)表示在前i(1<=i<=n)个物品中能够装入容量为就 j(1<=j<=C)的背包中的物品的最大价值，则可以得到如下的动态规划函数: (1) V(i,0)=V(0,j)=0 (2) V(i,j)=V(i-1,j) j贪心算法构造哈夫曼树
实验三.哈夫曼编码的贪心算法设计
北京理工大学《数据结构与算法设计》实验报告实验一
算法设计实验报告一(简单算法设计)
哈夫曼编码算法实现完整版
算法设计与实验报告讲解
0023算法笔记——【贪心算法】哈夫曼编码问题
算法设计实验报告
哈夫曼树建立、哈夫曼编码算法的实现
银行家算法设计实验报告
哈夫曼编码_贪心算法
算法设计与分析实验报告
南京邮电大学算法设计实验报告——动态规划法
4+四+贪心算法+习题参考答案
《算法设计与分析》实验报告
算法与设计实验报告