初三数学综合试题

合集下载

初三数学圆的综合的专项培优练习题(含答案)及答案解析

初三数学圆的综合的专项培优练习题(含答案)及答案解析一、圆的综合1．如图，四边形OABC 是平行四边形，以O 为圆心，OA 为半径的圆交AB 于D ，延长AO 交O 于E ，连接CD ，CE ，若CE 是⊙O 的切线，解答下列问题：（1）求证：CD 是⊙O 的切线；（2）若BC=4，CD=6，求平行四边形OABC 的面积．【答案】（1）证明见解析（2）24【解析】试题分析：（1）连接OD ，求出∠EOC=∠DOC ，根据SAS 推出△EOC ≌△DOC ，推出∠ODC=∠OEC=90°，根据切线的判定推出即可；（2）根据切线长定理求出CE=CD=4，根据平行四边形性质求出OA=OD=4，根据平行四边形的面积公式=2△COD 的面积即可求解．试题解析：（1）证明：连接OD ，∵OD=OA ，∴∠ODA=∠A ，∵四边形OABC 是平行四边形，∴OC ∥AB ，∴∠EOC=∠A ，∠COD=∠ODA ，∴∠EOC=∠DOC ，在△EOC 和△DOC 中，OE OD EOC DOC OC OC =⎧⎪∠=∠⎨⎪=⎩∴△EOC ≌△DOC （SAS ），∴∠ODC=∠OEC=90°，即OD ⊥DC ，∴CD 是⊙O 的切线；（2）由（1）知CD 是圆O 的切线，∴△CDO 为直角三角形，∵S △CDO =12CD•OD ，又∵OA=BC=OD=4，∴S△CDO=12×6×4=12，∴平行四边形OABC的面积S=2S△CDO=24．2．如图，⊙M交x轴于B、C两点，交y轴于A，点M的纵坐标为2．B（﹣33，O），C（3，O）．（1）求⊙M的半径；（2）若CE⊥AB于H，交y轴于F，求证：EH=FH．（3）在（2）的条件下求AF的长．【答案】（1）4；（2）见解析;（3）4．【解析】【分析】（1）过M作MT⊥BC于T连BM，由垂径定理可求出BT的长，再由勾股定理即可求出BM的长；（2）连接AE，由圆周角定理可得出∠AEC=∠ABC，再由AAS定理得出△AEH≌△AFH，进而可得出结论；（3）先由（1）中△BMT的边长确定出∠BMT的度数，再由直角三角形的性质可求出CG 的长，由平行四边形的判定定理判断出四边形AFCG为平行四边形，进而可求出答案．【详解】（1）如图（一），过M作MT⊥BC于T连BM，∵BC是⊙O的一条弦，MT是垂直于BC的直径，∴BT=TC=123∴124；（2）如图（二），连接AE，则∠AEC=∠ABC，∵CE⊥AB，∴∠HBC+∠BCH=90°在△COF中，∵∠OFC+∠OCF=90°，∴∠HBC=∠OFC=∠AFH，在△AEH和△AFH中，∵AFH AEHAHF AHE AH AH∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEH≌△AFH（AAS），∴EH=FH；（3）由（1）易知，∠BMT=∠BAC=60°，作直径BG，连CG，则∠BGC=∠BAC=60°，∵⊙O的半径为4，∴CG=4，连AG，∵∠BCG=90°，∴CG⊥x轴，∴CG∥AF，∵∠BAG=90°，∴AG⊥AB，∵CE⊥AB，∴AG∥CE，∴四边形AFCG为平行四边形，∴AF=CG=4．【点睛】本题考查的是垂径定理、圆周角定理、直角三角形的性质及平行四边形的判定与性质，根据题意作出辅助线是解答此题的关键．3．如图，⊙O的半径为6cm，经过⊙O上一点C作⊙O的切线交半径OA的延长于点B，作∠ACO的平分线交⊙O于点D，交OA于点F，延长DA交BC于点E．（1）求证：AC∥OD；（2）如果DE⊥BC，求»AC的长度．【答案】（1）证明见解析；（2）2π．【解析】试题分析：（1）由OC=OD，CD平分∠ACO，易证得∠ACD=∠ODC，即可证得AC∥OD；（2）BC切⊙O于点C，DE⊥BC，易证得平行四边形ADOC是菱形，继而可证得△AOC是等边三角形，则可得：∠AOC=60°，继而求得弧AC的长度．试题解析：（1）证明：∵OC=OD，∴∠OCD=∠ODC．∵CD平分∠ACO，∴∠OCD=∠ACD，∴∠ACD=∠ODC，∴AC∥OD；（2）∵BC切⊙O于点C，∴BC⊥OC．∵DE⊥BC，∴OC∥DE．∵AC∥OD，∴四边形ADOC 是平行四边形．∵OC=OD，∴平行四边形ADOC是菱形，∴OC=AC=OA，∴△AOC是等边三角形，∴∠AOC=60°，∴弧AC的长度=606180π⨯=2π．点睛：本题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式．此题难度适中，注意掌握数形结合思想的应用．4．如图，△ABC内接于⊙O，∠BAC的平分线交⊙O于点D，交BC于点E（BE＞EC），且BD＝23．过点D作DF∥BC，交AB的延长线于点F．（1）求证：DF为⊙O的切线；（2）若∠BAC＝60°，DE＝7，求图中阴影部分的面积．【答案】（1）详见解析；（2）32π．【解析】【分析】（1）连结OD，根据垂径定理得到OD⊥BC，根据平行线的性质得到OD⊥DF，根据切线的判定定理证明；（2）连结OB，连结OD交BC于P，作BH⊥DF于H，证明△OBD为等边三角形，得到∠ODB=60°，3PE，证明△ABE∽△AFD，根据相似三角形的性质求出AE，根据阴影部分的面积=△BDF的面积-弓形BD的面积计算．【详解】证明：（1）连结OD，∵AD平分∠BAC交⊙O于D，∴∠BAD=∠CAD，∴»»BD CD=，∴OD⊥BC，∵BC∥DF，∴OD⊥DF，∴DF为⊙O的切线；（2）连结OB，连结OD交BC于P，作BH⊥DF于H，∵∠BAC=60°，AD平分∠BAC，∴∠BAD=30°，∴∠BOD=2∠BAD=60°，∴△OBD为等边三角形，∴∠ODB=60°，3，∴∠BDF=30°，∵BC∥DF，∴∠DBP=30°，在Rt△DBP中，PD=123，3，在Rt△DEP中，∵37∴22(7)(3)=2，∵OP⊥BC，∴BP=CP=3，∴CE=3﹣2=1，∵∠DBE=∠CAE，∠BED=∠AEC，∴△BDE∽△ACE，∴AE：BE=CE：DE，即AE：5=17，∴57∵BE∥DF，∴△ABE∽△AFD，∴BE AE DF AD=，即5757125DF=，解得DF=12，在Rt△BDH中，BH=12BD=3，∴阴影部分的面积=△BDF的面积﹣弓形BD的面积=△BDF的面积﹣（扇形BOD的面积﹣△BOD的面积）=22160(23)3123(23)23604π⨯⨯⨯--⨯ =93﹣2π．【点睛】考查的是切线的判定，扇形面积计算，相似三角形的判定和性质，圆周角定理的应用，等边三角形的判定和性质，掌握切线的判定定理，扇形面积公式是解题的关键．5．如图1，是用量角器一个角的操作示意图，量角器的读数从M点开始（即M点的读数为0），如图2，把这个量角器与一块30°（∠CAB＝30°）角的三角板拼在一起，三角板的斜边AB与量角器所在圆的直径MN重合，现有射线C绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB，在旋转过程中，射线CP与量角器的半圆弧交于E．连接BE．（1）当射线CP经过AB的中点时，点E处的读数是，此时△BCE的形状是；（2）设旋转x秒后，点E处的读数为y，求y与x的函数关系式；（3）当CP旋转多少秒时，△BCE是等腰三角形？【答案】（1）60°，直角三角形；（2）y＝4x（0≤x≤45）；（3）7.5秒或30秒【解析】【分析】（1）根据圆周角定理即可解决问题；（2）如图2﹣2中，由题意∠ACE＝2x，∠AOE＝y，根据圆周角定理可知∠AOE＝2∠ACE，可得y＝2x（0≤x≤45）；（3）分两种情形分别讨论求解即可；【详解】解：（1）如图2﹣1中，∵∠ACB＝90°，OA＝OB，∴OA＝OB＝OC，∴∠OCA＝∠OAC＝30°，∴∠AOE＝60°，∴点E处的读数是60°，∵∠E＝∠BAC＝30°，OE＝OB，∴∠OBE＝∠E＝30°，∴∠EBC＝∠OBE+∠ABC＝90°，∴△EBC是直角三角形；故答案为60°，直角三角形；（2）如图2﹣2中，∵∠ACE＝2x，∠AOE＝y，∵∠AOE＝2∠ACE，∴y＝4x（0≤x≤45）．（3）①如图2﹣3中，当EB＝EC时，EO垂直平分线段BC，∵AC⊥BC，∵EO∥AC，∴∠AOE＝∠BAC＝30°，∠AOE＝15°，∴∠ECA＝12∴x＝7.5．②若2﹣4中，当BE＝BC时，易知∠BEC＝∠BAC＝∠BCE＝30°，∴∠OBE＝∠OBC＝60°，∵OE＝OB，∴△OBE是等边三角形，∴∠BOE＝60°，∴∠AOB＝120°，∠ACB＝60°，∴∠ACE＝12∴x＝30，综上所述，当CP旋转7.5秒或30秒时，△BCE是等腰三角形；【点睛】本题考查几何变换综合题、创新题目、圆周角定理、等腰三角形的判定和性质等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考压轴题．6．.如图，△ABC中，∠ACB＝90°，∠A＝30°，AB＝6．D是线段AC上一个动点（不与点A 重合），⊙D与AB相切，切点为E，⊙D交射线．．DC于点F，过F作FG⊥EF交直线．．BC于点G，设⊙D的半径为r．（1）求证AE＝EF；（2）当⊙D与直线BC相切时，求r的值；（3）当点G落在⊙D内部时，直接写出r的取值范围．【答案】(1)见解析,(2)r=3,(3)63 3r<<【解析】【分析】（1）连接DE，则∠ADE=60°=∠DEF+∠DFE，而∠DEF=∠DFE，则∠DEF=∠DFE=30°=∠A，即可求解；（2）如图2所示，连接DE，当圆与BC相切时，切点为F，∠A=30°，AB=6，则BF=3，AD=2r，由勾股定理，即可求解；（3）分点F在线段AC上、点F在线段AC的延长线上两种情况，分别求解即可．【详解】解：设圆的半径为r；（1）连接DE，则∠ADE=60°=∠DEF+∠DFE，而∠DEF=∠DFE，则∠DEF=∠DFE=30°=∠A，∴AE=EF；（2）如图2所示，连接DE，当圆与BC相切时，切点为F∠A=30°，AB=6，则BF=3，AD=2r ，由勾股定理得：（3r ）2+9=36，解得：r=3；（3）①当点F 在线段AC 上时，如图3所示，连接DE 、DG ，333,3933FC r GC FC r =-==-②当点F 在线段AC 的延长线上时，如图4所示，连接DE 、DG ，333,3339FC r GC FC r ===-两种情况下GC 符号相反，GC 2相同，由勾股定理得：DG 2=CD 2+CG 2，点G 在圆的内部，故：DG2＜r2，即：22(332)(339)2r r r +-<整理得：25113180r r -+<6335r <<【点睛】本题考查了圆的综合题：圆的切线垂直于过切点的半径；利用勾股定理计算线段的长．7．如图1，等腰直角△ABC 中，∠ACB=90°，AC=BC ，过点A ，C 的圆交AB 于点D ，交BC 于点E ，连结DE（1）若AD=7，BD=1，分别求DE ，CE 的长（2）如图2，连结CD ，若CE=3，△ACD 的面积为10，求tan ∠BCD（3）如图3，在圆上取点P 使得∠PCD=∠BCD （点P 与点E 不重合），连结PD ，且点D 是△CPF 的内心①请你画出△CPF ，说明画图过程并求∠CDF 的度数②设PC=a ，PF=b ，PD=c ，若（a-2c ）（b-2c ）=8，求△CPF 的内切圆半径长．【答案】（1）DE=1，CE=322）tan ∠BCD=14；（3）①135°；②2. 【解析】【分析】（1）由A 、C 、E 、D 四点共圆对角互补为突破口求解；（2）找∠BDF 与∠ODA 为对顶角，在⊙O 中，∠COD=2∠CAD ，证明△OCD 为等腰直角三角形，从而得到∠EDC+∠ODA=45°，即可证明∠CDF=135°；（3）过点D 做DH CB ⊥于点H ，以D 为圆心，DH 为半径画圆，过点P 做D e 切线PF 交CB 的延长线于点F ，结合圆周角定理得出∠CPD=∠CAD=45°，再根据圆的内心是三角形三个内角角平分线的交点，得出∠CPF=90°，然后根据角平分线性质得出114522DCF CFD PCF PFC ∠+∠=∠+∠=︒，最后再根据三角形内角和定理即可求解；证明∠DCF+∠CFD=45°，从而证明∠CPF 是直角，再求证四边形PKDN 是正方形，最后以△PCF 面积不变性建立等量关系，结合已知（2c ）（2c ）=8，消去字母a ，b 求出c 值，即求出△CPF 2c ．【详解】（1）由图可知：设BC=x ．在Rt △ABC 中，AC=BC ．由勾股定理得： AC 2+BC 2=AB 2，∵AB=AD+BD ，AD=7，BD=1， ∴x 2+x 2=82，解得：x=42．∵⊙O 内接四边形，∠ACD=90°， ∴∠ADE=90°， ∴∠EDB=90°， ∵∠B=45°，∴△BDE 是等腰直角三形． ∴DE=DB ，又∵DB=1， ∴DE=1，又∵CE=BC-BE ， ∴CE=42232-=．（2）如图所示：在△DCB 中过点D 作DM ⊥BE ，设BE=y ，则DM=12y ，又∵CE=3，∴BC=3+y ， ∵S △ACB =S ACD +S DCB ，∴()1114242103y y 222⨯=+⨯+⨯，解得：y=2或y=-11（舍去）． ∴EM=1，CM=CE+ME=1+3=4，又∵∠BCD=∠MCD ，∴tan ∠BCD=tan ∠MCD ，在Rt △DCM 中，tan ∠MCD=DM CM =14， ∴tan ∠BCD=14．（3）①如下图所示：过点D 做DH CB ⊥于点H ，以D 为圆心，DH 为半径画圆，过点P 做D e 切线PF 交CB 的延长线于点F ．∵∠CAD=45°， ∴∠CPD=∠CAD=45°，又∵点D 是CPF ∆的内心， ∴PD 、CD 、DF 都是角平分线，∴∠FPD=∠CPD =45°，∠PCD=∠DCF ，∠PFD=∠CFD ∴∠CPF=90° ∴∠PCF+∠PFC=90°∴114522DCF CFD PCF PFC ∠+∠=∠+∠=︒ ∴∠CDF=180°-∠DCF-∠CFD F=90°+45°=135°，即∠CDF 的度数为135°． ②如下图所示过点D 分别作DK ⊥PC ，DM ⊥CF ，DN ⊥PF 于直线PC ，CF 和PF 于点K ，M ，N 三点，设△PCF 内切圆的半径为m ，则DN=m ，∵点D 是△PCF 的内心， ∴DM=DN=DK ，又∵∠DCF+∠CFD+∠FDC=180°，∠FDC=45°， ∴∠DCF+∠CFD=45°，又∵DC ，DF 分别是∠PCF 和∠PFC 的角平分线， ∴∠PCF=2∠DCF ，∠PFC=2∠DFC ， ∴∠PCF+∠PFC=90°， ∴∠CPF=90°．在四边形PKDN 中，∠PND=∠NPK=∠PKD=90°， ∴四边形PKDN 是矩形，又∵KD=ND ，∴四边形PKDN 是正方形．又∵∠MBD=∠BDM=45°， ∠BDM=∠KDP ， ∴∠KDP=45°． ∵PC=a ，PF=b ，PD=c ，∴，∴NF=b -，CK=a -，又∵CK=CM ，FM=FN ，CF=CM+FM ， ∴CF=a b +，又∵S △PCF =S △PDF +S △PDC +S △DCF ，∴1111ab a b (a b 2222=+++-），化简得：)2a b c c +-------（Ⅰ），又∵若（c ）（c ）=8化简得：()2ab a b 2c 8++=------（Ⅱ），将（Ⅰ）代入（Ⅱ）得：c 2=8，解得：c =c =-∴m=c 222==，即△CPF 的内切圆半径长为2．【点睛】本题考查圆的内接四边形性质，圆的内心，圆心角、圆周角，同弧（或等弧）之间的相互关系，同时也考查直角三角形，勾股定理，同角或等角的三角函数值相等和三角形的面积公式，正方形，对顶角和整式的运算等知识点；难点是作辅助线和利用等式求△CPF 的内切圆半径长．8．如图，四边形为菱形，且，以为直径作，与交于点．请仅用无刻度的直尺按下列要求画图．(保留作图痕迹)(1)在如图中，过点作边上的高．(2)在如图中，过点作的切线，与交于点．【答案】(1)如图1所示．(答案不唯一),见解析；(2)如图2所示．(答案不唯一)，见解析.【解析】【分析】（1）连接AC交圆于一点F，连接PF交AB于点E,连接CE即为所求．（2）连接OF交BC于Q，连接PQ即为所求．【详解】(1)如图1所示．(答案不唯一)(2)如图2所示．(答案不唯一)【点睛】本题考查作图-复杂作图，菱形和圆的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．9．如图，△ABC中，AC＝BC＝10，cosC＝35，点P是AC边上一动点（不与点A、C重合），以PA长为半径的⊙P与边AB的另一个交点为D，过点D作DE⊥CB于点E．（1）当⊙P与边BC相切时，求⊙P的半径．（2）连接BP交DE于点F，设AP的长为x，PF的长为y，求y关于x的函数解析式，并直接写出x的取值范围．（3）在（2）的条件下，当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时，求相交所得的公共弦的长.【答案】（1）409R=;（2）25880320xy x xx=-++;（3）50105-.【解析】【分析】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，即可求解；（2）首先证明PD∥BE，则EB BFPD PF=，即：2024588x yxxx-+--=，即可求解；（3）证明四边形PDBE为平行四边形，则AG＝EP＝BD，即：AB＝DB+AD＝AG+AD＝45，即可求解．【详解】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC ＝HP CP ＝10R R -＝45，解得：R ＝409；（2）在△ABC 中，AC ＝BC ＝10，cosC ＝35，设AP ＝PD ＝x ，∠A ＝∠ABC ＝β，过点B 作BH ⊥AC ，则BH ＝ACsinC ＝8，同理可得：CH ＝6，HA ＝4，AB ＝45，则：tan ∠CAB ＝2， BP ＝228+(4)x -＝2880x x -+，DA ＝25x ，则BD ＝45﹣25x ，如下图所示，PA ＝PD ，∴∠PAD ＝∠CAB ＝∠CBA ＝β，tanβ＝2，则cosβ5，sinβ5， EB ＝BDcosβ＝（525x ）5＝4﹣25x ，∴PD ∥BE ，∴EB BFPD PF=，即：2024588x y x xx -+--=，整理得：y 25xx 8x 803x 20-++（3）以EP 为直径作圆Q 如下图所示，两个圆交于点G，则PG＝PQ，即两个圆的半径相等，则两圆另外一个交点为D，GD为相交所得的公共弦，∵点Q是弧GD的中点，∴DG⊥EP，∵AG是圆P的直径，∴∠GDA＝90°，∴EP∥BD，由（2）知，PD∥BC，∴四边形PDBE为平行四边形，∴AG＝EP＝BD，∴AB＝DB+AD＝AG+AD＝5设圆的半径为r，在△ADG中，AD＝2rcosβ5DG5AG＝2r，5＝52r51+，则：DG550﹣5相交所得的公共弦的长为50﹣5【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．10．如图，四边形ABCD是⊙O的内接四边形，AC为直径，»»BD AD=，DE⊥BC，垂足为E．（1）判断直线ED与⊙O的位置关系，并说明理由；（2）若CE=1，AC=4，求阴影部分的面积．【答案】（1）ED 与O e 相切.理由见解析；（2）2=33S π-阴影. 【解析】【分析】（1）连结OD ，如图，根据圆周角定理，由»»BD AD =得到∠BAD =∠ACD ，再根据圆内接四边形的性质得∠DCE =∠BAD ，所以∠ACD =∠DCE ；利用内错角相等证明OD ∥BC ，而DE ⊥BC ，则OD ⊥DE ，于是根据切线的判定定理可得DE 为⊙O 的切线；（2）作OH ⊥BC 于H ，易得四边形ODEH 为矩形，所以OD =EH =2，则CH =HE ﹣CE =1，于是有∠HOC =30°，得到∠COD =60°，然后根据扇形面积公式、等边三角形的面积公式和阴影部分的面积=S 扇形OCD ﹣S △OCD 进行计算即可．【详解】（1）直线ED 与⊙O 相切．理由如下：连结OD ，如图，∵»»BD AD =，∴∠BAD =∠ACD ．∵∠DCE =∠BAD ，∴∠ACD =∠DCE ．∵OC =OD ，∴∠OCD =∠ODC ，而∠OCD =∠DCE ，∴∠DCE =∠ODC ，∴OD ∥BC ． ∵DE ⊥BC ，∴OD ⊥DE ，∴DE 为⊙O 的切线；（2）作OH ⊥BC 于H ，则四边形ODEH 为矩形，∴OD =EH ．∵CE =1，AC =4，∴OC =OD =2，∴CH =HE ﹣CE =2﹣1=1．在Rt △OHC 中，∵OC =2，CH =1，∠OHC =90°，∠HOC =30°，∴∠COD =60°，∴阴影部分的面积=S 扇形OCD ﹣S △OCD26023360π⋅⋅=-•2223=π3-．【点睛】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．也考查了扇形面积的计算．11．已知四边形ABCD 是⊙O 的内接四边形，∠DAB ＝120°，BC ＝CD ，AD ＝4，AC ＝7，求AB 的长度．【答案】AB ＝3．【解析】【分析】作DE ⊥AC ，BF ⊥AC ，根据弦、弧、圆周角、圆心角的关系，求得BC CD =u u u r u u u r，进而得到∠DAC ＝∠CAB ＝60°，在Rt △ADE 中，根据60°锐角三角函数值，可求得DE ＝23，AE ＝2，再由Rt △DEC 中，根据勾股定理求出DC 的长，在△BFC 和△ABF 中，利用60°角的锐角三角函数值及勾股定理求出AF 的长，然后根据求出的两个结果，由AB ＝2AF ，分类讨论求出AB 的长即可. 【详解】作DE ⊥AC ，BF ⊥AC ，∵BC ＝CD ， ∴BC CD =u u u r u u u r， ∴∠CAB ＝∠DAC ， ∵∠DAB ＝120°， ∴∠DAC ＝∠CAB ＝60°， ∵DE ⊥AC ，∴∠DEA ＝∠DEC ＝90°， ∴sin60°＝4DE ，cos60°＝4AE， ∴DE ＝3AE ＝2， ∵AC ＝7，∴CE ＝5，∴DC= ∴BC ，∵BF ⊥AC ，∴∠BFA ＝∠BFC ＝90°，∴tan60°＝BF AF，BF 2+CF 2＝BC 2， ∴BF，∴()2227AF +-=， ∴AF ＝2或AF ＝32， ∵cos60°＝AF AB， ∴AB ＝2AF ，当AF ＝2时，AB ＝2AF ＝4，∴AB ＝AD ，∵DC ＝BC ，AC ＝AC ，∴△ADC ≌△ABC （SSS ），∴∠ADC ＝∠ABC ，∵ABCD 是圆内接四边形，∴∠ADC+∠ABC ＝180°，∴∠ADC ＝∠ABC ＝90°，但AC 2＝49，2222453AD DC +=+=，AC 2≠AD 2+DC 2，∴AB ＝4（不合题意，舍去），当AF ＝32时，AB ＝2AF ＝3， ∴AB ＝3．【点睛】此题主要考查了圆的相关性质和直角三角形的性质，解题关键是构造直角三角形模型，利用直角三角形的性质解题.12．如图，BD 为△ABC 外接圆⊙O 的直径，且∠BAE ＝∠C ．（1）求证：AE 与⊙O 相切于点A ；（2）若AE ∥BC ，BC ＝AC ＝2，求AD 的长．【答案】（1）证明见解析；（2）23【解析】【分析】（1）根据题目中已出现切点可确定用“连半径，证垂直”的方法证明切线，连接AO并延长交⊙O于点F，连接BF，则AF为直径，∠ABF＝90°，根据同弧所对的圆周角相等，则可得到∠BAE＝∠F，既而得到AE与⊙O相切于点A．（2））连接OC，先由平行和已知可得∠ACB＝∠ABC，所以AC＝AB，则∠AOC＝∠AOB，从而利用垂径定理可得AH＝1，在Rt△OBH中，设OB＝r，利用勾股定理解得r＝2，在Rt△ABD中，即可求得AD的长为3【详解】解：（1）连接AO并延长交⊙O于点F，连接BF，则AF为直径，∠ABF＝90°，∵»»，AB AB∴∠ACB＝∠F，∵∠BAE＝∠ACB，∴∠BAE＝∠F，∵∠FAB+∠F＝90°，∴∠FAB+∠BAE＝90°，∴OA⊥AE，∴AE与⊙O相切于点A．（2）连接OC，∵AE∥BC，∴∠BAE＝∠ABC，∵∠BAE＝∠ACB，∴∠ACB＝∠ABC，∴AC＝AB＝2，∴∠AOC＝∠AOB，∵OC＝OB，∴OA⊥BC，∴CH＝BH＝1BC32在Rt△ABH中，AH＝22AB BH-＝1，在Rt△OBH中，设OB＝r，∵OH2+BH2＝OB2，∴（r﹣1）2+（3）2＝r2，解得：r＝2，∴DB＝2r＝4，在Rt△ABD中，AD＝22BD AB-＝2242-＝23，∴AD的长为23．【点睛】本题考查了圆的综合问题，恰当的添加辅助线是解题关键.13．如图1，D是⊙O的直径BC上的一点，过D作DE⊥BC交⊙O于E、N，F是⊙O上的一点，过F的直线分别与CB、DE的延长线相交于A、P，连结CF交PD于M，∠C＝12∠P．（1）求证：PA是⊙O的切线；（2）若∠A＝30°，⊙O的半径为4，DM＝1，求PM的长；（3）如图2，在（2）的条件下，连结BF、BM；在线段DN上有一点H，并且以H、D、C 为顶点的三角形与△BFM相似，求DH的长度．【答案】（1）证明见解析；（2）PM＝32；（3）满足条件的DH的值为632-或122311+．【解析】【分析】（1）如图1中，作PH ⊥FM 于H ．想办法证明∠PFH=∠PMH ，∠C=∠OFC ，再根据等角的余角相等即可解决问题；（2）解直角三角形求出AD ，PD 即可解决问题；（3）分两种情形①当△CDH ∽△BFM 时，DH CD FM BF =． ②当△CDH ∽△MFB 时，DH CD FB MF=，分别构建方程即可解决问题；【详解】（1）证明：如图1中，作PH ⊥FM 于H ．∵PD ⊥AC ，∴∠PHM ＝∠CDM ＝90°，∵∠PMH ＝∠DMC ，∴∠C ＝∠MPH ，∵∠C ＝12∠FPM ，∴∠HPF ＝∠HPM ， ∵∠HFP+∠HPF ＝90°，∠HMP+∠HPM ＝90°，∴∠PFH ＝∠PMH ，∵OF ＝OC ，∴∠C ＝∠OFC ，∵∠C+∠CMD ＝∠C+∠PMF ＝∠C+∠PFH ＝90°，∴∠OFC+∠PFC ＝90°，∴∠OFP ＝90°，∴直线PA 是⊙O 的切线．（2）解：如图1中，∵∠A ＝30°，∠AFO ＝90°，∴∠AOF ＝60°，∵∠AOF ＝∠OFC+∠OCF ，∠OFC ＝∠OCF ，∴∠C ＝30°，∵⊙O 的半径为4，DM ＝1，∴OA ＝2OF ＝8，CD 33，∴OD ＝OC ﹣CD ＝43，∴AD ＝OA+OD ＝8+43 ＝123 ，在Rt △ADP 中，DP ＝AD•tan30°＝（12﹣3 ）×33 ＝43 ﹣1， ∴PM ＝PD ﹣DM ＝4 3﹣2．（3）如图2中，由（2）可知：BF ＝12BC ＝4，FM ＝3BF ＝43 ，CM ＝2DM ＝2，CD ＝3 ， ∴FM ＝FC ﹣CM ＝43﹣2，①当△CDH ∽△BFM 时，DH CD FM BF = ， ∴ 3432=- ，∴DH ＝63- ②当△CDH ∽△MFB 时，DH CD FB MF =， ∴34432DH =- ，∴DH ＝1223+ ， ∵DN ＝()22443833--=- ，∴DH ＜DN ，符合题意，综上所述，满足条件的DH 的值为63- 或1223+．【点睛】本题考查圆综合题、切线的判定、解直角三角形、相似三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，学会用分类讨论的思想思考问题.14．如图，是大半圆的直径，是小半圆的直径，点是大半圆上一点，与小半圆交于点，过点作于点. （1）求证：是小半圆的切线；（2）若，点在上运动（点不与两点重合），设，. ①求与之间的函数关系式，并写出自变量的取值范围；②当时，求两点之间的距离.【答案】（1）见解析；（2）①，，②两点之间的距离为或.【解析】【分析】（1）连接CO、CM，只需证到CD⊥CM．由于CD⊥OP，只需证到CM∥OP，只需证到CM 是△AOP的中位线即可．（2）①易证△ODC∽△CDP，从而得到CD2=DP•OD，进而得到y与x之间的函数关系式．由于当点P与点A重合时x=0，当点P与点B重合时x=4，点P在大半圆O上运动（点P不与A，B两点重合），因此自变量x的取值范围为0＜x＜4．②当y=3时，得到-x2+4x=3，求出x．根据x的值可求出CD、PD的值，从而求出∠CPD，运用勾股定理等知识就可求出P，M两点之间的距离．【详解】（1）连接，如图1所示∵是小半圆的直径，∴即∵∴∵∴∴，∵∴，∴∴.，即∵经过半径的外端，且∴直线是小半圆的切线.（2）①∵，，∴∴∴∽∴∴∵,,，∴当点与点重合时，；当点与点重合时，∵点在大半圆上运动（点不与两点重合），∴∴与之间的函数关系式为，自变量的取值范围是.②当时，解得,Ⅰ当时，如图2所示在中，∵，∴，∴∵，∴是等边三角形∵∴∴.Ⅱ当时，如图3所示，同理可得∵∴∴过点作，垂足为，连接，如图3所示∵，∴同理在中，∵，∴综上所述，当时，两点之间的距离为或.【点睛】考查了切线的判定、平行线的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质、特殊角的三角函数值、勾股定理等知识，综合性比较强．15．如图，已知四边形ABCD内接于⊙O，点E在CB的延长线上，连结AC、AE，∠ACB=∠BAE=45°．（1）求证：AE是⊙O的切线；（2）若AB=AD，AC=32，tan∠ADC=3，求BE的长．【答案】（1）证明见解析；（2）52 BE【解析】试题分析：（1）连接OA、OB，由圆周角定理得出∠AOB=2∠ACB=90°，由等腰直角三角形的性质得出∠OAB=∠OBA=45°，求出∠OAE=∠OAB+∠BAE=90°,即可得出结论；（2）过点A 作AF ⊥CD 于点F,由AB=AD ，得到∠ACD =∠ACB =45°，在Rt △AFC 中可求得AF＝3，在Rt △AFD 中求得DF ＝1，所以AB ＝AD ＝，CD = CF +DF =4，再证明△ABE ∽△CDA ，得出BE AB DA CD =，即可求出BE 的长度；试题解析：（1）证明：连结OA ，OB ，∵∠ACB =45°，∴∠AOB =2∠ACB = 90°，∵OA=OB ，∴∠OAB =∠OBA =45°，∵∠BAE =45°，∴∠OAE =∠OAB +∠BAE =90°，∴OA ⊥AE ．∵点A 在⊙O 上，∴AE 是⊙O 的切线．（2）解：过点A 作AF ⊥CD 于点F ，则∠AFC =∠AFD =90°．∵AB=AD ， ∴AB u u u r =AD u u u r∴∠ACD =∠ACB =45°，在Rt △AFC 中，∵AC =∠ACF =45°，∴AF=CF=AC ·sin ∠ACF =3，∵在Rt △AFD 中， tan ∠ADC=3AF DF =， ∴DF =1，∴AB AD ==且CD = CF +DF =4，∵四边形ABCD 内接于⊙O ，∴∠ABE =∠CDA ，∵∠BAE =∠DCA ，∴△ABE ∽△CDA ， ∴BE AB DA CD=，∴10=，10∴5BE=．2。

2022年北京市丰台区初三数学综合练习2 (二模)试题及答案解析

2022年北京市丰台区初三数学综合练习2（二模）一、选择题（本大题共8小题，共24.0分。

在每小题列出的选项中，选出符合题目的一项）1. 如图，下列水平放置的几何体中，侧面展开图是扇形的是A. B.C. D.2. 2021年我国原油产量约1.99亿吨，连续3年回升．将199000000用科学记数法表示应为( )A. 199×106B. 1.99×108C. 1.99×109D. 0.199×1093. 如图，AB//CD，∠ACD=80°，∠ACB=30°，∠B的度数为( )A. 50°B. 45°C. 30°D. 25°4. 下列多边形中，内角和最大的是 ( )A. B. C. D.5. 实数a，b在数轴上的对应点的位置如图所示，若实数c满足b<c<a，则c的值可以是( )A. −3B. −2C. 2D. 36. 同时抛掷两枚质地均匀的硬币，则两枚硬币全部正面向上的概率是( )A. 23B. 12C. 13D. 147. 若n为整数，且n<√77<n+1，则n的值是( )A. 7B. 8C. 9D. 108. 如图，某容器的底面水平放置，匀速地向此容器内注水，在注满水的过程中，水面的高度ℎ与时间t的函数关系的图象大致是A. B. C. D.二、填空题（本大题共8小题，共24.0分）9. 若√x−3在实数范围内有意义，则实数x的取值范围是．10. 方程 1 x =3x+2的解为________ ．11. 已知关于x的方程x2−2x+m=0有两个不相等的实数根，则m的取值范围是________12. 如图，PA，PB是⊙O的切线，A，B为切点，点C在⊙O上，若∠APB=60∘，则∠ACB= _____°．13. 如图，在平行四边形ABCD中，E，F分别是AB，CD的中点，连接EF.只需添加一个条件即可证明四边形EFCB是菱形，这个条件可以是(写出一个即可)．14. 在平面直角坐标系xOy中，若直线y=x与双曲线y=mx的交点为A，B，且点A，B的横坐标分别为x 1，x 2，则x 1+x 2的值是_______ ．15. 甲、乙两台包装机同时包装糖果，分别从中随机抽取5袋，测得它们的实际质量(单位：g)如表所示：甲1001029910198乙1009710497102那么包装机包装的5袋糖果的质量比较稳定(填“甲”或“乙”)．16. 某超市现有n个人在收银台排队等候结账．设结账人数按固定的速度增加，收银员结账的速度也是固定的．若同时开放2个收银台，需要20分钟可使排队等候人数为0；若同时开放3个收银台，需要12分钟可使排队等候人数为0.为减少顾客等待结账的时间，需要6分钟内使排队等候人数为0，则需要至少同时开放个收银台．三、计算题（本大题共2小题，共12.0分）17. 计算：|−3|−2sin45∘+√8+(π+√3)0．18. 解不等式组：{ 2x−3>x−2 , 3x−22<x+1 .四、解答题（本大题共10小题，共80.0分。

初三数学试题全册及答案

初三数学试题全册及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 0.33333…（3无限循环）B. √4C. πD. 1/3答案：C2. 一个二次函数y=ax^2+bx+c的顶点坐标为（1，-2），则下列哪个选项是正确的？A. a<0，b=2a，c=a-3B. a>0，b=-2a，c=a-3C. a<0，b=-2a，c=a-3D. a>0，b=2a，c=a-3答案：C3. 一个等腰三角形的两边长分别为3和5，那么这个三角形的周长是多少？A. 11B. 13C. 14D. 16答案：B4. 已知一个圆的半径为5，那么这个圆的面积是多少？A. 25πB. 50πC. 75πD. 100π答案：B5. 一个等差数列的首项为2，公差为3，那么这个数列的第5项是多少？A. 17B. 14C. 11D. 8答案：A6. 一个正六边形的边长为2，那么这个正六边形的面积是多少？A. 6√3B. 4√3C. 2√3D. √3答案：B7. 已知一个函数f(x)=2x+3，那么f(-1)的值是多少？B. 1C. 5D. -5答案：A8. 一个直角三角形的两条直角边长分别为3和4，那么这个三角形的斜边长是多少？A. 5B. √7C. √13D. 7答案：A9. 一个等比数列的首项为2，公比为2，那么这个数列的第4项是多少？A. 16C. 64D. 128答案：A10. 一个扇形的圆心角为60°，半径为4，那么这个扇形的面积是多少？A. 4πB. 8πC. 12πD. 16π答案：A二、填空题（每题3分，共30分）11. 一个二次函数y=ax^2+bx+c的顶点坐标为（-1，2），对称轴为直线x=-1，那么a的值为______。

答案：112. 一个等差数列的首项为1，公差为2，那么这个数列的第10项是______。

答案：1913. 一个正五边形的边长为a，那么这个正五边形的面积是______。

2023北京朝阳区初三一模数学试题及参考答案

北京市朝阳区九年级综合练习（一）一、选择题（共16分，每题2分）第1-8题均有四个选项，其中符合题意的选项只有一个．1.下图是某几何体的三视图，该几何体是（A ）长方体（B ）三棱柱（C ）圆锥（D ）圆柱第1题第3题第4题第7题2.我国已建成世界上规模最大的社会保障体系、医疗卫生体系，基本养老保险覆盖1 040 000 000人左右，将1 040 000 000用科学记数法表示应为（A ）1.04×1010 （B ）1.04×109 （C ）10.4×109 （D ） 0.104×10113．如上图，若数轴上的点A 表示下列四个无理数中的一个，则这个无理数是（A ）（B（C （D ）π4. 如上图，直线AB ，CD 相交于点O ，若∠AOC =60°，∠BOE =40°，则∠DOE 的度数为（A ）60° （B ）40°（C ）20° （D ）10°5. 经过某路口的汽车，只能直行或右转. 若这两种可能性大小相同，则经过该路口的两辆汽车都直行的概率为（A ）（B ）（C ）（D ）141312346．正六边形的外角和为（A ）180°（B ）360°（C ）540°（D ）720°7．某中学为了解学生对四类劳动课程的喜欢情况，从本校学生中随机抽取了200名进行问卷调查，根据数据绘制了如上面图所示的统计图. 若该校有2000名学生，估计喜欢木工的人数为（A ）64（B ）380（C ）640 （D ）7208. 下面的三个问题中都有两个变量：①矩形的面积一定，一边长y 与它的邻边x ;②某村的耕地面积一定，该村人均耕地面积S 与全村总人口n ;③汽车的行驶速度一定，行驶路程s 与行驶时间t .其中，两个变量之间的函数关系可以用形如的式子表示的是（A ）①②（B ）①③（C ）②③（D ）①②③二、填空题（共16分，每题2分）9在实数范围内有意义，则实数x 的取值范围是．10．分解因式：．11．若关于x 的一元二次方程260x x m ++=有两个相等的实数根，则实数m 的值为．12．方程的解为．13．在平面直角坐标系xOy 中，若反比例函数的图象经过点和点，则．14．如图，在△ABC 中，DE 是AC 的垂直平分线，AC =6. 若△ABD 的周长为13，则△ABC 的周长为．15．如图，在矩形ABCD 中，点E 在AD 边上，连接BE 并延长，交CD 的延长0ky k k x=≠（为常数，）2363a a -+=322x x=+6y x=()2A m ，()2B n -，m n +=第14题图第15题图线于点F . 若AB =2，BC =4，，则BF 的长为．16. 一个33人的旅游团到一家酒店住宿，酒店的客房只剩下4间一人间和若干间三人间，住宿价格是一人间每晚100元，三人间每晚130元.（说明：男士只能与男士同住，女士只能与女士同住. 三人间客房可以不住满，但每间每晚仍需支付130元.）（1）若该旅游团一晚的住宿房费为1530元，则他们租住了间一人间;（2）若该旅游团租住了3间一人间，且共有19名男士，则租住一晚的住宿房费最少为元.三、解答题（共68分，第17-20题，每题5分，第21题6分，第22题5分，第23-24题，每题6分，第25题5分，第26题6分，第27-28题，每题7分）17．计算：．18．解不等式组：19．已知，求代数式的值．20. 下面是证明“等腰三角形的两个底角相等”的两种添加辅助线的方法，选择其2AEDE=(02sin 45π-+-o 17242.3x x xx +⎧⎪+⎨⎪⎩＞-，≤230x x --=(2)(2)(2)x x x x +---中一种，完成证明.已知：如图，在△ABC 中，AB =AC .求证：∠B =∠C .方法一证明：如图，作△ABC 的中线AD .方法二证明：如图，作△ABC 的角平分线AD .21. 如图，在平行四边形ABCD 中，对角线AC ，BD 相交于点O ，点E ，F 在BD 上，AE ∥CF ，连接AF ，CE ．（1）求证：四边形AECF 为平行四边形；（2）若∠EAO +∠CFD =180°，求证：四边形AECF 是矩形．22. 在平面直角坐标系xOy 中，一次函数的图象经过点（0，1），（-2，2），与x轴交于点A .（1）求该一次函数的表达式及点A 的坐标；（2）当2x ≥时，对于x 的每一个值，函数的值大于一次函数0y kx b k =+≠（）2y x m =+的值，直接写出m 的取值范围.23. 如图，AB 是⊙O 的弦，过点O 作OC ⊥AB ，垂足为C ，过点A 作⊙O 的切线，交OC 的延长线于点D ，连接OB .（1）求证：∠B =∠D ；（2）延长BO 交⊙O 于点E ，连接AE ，CE ，若AD=，sinBCE 的长．24．某校为了解读书月期间学生平均每天阅读时间，在该校七、八、九年级学生中各随机抽取了15名学生，获得了他们平均每天阅读时间（单位：min ），并对数据进行了整理、描述，给出部分信息.a . 七、八年级学生平均每天阅读时间统计图：0y kx b k =+≠（）七年级学生平均每天阅读时间八年级学生平均每天阅读时间b . 九年级学生平均每天阅读时间：21 22 25 33 36 36 37 37 39 39 41 42 46 48 50c . 七、八、九年级学生平均每天阅读时间的平均数：年级七八九平均数26.435.236.8根据以上信息，回答下列问题：（1）抽取的15名九年级学生平均每天阅读时间的中位数是；（2）求三个年级抽取的45名学生平均每天阅读时间的平均数；（3）若七、八、九年级抽取的学生平均每天阅读时间的方差分别为，，，则，，之间的大小关系为.25．一位滑雪者从某山坡滑下并滑完全程，滑行距离s （单位：m ）与滑行时间t （单位：s ）近似满足“一次函数”、“二次函数”或“反比例函数”关系中的一种. 测得一些数据如下：滑行时间t /s 01234滑行距离s /m261220（1）s 是t 的函数（填“一次”、“二次”或“反比例”）；21s 22s 23s 21s 22s 23s（2）求s 关于t 的函数表达式；（3）已知第二位滑雪者也从坡顶滑下并滑完全程，且滑行距离与第一位滑雪者相同，滑行距离s （单位：m ）与滑行时间t （单位：s ）近似满足函数关系2522s t t =+. 记第一位滑雪者滑完全程所用时间为t 1，第二位滑雪者滑完全程所用时间为t 2，则t 1t 2（填“<”，“=”或“＞”）.26．在平面直角坐标系xOy 中，抛物线y =ax 2+（2m -6）x +1经过点()124m -，.（1）求a 的值；（2）求抛物线的对称轴（用含m 的式子表示）；（3）点()1m y -，，()2m y ，，()32m y +，在抛物线上，若231y y y ＜≤，求m 的取值范围.27. 如图，∠MON =α，点A 在ON 上，过点A 作OM 的平行线，与∠MON 的平分线交于点B ，点C 在OB 上（不与点O ，B 重合），连接AC ，将线段AC 绕点A 顺时针旋转180°-α，得到线段AD ，连接BD .（1）直接写出线段AO 与AB 之间的数量关系，并证明∠MOB =∠DBA ；（2）连接DC 并延长，分别交AB ，OM 于点E ，F . 若α=60°，用等式表示线段EF 与AC 之间的数量关系，并证明.28. 在平面直角坐标系xOy 中，对于点P ，C ，Q （点P 与点C 不重合），给出如下定义：若∠PCQ =90°，且1CQ CP k，则称点Q 为点P 关于点C 的“k -关联点”.已知点A （3，0），点B （0，），⊙O 的半径为r .（1）①在点D （0，3），E （0，-1.5），F （3，3）中，是点A 关于点O 的“1-关联点”的为；②点B 关于点O 的关联点”的坐标为；（2）点P 为线段AB 上的任意一点，点C 为线段OB 上任意一点（不与点B重合）.①若⊙O 上存在点P 关于点O 的关联点”，直接写出r 的最大值及最小值；②当r =⊙O 上不存在点P 关于点C 的“k -关联点”，直接写出k 的取值范围：.北京市朝阳区九年级综合练习（一）数学试卷答案及评分参考2023.4一、选择题（共16分，每题2分）题号12345678答案A B D C A B C A 二、填空题（共16分，每题2分）三、解答题（共68分，第17-20题，每题5分，第21题6分，第22题5分，第23-24题，每题6分，第25题5分，第26题6分，第27，28题，每题7分）17. 解：原式12=-++1=+.18. 解：原不等式组为17242.3x xxx+⎧⎪+⎨⎪⎩＞-，≤解不等式①，得 2.x>解不等式②，得 4.x≤∴原不等式组的解集为2 4.x<≤19. 解：(2)(2)(2)x x x x+---2242x x x=--+222 4.x x=--∵230x x--=，∴2 3.x x-=题号9101112答案5x≥23(1)a-9x=4题号13141516答案01951；1600①②∴原式22()4 2.x x =--=20. 方法一证明：∵AD 是△ABC 的中线， ∴BD =CD .在△ABD 和△ACD 中，AB AC AD AD BD CD =⎧⎪=⎨⎪=⎩，，，∴△ABD ≌△ACD . ∴∠B =∠C .方法二证明：∵AD 是△ABC 的角平分线， ∴∠BAD =∠CAD . 在△ABD 和△ACD 中，AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩，，，∴△ABD ≌△ACD . ∴∠B =∠C.21. 证明：（1）∵四边形ABCD 是平行四边形，∴OA =OC . ∵AE ∥CF ，∴∠EAO =∠FCO .∵∠AOE =∠COF ，∴△AEO ≌△CFO . ∴OE =OF .∴四边形AECF 为平行四边形.（2）∵∠EAO +∠CFD =180°，∠CFO +∠CFD =180°，∴∠EAO=∠CFO . ∵∠EAO =∠FCO ，∴∠FCO=∠CFO . ∴OC=OF . ∴AC=EF .∴四边形AECF 是矩形．22. 解：（1）∵一次函数的图象经过点（0，1），（-2，2），∴12 2.b k b =⎧⎨-+=⎩，解得 121.k b ⎧=-⎪⎨⎪=⎩ ∴该一次函数的表达式为11.2y x =-+令0y =，得 2.x =∴()20.A ，（2） 4.m ＞-23. （1）证明：如图，连接OA .∵AD 为⊙O 的切线，∴∠OAD =90°.∴∠CAD +∠OAB =90°.∵OC ⊥AB ，∴∠ACD =90°.∴∠CAD +∠D =90°.∴∠OAB =∠D .∵OA =OB ，∴∠OAB =∠B .∴∠B =∠D .（2）解：在Rt △ACD 中，AD=，sin D =sin B，可得sin 2AC AD D =⋅=.∴AB =2AC =4.根据勾股定理，得CD =4.∴tan B =tan D =12.∵BE 为⊙O 的直径，0y kx b k =+≠（）∴∠EAB =90°.在Rt △ABE 中,tan 2AE AB B =⋅=.在Rt △ACE 中，根据勾股定理，得CE=24．解：（1）37．（2）根据题意可知，三个年级抽取的45名学生平均每天阅读时间的平均数为 1526.41535.21536.832.8.45⨯+⨯+⨯=（3）＜＜．25．解：（1）二次.（2）设s 关于t 的函数表达式为s =at 2+bt ，根据题意，得242 6.a b a b +=⎧⎨+=⎩，解得11.a b =⎧⎨=⎩，∴s 关于t 的函数表达式为s =t 2+t.（3）＞.26．解：（1）∵抛物线y =ax 2+（2m -6）x +1经过点()124m -，，∴2m -4=a +（2m -6）+1.∴a =1（2）由（1）得抛物线的表达式为y =x 2+（2m -6）x +1.∴抛物线的对称轴为3.x m =-（3）①当m ＞0时，可知点()1m y -，，()2m y ，，()32m y +，从左至右分布.根据23y y ＜可得232m m m ++-＜.∴ 1.m ＞根据31y y ≤可得232m m m -++-≥.∴ 2.m ≤22s 21s 23s∴1 2.m ＜≤②当m ≤0时，∵3m m m +≤-＜-，∴21y y ≥，不符合题意.综上，m 的取值范围为1 2.m ＜≤27．解：（1）AO =AB .证明：∵OB 平分∠MON ， ∴∠MOB =∠NOB. ∵OM //AB ，∴∠MOB =∠ABO. ∴∠NOB =∠ABO. ∴AO =AB .根据题意，得AC =AD ，∠OAB =∠CAD .∴∠CAO =∠DAB.∴△OAC ≌△BAD. ∴∠COA =∠DBA. ∴∠MOB =∠DBA.（2）EF =.证明：如图，在OM 上截取OH =BE ，连接CH .∵△OAC ≌△BAD ，∴OC=BD.又OH =BE ，∴△OHC ≌△BED.∴CH=DE ，∠OHC=∠BED ，∵OM//AB ，∴∠MFC=∠BED.∴∠MFC=∠OHC.∴CF=CH.∴CF=DE.∴CD=EF.∵α=60°，∴∠CAD=180°－α=120°，作AK ⊥CD 于点K. ∵AC=AD ，∴∠ACK =30°，1.2CK CD =∴.CK AC =∴CD =.∴EF =.28．解：（1）①D .②（-3，0）或（3，0）.（2）① 3，32.②k .。

初三数学常考试题及答案

初三数学常考试题及答案一、选择题1. 已知一个二次函数的图像经过点A(-1,0)和点B(3,0)，且函数的开口向上，则该二次函数的对称轴是（）。

A. x = 0B. x = 1C. x = 2D. x = -1答案：B解析：二次函数的对称轴是其顶点的x坐标，由于函数图像经过点A(-1,0)和点B(3,0)，且开口向上，根据二次函数的性质，对称轴是这两点x坐标的平均值，即x = (-1 + 3) / 2 = 1。

2. 下列哪个选项是不等式2x - 3 > 0的解集？A. x > 3/2B. x < 3/2C. x > 3D. x < 3答案：A解析：将不等式2x - 3 > 0移项得到2x > 3，再除以2得到x > 3/2，因此选项A是正确的。

二、填空题3. 计算绝对值：|-7| = _______。

答案：7解析：绝对值表示一个数距离0的距离，因此|-7|表示-7距离0的距离，即7。

4. 计算平方根：√9 = _______。

答案：±3解析：平方根是一个数的平方等于给定数的那个数，9的平方根是3，因为3的平方是9。

同时，-3的平方也是9，所以9的平方根是±3。

三、解答题5. 已知一个直角三角形的两条直角边长分别为3和4，求斜边的长度。

答案：5解析：根据勾股定理，直角三角形的斜边长度等于两直角边长度的平方和的平方根。

即斜边长度= √(3² + 4²) = √(9 + 16) = √25 = 5。

6. 某工厂生产一种零件，每件成本为10元，售价为15元，若该工厂希望获得的利润不低于1000元，问至少需要生产多少件零件？答案：100件解析：设需要生产的零件数量为x件，则总利润为(15 - 10)x = 5x元。

根据题意，5x ≥ 1000，解得x ≥ 200。

因此，至少需要生产200件零件。

四、证明题7. 证明：如果一个三角形的两边之和大于第三边，那么这个三角形是存在的。

初三数学试题及答案人教版

初三数学试题及答案人教版初三数学试题及答案（人教版）一、选择题（每题2分，共10分）1. 若a，b，c为实数，且满足a+b+c=3，abc=1，则下列选项中正确的是：A. a^2+b^2+c^2=5B. a^2+b^2+c^2=7C. a^2+b^2+c^2=9D. a^2+b^2+c^2=112. 下列哪个不等式是正确的？A. |x-2| > |x+3|B. |x-2| < |x+3|C. |x-2| ≥ |x+3|D. |x-2| ≤ |x+3|3. 一个圆的半径为5，那么它的周长是：A. 10πB. 20πC. 30πD. 40π4. 函数y=2x^2+3x+1的顶点坐标是：A. (-1,0)B. (-1,1)C. (1,0)D. (1,1)5. 如果一个三角形的三边长分别为a，b，c，且满足a^2+b^2=c^2，那么这个三角形是：A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定二、填空题（每题2分，共10分）6. 若一个数的平方根等于它本身，那么这个数是________。

7. 一个数的绝对值是它本身，这个数是非负数，即这个数是________。

8. 一个直角三角形的两条直角边分别为3和4，那么它的斜边长为________。

9. 函数y=x^3-6x^2+11x-6的零点是________。

10. 一个圆的面积为25π，那么它的半径是________。

三、解答题（每题10分，共30分）11. 解一元二次方程：x^2-5x+6=0。

12. 证明：若a，b，c是三角形的三边，且满足a^2+b^2=c^2，那么这个三角形是直角三角形。

13. 求函数y=x^2-2x+1在x=2时的值。

四、证明题（每题15分，共30分）14. 证明：勾股定理。

15. 证明：若a，b，c是三角形的三边，且满足a+b>c，那么这个三角形是存在的。

五、综合题（每题20分，共20分）16. 一个长方形的长为10cm，宽为5cm，求其对角线的长度。

初三数学常考试题及答案

初三数学常考试题及答案一、选择题（本题共10分，每题2分）1. 下列哪个选项不是实数？A. πB. √2C. -1D. i2. 若a，b，c为实数，且a + b + c = 1，下列哪个等式一定成立？A. a^2 + b^2 + c^2 = 1B. a^3 + b^3 + c^3 = 1C. (a + b + c)^2 = a^2 + b^2 + c^2D. (a - b)^2 + (b - c)^2 + (c - a)^2 ≥ 03. 一个圆的半径为5，那么这个圆的面积是多少？A. 25πB. 50πC. 75πD. 100π4. 一个数的平方根是2，这个数是：A. 4B. -4C. 8D. -85. 下列哪个是一元二次方程的解？A. x + 2 = 0B. x^2 - 4x + 4 = 0C. x^2 + 4x + 4 = 0D. x^2 - 9 = 0二、填空题（本题共10分，每题2分）6. 一个直角三角形的两条直角边分别为3和4，那么它的斜边长为______。

7. 如果一个数的立方等于-27，那么这个数是______。

8. 一个正数的倒数是1/4，那么这个数是______。

9. 一个多项式f(x) = ax^3 + bx^2 + cx + d，如果f(2) = 5，f(-2) = -3，那么a + b + c + d = ______。

10. 如果一个数的平方加上8倍这个数再加上16等于0，那么这个数是______。

三、解答题（本题共30分，每题6分）11. 解方程：2x^2 - 5x - 3 = 0。

12. 证明：对于任意实数x，(x - 1)^2 + 3 ≥ 2。

13. 计算：(3x^2 - 2x + 1) / (x - 1)。

14. 已知一个长方体的长、宽、高分别是a、b、c，求证：长方体的体积V = abc。

15. 已知点A(-1, 2)，B(3, 4)，求直线AB的斜率。

四、综合题（本题共50分，每题10分）16. 一个圆的半径为7，求圆的周长和面积。

初三数学综合试题一10732

1
24、问渠那得清如许，为有源头活水来——朱熹
24、问渠那得清如许，为有源头活水来——朱熹初三数学综合试题一第一部分（100分）一、填空题（24分，每空2分） 1、当k＿＿＿时，关于x的方程（k+1）x2+2x+3=0是一元二次方程 2、方程x(x+2)=3(x+2) 的根是＿＿＿＿＿＿ 3、函数y=中自变量x的取值范围是＿＿＿＿＿ 4、点P的坐标为（3，－4），则点P关于原点的对称点P1的坐标是＿＿＿＿＿ 5、抛物线y=－x2－5的顶点坐标是________ 6、在Rt△ABC中，∠C=900，， tanA=，则cosA=_______ C B 7、圆内接四边形ABCD中，∠A：∠B：∠C=2：3：4，则∠D=____度 8、AB为⊙O的直径，弦CD⊥AB于M，AM=4，BM=9，则弦CD=_______ 9、若两圆共有三条公切线，则两圆的位置关系是______ A P 10、如图，PA切⊙O于A，∠PAB=500，∠ABC=700，则∠BAC=_______度（图10） 11、已知外切两圆半径分别为6和2，则两圆的外公切线长等于________ 12、已知⊙O的半径为6cm，⊙O的一条弦AB的长为6cm，则弦AB所对的圆周角的度数是____ 二、选择题（24分） 13、一元二次方程x2+x-3=0的根的情况是（） B、有两个相等的实数根 A、有两个不相等的实数根 C、没有实数根 D、不能确定 14、如果点P（a，b）在第四象限，则点P1（-b，-a）所在的象限是（） A、第一象限 B、第二象限 C、第三象限 D、第四象限 15、Rt△ABC中，∠C=900，a,b分别为∠A，∠B的对边，若sinA:sinB=2：3，则a:b= ( ) A、2：3 B、3：2 C、4：9 D 、9：4 16、直线y=－4x+3不经过的象限是（） A、第一象限 B第二象限 C、第三象限 D、第四象限 17、如图，PA，PB切⊙O于A、B，C是优弧AB上的点，∠C=640，则∠P等于（） A A、 260 B、620 P C

2024年北京初三九年级上学期数学期末考《圆的综合》

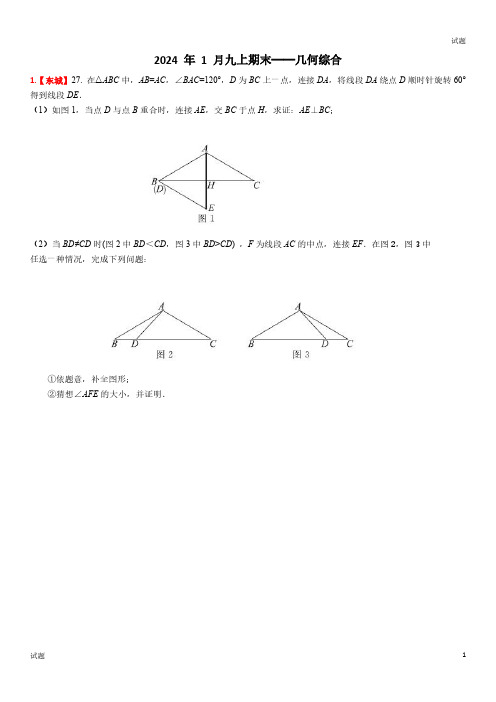
2024年1月九上期末——圆的综合1.【东城】24．如图，AB 为⊙O 的直径，点C 在⊙O 上，∠ACB 的平分线CD 交⊙O 于点D.过点D 作DE ∥AB ，交CB 的延长线于点E ．(1)求证：直线DE 是⊙O 的切线；(2)若∠BAC =30°，BC =CD 的长．2.【西城】24．如图，AB 是O 的直径，AB BC =，AC 交O 于点D ，点F 在OD 的延长线上且12FAD ABC ∠=∠．（1）求证：AF 是O 的切线；（2）若8AF =，4DF =，求AC 的长．3.【海淀】25.如图，AB 为半圆O 的直径，点C ，D 在半圆O 上，直线CM 与半圆O 相切于点C ，//CM AD .（1）若MCD ∠α=，求COA ∠的大小（用含α的式子表示）；（2）过点O 作OE CD ⊥交CM 于点E ，交CD 于点F ，若//CD AB ，6AB =，求CE 的长.4.【朝阳】24．如图，AC ，BD 是圆内接四边形ABCD 的对角线，AC ⊥BD 于点E ，BD 平分∠ADC .（1）求∠BAD 的度数；（2）点P 在DB 的延长线上，P A 是该圆的切线.①求证：PC 是该圆的切线；②若PA =AC =3，直接写出PD 的长.5.【石景山】24．如图，在ABC △中，AB AC =，以AB 为直径的O 交BC 于点D ，交AC 于点E ，点F 在AC 的延长线上，12CBF BAC ∠=∠．（1）求证：BF 是O 的切线；（2）若5AB =，1tan 2CBF ∠=，求CE 的长．6.【丰台】24．如图，△ABC 中，AB =AC ，以AB 为直径作⊙O 交BC 于点D ，作DE ⊥AC 交AC 于点E ，延长ED 与AB 的延长线交于点F ．（1）求证：DE 是⊙O 的切线；（2）若△ABC 为等边三角形，AE=3，求⊙O 半径的长．7.【昌平】24.如图，AB 是⊙O 的直径，点C 在⊙O 上，点D 为 AC 的中点，过点D 作⊙O 的切线，交BC 延长线于点P ，连接OD 交AC 于点E .（1）求证：四边形DECP 是矩形；（2）作射线AD 交BC 的延长线于点F ，若tan ∠CAB =43，BC =6，求DF 的长.8.【通州】25．如图，点C 在以AB 为直径的O 上，CD 平分ACB ∠交O 于点D ，交AB 于点E ，过点D 作DF AB ∥交CO 的延长线于点F ．（1）求证：直线DF 是O 的切线；（2）若30A ∠=︒，43AC =，求DF 的长．24题图9.【房山】24.如图,AB是⊙O的直径，AC，BC是弦，点D在AB的延长线上，且DCB DAC∠=∠，⊙O的切线AE与DC的延长线交于点E．（1）求证：CD是⊙O的切线；（2）若⊙O的半径为2，30∠=︒，求AE的长.D10.【大兴】24.如图，AB是⊙O的直径，点C在⊙O上，连接AC，BC，过点O作OD⊥BC于点D,过点C作直线CE交OD的延长线于点E,使得∠E=∠B.(1)求证：CE是⊙O的切线.(2)若DE=6,CE=35,求OD的长.11.【门头沟】25.如图，△ABC内接于⊙O，AB为直径，点D在⊙O上，过点D作⊙O切线与AC的延长线交于点E，ED∥BC，连接AD交BC于点F.（1）求证：∠BAD=∠DAE；（2）若AB=6，AD=5，求DF的长.12.【燕山】24．如图，在△ABC中，∠ACB＝90°，点D在AB上，以AD为直径作⊙O与BC相切于点E，连接DE并延长交AC的延长线于点F．(1)求证：AF＝AD；(2)若CE＝4，CF＝2，求⊙O的半径．13.【顺义】25．如图，AB为⊙O的弦，点C为AB的中点，CO的延长线交⊙O于点D，连接AD，BD，过点D作⊙O的切线交AO的延长线于点E．（1）求证：DE∥AB；（2）若⊙O的半径为3，tan∠ADC＝，求DE的长．14.【密云】24.如图，⊙O是△ABC的外接圆，∠ABC=45°，连接OC交AB于点E，过点A作OC的平行线交BC延长线于点D．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为4，AD=6，求线段CD的长．15.【平谷】24.如图，AB 为⊙O 的直径，弦CD ⊥AB 于H ，连接AC 、AD ，过点A 作⊙O 的切线与∠ADC 的平分线相交于点E ，DE 交AB 于点G ，交AC 于点F ，交⊙O 于点M ，连接AM ．（1）求证：AC=AD ；（2）若22tan =∠AMD ，CD=4，求AF 长．。

2024年北京市门头沟区九年级中考一模数学试题(原卷版)

门头沟区2024年初三年级综合练习（一）数学考生须知：1．本试卷共10页，共三道大题，28个小题．满分100分．考试时间120分钟．2．在试卷和答题卡上准确填写学校和姓名，并将条形码粘贴在答题卡相应位置处．3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．4．在答题卡上，选择题、作图题用2B 铅笔作答，其它试题用黑色字迹签字笔作答．5．考试结束，将试卷、答题卡和草稿纸一并交回．一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个．1. 下列几何体中，俯视图是三角形的是（　）A. B. C. D.2. 近几年全国各省市都在发展旅游业，让游客充分感受地域文化，据统计，某市2023年的游客接待量为210000000人次，将210000000用科学记数法表示为（）A. B. C. D. 3. 下图是手机的一些手势密码图形，其中既是轴对称图形又是中心对称图形的是（）A. B. C. D.4. 一个正n 边形的每一个外角都是60°，则这个正n 边形是（）A 正四边形 B. 正五边形 C. 正六边形 D. 正七边形5. 数轴上的两点所表示的数分别为a ，b ，且满足，下列结论正确的是（）A. B. C. D. 6. 如图，，平分交于点，，则（）.72.110⨯82.110⨯92.110⨯102.110⨯·0,0a b a b >+<0,0a b >>0,0a b <<0,0a b ><0,0a b <>AB CD AD BAC ∠CD D 130∠=︒CAB ∠=A. B. C. D. 7. 同时掷两枚质地均匀的骰子，朝上的一面点数之和为整数的平方的概率为（）A. B. C. D. 8. 如图，在等边三角形中，有一点P ，连接、、，将绕点B 逆时针旋转得到，连接、，有如下结论：①；②是等边三角形；③如果，那么．以上结论正确的是（）A. ①②B. ①③C. ②③D. ①②③二、填空题（本题共16分，每小题2分）9.的取值范围是__________．10 因式分解：______．11. 如图所示，为了验证某个机械零件的截面是个半圆，某同学用三角板放在了如下位置，通过实际操作可以得出结论，该机械零件的截面是半圆，其中蕴含的数学道理是_______．12. 在中，，，，点P 在线段上（不与B 、C 两点重合），如果的长度是个无理数，则的长度可以是______．（写出一个即可）.30︒45︒60︒90︒16736142936ABC PA PB PC BP 60︒BD PD AD BPC BDA ≌ BDP △150BPC ∠=︒²²²PA PB PC =+x 22mx mx m -+=ABC 90C ∠=︒3AB =2AC =BC AP AP13. 已知一元二次方程，有两个根，两根之和为正数，两根之积是负数，写出一组符合条件的a、b的值_________．14. “洞门初开，佳景自来”，园林建筑中的门洞设计有很多数学中的图形元素，如图中的门洞造型，由四个相同的半圆构成，且半圆的直径围成了正方形，如果半圆的直径为米，则该门洞的通过面积为_______平方米．15. 下面是某小区随机抽取的50户家庭的某月用电量情况统计表：月用电量x（千瓦时/户/月）户数（户）61511144已如月用电量第三档的标准为大于240小于等于400，如果该小区有500户家庭，估计用电量在第三档的家庭有______户．16. 5月20日是中国学生营养日，青少年合理膳食是社会公共卫生关注的问题之一．某食堂为了均衡学生的营养，特设置如下菜单，每种菜品所含的热量，脂肪和蛋白质如下：编号菜名类别热量/千焦脂肪/g蛋白质/g1宫保鸡丁荤菜1033187 2炸鸡排荤菜12541920 3糖醋鱼块荤菜211218144土豆炖牛肉荤菜109523165香菇油菜素菜911117 20x ax b++=1240x≤240300x<≤300350x<≤350400x<≤400x>6家常豆腐素菜102016137清炒冬瓜素菜564718韭菜炒豆芽素菜491239米饭主食3601810紫菜鸡蛋汤汤10058学校规定每份午餐由1份荤菜，2份素菜，1份汤和1碗米饭搭配．小明想要搭配一份营养午餐，那么他摄入的脂肪最低量是____________g ．（12岁岁的青少年男生午餐营养标准：摄入热量为2450千焦，摄入蛋白质为65g ，蛋白质越接近标准越营养）三、解答题（本题共68分，第17～21题每小题5分，第22～24题每小题6分，第25题5分，第26题6分，第27～28题每小题7分）解答应写出文字说明、证明过程或演算步骤．17. ．18. ．19. 已知，求代数式的值．20. 如图所示，在长为11、宽为10矩形内部，沿平行于矩形各边的方向割出三个完全相同的小矩形，求每个小矩形的面积．21. 如图，在四边形中，，，，点E 为中点，射线交的延长线于点F ，连接．的14-011(2021)22sin 45()3π---+︒-()2131242x x x x ⎧+>-⎪⎨-<+⎪⎩23210x x +-=22(1)(2)(2)3x x x x +-+-+ABCD AD BC ∥90A ∠=︒BD BC =CD BE AD CF（1）求证：四边形是菱形；（2）若，，求的长．22. 在平面直角坐标系中，一次函数的图象由的图象向上平移2个单位得到，反比例函数的图象过点．（1）求一次函数表达式及m 的值；（2）过点平行于x 轴的直线，分别与反比例函数一次函数的图象相交于点M 、N ，当时，画出示意图并直接写出n 的值．23. 某市统计局为研究我国省会及以上城市发展水平与人均之间关系，收集了年个城市的人均数据（单位：万元）以及城市排名，进行了相关的数据分析，下面给出了部分信息．．城市的人均的频数分布直方图（数据分成组：，，，，）：频数（城市个数）的BCFD 1AD =2CF =BF xOy ()0y kx b k =+≠1y x =()20m y m x=≠()14A ，()0P n ，2m y x =y kx b =+PM MN =GDP 202331GDP GDP a GDP 558x <≤811x <≤1114x <≤1417x <≤1720x <≤．城市的人均（万元）的数值在这一组的是：；．以下是个城市年的人均（万元）和城市排名情况散点图：根据以上信息，回答下列问题（1）某城市的人均为万元，该城市排名全国第_____；（2）在个城市年的人均和城市排名情况散点图中，请用“”画出城市排名的中位数所表示的点；（3）观察散点图，请你写出一条正确结论．24. 如图，在中，，的平分线交于点，过点作交于点．（1）求证：直线是以点为圆心，为半径的的切线；（2）如果：，，求的半径．25. 如图是某跳台滑雪场的横截面示意图，一名运动员经过助滑、起跳从地面上点O 的正上方4米处的A 点滑出，滑出后的路径形状可以看作是抛物线的一部分，通过测量运动员第一次滑下时，在距所在直线水平距离为d 米的地点，运动员距离地面高度为h 米．获得如下数据：水平距离d /米02468垂直高度h /米488的b GDP 1114x <≤12.313.213.613.8，，，c 312023GD GDP GDP 13.8GDP 312023GDP GDP GDP ABC 90C ∠=︒CAB ∠CB D D OD CB ⊥AB O CD O OA O 3sin 5CAB ∠=3BC =O OA 132172请解决以下问题：（1）在网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接；（2）结合表中所给数据或所画图象，直接写出运动员滑行过程中距离地面的最大高度为_____米；（3）求h 关于d 的函数表达式；（4）运动员第二次滑下时路径形状可表示为：，当第一次和第二次距离所在直线的水平距离分别为、，且时能成功完成空中动作，则该运动员_________（填写“能”或“不能”）完成空中动作．26. 在平面直角坐标系中，点，在抛物线上，设抛物线的对称轴为直线．（1）如果抛物线经过点，求的值；2C 215463h d d =-++OA 1d 2d 1223d d ≤≤-xoy ()1,A x m ()2,B x n ()240y ax bx a =++>x h =()2,4h（2）如果对于，，都有，求取值范围；（3）如果对于，或，存在，直接写出的取值范围．27. 如图，，，点在射线上，且，点在上且，连接，取的中点，连接并延长至，使，连接．（1）如图1，当点在线段上时．①用等式表示与的数量关系；②连接，，直接写出，的数量关系和位置关系；（2）如图2，当点在线段的延长线上时，依题意补全图形2，猜想②中的结论是否还成立，并证明．28. 在平面直角坐标系中，的半径为2，点P 、Q 是平面内的点，如果点P 关于点Q 的中心对称点在上，我们称圆上的点为点P 关于点Q 的“等距点”．（1）已知如图1点．①如图1，在点中，上存在点P 关于点Q 的“等距点”的是________；②如图2，点，上存在点P 关于点Q 的“等距点”，则m 的取值范围是________；（2）如图3，已知点，点P 在的图象上，若上存在点P 关于点Q 的“等距点”，14x h =-23x h =m n >h 142h x h -≤≤+21x ≤212x ≥m n >h AB BC =90ABC ∠=︒P AB 90CEP ∠=︒F EP EF EC =AF AF G EG H GH GE =AH P AB AH CE BH BE BH BE P AB xOy O O 40（，）P ()()()12330,2,1,1,1Q Q Q -，O (),Q m n O ()1,1Q y x b =-+O求b的取值范围．。

初三数学总复习资料_分专题试题及答案(90页)

绝对值符号去掉。
（2）已知| x | a(a 0) ，求 x 时，要注意 x a
考点 3 平方根与算术平方根
1、若 x 2 a(a 0) ，则 x 叫 a 做的_________，记作______；正数 a 的__________叫做算术平方根，0 的算术平方根是____。当 a 0 时， a 的算术平方根记作__________。
2
y
5、实数 a, b, c 在数轴上对应点的位置如图 2 所示，下列式子中正确的有（）
c
ba
-2 -1 0 1 2 3
图2
① b c 0 ② a b a c ③ bc ac ④ ab ac
A.1 个
B.2 个 C.3 个 D.4 个
6、 ①数轴上表示-2 和-5 的两点之间的距离是______数轴上表示 1 和-3 的两点之间的距离是
用根号形式表示的数并不都是无理数（如 4 ），也不是所有的无理数都可以写成根号的形
式（如）。
练习： 1、把下列各数填入相应的集合内：
7.5,
15, 4,
8 ,
2 ,
3 8,
,
0.25,
0.1 5
13 3
有理数集{ 正实数集{
}，无理数集{
}
}
2、在实数 4, 3 , 0, 2
2 1,
64, 3 27 , 1 中，共有___ 27
2、幂的运算法则：（以下的 m, n 是正整数）
(1)a m a n _____ ； (2)(a m )n ____ ； (3)(ab)n _____ ； (4)a m a n ______(a 0) ；
(5)(b )n ______ a
3、乘法公式：

2024年北京初三九年级上学期数学期末考《代数综合》

2024年1月九上期末——代数综合1.【东城】26.在平面直角坐标系xOy 中，点(2，c )在抛物线2(0)y ax bx c a =++>上，设该抛物线的对称轴为直线x t =.(1)求t 的值；(2)已知11()M x y ，，22()N x y ，是该抛物线上的任意两点，对于11m x m <<+，212m x m +<<+，都有12y y <,求m 的取值范围．2.【西城】26．在平面直角坐标系xOy 中，()1,A t y ，()1,B t y+，()23,C t y +三点都在抛物线224y ax ax =-+（0a >）上．（1）这个抛物线的对称轴为直线________．（2）若132y y y >≥，求t 的取值范围；（3）若无论t 取任何实数，点A ，B ，C 中都至少有两个点在x 轴的上方，直接写出a 的取值范围．3.【海淀】26.在平面直角坐标系xOy 中，点()1,A m -，点()3,B n 在抛物线2(0)y ax bx c a =++>上.设抛物线的对称轴为直线x t =.（1）当2t =时，①直接写出b 与a 满足的等量关系；②比较m ，n 的大小，并说明理由；（2）已知点()0,C x p 在该抛物线上，若对于034x <<，都有m p n >>，求t 的取值范围.4.【朝阳】26．在平面直角坐标系xOy 中，点(x 1，m )，(x 2，n )在抛物线y =ax 2+bx +c (a >0)上，设抛物线的对称轴为x =t .（1）若对于x 1=1，x 2=3，有m =n ，求t 的值；（2）若对于t -1<x 1<t ，2<x 2<3，存在m ＞n ，求t 的取值范围．5.【石景山】26．在平面直角坐标系xOy 中，抛物线2(0)y ax bx c a =++>经过点(33)A a c +,．（1）求该抛物线的对称轴；（2）点1(12)M a y -,，2(2)N a y +,在抛物线上.若12c y y <<，求a 的取值范围．6.【丰台】26．在平面直角坐标系xOy 中，点（m +2，1y ），（6，2y ）为抛物线22y x mx n =-+上两个不同的点．（1）求抛物线的对称轴（用含m 的式子表示）；（2）若12y n y <<，求m 的取值范围．7.【昌平】26.在平面直角坐标系xOy 中，点（0，3），（6，1y ）在抛物线()02≠++=a c bx ax y 上.（1）当31=y 时，求抛物线的对称轴；（2）若抛物线()02≠++=a c bx ax y 经过点（-1，-1），当自变量x 的值满足-1≤x ≤2时，y 随x 的增大而增大，求a 的取值范围；（3）当0>a 时，点（m -4，2y ），（m ，2y ）在抛物线c bx ax y ++=2上.若2y ＜1y ＜c ，请直接写出m 的取值范围.8.【通州】26．在平面直角坐标系xOy 中，()11,P x y ，()22,Q x y 是抛物线2221y x mx m =-+-上任意两点．（1）求抛物线的顶点坐标（用含m 的式子表示）；（2）若12x m =-，25x m =+，则1y ______2y ；（用“＜”，“＝”，或“＞”填空）（3）若对于114x -≤<，24x =，都有12y y ≤，求m 的取值范围．9.【房山】26.在平面直角坐标系xOy 中，点(1)m ，，(3)n ，在抛物线24(0)y ax bx a =++>上,设抛物线的对称轴为x t =.（1）当m n =时，求抛物线与y 轴交点的坐标及t 的值；（2）点00()(3)x n x ≠，在抛物线上，若4m n <<，求t 的取值范围及0x 的取值范围.10.【大兴】26.在平面直角坐标系xOy 中，点（2，m ）在抛物线2(0)y ax bx c a =++>上，设抛物线的对称轴为x=t .(1)当m =c 时，求t 的值；(2)点(-1,y 1),(3,y 2)在抛物线上，若c <m ,比较y 1，y 2的大小，并说明理由．11.【门头沟】26.在平面直角坐标系xOy 中，点M （1x ，1y ），N （2x ，2y ）为抛物线2y ax bx c=++(a >0)上任意两点，其中12x x <.（1）若抛物线的对称轴为x =2，当12x x 、为何值时，12y y c ==；（2）设抛物线的对称轴为x =t ，若对于124x x +>，都有12y y <，求t 的取值范围.12.【燕山】26．在平面直角坐标系xOy 中，点M (－1，m )，N (3，n )在抛物线2y ax bx c =++(a ＞0)上，设抛物线的对称轴为x ＝t ．(1)若m ＝n ，求t 的值；(2)若c ＜m ＜n ，求t 的取值范围．13.【顺义】26．在平面直角坐标系xOy 中，抛物线y ＝x 2﹣2ax +a 2﹣4与x 轴交于A ，B 两点（点A 在点B 左侧）．（1）若a ＝1，求抛物线的对称轴及A ，B 两点的坐标；（2）已知点（3﹣a ，y 1），（a +1，y 2），（﹣a ，y 3）在该抛物线上，若y 1，y 2，y 3中有且仅有一个大于0，求a 的取值范围．14.【密云】26．在平面直角坐标系xOy 中，点（2，m ）和（5，n ）在抛物线y =x 2+2bx 上，设抛物线的对称轴为x=t ．（1）若m=0，求b 的值；（2）若mn ＜0，求该抛物线的对称轴t 的取值范围．15.【平谷】26．在平面直角坐标系xOy 中，二次函数mx x y 22-=的图象上两个点A ),(11y x ，B ),(22y x ，点A 、B 之间的部分（包含点A 、点B ）记作图象G ，图象G 上y 的最大值与最小值的差记作y G ．（1）求这个二次函数的对称轴（用含m 的代数式表示）；（2）当m=1，x 1=0，x 2=3时，求y G 的值；（3）当121-=m x ，122+=m x 时，恒有y G ＞21y y -，求m 的取值范围．。

【初三数学】代数几何综合题(含答案)(共15页)

代数几何综合题代数几何综合题是初中数学中覆盖面最广、综合笥最强的题型，近几年的中考试题很多以代数几何综合题的形式出现，其命题的主要结合点是方程与几何、函数与几何等，解代数几何综合题最常用的数学方法是数形结合，由形导数，以数促形。

例1、如图，已知平面直角坐标系中三点A （2，0），B （0，2），P （x ，0）()x <0，连结BP ，过P 点作PC PB ⊥交过点A 的直线a 于点C （2，y ）（1）求y 与x 之间的函数关系式；（2）当x 取最大整数时，求BC 与PA 的交点Q 的坐标。

解：（1） PC PB BO PO ⊥⊥,∴∠+∠=︒∠+∠=︒∴∠=∠CPA OPB PBO OPB CPA PBO 9090, A （2，0），C （2，y ）在直线a 上 ∴∠=∠=︒BOP PAC 90∴∆∆BOP PAC ~∴=PO AC BOPA，∴=+||||||x y x 22， x y x y x<<∴=-0022，，∴=-+y x x 122（2） x <0，∴x 的最大整数值为-1 ,当x =-1时，y =-32，∴=CA 32BO a BOQ CAQ OQ AQ BOCA//~,，∴∴=∆∆ 设Q 点坐标为()m ，0，则AQ m =-2∴-=∴=m m m 223287，Q 点坐标为()870，说明:利用数形结合起来的思想，考查了相似三角形的判定及应用。

关键是搞清楚用坐标表示的数与线段的长度的关系。

练习1．如图，从⊙O 外一点A 作⊙O 的切线AB 、AC ，切点分别为B 、C ，⊙O 的直径BD 为6，连结CD 、AO.(1)求证：CD ∥AO ；（3分）(2)设CD ＝x ，AO ＝y ，求y 与x 之间的函数关系式，并写出自变量x 的取值范围；（3分） (3)若AO ＋CD ＝11，求AB 的长。

（4分）B2．如图，A、B两点的坐标分别是(x1，0)、(x2，O)，其中x1、x2是关于x的方程x2+2x+m-3=O 的两根，且x1<0<x2．(1)求m的取值范围；(2)设点C在y轴的正半轴上，∠ACB=90°，∠CAB=30°，求m的值；(3)在上述条件下，若点D在第二象限，△DAB≌△CBA，求出直线AD的函数解析式.3．一张矩形纸片OABC 平放在平面直角坐标系内，O 为原点，点A 在x 的正半轴上，点C 在y 轴的正半轴上，OA ＝5，OC ＝4。

2024北京门头沟初三二模数学试题及答案

门头沟区2024年初三年级综合练习（二）数学2024.5考生须知1．本试卷共8页，共三道大题，28个小题。

满分100分。

考试时间120分钟。

2．在试卷和答题卡上准确填写学校和姓名，并将条形码粘贴在答题卡相应位置处。

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4．在答题卡上，选择题、作图题用2B铅笔作答，其它试题用黑色字迹签字笔作答。

5．考试结束，将试卷、答题卡和草稿纸一并交回。

一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有．．一个．1.某几何体的展开图是由大小形状相等的两个正方形、四个长宽不等的矩形组成，则该几何体是A．正方体B．长方体C．四棱锥D．三棱柱2.目前所知病毒中最小的是一级口蹄疫病毒，它属于微核糖核酸病毒科鼻病毒属，其最大颗粒直径为23纳米，即0.000000023米，将0.000000023化成科学计数法为A．2.3×10-7B．2.3×10-8C．2.3×10-9D．0.23×10-10 3.下图是手机的一些手势密码图形，其中既是轴对称图形又是中心对称图形的是A B C D4.某个正多边形的一个内角是它的外角的2倍，则该正多边形是A．正方形B．正五边形C．正六边形D．正七边形5.数轴上的三点A、B、C所表示的数分别为a、b、c且满足0a b+＜，0b c⋅<，则原点在A.点A左侧B.点A点B之间（不含点A点B）C.点B点C之间（不含点B点C）D.点C右侧6.如图，AB∥CD，CE平分∠ACD．∠1=70°，∠2的度数为A．30︒B．35︒C．45︒D．70︒7.小明去商场购物，购买完后商家有一个抽奖答谢活动，有m 张奖券，其中含奖项的奖券有n 张，每名已购物的顾客只能抽取一次，小明抽之前有10名顾客已经抽过奖券，中奖的有3人，则小明中奖的概率为A ．n mB ．10n m -C ．310n m --D ．3n m-8.如图所示，两个体积不等的圆柱形水杯，大小水杯口均朝上，现往大水杯中均匀注水，注水过程中小水杯始终在原来位置，设水面上升高度为h ，注水时间为t ，下列图象能正确反应注水高度随时间变化关系的是二、填空题（本题共16分，每小题2分）9.如果分式11m m +-值为零，那么实数m 的取值是．10.如图所示的网格是正方形网格，点A ，B ，C 是网格线交点,则sin A =．11.在实数范围内进行因式分解:22mx m -=．12.如图，AB 是⊙O 的直径，弦CD AB ⊥于点E ，AC CD =，如果AC =则⊙O 的半径长为_____．13.某函数图象满足过点()02，，且当0x >时，y 随x 的增大而增大，写出一个满足条件的表达式_____.14.如图，在平面直角坐标系内，某图象上的点A 、B 为整数点，以点O 为位似中心将该图像扩大为原的2倍，则点A 的坐标为_____．15.某校抽测了某班级的10名学生竞赛成绩（均为整数），从低到高排序如下：x 1x 2x 3x 4x 5x 6x 7x 8x 9x 10如果x 4=83，x 7=86，该组数据的中位数是85，则x 5=_____．A BC D16.“谁知盘中餐，粒粒皆辛苦”知农爱农，珍惜粮食，传承美德，从校园做起。

数学九年级上册《一元二次方程》单元综合测试题(附答案)

人教版数学九年级上学期《一元二次方程》单元测试考试时间:100分钟;总分:120分一、单选题(每小题3分，共30分)1．(2019·临邑县实验中学初三期中)已知关于x 的方程:(1)20ax bx c ++=;(2)240x x -=;(3)1+(x-1)(x+1)=0;(4)23(2)(3)x x x -=-+;(5)210x x-=其中是一元二次方程有( )个. A.1个B.2个C.3个D.4个2．(2019·南山第二外国语学校集团海德学校初三期中)关于x 的一元二次方程的两根分别为13x =-，22x =，则这个方程可以为( ) A.(2)(3)0x x --= B.(2)(3)0x x ++= C.(2)(3)0x x +-=D.(2)(3)0x x -+=3．(2019·厦门市第五中学初三期中)方程226x =的根是( )和 B.0和3C.3和3-4．(2019·湖北初三期中)向阳村2016年的人均收入为12000元，2018年的人均收入为14520元，则人均收入的年平均增长为( ) A.10%或－210%B.12.1%C.11%D.10%5．(2019·湖北初三期中)一元二次方程x 2－1=1的常数项是( ) A.－1B.1C.0D.－26．方程2(2)3(2)x x -=-的解为( ) A.2x =B.5x =C.12x =，25x =D.12x =，23x =7．(2019·山东初三期中)已知关于x 的一元二次方程x 2－2x =m 有两个不相等的实数根，则m 的取值范围是( ) A.m ＜1B.m ＜－2C.m =0D.m ＞－18．(2019·广东初三期中)已知一元二次方程260x x c -+=有一根为2，另一根为( ) A.5B.4C.3D.29．(2019·青浦区华新中学初二月考)已知三角形的两条边分别是2和4，第三边是方程29180x x -+=的根，则这个三角形的周长为( ) A.9或12B.9C.12D.不能确定10．(2019·江苏东绛实验学校初三期中)某校初三篮球联赛中采用了单循环赛制(即参赛的每两个队之间都要比赛一场)，根据场地和时间等条件，赛程计划为7天，每天安排4场比赛．设有x 个队参加比赛，根据题意可列出方程( ) A.x (x ＋1)＝2B.x (x －1)＝28C.12x (x ＋1)＝28 D.12x (x －1)＝28 二、填空题(每小题4分，共24分) 11．关于x 的方程()221150aa a x --++=是一元二次方程，则a =_________.12．(2019·湖北初三期中)关于x 的方程(x+n)2=p 有两个相等的实数根，则p 的取值是__________. 13．(2019·湖北初三期中)实数x ，y 满足(x+y)2+x+y －2=0, 则2x+2y 值为_________．14．(2019·江苏初三期中)某型号的冰箱连续两次降价，每台售价由原来的2370元降到了1160元，若设平均每次降价的百分率为x ，则可列出的方程是__________________________________.15．(2019·江西省宜春实验中学初三期中)一元二次方程2410x x --=的两个根为12,,x x ,且2212x x +=____。

2024年北京初三九年级上学期数学期末考《几何综合》

2024年1月九上期末——几何综合1.【东城】27.在△ABC中，AB=AC，∠BAC=120°，D为BC上一点，连接DA，将线段DA绕点D顺时针旋转60°得到线段DE．（1）如图1，当点D与点B重合时，连接AE，交BC于点H，求证：AE⊥BC；（2）当BD≠CD时(图2中BD＜CD，图3中BD>CD)，F为线段AC的中点，连接EF．在图2，图3中任选一种情况，完成下列问题：①依题意，补全图形；②猜想∠AFE的大小，并证明．2.【西城】27．在ABC △中，90ACB ∠=︒，AC BC =，CM AB ⊥于点M ．点P 在射线CM 上，连接AP ，作CD AP ⊥于点D ．连接MD ，作CE MD ⊥于点E ，作//DF AB 交直线CE 于点F ，连接MF ．图1图2备用图（1）当点P 在线段CM 上时，在图1中补全图形，并直接写出ADM ∠的度数；（2）当点P 在线段CM 的延长线上时，利用图2探究线段DF 与AM 之间的数量关系，并证明；（3）取线段MF 的中点K ，连接BK ，若8AC =，直接写出线段BK 的长的最小值．3.【海淀】27.如图，在ABC △中，AB AC =，点D ，E 分别在边AC ，BC 上，连接DE ，EDC B ∠∠=.（1）求证：ED EC =；（2）连接BD ，点F 为BD 的中点，连接AF ，EF .①依题意补全图形；②若AF EF ⊥，求BAC ∠的大小.4.【朝阳】27．已知线段AB 和点C ，将线段AC 绕点A 逆时针旋转α（0°＜α＜90°），得到线段AD ，将线段BC 绕点B 顺时针旋转180°-α，得到线段BE ，连接DE ，F 为DE 的中点，连接AF ，BF .（1）如图1，点C 在线段AB 上，依题意补全图1，直接写出∠AFB 的度数；（2）如图2，点C 在线段AB 的上方，写出一个α的度数，使得3AF =成立，并证明.图1图25.【石景山】27．如图，在Rt ACB △中，90ACB ∠=°，60BAC ∠=°．D 是边BA 上一点（不与点B 重合且12BD BA <），将线段CD 绕点C 逆时针旋转60°得到线段CE ，连接DE ，AE ．（1）求CAE ∠的度数；（2）F 是DE 的中点，连接AF 并延长，交CD 的延长线于点G ，依题意补全图形．若G ACE ∠=∠，用等式表示线段FG ，AF ，AE 之间的数量关系，并证明．6.【丰台】27．已知在△ABC中，AB=AC，0°<∠BAC<90°，将线段AC绕点A逆时针旋转α得到线段AD，连接ＢD，CD．（1）如图1，当∠BAC=α时，∠ＡBD=（用含有α的式子表示）；（2）如图2，当α=90°时，连接BD，作∠BAD的角平分线交BC的延长线于点F，交BD于点E，连接DF．①依题意在图2中补全图形，并求∠DBC的度数；②用等式表示线段AF，CF，DF之间的数量关系，并证明．7.【昌平】27.在△ABC中，AB=AC，∠BAC=90°，点M为BC的中点，连接AM，点D为线段CM上一动点，过点D作DE⊥BC，且DE=DM，（点E在BC的上方），连接AE，过点E作AE的垂线交BC边于点F.（1）如图1，当点D为CM的中点时，①依题意补全图形；②直接写出BF和DE的数量关系为______________；（2）当点D在图2的位置时，用等式表示线段BF与DE之间的数量关系，并证明.图1图227题图127题图28.【通州】27．如图，ABC △中，90ACB ∠=︒，AC BC =，点D 在AB 的延长线上，取AD 的中点F ，连结CD 、CF ，将线段CD 绕点C 顺时针旋转90︒得到线段CE ，连结AE 、BE ．（1）依题意，请补全图形；（2）判断BE 、CF 的数量关系及它们所在直线的位置关系，并证明．9.【房山】27.如图，在等边三角形ABC 中，E ，F 分别是BC ，AC 上的点，且BE CF =，AE ，BF 交于点G .（1）AGF ∠=°；（2）过点A 作AD ∥BC （点D 在AE 的右侧），且AD BC =，连接DG .①依题意补全图形；②用等式表示线段AG ，BG 与DG 的数量关系，并证明.10.【大兴】27.在△ABC中,∠BAC=90°,AB=AC,点P为BA的延长线上一点,连接PC,以点P为中心,将线段PC顺时针旋转90°得到线段PD,连接BD.(1)依题意补全图形;(2)求证:∠ACP=∠DPB;(3)用等式表示线段BC,BP,BD之间的数量关系,并证明.11.【门头沟】27.如图，Rt△ABC中，∠ACB=90°，CA=CB，过点C在△ABC外作射线CP，且∠ACP=α，点A关于CP的对称点为点D，连接AD，BD，CD，其中AD，BD分别交射线CP于点M，N.（1）依题意补全图形；（2）当α=30°时，直接写出∠CNB的度数；（3）当0°<α<45°时，用等式表示线段BN，CM之间的数量关系，并证明．12.【燕山】27．如图，△ABC为等边三角形，点M为AB边上一点(不与点A，B重合)，连接CM，过点A作AD⊥CM于点D，将线段AD绕点A顺时针旋转60°得到线段AE，连接BE．(1)依题意补全图形，直接写出∠AEB的大小，并证明；(2)连接ED并延长交BC于点F，用等式表示BF与FC的数量关系，并证明．13.【顺义】27．在菱形ABCD中，∠B＝60°，点P是对角线AC上一点（不与点A重合），点E，F分别是边AB，AD上的点，且∠EPF＝60°，射线PE，PF分别与DA，BA的延长线交于点M，N．（1）如图1，若点P与C重合，且PA平分∠EPF，求证：AM＝AN；（2）连接BP，若∠ABP＝45°，BP＝3，且PA不平分∠EPF．①依题意补全图2；②用等式表示线段AM，AN的数量关系，并证明．14.【密云】27．如图，在Rt△ABC中，∠ACB=90°，AC=BC．点D为AB边上的一点，将线段CD绕点C逆时针旋转90°得到线段CE，连接AE、BE．（1）依据题意，补全图形；（2）直接写出∠A C E+∠B C D的度数；（3）若点F为BD中点，连接CF交AE于点P，用等式表示线段A E与CF之间的数量关系，并证明．15.【平谷】27.如图，△ABC中，AC=BC,∠ACB=90°，D为AB边中点，E为△ABC外部射线CD上一点，连接AE，过C作CF⊥AE于F.（1）依题意补全图形，（2）找出图中与∠EAD相等的角，并证明；（3）连接DF，猜想∠CFD的度数，并证明.。

全国通用版九年级下学期数学圆的综合题(含阴影面积)试题(无答案)

初三数学专题训练——圆的综合题（含求阴影面积）一．填空题（共14小题）1．如图，在Rt△AOB中，∠AOB＝90°，OA＝3，OB＝2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是．第1题图第2题图第3题图第4题图第5题图2．如图，已知直角三角形的两条直角边分别为a、b，以a为直径画一个半圆．若甲、乙两阴影部分的面积相等，则用a的代数式表示b＝．3．如图，在半径为2cm，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为．4．在Rt△ABC中，∠ACB＝90°，AC＝BC＝1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为，则图中阴影部分的面积是．5．如图，在矩形ABCD中，CD＝2，以点C为圆心，CD长为半径画弧，交AB边于点E，且E为AB中点，则图中阴影部分的面积为．̂交于点D，以O为圆心，OC的长6．如图，在扇形OAB中，C是OA的中点，CD⊥OA，CD与AB̂交OB于点E，若OA＝4，∠AOB＝120°，则图中阴影部分的面积为．（结为半径作CE果保留π）第6题图第7题图第8题图第9题图第10题图7．如图，在△ABC中，CA＝CB，∠ACB＝90°，AB=2√2，点D为AB的中点，以点D为圆心作圆心角为90°的扇形DEF，点C恰好在弧EF上，则图中阴影部分的面积为（结果保留π）．8．如图，在Rt△ABC中，∠ACB＝90°，AC＝2√3，以点C为圆心，CB的长为半径画弧，与AB ̂绕点D旋转180°后点B与点A恰好重合，则图中阴影部分的面积为．边交于点D，将BD̂的中点，D、E分别是OA、OB 9．如图，在圆心角为90°的扇形OAB中，半径OA＝2cm，C为AB的中点，则图中阴影部分的面积为cm2．10．如图，在Rt△ABC中，∠C＝90°，∠A＝30°，AB＝2．将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置，B，A，C′三点共线，则线段BC扫过的区域面积为．11．将△ABC绕点B逆时针旋转到△A′BC′，使A、B、C′在同一直线上，若∠BCA＝90°，∠BAC＝30°，AB＝4cm，则图中阴影部分面积为cm2．第11题图第12题图第13题图第14题图12．如图所示，⊙O是以坐标原点O为圆心，4为半径的圆，点P的坐标为（√2，√2），弦AB经过点P，则图中阴影部分面积的最小值＝．13．如图，以直角三角形的两条直角边AC、AB为直径，向三角形内作半圆，两半圆交于点D，CD ＝1，BD＝3，则图中阴影部分的面积为（平方单位）．14．如图，两个半径为1的14圆扇形A′OB′与AO′B叠放在一起，POQO'是正方形，则整个阴影图形的面积是．二．解答题（共14小题）15．如图，⊙O是△ABC的外接圆，AC是直径，过点O作OD⊥AB于点D，延长DO交⊙O于点P，过点P作PE⊥AC于点E，作射线DE交BC的延长线于F点，连接PF．（1）若∠POC＝60°，AC＝12，求劣弧PC的长；（结果保留π）（2）求证：OD＝OE；（3）求证：PF是⊙O的切线．16．如图，△ABC中，∠C＝90°，AC＝3，AB＝5，点O在BC边的中线AD上，⊙O与BC相切于点E，且∠OBA＝∠OBC．（1）求证：AB为⊙O的切线；（2）求⊙O的半径；（3）求tan∠BAD．17.如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB＝∠ADB．（1）求证：EA是⊙O的切线；（2）已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；（3）已知AF＝4，CF＝2．在（2）条件下，求AE的长．18．已知：如图，⊙O是△ABC的外接圆，AB为⊙O直径，BC＝6，AC＝8，OE⊥AE，垂足为E，交⊙O于点P，连结BP交AC于D．（1）求PE的长；（2）求△BOP的面积．19．如图，AB是⊙O的直径，M是OA的中点，弦CD⊥AB于点M，过点D作DE⊥CA交CA的延长线于点E．（1）连接AD，则∠OAD＝°；（2）求证：DE与⊙O相切；̂上，∠CDF＝45°，DF交AB于点N．若DE＝3，求FN的长．（3）点F在BC雅博学校初三数学专题训练——圆的综合题1．如图，在三角形ABC中，AB＝6，AC＝BC＝5，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF是⊙O的切线，D为切点，交CB的延长线于点E．（1）求证：DF⊥AC；（2）求tan∠E的值．2．如图，在等腰△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D且BD＝2AD，过点D 作DE⊥AC交BA延长线于点E，垂足为点F．（1）求tan∠ADF的值；（2）证明：DE是⊙O的切线；（3）若⊙O的半径R＝5，求EF的长．3．如图，在△ABC中，AB＝AC，以AB为直径的⊙O与边BC交于点D，DE⊥AC，垂足为E，交AB的延长线于点F．（1）求证：EF是⊙O的切线；̂的长．（2）若∠C＝60°，AC＝12，求BD（3）若tan C＝2，AE＝8，求BF的长．4．已知：如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC＝BD，连结AC，过点D作DE⊥AC，垂足为E．（1）求证：AB＝AC；（2）求证：DE为⊙O的切线；（3）若⊙O的半径为5，∠BAC＝60°，求DE的长．5．已知：如图，在△ABC中，AC＝BC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．（1）求证：点D是AB的中点；（2）求证：DE是⊙O的切线；（3）若⊙O的直径为18，cos B=13，求DE的长．6．已知，如图，△ABC中，AC＝BC，以BC为直径的⊙O交AB于E，过点E作EG⊥AC于G，交BC的延长线于F．（1）求证：AE＝BE；（2）求证：FE是⊙O的切线；（3）若FE＝4，FC＝2，求⊙O的半径及CG的长．6．如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA＝∠CBD．（1）求证：CD2＝CA•CB；（2）求证：CD是⊙O的切线；（3）过点B作⊙O的切线BE交CD的延长线于点E，若BC＝12，CA＝4，求BE的长．7．如图，⊙O是△ABC的外接圆，FH是⊙O的切线，切点为F，FH∥BC，连接AF交BC于E，∠ABC的平分线BD交AF于D，连接BF．（1）证明：AF平分∠BAC；（2）证明：BF＝FD；（3）若EF＝4，DE＝3，求AD的长．。

2023年北京市初三一模数学试题汇编：代数综合(第26题)

2023北京初三一模数学汇编代数综合（第26题）一、解答题1.（2023·北京西城·统考一模）已知抛物线24y ax bx =++的对称轴为直线x =t.（1）若点（2，4）在抛物线上，求t 的值；（2）若点12(,3),(,6)x x 在抛物线上，①当t =1时，求a 的取值范围；②若12t x x ≤<，且211x x −≥，直接写出a 的取值范围.2．（2023·北京朝阳·统考一模）在平面直角坐标系xOy 中，抛物线y=ax 2+（2m -6）x+1经过点()124m −，.（1）求a 的值；（2）求抛物线的对称轴（用含m 的式子表示）；（3）点()1m y −，，()2m y ，，()32m y +，在抛物线上，若231y y y ＜≤，求m 的取值范围.3．（2023·北京海淀·统考一模）在平面直角坐标系xOy 中，点0()A x m ,，0(4)B x n +,在抛物线 221y x bx =−+上. （1）当5b =，03x =时，比较m 与n 的大小，并说明理由；（2）若对于034x ≤≤，都有m <n <1，求b 的取值范围. 4．（2023·北京房山·统考一模）已知抛物线22=−+y x ax b 经过点（1，1）.（1）用含a 的式子表示b 及抛物线的顶点坐标；（2）若对于任意1−a ≤x ≤2+a ，都有y ≤1，求a 的取值范围.5. （2023·北京丰台·统考一模）在平面直角坐标系xOy 中，点A （-3，y 1），B （a +1，y 2）在抛物线221y x ax =−+ 上.（1）当2=a 时，求抛物线的顶点坐标，并直接写出y 1和y 2的大小关系；（2）抛物线经过点C （m ，y 3）.①当4=m 时，若y 1= y 3，则a 的值为________； ②若对于任意的4≤m ≤6都满足y 1＞y 3＞y 2，求a 的取值范围.6．（2023·北京门头沟·统考一模）在平面直角坐标系xOy 中，抛物线()2240y ax ax a a =−+−≠．（1）求该抛物线的顶点坐标；（2）当抛物线()2240y ax ax a a =−+−≠经过点()3,0时， ①求此时抛物线的表达式；②点()12,M n y −，()223,N n y +在抛物线上，且位于对称轴的两侧，当12y y >时，求n 的取值范围．7．（2023·北京顺义·统考一模）已知：抛物线y=ax 2-4ax -3(a >0)．（1）求此抛物线与y 轴的交点坐标及抛物线的对称轴；（2）已知点A （n ，y 1），B （n +1，y 2）在该抛物线上，且位于对称轴的同侧．若21−y y ≤4，求a 的取值范围．8．（2023·北京通州·统考一模）在平面直角坐标系xOy 中，已知点()()1,,2,n p −在二次函数22y x bx =−++的图象上．（1）当n p =时，求b 的值；（2）当()()20n n p −−>，求b 的取值范围．9.（2023·北京延庆·统考一模）在平面直角坐标系xOy 中，点A (4，m )在抛物线y=x 2−2bx +1上.（1）当m =1时，求b 的值；（2）点(x 0，n )在抛物线上，若存在0＜x 0＜b ，使得m = n ，直接写出b 的取值范围.10．（2023·北京燕山·统考一模）在平面直角坐标系xOy 中，抛物线245(0)y ax ax a =−+≠与y 轴交于点C ．(1) 求点C 的坐标及抛物线的对称轴；(2) 已知点(－1，1y )，(2，2y )，(6，3y )在该抛物线上，且1y ，2y ，3y 中有且只有一个小于0，求a 的取值范围．参考答案1．解：（1）∵ 点（2，4）在抛物线24y ax bx =++上，∴ 4a ＋2b ＋4＝4．∴ b ＝－2a ．∴ 12b t a=−=． ······································································· 2分（2）①当t ＝1时，b ＝-2a ，所以224y ax ax =−+．∵ 点（1x ，3），（2x ，6）在抛物线上，∴ 当a ＞0时，有a -2a ＋4≤3．得4-a ≤3，得a ≥1．当a ＜0时，有a -2a ＋4≥6．得4-a ≤6，得a ≤-2．综上，a 的取值范围是a ≤-2或a ≥1． ············································· 4分 ②a 的取值范围是0＜a ≤3．2．解：（1）∵抛物线y=ax 2+（2m -6）x+1经过点()124m −，， ∴2m -4=a +（2m -6）+1.∴a=1（2）由（1）得抛物线的表达式为y=x 2+（2m -6）x+1.∴抛物线的对称轴为3.x m =−（3）①当m ＞0时，可知点()1m y −，，()2m y ，，()32m y +，从左至右分布.根据23y y ＜可得232m m m ++−＜. ∴ 1.m ＞根据31y y ≤可得232m m m −++−≥. ∴ 2.m ≤∴1 2.m ＜≤②当m ≤0时，∵3m m m +≤-＜-，∴21y y ≥，不符合题意.综上，m 的取值范围为1 2.m ＜≤3.（本题满分6分）（1）m =n . …………………………………………………………………………………1分理由如下：∵ b =5，∴ 抛物线解析式为y =x 2−10x +1，∴ 对称轴为x =5.∵ x 0=3，∴ A （3，m ），B （7，n ）关于直线x =5对称.∴ m =n . ………………………………………………………………………………2分（2）当03x =时，∵ ()0A x m ，，()04B x n +，在抛物线221y x bx =−+上，∴ 106m b =−，5014n b =−.∵ 1m n <<，∴ 10650141b b −<−<.∴752b <<. 当04x =时， ∵ ()0A x m ，，()04B x n +，在抛物线221y x bx =−+上，∴ 178m b =−，6516n b =−.∵ 1m n <<，∴ 17865161b b −<−<.∴ 46b <<.∵ 对于034x ≤≤，都有1m n <<，∴ 45b <<.当45b <<时，设点()04x n +，关于抛物线的对称轴x b =的对称点为()1x n ，，∵ 点()04x n +，在抛物线上，∴ 点()1x n ，在抛物线上.由014x b b x +−=−，得1024x b x =−−.∵ 034x ≤≤，45b <<，∴ 103x <<.∵ 抛物线221y x bx =−+，∴ 抛物线与y 轴交于（0，1）.当x b <时，y 随x 的增大而减小.∵ 点（0，1），()1x n ，，()0x m ，在抛物线上，且100x x b <<<，∴ 1m n <<.综上所述，45b <<. ………………………………………………………………6分4.（1）把（1,1）代入表达式得，112a b =−+，∴a b 2= ……………………1分抛物线为22222()2y x ax a x a a a =−+=−−+抛物线顶点坐标为2(,2)a a a −+ ……………………2分（2）∵抛物线关于x =a 对称，开口向上，∴当1−a ≤x ≤2+a 时，由对称性得，x =2+a 时函数y 有最大值： y 最大=(a+2－a )2－a 2+2a=－a 2+2a+4. ……………………3分 ∵对于任意1−a ≤x ≤2+a ,都有y ≤1，∴－a 2+2a+4≤1 ……………………4分即a 2－2a －3≥0∴ a ≤－1或a ≥3 ……………………6分5.解：（1）当a =2时，223y x ，顶点坐标为（2,-3）； ……1分12y y . ……2分（2）①12； ……3分 ②∵对于任意的4≤m ≤6都满足y 1＞y 3＞y 2，∴点A 、B 、C 存在如下情况：情况1，如示意图，当31a m 时，可知32m a ， ∴312m a m ，解得332a. 情况2，如示意图，当31m a 时可知12m a a ， ∴11a m a m ， ∴1a m ，解得7a .综上所述，332a 或7a . ……6分（其它解法酌情给分）∴EF =2510533−=．…………………………………………………………………6分m ,y 3),y 2)A (-3,y 1A (-3,y 1,y 2)C (m ,6．（本小题满分6分）解：（1）212a x a−=−=，244y a a a =−+−=−，顶点为（1，4−）.……………………2分（2）①∵抛物线224y ax ax a =−+−（0a ≠）经过点（3，0），∴0964a a a =−+−．解得：1a =．∴此时抛物线的表达式为：223y x x =−−．……………………………………4分 ②∵点M （2n −，y 1），N （23n +，y 2）在抛物线上，且位于对称轴的两侧，∴当点M 位于对称轴的左侧，点N 位于对称轴的右侧时，21,23 1.n n −<⎧⎨+>⎩，解得：13n −＜＜．当点M 位于对称轴的右侧，点N 位于对称轴的左侧时，21,23 1.n n −>⎧⎨+<⎩，此不等式组无解，舍去．∴点M 位于对称轴的左侧，点N 位于对称轴的右侧．∵当0a >时，抛物线开口向上，在对称轴右侧，y 的值随x 值的增大而增大，又∵点M 关于对称轴1x =的对称点为M '（4n −，y 1），∴当12y y >时，423n n −>+．解得：n ∴综上所述：113n −<<．………………………………………………………6分7.解：（1）与y 轴交点坐标：（0，-3），对称轴：直线x =2. ………………… 2分（2）法1：假设A (2，y 1)，B (3，y 1+4)，将A 、B 两点坐标代入函数表达式得：1148349123y a a y a a =−−⎧⎨+=−−⎩ 解得a =4. ………………………………………………………………… 4分根据图象可知0<a ≤4. ………………………………………………… 6分法2：把A (n ，y 1)，B (n+1，y 2)，代入函数表达式得： 212243(1)4(1)3y an an y a n a n ⎧=−−⎨=+−+−⎩ ① 当A 、B 两点在对称轴右侧，即n ≥2时, ∵214y y −≤,∴22(1)4(1)3434a n a n an an +−+−−−−≤（）, ∴432a n a+≤.∵n ≥2, ∴4322a a+≥, ∴a ≤4.∵a >0,∴0<a ≤4.② 当A 、B 两点在对称轴左侧，即n+1≤2，n ≤1时, ∵214y y −≤,∴2243(1)4(1)34an an a n a n ⎡⎤−−−+−+−≤⎣⎦（）, ∴342a n a−≥. ∵n ≤1, ∴3412a a−≤, ∴a ≤4.∵a >0,∴0<a ≤4.综上所述，0<a ≤4. ……………………………………………………… 6分8.暂缺9．（本小题满分6分）解：（1）当m =1时，点A 的坐标为(4，1) ．∵点A 在抛物线y=x 2−2bx +1上，∴1=42−2b ×4+1上.∴b =2.（2）b ＞2且b ≠4.10．(本题满分6分)解：(1) 由题意，抛物线与y 轴交于点C (0，5)．对称轴为直线422a x a−=−=．……………………………………………3分 (2) ∵抛物线的对称轴为直线2x =，∴点(－1，1y )关于对称轴的对称点为(5，1y )，点(2，2y )在对称轴上，点(5，1y )，(6，3y )在对称轴右侧．当x ＝－1时，1y ＝45a a ++＝55a +，当x ＝2时，2y ＝485a a −+＝45a −+，当x ＝6时，3y ＝36245a a −+＝125a +．当0a >时，抛物线在对称轴右侧（即2x ≥时）y 随x 的增大而增大， ∴2y ＜1y ＜3y ．∵1y ，2y ，3y 中有且只有一个小于0， ............ 3分 (6)分∴2y ＜0，且1y ≥0，即450550，，a a −+<⎧⎨+≥⎩解得 54a >．当0a <时，抛物线在对称轴右侧（即2x ≥时）y 随x 的增大而减小， ∴3y ＜1y ＜2y ． ∵1y ，2y ，3y 中有且只有一个小于0，∴3y ＜0，且1y ≥0，即1250550，，a a +<⎧⎨+≥⎩解得 5112a −≤<−．综上所述，54a >或5112a −≤<−．…………………………………6分。

全国初三初中数学专题试卷带答案解析

全国初三初中数学专题试卷班级:___________ 姓名：___________ 分数：___________一、解答题1.如图，在平面直角坐标系中，抛物线y＝x2－x－与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C，对称轴与x轴交于点D，点E(4，n)在抛物线上．(1)求直线AE的解析式；(2)点P为直线CE下方抛物线上的一点，连接PC，PE.当△PCE的面积最大时，连接CD，CB，点K是线段CB 的中点，点M是CP上的一点，点N是CD上的一点，求KM＋MN＋NK的最小值．2.如图，抛物线y＝－x2＋bx＋c(a≠0)与x轴、y轴分别交于点A(3，0)，B(0，3)两点．(1)试求抛物线的解析式和直线AB的解析式；(2)动点E从O点沿OA方向以1个单位/秒的速度向终点A匀速运动，同时动点F沿AB方向以个单位/秒的速度向终点B匀速运动，E，F任意一点到达终点时另一个点停止运动，连接EF，设运动时间为t，当t为何值时，△AEF为直角三角形？3.如图，抛物线y＝ax2＋bx－2与x轴交于A，B两点，与y轴交于C点，已知A(3，0)，且M（1，）是抛物线上另一点．(1)求a，b的值；(2)连接AC，设点P是y轴上任一点，若以P，A，C三点为顶点的三角形是等腰三角形，求P点的坐标．4.如图，抛物线y＝－[(x－2)2＋n]与x轴交于点A(m－2，0)和B(2m＋3，0)(点A在点B的左侧)，与y轴交于点C，连接BC.(1)求m，n的值；(2)点N为抛物线上的一动点，且位于直线BC上方，连接CN，BN.求△NBC面积的最大值．5.如图，抛物线经过A(－1，0)，B(5，0)，C(0，－) 三点．(1)求抛物线的解析式；(2)在抛物线的对称轴上有一点P，使PA＋PC的值最小，求点P的坐标；(3)点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．全国初三初中数学专题试卷答案及解析一、解答题1.如图，在平面直角坐标系中，抛物线y ＝x 2－x －与x 轴交于A ，B 两点(点A 在点B 的左侧)，与y 轴交于点C ，对称轴与x 轴交于点D ，点E (4，n )在抛物线上． (1)求直线AE 的解析式；(2)点P 为直线CE 下方抛物线上的一点，连接PC ，PE .当△PCE 的面积最大时，连接CD ，CB ，点K 是线段CB的中点，点M 是CP 上的一点，点N 是CD 上的一点，求KM ＋MN ＋NK 的最小值．【答案】（1）y ＝x ＋；（2）3.【解析】（1）当y=0时，可求得点A 、B 坐标，将点E （4，n ）代入解析式求得点E 坐标，根据A 、E 两点坐标求直线AE 解析式；（2）先求出直线CE 的解析式，设过点P 作PF ∥y 轴，交CE 于点F .设点P 的坐标为，则点F，根据S △EPC ＝×PF×4求得S △EPC 最大时x 的值，作点K 关于CD 和CP 的对称点G ，H ，连接GH 分别交CD 和CP 于点N ，M .先证点G 与点O 重合，再求得点H 的坐标，由KM ＋MN ＋NK ＝MH ＋MN ＋ON .当点O ，N ，M ，H 在一条直线上时，KM ＋MN ＋NK 有最小值，最小值为OH ，求得OH 即可. 解：(1)当y ＝x 2－x －＝0时，解得x 1=-1,x 2=3,∴A (－1，0)，B (3，0)．当x ＝4时，y ＝，∴E （4，）.设直线AE 的解析式为y ＝kx ＋b ，将点A 和点E 的坐标代入得，解得k ＝，b ＝.∴直线AE 的解析式为y ＝x ＋. (2)当x=0时，二次函数y=-，则C （0，-），设直线CE 的解析式为y ＝mx －，将点E 的坐标（4，）代入得4m －＝，解得m ＝.∴直线CE 的解析式为y ＝x －.如图,过点P 作PF ∥y 轴，交CE 于点F .设点P 的坐标为，则点F ，则FP ＝－＝－x 2＋x .∴S △EPC ＝×（－x 2＋）×4＝－x 2＋x ＝－(x －2)2＋.∴当x ＝2时，△EPC 的面积最大，∴P (2，－).此时PC ∥x 轴．作点K 关于CD 和CP 的对称点G ，H ，连接GH 分别交CD 和CP 于点N ，M .∵K 是CB 的中点，∴K ，∴tan ∠KCP ＝.∵OD ＝1，OC ＝，∴tan ∠OCD ＝，∴∠OCD ＝∠KCP ＝30°，∴∠KCD ＝30°.∵K 是BC的中点，∠OCB ＝60°，∴OC ＝CK ，∴点O 与点K 关于CD 对称，∴点G 与点O 重合，∴点G (0，0)．∵点H 与点K 关于CP 对称，∴点H 的坐标为.∴KM ＋MN ＋NK ＝MH ＋MN ＋ON .当点O ，N ，M ，H 在一条直线上时，KM ＋MN ＋NK 有最小值，最小值为OH .∵OH ＝＝3，∴KM ＋MN ＋NK 的最小值为3.2.如图，抛物线y ＝－x 2＋bx ＋c (a ≠0)与x 轴、y 轴分别交于点A (3，0)，B (0，3)两点． (1)试求抛物线的解析式和直线AB 的解析式；(2)动点E 从O 点沿OA 方向以1个单位/秒的速度向终点A 匀速运动，同时动点F 沿AB 方向以个单位/秒的速度向终点B 匀速运动，E ，F 任意一点到达终点时另一个点停止运动，连接EF ，设运动时间为t ，当t 为何值时，△AEF 为直角三角形？【答案】（1）y ＝－x 2＋2x ＋3，y ＝－x ＋3；（2）当t 为或1时，△AEF 为直角三角形．【解析】（1）将点A 、B 坐标代入抛物线解析式，解得b 、c 即可得抛物线解析式.设直线AB 的解析式为y ＝kx ＋n ，将点A 、B 坐标代入即可解得直线AB 解析式；（2）先求出OA ＝3，AB ＝3，OE ＝t ，AF ＝t ，AE ＝3－t .由△AEF 为直角三角形，有∠AEF ＝90°和∠AFE ＝90°两种情况，分别利用相识求解. 解：(1)∵抛物线y ＝－x 2＋bx ＋c (a ≠0)经过A (3，0)，B (0，3)，∴ ，解得，∴抛物线的解析式为y ＝－x 2＋2x ＋3.设直线AB 的解析式为y ＝kx ＋n ，∴，解得，∴直线AB 的解析式为y＝－x ＋3.(2)由题意可知OA ＝3，AB ＝3，OE ＝t ，AF ＝t ，∴AE ＝3－t . ∵△AEF 为直角三角形，有∠AEF ＝90°和∠AFE ＝90°两种情况： ①当∠AEF ＝90°时，易证△AOB ∽△AEF ，∴，即，解得t ＝； ②当∠AFE ＝90°时，易证△AOB ∽△AFE ，∴ ，即，解得t ＝1.综上所述，当t 为或1时，△AEF 为直角三角形．3.如图，抛物线y ＝ax 2＋bx －2与x 轴交于A ，B 两点，与y 轴交于C 点，已知A (3，0)，且M （1，）是抛物线上另一点． (1)求a ，b 的值；(2)连接AC ，设点P 是y 轴上任一点，若以P ，A ，C 三点为顶点的三角形是等腰三角形，求P 点的坐标．【答案】（1）；（2）P 点的坐标为(0，2)或(0，－2)或或(0，－2－)．【解析】将A 、M 坐标代入抛物线解析式便可解得a 、b 的值；（2）分别求出A 、P 、C 的坐标，求得AP 、PC 、AC 的值，当△PAC 为等腰三角形时，分3种情况：①PA ＝CA ；②PC ＝CA ；③PC=PA 讨论. 解：(1)把A (3，0)，M （1，）代入y ＝ax 2＋bx －2，得，解得.(2)在y ＝ax 2＋bx －2中，当x ＝0时．y ＝－2，∴C (0，－2)，∴OC ＝2.如图，设P (0，m )，则PC ＝|m ＋2|.∵A (3，0)，∴OA ＝3，∴AC ＝＝ . 当△PAC 为等腰三角形时，有以下3种情况： ①当PA ＝CA 时，则OP 1＝OC ＝2，∴P 1(0，2)；②当PC ＝CA ＝时，即|m ＋2|＝，∴m ＝－2或m ＝－－2，∴P 2(0，－2)或P 4(0，－2－)；③当PC=PA 时，由PA==，则=|m ＋2|，解得m ＝，∴P 3.综上所述，P 点的坐标为(0，2)或(0，－2)或或(0，－2－)．4.如图，抛物线y ＝－[(x －2)2＋n ]与x 轴交于点A (m －2，0)和B (2m ＋3，0)(点A 在点B 的左侧)，与y 轴交于点C ，连接BC .(1)求m ，n 的值；(2)点N 为抛物线上的一动点，且位于直线BC 上方，连接CN ，BN .求△NBC 面积的最大值．【答案】（1）m ＝1，n ＝－9；（2）.【解析】（1）由抛物线解析式可得出抛物线的对称轴为直线x ＝2，又由点A 和点B 是抛物线与x 轴的交点，则A 和B 关于对称轴对称，则＝2，便可求得m ，得出点A 和点B 坐标，将A 坐标代入抛物线便求得n ；（2）过点N 作ND ∥y 轴交BC 于D .先求得BC 解析式，设点N 坐标(x ，－x 2＋x ＋3)，便可得点D 坐标，则得ND 的值，由S △NBC ＝S △NDC ＋S △NDB ＝×5×ND 得S △NBC 关于x 的二次函数，便可求得最大值.解：(1)∵抛物线的解析式为y ＝－[(x －2)2＋n ]＝－(x －2)2－n ，∴抛物线的对称轴为直线x ＝2.∵点A 和点B 关于直线x ＝2对称，∴＝2，解得m ＝1，∴点A 的坐标为(－1，0)，点B 的坐标为(5，0)．把A (－1，0)代入y ＝－[(x －2)2＋n ]得9＋n ＝0，解得n ＝－9.(2)过点N 作ND ∥y 轴交BC 于D .由(1)可得抛物线的解析式为y ＝－[(x －2)2－9]＝－x 2＋x ＋3.当x ＝0时，y ＝3，则点C 的坐标为(0，3)．设直线BC 的解析式为y ＝kx ＋b ，把B (5，0)，C (0，3)代入y ＝kx ＋b 得，解得.∴直线BC 的解析式为y ＝－x ＋3.设点N 的坐标为(x ，－x 2＋x ＋3)，则点D 的坐标为(x ，－x ＋3)，∴ND ＝－x 2＋x ＋3－(－x ＋3)＝－x 2＋3x ，∴S △NBC ＝S △NDC ＋S △NDB ＝×5×ND ＝(－x 2＋3x )＝－x 2＋x ＝－＋，当x ＝时，△NBC 面积最大，最大值为.5.如图，抛物线经过A (－1，0)，B (5，0)，C (0，－) 三点．(1)求抛物线的解析式；(2)在抛物线的对称轴上有一点P ，使PA ＋PC 的值最小，求点P 的坐标；(3)点M 为x 轴上一动点，在抛物线上是否存在一点N ，使以A ，C ，M ，N 四点构成的四边形为平行四边形？若存在，求点N 的坐标；若不存在，请说明理由．【答案】（1）y ＝x 2－2x －；（2）；（3）存在，点N 的坐标为或或.【解析】本题考查的是二次函数综合题，涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识，在解答（3）时要注意进行分类讨论．（1）设抛物线的解析式为y=ax 2+bx+c （a≠0），再把A （﹣1，0），B （5，0），C （0，）三点代入求出a 、b 、c 的值即可；（2）因为点A 关于对称轴对称的点B 的坐标为（5，0），连接BC 交对称轴直线于点P ，求出P 点坐标即可；（3）分点N 在x 轴下方或上方两种情况进行讨论．试题解析：（1）设抛物线的解析式为y=ax 2+bx+c （a≠0），∵A （﹣1，0），B （5，0），C （0，）三点在抛物线上，∴，解得．∴抛物线的解析式为：y=x 2﹣2x ﹣；（2）∵抛物线的解析式为：y=x 2﹣2x ﹣，∴其对称轴为直线x=﹣=﹣=2，连接BC ，如图1所示，∵B （5，0），C （0，﹣），∴设直线BC 的解析式为y=kx+b （k≠0），∴，解得，∴直线BC的解析式为y=x ﹣，当x=2时，y=1﹣=﹣，∴P （2，﹣）；（3）存在．如图2所示，①当点N 在x 轴下方时，∵抛物线的对称轴为直线x=2，C （0，﹣），∴N 1（4，﹣）； ②当点N 在x 轴上方时，如图2，过点N 2作N 2D ⊥x 轴于点D ，在△AN 2D 与△M 2CO 中，∴△AN 2D ≌△M 2CO （ASA ），∴N 2D=OC=，即N 2点的纵坐标为．∴x 2﹣2x ﹣=，解得x=2+或x=2﹣，∴N 2（2+，），N 3（2﹣，）．综上所述，符合条件的点N 的坐标为N 1（4，﹣），N 2（2+，）或N 3（2﹣，）．【考点】二次函数综合题．。

初三数学综合试题

初三数学圆的综合的专项培优练习题(含答案)及答案解析

2022年北京市丰台区初三数学综合练习2 (二模)试题及答案解析

初三数学试题全册及答案

2023北京朝阳区初三一模数学试题及参考答案

初三数学常考试题及答案

初三数学试题及答案人教版

初三数学常考试题及答案

初三数学综合试题一10732

2024年北京初三九年级上学期数学期末考《圆的综合》

2024年北京市门头沟区九年级中考一模数学试题(原卷版)

初三数学总复习资料_分专题试题及答案(90页)

2024年北京初三九年级上学期数学期末考《代数综合》

【初三数学】代数几何综合题(含答案)(共15页)

2024北京门头沟初三二模数学试题及答案

数学九年级上册《一元二次方程》单元综合测试题(附答案)

2024年北京初三九年级上学期数学期末考《几何综合》

全国通用版九年级下学期数学 圆的综合题(含阴影面积)试题(无答案)

2023年北京市初三一模数学试题汇编：代数综合(第26题)

全国初三初中数学专题试卷带答案解析

全国通用版九年级下学期数学圆的综合题(含阴影面积)试题(无答案)