粘性流体绕过物体的流动基本练习
粘性流体绕球体的流动

粘性流体绕球体的流动(一)绕流阻力绕流阻力由摩擦阻力和压差阻力两部分组成。
黏性流体绕流物体流动,由于流体的黏性在物体表面上产生切向应力而形成摩擦阻力,可见,摩擦阻力是作用在物体表面的切向应力在来流方向分力的总和,是黏性直接作用的结果;而压差阻力是黏性流体绕流物体时由于边界层分离,物体前后形成压强差而产生的。
压差阻力大小与物体行状有根大关系,也称形状阻力。
摩擦阻力和压差阻力之和统称为物体阻力。
对于流体纵向流过平板时一般只有摩擦阻力,绕流流线型物体时压差阻力很小,主要由摩擦阻力来决定。
而绕流圆柱体和球体等钝头体时,绕流阻力与摩擦阻力和压差阻力都有关,高雷诺数时,压差阻力却要比摩擦阻力大得多。
由于从理论上求解一个任意行状物体的阻力是十分困难的,目前都是自实验测得,工程上习惯借助无因次阻力系数来确定总阻力的大小,目摩擦阻力的计算公式相似,只是用阻力系数取代C D摩擦阻力系数C f,即式中:C D为无因次阻力系数;0.5ρν2A为单位体积来流的动能,Pa;A为物体垂直于运动方向或来流方向的投影面积,m2。
工程上遇到黏性流体绕球体的流动情况也很多,像燃料炉炉膛空气流中的煤粉颗粒、油滴、烟道烟气中的灰尘以及锅炉汽包内蒸汽空间中蒸汽夹带的水滴等,都可以近似地看作小圆球。
因此我们要经常研究固体微粒和液体细滴在流体中的运动情况。
比如,在气力输中要研究固体微粒在何种条件下才能被气流带走;在除尘器中要解决在何种条件下尘粒才能沉降;在煤粉燃烧技术中要研究煤粉颗粒的运动状况等问题。
当煤粉和灰尘等微小颗粒在空气、烟气或水等流体中运动时,由于这些微粒的尺寸以及流体与微粒间的相对运动速度都很小,所以在这些运动中雷诺数都很小,即它们的惯性力与黏性力相比要小得多,可以忽略不计。
又由于微粒表面的附面层板薄,于是质量力的影响也很小,也可略去(这种情况下的绕流运动常称为蠕流)。
这样,在稳定流动中,可把纳维托克斯方程简化为不可压缩流体的连续性方程1851年斯托克斯首先解决了黏性流体绕圆球作雷诺数很小(Re<1)的稳定流动时,圆球所受的阻力问题。
流体力学第八章 粘性不可压缩流体绕物体的流动

无滑移边界条件 y = 0时,u = 0
a=0
前缘
δ(x)
层流 x
边界层与势流衔接处, y = δ 时,u = V∞
V∞ = bδ + cδ + dδ
2 3
y = δ 时,τ = 0
流体力学
du τ =μ =0 dy
顺流平板层流边界层4
b + 2cδ + 3dδ 2 = 0
y V∞ 前缘 δ(x) 层流 x
∞ 0
δ* = ∫
u (1 − )dy U
δ*
μ=0 u=U
边界层内由粘性影响减少的流量=理想流 体流过物面时表面向外移动 δ*减少的流量
δ =∫
*
δ
0
u (1 − )dy U
流体力学
边界层内的厚度4
动量损失厚度
y dy y
u = u(y)
U
U
θ
μ≠0
μ=0 u=U
边界层内由于粘性的影响,动量流量比 理想流体流经该区域时有所减少
固体壁面上 y = 0 时
∂ u U dU =− 2 ν dx ∂y
2
dU =0 由 dx
∂ u = 2c = 0 2 ∂y
2
3V∞ V∞ a=c=0 , b= , d=− 3 2δ 2δ
流体力学
顺流平板层流边界层5
V∞ u= 2δ ⎛ y3 ⎞ ⎜3y − 2 ⎟ δ ⎠ ⎝
补充方程2-壁面切应力方程
3 ∞
= 1.771 ρμaV b
边界层内的流动状态1
V∞ 层流边界层 转捩区
紊流边界层 x
平板前缘开始
x ↑, δ ↑, Re ↑
层流边界层 转捩点 紊流边界层
流体流动习题
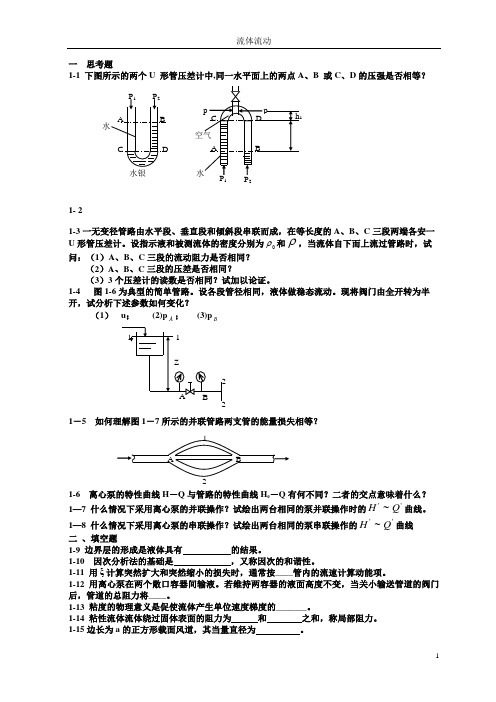
一 思考题1-1 下图所示的两个U 形管压差计中,同一水平面上的两点A 、B 或C 、D 的压强是否相等?1- 21-3一无变径管路由水平段、垂直段和倾斜段串联而成,在等长度的A 、B 、C 三段两端各安一U 形管压差计。
设指示液和被测流体的密度分别为0ρ和ρ,当流体自下而上流过管路时,试问:(1)A 、B 、C 三段的流动阻力是否相同?(2)A 、B 、C 三段的压差是否相同?(3)3个压差计的读数是否相同?试加以论证。
1-4 图1-6为典型的简单管路。
设各段管径相同,液体做稳态流动。
现将阀门由全开转为半开,试分析下述参数如何变化?(1) u ; (2)p A ; (3)p B1-5 如何理解图1-7所示的并联管路两支管的能量损失相等?1-6 离心泵的特性曲线H -Q 与管路的特性曲线H e -Q 有何不同?二者的交点意味着什么? 1—7 什么情况下采用离心泵的并联操作?试绘出两台相同的泵并联操作时的''~Q H曲线。
1—8 什么情况下采用离心泵的串联操作?试绘出两台相同的泵串联操作的''~Q H 曲线二 、填空题1-9 边界层的形成是液体具有 的结果。
1-10 因次分析法的基础是 ,又称因次的和谐性。
1-11 用ξ计算突然扩大和突然缩小的损失时,通常按____管内的流速计算动能项。
1-12 用离心泵在两个敞口容器间输液。
若维持两容器的液面高度不变,当关小输送管道的阀门后,管道的总阻力将____。
1-13 粘度的物理意义是促使流体产生单位速度梯度的_______。
1-14 粘性流体流体绕过固体表面的阻力为 和 之和,称局部阻力。
1-15边长为a 的正方形载面风道,其当量直径为 。
水银12mm/s的燃料油。
若保持油品作滞流流动,1-16 经内径为158mm的钢管输送运动粘度为902最大流速不能超过。
1-17 如果管内流体流量增大1倍以后,仍处于滞流状态,则流动阻力增大到原来的倍。
第8章 粘性流体绕物体的流动-复习

上式也称为广义牛顿定律。由上式可知切
应力与流体质点的角变形率大小成正比,而流
体的法向应力和流体的相当体积膨胀率 ,以及相应方向上的线变形率有关,因此在运
动的粘性流体中,和静止的状态不同,法向应
力在不同方向上大小可能不相等。
三、纳维-斯托克斯方程(简称N-S方程)
• 将式(8-10)代入式(8-9)可得: ( 8-11)
(8-9)
方程左端为单位质量流体的惯性力;右端第一项 为作用于单位质量流体上的质量力;第二项为作 用于单位质量流体上的表面力。
该方程是牛顿第二定律的一个严格的描述,在推 导过程中适用于各种流体。但是,方程中质量力 为已知,而表面应力各分量未知。?
二、本构方程
本构方程指确立应力和应变率之间关系的方程式。 例如弹性力学中的胡克定律。对于大多数流体应 力与应变变化率成正比,也就是说,应力与应变 变化率之间存在着线性关系,服从这种关系的流 体称为牛顿流体。 斯托克斯通过引入假设条件将牛顿内摩擦定律推
流体经过机翼翼型(或叶片叶型)的流动如图8-18所示, v p 以 和 表示无穷远处流体流动所具有的速度和压强。 流体绕过翼型前驻点后,沿上表面的流速先增加,直增 加到曲面上某一点M,然后降低。由伯努利方程可知, 相应的压强先降低(dp/dx<0),而后再升高(dp/dx>0)。 M点处边界层外边界上的速度最大,而压强最低。沿曲 面各点法向的速度剖面和压强变化曲线的示意如图8-19 所示。图中实线表示流线,虚线表示边界层的外边界。
●边界层的构成:
1.层流边界层,当 流边界层。
较小时,边界层内全为层流,称为层 Re
2.混合边界层:除前部起始部分有一小片层流区,其余大 部分为紊流区,称为混合边界层。
工程流体学第九章 粘性流体绕过物体的流动

当流体为理想流体时,运动粘度等于0,N-S方程简化为:
x x x x 1 p x y z fx t x y z x y y y y 1 p x y z fy t x y y z 1 p z z z z x y z fz y z z t x
第五节
边界层动量积分关系式
推导边界层动量积分关系式
1 p dx 2 x
在定常流动的流体中,沿边界 层划出一个单位宽度的微小控制 体,它的投影面ABDC由作为x轴的 物体壁面上的一微元距离BD、边界 层的外边界AC和彼此相距dx的两直 线AB和CD所围成。
Hale Waihona Puke bA pp
C
p p dx x
切向应力之间的关系 根据达朗伯原理,所有力矩之和等于零。
对z轴的力矩:
yx dy dy yx dxdz ( yx dy )dxdz 2 y 2 xy dx dx xy dydz ( xy 0 dx )dydz x 2 2
同理
xy yx
3422xyyy???????????????????????????????????22002642?xwyyd?yydy????????????????????????????????????????????340?0?72210xyyydydy??????????????????????2???????????????????342x2?2?0?0?36722630yyydydy???????????????????????????????????????ddee将式将式ccaa得式得式dd和式和式ee代入边界层动量积分关系式代入边界层动量积分关系式2?2?2367726301037630371260dddxdxddxxc????????????????????????或积分得因为在因为在平板壁面前缘点处边界层厚度为零平板壁面前缘点处边界层厚度为零即所以积分常数所以积分常数c0c0
长沙理工 流体力学是非题、选择题、思考题

第一章流体及其物理性质1、在高压下,流体(包括气体和液体)的粘性随着压力的升高而增大。
( )2、流体在静止时无粘性,只有内部发生相对运动时才有粘性。
( )3、。
流体在静止时无粘性,只有在流体微团发生相对运动时才有粘性。
( )4、当两流层之间残生相对运动时,单位面积上的内摩擦力与速度梯度成反比。
( )5、构成气体粘性主要因素是气体分子间的吸引力。
( )6、根据牛顿内摩擦定律,流层间的摩擦切应力与速度梯度成正比,而与压力无关。
( )7、理想流体必须具备两个条件:一是不具有粘性,二是不可压性。
( )8、流体在静止时无粘性,只有在内部发生相对运动时才有粘度。
( )9、在无粘性流体中,不管是否运动,都不会产生切应力。
( )10、流体的粘性随温度的升高而减小。
( )11、静止的不可压缩流体的密度并非处处都为同一常数,只有即为不可压缩流体,同时又是均质时,密度才时时处处都是同一常数。
( )12、静止流体无粘性,即切应力等于零。
( )13、由于粘性是流体的固有属性,因此粘性流体在静止是应该存在切应力。
( )第一章流体及其物理性质1、如果在某一瞬间使流体中每个流体微团的密度均相同,则这种流体一定是( )。
A、可压缩流体;B、不可压缩流体;C、均质流体;D、非均质流体;2、牛顿内摩擦定律告诉我们( )。
A、作用于流层上切向应力与压力成正比;B、作用于流层上切向应力与速度梯度成正比;C、作用于流层上切向应力与速度梯度成反比;D、作用于流层上切向应力与流层面积成反比;3、流体的特点是( )。
A、只能承受微小剪切力作用;B、受任何微小压力都能连续变形;C、当受到剪切力作用时,仅能产生一定程度的变形;D、受任何微小剪切力作用将发生连续变形;4、在地球的重力场中,流体的密度和重度的关系为( )。
A、gργ=;B、gργ=;C、ργg=;D、γρg=;5、流体是那样一种物质,它( )。
A、不断膨胀,直到充满任意容器;B、实际上是不可压缩的;C、不能承受切应力;D、在任意切应力作用下,不能保持静止;6、流体的力学特征为( )。
第4章 粘流基础(复习+习题)(略)

11/18/2010 11:52 PM
沈阳航空工业学院飞机设计教研室
第5页 共71页
4.1、流体的粘性及其对流动的影响 、
当理想流体绕过平板(无厚度)时,平板对流动不产生任何影响,在 平板表面,允许流体质点滑过平板,但不允许穿透平板(通常称作为 不穿透条件)。平板对流动无阻滞作用,平板阻力为零。 但如果是粘性流体,情况就不同了。由于存在粘性,紧贴平板表面的 流体质点粘附在平板上,与平板表面不存在相对运动(既不允许穿透, 也不允许滑动),这就是说,在边界面上流体质点必须满足不穿透条 件和不滑移条件。随着离开平板距离的增大,流体速度有壁面处的零 值迅速增大到来流的速度。这样在平板近区存在着速度梯度很大的流 动,因此流层之间的粘性切应力就不能忽略,对流动起控制作用。这 个区称为边界层区。平板对流动起阻滞作用,平板的阻力不为零。即
1 ∂v ∂u 1 ∂u ∂w - − ∆y + − ∆z ∂x ∂y 2 2 ∂z ∂x
11/18/2010 11:52 PM 沈阳航空工业学院飞机设计教研室 第12页 共71页
4.2、流体微团的运动形式与速度分解定理 、
如果令:
∂u ε xx = ∂x
11/18/2010 11:52 PM 沈阳航空工业学院飞机设计教研室 第9页 共71页
4.2、流体微团的运动形式与速度分解定理 、
1、流体微团运动的基本形式 流体微团在运动过程中,将发生刚体运动(平动和转动)与变形运动 (线变形和角变形运动)。 平动 转动
线变形
角变形
11/18/2010 11:52 PM
第4页 共71页
4.1、流体的粘性及其对流动的影响 、
1---binghan流体,泥浆、血浆、牙膏等 2---伪塑性流体,尼龙、橡胶、油漆、绝缘 3---牛顿流体,水、空气、汽油、酒精等 4---胀塑性流体,生面团、浓淀粉糊等 5---理想流体,无粘流体。 2、粘性流体运动特点 自然界中流体都是有粘性的,因此粘性对流体运动的影响是普遍 存在的。但对于具体的流动问题,粘性所起的作用并不一定相同。 特别是象水和空气这样的小粘性流体,对于某些问题忽略粘性的 作用可得到满意的结果。因此,为了简化起见,提出了理想流体 的概念和理论。 以下用若干流动事例说明粘性流动与无粘流动的差别。 (1)绕过平板的均直流动
第九章 粘性流体绕过物体的流动(12)

第十二节 物体阻力 自由沉降速度
• 二、减阻方法
(3)控制边界层,防止边界层分离。
将壁面附近被阻滞的流体设法吸去;
通过壁面注入流体,使被阻滞的流体获得更多的动量和能 量以增强其克服逆压梯度的能力。
第十二节 物体阻力 自由沉降速度
• 三、自由沉降速度
FD
小球受力:重力G、浮力F、沿流动方 向的阻力FD
翼型的阻力FD与翼型的翼弦b、翼展l、冲角α
第十二节 物体阻力 自由沉降速度
临界冲角升力系数达到最大值, 也是失速点
如果机翼的迎角大到了一定程度, 靠近机翼翼面附近的气流在绕过上 翼面时,由于自身粘性的作用,流 速会减慢,甚至减慢到零,而上游 尚未减速的气流仍然源源不断地流 过来,减速了的气流就成为了阻碍, 最后气流就不可能再沿着机翼表面 流动了,它将从表面抬起进入外层 的绕流,这就叫做边界层分离。
F
1 3 G d s g 6 1 3 F d g 6 v 2 1 2 2 FD CD CDd v f 2 8
G
第十二节 物体阻力 自由沉降速度
当FD+F>G 小球随流体向上运动
当FD+F<G 小球向下沉降
当FD+F=G 小球处于临界状态,及悬浮状态 小球处于悬浮状态时: FD F G 1 1 3 1 3 2 2 C Dd v f d g d m g 2 6 6
• 一、物体阻力 摩擦阻力是作用在物体表面的切向应力在来 流方向上的分力的和。
压差阻力是作用在物体表面的压强在来流方向 上的分力的总和。大小与物体表面形状有很大 关系,又称形状阻力。
第十二节 物体阻力 自由沉降速度
第十二节 物体阻力 自由沉降速度
圆柱体阻力系数与雷诺数关系
十一章粘性流体绕物流动

1 ~ 0 2 才成立。 则只有 Re 2 1 2 ~0 即 Re l
1
1 2 0
反比于
Re ,故随 Re , 。
上述方程是普朗特于1904年推出,称普朗 特边界层方程,又称二维恒定层流边界层。 方程中 p y 0,说明 p与 y无关,则
p dp x dx
Re c 5 10 3 10
5
6
对平板绕流 有层和紊的边界层称混合边界层。 边界层特点 (1) 与绕流长度相比,δ为小量,从前驻 点开始随x↑而增厚,随Re ↑而↓。 (2)在边界层内,沿法线方向,速度梯度很 大。外部为势流区。
(3)普朗特理论:边界层内惯性力与粘性力 量级相等。
vx 2 vx vx ~ 2 x y
U 2
l
U ~ 2
2
~ l 2 Ul
1 ~ l Re
(4)边界层内流态 实验测量表明边界层内 层流态向湍流态转捩的 雷诺数为 Rexcr 3.2 105
(5)沿曲面壁绕流时,边界层易分离并产生 尾涡。
第二节
边界层微分方程
先看数量级,然后将N—S方程化简得到 假定不可压缩流体恒定二维流动,μ不变, 略去质量力,则:
1 0 1
2
1 2 0
11 0
1 0
2 v y 2 v y p 1 v y v y vx + + + vy 2 2 y Re x x y y
1 0
0 0
l
2
1 0
1 0 01
用 V 除连续方程各项
v x v y + 0 x y
)
阴影面积 A V vx dy 取一
粘性流体绕过物体的流动基本练习

粘性流体绕过物体的流动1.应力是____ 。
(A)力(B) 一定质量的流体所受的力(C) 作用于流体界面上的力的分布强度(D) 随作用面的法线方向不同而可能改变的2.粘性流体分界面两侧____ 。
(A)速度连续(B) 切向速度分量可以不连续,法向速度分量连续(C) 法向速度分量可以不连续,切向速度分量连续(D) 切向、法向速度分量均可以不连续3.不计表面张力时,粘性流体分界面两侧____ 。
(A)应力连续(B) 切向应力分量可以不连续,法向应力分量连续(C) 切向应力分量连续,法向应力分量可以不连续(D) 切向、法向应力分量均可以不连续4.不可压缩流体____ 。
(A)满足(B) 满足(C) 即均质流体(ρ= 常数)情况比较简单的粘性流体具有精确解____ 。
(B)没有什么意义(B) 有助于揭示粘性流动的本质特征(C) 可用来评价数值方法的合理性(D) 可作为相近情况的求解基础5.对于斯托克斯流动____ 。
(A)可忽略惯性力(B) 可忽略粘性力(B)运动学性质与流体密度ρ无关(D) 运动学性质与粘性系数μ无关(E) 运动学性质与ρ、μ无关6.对于斯托克斯流动,由于运动学性质与流体密度ρ____关,所以压力、应力、合力等与ρ____关,阻力则与粘性系数μ成____比,与物体运动速度成____ 比,与物体的线性尺度____比。
(A) 有(B) 无(C) 正(D) 反7.描述粘性流体运动的微分方程有____ 。
(A)欧拉方程(B) 边界层方程(C) 纳维-斯托克斯方程(D) 斯托克斯方程8.低雷诺数流动的基本特点是____ 。
(A)惯性力比粘性力重要(B) 粘性力远比惯性力重要(C) 惯性力与粘性力同样重要(D) 惯性力与粘性力都不重要9.现代流体力学的标志性的开端是____ 。
(A)牛顿的内摩擦定律(B) 纳维-斯托克斯方程的建立(C) 普朗特提出的边界层的概念10.边界层流动的基本特点是____ 。
粘性流体的一元流动

粘性流体动的一元流动思考题及练习题1.湍流流动中,近壁面处的流动特征为()。
a)附加切应力大,速度梯度也大,b) 附加切应力为领,速度梯度很大,c)存在大的旋涡,消耗能量d)存在粘性底层,但摩擦切应力较湍流核心区小。
2.光华直圆管内的流动,层流与湍流的速度剖面差别为()。
a)后者较前者丰满,b)前者为二次函数,后者为三次函数,c) 前者为二次函数,后者为n次函数,d) 前者较均匀,后者均匀程度差。
3.“水力光滑”是指()。
a)光滑管内的水流b)摩擦切应力最小时的管流,c)粘性底层大于管壁粗糙度情况下的管流d)介于层流与湍流之间的管流。
4.等截面管内粘性不可压缩流体流动,沿流向的压力降主要与()参数有关。
a)流动速度b) 流动速度,粘性系数c) 流动速度,粘性系数和管径d) 流动速度,粘性系数,管径和管壁粗糙度。
5.对于同一等截面光滑直圆管内的不可压缩粘性流体的定常层流或湍流()。
a)层流流动时管轴线处的速度大于湍流时的速度b) 层流流动时管轴线处的速度小于湍流时的速度c) 层流流动时管轴线处的速度等于湍流时的速度d) 管轴线处的速度只取决于流量和过流断面面积。
6.水平放置的等截面管内不可压缩定常流动,由于粘性效应产生的损失是以()形式表现出来的。
a)压力降b)动能减少c)压力降和动能减少d) 维持旋涡的运动需要补充机械能。
7.粘性流体的流动状态分为几类?理想流体中是否有层流运动?8.简述牛顿内摩擦定律的适用条件。
9.举例说明湍流的利与害。
10.简述粘性底层(层流底层)的概念,其厚度如何确定,它对管壁的导热性影响如何。
11.湍流度的定义是什么?12.对于等截面光滑直圆管内的不可压缩流体的定常层流,若要用批托管测量管内流量,试简述其方法,并给出流量的计算公式。
13.在同一光滑直园管中的同一种不可压缩粘性流体定常流动中,层流与湍流状态下比较其阻力大小,并说明原因。
14.对于等截面光滑管内的不可压缩粘性流体的定常湍流,若要用批托管近似测量管内流量,试简述其方法,并给出流量的计算公式。
工程流体力学第八章--粘性流体绕物体的流动

v
2 f
2
vf
4 gd s 3 CD
在实际应用中,根据雷诺数的范围用下列三个公式求得
(1)当 Re 1
vf
1 18
g v
s
d2
(2)当 Re 10 ~ 1000
vf
( 4 39
g v 0.5
s
2
)3
d
(3)当 Re 1000 ~ 2105
共有九个分量 三个是法向应力 六个是切向应力
第一节 不可压缩粘性流体的运动微分方程
一、微元体的受力分析和运动微分方程的推导
作用于微元体各面上的x轴方向的应力
把作用于控制体上x方向的力叠加起来,得到作用 在微元体上的表面力在x方向的分量为:
x dxdydz yx dydxdz zx dzdxdy
①风洞实验技术。 ②机翼理论。 ③湍流理论。
一、边界层的概念
由于流体的易 变形性,流体与固 壁可实现分子量级 的粘附作用。通过 分子内聚力使粘附 在固壁上的流体质 点与固壁一起运动。
壁面不滑移条件
二、边界层的厚度d
y
U0
Ue
0.99Ue
Ue
o
边界层流动δ
Ue
dx) ux,y)
L
y
外部势流 u
2vz z 2
)
如果流动是不可压缩流体,则连续性方程为
vx v y vz 0 x y z
将式(8-6)依次求 2 p 、 2 p、 2 p ,然后相加,
x 2 y 2 z 2
并结合连续性方程,即得 2 p 2 p 2 p 2 p 0 x2 y 2 z 2
八粘性物体绕过物体的流动

粘性物体绕过物体的流动8-1.两无限长同心圆筒,半径分别为1R 与2R ,各以等角速度1ω与2ω绕中心轴旋转,两筒间充满不可压缩粘性液体,重力影响忽略不计。
试证明环形空间液体的角速度为:)()()(21222221222122221R R r R r R r R R --+ωωω-=8-2.粘性流体在两块无限大平板间作定常运动,上板移动速度为1V ,下板移动速度为2V ,试求流体的速度分布。
[2212212122V V h y V V h y x p h V ++⎪⎭⎫ ⎝⎛-+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-∂∂-=μ]8-3.液体的粘度系数为μ,密度为ρ,在重力场作用下沿一斜板流动,斜板与水平面的夹角为θ,宽度为无限大,液层厚度为h ,流动是稳定的,并平行于板面。
与液面接触的空气的粘度可以忽略不记。
试推导液层内平行斜面的速度分布函数,并推导板面的切应力和平均速度的计算式。
[)2(2sin 2y hy g -μθρ,θρsin gh ,μθρ3sin 2h ]8-4.流体在两平板缝隙间作定常层流流动,两平板相互间的倾角为θ(θ很小)缝隙的长度为l ,缝隙两端的高度分别为1h 与2h ,两端的压强分别为1p 和2p ,上板固定,下板水平放置并以速度V 作匀速运动,试证明缝隙间的压强分布为:)()(6)()()(2122212121221h h h x h h V p p l h h h x h h h p p +-+-++-=μ8-5.一直径为mm 1,密度为33/101.1m kg ⨯=ρ的质点自静止开始在密度为3/9.0m kg =ρ,粘度为3/03.0m s N ⋅的油中自由下落。
试求当小球达到自由沉降速度速度的%99时所用的时间,此时的雷诺数是多少?[s 0094.0,1089.0]8-6.沿平板流动的两种介质,一种是标准状态的空气,其流速为s m /30,另一种是C ︒20的水,其流速为s m /5.1,求二者在同一位置处的层流边界层的厚度之比[07.0]。
流体力学第九章 粘性流体绕过物体的流动

第四节 层流边界层微分方程
层流边界层微分方程组 普朗特边界层微分方程
第五节 边界层的动量积分方程
边界层内的流体是黏性流体的运动,理论上可以用N-S方程 来研究其运动规律。但由此得到的边界层微分方程中,非 线性项仍存在,因此即使对于外形很简单的绕流物体求解 也是很复杂的,目前只能对平板、楔形体绕流层流边界层 进行理论计算求得其解析解。但工程上遇到的很多问题, 如任意翼型的绕流问题和紊流边界层,一般来说求解比较 困难,为此人们常采用近似解法,其中应用的较为广泛的 是边界层动量积分方程解法。它是定常流动积分形式的动 量方程在边界层流动中的应用。
边界层定义:速度梯度很大的薄层。粘性在该薄层内起作用。
v y v
v 0.99
边界层流δ
v
y
外部势流 v
(x)
o L
x
Re>>1
s
尾涡区
u
图1平壁面绕流的边界层
图2 大Re数绕流流场划分
全流场分成二个流动区域(Plandtl BL Model) :
外流区(y>): 可略去粘性的作用,无粘流。 边界层(y<):沿壁面法向的速度梯度大,考虑粘性。
( CD D
1 2
V2 A
1.2
半管 半管
4 ×104
1.2
4 ×104
2.3
方柱 平板
3.5×104
2.0
104×106
1.98
椭柱
2:1
1×105
0.46
椭柱
三元物型
球 半球 半球 方块
8:1
2 ×105
0.20
( Re Vd n
CD D
1 2
V2 A
粘性流体流动
9.4 层流边界层微分方程
利用边界层每一处的厚度都很小的特征,来比较方程组中各项的数量级,权 衡主次,忽略次要项,大大简化该方程组。
l或 l 1
方程组无量纲化
0 y
vy vy v p p 2 v
x x l
y y l
9.3 边界层的基本概念 粘性流体在大雷诺数下平滑地绕流某静止物体
在紧靠物体表面的薄层内,流速将由物体表面上的零值迅速地增加 到与来流速度 v同数量级的大小,这种在大雷诺数下紧靠物体表面 流速从零急剧增加到与来流速度相同数量级的薄层称为边界层。
在边界层内,物体表面法线方向上的速度梯度很大,即使粘度很小的流体, 表现出的粘滞力也较大,决不能忽略。边界层内的流体有相当大的涡通量。 当边界层内的有旋流离开物体而流入下游时,在物体后形成尾涡区域。
o
x
l
vx
x
2vx 2vx v x v x 1 p vx vy 2 x y x y 2 x 2v y 2v y 1 p vx vy 2 2 x y y x y v x v y 0 x y v y v y
Re l v l
在边界层内, 可取
v x ~1 x 2 v x ~1 2 x
以及y与
是同一数量级,于是
v 1 x ~ y
2vx 1 ~ y 2 2
9.4 层流边界层微分方程 由连续方程
v v y x ~1 y x
一般在实际应用中规定从固体壁面沿外法线到速度达到势流速度的99%处距离为边界 层的厚度,以 表示。
边界层的外边界和流线并不重合,流线伸入边界层内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
粘性流体绕过物体的流动
1.应力是____ 。
(A)力(B) 一定质量的流体所受的力
(C) 作用于流体界面上的力的分布强度
(D) 随作用面的法线方向不同而可能改变的
2.粘性流体分界面两侧____ 。
(A)速度连续(B) 切向速度分量可以不连续,法向速度分量连续
(C) 法向速度分量可以不连续,切向速度分量连续
(D) 切向、法向速度分量均可以不连续
3.不计表面张力时,粘性流体分界面两侧____ 。
(A)应力连续(B) 切向应力分量可以不连续,法向应力分量连续
(C) 切向应力分量连续,法向应力分量可以不连续
(D) 切向、法向应力分量均可以不连续
4.不可压缩流体____ 。
(A)满足(B) 满足
(C) 即均质流体(ρ= 常数)情况比较简单的粘性流体具有精确解____ 。
(B)没有什么意义(B) 有助于揭示粘性流动的本质特征
(C) 可用来评价数值方法的合理性(D) 可作为相近情况的求解基础
5.对于斯托克斯流动____ 。
(A)可忽略惯性力(B) 可忽略粘性力
(B)运动学性质与流体密度ρ无关
(D) 运动学性质与粘性系数μ无关
(E) 运动学性质与ρ、μ无关
6.对于斯托克斯流动,由于运动学性质与流体密度ρ____关,所以压力、应力、合力等与
ρ____关,阻力则与粘性系数μ成____比,与物体运动速度成____ 比,与物体的线性尺度____比。
(A) 有(B) 无(C) 正(D) 反
7.描述粘性流体运动的微分方程有____ 。
(A)欧拉方程(B) 边界层方程
(C) 纳维-斯托克斯方程(D) 斯托克斯方程
8.低雷诺数流动的基本特点是____ 。
(A)惯性力比粘性力重要(B) 粘性力远比惯性力重要
(C) 惯性力与粘性力同样重要(D) 惯性力与粘性力都不重要
9.现代流体力学的标志性的开端是____ 。
(A)牛顿的内摩擦定律(B) 纳维-斯托克斯方程的建立
(C) 普朗特提出的边界层的概念
10.边界层流动的基本特点是____ 。
(A)惯性力比粘性力重要(B) 粘性力远比惯性力重要
(C) 惯性力与粘性力都不重要
(D) 贴近物面的薄层(即边界层)中惯性力与粘性力同样重要,薄层之外区域粘性可忽略
11. 在边界层厚度、排移厚度和动量损失厚度中,有较大人为规定因素的是
____。
(A) (B) (C)
12.基于平板长度L、排移厚度、动量损失厚度、前缘(x= 0)至所在位置x
的雷诺数分别记做、、和。
在典型的流动条件下,边界层从层流到湍流的过渡通常认为发生在____处。
(A) (B)
(C) (D)
13.就边界层中流动有层流向湍流过渡而言,____ 。
(A) 雷诺数的大小是唯一影响因素(B) 雷诺数的大小与此毫无关系
(C) 除雷诺数的大小外,还和来流条件、物面粗糙度等有关
14.利用测量边界层内近壁区平行于壁面顺流测量流速急剧变化的办法发现层流到湍流的
过渡的位置,其根据是____ 。
(A)边界层的横截面上,层流速度剖面近壁处变化较湍流的缓慢
(B) 边界层的横截面上,层流速度剖面近壁处变化较湍流的快
15.平板层流边界层厚度于与当地平板前缘距离x的关系是____ 。
(A)与x成正比(B) 与成正比
(C)与x成反比(D) 与成反比
(E) (A) 、(B)、(C)、(D)均不对
16.边界层的流动分离发生于____ 。
(A) 顺压梯度区(B) 零压梯度处(C) 逆压梯度区
17.边界层的流动分离____ 。
(A)只可能发生于层流边界层(B) 只可能发生于湍流边界层
(C) 在层流边界层和湍流边界层中均有可能发生
18.减少物体所受到的流体阻力____ 。
(A)只能靠减少摩擦阻力来实现(B) 只能靠减少压差阻力来实现
(C) 要靠同时减少摩擦阻力和压差阻力来实现
(D) 要根据问题的具体情况决定应采取减少摩擦阻力还是压差阻力的措施。
