(易错题精选)初中数学反比例函数易错题汇编含答案
中考数学压轴题专题反比例函数的经典综合题附答案

一、反比例函数真题与模拟题分类汇编(难题易错题)1.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y= (k>0,x>0)的图象上,点D的坐标为(,2).(1)求k的值;(2)若将菱形ABCD沿x轴正方向平移,当菱形的一个顶点恰好落在函数y= (k>0,x >0)的图象上时,求菱形ABCD平移的距离.【答案】(1)解:作DE⊥BO,DF⊥x轴于点F,∵点D的坐标为(,2),∴DO=AD=3,∴A点坐标为:(,5),∴k=5 ;(2)解:∵将菱形ABCD向右平移,使点D落在反比例函数y= (x>0)的图象上D′,∴DF=D′F′=2,∴D′点的纵坐标为2,设点D′(x,2)∴2= ,解得x= ,∴FF′=OF′﹣OF= ﹣ = ,∴菱形ABCD平移的距离为,同理,将菱形ABCD向右平移,使点B落在反比例函数y= (x>0)的图象上,菱形ABCD平移的距离为,综上,当菱形ABCD平移的距离为或时,菱形的一个顶点恰好落在函数图象上.【解析】【分析】(1)根据菱形的性质和D的坐标即可求出A的坐标,代入求出即可;(2)B和D可能落在反比例函数的图象上,根据平移求出即可.2.已知反比例函数y= 的图象经过点A(﹣,1).(1)试确定此反比例函数的解析式;(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;(3)已知点P(m, m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2 n+9的值.【答案】(1)解:由题意得1= ,解得k=﹣,∴反比例函数的解析式为y=﹣(2)解:过点A作x轴的垂线交x轴于点C.在Rt△AOC中,OC= ,AC=1,∴OA= =2,∠AOC=30°,∵将线段OA绕O点顺时针旋转30°得到线段OB,∴∠AOB=30°,OB=OA=2,∴∠BOC=60°.过点B作x轴的垂线交x轴于点D.在Rt△BOD中,BD=OB•sin∠BOD= ,OD= OB=1,∴B点坐标为(﹣1,),将x=﹣1代入y=﹣中,得y= ,∴点B(﹣1,)在反比例函数y=﹣的图象上(3)解:由y=﹣得xy=﹣,∵点P(m, m+6)在反比例函数y=﹣的图象上,其中m<0,∴m( m+6)=﹣,∴m2+2 m+1=0,∵PQ⊥x轴,∴Q点的坐标为(m,n).∵△OQM的面积是,∴OM•QM= ,∵m<0,∴mn=﹣1,∴m2n2+2 mn2+n2=0,∴n2﹣2 n=﹣1,∴n2﹣2 n+9=8.【解析】【分析】(1)由于反比例函数y= 的图象经过点A(﹣,1),运用待定系数法即可求出此反比例函数的解析式;(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;(3)把点P(m, m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2﹣2 n+9的值.3.如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2= (c≠0)的图象相交于点B(3,2)、C(﹣1,n).(1)求一次函数和反比例函数的解析式;(2)根据图象,直接写出y1>y2时x的取值范围;(3)在y轴上是否存在点P,使△PAB为直角三角形?如果存在,请求点P的坐标;若不存在,请说明理由.【答案】(1)解:把B(3,2)代入得:k=6∴反比例函数解析式为:把C(﹣1,n)代入,得:n=﹣6∴C(﹣1,﹣6)把B(3,2)、C(﹣1,﹣6)分别代入y1=ax+b,得:,解得:所以一次函数解析式为y1=2x﹣4(2)解:由图可知,当写出y1>y2时x的取值范围是﹣1<x<0或者x>3.(3)解:y轴上存在点P,使△PAB为直角三角形如图,过B作BP1⊥y轴于P1,∠B P1 A=0,△P1AB为直角三角形此时,P1(0,2)过B作BP2⊥AB交y轴于P2∠P2BA=90,△P2AB为直角三角形在Rt△P1AB中,在Rt△P1 AB和Rt△P2 AB∴∴P2(0,)综上所述,P1(0,2)、P2(0,).【解析】【分析】(1)利用待定系数法求出反比例函数解析式,进而求出点C坐标,最后用再用待定系数法求出一次函数解析式;(2)利用图象直接得出结论;(3)分三种情况,利用勾股定理或锐角三角函数的定义建立方程求解即可得出结论.4.已知:O是坐标原点,P(m,n)(m>0)是函数y= (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+ .(1)当n=1时,求点A的坐标;(2)若OP=AP,求k的值;(3)设n是小于20的整数,且k≠ ,求OP2的最小值.【答案】(1)解:过点P作PQ⊥x轴于Q,则PQ=n,OQ=m,当n=1时,s= ,∴a= = .(2)解:解法一:∵OP=AP,PA⊥OP,∴△OPA是等腰直角三角形.∴m=n= .∴1+ = •an.即n4﹣4n2+4=0,∴k2﹣4k+4=0,∴k=2.解法二:∵OP=AP,PA⊥OP,∴△OPA是等腰直角三角形.∴m=n.设△OPQ的面积为s1则:s1= ∴•mn= (1+ ),即:n4﹣4n2+4=0,∴k2﹣4k+4=0,∴k=2.(3)解:解法一:∵PA⊥OP,PQ⊥OA,∴△OPQ∽△OAP.设:△OPQ的面积为s1,则 =即: = 化简得:化简得:2n4+2k2﹣kn4﹣4k=0(k﹣2)(2k﹣n4)=0,∴k=2或k= (舍去),∴当n是小于20的整数时,k=2.∵OP2=n2+m2=n2+ 又m>0,k=2,∴n是大于0且小于20的整数.当n=1时,OP2=5,当n=2时,OP2=5,当n=3时,OP2=32+ =9+ = ,当n是大于3且小于20的整数时,即当n=4、5、6…19时,OP2的值分别是:42+ 、52+ 、62+ …192+ ,∵192+ >182+ >32+ >5,∴OP2的最小值是5.【解析】【分析】(1)利用△OPA面积定义构建关于a的方程,求出A的坐标;(2)由已知OP=AP,PA⊥OP,可得△OPA是等腰直角三角形,由其面积构建关于n的方程,转化为k的方程,求出k;(3)利用相似三角形的面积比等于相似比的平方构建关于k的方程,最值问题的基本解决方法就是函数思想,利用勾股定理用m、n的代数式表达OP2,,在n的范围内求出OP2的最值.5.如图,在平面直角坐标系中,直线与双曲线相交于点A(,6)和点B(-3,),直线AB与轴交于点C.(1)求直线AB的表达式;(2)求的值.【答案】(1)解:∵点A(,6)和点B(-3,)在双曲线,∴m=1,n=-2,∴点A(1,6),点B(-3,-2),将点A、B代入直线,得,解得,∴直线AB的表达式为:(2)解:分别过点A、B作AM⊥y轴,BN⊥y轴,垂足分别为点M、N,则∠AMO=∠BNO=90°,AM=1,BN=3,∴AM//BN,∴△ACM∽△BCN,∴【解析】【分析】根据反比例函数的解析式可得m和n的值,利用待定系数法求一次函数的表达式;作辅助线,构建平行线,根据平行线分线段成比例定理可得结论.6.如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折现”)(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;(2)如图2,双曲线y= 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.①试求△PAD的面积的最大值;②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.【答案】(1)解:如图1,新函数的性质:1.函数的最小值为0;2.函数图象的对称轴为直线x=3.由题意得,点A的坐标为(-3,0),分两种情况:①当x-3时,y=x+3;②当x<-3时,设函数解析式为y=kx+b,在直线y=x+3中,当x=-4时,y=-1,则点(-4,-1)关于x轴的对称点为(-4,1),把点(-4,1),(-3,0),代入y=kx+b中,得:,解得:,∴y=-x-3.综上,新函数的解析式为y=.(2)解:如图2,①∵点C(1,a)在直线y=x+3上,∴a=4,∵点C(1,4)在反比例函数y=上,∴k=4,∴反比例函数的解析式为y=.∵点D是线段AC上一动点,∴设点D的坐标为(m,m+3),且-3<m<1,∵DP∥x轴,且点P在双曲线上,∴点P的坐标为(,m+3),∴PD=-m,∴S△PAD=(-m)(m+3)=m2-m+2=(m+)2+,∵a=<0,∴当m=时,S有最大值,最大值为,又∵-3<<1,∴△PAD的面积的最大值为.②在点D的运动的过程中,四边形PAEC不能为平行四边形,理由如下:当点D为AC的中点时,其坐标为(-1,2),此时点P的坐标为(2,2),点E的坐标为(-5,2),∵DP=3,DE=4,∴EP与AC不能互相平分,∴四边形PAEC不能为平行四边形.【解析】【分析】(1)根据一次函数的性质,结合函数图象写出新函数的两条性质;利用待定系数法求新函数解析式,注意分两种情况讨论;(2)①先求出点C的坐标,再利用待定系数法求出反比例函数解析式,设出点D的坐标,进而得到点P的坐标,再根据三角形的面积公式得出函数解析式,利用二次函数的性质求解即可;②先求出A的中点D的坐标,再计算DP、DE的长度,如果对角线互相平分,则能成为平行四边形,如若对角线不互相平分,则不能成为平行四边形.7.如图,在矩形OABC中,OA=6,OC=4,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;(2)当k为何值时,△EFA的面积最大,最大面积是多少?【答案】(1)解:∵在矩形OABC中,OA=6,OC=4,∴B(6,4),∵F为AB的中点,∴F(6,2),又∵点F在反比例函数(k>0)的图象上,∴k=12,∴该函数的解析式为y= (x>0)(2)解:由题意知E,F两点坐标分别为E(,4),F(6,),∴,==== ,∴当k=12时,S有最大值.S最大=3【解析】【分析】)当F为AB的中点时,点F的坐标为(3,1),由此代入求得函数解析式即可;根据图中的点的坐标表示出三角形的面积,得到关于k的二次函数,利用二次函数求出最值即可.8.在平面直角坐标系中,我们定义点P(a,b)的“变换点”为Q.且规定:当a≥b时,Q 为(b,﹣a);当a<b时,Q为(a,﹣b).(1)点(2,1)的变换点坐标为________;(2)若点A(a,﹣2)的变换点在函数y= 的图象上,求a的值;(3)已知直线l与坐标轴交于(6,0),(0,3)两点.将直线l上所有点的变换点组成一个新的图形记作M.判断抛物线y=x2+c与图形M的交点个数,以及相应的c的取值范围,请直接写出结论.【答案】(1)(1,﹣2)(2)解:当a≥﹣2时,则A(a,﹣2)的变换点坐标为(﹣2,﹣a),代入y= 可得﹣a= ,解得a= ;当a<﹣2时,则A(a,﹣2)的变换点坐标为(a,2),代入y= 可得2= ,解得a= ,不符合题意;综上可知a的值为;(3)解:设直线l的解析式为y=kx+b (k≠0 ),将点(6,0)、(0,3)代入y=kx+b得:,解得,∴直线l的解析式为y=﹣ x+3.当x=y时,x=﹣ x+3,解得x=2.点C的坐标为(2,﹣2),点C的变换点的坐标为C′( 2,﹣2 ),点(6,0)的变换点的坐标为(0,﹣6),点(0,3)的变换点的坐标为(0,﹣3),当x≥2时,所有变换点组成的图形是以C′( 2,﹣2)为端点,过(0,﹣6 )的一条射线;即:y=2x﹣6,其中x≥2,当x<2时,所有变换点组成的图形是以C′(2,﹣2)为端点,过(0,﹣3)的一条射线,即y= x﹣3,其中,x<2.所以新的图形M是以C′(2,﹣2)为端点的两条射线组成的图形.如图所示:由和得:x2﹣x+c+3=0①和x2﹣2x+c+6=0②讨论一元二次方程根的判别式及抛物线与点C′的位置关系可得:①当方程①无实数根时,即:当c>﹣时,抛物线y=x2+c与图形M没有交点;②当方程①有两个相等实数根时,即:当c=﹣时,抛物线y=x2+c与图形M有一个交点;③当方程②无实数根,且方程①有两个不相等的实数根时,即:当﹣5<c<﹣时,抛物线y=x2+c与图形M有两个交点;④当方程②有两个相等实数根或y=x2+c恰好经过经过点C′时,即:当c=﹣5或c=﹣6时,抛物线y=x2+c与图形M有三个交点;⑤当方程②方程①均有两个不相等的实数根时,且两根均小于2,即:当﹣6<c<﹣5时,抛物线y=x2+c与图形M有四个交点;⑥当c<﹣6时,抛物线y=x2+c与图形M有两个交点.【解析】【解答】解:(1)∵2≥﹣1,∴点(2,1)的变换点坐标为(1,﹣2),故答案为:(1,﹣2);【分析】(1)由变换点的定义可求得答案;(2)由变换点的定义可求得A的变换点,代入函数解析式可求得a的值;(3)先求得直线y=x与直线l的交点坐标,然后分为当x≥2和x<2两种情况,求得M的关系式,然后在画出M的大致图象,然后将抛物线y=x2+c与M的函数关系式组成方程组,然后依据一元二次方程根的判别式进行判断即可.9.如图,已知二次函数的图象与y轴交于点A(0,4),与x 轴交于点B,C,点C坐标为(8,0),连接AB,AC.(1)请直接写出二次函数的解析式.(2)判断△ABC的形状,并说明理由.(3)若点N在x轴上运动,当以点A,N,C为顶点的三角形是等腰三角形时,请写出此时点N的坐标.【答案】(1)解:∵二次函数的图象与y轴交于点A(0,4),与x轴交于点B.C,点C坐标(8,0),∴解得∴抛物线表达式:(2)解:△ABC是直角三角形.令y=0,则解得x1=8,x2=-2,∴点B的坐标为(-2,0),由已知可得,在Rt△ABO中AB2=BO2+AO2=22+42=20,在Rt△AOC中AC2=AO2+CO2=42+82=80,又∴BC=OB+OC=2+8=10,∴在△ABC中AB2+AC2=20+80=102=BC2∴△ABC是直角三角形(3)解:∵A(0,4),C(8,0),AC= =4 ,①以A为圆心,以AC长为半径作圆,交轴于N,此时N的坐标为(-8,0),②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为( ,0)或( ,0)③作AC的垂直平分线,交g轴于N,此时N的坐标为(3,0),综上,若点N在轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(-8,0)、( ,0)、(3,0)、 ,0)【解析】【分析】(1)根据待定系数法即可求得;(2)根据拋物线的解析式求得B的坐标,然后根据勾股定理分别求得AB2=20,AC2=80,BC=10然后根据勾股定理的逆定理即可证得△ABC是直角三角形(3)分别以A.C两点为圆心,AC长为半径画弧,与m轴交于三个点,由AC的垂直平分线与c轴交于一个点,即可求得点N的坐标10.已知,抛物线的图象经过点,.(1)求这个抛物线的解析式;(2)如图1,是抛物线对称轴上一点,连接,,试求出当的值最小时点的坐标;(3)如图2,是线段上的一点,过点作轴,与抛物线交于点,若直线把分成面积之比为的两部分,请求出点的坐标.【答案】(1)解:将,的坐标分别代入.得解这个方程组,得,所以,抛物线的解析式为(2)解:如图1,由于点、关于轴对称,所以连接,直线与轴的交点即为所求的点,由,令,得,解得,,点的坐标为,又,易得直线的解析式为:.当时,,点坐标(3)解:设点的坐标为,所以所在的直线方程为.那么,与直线的交点坐标为,与抛物线的交点坐标为.由题意,得① ,即,解这个方程,得或(舍去).② ,即,解这个方程,得或(舍去),综上所述,点的坐标为,或,.【解析】【分析】(1)将点、的坐标代入可得出、的值,继而得出这个抛物线的解析式;(2)由于点、关于轴对称,所以连接,直线与轴的交点即为所求的点,利用待定系数法确定直线的解析式,然后求得该直线与轴的交点坐标即可;(3)如图2,交于,设,根据一次函数和二次函数图象上点的坐标特征,设点的坐标为,,.然后分类讨论:分别利用或,列关于的方程,然后分别解关于的方程,从而得到点坐标11.如图,二次函数y=x2+bx+c的图像与x轴交于A,B两点,B点坐标为(4,0),与y轴交于点C(0,4).点D为抛物线上一点(1)求抛物线的解析式及A点坐标;(2)若△BCD是以BC为直角边的直角三角形时,求点D的坐标;(3)若△BCD是锐角三角形,请直接写出点D的横坐标m的取值范围________.【答案】(1)解:将B(4,0),C(0,4)代入y=x2+bx+c得,,解得,所以抛物线的解析式为,令y=0,得,解得,,∴A点的坐标为(1,0)(2)解:设D点横坐标为,则纵坐标为,①当∠BCD=90°时,如下图所示,连接BC,过C点作CD⊥BC与抛物线交于点D,过D作DE⊥y轴与点E,由B、C坐标可知,OB=OC=4,∴△OBC为等腰直角三角形,∴∠OCB=∠OBC=45°,又∵∠BCD=90°,∴∠ECD+∠OCB=90°∴∠ECD=45°,∴△CDE为等腰直角三角形,∴DE=CE=a∴OE=OC+CE=a+4由D、E纵坐标相等,可得,解得,,当时,D点坐标为(0,4),与C重合,不符合题意,舍去.当时,D点坐标为(6,10);②当∠CBD=90°时,如下图所示,连接BC,过B点作BD⊥BC与抛物线交于点D,过B作FG⊥x轴,再过C作CF⊥FG于F,过D作DG⊥FG于G,∵∠COB=∠OBF=∠BFC=90°,∴四边形OBFC为矩形,又∵OC=OB,∴四边形OBFC为正方形,∴∠CBF=45°∵∠CBD=90°,∴∠CBF+∠DBG=90°,∴∠DBG=45°,∴△DBG为等腰直角三角形,∴DG=BG∵D点横坐标为a,∴DG=4-a,而BG=∴解得,,当时,D点坐标为(4,0),与B重合,不符合题意,舍去.当时,D点坐标为(2,-2);综上所述,D点坐标为(6,10)或(2,-2).(3)3+ <m <6或 3- <m <2【解析】【解答】解:(3)当BC为斜边构成Rt△BCD时,如下图所示,以BC中点O'为圆心,以BC为直径画圆,与抛物线交于D和D',∵BC为圆O'的直径,∴∠BDC=∠BD'C=90°,∵,∴D到O'的距离为圆O'的半径,∵D点横坐标为m,纵坐标为,O'点坐标为(2,2),∴即化简得:由图像易得m=0或4为方程的解,则方程左边必有因式,∴采用因式分解法进行降次解方程或或,解得,,,当时,D点坐标为(0,4),与C点重合,舍去;当时,D点坐标为(4,0),与B点重合,舍去;当时,D点横坐标;当时,D点横坐标为;结合(2)中△BCD形成直角三角形的情况,可得△BCD为锐角三角形时,D点横坐标m的取值范围为3+ <m <6或 3- <m <2.【分析】(1)利用待定系数法求抛物线的解析式,再令y=0,求A的坐标;(2)设D点横坐标为a,代入函数解析式可得纵坐标,分别讨论∠BCD=90°和∠CBD=90°的情况,作出图形进行求解;(3)当BC为斜边构成Rt△BCD时,以BC中点O'为圆心,以BC为直径画圆,与抛物线交于D和D',此时△BCD和△BCD'就是以BC为斜边的直角三角形,利用两点间距离公式列出方程求解,然后结合(2)找到m的取值范围.12.请完成下面题目的证明.如图,AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC,AC,且∠BOC<90°,直线BC与直线AD相交于点E,过点C作直线CG 与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE(1)求证:直线CG为⊙O的切线;(2)若点H为线段OB上一点,连接CH,满足CB=CH;①求证:△CBH∽△OBC;②求OH+HC的最大值.【答案】(1)证明:由题意可知:∠CAB=∠GAF,∵AB是⊙O的直径,∴∠ACB=90°∵OA=OC,∴∠CAB=∠OCA,∴∠OCA+∠OCB=90°,∵∠GAF=∠GCE,∴∠GCE+∠OCB=∠OCA+∠OCB=90°,∵OC是⊙O的半径,∴直线CG是⊙O的切线;(2)证明:①∵CB=CH,∴∠CBH=∠CHB,∵OB=OC,∴∠CBH=∠OCB,∴△CBH∽△OBC解:②由△CBH∽△OBC可知:∵AB=8,∴BC2=HB•OC=4HB,∴HB= ,∴OH=OB-HB=∵CB=CH,∴OH+HC=当∠BOC=90°,此时BC=∵∠BOC<90°,∴0<BC<令BC=x∴OH+HC= = =当x=2时,∴OH+HC可取得最大值,最大值为5【解析】【分析】(1)由题意可知:∠CAB=∠GAF,∠GAF=∠GCE,由圆的性质可知:∠CAB=∠OCA,所以∠OCA=∠GCE,从而可证明直线CG是⊙O的切线;(2)①由于CB=CH,所以∠CBH=∠CHB,易证∠CBH=∠OCB,从而可证明△CBH∽△OBC;②由△CBH∽△OBC可知:,所以HB= ,由于BC=HC,所以OH+HC=利用二次函数的性质即可求出OH+HC的最大值.13.如图1,抛物线y=ax2+bx﹣3经过点A,B,C,已知点A(﹣1,0),点B(3,0)(1)求抛物线的解析式(2)点D为抛物线的顶点,DE⊥x轴于点E,点N是线段DE上一动点①当点N在何处时,△CAN的周长最小?②若点M(m,0)是x轴上一个动点,且∠MNC=90°,求m的取值范围.【答案】(1)解:函数的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),故﹣3a=﹣3,解得:a=1,故函数的表达式为:y=x2﹣2x﹣3(2)解:①过点C作x轴的平行线交抛物线于点C'(2,﹣3),连接AC'交DE于点N,则此时△CAN的周长最小.设过点A、C'的一次函数表达式为y=kx+b,则:,解得:,故直线AC'的表达式为:y=﹣x﹣1,当x=1时,y=﹣2,故点N(1,﹣2);②如图2,过点C作CG⊥ED于点G.设NG=n,则NE=3﹣n.∵∠CNG+∠GCN=90°,∠CNG+∠MNE=90°,∴∠NCG=∠MNE,则tan∠NCG=n=tan∠MNE,故ME=﹣n2+3n,∴﹣1<0,故ME有最大值,当n时,ME,则m的最小值为:;如下图所示,当点N与点D重合时,m取得最大值.过C作CG⊥ED于G.∵y=x2﹣2x﹣3= y=(x-1)2﹣4,∴D(1,-4),∴CG=OE=1.∵EG=OC=3∴GD=4-3=1,∴CG=DG=1,∴∠CDG=45°.∵∠CDM=90°,∴∠EDM=45°,∴△EDM是等腰直角三角形,∴EM=ED=4,∴OM=OE+EM=1+4=5,∴m=5.故:m≤5.【解析】【分析】(1)函数的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),即可求解;(2)①过点C作x轴的平行线交抛物线于点C'(2,﹣3),连接AC'交DE于点N,则此时△CAN的周长最小,即可求解;②如图2,ME=﹣n2+3n,求出ME最大值,则可求出m的最小值;当点N与点D处时,m取得最大值,求解即可.14.在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).(1)抛物线的对称轴为直线x=-3,AB=4.求抛物线的表达式;(2)平移(1)中的抛物线,使平移后的抛物线经过点O,且与x正半轴交于点C,记平移后的抛物线顶点为P,若△OCP是等腰直角三角形,求点P的坐标;(3)当m=4时,抛物线上有两点M(x1, y1)和N(x2, y2),若x1<2,x2>2,x1+x2>4,试判断y1与y2的大小,并说明理由.【答案】(1)解:抛物线 y=-x2+mx+n的对称轴为直线x=-3,AB=4.∴点 A(-5,0),点B(-1,0).∴抛物线的表达式为y=-(x+5)( x+1)∴y=-x2-6x-5.(2)解:如图1,依题意,设平移后的抛物线表达式为:y=-x2+bx.∴抛物线的对称轴为直线x=,抛物线与x正半轴交于点C(b,0).∴b>0.记平移后的抛物线顶点为P,∴点P的坐标(,),∵△OCP是等腰直角三角形,∴ =∴b=2.∴点P的坐标(1,1).(3)解:如图2,当m=4时,抛物线表达式为:y=-x2+4x+n.∴抛物线的对称轴为直线 x=2.∵点M(x1, y1)和N(x2, y2)在抛物线上,且x1<2,x2>2,∴点M在直线x=2的左侧,点N在直线x=2的右侧.∵x1+x2>4,∴2-x1<x2-2,∴点M到直线x=2的距离比点N到直线x=2的距离近,∴y1>y2.【解析】【分析】(1)先根据抛物线和x轴的交点及线段的长,求出抛物线的解析式;(2)根据平移后抛物线的特点设出抛物线的解析式,再利用等腰直角三角形的性质求出抛物线解析式;(3)根据抛物线的解析式判断出点M,N的大概位置,再关键点M,N的横坐标的范围即可得出结论.15.如图,反比例函数y= 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).(1)求反比例函数与一次函数的表达式;(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.【答案】(1)解:把点A(2,6)代入y= ,得m=12,则y= .把点B(n,1)代入y= ,得n=12,则点B的坐标为(12,1).由直线y=kx+b过点A(2,6),点B(12,1)得,解得,则所求一次函数的表达式为y=﹣x+7(2)解:如图,直线AB与y轴的交点为P,设点E的坐标为(0,m),连接AE,BE,则点P的坐标为(0,7).∴PE=|m﹣7|.∵S△AEB=S△BEP﹣S△AEP=10,∴×|m﹣7|×(12﹣2)=10.∴|m﹣7|=2.∴m1=5,m2=9.∴点E的坐标为(0,5)或(0,9).【解析】【分析】(1)把点A的坐标代入反比例函数解析式,求出反比例函数的解析式,把点B的坐标代入已求出的反比例函数解析式,得出n的值,得出点B的坐标,再把A、B的坐标代入直线y=kx+b,求出k、b的值,从而得出一次函数的解析式;(2)设点E 的坐标为(0,m),连接AE,BE,先求出点P的坐标(0,7),得出PE=|m﹣7|,根据S△AEB=S△BEP﹣S△AEP=10,求出m的值,从而得出点E的坐标.。
中考数学复习反比例函数专项易错题含答案解析

一、反比例函数真题与模拟题分类汇编(难题易错题)1.如图,反比例函数y1= 的图象与一次函数y2= x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1= 的图象上.(1)求反比例函数的表达式;(2)观察图象回答:当x为何范围时,y1>y2;(3)求△PAB的面积.【答案】(1)解:把x=4代入y2= x,得到点B的坐标为(4,1),把点B(4,1)代入y1= ,得k=4.反比例函数的表达式为y1=(2)解:∵点A与点B关于原点对称,∴A的坐标为(﹣4,﹣1),观察图象得,当x<﹣4或0<x<4时,y1>y2(3)解:过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,设AP与y轴交于点C,如图,∵点A与点B关于原点对称,∴OA=OB,∴S△AOP=S△BOP,∴S△PAB=2S△AOP.y1= 中,当x=1时,y=4,∴P(1,4).设直线AP的函数关系式为y=mx+n,把点A(﹣4,﹣1)、P(1,4)代入y=mx+n,则,解得.故直线AP的函数关系式为y=x+3,则点C的坐标(0,3),OC=3,∴S△AOP=S△AOC+S△POC= OC•AR+ OC•PS= ×3×4+ ×3×1= ,∴S△PAB=2S△AOP=15.【解析】【分析】(1)把x=4代入y2= x,得到点B的坐标,再把点B的坐标代入y1=,求出k的值,即可得到反比例函数的表达式;(2)观察图象可知,反比例函数的图象在一次函数图象上方的部分对应的自变量的取值范围就是不等式y1>y2的解集;(3)过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,设AP与y轴交于点C,由点A与点B关于原点对称,得出OA=OB,那么S△AOP=S△BOP,S△PAB=2S△AOP.求出P点坐标,利用待定系数法求出直线AP的函数关系式,得到点C的坐标,根据S△AOP=S△AOC+S△POC求出S△AOP= ,则S△PAB=2S△AOP=15.2.如图,已知直线y=x+k和双曲线y= (k为正整数)交于A,B两点.(1)当k=1时,求A、B两点的坐标;(2)当k=2时,求△AOB的面积;(3)当k=1时,△OAB的面积记为S1,当k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为S n,若S1+S2+…+S n= ,求n的值.【答案】(1)解:当k=1时,直线y=x+k和双曲线y= 化为:y=x+1和y= ,解得,,∴A(1,2),B(﹣2,﹣1)(2)解:当k=2时,直线y=x+k和双曲线y= 化为:y=x+2和y= ,解得,,∴A(1,3),B(﹣3,﹣1)设直线AB的解析式为:y=mx+n,∴∴,∴直线AB的解析式为:y=x+2∴直线AB与y轴的交点(0,2),∴S△AOB= ×2×1+ ×2×3=4;(3)解:当k=1时,S1= ×1×(1+2)= ,当k=2时,S2= ×2×(1+3)=4,…当k=n时,S n= n(1+n+1)= n2+n,∵S1+S2+…+S n= ,∴ ×(…+n2)+(1+2+3+…n)= ,整理得:,解得:n=6.【解析】【分析】(1)两图像的交点就是求联立的方程组的解;(2)斜三角形△AOB的面积可转化为两水平(或竖直)三角形(有一条边为水平边或竖直边的三角形称为水平或竖直三角形)的面积和或差;(3)利用n个数的平方和公式和等差数列的和公式可求出.3.如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y= 相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.(1)求双曲线和抛物线的解析式;(2)计算△ABC的面积;(3)如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.【答案】(1)解:把点A的坐标代入双曲线的解析式得:k=﹣1×4=﹣4.所以双曲线的解析式为y=﹣.设点B的坐标为(m,﹣m).∵点B在双曲线上,∴﹣m2=﹣4,解得m=2或m=﹣2.∵点B在第四象限,∴m=2.∴B(2,﹣2).将点A、B、C的坐标代入得:,解得:.∴抛物线的解析式为y=x2﹣3x.(2)解:如图1,连接AC、BC.令y=0,则x2﹣3x=0,∴x=0或x=3,∴C(3,0),∵A(﹣1,4),B(2,﹣2),∴直线AB的解析式为y=﹣2x+2,∵点D是直线AB与x轴的交点,∴D(1,0),∴S△ABC=S△ADC+S△BDC= ×2×4+ ×2×2=6;(3)解:存在,理由:如图2,由原抛物线的解析式为y=x2﹣3x=(x﹣)2﹣,∴原抛物线的顶点坐标为(,﹣),∴抛物线向左平移个单位,再向上平移个单位,而平移前A(﹣1,4),B(2,﹣2),∴平移后点A(﹣,),B(,),∴点A关于y轴的对称点A'(,),连接A'B并延长交y轴于点P,连接AP,由对称性知,∠APE=∠BPE,∴△APB的内切圆的圆心在y轴上,∵B(,),A'(,),∴直线A'B的解析式为y=3x﹣,∴P(0,﹣).【解析】【分析】(1)首先将点A的坐标代入反比例函数的解析式求得k的值,然后再求得B的值,最后根据点A的坐标求出双曲线的解析式,进而得出点B的坐标,最后,将点A、B、O三点的坐标代入抛物线的解析式,求得a、b、c的值即可;(2)由点A和点B的坐标可求得直线AB的解析式,然后将y=0可求得点D的横坐标,最后用三角形的面积和求解即可;(3)先确定出平移后点A,B的坐标,进而求出点A关于y轴的对称点的坐标,求出直线BA'的解析式即可得出点P的坐标.4.如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=.(1)求该反比例函数和一次函数的解析式;(2)求△AOC的面积;(3)直接写出一次函数值大于反比例函数值时自变量x的取值范围.【答案】(1)解:作AD⊥x轴于D,如图,在Rt△OAD中,∵sin∠AOD= = ,∴AD= OA=4,∴OD= =3,∴A(﹣3,4),把A(﹣3,4)代入y= 得m=﹣4×3=﹣12,所以反比例函数解析式为y=﹣;把B(6,n)代入y=﹣得6n=﹣12,解得n=﹣2,把A(﹣3,4)、B(6,﹣2)分别代入y=kx+b得,解得,所以一次函数解析式为y=﹣x+2(2)解:当y=0时,﹣x+2=0,解得x=3,则C(3,0),所以S△AOC= ×4×3=6(3)解:当x<﹣3或0<x<6时,一次函数的值大于反比例函数的值【解析】【分析】(1)作AD⊥x轴于D,如图,先利用解直角三角形确定A(﹣3,4),再把A点坐标代入y= 可求得m=﹣12,则可得到反比例函数解析式;接着把B(6,n)代入反比例函数解析式求出n,然后把A和B点坐标分别代入y=kx+b得到关于a、b的方程组,再解方程组求出a和b的值,从而可确定一次函数解析式;(2)先确定C点坐标,然后根据三角形面积公式求解;(3)观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.5.如图,正方形AOCB的边长为4,反比例函数y= (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE.(1)求k的值;(2)反比例函数图象与线段BC交于点D,直线y= x+b过点D与线段AB交于点F,延长OF交反比例函数y= (x<0)的图象于点N,求N点坐标.【答案】(1)解:∵S△AOE=3S△OBE,∴AE=3BE,∴AE=3,∴E(﹣3,4)反比例函数y= (k≠0,且k为常数)的图象过点E,∴4= ,即k=﹣12(2)解:∵正方形AOCB的边长为4,∴点D的横坐标为﹣4,点F的纵坐标为4.∵点D在反比例函数的图象上,∴点D的纵坐标为3,即D(﹣4,3).∵点D在直线y= x+b上,∴3= ×(﹣4)+b,解得b=5.∴直线DF为y= x+5,将y=4代入y= x+5,得4= x+5,解得x=﹣2.∴点F的坐标为(﹣2,4),设直线OF的解析式为y=mx,代入F的坐标得,4=﹣2m,解得m=﹣2,∴直线OF的解析式为y=﹣2x,解,得.∴N(﹣,2 )【解析】【分析】(1)根据题意求得E的坐标,把点E(﹣3,4)代入利用待定系数法即可求出k的值;(2)由正方形AOCB的边长为4,故可知点D的横坐标为﹣4,点F的纵坐标为4.由于点D在反比例函数的图象上,所以点D的纵坐标为3,即D(﹣4,3),由点D在直线y= x+b上可得出b的值,进而得出该直线的解析式,再把y=4代入直线的解析式即可求出点F的坐标,然后根据待定系数法求得直线OF的解析式,然后联立方程解方程组即可求得.6.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= (m≠0)交于点A(2,﹣3)和点B(n,2).(1)求直线与双曲线的表达式;(2)对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.【答案】(1)解:∵双曲线y= (m≠0)经过点A(2,﹣3),∴m=﹣6.∴双曲线的表达式为y=﹣.∵点B(n,2)在双曲线y=﹣上,∴点B的坐标为(﹣3,2).∵直线y=kx+b经过点A(2,﹣3)和点B(﹣3,2),∴解得,∴直线的表达式为y=﹣x﹣1(2)解:符合条件的点P的坐标是(1,﹣6)或(6,﹣1).【解析】【分析】(1)把A的坐标代入可求出m,即可求出反比例函数解析式,把B点的坐标代入反比例函数解析式,即可求出n,把A,B的坐标代入一次函数解析式即可求出一次函数解析式;(2)根据图象和函数解析式得出即可.7.如图,在菱形ABCD中,, ,点E是边BC的中点,连接DE,AE.(1)求DE的长;(2)点F为边CD上的一点,连接AF,交DE于点G,连接EF,若 ,①求证:△△;②求DF的长.【答案】(1)解:连结BD(2)解:①②【解析】【分析】(1)连结BD ,根据菱形的性质及等边三角形的判定方法首先判定出△CDB是等边三角形,根据等边三角形的性质得出DE⊥BC,CE=2,然后利用勾股定理算出DE的长;(2)①首先判断出△AGD∽△EGF,根据相似三角形对应边成比例得出,又∠AGE=∠DGF,故△AGE∽△DGF;②根据相似三角形的性质及含30°直角三角形的边之间的关系及勾股定理得出EF的长,然后过点E作EH⊥DC于点H,在Rt△ECH中,利用勾股定理算出FH的长,从而根据线段的和差即可算出答案.8.如图,二次函数(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.(1)用含m的代数式表示a;(2)求证:为定值;(3)设该二次函数图象的顶点为F.探索:在x轴的负半轴上是否存在点G,连接CF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.【答案】(1)解:将C(0,-3)代入函数表达式得,,∴(2)证明:如答图1,过点D、E分别作x轴的垂线,垂足为M、N.由解得x1=-m,x2=3m.∴A(-m,0),B(3m,0).∵CD∥AB,∴点D的坐标为(2m,-3).∵AB平分∠DAE.∴∠DAM=∠EAN.∵∠DMA=∠ENA=900,∴△ADM∽△AEN, ∴ .设点E的坐标为(x, ),∴ ,∴x=4m.∴为定值.(3)解:存在,如答图2,连接FC并延长,与x轴负半轴的交点即为所求点G.由题意得:二次函数图像顶点F的坐标为(m,-4),过点F作FH⊥x轴于点H,在Rt△CGO和Rt△FGH中,∵tan∠CGO= , tan∠FGH= , ∴ = .∴OG="3m,"由勾股定理得,GF= ,AD=∴ .由(2)得,,∴AD∶GF∶AE=3∶4∶5.∴以线段GF、AD、AE的长度为三边长的三角形是直角三角形,此时点G的横坐标为-3m.【解析】【分析】1)将C点代入函数解析式即可求得.(2)令y=0求A、B的坐标,再根据,CD∥AB,求点D的坐标,由△ADM∽△AEN,对应边成比例,将求的比转化成求比,结果不含m即为定值.(3)连接FC并延长,与x轴负半轴的交点即为所求点G..过点F作FH⊥x轴于点H,在Rt△CGO和Rt△FGH中根据同角的同一个三角函数相等,可求OG(用m表示),然后利用勾股定理求GF和AD(用m表示),并求其比值,由(2)是定值,所以可得AD∶GF∶AE=3∶4∶5,由此可根据勾股定理逆定理判断以线段GF、AD、AE的长度为三边长的三角形是直角三角形,直接得点G的横坐标.9.【问题】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D 在直线l上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.(1)【探究发现】如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点D 移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;(2)【数学思考】如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程;(3)【拓展引申】如图4,在(1)的条件下,M是AB边上任意一点(不含端点A、B),N是射线BD上一点,且AM=BN,连接MN与BC交于点Q,这个数学兴趣小组经过多次取M点反复进行实验,发现点M在某一位置时BQ的值最大.若AC=BC=4,请你直接写出BQ的最大值.【答案】(1)解:∵∠ACB=90°,AC=BC∴∠CAB=∠CBA=45°∵CD∥AB∴∠CBA=∠DCB=45°,且BD⊥CD∴∠DCB=∠DBC=45°∴DB=DC即DB=DP(2)解:∵DG⊥CD,∠DCB=45°∴∠DCG=∠DGC=45°∴DC=DG,∠DCP=∠DGB=135°,∵∠BDP=∠CDG=90°∴∠CDP=∠BDG,且DC=DG,∠DCP=∠DGB=135°,∴△CDP≌△GDB(ASA)∴DB=DP(3)解:如图4,过点M作MH⊥MN交AC于点H,连接CM,HQ,∵MH⊥MN,∴∠AMH+∠NMB=90°∵CD∥AB,∠CDB=90°∴∠DBM=90°∴∠NMB+∠MNB=90°∴∠HMA=∠MNB,且AM=BN,∠CAB=∠CBN=45°∴△AMH≌△BNQ(ASA)∴AH=BQ∵∠ACB=90°,AC=BC=4,∴AB=4 ,AC-AH=BC-BQ∴CH=CQ∴∠CHQ=∠CQH=45°=∠CAB∴HQ∥AB∴∠HQM=∠QMB∵∠ACB=∠HMQ=90°∴点H,点M,点Q,点C四点共圆,∴∠HCM=∠HQM∴∠HCM=∠QMB,且∠A=∠CBA=45°∴△ACM∽△BMQ∴∴∴BQ= +2∴AM=2 时,BQ有最大值为2.【解析】【分析】(1)DB=DP,理由如下:根据等腰直角三角形的性质得出∠CAB=∠CBA=45°,根据二直线平行,内错角相等得出∠CBA=∠DCB=45°,根据三角形的内角和得出∠DCB=∠DBC=45°,最后根据等角对等边得出 DB=DC ,即DB=DP;(2)利用ASA判断出△CDP≌△GDB ,再根据全等三角形的对应边相等得出DB=DP;(3)如图4,过点M作MH⊥MN交AC于点H,连接CM,HQ,利用ASA判断出△AMH≌△BNQ 根据全等三角形的对应边相等得出AH=BQ,进而判断出点H,点M,点Q,点C四点共圆,根据圆周角定理得出∠HCM=∠HQM ,然后判断出△ACM∽△BMQ ,根据相似三角形的对应边成比例得出,根据比例式及偶数次幂的非负性即可得出求出答案.10.如图1,平面直角坐标系中,B、C两点的坐标分别为B(0,3)和C(0,﹣),点A在x轴正半轴上,且满足∠BAO=30°.(1)过点C作CE⊥AB于点E,交AO于点F,点G为线段OC上一动点,连接GF,将△OFG沿FG翻折使点O落在平面内的点O′处,连接O′C,求线段OF的长以及线段O′C的最小值;(2)如图2,点D的坐标为D(﹣1,0),将△BDC绕点B顺时针旋转,使得BC⊥AB于点B,将旋转后的△BDC沿直线AB平移,平移中的△BDC记为△B′D′C′,设直线B′C′与x轴交于点M,N为平面内任意一点,当以B′、D′、M、N为顶点的四边形是菱形时,求点M 的坐标.【答案】(1)解:如图1中,∵∠AOB=90°,∠OAB=30°,∴∠CBE=60°,∵CE⊥AB,∴∠CEB=90°,∠BCE=30°,∵C(0,- ),∴OC= ,OF=OC•tan30°= ,CF=2OF=3 ,由翻折可知:FO′=FO= ,∴CO′≥CF-O′F,∴CO′≥ ,∴线段O′C的最小值为(2)解:①如图2中,当B′D′=B′M=BD= 时,可得菱形MND′B′.在Rt△AMB′中,AM=2B′M=2 ,∴OM=AM-OA=2 -3 ,∴M(3 -2 ,0).②如图3中,当B′M是菱形的对角线时,由题意B′M=2OB=6,此时AM=12,OM=12-3,可得M(3 -12,0).③如图4中,当B′D′是菱形的对角线时,由∠D′B′M=∠DBO可得,所以B′M=则在RT△AM B′中,AM=2B′M= ,所以OM=OA-AM=3 - ,所以M(3 - ,0).④如图5中,当MD′是菱形的对角线时,MB′=B′D′= ,可得AM=2 ,OM=OA+AM=3 +2 ,所以M(3 +2 ,0).综上所述,满足条件的点M的坐标为(3 +2 ,0)或(3 -12,0)或(3 -,0)或(3 +2 ,0)【解析】【分析】(1)根据直角三角形的两锐角互余求出∠CBE的度数,由垂直的定义可求出∠BCE的度数,由点C的坐标求出OC的长,再在Rt△OCF中,利用解直角三角形求出OF的长;然后利用折叠的性质,可得到FO′的长,然后根据CO′≥CF-O′F,可求出线段O′C的最小值。
中考数学——反比例函数的综合压轴题专题复习附答案解析

一、反比例函数真题与模拟题分类汇编(难题易错题)1.在平面直角坐标系内,双曲线:y= (x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD.(1)求出双曲线的解析式;(2)连结CD,求四边形OCDB的面积.【答案】(1)解:过点A、C、D作x轴的垂线,垂足分别是M、E、F,∴∠AMO=∠CEO=∠DFB=90°,∵直线OA:y=x和直线AB:y=﹣x+10,∴∠AOB=∠ABO=45°,∴△CEO∽△DEB∴= =3,设D(10﹣m,m),其中m>0,∴C(3m,3m),∵点C、D在双曲线上,∴9m2=m(10﹣m),解得:m=1或m=0(舍去)∴C(3,3),∴k=9,∴双曲线y= (x>0)(2)解:由(1)可知D(9,1),C(3,3),B(10,0),∴OE=3,EF=6,DF=1,BF=1,∴S四边形OCDB=S△OCE+S梯形CDFE+S△DFB= ×3×3+ ×(1+3)×6+ ×1×1=17,∴四边形OCDB的面积是17【解析】【分析】(1)过点A、C、D作x轴的垂线,垂足分别是M、E、F,由直线y=x和y=﹣x+10可知∠AOB=∠ABO=45°,证明△CEO∽△DEB,从而可知 = =3,然后设设D(10﹣m,m),其中m>0,从而可知C的坐标为(3m,3m),利用C、D在反比例函数图象上列出方程即可求出m的值.(2)求分别求出△OCE、△DFB△、梯形CDFE的面积即可求出答案.2.如图.一次函数y=x+b的图象经过点B(﹣1,0),且与反比例函数(k为不等于0的常数)的图象在第一象限交于点A(1,n).求:(1)一次函数和反比例函数的解析式;(2)当1≤x≤6时,反比例函数y的取值范围.【答案】(1)解:把点B(﹣1,0)代入一次函数y=x+b得: 0=﹣1+b,∴b=1,∴一次函数解析式为:y=x+1,∵点A(1,n)在一次函数y=x+b的图象上,∴n=1+1,∴n=2,∴点A的坐标是(1,2).∵反比例函数的图象过点A(1,2).∴k=1×2=2,∴反比例函数关系式是:y=(2)解:反比例函数y= ,当x>0时,y随x的增大而减少,而当x=1时,y=2,当x=6时,y= ,∴当1≤x≤6时,反比例函数y的值:≤y≤2【解析】【分析】(1)根据题意首先把点B(﹣1,0)代入一次函数y=x+b求出一次函数解析式,又点A(1,n)在一次函数y=x+b的图象上,再利用一次函数解析式求出点A的坐标,然后利用代入系数法求出反比例函数解析式,(2)根据反比例函数的性质分别求出当x=1,x=6时的y值,即可得到答案.3.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y= (k>0,x>0)的图象上,点D的坐标为(,2).(1)求k的值;(2)若将菱形ABCD沿x轴正方向平移,当菱形的一个顶点恰好落在函数y= (k>0,x >0)的图象上时,求菱形ABCD平移的距离.【答案】(1)解:作DE⊥BO,DF⊥x轴于点F,∵点D的坐标为(,2),∴DO=AD=3,∴A点坐标为:(,5),∴k=5 ;(2)解:∵将菱形ABCD向右平移,使点D落在反比例函数y= (x>0)的图象上D′,∴DF=D′F′=2,∴D′点的纵坐标为2,设点D′(x,2)∴2= ,解得x= ,∴FF′=OF′﹣OF= ﹣ = ,∴菱形ABCD平移的距离为,同理,将菱形ABCD向右平移,使点B落在反比例函数y= (x>0)的图象上,菱形ABCD平移的距离为,综上,当菱形ABCD平移的距离为或时,菱形的一个顶点恰好落在函数图象上.【解析】【分析】(1)根据菱形的性质和D的坐标即可求出A的坐标,代入求出即可;(2)B和D可能落在反比例函数的图象上,根据平移求出即可.4.已知反比例函数y= 的图象经过点A(﹣,1).(1)试确定此反比例函数的解析式;(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;(3)已知点P(m, m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2 n+9的值.【答案】(1)解:由题意得1= ,解得k=﹣,∴反比例函数的解析式为y=﹣(2)解:过点A作x轴的垂线交x轴于点C.在Rt△AOC中,OC= ,AC=1,∴OA= =2,∠AOC=30°,∵将线段OA绕O点顺时针旋转30°得到线段OB,∴∠AOB=30°,OB=OA=2,∴∠BOC=60°.过点B作x轴的垂线交x轴于点D.在Rt△BOD中,BD=OB•sin∠BOD= ,OD= OB=1,∴B点坐标为(﹣1,),将x=﹣1代入y=﹣中,得y= ,∴点B(﹣1,)在反比例函数y=﹣的图象上(3)解:由y=﹣得xy=﹣,∵点P(m, m+6)在反比例函数y=﹣的图象上,其中m<0,∴m( m+6)=﹣,∴m2+2 m+1=0,∵PQ⊥x轴,∴Q点的坐标为(m,n).∵△OQM的面积是,∴OM•QM= ,∵m<0,∴mn=﹣1,∴m2n2+2 mn2+n2=0,∴n2﹣2 n=﹣1,∴n2﹣2 n+9=8.【解析】【分析】(1)由于反比例函数y= 的图象经过点A(﹣,1),运用待定系数法即可求出此反比例函数的解析式;(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;(3)把点P(m, m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2﹣2 n+9的值.5.已知:如图,正比例函数y=ax的图象与反比例函数y= 的图象交于点C(3,1)(1)试确定上述比例函数和反比例函数的表达式;(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?(3)点D(m,n)是反比例函数图象上的一动点,其中0<m<3,过点C作直线AC⊥x 轴于点A,交OD的延长线于点B;若点D是OB的中点,DE⊥x轴于点E,交OC于点F,试求四边形DFCB的面积.【答案】(1)解:将点C(3,1)分别代入y= 和y=ax,得:k=3,a= ,∴反比例函数解析式为y= ,正比例函数解析式为y= x;(2)解:观察图象可知,在第二象限内,当0<x<3时,反比例函数值大于正比例函数值;(3)解:∵点D(m,n)是OB的中点,又在反比例函数y= 上,∴OE= OA= ,点D(,2),∴点B(3,4),又∵点F在正比例函数y= x图象上,∴F(,),∴DF= 、BC=3、EA= ,∴四边形DFCB的面积为 ×( +3)× = .【解析】【分析】(1)利用待定系数法把C坐标代入解析式即可;(2)须数形结合,先找出交点,在交点的左侧与y轴之间,反比例函数值大于正比例函数值.(3)求出DF、BC、EA,代入梯形面积公式即可.6.已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.(1)k的值是________;(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 = ,则b的值是________.【答案】(1)﹣2(2)3【解析】【解答】解:(1)设点P的坐标为(m,n),则点Q的坐标为(m﹣1,n+2),依题意得:,解得:k=﹣2.故答案为:﹣2.(2)∵BO⊥x轴,CE⊥x轴,∴BO∥CE,∴△AOB∽△AEC.又∵ = ,∴ = = .令一次函数y=﹣2x+b中x=0,则y=b,∴BO=b;令一次函数y=﹣2x+b中y=0,则0=﹣2x+b,解得:x= ,即AO= .∵△AOB∽△AEC,且 = ,∴.∴AE= AO= b,CE= BO= b,OE=AE﹣AO= b.∵OE•CE=|﹣4|=4,即 b2=4,解得:b=3 ,或b=﹣3 (舍去).故答案为:3 .【分析】(1)设出点P的坐标,根据平移的特性写出Q点的坐标,由点P,Q均在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,即可得出关于k,m,n,b的四元次一方程组,两式作差即可求出k的值;(2)由BO⊥x轴,CE⊥x轴,找出△AOB∽△AEC.再由给定图形的面积比即可求出==,根据一次函数的解析式可以用含b的式子表示出OA,OB,由此即可得出线段CE,AE 的长,利用OE=AE﹣AO求出OE的长,再借助反比例函数K的几何意义得出关于b的一元二次方程,解方程即可得出结论。
人教中考数学 反比例函数 培优易错试卷练习(含答案)及答案

一、反比例函数真题与模拟题分类汇编(难题易错题)1.如图,已知A(﹣4,),B(﹣1,2)是一次函数y=kx+b与反比例函数(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?(2)求一次函数解析式及m的值;(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.【答案】(1)解:当﹣4<x<﹣1时,一次函数大于反比例函数的值;(2)把A(﹣4,),B(﹣1,2)代入y=kx+b得,解得,所以一次函数解析式为y= x+ ,把B(﹣1,2)代入y= 得m=﹣1×2=﹣2;(3)解:如下图所示:设P点坐标为(t,t+ ),∵△PCA和△PDB面积相等,∴• •(t+4)= •1•(2﹣t﹣),即得t=﹣,∴P点坐标为(﹣,).【解析】【分析】(1)观察函数图象得到当﹣4<x<﹣1时,一次函数图象都在反比例函数图象上方;(2)先利用待定系数法求一次函数解析式,然后把B点坐标代入y= 可计算出m的值;(3)设P点坐标为(t, t+ ),利用三角形面积公式可得到• •(t+4)= •1•(2﹣ t﹣),解方程得到t=﹣,从而可确定P点坐标.2.已知点A,B分别是x轴、y轴上的动点,点C,D是某个函数图象上的点,当四边形ABCD(A,B,C,D各点依次排列)为正方形时,我们称这个正方形为此函数图象的“伴侣正方形”.例如:在图1中,正方形ABCD是一次函数y=x+1图象的其中一个“伴侣正方形”.(1)如图1,若某函数是一次函数y=x+1,求它的图象的所有“伴侣正方形”的边长;(2)如图2,若某函数是反比例函数(k>0),它的图象的“伴侣正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;(3)如图3,若某函数是二次函数y=ax2+c(a≠0),它的图象的“伴侣正方形”为ABCD,C,D中的一个点坐标为(3,4),请你直接写出该二次函数的解析式.【答案】(1)解:(I)当点A在x轴正半轴、点B在y轴负半轴上时:正方形ABCD的边长为.(II)当点A在x轴负半轴、点B在y轴正半轴上时:设正方形边长为a,易得3a= ,解得a= ,此时正方形的边长为.∴所求“伴侣正方形”的边长为或(2)解:如图,作DE⊥x轴,CF⊥y轴,垂足分别为点E、F,易证△ADE≌△BAO≌△CBF.∵点D的坐标为(2,m),m<2,∴DE=OA=BF=m,∴OB=AE=CF=2﹣m.∴OF=BF+OB=2,∴点C的坐标为(2﹣m,2).∴2m=2(2﹣m),解得m=1.∴反比例函数的解析式为y=(3)解:实际情况是抛物线开口向上的两种情况中,另一个点都在(3,4)的左侧,而开口向下时,另一点都在(3,4)的右侧,与上述解析明显不符合a、当点A在x轴正半轴上,点B在y轴正半轴上,点C坐标为(3,4)时:另外一个顶点为(4,1),对应的函数解析式是y=﹣ x2+ ;b、当点A在x 轴正半轴上,点 B在 y轴正半轴上,点D 坐标为(3,4)时:不存在,c、当点A 在 x 轴正半轴上,点 B在 y轴负半轴上,点C 坐标为(3,4)时:不存在d、当点A在x 轴正半轴上,点B在y轴负半轴上,点D坐标为(3,4)时:另外一个顶点C为(﹣1,3),对应的函数的解析式是y= x2+ ;e、当点A在x轴负半轴上,点B在y轴负半轴上,点C坐标为(3,4)时,另一个顶点D的坐标是(7,﹣3)时,对应的函数解析式是y=﹣ x2+ ;f、当点A在x轴负半轴上,点B在y轴负半轴上,点C坐标为(3,4)时,另一个顶点D 的坐标是(﹣4,7)时,对应的抛物线为y= x2+ ;故二次函数的解析式分别为:y= x2+ 或y=﹣ x2+ 或y=﹣ x2+ 或y= x2+【解析】【分析】(1)先正确地画出图形,再利用正方形的性质确定相关点的坐标从而计算正方形的边长.(2)因为ABCD为正方形,所以可作垂线得到等腰直角三角形,利用点D(2,m)的坐标表示出点C的坐标,可求出m的值,即可得到反比例函数的解析式.(3)由抛物线开口既可能向上,也可能向下.当抛物线开口向上时,正方形的另一个顶点也是在抛物线上,这个点既可能在点(3,4)的左边,也可能在点(3,4)的右边,过点(3,4)向x轴作垂线,利用全等三角形确定线段的长即可确定抛物线上另一个点的坐标;当抛物线开口向下时也是一样地分为两种情况来讨论,即可得到所求的结论.3.如图,点P( +1,﹣1)在双曲线y= (x>0)上.(1)求k的值;(2)若正方形ABCD的顶点C,D在双曲线y= (x>0)上,顶点A,B分别在x轴和y 轴的正半轴上,求点C的坐标.【答案】(1)解:点P(,)在双曲线上,将x= ,y= 代入解析式可得:k=2;(2)解:过点D作DE⊥OA于点E,过点C作CF⊥OB于点F,∵四边形ABCD是正方形,∴AB=AD=BC,∠CBA=90°,∴∠FBC+∠OBA=90°,∵∠CFB=∠BOA=90°,∴∠FCB+∠FBC=90°,∴∠FBC=∠OAB,在△CFB和△AOB中,,∴△CFB≌△AOB(AAS),同理可得:△BOA≌△AED≌△CFB,∴CF=OB=AE=b,BF=OA=DE=a,设A(a,0),B(0,b),则D(a+b,a)C(b,a+b),可得:b(a+b)=2,a(a+b)=2,解得:a=b=1.所以点C的坐标为:(1,2).【解析】【分析】(1)由待定系数法把P坐标代入解析式即可;(2)C、D均在双曲线上,它们的坐标就适合解析式,设出C坐标,再由正方形的性质可得△CFB≌△AOB△BOA≌△AED≌△CFB,代入解析式得b(a+b)=2,a(a+b)=2,即可求出C坐标.4.如图,已知直线y= x与双曲线y=交于A、B两点,且点A的横坐标为 .(1)求k的值;(2)若双曲线y=上点C的纵坐标为3,求△AOC的面积;(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.【答案】(1)解:把x= 代入,得y= ,∴A(,1),把点代入,解得:;(2)解:∵把y=3代入函数,得x= ,∴C ,设过,两点的直线方程为:,把点,,代入得:,解得:,∴,设与轴交点为,则点坐标为,∴;(3)解:设点坐标,由直线解析式可知,直线与轴正半轴夹角为,∵以、、、为顶点的四边形是有一组对角为的菱形,在直线上,∴点只能在轴上,∴点的横坐标为,代入,解得纵坐标为:,根据,即得:,解得: .故点坐标为:或 .【解析】【分析】(1)先求的A点纵坐标,然后用待定系数法求解即可;(2)先求出C 点坐标,再用待定系数法求的直线AC的解析式,然后求得直线AC与x的交点坐标,再根据求解即可;(3)设点坐标,根据题意用关于a的式子表示出N的坐标,再根据菱形的性质得,求出a的值即可.5.在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(,),…,都是梦之点,显然梦之点有无数个.(1)若点P(2,b)是反比例函数 (n为常数,n≠0)的图象上的梦之点,求这个反比例函数解析式;(2)⊙O的半径是,①求出⊙O上的所有梦之点的坐标;②已知点M(m,3),点Q是(1)中反比例函数图象上异于点P的梦之点,过点Q的直线l与y轴交于点A,∠OAQ=45°.若在⊙O上存在一点N,使得直线MN∥l或MN⊥l,求出m的取值范围.【答案】(1)解:∵P(2,b)是梦之点,∴b=2∴P(2,2)将P(2,2)代入中得n=4∴反比例函数解析式是(2)解:①设⊙O上梦之点坐标是(,)∴∴=1或 =-1∴⊙O上所有梦之点坐标是(1,1)或(-1,-1)②由(1)知,异于点P的梦之点Q的坐标为(-2,-2)由已知MN∥l或MN⊥l∴直线MN为y=-x+b或y=x+b当MN为y=-x+b时,m=b-3由图可知,当直线MN平移至与⊙O相切时,且切点在第四象限时,b取得最小值,此时MN记为,其中为切点,为直线与y轴的交点∵△O 为等要直角三角形,∴O =∴O =2∴b的最小值是-2,∴m的最小值是-5当直线MN平移至与⊙O相切时,且切点在第二象限时,b取得最大值,此时MN记为,其中为切点,为直线与y轴的交点。
中考数学压轴题之反比例函数(中考题型整理,突破提升)及详细答案

则
,
解得
.
故直线 AP 的函数关系式为 y=x+3,
则点 C 的坐标(0,3),OC=3,
∴ S△ AOP=S△ AOC+S△ POC
= OC•AR+ OC•PS
又∵ 点 F 在反比例函数
(k>0)的图象上,∴ k=12,
∴ 该函数的解析式为 y= (x>0)
(2)解:由题意知 E,F 两点坐标分别为 E( ,4),F(6,
∴ 当 k=12 时,S 有最大值.S 最大=3
【解析】【分析】)当 F 为 AB 的中点时,点 F 的坐标为(3,1),由此代入求得函数解
C 与 D 横纵坐标乘积相等,求出 b 的值确定出 B 坐标,进而求出 k 的值,确定出双曲线解 析式;(3)抓住两个关键点,将 A 坐标代入双曲线解析式求出 b 的值;将 C 坐标代入双 曲线解析式求出 b 的值,即可确定出平行四边形与双曲线总有公共点时 b 的范围.
5.如图,正比例函数和反比例函数的图象都经过点 A(3,3),把直线 OA 向下平移后, 与反比例函数的图象交于点 B(6,m),与 x 轴、y 轴分别交于 C、D 两点.
(1)求 m 的值; (2)求过 A、B、D 三点的抛物线的解析式; (3)若点 E 是抛物线上的一个动点,是否存在点 E,使四边形 OECD 的面积 S1
, 是四边
形 OACD 面积 S 的 ?若存在,求点 E 的坐标;若不存在,请说明理由. 【答案】(1)解:∵ 反比例函数的图象都经过点 A(3,3),
(易错题精选)初中数学反比例函数易错题汇编及答案解析

1.使关于 x 的分式方程 =2 的解为非负数,且使反比例函数 y= 限时满足条件的所有整数 k 的和为( ). A.0 B.1 C.2 D.3 【答案】B 【解析】
图象过第一、三象
试题分析:分别根据题意确定 k 的值,然后相加即可.∵关于 x 的分式方程 =2 的解为
y1 )
、
B(1,
y2
)
、
C(2,
y3 )
三个点,
1 y1 k , 1 y2 k , 2 y3 k ,
y1
k
,
y2
k
,
y3
1k 2
,
而k 0,
y1 y3 y2 . 故选: B . 【点睛】
本题考查了反比例函数图象上点的坐标特征:反比例函数 y k ( k 为常数,且 k 0 ) x
∴反比例函数 y= a b 的图象过一、三象限, x
所以此选项正确; D. 由一次函数图象过二、四象限,得 a<0,交 y 轴负半轴,则 b<0, 满足 ab>0,与已知相矛盾 所以此选项不正确; 故选 C. 【点睛】 此题考查反比例函数的图象,一次函数的图象,解题关键在于确定 a、b 的大小
9.如图,点 P 是反比例函数 y k (x0)图象上一点,过 P 向 x 轴作垂线,垂足为 M,连 x
x
A. 3,1
B. 1, 3
C. 1,3
D. 3,1
【答案】A 【解析】 【分析】
先求出 k=-3,再依次判断各点的横纵坐标乘积,等于-3 即是在该双曲线上,否则不在. 【详解】
∵点 M 1,3 在双曲线 y k 上,
x ∴ k 13 3 ,
初三数学反比例函数的专项培优 易错 难题练习题(含答案)及详细答案

初三数学反比例函数的专项培优易错难题练习题(含答案)及详细答案一、反比例函数1.如图.一次函数y=x+b的图象经过点B(﹣1,0),且与反比例函数(k为不等于0的常数)的图象在第一象限交于点A(1,n).求:(1)一次函数和反比例函数的解析式;(2)当1≤x≤6时,反比例函数y的取值范围.【答案】(1)解:把点B(﹣1,0)代入一次函数y=x+b得: 0=﹣1+b,∴b=1,∴一次函数解析式为:y=x+1,∵点A(1,n)在一次函数y=x+b的图象上,∴n=1+1,∴n=2,∴点A的坐标是(1,2).∵反比例函数的图象过点A(1,2).∴k=1×2=2,∴反比例函数关系式是:y=(2)解:反比例函数y= ,当x>0时,y随x的增大而减少,而当x=1时,y=2,当x=6时,y= ,∴当1≤x≤6时,反比例函数y的值:≤y≤2【解析】【分析】(1)根据题意首先把点B(﹣1,0)代入一次函数y=x+b求出一次函数解析式,又点A(1,n)在一次函数y=x+b的图象上,再利用一次函数解析式求出点A的坐标,然后利用代入系数法求出反比例函数解析式,(2)根据反比例函数的性质分别求出当x=1,x=6时的y值,即可得到答案.2.如图,在平面直角坐标系中,反比例函数y= 的图象与一次函数y=ax+b的图象交于点A(﹣2,3)和点B(m,﹣2).(1)求反比例函数和一次函数的解析式;(2)直线x=1上有一点P,反比例函数图象上有一点Q,若以A、B、P、Q为顶点的四边形是以AB为边的平行四边形,直接写出点Q的坐标.【答案】(1)解:∵点A(﹣2,3)在反比例函数y= 的图形上,∴k=﹣2×3=﹣6,∴反比例函数的解析式为y=﹣,∵点B在反比例函数y=﹣的图形上,∴﹣2m=﹣6,∴m=3,∴B(3,﹣2),∵点A,B在直线y=ax+b的图象上,∴,∴,∴一次函数的解析式为y=﹣x+1(2)解:∵以A、B、P、Q为顶点的四边形是以AB为边的平行四边形,∴AB=PQ,AB∥PQ,设直线PQ的解析式为y=﹣x+c,设点Q(n,﹣),∴﹣ =﹣n+c,∴c=n﹣,∴直线PQ的解析式为y=﹣x+n﹣,∴P(1,n﹣﹣1),∴PQ2=(n﹣1)2+(n﹣﹣1+ )2=2(n﹣1)2,∵A(﹣2,3).B(3,﹣2),∴AB2=50,∵AB=PQ,∴50=2(n﹣1)2,∴n=﹣4或6,∴Q(﹣4. )或(6,﹣1)【解析】【分析】(1)先利用待定系数法求出反比例函数解析式,进而求出点B的坐标,再用待定系数法求出直线解析式;(2)先判断出AB=PQ,AB∥PQ,设出点Q的坐标,进而得出点P的坐标,即可求出PQ,最后用PQ=AB建立方程即可得出结论.3.如图,已知点D在反比例函数y= 的图象上,过点D作x轴的平行线交y轴于点B (0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= .(1)求反比例函数y= 和直线y=kx+b的解析式;(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.【答案】(1)解:∵A(5,0),∴OA=5.∵,∴,解得OC=2,∴C(0,﹣2),∴BD=OC=2,∵B(0,3),BD∥x轴,∴D(﹣2,3),∴m=﹣2×3=﹣6,∴,设直线AC关系式为y=kx+b,∵过A(5,0),C(0,﹣2),∴,解得,∴;(2)解:∵B(0,3),C(0,﹣2),∴BC=5=OA,在△OAC和△BCD中∴△OAC≌△BCD(SAS),∴AC=CD,∴∠OAC=∠BCD,∴∠BCD+∠BCA=∠OAC+∠BCA=90°,∴AC⊥CD;(3)解:∠BMC=45°.如图,连接AD,∵AE=OC,BD=OC,AE=BD,∴BD∥x轴,∴四边形AEBD为平行四边形,∴AD∥BM,∴∠BMC=∠DAC,∵△OAC≌△BCD,∴AC=CD,∵AC⊥CD,∴△ACD为等腰直角三角形,∴∠BMC=∠DAC=45°.【解析】【分析】(1)由正切定义可求C坐标,进而由BD=OC求出D坐标,求出反比例函数解析式;由A、C求出直线解析式;(2)由条件可判定△OAC≌△BCD,得出AC=CD,∠OAC=∠BCD,进而AC⊥CD;(3)由已知可得AE=OC,BD=OC,得出AE=BD,再加平行得四边形AEBD为平行四边形,推出△OAC≌△BCD,∴AC=CD,∵AC⊥CD,∴△ACD为等腰直角三角形,∴∠BMC=∠DAC=45°.4.如图,已知A是双曲线y= (k>0)在第一象限内的一点,O为坐标原点,直线OA交双曲线于另一点C,当OA在第一象限的角平分线上时,将OA向上平移个单位后,与双曲线在第一象限交于点M,交y轴于点N,若 =2,(1)求直线MN的解析式;(2)求k的值.【答案】(1)解:∵OA在第一象限的角平分线上,∴直线OA的解析式为y=x,∴将OA向上平移个单位后,N(0,),可设直线MN的解析式为y=x+b,把N(0,)代入,可得b= ,∴直线MN的解析式为y=x+(2)解:如图所示,过A作AB⊥y轴于B,过M作MD⊥y轴于D,则∠MDN=∠ABO=90°,由平移可得,∠MND=∠AOB=45°,∴△MDN∽△ABO,∴ = =2,设A(a,a),则AB=a,∴MD= a=DN,∴DO= a+ ,∴M( a, a+ ),∵双曲线经过点A,M,∴k=a×a= a×( a+ ),解得a=1,∴k=1.【解析】【分析】(1)第一三象限角平分线为y=x,向上平移为y=x+b,可求出N点坐标,代入y=x+b,即可求出;(2)通过作垂线构造相似三角形,即△MDN∽△ABO,把A、M坐标代入解析式即可求出a,进而求出k.5.如图,四边形ABCD的四个顶点分别在反比例函数与(x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.(1)当m=4,n=20时.①若点P的纵坐标为2,求直线AB的函数表达式.②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.【答案】(1)①当x=4时,∴点B的坐标是(4,1)当y=2时,由得得x=2∴点A的坐标是(2,2)设直线AB的函数表达式为∴解得∴直线AB的函数表达式为②四边形ABCD为菱形,理由如下:如图,由①得点B(4,1),点D(4,5)∵点P为线段BD的中点∴点P的坐标为(4,3)当y=3时,由得,由得,∴PA= ,PC=∴PA=PC而PB=PD∴四边形ABCD为平行四边形又∵BD⊥AC∴四边形ABCD是菱形(2)四边形ABCD能成为正方形当四边形ABCD时正方形时,PA=PB=PC=PD(设为t,t≠0),当x=4时,∴点B的坐标是(4,)则点A的坐标是(4-t,)∴,化简得t=∴点D的纵坐标为则点D的坐标为(4,)所以,整理得m+n=32【解析】【分析】(1)①分别求出点A,B的坐标,运用待定系数法即可求出直线AB的表达示;②由特殊的四边形可知,对角线互相垂直的是菱形和正方形,则可猜测这个四边形是菱形或是正方形,先证明其为菱形先,则需要证明四边形ABCD是平行四边形,运用“对角线互相平分的四边形是平行四边形”的判定定理证明会更好些;再判断对角线是否相等,若不相等则不是正方形;(2)要使m,n有具体联系,根据A,B,C,D分别在两个函数图象,且由正方形的性质,可用只含m的代数式表示出点D或点C的坐标代入y= ,即可得到只关于m和n的等式.6.阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。
南京精选中考数学易错题专题复习反比例函数
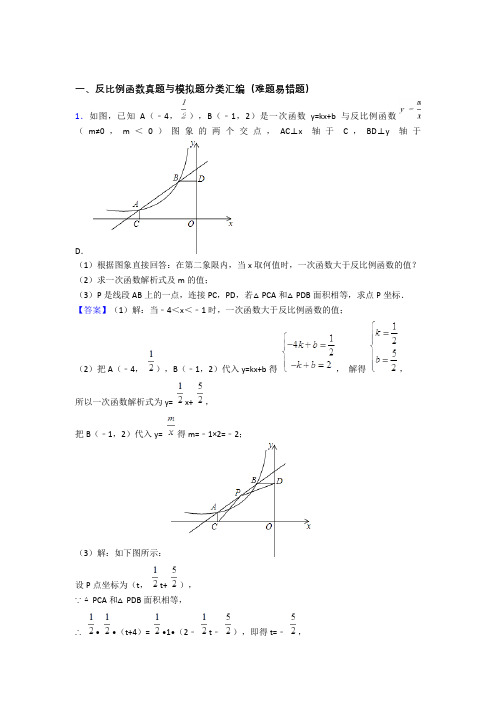
一、反比例函数真题与模拟题分类汇编(难题易错题)1.如图,已知A(﹣4,),B(﹣1,2)是一次函数y=kx+b与反比例函数(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?(2)求一次函数解析式及m的值;(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.【答案】(1)解:当﹣4<x<﹣1时,一次函数大于反比例函数的值;(2)把A(﹣4,),B(﹣1,2)代入y=kx+b得,解得,所以一次函数解析式为y= x+ ,把B(﹣1,2)代入y= 得m=﹣1×2=﹣2;(3)解:如下图所示:设P点坐标为(t,t+ ),∵△PCA和△PDB面积相等,∴• •(t+4)= •1•(2﹣t﹣),即得t=﹣,∴P点坐标为(﹣,).【解析】【分析】(1)观察函数图象得到当﹣4<x<﹣1时,一次函数图象都在反比例函数图象上方;(2)先利用待定系数法求一次函数解析式,然后把B点坐标代入y= 可计算出m的值;(3)设P点坐标为(t, t+ ),利用三角形面积公式可得到• •(t+4)= •1•(2﹣ t﹣),解方程得到t=﹣,从而可确定P点坐标.2.已知反比例函数y= 的图象经过点A(﹣,1).(1)试确定此反比例函数的解析式;(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;(3)已知点P(m, m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2 n+9的值.【答案】(1)解:由题意得1= ,解得k=﹣,∴反比例函数的解析式为y=﹣(2)解:过点A作x轴的垂线交x轴于点C.在Rt△AOC中,OC= ,AC=1,∴OA= =2,∠AOC=30°,∵将线段OA绕O点顺时针旋转30°得到线段OB,∴∠AOB=30°,OB=OA=2,∴∠BOC=60°.过点B作x轴的垂线交x轴于点D.在Rt△BOD中,BD=OB•sin∠BOD= ,OD= OB=1,∴B点坐标为(﹣1,),将x=﹣1代入y=﹣中,得y= ,∴点B(﹣1,)在反比例函数y=﹣的图象上(3)解:由y=﹣得xy=﹣,∵点P(m, m+6)在反比例函数y=﹣的图象上,其中m<0,∴m( m+6)=﹣,∴m2+2 m+1=0,∵PQ⊥x轴,∴Q点的坐标为(m,n).∵△OQM的面积是,∴OM•Q M= ,∵m<0,∴mn=﹣1,∴m2n2+2 mn2+n2=0,∴n2﹣2 n=﹣1,∴n2﹣2 n+9=8.【解析】【分析】(1)由于反比例函数y= 的图象经过点A(﹣,1),运用待定系数法即可求出此反比例函数的解析式;(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;(3)把点P(m, m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2﹣2 n+9的值.3.如图,已知直线y=ax+b与双曲线y= (x>0)交于A(x1, y1),B(x2, y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).【答案】(1)解:∵直线y=ax+b与双曲线y= (x>0)交于A(1,3),∴k=1×3=3,∴y= ,∵B(3,y2)在反比例函数的图象上,∴y2= =1,∴B(3,1),∵直线y=ax+b经过A、B两点,∴解得,∴直线为y=﹣x+4,令y=0,则x=4,∴P(4,O)(2)解:如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG 交于H,则AD∥BG∥x轴,AE∥BF∥y轴,∴= ,= = ,∵b=y1+1,AB=BP,∴= ,= = ,∴B(,y1)∵A,B两点都是反比例函数图象上的点,∴x1•y1= • y1,解得x1=2,代入= ,解得y1=2,∴A(2,2),B(4,1)(3)解:根据(1),(2)中的结果,猜想:x1, x2, x0之间的关系为x1+x2=x0【解析】【分析】(1)先把A(1,3)),B(3,y2)代入y= 求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出 = , = = ,根据题意得出 = , = = ,从而求得B(, y1),然后根据k=xy得出x1•y1= • y1,求得x1=2,代入 = ,解得y1=2,即可求得A、B的坐标;(3)合(1),(2)中的结果,猜想x1+x2=x0.4.如图,点P( +1,﹣1)在双曲线y= (x>0)上.(1)求k的值;(2)若正方形ABCD的顶点C,D在双曲线y= (x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.【答案】(1)解:点P(,)在双曲线上,将x= ,y= 代入解析式可得:k=2;(2)解:过点D作DE⊥OA于点E,过点C作CF⊥OB于点F,∵四边形ABCD是正方形,∴AB=AD=BC,∠CBA=90°,∴∠FBC+∠OBA=90°,∵∠CFB=∠BOA=90°,∴∠FCB+∠FBC=90°,∴∠FBC=∠OAB,在△CFB和△AOB中,,∴△CFB≌△AOB(AAS),同理可得:△BOA≌△AED≌△CFB,∴CF=OB=AE=b,BF=OA=DE=a,设A(a,0),B(0,b),则D(a+b,a)C(b,a+b),可得:b(a+b)=2,a(a+b)=2,解得:a=b=1.所以点C的坐标为:(1,2).【解析】【分析】(1)由待定系数法把P坐标代入解析式即可;(2)C、D均在双曲线上,它们的坐标就适合解析式,设出C坐标,再由正方形的性质可得△CFB≌△AOB△BOA≌△AED≌△CFB,代入解析式得b(a+b)=2,a(a+b)=2,即可求出C坐标.5.如图,已知函数的图象与一次函数的图象相交不同的点A、B,过点A作AD⊥轴于点D,连接AO,其中点A的横坐标为,△AOD的面积为2.(1)求的值及 =4时的值;(2)记表示为不超过的最大整数,例如:,,设 ,若,求值【答案】(1)解:设A(x0, y0),则OD=x0, AD=y0,∴S△AOD= OD•AD= x0y0=2,∴k=x0y0=4;当x0=4时,y0=1,∴A(4,1),代入y=mx+5中得4m+5=1,m=-1(2)解:∵,∴=mx+5,整理得,mx2+5x-4=0,∵A的横坐标为x0,∴mx02+5x0=4,当y=0时,mx+5=0,x=- ,∵OC=- ,OD=x0,∴m2•t=m2•(OD•DC),=m2•x0(- -x0),=m(-5x0-mx02),=-4m,∵- <m<- ,∴5<-4m<6,∴[m2•t]=5【解析】【分析】(1)根据反比例函数比例系数k的几何意义,即可得出k的值;根据反比例函数图像上的点的坐标特点,即可求出A点的坐标,再将A点的坐标代入直线y=mx+5中即可求出m的值;(2)解联立直线与双曲线的解析式所组成的方程组,得出mx2+5x-4=0,将A点的横坐标代入得出mx02+5x0=4,根据直线与x轴交点的坐标特点,表示出OC,OD的长,由m2•t=m2•(OD•DC)=-4m,根据m的取值范围得出5<-4m<6,从而答案。
备战中考数学反比例函数(大题培优 易错 难题)及答案解析

一、反比例函数真题与模拟题分类汇编(难题易错题)1.如图,反比例函数y= 的图象与一次函数y= x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.【答案】(1)解:k=4,S△PAB=15.提示:过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,设AP与y轴交于点C,如图1,把x=4代入y= x,得到点B的坐标为(4,1),把点B(4,1)代入y= ,得k=4.解方程组,得到点A的坐标为(﹣4,﹣1),则点A与点B关于原点对称,∴OA=OB,∴S△AOP=S△BOP,∴S△PAB=2S△AOP.设直线AP的解析式为y=mx+n,把点A(﹣4,﹣1)、P(1,4)代入y=mx+n,求得直线AP的解析式为y=x+3,则点C的坐标(0,3),OC=3,∴S△AOP=S△AOC+S△POC= OC•AR+ OC•PS= ×3×4+ ×3×1= ,∴S△PAB=2S△AOP=15;(2)解:过点P作PH⊥x轴于H,如图2.B(4,1),则反比例函数解析式为y= ,设P(m,),直线PA的方程为y=ax+b,直线PB的方程为y=px+q,联立,解得直线PA的方程为y= x+ ﹣1,联立,解得直线PB的方程为y=﹣ x+ +1,∴M(m﹣4,0),N(m+4,0),∴H(m,0),∴MH=m﹣(m﹣4)=4,NH=m+4﹣m=4,∴MH=NH,∴PH垂直平分MN,∴PM=PN,∴△PMN是等腰三角形;(3)解:∠PAQ=∠PBQ.理由如下:过点Q作QT⊥x轴于T,设AQ交x轴于D,QB的延长线交x轴于E,如图3.可设点Q为(c,),直线AQ的解析式为y=px+q,则有,解得:,∴直线AQ的解析式为y= x+ ﹣1.当y=0时, x+ ﹣1=0,解得:x=c﹣4,∴D(c﹣4,0).同理可得E(c+4,0),∴DT=c﹣(c﹣4)=4,ET=c+4﹣c=4,∴DT=ET,∴QT垂直平分DE,∴QD=QE,∴∠QDE=∠QED.∵∠MDA=∠QDE,∴∠MDA=∠QED.∵PM=PN,∴∠PMN=∠PNM.∵∠PAQ=∠PMN﹣∠MDA,∠PBQ=∠NBE=∠PNM﹣∠QED,∴∠PAQ=∠PBQ.【解析】【分析】(1)过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,设AP 与y轴交于点C,如图1,可根据条件先求出点B的坐标,然后把点B的坐标代入反比例函数的解析式,即可求出k,然后求出直线AB与反比例函数的交点A的坐标,从而得到OA=OB,由此可得S△PAB=2S△AOP,要求△PAB的面积,只需求△PAO的面积,只需用割补法就可解决问题;(2)过点P作PH⊥x轴于H,如图2.可用待定系数法求出直线PB的解析式,从而得到点N的坐标,同理可得到点M的坐标,进而得到MH=NH,根据垂直平分线的性质可得PM=PN,即△PMN是等腰三角形;(3)过点Q作QT⊥x轴于T,设AQ交x轴于D,QB的延长线交x轴于E,如图3.可设点Q为(c,),运用待定系数法求出直线AQ的解析式,即可得到点D的坐标为(c﹣4,0),同理可得E(c+4,0),从而得到DT=ET,根据垂直平分线的性质可得QD=QE,则有∠QDE=∠QED.然后根据对顶角相等及三角形外角的性质,就可得到∠PAQ=∠PBQ.2.如图,已知抛物线y=﹣x2+9的顶点为A,曲线DE是双曲线y= (3≤x≤12)的一部分,记作G1,且D(3,m)、E(12,m﹣3),将抛物线y=﹣x2+9水平向右移动a个单位,得到抛物线G2.(1)求双曲线的解析式;(2)设抛物线y=﹣x2+9与x轴的交点为B、C,且B在C的左侧,则线段BD的长为________;(3)点(6,n)为G1与G2的交点坐标,求a的值.(4)解:在移动过程中,若G1与G2有两个交点,设G2的对称轴分别交线段DE和G1于M、N两点,若MN<,直接写出a的取值范围.【答案】(1)把D(3,m)、E(12,m﹣3)代入y= 得,解得,所以双曲线的解析式为y= ;(2)2(3)解:把(6,n)代入y= 得6n=12,解得n=2,即交点坐标为(6,2),抛物线G2的解析式为y=﹣(x﹣a)2+9,把(6,2)代入y=﹣(x﹣a)2+9得﹣(6﹣a)2+9=2,解得a=6± ,即a的值为6± ;(4)抛物线G2的解析式为y=﹣(x﹣a)2+9,把D(3,4)代入y=﹣(x﹣a)2+9得﹣(3﹣a)2+9=4,解得a=3﹣或a=3+ ;把E(12,1)代入y=﹣(x﹣a)2+9得﹣(12﹣a)2+9=1,解得a=12﹣2 或a=12+2;∵G1与G2有两个交点,∴3+ ≤a≤12﹣2 ,设直线DE的解析式为y=px+q,把D(3,4),E(12,1)代入得,解得,∴直线DE的解析式为y=﹣ x+5,∵G2的对称轴分别交线段DE和G1于M、N两点,∴M(a,﹣ a+5),N(a,),∵MN<,∴﹣ a+5﹣<,整理得a2﹣13a+36>0,即(a﹣4)(a﹣9)>0,∴a<4或a>9,∴a的取值范围为9<a≤12﹣2 .【解析】【解答】解:(2)当y=0时,﹣x2+9=0,解得x1=﹣3,x2=3,则B(﹣3,0),而D(3,4),所以BE= =2 .故答案为2 ;【分析】(1)把D(3,m)、E(12,m﹣3)代入y= 得关于k、m的方程组,然后解方程组求出m、k,即可得到反比例函数解析式和D、E点坐标;(2)先解方程﹣x2+9=0得到B(﹣3,0),而D(3,4),然后利用两点间的距离公式计算DE的长;(3)先利用反比例函数图象上点的坐标特征确定交点坐标为(6,2),然后把(6,2)代入y=﹣(x ﹣a)2+9得a的值;(4)分别把D点和E点坐标代入y=﹣(x﹣a)2+9得a的值,则利用图象和G1与G2有两个交点可得到3+ ≤a≤12﹣2 ,再利用待定系数法求出直线DE的解析式为y=﹣ x+5,则M(a,﹣ a+5),N(a,),于是利用MN<得到﹣ a+5﹣<,然后解此不等式得到a<4或a>9,最后确定满足条件的a的取值范围.3.已知一次函数y=kx+b与反比例函数y= 交于A(﹣1,2),B(2,n),与y轴交于C 点.(1)求反比例函数和一次函数解析式;(2)如图1,若将y=kx+b向下平移,使平移后的直线与y轴交于F点,与双曲线交于D,E两点,若S△ABD=3,求D,E的坐标.(3)如图2,P为直线y=2上的一个动点,过点P作PQ∥y轴交直线AB于Q,交双曲线于R,若QR=2QP,求P点坐标.【答案】(1)解:点A(﹣1,2)在反比例函数y= 的图象上,∴m=(﹣1)×2=﹣2,∴反比例函数的表达式为y=﹣,∵点B(2,n)也在反比例函数的y=﹣图象上,∴n=﹣1,即B(2,﹣1)把点A(﹣1,2),点B(2,﹣1)代入一次函数y=kx+b中,得,解得:k=﹣1,b=1,∴一次函数的表达式为y=﹣x+1,答:反比例函数的表达式是y=﹣,一次函数的表达式是y=﹣x+1;(2)解:如图1,连接AF,BF,∵DE∥AB,∴S△ABF=S△ABD=3(同底等高的两三角形面积相等),∵直线AB的解析式为y=﹣x+1,∴C(0,1),设点F(0,m),∴AF=1﹣m,∴S△ABF=S△ACF+S△BCF= CF×|x A|+ CF×|x B|= (1﹣m)×(1+2)=3,∴m=﹣1,∴F(0,﹣1),∵直线DE的解析式为y=﹣x+1,且DE∥AB,∴直线DE的解析式为y=﹣x﹣1①.∵反比例函数的表达式为y=﹣②,联立①②解得,或∴D(﹣2,1),E(1,﹣2);(3)解:如图2由(1)知,直线AB的解析式为y=﹣x﹣1,双曲线的解析式为y=﹣,设点P(p,2),∴Q(p,﹣p﹣1),R(p,﹣),PQ=|2+p+1|,QR=|﹣p﹣1+ |,∵QR=2QP,∴|﹣p﹣1+ |=2|2+p+1|,解得,p= 或p= ,∴P(,2)或(,2)或(,2)或(,2).【解析】【分析】(1)把A的坐标代入反比例函数的解析式可求得m的值,从而可得到反比例函数的解析式;把点A和点B的坐标代入一次函数的解析式可求得一次函数的解析式;(2)依据同底等高的两个三角形的面积相等可得到S△ABF=S△ABD=3,再利用三角形的面积公式可求得点F的坐标,即可得出直线DE的解析式,即可求出交点坐标;(3)设点P(p,2),则Q(p,﹣p﹣1),R(p,﹣),然后可表示出PQ与QR的长度,最后依据QR=2QP,可得到关于p的方程,从而可求得p的值,从而可得到点P的坐标.4.如图,Rt△ABO的顶点A是双曲线y= 与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= .(1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.【答案】(1)解:设A点坐标为(x,y),且x<0,y>0,则S△ABO= •|BO|•|BA|= •(﹣x)•y= ,∴xy=﹣3,又∵y= ,即xy=k,∴k=﹣3.∴所求的两个函数的解析式分别为y=﹣,y=﹣x+2;(2)解:由y=﹣x+2,令x=0,得y=2.∴直线y=﹣x+2与y轴的交点D的坐标为(0,2),A、C两点坐标满足∴交点A为(﹣1,3),C为(3,﹣1),∴S△AOC=S△ODA+S△ODC= OD•(|x1|+|x2|)= ×2×(3+1)=4.【解析】【分析】两解析式的k一样,根据面积计算双曲线中的k较易,由公式=2S△ABO,可求出k;(2)求交点就求两解析式联立的方程组的解,可分割△AOC为S△ODA+S△ODC,即可求出.5.如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=.(1)求该反比例函数和一次函数的解析式;(2)求△AOC的面积;(3)直接写出一次函数值大于反比例函数值时自变量x的取值范围.【答案】(1)解:作AD⊥x轴于D,如图,在Rt△OAD中,∵sin∠AOD= = ,∴AD= OA=4,∴OD= =3,∴A(﹣3,4),把A(﹣3,4)代入y= 得m=﹣4×3=﹣12,所以反比例函数解析式为y=﹣;把B(6,n)代入y=﹣得6n=﹣12,解得n=﹣2,把A(﹣3,4)、B(6,﹣2)分别代入y=kx+b得,解得,所以一次函数解析式为y=﹣x+2(2)解:当y=0时,﹣x+2=0,解得x=3,则C(3,0),所以S△AOC= ×4×3=6(3)解:当x<﹣3或0<x<6时,一次函数的值大于反比例函数的值【解析】【分析】(1)作AD⊥x轴于D,如图,先利用解直角三角形确定A(﹣3,4),再把A点坐标代入y= 可求得m=﹣12,则可得到反比例函数解析式;接着把B(6,n)代入反比例函数解析式求出n,然后把A和B点坐标分别代入y=kx+b得到关于a、b的方程组,再解方程组求出a和b的值,从而可确定一次函数解析式;(2)先确定C点坐标,然后根据三角形面积公式求解;(3)观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.6.如图,已知矩形OABC中,OA=3,AB=4,双曲线y= (k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD(1)求k的值和点E的坐标;(2)点P是线段OC上的一个动点,是否存在点P,使∠APE=90°?若存在,求出此时点P 的坐标,若不存在,请说明理由.【答案】(1)解:∵AB=4,BD=2AD,∴AB=AD+BD=AD+2AD=3AD=4,∴AD= ,又∵OA=3,∴D(,3),∵点D在双曲线y= 上,∴k= ×3=4;∵四边形OABC为矩形,∴AB=OC=4,∴点E的横坐标为4.把x=4代入y= 中,得y=1,∴E(4,1);(2)解:(2)假设存在要求的点P坐标为(m,0),OP=m,CP=4﹣m.∵∠APE=90°,∴∠APO+∠EPC=90°,又∵∠APO+∠OAP=90°,∴∠EPC=∠OAP,又∵∠AOP=∠PCE=90°,∴△AOP∽△PCE,∴,∴,解得:m=1或m=3,∴存在要求的点P,坐标为(1,0)或(3,0).【解析】【分析】(1)由矩形OABC中,AB=4,BD=2AD,可得3AD=4,即可求得AD的长,然后求得点D的坐标,即可求得k的值,继而求得点E的坐标;(2)首先假设存在要求的点P坐标为(m,0),OP=m,CP=4﹣m,由∠APE=90°,易证得△AOP∽△PCE,然后由相似三角形的对应边成比例,求得m的值,继而求得此时点P的坐标.7.【阅读理解】我们知道,当a>0且b>0时,(﹣)2≥0,所以a﹣2 +≥0,从而a+b≥2 (当a=b时取等号),【获得结论】设函数y=x+ (a>0,x>0),由上述结论可知:当x= 即x= 时,函数y有最小值为2(1)【直接应用】若y1=x(x>0)与y2= (x>0),则当x=________时,y1+y2取得最小值为________.(2)【变形应用】若y1=x+1(x>﹣1)与y2=(x+1)2+4(x>﹣1),则的最小值是________(3)【探索应用】在平面直角坐标系中,点A(﹣3,0),点B(0,﹣2),点P是函数y= 在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S①求S与x之间的函数关系式;②求S的最小值,判断取得最小值时的四边形ABCD的形状,并说明理由.【答案】(1)1;2(2)4(3)解:①设P(x,),则C(x,0),D(0,),∴AC=x+3,BD= +2,∴S= AC•BD= (x+3)( +2)=6+x+ ;②∵x>0,∴x+ ≥2 =6,∴当x= 时,即x=3时,x+ 有最小值6,∴此时S=6+x+ 有最小值12,∵x=3,∴P(3,2),C(3,0),D(0,2),∴A、C关于x轴对称,D、B关于y轴对称,即四边形ABCD的对角线互相垂直平分,∴四边形ABCD为菱形.【解析】【解答】解:(1)∵x>0,∴y1+y2=x+ ≥2 =2,∴当x= 时,即x=1时,y1+y2有最小值2,故答案为:1;2;(2)∵x>﹣1,∴x+1>0,∴ = =(x+1)+ ≥2 =4,∴当x+1= 时,即x=1时,有最小值4,故答案为:4;【分析】(1)直接由结论可求得其取得最小值,及其对应的x的值;(2)可把x+1看成一个整体,再利用结论可求得答案;(3)①可设P(x,),则可表示出C、D的坐标,从而可表示出AC和BD,再利用面积公式可表示出四边形ABCD的面积,从而可得到S 与x的函数关系式;②再利用结论可求得其最得最小值时对应的x的值,则可得到P、C、D的坐标,可判断A、C关于x轴对称,B、D关于y轴对称,可判断四边形ABCD为菱形.8.已知二次函数的图象经过三点(1,0),(-3,0),(0,).(1)求该二次函数的解析式;(2)若反比例函数图像与二次函数的图像在第一象限内交于点 , 落在两个相邻的正整数之间,请写出这两个相邻的正整数;(3)若反比例函数的图像与二次函数的图像在第一象限内的交点为A,点A的横坐标为满足,试求实数的取值范围。
反比例函数易错题汇编含答案

故选:B.
【点睛】
本题考查函数的图象性质与中心对称图形的性质,熟练掌握相关知识是解题的关键.
7.下列各点中,在反比例函数 图象上的是()
A.(3,1)B.(-3,1)C.(3, )D.( ,3)
【答案】A
故选A.
8.如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于点A,反比例函数y= (x>0)的图象与线段AB相交于点C,且C是线段AB的中点,若△OAB的面积为3,则k的值为()
A. B.1C.2D.3
【答案】D
【解析】
【分析】
连接OC,如图,利用三角形面积公式得到S△AOC= S△OAB= ,再根据反比例函数系数k的几何意义得到 |k|= ,然后利用反比例函数的性质确定k的值.
【详解】
∵反比例函数y= (k>0)的图象在一、三象限,
∴在每个象限内y随x的增大而减小,
∵A(-3,y1)、B(-1,y2)在第三象限双曲线上,
∴y2<y1<0,
∵C(1,y3)在第一象限双曲线上,
∴y3>0,
∴y3>y1>y2,
故选:B.
【点睛】
此题考查反比例函数的图象和性质,解题关键在于当k>0,时,在每个象限内y随x的增大而减小;当k<0时,y随x的增大而增大,注意“在每个象限内”的意义,这种类型题目用图象法比较直观得出答案.
【答案】D
【解析】
【详解】
∵点(2,-4)在反比例函数y= 的图象上,
∴k=2×(-4)=-8.
∵A中2×4=8;B中-1×(-8)=8;C中-2×(-4)=8;D中4×(-2)=-8,
(易错题精选)初中数学反比例函数易错题汇编附答案解析

(易错题精选)初中数学反比例函数易错题汇编附答案解析一、选择题1.如图,菱形ABCD的两个顶点B、D在反比例函数y=的图象上,对角线AC与BD的交点恰好是坐标原点O,已知点A(1,1),∠ABC=60°,则k的值是()A.﹣5 B.﹣4 C.﹣3 D.﹣2【答案】C【解析】分析:根据题意可以求得点B的坐标,从而可以求得k的值.详解:∵四边形ABCD是菱形,∴BA=BC,AC⊥BD,∵∠ABC=60°,∴△ABC是等边三角形,∵点A(1,1),∴OA=,∴BO=,∵直线AC的解析式为y=x,∴直线BD的解析式为y=-x,∵OB=,∴点B的坐标为(−,),∵点B在反比例函数y=的图象上,∴,解得,k=-3,故选C.点睛:本题考查反比例函数图象上点的坐标特征、菱形的性质,解答本题的关键是明确题意,利用反比例函数的性质解答.2.如图,反比例函数y=2x的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为( )A .1B .2C .4D .8【答案】C【解析】【分析】 由反比例函数的系数k 的几何意义可知:2OA AD =g ,然后可求得OA AB g 的值,从而可求得矩形OABC 的面积.【详解】解:Q 反比例函数2y x=, 2OA AD ∴=g . D Q 是AB 的中点,2AB AD ∴=.∴矩形的面积2224OA AB AD OA ===⨯=g g .故选:C .【点睛】本题主要考查的是反比例函数k 的几何意义,掌握反比例函数系数k 的几何意义是解题的关键.3.在同一直角坐标系中,函数y=k(x -1)与y=(0)k k x<的大致图象是 A . B . C . D .【答案】B【解析】【分析】【详解】解:k<0时,y=(0)k k x<的图象位于二、四象限, y=k(x -1)的图象经过第一、二、四象限,观察可知B 选项符合题意,故选B.4.下列函数中,当x >0时,函数值y 随自变量x 的增大而减小的是( ) A .y =x 2B .y =xC .y =x+1D .1y x = 【答案】D【解析】【分析】需根据函数的性质得出函数的增减性,即可求出当x >0时,y 随x 的增大而减小的函数.【详解】解:A 、y =x 2是二次函数,开口向上,对称轴是y 轴,当x >0时,y 随x 的增大而增大,错误;B 、y =x 是一次函数k =1>0,y 随x 的增大而增大,错误;C 、y =x+1是一次函数k =1>0,y 随x 的增大而减小,错误;D 、1y x=是反比例函数,图象无语一三象限,在每个象限y 随x 的增大而减小,正确; 故选D .【点睛】本题综合考查了二次函数、一次函数、反比例函数的性质,熟练掌握函数的性质是解题的关键.5.如图,点A 是反比例函数y =k x(x <0)的图象上的一点,过点A 作平行四边形ABCD ,使点B 、C 在x 轴上,点D 在y 轴上.已知平行四边形ABCD 的面积为8,则k 的值为( )A .8B .﹣8C .4D .﹣4【答案】B【解析】【分析】 作AE ⊥BC 于E ,由四边形ABCD 为平行四边形得AD ∥x 轴,则可判断四边形ADOE 为矩形,所以S 平行四边形ABCD =S 矩形ADOE ,根据反比例函数k 的几何意义得到S 矩形ADOE =|k|.【详解】解:作AE⊥BC于E,如图,∵四边形ABCD为平行四边形,∴AD∥x轴,∴四边形ADOE为矩形,∴S平行四边形ABCD=S矩形ADOE,而S矩形ADOE=|k|,∴|k|=8,而k<0∴k=-8.故选:B.【点睛】本题考查了反比例函数y=kx(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.6.如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=8x上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )A.85B.235C.3.5 D.5【答案】B 【解析】【分析】设点D(m,8m),过点D作x轴的垂线交CE于点G,过点A过x轴的平行线交DG于点H,过点A作AN⊥x轴于点N,根据AAS先证明△DHA≌△CGD、△ANB≌△DGC可得AN=DG=1=AH,据此可得关于m的方程,求出m的值后,进一步即可求得答案.【详解】解:设点D(m,8m),过点D作x轴的垂线交CE于点G,过点A过x轴的平行线交DG于点H,过点A作AN⊥x轴于点N,如图所示:∵∠GDC+∠DCG=90°,∠GDC+∠HDA=90°,∴∠HDA=∠GCD,又AD=CD,∠DHA=∠CGD=90°,∴△DHA≌△CGD(AAS),∴HA=DG,DH=CG,同理△ANB≌△DGC(AAS),∴AN=DG=1=AH,则点G(m,8m﹣1),CG=DH,AH=﹣1﹣m=1,解得:m=﹣2,故点G(﹣2,﹣5),D(﹣2,﹣4),H(﹣2,1),则点E(﹣85,﹣5),GE=25,CE=CG﹣GE=DH﹣GE=5﹣25=235,故选:B.【点睛】本题考查了正方形的性质、反比例函数图象上点的坐标特点和全等三角形的判定与性质,构造全等、充分运用正方形的性质是解题的关键.7.函数kyx=与y kx k=-(0k≠)在同一平面直角坐标系中的大致图象是()A .B .C .D .【答案】C【解析】【分析】分k>0和k<0两种情况确定正确的选项即可.【详解】当k:>0时,反比例函数的图象位于第一、三象限,一次函数的图象交 y 轴于负半轴,y 随着x 的增大而增大,A 选项错误,C 选项符合;当k<0时,反比例函数的图象位于第二、四象限,一次函数的图象交y 轴于正半轴,y 随着x 的增大而增减小,B. D 均错误,故选:C.【点睛】此题考查反比例函数的图象,一次函数的图象,熟记函数的性质是解题的关键.8.已知点()1,3M -在双曲线k y x =上,则下列各点一定在该双曲线上的是( ) A .()3,1-B .()1,3--C .()1,3D .()3,1 【答案】A【解析】【分析】先求出k=-3,再依次判断各点的横纵坐标乘积,等于-3即是在该双曲线上,否则不在.【详解】∵点()1,3M -在双曲线k y x=上, ∴133k =-⨯=-,∵3(1)3⨯-=-,∴点(3,-1)在该双曲线上,∵(1)(3)13313-⨯-=⨯=⨯=,∴点()1,3--、()1,3、()3,1均不在该双曲线上,故选:A.【点睛】此题考查反比例函数解析式,正确计算k 值是解题的关键.9.如图所示是一块含30°,60°,90°的直角三角板,直角顶点O 位于坐标原点,斜边AB垂直于x 轴,顶点A 在函数y 1=1k x(x>0)的图象上,顶点B 在函数y 2= 2k x (x>0)的图象上,∠ABO=30°,则21k k =( )A .-3B .3C .13D .- 13【答案】A【解析】【分析】 根据30°角所对的直角边等于斜边的一半,和勾股定理,设出适当的常数,表示出其它线段,从而得到点A 、B 的坐标,表示出k 1、k 2,进而得出k 2与k 1的比值.【详解】如图,设AB 交x 轴于点C ,又设AC=a.∵AB ⊥x 轴 ∴∠ACO=90°在Rt △AOC 中,OC=AC·tan ∠OAB=a·tan60°3∴点A 3a ,a )同理可得 点B 3,-3a )∴k 1332 , k 23a×(-3a )3a∴213333k a k a==-. 故选A.【点睛】考查直角三角形的边角关系,反比例函数图象上点的坐标特征,设适合的常数,用常数表示出k ,是解决问题的方法.10.对于反比例函数2y x=-,下列说法不正确的是( ) A .图象分布在第二、四象限B .当0x >时,y 随x 的增大而增大C .图象经过点(1,-2)D .若点()11,A x y ,()22,B x y 都在图象上,且12x x <,则12y y <【答案】D【解析】【分析】根据反比例函数图象的性质对各选项分析判断后利用排除法求解.【详解】A. k=−2<0,∴它的图象在第二、四象限,故本选项正确;B. k=−2<0,当x>0时,y 随x 的增大而增大,故本选项正确;C.∵221-=-,∴点(1,−2)在它的图象上,故本选项正确; D. 若点A (x 1,y 1),B (x 2,y 2)都在图象上,,若x 1<0< x 2,则y 2<y 1,故本选项错误. 故选:D.【点睛】本题考查了反比例函数的图象与性质,掌握反比例函数的性质是解题的关键.11.已知反比例函数y =﹣2x的图象上有三个点(x 1,y 1)、(x 2,y 2)、(x 3,y 3),若x 1>x 2>0>x 3,则下列关系是正确的是( )A .y 1<y 2<y 3B .y 2<y 1<y 3C .y 3<y 2<y 1D .y 2<y 3<y 1【答案】B【解析】【分析】根据函数的解析式得出图象所在的象限和增减性,再进行比较即可.【详解】 解:∵反比例函数y =﹣2x, ∴函数图象在第二、四象限,且在每个象限内,y 随x 的增大而增大,∵函数的图象上有三个点(x 1,y 1),(x 2,y 2)、(x 3,y 3),且x 1>x 2>0>x 3, ∴y 2<y 1<0,y 3>0∴. y 2<y 1<y 3故选:B .【点睛】本题考查了反比例函数图象上点的坐标特征和函数的图象和性质,能灵活运用函数的图象和性质进行推理是解此题的关键.12.如图所示,Rt AOB ∆中,90AOB ∠=︒ ,顶点,A B 分别在反比例函数()10y x x =>与()50y x x=-<的图象器上,则tan BAO ∠的值为( )A 5B 5C 25D 10【答案】B【解析】【分析】过A 作AC ⊥x 轴,过B 作BD ⊥x 轴于D ,于是得到∠BDO=∠ACO=90°,根据反比例函数的性质得到S △BDO =52,S △AOC =12,根据相似三角形的性质得到=5OB OA =,根据三角函数的定义即可得到结论. 【详解】解:过A 作AC ⊥x 轴,过B 作BD ⊥x 轴于D , 则∠BDO=∠ACO=90°,∵顶点A ,B 分别在反比例函数()10y x x =>与()50y x x =-<的图象上, ∴S △BDO =52,S △AOC =12, ∵∠AOB=90°,∴∠BOD+∠DBO=∠BOD+∠AOC=90°,∴∠DBO=∠AOC ,∴△BDO ∽△OCA ,∴251522BODOACSOBS OA⎛⎫==÷=⎪⎝⎭△△,∴5OBOA=,∴tan∠BAO=5OBOA=.故选B.【点睛】本题考查了反比例函数的性质以及直角三角形的性质,三角形相似的判定和性质.解题时注意掌握数形结合思想的应用,注意掌握辅助线的作法.13.如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数1(0)ky xx=>和2(0)ky xx=>的图象于点P和Q,连接OP和OQ.则下列结论正确的是()A.∠POQ不可能等于90°B.12PMQMkk=C.这两个函数的图象一定关于x轴对称D.△POQ的面积是()1212k k+【答案】D【解析】【分析】【详解】解:根据反比例函数的性质逐一作出判断:A .∵当PM=MO=MQ 时,∠POQ=90°,故此选项错误;B .根据反比例函数的性质,由图形可得:1k >0,2k <0,而PM ,QM 为线段一定为正值,故12PM QM k k =,故此选项错误; C .根据1k ,2k 的值不确定,得出这两个函数的图象不一定关于x 轴对称,故此选项错误;D .∵|1k |=PM•MO ,|2k |=MQ•MO ,∴△POQ 的面积=12MO•PQ=12MO (PM+MQ )=12MO•PM+12MO•MQ=()1212k k +. 故此选项正确.故选D .14.若A (-3,y 1)、B (-1,y 2)、C (1,y 3)三点都在反比例函数y=k x (k >0)的图象上,则y 1、y 2、y 3的大小关系是( )A . y 1>y 2>y 3B . y 3>y 1>y 2C . y 3>y 2>y 1D . y 2>y 1>y 3 【答案】B【解析】【分析】反比例函数y=k x(k >0)的图象在一、三象限,根据反比例函数的性质,在每个象限内y 随x 的增大而减小,而A (-3,y 1)、B (-1,y 2)在第三象限双曲线上的点,可得y 2<y 1<0,C (1,y 3)在第一象限双曲线上的点y 3>0,于是对y 1、y 2、y 3的大小关系做出判断.【详解】∵反比例函数y=k x(k >0)的图象在一、三象限, ∴在每个象限内y 随x 的增大而减小,∵A (-3,y 1)、B (-1,y 2)在第三象限双曲线上,∴y 2<y 1<0,∵C (1,y 3)在第一象限双曲线上,∴y 3>0,∴y 3>y 1>y 2,故选:B .【点睛】此题考查反比例函数的图象和性质,解题关键在于当k >0,时,在每个象限内y 随x 的增大而减小;当k <0时,y 随x 的增大而增大,注意“在每个象限内”的意义,这种类型题目用图象法比较直观得出答案.15.矩形ABCO如图摆放,点B在y轴上,点C在反比例函数ykx=(x>0)上,OA=2,AB=4,则k的值为()A.4 B.6 C.325D.425【答案】C【解析】【分析】根据矩形的性质得到∠A=∠AOC=90°,OC=AB,根据勾股定理得到OB22OA AB=+=5C作CD⊥x轴于D,根据相似三角形的性质得到CD855=,OD45=求得8545,)于是得到结论.【详解】解:∵四边形ABCO是矩形,∴∠A=∠AOC=90°,OC=AB,∵OA=2,AB=4,∴过C作CD⊥x轴于D,∴∠CDO=∠A=90°,∠COD+∠COB=∠COB+∠AOB=90°,∴∠COD=∠AOB,∴△AOB∽△DOC,∴OB AB OA OC CD OD==,∴25424CD OD==,∴CD85=,OD45=,∴4585),∴k325 =,故选:C.【点睛】本题考查了反比例函数图象上点的坐标特征,反比例函数的性质,矩形的性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.16.在函数()0k y k x=<的图象上有()11,A y ,()21,B y -,()32,B y -三个点,则下列各式中正确的是( ) A .123y y y <<B .132y y y <<C .321y y y <<D .231y y y <<【答案】B【解析】【分析】根据反比例函数图象上点的坐标特征得到11y k ⨯=,21y k -⨯=,32y k -⨯=,然后计算出1y 、2y 、3y 的值再比较大小即可.【详解】 解:(0)k y k x=<Q 的图象上有1(1,)A y 、2(1,)B y -、3(2,)C y -三个点, 11y k ∴⨯=,21y k -⨯=,32y k -⨯=, 1y k ∴=,2y k =-,312y k =-, 而k 0<,132y y y ∴<<.故选:B .【点睛】 本题考查了反比例函数图象上点的坐标特征:反比例函数k y x=(k 为常数,且0k ≠)的图象是双曲线,图象上的点(),x y 的横纵坐标的积是定值k ,即xy k =.17.已知反比例函数b y x=与一次函数y ax c =+有一个交点在第四象限,该交点横坐标为1,抛物线2y ax bx c =++与x 轴只有一个交点,则一次函数b c y x a a=+的图象可能是( )A .B .C .D .【答案】B【解析】【分析】根据题意得b <0,a+c <0,240b ac =>,可得a <0,c <0,进而即可判断一次函数b c y x a a =+的图象所经过的象限. 【详解】 ∵反比例函数b y x=与一次函数y ax c =+有一个交点在第四象限, ∴反比例函数的图象在二、四象限,即b <0,∵该交点横坐标为1,∴y=a+c <0,∵抛物线2y ax bx c =++与x 轴只有一个交点, ∴240b ac -=,即:240b ac =>,∴a <0,c <0,∴0b a>,0c a >, ∴b c y x a a=+的图象过一、二、三象限. 故选B .【点睛】 本题主要考查反比例函数与一次函数的图象和性质,掌握函数图象上点的坐标特征以及函数解析式的系数的几何意义,是解题的关键.18.如图,矩形ABCD 的顶点A ,B 在x 轴的正半轴上,反比例函数k y x =在第一象限内的图象经过点D ,交BC 于点E .若4AB =,2CE BE =,34AD OA =,则线段BC 的长度为( )A .1B .32C .2D .23【解析】【分析】设OA 为4a ,则根据题干中的比例关系,可得AD=3a ,CE=2a ,BE=a ,从而得出点D 和点E 的坐标(用a 表示),代入反比例函数可求得a 的值,进而得出BC 长.【详解】设OA=4a 根据2CE BE =,34AD OA =得:AD=3a ,CE=2a ,BE=a ∴D(4a ,3a),E(4a+4,a)将这两点代入解析得; 3444k a a k a a ⎧=⎪⎪⎨⎪=⎪+⎩解得:a=12∴BC=AD=32 故选:B【点睛】本题考查反比例函数和矩形的性质,解题关键是用含有字母的式子表示出点D 、E 的坐标,然后代入解析式求解.19.如图,Rt ABO ∆中,90AOB ∠=︒,3AO BO =,点B 在反比例函数2y x =的图象上,OA 交反比例函数()0k y k x=≠的图象于点C ,且2OC CA =,则k 的值为( )A .2-B .4-C .6-D .8-【答案】D【分析】过点A 作AD ⊥x 轴,过点C 作CE ⊥x 轴,过点B 作BF ⊥x 轴,利用AA 定理和平行证得△COE ∽△OBF ∽△AOD ,然后根据相似三角形的性质求得21()9BOF OAD S OB S OA ==V V ,24()9COE AOD S OC S OA ==V V ,根据反比例函数比例系数的几何意义求得212BOF S ==V ,从而求得4COE S =V ,从而求得k 的值.【详解】解:过点A 作AD ⊥x 轴,过点C 作CE ⊥x 轴,过点B 作BF ⊥x 轴∴CE ∥AD ,∠CEO=∠BFO=90°∵90AOB ∠=︒∴∠COE+∠FOB=90°,∠ECO+∠COE=90°∴∠ECO=∠FOB∴△COE ∽△OBF ∽△AOD又∵3AO BO =,2OC CA = ∴13OB OA =,23OC OA = ∴21()9BOF OAD S OB S OA ==V V ,24()9COE AOD S OC S OA ==V V ∴4COE BOFS S =V V ∵点B 在反比例函数2y x =的图象上 ∴212BOF S ==V ∴4COE S =V ∴42k =,解得k=±8 又∵反比例函数位于第二象限,∴k=-8故选:D .【点睛】本题考查反比例函数的性质和相似三角形的判定和性质,正确添加辅助线证明三角形相似,利用数形结合思想解题是关键.20.如图,四边形OABF中,∠OAB=∠B=90°,点A在x轴上,双曲线kyx=过点F,交AB于点E,连接EF.若BF2OA3=,S△BEF=4,则k的值为()A.6 B.8 C.12 D.16【答案】A【解析】【分析】由于23BFOA=,可以设F(m,n)则OA=3m,BF=2m,由于S△BEF=4,则BE=4m,然后即可求出E(3m,n-4m),依据mn=3m(n-4m)可求mn=6,即求出k的值.【详解】如图,过F作FC⊥OA于C,∵23 BFOA,∴OA=3OC,BF=2OC ∴若设F(m,n)则OA=3m,BF=2m ∵S△BEF=4∴BE=4 m则E(3m,n-4m)∵E在双曲线y=kx上∴mn=3m(n-4m)∴mn=6即k=6.故选A.【点睛】此题主要考查了反比例函数的图象和性质、用坐标表示线段长和三角形面积,表示出E点坐标是解题关键.。
中考数学培优易错难题(含解析)之反比例函数附答案解析.doc

中考数学培优易错难题(含解析)之反比例函数附答案解析一、反比例函数1.如图,点 P( x,y1)与 Q( x, y2)分别是两个函数图象C1与 C2上的任一点.当a≤ x≤b 时,有﹣ 1≤ya≤ x≤b 1﹣y2≤1成立,则称这两个函数在a≤ x≤b上是“相邻函数”,否则称它们在上是“非相邻函数”.例如,点 P( x, y1)与 Q ( x, y2)分别是两个函数 y=3x+1 与 y=2x﹣ 1 图象上的任一点,当﹣ 3≤x≤﹣ 1 时, y1﹣ y2=( 3x+1)﹣( 2x﹣ 1 ) =x+2,通过构造函数y=x+2 并研究它在﹣ 3≤ x﹣≤1 上的性质,得到该函数值的范围是﹣1≤ y≤1,所以﹣ 1≤y1﹣ y2≤1成立,因此这两个函数在﹣3≤x﹣≤ 1 上是“相邻函数”.(1)判断函数 y=3x+2 与 y=2x+1 在﹣ 2≤x≤0上是否为“相邻函数”,并说明理由;(2)若函数 y=x2﹣ x 与 y=x﹣a 在 0≤x≤2上是“相邻函数”,求 a 的取值范围;(3)若函数 y= 与 y=﹣ 2x+4 在 1≤x≤2上是“相邻函数”,直接写出 a 的最大值与最小值.【答案】(1)解:是“相邻函数”,理由如下: y1﹣ y2=( 3x+2)﹣( 2x+1) =x+1,构造函数 y=x+1,∵y=x+1 在﹣ 2 ≤ x ≤0是随着, x 的增大而增大,∴当 x=0 时,函数有最大值1,当 x=﹣ 2 时,函数有最小值﹣1,即﹣ 1 ≤ y ≤1,∴﹣ 1 ≤y1 2≤1,﹣ y即函数 y=3x+2 与 y=2x+1 在﹣ 2≤x≤0上是“相邻函数”(2)解: y1﹣ y2=( x2﹣ x)﹣( x﹣ a) =x2﹣2x+a,构造函数 y=x2﹣2x+a,∵y=x2﹣ 2x+a=( x﹣ 1)2+( a﹣ 1),∴顶点坐标为:( 1, a﹣ 1),又∵ 抛物线 y=x2﹣2x+a 的开口向上,∴当 x=1 时,函数有最小值a﹣ 1,当 x=0 或 x=2 时,函数有最大值a,即 a﹣ 1 ≤ y ,≤a∵函数 y=x2﹣ x 与 y=x﹣ a 在 0≤x≤2上是“相邻函数”,∴﹣ 1 ≤y1﹣ y2≤1,即,∴0 ≤ a ≤1(3)解: y1﹣ y2=﹣(﹣2x+4)=+2x﹣ 4,构造函数y= +2x﹣4,∵y=+2x﹣ 4∴当 x=1 时,函数有最小值a﹣ 2,当 x=2 时,函数有最大值,即a﹣2≤y≤,∵函数 y=与y=﹣2x+4在1≤x≤2上是“相邻函数”,∴﹣ 1 ≤y1 2,﹣ y ≤1,即∴1 ≤ a ≤2;∴a 的最大值是 2,a 的最小值 1【解析】【分析】( 1) y1﹣y 2=(3x+2)﹣(2x+1)=x+1,构造函数y=x+1,因为 y=x+1 在﹣2≤x≤0,是随着 x 的增大而增大,所以当x=0 时,函数有最大值1,当 x=﹣2 时,函数有最小值﹣ 1,即﹣ 1≤y≤1,所以﹣ 1≤y1 2﹣ y ≤1,即函数 y=3x+2 与 y=2x+1 在﹣ 2≤ x≤0上是“相邻函数”;( 2 ) y1﹣ y2=( x2﹣ x)﹣( x﹣ a) =x2﹣ 2x+a,构造函数y=x2﹣ 2x+a,因为y=x2﹣2x+a=( x﹣ 1)2+( a﹣ 1),所以顶点坐标为:(1, a﹣1 ),又抛物线y=x2﹣ 2x+a 的开口向上,所以当x=1 时,函数有最小值a﹣ 1,当 x=0 或 x=2 时,函数有最大值a,即 a﹣1≤ y≤a,因为函数2﹣ x 与 y=x﹣ a 在 0≤x≤2上是“相邻函数”,所以﹣ 1≤y1 2y=x ﹣ y ≤1,即0≤ a≤1;( 3)当 x=1 时,函数有最小值a﹣ 2,当 x=2 时,函数有最大值,因为函数y=与 y=﹣ 2x+4 在 1≤x≤2上是“相邻函数”,﹣ 1≤y2, a1﹣y2≤1,即1≤a≤2,所以a的最大值是的最小值 1.2.如图,已知 A 是双曲线y=(k>0)在第一象限内的一点,O 为坐标原点,直线OA 交双曲线于另一点C,当 OA 在第一象限的角平分线上时,将OA 向上平移个单位后,与双曲线在第一象限交于点M ,交 y 轴于点 N,若=2,(1)求直线 MN 的解析式;(2)求 k 的值.【答案】(1)解:∵OA 在第一象限的角平分线上,∴直线 OA 的解析式为y=x,∴将 OA 向上平移个单位后,N(0,),可设直线MN 的解析式为y=x+b,把 N( 0,)代入,可得b=,∴直线 MN 的解析式为y=x+( 2 )解:如图所示,过 A 作 AB⊥ y 轴于 B ,过 M 作 MD⊥ y 轴于 D ,则∠MDN= ∠ ABO=90 ,°由平移可得,∠ MND=∠ AOB=45°,∴△ MDN ∽△ ABO,∴= =2,设A( a, a),则 AB=a,∴MD= a=DN,∴DO= a+,∴M (a,a+),∵双曲线经过点A, M,∴k=a × a=a (×a+),解得 a=1,∴k=1.【解析】【分析】( 1)第一三象限角平分线为y=x,向上平移为y=x+b,可求出 N 点坐标,代入 y=x+b,即可求出 ; (2)通过作垂线构造相似三角形,即△ MDN∽ △ABO,把A、M坐标代入解析式即可求出a,进而求出k.3.如图,在平面直角坐标系中,矩形OADB 的顶点A, B 的坐标分别为A(﹣ 6, 0), B(0, 4).过点C(﹣ 6, 1)的双曲线y=(k≠0)与矩形OADB 的边 BD 交于点 E.(1)填空: OA=________, k=________,点 E 的坐标为 ________;(2)当 1≤t ≤6时,经过点M( t ﹣ 1,﹣t2+5t﹣)与点N(﹣ t ﹣3,﹣t2+3t ﹣)的直线交 y 轴于点 F,点 P 是过 M, N 两点的抛物线y= ﹣x2+bx+c 的顶点.①当点 P 在双曲线y=上时,求证:直线MN 与双曲线y=没有公共点;②当抛物线y=﹣x2+bx+c 与矩形 OADB 有且只有三个公共点,求t 的值;③当点 F 和点 P 随着 t 的变化同时向上运动时,求t 的取值范围,并求在运动过程中直线MN 在四边形OAEB中扫过的面积.【答案】(1) 6; -6;(﹣,4)(2)解:①设直线 MN 解析式为: y1=k1x+b1由题意得:解得∵抛物线 y=﹣过点M、N∴解得∴抛物线解析式为:y=﹣x2﹣ x+5t﹣ 2∴顶点 P 坐标为(﹣ 1, 5t﹣)∵P 在双曲线y=﹣上∴( 5t﹣)×(﹣1)=﹣ 6∴t=此时直线MN 解析式为:联立∴8x2+35x+49=0∵△ =352﹣ 4×8×48=1225﹣ 1536 < 0∴直线 MN 与双曲线y=﹣没有公共点.②当抛物线过点B,此时抛物线y=﹣x2+bx+c 与矩形 OADB 有且只有三个公共点∴4=5t ﹣2,得 t=当抛物线在线段DB 上,此时抛物线与矩形OADB有且只有三个公共点∴,得 t=∴t= 或 t=③ ∵点 P 的坐标为(﹣1, 5t﹣)∴y P=5t ﹣当1≤t ≤6时, y P随 t 的增大而增大此时,点 P 在直线 x=﹣1 上向上运动∵点 F 的坐标为( 0,﹣)∴y F=﹣∴当 1 ≤ t ≤4时,随者y F随 t 的增大而增大此时,随着t 的增大,点 F 在 y 轴上向上运动∴1 ≤ t ≤4当t=1 时,直线 MN : y=x+3 与 x 轴交于点 G(﹣ 3,0),与 y 轴交于点 H(0 ,3)当t=4﹣时,直线MN过点A.当1≤t ≤4时,直线 MN 在四边形 AEBO中扫过的面积为S=【解析】【解答】解:(1)∵A 点坐标为(﹣ 6, 0)∴O A=6∵过点 C(﹣ 6,1)的双曲线y=∴k=﹣ 6y=4 时, x=﹣∴点 E 的坐标为(﹣,4)故答案为: 6,﹣ 6,(﹣,4)【分析】( 1)根据 A 点的坐标即可得出OA 的长,将 C 点的坐标代入双曲线y= ,即可求出 k 的值,得出双曲线的解析式,根据平行于x 轴的直线上的点的坐标特点得出点 E 的纵坐标为4,将y=4 代入双曲线的解析式即可算出对应的自变量的值,从而得出 E 点的坐标;( 2 )①用待定系数法求出直线MN解析式,将M,N两点的坐标代入抛物线y=﹣ x2+bx+c,得出关于 b,c 的方程组,求解得出 b,c 的值,根据顶点坐标公式表示出P 点的坐标,再将 P 点的坐标代入双曲线即可求出t 的值,从而得出直线MN 解析式,解联立直线 MN 解析式与双曲线的解析式组成的方程组,根据根的判别式的值小于0,得出直线 MN与双曲线没有公共点;② 当抛物线过点B,此时抛物线 y=﹣x2+bx+c 与矩形 OADB 有且只有三个公共点,故4=5t﹣2,求解得出t 的值,当抛物线在线段DB 上,此时抛物线与矩形 OADB 有且只有三个公共点,故,求解得出 t 的值,综上所述得出答案;③根据 P 点的坐标判断出当1≤t ≤6时, y P随 t 的增大而增大,此时,点P 在直线 x=﹣1 上向上运动进而表示出 F 点的坐标,将 F 点的纵坐标配成顶点式,得出当1≤t ≤4时,随者 y F 随t 的增大而增大,此时,随着t 的增大,点 F 在 y 轴上向上运动,故 1≤ t ≤4,当 t=1 时,直线 MN: y=x+3 与 x 轴交于点 G(﹣ 3, 0),与 y 轴交于点 H( 0,3),当 t=4﹣时,直线 MN 过点 A.根据割补法算出当1≤t ≤4时,直线 MN 在四边形 AEBO中扫过的面积。
(易错题精选)初中数学反比例函数知识点总复习(1)

(易错题精选)初中数学反比例函数知识点总复习(1)一、选择题1.若A (-3,y 1)、B (-1,y 2)、C (1,y 3)三点都在反比例函数y=k x (k >0)的图象上,则y 1、y 2、y 3的大小关系是( )A . y 1>y 2>y 3B . y 3>y 1>y 2C . y 3>y 2>y 1D . y 2>y 1>y 3 【答案】B【解析】【分析】反比例函数y=k x(k >0)的图象在一、三象限,根据反比例函数的性质,在每个象限内y 随x 的增大而减小,而A (-3,y 1)、B (-1,y 2)在第三象限双曲线上的点,可得y 2<y 1<0,C (1,y 3)在第一象限双曲线上的点y 3>0,于是对y 1、y 2、y 3的大小关系做出判断.【详解】∵反比例函数y=k x(k >0)的图象在一、三象限, ∴在每个象限内y 随x 的增大而减小,∵A (-3,y 1)、B (-1,y 2)在第三象限双曲线上,∴y 2<y 1<0,∵C (1,y 3)在第一象限双曲线上,∴y 3>0,∴y 3>y 1>y 2,故选:B .【点睛】此题考查反比例函数的图象和性质,解题关键在于当k >0,时,在每个象限内y 随x 的增大而减小;当k <0时,y 随x 的增大而增大,注意“在每个象限内”的意义,这种类型题目用图象法比较直观得出答案.2.在平面直角坐标系中,分别过点(),0A m ,()2,0B m﹢作x 轴的垂线1l 和2l ,探究直线1l 和2l 与双曲线 3y x= 的关系,下列结论中错误..的是 A .两直线中总有一条与双曲线相交B .当m =1时,两条直线与双曲线的交点到原点的距离相等C .当20m -﹤﹤ 时,两条直线与双曲线的交点在y 轴两侧D .当两直线与双曲线都有交点时,这两交点的最短距离是2【答案】D【解析】【分析】根据题意给定m 特定值、非特定值分别进行讨论即可得.【详解】当m =0时,2l 与双曲线有交点,当m =-2时,1l 与双曲线有交点,当m 0m 2≠≠,﹣时,12l l 与和双曲线都有交点,所以A 正确,不符合题意;当m 1=时,两交点分别是(1,3),(3,1)B 正确,不符合题意;当2m 0-﹤﹤ 时,1l 在y 轴的左侧,2l 在y 轴的右侧,所以C 正确,不符合题意;两交点分别是33m (m 2m m 2++,和,),当m 无限大时,两交点的距离趋近于2,所以D 不正确,符合题意,故选D.【点睛】本题考查了垂直于x 轴的直线与反比例函数图象之间的关系,利用特定值,分情况进行讨论是解本题的关键,本题有一定的难度.3.对于反比例函数2y x=,下列说法不正确的是( ) A .点(﹣2,﹣1)在它的图象上 B .它的图象在第一、三象限C .当x >0时,y 随x 的增大而增大D .当x <0时,y 随x 的增大而减小 【答案】C【解析】【详解】由题意分析可知,一个点在函数图像上则代入该点必定满足该函数解析式,点(-2,-1)代入可得,x=-2时,y=-1,所以该点在函数图象上,A 正确;因为2大于0所以该函数图象在第一,三象限,所以B 正确;C 中,因为2大于0,所以该函数在x >0时,y 随x 的增大而减小,所以C 错误;D 中,当x <0时,y 随x 的增大而减小,正确,故选C.考点:反比例函数【点睛】本题属于对反比例函数的基本性质以及反比例函数的在各个象限单调性的变化4.如图,A ,B 是反比例函数y=4x在第一象限内的图象上的两点,且A ,B 两点的横坐标分别是2和4,则△OAB 的面积是( )A .4B .3C .2D .1【答案】B【解析】 【分析】先根据反比例函数图象上点的坐标特征及A ,B 两点的横坐标,求出A (2,2),B (4,1).再过A ,B 两点分别作AC ⊥x 轴于C ,BD ⊥x 轴于D ,根据反比例函数系数k 的几何意义得出S △AOC =S △BOD =12×4=2.根据S 四边形AODB =S △AOB +S △BOD =S △AOC +S 梯形ABDC ,得出S △AOB =S 梯形ABDC ,利用梯形面积公式求出S 梯形ABDC =12(BD+AC )•CD=12×(1+2)×2=3,从而得出S △AOB =3.【详解】∵A ,B 是反比例函数y=4x在第一象限内的图象上的两点, 且A ,B 两点的横坐标分别是2和4,∴当x=2时,y=2,即A (2,2),当x=4时,y=1,即B (4,1),如图,过A ,B 两点分别作AC ⊥x 轴于C ,BD ⊥x 轴于D , 则S △AOC =S △BOD =12×4=2, ∵S 四边形AODB =S △AOB +S △BOD =S △AOC +S 梯形ABDC ,∴S △AOB =S 梯形ABDC ,∵S 梯形ABDC =12(BD+AC )•CD=12×(1+2)×2=3, ∴S △AOB =3,故选B .【点睛】本题考查了反比例函数()0k y k x=≠中k 的几何意义,反比例函数图象上点的坐标特征,梯形的面积,熟知反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S与k的关系为S=12|k|是解题的关键.5.在反比例函数y=93mx+图象上有两点A(x1,y1)、B(x2,y2),y1<0<y2,x1>x2,则有()A.m>﹣13B.m<﹣13C.m≥﹣13D.m≤﹣13【答案】B【解析】【分析】先根据y1<0<y2,有x1>x2,判断出反比例函数的比例系数的正负,求出m的取值范围即可.【详解】∵在反比例函数y=93mx+图象上有两点A(x1,y1)、B(x2,y2),y1<0<y2,x1>x2,∴反比例函数的图象在二、四象限,∴9m+3<0,解得m<﹣13.故选:B.【点睛】此题主要考查了反比例函数的性质,以及反比例函数图象上点的坐标特点,关键是掌握反比例函数的性质6.下列函数:①y=-x;②y=2x;③1yx=-;④y=x2.当x<0时,y随x的增大而减小的函数有()A.1 个B.2 个C.3 个D.4 个【答案】B【解析】【分析】分别根据一次函数、反比例函数及二次函数的性质进行逐一判断即可.【详解】一次函数y=-x中k<0,∴y随x的增大而减小,故本选项正确;∵正比例函数y=2x中,k=2,∴当x<0时,y随x的增大而增大,故本选项错误;∵反比例函数1yx-=中,k=-1<0,∴当x<0时函数的图像在第二象限,此时y随x的增大而增大,故本选项错误;∵二次函数y=x2,中a=1>0,∴此抛物线开口向上,当x<0时,y随x的增大而减小,故本选项正确.故选B .【点睛】本题考查的是一次函数、反比例函数及二次函数的性质,解题关键是根据题意判断出各函数的增减性.7.如图,正方形OABC 的边长为6,D 为AB 中点,OB 交CD 于点Q ,Q 是y =k x上一点,k 的值是( )A .4B .8C .16D .24【答案】C【解析】【分析】 延长根据相似三角形得到:1:2BQ OQ =,再过点Q 作垂线,利用相似三角形的性质求出QF 、OF ,进而确定点Q 的坐标,确定k 的值.【详解】解:过点Q 作QF OA ⊥,垂足为F ,OABC Q 是正方形,6OA AB BC OC ∴====,90ABC OAB DAE ∠=∠=︒=∠,D Q 是AB 的中点,12BD AB ∴=, //BD OC Q ,OCQ BDQ ∴∆∆∽,∴12BQ BD OQ OC ==, 又//QF AB Q ,OFQ OAB ∴∆∆∽,∴22213QF OF OQ AB OA OB ====+, 6AB =Q , 2643QF ∴=⨯=,2643OF =⨯=, (4,4)Q ∴,Q 点Q 在反比例函数的图象上,4416k ∴=⨯=,故选:C .【点睛】本题考查了待定系数法求反比例函数、相似三角形的性质和判定,利用相似三角形性质求出点Q 的坐标是解决问题的关键.8.如图,矩形ABCD 的边AB 在x 轴上,反比例函数k y x=(0)k ≠的图象过D 点和边BC 的中点E ,连接DE ,若CDE ∆的面积是1,则k 的值是( )A .4B .3C .25D .2【答案】A【解析】【分析】 设E 的坐标是(m ,n ),k=mn ,则C 的坐标是(m ,2n ),求得D 的坐标,然后根据三角形的面积公式求得mn 的值,即k 的值.【详解】解:设E 的坐标是(m ,n ),k=mn ,则C 的坐标是(m ,2n ),在y=mn x 中,令y=2n ,解得:x=2m , ∵S △CDE =1,∴12|n|•|m-2m|=1,即12n×2m=1,∴mn=4.∴k=4.故选:A.【点睛】本题考查了待定系数法求函数的解析式,利用mn表示出三角形的面积是关键.9.如图,直线l与x轴、y轴分别交于A、B两点,与反比例函数y=kx的图象在第一象限相交于点C.若AB=BC,△AOB的面积为3,则k的值为()A.6 B.9 C.12 D.18【答案】C【解析】【分析】设OB=a,根据相似三角形性质即可表示出点C,把点C代入反比例函数即可求得k.【详解】作CD⊥x轴于D,设OB=a,(a>0)∵△AOB的面积为3,∴12OA•OB=3,∴OA=6a,∵CD∥OB,∴OD=OA=6a,CD=2OB=2a,∴C(6a,2a),∵反比例函数y=kx经过点C,∴k=6a×2a=12,故选C.【点睛】本题考查直线和反比例函数的交点问题,待定系数法求函数解析式,会运用相似求线段长度是解题的关键.10.如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于点A,反比例函数y=kx(x>0)的图象与线段AB相交于点C,且C是线段AB的中点,若△OAB的面积为3,则k的值为 ()A.13B.1 C.2 D.3【答案】D 【解析】【分析】连接OC,如图,利用三角形面积公式得到S△AOC=12S△OAB=32,再根据反比例函数系数k的几何意义得到12|k|=32,然后利用反比例函数的性质确定k的值.【详解】连接OC,如图,∵BA⊥x轴于点A,C是线段AB的中点,∴S△AOC=12S△OAB=32,而S △AOC =12|k|, ∴12|k|=32, 而k >0,∴k=3.故选:D .【点睛】此题考查反比例函数系数k 的几何意义,解题关键在于掌握在反比例函数y=k x图象中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.11.如图,在平面直角坐标系中,等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA x ⊥轴,点C 在函数()0k y x x=>的图象上,若1AB =,则k 的值为( )A .1B .22C 2D .2【答案】A【解析】【分析】 根据题意可以求得 OA 和 AC 的长,从而可以求得点 C 的坐标,进而求得 k 的 值,本题得以解决.【详解】Q 等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA ⊥x 轴,1AB =,45BAC BAO ︒∴∠=∠=,22OA OB ∴==,2AC =, ∴点C 的坐标为22⎝,Q 点C 在函数()0k y x x =>的图象上, 2212k ∴=⨯=, 故选:A .【点睛】本题考查反比例函数图象上点的坐标特征、等腰直角三角形,解答本题的关键 是明确题意,利用数形结合的思想解答.12.如图,已知在平面直角坐标系中,点O 是坐标原点,AOB V 是直角三角形,90AOB ∠=︒,2OB OA =,点B 在反比例函数2y x =上,若点A 在反比例函数k y x=上,则k 的值为( )A .12B .12-C .14D .14- 【答案】B【解析】【分析】通过添加辅助线构造出相似三角形,再根据相似三角形的性质可求得1,2x A x ⎛⎫- ⎪⎝⎭,然后由点的坐标即可求得答案.【详解】解:过点B 作BE x ⊥于点E ,过点A 作AF x ⊥于点F ,如图:∵点B 在反比例函数2y x =上 ∴设2,B x x ⎛⎫ ⎪⎝⎭∴OE x =,2BE x=∵90AOB ∠=︒ ∴90AOD BOD ∠+∠=︒∴90BOE AOF ∠+∠=︒∵BE x ⊥,AF x ⊥∴90BEO OFA ∠=∠=︒∴90OAF AOF ∠+∠=︒∴BOE OAF ∠=∠∴BOE OAF V V ∽∵2OB OA = ∴12OF AF OA BE OE BO === ∴121122OF BE x x =⋅=⋅=,11222x AF OE x =⋅=⋅= ∴1,2x A x ⎛⎫- ⎪⎝⎭ ∵点A 在反比例函数k y x=上 ∴12x k x=- ∴12k =-. 故选:B【点睛】本题考查了反比例函数与相似三角形的综合应用,点在函数图象上则点的坐标就满足函数解析式,结合已知条件能根据相似三角形的性质求得点A 的坐标是解决问题的关键.13.反比例函数k y x=的图象在第二、第四象限,点()()()1232,,4,,5,A y B y C y -是图象上的三点,则123,,y y y 的大小关系是( )A .123y y y >>B .132y y y >>C .312y y y >>D .231y y y >> 【答案】B【解析】【分析】根据反比例函数图像在第二、四象限,反比例函数图像在第二、四象限,y 随x 的增大而增大,再根据三点横坐标的特点即可得出结论.【详解】 解:∵反比例函数ky x=图象在第二、四象限, ∴反比例函数图象在每个象限内y 随x 的增大而增大,∵-2<4<5, ∴点B 、C 在第四象限,点A 在第二象限, ∴23y y <<0,10y > ,∴132y y y >>.故选B.【点睛】本题考查了反比例函数图象上点的坐标特征,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答本题的关键.14.如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A 在反比例函数y=6x(x >0)的图象上,则经过点B 的反比例函数解析式为( )A .y=﹣6xB .y=﹣4xC .y=﹣2xD .y=2x【答案】C【解析】【分析】直接利用相似三角形的判定与性质得出13BCO AOD S S =V V ,进而得出S △AOD =3,即可得出答案. 【详解】过点B 作BC ⊥x 轴于点C ,过点A 作AD ⊥x 轴于点D ,∵∠BOA =90°,∴∠BOC +∠AOD =90°,∵∠AOD +∠OAD =90°,∴∠BOC=∠OAD,又∵∠BCO=∠ADO=90°,∴△BCO∽△ODA,∵BOAO=tan30°=3,∴13BCOAODSSVV,∵12×AD×DO=12xy=3,∴S△BCO=12×BC×CO=13S△AOD=1,∵经过点B的反比例函数图象在第二象限,故反比例函数解析式为:y=﹣2x.故选C.【点睛】此题主要考查了相似三角形的判定与性质,反比例函数数的几何意义,正确得出S△AOD=2是解题关键.15.点(2,﹣4)在反比例函数y=kx的图象上,则下列各点在此函数图象上的是()A.(2,4)B.(﹣1,﹣8)C.(﹣2,﹣4)D.(4,﹣2)【答案】D【解析】【详解】∵点(2,-4)在反比例函数y=kx的图象上,∴k=2×(-4)=-8.∵A中2×4=8;B中-1×(-8)=8;C中-2×(-4)=8;D中4×(-2)=-8,∴点(4,-2)在反比例函数y=kx的图象上.故选D.【点睛】本题考查了反比例函数图象上点的坐标特征,解题的关键是求出反比例系数k ,解决该题型题目时,结合点的坐标利用反比例函数图象上点的坐标特征求出k 值是关键.16.在函数()0k y k x=<的图象上有()11,A y ,()21,B y -,()32,B y -三个点,则下列各式中正确的是( ) A .123y y y <<B .132y y y <<C .321y y y <<D .231y y y <<【答案】B【解析】【分析】根据反比例函数图象上点的坐标特征得到11y k ⨯=,21y k -⨯=,32y k -⨯=,然后计算出1y 、2y 、3y 的值再比较大小即可.【详解】 解:(0)k y k x=<Q 的图象上有1(1,)A y 、2(1,)B y -、3(2,)C y -三个点, 11y k ∴⨯=,21y k -⨯=,32y k -⨯=, 1y k ∴=,2y k =-,312y k =-, 而k 0<,132y y y ∴<<.故选:B .【点睛】 本题考查了反比例函数图象上点的坐标特征:反比例函数k y x=(k 为常数,且0k ≠)的图象是双曲线,图象上的点(),x y 的横纵坐标的积是定值k ,即xy k =.17.已知反比例函数2y x =-,下列结论不正确的是 A .图象必经过点(-1,2)B .y 随x 的增大而增大C .图象在第二、四象限内D .若x >1,则y >-2 【答案】B【解析】【分析】此题可根据反比例函数的性质,即函数所在的象限和增减性对各选项作出判断.【详解】解: A 、把(-1,2)代入函数解析式得:2=-21-成立,故点(-1,2)在函数图象上,故选项正确;B 、由k=-2<0,因此在每一个象限内,y 随x 的增大而增大,故选项不正确;C 、由k=-2<0,因此函数图象在二、四象限内,故选项正确;D 、当x=1,则y=-2,又因为k=-2<0,所以y 随x 的增大而增大,因此x >1时,-2<y <0,故选项正确;故选B .【点睛】本题考查反比例函数的图像与性质.18.如图,点A 在反比例函数3(0)y x x =-<的图象上,点B 在反比例函数3(0)y x x=>的图象上,点C 在x 轴的正半轴上,则平行四边形ABCO 的面积是( )A .6B .5C .4D .3【答案】A【解析】【分析】 因为四边形ABCO 是平行四边形,所以点A 、B 纵坐标相等,即可求得A 、B 横坐标,则AB 的长度即可求得,然后利用平行四边形面积公式即可求解.【详解】解:∵四边形ABCO 是平行四边形∴点A 、B 纵坐标相等设纵坐标为b ,将y=b 带入3(0)y x x =-<和3(0)y x x=>中, 则A 点横坐标为3b -,B 点横坐标为3b ∴AB=336()b b b--= ∴66ABCO S b b =⨯=Y 故选:A . 【点睛】本题考查了反比例函数以及平行四边形面积公式,本题关键在于两点间距离的求法.19.若点()11,A y -,()22,B y -,()33,C y 在反比例函数8y x=-的图象上,则y 1,y 2,y 3的大小关系是( )A .123y y y <<B .213y y y <<C .132y y y <<D .321y y y << 【答案】D【解析】【分析】由于反比例函数的系数是-8,故把点A 、B 、C 的坐标依次代入反比例函数的解析式,求出123,,y y y 的值即可进行比较.【详解】解:∵点()11,A y -、()22,B y -、()33,C y 在反比例函数8y x =-的图象上, ∴1881y =-=-,2842y =-=-,383y =-, 又∵8483-<<, ∴321y y y <<.故选:D .【点睛】本题考查的是反比例函数的图象和性质,难度不大,理解点的坐标与函数图象的关系是解题的关键.20.如图,二次函数2y ax bx c =++的图象如图所示,则一次函数y ax c =+和反比例函数b y x=在同平面直角坐标系中的图象大致是( )A .B .C .D .【答案】D【解析】【分析】直接利用二次函数图象经过的象限得出a ,b ,c 的值取值范围,进而利用一次函数与反比例函数的性质得出答案.【详解】∵二次函数y=ax2+bx+c的图象开口向下,∴a<0,∵二次函数y=ax2+bx+c的图象经过原点,∴c=0,∵二次函数y=ax2+bx+c的图象对称轴在y轴左侧,∴a,b同号,∴b<0,∴一次函数y=ax+c,图象经过第二、四象限,反比例函数y=bx图象分布在第二、四象限,故选D.【点睛】此题主要考查了反比例函数、一次函数、二次函数的图象,正确把握相关性质是解题关键.。
反比例函数易错题汇编及答案解析

反比例函数易错题汇编及答案解析一、选择题1. 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x 轴平行,A, B两点k的纵坐标分别为4, 2,反比例函数y (x>0)的图象经过A, B两点,若菱形ABCD的xA. 2B. 3C. 4D. 6【答案】C【解析】【分析】过点A作x轴的垂线,交CB的延长线于点E,根据A, B两点的纵坐标分别为4, 2,可得出横坐标,即可求得AE, BE的长,根据菱形的面积为2 5,求得AE的长,在Rt A AEB 中,即可得出k的值.【详解】k••• A, B两点在反比例函数y — ( x>0)的图象,且纵坐标分别为4, 2,xk k二A( , 4), B ( , 2),4 21 1 1二AE= 2, BE k k k,2 4 4•••菱形ABCD的面积为2話,••• BCX AE= 2即BC 話,• - AB= BC J5 ,在 RtMEB 中,BEAB 2 AE 2 11-k = 14故选:C. 【点睛】本题考查了菱形的性质以及反比例函数图象上点的坐标特征,熟记菱形的面积公式是解题 的关键.k2. 如图,直线l 与x 轴、y 轴分别交于A 、B 两点,与反比例函数 y = 的图象在第一象限x【答案】C 【解析】 【分析】设0B = a ,根据相似三角形性质即可表示出点 C,把点C 代入反比例函数即可求得 k .【详解】作CD 丄x 轴于D, 设 0B = a , (a > 0) •••△ AOB 的面积为3,1•••严。
B = 3,6 0A = a•「CD // OB , .•.0D = 0A = 6 , CD = 20B = 2a ,a6.C (— , 2a ),ak「•反比例函数y = 经过点C ,xC. 12D . 183,则k 的值为(••• k = 6x 2殳12,ah丿X 0【点睛】本题考查直线和反比例函数的交点问题,待定系数法求函数解析式,会运用相似求线段长度是解题的关键.3. 如图,菱形OABC的顶点C的坐标为(3, 4),顶点A在x轴的正半轴上.反比例函数【答案】D【解析】【分析】【详解】如图,过点C作CD丄x轴于点D,•••点C 的坐标为(3, 4),二OD=3, CD=4.•根据勾股定理,得:OC=5.•••四边形OABC是菱形,•点B的坐标为(8, 4)D. 32C. 24•••点B 在反比例函数・(x>0)的图象上,•••四边形ABCD 为平行四边形,••• AD // x 轴,•••四边形ADOE 为矩形,•- S 平行四边形ABCD =S 矩形ADOE, 而S 矩形 ADOE =|k| ,•|k|=8 , 而k v 0 二 k=-8. 故选:B . 【点睛】kk本题考查了反比例函数 y=— ( k ^0系数k 的几何意义:从反比例函数y=— (20图象xx故选D.4.如图,点A 是反比例函数 ky = k(x v 0)的图象上的一点,过点 A 作平行四边形xABCD,使点B C 在x 轴上, 点D 在y 轴上•已知平行四边形 ABCD 的面积为8,则k 的值C. D .- 4【答案】B 【解析】 【分析】作AE 丄BC 于E ,由四边形 ABCD 为平行四边形得 形,所以S 平行四边形ABCD =S 矩形ADOE,根据反比例函数【详解】AD / x 轴,则可判断四边形 ADOE 为矩 k 的几何意义得到 S 矩形ADoE =|k|.8上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为 |k| .5.如图直线y = mx 与双曲线y=k 交于点xA 、B ,过A 作AM 丄x 轴于M 点,连接BM ,若C. 3 D .【解析】 【分析】此题可根据反比例函数图象的对称性得到 结合反比例函数系数 k 的几何意义得到 【详解】A 、B 两点关于原点对称,再由 k 的值.S A ABM =2S A AOM 并o 1S ZABM = 2S AOM = 2 , S/AOM = — | k|2则k =±2又由于反比例函数图象位于一三象限, k >0,所以k = 2.故选B . 【点睛】根据双曲线的对称性可得:OA=OB 则 1,k本题主要考查了反比例函数y = 中k 的几何意义,即过双曲线上任意x线,所得矩形面积为|k|,是经常考查的一个知识点.x 轴、y 轴垂OABF 中,/ OAB =Z B = 90 °点 A 在x 轴上,双曲线k y —过点F ,交xD . 166.如图,四边形A . 6B . 8 C. 12【答案】A【解析】【分析】由于BF 2,可以设F (m, n)贝U 0A=3m, BF=2m,由于S\BE(=4,贝U BE二4,然后即可OA 3 m4 4求出E (3m, n-),依据mn=3m (n-)可求mn=6,即求出k的值. m m【详解】如图,过F作FC丄OA于C,BF 2OA 3•••OA=3OC, BF=2OC •••若设F ( m, n) 则OA=3m, BF=2m■/ S^BEF=4BE= —则E (3m , n- 4)mk■/ E在双曲线y= 上x4•mn=3m (n-_m•mn=6即k=6.故选A.【点睛】此题主要考查了反比例函数的图象和性质、用坐标表示线段长和三角形面积,表示出坐标是解题关键.7.如图,在x轴的上方,直角/B O A绕原点O按顺时针方向旋转•若/B O A的两边分别与1函数y 、yx -的图象交于B、A两点,则/ OAB大小的变化趋势为() xA.逐渐变小【答案】D【解析】B.逐渐变大C.时大时小D.保持不变【分析】如图,作辅助线;首先证明ABEO^^ OFA,,得到更OF OE;设B为(a,丄),A为AF a2 1 (b, b),得到OE=-a,EB=;,2OF=b, AF=-,进而得到a2b22,此为解决问题的关b键性结论;运用三角函数的定义证明知tan / OAB=_12为定值,即可解决问题.2【详解】解:分别过B和A作BE丄x轴于点^△BEC^^ OFAAF丄x轴于点F,BE OEOF AF,设点B为(a, -),A 为(b, f )a b则OE=-a, EB=1, OF=b, AF=2, a b可代入比例式求得a2b22,即a2根据勾股定理可得:OB/• tan / OAB= -----OA•••/ OAB大小是一个定值,因此/ OAB的大小保持不变故选D【点睛】该题主要考查了反比例函数图象上点的坐标特征、相似三角形的判定等知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用相似三角形的判定等知识点来分析、判断、推理或解答.k-1 3-k&使关于x的分式方程X- 1=2的解为非负数,且使反比例函数y=尤图象过第一、三象限时满足条件的所有整数k的和为().A. 0B. 1C. 2D. 3【答案】B【解析】试题分析:分别根据题意确定k的值,然后相加即可.•••关于x的分式方程I =2的解为it + 1 3-k非负数,••• x= 2 >0解得:心1 ,••反比例函数y=女图象过第一、三象限,••• 3- k>0,解得:k v 3 ,• -1 <k< 3,整数为-1,0,1, 2, • x旳或1,•和为-1+2=1,故选,B.考点:反比例函数的性质.9.如图,YABDC的顶点A,B的坐标分别是A (0, 3),B 1, 0 ,顶点C,D在双曲线ky 上,边BD交y轴于点E,且四边形ACDE的面积是ABE面积的3倍,贝U k的值x为:()【答案】A【解析】【分析】过D作DF//y轴,过C作CF//X轴,交点为F,利用平行四边形的性质证明DCF ABO,利用平移写好C,D的坐标,由四边形ACDE的面积是ABE面积的3倍,得到DB 2BE,利用中点坐标公式求横坐标,再利用反比例函数写D的坐标,列方程求解k .【详解】解:过D作DF// y轴,过C作CF //X轴,交点为F ,则CF DF ,QY ABDC ,CDF , BAO的两边互相平行,AB DC,CDF BAO,Q DFC BOA 90 ,DCF ABO,CF BO, DF AO,k设C(m,—),mk由A(0, 3),B 1, 0结合平移可得:D(m 1,- 3),mQ四边形ACDE的面积是ABE面积的3倍,1—(DE CA)h BD13 — h BE BE ,2Q h BD h BE , AC BD,DE AC 3BEDE BD BE4BE,C. 3D. 12DB 2BE,k QD(m 1,3), B(1,0),X E 0,m一m 1 1小由中点坐标公式知:0,2m 2 ,k Q D(m 1,), m 1k k 3 ,2 1 2k 6.故选A .【点睛】本题考查的是反比例函数的图像与性质,平行四边形的性质,平移性质,中点坐标公式, 掌握以上知识点是解题关键.2 110.方程x 23x 1 0的根可视为函数 y=x+3的图象与函数y —的图象交点的横坐 x 标,则方程x 3 2x 1 0的实根x o 所在的范围是( )据四个选项中X 的取值代入两函数解析式,找出抛物线的图象在反比例函数上方和反比例 函数的图象在抛物线的上方两个点即可判定推断方程 x 3+2x-1=o 的实根x 所在范围.【详解】1 解:依题意得方程 x 3 2x 1 0的实根是函数y x2 2与y的图象交点的横坐标,xA . 0<x o < —4【答案】C 【解析】 【分析】1 1B . — <x o <4 3 1 1C. 一 <x o <3 2D . 1<X o <12首先根据题意推断方程 x 3+2x-仁0的实根是函数 y=x 2+2与y-的图象交点的横坐标,再根x这两个函数的图象如图所示,它们的交点在第一象限.当x=!时, y 2 x22-1, y14,此时抛物线的图象在反比例函数下方;416x1 当x=—时, y 2 x22舟,y13,此时抛物线的图象在反比例函数下方;3x1 当x=—时, y 2 x221, y12,此时抛物线的图象在反比例函数上方;2x当x=1时,y 2 x23, y -x1,此时抛物线的图象在反比例函数上方.1 1二方程x3 2x 1 0的实根x o所在范围为:—vx°v •3 2故选C.【点睛】此题考查了学生从图象中读取信息的数形结合能力•解决此类识图题,同学们要注意分析其中的关键点”,还要善于分析各图象的变化趋势.1-k11. 函数y= 与y=2x的图象没有交点,则k的取值范围是()xA. k<0B. k<1C. k>0D. k>1【答案】D【解析】【分析】由于两个函数没有交点,那么联立两函数解析式所得的方程无解.由此可求出k的取值范围.【详解】1-k 1-k 1-k令=2x,化简得:x2= ;由于两函数无交点,因此v 0,即卩k> 1.x 2 2故选D.【点睛】函数图象交点坐标为两函数解析式组成的方程组的解.如果两函数无交点,那么联立两函数解析式所得的方程(组)无解.12. 如图,过点C 1,2分别作x轴、y轴的平行线,交直线y x 5于A、B两点,k若反比例函数y (x 0)的图象与VABC有公共点,贝U k的取值范围是()xQc . 25 A. 2 k —4、XB. 2 k 6C. 2 k 4D. 4 k 6【答案】A【解析】【分析】由点C的坐标结合直线AB的解析式可得出点A、B的坐标,求出反比例函数图象过点C时的k值,将直线AB的解析式代入反比例函数解析式中,令其根的判别式△为可求出k的取值范围,取其最大值,找出此时交点的横坐标,进而可得出此点在线段AB上,综上即可得出结论.【详解】解:令y = -X+ 5 中x= 1,贝y y = 4,二B (1 , 4);令y= -x+ 5 中y= 2,则x= 3,•- A (3, 2),当反比例函数y kxk (x> 0)的图象过点C时,有2 =1解得:k= 2,将y= - x+ 5代入y k 2中,整理得:X2-5X+ k= 0 , x•••△=( -5) 2-4k >025 5当k= 时,解得:x =4 25•/ 1 v v 3,2k 25•••若反比例函数y (x> 0)的图象与A ABC有公共点,则k的取值范围是2< k<x 4故选:A .【点睛】本题考查了反比例函数与一次函数的交点问题,解题的关键是求出反比例函数图象过点A 、C 时的k 值以及直线与双曲线有一个交点时 k 的值.13. 如图,在平面直角坐标系中,点 ky= (x>0)的图象与线段 AB 相交于点x13连接OC,如图,利用三角形面积公式得到S AAOC = S AOAB =,再根据反比例函数系数k 的2 一1 3 几何意义得到—|k|=,然后利用反比例函数的性质确定22••• BA 丄x 轴于点A , C 是线段AB 的中点,o 13…S A AOC = — S OAB =—,2 2 而 S ZAOC = — |k| ,21 3 二 2|k|= 3,B 在第一象限,BA 丄x 轴于点A ,反比例函数C ,且C 是线段AB 的中点,若△OAB 的面积为3,则kB . 1C. 2 D . 3k 的值.A.-3【答案】D 【解析】 【分析】【详解】而 k >0,k=3.故选:D . 【点睛】k此题考查反比例函数系数 k 的几何意义,解题关键在于掌握在反比例函数 y= 图象中任取x一点,过这一个点向 x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值|k| .k 在第一象限的图象如图所示,则k 的值可能是()xA . 3B . 5 C. 6 D . 8【答案】B 【解析】 【分析】根据点(1, 3)在反比例函数图象下方,点( 3, 2)在反比例函数图象上方可得出 k 的取值范围,即可得答案• 【详解】•••点(1, 3)在反比例函数图象下方,••• k>3,•••点(3, 2)在反比例函数图象上方, • —<2,即 k<6,33<k<6,故选:B. 【点睛】本题考查了反比例函数的图象的性质,熟记k=xy 是解题关键.2 一15.如图,在平面直角坐标系中,函数y kx 与y的图象交于 A 、B 两点,过A 作yx4轴的垂线,交函数 y的图象于点 C,连接BC,则△ABC 的面积为()x14.反比例函数yA . 2【答案】C 【解析】 【分析】连接0C,根据图象先证明 △AOC 与A COB 的面积相等,再根据题意分别计算出 A AOD 与△ODC 的面积即可得 A ABC 的面积. 【详解】连接0C,设AC 丄y 轴交y 轴为点D , 如图,2 •••反比例函数y 二 为对称图形,x•••0为AB 的中点,二 S A AOC F S COB ,24 •.•由题意得A 点在y=-上,B 点在y= 上,xxC1 1…S A AOD = X OC K AD= xy=1 ;2 211S^OD =X OC X 0D=xy=2: 2 2S ZA OC = S^AOD + S A .COD =3 ,•- S A ABC = S^AOC +S A COB =6. 故答案选C. 【点睛】本题考查了一次函数与反比例函数的交点问题与三角形面积公式,解题的关键是熟练的掌 握一次函数与反比例函数的交点问题与三角形面积运算C. 6 D .816.如图,点A , B 是双曲线y 18图象上的两点,连接 AB ,线段AB 经过点O ,点xkC 为双曲线y在第二象限的分支上一点,当 VABC 满足AC BC 且x和1 丿“ .r •/ AC BC, OA OB •••OC 丄 AB , •••/ CFO=Z COA =Z AEO = 90° °•••/ COF ^Z AOE = 90°, / AOE +Z EAO= 90° ° •••/ COF =Z OAE, • △ CF3A OEA,SCOF (OC )2 s^OE (O A ),AC: AB 13:24 时,k 的值为()•25 A.-16【答案】B 【解析】 B .25C.25D . 25【分析】 如图作AE 丄x 轴于E, CF 丄x 轴于F .连接OC .首先证明△CF3A OEA,推出S COF S AOE OC 2(OA ),因为CA : AB = 13:24, AO = OB ,推出 CA : OA = 13: 12,推出 CO OA =5: 12,S COF 可得出S — SAOE(OC )2 __25 OA 14425,因为S" 9,可得沁=-,再根据反比例函数的几何意义即可解决问题. 【详解】CF 丄x 轴于F .连接OC.•/ CA: AB= 13: 24, AO= OB,••• CA:OA= 13 : 12,••• CO: OA= 5: 12,S COF ,OC\2 25()=-SAOE 144• ' Sm oE= 9,• - S A COF= 2516• |k| 25 "2 16•/ k v 0,258故选:B.【点睛】本题主要考查反比例函数图象上的点的特征、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,根据相似三角形解决问题,属于中考选择题中的压轴题.217.若反比例函数y 2m 1 x m 2的图象在第二、四象限,贝U m的值是()1A. -1或1B.小于一的任意实数C. -1D.不能确定2【答案】C【解析】【分析】根据反比例函数的定义列出方程m221且2m 1 0求解即可.【详解】解: Q y2(2m 1)x m 2是反比例函数,2 m2 1 , 2m 10, 解之得m1.又因为图象在第二,四象限,所以2m 1 0 ,1解得m ,即m的值是1.2故选:C .【点睛】k对于反比例函数y — k 0 .( 1) k 0,反比例函数图像分布在一、三象限;(2)xk 0,反比例函数图像分布在第二、四象限内.18.已知抛物线y=x 2+2x+k+1与x 轴有两个不同的交点,则一次函数y=kx - k 与反比例函数ky=—在同一坐标系内的大致图象是()【解析】【分析】依据抛物线 y=x 2+2x+k+1与x 轴有两个不同的交点,即可得到k v 0,进而得出k次函数y=kx - k 的图象经过第一二四象限,反比例函数 y=的图象在第二四象限,据此即x可作出判断•【详解】•••抛物线y=x 2+2x+k+1与x 轴有两个不同的交点,=4- 4 (k+1) > 0,解得k v 0,.一次函数y=kx - k 的图象经过第一二四象限,k反比例函数y=k 的图象在第二四象限,x故选D .【点睛】本题考查了二次函数的图象与x 轴的交点问题、反比例函数图象、一次函数图象等,根据抛物线与 x 轴的交点情况确定出 k 的取值范围是解本题的关键•k19. 如图,矩形 ABCD 的顶点A , B 在x 轴的正半轴上,反比例函数 y —在第一象限x内的图象经过点D,交BC 于点E .卄 m , CE 右 AB 4 ,BE2 AD,OA3 4,则线段BC 的长度为())f ||\ocXf jdA . 13 B.-2C. 2D. 2虫【答案】B【解析】【分析】设OA 为4a ,则根据题干中的比例关系,可得 AD=3a , CE=2q BE=a,从而得出点 D 和点E 的坐标(用a 表示),代入反比例函数可求得 a 的值,进而得出 BC 长.【详解】 设 OA=4a ••• D(4a , 3a), E(4a+4, a)将这两点代入解析得;k 4a 41解得:a=-2 3 ••• BC=AD=-2故选:B 【点睛】本题考查反比例函数和矩形的性质,解题关键是用含有字母的式子表示出点 D 、E 的坐标,然后代入解析式求解•20. 若函数y m ^的图象在其象限内y 的值随x 值的增大而增大,贝U m 的取值范围是x( )A . m > - 2B . m v - 2 C. m >2D . m v 2【答案】B 【解析】 【分析】根据反比例函数的性质,可得 m+2v 0,从而得出m 的取值范围.【详解】•••函数y m -2的图象在其象限内y 的值随x 值的增大而增大,x•. m+2 v 0, 解得m v -2. 故选B .根据BE4 得:A D =3a ,CE =2a BE =a3ak 4a。
(专题精选)初中数学反比例函数易错题汇编附答案解析

(专题精选)初中数学反比例函数易错题汇编附答案解析一、选择题1.已知反比例函数ky x=的图象分别位于第二、第四象限,()11,A x y 、()22,B x y 两点在该图象上,下列命题:①过点A 作AC x ⊥轴,C 为垂足,连接OA .若ACO ∆的面积为3,则6k =-;②若120x x <<,则12y y >;③若120x x +=,则120y y +=其中真命题个数是( )A .0B .1C .2D .3【答案】D 【解析】 【分析】根据反比例函数的性质,由题意可得k <0,y 1=,,sin cos 22x x x ππ⎡⎤∃∈-≤⎢⎥⎣⎦,y 2=2k x ,然后根据反比例函数k 的几何意义判断①,根据点位于的象限判断②,结合已知条件列式计算判断③,由此即可求得答案. 【详解】 ∵反比例函数ky x=的图象分别位于第二、第四象限, ∴k<0,∵()11,A x y 、()22,B x y 两点在该图象上, ∴y 1=,,sin cos 22x x x ππ⎡⎤∃∈-≤⎢⎥⎣⎦,y 2=2k x ,∴x 1y 1=k ,x 2y 2=k ,①过点A 作AC x ⊥轴,C 为垂足, ∴S △AOC =1OC?AC 2=11x ?y k =322=, ∴6k=-,故①正确;②若120x x <<,则点A 在第二象限,点B 在第四象限,所以12y y >,故②正确; ③∵120x x +=, ∴()121212120k x x k k y y x x x x ++=+==,故③正确, 故选D. 【点睛】本题考查了反比例函数的性质,反比例函数图象上点的坐标特征等,熟练掌握和灵活运用相关知识是解题的关键.2.如图,ABDC Y 的顶点,A B 的坐标分别是()(), 0,3 1, 0A B -,顶点,C D 在双曲线ky x =上,边BD 交y 轴于点E ,且四边形ACDE 的面积是ABE ∆面积的3倍,则k 的值为:( )A .6-B .4-C .3-D .12-【答案】A 【解析】 【分析】过D 作DF//y 轴,过C 作//CF x 轴,交点为F ,利用平行四边形的性质证明,DCF ABO ∆≅∆利用平移写好,C D 的坐标,由四边形ACDE 的面积是ABE ∆面积的3倍,得到2,DB BE =利用中点坐标公式求横坐标,再利用反比例函数写D 的坐标,列方程求解k . 【详解】解:过D 作DF//y 轴,过C 作//CF x 轴,交点为F , 则,CF DF ⊥ABDC QY ,,CDF BAO ∴∠∠的两边互相平行,,AB DC =CDF BAO ∴∠=∠, 90,DFC BOA ∠=∠=︒Q ,DCF ABO ∴∆≅∆ ,,CF BO DF AO ∴==设(,),k C m m由()(), 0,3 1, 0A B -结合平移可得:(1,3)kD m m++, Q 四边形ACDE 的面积是ABE ∆面积的3倍,11()322BD BE DE CA h h BE ∴+=⨯⨯, ,,BD BE h h AC BD ==Q3DE AC BE ∴+=, 4,DE BD BE BE ∴++= 2,DB BE ∴=(1,3),(1,0),0,E kD m B x m++=Q ∴ 由中点坐标公式知:110,2m ++= 2m ∴=- ,(1,)1kD m m ++Q ,3212k k ∴=+-+-, 6.k ∴=- 故选A .【点睛】本题考查的是反比例函数的图像与性质,平行四边形的性质,平移性质,中点坐标公式,掌握以上知识点是解题关键.3.如图,在平面直角坐标系中,点A 是函数()0ky x x=>在第一象限内图象上一动点,过点A 分别作AB x ⊥轴于点B AC y ⊥、轴于点C ,AB AC 、分别交函数()10y x x=>的图象于点E F 、,连接OE OF 、.当点A 的纵坐标逐渐增大时,四边形OFAE 的面积( )A .不变B .逐渐变大C .逐渐变小D .先变大后变小【答案】A 【解析】 【分析】根据反比例函数系数k 的几何意义得出矩形ACOB 的面积为k ,BOE S V COF S =V 12=,则四边形OFAE 的面积为定值1k -. 【详解】 ∵点A 是函数(0ky x x=>)在第一象限内图象上,过点A 分别作AB ⊥x 轴于点B ,AC ⊥y 轴于点C ,∴矩形ACOB 的面积为k , ∵点E 、F 在函数1y x=的图象上, ∴BOE S V COF S =V 12=, ∴四边形OFAE 的面积11122k k =--=-, 故四边形OFAE 的面积为定值1k -,保持不变, 故选:A . 【点睛】本题考查了反比例函数中系数k 的几何意义,根据反比例函数系数k 的几何意义可求出四边形和三角形的面积是解题的关键.4.如图,点P 是反比例函数(0)ky k x=≠的图象上任意一点,过点P 作PM x ⊥轴,垂足为M . 连接OP . 若POM ∆的面积等于2. 5,则k 的值等于 ( )A .5-B .5C . 2.5-D .2. 5【答案】A 【解析】 【分析】利用反比例函数k 的几何意义得到12|k|=2,然后根据反比例函数的性质和绝对值的意义确定k 的值. 【详解】解:∵△POM 的面积等于2.5, ∴12|k|=2.5, 而k <0, ∴k=-5, 故选:A . 【点睛】本题考查了反比例函数系数k 的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了反比例函数的性质.5.已知点()11,A y -、()22,B y -都在双曲线32my x+=上,且12y y >,则m 的取值范围是( ) A .0m < B .0m >C .32m >-D .32m <-【答案】D 【解析】 【分析】根据已知得3+2m <0,从而得出m 的取值范围. 【详解】∵点()11,A y -、()22,B y -两点在双曲线32my x+=上,且y 1>y 2, ∴3+2m <0,∴32 m<-,故选:D.【点睛】本题考查了反比例函数图象上点的坐标特征,当k>0时,该函数图象位于第一、三象限,当k<0时,函数图象位于第二、四象限.6.如图,A,B是反比例函数y=4x在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是()A.4 B.3 C.2 D.1【答案】B【解析】【分析】先根据反比例函数图象上点的坐标特征及A,B两点的横坐标,求出A(2,2),B(4,1).再过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,根据反比例函数系数k的几何意义得出S△AOC=S△BOD=12×4=2.根据S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,得出S△AOB=S梯形ABDC,利用梯形面积公式求出S梯形ABDC=12(BD+AC)•CD=12×(1+2)×2=3,从而得出S△AOB=3.【详解】∵A,B是反比例函数y=4x在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,∴当x=2时,y=2,即A(2,2),当x=4时,y=1,即B(4,1),如图,过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,则S△AOC=S△BOD=12×4=2,∵S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,∴S△AOB=S梯形ABDC,∵S梯形ABDC=12(BD+AC)•CD=12×(1+2)×2=3,∴S△AOB=3,故选B.【点睛】本题考查了反比例函数()0ky k x=≠中k 的几何意义,反比例函数图象上点的坐标特征,梯形的面积,熟知反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 与k 的关系为S=12|k|是解题的关键.7.如图,在x 轴的上方,直角∠BOA 绕原点O 按顺时针方向旋转.若∠BOA 的两边分别与函数1y x=-、2y x =的图象交于B 、A 两点,则∠OAB 大小的变化趋势为( )A .逐渐变小B .逐渐变大C .时大时小D .保持不变【答案】D 【解析】 【分析】如图,作辅助线;首先证明△BEO ∽△OFA ,,得到BE OE OF AF =;设B 为(a ,1a-),A 为(b ,2b ),得到OE=-a ,EB=1a-,OF=b ,AF=2b ,进而得到222a b =,此为解决问题的关键性结论;运用三角函数的定义证明知tan ∠OAB=22为定值,即可解决问题. 【详解】解:分别过B 和A 作BE ⊥x 轴于点E ,AF ⊥x 轴于点F , 则△BEO ∽△OFA , ∴BE OEOF AF=, 设点B 为(a ,1a-),A 为(b ,2b ),则OE=-a ,EB=1a-,OF=b ,AF=2b ,可代入比例式求得222a b =,即222a b =, 根据勾股定理可得:OB=22221OE EB a a +=+,OA=22224OF AF b b +=+, ∴tan ∠OAB=2222222212244b a OB a b OA b b bb++==++=222214()24b b b b ++=22∴∠OAB 大小是一个定值,因此∠OAB 的大小保持不变. 故选D【点睛】该题主要考查了反比例函数图象上点的坐标特征、相似三角形的判定等知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用相似三角形的判定等知识点来分析、判断、推理或解答.8.如图,,A B 是双曲线ky x=上两点,且,A B 两点的横坐标分别是1-和5,ABO -∆的面积为12,则k 的值为( )A .3-B .4-C .5-D .6-【答案】C 【解析】【分析】分别过点A 、B 作AD ⊥x 轴于点D ,BE ⊥x 轴于点E ,根据S △AOB =S 梯形ABED +S △AOD - S △BOE =12,故可得出k 的值. 【详解】分别过点A 、B 作AD ⊥x 轴于点D ,BE ⊥x 轴于点E ,∵双曲线ky x=的图象的一支在第二象限 ∴k<0,∵A ,B 两点在双曲线ky x =的图象上,且A ,B 两点横坐标分别为:-1,-5, ∴A (-1,-k ),B (-5, 5k-)∴S △AOB =S 梯形ABED +S △AOD - S △BOE=1||11||(||)(51)1||525225k k k k ⨯+⨯-+⨯⨯-⨯⨯=12||5k =12, 解得,k=-5 故选:C . 【点睛】本题考查反比例函数系数k 的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.9.如图,点P 是反比例函数y =kx(x <0)图象上一点,过P 向x 轴作垂线,垂足为M ,连接OP .若Rt △POM 的面积为2,则k 的值为( )A .4B .2C .-4D .-2【答案】C 【解析】 【分析】根据反比例函数的比例系数k的几何意义得到S△POD=12|k|=2,然后去绝对值确定满足条件的k的值.【详解】解:根据题意得S△POD=12|k|,所以12|k||=2,而k<0,所以k=-4.故选:C.【点睛】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.10.如图,菱形ABCD的两个顶点B、D在反比例函数y=的图象上,对角线AC与BD的交点恰好是坐标原点O,已知点A(1,1),∠ABC=60°,则k的值是()A.﹣5 B.﹣4 C.﹣3 D.﹣2【答案】C【解析】分析:根据题意可以求得点B的坐标,从而可以求得k的值.详解:∵四边形ABCD是菱形,∴BA=BC,AC⊥BD,∵∠ABC=60°,∴△ABC是等边三角形,∵点A (1,1),∴OA=, ∴BO=,∵直线AC 的解析式为y=x ,∴直线BD 的解析式为y=-x ,∵OB=,∴点B 的坐标为(−,), ∵点B 在反比例函数y=的图象上, ∴,解得,k=-3,故选C .点睛:本题考查反比例函数图象上点的坐标特征、菱形的性质,解答本题的关键是明确题意,利用反比例函数的性质解答.11.如图,在平面直角坐标系中,等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA x ⊥轴,点C 在函数()0k y x x=>的图象上,若1AB =,则k 的值为( )A .1B .22C 2D .2【答案】A【解析】【分析】 根据题意可以求得 OA 和 AC 的长,从而可以求得点 C 的坐标,进而求得 k 的值,本题得以解决.【详解】Q 等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA ⊥x 轴,1AB =,45BAC BAO ︒∴∠=∠=,2OA OB ∴==,AC =,∴点C 的坐标为⎝,Q 点C 在函数()0k y x x=>的图象上,12k ∴==, 故选:A .【点睛】本题考查反比例函数图象上点的坐标特征、等腰直角三角形,解答本题的关键 是明确题意,利用数形结合的思想解答.12.若A (-3,y 1)、B (-1,y 2)、C (1,y 3)三点都在反比例函数y=k x (k >0)的图象上,则y 1、y 2、y 3的大小关系是( )A . y 1>y 2>y 3B . y 3>y 1>y 2C . y 3>y 2>y 1D . y 2>y 1>y 3 【答案】B【解析】【分析】反比例函数y=k x(k >0)的图象在一、三象限,根据反比例函数的性质,在每个象限内y 随x 的增大而减小,而A (-3,y 1)、B (-1,y 2)在第三象限双曲线上的点,可得y 2<y 1<0,C (1,y 3)在第一象限双曲线上的点y 3>0,于是对y 1、y 2、y 3的大小关系做出判断.【详解】∵反比例函数y=k x(k >0)的图象在一、三象限, ∴在每个象限内y 随x 的增大而减小,∵A (-3,y 1)、B (-1,y 2)在第三象限双曲线上,∴y 2<y 1<0,∵C (1,y 3)在第一象限双曲线上,∴y 3>0,∴y 3>y 1>y 2,故选:B .【点睛】此题考查反比例函数的图象和性质,解题关键在于当k >0,时,在每个象限内y 随x 的增大而减小;当k <0时,y 随x 的增大而增大,注意“在每个象限内”的意义,这种类型题目用图象法比较直观得出答案.13.如图,已知在平面直角坐标系中,点O 是坐标原点,AOB V 是直角三角形,90AOB ∠=︒,2OB OA =,点B 在反比例函数2y x =上,若点A 在反比例函数k y x=上,则k 的值为( )A .12B .12-C .14D .14- 【答案】B【解析】【分析】通过添加辅助线构造出相似三角形,再根据相似三角形的性质可求得1,2x A x ⎛⎫-⎪⎝⎭,然后由点的坐标即可求得答案.【详解】解:过点B 作BE x ⊥于点E ,过点A 作AF x ⊥于点F ,如图:∵点B 在反比例函数2y x =上 ∴设2,B x x ⎛⎫ ⎪⎝⎭∴OE x =,2BE x=∵90AOB ∠=︒ ∴90AOD BOD ∠+∠=︒∴90BOE AOF ∠+∠=︒∵BE x ⊥,AF x ⊥∴90BEO OFA ∠=∠=︒∴90OAF AOF ∠+∠=︒∴BOE OAF ∠=∠∴BOE OAF V V ∽∵2OB OA = ∴12OF AF OA BE OE BO ===∴121122OF BE x x =⋅=⋅=,11222x AF OE x =⋅=⋅= ∴1,2x A x ⎛⎫- ⎪⎝⎭∵点A 在反比例函数k y x=上 ∴12x k x=- ∴12k =-. 故选:B【点睛】本题考查了反比例函数与相似三角形的综合应用,点在函数图象上则点的坐标就满足函数解析式,结合已知条件能根据相似三角形的性质求得点A 的坐标是解决问题的关键.14.矩形ABCO 如图摆放,点B 在y 轴上,点C 在反比例函数y k x=(x >0)上,OA =2,AB =4,则k 的值为( )A .4B .6C .325D .425【答案】C【解析】【分析】 根据矩形的性质得到∠A=∠AOC=90°,OC=AB ,根据勾股定理得到OB 22OA AB =+=25,过C 作CD ⊥x 轴于D ,根据相似三角形的性质得到CD 85=,OD 45=, 求得C (8545,)于是得到结论. 【详解】解:∵四边形ABCO 是矩形,∴∠A =∠AOC =90°,OC =AB ,∵OA =2,AB =4,∴过C 作CD ⊥x 轴于D ,∴∠CDO =∠A =90°,∠COD+∠COB =∠COB+∠AOB =90°,∴∠COD =∠AOB ,∴△AOB ∽△DOC ,∴OB AB OA OC CD OD ==, ∴2542CD OD==, ∴CD 855=,OD 45=, ∴C(455,855), ∴k 325=, 故选:C .【点睛】本题考查了反比例函数图象上点的坐标特征,反比例函数的性质,矩形的性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.15.如图,若直线2y x n =-+与y 轴交于点B ,与双曲线()20y x x=-<交于点(),1A m ,则AOB V 的面积为( )A .6B .5C .3D .1.5【答案】C【解析】【分析】 先根据题意求出A 点坐标,再求出一次函数解析式,从而求出B 点坐标,则问题可解.【详解】解:由已知直线2y x n =-+与y 轴交于点B ,与双曲线()20y x x =-<交于点(),1A m ∴21m=-则m=-2 把A (-2,1)代入到2y x n =-+,得()122n =-⨯-+∴n=-3∴23y x =--则点B (0,-3)∴AOB V 的面积为132=32⨯⨯ 故应选:C【点睛】本题考查的是反比例函数与一次函数的综合问题,解题关键是根据题意应用数形结合思想.16.如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A 在反比例函数y=6x(x >0)的图象上,则经过点B 的反比例函数解析式为( )A .y=﹣6xB .y=﹣4xC .y=﹣2xD .y=2x【答案】C 【解析】【分析】直接利用相似三角形的判定与性质得出13 BCOAODSS= VV,进而得出S△AOD=3,即可得出答案.【详解】过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,∵∠BOA=90°,∴∠BOC+∠AOD=90°,∵∠AOD+∠OAD=90°,∴∠BOC=∠OAD,又∵∠BCO=∠ADO=90°,∴△BCO∽△ODA,∵BOAO=tan30°=3,∴13BCOAODSS=VV,∵12×AD×DO=12xy=3,∴S△BCO=12×BC×CO=13S△AOD=1,∵经过点B的反比例函数图象在第二象限,故反比例函数解析式为:y=﹣2x.故选C.【点睛】此题主要考查了相似三角形的判定与性质,反比例函数数的几何意义,正确得出S△AOD=2是解题关键.17.如图,点A,B是双曲线18yx=图象上的两点,连接AB,线段AB经过点O,点C为双曲线kyx=在第二象限的分支上一点,当ABCV满足AC BC=且:13:24AC AB=时,k的值为().A.2516-B.258-C.254-D.25-【答案】B【解析】【分析】如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.首先证明△CFO∽△OEA,推出2()COFAOES OCS OA∆∆=,因为CA:AB=13:24,AO=OB,推出CA:OA=13:12,推出CO:OA=5:12,可得出2()COFAOES OCS OA∆∆==25144,因为S△AOE=9,可得S△COF=2516,再根据反比例函数的几何意义即可解决问题.【详解】解:如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.∵A、B关于原点对称,∴OA=OB,∵AC=BC,OA=OB,∴OC⊥AB,∴∠CFO=∠COA=∠AEO=90°,∴∠COF+∠AOE=90°,∠AOE+∠EAO=90°,∴∠COF=∠OAE,∴△CFO∽△OEA,∴2()COFAOES OCS OA∆∆=,∵CA:AB=13:24,AO=OB,∴CA:OA=13:12,∴CO:OA=5:12,∴2()COF AOE S OC S OA ∆∆==25144, ∵S △AOE =9,∴S △COF =2516, ∴||25216k =, ∵k <0, ∴258k =- 故选:B .【点睛】本题主要考查反比例函数图象上的点的特征、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,根据相似三角形解决问题,属于中考选择题中的压轴题.18.若反比例函数()2221my m x -=-的图象在第二、四象限,则m 的值是( ) A .-1或1B .小于12的任意实数C .-1D .不能确定 【答案】C【解析】【分析】根据反比例函数的定义列出方程221m -=-且210m -<求解即可.【详解】解:22(21)m y m x -=-Q 是反比例函数,∴221m -=-,210m -≠,解之得1m =±.又因为图象在第二,四象限,所以210m -<, 解得12m <,即m 的值是1-. 故选:C .【点睛】 对于反比例函数()0k y k x=≠.(1)0k >,反比例函数图像分布在一、三象限;(2)k 0< ,反比例函数图像分布在第二、四象限内.19.反比例函数21k y x+=的图象上有两点()11,A a y -,()21,B a y +,若12y y <,则a 的取值范围( )A .1a <-B .1a >C .11a -<<D .这样的a 值不存在【答案】C【解析】【分析】由210k +>得出在同一分支上,反比例函数y 随x 的增大而减小,然后结合反比例函数的图象进行求解.【详解】 210k +>Q ,∴在同一分支上,反比例函数y 随x 的增大而减小,11a a -<+Q ,12y y <,∴点A ,B 不可能在同一分支上,只能为位于不同的两支上,10a ∴-<且10a +>,11a ∴-<<,故选C .【点睛】本题考查反比例函数的图象与性质,熟练掌握反比例函数的性质是解题的关键,注意反比例函数的图象有两个分支.20.若函数2m y x+=的图象在其象限内y 的值随x 值的增大而增大,则m 的取值范围是( )A .m >﹣2B .m <﹣2C .m >2D .m <2 【答案】B【解析】【分析】根据反比例函数的性质,可得m+2<0,从而得出m 的取值范围.【详解】 ∵函数2m y x+=的图象在其象限内y 的值随x 值的增大而增大, ∴m+2<0,解得m <-2.故选B .。
中考数学反比例函数(大题培优 易错 难题)含答案解析
中考数学反比例函数(大题培优易错难题)含答案解析一、反比例函数1.如图,平行于y轴的直尺(一部分)与双曲线y= (k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm.(1)求k的值;(2)求经过A、C两点的直线的解析式;(3)连接OA、OC,求△OAC的面积.【答案】(1)解:∵AB=5﹣2=3cm,OB=2cm,∴A的坐标是(2,3),代入y= 得3= ,解得:k=6(2)解:OD=2+2=4,在y= 中令x=4,解得y= .则C的坐标是(4,).设AC的解析式是y=mx+n,根据题意得:,解得:,则直线AC的解析式是y=﹣ x+(3)解:直角△AOB中,OB=2,AB=3,则S△AOB= OB•AB= ×2×3=3;直角△ODC中,OD=4,CD= ,则S△OCD= OD•CD= ×4× =3.在直角梯形ABDC中,BD=2,AB=3,CD= ,则S梯形ABDC= (AB+DC)•BD= (3+ )×2= .则S△OAC=S△AOB+S梯形ABDC﹣S△OCD=3+ ﹣3=【解析】【分析】(1)首先求得A的坐标,然后利用待定系数法求得函数的解析式;(2)首先求得C的坐标,然后利用待定系数法求得直线的解析式;(3)根据S△OAC=S△AOB+S梯形ABDC﹣S△OCD利用直角三角形和梯形的面积公式求解.2.如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b 时,有﹣1≤y1﹣y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b 上是“非相邻函数”.例如,点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x﹣1图象上的任一点,当﹣3≤x≤﹣1时,y1﹣y2=(3x+1)﹣(2x﹣1)=x+2,通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质,得到该函数值的范围是﹣1≤y≤1,所以﹣1≤y1﹣y2≤1成立,因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”.(1)判断函数y=3x+2与y=2x+1在﹣2≤x≤0上是否为“相邻函数”,并说明理由;(2)若函数y=x2﹣x与y=x﹣a在0≤x≤2上是“相邻函数”,求a的取值范围;(3)若函数y= 与y=﹣2x+4在1≤x≤2上是“相邻函数”,直接写出a的最大值与最小值.【答案】(1)解:是“相邻函数”,理由如下:y1﹣y2=(3x+2)﹣(2x+1)=x+1,构造函数y=x+1,∵y=x+1在﹣2≤x≤0,是随着x的增大而增大,∴当x=0时,函数有最大值1,当x=﹣2时,函数有最小值﹣1,即﹣1≤y≤1,∴﹣1≤y1﹣y2≤1,即函数y=3x+2与y=2x+1在﹣2≤x≤0上是“相邻函数”(2)解:y1﹣y2=(x2﹣x)﹣(x﹣a)=x2﹣2x+a,构造函数y=x2﹣2x+a,∵y=x2﹣2x+a=(x﹣1)2+(a﹣1),∴顶点坐标为:(1,a﹣1),又∵抛物线y=x2﹣2x+a的开口向上,∴当x=1时,函数有最小值a﹣1,当x=0或x=2时,函数有最大值a,即a﹣1≤y≤a,∵函数y=x2﹣x与y=x﹣a在0≤x≤2上是“相邻函数”,∴﹣1≤y1﹣y2≤1,即,∴0≤a≤1(3)解:y1﹣y2= ﹣(﹣2x+4)= +2x﹣4,构造函数y= +2x﹣4,∵y= +2x﹣4∴当x=1时,函数有最小值a﹣2,当x=2时,函数有最大值,即a﹣2≤y≤ ,∵函数y= 与y=﹣2x+4在1≤x≤2上是“相邻函数”,∴﹣1≤y1﹣y2≤1,即,∴1≤a≤2;∴a的最大值是2,a的最小值1【解析】【分析】(1)y1﹣y2=(3x+2)﹣(2x+1)=x+1,构造函数y=x+1,因为y=x+1在﹣2≤x≤0,是随着x的增大而增大,所以当x=0时,函数有最大值1,当x=﹣2时,函数有最小值﹣1,即﹣1≤y≤1,所以﹣1≤y1﹣y2≤1,即函数y=3x+2与y=2x+1在﹣2≤x≤0上是“相邻函数”;(2)y1﹣y2=(x2﹣x)﹣(x﹣a)=x2﹣2x+a,构造函数y=x2﹣2x+a,因为y=x2﹣2x+a=(x﹣1)2+(a﹣1),所以顶点坐标为:(1,a﹣1),又抛物线y=x2﹣2x+a的开口向上,所以当x=1时,函数有最小值a﹣1,当x=0或x=2时,函数有最大值a,即a﹣1≤y≤a,因为函数y=x2﹣x与y=x﹣a在0≤x≤2上是“相邻函数”,所以﹣1≤y1﹣y2≤1,即0≤a≤1;(3)当x=1时,函数有最小值a﹣2,当x=2时,函数有最大值,因为函数y=与y=﹣2x+4在1≤x≤2上是“相邻函数”,﹣1≤y1﹣y2≤1,即1≤a≤2,所以a的最大值是2,a 的最小值1.3.已知一次函数y=kx+b与反比例函数y= 交于A(﹣1,2),B(2,n),与y轴交于C 点.(1)求反比例函数和一次函数解析式;(2)如图1,若将y=kx+b向下平移,使平移后的直线与y轴交于F点,与双曲线交于D,E两点,若S△ABD=3,求D,E的坐标.(3)如图2,P为直线y=2上的一个动点,过点P作PQ∥y轴交直线AB于Q,交双曲线于R,若QR=2QP,求P点坐标.【答案】(1)解:点A(﹣1,2)在反比例函数y= 的图象上,∴m=(﹣1)×2=﹣2,∴反比例函数的表达式为y=﹣,∵点B(2,n)也在反比例函数的y=﹣图象上,∴n=﹣1,即B(2,﹣1)把点A(﹣1,2),点B(2,﹣1)代入一次函数y=kx+b中,得,解得:k=﹣1,b=1,∴一次函数的表达式为y=﹣x+1,答:反比例函数的表达式是y=﹣,一次函数的表达式是y=﹣x+1;(2)解:如图1,连接AF,BF,∵DE∥AB,∴S△ABF=S△ABD=3(同底等高的两三角形面积相等),∵直线AB的解析式为y=﹣x+1,∴C(0,1),设点F(0,m),∴AF=1﹣m,∴S△ABF=S△ACF+S△BCF= CF×|x A|+ CF×|x B|= (1﹣m)×(1+2)=3,∴m=﹣1,∴F(0,﹣1),∵直线DE的解析式为y=﹣x+1,且DE∥AB,∴直线DE的解析式为y=﹣x﹣1①.∵反比例函数的表达式为y=﹣②,联立①②解得,或∴D(﹣2,1),E(1,﹣2);(3)解:如图2由(1)知,直线AB的解析式为y=﹣x﹣1,双曲线的解析式为y=﹣,设点P(p,2),∴Q(p,﹣p﹣1),R(p,﹣),PQ=|2+p+1|,QR=|﹣p﹣1+ |,∵QR=2QP,∴|﹣p﹣1+ |=2|2+p+1|,解得,p= 或p= ,∴P(,2)或(,2)或(,2)或(,2).【解析】【分析】(1)把A的坐标代入反比例函数的解析式可求得m的值,从而可得到反比例函数的解析式;把点A和点B的坐标代入一次函数的解析式可求得一次函数的解析式;(2)依据同底等高的两个三角形的面积相等可得到S△ABF=S△ABD=3,再利用三角形的面积公式可求得点F的坐标,即可得出直线DE的解析式,即可求出交点坐标;(3)设点P(p,2),则Q(p,﹣p﹣1),R(p,﹣),然后可表示出PQ与QR的长度,最后依据QR=2QP,可得到关于p的方程,从而可求得p的值,从而可得到点P的坐标.4.已知:如图,正比例函数y=ax的图象与反比例函数y= 的图象交于点C(3,1)(1)试确定上述比例函数和反比例函数的表达式;(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?(3)点D(m,n)是反比例函数图象上的一动点,其中0<m<3,过点C作直线AC⊥x 轴于点A,交OD的延长线于点B;若点D是OB的中点,DE⊥x轴于点E,交OC于点F,试求四边形DFCB的面积.【答案】(1)解:将点C(3,1)分别代入y= 和y=ax,得:k=3,a= ,∴反比例函数解析式为y= ,正比例函数解析式为y= x;(2)解:观察图象可知,在第二象限内,当0<x<3时,反比例函数值大于正比例函数值;(3)解:∵点D(m,n)是OB的中点,又在反比例函数y= 上,∴OE= OA= ,点D(,2),∴点B(3,4),又∵点F在正比例函数y= x图象上,∴F(,),∴DF= 、BC=3、EA= ,∴四边形DFCB的面积为 ×( +3)× = .【解析】【分析】(1)利用待定系数法把C坐标代入解析式即可;(2)须数形结合,先找出交点,在交点的左侧与y轴之间,反比例函数值大于正比例函数值.(3)求出DF、BC、EA,代入梯形面积公式即可.5.如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y= 相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.(1)求双曲线和抛物线的解析式;(2)计算△ABC的面积;(3)如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.【答案】(1)解:把点A的坐标代入双曲线的解析式得:k=﹣1×4=﹣4.所以双曲线的解析式为y=﹣.设点B的坐标为(m,﹣m).∵点B在双曲线上,∴﹣m2=﹣4,解得m=2或m=﹣2.∵点B在第四象限,∴m=2.∴B(2,﹣2).将点A、B、C的坐标代入得:,解得:.∴抛物线的解析式为y=x2﹣3x.(2)解:如图1,连接AC、BC.令y=0,则x2﹣3x=0,∴x=0或x=3,∴C(3,0),∵A(﹣1,4),B(2,﹣2),∴直线AB的解析式为y=﹣2x+2,∵点D是直线AB与x轴的交点,∴D(1,0),∴S△ABC=S△ADC+S△BDC= ×2×4+ ×2×2=6;(3)解:存在,理由:如图2,由原抛物线的解析式为y=x2﹣3x=(x﹣)2﹣,∴原抛物线的顶点坐标为(,﹣),∴抛物线向左平移个单位,再向上平移个单位,而平移前A(﹣1,4),B(2,﹣2),∴平移后点A(﹣,),B(,),∴点A关于y轴的对称点A'(,),连接A'B并延长交y轴于点P,连接AP,由对称性知,∠APE=∠BPE,∴△APB的内切圆的圆心在y轴上,∵B(,),A'(,),∴直线A'B的解析式为y=3x﹣,∴P(0,﹣).【解析】【分析】(1)首先将点A的坐标代入反比例函数的解析式求得k的值,然后再求得B的值,最后根据点A的坐标求出双曲线的解析式,进而得出点B的坐标,最后,将点A、B、O三点的坐标代入抛物线的解析式,求得a、b、c的值即可;(2)由点A和点B的坐标可求得直线AB的解析式,然后将y=0可求得点D的横坐标,最后用三角形的面积和求解即可;(3)先确定出平移后点A,B的坐标,进而求出点A关于y轴的对称点的坐标,求出直线BA'的解析式即可得出点P的坐标.6.如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折现”)(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;(2)如图2,双曲线y= 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.①试求△PAD的面积的最大值;②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.【答案】(1)解:如图1,新函数的性质:1.函数的最小值为0;2.函数图象的对称轴为直线x=3.由题意得,点A的坐标为(-3,0),分两种情况:①当x-3时,y=x+3;②当x<-3时,设函数解析式为y=kx+b,在直线y=x+3中,当x=-4时,y=-1,则点(-4,-1)关于x轴的对称点为(-4,1),把点(-4,1),(-3,0),代入y=kx+b中,得:,解得:,∴y=-x-3.综上,新函数的解析式为y=.(2)解:如图2,①∵点C(1,a)在直线y=x+3上,∴a=4,∵点C(1,4)在反比例函数y=上,∴k=4,∴反比例函数的解析式为y=.∵点D是线段AC上一动点,∴设点D的坐标为(m,m+3),且-3<m<1,∵DP∥x轴,且点P在双曲线上,∴点P的坐标为(,m+3),∴PD=-m,∴S△PAD=(-m)(m+3)=m2-m+2=(m+)2+,∵a=<0,∴当m=时,S有最大值,最大值为,又∵-3<<1,∴△PAD的面积的最大值为.②在点D的运动的过程中,四边形PAEC不能为平行四边形,理由如下:当点D为AC的中点时,其坐标为(-1,2),此时点P的坐标为(2,2),点E的坐标为(-5,2),∵DP=3,DE=4,∴EP与AC不能互相平分,∴四边形PAEC不能为平行四边形.【解析】【分析】(1)根据一次函数的性质,结合函数图象写出新函数的两条性质;利用待定系数法求新函数解析式,注意分两种情况讨论;(2)①先求出点C的坐标,再利用待定系数法求出反比例函数解析式,设出点D的坐标,进而得到点P的坐标,再根据三角形的面积公式得出函数解析式,利用二次函数的性质求解即可;②先求出A的中点D的坐标,再计算DP、DE的长度,如果对角线互相平分,则能成为平行四边形,如若对角线不互相平分,则不能成为平行四边形.7.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= (m≠0)交于点A(2,﹣3)和点B(n,2).(1)求直线与双曲线的表达式;(2)对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.【答案】(1)解:∵双曲线y= (m≠0)经过点A(2,﹣3),∴m=﹣6.∴双曲线的表达式为y=﹣.∵点B(n,2)在双曲线y=﹣上,∴点B的坐标为(﹣3,2).∵直线y=kx+b经过点A(2,﹣3)和点B(﹣3,2),∴解得,∴直线的表达式为y=﹣x﹣1(2)解:符合条件的点P的坐标是(1,﹣6)或(6,﹣1).【解析】【分析】(1)把A的坐标代入可求出m,即可求出反比例函数解析式,把B点的坐标代入反比例函数解析式,即可求出n,把A,B的坐标代入一次函数解析式即可求出一次函数解析式;(2)根据图象和函数解析式得出即可.8.如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y= 的图象经过D点.(1)证明四边形ABCD为菱形;(2)求此反比例函数的解析式;(3)已知在y= 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.【答案】(1)解:∵A(0,4),B(﹣3,0),C(2,0),∴OA=4,OB=3,OC=2,∴AB= =5,BC=5,∴AB=BC,∵D为B点关于AC的对称点,∴AB=AD,CB=CD,∴AB=AD=CD=CB,∴四边形ABCD为菱形(2)解:∵四边形ABCD为菱形,∴D点的坐标为(5,4),反比例函数y= 的图象经过D点,∴4= ,∴k=20,∴反比例函数的解析式为:y=(3)解:∵四边形ABMN是平行四边形,∴AN∥BM,AN=BM,∴AN是BM经过平移得到的,∴首先BM向右平移了3个单位长度,∴N点的横坐标为3,代入y= ,得y= ,∴M点的纵坐标为:﹣4= ,∴M点的坐标为:(0,)【解析】【分析】(1)由A(0,4),B(﹣3,0),C(2,0),利用勾股定理可求得AB=5=BC,又由D为B点关于AC的对称点,可得AB=AD,BC=DC,即可证得AB=AD=CD=CB,继而证得四边形ABCD为菱形;(2)由四边形ABCD为菱形,可求得点D 的坐标,然后利用待定系数法,即可求得此反比例函数的解析式;(3)由四边形ABMN 是平行四边形,根据平移的性质,可求得点N的横坐标,代入反比例函数解析式,即可求得点N的坐标,继而求得M点的坐标.9.如图,已知二次函数的图象与y轴交于点A(0,4),与x 轴交于点B,C,点C坐标为(8,0),连接AB,AC.(1)请直接写出二次函数的解析式.(2)判断△ABC的形状,并说明理由.(3)若点N在x轴上运动,当以点A,N,C为顶点的三角形是等腰三角形时,请写出此时点N的坐标.【答案】(1)解:∵二次函数的图象与y轴交于点A(0,4),与x轴交于点B.C,点C坐标(8,0),∴解得∴抛物线表达式:(2)解:△ABC是直角三角形.令y=0,则解得x1=8,x2=-2,∴点B的坐标为(-2,0),由已知可得,在Rt△ABO中AB2=BO2+AO2=22+42=20,在Rt△AOC中AC2=AO2+CO2=42+82=80,又∴BC=OB+OC=2+8=10,∴在△ABC中AB2+AC2=20+80=102=BC2∴△ABC是直角三角形(3)解:∵A(0,4),C(8,0),AC= =4 ,①以A为圆心,以AC长为半径作圆,交轴于N,此时N的坐标为(-8,0),②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为( ,0)或( ,0)③作AC的垂直平分线,交g轴于N,此时N的坐标为(3,0),综上,若点N在轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(-8,0)、( ,0)、(3,0)、 ,0)【解析】【分析】(1)根据待定系数法即可求得;(2)根据拋物线的解析式求得B的坐标,然后根据勾股定理分别求得AB2=20,AC2=80,BC=10然后根据勾股定理的逆定理即可证得△ABC是直角三角形(3)分别以A.C两点为圆心,AC长为半径画弧,与m轴交于三个点,由AC的垂直平分线与c轴交于一个点,即可求得点N的坐标10.综合实践问题情景:某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无盖纸盒.操作探究:(1)若准备制作一个无盖的正方体形纸盒,如图1,下面的哪个图形经过折叠能围成无盖正方体形纸盒?(2)如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字?(3)如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒.①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕.②若四角各剪去了一个边长为xcm的小正方形,用含x的代数式表示这个纸盒的高为________cm,底面积为________cm2,当小正方形边长为4cm时,纸盒的容积为________cm3.【答案】(1)解:A.有田字,故A不能折叠成无盖正方体;B.只有4个小正方形,无盖的应该有5个小正方形,不能折叠成无盖正方体;C.可以折叠成无盖正方体;D.有6个小正方形,无盖的应该有5个小正方形,不能折叠成无盖正方体.故答案为:C.(2)解:正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,所以与“保”字相对的字是“卫”(3)x;(20﹣2x)2;576【解析】【解答】(3)解:①如图,②设剪去的小正方形的边长为x(cm),用含字母x的式子表示这个盒子的高为xcm,底面积为(20﹣2x)2cm2,当小正方形边长为4cm时,纸盒的容积为=x(20﹣2x)2=4×(20﹣2×4)2=576(cm3).故答案为:x,(20﹣2x)2, 576【分析】(1)由平面图形的折叠及正方体的展开图解答本题;(2)正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,据此作答;(3)①根据题意,画出图形即可;②根据正方体底面积、体积,即可解答.11.【问题】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D 在直线l上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.(1)【探究发现】如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点D 移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;(2)【数学思考】如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程;(3)【拓展引申】如图4,在(1)的条件下,M是AB边上任意一点(不含端点A、B),N是射线BD上一点,且AM=BN,连接MN与BC交于点Q,这个数学兴趣小组经过多次取M点反复进行实验,发现点M在某一位置时BQ的值最大.若AC=BC=4,请你直接写出BQ的最大值.【答案】(1)解:∵∠ACB=90°,AC=BC∴∠CAB=∠CBA=45°∵CD∥AB∴∠CBA=∠DCB=45°,且BD⊥CD∴∠DCB=∠DBC=45°∴DB=DC即DB=DP(2)解:∵DG⊥CD,∠DCB=45°∴∠DCG=∠DGC=45°∴DC=DG,∠DCP=∠DGB=135°,∵∠BDP=∠CDG=90°∴∠CDP=∠BDG,且DC=DG,∠DCP=∠DGB=135°,∴△CDP≌△GDB(ASA)∴DB=DP(3)解:如图4,过点M作MH⊥MN交AC于点H,连接CM,HQ,∵MH⊥MN,∴∠AMH+∠NMB=90°∵CD∥AB,∠CDB=90°∴∠DBM=90°∴∠NMB+∠MNB=90°∴∠HMA=∠MNB,且AM=BN,∠CAB=∠CBN=45°∴△AMH≌△BNQ(ASA)∴AH=BQ∵∠ACB=90°,AC=BC=4,∴AB=4 ,AC-AH=BC-BQ∴CH=CQ∴∠CHQ=∠CQH=45°=∠CAB∴HQ∥AB∴∠HQM=∠QMB∵∠ACB=∠HMQ=90°∴点H,点M,点Q,点C四点共圆,∴∠HCM=∠HQM∴∠HCM=∠QMB,且∠A=∠CBA=45°∴△ACM∽△BMQ∴∴∴BQ= +2∴AM=2 时,BQ有最大值为2.【解析】【分析】(1)DB=DP,理由如下:根据等腰直角三角形的性质得出∠CAB=∠CBA=45°,根据二直线平行,内错角相等得出∠CBA=∠DCB=45°,根据三角形的内角和得出∠DCB=∠DBC=45°,最后根据等角对等边得出 DB=DC ,即DB=DP;(2)利用ASA判断出△CDP≌△GDB ,再根据全等三角形的对应边相等得出DB=DP;(3)如图4,过点M作MH⊥MN交AC于点H,连接CM,HQ,利用ASA判断出△AMH≌△BNQ 根据全等三角形的对应边相等得出AH=BQ,进而判断出点H,点M,点Q,点C四点共圆,根据圆周角定理得出∠HCM=∠HQM ,然后判断出△ACM∽△BMQ ,根据相似三角形的对应边成比例得出,根据比例式及偶数次幂的非负性即可得出求出答案.12.在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.(1)求抛物线的顶点坐标;(2)横、纵坐标都是整数的点叫做整点.①当m=1时,求线段AB上整点的个数;②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.【答案】(1)解:将抛物线表达式变为顶点式,则抛物线顶点坐标为(1,-1);(2)解:①m=1时,抛物线表达式为,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个;②抛物线顶点为(1,-1),则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;又有抛物线表达式,令y=0,则,得到A、B两点坐标分别为(,0),(,0),即5个整点是以(1,0)为中心向两侧分散,进而得到,∴.【解析】【分析】(1)将抛物线表达式变为顶点式,即可得到顶点坐标;(2)①m=1时,抛物线表达式为,即可得到A、B的坐标,可得到线段AB上的整点个数;②抛物线顶点为(1,-1),则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;令y=0,则,解方程可得到A、B两点坐标分别为(,0),(,0),即5个整点是以(1,0)为中心向两侧分散,进而得到,即可得到结论.。
九年级数学反比例函数的专项培优 易错 难题练习题(含答案)及详细答案

九年级数学反比例函数的专项培优易错难题练习题(含答案)及详细答案一、反比例函数1.如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2= (c≠0)的图象相交于点B(3,2)、C(﹣1,n).(1)求一次函数和反比例函数的解析式;(2)根据图象,直接写出y1>y2时x的取值范围;(3)在y轴上是否存在点P,使△PAB为直角三角形?如果存在,请求点P的坐标;若不存在,请说明理由.【答案】(1)解:把B(3,2)代入得:k=6∴反比例函数解析式为:把C(﹣1,n)代入,得:n=﹣6∴C(﹣1,﹣6)把B(3,2)、C(﹣1,﹣6)分别代入y1=ax+b,得:,解得:所以一次函数解析式为y1=2x﹣4(2)解:由图可知,当写出y1>y2时x的取值范围是﹣1<x<0或者x>3.(3)解:y轴上存在点P,使△PAB为直角三角形如图,过B作BP1⊥y轴于P1,∠B P1 A=0,△P1AB为直角三角形此时,P1(0,2)过B作BP2⊥AB交y轴于P2∠P2BA=90,△P2AB为直角三角形在Rt△P1AB中,在Rt△P1 AB和Rt△P2 AB∴∴P2(0,)综上所述,P1(0,2)、P2(0,).【解析】【分析】(1)利用待定系数法求出反比例函数解析式,进而求出点C坐标,最后用再用待定系数法求出一次函数解析式;(2)利用图象直接得出结论;(3)分三种情况,利用勾股定理或锐角三角函数的定义建立方程求解即可得出结论.2.如图,四边形OP1A1B1、A1P2A2B2、A2P3A3B3、…、A n﹣1P n A n B n都是正方形,对角线OA1、A1A2、A2A3、…、A n﹣1A n都在y轴上(n≥1的整数),点P1(x1,y1),点P2(x2,y2),…,P n(x n, y n)在反比例函数y= (x>0)的图象上,并已知B1(﹣1,1).(1)求反比例函数y= 的解析式;(2)求点P2和点P3的坐标;(3)由(1)、(2)的结果或规律试猜想并直接写出:△P n B n O的面积为 ________ ,点P n的坐标为________ (用含n的式子表示).【答案】(1)解:在正方形OP1A1B1中,OA1是对角线,则B1与P1关于y轴对称,∵B1(﹣1,1),∴P1(1,1).则k=1×1=1,即反比例函数解析式为y=(2)解:连接P2B2、P3B3,分别交y轴于点E、F,又点P1的坐标为(1,1),∴OA1=2,设点P2的坐标为(a,a+2),代入y=得a=-1,故点P2的坐标为(-1,+1),则A1E=A2E=2-2,OA2=OA1+A1A2=2,设点P3的坐标为(b,b+2),代入y=(>0)可得b=-,故点P3的坐标为(-,+)(3)1;(-,+)【解析】【解答】解:(3)∵=2=2×=1,=2=2×=1,…∴△P n B n O的面积为1,由P1(1,1)、P2(﹣1, +1)、P3(﹣,+ )知点P n的坐标为(﹣,+ ),故答案为:1、(﹣, +).【分析】(1)由四边形OP1A1B1为正方形且OA1是对角线知B1与P1关于y轴对称,得出点P1(1,1),然后利用待定系数法求解即可;(2)连接P2B2、P3B3,分别交y轴于点E、F,由点P1坐标及正方形的性质知OA1=2,设P2的坐标为(a,a+2),代入解析式求得a的值即可,同理可得点P3的坐标;(3)先分别求得S△P1B1O、S△P2B2O的值,然后找出其中的规律,最后依据规律进行计算即可.3.平面直角坐标系xOy中,点A、B分别在函数y1= (x>0)与y2=﹣(x<0)的图象上,A、B的横坐标分别为a、b.(1)若AB∥x轴,求△OAB的面积;(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;(3)作边长为2的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于3的任意实数a,CD边与函数y1= (x>0)的图象都有交点,请说明理由.【答案】(1)解:由题意知,点A(a,),B(b,﹣),∵AB∥x轴,∴,∴a=﹣b;∴AB=a﹣b=2a,∴S△OAB= •2a• =3(2)解:由(1)知,点A(a,),B(b,﹣),∴OA2=a2+()2, OB2=b2+(﹣)2,∵△OAB是以AB为底边的等腰三角形,∴OA=OB,∴OA2=OB2,∴a2+()2=b2+(﹣)2,∴a2﹣b2=()2﹣()2,∴(a+b)(a﹣b)=( + )(﹣)= ,∵a>0,b<0,∴ab<0,a﹣b≠0,∵a+b≠0,∴1= ,∴ab=3(舍)或ab=﹣3,即:ab的值为﹣3;(3)解:对大于或等于3的任意实数a,CD边与函数y1= (x>0)的图象都有交点.理由:如图,∵a≥3,AC=2,∴直线CD在y轴右侧且平行于y轴,∴直线CD一定与函数y1= (x>0)的图象有交点,∵四边形ACDE是边长为2的正方形,且点D在点A(a,)的左上方,∴C(a﹣2,),∴D(a﹣2, +2),设直线CD与函数y1= (x>0)相交于点F,∴F(a﹣2,),∴FC= ﹣ = ,∴2﹣FC=2﹣ = ,∵a≥3,∴a﹣2>0,a﹣3≥0,∴≥0,∴2﹣FC≥0,∴FC≤2,∴点F在线段CD上,即:对大于或等于3的任意实数a,CD边与函数y1= (x>0)的图象都有交点.【解析】【分析】(1)先判断出a=﹣b,即可得出AB=2a,再利用三角形的面积公式即可得出结论;(2)利用等腰三角形的两腰相等建立方程求解即可得出结论;(3)先判断出直线CD和函数y1= (x>0)必有交点,根据点A的坐标确定出点C,F的坐标,进而得出FC,再判断FC与2的大小即可.4.如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=.(1)求该反比例函数和一次函数的解析式;(2)求△AOC的面积;(3)直接写出一次函数值大于反比例函数值时自变量x的取值范围.【答案】(1)解:作AD⊥x轴于D,如图,在Rt△OAD中,∵sin∠AOD= = ,∴AD= OA=4,∴OD= =3,∴A(﹣3,4),把A(﹣3,4)代入y= 得m=﹣4×3=﹣12,所以反比例函数解析式为y=﹣;把B(6,n)代入y=﹣得6n=﹣12,解得n=﹣2,把A(﹣3,4)、B(6,﹣2)分别代入y=kx+b得,解得,所以一次函数解析式为y=﹣x+2(2)解:当y=0时,﹣x+2=0,解得x=3,则C(3,0),所以S△AOC= ×4×3=6(3)解:当x<﹣3或0<x<6时,一次函数的值大于反比例函数的值【解析】【分析】(1)作AD⊥x轴于D,如图,先利用解直角三角形确定A(﹣3,4),再把A点坐标代入y= 可求得m=﹣12,则可得到反比例函数解析式;接着把B(6,n)代入反比例函数解析式求出n,然后把A和B点坐标分别代入y=kx+b得到关于a、b的方程组,再解方程组求出a和b的值,从而可确定一次函数解析式;(2)先确定C点坐标,然后根据三角形面积公式求解;(3)观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.5.如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点在轴正半轴上,顶点B在第一象限,线段,的长是一元二次方程的两根,,.(1)直接写出点的坐标________点 C的坐标________;(2)若反比例函数的图象经过点,求k的值;(3)如图过点作轴于点;在轴上是否存在点,使以,,为顶点的三角形与以,,为顶点的三角形相似?若存在,直接写出满足条件的点的坐标;若不存在,请说明理由.【答案】(1);(2)解:如图,过点作,垂足为,∵,∴,设,∵ =12,∴EC=12-x,在RtΔBEC中,,∴整理得:,解得:(不合题意舍去),,∴,,∴,把代入,得(3)解:存在.如图2,若点P在OD上,若△PDB∽△AOP,则,即,解得:OP=2或OP=6,∴P(0,2)或P(0,6);如图3,若点P在OD上方,△PDB∽△AOP,则,即,解得:OP=12,∴P(0,12);如图4,若点P在OD上方,△BDP∽△AOP,则,即,解得:OP=4+2 或OP=4-2 (不合题意舍去),∴P(0,4+2 );如图5,若点P在y轴负半轴,△PDB∽△AOP,则,即,解得:OP=-4+2 或-4-2 (不合题意舍去),则P点坐标为(0,4-2 )故点的坐标为:或或或或【解析】【解答】解:(1)解一元二次方程,解得:,所以,所以,;【分析】(1)首先利用直接开平方法求出方程的两根,从而得出OA=OC=6,进而得出A,C两点的坐标;(2)如图,过点作,垂足为,根据等腰直角三角形的性质得出,设,EC=12-x,在RtΔBEC中利用勾股定理建立方程,求解并检验即可得出BE,OE 的长从而得出B点的坐标,然后利用待定系数法即可求出反比例函数的解析式;(3)存在.如图2,若点P在OD上,若△PDB∽△AOP,根据相似三角形对应边成比例得出,根据比例式列出方程,求解即可得出P点的坐标;如图3,若点P在OD上方,△PDB∽△AOP,根据相似三角形对应边成比例得出则根据比例式列出方程,求解并检验即可得出P点的坐标;如图4,若点P在OD上方,△PDB∽△AOP,根据相似三角形对应边成比例得出,根据比例式列出方程,求解并检验即可得出P 点的坐标;如图5,若点P在y轴负半轴,△PDB∽△AOP,根据相似三角形对应边成比例得出,根据比例式列出方程,求解并检验即可得出P点的坐标,综上所述即可得出答案。
(易错题精选)初中数学反比例函数难题汇编及解析

(易错题精选)初中数学反比例函数难题汇编及解析一、选择题1.下列函数:①y=-x;②y=2x;③1yx=-;④y=x2.当x<0时,y随x的增大而减小的函数有()A.1 个B.2 个C.3 个D.4 个【答案】B【解析】【分析】分别根据一次函数、反比例函数及二次函数的性质进行逐一判断即可.【详解】一次函数y=-x中k<0,∴y随x的增大而减小,故本选项正确;∵正比例函数y=2x中,k=2,∴当x<0时,y随x的增大而增大,故本选项错误;∵反比例函数1yx-=中,k=-1<0,∴当x<0时函数的图像在第二象限,此时y随x的增大而增大,故本选项错误;∵二次函数y=x2,中a=1>0,∴此抛物线开口向上,当x<0时,y随x的增大而减小,故本选项正确.故选B.【点睛】本题考查的是一次函数、反比例函数及二次函数的性质,解题关键是根据题意判断出各函数的增减性.2.如图,是反比例函数3yx=和7yx=-在x轴上方的图象,x轴的平行线AB分别与这两个函数图象相交于点,A B,点P在x轴上.则点P从左到右的运动过程中,APB△的面积是()A.10 B.4 C.5 D.从小变大再变小【答案】C【解析】【分析】连接AO 、BO ,由AB ∥x 轴,得ABP ABO S S =V V ,结合反比例函数比例系数的几何意义,即可求解.【详解】连接AO 、BO ,设AB 与y 轴交于点C .∵AB ∥x 轴,∴ABP ABO S S =V V ,AB ⊥y 轴, ∵73522ABO BOC AOC S S S -=+=+=V V V , ∴APB △的面积是:5.故选C .【点睛】本题主要考查反比例函数比例系数的几何意义,掌握反比例函数图象上的点与原点的连线,反比例函数图象上的点垂直于坐标轴的垂线段以及坐标轴所围成的三角形面积等于反比例函数比例系数绝对值的一半,是解题的关键.3.如图,反比例函数y =2x的图象经过矩形OABC 的边AB 的中点D ,则矩形OABC 的面积为( )A .1B .2C .4D .8【答案】C【解析】【分析】 由反比例函数的系数k 的几何意义可知:2OA AD =g ,然后可求得OA AB g 的值,从而可求得矩形OABC 的面积.【详解】解:Q 反比例函数2y x=, 2OA AD ∴=g . D Q 是AB 的中点,2AB AD ∴=.∴矩形的面积2224OA AB AD OA ===⨯=g g .故选:C .【点睛】本题主要考查的是反比例函数k 的几何意义,掌握反比例函数系数k 的几何意义是解题的关键.4.如图,在平面直角坐标系中,点A 是函数()0k y x x=>在第一象限内图象上一动点,过点A 分别作AB x ⊥轴于点B AC y ⊥、轴于点C ,AB AC 、分别交函数()10y x x=>的图象于点E F 、,连接OE OF 、.当点A 的纵坐标逐渐增大时,四边形OFAE 的面积( )A .不变B .逐渐变大C .逐渐变小D .先变大后变小【答案】A【解析】【分析】 根据反比例函数系数k 的几何意义得出矩形ACOB 的面积为k ,BOE S V COF S =V 12=,则四边形OFAE 的面积为定值1k -.【详解】∵点A 是函数(0k y x x =>)在第一象限内图象上,过点A 分别作AB ⊥x 轴于点B ,AC ⊥y 轴于点C ,∴矩形ACOB 的面积为k ,∵点E 、F 在函数1y x =的图象上, ∴BOE S V COF S =V 12=, ∴四边形OFAE 的面积11122k k =--=-, 故四边形OFAE 的面积为定值1k -,保持不变,故选:A .【点睛】本题考查了反比例函数中系数k 的几何意义,根据反比例函数系数k 的几何意义可求出四边形和三角形的面积是解题的关键.5.ABC ∆的面积为2,边BC 的长为x ,边BC 上的高为y ,则y 与x 的变化规律用图象表示大致是( )A .B .C .D .【答案】A【解析】【分析】根据三角形面积公式得出y 与x 的函数解析式,根据解析式作出图象进行判断即可.【详解】根据题意得 122xy = ∴4y x=∵00x y >>,∴y 与x 的变化规律用图象表示大致是故答案为:A .【点睛】本题考查了反比例函数的图象问题,掌握反比例函数图象的性质是解题的关键.6.下列函数中,当x >0时,函数值y 随自变量x 的增大而减小的是( ) A .y =x 2B .y =xC .y =x+1D .1y x = 【答案】D【解析】【分析】需根据函数的性质得出函数的增减性,即可求出当x >0时,y 随x 的增大而减小的函数.【详解】解:A 、y =x 2是二次函数,开口向上,对称轴是y 轴,当x >0时,y 随x 的增大而增大,错误;B 、y =x 是一次函数k =1>0,y 随x 的增大而增大,错误;C 、y =x+1是一次函数k =1>0,y 随x 的增大而减小,错误;D 、1y x=是反比例函数,图象无语一三象限,在每个象限y 随x 的增大而减小,正确;故选D .【点睛】本题综合考查了二次函数、一次函数、反比例函数的性质,熟练掌握函数的性质是解题的关键.7.在平面直角坐标系xoy 中,函数()20y x x =<的图象与直线1l :()103y x b b =+<交于点A ,与直线2l :x b =交于点B ,直线1l 与2l 交于点C ,记函数()20y x x =<的图象在点A 、B 之间的部分与线段AC ,线段BC 围城的区域(不含边界)为W ,当4233b -≤≤-时,区域W 的整点个数为( ) A .3个 B .2个 C .1个 D .没有【答案】D【解析】【分析】根据解析式画出函数图象,根据图形W 得到整点个数进行选择.【详解】∵()20y x x=<,过整点(-1,-2),(-2,-1), 当b=43-时,如图:区域W 内没有整点,当b=23-时,区域W 内没有整点,∴4233b-≤≤-时图形W增大过程中,图形内没有整点,故选:D.【点睛】此题考查函数图象,根据函数解析式正确画出图象是解题的关键.8.如图,四边形OABF中,∠OAB=∠B=90°,点A在x轴上,双曲线kyx=过点F,交AB于点E,连接EF.若BF2OA3=,S△BEF=4,则k的值为()A.6 B.8 C.12 D.16【答案】A【解析】【分析】由于23BFOA=,可以设F(m,n)则OA=3m,BF=2m,由于S△BEF=4,则BE=4m,然后即可求出E(3m,n-4m),依据mn=3m(n-4m)可求mn=6,即求出k的值.【详解】如图,过F作FC⊥OA于C,∵23BF OA =, ∴OA=3OC ,BF=2OC∴若设F (m ,n )则OA=3m ,BF=2m∵S △BEF =4∴BE=4m则E (3m ,n-4m ) ∵E 在双曲线y=k x 上 ∴mn=3m (n-4m) ∴mn=6即k=6.故选A .【点睛】 此题主要考查了反比例函数的图象和性质、用坐标表示线段长和三角形面积,表示出E 点坐标是解题关键.9.如图,ABDC Y 的顶点,A B 的坐标分别是()(), 0,3 1, 0A B -,顶点,C D 在双曲线k y x=上,边BD 交y 轴于点E ,且四边形ACDE 的面积是ABE ∆面积的3倍,则k 的值为:( )A .6-B .4-C .3-D .12-【答案】A【解析】【分析】 过D 作DF//y 轴,过C 作//CF x 轴,交点为F ,利用平行四边形的性质证明,DCF ABO ∆≅∆利用平移写好,C D 的坐标,由四边形ACDE 的面积是ABE ∆面积的3倍,得到2,DB BE =利用中点坐标公式求横坐标,再利用反比例函数写D 的坐标,列方程求解k .【详解】解:过D 作DF//y 轴,过C 作//CF x 轴,交点为F ,则,CF DF ⊥ABDC QY ,,CDF BAO ∴∠∠的两边互相平行,,AB DC =CDF BAO ∴∠=∠,90,DFC BOA ∠=∠=︒Q,DCF ABO ∴∆≅∆,,CF BO DF AO ∴== 设(,),k C m m由()(), 0,3 1, 0A B -结合平移可得:(1,3)k D m m ++, Q 四边形ACDE 的面积是ABE ∆面积的3倍,11()322BD BE DE CA h h BE ∴+=⨯⨯, ,,BD BE h h AC BD ==Q3DE AC BE ∴+=,4,DE BD BE BE ∴++=2,DB BE ∴=(1,3),(1,0),0,E k D m B x m++=Q ∴ 由中点坐标公式知:110,2m ++= 2m ∴=- ,(1,)1k D m m ++Q , 3212k k ∴=+-+-, 6.k ∴=-故选A .【点睛】本题考查的是反比例函数的图像与性质,平行四边形的性质,平移性质,中点坐标公式,掌握以上知识点是解题关键.10.如图,在平面直角坐标系中,将△OAB (顶点为网格线交点)绕原点O 顺时针旋转90°,得到△OA ′B ′,若反比例函数y=k x的图象经过点A 的对应点A′,则k 的值为( )A .6B .﹣3C .3D .6【答案】C【解析】【分析】直接利用旋转的性质得出A′点坐标,再利用反比例函数的性质得出答案.【详解】如图所示:∵将△OAB (顶点为网格线交点)绕原点O 顺时针旋转90°,得到△OA ′B ′,反比例函数y=k x 的图象经过点A 的对应点A′, ∴A ′(3,1), 则把A′代入y=k x , 解得:k=3.故选C .【点睛】此题主要考查了反比例函数图象上点的坐标特征,正确得出A′点坐标是解题关键.11.如图,A 、C 是函数1y x=的图象上任意两点,过点A 作y 轴的垂线,垂足为B ,过点C 作y 轴的垂线,垂足为D .记Rt AOB ∆的面积为1S ,Rt COD ∆的面积为2S ,则1S 和2S 的大小关系是( )A .12S S >B .12S S <C .12=S SD .由A 、C 两点的位置确定【答案】C【解析】【分析】 根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系即S=12k|. 【详解】由题意得:S 1=S 2=12|k|=12. 故选:C .【点睛】本题主要考查了反比例函数y =k x中k 的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系即S=12|k|,是经常考查的一个知识点;这里体现了数形结合的思想.12.如图,在平面直角坐标系中,点B 在第一象限,BA ⊥x 轴于点A ,反比例函数y=k x(x>0)的图象与线段AB 相交于点C ,且C 是线段AB 的中点,若△OAB 的面积为3,则k 的值为 ( )A .13B .1C .2D .3【答案】D【解析】【分析】连接OC ,如图,利用三角形面积公式得到S △AOC =12S △OAB =32,再根据反比例函数系数k 的几何意义得到12|k|=32,然后利用反比例函数的性质确定k 的值. 【详解】连接OC ,如图,∵BA ⊥x 轴于点A ,C 是线段AB 的中点,∴S △AOC =12S △OAB =32, 而S △AOC =12|k|, ∴12|k|=32, 而k >0,∴k=3.故选:D .【点睛】此题考查反比例函数系数k 的几何意义,解题关键在于掌握在反比例函数y=k x图象中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.13.如图,在某温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体的体积(mL)V 与气体对气缸壁产生的压强(kPa)P 的关系可以用如图所示的函数图象进行表示,下列说法正确的是( )A .气压P 与体积V 的关系式为(0)P kV k =>B .当气压70P =时,体积V 的取值范围为70<V<80C .当体积V 变为原来的一半时,对应的气压P 也变为原来的一半D .当60100V 剟时,气压P 随着体积V 的增大而减小 【答案】D【解析】【分析】A.气压P与体积V表达式为P= kV,k>0,即可求解;B.当P=70时,600070V ,即可求解;C.当体积V变为原来的一半时,对应的气压P变为原来的两倍,即可求解;D.当60≤V≤100时,气压P随着体积V的增大而减小,即可求解.【详解】解:当V=60时,P=100,则PV=6000,A.气压P与体积V表达式为P= kV,k>0,故本选项不符合题意;B.当P=70时,V=600070>80,故本选项不符合题意;C.当体积V变为原来的一半时,对应的气压P变为原来的两倍,本选项不符合题意;D.当60≤V≤100时,气压P随着体积V的增大而减小,本选项符合题意;故选:D.【点睛】本题考查的是反比例函数综合运用.现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,进而根据字母代表的意思求解.14.若A(-3,y1)、B(-1,y2)、C(1,y3)三点都在反比例函数y=kx(k>0)的图象上,则y1、y2、y3的大小关系是()A. y1>y2>y3B. y3>y1>y2C. y3>y2>y1D. y2>y1>y3【答案】B【解析】【分析】反比例函数y=kx(k>0)的图象在一、三象限,根据反比例函数的性质,在每个象限内y随x的增大而减小,而A(-3,y1)、B(-1,y2)在第三象限双曲线上的点,可得y2<y1<0,C(1,y3)在第一象限双曲线上的点y3>0,于是对y1、y2、y3的大小关系做出判断.【详解】∵反比例函数y=kx(k>0)的图象在一、三象限,∴在每个象限内y随x的增大而减小,∵A(-3,y1)、B(-1,y2)在第三象限双曲线上,∴y2<y1<0,∵C(1,y3)在第一象限双曲线上,∴y3>0,∴y3>y1>y2,故选:B.【点睛】此题考查反比例函数的图象和性质,解题关键在于当k >0,时,在每个象限内y 随x 的增大而减小;当k <0时,y 随x 的增大而增大,注意“在每个象限内”的意义,这种类型题目用图象法比较直观得出答案.15.如图所示,已知()121,,2,2A y B y ⎛⎫ ⎪⎝⎭为反比例函数1y x =图象上的两点,动点(),0P x 在x 轴正半轴上运动,当AP BP -的值最大时,连结OA ,AOP ∆的面积是 ( )A .12B .1C .32D .52【答案】D【解析】【分析】先根据反比例函数解析式求出A ,B 的坐标,然后连接AB 并延长AB 交x 轴于点P ',当P 在P '位置时,PA PB AB -=,即此时AP BP -的值最大,利用待定系数法求出直线AB 的解析式,从而求出P '的坐标,进而利用面积公式求面积即可.【详解】当12x =时,2y = ,当2x =时,12y = , ∴11(,2),(2,)22A B .连接AB 并延长AB 交x 轴于点P ',当P 在P '位置时,PA PB AB -=,即此时AP BP -的值最大.设直线AB 的解析式为y kx b =+ , 将11(,2),(2,)22A B 代入解析式中得 122122k b k b ⎧+=⎪⎪⎨⎪+=⎪⎩解得152k b =-⎧⎪⎨=⎪⎩ , ∴直线AB 解析式为52y x =-+. 当0y =时,52x =,即5(,0)2P ', 115522222AOP A S OP y '∴=⋅=⨯⨯=V . 故选:D .【点睛】 本题主要考查一次函数与几何综合,掌握待定系数法以及找到AP BP -何时取最大值是解题的关键.16.若反比例函数()2221my m x -=-的图象在第二、四象限,则m 的值是( ) A .-1或1B .小于12的任意实数C .-1D .不能确定 【答案】C【解析】【分析】根据反比例函数的定义列出方程221m -=-且210m -<求解即可.【详解】解:22(21)m y m x -=-Q 是反比例函数,∴221m -=-,210m -≠,解之得1m =±.又因为图象在第二,四象限,所以210m -<, 解得12m <,即m 的值是1-. 故选:C . 【点睛】 对于反比例函数()0k y k x=≠.(1)0k >,反比例函数图像分布在一、三象限;(2)k 0< ,反比例函数图像分布在第二、四象限内.17.如图,点A 是反比例函数2(0)y x x=>的图象上任意一点,AB x P 轴交反比例函数3y x=-的图象于点B ,以AB 为边作ABCD Y ,其中C 、D 在x 轴上,则ABCD S Y 为( )A .2.5B .3.5C .4D .5【答案】D【解析】【分析】 过点B 作BH ⊥x 轴于H ,根据坐标特征可得点A 和点B 的纵坐标相同,由题意可设点A 的坐标为(2a,a ),点B 的坐标为(3a -,a ),即可求出BH 和AB ,最后根据平行四边形的面积公式即可求出结论.【详解】解:过点B 作BH ⊥x 轴于H∵四边形ABCD 为平行四边形∴//AB x 轴,CD=AB∴点A 和点B 的纵坐标相同由题意可设点A 的坐标为(2a ,a ),点B 的坐标为(3a -,a ) ∴BH=a ,CD=AB=2a -(3a -)=5a∴ABCD S Y =BH·CD=5 故选D .【点睛】此题考查的是反比例函数与几何图形的综合题,掌握利用反比例函数求几何图形的面积是解决此题的关键.18.如图,△AOB 是直角三角形,∠AOB =90°,△AOB 的两边分别与函数12,y y x x=-=的图象交于B 、A 两点,则等于( )A .22B .12C .14D .33【答案】A【解析】【分析】过点A,B 作AC ⊥x 轴,BD ⊥x 轴,垂足分别为C,D.根据条件得到△ACO ∽△ODB.根据反比例函数比例系数k 的几何意义得出2()S OBD OB S AOC OA ∆=∆=121=12利用相似三角形面积比等于相似比的平方得出2OB OA =【详解】 ∵∠AOB =90°,∴∠AOC +∠BOD =∠AOC +∠CAO =90°,∠CAO =∠BOD ,∴△ACO ∽△BDO ,∴2()S OBD OB S AOC OA∆=∆ , ∵S △AOC =12 ×2=1,S △BOD =12×1=12, ∴2()OB OA =121=12 , ∴2OB OA = 故选A .【点睛】此题考查了反比例函数图象上点的坐标特征和相似三角形的判定与性质,解题关键在于做辅助线,然后得到相似三角形再进行求解19.如图,平行于x 轴的直线与函数y =1k x(k 1>0,x >0),y =2k x (k 2>0,x >0)的图象分别相交于A ,B 两点,点A 在点B 的右侧,C 为x 轴上的一个动点,若△ABC 的面积为6,则k 1﹣k 2的值为( )A .12B .﹣12C .6D .﹣6【答案】A【解析】【分析】 △ABC 的面积=12•AB•y A ,先设A 、B 两点坐标(其y 坐标相同),然后计算相应线段长度,用面积公式即可求解.【详解】 解:设:A 、B 点的坐标分别是A (1k m ,m )、B (2k m ,m ), 则:△ABC 的面积=12•AB•y A =12•(1k m ﹣2k m )•m =6, 则k 1﹣k 2=12.故选:A .【点睛】此题主要考查了反比例函数系数的几何意义,以及图象上点的特点,求解函数问题的关键是要确定相应点坐标,通过设A 、B 两点坐标,表示出相应线段长度即可求解问题.20.如图,菱形ABCD的两个顶点B、D在反比例函数y=的图象上,对角线AC与BD的交点恰好是坐标原点O,已知点A(1,1),∠ABC=60°,则k的值是()A.﹣5 B.﹣4 C.﹣3 D.﹣2【答案】C【解析】分析:根据题意可以求得点B的坐标,从而可以求得k的值.详解:∵四边形ABCD是菱形,∴BA=BC,AC⊥BD,∵∠ABC=60°,∴△ABC是等边三角形,∵点A(1,1),∴OA=,∴BO=,∵直线AC的解析式为y=x,∴直线BD的解析式为y=-x,∵OB=,∴点B的坐标为(−,),∵点B在反比例函数y=的图象上,∴,解得,k=-3,故选C.点睛:本题考查反比例函数图象上点的坐标特征、菱形的性质,解答本题的关键是明确题意,利用反比例函数的性质解答.。
(易错题精选)初中数学反比例函数难题汇编含解析

(易错题精选)初中数学反比例函数难题汇编含解析一、选择题1.如图,一次函数1y ax b =+和反比例函数2k y x=的图象相交于A ,B 两点,则使12y y >成立的x 取值范围是( )A .20x -<<或04x <<B .2x <-或04x <<C .2x <-或4x >D .20x -<<或4x >【答案】B【解析】【分析】 根据图象找出一次函数图象在反比例函数图象上方时对应的自变量的取值范围即可.【详解】观察函数图象可发现:2x <-或04x <<时,一次函数图象在反比例函数图象上方, ∴使12y y >成立的x 取值范围是2x <-或04x <<,故选B .【点睛】本题考查了反比例函数与一次函数综合,函数与不等式,利用数形结合思想是解题的关键.2.已知点A (﹣2,y 1),B (a ,y 2),C (3,y 3)都在反比例函数4y x =的图象上,且﹣2<a <0,则( )A .y 1<y 2<y 3B .y 3<y 2<y 1C .y 3<y 1<y 2D .y 2<y 1<y 3 【答案】D【解析】【分析】根据k >0,在图象的每一支上,y 随x 的增大而减小,双曲线在第一三象限,逐一分析即可.【详解】∵反比例函数y=4x中的k=4>0, ∴在图象的每一支上,y 随x 的增大而减小,双曲线在第一三象限,∵-2<a <0,∴0>y 1>y 2,∵C (3,y 3)在第一象限,∴y 3>0,∴213y y y <<,故选D .【点睛】本题考查了反比例函数的性质,熟练地应用反比例函数的性质是解题的关键.3.如图,在平面直角坐标系中,点A 是函数()0k y x x=>在第一象限内图象上一动点,过点A 分别作AB x ⊥轴于点B AC y ⊥、轴于点C ,AB AC 、分别交函数()10y x x=>的图象于点E F 、,连接OE OF 、.当点A 的纵坐标逐渐增大时,四边形OFAE 的面积( )A .不变B .逐渐变大C .逐渐变小D .先变大后变小【答案】A【解析】【分析】 根据反比例函数系数k 的几何意义得出矩形ACOB 的面积为k ,BOE S V COF S =V 12=,则四边形OFAE 的面积为定值1k -.【详解】 ∵点A 是函数(0k y x x =>)在第一象限内图象上,过点A 分别作AB ⊥x 轴于点B ,AC ⊥y 轴于点C ,∴矩形ACOB 的面积为k ,∵点E 、F 在函数1y x =的图象上, ∴BOE S V COF S =V 12=, ∴四边形OFAE 的面积11122k k =--=-,故四边形OFAE 的面积为定值1k -,保持不变,故选:A .【点睛】本题考查了反比例函数中系数k 的几何意义,根据反比例函数系数k 的几何意义可求出四边形和三角形的面积是解题的关键.4.在同一直角坐标系中,函数y=k(x -1)与y=(0)k k x<的大致图象是 A . B . C . D .【答案】B【解析】【分析】【详解】解:k<0时,y=(0)k k x<的图象位于二、四象限, y=k(x -1)的图象经过第一、二、四象限,观察可知B 选项符合题意,故选B.5.已知点()11,A y -、()22,B y -都在双曲线32m y x +=上,且12y y >,则m 的取值范围是( )A .0m <B .0m >C .32m >-D .32m <- 【答案】D【解析】【分析】根据已知得3+2m <0,从而得出m 的取值范围.【详解】∵点()11,A y -、()22,B y -两点在双曲线32m y x+=上,且y 1>y 2, ∴3+2m <0, ∴32m <-, 故选:D .【点睛】本题考查了反比例函数图象上点的坐标特征,当k >0时,该函数图象位于第一、三象限,当k <0时,函数图象位于第二、四象限.6.如图,点A 、B 在函数k y x=(0x >,0k >且k 是常数)的图像上,且点A 在点B 的左侧过点A 作AM x ⊥轴,垂足为M ,过点B 作BN y ⊥轴,垂足为N ,AM 与BN 的交点为C ,连结AB 、MN .若CMN ∆和ABC ∆的面积分别为1和4,则k 的值为( )A .4B .2C 522D .6【答案】D【解析】 【分析】 设点M (a ,0),N (0,b ),然后可表示出点A 、B 、C 的坐标,根据CMN ∆的面积为1可求出ab =2,根据ABC ∆的面积为4列方程整理,可求出k .【详解】解:设点M (a ,0),N (0,b ),∵AM ⊥x 轴,且点A 在反比例函数k y x =的图象上, ∴点A 的坐标为(a ,k a ), ∵BN ⊥y 轴,同理可得:B (k b ,b ),则点C (a ,b ), ∵S △CMN =12NC•MC =12ab =1, ∴ab =2,∵AC =k a −b ,BC =k b−a , ∴S △ABC =12AC•BC =12(k a −b)•(k b −a)=4,即8k ab k ab a b--⋅=, ∴()2216k -=,解得:k =6或k =−2(舍去),故选:D .【点睛】本题考查反比例函数图象上点的坐标特征、三角形的面积计算等,解答本题的关键是明确题意,利用三角形的面积列方程求解.7.如图,反比例函数11k y x=的图象与正比例函数22y k x =的图象交于点(2,1),则使y 1>y 2的x 的取值范围是( )A .0<x <2B .x >2C .x >2或-2<x <0D .x <-2或0<x <2【答案】D【解析】【分析】 先根据反比例函数与正比例函数的性质求出B 点坐标,由函数图象即可得出结论.【详解】∵反比例函数与正比例函数的图象均关于原点对称,∴A 、B 两点关于原点对称.∵A (2,1),∴B (-2,-1).∵由函数图象可知,当0<x <2或x <-2时函数y 1的图象在y 2的上方,∴使y 1>y 2的x 的取值范围是x <-2或0<x <2.故选D.8.在平面直角坐标系xoy 中,函数()20y x x =<的图象与直线1l :()103y x b b =+<交于点A ,与直线2l :x b =交于点B ,直线1l 与2l 交于点C ,记函数()20y x x =<的图象在点A 、B 之间的部分与线段AC ,线段BC 围城的区域(不含边界)为W ,当4233b -≤≤-时,区域W 的整点个数为( ) A .3个 B .2个 C .1个 D .没有【答案】D【解析】【分析】根据解析式画出函数图象,根据图形W 得到整点个数进行选择.【详解】 ∵()20y x x =<,过整点(-1,-2),(-2,-1), 当b=43-时,如图:区域W 内没有整点,当b=23-时,区域W 内没有整点,∴4233b -≤≤-时图形W 增大过程中,图形内没有整点, 故选:D.【点睛】 此题考查函数图象,根据函数解析式正确画出图象是解题的关键.9.如图,ABDC Y 的顶点,A B 的坐标分别是()(), 0,3 1, 0A B -,顶点,C D 在双曲线k y x=上,边BD 交y 轴于点E ,且四边形ACDE 的面积是ABE ∆面积的3倍,则k 的值为:( )A .6-B .4-C .3-D .12-【答案】A【解析】【分析】 过D 作DF//y 轴,过C 作//CF x 轴,交点为F ,利用平行四边形的性质证明,DCF ABO ∆≅∆利用平移写好,C D 的坐标,由四边形ACDE 的面积是ABE ∆面积的3倍,得到2,DB BE =利用中点坐标公式求横坐标,再利用反比例函数写D 的坐标,列方程求解k .【详解】解:过D 作DF//y 轴,过C 作//CF x 轴,交点为F ,则,CF DF ⊥ABDC QY ,,CDF BAO ∴∠∠的两边互相平行,,AB DC =CDF BAO ∴∠=∠,90,DFC BOA ∠=∠=︒Q,DCF ABO ∴∆≅∆,,CF BO DF AO ∴== 设(,),k C m m由()(), 0,3 1, 0A B -结合平移可得:(1,3)k D m m ++, Q 四边形ACDE 的面积是ABE ∆面积的3倍,11()322BD BE DE CA h h BE ∴+=⨯⨯, ,,BD BE h h AC BD ==Q3DE AC BE ∴+=,4,DE BD BE BE ∴++=2,DB BE ∴=(1,3),(1,0),0,E k D m B x m++=Q ∴ 由中点坐标公式知:110,2m ++= 2m ∴=- ,(1,)1k D m m ++Q , 3212k k ∴=+-+-, 6.k ∴=-故选A .【点睛】本题考查的是反比例函数的图像与性质,平行四边形的性质,平移性质,中点坐标公式,掌握以上知识点是解题关键.10.函数k y x=与y kx k =-(0k ≠)在同一平面直角坐标系中的大致图象是( ) A . B . C . D .【答案】C【解析】【分析】分k>0和k<0两种情况确定正确的选项即可.【详解】当k:>0时,反比例函数的图象位于第一、三象限,一次函数的图象交 y 轴于负半轴,y 随着x 的增大而增大,A 选项错误,C 选项符合;当k<0时,反比例函数的图象位于第二、四象限,一次函数的图象交y 轴于正半轴,y 随着x 的增大而增减小,B. D 均错误,故选:C.【点睛】此题考查反比例函数的图象,一次函数的图象,熟记函数的性质是解题的关键.11.函数y =1-k x 与y =2x 的图象没有交点,则k 的取值范围是( ) A .k<0B .k<1C .k>0D .k>1【答案】D【解析】【分析】由于两个函数没有交点,那么联立两函数解析式所得的方程无解.由此可求出k 的取值范围.【详解】 令1-k x =2x ,化简得:x 2=1-2k ;由于两函数无交点,因此1-2k <0,即k >1. 故选D .【点睛】 函数图象交点坐标为两函数解析式组成的方程组的解.如果两函数无交点,那么联立两函数解析式所得的方程(组)无解.12.如图,二次函数2y ax bx c =++的图象如图所示,则一次函数y ax c =+和反比例函数b y x=在同平面直角坐标系中的图象大致是( )A .B .C .D .【答案】D【解析】【分析】直接利用二次函数图象经过的象限得出a,b,c的值取值范围,进而利用一次函数与反比例函数的性质得出答案.【详解】∵二次函数y=ax2+bx+c的图象开口向下,∴a<0,∵二次函数y=ax2+bx+c的图象经过原点,∴c=0,∵二次函数y=ax2+bx+c的图象对称轴在y轴左侧,∴a,b同号,∴b<0,∴一次函数y=ax+c,图象经过第二、四象限,反比例函数y=bx图象分布在第二、四象限,故选D.【点睛】此题主要考查了反比例函数、一次函数、二次函数的图象,正确把握相关性质是解题关键.13.如图,在平面直角坐标系中,函数y =kx 与y =-2x的图象交于 A、B 两点,过 A 作 y轴的垂线,交函数4yx=的图象于点 C,连接 BC,则△ABC 的面积为()A.2 B.4 C.6 D.8【答案】C【解析】【分析】连接OC,根据图象先证明△AOC与△COB的面积相等,再根据题意分别计算出△AOD与△ODC的面积即可得△ABC的面积.【详解】连接OC,设AC⊥y轴交y轴为点D,如图,∵反比例函数y=-2x为对称图形, ∴O 为AB 的中点,∴S △AOC =S △COB , ∵由题意得A 点在y=-2x 上,B 点在y=4x 上, ∴S △AOD =12×OD×AD=12xy=1; S △COD =12×OC×OD=12xy=2; S △AOC = S △AOD + S △COD =3,∴S △ABC = S △AOC +S △COB =6.故答案选C.【点睛】本题考查了一次函数与反比例函数的交点问题与三角形面积公式,解题的关键是熟练的掌握一次函数与反比例函数的交点问题与三角形面积运算.14.若反比例函数()2221my m x -=-的图象在第二、四象限,则m 的值是( ) A .-1或1B .小于12的任意实数C .-1D .不能确定 【答案】C【解析】【分析】根据反比例函数的定义列出方程221m -=-且210m -<求解即可.【详解】解:22(21)m y m x -=-Q 是反比例函数,∴221m -=-,210m -≠,解之得1m =±.又因为图象在第二,四象限,所以210m -<,解得12m <,即m 的值是1-. 故选:C . 【点睛】对于反比例函数()0k y k x=≠.(1)0k >,反比例函数图像分布在一、三象限;(2)k 0< ,反比例函数图像分布在第二、四象限内.15.如图,点A 在反比例函数3(0)y x x =-<的图象上,点B 在反比例函数3(0)y x x=>的图象上,点C 在x 轴的正半轴上,则平行四边形ABCO 的面积是( )A .6B .5C .4D .3【答案】A【解析】【分析】 因为四边形ABCO 是平行四边形,所以点A 、B 纵坐标相等,即可求得A 、B 横坐标,则AB 的长度即可求得,然后利用平行四边形面积公式即可求解.【详解】解:∵四边形ABCO 是平行四边形∴点A 、B 纵坐标相等设纵坐标为b ,将y=b 带入3(0)y x x =-<和3(0)y x x=>中, 则A 点横坐标为3b -,B 点横坐标为3b ∴AB=336()b b b--= ∴66ABCO S b b=⨯=Y 故选:A .【点睛】 本题考查了反比例函数以及平行四边形面积公式,本题关键在于两点间距离的求法.16.如图,矩形ABCD 的边AB 在x 轴上,反比例函数(0)k y k x=≠的图象过D 点和边BC的中点E ,连接DE ,若△CDE 的面积是1,则k 的值是( )A .3B .4C .25D .6 【答案】B 【解析】【分析】 设E 的坐标是m n k mn =(,),, 则C 的坐标是2m n (,),求得D 的坐标,然后根据三角形的面积公式求得mn 的值,即k 的值.【详解】设E 的坐标是m n k mn =(,),,, 则C 的坐标是(m ,2n ),在mn y x = 中,令2y n =,解得:2m x =, ∵1CDE S =V ,∴111,12222m m n m n -=⨯=g 即 ∴4mn =∴4k =故选:B【点睛】本题考查了待定系数法求函数的解析式,利用mn 表示出三角形的面积是关键.17.如图,点A 是反比例函数2(0)y x x=>的图象上任意一点,AB x P 轴交反比例函数3y x=-的图象于点B ,以AB 为边作ABCD Y ,其中C 、D 在x 轴上,则ABCD S Y 为( )A .2.5B .3.5C .4D .5【答案】D【解析】【分析】过点B 作BH ⊥x 轴于H ,根据坐标特征可得点A 和点B 的纵坐标相同,由题意可设点A 的坐标为(2a ,a ),点B 的坐标为(3a -,a ),即可求出BH 和AB ,最后根据平行四边形的面积公式即可求出结论.【详解】解:过点B 作BH ⊥x 轴于H∵四边形ABCD 为平行四边形∴//AB x 轴,CD=AB∴点A 和点B 的纵坐标相同由题意可设点A 的坐标为(2a ,a ),点B 的坐标为(3a -,a ) ∴BH=a ,CD=AB=2a -(3a -)=5a∴ABCD S Y =BH·CD=5 故选D .【点睛】此题考查的是反比例函数与几何图形的综合题,掌握利用反比例函数求几何图形的面积是解决此题的关键.18.已知反比例函数b y x=与一次函数y ax c =+有一个交点在第四象限,该交点横坐标为1,抛物线2y ax bx c =++与x 轴只有一个交点,则一次函数b c y x a a=+的图象可能是( ) A . B . C . D .【答案】B【解析】【分析】根据题意得b <0,a+c <0,240b ac =>,可得a <0,c <0,进而即可判断一次函数b c y x a a=+的图象所经过的象限. 【详解】 ∵反比例函数b y x=与一次函数y ax c =+有一个交点在第四象限, ∴反比例函数的图象在二、四象限,即b <0,∵该交点横坐标为1,∴y=a+c <0,∵抛物线2y ax bx c =++与x 轴只有一个交点, ∴240b ac -=,即:240b ac =>,∴a <0,c <0, ∴0b a>,0c a >, ∴b c y x a a=+的图象过一、二、三象限. 故选B .【点睛】 本题主要考查反比例函数与一次函数的图象和性质,掌握函数图象上点的坐标特征以及函数解析式的系数的几何意义,是解题的关键.19.若点A (﹣4,y 1)、B (﹣2,y 2)、C (2,y 3)都在反比例函数1y x =-的图象上,则y 1、y 2、y 3的大小关系是( )A .y 1>y 2>y 3B .y 3>y 2>y 1C .y 2>y 1>y 3D .y 1>y 3>y 2 【答案】C【解析】【分析】根据反比例函数图象上点的坐标特征求出y 1、y 2、y 3的值,比较后即可得出结论.【详解】∵点A(﹣4,y 1)、B(﹣2,y 2)、C(2,y 3)都在反比例函数1y x =-的图象上, ∴11144y =-=-,21122y =-=-,312y =-, 又∵﹣12<14<12, ∴y 3<y 1<y 2,故选C.【点睛】本题考查了反比例函数图象上点的坐标特征,反比例函数值的大小比较,熟知反比例函数图象上的点的坐标满足反比例函数的解析式是解题的关键.20.若一个圆锥侧面展开图的圆心角是270°,圆锥母线l与底面半径r之间的函数关系图象大致是()A.B.C.D.【答案】A【解析】【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长得到2πr=270180lπ⋅⋅,整理得l=43r(r>0),然后根据正比例函数图象求解.【详解】解:根据题意得2πr=270180lπ⋅⋅,所以l=43r(r>0),即l与r为正比例函数关系,其图象在第一象限.故选A.【点睛】本题考查圆锥的计算;函数的图象.。
反比例函数易错题汇编及答案

两交点分别是 ),两交点的距离是 ,当 无限大时,两交点的距离趋近于2,所以 不正确,符合题意,
故选D.
【点睛】
本题考查了垂直于x轴的直线与反比例函数图象之间的关系,利用特定值,分情况进行讨论是解本题的关键,本题有一定的难度.
4.如图直线y=mx与双曲线y= 交于点A、B,过A作AM⊥x轴于M点,连接BM,若S△AMB=2,则k的值是()
根据函数与不等式的关系:函数图象在上方的函数值大,可判断D选项.
【详解】
解:由反比例函数y2=﹣ (x<0)经过C,点C的横坐标为﹣1,得
y=﹣ =5,即C(﹣1,5).
反比例函数与一次函数交于C、D点,
5=﹣1+b,
解得b=6,故A错误;
CE⊥y轴于E点,E(0,﹣5),BE=6﹣5=1.
反比例函数与一次函数交于C、D点,联立 ,
【答案】B
【解析】
【分析】
此题可根据反比例函数的性质,即函数所在的象限和增减性对各选项作出判断.
【详解】
解:A、把(-1,2)代入函数解析式得:2=- 成立,故点(-1,2)在函数图象上,故选项正确;
B、由k=-2<0,因此在每一个象限内,y随x的增大而增大,故选项不正确;
C、由k=-2<0,因此函数图象在二、四象限内,故选项正确;
D、当x=1,则y=-2,又因为k=-2<0,所以y随x的增大而增大,因此x>1时,-2<y<0,故选项正确;
故选B.
【点睛】
本题考查反比例函数的图像与性质.
16.如图,点 是反比例函数 的图象上任意一点, 轴交反比例函数 的图象于点 ,以 为边作 ,其中 、 在 轴上,则 为()
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(易错题精选)初中数学反比例函数易错题汇编含答案一、选择题1.矩形ABCO如图摆放,点B在y轴上,点C在反比例函数ykx=(x>0)上,OA=2,AB=4,则k的值为()A.4 B.6 C.325D.425【答案】C【解析】【分析】根据矩形的性质得到∠A=∠AOC=90°,OC=AB,根据勾股定理得到OB22OA AB=+=5C作CD⊥x轴于D,根据相似三角形的性质得到CD85=,OD45=求得8545,)于是得到结论.【详解】解:∵四边形ABCO是矩形,∴∠A=∠AOC=90°,OC=AB,∵OA=2,AB=4,∴过C作CD⊥x轴于D,∴∠CDO=∠A=90°,∠COD+∠COB=∠COB+∠AOB=90°,∴∠COD=∠AOB,∴△AOB∽△DOC,∴OB AB OA OC CD OD==,2542CD OD==,∴CD855=,OD45=,∴C(455,855),∴k325 =,故选:C.【点睛】本题考查了反比例函数图象上点的坐标特征,反比例函数的性质,矩形的性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.2.如图, 在同一坐标系中(水平方向是x轴),函数kyx=和3y kx=+的图象大致是()A.B.C.D.【答案】A【解析】【分析】根据一次函数及反比例函数的图象与系数的关系作答.【详解】解:A、由函数y=kx的图象可知k>0与y=kx+3的图象k>0一致,正确;B 、由函数y=k x 的图象可知k >0与y=kx+3的图象k >0,与3>0矛盾,错误; C 、由函数y=k x 的图象可知k <0与y=kx+3的图象k <0矛盾,错误; D 、由函数y=k x的图象可知k >0与y=kx+3的图象k <0矛盾,错误. 故选A .【点睛】 本题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.3.已知点A (﹣2,y 1),B (a ,y 2),C (3,y 3)都在反比例函数4y x =的图象上,且﹣2<a <0,则( )A .y 1<y 2<y 3B .y 3<y 2<y 1C .y 3<y 1<y 2D .y 2<y 1<y 3 【答案】D【解析】【分析】根据k >0,在图象的每一支上,y 随x 的增大而减小,双曲线在第一三象限,逐一分析即可.【详解】∵反比例函数y=4x中的k=4>0, ∴在图象的每一支上,y 随x 的增大而减小,双曲线在第一三象限,∵-2<a <0,∴0>y 1>y 2,∵C (3,y 3)在第一象限,∴y 3>0,∴213y y y <<,故选D .【点睛】本题考查了反比例函数的性质,熟练地应用反比例函数的性质是解题的关键.4.如图,点A 是反比例函数y =k x(x <0)的图象上的一点,过点A 作平行四边形ABCD ,使点B 、C 在x 轴上,点D 在y 轴上.已知平行四边形ABCD 的面积为8,则k 的值为( )A .8B .﹣8C .4D .﹣4【答案】B【解析】【分析】 作AE ⊥BC 于E ,由四边形ABCD 为平行四边形得AD ∥x 轴,则可判断四边形ADOE 为矩形,所以S 平行四边形ABCD =S 矩形ADOE ,根据反比例函数k 的几何意义得到S 矩形ADOE =|k|.【详解】解:作AE ⊥BC 于E ,如图,∵四边形ABCD 为平行四边形,∴AD ∥x 轴,∴四边形ADOE 为矩形,∴S 平行四边形ABCD =S 矩形ADOE ,而S 矩形ADOE =|k|,∴|k|=8,而k <0∴k=-8.故选:B .【点睛】本题考查了反比例函数y=k x (k≠0)系数k 的几何意义:从反比例函数y=k x(k≠0)图象上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.5.如图,点P 是反比例函数(0)k y k x=≠的图象上任意一点,过点P 作PM x ⊥轴,垂足为M . 连接OP . 若POM ∆的面积等于2. 5,则k 的值等于 ( )A.5-B.5 C. 2.5-D.2. 5【答案】A【解析】【分析】利用反比例函数k的几何意义得到12|k|=2,然后根据反比例函数的性质和绝对值的意义确定k的值.【详解】解:∵△POM的面积等于2.5,∴12|k|=2.5,而k<0,∴k=-5,故选:A.【点睛】本题考查了反比例函数系数k的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了反比例函数的性质.6.如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=﹣5x(x<0)的图象交于C,D两点,点C的横坐标为﹣1,过点C作CE⊥y轴于点E,过点D作DF ⊥x轴于点F.下列说法正确的是()A.b=5B.BC=ADC.五边形CDFOE的面积为35D.当x<﹣2时,y1>y2【答案】B【解析】【分析】根据函数值与相应自变量的关系,可得C 点坐标,根据待定系数法,可得一次函数解析式,可判断A 选项;根据解方程组,可得C 、D 点的坐标,根据全等三角形的判定与性质,可判断B 选项; 根据图形的分割,可得梯形、矩形,根据面积的和差,可判断C 选项;根据函数与不等式的关系:函数图象在上方的函数值大,可判断D 选项.【详解】解:由反比例函数y 2=﹣5x (x <0)经过C ,点C 的横坐标为﹣1,得 y =﹣51-=5,即C (﹣1,5). 反比例函数与一次函数交于C 、D 点,5=﹣1+b ,解得b =6,故A 错误;CE ⊥y 轴于E 点,E (0,﹣5),BE =6﹣5=1.反比例函数与一次函数交于C 、D 点,联立65y x y x =+⎧⎪⎨=-⎪⎩, x 2+6x +5=0解得x 1=﹣5,x 2=﹣1,当x =﹣5时,y =﹣5+6=1,即D (﹣5,1),即DF =1,在△ADF 和△CBE 中,DAF BCE AFD CEB DF BE ∠=∠⎧⎪∠=∠⎨⎪=⎩,△ADF ≌△CBE (AAS ),AD =BC ,故B 正确;作CG ⊥x 轴,S △CDFOE =S 梯形DFGC +S 矩形CGOE=()(15)422DF CG FG OG CG ++⨯+g +1×5=17,故C 错误; 由一次函数图象在反比例函数图象上方的部分,得﹣5<x <﹣1,即当﹣5<x <﹣1时,y 1>y 2,故D 错误;故选:B .【点睛】本题考查了反比例函数综合题,利用了自变量与函数值的对应关系,点的坐标与函数解析式的关系,全等三角形的判定与性质,图形分割法求图形的面积,函数图象与不等式的关系.7.函数k y x=与y kx k =-(0k ≠)在同一平面直角坐标系中的大致图象是( ) A . B . C . D .【答案】C【解析】【分析】分k>0和k<0两种情况确定正确的选项即可.【详解】当k:>0时,反比例函数的图象位于第一、三象限,一次函数的图象交 y 轴于负半轴,y 随着x 的增大而增大,A 选项错误,C 选项符合;当k<0时,反比例函数的图象位于第二、四象限,一次函数的图象交y 轴于正半轴,y 随着x 的增大而增减小,B. D 均错误,故选:C.【点睛】此题考查反比例函数的图象,一次函数的图象,熟记函数的性质是解题的关键.8.如图,二次函数2y ax bx c =++的图象如图所示,则一次函数y ax c =+和反比例函数b y x=在同平面直角坐标系中的图象大致是( )A.B.C.D.【答案】D【解析】【分析】直接利用二次函数图象经过的象限得出a,b,c的值取值范围,进而利用一次函数与反比例函数的性质得出答案.【详解】∵二次函数y=ax2+bx+c的图象开口向下,∴a<0,∵二次函数y=ax2+bx+c的图象经过原点,∴c=0,∵二次函数y=ax2+bx+c的图象对称轴在y轴左侧,∴a,b同号,∴b<0,∴一次函数y=ax+c,图象经过第二、四象限,反比例函数y=bx图象分布在第二、四象限,故选D.【点睛】此题主要考查了反比例函数、一次函数、二次函数的图象,正确把握相关性质是解题关键.9.如图,点P是反比例函数y=kx(x<0)图象上一点,过P向x轴作垂线,垂足为M,连接OP.若Rt△POM的面积为2,则k的值为()A.4 B.2 C.-4 D.-2【答案】C【解析】【分析】根据反比例函数的比例系数k的几何意义得到S△POD=12|k|=2,然后去绝对值确定满足条件【详解】解:根据题意得S△POD=12|k|,所以12|k||=2,而k<0,所以k=-4.故选:C.【点睛】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.10.若A(-3,y1)、B(-1,y2)、C(1,y3)三点都在反比例函数y=kx(k>0)的图象上,则y1、y2、y3的大小关系是()A. y1>y2>y3B. y3>y1>y2C. y3>y2>y1D. y2>y1>y3【答案】B【解析】【分析】反比例函数y=kx(k>0)的图象在一、三象限,根据反比例函数的性质,在每个象限内y随x的增大而减小,而A(-3,y1)、B(-1,y2)在第三象限双曲线上的点,可得y2<y1<0,C(1,y3)在第一象限双曲线上的点y3>0,于是对y1、y2、y3的大小关系做出判断.【详解】∵反比例函数y=kx(k>0)的图象在一、三象限,∴在每个象限内y随x的增大而减小,∵A(-3,y1)、B(-1,y2)在第三象限双曲线上,∴y2<y1<0,∵C(1,y3)在第一象限双曲线上,∴y3>0,∴y3>y1>y2,【点睛】此题考查反比例函数的图象和性质,解题关键在于当k >0,时,在每个象限内y 随x 的增大而减小;当k <0时,y 随x 的增大而增大,注意“在每个象限内”的意义,这种类型题目用图象法比较直观得出答案.11.已知反比例函数y=﹣8x ,下列结论:①图象必经过(﹣2,4);②图象在二,四象限内;③y 随x 的增大而增大;④当x >﹣1时,则y >8.其中错误的结论有( )个 A .3 B .2 C .1 D .0【答案】B【解析】【分析】根据反比例函数的性质,逐一进行判断即可得答案.【详解】①当x=﹣2时,y=4,即图象必经过点(﹣2,4);②k=﹣8<0,图象在第二、四象限内;③k=﹣8<0,每一象限内,y 随x 的增大而增大,错误;④k=﹣8<0,每一象限内,y 随x 的增大而增大,若0>x >﹣1,﹣y >8,故④错误, 故选B .【点睛】本题考查了反比例函数的性质,熟练掌握反比例函数的性质是解题关键.12.如图所示,已知()121,,2,2A y B y ⎛⎫ ⎪⎝⎭为反比例函数1y x =图象上的两点,动点(),0P x 在x 轴正半轴上运动,当AP BP -的值最大时,连结OA ,AOP ∆的面积是 ( )A .12B .1C .32D .52【答案】D【解析】【分析】先根据反比例函数解析式求出A ,B 的坐标,然后连接AB 并延长AB 交x 轴于点P ',当P 在P '位置时,PA PB AB -=,即此时AP BP -的值最大,利用待定系数法求出直线AB 的解析式,从而求出P '的坐标,进而利用面积公式求面积即可.【详解】当12x=时,2y=,当2x=时,12y=,∴11(,2),(2,)22A B.连接AB并延长AB交x轴于点P',当P在P'位置时,PA PB AB-=,即此时AP BP-的值最大.设直线AB的解析式为y kx b=+,将11(,2),(2,)22A B代入解析式中得122122k bk b⎧+=⎪⎪⎨⎪+=⎪⎩解得152kb=-⎧⎪⎨=⎪⎩,∴直线AB解析式为52y x=-+.当0y=时,52x=,即5(,0)2P',115522222AOP AS OP y'∴=⋅=⨯⨯=V.故选:D.【点睛】本题主要考查一次函数与几何综合,掌握待定系数法以及找到AP BP-何时取最大值是解题的关键.13.如图,点A,B是双曲线18yx=图象上的两点,连接AB,线段AB经过点O,点C为双曲线kyx=在第二象限的分支上一点,当ABCV满足AC BC=且:13:24AC AB=时,k的值为().A.2516-B.258-C.254-D.25-【答案】B【解析】【分析】如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.首先证明△CFO∽△OEA,推出2()COFAOES OCS OA∆∆=,因为CA:AB=13:24,AO=OB,推出CA:OA=13:12,推出CO:OA=5:12,可得出2()COFAOES OCS OA∆∆==25144,因为S△AOE=9,可得S△COF=2516,再根据反比例函数的几何意义即可解决问题.【详解】解:如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.∵A、B关于原点对称,∴OA=OB,∵AC=BC,OA=OB,∴OC⊥AB,∴∠CFO=∠COA=∠AEO=90°,∴∠COF+∠AOE=90°,∠AOE+∠EAO=90°,∴∠COF=∠OAE,∴△CFO∽△OEA,∴2()COFAOES OCS OA∆∆=,∵CA:AB=13:24,AO=OB,∴CA:OA=13:12,∴CO:OA=5:12,∴2()COF AOE S OC S OA ∆∆==25144, ∵S △AOE =9,∴S △COF =2516, ∴||25216k =, ∵k <0, ∴258k =- 故选:B .【点睛】本题主要考查反比例函数图象上的点的特征、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,根据相似三角形解决问题,属于中考选择题中的压轴题.14.若反比例函数()2221my m x -=-的图象在第二、四象限,则m 的值是( ) A .-1或1B .小于12的任意实数C .-1D .不能确定 【答案】C【解析】【分析】根据反比例函数的定义列出方程221m -=-且210m -<求解即可.【详解】解:22(21)m y m x -=-Q 是反比例函数,∴221m -=-,210m -≠,解之得1m =±.又因为图象在第二,四象限,所以210m -<, 解得12m <,即m 的值是1-. 故选:C .【点睛】 对于反比例函数()0k y k x=≠.(1)0k >,反比例函数图像分布在一、三象限;(2)k 0< ,反比例函数图像分布在第二、四象限内.15.点(2,﹣4)在反比例函数y=k x 的图象上,则下列各点在此函数图象上的是( ) A .(2,4)B .(﹣1,﹣8)C .(﹣2,﹣4)D .(4,﹣2) 【答案】D【解析】【详解】∵点(2,-4)在反比例函数y=k x的图象上, ∴k =2×(-4)=-8. ∵A 中2×4=8;B 中-1×(-8)=8;C 中-2×(-4)=8;D 中4×(-2)=-8,∴点(4,-2)在反比例函数y=k x 的图象上. 故选D .【点睛】本题考查了反比例函数图象上点的坐标特征,解题的关键是求出反比例系数k ,解决该题型题目时,结合点的坐标利用反比例函数图象上点的坐标特征求出k 值是关键.16.如图,矩形ABCD 的边AB 在x 轴上,反比例函数(0)k y k x=≠的图象过D 点和边BC 的中点E ,连接DE ,若△CDE 的面积是1,则k 的值是( )A .3B .4C .25D .6【答案】B【解析】【分析】 设E 的坐标是m n k mn =(,),, 则C 的坐标是2m n (,),求得D 的坐标,然后根据三角形的面积公式求得mn 的值,即k 的值.【详解】设E 的坐标是m n k mn =(,),,, 则C 的坐标是(m ,2n ),在mn y x = 中,令2y n =,解得:2m x =, ∵1CDE S =V ,∴111,1 2222m mn m n-=⨯= g即∴4mn=∴4k=故选:B【点睛】本题考查了待定系数法求函数的解析式,利用mn表示出三角形的面积是关键.17.已知抛物线y=x2+2x+k+1与x轴有两个不同的交点,则一次函数y=kx﹣k与反比例函数y=kx在同一坐标系内的大致图象是()A.B.C.D.【答案】D【解析】【分析】依据抛物线y=x2+2x+k+1与x轴有两个不同的交点,即可得到k<0,进而得出一次函数y=kx﹣k的图象经过第一二四象限,反比例函数y=kx的图象在第二四象限,据此即可作出判断.【详解】∵抛物线y=x2+2x+k+1与x轴有两个不同的交点,∴△=4﹣4(k+1)>0,解得k<0,∴一次函数y=kx﹣k的图象经过第一二四象限,反比例函数y=kx的图象在第二四象限,故选D.【点睛】本题考查了二次函数的图象与x轴的交点问题、反比例函数图象、一次函数图象等,根据抛物线与x轴的交点情况确定出k的取值范围是解本题的关键.18.如图,△AOB是直角三角形,∠AOB=90°,△AOB的两边分别与函数12,y yx x =-=的图象交于B、A两点,则等于()A .22B .12C .14D .3 【答案】A【解析】【分析】过点A,B 作AC ⊥x 轴,BD ⊥x 轴,垂足分别为C,D.根据条件得到△ACO ∽△ODB.根据反比例函数比例系数k 的几何意义得出2()S OBD OB S AOC OA ∆=∆=121=12利用相似三角形面积比等于相似比的平方得出2OB OA = 【详解】 ∵∠AOB =90°,∴∠AOC +∠BOD =∠AOC +∠CAO =90°,∠CAO =∠BOD ,∴△ACO ∽△BDO ,∴2()S OBD OB S AOC OA∆=∆ , ∵S △AOC =12 ×2=1,S △BOD =12×1=12, ∴2()OB OA =121=12 , ∴2OB OA =, 故选A .【点睛】此题考查了反比例函数图象上点的坐标特征和相似三角形的判定与性质,解题关键在于做辅助线,然后得到相似三角形再进行求解19.若点A (﹣4,y 1)、B (﹣2,y 2)、C (2,y 3)都在反比例函数1y x =-的图象上,则y 1、y 2、y 3的大小关系是( )A .y 1>y 2>y 3B .y 3>y 2>y 1C .y 2>y 1>y 3D .y 1>y 3>y 2 【答案】C【解析】【分析】根据反比例函数图象上点的坐标特征求出y 1、y 2、y 3的值,比较后即可得出结论.【详解】∵点A(﹣4,y 1)、B(﹣2,y 2)、C(2,y 3)都在反比例函数1y x =-的图象上, ∴11144y =-=-,21122y =-=-,312y =-, 又∵﹣12<14<12, ∴y 3<y 1<y 2,故选C.【点睛】本题考查了反比例函数图象上点的坐标特征,反比例函数值的大小比较,熟知反比例函数图象上的点的坐标满足反比例函数的解析式是解题的关键.20.如图,过点()1,2C 分别作x 轴、y 轴的平行线,交直线5y x =-+于A 、B 两点,若反比例函数(0)k y x x=>的图象与ABC V 有公共点,则k 的取值范围是( )A .2524k ≤≤B .26k ≤≤C .24k ≤≤D .46k ≤≤【答案】A【解析】【分析】 由点C 的坐标结合直线AB 的解析式可得出点A 、B 的坐标,求出反比例函数图象过点C 时的k 值,将直线AB 的解析式代入反比例函数解析式中,令其根的判别式△≥0可求出k 的取值范围,取其最大值,找出此时交点的横坐标,进而可得出此点在线段AB上,综上即可得出结论.【详解】解:令y=−x+5中x=1,则y=4,∴B(1,4);令y=−x+5中y=2,则x=3,∴A(3,2),当反比例函数kyx=(x>0)的图象过点C时,有2=1k,解得:k=2,将y=−x+5代入kyx=中,整理得:x2−5x+k=0,∵△=(−5)2−4k≥0,∴k≤254,当k=254时,解得:x=52,∵1<52<3,∴若反比例函数kyx=(x>0)的图象与△ABC有公共点,则k的取值范围是2≤k≤254,故选:A.【点睛】本题考查了反比例函数与一次函数的交点问题,解题的关键是求出反比例函数图象过点A、C时的k值以及直线与双曲线有一个交点时k的值.。
