资料分析十大估算方法
李委明十大速算技巧(完美修正版)

李委明十大速算技巧★【速算技巧一:估算法】“估算法”毫无疑问是资料分析题当中的速算第一法,在所有计算进行之前必须考虑能否先行估算。
所谓估算,是在精度要求并不太高的情况下,进行粗略估值的速算方式,一般在选项相差较大,或者在被比较数据相差较大的情况下使用。
估算的方式多样,需要各位考生在实战中多加训练与掌握。
进行估算的前提是选项或者待比较的数字相差必须比较大,并且这个差别的大小决定了“估算”时候的精度要求。
★【速算技巧二:直除法】李委明提示:“直除法”是指在比较或者计算较复杂分数时,通过“直接相除”的方式得到商的首位(首一位或首两位),从而得出正确答案的速算方式。
“直除法”在资料分析的速算当中有非常广泛的用途,并且由于其“方式简单”而具有“极易操作”性。
“直除法”从题型上一般包括两种形式:一、比较多个分数时,在量级相当的情况下,首位最大/小的数为最大/小数;二、计算一个分数时,在选项首位不同的情况下,通过计算首位便可选出正确答案。
“直除法”从难度深浅上来讲一般分为三种梯度:一、简单直接能看出商的首位;二、通过动手计算能看出商的首位;三、某些比较复杂的分数,需要计算分数的“倒数”的首位来判定答案。
【例1】中最大的数是()。
【解析】直接相除:=30+,=30-,=30-,=30-,明显为四个数当中最大的数。
【例2】32409/4103、32895/4701、23955/3413、12894/1831中最小的数是()。
【解析】32409/4103、23955/3413、12894/1831都比7大,而32895/4701比7小,因此四个数当中最小的数是32895/4701。
李委明提示:即使在使用速算技巧的情况下,少量却有必要的动手计算还是不可避免的。
【例3】6874.32/760.31、3052.18/341.02、4013.98/447.13、2304.83/259.74中最大的数是()。
【解析】在本节及以后的计算当中由于涉及到大量的估算,因此我们用a+表示一个比a大的数,用a-表示一个比a小的数。
行测资料分析题十大速算解题技巧全解

★【速算技巧八:放缩法】
要点:
"放缩法"是指在数字的比较计算当中,如果精度要求并不高, 我们可以将中间结果进行 大胆的”放"(大)或者"缩"(缩小),从而迅速得到待比较数字大小关系的速算方式。
1、"从2004年到2007年的平均增长率"一般表示不包括2004年的增长率;
2、"2004、2005、2006、2007年的平均增长率"一般表示包括2004年的增长率。
注意几点问题:
1、r一定是介于a、b之间的,"十字交叉”相减的时,一个r在前,另一个r在后;
上再乘以各自的增长率。
等速率增长结论:
时可以采取的一种速算方式。
适用形式:
若差分数与小分数相等,则大分数与小分数相等。
比如上文中就是"11/1.4代替324/53.1与313/51.7作比较”,因为11/
1.4>313/51.7(可以通过”直除法”或者”化同法”简单得到),所以324/53.1>313/51.7。
特别注意:
、”差分法”本身是一种”精算法”而非"估算法”,得出来的大小关系是精确的关系而非
A'=A/( 1+r)~A ( 1-r)
(实际上左式略大于右式,r越小,则误差越小,误差量级为「人2)
平均增长率近似公式:
如果N年间的增长率分别为r1、r2、r3••…rn,则平均增长率:
r-上述各个数的算术平均数
(实际上左式略小于右式,增长率越接近,误差越小)
有哪些估算方法有哪些

有哪些估算方法有哪些估算方法是指通过一系列计算步骤来推测或预测某个变量的值或结果的方法。
在各个学科领域和实际应用中都有各种估算方法的应用,包括数学、统计学、经济学、工程学、计算机科学等等。
本文将介绍一些常见的估算方法。
一、数学估算方法:1. 近似方法:近似方法是通过对某个数值进行简化或缩小范围的处理,得到一个接近真实结果的估算值。
例如,将π取为3.14来计算圆的面积。
2. 插值方法:插值方法是在已知数据点之间预测缺失值的方法。
最简单的线性插值是通过已知数据点构建一条直线,并在这条直线上预测缺失值。
3. 数值积分方法:数值积分方法是通过将连续函数划分为若干离散区间,再计算这些区间上的面积之和来估算函数的积分值。
4. 数值微分方法:数值微分方法是通过近似计算函数的导数值,来估计函数的局部变化率。
常见的数值微分方法包括差分法和有限差分法。
二、统计学估算方法:1. 抽样方法:抽样方法是通过从总体中抽取一部分样本,并对样本进行测量、观察、分析来估算总体参数。
常见的抽样方法包括简单随机抽样、系统抽样、分层抽样等。
2. 参数估计方法:参数估计方法是通过样本数据来估计总体参数的值。
常见的参数估计方法包括最大似然估计、矩估计和贝叶斯估计等。
3. 区间估计方法:区间估计方法是通过样本数据来估计总体参数的范围。
常见的区间估计方法包括置信区间估计和预测区间估计等。
4. 回归分析方法:回归分析方法是一种通过建立统计模型来估算自变量与因变量之间关系的方法。
常见的回归分析方法包括线性回归、多元回归和非线性回归等。
三、经济学估算方法:1. 成本法:成本法是通过对企业生产成本和资源利用情况进行估计,来推断其经济效益和价值的方法。
2. 动态规划方法:动态规划方法是一种通过递归的方式,将问题分解为更小的子问题,并最终求解整个问题的方法。
动态规划方法在资源分配、项目管理等经济学领域有广泛应用。
3. 投资评估方法:投资评估方法是一种通过分析和计算投资项目的成本、收益和风险等因素,来判断项目的可行性和价值的方法。
十大速算技巧(完整版)

十大速算技巧(完整版)★【速算技巧一:估算法】“估算法”毫无疑问是资料分析题当中的速算第一法,在所有计算进行之前必须考虑能否先行估算。
所谓估算,是在精度要求并不太高的情况下,进行粗略估值的速算方式,一般在选项相差较大,或者在被比较数据相差较大的情况下使用。
估算的方式多样,需要各位考生在实战中多加训练与掌握。
进行估算的前提是选项或者待比较的数字相差必须比较大,并且这个差别的大小决定了“估算”时候的精度要求。
★【速算技巧二:直除法】李委明提示:“直除法”是指在比较或者计算较复杂分数时,通过“直接相除”的方式得到商的首位(首一位或首两位),从而得出正确答案的速算方式。
“直除法”在资料分析的速算当中有非常广泛的用途,并且由于其“方式简单”而具有“极易操作”性。
“直除法”从题型上一般包括两种形式:一、比较多个分数时,在量级相当的情况下,首位最大/小的数为最大/小数;二、计算一个分数时,在选项首位不同的情况下,通过计算首位便可选出正确答案。
“直除法”从难度深浅上来讲一般分为三种梯度:一、简单直接能看出商的首位;二、通过动手计算能看出商的首位;三、某些比较复杂的分数,需要计算分数的“倒数”的首位来判定答案。
【例1】中最大的数是()。
【解析】直接相除:=30+,=30-,=30-,=30-,明显为四个数当中最大的数。
【例2】32409/4103、32895/4701、23955/3413、12894/1831中最小的数是()。
【解析】32409/4103、23955/3413、12894/1831都比7大,而32895/4701比7小,因此四个数当中最小的数是32895/4701。
李委明提示:即使在使用速算技巧的情况下,少量却有必要的动手计算还是不可避免的。
【例3】6874.32/760.31、3052.18/341.02、4013.98/447.13、2304.83/259.74中最大的数是()。
在本节及以后的计算当中由于涉及到大量的估算,因此我们用a+表示一个比a大的数,用a-表示一个比a小的数。
公务员考试十大速算技巧(完整版)

★【速算技巧一:估算法】 “估算法”毫无疑问是资料分析题当中的速算第一法,在所有计算进行之前必须考虑能否先行估算。
所谓估算,是在精度要求并不太高的情况下,进行粗略估值的速算方式,一般在选项相差较大,或者在被比较数据相差较大的情况下使用。
估算的方式多样,需要各位考生在实战中多加训练与掌握。
进行估算的前提是选项或者待比较的数字相差必须比较大,并且这个差别的大小决定了“估算”时候的精度要求。
★【速算技巧二:直除法】李委明提示:“直除法”是指在比较或者计算较复杂分数时,通过“直接相除”的方式得到商的首位(首一位或首两位),从而得出正确答案的速算方式。
“直除法”在资料分析的速算当中有非常广泛的用途,并且由于其“方式简单”而具有“极易操作”性。
“直除法”从题型上一般包括两种形式:一、比较多个分数时,在量级相当的情况下,首位最大/小的数为最大/小数;二、计算一个分数时,在选项首位不同的情况下,通过计算首位便可选出正确答案。
“直除法”从难度深浅上来讲一般分为三种梯度:一、简单直接能看出商的首位;二、通过动手计算能看出商的首位;三、某些比较复杂的分数,需要计算分数的“倒数”的首位来判定答案。
【例1】56.10134.489294.13343.559310.7454.813222.0349.738、、、中最大的数是( )。
【解析】直接相除:30.2294.837=30+,10.7454.8132=30-,94.13343.5593=30-,56.10134.4892=30-, 明显30.2294.837为四个数当中最大的数。
【例2】324094103、328954701、239553413、128941831中最小的数是( )。
【解析】32409/4103、23955/3413、12894/1831都比7大,而32895/4701比7小,因此四个数当中最小的数是32895/4701。
李委明提示:即使在使用速算技巧的情况下,少量却有必要的动手计算还是不可避免的。
资料分析估算方法(秒杀)

资料分析估算方法 第一节文字资料分析出题方式是:给出一段文字,文字里面含有很多数据,下提出5个问题,考察对文字数据的分析。
文字分析的估算方法有: 1、 多年增长:两个增长率:第一个增长率为r1,第二个增长率为r2,共同的增长率为r1+r2+r1×r2。
比如:第一年的增长率为r1,第二年的增长率为r2,这两年共同的增长率为r1+r2+r1×r2。
再比如:前五年增长率为r1,后五年增长率为r2,这十年的增长率为r1+r2+r1×r2。
多年持续增长:新量=原量×(1+r )年数>原量×(1+r ×年数),其中r 为增长率,年数表示经过的年份的数量。
(注意:翻几番是原量×2番数,2着区别很大。
)2、三角上溯:增加得快是速率,增长得多是数量,三角上溯是增长率的增量,比如2008年到2009年的增长率为50%,2009年到2010年的增长率为60%,增长率的增长量为10个百分点。
3、总量不同:乘法估算,总量1×比例1-总量2×比例24、定性分析:分子乘以M 大于分母,则此分数>1/M ,反之小于。
比如19/37,有19×2>37,则19/37>1/2。
5、除法估算:资料分析中最重要的估算。
提问有分总(分量和总量)和增减,选项有百分比(%)和数字,按照这4个特征可以把除法分成4个部分:1除估算法:首数法,除出商的前两位数字(最多除到商的第三位),选择答案。
在国考的资料分析中,选项的差异在前两位(最多第三位)就会体现,所以通过判断选项的前两位(最多第三位)就能选出答案。
2除估算法:可以除2次、使用两次首数估算法;也可以把其中的1除化为3除估算法:3除化1除,3除的格式是BA ÷DC ,我们把其中的BA 或者DC 估算成一个简单的分数比如1/2,3/4等等,此时3除就相当于1除了。
资料分析速算技巧

二、"差分法"与"化同法"经常联系在一起使用,"化同法紧接差分法"与"差分法紧接
化同法"是资料分析速算当中经常遇到的两种情形。
三、"差分法"得到"差分数"与"小分数"做比较的时候,还经常需要用到"直除法"。
四、如果两个分数相隔非常近,我们甚至需要反复运用两次"差分法",这种情况相
正包括的主要内容。
★【速算技巧八:放缩法】
要点:
"放缩法"是指在数字的比较计算当中,如果精度要求并不高,我们可以将中间结果
进行大胆的"放"(扩大)或者"缩"(缩小),从而迅速得到待比较数字大小关系的
速算方式。
要点:
若A>B>0,且C>D>0,则有:
1) A+C>B+D
2) A-D>B-C
乘/除以5、25、125的速算技巧:
A× 5型速算技巧:A×5= 10A÷2; A÷ 5型速算技巧:A÷5= 0.1A×2
例 8739.45×5=87394.5÷2=43697.25
36.843÷5=3.6843×2=7.3686
A× 25型速算技巧:A×25= 100A÷4; A÷ 25型速算技巧:A÷25= 0.01A×4
资料分析速算技巧
很多考生朋友对于资料分析的计算特别头痛,事实上资料分析的计算是极具技巧的,历史上曾经考过的资料分析试题计算当中99%以上是可以简化,所以答应很多朋友总结出来之后供大家借鉴与参考,希望能给各位考生的资料分析计算带来一点帮助。
估算的方法与技巧

估算的方法与技巧估算是我们日常生活中常常需要用到的技能,它帮助我们快速、粗略地估计各种数量和情况。
无论是在购物、旅行、做决策还是解决问题时,估算都可以发挥作用。
下面我将分享一些估算的方法和技巧,希望对您有所帮助。
1. 分析局部,综合整体:估算时,可以先将问题分解成小部分,估算每个部分,然后将它们综合起来得到整体估算。
例如,在估算一项工程的成本时,可以考虑各个子项的费用,然后相加得出总成本的估计。
2. 比较和对比法:将待估量与已知的量进行比较,以便更容易估算。
例如,如果您要估算某个物体的重量,可以将它与已知重量的物体进行比较,然后估算出大致的重量。
3. 利用参考点:有时候,我们可以使用已知的参考点来估算未知的量。
例如,如果您知道某个城市的人口数量,可以用这个数字来估算附近城市的人口数量。
4. 回归估算法:这种方法通过观察已知数据的趋势来估算未知数据。
例如,如果您有一组销售数据,可以使用回归分析来预测未来销售额。
5. 精确估算和快速估算:有时候,我们需要做快速的估算来做出决策,而有时需要更精确的估算。
在不同情境下,选择合适的估算方法很重要。
6. 多次估算:如果您对估算的结果不太确定,可以多次估算,然后取平均值。
这样可以降低误差。
7. 使用大概数值:有时候,不需要非常精确的估算,只需要一个大致的数值即可。
在这种情况下,可以省略一些细节,快速估算。
8. 借助工具和技术:现代科技提供了各种估算工具,如计算器、电子表格和统计软件,可以帮助我们更准确地估算各种数据。
9. 不断练习:估算是一项技能,需要不断练习和改进。
通过在日常生活中多次估算,您可以逐渐提高准确性和速度。
总之,估算是一项有用的技能,可以帮助我们在各种情况下做出快速而合理的决策。
通过使用上述方法和技巧,您可以提高估算的准确性和效率,更好地应对各种估算任务。
希望这些建议能对您有所帮助。
最新公务员考试十大速算技巧(完整版)

★【速算技巧一:估算法】 “估算法”毫无疑问是资料分析题当中的速算第一法,在所有计算进行之前必须考虑能否先行估算。
所谓估算,是在精度要求并不太高的情况下,进行粗略估值的速算方式,一般在选项相差较大,或者在被比较数据相差较大的情况下使用。
估算的方式多样,需要各位考生在实战中多加训练与掌握。
进行估算的前提是选项或者待比较的数字相差必须比较大,并且这个差别的大小决定了“估算”时候的精度要求。
★【速算技巧二:直除法】李委明提示:“直除法”是指在比较或者计算较复杂分数时,通过“直接相除”的方式得到商的首位(首一位或首两位),从而得出正确答案的速算方式。
“直除法”在资料分析的速算当中有非常广泛的用途,并且由于其“方式简单”而具有“极易操作”性。
“直除法”从题型上一般包括两种形式:一、比较多个分数时,在量级相当的情况下,首位最大/小的数为最大/小数;二、计算一个分数时,在选项首位不同的情况下,通过计算首位便可选出正确答案。
“直除法”从难度深浅上来讲一般分为三种梯度:一、简单直接能看出商的首位;二、通过动手计算能看出商的首位;三、某些比较复杂的分数,需要计算分数的“倒数”的首位来判定答案。
【例1】56.10134.489294.13343.559310.7454.813222.0349.738、、、中最大的数是( )。
【解析】直接相除:30.2294.837=30+,10.7454.8132=30-,94.13343.5593=30-,56.10134.4892=30-, 明显30.2294.837为四个数当中最大的数。
【例2】324094103、328954701、239553413、128941831中最小的数是( )。
【解析】32409/4103、23955/3413、12894/1831都比7大,而32895/4701比7小,因此四个数当中最小的数是32895/4701。
李委明提示:即使在使用速算技巧的情况下,少量却有必要的动手计算还是不可避免的。
资料分析解题技巧和练习
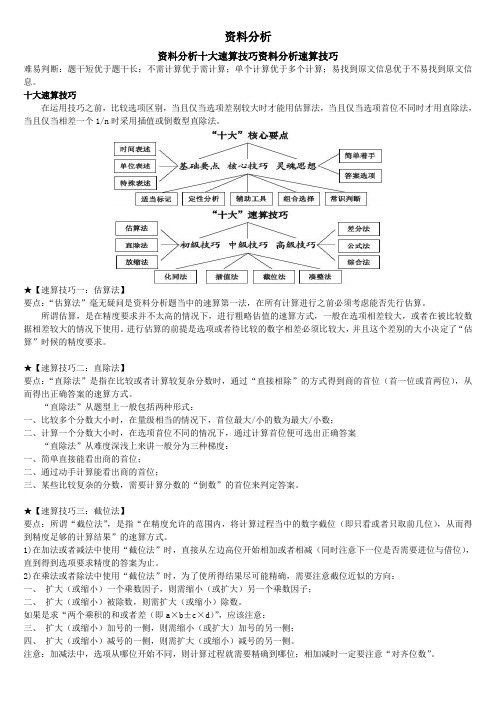
资料分析资料分析十大速算技巧资料分析速算技巧难易判断:题干短优于题干长;不需计算优于需计算;单个计算优于多个计算;易找到原文信息优于不易找到原文信息。
十大速算技巧在运用技巧之前,比较选项区别,当且仅当选项差别较大时才能用估算法,当且仅当选项首位不同时才用直除法,当且仅当相差一个1/n时采用插值或倒数型直除法。
★【速算技巧一:估算法】要点:“估算法”毫无疑问是资料分析题当中的速算第一法,在所有计算进行之前必须考虑能否先行估算。
所谓估算,是在精度要求并不太高的情况下,进行粗略估值的速算方式,一般在选项相差较大,或者在被比较数据相差较大的情况下使用。
进行估算的前提是选项或者待比较的数字相差必须比较大,并且这个差别的大小决定了“估算”时候的精度要求。
★【速算技巧二:直除法】要点:“直除法”是指在比较或者计算较复杂分数时,通过“直接相除”的方式得到商的首位(首一位或首两位),从而得出正确答案的速算方式。
“直除法”从题型上一般包括两种形式:一、比较多个分数大小时,在量级相当的情况下,首位最大/小的数为最大/小数;二、计算一个分数大小时,在选项首位不同的情况下,通过计算首位便可选出正确答案“直除法”从难度深浅上来讲一般分为三种梯度:一、简单直接能看出商的首位;二、通过动手计算能看出商的首位;三、某些比较复杂的分数,需要计算分数的“倒数”的首位来判定答案。
★【速算技巧三:截位法】要点:所谓“截位法”,是指“在精度允许的范围内,将计算过程当中的数字截位(即只看或者只取前几位),从而得到精度足够的计算结果”的速算方式。
1)在加法或者减法中使用“截位法”时,直接从左边高位开始相加或者相减(同时注意下一位是否需要进位与借位),直到得到选项要求精度的答案为止。
2)在乘法或者除法中使用“截位法”时,为了使所得结果尽可能精确,需要注意截位近似的方向:一、扩大(或缩小)一个乘数因子,则需缩小(或扩大)另一个乘数因子;二、扩大(或缩小)被除数,则需扩大(或缩小)除数。
估算的方法与技巧

估算的方法与技巧估算是指通过一定的方法和技巧,根据已知的信息或数据,推测或估计未知的信息或数据。
在各个领域,估算都是一个非常重要的技能,它能帮助我们在缺乏准确数据的情况下,做出合理的决策或预测。
本文将介绍一些常用的估算方法和技巧。
一、比例估算法比例估算法是一种简单而常用的估算方法。
它基于已知数据的比例关系,推测未知数据的大小。
例如,假设我们已知某个城市的总人口和男女比例,我们可以通过比例估算法推测出该城市男性和女性人口的数量。
比例估算法的关键是准确把握已知数据之间的比例关系,从而得出合理的估算结果。
二、抽样估算法抽样估算法是一种常用的统计估算方法。
它基于对样本的观察和测量,推测总体的特征或参数。
例如,在进行市场调研时,我们可以通过对一部分消费者的调查,估算出整个市场的需求量或偏好。
抽样估算法的关键是选择具有代表性的样本,并进行科学的统计分析,从而得出可靠的估算结果。
三、线性插值法线性插值法是一种常用的数值计算方法,用于在已知数据点之间,推测未知数据点的值。
它基于已知数据点之间的线性关系,通过插值计算出未知数据点的值。
例如,在绘制曲线图时,我们可以通过已知的几个数据点,使用线性插值法估算出其他数据点的值。
线性插值法的关键是准确把握已知数据点之间的线性关系,从而得出准确的估算结果。
四、指标估算法指标估算法是一种基于相关指标的估算方法。
它通过已知指标之间的关系,推测未知指标的数值。
例如,在经济领域,我们可以通过已知的相关指标(如GDP、就业率等),估算出其他指标(如消费水平、生活质量等)的数值。
指标估算法的关键是找到合适的指标之间的关系,并进行合理的计算,从而得出可靠的估算结果。
五、经验估算法经验估算法是一种基于经验和专业知识的估算方法。
它通过对过去的经验和专业知识的总结和归纳,推测未来的情况或结果。
例如,在项目管理中,我们可以通过以往的类似项目的经验,估算出新项目的时间和成本。
经验估算法的关键是准确把握过去的经验和专业知识,并进行合理的推断,从而得出合理的估算结果。
李委明十大速算技巧(完整版)

李委明十大速算技巧★【速算技巧一:估算法】“估算法”毫无疑问是资料分析题当中的速算第一法,在所有计算进行之前必须考虑能否先行估算。
所谓估算,是在精度要求并不太高的情况下,进行粗略估值的速算方式,一般在选项相差较大,或者在被比较数据相差较大的情况下使用。
估算的方式多样,需要各位考生在实战中多加训练与掌握。
进行估算的前提是选项或者待比较的数字相差必须比较大,并且这个差别的大小决定了“估算”时候的精度要求。
★【速算技巧二:直除法】李委明提示:“直除法”是指在比较或者计算较复杂分数时,通过“直接相除”的方式得到商的首位(首一位或首两位),从而得出正确答案的速算方式。
“直除法”在资料分析的速算当中有非常广泛的用途,并且由于其“方式简单”而具有“极易操作”性。
“直除法”从题型上一般包括两种形式:一、比较多个分数时,在量级相当的情况下,首位最大/小的数为最大/小数;二、计算一个分数时,在选项首位不同的情况下,通过计算首位便可选出正确答案。
“直除法”从难度深浅上来讲一般分为三种梯度:一、简单直接能看出商的首位;二、通过动手计算能看出商的首位;三、某些比较复杂的分数,需要计算分数的“倒数”的首位来判定答案。
【例1】中最大的数是()。
【解析】直接相除:=30+,=30-,=30-,=30-,明显为四个数当中最大的数。
【例2】32409/4103、32895/4701、23955/3413、12894/1831中最小的数是()。
【解析】32409/4103、23955/3413、12894/1831都比7大,而32895/4701比7小,因此四个数当中最小的数是32895/4701。
李委明提示:即使在使用速算技巧的情况下,少量却有必要的动手计算还是不可避免的。
【例3】6874.32/760.31、3052.18/341.02、4013.98/447.13、2304.83/259.74中最大的数是()。
在本节及以后的计算当中由于涉及到大量的估算,因此我们用a+表示一个比a大的数,用a-表示一个比a小的数。
资料分析常用速算技巧

资料分析常用速算技巧
一、直接估算法(数值精度不高,选项差距大)
直接估算结果的大小的判断(其中a、b均为正数)
常用的几个分数值:
%3.3331≈ %7.6632
≈ %254
1
≈ %754
3
≈
%7.1661
≈
%3.836
5
≈ %3.147
1
≈ %5.128
1
≈
%5.378
3
≈
%5.378
5
≈
%5.878
7
≈ %1.1191≈ %2.2292
≈ %09.911
1
≈
%18.1811
2
≈ 二、乘除转化法
1. 在计算精度允许的条件下,将计算过程中的除法(乘法)转化成乘法(除法)。
2.一般要求X 在-5%-5%范围内,在选项误差允许的情况下,可以适当将X 的范围扩大为-10%-10%。
三、拆分消除法
在计算性题目中,拆分消去法一般包含以下两种基本形式: 1.在乘法或除法运算中,将某个数拆分成两个或多个容易计算的数,从而快速得到运算结果。
2.在一些多步计算题中,先列出最终算式,然后通过整理消去相同或相近的数值,从而简化运算。
四、首尾数法
1.首数法是根据首位数(首一位或者首两位)来确定答案。
2.尾数法是根据尾数(最后-位或者两位)来确定答案。
3.在做商或做差时,一般采用首数法。
4.在求和、求积或做差时,一般采用尾数法。
有哪些估算的方法有哪些

有哪些估算的方法有哪些估算是指根据已有的信息和经验,对未知或不确定的事物进行近似计算或推测。
在现实生活和各个领域中,估算是一种常见的应用技巧。
下面将介绍一些常见的估算方法。
1. 顶部估算法:顶部估算法是一种简单而迅速的估算方法。
它通过将问题的上限或最大可能值确定为估算结果,这样做可以在短时间内得到一个大致的估计。
这种方法最适合在没有足够信息或数据进行精确估算时使用。
2. 底部估算法:底部估算法与顶部估算法相反,它将问题的下限或最小可能值作为估算结果。
这种方法适用于在具备一些基本信息或边界条件的情况下进行估算。
3. 平均估算法:平均估算法是通过计算事物的平均值来进行估算的方法。
它适用于已有一些数据或样本的情况下,可以通过对这些数据进行加总,然后除以样本量得到的平均值进行估算。
4. 比例估算法:比例估算法是通过建立已知事物与未知事物之间的比例关系来进行估算的方法。
这种方法适用于已知的类似事物与未知事物之间具有相似特征或规律的情况。
5. 类比估算法:类比估算法是通过找到一个类似的事物或情景并将其应用于待估算的问题中。
这种方法基于相似性原理,适用于在没有具体数据或信息的情况下进行估算。
6. 经验法:经验法是通过对已有经验或知识进行应用来进行估算的方法。
它基于个人或群体在某个领域积累的经验和知识,通过将这些经验应用到新的情况中进行估算。
7. 渐进法:渐进法是通过逐步分析问题的不同部分或细节,然后将它们整合起来进行估算的方法。
这种方法适用于复杂的问题,通过分步骤的估算可以减少误差和提高准确性。
8. 整合估算法:整合估算法是通过整合不同来源的信息或数据来进行估算的方法。
这种方法基于多种信息来源的考虑,并通过综合分析来得出估算结果。
9. 概率估算法:概率估算法是通过概率理论和统计方法进行估算的方法。
它适用于有相关数据或概率分布的情况,通过计算概率来得出估算结果。
10. 历史数据估算法:历史数据估算法是通过分析过去的数据来进行估算的方法。
公务员考试十大速算技巧(完整版)

★【速算技巧一:估算法】 “估算法”毫无疑问是资料分析题当中的速算第一法,在所有计算进行之前必须考虑能否先行估算。
所谓估算,是在精度要求并不太高的情况下,进行粗略估值的速算方式,一般在选项相差较大,或者在被比较数据相差较大的情况下使用。
估算的方式多样,需要各位考生在实战中多加训练与掌握。
进行估算的前提是选项或者待比较的数字相差必须比较大,并且这个差别的大小决定了“估算”时候的精度要求。
★【速算技巧二:直除法】李委明提示:“直除法”是指在比较或者计算较复杂分数时,通过“直接相除”的方式得到商的首位(首一位或首两位),从而得出正确答案的速算方式。
“直除法”在资料分析的速算当中有非常广泛的用途,并且由于其“方式简单”而具有“极易操作”性。
“直除法”从题型上一般包括两种形式:一、比较多个分数时,在量级相当的情况下,首位最大/小的数为最大/小数;二、计算一个分数时,在选项首位不同的情况下,通过计算首位便可选出正确答案。
“直除法”从难度深浅上来讲一般分为三种梯度:一、简单直接能看出商的首位;二、通过动手计算能看出商的首位;三、某些比较复杂的分数,需要计算分数的“倒数”的首位来判定答案。
【例1】56.10134.489294.13343.559310.7454.813222.0349.738、、、中最大的数是( )。
【解析】直接相除:30.2294.837=30+,10.7454.8132=30-,94.13343.5593=30-,56.10134.4892=30-, 明显30.2294.837为四个数当中最大的数。
【例2】324094103、328954701、239553413、128941831中最小的数是( )。
【解析】32409/4103、23955/3413、12894/1831都比7大,而32895/4701比7小,因此四个数当中最小的数是32895/4701。
李委明提示:即使在使用速算技巧的情况下,少量却有必要的动手计算还是不可避免的。
公务员行测资料分析_速算十大技巧

公务员行测资料分析_速算十大技巧随着公务员考试的日益严格,越来越多的考生开始关注公务员行测的资料分析。
而在行测中最重要的一点便是速算技巧。
本文将为大家介绍公务员行测中常用的十大速算技巧。
一、近似计算法在实际生活中,我们常常需要快速进行估算,比如购物时对价格进行快速的估算。
在公务员行测中,这种技巧也同样常用。
例如,算一个近似的数字,比如13,我们可以选择用数字13后面的数字零来代替,从而得出130。
这类似的技巧在行测中经常用到。
二、快速乘法如果要计算两个数字相乘,我们可以将其中一个数字拆分成两个数字。
例如,将8拆成5+3,那么10×8变成10×5+10×3=50+30=80。
这个技巧在繁琐的计算中尤其有效。
三、快速除法快速除法和快速乘法类似。
如果要计算一个数字除以另一个数字,我们可以将被除数拆成两个部分,比如27可以拆成20+7。
现在,如果要将2738除以27,我们可以将2738拆成2700+38,由于27是3×9的形式,因此,我们可以将38除以9,从而得出解答。
四、倍数转换如果需要计算一个数字的倍数,比如40的6倍,我们可以将40乘以6,然后除以2,即40×6÷2=120。
这种技巧很适合快速计算两个数字的倍数。
五、相近数相乘在公务员行测中,有时会出现需要进行大数字的乘法计算,此时,我们可以将其中的两个数字逐位相乘,然后将结果相加,这样可以缩短计算时间。
六、快速平方计算数字的平方有很多种方式。
其中一种方法是,将该数字的一半平方数加上其一半的平方数,比如22的平方等于11的平方加上11的平方,即11×11+11×11=242。
七、减一术如果需要将一个数字减1,我们可以在使用减法的同时使用加法,即42-1=42+(-1)=41。
八、倍数增加对于一个数字,如果需要计算其某个倍数,我们可以将该数字减去一个基础数字,然后将结果加上另一个数字,从而得到该数字的倍数。
公务员考试资料分析的速算与估算技巧

公务员考试资料分析的速算与估算技巧在公务员考试中,资料分析是一个重要的模块,它不仅考查我们对数据的理解和分析能力,还对我们的计算速度和精度有较高要求。
要在有限的时间内准确完成大量的计算,掌握速算与估算技巧就显得至关重要。
一、速算技巧1、尾数法尾数法是通过计算式子的尾数来快速得出答案的方法。
适用于选项尾数不同的加减运算。
例如:计算 345 + 256 + 178 的和,我们只需要计算这三个数的尾数 5 + 6 + 8 = 19 的尾数 9,然后对比选项的尾数,即可快速选出正确答案。
2、首数法首数法用于除法运算,通过观察商的首位数来确定答案。
当选项的首位数字不同时,我们可以先计算出商的首位数字,从而快速排除错误选项。
比如计算 4567÷56,首位商 8,即可排除首位不是 8 的选项。
3、特征数字法将百分数转化为分数来简化计算。
比如,125%可以转化为1/8,25%转化为 1/4,333%转化为 1/3 等等。
在计算时,将百分数替换为对应的分数,能大大简化运算。
4、错位加减法这是一种用于解决乘法运算的技巧。
例如,计算 345×11,我们可以将 345 错位相加得到 3795。
对于较为复杂的乘法,如 345×102,可以将 345×100 + 345×2 转化为 34500 + 690 = 35190。
5、分数比较法在比较分数大小时,若分子分母的差值相同,分子大的分数大;若分子分母同比例变化,分子分母变化幅度大的分数大。
二、估算技巧1、截位法根据选项的差距,对数字进行截位处理。
如果选项差距较大,可以大胆地截位;若选项差距较小,则需要谨慎截位。
比如计算4567÷123,若选项差距大,可将 123 截位为 100 计算。
2、放缩法通过对数字进行放大或缩小,来简化计算并确定答案的范围。
比如计算 23×18,可将 18 放大为 20,计算 23×20 = 460,从而知道原式的结果小于 460。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
★【速算技巧一:估算法】要点:"估算法"毫无疑问是资料分析题当中的速算第一法,在所有计算进行之前必须考虑能否先行估算。
所谓估算,是在精度要求并不太高的情况下,进行粗略估值的速算方式,一般在选项相差较大,或者在被比较数据相差较大的情况下使用。
估算的方式多样,需要各位考生在实战中多加训练与掌握。
进行估算的前提是选项或者待比较的数字相差必须比较大,并且这个差别的大小决定了"估算"时候的精度要求。
★【速算技巧二:直除法】李委明提示:“直除法”是指在比较或者计算较复杂分数时,通过“直接相除”的方式得到商的首位(首一位或首两位),从而得出正确答案的速算方式。
“直除法”在资料分析的速算当中有非常广泛的用途,并且由于其“方式简单”而具有“极易操作”性。
“直除法”从题型上一般包括两种形式:一、比较多个分数时,在量级相当的情况下,首位最大/小的数为最大/小数;二、计算一个分数时,在选项首位不同的情况下,通过计算首位便可选出正确答案。
“直除法”从难度深浅上来讲一般分为三种梯度:一、简单直接能看出商的首位;二、通过动手计算能看出商的首位;三、某些比较复杂的分数,需要计算分数的“倒数”的首位来判定答案。
【例1】中最大的数是()。
【解析】直接相除:=30+,=30-,=30-,=30-,明显为四个数当中最大的数。
【例2】32409/4103、32895/4701、23955/3413、12894/1831中最小的数是()。
【解析】32409/4103、23955/3413、12894/1831都比7大,而32895/4701比7小,因此四个数当中最小的数是32895/4701。
李委明提示:即使在使用速算技巧的情况下,少量却有必要的动手计算还是不可避免的。
【例3】6874.32/760.31、3052.18/341.02、4013.98/447.13、2304.83/259.74中最大的数是()。
在本节及以后的计算当中由于涉及到大量的估算,因此我们用a+表示一个比a大的数,用a-表示一个比a小的数。
【解析】只有6874.32/760.31比9大,所以四个数当中最大的数是6874.32/760.31。
【例4】5794.1/27591.43、3482.2/15130.87、4988.7/20788.33、6881.3/26458.46中最大的数是()。
【解析】本题直接用“直除法”很难直接看出结果,我们考虑这四个数的倒数:27591.43/5794.1、15130.87/3482.2、20788.33/4988.7、26458.46/6881.3,利用直除法,它们的首位分别为“4”、“4”、“4”、“3”,所以四个倒数当中26458.46/6881.3最小,因此原来四个数当中6881.3/26458.46最大。
【例5】阅读下面饼状图,请问该季度第一车间比第二车间多生产多少?()A.38.5%B.42.8%C.50.1%D.63.4%【解析】5632-3945/3945=1687/3945=0.4+=40%+,所以选B。
【例6】某地区去年外贸出口额各季度统计如下,请问第二季度出口额占全年的比例为多少?()第一季度第二季度第三季度第四季度全年出口额(亿元)4573 5698 3495 3842 17608A.29.5%B.32.4%C.33.7%D.34.6%【解析】5698/17608=0.3+=30%+,其倒数17608/5698=3+,所以5698/17608=(1/3)-,所以选B。
【例7】根据下图资料,己村的粮食总产量为戊村粮食总产量的多少倍?()A.2.34B.1.76C.1.57D.1.32【解析】直接通过直除法计算516.1÷328.7:根据首两位为1.5*得到正确答案为C。
★【速算技巧三:截位法】所谓"截位法",是指"在精度允许的范围内,将计算过程当中的数字截位(即只看或者只取前几位),从而得到精度足够的计算结果"的速算方式。
在加法或者减法中使用"截位法"时,直接从左边高位开始相加或者相减(同时注意下一位是否需要进位与借位),直到得到选项要求精度的答案为止。
在乘法或者除法中使用"截位法"时,为了使所得结果尽可能精确,需要注意截位近似的方向:一、扩大(或缩小)一个乘数因子,则需缩小(或扩大)另一个乘数因子;二、扩大(或缩小)被除数,则需扩大(或缩小)除数。
如果是求"两个乘积的和或者差(即a×b±c×d)",应该注意:三、扩大(或缩小)加号的一侧,则需缩小(或扩大)加号的另一侧;四、扩大(或缩小)减号的一侧,则需扩大(或缩小)减号的另一侧。
到底采取哪个近似方向由相近程度和截位后计算难度决定。
一般说来,在乘法或者除法中使用"截位法"时,若答案需要有N位精度,则计算过程的数据需要有N+1位的精度,但具体情况还得由截位时误差的大小以及误差的抵消情况来决定;在误差较小的情况下,计算过程中的数据甚至可以不满足上述截位方向的要求。
所以应用这种方法时,需要考生在做题当中多加熟悉与训练误差的把握,在可以使用其它方式得到答案并且截位误差可能很大时,尽量避免使用乘法与除法的截位法。
★【速算技巧四:化同法】要点:所谓"化同法",是指"在比较两个分数大小时,将这两个分数的分子或分母化为相同或相近,从而达到简化计算"的速算方式。
一般包括三个层次:一、将分子(或分母)化为完全相同,从而只需要再看分母(或分子)即可;二、将分子(或分母)化为相近之后,出现"某一个分数的分母较大而分子较小"或"某一个分数的分母较小而分子较大"的情况,则可直接判断两个分数的大小。
三、将分子(或分母)化为非常接近之后,再利用其它速算技巧进行简单判定。
事实上在资料分析试题当中,将分子(或分母)化为完全相同一般是不可能达到的,所以化同法更多的是"化为相近"而非"化为相同"。
★【速算技巧五:差分法】李委明提示:“差分法”是在比较两个分数大小时,用“直除法”或者“化同法”等其他速算方式难以解决时可以采取的一种速算方式。
适用形式:两个分数作比较时,若其中一个分数的分子与分母都比另外一个分数的分子与分母分别仅仅大一点,这时候使用“直除法”、“化同法”经常很难比较出大小关系,而使用“差分法”却可以很好地解决这样的问题。
基础定义:在满足“适用形式”的两个分数中,我们定义分子与分母都比较大的分数叫“大分数”,分子与分母都比较小的分数叫“小分数”,而这两个分数的分子、分母分别做差得到的新的分数我们定义为“差分数”。
例如:324/53.1与313/51.7比较大小,其中324/53.1就是“大分数”,313/51.7就是“小分数”,而324-313/53.1-51.7=11/1.4就是“差分数”。
“差分法”使用基本准则——“差分数”代替“大分数”与“小分数”作比较:1、若差分数比小分数大,则大分数比小分数大;2、若差分数比小分数小,则大分数比小分数小;3、若差分数与小分数相等,则大分数与小分数相等。
比如上文中就是“11/1.4代替324/53.1与313/51.7作比较”,因为11/1.4>313/51.7(可以通过“直除法”或者“化同法”简单得到),所以324/53.1>313/51.7。
特别注意:一、“差分法”本身是一种“精算法”而非“估算法”,得出来的大小关系是精确的关系而非粗略的关系;二、“差分法”与“化同法”经常联系在一起使用,“化同法紧接差分法”与“差分法紧接化同法”是资料分析速算当中经常遇到的两种情形。
三、“差分法”得到“差分数”与“小分数”做比较的时候,还经常需要用到“直除法”。
四、如果两个分数相隔非常近,我们甚至需要反复运用两次“差分法”,这种情况相对比较复杂,但如果运用熟练,同样可以大幅度简化计算。
【例1】比较7/4和9/5的大小【解析】运用“差分法”来比较这两个分数的大小关系:大分数小分数9/5 7/49-7/5-1=2/1(差分数)根据:差分数=2/1>7/4=小分数因此:大分数=9/5>7/4=小分数李委明提示:使用“差分法”的时候,牢记将“差分数”写在“大分数”的一侧,因为它代替的是“大分数”,然后再跟“小分数”做比较。
【例2】比较32.3/101和32.6/103的大小【解析】运用“差分法”来比较这两个分数的大小关系:小分数大分数32.3/101 32.6/10332.6-32.3/103-101=0.3/2(差分数)根据:差分数=0.3/2=30/200<32.3/101=小分数(此处运用了“化同法”)因此:大分数=32.6/103<32.3/101=小分数[注释]本题比较差分数和小分数大小时,还可采用直除法,读者不妨自己试试。
李委明提示(“差分法”原理):以例2为例,我们来阐述一下“差分法”到底是怎样一种原理,先看下图:上图显示了一个简单的过程:将Ⅱ号溶液倒入Ⅰ号溶液当中,变成Ⅲ号溶液。
其中Ⅰ号溶液的浓度为“小分数”,Ⅲ号溶液的浓度为“大分数”,而Ⅱ号溶液的浓度为“差分数”。
显然,要比较Ⅰ号溶液与Ⅲ号溶液的浓度哪个大,只需要知道这个倒入的过程是“稀释”还是“变浓”了,所以只需要比较Ⅱ号溶液与Ⅰ号溶液的浓度哪个大即可。
【例3】比较29320.04/4126.37和29318.59/4125.16的大小【解析】运用“差分法”来比较这两个分数的大小关系:29320.04/4126.37 29318.59/4125.161.45/1.21根据:很明显,差分数=1.45/1.21<2<29318.59/4125.16=小分数因此:大分数=29320.04/4126.37<29318.59/4125.16=小分数[注释]本题比较差分数和小分数大小时,还可以采用“直除法”(本质上与插一个“2”是等价的)。
【例4】下表显示了三个省份的省会城市(分别为A、B、C城)2006年GDP及其增长情况,请根据表中所提供的数据回答:1.B、C两城2005年GDP哪个更高?2.A、C两城所在的省份2006年GDP量哪个更高?GDP(亿元)GDP增长率占全省的比例A城873.2 12.50% 23.9%B城984.3 7.8% 35.9%C城1093.4 17.9% 31.2%【解析】一、B、C两城2005年的GDP分别为:984.3/1+7.8%、1093.4/1+17.9%;观察特征(分子与分母都相差一点点)我们使用“差分法”:984.3/1+7.8% 1093.4/1+17.9%109.1/10.1%运用直除法,很明显:差分数=109.1/10.1%>1000>984.3/1+7.8%=小分数,故大分数>小分数所以B、C两城2005年GDP量C城更高。
