《信息论》期末考试B卷答案
《信息论》期末考试试题(A卷)标准答案

(1) 每幅画面所含信息量: H log 2 10 信息传输速率:
9.97 105 bit
(2 分)
R 30 H 30 log 2 10300000 29.90 Mbps
(2) AWGN 信道容量:
(1 分)
C W log 2 (1 SNR) 6 106 log 2 (1 1000) 59.80 Mbps
(2+1 分) (3 分)
(3)求为实现电视信号可靠传输信道所需的最小带宽和对应的信号平均功率; (3+2 分) (4)求信息传输速率达到容量时的频谱利用率和对应的 Eb / N 0 (dB ) 。 解 信噪比换算: SNR 10
SNR[ dB ]/10
(3+2 分)
1030/10 1000
的符号熵为 (2/5)H(1/2,1/4,1/4)+ (3/5)H(1/3)=1.151 比特/符号。 4.设试验信道输入与输出符号集均为 {1, 2,3, 4} ,输入概率分别为 1/2,1/4,1/8,1/8,失 真测度为 d(i, j)= (i - j)2 ,1 i, j 4 ; 则 Dmin 0 , Dmax 9/8=1.125 。
3 次扩展信源符号 000 001 010 100 011 101 110 111 平均码长 概 率 0.729 0.081 0.081 0.081 0.009 0.009 0.009 0.001 编 0 100 101 110 11100 11101 11110 11111 0.5327 码
(5 分)
个二元一一对应信道传输,且每秒只传送两个符号; (1) 若要求信息无失真传输,信源能否不进行编码而直接与信道相接? (3 分) (2) 能否采用适当的编码方式然后通过信道进行无失真传输?为什么? (2+3 分) (3) 确定一种编码方式并进行编码,使得传输满足不失真要求;同时请说明信源采用这 种编码后, 编码器输出与信道输入之间应设置何种装置? (10+2 分) 解
《信息论》期末考试试题(A 卷) 标准答案

(2) 通过错误概率为 p, 0 ≤ p ≤ 1/ 2 的二元删除信道,求最佳译码准则的判决
函数和平均译码错误率;
(2+2=4 分)
(3) 通过(1)与(2)的串联信道,求最佳译码准则的判决函数和平均译码错误
率,并与(1)和(2)的平均译码错误率进行比较,得到怎样的结论?
(2+2+3=7 分)
(4) 根据(3)的结果,求信源经过串联信道后信息量损失的上界? (3 分)
①确定
σ12
,
σ
2 2
和
P
的关系;
②写出信道容量表达式;
(3+3+3=9 分)
③写出达到容量时信道的输入概率密度 p(x1, x2 ) ; 解:
(1) E[x12 ] = 0 ,则
(3+3=6 分)
①
σ
2 1
≥
σ
2 2
+
P
,
②
C
=
1 2
log(1 +
P σ 22
)
,
(2) E[x22 ] > 0 ,则
从零均值的高斯分布,且相互独立,方差分别为 σ12
和σ22
,且 σ12
>
σ
2 2
,信道输
入均值为零, E x12 + x22 ≤ P ;
(1) 当达到信道容量时, E[x12 ] = 0 ;
(3+3=6 分)
①确定σ12 ,σ 22 和 P 的关系;
②写出信道容量表达式;
(2) 当达到信道容量时, E[x22 ] > 0 ;
(2 分)
(3) 写出香农第三定理中存在平均失真不大于 D 的信源编码充要条件;
信息论与编码期末考试题(全套)

三、(16分)已知信源
(1)用霍夫曼编码法编成二进制变长码;(6分)
(2)计算平均码长 ;(4分)
(3)计算编码信息率 ;(2分)
(4)计算编码后信息传输率 ;(2分)
(5)计算编码效率 。(2分)
四、(10分)某信源输出A、B、C、D、E五种符号,每一个符号独立出现,出现概率分别为1/8、1/8、1/8、1/2、1/8。如果符号的码元宽度为0.5 。计算:
(1)信息就是一种消息。()
(2)信息论研究的主要问题是在通信系统设计中如何实现信息传输、存储和处理的有效性和可靠性。()
(3)概率大的事件自信息量大。()
(4)互信息量可正、可负亦可为零。()
(5)信源剩余度用来衡量信源的相关性程度,信源剩余度大说明信源符号间的依赖关系较小。()
(6)对于固定的信源分布,平均互信息量是信道传递概率的下凸函数。()
7、根据是否允许失真,信源编码可分为和。
8、若连续信源输出信号的平均功率为 ,则输出信号幅度的概率密度是时,信源具有最大熵,其值为值。
9、在下面空格中选择填入数学符号“ ”或“ ”
(1)当X和Y相互独立时,H(XY)H(X)+H(X/Y)H(Y)+H(X)。
(2)
(3)假设信道输入用X表示,信道输出用Y表示。在无噪有损信道中,H(X/Y) 0,
5.各码字的长度符合克拉夫特不等式,是唯一可译码存在的充分和必要条件.()
6.连续信源和离散信源的熵都具有非负性.()
7.信源的消息通过信道传输后的误差或失真越大,信宿收到消息后对信源存在的不确
定性就越小,获得的信息量就越小.
8.汉明码是一种线性分组码.()
《信息论基础》试卷(期末)(B卷)

《信息论基础》试卷(期末)(B卷)重庆邮电⼤学2007/2008学年2学期《信息论基础》试卷(期末)(B 卷)(半开卷)⼀、填空题(共20分,每空1分)1、通信系统中,编码的主要⽬的有两个,分别是和。
2、离散⽆记忆信源存在剩余度的原因是。
3、当时,信源熵为最⼤值。
⼋进制信源的最⼤熵为,最⼩熵为。
4、⽆失真信源编码的平均码长最⼩理论极限制为。
5、⼀个事件发⽣概率为0.125,则⾃相关量为。
6、根据信原输出随机序列中随机变量前后之间有⽆统计依赖性,信原可以分为和。
7、噪声瞬时值的概率密度函数服从分布,同时功率谱密度为的噪声称为⾼斯⽩噪声。
8、当时,信源与信道达到匹配。
9、若连续信源输出信号的平均功率为2σ,则输出信号幅度的概率密度是⾼斯分布或正态分布或时,信源具有最⼤熵,其值为值。
9、在下⾯空格中选择填⼊数学符号“,,,=≥≤>”或“?” (1)H(XY) H(Y)+H(X|Y) H(Y)+H(X)(2)假设信道输⼊⽤X 表⽰,信道输出⽤Y 表⽰。
在有噪⽆损信道中, H(X/Y) 0, H(Y/X) 0, I(X;Y) H(X)。
⼆、(6分)若连续信源输出的幅度被限定在【1,3】区域内,当输出信号的概率密度是均匀分布时,计算该信源的相对熵,并说明该信源的绝对熵为多少。
三、(16分)已知信源12345S P 0.250.20.20.20.15s s s s s =(1)⽤霍夫曼编码法编成⼆进制变长码;(4分)(2)计算平均码长—L ;(4分)(3)计算编码信息率R ';(4分)(4)计算编码后信息传输率R ;(2分)(5)计算编码效率η。
(2分)四、(12分)已知⼀个平均功率受限的连续信号,通过带宽W 10MHz =的⾼斯⽩噪声信道,试计算(1)若信噪⽐为10,信道容量为多少?(4分)(2)若信道容量不变,信噪⽐降为5,信道带宽为多少?(4分)(3)若信道通频带减为5MHz 时,要保持相同的信道容量,信道上的信号与噪声的平均功率⽐值应等于多少?(4分)五、(16分)某个信息源发出符号的概率为:12()(),P a P a =3()0.4,P a =假设该信息源发出的符号前后有关联,其依赖关系为:112122321333312133(|);(|);(|);(|);(|);(|);443344P a a P a a P a a P a a P a a P a a ======(1)画出状态转移图(4分)(2)计算稳态概率(4分)(3)计算信源的极限熵(4分)(4)计算稳态下H1,H2及其对应的剩余度。
北邮信息论期末考试试题标准答案

l 如果对数的底不定,可以不写单位。
9
8
C = C1 = log2 (5 / 3) 比特/自由度 (共 4 分,步骤酌情给分)
信道输入概率分布为
p(x) =
1
− x2
e 18
3 2π
(2 分)
信道输入的熵为
h( X ) =
1 log(2π e ×9) = 2
1 2
log
2
(18π
e)
比特/自由度
(2 分)
注:
l 对数可以化到最简,不必算出结果;
北京邮电大学 2008——2009 学年第 一 学期
《信息论》期末考试试题(B 卷)标准答案
姓名
班级
学号
分数
注:所有答案均写在答题纸上,试卷和答题纸一起上交。
一、判断题(正确打√,错误打×)(共 10 分,每小题 1 分)
(1) 差熵为零的连续信源的输出平均不确定性为零; (2) 在通过一一对应的变换后,连续信源的差熵一定会变化;
=
∫
p( x)[ 1 2
log(2π
e
×
9)]dx
=
1 2
log2 (18π
e)
比特/自由度
(4 分)
(3)
I ( X ;Y ) = h(Y ) − h(Y | X )
C = max h(Y ) − h(Y | X )
Y 为高斯分布时达到容量
C = 1 log(2π e× 25) − 1 log(2π e ×9)
ML 准则确定译码函数,并求信息传输速率和平均译码错误率;
(2+2+2 分)
(4) 如果利用 n 长重复码传送 0、1 符号,求信息传输速率和平均译码错
信息理论与编码-期末试卷A及答案

一、填空题(每空1分,共35分) 1、1948年,美国数学家 发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。
信息论的基础理论是 ,它属于狭义信息论。
2、信号是 的载体,消息是 的载体。
3、某信源有五种符号}{,,,,a b c d e ,先验概率分别为5.0=a P ,25.0=b P ,125.0=c P ,0625.0==e d P P ,则符号“a ”的自信息量为 bit ,此信源的熵为 bit/符号。
4、某离散无记忆信源X ,其概率空间和重量空间分别为1234 0.50.250.1250.125X x x x x P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦和12340.5122X x x x x w ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,则其信源熵和加权熵分别为 和 。
5、信源的剩余度主要来自两个方面,一是,二是 。
6、平均互信息量与信息熵、联合熵的关系是 。
7、信道的输出仅与信道当前输入有关,而与过去输入无关的信道称为 信道。
8、马尔可夫信源需要满足两个条件:一、 ; 二、。
9、若某信道矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡010001000001100,则该信道的信道容量C=__________。
10、根据是否允许失真,信源编码可分为 和 。
12、在现代通信系统中,信源编码主要用于解决信息传输中的 性,信道编码主要用于解决信息传输中的 性,保密密编码主要用于解决信息传输中的安全性。
13、差错控制的基本方式大致可以分为 、 和混合纠错。
14、某线性分组码的最小汉明距dmin=4,则该码最多能检测出 个随机错,最多能纠正 个随机错。
15、码字101111101、011111101、100111001之间的最小汉明距离为 。
16、对于密码系统安全性的评价,通常分为 和 两种标准。
17、单密钥体制是指 。
18、现代数据加密体制主要分为 和 两种体制。
19、评价密码体制安全性有不同的途径,包括无条件安全性、 和 。
最新《信息论》试题及答案

期终练习一、某地区的人群中,10%是胖子,80%不胖不瘦,10%是瘦子。
已知胖子得高血压的概率是15%,不胖不瘦者得高血压的概率是10%,瘦子得高血压的概率是5%,则“该地区的某一位高血压者是胖子”这句话包含了多少信息量。
解:设事件A :某人是胖子; B :某人是不胖不瘦 C :某人是瘦子 D :某人是高血压者根据题意,可知:P (A )=0.1 P (B )=0.8 P (C )=0.1 P (D|A )=0.15 P (D|B )=0.1 P (D|C )=0.05而“该地区的某一位高血压者是胖子” 这一消息表明在D 事件发生的条件下,A 事件的发生,故其概率为P (A|D )根据贝叶斯定律,可得:P (D )=P (A )* P (D|A )+P (B )* P (D|B )+P (C )* P (D|C )=0.1 P (A|D )=P (AD )/P (D )=P (D|A )*P (A )/ P (D )=0.15*0.1/0.1=0.15 故得知“该地区的某一位高血压者是胖子”这一消息获得的多少信息量为: I (A|D ) = - logP (A|D )=log (0.15)≈2.73 (bit ) 二、设有一个马尔可夫信源,它的状态集为{S 1,S 2,S 3},符号集为{a 1,a 2,a 3},以及在某状态下发出符号集的概率是(|)k i p a s (i ,k=1,2,3),如图所示(1)求图中马尔可夫信源的状态极限概率并找出符号的极限概率(2)计算信源处在某一状态下输出符号的条件熵H(X|S=j) (j=s 1,s 2,s 3) (3)求出马尔可夫信源熵H ∞解:(1)该信源达到平稳后,有以下关系成立:13212312123()()31()()()4211()()()42()()()1Q E Q E Q E Q E Q E Q E Q E Q E Q E Q E Q E =⎧⎪⎪=+⎪⎨⎪=+⎪⎪++=⎩可得1232()73()72()7Q E Q E Q E ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩3111322133313()()(|)72()()(|)73()()(|)7i i i i i i i i i p a Q E p a E p a Q E p a E p a Q E p a E =========∑∑∑(2)311113222133331(|)(|)log (|) 1.5bit/(|)(|)log (|)1bit/(|)(|)log (|)0bit/k k k kk k k k k H X S p a S p a S H X S p aS p a S H X S p a S p a S ====-==-==-=∑∑∑(符号)(符号)(符号)(3)31()(|)2/7*3/23/7*12/7*06/7iii H Q E H X E ∞==⨯=++=∑(比特/符号)三、二元对称信道的传递矩阵为0.60.40.40.6⎡⎤⎢⎥⎣⎦(1)若P(0)=3/4,P(1)=1/4,求H (X ),H (X|Y )和I (X ;Y )(2)求该信道的信道容量及其最大信道容量对应的最佳输入分布 解:⑴()H X =21()log ()iii p x p x ==-∑=0.75log 750.25log 25--≈0.811(比特/符号)1111212()()(|)()(|)p y p x p y x p x p y x =+=0.75*0.6+0.25*0.4=0.55 2121222()()(|)()(|)p y p x p y x p x p y x =+=0.75*0.4+0.25*0.6=0.45()0.55log0.550.45log0.45H Y =--=≈0.992(比特/符号)122(|)()(|)()(|)0.75(0.6,0.4)0.25(0.4,0.6)(0.6log 0.60.4log 0.4)0.971/H Y X p x H Y x p x H Y x H H =+=⨯+⨯=-+≈(比特符号)(|)()()()(|)()H X Y H XY H Y H X H Y X H Y =-=+-≈0.811+0.971-0.992=0.79 (比特/符号)I (X ;Y )=H (X )-H (X =0.811-0.79=0.021(比特/符号)(2)此信道为二元对称信道,所以信道容量为C=1-H(p)=1-H(0.6)=1-0.971=0.029(比特/符号) 当输入等概分布时达到信道容量四、求信道22042240p p p p εεεεεε⎡⎤-- ⎢⎥-- ⎢⎥⎣⎦的信道容量,其中1p p =-。
信息论试卷含答案

《信息论基础》参考答案一、填空题(共15分,每空1分)1、信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。
2、信源的剩余度主要来自两个方面,一是信源符号间的相关性,二是信源符号的统计不均匀性。
3、三进制信源的最小熵为0,最大熵为32log bit/符号。
4、无失真信源编码的平均码长最小理论极限制为信源熵(或H(S)/logr= H r (S))。
5、当R=C 或(信道剩余度为0)时,信源与信道达到匹配。
6、根据信道特性是否随时间变化,信道可以分为恒参信道和随参信道。
7、根据是否允许失真,信源编码可分为无失真信源编码和限失真信源编码。
8、若连续信源输出信号的平均功率为2σ,则输出信号幅度的概率密度是高斯分布或正态分布或()222x f x σ-=时,信源具有最大熵,其值为值21log 22e πσ。
9、在下面空格中选择填入数学符号“,,,=≥≤〉”或“〈”(1)当X 和Y 相互独立时,H (XY )=H(X)+H(X/Y)=H(Y)+H(X)。
(2)()()1222H X X H X =≥()()12333H X X X H X = (3)假设信道输入用X 表示,信道输出用Y 表示。
在无噪有损信道中,H(X/Y)> 0, H(Y/X)=0,I(X;Y)<H(X)。
二、(6分)若连续信源输出的幅度被限定在【2,6】区域内,当输出信号的概率密度是均匀分布时,计算该信源的相对熵,并说明该信源的绝对熵为多少。
()1,2640,x f x ⎧≤≤⎪=⎨⎪⎩其它()()()62log f x f x dx ∴=-⎰相对熵h x=2bit/自由度该信源的绝对熵为无穷大。
三、(16分)已知信源1234560.20.20.20.20.10.1S s s s s s s P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)用霍夫曼编码法编成二进制变长码;(6分) (2)计算平均码长L ;(4分)(3)计算编码信息率R ';(2分)(4)计算编码后信息传输率R ;(2分) (5)计算编码效率η。
(完整word版)信息论试卷

一、选择题1、下列那位创立了信息论.(C)A.牛顿B.高斯C.香农D.哈夫曼2、下列不属于消息的是。
(B)A.文字B.信号C.图像D.语言3、同时扔两个正常的骰子,即各面呈现的概率都是1/6,若点数之和为2,则得到的自信息量为(B)。
A.-log36 bitB.log36 bitC.-log18 bitD.log18 bit4、下列说法不正确的是(C)A.异字头码肯定是唯一可译的B.逗点码是唯一可译的C.唯一可译码不必满足Kraft 不等式D.无逗点码可以唯一可译5、下述编码中那个可能是任何概率分布对应的Huffman编码(A)A.{0,10,11}B.{00,01,10,110}C.{01,10}D.{001,011,100,101}6、下列物理量不满足非负性的是(D)A.H(X)B.I(X;Y)C.H(Y|X)D.I(x j;y j)7、信源的输出与信道的输入匹配的目的不包括(D)A.符号匹配B.信息匹配C.降低信道剩余度D.功率匹配8、在串联系统中,有效信息量的值(B)A.趋于变大B.趋于变小C.不变D.不确定二、判断题1、信息论研究的主要问题是在通信系统设计中如何实现信息传输、存储和处理的有效性和可靠性。
(T)2、信息是先验概率和后验概率的函数,信息量是事件数目的指数函数。
(F)提示:对数函数3、两个事件之间的互信息量可正,可负,也可能为0。
(T)4、在通讯系统中,无论对接收到的信息怎样处理,信息只会减少,绝不可能增加。
(T )5、Huffman 编码是唯一的.(F)提示:不唯一6、概率大的事件自信息量大。
(F )提示:小7、在事件个数相同条件下,事件等概率出现情况下的熵值最大。
(T)8、平稳的离散无记忆信道不可用一维概率描述。
(F)提示:可以三、填空题1、必然事件的自信息是 0 .2、根据码字所含的码元的个数,编码可分为 等长 编码和 不等长 编码。
3、不等长D 元码,码字最长限定为N,则至多有 D(D N - 1)/(D — 1) 个码字。
《信息论》期末考试试题( 卷)标准答案

2.(共 10 分)有两枚硬币,第一枚是正常的硬币,它的一面是国徽,另一面是 面值;第二枚是不正常的硬币,它的两面都是面值。现随机地抽取一枚硬币,进 行 2 次抛掷试验,观察硬币朝上的一面,其结果为:面值、面值。
1)求该试验结果与事件“取出的是第一枚硬币”之间的互信息;(4 分)
=
E( XS + αS 2 ) σ SσU
=
αQ σ SσU
I (U ; S) = H (U ) + H (S ) − H (US )
=
1 2
log
2πe σ
2 U
+
1 2
log
2πeσ
2 S
+
log 2πeσUσ S
1− ρ2
=
1 2
log
σ
σ σ2 2
SU
σ2 2
US
− (αQ)
2
=
1 log P + α 2Q
2 1 d = 1 0 7)若失真矩阵为 3 1 ,输入等概,则 Dmin = 2/3 , Dmax = 2/3 。
三、简答题(6 分)
1.仙农第二定理指出了“高效率、高可靠性”的信道编码存在性,
1)“高效率”的含义是什么?
(1 分)
2)“高可靠性” 的含义是什么?
(1 分)
3)存在这种信道编码的必要条件是什么?
1− ρ2
=
1 log
σ
2 U
σ
2 Y
2
σ
2 U
σ
2 Y
−
(P
+ αQ)2
=
1 log
(P + Q + N )(P + α 2Q)
信息论与编码考题标准答案

信 息 论 与 编 码 考题与标准答案第一题 选择题1.信息是( b )a. 是事物运动状态或存在方式的描述b.是事物运动状态或存在方式的不确定性的描述c.消息、文字、图象d.信号 2.下列表达式哪一个是正确的(e )a. H (X /Y )=H (Y /X )b. )();(0Y H Y X I <≤c.)/()(),(X Y H X H Y X I -=d. )()/(Y H Y X H ≤e. H (XY )=H (X )+H (Y /X )3.离散信源序列长度为L ,其序列熵可以表示为( b )a. )()(1X LH X H =b.c. ∑==Ll lXH X H 1)()(d. )()(X H X H L =4.若代表信源的N 维随机变量的取值被限制在一定的范围之内,则连续信源为( c ),具有最大熵。
a. 指数分布b. 正态分布c. 均匀分布d. 泊松分布 5.对于平均互信息);(Y X I ,下列说法正确的是( b )a. 当)(i x p 一定时,是信道传递概率)(i j x y p 的上凸函数,存在极大值b. 当)(i x p 一定时,是信道传递概率)(i j x y p 的下凸函数,存在极小值c.当)(i j x y p 一定时,是先验概率)(i x p 的上凸函数,存在极小值d.当)(i j x y p 一定时,是先验概率)(i x p 的下凸函数,存在极小值 6.当信道输入呈( c )分布时,强对称离散信道能够传输最大的平均信息量,即达到信道容量 a. 均匀分布 b. 固定分布 c. 等概率分布 d. 正态分布7.当信道为高斯加性连续信道时,可以通过以下哪些方法提高抗干扰性(b d ) a. 减小带宽 b. 增大发射功率 c. 减小发射功率 d.增加带宽第二题 设信源 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡6.04.0)(21x x X p X 通过一干扰信道,接收符号为Y={y 1,y 2},信道传递矩阵为⎥⎦⎤⎢⎣⎡43416165 求:(1) 信源 X 中事件 x 1 和 x 2 分别含有的自信息量。
信息论考试卷及答案
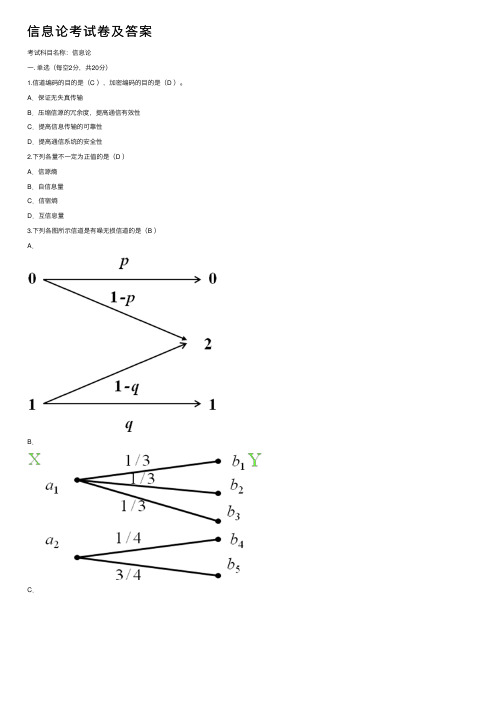
信息论考试卷及答案考试科⽬名称:信息论⼀. 单选(每空2分,共20分)1.信道编码的⽬的是(C ),加密编码的⽬的是(D )。
A.保证⽆失真传输B.压缩信源的冗余度,提⾼通信有效性C.提⾼信息传输的可靠性D.提⾼通信系统的安全性2.下列各量不⼀定为正值的是(D )A.信源熵B.⾃信息量C.信宿熵D.互信息量3.下列各图所⽰信道是有噪⽆损信道的是(B )A.B.C.D.4.下表中符合等长编码的是( A )5.联合熵H(XY)与熵H(X)及条件熵H(X/Y)之间存在关系正确的是(A )A.H(XY)=H(X)+H(Y/X)B.H(XY)=H(X)+H(X/Y)C.H(XY)=H(Y)+H(X)D.若X和Y相互独⽴,H(Y)=H(YX)6.⼀个n位的⼆进制数,该数的每⼀位可从等概率出现的⼆进制码元(0,1)中任取⼀个,这个n位的⼆进制数的⾃信息量为(C )A.n2B.1 bitC.n bitnD.27.已知发送26个英⽂字母和空格,其最⼤信源熵为H0 = log27 = 4.76⽐特/符号;在字母发送概率不等时,其信源熵为H1 = 4.03⽐特/符号;考虑字母之间相关性时,其信源熵为H2 = 3.32⽐特/符号;以此类推,极限熵H=1.5⽐特/符号。
问若⽤⼀般传送⽅式,冗余度为( B )∞A.0.32B.0.68C .0.63D .0.378. 某对称离散信道的信道矩阵为,信道容量为( B )A .)61,61,31,31(24log H C -= B .)61,61,31,31(4log H C -= C .)61,61,31,31(2log H C -= D .)61,31(2log H C -= 9. 下⾯不属于最佳变长编码的是( D )A .⾹农编码和哈夫曼编码B .费诺编码和哈夫曼编码C .费诺编码和⾹农编码D .算术编码和游程编码⼆. 综合(共80分)1. (10分)试写出信源编码的分类,并叙述各种分类编码的概念和特性。
信息理论与编码-期末试卷A及答案

一、填空题(每空1分,共35分)1、1948年,美国数学家 发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。
信息论的基础理论是 ,它属于狭义信息论。
2、信号是 的载体,消息是 的载体。
3、某信源有五种符号}{,,,,a b c d e ,先验概率分别为5.0=a P ,25.0=b P ,125.0=c P ,0625.0==e d P P ,则符号“a ”的自信息量为 bit ,此信源的熵为 bit/符号。
4、某离散无记忆信源X ,其概率空间和重量空间分别为1234 0.50.250.1250.125X x x x x P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦和12340.5122X x x x x w ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,则其信源熵和加权熵分别为 和 。
5、信源的剩余度主要来自两个方面,一是 ,二是 。
6、平均互信息量与信息熵、联合熵的关系是 。
7、信道的输出仅与信道当前输入有关,而与过去输入无关的信道称为 信道。
8、马尔可夫信源需要满足两个条件:一、 ;二、 。
9、若某信道矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡010001000001100,则该信道的信道容量C=__________。
10、根据是否允许失真,信源编码可分为 和 。
11、信源编码的概率匹配原则是:概率大的信源符号用 ,概率小的信源符号用 。
(填短码或长码)12、在现代通信系统中,信源编码主要用于解决信息传输中的 性,信道编码主要用于解决信息传输中的 性,保密密编码主要用于解决信息传输中的安全性。
13、差错控制的基本方式大致可以分为 、 和混合纠错。
14、某线性分组码的最小汉明距dmin=4,则该码最多能检测出 个随机错,最多能纠正 个随机错。
15、码字1、0、1之间的最小汉明距离为 。
16、对于密码系统安全性的评价,通常分为 和 两种标准。
17、单密钥体制是指 。
18、现代数据加密体制主要分为 和 两种体制。
信息论与编码期末复习试题2套含答案(大学期末复习资料)

莆田学院期末考试试卷(A)卷2011 — 2012 学年第一学期课程名称:信息论与编码适用年级/专业: 09/电信(通信)试卷类别开卷()闭卷(√)学历层次本科考试用时 120分钟《.考生注意:答案要全部抄到答题纸上,做在试卷上不给分.........................》.一、简答题(每小题8分,共32分)1.对于一个一般的通信系统,试给出其系统模型框图,并结合此图,解释数据处理定理。
2. 香农信息论研究了哪些内容?试讲述香农第二编码定理。
3. 什么是唯一可译码?什么是即时码(前缀码)?构造唯一可译码的充要条件?(10分)4. 什么是信源编码?什么是信道编码?为何要进行这两者编码?二、证明题(每小题6分,共6分)对于任意的事件X、Y,试证明下列不等式成立:H(X|Y)<=H(X),并说明等式成立的条件。
三、计算题(第1、5题各16分,第2题12分,第3题10分,第4题8分,共62分)1.(16分)一黑白气象传真图的消息只有黑色和白色两种,即信源X={黑,白}。
设黑色出现的概率为P(黑)=0.3,白色的出现概率P(白)=0.7。
求(1)假设图上黑白消息出现前后没有关联,求熵H(X);(2)假设消息前后有关联,其依赖关系为P(白/白)=0.9,P(黑/白)=0.1,P(白/黑)=0.2,P(黑/黑)=0.8,求此一阶马尔可夫信源的熵H2(X);(3)分别求上述两种信源的剩余度,比较和的大小,并说明其物理意义。
2.(12分)一信源产生概率为P(1)=0.005, P(0)=0.995的统计独立二进制数符。
这些数符组成长度为100的数符组。
我们为每一个少于3个“1”的源数符组提供一个二进制码字,所有码字的长度相等。
(1)求出为所规定的所有源符组都提供码字所需的最小码长。
(2)求信源发出一数符组,而编码器无相应码字的概率。
3.(10分)已知一个(6,3)线性分组码的全部码字为001011,110011,010110,101110,100101,111000,011101,000000。
《信息论》期末考试试题(A 卷)标准答案

北京邮电大学2006——2007学年第 一 学期《信息论》期末考试试题(A 卷)标准答案姓名 班级 学号 分数一、判断题(正确打√,错误打×)(共10分,每小题1分)1)异前置码是即时码; (√) 2)最大似然准则等价于最小汉明距离准则; (×) 3)离散信源记忆的长度越大,信源的符号熵越小; (√) 4)一维高斯信源的熵只与其均值和方差有关; (×) 5)为达到并联加性高斯噪声信道容量,在信道输入总功率给定条件下应给噪声方差大的子信道分配更多的功率; (×) 6)只要信息传输速率小于信道容量,总可以找到一种编码方式使得当编码序列足够长时传输差错率任意小; (√) 7)离散无记忆信源的N 次扩展源的熵是原信源熵的N 倍; (√) 8)仙农的AWGN 信道容量公式是在信道输入的平均功率和幅度受限条件下推导出来的; (×) 9)当马氏源的初始状态s 和输出nx x x ,,,10 给定后,那么状态1,21,,+n s s s 就能唯一确定; (√) 10)当平均失真大于其上限D max 时,率失真函数R (D )= 0 。
(√)二、填空题(共20分,每空2分)1) 设信源的熵为0.8比特/符号,对信源序列进行单符号编码,码序列为0、1二元序列,如果编码效率为100%,那么每信源符号平均码长为 0.8 ,码序列中“0 ”符号出现的概率为 1/2 ,信息传输速率为 1 比特/码符号。
2) 一阶平稳马氏源的符号转移概率为2.0)0|0(12|=X X p ,6.0)1|1(12|=X X p ,那么符号的平稳分布为=)0(X p 1/3 ,=)1(X p 2/3 ;信源的符号熵为 0.8879 比特/符号。
3)一维连续随机变量X在[a,b]区间内均匀分布时,其信源熵为log2(b-a)。
4)在输入平均功率相同的情况下, 高斯分布使加性噪声信道容量最小。
5) 二元等概信源的熵为 1 比特/符号,当信源输出序列长度L足够长时,典型序列的个数约等于2L。
信息论期末考试试题 答案

安徽大学2011—2012学年第1学期 《信息论》考试试卷参考答案(AB 合卷)一、 填空题 1、()(;)log()()p xy I x y p x p y =;2、事物运动状态或存在方式的不确定性的描述;3、(|)log(|)(|)p xy z p x z p y z ;4、信源 编码器 信道 译码器 信宿;5、保密性 认证性;6、0.72;7、 , ;8、(;)C I X Y - ;9、4.6 ; 10、0H ≥1H ≥4H ≥6H ≥∞H ; 11、()()1log log N L H S H S r N r N≤<+; 12、()f x 在q F 上不可约; 13、()g x |1n x -; 14、2F 、22F 、32F 、42F 、62F 、122F ; 15、8,4.二、判断题1、╳2、√3、√4、╳5、╳6、√7、√8、╳9、 ╳三、计算题 1、解:1111()log log 12222H X =--=1()log24H Y =-= 1()log 38H Z =-=当Z Y X ,,为统计独立时:()()()()1236H XYZ H X H Y H Z =++=++=2、解:二次扩展信源为2111213212223313233,,,,,,,,411111111,,,,,,,,9999363693636x x x x x x x x x x x x x x x x x x X P ⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦信源熵:22HX H X =()()22112log 2log )3366=-+⨯(=2log3-2/3比特/二符号 3、解:1)信道到矩阵为1/31/61/31/61/61/31/61/3P ⎛⎫= ⎪⎝⎭,故此信道为对称信道1111log 4(,,,)3636C H =-5l o g 33=-(比特/符号)相应的最佳输入概率分布为等概率分布。
(2)信道到矩阵为1/21/31/61/61/21/31/31/61/2P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,故此信道为对称信道111l o g 3(,,)236C H =-12log 323=- (比特/符号) 相应的最佳输入概率分布为等概率分布。
信息理论与编码-期末试卷A及答案

一、填空题(每空1分,共35分) 1、1948年,美国数学家 发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。
信息论的基础理论是 ,它属于狭义信息论。
2、信号是 的载体,消息是 的载体。
3、某信源有五种符号}{,,,,a b c d e ,先验概率分别为5.0=a P ,25.0=b P ,125.0=c P ,0625.0==e d P P ,则符号“a ”的自信息量为 bit ,此信源的熵为 bit/符号。
4、某离散无记忆信源X ,其概率空间和重量空间分别为1234 0.50.250.1250.125X x x x x P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦和12340.5122X x x x x w ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,则其信源熵和加权熵分别为 和 。
5、信源的剩余度主要来自两个方面,一是 ,二是 。
6、平均互信息量与信息熵、联合熵的关系是 。
7、信道的输出仅与信道当前输入有关,而与过去输入无关的信道称为 信道。
8、马尔可夫信源需要满足两个条件:一、 ; 二、 。
9、若某信道矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡010001000001100,则该信道的信道容量C=__________。
10、根据是否允许失真,信源编码可分为 和 。
11、信源编码的概率匹配原则是:概率大的信源符号用 ,概率小的信源符号用 。
(填短码或长码)12、在现代通信系统中,信源编码主要用于解决信息传输中的 性,信道编码主要用于解决信息传输中的 性,保密密编码主要用于解决信息传输中的安全性。
13、差错控制的基本方式大致可以分为 、 和混合纠错。
14、某线性分组码的最小汉明距dmin=4,则该码最多能检测出 个随机错,最多能纠正 个随机错。
15、码字101111101、011111101、100111001之间的最小汉明距离为 。
16、对于密码系统安全性的评价,通常分为 和 两种标准。
17、单密钥体制是指 。
信息论与编码期末复习试题含参考答案

信息论与编码期末复习试题含参考答案在无失真的信源中,信源输出由 H (X ) 来度量;在有失真的信源中,信源输出由 R (D ) 来度量。
要使通信系统做到传输信息有效、可靠和保密,必须首先 信源 编码,然后_____加密____编码,再______信道_____编码,最后送入信道。
带限AWGN 波形信道在平均功率受限条件下信道容量的基本公式,也就是有名的香农公式是;当归一化信道容量C/W 趋近于零时,也即信道完全丧失了通信能力,此时E b /N 0为 -1.6 dB ,我们将它称作香农限,是一切编码方式所能达到的理论极限。
保密系统的密钥量越小,密钥熵H (K )就越 小 ,其密文中含有的关于明文的信息量I (M ;C )就越 大 。
已知n =7的循环码,则信息位长度k 为 3 ,校验多项式h(x)= 。
设输入符号表为X ={0,1},输出符号表为Y ={0,1}。
输入信号的概率分布为p =(1/2,1/2),失真函数为d (0,0) = d (1,1) = 0,d (0,1) =2,d (1,0) = 1,则D min = 0 ,R (D min )= 1bit/symbol ,相应的编码器转移概率矩阵[p(y/x )]=;D max = 0.5 ,R (D max )= 0 ,相应的编码器转移概率矩阵[p(y/x )]=。
已知用户A 的RSA 公开密钥(e,n )=(3,55),,则 log(1)C W SNR =+42()1g x x x x =+++31x x ++1001⎡⎤⎢⎥⎣⎦1010⎡⎤⎢⎥⎣⎦5,11p q ==()φn =40 ,他的秘密密钥(d,n )=(27,55) 。
若用户B 向用户A 发送m =2的加密消息,则该加密后的消息为 8 。
二、判断题可以用克劳夫特不等式作为唯一可译码存在的判据。
(√ ) 线性码一定包含全零码。
(√ )算术编码是一种无失真的分组信源编码,其基本思想是将一定精度数值作为序列的编码,是以另外一种形式实现的最佳统计匹配编码。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1 页 共5 页
北方民族大学试卷
课程代码: 01100622 课程: 信息理论及编码 B 卷答案
说明:此卷为《信息理论及编码》B 卷答案
一、概念简答题(每小题6分,共30分)
1、比较平均自信息(信源熵)与平均互信息的异同。
答:平均自信息为 ()()()1
log q
i
i
i H X P a P a ==-
∑,表示信源的平均不确定度,也表示平
均每个信源消息所提供的信息量。
………………………………………(3分)
平均互信息()()()
()
,;log X Y
y
P x I X Y P xy P y =
∑。
表示从Y 获得的关于每个X 的平均信息量,
也表示发X 前后Y 的平均不确定性减少的量,还表示通信前后整个系统不确定性减少的量。
………………………………………(3分)
2、简述香农第一定理。
答:对于离散信源S 进行r 元编码,只要其满足
()
_
log H s N
N
r
L ≥
,…………………(3分) 当N 足够长,总可以实现无失真编码。
………………………………………(3分)
3、简述唯一可译变长码的判断方法?
答:将码C 中所有可能的尾随后缀组成一个集合F ,当且仅当集合F 中没有包含任一码字时,码C 为唯一可译变长码。
构成集合F 的方法:…………………(2分)
首先,观察码C 中最短的码字是否是其他码字的前缀。
若是,将其所有可能的尾随后缀排列出。
而这些尾随后缀又可能是某些码字的前缀,再将由这些尾随后缀产生的新的尾随后缀列出。
依此下去,直至没有一个尾随后缀是码字的前缀或没有新的尾随后缀产生为止。
…………………(2分) 接着,按照上述步骤将次短的码字直至所有码字可能产生的尾随后缀全部列出,得到尾随后缀集合F 。
…………………(2分)
4、简述最大离散熵定理。
第2 页 共5 页
答:最大离散熵定理为:对于离散无记忆信源,当信源等概率分布时熵最大。
……(3分)
对于有m 个符号的离散信源,其最大熵为log m 。
…………………………(3分)
5、什么是汉明距离;两个二元序列1230210,0210210i j αβ==,求其汉明距离。
答:长度相同的两个码字之间对应位置上不同的码元的个数,称为汉明距离。
…………………(3分)
(),5i j D αβ=………………………………………(3分)
二、判断题(每小题2分,共10分)
1、信息是事物运动状态或存在方式的不确定性的描述。
( √ )
2、当信源与信道连接时,若信息传输率达到了信道容量,则称此信源与信道达到匹配。
( √ )
3、二元霍夫曼码一定是最佳即时码。
( √ )
4、单符号离散信源的自信息和信源熵都是一个确定值。
( × )
5、平均错误概率只与译码准则有关系。
( × )
三、计算题(每小题10分,共40分)
1、设离散无记忆信源()1
23
40
123
31118844a a a a X P x ====⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢
⎥⎣⎦。
其发生的消息为()202123021302201320200231201320,求:(1)此消息的自信息是多少?(2)在此消息中平均每个符号携带的自信息是多少? 答: (1)自信息量()()()()()()
9log 05log 111log 25log 359.74I a P P P P =----≈比特……………(5分)
(2)()
259.74
1.9930
I =≈比特符号………………………………………(5分)
2、计算以下2个信道的信道容量C :
11
1
1133661111636
3P ⎡⎤
⎢⎥
=⎢
⎥⎢⎥
⎢⎥⎣⎦, 200
101
00000010
10
0P ⎡⎤⎢⎥⎢
⎥=⎢⎥⎢⎥⎣⎦
答:1P 为准对称信道,其信道容量∑=-
'''-=n
k k k
s M N
p p p H r C 1
211log ),,,(log ………………(2分)
第3 页 共5 页
其中3个子矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=316161311B ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=31312B ,⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡=61613B ,所以61
,31,21321===N N N
3
1,32,21321===M M M ,
则)/(0407.0)31
log 6132log 3121log 21()61,61,31,31(2log 1symbol bit H C =++--=………(4分)
2P 为一一对应信道,其信道容量)/(24log )(max 22symbol
bit X H C ===………………(4分)
3、信源空间为⎥
⎦
⎤⎢⎣⎡=⎥⎦⎤⎢
⎣⎡05.005.005.005.01.01.02.04.0)(87654
321s s s s s s s s s P S ,试构造二元霍夫曼码,并计算其平均码长和编码效率。
答:霍夫曼编码如下表所示
………………(6分)
平均码长信源符号)(码符号/6.224.022.0231.04405.0=⨯+⨯+⨯⨯+⨯⨯=L ………(2分) 编码效率97.06.2)05.01
log 05.041.01log 1.022.01log 2.04.01log 4.0()(=⨯+⨯++==L
S H η(2
分)
4、设某二元码为{}00000011011011111010C =。
(1)计算此码的最小距离min d ;(2)计算此码的码率R ,假设码字等概率分布;(3)采用最小距离译码准则,接收到序列00100,01010,00111和
00101应译成什么码字。
答:(1) min 3d =………………(3分)
第4 页 共5 页
(2) ()
log log 4
0.45
m R n =
==比特码符号………………(3分)
(3)序列00100译成00000,………………(1分)
序列01010译成11010,………………(1分) 序列00111译成10111,………………(1分) 序列00101译成01101………………(1分)
四、综合题(20分)
1、二元对称信道的信道矩阵为⎥
⎦
⎤
⎢
⎣⎡=9.01.01.09.0P ,信道传输速度为1500二元符号/秒,设信源为等概率分布,信源消息序列共有13000个二元符号,问:
(1)试计算能否在10秒内将信源消息序列无失真传送完?
(2)若信源概率分布为3.0)1(,7.0)0(==P P ,求无失真传送以上信源消息序列至少需要多长时间? 答:(1)此信道为二元对称信道,信源等概分布时,信道传输率达最大-C 。
信源熵
)/(12l o g )(s y m b o l b i t S H ==………………(1分)
)/(531.0469.011.0log 1.09.0log 9.01)(122symbol bit P H C =-=--=-=………………(1分)
)(113000)(7965531.0101500bit bit ⨯<=⨯⨯,所以10秒内不能传完。
………………(3分)
(2)信源不等概分布,信息传输率达不到C
)/(88129.052109.03602.03
.01
log 3.07.01log
7.0)(symbol bit S H =+=+=………………(1分) 130000个信源符号所含信息量为:)(77.11456)(130000
bit S H =⨯………………(2分) [][]34.066.09.01.01.09.03.07.0)(=⎥
⎦⎤
⎢⎣⎡⨯=y P ………………(1分) ⎥
⎦
⎤
⎢⎣⎡=⎥⎦⎤⎢⎣⎡⨯⨯⨯⨯=27.003.007.063.03.09.03.01.07.01.07.09.0)(xy P ………………(1分) 信息传输率:
)/(4558.034
.09
.0log 27.066.01.0log 03.034.01.0log 07.066.09.0log
63.0)
()/(log )();(2
symbol bit y P x y P y x P Y X I R XY
j i j j i =+++===∑………(5分)
要无失真传送130000个二元符号的信源消息序列至少需要的时间:
第5 页 共5 页
s T 757.161500
4558.077
.11456=⨯≥
………………(5分)。
