数学专业英语翻译
数学专业英语词汇英汉对照

1 概率论与数理统计词汇英汉对照表A absolute value 绝对值accept 接受acceptable region 接受域additivity 可加性adjusted 调整的alternative hypothesis 对立假设analysis 分析analysis of covariance 协方差分析analysis of variance 方差分析arithmetic mean 算术平均值association 相关性assumption 假设assumption checking 假设检验availability 有效度average 均值B balanced 平衡的band 带宽bar chart 条形图beta-distribution 贝塔分布between groups 组间的bias 偏倚binomial distribution 二项分布binomial test 二项检验C calculate 计算case 个案category 类别center of gravity 重心central tendency 中心趋势chi-square distribution 卡方分布chi-square test 卡方检验classify 分类cluster analysis 聚类分析coefficient 系数coefficient of correlation 相关系数collinearity 共线性column 列compare 比较comparison 对照components 构成,分量compound 复合的confidence interval 置信区间consistency 一致性constant 常数continuous variable 连续变量control charts 控制图correlation 相关covariance 协方差covariance matrix 协方差矩阵critical point 临界点critical value 临界值crosstab 列联表cubic 三次的,立方的cubic term 三次项cumulative distribution function 累加分布函数curve estimation 曲线估计D data 数据default 默认的definition 定义deleted residual 剔除残差density function 密度函数dependent variable 因变量description 描述design of experiment 试验设计deviations 差异df.(degree of freedom)自由度diagnostic 诊断dimension 维discrete variable 离散变量discriminant function 判别函数discriminatory analysis 判别分析distance 距离distribution 分布D-optimal design D-优化设计E eaqual 相等effects of interaction 交互效应efficiency 有效性eigenvalue 特征值equal size 等含量equation 方程error 误差estimate 估计estimation of parameters 参数估计estimations 估计量evaluate 衡量exact value 精确值expectation 期望expected value 期望值exponential 指数的exponential distributon 指数分布extreme value 极值F factor 因素,因子factor analysis 因子分析factor score 因子得分factorial designs 析因设计factorial experiment 析因试验fit 拟合fitted line 拟合线fitted value 拟合值fixed model 固定模型fixed variable 固定变量fractional factorial design 部分析因设计frequency 频数F-test F检验full factorial design 完全析因设计function 函数G gamma distribution 伽玛分布geometric mean 几何均值group 组H harmomic mean 调和均值heterogeneity 不齐性histogram 直方图homogeneity 齐性homogeneity of variance 方差齐性hypothesis 假设hypothesis test 假设检验I independence 独立independent variable 自变量independent-samples 独立样本index 指数index of correlation 相关指数interaction 交互作用interclass correlation 组内相关interval estimate 区间估计intraclass correlation 组间相关inverse 倒数的iterate 迭代K kernal 核Kolmogorov-Smirnov test柯尔莫哥洛夫-斯米诺夫检验kurtosis 峰度L large sample problem 大样本问题layer 层least-significant difference 最小显著差数least-square estimation 最小二乘估计least-square method 最小二乘法level 水平level of significance 显著性水平leverage value 中心化杠杆值life 寿命life test 寿命试验likelihood function 似然函数likelihood ratio test 似然比检验linear 线性的linear estimator 线性估计linear model 线性模型linear regression 线性回归linear relation 线性关系linear term 线性项logarithmic 对数的logarithms 对数logistic 逻辑的lost function 损失函数M main effect 主效应matrix 矩阵maximum 最大值maximum likelihood estimation 极大似然估计mean squared deviation(MSD)均方差mean sum of square 均方和measure 衡量media 中位数M-estimator M估计minimum 最小值missing values 缺失值mixed model 混合模型mode 众数model 模型Monte Carle method 蒙特卡罗法moving average 移动平均值multicollinearity 多元共线性multiple comparison 多重比较multiple correlation 多重相关multiple correlation coefficient 复相关系数multiple correlation coefficient 多元相关系数multiple regression analysis 多元回归分析multiple regression equation 多元回归方程multiple response 多响应multivariate analysis 多元分析N negative relationship 负相关nonadditively 不可加性nonlinear 非线性nonlinear regression 非线性回归noparametric tests 非参数检验normal distribution 正态分布null hypothesis 零假设number of cases 个案数O one-sample 单样本one-tailed test 单侧检验one-way ANOVA 单向方差分析one-way classification 单向分类optimal 优化的optimum allocation 最优配制order 排序order statistics 次序统计量origin 原点orthogonal 正交的outliers 异常值P paired observations 成对观测数据paired-sample 成对样本parameter 参数parameter estimation 参数估计partial correlation 偏相关partial correlation coefficient 偏相关系数partial regression coefficient 偏回归系数percent 百分数percentiles 百分位数pie chart 饼图point estimate 点估计poisson distribution 泊松分布polynomial curve 多项式曲线polynomial regression 多项式回归polynomials 多项式positive relationship 正相关power 幂P-P plot P-P概率图predict 预测predicted value 预测值prediction intervals 预测区间principal component analysis 主成分分析proability 概率probability density function 概率密度函数probit analysis 概率分析proportion 比例Q qadratic 二次的Q-Q plot Q-Q概率图quadratic term 二次项quality control 质量控制quantitative 数量的,度量的quartiles 四分位数R random 随机的random number 随机数random number 随机数random sampling 随机取样random seed 随机数种子random variable 随机变量randomization 随机化range 极差rank 秩rank correlation 秩相关rank statistic 秩统计量regression analysis 回归分析regression coefficient 回归系数regression line 回归线reject 拒绝rejection region 拒绝域relationship 关系reliability 可靠性repeated 重复的report 报告,报表residual 残差residual sum of squares 剩余平方和response 响应risk function 风险函数robustness 稳健性root mean square 标准差row 行run 游程run test 游程检验S sample 样本sample size 样本容量sample space 样本空间sampling 取样sampling inspection 抽样检验scatter chart 散点图S-curve S形曲线separately 单独地sets 集合sign test 符号检验significance 显著性significance level 显著性水平significance testing 显著性检验significant 显著的,有效的significant digits 有效数字skewed distribution 偏态分布skewness 偏度small sample problem 小样本问题smooth 平滑sort 排序soruces of variation 方差来源space 空间spread 扩展square 平方standard deviation 标准离差standard error of mean 均值的标准误差standardization 标准化standardize 标准化statistic 统计量statistical quality control 统计质量控制std. residual 标准残差stepwise regression analysis 逐步回归stimulus 刺激strong assumption 强假设stud. deleted residual 学生化剔除残差stud. residual 学生化残差subsamples 次级样本sufficient statistic 充分统计量sum 和sum of squares 平方和summary 概括,综述T table 表t-distribution t分布test 检验test criterion 检验判据test for linearity 线性检验test of goodness of fit 拟合优度检验test of homogeneity 齐性检验test of independence 独立性检验test rules 检验法则test statistics 检验统计量testing function 检验函数time series 时间序列tolerance limits 容许限total 总共,和transformation 转换treatment 处理trimmed mean 截尾均值true value 真值t-test t检验two-tailed test 双侧检验U unbalanced 不平衡的unbiased estimation 无偏估计unbiasedness 无偏性uniform distribution 均匀分布V value of estimator 估计值variable 变量variance 方差variance components 方差分量variance ratio 方差比various 不同的vector 向量W weight 加权,权重weighted average 加权平均值within groups 组内的Z Z score Z分数2. 最优化方法词汇英汉对照表A active constraint 活动约束active set method 活动集法analytic gradient 解析梯度approximate 近似arbitrary 强制性的argument 变量attainment factor 达到因子B bandwidth 带宽be equivalent to 等价于best-fit 最佳拟合bound 边界C coefficient 系数complex-value 复数值component 分量constant 常数constrained 有约束的constraint 约束constraint function 约束函数continuous 连续的converge 收敛cubic polynomial interpolation method 三次多项式插值法curve-fitting 曲线拟合D data-fitting 数据拟合default 默认的,默认的define 定义diagonal 对角的direct search method 直接搜索法direction of search 搜索方向discontinuous 不连续E eigenvalue 特征值empty matrix 空矩阵equality 等式exceeded 溢出的F feasible 可行的feasible solution 可行解finite-difference 有限差分first-order 一阶G Gauss-Newton method 高斯-牛顿法goal attainment problem 目标达到问题gradient 梯度gradient method 梯度法Hhandle 句柄Hessian matrix 海色矩阵I independent variables 独立变量inequality 不等式infeasibility 不可行性infeasible 不可行的initial feasible solution 初始可行解initialize 初始化inverse 逆invoke 激活iteration 迭代iteration 迭代J Jacobian 雅可比矩阵L Lagrange multiplier 拉格朗日乘子large-scale 大型的least square 最小二乘least squares sense 最小二乘意义上的Levenberg-Marquardt method列文伯格-马夸尔特法line search 一维搜索linear 线性的linear equality constraints 线性等式约束linear programming problem 线性规划问题local solution 局部解M medium-scale 中型的minimize 最小化mixed quadratic and cubic polynomial interpolation and extrapolation method 混合二次、三次多项式内插、外插法multiobjective 多目标的N nonlinear 非线性的norm 范数O objective function 目标函数observed data 测量数据optimization routine 优化过程optimize 优化optimizer 求解器over-determined system 超定系统P parameter 参数partial derivatives 偏导数polynomial interpolation method多项式插值法Q quadratic 二次的quadratic interpolation method 二次内插法quadratic programming 二次规划R real-value 实数值residuals 残差robust 稳健的robustness 稳健性,鲁棒性S scalar 标量semi-infinitely problem 半无限问题Sequential Quadratic Programming method序列二次规划法simplex search method 单纯形法solution 解sparse matrix 稀疏矩阵sparsity pattern 稀疏模式sparsity structure 稀疏结构starting point 初始点step length 步长subspace trust region method 子空间置信域法sum-of-squares 平方和symmetric matrix 对称矩阵T termination message 终止信息termination tolerance 终止容限the exit condition 退出条件the method of steepest descent 最速下降法transpose 转置U unconstrained 无约束的under-determined system 负定系统V variable 变量vector 矢量W weighting matrix 加权矩阵3 样条词汇英汉对照表A approximation 逼近array 数组a spline in b-form/b-spline b样条a spline of polynomial piece /ppform spline 分段多项式样条B bivariate spline function 二元样条函数break/breaks 断点C coefficient/coefficients 系数cubic interpolation 三次插值/三次内插cubic polynomial 三次多项式cubic smoothing spline 三次平滑样条cubic spline 三次样条cubic spline interpolation三次样条插值/三次样条内插curve 曲线D degree of freedom 自由度dimension 维数E end conditions 约束条件I input argument 输入参数interpolation 插值/内插interval 取值区间K knot/knots 节点L least-squares approximation 最小二乘拟合M multiplicity 重次multivariate function 多元函数O optional argument 可选参数order 阶次output argument 输出参数P point/points 数据点R rational spline 有理样条rounding error 舍入误差(相对误差)S scalar 标量sequence 数列(数组)spline 样条spline approximation 样条逼近/样条拟合spline function 样条函数spline curve 样条曲线spline interpolation 样条插值/样条内插spline surface 样条曲面smoothing spline 平滑样条T tolerance 允许精度U univariate function 一元函数V vector 向量W weight/weights 权重4 偏微分方程数值解词汇英汉对照表A absolute error 绝对误差absolute tolerance 绝对容限adaptive mesh 适应性网格B boundary condition 边界条件C contour plot 等值线图converge 收敛coordinate 坐标系D decomposed 分解的decomposed geometry matrix 分解几何矩阵diagonal matrix 对角矩阵Dirichlet boundary conditionsDirichlet边界条件E eigenvalue 特征值elliptic 椭圆形的error estimate 误差估计exact solution 精确解G generalized Neumann boundary condition 推广的Neumann边界条件geometry 几何形状geometry description matrix 几何描述矩阵geometry matrix 几何矩阵graphical user interface(GUI)图形用户界面H hyperbolic 双曲线的I initial mesh 初始网格J jiggle 微调L Lagrange multipliers 拉格朗日乘子Laplace equation 拉普拉斯方程linear interpolation 线性插值loop 循环M machine precision 机器精度mixed boundary condition 混合边界条件N Neuman boundary condition Neuman边界条件node point 节点nonlinear solver 非线性求解器normal vector 法向量P Parabolic 抛物线型的partial differential equation 偏微分方程plane strain 平面应变plane stress 平面应力Poisson's equation 泊松方程polygon 多边形positive definite 正定Q quality 质量R refined triangular mesh 加密的三角形网格relative tolerance 相对容限relative tolerance 相对容限residual 残差residual norm 残差范数S singular 奇异的。
数学专业英语翻译2-7

7-B The limit of a sequence
The main question we are concerned with here is to decide whether or not the terms f(n) tend to a finite limit as n increases infinitely. 这里我们关心的主要问题是当n无限增加时,项 f(n) 是否会趋于一个有限的极限。
如果对每一个正整数 n都有一个实数或复数an与之对 应, 则有序集a1 , a2, …, an ,… 称为一个无穷序列.
The important thing here is that each member of the set has been labeled with an integer so that we may speak of the first term a1, the second term a2, and, in general, the nth term an. 这里重要的是集合中的每一个元素都由一个整数标 记,因此我们可以说第一项 , 第二项, 一般的,第n项
This particular rule is known as a recursion formula and it defines a famous sequence whose terms are called Fibonacci numbers. The first few terms are 1,1,2,3,5,8,13,21,34. 这个特殊的规则就是常见的递推公式,它定义了一个 著名的序列,其中的项称为菲波那契数。前几项是…...
数学专业词汇及翻译

数学专业词汇及翻译一、字母顺序表 (1)二、常用的数学英语表述 (7)三、代数英语(高端) (13)一、字母顺序表1、数学专业词汇Aabsolute value 绝对值 accept 接受 acceptable region 接受域additivity 可加性 adjusted 调整的 alternative hypothesis 对立假设analysis 分析analysis of covariance 协方差分析analysis of variance 方差分析 arithmetic mean 算术平均值 association 相关性assumption 假设 assumption checking 假设检验availability 有效度average 均值Bbalanced 平衡的 band 带宽 bar chart 条形图beta-distribution 贝塔分布 between groups 组间的 bias 偏倚 binomial distribution 二项分布 binomial test 二项检验Ccalculate 计算 case 个案 category 类别 center of gravity 重心central tendency 中心趋势chi-square distribution 卡方分布chi-square test 卡方检验classify 分类cluster analysis 聚类分析coefficient 系数 coefficient of correlation 相关系数collinearity 共线性 column 列 compare 比较 comparison 对照 components 构成,分量compound 复合的 confidence interval 置信区间 consistency 一致性 constant 常数continuous variable 连续变量 control charts 控制图 correlation 相关 covariance 协方差 covariance matrix 协方差矩阵critical point 临界点critical value 临界值crosstab 列联表cubic 三次的,立方的cubic term 三次项cumulative distribution function 累加分布函数 curve estimation 曲线估计Ddata 数据default 默认的definition 定义deleted residual 剔除残差density function 密度函数dependent variable 因变量description 描述design of experiment 试验设计deviations 差异df.(degree of freedom) 自由度diagnostic 诊断dimension 维discrete variable 离散变量discriminant function 判别函数discriminatory analysis 判别分析distance 距离distribution 分布D-optimal design D-优化设计Eeaqual 相等 effects of interaction 交互效应 efficiency 有效性eigenvalue 特征值equal size 等含量equation 方程error 误差estimate 估计estimation of parameters 参数估计estimations 估计量evaluate 衡量exact value 精确值expectation 期望expected value 期望值exponential 指数的exponential distributon 指数分布extreme value 极值F factor 因素,因子 factor analysis 因子分析 factor score 因子得分 factorial designs 析因设计factorial experiment 析因试验fit 拟合fitted line 拟合线fitted value 拟合值 fixed model 固定模型 fixed variable 固定变量fractional factorial design 部分析因设计frequency 频数F-test F检验full factorial design 完全析因设计function 函数Ggamma distribution 伽玛分布geometric mean 几何均值group 组Hharmomic mean 调和均值 heterogeneity 不齐性histogram 直方图homogeneity 齐性homogeneity of variance 方差齐性hypothesis 假设 hypothesis test 假设检验Iindependence 独立independent variable 自变量independent-samples 独立样本 index 指数 index of correlation 相关指数 interaction 交互作用 interclass correlation 组内相关 interval estimate 区间估计intraclass correlation 组间相关inverse 倒数的iterate 迭代Kkernal 核 Kolmogorov-Smirnov test柯尔莫哥洛夫-斯米诺夫检验 kurtosis 峰度Llarge sample problem 大样本问题layer 层least-significant difference 最小显著差数least-square estimation 最小二乘估计least-square method 最小二乘法 level 水平 level of significance 显著性水平leverage value 中心化杠杆值life 寿命life test 寿命试验likelihood function 似然函数 likelihood ratio test 似然比检验linear 线性的linear estimator 线性估计linear model 线性模型linear regression 线性回归linear relation 线性关系linear term 线性项logarithmic 对数的logarithms 对数 logistic 逻辑的 lost function 损失函数Mmain effect 主效应matrix 矩阵maximum 最大值maximum likelihood estimation 极大似然估计 mean squared deviation(MSD) 均方差 mean sum of square 均方和 measure 衡量 media 中位数 M-estimator M估计minimum 最小值missing values 缺失值mixed model 混合模型 mode 众数model 模型Monte Carle method 蒙特卡罗法moving average 移动平均值multicollinearity 多元共线性multiple comparison 多重比较multiple correlation 多重相关multiple correlation coefficient 复相关系数multiple correlation coefficient 多元相关系数multiple regression analysis 多元回归分析multiple regression equation 多元回归方程 multiple response 多响应 multivariate analysis 多元分析Nnegative relationship 负相关nonadditively 不可加性nonlinear 非线性nonlinear regression 非线性回归noparametric tests 非参数检验 normal distribution 正态分布null hypothesis 零假设 number of cases 个案数Oone-sample 单样本 one-tailed test 单侧检验 one-way ANOVA 单向方差分析one-way classification 单向分类optimal 优化的optimum allocation 最优配制 order 排序order statistics 次序统计量 origin 原点orthogonal 正交的 outliers 异常值Ppaired observations 成对观测数据paired-sample 成对样本parameter 参数parameter estimation 参数估计 partial correlation 偏相关partial correlation coefficient 偏相关系数 partial regression coefficient 偏回归系数percent 百分数percentiles 百分位数pie chart 饼图point estimate 点估计poisson distribution 泊松分布polynomial curve 多项式曲线polynomial regression 多项式回归polynomials 多项式positive relationship 正相关 power 幂P-P plot P-P概率图predict 预测predicted value 预测值prediction intervals 预测区间principal component analysis 主成分分析 proability 概率probability density function 概率密度函数 probit analysis 概率分析proportion 比例Qqadratic 二次的 Q-Q plot Q-Q概率图 quadratic term 二次项quality control 质量控制 quantitative 数量的,度量的 quartiles 四分位数Rrandom 随机的 random number 随机数 random number 随机数random sampling 随机取样random seed 随机数种子random variable 随机变量 randomization 随机化 range 极差rank 秩 rank correlation 秩相关 rank statistic 秩统计量 regression analysis 回归分析regression coefficient 回归系数regression line 回归线reject 拒绝rejection region 拒绝域relationship 关系reliability 可*性repeated 重复的report 报告,报表 residual 残差 residual sum of squares 剩余平方和response 响应risk function 风险函数robustness 稳健性 root mean square 标准差 row 行 run 游程run test 游程检验Sample 样本sample size 样本容量sample space 样本空间sampling 取样 sampling inspection 抽样检验 scatter chart 散点图S-curve S形曲线separately 单独地sets 集合sign test 符号检验significance 显著性significance level 显著性水平significance testing 显著性检验 significant 显著的,有效的 significant digits 有效数字 skewed distribution 偏态分布 skewness 偏度 small sample problem 小样本问题 smooth 平滑 sort 排序 soruces of variation 方差来源 space 空间 spread 扩展square 平方 standard deviation 标准离差 standard error of mean 均值的标准误差standardization 标准化 standardize 标准化 statistic 统计量 statistical quality control 统计质量控制 std. residual 标准残差 stepwise regression analysis 逐步回归stimulus 刺激strong assumption 强假设stud. deleted residual 学生化剔除残差stud. residual 学生化残差 subsamples 次级样本 sufficient statistic 充分统计量sum 和 sum of squares 平方和 summary 概括,综述Ttable 表t-distribution t分布test 检验test criterion 检验判据test for linearity 线性检验 test of goodness of fit 拟合优度检验 test of homogeneity 齐性检验test of independence 独立性检验test rules 检验法则 test statistics 检验统计量 testing function 检验函数time series 时间序列tolerance limits 容许限total 总共,和transformation 转换 treatment 处理 trimmed mean 截尾均值 true value 真值 t-test t检验 two-tailed test 双侧检验unbalanced 不平衡的unbiased estimation 无偏估计unbiasedness 无偏性 uniform distribution 均匀分布Vvalue of estimator 估计值 variable 变量 variance 方差 variance components 方差分量 variance ratio 方差比 various 不同的 vector 向量Wweight 加权,权重weighted average 加权平均值within groups 组内的ZZ score Z分数2. 最优化方法词汇英汉对照表Aactive constraint 活动约束 active set method 活动集法 analytic gradient 解析梯度approximate 近似 arbitrary 强制性的 argument 变量 attainment factor 达到因子Bbandwidth 带宽be equivalent to 等价于best-fit 最佳拟合bound 边界Ccoefficient 系数complex-value 复数值component 分量constant 常数constrained 有约束的constraint 约束constraint function 约束函数continuous 连续的converge 收敛cubic polynomial interpolation method三次多项式插值法 curve-fitting 曲线拟合Ddata-fitting 数据拟合default 默认的,默认的define 定义diagonal 对角的direct search method 直接搜索法direction of search 搜索方向 discontinuous 不连续eigenvalue 特征值empty matrix 空矩阵equality 等式exceeded 溢出的Ffeasible 可行的 feasible solution 可行解 finite-difference 有限差分 first-order 一阶GGauss-Newton method 高斯-牛顿法 goal attainment problem 目标达到问题 gradient 梯度 gradient method 梯度法Hhandle 句柄 Hessian matrix 海色矩阵Independent variables 独立变量inequality 不等式infeasibility 不可行性infeasible 不可行的initial feasible solution 初始可行解initialize 初始化inverse 逆 invoke 激活 iteration 迭代 iteration 迭代JJacobian 雅可比矩阵LLagrange multiplier 拉格朗日乘子large-scale 大型的least square 最小二乘 least squares sense 最小二乘意义上的 Levenberg-Marquardt method 列文伯格-马夸尔特法line search 一维搜索linear 线性的linear equality constraints 线性等式约束linear programming problem 线性规划问题 local solution 局部解M medium-scale 中型的minimize 最小化mixed quadratic and cubic polynomialinterpolation and extrapolation method 混合二次、三次多项式内插、外插法multiobjective 多目标的Nnonlinear 非线性的 norm 范数Oobjective function 目标函数observed data 测量数据optimization routine 优化过程optimize 优化optimizer 求解器over-determined system 超定系统Pparameter 参数partial derivatives 偏导数polynomial interpolation method 多项式插值法Qquadratic 二次的 quadratic interpolation method 二次内插法quadratic programming 二次规划Rreal-value 实数值 residuals 残差 robust 稳健的 robustness 稳健性,鲁棒性S scalar 标量semi-infinitely problem 半无限问题Sequential Quadratic Programming method 序列二次规划法 simplex search method 单纯形法solution 解sparse matrix 稀疏矩阵sparsity pattern 稀疏模式 sparsity structure 稀疏结构 starting point 初始点step length 步长subspace trust region method 子空间置信域法sum-of-squares 平方和 symmetric matrix 对称矩阵Ttermination message 终止信息 termination tolerance 终止容限 the exit condition 退出条件 the method of steepest descent 最速下降法 transpose 转置Uunconstrained 无约束的 under-determined system 负定系统Vvariable 变量 vector 矢量Wweighting matrix 加权矩阵3 样条词汇英汉对照表Aapproximation 逼近 array 数组 a spline in b-form/b-spline b 样条 a spline of polynomial piece /ppform spline 分段多项式样条Bbivariate spline function 二元样条函数 break/breaks 断点Ccoefficient/coefficients 系数cubic interpolation 三次插值/三次内插cubic polynomial 三次多项式 cubic smoothing spline 三次平滑样条 cubic spline 三次样条cubic spline interpolation 三次样条插值/三次样条内插 curve 曲线Ddegree of freedom 自由度 dimension 维数Eend conditions 约束条件input argument 输入参数interpolation 插值/内插 interval取值区间Kknot/knots 节点Lleast-squares approximation 最小二乘拟合Mmultiplicity 重次 multivariate function 多元函数Ooptional argument 可选参数 order 阶次 output argument 输出参数P point/points 数据点Rrational spline 有理样条 rounding error 舍入误差(相对误差)Sscalar 标量sequence 数列(数组)spline 样条spline approximation 样条逼近/样条拟合spline function 样条函数 spline curve 样条曲线spline interpolation 样条插值/样条内插spline surface 样条曲面 smoothing spline 平滑样条Ttolerance 允许精度Uunivariate function 一元函数Vvector 向量Wweight/weights 权重4 偏微分方程数值解词汇英汉对照表Aabsolute error 绝对误差 absolute tolerance 绝对容限 adaptive mesh 适应性网格Bboundary condition 边界条件Ccontour plot 等值线图 converge 收敛 coordinate 坐标系Ddecomposed 分解的 decomposed geometry matrix 分解几何矩阵diagonal matrix 对角矩阵Dirichlet boundary conditions Dirichlet边界条件Eeigenvalue 特征值elliptic 椭圆形的error estimate 误差估计exact solution 精确解Ggeneralized Neumann boundary condition 推广的Neumann 边界条件 geometry 几何形状geometry description matrix 几何描述矩阵 geometry matrix 几何矩阵 graphical user interface(GUI)图形用户界面Hhyperbolic 双曲线的Iinitial mesh 初始网格Jjiggle 微调LLagrange multipliers 拉格朗日乘子Laplace equation 拉普拉斯方程linear interpolation 线性插值 loop 循环Mmachine precision 机器精度 mixed boundary condition 混合边界条件NNeuman boundary condition Neuman边界条件 node point 节点 nonlinear solver 非线性求解器 normal vector 法向量PParabolic 抛物线型的 partial differential equation 偏微分方程plane strain 平面应变 plane stress 平面应力 Poisson's equation 泊松方程 polygon 多边形 positive definite 正定Qquality 质量Rrefined triangular mesh 加密的三角形网格relative tolerance 相对容限 relative tolerance 相对容限 residual 残差 residual norm 残差范数Ssingular 奇异的二、常用的数学英语表述1.Logicthere existfor allp?q p implies q / if p, then qp?q p if and only if q /p is equivalent to q / p and q are equivalent2.Setsx∈A x belongs to A / x is an element (or a member) of Ax?A x does not belong to A / x is not an element (or a member) of AA?B A is contained in B / A is a subset of BA?B A contains B / B is a subset of AA∩B A cap B / A meet B / A intersection BA∪B A cup B / A join B / A union BA\B A minus B / the diference between A and BA×B A cross B / the cartesian product of A and B3. Real numbersx+1 x plus onex-1 x minus onex±1 x plus or minus onexy xy / x multiplied by y(x - y)(x + y) x minus y, x plus yx y x over y= the equals signx = 5 x equals 5 / x is equal to 5x≠5x (is) not equal to 5x≡y x is equivalent to (or identical with) yx ≡ y x is not equivalent to (or identical wit h) yx > y x is greater than yx≥y x is greater than or equal to yx < y x is less than yx≤y x is less than or equal to y0 < x < 1 zero is less than x is less than 10≤x≤1zero is less than or equal to x is less than or equal to 1 | x | mod x / modulus xx 2 x squared / x (raised) to the power 2x 3 x cubedx 4 x to the fourth / x to the power fourx n x to the nth / x to the power nx ?n x to the (power) minus nx (square) root x / the square root of xx 3 cube root (of) xx 4 fourth root (of) xx n nth root (of) x( x+y ) 2 x plus y all squared( x y ) 2 x over y all squaredn! n factorialx ^ x hatx ˉ x barx ?x tildex i xi / x subscript i / x suffix i / x sub i∑ i=1 n a i the sum from i equals one to n a i / the sum as i runs from 1 to n of the a i4. Linear algebra‖ x ‖the norm (or modulus) of xOA →OA / vector OAOA ˉ OA / the length of the segment OAA T A transpose / the transpose of AA ?1 A inverse / the inverse of A5. Functionsf( x ) fx / f of x / the function f of xf:S→T a function f from S to Tx→y x maps to y / x is sent (or mapped) to yf'( x ) f prime x / f dash x / the (first) derivative of f with respect to xf''( x ) f double-prime x / f double-dash x / the second derivative of f with r espect to xf'''( x ) triple-prime x / f triple-dash x / the third derivative of f with respect to xf (4) ( x ) f four x / the fourth derivative of f with respect to xf ? x 1the partial (derivative) of f with respect to x12 f ? x 1 2the second partial (derivative) of f with respect to x1∫ 0 ∞the i ntegral from zero to infinitylim?x→0 the limit as x approaches zerolim?x→0 + the limit as x approaches zero from abovelim?x→0 ?the limit as x approaches zero from belowlog e y log y to the base e / log to the base e of y / natural log (of) yln?y log y to the base e / log to the base e of y / natural log (of) y一般词汇数学mathematics, maths(BrE), math(AmE)公理axiom定理theorem计算calculation运算operation证明prove假设hypothesis, hypotheses(pl.)命题proposition算术arithmetic加plus(prep.), add(v.), addition(n.)被加数augend, summand加数addend和sum减minus(prep.), subtract(v.), subtraction(n.)被减数minuend减数subtrahend差remainder乘times(prep.), multiply(v.), multiplication(n.)被乘数multiplicand, faciend乘数multiplicator积product除divided by(prep.), divide(v.), division(n.)被除数dividend除数divisor商quotient等于equals, is equal to, is equivalent to 大于is greater than 小于is lesser than大于等于is equal or greater than小于等于is equal or lesser than运算符operator数字digit数number自然数natural number整数integer小数decimal小数点decimal point分数fraction分子numerator分母denominator比ratio正positive负negative零null, zero, nought, nil十进制decimal system二进制binary system十六进制hexadecimal system权weight, significance进位carry截尾truncation四舍五入round下舍入round down上舍入round up有效数字significant digit无效数字insignificant digit代数algebra公式formula, formulae(pl.)单项式monomial多项式polynomial, multinomial系数coefficient未知数unknown, x-factor, y-factor, z-factor 等式,方程式equation一次方程simple equation二次方程quadratic equation三次方程cubic equation四次方程quartic equation不等式inequation阶乘factorial对数logarithm指数,幂exponent乘方power二次方,平方square三次方,立方cube四次方the power of four, the fourth power n次方the power of n, the nth power开方evolution, extraction二次方根,平方根square root三次方根,立方根cube root四次方根the root of four, the fourth root n次方根the root of n, the nth root集合aggregate元素element空集void子集subset交集intersection并集union补集complement映射mapping函数function定义域domain, field of definition值域range常量constant变量variable单调性monotonicity奇偶性parity周期性periodicity图象image数列,级数series微积分calculus微分differential导数derivative极限limit无穷大infinite(a.) infinity(n.) 无穷小infinitesimal积分integral定积分definite integral不定积分indefinite integral 有理数rational number无理数irrational number实数real number虚数imaginary number复数complex number矩阵matrix行列式determinant几何geometry点point线line面plane体solid线段segment射线radial平行parallel相交intersect角angle角度degree弧度radian锐角acute angle直角right angle钝角obtuse angle平角straight angle周角perigon底base边side高height三角形triangle锐角三角形acute triangle直角三角形right triangle直角边leg斜边hypotenuse勾股定理Pythagorean theorem钝角三角形obtuse triangle不等边三角形scalene triangle等腰三角形isosceles triangle等边三角形equilateral triangle四边形quadrilateral平行四边形parallelogram矩形rectangle长length宽width附:在一个分数里,分子或分母或两者均含有分数。
数学专业英语2-10翻译

Although dependence and independence are properties of sets of elements, we also apply these terms to the elements themselves. For example, the elements in an independent set are called independent elements.虽然相关和无关是元素集的属性,我们也适用于这些元素本身。
例如,在一个独立设定的元素被称为独立元素。
If s is finite set, the foregoing definition agrees with that given in Chapter 8 for the space n V . However, the present definition is not restricted to finite sets.如果S 是有限集,同意上述定义与第8章中给出的空间n V ,然而,目前的定义不局限于有限集。
If a subset T of a set S is dependent, then S itself is dependent. This is logically equivalent to the statement that every subset of an independent set is independent.如果集合S 的子集T 是相关的,然后S 本身是相关的,这在逻辑上相当于每一个独立设置的子集是独立的语句。
If one element in S is a scalar multiple of another, then S is dependent. 如果S 中的一个元素是另一个集中的多个标量的,则S 是相关的。
If S ∈0,then S is dependent. 若S ∈0,则 S 是相关的。
数学专业英语翻译2-5

Mathematical English
Chapter 2 精读课文---入门必读
一个几何图形是满足一个或多个特殊条件的点集,比如平面 上的曲线。通过把这些条件转化成含有坐标x和y的表达式, 我们就得到了一个或多个能刻画该图形特征的方程。例如, 如图2-5-2所示的中心在原点,半径为r的圆,令P是原上任意 一点,假设P的坐标为(x, y).
本小节重点掌握
1 计算图形的面积是积分的一个重要应用。 2 微积分与解析几何在他们的发展史上已经互相交融在一起 了。
5-A the coordinate system of Cartesian geometry
As mentioned earlier, one of the applications of the integral is the calculation of area. Ordinarily , we do not talk about area by itself ,instead, we talk about the area of something . This means that we have certain objects (polygonal regions, circular regions, parabolic segments etc.) whose areas we wish to measure. If we hope to arrive at a treatment of area that will enable us to deal with many different kinds of objects, we must first find an effective way to describe these objects.
数学专业英语翻译
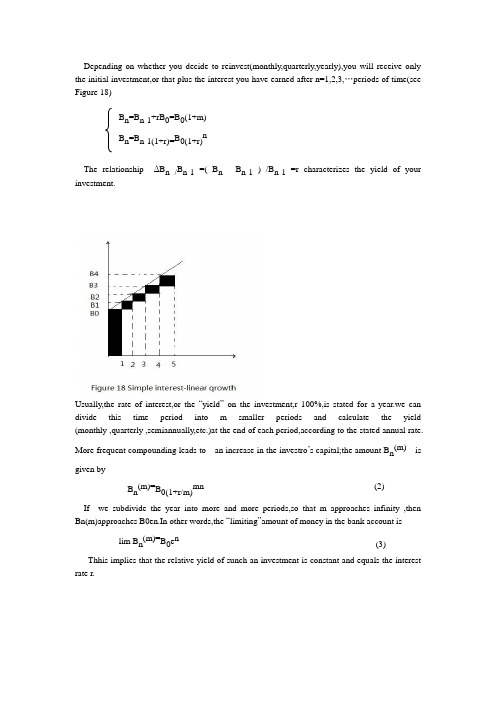
Depending on whether you decide to reinvest(monthly,quarterly,yearly),you will receive only the initial investment,or that plus the interest you have earned after n=1,2,3,…periods of time(see Figure 18)B n=B n-1+rB0=B0(1+m)B n=B n-1(1+r)=B0(1+r)nThe relationship ΔB n /B n-1 =( B n- B n-1 ) /B n-1 =r characterizes the yield of your investment.Usually,the rate of interest,or the “yield”on the investment,r 100%,is stated for a year.we can divide this time period into m smaller periods and calculate the yield (monthly ,quarterly ,semiannually,etc.)at the end of each period,according to the stated annual rate.More frequent compounding leads to an increase in the investro’s capital;the amount B n(m)is given byB n(m)=B0(1+r/m)mn (2)If we subdivide the year into more and more periods,so that m approaches infinity ,then Bn(m)approaches B0en.In other words,the “limiting”amount of money in the bank account islim B n(m)=B0e n(3)Thhis implies that the relative yield of sunch an investment is constant and equals the interest rate r.The three methods of calculating interest discussed above are called simple ,compound ,and continuous .Formulas (1),(2)and (3)provide ways to calculate the amount in the investor’s bank account and clearly show the dependence of the value of money on time.On the other hand,we have the bank’s interest rate R,s that if we invest the amount (1-R)B1,at time 1 ,say after one year,we will receive the amount B1.This is equivalent to the issuance of a bond with a nominal value B1(to be paid to the bond holder at the end of this year),but now the bond sells for a lower price(decreased by the amount of the lending rate R over one period ,that is m=1).So today’s price is determined by the formula(1-R)B1,which is equal to the discounted price B1/(1+r) .Therefore,we can view the bank account as a coupon-free bond in the sense of a risk-free asset of the financial market.The lack of ,or very small,changes in interest rates characterize the stability of financial and economic systems ,for which the corresponding bank acccount serves as the basic non-risky asset.Reality shows that such suggestions present limits in The idealization of mathematical models for financial markets.译文:依赖于你是否决定再投资(平稳的,按季度的,一年一次的),你将仅仅收到最初的投资,否则就会加上n=1,2,3…个时期后你所赚的利息。
《数学专业英语》常用英文表达

7
max, min maximum value, minimum value Eample: max f ( x) Maximum value of f(x)
max(a1 ,an ) Maximum value of the series
a1 to an Powers and roots Example: x 2 x squared
10
Function f
2 Example: f ( x ) ax bx c , a 0. The function of x
equals a times the square of x plus b times x plus c, where a is not equal to zero.
Imaginary number and two common irrational numbers
, ratio of the circumference of a circle to its
diameter,approximate value 3.1415926
9
1 x i 1, e lim(1 ) x x
Example:
f ( x ) f double-prime x, f double-dashed x f ( x ) f triple-prime x, f triple-dashed x (4) f ( x ) f four x
8
xn x 1
Example:
3
x x
4 n
x x
fourth root (of) x
nth root (of) x
Example: 24 16 Two to the fourth power is sixteen
数学专业英语

数学专业英语Lesson 1Mathematics as a Language of Scienceassert vt. 断言;坚持主张;维护表明qualitative adj. 性质的;定性的quantitative adj. 量的;数量的;定量的;与数量有关的astronomy n. 天文学postulate n. 假定, 基本条件, 基本原理 vt. 要求, 假定 vi. 要求hypothetical adj. 假设的, 假定的,爱猜想的Lesson 2deduction n. 减除, 扣除, 减除额, 推论, 演绎induction n. 归纳;归纳法;归纳所得之结论verification n. 验证;证实correlate vt. 使相互关联 vi. 和...相关discard vt. 丢弃, 抛弃 v. 放弃discredit n. 不信任;失信consistent adj. 一致的, 调和的, 坚固的, [数、统]相容的inadequacy n. 不充分 ,不适当,不适合,不足额conic, conical adj 圆锥的;圆锥形的ellipse n. 椭圆, 椭圆形 ellipt (n.)hyperbolic adj. 双曲线的 hyperbola (n.)parabolic adj. 用寓言表达的: 抛物线的,像抛物线的 parabola (n.) algebraic adj. 代数的, 关于代数学的mineralogy n. 矿物学refraction n. 折光, 折射stimulus n. 刺激物, 促进因素, 刺激, 刺激impetus n. 冲力推动力;刺激Lesson 3Axioms, definitions and Theoremsaxiom n. [数]公理definition n. 阐明;确定定义;界说extravagant adj. 奢侈的, 浪费的, 过分的, 放纵的collinear adj. 在同一直线上的, 同线的convex adj. 凸出的;凸面的segment n. 部分;片段;节, 弓形;圆缺;弧形, 线段conswquently adv. 从而, 因此in terms of adv. 根据, 按照, 用...的话, 在...方面pretense n. 主张, 要求, 伪称, 借口, 自称Lesson 4Geometry and Geometrical termsterm n. 学期, 期限, 期间, 条款, 条件, 术语triangle n. [数]三角形, 三人一组, 三角关系parallelogram n. 平行四边形straight angle n. [数]平角right angle n. 直角acute angle n. 锐角obtuse angle n. 钝角reflex angle n. 优角rectilinear adj 直线的;由直线组成的;循直线进行的isosceles triangle n. 等腰三角形equilateral triangle n. 等边三角形right triangle n. 直角三角形obtuse triangle n. 钝角三角形acute triangle n. 锐角三角形equiangular triangle n. 正三角形,等角三角形hypotenuse n. (直角三角形的)斜边circle 圆center 中心;中央;圆心diameter n. 直径radius n. 半径, 范围, 辐射光线, 有效航程, 范围, 界限circumference n. 圆周, 周围Lesson 5The Method of Limitslimit n. 限度,极限,极点infinite adj. 无限的;无穷的infinitesimal adj. 无穷小的, 极小的, 无限小的calculus n. 微积分学, 结石exemplify vt. 例证, 例示, 作为...例子inscribe v. 记下polygon n. [数]多角形, 多边形diminish v. (使)减少, (使)变小curvilinear adj 曲线的, 由曲线组成的intuition n. 直觉, 直觉的知识integral n. [数学] 积分, 完整, 部分defective adj. 有缺陷的, (智商或行为有)欠缺的differential coefficient 微分系数arithmetical adj. 算术的, 算术上的convergence n. 集中, 收敛criterion n. (批评判断的)标准, 准据, 规范sequence n. 次序, 顺序, 序列irrational numbers n. [数]无理数domain ,定义域contradiction 矛盾reversal n. 颠倒, 反转, 反向, 逆转, 撤销Lesson 6Functioncontinuous variable 连续变量;[连续变数]variation 变分, 变化interval 区间independent variable 自变量dependent variable 应变量rectangular coordinate 直角坐标abscissa n. 〈数〉横坐标ordinate n. [数]纵线, 纵座标gradient adj. 倾斜的n. 梯度, 倾斜度, 坡度slope n. 斜坡, 斜面, 倾斜 v. (使)顺斜Lesson 7Differential and Integral calculusdifferential adj. 微分的n. 微分 (differentiation)Integral n. [数学] 积分, 完整, 部分 (integration)calculus n. 微积分学, 结石interrelation n. 相互关系trigonometry n. 三角法exponential adj. 指数的, 幂数的logarithm n. [数] 对数derivative n. 导数;微商tangent n. 切线, [数]正切counterclockwise adj. 反时针方向的adv. 反时针方向 (clockwise) definite integral 定积分approximation n. 接近, 走近, [数]近似值culminate v. 达到顶点mean n. 平均数, 中间, 中庸differential equation 微分方程extreme value n. 极值multiple integral 多重积分double integralline integralfunctional analysis 泛函分析Lesson 8 The Concept of Cardinal Number (I)cardinal number n. 基数(如: 1, 2, 3, ... 有别于序数)denumerable adj. 可数的aggregate n. 合计, 总计, 集合体adj. 合计的, 集合的, 聚合的v. 聚集, 集合, 合计purport n. 主旨 v. 声称fancier n. 空想家, 培育动物(或植物)的行家, 爱好者sniff v. 用力吸, 嗅, 闻到, 发觉, 轻视, 用力吸气n. 吸, 闻, 吸气声, 嗤之以鼻scheme n. 安排, 配置, 计划, 阴谋, 方案, 图解, 摘要v. 计划, 设计, 图谋, 策划, * n.(计算数学)方法,格式superior n. 长者, 高手, 上级adj. 较高的, 上级的, 上好的, 出众的, 高傲的cumbersome adj. 讨厌的, 麻烦的, 笨重的instruction n. 指示, 用法说明(书), 教育, 指导, 指令drastically adv. 激烈地, 彻底地conservation 守衡律quadrature n. 求积, 求积分interpolation n. 插值extrapolation n. [数]外推法, 推断internal point 内点identical adj. 同一的, 同样的generalized solution 广义解functional 泛函hydrodynamics 流体力学,水动力学divergence 发散(性),梯度,发散量play an important (fundamental ... ) role 起着重要的(...)作用integro-interpolation method 积分插值法Variational method 变分方法comparatively adv. 比较地, 相当地deficiency n. 缺乏, 不足fictive adj. 虚构的, 想象上的, 虚伪的self-adjoint (nonself-adjoint) 自治的,自伴的,自共轭的finite element method 有限元法spline approximation 样条逼近Particles-in-the-Cell 网格质点法herald n. 使者, 传令官, 通报者, 先驱, 预兆vt. 预报, 宣布, 传达, 欢呼advection n. 水平对流phenomenological adj. 现象学的, 现象的fluctuation n. 波动, 起伏optimism n. 乐观, 乐观主义pessimism n. 悲观, 悲观主义unjustified adj 未被证明其正确的mean-square 均方dispersion n. [数] 离差, 差量Polynomial n adj. [数]多项式的interpolation 插值arithmetic n. 算术, 算法rounding errors 舍入误差multiple n. 倍数, 若干subjective adj. 主观的, 个人的objective adj. 客观的,outcome n. 结果, 成果pattern n. 样品toss v. 投, 掷exhaust vt. 用尽, 耗尽, 抽完, 使精疲力尽divisible adj. 可分的dice, die n. 骰子assign vt. 分配, 指派attach vt. 缚上, 系上, 贴上v. 配属, 隶属于pitfall n. 缺陷chairperson 主席mechanics n. (用作单数)机械学、力学, (用作复数)技巧, 结构statics n. [物]静力学dynamics n. 动力学adequately adv. 充分地celestial adj. 天上的macroscopic adj. 肉眼可见的, 巨观的classical field theory 经典场理论rigit adj. 刚硬的, 刚性的, 严格的elastic adj. 弹性的plastic n. 可塑的,塑性的,塑料的quantum n. 量, 额, [物] 量子, 量子论inception n. 起初, 获得学位pertain v. 适合, 属于gravitation n. 地心吸力, 引力作用tide n. 潮, 潮汐, 潮流, 趋势monumental adj. 纪念碑的, 纪念物的, 不朽的, 非常的encompass v. 包围, 环绕, 包含或包括某事物ingredient n. 成分, 因素acquainted adj. 有知识的, 知晓的synonymous adj. 同义的configuration n. 构造, 结构, 配置, 外形reference n. 提及, 涉及, 参考, 参考书目inertia n. 惯性, 惯量attribute 特性momentum n. 动量proportional adj. 比例的, 成比例的, 相称的, 均衡的designate 指明negligible adj. 可以忽略的, 不予重视的projectile n. 射弹 adj. 发射的ballistics n. 弹道学, 发射学intractable adj. 难处理的{Mechanics of a Particlein consequence of adv. 由于的...缘故exert vt. 尽(力), 施加(压力等), 努力v. 发挥, 竭尽全力, 尽galaxy n. 星系, 银河, 一群显赫的人, 一系列光彩夺目的东furnish vt. 供应, 提供, 装备, 布置v. 供给torque n. 扭矩, 转矩moment 力矩的friction 摩擦dissipation n. 消散, 分散, 挥霍, 浪费, 消遣, 放荡, 狂饮infer v. 推断Hooke s Law and Its Consequenceselasticity n. 弹力, 弹性constitutive adj. 构成的, 制定的atomistic adj. 原子论的crack n. 裂缝, 噼啪声v. (使)破裂, 裂纹, (使)爆裂continuum mechanics n. 连续介质力学superposition n. 重叠, 重合, 叠合strain n. 过度的疲劳, 紧张, 张力, 应变vt. 扭伤, 损伤v. 拉紧, 扯紧, (使)紧张, 尽力thermodynamics n. [物] 热力学reckon vt. 计算, 总计, 估计, 猜想vi. 数, 计算, 估计, 依赖, 料想lesson 20strength 强度load 载荷empirical 以经验为依据的member 构件isolated 孤立的segment 部分、段、节stress 应力strain 应变tension 拉伸shear 剪切bend 弯曲torsion 扭转、扭力insofar 在……范围cohesive 内聚性的tensile 拉力、张力stiffness 硬度furnish 供给Lesson 23 Fluid Mechanicseruption 喷发、爆发turbulent 湍流laminar 层流isothermal 等温isotropic 各向同性prevalent 普遍的、流行的tornado 旋风、飓风eddy 旋涡viscosity 粘性、粘度nonviscous 无粘性的rotation 旋转adiabatic 绝热的reversible 可逆的isentropic 等熵的instant 瞬时的streamline 流线stream tube 流管tangential 切线的incompressible 不可压缩的resultant 合成的,组合的downstream 下游的,顺流的elbow 弯管,肘similitude 相似性hydraulic 水力的,水力学的predominante 占主导地位spillway (河或水坝的)放水道,泄洪道prototype 原型,样板Lesson 24 Mechanical Vibration repetitive 重复的,反复的periodic 周期的,定期的tidal 潮的,像潮的stationary 固定的,不动的vibratory 振动的,摆动的propagation 传播couple v .连接,连合acoustic 听觉的,声学的annoyance 烦恼,困惑adjacent 接近的,邻近的damp 阻尼,衰减restore 复职,归还neutral 平衡exciting force 激励力resonant adj. 共振的,谐振的stiffness 刚度,刚性proportionality 成比例地inclusion 包含,包括magnitude 数值,大小substantially adv. 实质上的perturb 干扰,扰乱resonance n. 共振vibratory adj. 振动的, 可知的perceptible 可见的,可知的adudible 听得见的,可闻的foregoing 前述的impulsive 冲击的shock 冲击Fourier series 傅里叶级数excitation 激发,激励discrete 分离,离散的contend with 向…作斗争compressor 压气机fatigue 疲劳perceptible 可见的,可知觉的shredder 切菜器disposal 处理urban 都市的metropolitan 大都市的at-grade 在同一水平面上elevated 高架的guideway 导轨Lesson 25 A prefect to the Continuum Mechanics preface 序言continuum连续 pl. continuua rigid body 刚体contemporary 当代的,同时期的widespread 分布广的, 普及的accommodate 容纳,使适应medium 介质plasticity 塑性residual 剩余的,残留的creep 蠕变,爬行,塑性变形aging 老化polymeric聚合(物)的sandy 沙的,沙质的aubterranean 地下的,隐藏的essence 精髓,本质thermodynamics 热力学self-similar 自相似expedient 方便的sonsolidate 把…联合为一体,统一justify 证明…有理radically 根本地,本质上deliberate 从容不迫的,深思熟虑Lesson 33 what is a computer Attribute v. 赋予medieval 中世纪的astronomer 天文学家Mars 火星resemble vt. 像,相似tedious adj. 冗长乏味的pulp 浆状物,果肉filter vt.过滤underlying adj. 潜在的, 基本的ore n. 矿沙,矿石perceive v. 察觉,看见intervention n. 干涉,插入intelligent adj. 有智力的,聪明的Lesson 34 A computer system manipulate vt. 操纵,使用chip n. 芯片etch vt. 蚀刻,蚀镂fingernail 指甲mount vt. 安装,安置assemble vt. 集合,聚集cabinet 橱柜execute vt. 执行,实现paycheck n.支付薪金的支票bar chart 直方图joystick 游戏杆encounter vt. 遇到,遇上Mathematical Modelingindustry n. 工业, 产业, 行业, 勤奋commerce n. 商业complexity n. 复杂(性), 复杂的事物, 复杂性career n. (原意:道路, 轨道)事业, 生涯, 速度outset n. 开端, 开始essence n. 基本, [哲]本质, 香精advocation n. (=advocacy)拥护支持provision n. 供应, (一批)供应品, 预备, 防备, 规定publicize v. 宣扬roundabout adj. 迂回的, 转弯抹角的n. 道路交叉处的环形路, 迂回路线, 兜圈子的话trial-error vt. n. 试制, 试生产maneuverability n. 可操作性, 机动性vehicle n. 交通工具, 车辆, 媒介物, 传达手段junction n. 连接, 接合, 交叉点, 汇合处ponder v. 沉思, 考虑contrive v. 发明, 设计, 图谋snooker n. (=snooker pool)彩色台球, 桌球context n. 上下文, 文章的前后关系deviation n. 背离数学专业英语-Groups and RingsDuring the present century modern abstract algebra has become more and more important as a tool for research not only in other branches of mathematics bu t even in other sciences .Many discoveries in abstract algebra itself have been made during the past years and the spirit of algebraic research has definitely t ended toward more abstraction and rigor so as to obtain a theory of greatest p ossible generality. In particular, the concepts of group ,ring,integral domain and field have been emphasized.The notion of an abstract group is fundamental in all sciences ,and it is certai nly proper to begin our subject with this concept. Commutative additive groupsare made into rings by assuming closure with respect to a second operation h aving some of the properties of ordinary multiplication. Integral domains and fi elds are rings restricted in special ways and may be fundamental concepts and their more elementary properties are the basis for modern algebra.GroupsDEFINITION A non-empty set G of elements a,b,…is said to form a group with respect to 0 if:I.G is closed with respect to 0II.The associative law holds in G, that isaо(bоc)=(aоb)оcfor every a, b, c of GⅢ. For every a and b of G there exist solutions χand Уin G of the equ ationsaοχ=b yοa=bA group is thus a system consisting of a set of elements and operation οwit h respect to which G forms a group. We shall generally designate the entire s ystem by the set G of its elements and shall call G a group. The notation use d for the operation is generally unimportant and may be taken in as convenien t a way as possible.DEFINITION A group G is called commutative or abelian ifaοb=bοaFor every a and b of G.An elementary physical example of an abelian group is a certain rotation grou p. We let G consist of the rotations of the spoke of a wheel through multiples of 90ºand aοb be the result of the rotation a followed by the rotation b. T he reader will easily verify that G forms a group with respect to οand that aοb=bοa. There is no loss of generality when restrict our attention to multipl icative groups, that is, write ab in stead of aοb.EQUIVALENCEIn any study of mathematical systems the concept of equivalence of systems of the same kind always arises. Equivalent systems are logically distinct but weusually can replace any one by any other in a mathematical discussion with no loss of generality. For groups this notion is given by the definition: let G an d G´be groups with respective operations o and o´,and let there be a1-1 corr espondenceS : a a´ (a in G and a´in G´)between G and G´such that(aοb)´=a´οb´for all a, b of G. then we call G and G´equivalent(or simply, isomorphic)grou ps.The relation of equivalence is an equivalence relation in the technical sense in the set of all groups. We again emphasize that while equivalent groups may be logically distinct they have identical properties.The groups G and G´of the above definition need not be distinct of course a nd o´may be o. when this is the case the self-equivalence S of G is called a n automorphism.I: a aOf G, but other automorphisms may also exist.RingsA ring is an additive abelian groupB such thatI.the set B is closed with respect to a second operation designated by multiplication; that is , every a and b of B define a unique element ab of B. II.multiplication is associative; that isa (bc) = (ab)cfor every a, b, c of B.Ⅲ. The distributive lawsa (b+c) = ab +ac (b+c) a=ba +cahold for every a, b, c of B.The concept of equivalence again arises. We shall writeB ≌B′to mean that B and B′are equivalent.VocabularyGroup 群rigor 严格ring 环 generalization 推广integral domain 整环Abelian group 阿贝尔群commutative additive group 可交换加法群 rotation 旋转automorphism 自同构数学专业英语-Historical introduction of CalculusThe Two Basic Concepts of CalculusThe remarkable progress that has been made in science and technology during the last century is due in large part to the development of mathematics. That branch of mathematics known as integral and differential calculus serves as a natural and powerful tool for attacking a variety of problems that arise in phys ics,engineering,chemistry,geology,biology, and other fields including,rather recentl y,some of the social sciences.To give the reader an idea of the many different types of problems that can b e treatedby the methods of calculus,we list here a few sample questions.With what speed should a rocket be fired upward so that it never returns to e arth? What is the radius of the smallest circular disk that can cover every isosceles triangle of a given perimeter L? What volume of material is removed fr om a solid sphere of radius 2 r if a hole of redius r is drilled through the ce nter? If a strain of bacteria grows at a rate proportional to the amount present and if the population doubles in one hour,by how much will it increase at th e end of two hours? If a ten-pound force stretches an elastic spring one inch,h ow much work is required to stretch the spring one foot?These examples,chosen from various fields,illustrate some of the technical quest ions that can be answered by more or less routine applications of calculus.Calculus is more than a technical tool-it is a collection of fascinating and ex eiting idea that have interested thinking men for centuries.These ideas have to do with speed,area,volume,rate of growth,continuity,tangent line,and otherconcept s from a varicty of fields.Calculus forces us to stop and think carefully about the meanings of these concepts. Another remarkable feature of the subject is it s unifying power.Most of these ideas can be formulated so that they revolve a round two rather specialized problems of a geometric nature.We turn now to a brief description of these problems.Consider a cruve C which lies above a horizontal base line such as that show n in Fig.1. We assume this curve has the property that every vertical line inter sects it once at most.The shaded portion of the figure consists of those pointe which lie below the curve C , above the horizontal base,and between two para llel vertical segments joining C to the base.The first fundamental problem of c alculus is this: To assign a number which measures the area of this shaded re gion.Consider next a line drawn tangent to the curve,as shown in Fig.1. The second fundamental problem may be stated as follows:To assign a number which me asures the steepness of this line.Basically,calculus has to do with the precise formulation and solution of these two special problems.It enables us to define the concepts of area and tangent l ine and to calculate the area of a given region or the steepness of a given an gent line. Integral calculus deals with the problem of area while differential cal culus deals with the problem of tangents.Historical BackgroundThe birth of integral calculus occurred more than 2000 years ago when the Gr eeks attempted to determine areas by a procees which they called the method of exhaustion.The essential ideas of this ,method are very simple and can be d escribed briefly as follows:Given a region whose area is to be determined,we inscribe in it a polygonal region which approximates the given region and whos e area we can easily compute.Then we choose another polygonal region which gives a better approximation,and we continue the process,taking polygons with more and more sides in an attempt to exhaust the given region.The method is illustrated for a scmicircular region in Fig.2. It was used successfully by Arch imedes(287-212 B.C.) to find exact formulas for the area of a circle and a fe w other special figures.The development of the method of exhaustion beyond the point to which Ar chimcdcs carried it had to wait nearly eighteen centuries until the use of algeb raic symbols and techniques became a standard part of mathematics. The eleme ntary algebra that is familiar to most high-school students today was completel y unknown in Archimedes’time,and it would have been next to impossible to extend his method to any general class of regions without some convenient w ay of expressing rather lengthy calculations in a compact and simpolified form.A slow but revolutionary change in the development of mathematical notations began in the 16th century A.D. The cumbersome system of Roman numerals was gradually displaced by the Hindu-Arabic characters used today,the symbol s “+”and “-”were introduced for the forst time,and the advantages of the decimal notation began to be recognized.During this same period,the brilliant su ccesse of the Italian mathematicians Tartaglia,Cardano and Ferrari in finding al gebraic solutions of cubic and quadratic equations stimulated a great deal of ac tivity in mathematics and encouraged the growth and acceptance of a new and superior algebraic language. With the wide spread introduction of well-chosen algebraic symbols,interest was revived in the ancient method of exhaustion an d a large number of fragmentary results were discovered in the 16 th century by such pioneers as Cavalieri, Toricelli, Roberval, Fermat, Pascal, and Wallis.Fig.2. The method of exhaustion applied to a semicircular region.Gradually the method of exhaustion was transformed into the subject now calle d integral calculus,a new and powerful discipline with a large variety of applic ations, not only to geometrical problems concerned with areas and volumes but also to jproblems in other sciences. This branch of mathematics, which retaine d some of the original features of the method of exhaustion,received its bigges t impetus in the 17 th century, largely due to the efforts of Isaac Newion (16 42—1727) and Gottfried Leibniz (1646—1716), and its development continued well into the 19 th century before the subject was put on a firm mathematical basis by such men as Augustin-Louis Cauchy (1789-1857) and Bernhard Riem ann (1826-1866).Further refinements and extensions of the theory are still being carried o ut in contemporary mathematicsVocabularygeology 地质学decimal 小数,十进小数biology 生物学discipline 学科social sciences 社会科学 contemporary 现代的disk (disc) 圆盘bacteria 细菌isosceles triangle 等腰三角形 elastic 弹性的perimeter 周长 impetus 动力volume 体积 proportional to 与…成比例center 中心 inscribe 内接steepness 斜度 solid sphere 实心球method of exhaustion 穷举法 refinement 精炼,提炼polygon 多边形,多角形 cumbersome 笨重的,麻烦的polygonal 多角形fragmentary 碎片的,不完全的approximation 近似,逼近 background 背景学专业英语-How to Organize a paper (For Beginers)?The usual journal article is aimed at experts and near-experts, who are the peo ple most likely to read it. Your purpose should be say quickly what you have done is good, and why it works. Avoid lengthy summaries of known results, and minimize the preliminaries to the statements of your main results. There ar e many good ways of organizing a paper which can be learned by studying pa pers of the better expositors. The following suggestions describe a standard acc eptable style.Choose a title which helps the reader place in the body of mathematics. A use less title: Concerning some applications of a theorem of J. Doe. A. good titlecontains several well-known key words, e. g. Algebraic solutions of linear parti al differential equations. Make the title as informative as possible; but avoid re dundancy, and eschew the medieval practice of letting the title serve as an infl ated advertisement. A title of more than ten or twelve words is likely to be m iscopied, misquoted, distorted, and cursed.The first paragraph of the introduction should be comprehensible to any mathe matician, and it should pinpoint the location of the subject matter. The main p urpose of the introduction is to present a rough statement of the principal resul ts; include this statement as soon as it is feasible to do so, although it is som etimes well to set the stage with a preliminary paragraph. The remainder of th e introduction can discuss the connections with other results.It is sometimes useful to follow the introduction with a brief section that estab lishes notation and refers to standard sources for basic concepts and results. N ormally this section should be less than a page in length. Some authors weave this information unobtrusively into their introductions, avoiding thereby a dull section.The section following the introduction should contain the statement of one or more principal results. The rule that the statement of a theorem should precede its proof a triviality. A reader wants to know the objective of the paper, as well as the relevance of each section, as it is being read. In the case of a ma jor theorem whose proof is long, its statement can be followed by an outline of proof with references to subsequent sections for proofs of the various parts.Strive for proofs that are conceptual rather than computational. For an example of the difference, see A Mathematician’s Miscellany by J.E.Littlewood, in wh ich the contrast between barbaric and civilized proofs is beautifully and amusin gly portrayed. To achieve conceptual proofs, it is often helpful for an author t o adopt an initial attitude such as one would take when communicating mathe matics orally (as when walking with a friend). Decide how to state results wit h a minimum of symbols and how to express the ideas of the proof without c omputations. Then add to this framework the details needed to clinch the resul ts.Omit any computation which is routine (i.e. does not depend on unexpected tri cks). Merely indicate the starting point, describe the procedure, and state the o utcome.It is good research practice to analyze an argument by breaking it into a succe ssion of lemmas, each stated with maximum generality. It is usually bad practi ce to try to publish such an analysis, since it is likely to be long and unintere sting. The reader wants to see the path-not examine it with a microscope. A part of the argument is worth isolating as a lemma if it is used at least twice l ater on.The rudiments of grammar are important. The few lines written on the blackbo ard during an hour’s lecture are augmented by spoken commentary, and aat t he end of the day they are washed away by a merciful janitor. Since the publ ished paper will forever speak for its author without benefit of the cleansing s ponge, careful attention to sentence structure is worthwhile. Each author must develop a suitable individual style; a few general suggestions are nevertheless a ppropriate.The barbarism called the dangling participle has recently become more prevalen t, but not less loathsome. “Differentiating both sides with respect to x, the eq uation becomes---”is wrong, because “the equation”cannot be the subject th at does the differentiation. Write instead “differentiating both sides with respec t to x, we get the equation---,”or “Differentiation of both sides with respect to x leads to the equation---”Although the notion has gained some currency, it is absurd to claim that infor mal “we”has no proper place in mathematical exposition. Strict formality is appropriate in the statement of a theorem, and casual chatting should indeed b e banished from those parts of a paper which will be printed in italics. But fif teen consecutive pages of formality are altogether foreign to the spirit of the t wentieth century, and nearly all authors who try to sustain an impersonal digni fied text of such length succeed merely in erecting elaborate monuments to slu msiness.A sentence of the form “if P,Q”can be understood. However “if P,Q,R,S,T”is not so good, even if it can be deduced from the context that the third co mma is the one that serves the role of “then.”The reader is looking at the paper to learn something, not with a desire for mental calisthenics.Vocabularypreliminary 序,小引(名)开端的,最初的(形)eschew 避免medieval 中古的,中世纪的inflated 夸张的comprehensible 可领悟的,可了解的pinpoint 准确指出(位置)weave 插入,嵌入unobtrusivcly 无妨碍地triviality 平凡琐事barbarism 野蛮,未开化portray 写真,描写clinch 使终结rudiment 初步,基础commentary 注解,说明janitor 看守房屋者sponge 海绵dangling participle 不连结分词prevalent 流行的,盛行loathsome 可恶地absurd 荒谬的banish 排除sustain 维持,继续slumsiness 粗俗,笨拙monument 纪念碑calisthenics 柔软体操,健美体操notes1. 本课文选自美国数学会出版的小册子A mamual for authors of mathematical paper的一节,本文对准备投寄英文稿件的读者值得一读。
数学专业英语翻译2-6

It may be done by a formula as the 18th century mathematics presumed but it can equally well be done by a tabulation such as a statistical chart, or by some other form of description.
EXAMPLE 1. The force F necessary to stretch a steel spring a distance x beyond its natural length is proportional to x. That is, F=cx, where c is a number independent of x called the spring constant.
这个公式是在17世纪中叶被胡克发现的,叫做胡克定 律,它用来表示力关于位移的函数。
EXAMPLE 2. The volume of a cube is a function of its edge-length. If the edges have length x, the volume V is given by the formula V=x3.
Today, the meaning of function is essentially this: Given two sets, say X and Y, a function is a correspondence which associates with each element of X one and one only element of Y.
数学专业课程术语翻译大全.

数学专业课程术语翻译大全Advanced Computational Fluid Dynamics 高等计算流体力学Advanced Mathematics 高等数学Advanced Numerical Analysis 高等数值分析Algorithmic Language 算法语言Analogical Electronics 模拟电子电路Artificial Intelligence Programming 人工智能程序设计Audit 审计学Automatic Control System 自动控制系统Automatic Control Theory 自动控制理论Auto-Measurement Technique 自动检测技术Basis of Software Technique 软件技术基础Calculus 微积分Catalysis Principles 催化原理Chemical Engineering Document Retrieval 化工文献检索Circuitry 电子线路College English 大学英语College English Test (Band 4 CET-4College English Test (Band 6 CET-6College Physics 大学物理Communication Fundamentals 通信原理Comparative Economics 比较经济学Complex Analysis 复变函数论Computational Method 计算方法Computer Graphics 图形学原理computer organization 计算机组成原理computer architecture 计算机系统结构Computer Interface Technology 计算机接口技术Contract Law 合同法Cost Accounting 成本会计Circuit Measurement Technology 电路测试技术Database Principles 数据库原理Design & Analysis System 系统分析与设计Developmental Economics 发展经济学discrete mathematics 离散数学Digital Electronics 数字电子电路Digital Image Processing 数字图像处理Digital Signal Processing 数字信号处理Econometrics 经济计量学Economical Efficiency Analysis for Chemical Technology 化工技术经济分析Economy of Capitalism 资本主义经济Electromagnetic Fields & Magnetic Waves 电磁场与电磁波Electrical Engineering Practice 电工实习Enterprise Accounting 企业会计学Equations of Mathematical Physics 数理方程Experiment of College Physics 物理实验Experiment of Microcomputer 微机实验Experiment in Electronic Circuitry 电子线路实验Fiber Optical Communication System 光纤通讯系统Finance 财政学Financial Accounting 财务会计Fine Arts 美术Functions of a Complex Variable 单复变函数Functions of Complex Variables 复变函数Functions of Complex Variables & Integral Transformations 复变函数与积分变换Fundamentals of Law 法律基础Fuzzy Mathematics 模糊数学General Physics 普通物理Graduation Project(Thesis 毕业设计(论文Graph theory 图论Heat Transfer Theory 传热学History of Chinese Revolution 中国革命史Industrial Economics 工业经济学Information Searches 情报检索Integral Transformation 积分变换Intelligent robot(s; Intelligence robot 智能机器人International Business Administration 国际企业管理International Clearance 国际结算International Finance 国际金融International Relation 国际关系International Trade 国际贸易Introduction to Chinese Tradition 中国传统文化Introduction to Modern Science & Technology 当代科技概论Introduction to Reliability Technology 可靠性技术导论Java Language Programming Java 程序设计Lab of General Physics 普通物理实验Linear Algebra 线性代数Management Accounting 管理会计学Management Information System 管理信息系统Mechanic Design 机械设计Mechanical Graphing 机械制图Merchandise Advertisement 商品广告学Metalworking Practice 金工实习Microcomputer Control Technology 微机控制技术Microeconomics & Macroeconomics 西方经济学Microwave Technique 微波技术Military Theory 军事理论Modern Communication System 现代通信系统Modern Enterprise System 现代企业制度Monetary Banking 货币银行学Motor Elements and Power Supply 电机电器与供电Moving Communication 移动通讯Music 音乐Network Technology 网络技术Numeric Calculation 数值计算Oil Application and Addition Agent 油品应用及添加剂Operation & Control of National Economy 国民经济运行与调控Operational Research 运筹学Optimum Control 最优控制Petroleum Chemistry 石油化学Petroleum Engineering Technique 石油化工工艺学Philosophy 哲学Physical Education 体育Political Economics 政治经济学principle of compiling 编译原理Primary Circuit (反应堆一回路Principle of Communication 通讯原理Principle of Marxism 马克思主义原理Principle of Mechanics 机械原理Principle of Microcomputer 微机原理Principle of Sensing Device 传感器原理Principle of Single Chip Computer 单片机原理Principles of Management 管理学原理Probability Theory & Stochastic Process 概率论与随机过程Procedure Control 过程控制Programming with Pascal Language Pascal语言编程Programming with C Language C语言编程Property Evaluation 工业资产评估Public Relation 公共关系学Pulse & Numerical Circuitry 脉冲与数字电路Refinery Heat Transfer Equipment 炼厂传热设备Satellite Communications 卫星通信Semiconductor Converting Technology 半导体变流技术Set Theory 集合论Signal & Linear System 信号与线性系统Social Research 社会调查software engineering 软件工程SPC Exchange Fundamentals 程控交换原理Specialty English 专业英语Statistics 统计学Stock Investment 证券投资学Strategic Management for Industrial Enterprises 工业企业战略管理Technological Economics 技术经济学Television Operation 电视原理Theory of Circuitry 电路理论Turbulent Flow Simulation and Application 湍流模拟及其应用Visual C++ Programming Visual C++程序设计Windows NT Operating System Principles Windows NT操作系统原理Word Processing 数据处理Topology 拓扑学Differential Geometry 微分几何Mathematical Modeling 数学模型(NonlinearOrdinary Differential Equation (非线性常微分方程Partial Differential Equation 偏微分方程Modern Algebra 抽象代数Mathematical Finace 数学金融学Basic Control Theory 控制理论基础Functional Analysis泛函分析Mathematical Finance 数学金融学。
数学各种专业的英语词汇翻译

1. 有关数*算add,plus 加subtract 减difference 差multiply, times 乘product 积divide 除divisible 可被整除的divided evenly 被整除dividend 被除数,红利divisor 因子,除数quotient 商remainder 余数factorial 阶乘power 乘方radical sign, root sign 根号round to 四舍五入to the nearest 四舍五入2. 有关集合union 并集proper subset 真子集solution set 解集3.有关代数式、方程和不等式algebraic term 代数项like terms, similar terms 同类项numerical coefficient 数字系数literal coefficient 字母系数inequality 不等式triangle inequality 三角不等式range 值域original equation 原方程equivalent equation 同解方程,等价方程linear equation 线性方程(e.g. 5x +6=22)4.有关分数和小数proper fraction 真分数improper fraction 假分数mixed number 带分数vulgar fraction,common fraction 普通分数simple fraction 简分数complex fraction 繁分数numerator 分子denominator 分母(least) common denominator (最小)公分母quarter 四分之一decimal fraction 纯小数infinite decimal 无穷小数recurring decimal 循环小数tenths unit 十分位5. 基本数学概念arithmetic mean 算术平均值weighted average 加权平均值geometric mean 几何平均数exponent 指数,幂base 乘幂的底数,底边cube 立方数,立方体square root 平方根cube root 立方根common logarithm 常用对数digit 数字constant 常数variable 变量inverse function 反函数complementary function 余函数linear 一次的,线性的factorization 因式分解absolute value 绝对值,e.g.|-32|=32round off 四舍五入主题:数学专业英语词汇6.有关数论natural number 自然数positive number 正数negative number 负数odd integer, odd number 奇数even integer, even number 偶数integer, whole number 整数positive whole number 正整数negative whole number 负整数consecutive number 连续整数real number, rational number 实数,有理数irrational(number)无理数inverse 倒数composite number 合数 e.g. 4,6,8,9,10,12,14,15……prime number 质数 e.g. 2,3,5,7,11,13,15……注意:所有的质数(2除外)都是奇数,但奇数不一定是质数reciprocal 倒数common divisor 公约数multiple 倍数(least)common multiple (最小)公倍数(prime) factor (质)因子common factor 公因子ordinary scale, decimal scale 十进制nonnegative 非负的tens 十位units 个位mode 众数median 中数common ratio 公比7.数列arithmetic progression(sequence) 等差数列geometric progression(sequence) 等比数列8.其它approximate 近似(anti)clockwise (逆) 顺时针方向cardinal 基数ordinal 序数direct proportion 正比distinct 不同的estimation 估计,近似parentheses 括号proportion 比例permutation 排列combination 组合table 表格trigonometric function 三角函数unit 单位,位几何部分1. 所有的角alternate angle 内错角corresponding angle 同位角vertical angle 对顶角central angle 圆心角interior angle 内角exterior angle 外角supplementary angles 补角complementary angle 余角adjacent angle 邻角acute angle 锐角obtuse angle 钝角right angle 直角round angle 周角straight angle 平角included angle 夹角2.所有的三角形equilateral triangle 等边三角形scalene triangle 不等边三角形isosceles triangle 等腰三角形right triangle 直角三角形oblique 斜三角形inscribed triangle 内接三角形3.有关收敛的平面图形,除三角形外semicircle 半圆concentric circles 同心圆quadrilateral 四边形pentagon 五边形hexagon 六边形heptagon 七边形octagon 八边形nonagon 九边形decagon 十边形polygon 多边形parallelogram 平行四边形equilateral 等边形plane 平面square 正方形,平方rectangle 长方形regular polygon 正多边形rhombus 菱形trapezoid 梯形4.其它平面图形arc 弧line, straight line 直线line segment 线段parallel lines 平行线segment of a circle 弧形5.有关立体图形cube 立方体,立方数rectangular solid 长方体regular solid/regular polyhedron 正多面体circular cylinder 圆柱体cone 圆锥sphere 球体solid 立体的6.有关图形上的附属物altitude 高depth 深度side 边长circumference, perimeter 周长radian 弧度surface area 表面积volume 体积arm 直角三角形的股cross section 横截面center of a circle 圆心chord 弦radius 半径angle bisector 角平分线diagonal 对角线diameter 直径edge 棱face of a solid 立体的面hypotenuse 斜边included side 夹边leg 三角形的直角边median of a triangle 三角形的中线base 底边,底数(e.g. 2的5次方,2就是底数)opposite 直角三角形中的对边midpoint 中点endpoint 端点vertex (复数形式vertices)顶点tangent 切线的transversal 截线intercept 截距7.有关坐标coordinate system 坐标系rectangular coordinate 直角坐标系origin 原点abscissa 横坐标ordinate 纵坐标number line 数轴quadrant 象限slope 斜率complex plane 复平面8.其它plane geometry 平面几何trigonometry 三角学bisect 平分circumscribe 外切inscribe 内切intersect 相交perpendicular 垂直pythagorean theorem 勾股定理congruent 全等的multilateral 多边的其它1.单位类cent 美分penny 一美分硬币nickel 5美分硬币dime 一角硬币dozen 打(12个)score 廿(20个)Centigrade 摄氏Fahrenheit 华氏quart 夸脱gallon 加仑(1 gallon = 4 quart) yard 码meter 米micron 微米inch 英寸foot 英尺minute 分(角度的度量单位,60分=1度)square measure 平方单位制cubic meter 立方米pint 品脱(干量或液量的单位)2.有关文字叙述题,主要是有关商业intercalary year(leap year) 闰年(366天)common year 平年(365天) depreciation 折旧down payment 直接付款discount 打折margin 利润profit 利润interest 利息simple interest 单利compounded interest 复利dividend 红利decrease to 减少到decrease by 减少了increase to 增加到increase by 增加了denote 表示list price 标价markup 涨价per capita 每人ratio 比率retail price 零售价tie 打。
数学专业英语课文翻译2-9,2-10

No matter what the students’ field of major interest is , knowledge of the rudiments of matrices is likely to broaden the range of literature that he can read with understanding .
2.9 微分方程简介 Introduction to Differential Equations
New Words & Expressions:
approximate evaluation 近似估计 initial 初始的
disintegrate 解体,衰变
differentiable 可微的 exponential 指数的 数
Or a radioactive substance may be disintegrating at a known rate and we may be required to determine the amount of material present after a given time.
又如,某种放射性物质可能正在以已知的速度进行衰 变,需要我们确定在给定的时间后遗留物质的总量。
※In examples like these, we are trying to determine an unknown function from prescribed information expressed in the form of an equation involving at least one of the derivatives of the unknown function . 在类似的例子中,我们力求由方程的形式表述的信息 来确定未知函数,而这种方程至少包含了未知函数的 一个导数。
数学专业外语词汇

第一节number ['nʌmbə] n. 号码;数字;数;算术;(杂志等的)期 vi. 计入;总数达到 vt. 编号;计入;数…的数目;使为数有限form [fɔ:m] n. 形式,形状;形态,外形;表格;方式vt. 构成,组成;排列,组织;产生,塑造vi. 形成,构成;排列geometry [dʒi'ɔmitri] n. 几何学trigonometry [,triɡə'nɔmitri] n. 三角学algebra ['ældʒibrə] n. 代数学equation [i'kweiʒən, -ʃən] n. 方程式,等式;相等;反应式function ['fʌŋkʃən] n. 功能;函数;职责;盛大的集会 vi. 行使职责;运行;活动conception [kən'sepʃən] n. 概念;设想;怀孕;开始proposition [,prɔpə'ziʃən] n. 命题;提议,议题;[修辞]主题 vt. 向…提议;向...求欢axiom ['æksiəm] n. 公理;格言;自明之理postulate ['pɔstjuleit, -tʃə-] vt. 要求;假定;视…为理所当然 n. 假定;基本条件definition [,difi'niʃən] n. 定义;清晰度;解说theorem ['θiərəm, 'θi:ə-] n. 定理;原理symbol ['simbəl] n. 符号;象征;标志sign [sain] n. 符号;记号;迹象;手势 vi. 签名;签署 vt. 签署;示意branch [brɑ:ntʃ, bræntʃ] vt. 分支;出现分歧 vi. 分支;出现分歧n. 树枝,分枝;分部;支流deduce [di'dju:s] vt. 推论,推断;演绎出;推导computation [,kɔmpju'teiʃən] n. 估计,计算numeral ['nju:mərəl] n. 数字 adj. 表示数字的;数字的operation [,ɔpə'reiʃən] n. 操作;手术;经营;运算addition [ə'diʃən] n. 添加;增加物;加法subtraction [səb'trækʃən] n. 减少;减法;差集multiplication [,mʌltipli'keiʃən] n. 乘法;增加division [di'viʒən] n. 除法;部门;分割;师(军队);[体]赛区equality [i:'kwɔləti] n. 平等;相等;[数]等式equal ['i:kwəl] adj. 相等的;胜任的;平等的vt. 等于;比得上n. 同辈;对手;匹敌;相等的事物measure ['meʒə] n. 措施;程度;测量;尺寸vt. 测量;估量;权衡 vi. 测量;估量measurement ['meʒəmənt] n. 测量;尺寸;度量;量度制;观测notation [nəu'teiʃən] n. 符号;注释;记号法;乐谱constant ['kɔnstənt] adj. 不变的;恒定的;经常的n. 常数;恒量variable ['vεəriəbl] adj. 易变的,多变的;可变的;[生]变异的,畸变的;[数]变量的 n. 可变物,可变因素;[数]变量formula ['fɔ:mjulə] n. 公式,准则;配方;婴儿食品figure ['fiɡə] n. 图形;数字;(人的)体形;人物;画像;价格vi. 出现;计算;扮演角色 vt. 描绘;计算;认为;象征chart [tʃɑ:t] n. 图表;海图;图纸 vt. 绘制…的图表;在海图上标出;详细计划even ['i:vən] adj. 偶数的;相等的;平坦的 adv. 甚至;还;实际上;即使vt. 使平坦;使相等 vi. 变平;变得可比较;成为相等identity [ai'dentəti] n. 身份;同一性,一致;恒等式;特性arithmetic [ə'riθmətik, ,æriθ'metik] n. 算术,算法statement ['steitmənt] n. 声明;陈述,叙述;报表,清单algebraic [,ældʒi'breiik,-kəl] adj. [数] 代数的;关于代数学的root [ru:t, rut] n. 根;根源;祖先;词根vi. 生根;根除 vt. 生根,固定;根源在于numeric [nju:'merik] n. 数;数字 adj. 数字的;数值的(等于numerical [nju:'merikəl] ) performance [pə'fɔ:məns] n. 性能;表演;执行;绩效;操作term [tə:m] n. 学期;术语;条款;期限vt. 把…叫做set [set] n. 集合;一套;布景;装置;趋势vt. 树立;点燃;放;点缀;使凝结vi. 凝固;结果;定型adj. 固定的;规定的;固执的involve [in'vɔlv] vt. 包含;牵涉;使陷于;潜心于indicate ['indikeit] vt. 指出;表明;象征;预示untrue [,ʌn'tru:] adj. 不真实的;不合标准的;不忠实的;不正当的true [tru:] adj. 真实的;正确的 adv. 准确地;真实地 n. 真实;准确 vt. 装准fraction ['frækʃən] n. 小部分;部分;稍微;[数]分数dimension [di'menʃən, dai-] n. 维;尺寸;次元;容积 vt. 标出尺寸 adj. 规格的短语:mathematical analysis数学分析 higher algebra高等代数higher mathematics高等数学 differential equation微分方程function theory 函数论 dependent variable 因变量 independent variable自变量logical deduction逻辑推理 reasoning method推理方法 even number偶数military operation军事行动 odd number 奇数 equation of condition条件等式quadratic equation二次方程 linear equation线性方程 of one dimension一维第二节institution [,insti'tju:ʃən] n. 制度;(社会或宗教等)公共机构;习俗;建立prerequisite ['pri:'rekwizit] n. 先决条件 adj. 首要必备的inundate ['inʌndeit, in'ʌn-] vt. 泛滥;淹没;浸水;(洪水般的)扑来vanish ['væniʃ] vi. 消失;突然不见;[数]成为零 vt. 使不见,使消失 n. [语]弱化音matriculation [mə,trikju'leiʃən] n. 入学考试;大学入学许可;录取入学surveyor [sə'veiə, sə:-] n. 测量员;检验员architect ['ɑ:kitekt] n. 建筑师draftsman ['drɑ:ftsmən, 'dræft-] n. 绘图员;起草者;立案者machinist [mə'ʃi:nist] n. 机械工;机械师;机械安装修理工stonecutter ['stəun,kʌtə] n. 石匠;琢石机;石工critical ['kritikəl] adj. 批评的,爱挑剔的;决定性的;危险的;临界的;鉴定的;评论的byproduct ['bai,prɔdʌkt] n. 副产品perseverance [,pə:si:'viərəns] n. 坚持不懈;不屈不挠originality [ə,ridʒə'næləti] n. 独创性,创造力;创意;新奇;原始orderliness ['ɔ:dəlinis] n. 秩序井然;整洁,整齐appreciation [ə,pri:ʃi'eiʃən] n. 感谢;增值;欣赏,鉴别abound [ə'baund] vi. 充满;富于numerical [nju:'merikəl] adj. 数字的;数值的;用数字表示的(等于numericcube [kju:b] n. 立方体;立方;骰子 vt. 使成立方形;使自乘二次;量…的体积position [pə'ziʃən] n. 位置,方位;职位,工作;姿态;站位;vt. 安置;把……放在适当位置sphere [sfiə] n. 范围;球体 vt. 包围;放入球内;使…成球形 adj. 球体的cylinder ['silində] n. 汽缸;圆筒;圆柱状物;柱面cone [kəun] n. 圆锥体,圆锥形;球果 vt. 使成锥形geometrical adj. 几何的,几何学的triangle ['traiæŋɡl] n. 三角(形);三角形之物;三人一组;三角关系surface ['sə:fis] n. 表面;外观;表层 adj. 表面的,肤浅的vi. 浮出水面 vt. 使浮出水面;使成平面pyramid ['pirəmid] n. 金字塔;角锥体 vi. 渐增;上涨;成金字塔状vt. 使…渐增;使…上涨;使…成金字塔状plane [plein] n. 平面;飞机;程度,水平 vi. 刨;翱翔;乘飞机旅行vt. 刨平;用刨子刨;掠过水面 adj. 平的;平面的solid ['sɔlid] adj. 固体的;结实的;可靠的;一致的;立体的 n. 固体;立方体breadth[bredθ] n. 宽度,幅度;宽宏thickness ['θiknis] n. 厚度;层;含混不清;浓度line [lain] n. 绳;排;路线,航线 vi. 排队;站成一排vt. 划线于;排成一行;以线条标示;使…起皱纹segment ['seɡmənt, seɡ'ment, 'seɡment] vi. 分割 n. 段;部分 vt. 分割ray [rei] n. 射线;光线 vt. 放射;显出 vi. 放射光线;浮现equidistant [,i:kwi'distənt] adj. 等距的;距离相等的curve [kə:v] n. 曲线;弯曲;曲线球;曲线图表 vt. 使弯曲;弯vi. 成曲形 adj. 弯曲的;曲线形的curved [kə:vd] adj. 弯曲的;弄弯的 n. 倒弧角 vt. 弯曲(curve的过去式)side [said] n面;侧面;旁边 vi. 支持;赞助;偏袒 adj. 旁的,侧的 vt. 同意,支持angle ['æŋɡl] vi. 钓鱼;谋取 n. 角度,角radius ['reidiəs] n. 半径,半径范围;辐射光线;有效航程;桡骨diameter [dai'æmitə] n. 直径infinitely ['infinitli] adv. 无限地;极其endpoint ['end,pɔint] n. 端点;末端,终结点center ['sentə] n. 中心,中央;中锋;中心点 vi. 居中,被置于中心vt. 集中,使聚集在一点;定中心 adj. 中央的,位在正中的terminate ['tə:mineit] vt. 使终止;使结束;解雇 vi. 结束,终止;结果 adj. 结束的circle ['sə:kl] n. 圆;圆形物;循环,周期;圈子vi. 盘旋,旋转;环行vt. 画圆圈;环绕…移动semicircle ['semi,sə:kl] n. 半圆,半圆形arc [ɑ:k] n. 弧(度);弧形物;天穹;弧光(全称electric arc)adj. 圆弧的;反三角函数的 vt. 走弧线;形成电弧chord [kɔ:d] n. 弦;和弦circumference [sə'kʌmfərəns] n. 圆周;周长;胸围hypotenuse [hai'pɔtənju:z] n. 直角三角形的斜边短语: minor arc 劣弧 major arc 优弧line segment 直线段 broken line 折线acute angle 锐角 obtuse angle 钝角 right angle 直角right triangle 直角三角形 adjacent side 邻边第三节set [set] n. 集合;一套;布景;装置;趋势vt. 树立;点燃;放;点缀;使凝结vi. 凝固;结果;定型adj. 固定的;规定的;固执的subset ['sʌbset] n. [数] 子集;子设备;小团体notation [nəu'teiʃən] n. 符号;注释;记号法;乐谱roster ['rɔstə, 'rəu-] n. 执勤人员表;花名册;逐项登记表denote [di'nəut] vt. 表示,指示designate ['deziɡneit, 'deziɡnit] vt. 标出;指定;把…定名为;指派adj. 指定的;选定的brace [breis] n. 支柱;大括号;曲柄vt. 支撑;激励;振作起来;撑牢vi. 支持;打起精神adj. 曲柄的integer ['intidʒə] n. 整数;完整的事物;整体Even integer:偶数 Even integer/number:偶数 Consecutive even integer:连续偶数even ['i:vən] adj. 偶数的;相等的;平坦的adv. 甚至;还;实际上;即使vt. 使平坦;使相等 vi. 变平;变得可比较;成为相等positive ['pɔzətiv, -zi-] adj. 确定的,肯定的;积极的;正的,阳性的;绝对的;实际的,真实的 n. 正片;正数 positive number正数underlying [,ʌndə'laiiŋ] adj. 在下面的;优先的;根本的;潜在的v. 放在…的下面;为…的基础;优先于(underlie的ing形式)universal [,ju:ni'və:səl] adj. 通用的;宇宙的;普遍的;全体的;全世界的n. 一般概念;普通性universal set 全集 void set/empty set 空集 the underlying set 基础集、底集dummy ['dʌmi] adj. 假的;虚拟的n. 仿制品;傀儡;哑巴diagram ['daiəɡræm] n. 图表;图解 vt. 用图解法表示Venn diagram 文氏图维恩图解 be divisible by:可被....整除proper subset 真子集 be said to be被称为 rule out 排除;取消;划去the reference to参考所提到后提及 be referred to as被称为…be contained in包括在包含于 take the place of 代替取代顶替vary from one application to another有所变动,从一个应用到另一个地方第四节integer ['intidʒə] n. 整数;完整的事物;整体irrational [i'ræʃənəl] adj. 无理性的;不合理的;荒谬的 n. 无理数axiom ['æksiəm] n. 公理;格言;自明之理sum [sʌm] n. 总数;金额 vi. 概括 vt. 总结;合计difference ['difərəns] n. 差异;不同;争执product ['prɔdəkt, -ʌkt] n. 产品;结果;作品;乘积quotient ['kwəuʃənt] n. [数]商;系数;份额ordered ['ɔ:dəd] adj. 安排好的;整齐的;[数]有序的 v. 命令;点餐interchangeably [intə'tʃeindʒəbli] adv. [数] 可交换地distinguished [dis'tiŋɡwiʃt] adj. 著名的;高贵的;卓著的 v. 区别(distinguish的过去式)illuminating [i'lju:mineitiŋ] adj. 照亮的,照明的;启蒙的,有启发性的v. 照明,阐释(illuminate的现在分词形式)fraction ['frækʃən] n. 小部分;部分;稍微;[数]分数illustrate ['iləstreit] vt. 阐明,举例说明;图解 vi. 举例denominator [di'nɔmineitə] n. [数] 分母;命名者numerator ['nju:məreitə] n. 分子;计算者;计算器decimal ['desiməl] adj. 小数的;十进位的 n. 小数短语:rational number 有理数 irrational number 无理数 entirely complete 完整的field axiom 域公理 order axiom 序公理 inductive set 归纳集 real axis实轴real line 实直线 a type of reasoning 一种推理方式the intuitive meaning 直观意义 deducible from sth. 可由...推导出来的proof by induction 用数学归纳法证明 decimal fraction 十进制小数第五节integral ['intiɡrəl] adj. 完整的,整体的;[数学]积分的n. [数学]积分;部分;完整area ['εəriə] n. 面积;区域,地区;范围calculation [,kælkju:leiʃən] n. 计算;估计;深思熟虑;计算的结果measure ['meʒə] n. 措施;程度;测量;尺寸vt. 测量;估量;权衡vi. 测量;估量circular ['sə:kjulə] adj. 圆形的;循环的;间接的n. 通知,传单polygonal [pə'liɡənəl] adj. [数] 多边形的;[数] 多角形的region ['ri:dʒən] n. 地区;范围;部位Circular Region:圆形选择;圆形区域;圆形选区 Circular Region:圆形区域Circular Selection Region:圆形选择区域 polygonal regions 多边形区域parabolic [,pærə'bɔlik] adj. 比喻的;抛物线的;寓言的coordinate [kəu'ɔ:dinit, kəu'ɔ:dineit] n. 坐标;同等的人或物adj. 同等的;并列的vt. 调整;整合vi. 协调axis ['æksis] n. 轴;轴线;轴心国parabolic segment:抛物线段抛物弓形 the unit distance单位长度horizontal ['hɔri'zɔntəl] adj. 水平的;地平线的;同一阶层的n. 水平线,水平面;水平位置coordinate system 坐标系 the origin 坐标原点perpendicular [,pə:pən'dikjulə] adj. 垂直的,正交的;直立的;陡峭的n. 垂线;垂直的位置vertical ['və:tikəl] adj. 垂直的,直立的;头顶的,顶点的,竖直的n. 垂直线,垂直面the procedure for points 找点的程序 an ordered pair一个有序对abscissa [æb'sisə] n. 横线;[数]横坐标scale [skeil] n. 刻度;比例;数值范围;天平;规模;鳞vi. 攀登;衡量;生水垢;剥落vt. 攀登;测量;刮鳞;依比例决定quadrant ['kwɔdrənt] n. 象限;象限仪;四分之一圆ordinate ['ɔ:dinət, -neit] n. 纵坐标;[数]纵线three-dimensional ['θri:di'menʃənəl, -dai-] adj. 三维的;立体的;真实的intersect [,intə'sekt] vi. 相交,交叉vt. 横断,横切;贯穿distance ['distəns] n. 距离;远方;疏远;间隔vt. 把…远远甩在后面;疏远distances from sth 到……的距离 Rene Descartes勒奈·笛卡尔(法国哲学家)rudiment ['ru:dimənt] n. 雏形;基本原理rudiments n. 入门;初步;基础知识analytic [,ænə'litik,-kəl] adj. 分析的;解析的;善于分析的analytic geometry解析几何;分析几何学cartesianadj. 笛卡尔哲学的;笛卡尔的n. 笛卡尔信徒also known as Cartesian geometry 也被称为笛卡尔几何Pythagoras [pai'θæɡəræs; pi-] n. 毕达哥拉斯(古希腊哲学家,数学家)pythagoras theorem / the theorem of pythagoras 毕达哥拉斯定理;勾股定理comprise [kəm'praiz] vt. 包含;由…组成succinctly [sək'siŋktli] adv. 简洁地;简便地第六节cube [kju:b] n. 立方体;立方;骰子 vt. 使成立方形;使自乘二次;量…的体积edge [edʒ] n. 边缘;刀刃;优势;锋利vt. 使锐利;将…开刃;给…加上边 vi. 缓缓移动;侧着移动prime [praim] adj. 基本的;最好的;主要的 adv. 极好地n. 初期;青年;全盛时期;精华 vt. 填装;使准备好 vi. 作准备displacement [dis'pleismənt] n. 取代,移位;排水量generalization [,dʒenərəlai'zeiʃən, -li'z-] n. 概括;普遍化;一般化domain [dəu'mein] n. 领域;产业;地产;[计]域名;区域,定义域range [reindʒ] n. 范围;山脉;排;幅度 vi. 平行,列为一行;延伸;漫游;射程达到vt. 使并列;归类于;漫游;来回走动;放牧schematically [ski'mætikli] adv. 计划性地;按照图式;图解式地totality [təu'tæləti] n. 全体;总数;[天]全食output ['autput, ,aut'put] n. 产量;输出,输出量;出产 vt. 输出plot [plɔt] n. 阴谋;情节;图 vt. 密谋;划分;标绘;绘图 vi. 密谋策划;绘制stretch [stretʃ] vt. 伸展,张开;vi. 伸展;adj. 可伸缩的;n. 伸展,延伸短语:non-negative 非负的 function idea 函数思想real-value function 实值函数 the triangle inequality 三角不等式real variable实变量 the identity function恒等函数 schematic representation 图解表示absolute-value function 绝对值函数 Gallup poll 盖洛普民意测验 Hooke’s law 胡克定律第七节succession [sək'seʃən] n. 连续;继位;继承权;[农业]轮栽sequence ['si:kwəns] n. 序列;顺序;续发事件vt. 按顺序排好series ['siəri:z, -riz] n. 系列,连续;丛书;[电]串联;[数]级数infinite ['infinət] adj. 无限的,无穷的;无数的;极大的n. 无限;无限的东西(如空间,时间);无穷大infinite sequence [数] 无穷序列;无限序列successor [sək'sesə] n. 继承者;后续的事物event [i'vent] n. 事件,大事;结果;项目instruction [in'strʌkʃən] n. 指令,命令;指示;用法说明;教导recursion [ri'kə:ʃən, -ʒən] n. 递归,循环;递归式recursion formula [数] 递推公式;[数] 递归公式Fibonacci [,fibə'na:si] n. 斐波纳契(一种整数数列) Fibonacci numbers斐波纳契数列subscript ['sʌbskript] adj. 写在下方的;下标的;脚注的n. 下标;脚注the real part 实部 the imaginary part 虚部complex-valued sequence 复值序列 real-valued sequence 实值序列if and only if 当且仅当 converge to 收敛于phrase [freiz] n. 成语;习语;措词 vt. 用短语表达;用语言表达vi. 用话表示convergent [kən'və:dʒənt] adj. 收敛的;会聚性的;趋集于一点的assume [ə'sju:m, ə'su:m] vt. 假定;承担;呈现;采取vi. 装腔作势;多管闲事suggest [sə'dʒest, səɡ-] vt. 提议,建议;启发;使人想起convergence [kən'və:dʒəns] n. 会聚,集合;[数]收敛convey [kən'vei] vt. 传达;让与;运输divergent [dai'və:dʒənt, di-] adj. 相异的,分歧的;散开的diverge [dai'və:dʒ, di-] vi. 分歧;分叉;偏离;离题vt. 使分叉;使偏离imply [im'plai] vt. 暗示;意味;隐含hold [həuld] vt. 持有;保存;拥有;拘留;约束或控制vi. 持续;支持;有效n. 保留;控制divergence [dai'və:dʒəns, di-] n. 分歧、发散carry over to 继续做下去 converselyadv. 相反地the positive invegers=the set of all postive integers 正整数集separately ['sepəritli] adv. 分别地;分离地;个别地第八节derivative [di'rivətiv] n. 衍生物,派生物;导数 adj. 引出的;派生的numerator ['nju:məreitə] n. 分子;计算者;计算器fraction ['frækʃən] n. 小部分;部分;稍微;[数]分数constant ['kɔnstənt] 英 adj. 不变的;恒定的;经常的 n. 常数;恒量interval ['intəvəl] n. 间隔;幕间休息;间距;区间,线节velocity [vi'lɔsəti] n. 速率;迅速;周转率,速度acceleration [ək,selə'reiʃən] n. 加速,促进;加速度average ['ævəridʒ] n. 平均;平均数;[商]海损 adj. 平均的;普通的vt. 算出…的平均数;将…平均分配;使…平衡 vi. 平均为;呈中间色altitude ['æltitju:d] n. 高度;高地;[数]顶垂线;(等级和地位等的)高级approach [ə'prəutʃ] n. 接近;方法;途径 vt. 接近;着手处理 vi. 靠近,逼近,趋于tangent ['tændʒənt] adj. 切线的,相切的;接触的;离题的 n. 切线,正切steepness ['sti:pnis] n. 险峻;不合道理,陡峭bound [baund] adj. 受约束的;装有封面的;有义务的 vt. 束缚;使跳跃n. 跳跃;范围,界 vi. 弹起;限制slope [sləup] n. 倾斜;斜率;斜坡;扛枪姿势;坡度 vi. 倾斜;逃走vt. 扛;倾斜;使倾斜短语:the first derivative 一阶导数 the second derivative二阶导数 open interval开区间difference quatient差商 position function位置函数 instantaneous velocity即时速度linear function线性函数 rectilinear motion直线运动 average rate平均变化率geometric interpretation几何解释 average value平均值 approach zero 趋于0 respective coordinate 相应的坐标 without bound =boundless 无界的第九节terminology [,tə:mi'nɔlədʒi] n. 术语,术语学;用辞polynomial [,pɔli'nəumiəl] n. [数] 多项式;由 2 字以上组成的学名adj. 多项式的;多词学名(指由两个以上的词构成的学名logarithm ['lɔɡəriðəm, 'lɔ:ɡ-] n. [数] 对数exponential [,ekspəu'nenʃəl] 英汉翻译adj. 指数的 n. 指数nature ['neitʃə] n. 自然;性质;种类;本性integral ['intiɡrəl] adj. 完整的,整体的;[数学]积分的 n. [数学]积分;部分;完整integrate ['intiɡreit, 'intiɡrit, -ɡreit] vt. 使…完整;使…成整体;求…的积分;表示…的总和vi. 求积分;取消隔离;成为一体 adj. 完全的;整合的 n. 集成体;一体化integration [,inti'ɡreiʃən] n. 综合;集成,积分displacement [dis'pleismənt] n. 取代,移位;排水量;位移mechanics [mi'kæniks] n. 力学(用作单数);机械学(用作单数);结构;技术disintegrate [dis'intiɡreit] vt. 使分解;使碎裂;使崩溃;[核]使衰变vi. 碎裂;瓦解;[核]衰变astronomy [ə'strɔnəmi] n. 天文学短语:differential equation微分方程 ordinary differential equationchang常微分方程partial differential equation 偏微分方程 rational function有理函数logarithm function对数函数 trigonometric function三角函数exponential function指数函数 inverse trigonometric function反三角函数approximate evaluation近似估计 initial-value problem初值问题initial condition 初始条件 mathematical physics数学物理第十节set [set] n. 集合;一套;布景;装置;趋势vt. 树立;点燃;放;点缀;使凝结vi. 凝固;结果;定型adj. 固定的;规定的;固执的linear ['liniə] adj. 线的,线型的;直线的,线状的;长度的linear space【数学】线性空间,向量空间(=vector space)dependent [di'pendənt] adj. 依靠的;从属的;取决于…的;相关的n. 依赖他人者;受赡养者logically equivalent t逻辑上等价于 the empty set 空集induction [in'dʌkʃən] n. 感应;归纳法;感应现象differentiate [,difə'renʃieit] vi. 区分,区别vt. 区分,区别,求各种数学名词的英语翻译 ... differentiate [,difə'renʃieit] 求...的导数differential mean value theorem 微分中值定理differentiate from first principle 从基本原理求导数 ...by induction hypothesis 通过归纳假设;归纳法的假设hypothesis [hai'pɔθisis] n. 假设hold [həuld] vt. 持有;保存;拥有;拘留;约束或控制vi. 持续;支持;有效n. 保留;控制coefficient [,kəui'fiʃənt] n. 协同因素;[数]系数;[物]率adj. 合作的;共同作用的the result holds trivially 这结果显然成立 finite basis有限基basis ['beisis] n. 底部;基础;主要成分;基本原则或原理span [/spæn/] n. 跨度,跨距;范围vt. 跨越;持续;以手指测量the subspace spanned by S 有S张成的子空间 lnear combination [数] 线性组合combination [,kɔmbi'neiʃən] n. 结合;化合;联合;组合valid ['vælid] adj. 正当的;有效的,有根据的,成立的component [kəm'pəunənt] adj. 组成的,构成的n. 成分;元件;组件;分量ordered basis:有序基底 be valid for适用于;对……成立unique [ju:'ni:k] adj. 唯一的,独一无二的;独特的,稀罕的 n. 独一无二的人uniquely [ju:'ni:kli] adv. 独特地;珍奇地dimension [di'menʃən, dai-] n. 维;尺寸;次元;容积 vt. 标出尺寸 adj. 规格的vector ['vektə] n. 矢量;带菌者;航线 vt. 用无线电导finite dimensional 有限维的 finite dimensional vector space:有限维向量空endlich-dimensional finite-dimensional 有限维 infinite dimensional [数] 无限维的multiple ['mʌltipl] adj. 多样的;许多的;多重的n. 并联;倍数tuple ['tʌpl] n. 元组,重数 n-tuple n-元组 the Ordered n-tuple 有序n-元组multiply ['mʌltiplai] vt. 乘;使相乘;使增加;使繁殖vi. 繁殖;增加;乘adv. 多样地;复合地adj. 多样的;多层的multiplication [,mʌltipli'keiʃən] n. 乘法;增加第十一节statement['steitmənt] n. 声明;陈述,叙述;报表,清单subject of the statement 语句的主语predicate['predikeit] vt. 断定为…;使…基于 vi. 断言,断定n. 谓语,述语adj. 谓语的;述语的proposition[,prɔpə'ziʃən] n. [数] 命题;提议;主题;议题 vt. 向…提议;向…求欢universe['ju:nivə:s] n. 宇宙;世界;领域propositional[prɔpə'ziʃənəl] adj. 命题的;建议的universe of discourse论域,通集 propositional function 命题函数assertion[ə'sə:ʃən] n. 断言,声明;主张,要求;坚持quantifier['kwɔntifaiə] n. [数][语] 量词;数量词;精于计算的人assert [ə'sə:t] vt. 维护,坚持;断言;主张;声称quantification[,kwɔntifi'keiʃən] n. [统计] 定量,量化connective[kə'nektiv] a dj. 连合的,连接的 n. 连接词;连接物universal quantifier 全称量词 universal quantification全称量词化true[tru:] adj. 真实的;正确的 adv. 真实地;准确地 n. 真实;准确 vt. 装准existential quantifier 存在量词 existential quantification 存在量词化 true value真假值false [fɔ:ls] adj. 错误的;虚伪的;伪造的 adv. 欺诈地inclusive[in'klu:siv] adj. 包括的,包含的preferable ['prefərəbl] adj. 更好的,更可取的;更合意的exclusive [ik'sklu:siv] adj. 独有的;排外的;专一的n. 独家新闻;独家经营的项目;排外者execute['eksikju:t] vt. 实行;执行;处死rule of inference 推演规则Phrase [ freiz] n. 成语;习语;措词 vt. 用短语表达;用语言表达vi. 用话表示ambiguous[æm'biɡjuəs] adj. 模糊不清的;引起歧义的eliminate[i'limineit] vt. 消除;排除unambiguous [,ʌnæm'bigjuəs] adj. 不含糊的;清楚的;明白的obscure [əb'skjuə] adj. 模糊的;晦涩的;昏暗的vt. 遮掩;使变暗;使难理解disjunction[dis'dʒʌŋkʃən] n. 分离;析取;分裂;折断negation[ni'ɡeiʃən] n. 否定,否认;拒绝conjunction[kən'dʒʌŋkʃən] n. 结合;[语] 连接词;同时发生propositional connective 命题连词 artificial intelligence人工智能第十二节probability [,prɔbə'biləti] n. 机率;可能性;或然率probability theory概率论 probability space概率空间event [i'vent] n. 事件,大事;结果;项目universal set 通集 impossible event 不可能事件 certain event必然事件Boolean ['bu:liən] algebra 布尔代数outcome ['autkʌm] n. 结果,结局;成果sample ['sɑ:mpl] vt. 取样;尝试;抽样检查 n. 样品;样本;例子adj. 试样的,样品的;作为例子的mutually ['mju:tʃuəli, -tjuəli] adv. 互相地;互助exclusive[ik'sklu:siv] adj. 独有的;排外的;专一的 n. 独家新闻;独家经营的项目;排外者equally likely 同等可能的 probability zero 零概率finitely ['fainaitli] a dv.有限地additive measure有限可加测度discernible [di'sə:nəbl, -'zə:-] adj. 可辨别的;可识别的population[,pɔpju'leiʃən] n. 人口;[生物] 种群,[生物] 群体;全体居民long-lasting ['lɔ:ŋla:stiŋ\] adj. 持续时间长的statistics [stə'tistiks] n. 统计;统计学;[统计] 统计资料relief [ri'li:f] n. 救济;减轻,解除;安慰mathematical statistics 数理统计 rigid law刚性定律transient['trænziənt]adj. 短暂的;路过的n. 瞬变现象;过往旅客;候鸟unrealistic [,ʌnriə'listik] adj. 不切实际的;不实在的feasible ['fi:zəbl] adj. 可行的;可能的;可实行的trial['traiəl] n. 试验;审讯;努力;磨炼adj. 试验的;审讯的monumental[,mɔnju'mentəl] adj. 不朽的;纪念碑的;非常的expenditure[iks'penditʃə] n. 支出,花费;经费,消费额sustain[sə'stein] vt. 维持;支撑,承担;忍受;供养;证实destructive nature破坏性,有害的性质highlight['hailait] vt. 突出;强调;使显著;加亮n. 最精彩的部分;最重要的事情;加亮区inference['infərəns] n. 推理;推论;推断elucidate[i'lu:si,deit] vt. 阐明;说明allergy['ælədʒi] n. 过敏症;反感;厌恶trait [trei, treit] n. 特性,特点;品质;少许digress[dai'ɡres] vi. 离题;走向岔道sampling unit 样本单位,样本个体measurement['meʒəmənt] n. 测量;[计量] 度量;尺寸;量度制exhaustive [iɡ'zɔ:stiv] adj. 详尽的;彻底的;消耗的variability [,vεəriə'biləti] n. 可变性,变化性;[生物][数] 变异性deck [dek] n. 甲板;行李仓;露天平台 vt. 装饰;装甲板;打扮combinatorial analysis组合分析Bridge [bridʒ] n. 桥;桥牌;桥接器;船桥 vt. 架桥;渡过。
数学专业英语课后翻译

2.1 数学、方程与比例(1)数学来源于人类的社会实践,包括工农业的劳动,商业、军事和科学技术研究等活动。
Mathematics comes from man’s social practice, for example, industrial and agricultural production, commercial activities, military operations and scientific and technological researches.(2)如果没有运用数学,任何一个科学技术分支都不可能正常地发展。
No modern scientific and technological branches could be regularly developed without the application of mathematics.(3)符号在数学中起着非常重要的作用,它常用于表示概念和命题。
Notations are a special and powerful tool of mathematics and are used to express conceptions and propositions very often.(4)17 世纪之前,人们局限于初等数学,即几何、三角和代数,那时只考虑常数。
Before 17th century, man confined himself to the elementary mathematics, i. e. , geometry, trigonometry and algebra, in which only the constants were considered.(5)方程与算数的等式不同在于它含有可以参加运算的未知量。
Equation is different from arithmetic identity in that it contains unknown quantity which can join operations.(6)方程又称为条件等式,因为其中的未知量通常只允许取某些特定的值。
数学专业英语翻译2-4

New Words & Expressions:
irrational number 无理数 the order axiom 序公理 ordered 有序的 product 积 quotient 商 rational 有理的 rational number 有理数 reasoning 推理 scale 尺度,刻度 尺度, sum 和
This property of P forms the logical basis for a type of reasoning that mathematicians call proof by induction, a detailed discussion of which is given in Part 4 of this introduction.
现在我们来定义正整数,就是属于每一个归纳集的实数。 现在我们来定义正整数,就是属于每一个归纳集的实数。
Let P denote the set of all positive integers. Then P is itself an inductive set because (a) it contains 1, and (b) it contains x+1 whenever it contains x. Since the members of P belong to every inductive set, we refer to P as the smallest inductive set. 表示所有正整数的集合。 用 P表示所有正整数的集合。那么 本身是一个归纳 表示所有正整数的集合 那么P本身是一个归纳 集 , 因为其中含1, 满足(a); 只要包含x就包含 因为其中含 , 满足 ; 只要包含 就包含x+1, 就包含 满足(b)。由于P中的元素属于每一个归纳集 因此P 中的元素属于每ห้องสมุดไป่ตู้个归纳集, 满足 。由于 中的元素属于每一个归纳集,因此 是最小的归纳集。 是最小的归纳集。
数学专业英语翻译3.4.5

3.4数学的应用与应用数学3.4.5Construction of mathematical model(建立数学模型)In the preceding discussion we viewed modeling as a process and considered briefly the form of the model.Now let's focus attention on the construction of mathematical models.(在前面的讨论中,我们将建模视为一个过程,并简要地仔细思考了模型的形式。
现在让我们把注意力集中在数学模型的构建上。
)We begin by presenting an outline of a peocedure that is helpful in constructing models.In the next section,we illustrate the various steps in the procedure by discussing several real-world examples.(我们首先介绍一种有助于构建模型的概述。
在下一节中,我们通过讨论几个实际示例来说明过程中的各个步骤。
)STEP1Identify the problem(确定问题)What is the problem you would like to explore?Typically this is a difficult step because in real-life situations no one simply hands you a mathematical problem to solve.(你想探索的问题是什么?通常这是一个困难的步骤,因为在现实生活中,没有人只是给你一个数学问题来解决。
)Usually you have to sort through large amounts of data and identify some particular aspect of the situation to study.Moreover,it is imperative to be sufficiently precise(ultimately)in the formulation of the problem to allow for translation of the verbal statements describing the problem into mathematical symbology.(通常你必须对大量数据进行排序,并确定要研究的某些特定情况。
数学专业英语翻译2-3

We use the special notation x S to mean that “x is an element of S” or “x belongs to S”. If x does not belong to S, we write x S .
When convenient, we shall designate sets by displaying the elements in braces; for example, the set of positive even integers less than 10 is displayed as {2,4,6,8} whereas the set of all positive even integers is displayed as {2,4,6,…}, the three dots taking the place of “and so on.”
Sets usually are denoted by capital letters; elements are designated by lower-case letters.
集合论的概念已经被广泛使用,遍及现代数学,因此对大学生 来说,理解它的概念是必要的。集合是数学家们用抽象的方式 来表述一些事物的集体的工具。 集合通常用大写字母表示,元素用小写字母表示。
and we write A≠B.
集合相等的定义 如果两个集合A和B确切包含同样的元素,则 称二者相等,此时记为A=B。如果一个集合包含了另一个集 合以外的元素,则称二者不等,记为A≠B。
EXAMPLE 1. According to this definition, the two sets {2,4,6,8} and {2,8,6,4} are equal since they both consist of the four integers 2,4,6 and 8. Thus, when we use the roster notation to describe a set, the order in which the elements appear is irrelevant.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一段翻译(2):what is the exact value of the number pai?a mathematician made an experiment in order to find his own estimation of the number pai.in his experiment,he used an old bicycle wheel of diameter 63.7cm.he marked the point on the tire where the wheel was touching the ground and he rolled the wheel straight ahead by turning it 20 times.next,he measured the distance traveled by the wheel,which was 39.69 meters.he divided the number 3969 by 20*63.7 and obtained 3.115384615 as an approximation of the number pai.of course,this was just his estimate of the number pai and he was aware that it was not very accurate.数π的精确值是什么?一位数学家做了实验以便找到他自己对数π的估计。
在试验中,他用了一直径63.1厘米的旧自行车轮。
他在车轮接触地面的轮胎上做了标记,而且将车轮向前转动20次。
接下来,他测量了车轮经过的距离,是39.69米。
他用3969除20*63.7得到了数π的近似值3.115384615。
当然,这只是对数π的估计值,并且他也意识到不是很准确。
第二段翻译(5):one of the first articles which we included in the "History Topics" section archive was on the history of pai.it is a very popular article and has prompted many to ask for a similar article about the number e.there is a great contrast between the historical developments of these two numbers and in many ways writing a history of e is a much harder task than writing one of pai.the number e is,compared to pai,a relative newcomer on the mathematical scene.我们包括在“历史专题”部分档案中的第一篇文章就是历史上的π,这是一篇很流行的文章,也促使许多人想了解下一些有关数e的类似文章。
这两个数字的历史发展中有着很大的反差并且在许多方面写数e的历史是比写π的历史更为艰巨的任务。
与π相比,数e在数学界相对较晚。
第三段翻译(24):the path to the development of the integral is a branching one,where similar discoveries were made simultaneously by different people.the history of the technique that is currently known as integration began with attempts to find the area underneath curves.the foundations for the discovery of the integral were first laid by Cavalieri,an Italian Mathematician,in around 1635.Cavalieri's work centered around the observation that a curve can be considered to be sketched by a moving point and an area to be sketched by a moving line.积分发展的道路是一个分支,不同的人在同一时间作了类似的发现。
目前众所周知的积分这一历史方法最初是为了求出曲线下方的面积。
积分的的第一奠基人是Cavalieri(卡瓦列里),一位意大利数学家,时间大约为1635年。
Cavalieri(卡瓦列里)的工作集中在观察,即一个曲线可以被视为是移动的点所勾勒且和面积由移动的线勾勒出。
第四段翻译(35):Pierre De Fermat's method for finding a tangent was developed during the 1630's,and though never rigorously formulated,is almost exactly the method used bu Newton and cking a formal concept of a limit,Fermat was unable to properly justify his work.however,by examining his techniques,it is obvious that he understood precisely the method used in differentiation today. in order to understand Fermat's mathod,it is first necessary to consider his technique for finding maxima.Fermat's first documented problem in differentiation involved finding the maxima of an equation,and it is clearly this work that led to his technique for finding tangents.找到一个切线的Pierre De Ferma(皮埃尔·德·费马)方法发展于1630,尽管从来没有严格的规定,却几乎是被Newton(牛顿)和Leibniz(莱布尼茨)完全采用的方法。
缺乏一个正式的概念限制,Fermat(费马)无法严格地证明他的工作是正确的。
然而,通过查看他的技术,很显然,他准确地明白今天在微分中使用的方法。
为了理解Fermat(费马)方法,首先要考虑的是他的方法是寻找最大值。
Fermat(费马)第一个记录在微分的问题中涉及找到一个极大等式,很显然这项工作导致了他寻找切线的方法。
第五段翻译(39):the notation of Leibniz most closely resembles that which is used in modern calculus and his approach to discovering the inverse relationship between the integral and differential will be examined.though Newton independently arrived at the same conclusion,his path to discovery is slightly less accessible to the modern reader.Leibniz(莱布尼茨)符号最接近用于现代的微积分,他发现积分和微分之间的逆关系的方法也会被审查。
虽然Newton(牛顿)独立地得出同样的结论,但他的发现途径略少接触到现代读者。
第六段翻译(46):both Torricelli and Barrow considered the problem of motion with variable speed.the derivative of the distance is velocity and the inverse operation takes one from the velocity to the distance.hence an awareness of the inverse of differentiation began to evolve naturally and the idea that integral and derivative were inverses to each other were familiar to Barrow.in fact,although Barrow never explicitly stated the fundamental theorem of the calculus,he was working towards the result and Newton was to continue with this direction and state the Fundamental Theorem of the Calculus explicitly.Torricelli(托里拆利)和Barrow(巴罗)都在考虑变速运动的问题。
距离衍生出速度,逆运算就可以使得速度到距离的一个成为可能。
因此微分的逆的意思开始自然演变,积分和微分是相互的逆的构想对于Barrow(巴罗)很熟悉了。
事实上,虽然Barrow(巴罗)从未明确表示微积分基本定理,他一直在向着这个结果努力,Newton(牛顿)也在继续着这个方向并明确地说明了微积分基本定理。
第七段翻译(48):for Newton integration consisted of finding fluents for a given fluxion so the fact that integration and differentiation were inverses was implied. Leibniz used integration as a sum,in a rather similar way to Cavalieri.he was also happy to use"infinitesimals"dx and dy where Newton used x' and y' which were finite velocities.of course neither Leibniz nor Newton thought in terms of functions,however,but both always thought in terms of graphs.for Newton the calculus was geometrical while Leibniz took it towards analysis.由于Newton(牛顿)积分包括对一个给定的流数找变数,因此这样一个事实即积分和微分是相互的逆就被暗示了。
