现代电力系统分析-往年试卷与复习资料 (6)
电力系统分析试题+答案

一、填空题1.降压变压器高压侧的主分接头电压为220kv ,若选择+2×2.5%的分接头,则该分接头电压为 231KV 。
2.电力系统中性点有效接地方式指的是 中性点直接接地 。
3.输电线路的电气参数包括电抗、电导、电纳和 电阻 。
4.输电线路的电压偏移是指线路始端或末端母线的实际运行电压与线路 额定电压 的数值差。
5.电力系统的潮流分布一般是用各节点的电压和 功率 表示。
6.调整发电机组输出的有功功率用来调整电力系统运行的 频率 。
7.复合故障一般是指某一时刻在电力系统 二个及以上地方 发生故障。
8.用对称分量法计算不对称故障,当三相阻抗完全对称时,则其序阻抗矩阵Zsc 的非对角元素为 零 。
9.系统中发生单相接地短路时故障点短路电流的大小是零序电流的 3 倍。
10.减小输出电元件的电抗将 提高(改善) 系统的静态稳定性。
二、单项选择题在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
11.同步发电机的转速和系统频率之间是否有严格的关系( ② )①否 ②是 ③不一定 ④根据发电机的形式定12.三绕组变压器的结构、通常将高压绕组放在( ③ )①内层 ②中间层 ③外层 ④独立设置13.中性点以消弧线圈接地的电力系统,通常采用的补偿方式是( ③ )①全补偿 ②欠补偿 ③过补偿 ④有时全补偿,有时欠补偿14.三相导线的几何均距越大,则导线的电抗( ① )①越大 ②越小 ③不变 ④无法确定15.变压器的电导参数G T ,主要决定于哪一个实验数据( ① )①△P O ②△P K ③U K % ④I O %16.当功率的有名值为s =P +jQ 时(功率因数角为ϕ)取基准功率为S n ,则有功功率的标么值为( ③ ) ①ϕcos S P n ⋅ ②ϕsin S P n ⋅ ③n S P ④nS cos P ϕ⋅17.环网中功率的自然分布是( ④ )①与电阻成正比分布 ②与电抗成正比分布③与阻抗成正比分布 ④与阻抗成反比分布18.电力系统中PQ 节点的数量( ② )①全都是 ②大量的 ③少量的 ④必有且一般只设一个19.潮流计算中,要求某些节点之间电压的相位差应满足的约束条件是(④ )①|-j i δδ|>|-j i δδ|min ②|-j i δδ|<|-j i δδ|min③|-j i δδ|>|-j i δδ|max ④|-j i δδ|<|-j i δδ|max20.在同一时间内,电力网的电能损耗与供电量之比的百分值称为( ② )①负载率 ②网损率 ③供电率 ④厂用电率21.电力系统的频率主要决定于( ① )①有功功率的平衡 ②无功功率的平衡③电压质量 ④电流的大小22.关于顺调压电压调整方式的描述,错误的是( ② )①高峰负荷时允许中枢点电压略低②低谷负荷时允许中枢点电压略低③适用于用户对电压要求不高的场合④适用于供电线路不长的场合23.通过改变变压器变比,实质上( ③ )①改变了电压损耗的数值 ②改变了负荷变化时次级电压的变化幅度③改变了电力网的无功功率分布 ④增加了整个电力系统的无功功率容量24.三相短路时,非周期分量极小值,只能是在某种情况(① )①一相中出现 ②同时在两相中出现③三相均不出现 ④只有故障相出现其它相不出现25.同步机的各种电抗间关系为(③ )①'x "x x x d d q d >>> ②"x 'x x x d d d q >>>③ "x 'x x x d d q d >>> ④"x x 'x x d q d d >>>26.若ac 两相发生短路,则基准相选择为( ② )①a 相 ②b 相 ③c 相 ④a 相和c27.下网K 点发生两相短路接地,其复合序网为图所示( ③ )(其中,1,2,0分别为正序、负序、零序阻抗)28.越靠近电源点负序电压越( ① )①低 ②高 ③不变 ④无法确定29.作为判据0d dP E >δ主要应用于分析简单系统的( ③ ) ①暂态稳定 ②故障计算 ③静态稳定 ④调压计算30.分析简单系统的暂态稳定性可以应用( ② )①等耗量微增率准则 ②等面积定则 ③小干扰法 ④对称分量法三、简答题31.电力变压器的主要作用是什么?答:电力变压器的主要作用是升高或降低电压,另外还起到将不同电压等级电网相联系的作用。
电力系统分析复习题(附参考答案)

电力系统分析复习题(附参考答案)一、单选题(共58题,每题1分,共58分)1.三绕组变压器的(____)没有分接头。
A、$低压侧$B、$三侧都可以装C、高压侧$D、$中压侧$正确答案:A2.要保证良好的电压质量,(____)必须保持平衡。
A、有功功率$B、$视在功率$C、$无功功率$D、$波形质量正确答案:C3.电网中无功功率的流向是(____)。
A、从电压高的节点流向电压低的节点$B、$从相位滞后相流向相位超前相C、$从相位超前相流向相位滞后相$D、$从电压低的节点流向电压高的节点$正确答案:A4.一般说,在我国,高压电网的电压等级是(____)。
A、$330-1000kVB、$l-35kV之间$C、$35-220kV$D、1kV以下$正确答案:C5.冲击电流主要用于检验电气设备和载流导体的(____)。
A、$动稳定性$B、$载流量$C、$耐压等级D、热稳定性$正确答案:A6.三相导线的几何均距越大,则导线的电抗(____)。
A、$越小$B、$不确定C、$不变$D、越大$正确答案:D7.220kV电力线路的平均额定电压为(____)。
A、$220kV$B、$221kV$C、230kV$D、$242kV正确答案:C8.在变压器的参数计算中,不能用空载试验特性数据求的是(____)。
A、$电导和电纳$B、$电阻和电抗C、电抗和电导$D、$电阻和电纳$正确答案:B9.某110kV线路某点的实际电压为115.5kV,则电压偏移为(____)。
A、4%$B、$5%C、$10%$D、$2.5%$正确答案:B10.发电机的额定电压比所连线路的额定电压高(____)。
A、5%$B、$0%$C、$10%衡$D、$7.5%正确答案:A11.关于电力元件的正序阻抗、负序阻抗和零序阻抗阻抗,下述说法中错误的是(____)。
A、$电抗器正序阻抗、负序阻抗和零序阻抗相等B、$静止元件的正序阻抗、负序阻抗和零序阻抗都不相同$C、静止元件的正序阻抗等于负序阻抗$D、$旋转元件的正序阻抗、负序阻抗和零序阻抗严格讲各不相同$正确答案:B12.在枯水季节,宜选(____)作为主调频电厂。
电力系统分析复习题(包括答案)汇编

电力系统分析复习题2. 综合负荷、供电负荷和发电负荷的区别及关系答:综合用电负荷加上电力网的功率损耗就是各发电厂应该供给的功率,称为电力系统的供电负荷。
供电负荷再加上发电厂厂用电消耗的功率就是各发电厂应该发出的功率,称为电力系统的发电负荷。
2.电压降落、电压损耗、电压偏移的定义有所不同答:网络元件电压降落是指元件首末端两点电压的相量差,即12()V V R jX I -=+;把两点间电压绝对值之差称为电压损耗,用V ∆表示,12V V V ∆=-;电压偏移是指网络中某点的实际电压同网络该处的额定电压之差,可以用KV 表示,也可以用额定电压的百分数表示。
若某点的实际电压为V ,该处的额定电压为N V ,则用百分数表示的电压偏移为电压偏移(%)100N NV V V -=⨯5.输电线路何时作为无功电源、何时作为无功负荷答:35KV 及以下的架空线路的充电功率甚小,一般说,这种线路都是消耗无功功率的;110KV 及以上的架空线路当传输功率较大时,电抗中消耗的无功功率将大于电纳中产生的无功功率,线路成为无功负载,当传输功率较小(小于自然功率)时,电纳中生产的无功功率,除了抵偿电抗中的损耗以外,还有多余,这时线路就成为无功电源。
(0180δ<:无功电源;0180δ>,无功负荷)1.两端供电网络功率分布的计算公式﹝掌握假设的条件和两个功率分量 式11-7﹞答:**121**22112112*****11112222,******22112112()()()()b b a b N a a LD cir b b a a a a a b N a a LD cir b b a a Z Z S Z S V V V S S S Z Z Z Z Z Z Z S Z Z S V V V S S S Z Z Z Z Z Z ⎧++-⎪=+=+⎪++++⎪⎨⎪++-=-=-⎪⎪++++⎩ ① 第一部分由负荷功率和网络参数确定,阻抗共轭值成反比的关系分配②第二部分与负荷无关,它可以在网络中负荷切除的情况下,由两个供电点的电压差和网络参数确定。
(完整word版)《现代电力系统分析》期末复习材料

电力系统潮流计算的目的是什么?电力系统潮流计算是对电力系统正常和故障条件下稳态运行状态的计算。
潮流计算的目标是求取电力系统在给定运行方式下的节点电压和功率分布,用以检查系统各元件是否过负荷、各点电压是否满足要求、功率的分布和分配是否合理以及功率损耗等。
潮流计算既是对电力系统规划设计和运行方式的合理性、可靠性及经济性进行定量分析的依据,又是电力系统静态及暂态稳定计算的基础。
在进行电力系统分析时,控制变量和状态变量含义是什么?如何划分控制变量和状态变量?控制变量是指可通过人为方式进行调节,从而改变电力系统运行状态的量;状态变量是指表征电力系统运行状态的量。
控制变量包括除平衡节点外其他发电机节点的有功功率、各发电机节点的电压幅值及各调压变压器的变比,通常用u 表示;状态变量包括除发电机节点外其他节点的电压幅值以及除平衡节点外其他节点的电压相位,通常用x 表示。
电力系统潮流中有功功率、无功功率的控制是如何实现的?有功功率控制:电力系统负荷的变化会引起电力系统频率的变化,系统中所有并列运行的发电机组都装有调速器,有可调容量的机组的调速器均将反应系统频率的变化,按各自的静态调节特性,及时调节各发电机的出力(通过调节原动机动力元素—蒸汽或水等输入量),改变机组的出力,使有功功率重新达到平衡;同时,还可通过发电机组调速器的转速整定元件来实现有功功率的控制。
无功功率控制:调节发电机的励磁电流可改变发电机发出的无功功率,同时,并联电容、同步调相机和静止补偿器等无功功率补偿设备,也可实现无功功率的调节。
电力系统有功功率与频率是什么关系?互联成网的电力系统在稳定运行方式下具有同一频率,当系统中出现功率不平衡时,如有功功率电源不足或负荷增大时,将会引起系统频率的下降;反之,将造成系统频率过高。
频率过高或过低都会对电力系统造成不良影响,可通过调节发电机组的有功出力及转速整定元件调节系统频率,保证系统频率偏移在规定范围以内。
电力系统分析测试题(含参考答案)

电力系统分析测试题(含参考答案)一、单选题(共137题,每题1分,共137分)1.架空输电线路采用分裂导线的目的是()。
A、改善输电线路的电晕条件。
B、减小线路电抗;C、减小线路电阻;D、增大线路电纳;正确答案:B2.在短路冲击电流的工程计算中,常常需要选定短路冲击系数Kim数值。
当在发电机机端短路时,对发电机而言,其短路冲击系数Kim应取为()。
A、1.95B、1.85C、1.8D、1.9正确答案:D3.单相接地短路时,故障处故障相短路电流与正序分量电流的关系是()。
A、故障相短路电流为正序分量电流的B、故障相短路电流为正序分量电流的3倍;C、故障相电流等于正序分量电流。
正确答案:B4.电力系统的基本技术参数不包括:A、频率B、电流C、电压D、畸变率正确答案:D5.500kv超高压输电线路两端装设并联电抗器的目的是( )。
A、防止输电线路轻载时末端电压降低。
B、防止输电线路重载时末端电压降低;C、防止输电线路轻载时末端电压升高;正确答案:C6.如果某发电厂装有四台机组,正常运行时四台机组都没有达到额定出力,且有、,当发电厂有功负荷增大时,应首先增加出力的发电机组是()。
A、4号机组。
B、2号机组;C、3号机组;D、1号机组;正确答案:D7.在无功电源并不缺乏的电力系统中,关于是否需要增加无功补偿装置,下述说法中正确的是()。
A、绝对不应增加无功补偿装置;B、可以增加无功补偿装置,但应遵守最优网损微增率准则;C、可以增加无功补偿装置,但应遵守等网损微增率准则;D、应增加无功补偿装置,直到各节点的网损微增率均为正值为止。
正确答案:B8.线路始端的额定电压为线路额定电压的().A、105%B、110%C、100%D、95%正确答案:B9.系统中供电可靠性高,同时对系统的绝缘水平要求也高。
A、大电流接地B、不接地C、部分接地D、直接接地正确答案:C10.电力系统潮流计算时,平衡节点的待求量是()。
A、节点电压相角和发电机无功功率。
电力系统分析试题及答案

电力系统分析试题及答案# 电力系统分析试题及答案一、选择题1. 电力系统的主干部分是()。
A. 发电机B. 输电线路C. 变电站D. 负荷答案: B. 输电线路2. 电力系统的频率标准为()Hz。
A. 50B. 60C. 120D. 180答案: A. 503. 电力系统中,短路故障通常发生在()。
A. 发电机内部B. 变电站C. 输电线路D. 负荷端答案: C. 输电线路二、填空题1. 电力系统的稳定性分析通常分为______稳定性和______稳定性。
答案:静态;动态2. 在电力系统中,无功功率的流动主要影响系统的______。
答案:电压水平3. 电力系统的损耗主要包括______损耗和______损耗。
答案:铜损;铁损三、简答题1. 简述电力系统的基本组成及其功能。
答案:电力系统由发电站、变电站、输电线路和配电网组成。
发电站的功能是将其他形式的能量转换为电能;变电站的功能是调整电压,以适应不同电压等级的输电和用电需求;输电线路的功能是将电能从发电站输送到变电站或直接到用户;配电网的功能是将电能分配给最终用户。
2. 什么是电力系统的静态稳定和动态稳定?答案:静态稳定是指在电力系统受到小扰动后,系统能够自动恢复到初始运行状态的能力。
动态稳定则是指在系统受到较大扰动或连续扰动时,系统能够在一定时间内恢复到新的稳定状态的能力。
四、计算题1. 假设一个简单的电力系统,其中包含一个发电机、一个变电站和一个负荷。
发电机的输出功率为100MW,变电站的损耗为5%,负荷的功率需求为95MW。
请计算输电线路的损耗。
答案:首先计算变电站的损耗:100MW * 5% = 5MW。
然后计算到达负荷之前的功率:100MW - 5MW = 95MW。
由于负荷的功率需求正好是95MW,所以输电线路的损耗为0MW。
2. 如果上述系统中,输电线路的电阻为0.5欧姆,线路的电流为200A,计算输电线路的损耗。
答案:根据公式 P_loss = I^2 * R,其中 P_loss 是损耗功率,I 是电流,R 是电阻。
电力系统分析考试试卷

电力系统分析考试试卷一、选择题(每题2分,共20分)1. 电力系统的基本组成包括哪些部分?A. 发电机、变压器、输电线路B. 发电机、变压器、配电设备C. 发电机、变电站、用电设备D. 发电机、变电站、输电线路2. 电力系统中,短路故障通常发生在哪些设备上?A. 发电机B. 变压器C. 输电线路D. 用电设备3. 电力系统中,下列哪种设备不参与电能的转换?A. 发电机B. 变压器C. 电动机D. 断路器4. 电力系统稳态分析主要研究的是哪些方面的性能?A. 系统稳定性B. 系统可靠性C. 系统经济性D. 系统安全性5. 电力系统中,电压等级的划分主要依据是什么?A. 电压大小B. 电流大小C. 功率大小D. 频率大小...(此处省略其他选择题)二、简答题(每题10分,共30分)1. 简述电力系统的基本功能及其重要性。
2. 解释什么是电力系统的负荷预测,并说明其在电力系统规划中的作用。
3. 描述电力系统中的无功功率和有功功率的区别及其在电力系统中的作用。
三、计算题(每题15分,共30分)1. 给定一个简单的电力系统网络,包含一个发电机和两个负载,计算在不同负载条件下的节点电压和线路损耗。
(提供具体的网络参数和负载条件)2. 假设一个电力系统中发生了三相短路故障,请根据给定的系统参数,计算短路电流的大小,并分析其对系统的影响。
四、论述题(20分)1. 论述电力系统自动化技术的发展对提高电力系统运行效率和安全性的作用。
五、案例分析题(20分)1. 给出一个具体的电力系统故障案例,要求分析故障原因,影响范围,并提出相应的预防和应对措施。
试卷结束语:请注意检查答案的准确性,并合理安排答题时间。
祝各位考生考试顺利,取得优异成绩。
现代电力系统分析-往年试卷与复习资料 (6)

一、潮流计算方法之间的区别联系高斯-赛德尔法:原理简单,导纳矩阵对称且高度稀疏,占用内存小。
收敛速度很慢,迭代次数随节点数直接上升,计算量急剧增加,不适用大规模系统。
牛顿-拉夫逊法:收敛速度快,迭代次数和网络规模基本无关。
相对高斯-赛德尔法,内存量和每次迭代所需时间较多,其可靠的收敛还取决于一个良好的启动初值。
PQ 分解法(快速解耦法):PQ 分解法实际上是在极坐标形式的牛顿法的基础上,在交流高压电网中,输电线路等元件的R<<X ,即有功功率主要取决于电压相角,而无功功率主要取决于电压幅值,根据这种特性对方程组进行简化,从而实现了有功和无功的解耦。
两大条件:(1)线路两端的相角相差不大(小于10°~20°),而且||||ij ij G B ≤,于是可以认为:cos 1;sin ij ij ij ij G B θθ≈≤; (2)与节点无功功率相对应的导纳2/i i Q U 通常远小于节点的自导纳ii B ,也即2i i ii Q U B <<。
1. PQ 分解法用一个1n -阶和一个1n m --阶的方程组代替牛顿法中22n m --阶方程组,显著减少了内存需量和计算量。
2. 计算过程中B '、B ''保持不变,不同于牛顿法每次迭代都要重新形成雅可比矩阵,因此显著提高了计算速度。
3.雅可比矩阵J 不对称,而B '、B ''都是对称的,使求逆等运算量和所需的存储容量都大为减少。
4. PQ 分解法的迭代次数要比牛顿法多,但是每次迭代所需时间比牛顿法少,所以总的计算速度仍是PQ 分解法快。
在低压配电网中PQ 分解法不适用。
交流高压电网的输电线路的元件满足R<<X ,PQ 分解法正是基于此条件简化而来;而低电压配电网络一般R/X 比值很大,大R/X 比值病态问题也正是PQ 分解法应用中的一个最大障碍。
《电力系统分析》(高起专)复习 学习材料 试题与参考答案

复习学习材料试题与参考答案《电力系统分析》(高起专) 一、单选题1.变压器电抗计算式:应取的单位是(A)A.kVA和kV;B.kW和kV;C.MW和kV;D.MVA和kV2.同步调相机可以向系统中(D)A.发出感性无功B.吸收感性无功C.只能发出感性无功D.既可发出也可吸收感性无功3.系统振荡时,应迅速减小原动机功率,并且要(B)。
A.减小励磁电流;B.增大励磁电流;C.保持励磁电流不变;D.断开励磁电流4.频率的一次调整是(A)A.由发电机组的调速系统完成的B.由发电机组的调频系统完成的C.由负荷的频率特性完成的D.由无功补偿设备完成的5.凸极同步发电机a、b、c坐标下的磁链方程中,电感系数为常数的有(C)。
A.定子各相绕组自感系数B.定子各相绕组互感系数C.转子各绕组互感系数6.既可以提高系统静态稳定性,又可以提高系统暂态稳定性的措施是(D)A.快速切除故障B.重合闸C.增大原动机功率PTD.增大发电机励磁7.采用分裂导线的目的是(A )A.减小电抗B.增大电抗C.减小电纳D.增大电阻8.自动调节励磁装置可以(A),因而可以提高系统的稳定性A.提高发电机电势B.稳定发电机电势C.降低发电机电势D.减少原动机功率PT9.若变压器绕组接法形式为,则在零序等值电路中,变压器的原边相当于(A )。
A.断路B.短路C.通路10.可通过(C)减小输电线路有功损耗A.增大线路有功功率B.增大线路无功功率C.提高线路两端电压D.增大输电线路电阻11.当其发生三相短路瞬间,定子绕阻中的电流除有基频分量,还有(A)。
A.直流分量B.倍频分量C.直流分量和倍频分12.额定电压等级为110kV系统的平均额定电压是(B)A.112kVB.115kVC.142kVD.121kV13.频率的一次调整是( A)A.由发电机组的调速系统完成的B.由发电机组的调频系统完成的C.由负荷的频率特性完成的D.由无功补偿设备完成的14.隐极同步发电机,机端发生三相短路瞬间,定子绕阻中的电流除有基频分量,还有(C)A.直流分量B.倍频分量C.直流分量和倍频分量D.零序分量15.电力系统中用户用电设备消耗功率总和称为(B)A.发电负荷B.用电负荷C.供电负荷D.备用负荷16.同步调相机可以向系统中(D)A.发出感性无功B.吸收感性无功C.只能发出感性无功D.既可发出也可吸收感性无功17.消弧线圈采用全补偿,当系统发生单相接地时,可能会使系统(A)A.产生谐振B.失去稳定C.保护误动D.接地电流增加18.可通过(C)减小输电线路有功损耗A.增大线路有功功率B.增大线路无功功率C.提高线路两端电压D.增大输电线路电阻19.下列选项中,(C)属于与频率无关的负荷。
《电力系统分析》复习题及答案

《电力系统分析》复习题1一、填空题1、电力网络主要由电力线路和( 变压器或变、配电装置或变电所 )组成。
2、电能生产最基本首要的要求是( 保证安全可靠持续供电 )。
3、连接额定电压分别为220kV 和35kV 两个电力网的一台降压变压器,变压器的两侧均接线路,则此变压器的变比为( 220/38.5或5.7 )。
4、在我国110kV 以上电力系统的中性点运行方式一般为(直接接地)。
5、电压降落指元件两端电压的(相量差)。
6、在电磁环网中,由于变压器变比不匹配而产生的功率称为(循环功率;)。
7、电力系统频率的一次调整,通过调节发电机组上的(调速器)完成。
8、双绕组变压器的分接头在( 高压绕组 )侧。
9、短路冲击电流指的是(短路电流最大可能的瞬时值)。
10、经过派克变换后同步发电机等效的dd 、qq 绕组之间的互感为(0)。
二、单项选择题1、电导是反映电流流经导线而产生的__D__的参数。
A 热效应;B 磁场效应;C 电场效应;D 电晕和漏磁损耗 2、100km 的架空线属于___B____。
A 长线;B 短线;C 中等长度线;D 都不对3、长线路、重负荷的中枢点采用的调压方式是____B_____。
A 顺调压 B 逆调压 C 常调压4、潮流方程是由____B_____推导得来的。
A 回路电流方程;B 节点电压方程;C 支路电压方程;D 割集方程 5、P-V 节点是_______B_____的节点。
A 节点的有功功率和电压未知;B 节压已知;C 节点的电压和相角未知;D 节点的电压和相角已知6、高压电网中,电能传输时产生的电压损耗主要是____D______引起的。
A 有功电流流过电阻;B 有功电流流过电抗;C 无功电流流过电阻;D 无功电流流过电抗7、短路后没有零序电流的不对称短路是___B______。
A 单相短路;B 两相短路;C 三相短路;D 两相短路接地8、电力系统进行潮流的调整和控制措施,错误的是____D_____。
电力系统分析试卷及答案完整版

电力系统分析试卷及答案HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】电力系统分析练习题一、简答题1、电力线路的正序电抗与零序电抗是否相等?2、在220kV及以上的超高压架空线路上,普遍采用分裂导线,采用分裂导线后,线路电感、线路并联电容会增大还是变小?3、动力系统、电力系统和电力网的基本构成形式如何?4、电力变压器的主要作用是什么?5、采用标么值计算有什么优点?6、对电力系统运行的要求是什么?7、试画出单相变压器等值电路。
8、试画出电力线路等值电路。
二、如图所示的电力系统1.确定发电机G,变压器T-1、T-2、T-3,线路L-1、L-2、L-3及电容器Y c的额定电压;2.给出其稳态分析时的等值电路;3.输电线路L-3阻抗为5+j20Ω(忽略并联支路),末端有功功率为10MW,功率因数为0.80(感性),末端电压为35kV,计算线路L-3的功率损耗和电压损耗;4.条件同3,但功率因数提高到0.90(感性),请问线路L-3的功率损耗和电压损耗会增加还是减少三、电力系统接线如下图所示,电网各级电压示于图中,求1)发电机和各变压器高低压侧额定电压;2)设T-1 高压侧工作于+2.5%抽头,T-2工作于主抽头,T-3高压侧工作于-5%抽头,求各变压器实际变比。
四93kW,短路电压耗、G、B。
五、一容量比为90/90/60兆伏安,额定电压为220/38.5/11千伏的三绕组变压器。
工厂给出试验数据为:ΔP s’(1-2)=560千瓦,ΔP s’(2-3)=178千瓦,ΔP s’(3-1)=363千瓦,V S(1-2)%=13.15, VS(2-3)%=5.7, VS(3-1)%=20.4,ΔP=187千瓦,I0 %=0.856。
试求归算到220千伏侧的变压器参数。
(注:功率值未归算,电压值已归算)六、已知某一变压器参数如表1所示。
表1变压器绕组电阻、漏抗、励磁支路电导和励磁支路电纳的计算公式分别为:1、试计算变压器绕组电阻、漏抗的有名值;2、设S B=100MVA ,110kV 级为基本级,U B=121kV ,试计算变压器绕组电阻、漏抗的标幺值。
《电力系统分析》复习题及答案

《电⼒系统分析》复习题及答案《电⼒系统分析》复习题1⼀、填空题1、电⼒⽹络主要由电⼒线路和(变压器或变、配电装置或变电所)组成。
2、电能⽣产最基本⾸要的要求是( 保证安全可靠持续供电 )。
3、连接额定电压分别为220kV 和35kV 两个电⼒⽹的⼀台降压变压器,变压器的两侧均接线路,则此变压器的变⽐为(220/38.5或5.7 )。
4、在我国110kV 以上电⼒系统的中性点运⾏⽅式⼀般为(直接接地)。
5、电压降落指元件两端电压的(相量差)。
6、在电磁环⽹中,由于变压器变⽐不匹配⽽产⽣的功率称为(循环功率;)。
7、电⼒系统频率的⼀次调整,通过调节发电机组上的(调速器)完成。
8、双绕组变压器的分接头在(⾼压绕组)侧。
9、短路冲击电流指的是(短路电流最⼤可能的瞬时值)。
10、经过派克变换后同步发电机等效的dd 、qq 绕组之间的互感为(0)。
⼆、单项选择题1、电导是反映电流流经导线⽽产⽣的__D__的参数。
A 热效应;B 磁场效应;C 电场效应;D 电晕和漏磁损耗 2、100km 的架空线属于___B____。
A 长线;B 短线;C 中等长度线;D 都不对3、长线路、重负荷的中枢点采⽤的调压⽅式是____B_____。
A 顺调压 B 逆调压 C 常调压4、潮流⽅程是由____B_____推导得来的。
A 回路电流⽅程;B 节点电压⽅程;C ⽀路电压⽅程;D 割集⽅程 5、P-V 节点是_______B_____的节点。
A 节点的有功功率和电压未知;B 节压已知;C 节点的电压和相⾓未知;D 节点的电压和相⾓已知B 有功电流流过电抗;C ⽆功电流流过电阻;D ⽆功电流流过电抗7、短路后没有零序电流的不对称短路是___B______。
A 单相短路;B 两相短路;C 三相短路;D 两相短路接地8、电⼒系统进⾏潮流的调整和控制措施,错误的是____D_____。
A 串联电感 B 串联电容 C 附加串联加压器 D 并联电感三、简答题1、试写出发⽣A 、C 两相短路故障,故障处的相量边界条件和序分量边界条件?答:相边界条件=+==00fc fa fb fc fa I I I U U序边界条件=+==00)2()1()0()2()1(fb fb fb fb fb I I I U U2、电⼒⽹络接线如图所⽰,画出零序⽹络。
电力系统分析考试题含参考答案

电力系统分析考试题含参考答案一、选择题(每题5分,共25分)1. 电力系统中,描述电压、电流随时间变化的函数称为()。
A. 电压函数B. 电流函数C. 电压电流函数D. 微分方程答案:C2. 在电力系统中,为了提高系统的稳定性,通常采用()。
A. 增大输电线路的电阻B. 增大发电机的电抗C. 提高系统的电压等级D. 增加系统的负载答案:C3. 电力系统中的无功功率主要由()产生。
A. 同步电机B. 感应电机C. 变压器D. 电容器答案:A4. 在电力系统分析中,常用的潮流计算方法有()。
A. 高斯消元法B. 牛顿-拉夫森法C. 矩阵求逆法D. 以上都是答案:D5. 电力系统短路计算的主要目的是()。
A. 确定系统的稳定性B. 确定系统的电压等级C. 校验设备的承受能力D. 确定系统的无功需求答案:C二、填空题(每题5分,共25分)6. 电力系统中,描述电压、电流随时间变化的函数称为_________。
答案:电压电流函数7. 电力系统的稳定性主要取决于系统的_________和_________。
答案:电压等级、无功功率8. 在电力系统中,常用的潮流计算方法有_________、_________和_________。
答案:高斯消元法、牛顿-拉夫森法、矩阵求逆法9. 电力系统短路计算的主要目的是_________。
答案:校验设备的承受能力三、简答题(每题10分,共30分)10. 请简述电力系统分析的主要任务。
答案:电力系统分析的主要任务包括潮流计算、短路计算、稳定性分析、无功优化等。
潮流计算是为了确定电力系统中各节点的电压和功率分布;短路计算是为了校验系统在发生短路时设备的承受能力;稳定性分析是为了保证电力系统在运行过程中具有良好的稳定性;无功优化是为了在满足系统稳定性的前提下,经济地配置无功功率资源,提高系统的电压水平。
11. 请简述电力系统中的有功功率和无功功率的作用。
答案:有功功率主要用于完成电力系统的功率传输,满足用户的电力需求;无功功率主要用于维持电力系统的电压水平,提高系统的稳定性。
电力系统分析复习资料

一、单选题(共20题,40分)1、输电线路单位长度的电阻主要决定于(2.0)A、材料和对地高度B、电晕损耗和电压C、几何均距和半径D、材料和粗细正确答案: D2、n节点电力系统中,已知PQ节点的数目为N-1,则PV节点数目为( )。
(2.0)A、 1B、 2C、 0D、无法确定正确答案: C3、如果高压输电线路首末端电压之间的关系为,在忽略线路电阻影响的情况下,下述说法中正确的是( )。
(2.0)A、有功功率从首端流向末端无功功率从末端流向首端B、有功功率和无功功率都是从首端流向末端C、无功动率从首端流向未端有功功率从首端流向末端D、有功功率和无功功率都从末端流向首端正确答案: A4、电力系统的综合用电负荷加上网络中的供电损耗称为(2.0)A、供电负荷B、发电负荷C、工业负荷D、厂用电负荷正确答案: A5、在电力系统受到大扰动后的暂态过程中,发电机组的调节系统已发挥作用的阶段是( )。
(2.0)A、起始阶段B、初始阶段C、中间阶段D、起始阶段和中间阶段正确答案: C6、在接线变压器三角形侧两相短路时,关于变压器星形侧三相线路中的电流,下述说法中正确的是( )。
(2.0)A、变压器星形侧三相线路中都有电流流过,其中故障相中的滞后相电流为其它两相的两倍B、变压器星形侧三相线路中都有电流流过,其中故障相中的超前相电流为其它两相的两倍C、变压器星形侧三相线路中只有故障相有电流流过D、变压器星形侧三相线路中都有电流流过,其中非故障相中电流为故障相电流的两倍。
正确答案: A7、常规电网潮流计算时,( )是对称矩阵。
(2.0)A、混合参数矩阵B、节点支路关联矩阵C、雅克比矩阵D、节点导纳矩阵正确答案: D8、冲击电流主要用来校验设备(2.0)A、是否超过额定电流B、是否超过发热允许电流C、电动力稳定度D、超过经济电流正确答案: C9、构成电力网的主要设备有(2.0)A、变压器,用户B、变压器,电力线路C、电缆,架空线D、电阻,电容正确答案: B10、联合电力系统的接线图及参数如下,联络线的功率传输限制为300MW,频率偏移超出才进行二次调频,当子系统A出现功率缺额200MW时,如系统A不参加一次调频,则联络(2.0)A、 B系统向A系统输送181MW有功功率,联络线功率没有越限B、 A系统向B系统输送181MW有功功率,联络线功率没有越限C、 B系统向A系统输送281MW有功功率,联络线功率没有越限D、 B系统向A系统输送81MW有功功率,联络线功率没有越限。
电力系统分析基础试卷及复习资料
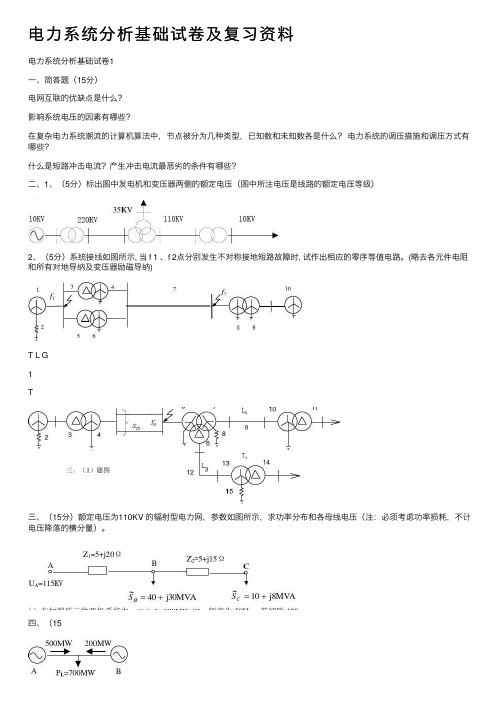
电⼒系统分析基础试卷及复习资料电⼒系统分析基础试卷1⼀、简答题(15分)电⽹互联的优缺点是什么?影响系统电压的因素有哪些?在复杂电⼒系统潮流的计算机算法中,节点被分为⼏种类型,已知数和未知数各是什么?电⼒系统的调压措施和调压⽅式有哪些?什么是短路冲击电流?产⽣冲击电流最恶劣的条件有哪些?⼆、1、(5分)标出图中发电机和变压器两侧的额定电压(图中所注电压是线路的额定电压等级)2、(5分)系统接线如图所⽰, 当 f 1 、f 2点分别发⽣不对称接地短路故障时, 试作出相应的零序等值电路。
(略去各元件电阻和所有对地导纳及变压器励磁导纳)T L G1T三、(15分)额定电压为110KV 的辐射型电⼒⽹,参数如图所⽰,求功率分布和各母线电压(注:必须考虑功率损耗,不计电压降落的横分量)。
四、(15P GN =500MW σ%=4 P GN =450MW σ%=5 负荷的单位调节功率K L*=1.5负荷后,系统的频率和发电机的出⼒各为多少?五、(15分)设由电站1向⽤户2供电线路如图,为了使⽤户2能维持额定电压运⾏,问在⽤户处应装电容器的容量是多少?(忽略电压降落的横分量影响)六、(15(注:图中参数为归算到统⼀基准值下的标么值SB=100MV A,UB=Uav)故障点A相各序电流和电压的有名值、A相各序电流向量图。
中性点电位Un是多少KV?Xn是否流过正、负序电流?Xn的⼤⼩是否对正、负序电流有影响?七、(15分)电⼒系统接线如图所⽰,元件参数标于图中,当f点发⽣三相短路时,若要使短路后的短路功率Sf不⼤于250MV A,试求(SB=100MV A,UB= Uav)线路允许的电抗有名值XL?发电机G1、G2的计算电抗?⼀、简答题(25分)电⼒系统为什么不采⽤⼀个统⼀的电压等级,⽽要设置多级电压?什么是电压损耗、电压降落、电压偏移?电⼒系统采⽤分裂导线有何作⽤?简要解释基本原理。
在复杂电⼒系统潮流的计算机算法中,节点被分为⼏种类型,已知数和未知数各是什么?什么是电⼒系统短路故障?故障的类型有哪些?⼆、(15分)在如图所⽰的两机系统中,PGN1=450MW,σ1%=5;PGN2=500MW,σ2%=4。
电力系统分析题库与答案

电力系统分析题库与答案一、单选题(共137题,每题1分,共137分)1.在抑制电力系统大区域之间的低频振荡时,发电机可以通过投入()来参与系统的振荡,提高系统的阻尼水平。
A、AGCB、AVRC、ALFCD、PSS正确答案:D2.关于电力系统的电压调整,下述说法中正确的是( B )。
A、只要保证电力系统在所要求的电压水平下的无功功率平衡,就可以将电力系统中所有用电设备的电压限制在允许的范围;B、要维持电力系统用电设备的电压在允许的范围,首要的条件是要满足在所要求的电压水平下的电力系统的无功率平衡;C、在任何情况下都可以通过改变变压器变比,将电力系统中所有用电设备的电压限制在允许范围;D、当无功负荷变化时,不必改变系统无功电源的总出力,只要调整电力系统的无功潮流分布总可以将电力系统用电设备的电压控制在允许范围。
正确答案:B3.现代电网的特点叙述错误的是( )A、具有足够的调峰、调频、调压容量B、有高度自动化的监控系统C、由超高压系统构成主网架D、各电网之间联系较弱正确答案:D4.电网潮流计算中,功率分点总是网络中()电压点。
A、任意B、最低C、发电机D、最高正确答案:B5.下面所列各组电力网接线方式中,完全属于有备用接线的一组是()。
A、双回线路辐射网、环网、单回路链式网B、两端供电网、环网、双回线路辐射网C、单回路辐射网、两端供电网、单回路干线网正确答案:B6.无限大电源供电情况下突然发生三相短路时,各相短路电流中非周期分量的关系是()。
A、不相等。
B、三相可能相等,也可能不相等;C、三相相等;正确答案:A7.电力系统中不可以作为无功功率电源的设备有:A、断路器B、调相机C、静止补偿器D、发电机8.电力系统发生振荡时,各点电压和电流()A、均作往复性摆动B、均会发生突变C、在振荡的频率高时会发生突变D、保持不变正确答案:A9.中性点直接接地的系统发生单相接地时,接地点非故障相对地电压( )。
A、等于0B、不变C、增大2倍D、增大1.732倍正确答案:B10.电力系统中无功功率电源的最优分布是按照()确定的。
电力系统分析复习题(包括答案)

电力系统分析复习题9-11.综合负荷的定义答:系统中所有电力用户的用电设备所消耗的电功率总和就是电力系统的负荷,亦称电力系统的综合用电负荷。
它是把不同地区、不同性质的所有的用户的负荷总加起来而得到的。
2. 综合负荷、供电负荷和发电负荷的区别及关系答:综合用电负荷加上电力网的功率损耗就是各发电厂应该供给的功率,称为电力系统的供电负荷。
供电负荷再加上发电厂厂用电消耗的功率就是各发电厂应该发出的功率,称为电力系统的发电负荷。
9-21.负荷曲线的定义答:反映一段时间内负荷随时间而变化的规律用负荷曲线来描述2.日负荷曲线和年负荷曲线的慨念答:负荷曲线按时间长短分,分为日负荷曲线和年负荷曲线。
日负荷曲线描述了一天24小时负荷的变化情况;年负荷曲线描述了一年内负荷变化的情况。
3.日负荷曲线中最大负荷、最小负荷、平均负荷、负荷率、最小负荷系数的慨念 答:负荷曲线中的最大值称为日最大负荷max P (又称峰荷),最小值称为日最小负荷min P (又称谷荷);平均负荷是指某一时期(日,月,年)内的负荷功率的平均值,24024d av W P Pdt =⎰;负荷率m k 是日平均负荷av P 与日最大负荷max P 之比,即maxav m P k P =;最小负荷系数α是日最小负荷min P 跟日最大负荷max P 之比,即min maxP P α=。
4.日负荷曲线的作用答:日负荷曲线对电力系统的运行非常重要,它是安排日发电计划和确定系统运行方式的重要依据。
5.年最大负荷曲线的定义和作用答:年最大负荷曲线描述一年内每月(或每日)最大有功功率负荷变化的情况,它主要用来安排发电设备的检修计划,同时也为制订发电机组或发电厂的扩建或新建计划提供依据。
6.年持续负荷曲线的定义、最大负荷利用时数的慨念、年持续负荷曲线的用途答:年持续负荷曲线是按一年中系统负荷的数值大小及其持续小时数顺序排列而绘制成,作用是安排发电计划和进行可靠性估算。
电力系统分析题库(附答案)

电力系统分析题库(附答案)一、单选题(共56题,每题1分,共56分)1.某线路首端电压10.5kV,末端电压10.2kV,首端电压偏移百分数为(____)。
A、0.0294B、0.0286C、0.03D、0.05正确答案:D2.采用分裂导线可以实现(____)。
A、增大电阻B、增大电抗C、减小电抗D、减小电纳正确答案:C3.输电线路等效电路中消耗无功功率的是电抗和(____)。
A、电流B、电阻C、电导D、电纳正确答案:D4.500kV系统中性点运行方式经常采用(____)。
A、直接接地B、不接地C、经电抗接地D、经电阻接地正确答案:A5.以高压甚至超高压将发电厂、变电所或变电所之间连接起来的送电网络称为(____)。
A、发电网B、输电网C、配电网D、以上都对正确答案:B6.事故备用一般约为最大负荷的(____),但不得小于系统中最大机组容量。
A、5%-7%;B、2%-5%;C、5%-10%D、4%-5%;正确答案:C7.下面能够提高三相短路情况下电力系统并列运行暂态稳定性的一组措施是(____)。
A、快速切除故障、变压器中性点经小电阻接地、发电机装设强励装置B、快速切除故障、快速关闭汽轮发电机气门、线路装设重合闸C、快速切除故障、快速关闭汽轮发电机气门、变压器中性点经小电阻接地D、快速切除故障、线路装设重合闸、变压器中性点经小电阻接地正确答案:B8.(____)电网采用中性点直接接地方式A、35kV及以下B、35kV及以上C、110kV及以下D、110kV及以上正确答案:D9.一般线路的平均额定电压比线路的额定电压高(____)。
A、0.075B、0.05C、0D、0.1正确答案:B10.关于短路故障时正序电压、负序电压和零序电压的分布,下述说法中正确的是(____)。
A、故障处正序电压、负序电压和零序电压均最高B、发电机机端正序电压、负序电压、零序电压均为最高C、发电机机端正序电压最高、短路点负序电压和零序电压最高D、发电机中性点负序电压和零序电压最高.正序电压最低正确答案:C11.中性点不直接接地系统发生单相接地时,可继续运行最多不超过(____)。
电力系统分析复习资料

电力系统分析复习资料一、填空题1.依据一次能源的不同,发电厂可分为火力发电厂、水力发电厂、 、风力发电厂等。
2.采用分裂导线的目的是 。
3.电力系统中一级负荷、二级负荷和三级负荷的划分依据是用户对供电 要求。
4.潮流计算中的电压数值约束条件是由 决定的。
5.发电机定子三相短路时为维持定了绕组的磁链守恒的定子绕组产生 分量电流。
6.从发电厂电源侧的电源功率中减去变压器的功率损耗,得到的直接连接在发电厂负荷测母线上的电源功率称为 。
7.电力系统零序等值电路与正序等值电路 。
8.短路电流最大可能的瞬时值称为 。
9.简单系统静态稳定依据为 。
10.减少原动机出力将 系统的暂态稳定性。
二、单项选择题11.在有名单位制中,功率的表达式为( )①S =1.723×V ×I ②S =V ×I ③S =3×V ×I ④S =VICOS φ12.电力系统的中性点是指( )①变压器的中性点 ②星形接线变压器的中性点③发电机的中性点 ④②和③13.我国电力系统的额定电压等级为( )①3、6、10、35、110、220(KV ) ②3、6、10、35、66、110、220(KV ) ③3、6、10、110、220、330(KV ) ④3、6、10、35、60、110、220、330、500(KV )14.有备用电源接线方式的优缺点是( )①可靠性高、电压高②可靠性高、造价高③供电可靠性和电压质量高、造价高、调度复杂④供电可靠性高、调度方便、造价15.电能质量是指( )①电压的大小 ②电压的大小和波形质量③电压大小,电流大小 ④电压大小,波形质量,频率16.牛顿一拉夫逊迭代的主要优点是( )①简单 ②收敛快 ③准确 ④占用内存小17.无限大功率供电系统,发生三相短路,短路电流非周期分量起始值( ) ①cp bp ap i i i == ②cp bp ap i i i ≠≠③cp bp ap i i i ≠= ④cp bp ap i i i =≠18.短路电流量大的短路为( )①单相短路 ②两相短路 ③两相短路接地 ④三相短路19.理想同发电机,q 轴电抗的大小顺序是( )①xq=xq ″ ②xq >xq ″ ③xq <xq ″ ④都不对20.通常逆调压的调压范围是(基准为U N)()①0~5% ②2.5~%7.5% ③5%~10% ④0~10%21.仅改变变压器变化调压的是()①典型的顺调压②典型的逆调压③典型的常调压④均不对22.a为旋转因子a+a2等于多少()①0 ②1 ③-1 ④223.输电线路的正序阻抗与负序阻抗相比,其值要()①大②小③相等④都不是24.系统中发生单接地故障时,零序回路中不包含()①零序电流②零序电压③零序阻抗④电源电势25.单相短路中,附加阻抗Z△为()①Z0Σ②Z2Σ③Z0Σ+ Z2Σ④Z0Σ∥Z2Σ26.在发电机稳态运行状态中,机械功率P T与电磁功率相比,将()①大②小③相等④无关系27.P-δ曲线被称为()①耗量特性曲线②负荷曲线③正弦电压曲线④功角曲线28.等面积定则主要用于分析简单系统的()①潮流计算②故障计算③调压计算④暂态稳定分析29.系统备用容量中,哪种可能不需要()①负荷备用②国民经济备用③事故备用④检修备用30.单相短路的序分量电流边界条件是()①i1+i2+i0=0 ②i1=i2=i0 ③i1+i2=0 ④i1=i2三、简答题31.列出三种提高系统静态稳定的措施?32.解释采用减少原动机输出功率的方法能够改善系统的暂态稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
消去节点 k 之前, jk 个节点间原有的支路数为
则
k
消除后所增加的新支路数为(即注入元个数为 dk
) bk
1 2
jk .(
jk
1) dk
动态优化法:(1)按上式分别统计消去网络各节点时增加的出线数,选其中出 线数最少的被消节点编为 1 号节点,消
去节点 1 。
(2)修改其余节点的出线数目,然后对余下节点重复出节点 2,3,、、、,直到所有节点编完为止。
一、潮流计算方法之间的区别联系 高斯-赛德尔法:原理简单,导纳矩阵对称且高度稀疏,占用内存小。 收敛速度很慢,迭代次数随节点数直接上升,计算量急剧增加,不适用大规模系统。 牛顿-拉夫逊法:收敛速度快,迭代次数和网络规模基本无关。 相对高斯-赛德尔法,内存量和每次迭代所需时间较多,其可靠的收敛还取决于一个良好的启动初值。 PQ 分解法(快速解耦法): PQ 分解法实际上是在极坐标形式的牛顿法的基础上,在交流高压电网中,输电线路等元件的 R<<X,即有功功率主要 取决于电压相角,而无功功率主要取决于电压幅值,根据这种特性对方程组进行简化,从而实现了有功和无功的解耦。
1.静态优化法:按静态节点支路数的多少编号。 统计电力网络节点的出线支路数,然后按出线支路数从少到多的顺序编号,当有 m 个节点的出线数相同时,则可按任 意次序对此 m 个节点进行编号。
其依据是:在 Y 阵中,出线数最少的节点所对应的行中非零元素也最少,因此在消去过程中产生注入元的可能性 也最小。
2.半动态优化法: 动态地按最少出线支路数编号。 静态优化法中,各节点的出线数是按原始网 络统计 出来的,在编号过程中认为固定不变。而事实上在节点消去
(1)利用常规牛顿潮流算法每次迭代所求出的修正向量 x(k) (J(x(k) )1 f(x(k) ) 作为搜索方向,并称之为目标函数在
x(k)处的牛顿方向。 (2)最优步长因子的确定方法:
采用直角坐标的潮流方程的泰勒展开式可以精确的表示为 f(x) ys y(x) ys y(x(0) ) J(x(0) ) x y(x)
上式中 Jc 为常数对称阵,故只需在迭代求解前进行一次三角因子分解即可。
本算法的计算速度较岩本伸一提出的保留非线性算法快近 40-50%,与 PQ 分解法相当。但在具有大 R/X 比值的系统 以及具有串联电容支路的系统中,本算法比 PQ 分解法具有更可靠的收敛性。
三、最小化潮流算法(带最优乘子的牛顿潮流算法)原理 将潮流问题转化为求使标量函数 F(x)为最小值时的 x 的值问题。根据数学规划方法可有如下:
x1x
ys 在初值 x0 附近展开成没有截断误差的式子: ys y
x0
J
x
1
H
x2x
2
xn
x
其中: x x x(0) x1, x2, , xn T 为修正量向量。
对上式的第三项进行研究表明,可以写成: ys y x0 J x y x
过程中,每消去一个节点以后,与该节点相联的各节点的出线支路数将发生变化(增加、减少或维持不变)
因此,如果在每消去一个节点后,立即修正尚未编号的出线支路数,然后选其中出线支路数最少的节点编号,就
可以预期达到更好的效果。
所谓半动态优化法就是出线支路数的统计考虑了节点消去后的变动。
3.动态优化法:按动态增加支路数最少编号。 用以上两种方法编号,只能使消去过程中出现新支路的可能性减少,但并不一定保证在消去这些节点时出现的新
则是相对于始终不变的初始值 x(0)的修正量;
4.保留非线性快速朝流算法达到收敛所需的迭代次数要比牛顿法多,但由于每次迭代所需计算量比牛顿法省很多,所以
总的计算速度比牛顿法可提高很多;
5.由于不具对称性的雅可比矩阵三角分解后,其上下三角元素都需要保存,而牛顿法只需要保存上三角元素,因此,此 算法的矩阵存储量要比牛顿法增加 35%—40%; 6.由于采用恒定雅克比进行迭代,因此初始值的选择对保留非线性快速潮流法的收敛性有很大影响。
(5)判断 F(x(k+1)) <ε 是否成立。若成立,x(k+1)为所求的解。否则,令 k=k+1,转(3),重复循环计算,到满足为止。 关键的两个问题:
(1)如何确定第 k 次迭代的寻优方向 x(k) ; (2)如何确定第 k 次迭代的步长因子 (k) 。
带有最优乘子的牛顿潮流算法:即数学规划与牛顿法结合
Ps:直角坐标形式包括二阶项的快速潮流算法(Nagendra Rao) 首先假定系统中除一个平衡节点外,其余均为 PQ 节点。 特点:1.为了简化计算,先对导纳矩阵的对角元进行改造,即令各节点的对地并联支路作为恒定阻抗负荷处理,而不包 含在导纳矩阵之中; 2.所有节点的电压初值都取为平衡节点的电压。
算量。
2. 计算过程中 B 、 B 保持不变,不同于牛顿法每次迭代都要重新形成雅可比矩阵,因此显著提高了计算速度。 3.雅可比矩阵 J 不对称,而 B 、 B 都是对称的,使求逆等运算量和所需的存储容量都大为减少。
4. PQ 分解法的迭代次数要比牛顿法多,但是每次迭代所需时间比牛顿法少,所以总的计算速度仍是 PQ 分解法快。 在低压配电网中 PQ 分解法不适用。交流高压电网的输电线路的元件满足 R<<X,PQ 分解法正是基于此条件简化而来; 而低电压配电网络一般 R/X 比值很大,大 R/X 比值病态问题也正是 PQ 分解法应用中的一个最大障碍。
B
e
此时修正方程中的雅可比矩阵已经是由导纳阵元素组成的常数对称矩阵。
对二阶项进行处理可得
RP RQ
es es
J
d
RU 2es
Jc
f
ePQ
令上式左边为
RP' RQ'
,从而
f ePQ
J
1 c
RP' RQ'
3
② 给控制变量以初值 u(0) ,令迭代计数 k 0 ;
③ 将 u(k) 代入潮流方程(即式(3)),求得状态变量 x(k) ,同时也获得雅可比矩阵 J g x
两大条件:(1)线路两端的相角相差不大(小于 10°~20°),而且| Gij || Bij | ,于是可以认为:cosij 1;Gij sinij Bij ;
(2)与节点无功功率相对应的导纳 Qi / Ui2 通常远小于节点的自导纳 Bii ,也即 Qi Ui2Bii 。 1. PQ 分解法用一个 n 1阶和一个 n m 1阶的方程组代替牛顿法中 2n m 2 阶方程组,显著减少了内存需量和计
引入一个标量乘子 μ 以调节变量 x 的修正步长,上式可以写为:
f(x) ys y(x(0) ) J(x(0) ) ( x) y( x) 0
ys y(x(0) ) J(x(0) ) (x) 2 y(x) 0
在此 f(x) [f1(x), f2 (x),..., fn (x)]T a [a1, a2, ..., an ]T ys y(x(0) )
令: b [b1, b2,...bn ]T J x c [c1, c2,..., cn ]T y(x)
于是上式写为: f(x) a b 2 c 0
n
n
所以目标函数可以写为: F(x) fi2 (x) (ai bi 2 ci )2 ()
二、保留非线性快速潮流算法原理,与牛顿法比较? 保留非线性快速潮流算法(Iwamoto-Tamura)原理:普通牛顿法求解非线性方程时采用了逐次线性化的方法,忽略了 泰勒级数的高阶项或非线性项,而保留非线性快速朝流算法考虑了泰勒级数的二阶项,也称二阶潮流算法。
潮流方程组可写成矩阵形式: f (x) y x ys 0
i 1
i1
F(x)对
μ
求导,并令其等于零:
d() d
d d
[
n i 1
(ai
bi
ci 2 )2 ]
n
2 (ai bi ci 2 ) (bi 2 ci ) 0
i 1
上式展开可得: g0 g1 g2 2 g3 3 0
应用经典的函数求极值的方法可得:
L x
f x
g x
T
W x
0
1
L
u
f u
g u
T
W u
0
2
L
g ( x, u)
0
3
① 输入原始数据,如各机组的耗量特性,运行限制及潮流计算等数据;
显然,这种方法的工作量比以上两种方法大得多。
五.最优潮流法的原理,与基本潮流法的比较,目标函数,等式,不等式约束条件,并介绍简化梯度法的原理; 最优潮流就是当系统的机构参数及负荷情况给定时,通过控制变量的优选,所能找到的能满足所有指定的约束条
件,并使系统的某一个性能或目标函数达到最优时的潮流分布。 最优潮流与基本潮流比较有以下不同:
4.基本潮流计算所完成的仅仅是一种计算功能,即从给定的 u 求出相应的 x;而最优潮流计算则能够根据特定目标函数 并在满足相应约束条件的情况下,自动优选控制变量,这便具有指导系统进行优化调整的决策能力。
简化梯度法:
同时计及等式和不等式约束条件的最优潮流的数学模型为: 根据拉格朗日乘子法构造出函数:
L(x,u, ) f (x,u) T g(x,u) W (x,u) 为不等式约束的惩罚函数。
