第3章 蛮力法资料
蛮力法

i 0 nm
1 [(m 1) 1] (n m 1)m
j 0 i 0
m 1
nm
第三章 蛮力法
3.2 最近对问题 算法:BruteForceClosetPoints(P)
//该算法实现了蛮力法球平面中距离最近的两个点 //输入:一个n个(n>1)个点的列表,P1=(X1,Y1)…… ,Pn=(Xn,Yn) //输出:最近的两个点得下标,index1和index2
C( n )
n 1 i 1
1
i 1 j i 1k 1 n n) n( n i )
j i 1
n[(n 1)(n 2) 1] n 2 ( n 1) / 2
第三章 蛮力法
3.4 旅行商问题 算法:TSP(P[1..n],V[1..n][1..n])
C( n )
i 1 n 1
j i 1
2 [2(n i)] 2[(n 1 1)(n 1)] / 2 n(n 1)
i 1
n
n 1
第三章 蛮力法
3.3 凸包问题 算法:BruteForceConvexHull(P)
//该算法实现了蛮力法求平面中距离最近的两个点 //输入:一个n个(n>1)个点的列表,P1=(X1,Y1)…… ,Pn=(Xn,Yn) //输出:最小凸集合集合S
2 3 n C( n) c11 cn cn cn 2n 1 n
第三章 蛮力法
3.4 旅行商问题 效率分析: TSP(P[1..n],V[1..n][1..n]) //对于具有n个节点的哈密顿回路而言,必须生成一个由n+1 个节点构成的序列,其入口和出口假设为节点1,那么蛮 力法必须生成所有其他的n-1个节点构成一条完整的路径 //显然,对于这样一个算法而言,蛮力法求旅行商问题总是 一个效率为θ((n-1)!)的算法
蛮力法

搜索所有的解空间 搜索所有的路径 直接计算 模拟和仿真
一个简单的例子——百元买百鸡问题
3.1.5 蛮力法解题步骤
用蛮力法解决问题,通常可以从两个方面进行算 法设计:
找出枚举范围:分析问题所涉及的各种情况。 找出约束条件:分析问题的解需要满足的条件,并
用逻辑表达式表示。
逻辑清晰,编写程序简洁 对于一些重要的问题(比如:排序、查找、矩阵 乘法和字符串匹配),可以产生一些合理的算法 解决问题的实例很少时,可以花费较少的代价 可以解决一些小规模的问题(使用优化的算法没 有必要,而且某些优化算法本身较复杂) 可以作为其他高效算法的衡量标准
3.1.4 使用蛮力法的几种情况
问题描述:旅行家要旅行n个城市然后回到出发 城市,要求各个城市经历且仅经历一次,并要求 所走的路程最短。该问题又称为货郎担问题、邮 递员问题、售货员问题,是图问题中最广为人知 的问题。 用蛮力法解决TSP问题,可以找出所有可能的旅 行路线,从中选取路径长度最短的简单回路。 求解: 一个加权连通图中的最短哈密顿回路问题。
2.2.1 如果weight+wj<C,则 weight=weight+wj;value=value+vj; 2.2.2 否则,转步骤2考察下一个子集;
2.3 如果maxValue<value,则maxValue=value;S=T;
3. 输出子集S中的各元素。
3.2.4 TSP——图问题
思考:求所有的三位数,它除以11所得的余数等于 它的三个数字的平方和。——找出枚举范围和约 束条件
分析:
枚举范围:100~999,共900个。 约束条件:设三位数的百位、十位、个位的数字分 别为x,y,z。则有x2+y2+z2≤10,进而1≤x≤3, 0≤y≤3, 0≤z≤3。
蛮力法、动态规划法 求解01背包问题

else
v[i][j]=v[i-1][j];
}
else v[i][j]=v[i-1][j];
}
return v[n][m];
}
int main()
{
int m,n;int i,j;
cout<<"请输入背包的承重量:"<<endl;
2)复杂度分析:2n
2、动态规划法
1)基本思想:Dynamic programming is a technique for solving problems with overlapping subproblems.The function:
V(i,0)=V(0,j)=0;(1)
V(i-1,j)j<w
if (cur_weight <= capacity && cur_value > max_value) {
max_value = cur_value;
}
return;
}
c[d] = 0;
MFKnapsack(capacity, values, weights, c,
d + 1, max_value);
cout << MFKnapsack(capacity, values, weights, n) << endl;
return 0;
}
(2)Dynamic Programming
#include<iostream.h>
#include<string.h>
int v[10][100];//对应每种情况的最大价值
蛮力法的魅力

蛮力法的魅力摘要:蛮力法是我们算法中最常使用的算法,虽然巧妙和高效的算法很少来自于蛮力法,但是蛮力法依然是一种重要的算法设计技术。
在实际理论上,蛮力法可以解决可计算领域的各种问题,只是效率的高低不同而已。
因此蛮力法经常用来解决一些较小规模的问题。
蛮力法对于一些重要的问题可以产生一些合理的算法,他们具备一些实用价值,而且不受问题规模的限制。
蛮力法也可以作为某类问题时间性能的底限,来衡量同样问题的更高效算法。
本文将对蛮力法进行深入了解,发掘出蛮力法的价值。
关键字:蛮力法效率算法应用简单结合引言:蛮力法,由于对于解决一些问题时的低效,不够有技巧性,一直为人们所“诟病”。
但是,遍观我们所学的算法,只有蛮力法是可以适合于任何问题的。
而且,简单的招式,练到极致,就是绝招。
我们在解决的问题的时候,首先考虑的也是蛮力法。
只有当蛮力法不能高效处理问题时,我们才会思考其他算法。
这也就说明,蛮力法对于我们设计算法,仍是必不可少的。
1 蛮力法的原理顾名思义,蛮力法即是顺序往下寻找方法,直到问题的解决。
它所依赖的技术是扫描技术,关键是依次处理所有元素。
蛮力法的思想非常简单,没有很多条件的限制,比如动态规划法,必须满足最有性原理才可以使用。
它的方法上也没有缺陷,对于分治法,一旦子问题的规模不同,便不能在使用。
而蛮力法则没有这个要求。
因此,简单,易上手,是蛮力法的基本原理。
1 蛮力法与其他算法的比较大部分算法都是在蛮力法的基础上改进而来的。
这里比较蛮力法中的冒泡排序与分治法中的快速排序。
对于蛮力法,是所以元素都要经过比较之后再排序,显然这是不可取的。
比如2比1大,3比2大,那1和3就没必要再进行比较。
快速排序,就是有选择性的进行比较。
将序列分为两个子序列,用递归实现,从而使得算法的时间复杂度变为nlog2n,这就是技巧的体现(减治法也是如此),从中也可以看出,在蛮力法的基础上,我们可以改造出更好的算法,体现了蛮力法的重要性。
蛮力算法

17
main1( ) { int *a,i,j,n; input(n); a=calloc(n+1,sizeof(int)); //申请存储空间 for (i=1; i<=n;i++) a[i]=1; for (i=1; i<=n;i++) for (j=i; j<=n;j=j+i) a[i]=1-a[i]; for (i=1; i<=n;i++) if (a[i]=0) print(i,”is free.”); } 算法分析1:以一次开关锁计算,算法的时间复杂度为 n(1+1/2+1/3+……+1/n)=O(nlogn)。
3
【例3.1】百钱百鸡问题。中国古代数学家张丘建在《算经》 中提出了著名的“百钱百鸡问题”:鸡翁一,值钱五;鸡母一, 值钱三;鸡雏三,值钱一;百钱买百鸡,翁、母、雏各几何? 算法设计1: 通过对问题的理解,可能会想到列出两个三元一次方程, 去解这个不定解方程,就能找出问题的解。这确实是一种办法, 但这里我们要用“懒惰”的枚举策略进行算法设计: 设x,y,z分别为公鸡、母鸡、小鸡的数量。 尝试范围:由题意给定共100钱要买百鸡,若全买公鸡最多 买100/5=20只,显然x的取值范围1~20之间;同理,y的取值范 围在1~33之间,z的取值范围在1~100之间。 约束条件: x+y+z=100 且 5*x+3*y+z/3=100
第3章 蛮力法

结果: 结果: 1. 冒泡排序算法效率属于 Θ( n 2 ) 类型;(与选择排序一样 类型; 与选择排序一样 与选择排序一样) 2. 键值交换次数在最坏情况下(输入降序列表,每次比较后均要交换) 键值交换次数在最坏情况下(输入降序列表,每次比较后均要交换) 这比选择排序差。因此, 和键值比较次数一样即均为 Θ( n2 ) ,这比选择排序差。因此,该算法 在简单排序问题上不是一个好的选择。 在简单排序问题上不是一个好的选择。“如果不是因为它有一个好记 的名字,我们很可能对它不会有任何的了解” 的名字,我们很可能对它不会有任何的了解”。
蛮力算法策略: 滑动匹配 滑动匹配) 蛮力算法策略:(滑动匹配 模式在文本上从左向右滑动一个字符,比较对应字符(从左到右), 模式在文本上从左向右滑动一个字符,比较对应字符(从左到右), 个字符都已匹配,算法停止。否则,继续滑动、比较。 若全部 m 个字符都已匹配,算法停止。否则,继续滑动、比较。 注意: (n注意:最后一轮比较的起始位置在 (n-m) 处:(n-1)-(n-m)+1=m
p0 ... p j ... pm −1 ⇒
b
b
b
t n− m ... t n−1 1 24 4 3
m个
11
字符串匹配 (String Matching) 的蛮力算法 BruteForceStringMatch(T [0...n − 1], P[0...m − 1]) { for ( i ← 0) to ( n − m ) do // 模式P滑动循环 { // while结束时j < m : 进入下一轮 i 循环 j ← 0; // 每次比较从P[0]开始 while ( j < m ) and ( P[ j ] = T [i + j ]) do { j ← j + 1; } // 比较下一个字符 if ( j = m ) return ( i ); // 考虑while结束时 j 值 return } return ( −1); // 滑动到文本尾,没找到匹配 } // 可用限位:模式添加到文本最后。去掉j < m
蛮力法

2 其它范例
蛮力法的表现形式非常多。本节将通过蛮力策略, 蛮力法的表现形式非常多。本节将通过蛮力策略,用 算法模拟问题中所描述的全部过程和全部状态, 算法模拟问题中所描述的全部过程和全部状态,来找出问 题的解,并与经过数学建模后的算法进行效率上的比较。 题的解,并与经过数学建模后的算法进行效率上的比较。
8
1 枚举法
枚举法( 穷举法) 是蛮力策略的一种表现形式, 枚举法 ( 穷举法 ) 是蛮力策略的一种表现形式 , 根据问题 中条件将可能情况一一列举出来, 逐一尝试从中找出满足 中条件将可能情况一一列举出来 , 问题条件的解。 但有时一一列举出的情况数目很大, 问题条件的解 。 但有时一一列举出的情况数目很大 , 则需 要进一步考虑, 排除一些明显不合理的情况, 要进一步考虑 , 排除一些明显不合理的情况 , 尽可能减少 问题可能解的列举数目。 问题可能解的列举数目。 通常从两个方面进行算法设计: 通常从两个方面进行算法设计: 1)找出枚举范围:分析问题所涉及的各种情况。 找出枚举范围:分析问题所涉及的各种情况。 找出约束条件:分析问题的解需要满足的条件, 2)找出约束条件:分析问题的解需要满足的条件,并 用逻辑表达式表示。 用逻辑表达式表示。
16
main() () {int A,B,C,D,E,F; for(A=3;A<=9;A++) for(D=1;D<=9;D++) { E = D*100000+D*10000+D*1000+D*100+D*10+D; if(E mod A=0) F=E\A; if(F\10000=A and (F mod 100)\10=A) and (F\1000=F mod 10) print( F,”*”,A,”=”,E); , ” , , } }
3-蛮力法

14
字符串匹配
问题:给定一个n个字符组成的串,称为文本,一个 m(m≤n)个字符组成的串称为模式,从文本中寻找 匹配模式的子串。
16
字符串匹配
流程图或伪代码
算法 bruteForceStringMatch(T[0..n-1],P[0..m-1]) //蛮力字符串匹配算法实现 //输入1:一个n个字符的数组T[0..n-1]代表一段文本 //输入2:一个m个字符的数组P[0..m-1]代表一个模式 //输出:若查找成功,返回文本第一个匹配子串中的第一 个字符的位置,否则返回-1 for i←0 to n-m do j←0 while j<m and P[j]=T[i+j] j←j+1 if j=m return i return -1 17
8
排序问题
正确性证明 算法分析
输入规模:序列元素个数n 基本操作:比较次数A[j] < A[min] 影响基本操作执行次数的因素:n 建立基本操作求和表达式 利用求和公式分析算法时间复杂性
T ( n)
n 2 n 1 i Байду номын сангаас0 j i 1
1 [n (i 1)] [n i 1]
7
排序问题
小规模实例分析
1 89 17 17 17 17 17 17
2 45 45 29 29 29 29 29
3 68 68 68 34 34 34 34
蛮力法

2 查找问题中的蛮力法—串的匹配
BF算法
KMP算法
下一次开始位置 下一次开始位置
本趟开始位置
i 回溯
ii
S 模式T
si
…
tj
回溯
j
j
回溯next[j]
……
3 排序问题中的蛮力法—选择排序
选择排序开始的时候,扫描整个序列,找到整个序列的最小记
录和序列中的第一个记录交换,从而将最小记录放到它在有序
区的最终位置上,然后再从第二个记录开始扫描序列,找到n-1
个序列中的最小记录,再和第二个记录交换位置。一般地,第i
趟排序从第i个记录开始扫描序列,在n-i+1(1≤i≤n-1)个记录中
找到关键码最小的记录,并和第i个记录交换作为有序序列的第i
个记录。
4 组合问题中的蛮力法—任务分配问题
可以用一个n元组(j1, j2, …, jn)来描述任务分配问题的一个可能 解,其中第i个分量ji(1≤i≤n)表示在第i行中选择的列号,因此 用蛮力法解决任务分配问题要求生成整数1~n的全排列,然后把 成本矩阵中的相应元素相加来求得每种分配方案的总成本,最 后选出具有最小和 18
是否最短
否 是 否 是 否 否
蛮力法求解TSP问题存在的问题
注意到图中有3对不同的路径,对每对路径来说,不同 的只是路径的方向,因此,可以将这个数量减半,则 可能的解有(n-1)!/2个。随着n的增长,TSP问题的可 能解也在迅速地增长。
一个10城市的TSP问题有大约180,000个可能解。 一个20城市的TSP问题有大约
依次处理所有元素是蛮力法的关键,为 了避免陷入重复试探,应保证处理过的 元素不再被处理。
第三章 蛮力法PPT课件

个定值。设此值为SN ,则不难解
出:SN = N 2 ·(N 2 +1)/2N= N ·(N 2 +1) /2。
.
19
外延法(由巴谢提出)构造奇阶幻方
.
20
H·Coxeter构造幻方的方法
首先在正方形最上面一 行的正中间的小方格内 填写1,然后到它的左 上方的小格内填写下一 个数(注意:我们认为正 方形的同一行或同一行 的头尾是相连的)。如果 走到某个小方格,而该 格已填了数,那末就改 走到原方格的下面一个 方格。
axbyc13穷举查找14穷举查找15穷举查找分配问题n个任务分配给n个人任务j分配给人i的成本是cij16小结蛮力法是一种简单直接地解决问题的方法通常直接基于问题的描述和所涉及的概念定义
算法分析与设计
Analysis and Design of Computer Algorithms
第三章 蛮力法 Brute Force
.
21
习题3.4-10
.
22
直线方程:ax+by=c a=y2-y1 , b=x1-x2, c=x1y2-y1x2
.
12
旅行商问题
穷举查找
.
13
背包问题
穷举查找
.
14
穷举查找
分配问题
N个任务分配给n个人,任务j分配给人i的成本是C[I,j]
.
15
小结
蛮力法是一种简单直接地解决问题的方法,通常 直接基于问题的描述和所涉及的概念定义。
算法 解决问题的实例很少时,它让你花费较少的代
价 可以解决一些小规模的问题 可以作为其他高效算法的衡量标准
.
3
教学内容
第4章 蛮力法

for (i=0;i<n;i++)
//两重循环穷举所有的连续子序列
{ for (j=i;j<n;j++) { thisSum=0; for (k=i;k<=j;k++) thisSum+=a[k]; if (thisSum>maxSum) //通过比较求最大连续子序列之和 maxSum=thisSum; }
第4章 蛮力法
4.1 蛮力法概述 4.2 蛮力法的基本应用 4.3 递归在蛮力法中的应用
4.1 蛮力法概述
• 蛮力法也称穷举法,枚举法,暴力法,是一种简单直接地 解决问题的方法,是算法中最常用的方法之一
• 通常直接基于问题的描述和所涉及的概念定义,找出所有 可能的解。然后选择其中的一种或多种解,若该解不可行 则试探下一种可能的解。
//进行n-1趟排序
{
} }
exchange=false;
//本趟排序前置exchange为false
for (j=n-1;j>i;j--)
//无序区元素比较,找出最小元素
if (a[j]<a[j-1])
//当相邻元素反序时
{ swap(a[j],a[j-1]); //a[j]与a[j-1]进行交换
for (m=2;m<=1000;m++) { 求出m的所有因子之和s;
if (m==s) 输出s; }
对应的程序如下:
void main() { int m,i,s;
for (m=2;m<=1000;m++) { s=0;
for (i=1;i<=m/2;i++) if (m%i==0) s+=i; //i是m的一个因子
ACM蛮力(穷举)ppt课件

• 穷举范围:即把所有的三位正整数100~999按题 意一一进行判断。
• 判断式:如果一个三位正整数n的百位、十位、 个位上的数字分别为i、j、k,则判断式为: n = i3 + j3 + k3
• 如何分解三位数n的百位、十位、个位: 百位:i = n/100; 十位:j = ( n/10 )%10; 个位:k = n%10;
精品课件
8
• 另一方法是:把x可能值0~20、y可能值0~33和z 可能值0~99用三重循环来组合,若x、y、z值使 5x+3y+z/3=100和x+y+z=100同时成立,则该组x、 y、z即为一组所求值。即: 穷举范围:
x : 0~20 , y : 0~33 , z : 0~99 判断式:
z%3==0&&5*x+3*y+z/3==100&&x+y+z==100
1: cock=0 hen=25 chicken=75 2: cock=4 hen=18 chicken=78 3: cock=8 hen=11 chicken=81 4: cock=12 hen=4 chicken=84
精品课件
11
例2:打印出所有的“水仙花数”。所谓“水仙花 数”是指一个三位正整数,其各位数字的立方和 等于该数本身,例如:153=13+53+33 。
设买 x 只公鸡,y 只母鸡,z 只小鸡,则有: x+y+z=100 5x+3y+z/3=100
且:x、y、z 都是整数; 0 ≤ x ≤ 20; 0 ≤ y ≤ 33; 0 ≤ z ≤ 99; z%3=0。
精品课件
蛮力法 (2)

11
【例】贴纸问题 有A、B、C、D、E五人,每人额头上都帖了一张黑或白的纸。五人对 坐,每人都可以看到其他人额头上的纸的颜色。五人相互观察后, A说:“我看见有三人额头上帖的是白纸,一人额头上帖的是黑纸” B说:“我看见其他四人额头上帖的都是黑纸” C说:“我看见有一人额头上帖的是白纸,其他三人额头上帖的是黑纸” D说:“我看见其他四人额头上帖的都是白纸” E说:什么也没有说 现在已知额头上帖黑纸的人说的都是谎话,额头上贴白纸的人说的都 是实话,请你编写程序,求出这五个人谁的额头上帖的白纸,谁的额 头上帖的黑纸。
蛮力算法的优缺点:
(1)可以用来解决广阔领域的问题; (2)算法设计思想简单明了; (3)可以解决一些小规模的问题; (4)算法的效率不高,随着问题规模的增大,算法效率急剧下降; (5)问题规模过大时,在时间上,有些蛮力算法不可行。
15
作业1:用蛮力算法求解古堡问题
福尔摩斯到某古堡探险,看到门上写着一个奇怪的算式: ABCDE * ? = EDCBA 他对华生说:“ABCDE应该代表不同的数字,问号也代表某个数字!” 华生:“我猜也是!” 于是,两人沉默了好久,还是没有算出合适的结果来。 请你利用计算机的优势,找到破解的答案。 把 ABCDE 所代表的数字写出来。
蛮力法
1
蛮力法
蛮力法是基于计算机运算速度快这一特性,在解决问题 时采取的一种“懒惰” 策略。这种策略不经过(或者说经过 很少)思考,把问题所有情况或所有过程交给计算机去一 一尝试,从中找出问题的解。 蛮力策略应用:选择排序、冒泡排序、插入排序、顺序 查找、朴素的字符串匹配等。比较常用还有枚举法、盲目
搜索算法等。
2
1 枚举法
枚举法(穷举法)是蛮力策略的一种表现形式,根据问题 中条件将可能情况一一列举出来,逐一尝试从中找出满足 问题条件的解。但有时一一列举出的情况数目很大,则需 要进一步考虑,排除一些明显不合理的情况,尽可能减少 问题可能解的列举数目。 通常从两个方面进行算法设计: 1)找出枚举范围:分析问题所涉及的各种情况。 2)找出约束条件:分析问题的解需要满足的条件,并 用逻辑表达式表示。
第3章 蛮力法

1
清华大学出版社
算法设计与分析
2
ii
第 a b a bc a b c a c ba b
趟
a
i=2,j=1失败 i回溯到3,j回溯到1
jj
i ii i i i
第
a b a b c a b c a c ba b
趟 a b c a c i=7,j=5失败 jj j j j j i回溯到4,j回溯到1
3
清华大学出版社
清华大学出版社
算法设计与分析
再比较tnext[k]和tj,此时仍会出现两种情况,当tnext[k]=tj时, 与情况(1)类似,next[j]=next[k]+1;当tnext[k]≠tj时,与情况 (2)类似,再找t1 … tj-1的后缀中第3大真前缀,重复(2) 的过程,直到找到t1 … tj-1的后缀中的最大真前缀,或确定 t1 … tj-1的后缀中不存在真前缀,此时,next[j+1]=1。
例如:S="aaaaaaaaaaab"
T="aaab"
设匹配成功发生在si处,则在i-1趟不成功的匹配中共 比较了(i-1)×m次,第i趟成功的匹配共比较了m次,所 以总共比较了i×m次,因此平均比较次数是:
nm1
nm1 1
m(n m 2)
i1
pi (i m)
时,t1=t3,next[4]=2;j=5时,t2≠t4, 令k=next[2]=1,t1=t4,next[5]=k+1=2; j=6时,t2=t5,next[6]=3;j=7时,t3=t6,next[7]=4; j=8时,t4≠t7,k=next[4]=2,t2=t7,next[8]=k+1=3。
蛮力法

算法设计2: 在公鸡(x)、母鸡(y)的数量确定后,小 鸡 的数量 z就固定为100-x-y,无需再进行枚举了 此时约束条件只有一个:5*x+3*y+z/3=100 算法2如下:
8
Z能被3整除时,才会判断“5*x+3*y+z/3=100
main( ) 枚举尝试20*33=660次 { int x,y,z; for(x=1;x<=20;x=x+1) for(y=1;y<=33;y=y+1) { z=100-x-y; if(z%3==0&&5*x+3*y+z/3==100) { print("the cock number is",x);
蛮力字符串匹配:即朴素模式串匹配
4
蛮力法解题步骤
根据问题中的条件将可能的情况一一列举出 来,逐一尝试从中找出满足问题条件的解。但有 时一一列举出的情况数目很大,如果超过了我们 所能忍受的范围,则需要进一步考虑,排除一些 明显不合理的情况,尽可能减少问题可能解的列 举数目。 用蛮力法解决问题,通常可以从两个方面进行算 法设计:
16
1)找出枚举范围:分析问题所涉及的各种情况。
2)找出约束条件:分析问题的解需要满足的条件,并用 逻辑表达式表示。
5
例1 百钱百鸡问题。中国古代数学家张丘建在他的 《算经》中提出了著名的“百钱百鸡问题”:鸡翁一, 值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买 百鸡,翁、母、雏各几何?
算法设计1:
通过对问题的理解,可能会想到列出两个三元一次方程, 去解这个不定解方程,就能找出问题的解。这确实是一种 办法,但这里我们要用“懒惰”的枚举策略进行算法设计: 设x,y,z分别为公鸡、母鸡、小鸡的数量。
蛮力法求解旅行商问题
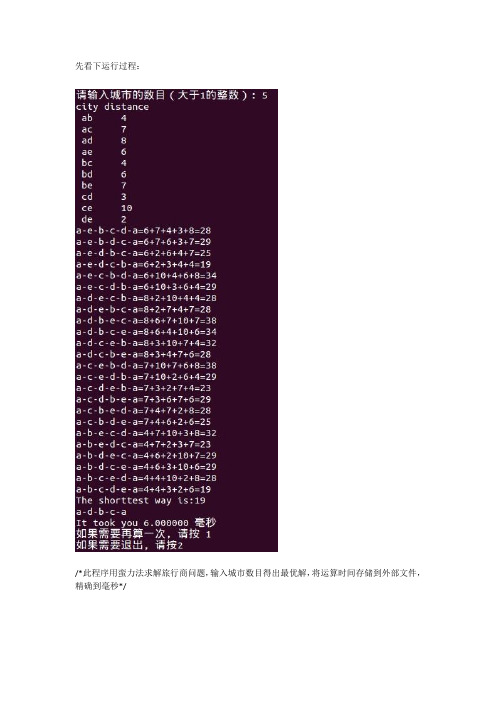
先看下运行过程:/*此程序用蛮力法求解旅行商问题,输入城市数目得出最优解,将运算时间存储到外部文件,精确到毫秒*/#include<stdio.h>#include<stdlib.h>#include<string.h>#include <time.h>#include <sys/time.h>#include <assert.h>#define MAXSIZE 99999//#define CITYNUM 5 /*4个城市的话,其实全排列的只有3个,另外一个是起点固定的*///#define TOTLE 15 /*4个城市对应的道路一共有6条*/#define MAX 32int CITYNUM=0;int TOTLE=0;char city[MAXSIZE]={0}; /*和下面这个数组组成两个城市之间的道路*/char citytwo[MAXSIZE]={0};int distance[MAXSIZE]={0}; /*存放城市间距离*/int valueall[MAXSIZE]={0}; /*最后放每次运算的路径值*/int all=0; /*对应上面的*/char backarray[MAXSIZE]={0};long int bbb=0;int ccc=0;/*文件里存了全部的道路和距离比如:ab 7,读取数据到三个数组*/void read(){int nn = 1, ii = 1;int i = 1;int p ;FILE *fp;fp = fopen("in.dat", "rb");while(!feof(fp)){p=fscanf(fp,"%c %c %d\n",&city[nn],&citytwo[nn], &distance[nn]); /*读取的时候遇到回车所以fscanf时候加\n*/if((p != EOF)){nn++;i++;TOTLE++;}else{break;}}fclose(fp);printf("city ");printf("distance\n");for(ii = 1; ii < nn;ii++){printf(" %c%c %d\n", city[ii],citytwo[ii],distance[ii]);}}/*两两互换*/void swap(int *l, int *r){int temp;temp = *l;*l = *r;*r = temp;}/*打印各种东西...*/void print(int ncount, int *val){int n=0;int i;int ii=0;int nnn=0;int sum=0; /*每次运算加起来的最后路程*/int value[MAXSIZE]={0}; /*存放每次运算上面那个结果*/printf("a-");for(;n < ncount;n++){printf("%c-", val[n]);backarray[bbb]=val[n];bbb++;}printf("a");printf("=");/*起点城市*/for(i=0;i<TOTLE;i++){if(val[0]==citytwo[i+1]&&city[i+1]=='a'){printf("%d+", distance[i+1]);value[nnn]=distance[i+1];nnn++;}}/*中间的全排列城市*/for(i=0;i<ncount;i++){for(ii=1;ii<=TOTLE;ii++){if(val[i]==city[ii] && val[i+1]==citytwo[ii]){printf("%d+", distance[ii]);value[nnn]=distance[ii];nnn++;continue;}else if(val[i]==citytwo[ii] && val[i+1]==city[ii]){printf("%d+", distance[ii]);value[nnn]=distance[ii];nnn++;continue;}}}/*最后返回起点*/for(i=0;i<TOTLE;i++){if(val[ncount-1]==citytwo[i+1] && city[i+1]=='a'){printf("%d=", distance[i+1]);value[nnn]=distance[i+1];nnn++;}}/*存放走一次的路径*/for(i=0;i<nnn;i++){sum=sum+value[i];}printf("%d", sum);/*存入数组*/valueall[all]=sum;all++;printf("\n");}/*蛮力法穷举*/void func(int ncount, int n, int *val){if(1 == n){print(ncount, val);}else{int i = 0;int *pnew = (int *)malloc(sizeof(int)*ncount);for(;i < n;i++){memcpy(pnew, val, sizeof(int)*ncount);swap(pnew +ncount -n, pnew+ncount-1-i);func(ncount, n-1, pnew);}free(pnew);}}/*自动生成文件*/void become()int i,j;FILE *fp;fp = fopen("in.dat","w");//srand(unsigned(time(NULL)));for(i=0;i<CITYNUM;i++){for(j=i+1;j<=CITYNUM;j++){fprintf(fp,"%c %c %d\n",i+'a',j+'a',rand()%10+1);}}fclose(fp);}void del(){remove("in.dat");}int main(){printf("请输入城市的数目(大于1的整数):");scanf(" %d",&CITYNUM);CITYNUM=CITYNUM-1;become();float time_usea=0;float time_useb=0;struct timeval starta;struct timeval enda;struct timeval startb;struct timeval endb;int i = 0, ncount = CITYNUM, *val = 0;int temp;int loop;int n=0,d,cnt=0;char sa[10],sb[10];int j;gettimeofday(&starta,NULL);read();val = (int *)malloc(sizeof(int)*ncount);/* a 城市是起点,从b 城市开始全排列,把所有城市存在val中*/ for(i = 0;i < ncount;i++){val[i] ='b'+i;}func(ncount, ncount, val);/*for(i=0;i<all;i++){if(i%10==0){printf("%d ",valueall[i]);printf("\n");}else{printf("%d ",valueall[i]);}}*//*找到最短路程*/temp = valueall[0];for(i=1;i<all;i++){if(temp > valueall[i]){temp=valueall[i];ccc = i;}}printf("The shorttest way is:%d\n",temp);printf("a-");for(i=ccc*(CITYNUM-1);i<ccc*(CITYNUM-1)+(CITYNUM-1);i++){printf("%c-",backarray[i]);}printf("a");printf("\n");gettimeofday(&enda,NULL);time_usea=(__sec)*1000+(__usec)/1000;//毫秒printf("It took you %f 毫秒\n",time_usea);//printf("b = %ld,all=%d,ccc=%d\n",bbb,all,ccc);free(val);FILE *fp = NULL;fp = fopen("OUT.DAT", "a+");if(NULL == fp){printf("wrong");return 0;}fprintf(fp, "蛮力: %d %f\n", n,time_usea);//fprintf(fp, "分支: %d %f\n", n,time_useb/1000);fclose(fp);del();printf("如果需要再算一次,请按1\n");printf("如果需要退出,请按2\n");scanf("%d",&loop);switch(loop){case 1:return main();case 2:return;default:return;}return 0;}。
蛮力法详解

算法3.1——顺序查找
int SeqSearch1(int r[ ], int n, int k) //数组r[1] ~ r[n]存放查找集合
{ i=n;
基本语句 ?
while (i>0 && r[i]!=k)
i--;
return i;
}
算法3.1的基本语句是i>0和r[i]!=k,其执行次数为:
n
2020/6/14
Chapter 3 Brute force method
教学要求 理解 掌握
√
√ √ √
√ √ √
熟练掌握 √ √
√
4
3.1 概述:蛮力法的设计思想
蛮力法中“力”是指计算机的“计算能 力”,不是人的智“力”。
蛮力法的设计思想:直接基于问题的描述, 从有限集合中,逐一列举集合的所有元素, 对每一个元素逐一判断和处理,从而找出 问题的解。
如已知:公钥为:KU={e, n},私钥为: KR={d, n},则 对明文m的加密/解密算法如下:
加密 明文: M<n 密文: C=Me (mod n)
密文: 明文:
解密 C M=Cd (mod n)
注:计算an算法的效率直接影响到RSA算法的性能
2020/6/14
Chapter 3 Brute force method
2020/6/14
Chapter 3 Brute force method
7
蛮力法的设计思想
因要穷举待处理的元素,故蛮力法的时间性能往往最低, 但基于以下原因,蛮力法也是一种重要的算法设计技术:
(1)理论上,蛮力法可以解决可计算领域的各种问题。 (2)蛮力法经常用来解决一些较小规模的问题。 (3)对于一些重要的问题(例如排序、查找等)蛮力法 可以产生一些合理的算法,他们具备一些实用价值,而且 不受问题规模的限制。 (4)蛮力法可以作为某类问题时间性能(不是复杂性, 两者恰好相反)的下界,来衡量同样问题的更高效算法。
第6讲 迭代法和蛮力法

Design and Analysis of Computer Algorithms
4.1.3
迭代法解方程
迭代法解方程的实质是按照下列步骤构造一个序列 x0,x1,…,xn,来逐步逼近方程f(x)=0的解:
1)选取适当的初值x0;
2)确定迭代格式,即建立迭代关系,需要将方程f(x)=0 改写为x=φ (x)的等价形式;
大连海事大学
Design and Analysis of Computer Algorithms
算法2:
递推迭代表达式 1 2 3 4 5 6 7 8 9 a b c=a+b a=b+c b=a+c c=a+b a=b+c b=a+c …… 由此归纳出可以用“c=a+b; a=b+c; b=c+a;”做循环“不变 式”。 算法2如下: main( ) 算法2,最后输出的 { int i,a=1,b=1; 并不是12项,而是 2+3*4共14项。 print(a,b); for(i=1; i<=4;i++) { c=a+b; a=b+c; b=c+a; print(a,b,c); } }
大连海事大学
Design and Analysis of Computer Algorithms
【例2】求两个整数的最大公约数。 数学建模:辗转相除法是根据递推策略设计的。
不妨设两个整数 a>b 且 a 除以 b 商 x 余 c ;则 a-bx=c ,不难看出 a 、 b 的最大公约数也是 c 的约数(一个数能整除等式左边就一定能整 除等式的右边),则a、b的最大公约数与b、c的最大公约数相同。 同样方法推出b、c的最大公约数与……,直到余数为0时,除数即 为所求的最大公约数。
(word完整版)浙教版七年级下科学第三章运动和力复习提纲(2021年整理)

(word完整版)浙教版七年级下科学第三章运动和力复习提纲(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((word完整版)浙教版七年级下科学第三章运动和力复习提纲(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(word完整版)浙教版七年级下科学第三章运动和力复习提纲(word版可编辑修改)的全部内容。
第三章运动和力复习提纲一.机械运动1.机械运动:物体空间位置发生了变化的运动.也是最简单、最基本的运动形式。
2.参照物:在研究机械运动时,被选作标准的物体叫做参照物。
参照物的选择是任意的(除研究对象本身外),科学中一般取地面或相对于地面静止的物体作为参照物,可以不加以说明;若选取其他合适的物体做参照物研究机械运动时,则要作出说明.3.运动和静止的相对性: 运动和静止是相对参照物而言的。
选择不同的参照物对同一物体运动的描述结果可能是不同的。
4.机械运动的分类:根据运动路线的形状,可分为直线运动和曲线运动;而直线运动根据运动快慢是否变化,可分为匀速直线运动和变速直线运动。
匀速直线运动是最简单的机械运动,即运动的方向和快慢不发生变化的运动.5.比较物体的快慢有两种方法:⑴相同时间比较路程,路程大的速度快;⑵相同的路程比较时间,用时少的速度快。
6.速度和平均速度⑴速度是表示物体运动快慢的科学量.①定义:物体在单位时间内通过的路程叫做速度。
②计算公式:v=s/t ;变形公式:s=vt t=s/v③速度单位:国际单位:米/秒,记作:m/s常用单位:千米/时,记作:Km/h换算关系:1米/秒 = 3.6千米/时“1米/秒”表示:物体在1秒内通过的路程为1米。
回朔法与蛮力法

首页
上页
下页
退出
第六章
深度优先搜索(Depth_First Search):
图的深度优先搜索方法类似于树的先根序遍历。 例:如图深度优先搜索结果为:v1 v2 v4 v1 Boolean visited[MAX]; v2 v3 v5 v8 v6
Status (*VisitFunc)(int v); void DFSTraverse(graph G, Status (*Visit)(int v)){ VisitFunc = Visit ; for ( v=0;v<G.vexnum;++v) visited[v] = FALSE; for ( v=0;v<G.vexnum;++v) if( !visited[v]) DFS(G,v); }
首页
上页
下页
退出
第六章
n后问题
在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象 棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线 上的棋子。n后问题等价于在n×n格的棋盘上放置n个皇后,任 何2个皇后不放在同一行或同一列或同一斜线上。
1 2 3 4 5 6 7 8 Q Q Q Q Q Q Q
首页 上页 下页 退出
第六章
装载问题
有一批共n个集装箱要装上2艘载重量分别为 c1和c2的轮船,其 n 中集装箱i的重量为wi,且 wi c1 c2
装载问题要求确定是否有一个合理的装载方案可将这批集装箱 装上这2艘轮船。如果有,找出一种装载方案。 容易证明,如果一个给定装载问题有解,则采用下面的策略可 得到最优装载方案。 (1)首先将第一艘轮船尽可能装满; (2)将剩余的集装箱装上第二艘轮船。 将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集, 使该子集中集装箱重量之和最接近。由此可知,装载问题等价 于以下特殊的0-1背包问题。 n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.3.1 选择排序
3.3.2 起泡排序
2020/9/10
算法设计与分析--蛮力法
14
3.3.1 选择排序
选择排序第i趟排序从第i个记录开始扫描序列, 在n-i+1(1≤i≤n-1)个记录中找到关键码最小的记 录,并和第i个记录交换作为有序序列的第i个记录。
交换
r1 ≤r2 … … ≤ri-1 ri ri+1 … rmin … rn
2020/9/10
算法设计与分析--蛮力法
9
改进的顺序查找
将待查值放在查找方向的尽头处,免去了在查找过 程中每一次比较后都要判断查找位置是否越界,从 而提高了查找速度。
哨兵
0123456789 k 10 15 24 6 12 35 40 98 55
查找方向
i
2020/9/10
算法设计与分析--蛮力法
while (i>0 && r[i]!=k)
i--;
return i;
}
算法3.1的基本语句是i>0和r[i]!=k,其执行次数为:
n
i 1
pibi
n i 1
pici
1 n
n i 1
(n
i
1)
1 n
n i 1
(n
i
1)
n
1
O(n)
其中pi是第i个元素的查找概率,而bi和ci分别是基本语句 i>0和r[i]!=k的执行次数
第3章 蛮力法
3.1 概述 3.2 查找问题中的蛮力法 3.3 排序问题中的蛮力法 3.4 组合问题中的蛮力法 3.5 图问题中的蛮力法 3.6 几何问题中的蛮力法
2020/9/10
算法设计与分析--蛮力法
1
3.1 概述
3.1.1 蛮力法的设计思想
蛮力法(穷举法),是一种简单而直接地解决问题的方 法。设计思想:直接基于问题的描述。
12
3.2.2 串匹配问题 (略)
串匹配问题——给定两个串S=“s1s2…sn” 和T=“t1t2…tm”,在 主串S中查找子串T的过程称为串匹配,也称模式匹配。
➢ 串匹配问题属于易解问题。 ➢ 串匹配问题的特征:
(1)算法的一次执行时间不容忽视:问题规模 n 很大, 常常需要在大量信息中进行匹配; (2)算法改进所取得的积累效益不容忽视:串匹配操作 经常被调用,执行频率高。
0 1 23 456 7 8 9 10 15 24 6 12 35 40 98 55
查找方向
i
2020/9/10
算法设计与分析--蛮力法
8
算法3.1——顺序查找
int SeqSearch1(int r[ ], int n, int k) //数组r[1] ~ r[n]存放查找集合
{ i=n;
基本语句 ?
系数相差一半
n
i 1
pici
1 n
n i 1
(n i
1)Βιβλιοθήκη n 1 2O(n)
2020/9/10
算法设计与分析--蛮力法
11
❖ 一般观点: 用蛮力法设计的算法,都可以对算法的
第一个版本进行一定程度的改良,改进其时 间性能,但只能减少系数,而数量级不会改 变。
2020/9/10
算法设计与分析--蛮力法
2020/9/10
算法设计与分析--蛮力法
3
蛮力法所依赖的基本技术——扫描技术
关键——依次处理所有元素
基本的扫描技术——遍历 (1)集合的遍历 (2)线性表的遍历 (3)树的遍历 (4)图的遍历
2020/9/10
算法设计与分析--蛮力法
4
蛮力法也是一种重要的算法设计技术,原因如下:
(1)理论上,蛮力法可以解决可计算领域的各 种问题。
2020/9/10
算法设计与分析--蛮力法
13
3.3 排序问题中的蛮力法
排序:给定一个记录序列(r1,r2,…,rn),其相应的 关键字分别为(k1,k2,…,kn) ,排序是将这些记录 排列成顺序为(rs1,rs2,…,rsn)的一个序列,使得相 应的关键字满足ks1ks2 … ksn(升序或非降序)或 ks1 ks2 … ksn (降序或非升序) 。
10
算法3.2——改进的顺序查找
int SeqSearch2(int r[ ], int n, int k) //数组r[1] ~ r[n]存放查找集合 { r[0]=k; i=n; while (r[i]!=k)
i --; return i; }
算法3.2的基本语句是r[i]!=k,其执行次数为: 数量级相同,
有序区 已经位于最终位置
无序区 rmin为无序区的最小记录
2020/9/10
算法设计与分析--蛮力法
15
算法3.6——选择排序
void SelectSort(int r[ ], int n) //数组下标从1开始 {
for (i=1; i<=n-1; i++) //对n个记录进行n-1趟简单选择排序 {
2020/9/10
算法设计与分析--蛮力法
6
3.2 查找问题中的蛮力法
3.2.1 顺序查找 3.2.2 串匹配问题
2020/9/10
算法设计与分析--蛮力法
7
3.2.1 顺序查找
顺序查找从表的一端向另一端逐个将元素与给
定值进行比较,若相等,则查找成功,给出该元素 在表中的位置;若整个表检测完仍未找到与给定值 相等的元素,则查找失败,给出失败信息。
例:计算an
an=a×a×…×a n次
2020/9/10
算法设计与分析--蛮力法
2
应用实例: 计算an的值是RSA算法的主要组成 部分。 RSA算法的加密和解密过程都需要一 个整数的整数次幂再取模。
例如,设公钥为(5,119),私钥为(77,119),明 文m=19,则加密得密文c为:
c=195 mod 119=2 476 099 mod 119=66 解密得明文m为: m=6677 mod 119=19 计算an算法的效率直接影响到RSA算法的性能。
(2)蛮力法经常用来解决一些较小规模的问 题。
(3)对于一些重要的问题(如:排序、查找) 蛮力法可以产生一些合理的算法。
(4)蛮力法可以作为某类问题时间性能的底 限,来衡量同样问题的更高效算法。
2020/9/10
算法设计与分析--蛮力法
5
举例:百元买百鸡问题
已知公鸡5元一只,母鸡3元一只,小 鸡1元三只,用100元钱买100只鸡,问公鸡、 母鸡、小鸡各多少只?
