小学数学经典习题及解析
六年级数学上册解决问题解答应用题练习题50(经典版)带答案解析

六年级数学上册解决问题解答应用题练习题50(经典版)带答案解析一、六年级数学上册应用题解答题1.某地为提倡节约用电,推行“阶梯电价“.其计费规则为:居民用电300度及以内,每度电0.5元;用电超过300度至500度部分,每度电加价10%;用电超过500度部分,每度电加价50%,张阿姨家七月份交了216元电费,这个月她家一共用电多少度?解析:410度【详解】300×0.5=150(元)0.5×(1+10%)=0.6(元)(500﹣300)×0.6=200×0.6=120(元)150+120=270(元)270>216(216﹣150)÷0.6=66÷0.6=110(度)300+110=410(度)答:这个月她家一共用电410度.2.三个小朋友跳绳,一共跳了252下。
小青跳了总数的37,小明跳的比小光跳的少25。
三个小朋友分别跳了多少下?解析:小青108下,小光90下,小明54下【详解】略3.求实小学原来男、女生人数之比为16:13,这学期又转来几名女生,这样男、女生人数之比为6:5,这时男、女生人数共有880人,转来的女生有多少人?解析:10人【详解】880÷(6+5)=80(人),80×6=480(人),480÷16=30(人),30×13=390(人),80×5-390=10(人).答:转来的女生有10人.4.下图中,涂色部分甲比乙的面积大211.25cm。
求BC的长。
解析:6厘米【分析】因为涂色部分甲比乙的面积大211.25cm,也就是(甲+空白扇形)-(乙+空白扇形)=11.25cm2,即半圆面积-三角形面积=11.25cm2,所以三角形面积=半圆面积-11.25,通过圆形面积公式和三角形面积公式进而可计算出BC的长。
【详解】根据分析,列式如下:[3.14×(10÷2)2÷2-11.25]×2÷10=[39.25-11.25]×2÷10=28×2÷10=5.6(厘米)答:BC的长是5.6厘米。
小学二年级上册数学练习题100道及答案解析

小学二年级上册数学练习题100道及答案解析1. 小明有10 个苹果,小红比小明多5 个,小红有多少个苹果?答案:10 + 5 = 15(个)解析:求比一个数多几的数是多少,用加法计算。
2. 树上有8 只鸟,飞走了3 只,又飞来了2 只,现在树上有几只鸟?答案:8 - 3 + 2 = 7(只)解析:先算出飞走3 只后剩下的鸟的数量,再加上又飞来的鸟的数量。
3. 妈妈买了15 个梨,小明吃了6 个,还剩下几个梨?答案:15 - 6 = 9(个)解析:用总数减去吃掉的数量就是剩下的数量。
4. 一盒铅笔有8 支,3 盒铅笔一共有多少支?答案:8×3 = 24(支)解析:求几个相同加数的和用乘法计算。
5. 停车场原来有12 辆车,开走了5 辆,又开来了4 辆,现在停车场有多少辆车?答案:12 - 5 + 4 = 11(辆)解析:先算开走5 辆后剩下的车,再加上开来的车。
6. 一只兔子有4 条腿,5 只兔子一共有多少条腿?答案:4×5 = 20(条)解析:一只兔子4 条腿,5 只兔子的腿数用乘法计算。
7. 教室里有20 个同学,出去了8 个女生,还剩下多少个同学?答案:20 - 8 = 12(个)解析:用总人数减去出去的女生人数。
8. 每件衣服需要5 颗扣子,做6 件衣服需要多少颗扣子?答案:5×6 = 30(颗)解析:一件衣服5 颗扣子,6 件衣服需要的扣子数用乘法。
9. 小明有30 元钱,买一个书包花了18 元,还剩下多少钱?答案:30 - 18 = 12(元)解析:用总钱数减去花掉的钱数。
10. 有4 组同学在做游戏,每组6 人,一共有多少人在做游戏?答案:4×6 = 24(人)解析:组数乘以每组的人数就是总人数。
11. 一支钢笔7 元,买8 支钢笔需要多少钱?解析:单价乘以数量等于总价。
12. 小丽做了15 朵花,小美比小丽少做3 朵,小美做了多少朵花?答案:15 - 3 = 12(朵)解析:小丽做的花的数量减去3 就是小美做的花的数量。
小学数学经典题型和倍问题应用题知识点讲解练习题及参考答案

小学数学和倍问题知识点讲解+练习题+参考答案一、【定义】已知两个数的和及大数是小数的几倍(或小数是大数的几分之几),要求这两个数各是多少,这类题型叫做和倍问题。
二、【数量关系】总和÷(几倍+1)=较小的数总和-较小的数=较大的数较小的数×几倍=较大的数三、【解题思路和方法】简单的题目:直接套用公式;复杂的题目:变通后再利用公式。
例1果园里有杏树和桃树共248棵,桃树的棵数是杏树的3倍,求杏树、桃树各多少棵?解(1)杏树有多少棵? 248÷(3+1)=62(棵)(2)桃树有多少棵? 62×3=186(棵)答:杏树有62棵,桃树有186棵。
例2东西两个仓库共存粮480吨,东库存粮数是西库存粮数的1.4倍,求两库各存粮多少吨?解(1)西库存粮数=480÷(1.4+1)=200(吨)(2)东库存粮数=480-200=280(吨)答:东库存粮280吨,西库存粮200吨。
例3 甲站原有车52辆,乙站原有车32辆,若每天从甲站开往乙站28辆,从乙站开往甲站24辆,几天后乙站车辆数是甲站的2倍?解每天从甲站开往乙站28辆,从乙站开往甲站24辆,相当于每天从甲站开往乙站(28-24)辆。
把几天以后甲站的车辆数当作1倍量,这时乙站的车辆数就是2倍量,两站的车辆总数(52+32)就相当于(2+1)倍,那么,几天以后甲站的车辆数减少为(52+32)÷(2+1)=28(辆)所求天数为(52-28)÷(28-24)=6(天)答:6天以后乙站车辆数是甲站的2倍。
例4 甲乙丙三数之和是170,乙比甲的2倍少4,丙比甲的3倍多6,求三数各是多少?解乙丙两数都与甲数有直接关系,因此把甲数作为1倍量。
因为乙比甲的2倍少4,所以给乙加上4,乙数就变成甲数的2倍;又因为丙比甲的3倍多6,所以丙数减去6就变为甲数的3倍;这时(170+4-6)就相当于(1+2+3)倍。
那么,甲数=(170+4-6)÷(1+2+3)=28乙数=28×2-4=52丙数=28×3+6=90答:甲数是28,乙数是52,丙数是90。
六年级数学解决问题解答应用题练习题30篇(经典版)带答案解析

六年级数学解决问题解答应用题练习题30篇(经典版)带答案解析一、苏教小学数学解决问题六年级下册应用题1.一瓶装满的矿泉水,内直径是6cm,明明喝了一些,瓶里剩下水的高度是8cm,把瓶盖拧紧后倒置放平,无水部分高是10cm,这瓶矿泉水原有多少水?2.一个圆柱体的侧面积是31.4平方厘米,底面周长是6.28厘米,这个圆柱体的体积是多少立方厘米?3.小军家离学校1千米,离图书馆2千米.他从家出发,走了15分钟,每分钟走64米.(1)如果向东走,离学校还有多少米?(2)如果向北走,小军现在走到什么位置?(先列式计算,再用★在图上标注出来)4.一个圆柱形的容器,底面周长是62.8厘米,容器里面水面高0.8分米,现把一个小圆柱体和一个与圆柱等底、高是圆柱一半的圆锥放入容器中,结果圆锥完全浸没在水中,圆柱有在水面之上,容器内的水比放入前上升了3厘米,求圆柱和圆锥的体积?5.鸡和免一共有8只,它们的腿有22条。
鸡和兔各有多少只?6.张宏上个月收集了13张邮票,有8角和1元2角这两种面值。
这些邮票的总面值是14元。
两种面值的邮票各有多少张?7.在一幅比例尺是1:18000000的地图上,量得甲、乙两地的距离是6厘米。
张师傅凌晨4时从甲地出发,平均每时行驶90千米,到达乙地时是几时?8.会议大厅里有10根底面直径0.6米,高6米的圆柱形柱子,现在要刷上油漆,每平方米用油漆0.5千克,刷这些柱子要用油漆多少千克?9.一个圆锥形沙堆,底面积是28.26m²,高是2.5m。
用这堆沙在10m宽的公路上铺2cm 厚的路面,能铺多少米?10.为了测量一个空瓶子的容积,一个学习小组进行了如下实验。
①测量出整个瓶子的高度是22厘米;②测量出瓶子圆柱形部分的内直径是6厘米;③给瓶子里注入一些水,把瓶子正放时,测量出水的高度是5厘米;④把瓶盖拧紧,将瓶子倒置放平,无水部分是圆柱形,测量出无水部分圆柱的高度是12厘米。
(1)要求这个瓶子的容积,上面记录中的哪些信息是必须有的?________(填实验序号)(2)请根据选出的信息,求出这个瓶子的容积。
小学数学加减乘除练习题解析与详细解答

小学数学加减乘除练习题解析与详细解答在小学数学学习过程中,加减乘除是最基础的四则运算。
掌握了这四种运算的方法和技巧,才能够更好地解决实际问题。
本文将对小学数学中的加减乘除练习题进行解析与详细解答,帮助同学们更好地掌握这些知识点。
一、加法解析与详细解答加法是数学中最常见的运算之一。
通过加法运算,两个或多个数可以合并在一起,得到它们的总和。
例如,计算下列加法题目:1. 23 + 18 = ?解析:首先,我们从个位数开始相加,3 + 8 = 11。
将11的个位数1写在十位上,进位1写在百位上。
接下来,计算十位数,2 + 1 + 1 = 4。
因此,答案是41。
详细解答:23 + 18 = 41二、减法解析与详细解答减法是加法的逆运算,通过减法运算,我们可以计算两个数之间的差值。
例如,计算下列减法题目:1. 57 - 28 = ?解析:从个位数开始相减,7 - 8 不足以相减,因此需要向十位借位。
将十位的5借位给个位,得到17 - 8 = 9。
然后,十位数直接相减,5 -2 = 3。
因此,答案是29。
详细解答:57 - 28 = 29三、乘法解析与详细解答乘法是一种重复相加的运算。
通过乘法运算,我们可以计算两个或多个数的积。
例如,计算下列乘法题目:1. 6 × 4 = ?解析:将4写下来,在6的上方画一条横线。
然后,每个空格内填入6的倍数分别是6、12、18、24。
最后,将这四个数相加得到答案24。
详细解答:6 × 4 = 24四、除法解析与详细解答除法是乘法的逆运算,通过除法运算,我们可以计算两个数之间的商。
例如,计算下列除法题目:1. 24 ÷ 3 = ?解析:将24分成3个相等的部分,每个部分是8。
因此,答案是8。
详细解答:24 ÷ 3 = 8通过以上的解析与详细解答,我们可以看到小学数学中的四则运算加减乘除的基本方法和步骤。
掌握这些方法和技巧,同学们就能够更加轻松地解决相关的练习题。
小学六年级数学上册练习题100道及答案解析

小学六年级数学上册练习题100道及答案解析1. 一个长方形,长是20 厘米,宽是长的3/5 ,这个长方形的面积是多少平方厘米?答案:宽= 20×3/5 = 12(厘米),面积= 20×12 = 240(平方厘米)解析:先求出宽,再用长乘以宽得到面积。
2. 一桶油重50 千克,用去了2/5 ,还剩多少千克?答案:50×(1 - 2/5) = 30(千克)解析:用总量乘以剩下的比例。
3. 一本书有300 页,第一天看了全书的1/6 ,第二天看了全书的1/5 ,两天一共看了多少页?答案:300×(1/6 + 1/5) = 110(页)解析:分别算出第一天和第二天看的页数,然后相加。
4. 果园里有苹果树80 棵,梨树的棵数是苹果树的3/4 ,桃树的棵数是梨树的2/3 ,桃树有多少棵?答案:梨树= 80×3/4 = 60(棵),桃树= 60×2/3 = 40(棵)解析:逐步计算梨树和桃树的棵数。
5. 一个正方形的边长是15 分米,它的周长是多少分米?面积是多少平方分米?答案:周长= 15×4 = 60(分米),面积= 15×15 = 225(平方分米)解析:根据正方形的周长和面积公式计算。
6. 一根绳子长40 米,第一次用去1/4 ,第二次用去1/5 ,两次一共用去多少米?答案:40×(1/4 + 1/5) = 18(米)解析:先算出两次分别用去的长度,再相加。
7. 一套西服原价800 元,现在打八折出售,现在的价格是多少元?答案:800×80% = 640(元)解析:原价乘以折扣得到现价。
8. 一个圆形花坛的半径是8 米,它的占地面积是多少平方米?答案:3.14×8²= 200.96(平方米)解析:根据圆的面积公式计算。
9. 六年级有学生180 人,其中男生占5/9 ,女生有多少人?答案:180×(1 - 5/9) = 80(人)解析:先算出女生占的比例,再用总人数乘以比例。
小学数学三年级下册第一单元经典练习题(含答案解析)

一、选择题1.黑板在教室的西面,那么同学们坐在黑板的()面.A. 东B. 南C. 西A解析: A【解析】【解答】黑板在教室的西面,那么同学们坐在黑板的东面。
故答案为:A。
【分析】西的相对方向是东。
2.明明上学时往东北方向走600米,他放学回家时要往()方向走600米。
A. 东北B. 东南C. 西北D. 西南D 解析: D【解析】【解答】解:明明上学时往东北方向走600米,他放学回家时要往西南方向走600米。
故答案为:D。
【分析】东北和西南是相对的方向,上学和放学走的方向是相对的。
3.上体育课时,同学们面向东站好队,体育委员下口令“向右转”,这时同学们面向()站立。
A. 东B. 南C. 西B解析: B【解析】【解答】解:面向东方,右面是南方的方向,所以这时同学们面向南站立。
故答案为:B。
【分析】根据方位图作答即可。
4.晴朗有夜晚,我们可以利用( )来辩别方向。
A. 星星B. 月亮C. 北斗星C解析: C【解析】【解答】解:晴朗有夜晚,我们可以利用北斗星来辩别方向。
故答案为:C。
【分析】夜晚可以利用北极星辨别方向,面对北极星,顺时针方向看,前面是北,右面是东,后面是南,左边是西。
5.教室里,张强的座位在小花的东南方向,那么小花的座位在张强的( )方向。
A. 东北B. 西北C. 西南B解析: B【解析】【解答】解:小花的座位在张强的西北方向。
故答案为:B。
【分析】东南方向与西北方向相对,所以小花的座位在张强的西北方向。
6.江勇放学回家往东走,学校在他家的( )。
A. 东面B. 西面C. 南面D. 北面B 解析:B【解析】【解答】解:江勇放学回家往东走,学校在他家的西面.故答案为:B【分析】以他家为中心,学校在他家的西面,他才会从学校往东走.7.从地图中,可以看出邮局在书店的()面.A. 东北B. 西北C. 南面A解析:A【解析】【解答】从地图中可以看出:邮局在书店的东北面.故答案为:A.【分析】观察此地图可知,图中是按“上北下南,左西右东”来规定方向的,据此解答. 8.小红座位的西南方向是小丽,那么小红在小丽的( )方向。
五年级数学解决问题解答应用题练习题50经典题型带答案解析

五年级数学解决问题解答应用题练习题50经典题型带答案解析一、五年级数学上册应用题解答题1.市内固定电话的收费标准是前3分钟一共收费0.20元,以后每分钟0.15元。
小丽用固定电话给本市的姥爷打电话,一共花了1.40元。
小丽一共打了几分钟电话?2.为鼓励居民节约用水,许昌市自来水公司制定下列收费办法:每户每月用水12吨以内(含12吨),每吨收费3.4吨。
超出12吨部分,按4.6元/吨收取。
(1)小明家十月份用水14吨,该交费多少元?(2)兰兰家十月份交水费73元,她家十月份用水多少吨?3.为了鼓励居民节约用水,某市采用了“阶梯水价”的分段计费方式,收费标准如下表:每月用水量收费标准第一段0-15吨(含15吨) 3.4元/吨第二段超过15吨的部分 5.5元/吨(1)小强家上月用水14吨,应交水费多少元?(2)小强家某个月共交水费62元,那么他家该月用水多少吨?4.一条路上有A、O、B三个地点,O在A与B之间,A与O相距1360米。
甲、乙两人同时分别从A和O点出发向B点行进,出发10分钟后,甲、乙两人离O点的距离相等;40分钟后,甲、乙两人第一次在B点相遇,那么O与B两点的距离是多少米?5.某市的出租车收费标准如下:乘车路程2千米(包括2千米)收费6元,超过2千米的部分每千米收费1.2元(不足1千米按1千米计算),张老师打车上班花了10.8元,张老师家距离学校多少千米?6.文钟在计算4.68除以一个数时,由于商的小数点向左多点了一位,结果得0.36.这道题的除数是多少?7.为了鼓励居民节约用水,自来水公司规定:每户每月用水10吨以内(含10吨),按每吨2.5元收费;超过10吨的,其超出的部分按每吨5.5元收费。
(1)小强家上月用水12吨,应交水费多少元?(2)小华家上个月共交水费52.5元,那么他家上月用水多少吨?8.育英小学五年级一班实行垃圾分类处理,11月份共收集垃圾21.7kg,其中可回收利用的垃圾是不可回收利用垃圾的5.2倍,两种垃圾各多少kg?9.帮妈妈卖水果。
小学数学鸡兔同笼经典习题及答案

1.一个笼子里有若干只鸡和兔,共有35个头和94只脚,请问笼子里有多少只兔子和鸡?解答:设鸡的数量为x,兔的数量为y,则有以下方程组:x + y = 35 (头数方程)2x + 4y = 94 (脚数方程)解得x = 23,y=12,因此笼子里有23只鸡和12只兔子。
2.有一只笼子里装有鸡和兔子,共有48只脚和20个头,请问笼子里有多少只鸡和兔子?解答:设鸡的数量为x,兔的数量为y,则有以下方程组:x + y = 20 (头数方程)2x + 4y = 48 (脚数方程)解得x = 8,y=12,因此笼子里有8只鸡和12只兔子。
3.一只笼子里共有鸡和兔子46只,它们的脚数为124只,请问笼子里有几只鸡和兔子?解答:设鸡的数量为x,兔的数量为y,则有以下方程组:x + y = 46 (头数方程)2x + 4y = 124 (脚数方程)解得x = 22,y=24,因此笼子里有22只鸡和24只兔子。
4.一个笼子里面关着若干只鸡和兔子。
如果数了一下它们的头共有34个,数了一下它们的脚共有94只,那么笼子里应该有几只兔子和几只鸡?解答:设鸡的数量为x,兔的数量为y,则有以下方程组:x + y = 34 (头数方程)2x + 4y = 94 (脚数方程)解得x = 18,y=16,因此笼子里有18只鸡和16只兔子。
5.一个笼子里面有若干只鸡和兔子,如果数了一下这些动物的头一共有24个,数了一下它们的腿一共有64只,那么笼子里应该有几只兔子和几只鸡?解答:设鸡的数量为x,兔的数量为y,则有以下方程组:x + y = 24 (头数方程)2x + 4y = 64 (脚数方程)解得x = 12,y=12,因此笼子里有12只鸡和12只兔子。
6.一个笼子里面有若干只鸡和兔子,如果数了一下这些动物的头一共有27个,数了一下它们的腿一共有84只,那么笼子里应该有几只兔子和几只鸡?解答:设鸡的数量为x,兔的数量为y,则有以下方程组:x + y = 27 (头数方程)2x + 4y = 84 (脚数方程)解得x = 15,y=12,因此笼子里有15只鸡和12只兔子。
小学数学练习题及答案解析

小学数学练习(满分120分,考试时间为60分钟)一、选择题(请在答卷卡上填涂信息点,每小题2分,共10分)1. 下面四个算式中( )的结果最大.(a 是不等于0的自然数)A. a -56B. a ×56C. a +56D. 无法确定 【参考答案】C【考核知识点】分数计算【解析】一个数加上一个不为零的数要大于减去这个不为零的数;一个不为零的数乘小于1的数比它本身要小,所以C 答案结果最大.2. 周长都相等的圆、正方形和三角形,它们的面积( ).A. 圆最大B.正方形最大C. 长方形最大D. 一样大【参考答案】A【考核知识点】图形面积【解析】周长一样,圆的面积最大;面积一样则长方形的周长最长.3. 如图,E 是梯形ABCD 下底BC 边的中点,则图中与阴影三角形CDE 面积相等的三角形共有( ).A. 1个B. 2个C. 3个D. 4个【参考答案】C【考核知识点】三角形的面积【解析】 等底等高的三角形,面积相等;因为E 点是BC 边的中点,所以BE =EC,三角形ABE 、三角形DBE 、三角形AEC 的面积都与三角形DEC 面积相等.4. 白菜2元一斤,菜心3元一斤,小亮有10元钱,则他可以买( ).A. 1斤白菜4菜心B. 2斤白菜2菜心C. 2斤白菜3菜心D. 4斤白菜1菜心【参考答案】B【考核知识点】价格问题【解析】利用“单价×数量=总价”即可以一一排除,得出答案为B 选项.5. 下面各数,在读数时一个“零”字也不用读的是( ).A. 620080000B. 35009000C. 700200600D. 80500000【参考答案】B【考核知识点】大数的读写【解析】此题主要考查学生对以大数的读写知识点.大数的读写,先四位为一级,从右往左先分级,对于同一级的中间连续有多个0,只需读一个0,每级末尾的0不用读.二、判断题(请在答卷上填涂信息点,判对则填A ;判错则填B.每小题2分,共10分)1. 一件工程,20人去做,15天完成;如果30人去做,10天就可以完成. ( )【参考答案】A【考核知识点】工程问题【解析】根据题意可以把工作总量看成1,即每个人的工作效率是1÷20÷15=3001.因此当30人做,所需时间为1÷(3001×30)=10天.2. 27化成小数后是一个无限不循环小数. ( ) 【参考答案】B【考核知识点】循环小数【解析】任何一个最简分数化成小数时,分母如果只包含2和5的因数就可以化成有限小数;如果含有2和5以外的因数就只能化成无限循环小数.3. 一个长方形的长和宽都增加5厘米,那么它的面积增加25平方厘米.( )【参考答案】B【考核知识点】图形的面积【解析】如下图,当长方形的长和宽都增加5厘米后,增加的面积应该为图中的阴影部分面积,可知增加的面积不只是25平方厘米.4. 把一个不为零的数扩大100倍,只需要在这个数的末尾添上两个零.()【参考答案】B【考核知识点】数的扩大或缩小【解析】此题忽略了这个数是小数的情况,如果这个数是小数的话,应该是这个数的小数点向右边移动两位,所以题目的观点不够全面.5. 已知一刀可以把一个平面切成2块,两刀最多可以把一个平面切成4块,三刀最多可以切成7块……,由此可以推测,五刀最多可以切成16块.()【参考答案】A【考核知识点】找规律【解析】一个平面,切一刀,1+1=2块,以此类推1+1+2+3+4+5=16,也就是5刀可以切成16块.三、填空题(每小题2分,共20分)1. 数102.6连续减去个1.9,结果是0.【参考答案】54【考核知识点】求一个数里包含多少个另一个数,用除法计算【解析】一个数连续减去一个不为零的数,最后结果等于0.证明大的数是小的数的倍数,则可以用除法进行计算,102.6÷1.9=54.2. 2000名学生排成一排按1,2,3,4,5,6,7,6,5,4,3,2,1,1,2,3,4,5,6,7,6,5,4,3,2,1,1,2……循环报数,则第2000名学生所报的数是 .【参考答案】3【考核知识点】周期问题【解析】根据题意,可知一个周期的个数为13,用2000÷13=153·······11,余数是11,对应的数是周期中的第11位数,即可知是3.3. 如果a ※b 表示a +b 2,那么5※(4※8)= . 【参考答案】5.5或112【考核知识点】新定义运算【解析】根据“a ※b 表示a +b 2”将数值代入计算,注意有括号需先算括号里面的,再算括号外面的.4. 一个长8厘米,宽5厘米的长方形,如右图所示折一折,得到右边的图形,阴影部分四个三角形的周长之和是 厘米.【参考答案】26【考核知识点】图形周长【解析】根据图示,找到围成阴影部分的所有线段,可以发现围成阴影部分的周长即是原来围成这个长方形的周长,则求阴影部分的周长即是求原来长方形的周长,所以(8+5)×2=26(厘米).5. 甲、乙、丙三个同学到图书馆去借书,甲每6天去一次,乙每8天去一次,丙每9天去一次,如果2015年1月5日他们三人在图书馆相遇,那么下一次他们一起到图书馆相遇是 月 日.【参考答案】3月18【考核知识点】公倍数和公因数【解析】甲每6天去一次,乙每8天去一次,丙每9天去一次,可知:他们从2015年1月5日到下一次他们三人在图书馆相遇之间的天数是6、8、9的最小公倍数.又知6,8,9的最小公倍数是72,那么1月5日加上72天后就是3月18号,注意其中2015年的2月份只有28日.6. 甲数比乙数多三分之一,甲数与乙数的比是 .【参考答案】4:3【考核知识点】分数和比【解析】单位“1”做分母,那么乙数有3份,甲数有3+1=4份,那么甲数与乙数的比就可以得出4:3.7. 一个正方体木块,棱长4厘米,把它的外表都涂成绿色,然后切割成棱长为1厘米的小正方体,那么没有一个面是绿色的小正方体有个.【参考答案】8【考核知识点】立体图形的表面积和体积【解析】由题意得问题所问是包在正方体里面的小的正方体的个数,也就是棱长为(4-1-1=2cm),那么没有涂色的个数为2×2×2=8个.8. 王叔叔记得李叔叔的七位电话号码的前五位数:76045□□,还记得其中最大数字是7,各个数字又不重复,但忘记最后两位数字是什么了.王叔叔要拨通李叔叔的电话,最多要试拨打次.【参考答案】6【考核知识点】排列组合【解析】由题意得,这两个数字为1,2,3中取出2个再排列,那么可以得的可能是6种:12,13,21,23,31,32.9、一辆汽车上山速度是每小时行40千米,下山速度是每小时行60千米.由此可知这辆车上、下山的平均速度是每小时千米.【参考答案】48千米【考核知识点】行程问题【解析】根据“平均速度=总路程÷总时间”,可得:上、下山的总路程为2,则总时间是1÷40+1÷60=124,那么平均速度为:2÷124=48(千米/时).10、社会主义核心价值观是:富强、民主、文明、和谐;自由、平等、公正、法制;爱国、敬业、诚信、友善,一共包括24个字,现有4,4,10,10这四个数,仅使用加减乘除运算符号和括号,列出一条算式,算出结果是24.这条算式是 .【参考答案】(10×10-4)÷4【考核知识点】四则运算、数字谜【解析】注意加、减、乘、除的运算顺序及括号的使用.四、计算题(3小题,共34分)1、直接写出得数.(每小题1分,共10分)(1)25 +16 = (2)13-414= (3)0.75×4= (4)5.6÷0.04= (5)3×51÷7= (6)8.5-3.5×2=(7)5×57 ÷57 ×5= (8)(13 -17)×21= (9)0.375÷14 +1= (10)3÷(112+3)= 【参考答案】1730 834 3 140 1537 1.5 25 4 2.5 23 【考核知识点】基础计算【解析】将小数化分数或分数化小数计算,注意约分.2、用尽量简便的方法计算,并写出计算过程.(每小题4分共12分,不能体现简便计算则不能得分)(1)(437+1.9-2.85)+(1.1-2.15) 【参考答案】=437+1.9-2.85+1.1-2.15 =437+(1.9+1.1)-(2.85+2.15) =437+3-5 =237 【考核知识点】带符号搬家、减法性质【解析】同级运算,可带符号搬家,注意是带数字前面的符号;利用减法性质凑整.(2)10÷8+3.96×12.5%+2.04×18【参考答案】=10×18 +3.96×18 +2.04×18=18×(10+3.96+2.04) =18×16 =2【考核知识点】乘法分配律【解析】将“÷”变成“×”,除以一个数等于乘这个数的倒数;把百分数化成分数,再利用乘法分配律计算.(3)32-0.8×(10.25+14.75)÷1.25【参考答案】=32-0.8×25÷1.25=32-20×45=32-16=16【考核知识点】四则运算【解析】按照运算顺序运算,注意将小数化成分数的方法.3、解方程(每小题4分,共12分)(1)8x ÷0.7=8【参考答案】解:8x =8×0.7x =5.6÷8x =0.7【考核知识点】解方程【解析】 先通过等号两边同时×0.7消掉0.7,再两边同时÷8消掉8,得出x =0.7.(2)17 m +14 =14m【参考答案】解:14 m -17 m =14328 m =14m =14 ÷328m =73 【考核知识点】移项解方程【解析】等号两边都有x 的方程需要将含有x 的项都移到等号的一边,注意是小的移到大的一边,移动的过程需要变号.另外,可用“加数=和-另一个加数”,然后根据天平法则解方程.(3)0.4:x =(1+18):5 【参考答案】解:(1+18)x =0.4×5 98x =2 x =2÷98x =169 【考核知识点】解比例【解析】根据“內项积=外项积”,再按照常规解方程方法进行求解,另外,也可以把“:”转化成“÷”来解方程.五、解答题(6小题,共46分)1.(6分)做一种零件,8人0.5小时完成64个,照这样计算,3小时要完成144个零件,需要多少个工人?【参考答案】 64÷8÷0.5=16(个) 144÷3÷16=3(人)【考核知识点】归一问题【解析】用连除,先求出一个人一小时可以完成几个;再用连除,平均分.2.(6分)小雨在超市用若干元钱买了某种品牌的饮料28盒,过一段时间再去逛超市,发现这种饮料进行降价销售,每盒降价0.6元,他用同样的钱比上次多买了3盒,求这种饮料降价前每盒多少元?【参考答案】28×0.6÷3=5.6(元/盒) 5.6+0.6=6.2(元/盒)【考核知识点】价格问题【解析】根据题意可知,每盒降价0.6元,则28盒共应节约了28×0.6=16.8(元),用同样的钱比上次多买了3盒,即16.8元买了3盒,现在每盒16.8÷3=5.6(元),所以这种饮料降价前每盒为5.6+0.6=6.2(元).3.(8分)一块正方形的草地,边长为3米,在两个对角的顶点处各种一棵树,树上各栓一只羊,绳长都是3米.问两只羊都能吃到草的草地面积有多大?(圆周率取3.14)【参考答案】14×3.14×32=7.065(平方米) 3×3÷2=4.5(平方米)(7.065-4.5)×2=5.13(平方米)【考核知识点】圆的面积、阴影部分的面积【解析】根据题意,画图①,可知图②中阴影部分的面积即为两只羊都能吃到草的草地面积.4. (8分)甲、乙两人分别从A、B两地出发相向而行,到达目的地后马上调头返回到出发点,他们第一次相遇时距A地800米,第二次相遇时距B地500米.A、B两地相距多少米?【参考答案】1900米【考核知识点】直线多次相遇问题【解析】他们第一次相遇时两车共走一个全程,甲车走了800米;第二次相遇时两车共走了三个全程,甲车应走800×3=2400(米).而甲车走的路程恰好是一个全程+500米,所以A、B 两地相距2400-500=1900(米).5. (8分)两根蜡烛,一根较细,长30厘米,可燃烧3小时;一根较粗,长20厘米,可燃烧4小时.同时点燃这两根蜡烛.(1)请你仔细观察图1中细蜡烛燃烧过程的图示,然后把粗蜡烛的燃烧情况表示在图2的方格图中.【参考答案】【考核知识点】数形结合【解析】根据图1可知,细蜡烛在燃烧过程中,每个小时的长度变化是一样的,1小时长度缩短30÷3=10(厘米),所以粗蜡烛在燃烧过程中每小时的长度缩短20÷4=5(厘米),由此可以画出图形.(2)请将图1图2两个图画在同一幅图(图3)中,请写出点燃几个小时后两根蜡烛一样高?此时高度是多少?【参考答案】答:点燃2小时后两根蜡烛一样高,此时高度是10厘米.【考核知识点】数形结合【解析】根据图1和图2可画出图形.由图形可看出,2小时后,粗、细两根蜡烛的燃烧过程图相交于一点,此时对于的蜡烛高度为10厘米.6. (10分)如图,房间里地面是长方形形状,它由9个不同大小的正方形地砖拼接铺成,其中最小的地砖边长为1,试求这个房间的地面面积.【参考答案】1056【考核知识点】数形结合、用方程解决问题【解析】如右下图所示,黑色部分正方形边长为1,其他正方形边长未知.所以可以设AB的长度为x,那么1号正方形边长为(x+1),2号正方形边长为(x+2),3号正方形边长为(x+3),4号正方形边长为(x+4),5号正方形边长为4号正方形边长与AB的差,也就是x+4-x=4,6号正方形边长为(x+8),7号正方形边长为(2x+3),8号正方形边长为(x+12). 根据长方形的宽相等可以列方程:(x+3)+(x+2)+(2x+3)=(x+8)+(x+12)解得:x=6所以长方形的长为:(2x+3)+(x+12)=(2×6+3)+(6+12)=15+18=33宽为:(x+8)+(x+12)=(6+8)+(6+12)=14+18=32长方形的面积为:33×32=1056。
小学生奥数练习题及答案解析

小学生奥数练习题及答案解析1.小学生奥数练习题及答案解析篇一1、两块同样长的布,第一块用去32米,第二块用去20米,结果所余的米数第二块是第一块的3倍。
两块布原来各长多少米?【解析】设块布原来长x米所以x-20=3×(x-32),解得x=38米2、一个正方形,被分成5个相等的长方形,每个长方形的周长是60厘米,正方形的周长是多少厘米【解析】假设正方形的边长为x厘米所以,解得x=25厘米因此正方形的周长为25×4=100厘米2.小学生奥数练习题及答案解析篇二1、甲袋盐的重量是乙袋盐的3倍,如果从甲袋中取出15千克盐倒入乙袋中,那么两袋盐的重量就相等了,问两袋盐有重量多少千克?【解析】因为从甲袋中取出15千克盐倒入乙袋中,那么两袋盐的重量就相等了,说明甲袋盐的重量比乙袋多15×2=30千克,又因为甲袋盐的重量是乙袋盐的3倍,即甲袋比乙袋多2倍的乙袋盐,所以乙袋盐的重量为30÷2=15千克,甲袋盐的重量为15×3=45千克2、两堆煤重量相等,现从甲堆运走24吨煤,乙堆又运入8吨,这时乙堆煤的重量是甲堆的3倍,问两堆煤原来各有多少吨煤?【解析】设原来两堆煤重量都是x吨,那么甲堆运走24吨煤后剩下x-24吨,乙堆又运入8吨还有x+8吨,所以x+8=3×(x-24),解得x=40吨3.小学生奥数练习题及答案解析篇三1、甲、乙、丙三个数,甲、乙的和比丙多59,乙、丙的和比甲多49,甲、丙的和比乙多85,求这三个数。
【解析】甲+乙=丙+59......(1)乙+丙=甲+49......(2)甲+丙=乙+85 (3)相加得到:甲+乙+丙=59+49+85=193 (4)(4)-(1)得:丙=134-丙,解得丙=67;(4)-(2)得:甲=144-甲,解得甲=72;(4)-(3)得:乙=108-乙,解得乙=542、小明期末考试语文、数学、英语的平均分是95分,数学比语文多6分,英语比语文多9分,求三门功课各多少分?【解析】数学=语文+6,英语=语文+9,数学+语文+英语=3×95=2853×语文+6+9=285,解得:语文=90所以数学为90+6=96分,英语为90+9=99分4.小学生奥数练习题及答案解析篇四1、一个筐里装着52个苹果,另一个筐里装着一些梨。
小学数学50道经典奥数题及解析

小学数学50道经典奥数题及解析1. 小明的妈妈给他买了一些贴纸,其中3/4是花纹贴纸,剩下的是字母贴纸。
如果小明得到了60个字母贴纸,那么他一共收到了多少个贴纸?解析:假设小明一共收到了x个贴纸,则有3/4x是花纹贴纸,剩下的x - 3/4x = 1/4x 是字母贴纸。
根据题目可得:1/4x = 60。
解方程可得:x = 240。
所以小明一共收到了240个贴纸。
2. 某个数的三分之一加上四分之一等于40,这个数是多少?解析:设这个数为x,根据题目可得:1/3x + 1/4x = 40。
化简方程可得:7/12x = 40。
解方程可得:x = 40 * 12 / 7 = 68.57。
所以这个数约等于68.57。
3. 甲、乙、丙三个人合作种地,甲每天种地的1/5,乙每天种地的1/4,丙每天种地的1/3。
如果三个人连续工作8天,他们一共种了多少地?解析:甲、乙、丙三个人每天种地的比例为1/5:1/4:1/3。
将分母相同化简后相加可得:12/60 + 15/60 + 20/60 = 47/60。
所以三个人连续工作8天一共种了(47/60) * 8 = 6.27 地。
4. 一个两位数,各位数字的和是9,除以6的余数是3。
这个两位数是多少?解析:设这个两位数为10a + b,其中a为十位上的数字,b为个位上的数字。
根据题目可得:a + b = 9,并且(10a + b) % 6 = 3。
列举10的倍数加上3的倍数得到的数,最终找到满足条件的两位数为33。
所以这个两位数是33。
5. 甲、乙、丙三个人一起喝了一桶水,甲喝了其中的1/4,乙喝了剩下的1/3,丙喝了剩下的1/2。
如果桶中还有1升水,那么这桶水一共有多少升?解析:设桶中水的总体积为x,根据题意可得:(3/4) * (2/3) * (1/2) * x = 1。
化简方程可得:x = 4/3。
所以这桶水一共有(4/3 + 1) = 7/3升,约等于2.33升。
小学数学经典题型和差问题应用题知识点讲解练习题及参考答案

小学数学和差问题知识点讲解+练习题+参考答案一、【含义】已知大、小两个数的和与差,求这两个数各是多少,我们称这类问题为和差问题。
二、【数量关系】较大的数=(和+差)÷ 2较小的数=(和-差)÷ 2三、【解题思路和方法】简单的题目:直接套用公式;复杂的题目:变通后再用公式。
例1 甲乙两班共有学生98人,甲班比乙班多6人,求两班各有多少人?解甲班人数=(98+6)÷2=52(人)乙班人数=(98-6)÷2=46(人)答:甲班有52人,乙班有46人。
例2 长方形的长和宽之和为18厘米,长比宽多2厘米,求长方形的面积。
解长=(18+2)÷2=10(厘米)宽=(18-2)÷2=8(厘米)长方形的面积=10×8=80(平方厘米)答:长方形的面积为80平方厘米。
例3有甲乙丙三袋化肥,甲乙两袋共重32千克,乙丙两袋共重30千克,甲丙两袋共重22千克,求三袋化肥各重多少千克。
解甲乙两袋、乙丙两袋都含有乙,从中可以看出甲比丙多(32-30)=2千克,且甲是大数,丙是小数。
由此可知甲袋化肥重量=(22+2)÷2=12(千克)丙袋化肥重量=(22-2)÷2=10(千克)乙袋化肥重量=32-12=20(千克)答:甲袋化肥重12千克,乙袋化肥重20千克,丙袋化肥重10千克。
例4 甲乙两车原来共装苹果97筐,从甲车取下14筐放到乙车上,结果甲车比乙车还多3筐,两车原来各装苹果多少筐?解“从甲车取下14筐放到乙车上,结果甲车比乙车还多3筐”,这说明甲车是大数,乙车是小数,甲与乙的差是(14×2+3),甲与乙的和是97,因此甲车筐数=(97+14×2+3)÷2=64(筐)乙车筐数=97-64=33(筐)答:甲车原来装苹果64筐,乙车原来装苹果33筐。
四、知识巩固题。
1.期末考试王平和李杨语文成绩的总和是188分,李杨比王平少4分,两人各考了多少分?2.两袋花生共重150千克,第二袋比第一袋多10千克,两袋大米各重多少千克?3.亮亮家养的白兔和黑兔一共有22只,如果再买4只白兔,白兔和黑兔的只数一样多,小勇家养的白兔和黑兔各多少只?4.小明和小华在一次数学竞赛中,小明小华一共考了160分,小明比小华多得40分,小明和小华各得多少分?5.两筐苹果共重150千克,第一筐比第二筐少10千克,两筐水果各多少千克?6.小明家的果园共260棵桃树和梨树,其中桃树的棵数比梨树多20棵,桃树和梨树各有多少棵?7.丽丽家养了30只鸡,母鸡比公鸡多8只,请问小红家养母鸡、公鸡各多少只?8.光明高中男生、女生共816人,男生人数比女生人数多74人,男、女生各多少人?9.四年级一班和二班共有85人,一班比二班多3人,问一班、二班各有多少人?10.甲、乙两桶油共重30千克,如果把甲桶中6千克油倒入乙桶,那么两桶油重量相等,问甲、乙两桶原有多少油?五、参考答案。
小学数学经典练习题及答案

小学数学经典练习题及答案【小学数学经典练习题及答案】第一部分:加法与减法(500字)题目1:小明有3个苹果,他又买了2个苹果,请问他一共有几个苹果?答案:小明一共有5个苹果。
题目2:一列火车上有8节车厢,下来了3节车厢,请问还有几节车厢?答案:火车上还有5节车厢。
题目3:小华家有15本书,他借给小明4本书,请问小华家还有几本书?答案:小华家还有11本书。
题目4:班级里有20个男生和15个女生,请问男生比女生多几个?答案:男生比女生多5个。
题目5:小明做了一个游戏,开始时有7个红球和9个蓝球,他将其中的3个红球和2个蓝球放入盒子里,请问还剩下几个球?答案:还剩下4个红球和7个蓝球。
第二部分:乘法与除法(500字)题目1:小丽买了4包糖果,每包有5颗,请问她一共买了几颗糖果?答案:小丽一共买了20颗糖果。
题目2:小明的家里有24只鸡,分成3组,请问每组有多少只鸡?答案:每组有8只鸡。
题目3:某个果园里有15棵苹果树,每棵树上结了8个苹果,请问一共有几个苹果?答案:一共有120个苹果。
题目4:班级里有32个学生,老师要将他们平均分成4个小组,请问每个小组有几个学生?答案:每个小组有8个学生。
题目5:小华有50元,他想买5本书,每本书的价格一样,请问每本书多少钱?答案:每本书10元。
第三部分:数的大小与顺序(500字)题目1:请将以下数字从小到大排列:19、36、5、12、8。
答案:5、8、12、19、36。
题目2:请将以下数字从大到小排列:45、10、29、33、16。
答案:45、33、29、16、10。
题目3:小明把一大桶水平均分给4个同学,每个同学得到了多少水?答案:每个同学得到了1/4桶水。
题目4:请按千位数字从小到大的顺序排列以下数字:2734、5019、3567、1002、4526。
答案:1002、2734、3567、4526、5019。
题目5:请将下面的数字从小到大排列:2/5、2/3、1/2、3/4、1/3。
小学数学三年级下册第三单元经典练习题(含答案解析)
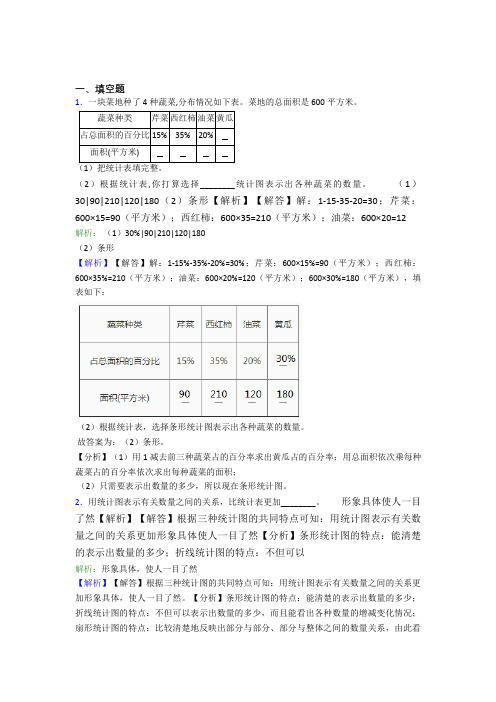
一、填空题1.一块菜地种了4种蔬菜,分布情况如下表。
菜地的总面积是600平方米。
蔬菜种类芹菜西红柿油菜黄瓜占总面积的百分比15%35%20%面积(平方米)(1)把统计表填完整。
(2)根据统计表,你打算选择________统计图表示出各种蔬菜的数量。
(1)30|90|210|120|180(2)条形【解析】【解答】解:1-15-35-20=30;芹菜:600×15=90(平方米);西红柿:600×35=210(平方米);油菜:600×20=12解析:(1)30%|90|210|120|180(2)条形【解析】【解答】解:1-15%-35%-20%=30%;芹菜:600×15%=90(平方米);西红柿:600×35%=210(平方米);油菜:600×20%=120(平方米);600×30%=180(平方米),填表如下:(2)根据统计表,选择条形统计图表示出各种蔬菜的数量。
故答案为:(2)条形。
【分析】(1)用1减去前三种蔬菜占的百分率求出黄瓜占的百分率;用总面积依次乘每种蔬菜占的百分率依次求出每种蔬菜的面积;(2)只需要表示出数量的多少,所以现在条形统计图。
2.用统计图表示有关数量之间的关系,比统计表更加________。
形象具体使人一目了然【解析】【解答】根据三种统计图的共同特点可知:用统计图表示有关数量之间的关系更加形象具体使人一目了然【分析】条形统计图的特点:能清楚的表示出数量的多少;折线统计图的特点:不但可以解析:形象具体,使人一目了然【解析】【解答】根据三种统计图的共同特点可知:用统计图表示有关数量之间的关系更加形象具体,使人一目了然。
【分析】条形统计图的特点:能清楚的表示出数量的多少;折线统计图的特点:不但可以表示出数量的多少,而且能看出各种数量的增减变化情况;扇形统计图的特点:比较清楚地反映出部分与部分、部分与整体之间的数量关系,由此看出统计图比统计表具有的优点。
小学数学二年级下册第七单元经典习题(含答案解析)

一、选择题1.用、、三张卡片摆三位数,能摆成()个不同三位数。
A. 2个B. 4个C. 6个B解析: B【解析】【解答】解:能摆成4个不同的三位数。
故答案为:B。
【分析】因为要组成三位数,所以每个数放在首位,都有2种摆法,而0不能放在首位,所以一共有4种摆法。
2.一个四位数,它的千位上的数字和十位上的相同,百位上的数字和个位上的数字相同,它的个位上的数字是2,十位上的数字是个位上的4倍,这个数是()。
A. 4242B. 8282C. 2828B解析: B【解析】【解答】个位和百位上数字都是2,十位和千位上的数字都是2×4=8,这个数是8282。
故答案为:B。
【分析】先确定十位数字和千位数字,从高位到低位写出这个数。
整数的右边起依次是个位、十位、百位、千位。
3.估算576+284,下面说法正确的是()。
A. 它们的和比1000大一些。
B. 它们的和700小一些。
C. 576<600,284<300,它们的和一定小于900。
C解析: C【解析】【解答】576+284≈600+300=900故答案为:C。
【分析】根据估算方法,把两个加数分别看成整百数,都多看了,因此,估算求出的和大于实际的和。
4.195+495的和接近()。
A. 500B. 600C. 700C解析: C【解析】【解答】195≈200,495≈500,200+500=700。
故答案为:C。
【分析】根据整数的估算方法,先求出加数的近似数,再求和即可。
5.202与394的和大约是()。
A. 500B. 200C. 600C解析: C【解析】【解答】解:202+394≈600故答案为:C。
【分析】把202看作200,把394看作400,由此估算出两个数的和即可。
6.293+587的结果大约是()。
A. 900B. 800C. 700A解析: A【解析】【解答】293+587≈300+600=900故答案为:A。
【分析】估算和是多少时,先把加数看作与它最接近的整十、整百数,然后相加求和即可。
小学数学加减乘除练习题解析与详解

小学数学加减乘除练习题解析与详解在小学的数学学习中,加减乘除是最基本的运算。
通过不断的练习,孩子们能够掌握这些运算的技巧和方法,提高他们的数学能力。
本文将为大家解析和详解一些常见的小学数学加减乘除练习题。
一、加法1. 加法的定义加法是两个或多个数相加得到一个数的运算。
例如,2 + 3 = 5,表示将2和3相加等于5。
2. 加法的性质加法具有交换律、结合律和加零律。
- 交换律:a + b = b + a- 结合律:(a + b) + c = a + (b + c)- 加零律:a + 0 = a3. 加法的练习题解析与详解(1)题目:5 + 3 = ?解析:这是一个加法的题目,我们只需要将5和3相加即可。
详解:5 + 3 = 8(2)题目:12 + 8 = ?解析:这是一个两位数加一位数的题目,我们可以将12拆分成10和2,然后分别与8相加。
详解:12 + 8 = 10 + 2 + 8 = 20二、减法1. 减法的定义减法是一个数减去另一个数得到一个差的运算。
例如,7 - 4 = 3,表示将7减去4得到3。
2. 减法的性质减法具有不满足交换律、结合律和减零律,但具有减去零的性质。
- 减去零:a - 0 = a3. 减法的练习题解析与详解(1)题目:9 - 5 = ?解析:这是一个减法的题目,我们只需要将9减去5即可。
详解:9 - 5 = 4(2)题目:18 - 7 = ?解析:这是一个两位数减一位数的题目,我们可以直接将18减去7。
详解:18 - 7 = 11三、乘法1. 乘法的定义乘法是两个数相乘得到一个积的运算。
例如,3 × 4 = 12,表示将3和4相乘等于12。
2. 乘法的性质乘法具有交换律和结合律,但不具有乘一的性质。
- 交换律:a × b = b × a- 结合律:(a × b) × c = a × (b × c)3. 乘法的练习题解析与详解(1)题目:6 × 2 = ?解析:这是一个乘法的题目,我们只需要将6和2相乘即可。
小学数学除法练习题解析

小学数学除法练习题解析除法是小学数学中的重要内容之一,也是孩子们学习数学的一个里程碑。
通过解析小学数学除法练习题,我们可以帮助孩子们更好地理解和掌握除法运算。
本文将为您详细解析一些小学数学除法练习题。
题目一:求商及余数24 ÷ 3 = ?解析:此题要求我们计算24除以3的商及余数。
我们首先用长除法的方法解题。
8- ------3 | 2421- -----3通过长除法可知,24除以3的商为8,余数为0。
因此,24 ÷3 = 8。
题目二:多位数的除法运算1584 ÷ 6 = ?解析:这是一个多位数除以个位数的除法运算。
同样,我们用长除法的方法解题。
- -------6 | 1 5 8 41 5- -------8 47 8- -------6通过长除法可知,1584除以6的商为264,余数为6。
因此,1584 ÷ 6 = 264。
题目三:小数的除法运算5.4 ÷ 0.6 = ?解析:这是一个小数除以小数的除法运算。
为了便于计算,我们可以将除数和被除数都乘以10,将小数转化为整数。
54 ÷ 6 = ?同样,我们用长除法的方法解题。
9- -----4- -----通过长除法可知,54除以6的商为9,余数为0。
因此,5.4 ÷ 0.6 = 9。
通过以上几个例题,我们可以看出,在小学数学中,除法是一个重要的运算。
通过理解和掌握除法的计算方法,孩子们可以更好地解决数学问题,并发展他们的逻辑思维能力和数学推理能力。
使用合适的解法和步骤来解答除法题目,可以帮助孩子们准确地计算出商和余数。
长除法是小学阶段最常用的解题方法,可以帮助孩子们有条不紊地进行计算。
同时,练习除法运算也可以提高孩子们的注意力和耐心,培养他们的逻辑思维和问题解决能力。
除法是数学学习过程中的一个重要环节。
希望通过本文对小学数学除法练习题的解析,能够帮助学生们更好地掌握除法运算,提高他们的数学能力。
小学生数学加减乘除练习题解析

小学生数学加减乘除练习题解析数学是小学生学习的基础学科之一,掌握好数学的基本运算加减乘除对于小学生来说至关重要。
本文将为大家解析一些小学生常见的数学加减乘除练习题,帮助他们更好地理解和掌握这些运算。
一、加法运算加法是指将两个或多个数相加的运算。
首先我们先来解析一道简单的加法题目。
例题:小明有3个苹果,小红给了他2个苹果,小明一共有多少个苹果?解析:题目中给出了小明开始时有3个苹果,然后小红给了他2个苹果,所以我们需要将3和2相加。
计算过程如下:3+ 2-----5所以答案是5,小明一共有5个苹果。
二、减法运算减法是指将一个数减去另一个数的计算方法。
下面我们解析一个减法题目。
例题:小明有5个橙子,他吃了3个,还剩下几个橙子?解析:题目中给出了小明开始时有5个橙子,然后他吃了3个橙子,所以我们需要用5减去3。
计算过程如下:5- 3-----2所以答案是2,小明还剩下2个橙子。
三、乘法运算乘法是指将两个数相乘的计算方法。
接下来我们来解析一个乘法题目。
例题:小明有3个篮球,每个篮球的价格是5元,他一共需要支付多少钱?解析:题目中给出了小明有3个篮球,每个篮球的价格是5元,所以我们需要计算3乘以5。
计算过程如下:3× 5-----15所以答案是15,小明需要支付15元。
四、除法运算除法是指将一个数分成若干等分的计算方法。
下面我们解析一个除法题目。
例题:小明有6个橙子,他要把它们分给他的2个朋友,每个朋友分到几个?解析:题目中给出了小明有6个橙子,他要分给2个朋友,所以我们需要用6除以2。
计算过程如下:6÷ 2-----3所以答案是3,每个朋友分到3个橙子。
通过以上的加减乘除练习题的解析,我们可以看到每个题目都有一个明确的问题和对应的计算过程,通过正确地进行运算,我们可以得到准确的答案。
希望小学生们通过不断的练习和解析加深对数学运算的理解,提高自己的计算能力。
总结:数学加减乘除是小学生学习数学的基础,掌握好这些运算对学习其他数学知识起到重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结果就是草的生长速率。所以草的生长速率是45/3=15(牛/天);
原有的草量依此反推。
公式就是A头B天的吃草量减去B天乘以草的生长速率。
所以原有的草量=27X6-6X15=72(牛/天)。
将未知吃草量的牛分为两个部分:
例1:小军今年8岁,爸爸今年34岁,几年后,爸爸的年龄的小军的3倍?
岁差不会变,今年的岁数差点34-8=26,到几年后仍然不会变。
已知差及倍数,转化为差比问题。
26/(3-1)=13,几年后爸爸的年龄是13X3=39岁,小军的年龄是13X1=13岁,所以应该是5年后。
例2:姐姐今年13岁,弟弟今年9岁,当姐弟俩岁数的和是40岁时,两人各应该是多少岁?
一、和差问题
已知两数的和与差,求这两个数。
口诀:
和加上差,越加越大;
除以2,便是大的;
和减去差,越减越小;
除以2,便是小的。
例:已知两数和是10,差是2,求这两个数。
按口诀,则大数=(10+2)/2=6,小数=(10-2)/2=4。
二、鸡兔同笼问题
口诀:
假设全是鸡,假设全是兔。
所以甲数为:4X7=28,乙数为:4X4=16。
七、工程问题
口诀:
工程总量设为1,
1除以时间就是工作效率。
单独做时工作效率是自己的,
一齐做时工作效率是众人的效率和。
1减去已经做的便是没有做的,
没有做的除以工作效率就是结果。
例:一项工程,甲单独做4天完成,乙单独做6天完成。甲乙同时做2天后,由乙单独做,几天完
四、路程问题
(1)相遇问题
口诀:
相遇那一刻,路程全走过。
除以速度和,就把时间得。
例:甲乙两人从相距120千米的两地相向而行,甲的速度为40千米/小时,乙的速度为20千米/小
时,多少时间相遇?
相遇那一刻,路程全走过。即甲乙走过的路程和恰好是两地的距离120千米。
除以速度和,就把时间得。即甲乙两人的总速度为两人的速度之和40+20=60(千米/小时),所
成?
[1-(1/6+1/4)X2]/(1/6)=1(天)
八、植树问题。
口诀:
植树多少颗,
要问路如何?
直的减去1,
圆的是结果。
例1:在一条长为120米的马路上植树,间距为4米,植树多少颗?
路是直的。所以植树120/4-1=29(颗)。
例2:在一条长为120米的圆形花坛边植树,间距为4米,植树多少颗?
例2:士兵背子弹。每人45发则多680发;每人50发则多200发,多少士兵多少子弹?
全盈问题。大的减去小的,则公式为:(680-200)/(50-45)=96(人)则子弹为
96X50+200=5000(发)。
例3:学生发书。每人10本则差90本;每人8本则差8本,多少学生多少书?
全亏问题。大的减去小的。则公式为:(90-8)/(10-8)=41(人),相应书为41X10-
一小部分先吃新草,个数就是草的比率;
这就是说将要求的21头牛分为两部分,一部分15头牛吃新生的草;
剩下的21-15=6去吃原有的草,
所以所求的天数为:原有的草量/分配剩下的牛=72/6=12(天)
十一、年龄问题
口诀:
岁差不会变,同时相加减。
岁数一改变,倍数也改变。
抓住这三点,一切都简单。
90=320(本)
十、牛吃草问题
口诀:
每牛每天的吃草量假设是份数1,
A头B天的吃草量算出是几?
M头N天的吃草量又是几?
大的减去小的,除以二者对应的天数的差值,
结果就是草的生长速率。
原有的草量依此反推。
公式就是A头B天的吃草量减去B天乘以草的生长速率。
将未知吃草量的牛分为两个部分:
口诀:
加糖先求水,水完求糖水。
糖水减糖水,求出便解题。
例:有20千克浓度为15%的糖水,加糖多少千克后,浓度变为20%?
加糖先求水,原来含水为:20X(1-15%)=17(千克)
水完求糖水,含17千克水在20%浓度下应有多少糖水,17/(1-20%)=21.25(千克)
糖水减糖水,后的糖水量减去原来的糖水量,21.25-20=1.25(千克)
2=16(点)。
糖水减糖水,便是加糖量。
例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?
加水先求糖,原来含糖为:20X15%=3(千克)
糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3/10%=30(千克)
糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)
(2)加糖浓化
不要看商,
只要看余。
例:如果时钟现在表示的时间是18点整,那么分针旋转1990圈后是几点钟?
分针旋转一圈是1小时,旋转24圈就是时针转1圈,也就是时针回到原位。1980/24的余数是22,
所以相当于分针向前旋转22个圈,分针向前旋转22个圈相当于时针向前走22个小时,时针向前走
22小时,也相当于向后24-22=2个小时,即相当于时针向后拔了2小时。即时针相当于是18-
和乘以比例,所以甲数为27X2/9=6,乙数为:27X3/9=9,丙数为:27X4/9=12。
六、差比问题(差倍问题)
口诀:
我的比你多,倍数是因果。
分子实际差,分母倍数差。 商Biblioteka 一倍的, 乘以各自的倍数,
两数便可求得。
例:甲数比乙数大12,甲:乙=7:4,求两数。
先求一倍的量,12/(7-4)=4,
多了几只脚,少了几只足?
除以脚的差,便是鸡兔数。
例:鸡免同笼,有头36,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36X2)/(4-2)=24
求鸡时,假设全是兔,则鸡数=(4X36-120)/(4-2)=12
三、浓度问题
(1)加水稀释
口诀:
加水先求糖,糖完求糖水。
一小部分先吃新草,个数就是草的比率;
原有的草量除以剩余的牛数就将需要的天数求知。
例:整个牧场上草长得一样密,一样快。27头牛6天可以把草吃完;23头牛9天也可以把草吃完。
问21头多少天把草吃完。
每牛每天的吃草量假设是1,则27头牛6天的吃草量是27X6=162,23头牛9天的吃草量是
23X9=207;
以相遇的时间就为120/60=2(小时)
(2)追及问题
口诀:
慢鸟要先飞,快的随后追。
先走的路程,除以速度差,
时间就求对。
例:姐弟二人从家里去镇上,姐姐步行速度为3千米/小时,先走2小时后,弟弟骑自行车出发速
度6千米/小时,几时追上?
先走的路程,为3X2=6(千米)
速度的差,为6-3=3(千米/小时)。
岁差不会变,今年的岁数差13-9=4几年后也不会改变。
几年后岁数和是40,岁数差是4,转化为和差问题。
则几年后,姐姐的岁数:(40+4)/2=22,弟弟的岁数:(40-4)/2=18,所以答案是9年后。
十二、余数问题
口诀:
余数有(N-1)个,
最小的是1,最大的是(N-1)。
周期性变化时,
路是圆的,所以植树120/4=30(颗)。
九、盈亏问题
口诀:
全盈全亏,大的减去小的;
一盈一亏,盈亏加在一起。
除以分配的差,
结果就是分配的东西或者是人。
例1:小朋友分桃子,每人10个少9个;每人8个多7个。求有多少小朋友多少桃子?
一盈一亏,则公式为:(9+7)/(10-8)=8(人),相应桃子为8X10-9=71(个)
所以追上的时间为:6/3=2(小时)。
五、和比问题
已知整体求部分。
口诀:
家要众人合,分家有原则。
分母比数和,分子自己的。
和乘以比例,就是该得的。
例:甲乙丙三数和为27,甲;乙:丙=2:3:4,求甲乙丙三数。
分母比数和,即分母为:2+3+4=9;
分子自己的,则甲乙丙三数占和的比例分别为2/9,3/9,4/9。
