第4章-控制系统的根轨迹分析法PPT课件
合集下载
4-4 第四节 控制系统的根轨迹分析法 自动控制原理课件

时间。这些性能指标和闭环极点的关系如下:
% e 1 2 100% ectg 100%
ts
3
n
3
(为极点实部 )
n
j 1 2n
%和 的关系如下图 %
80
60
若闭环极点落在下图中红线包围
的区域中,有:
% ectg 和ts
3
40
20
0 30 60 90
上述结论也可应用于具有主导极点的高阶系统中。如下例:
是稳定的(为什么?);
kg 64 kg 14
当 kg 195和14 kg 64 时, 系统是不稳定的。
kg 14 kg 64
kg 195
左图是用Matlab工具绘
制的。
条件稳定系统:参数在一定的范围内取值才能使系统稳定,这 样的系统叫做条件稳定系统。
下面的系统就是条件稳定系统的例子:
A B
这是一个三阶系统,从根轨迹上看出,随着kg 的增加, 主导极点越显著。所以可以用二阶系统的性能指标近似计
算。 下面计算超调量和阻尼角的关系。由于:
% ectg1 100%, 当 % 18%时解得: 60
在根轨迹图上画两条与实轴夹角为 60的直线,与根轨 迹交与A、B两点。 则A、B两点就是闭环共轭主导极点, 这时系统的超调量为18%。通过求A、B两点的坐标,可以 确定这时的根轨迹增益kg ,进而求得开环放大系数k。
[例4-12]单位反馈系统的开环传递函数为:Gk
(s)
s(s
kg 4)( s
6)
若要求闭环单位阶跃响应的最大超调量 % 18% ,试确定 开环放大系数。
[解]:首先画出根 轨迹如右。由图 可以看出:根轨 迹与虚轴的交点 为+j5,-j5,这时的 临界增益 kgp 240 当 kg 240 时, 闭环系统不稳定。
自动控制理论 第四章根轨迹分析法PPT课件

s3 不是根轨迹上的点。
根据相角方程得系 统的根轨迹为:
第一节 根轨迹的基本概念
作业习题: 4-2 4-3 4-7
返回
第四章 根轨迹分析法
第二节 绘制根轨迹的基本方法
根据根轨迹方程,无需对闭环特征方程式 求解,只需寻找所有满足相角方程的 s ,便可 得到闭环特征方程式根的轨迹。同时,可由幅
值方程来确定根轨迹所对应的Kr值。
闭s环s22 +特K2rs=征0+↑KKr 方1r=程s110 式 特征-2 方程-1的根0 σ
(1R)左(从s) 半根- 平轨s面(迹sK+r为2可) 稳C知(s定): 极点;右半平面为 不稳Kr定极s1点;虚s2轴 上为0临界0极点。-2
(2)有01<2呈Kr过<-11-阻1+时j 尼,状-系1-1-态j统。
根据根轨迹的基本特征和关键点,就能比较 方便地近似绘制出根轨迹曲线。
根轨迹基本特征为以下八条:
第二节 绘制根轨迹的基本方法
一、根轨迹的对称性和分布性 二、根轨迹的起点和终点 三、实轴上的根轨迹段 四、根轨迹的渐近线 五、根轨迹的分离点和会合点 六、根轨迹的出射角和入射角 七、根轨迹与虚轴的交点 八、开环极点与闭环极点的关系
p2
p1
-2
0σ
环传递函数的极点
第二节 绘制根轨迹的基本方法
2. 终点
根轨迹方程:
m
i
n=1((ss--pzji))=
-
1 Kr
m
j =1
Kr
i n=1((ss--pzji))=0
j =1
m
则 i =1(s-zi) =0 即 s=zi
8 8
m条根轨迹终止于开环传递函数的零点
根轨迹法(自动控制原理)ppt课件精选全文完整版

1 K (s z1 )( s z2 )....( s zm ) 0 (s p1 )( s p2 )....( s pn )
课程:自动控制原理
第4章 根轨迹法
➢ 以K为参变量的根轨迹上的每一点都必须满足以上方程, 相应地,称之为‘典型根轨迹方程’。
也可以写成
m
n
(s zl ) K (s pi ) 0
可见,根轨迹可以清晰地描绘闭环极点与开环增益K之间的 关系。
课程:自动控制原理
第4章 根轨迹法
2.根轨迹的基本条件
❖ 考察图示系统,其闭环传递函数为:
Y(s) G(s) R(s) 1 G(s)H(s)
闭环特征方程为:
1 G(s)H(s) 0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根,所以根轨 迹上的每一点都应满足:
l 1
i 1
对应的幅值条件为:
相角条件为:
n
( s pi ) K i1
m
(s zl )
l 1
m
n
(s zl ) (s pi ) (2k 1)180
k 1,2,
l 1
i 1
课程:自动控制原理
第4章 根轨迹法
❖ 上述相角条件,即为绘制根轨迹图的依据。具体绘制方法 是:在复平面上选足够多的试验点,对每一个试验点检查 它是否满足相角条件,如果是则该点在根轨迹上,如果不 是则该点不在根轨迹上,最后将在根轨迹上的试验点连接 就得到根轨迹图。
显然,位于实轴上的两个相邻的开环极点之间一定有分离 点,因为任何一条根轨迹不可能开始于一个开环极点终止 于另一个开环极点。同理,位于实轴上的两个相邻的开环 零点之间也一定有分离点。
课程:自动控制原理
第4章 根轨迹法
课程:自动控制原理
第4章 根轨迹法
➢ 以K为参变量的根轨迹上的每一点都必须满足以上方程, 相应地,称之为‘典型根轨迹方程’。
也可以写成
m
n
(s zl ) K (s pi ) 0
可见,根轨迹可以清晰地描绘闭环极点与开环增益K之间的 关系。
课程:自动控制原理
第4章 根轨迹法
2.根轨迹的基本条件
❖ 考察图示系统,其闭环传递函数为:
Y(s) G(s) R(s) 1 G(s)H(s)
闭环特征方程为:
1 G(s)H(s) 0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根,所以根轨 迹上的每一点都应满足:
l 1
i 1
对应的幅值条件为:
相角条件为:
n
( s pi ) K i1
m
(s zl )
l 1
m
n
(s zl ) (s pi ) (2k 1)180
k 1,2,
l 1
i 1
课程:自动控制原理
第4章 根轨迹法
❖ 上述相角条件,即为绘制根轨迹图的依据。具体绘制方法 是:在复平面上选足够多的试验点,对每一个试验点检查 它是否满足相角条件,如果是则该点在根轨迹上,如果不 是则该点不在根轨迹上,最后将在根轨迹上的试验点连接 就得到根轨迹图。
显然,位于实轴上的两个相邻的开环极点之间一定有分离 点,因为任何一条根轨迹不可能开始于一个开环极点终止 于另一个开环极点。同理,位于实轴上的两个相邻的开环 零点之间也一定有分离点。
课程:自动控制原理
第4章 根轨迹法
自动控制原理第四章-根轨迹分析法

jω
×
p4 z 2
×
p3
×
×
p 2 z1 p1
σ
规则4:根轨迹的分会点(分离点和会合点)d。 (1)定义:分会点是指根轨迹离开实轴进入复平面的点(分 离点)或由复平面进入实轴的点(汇合点),位于相邻两极点 或两零点之间。
(2)位置:大部分的分会点在实轴上,若出现在复平面内时,则 成对出现。
(3)特点:分会点对应于闭环特征方程有重根的点;根轨迹离开
(4)与虚轴的交点:
方法1:闭环特征方程为s3 + 6s2 + 8s + K*= 0 令s = jω得:-jω3 -6ω2 + j8ω + K* = 0
-6ω2 + K* = 0 即
-ω3 + 8ω= 0
K* = 48 ω= 2.8 s-1
方法2:闭环特征方程为 s3 + 6s2 + 8s + K*= 0 列劳斯表如下:
规则1:根轨迹的起点和终点。 根轨迹起始于开环极点,终止开环零点或无穷远。
m
i 1
s
zi
n
s
l 1
pl
1 K
K
K
0 s pl
s s
zi , m条 (, n
m)条
规则2: 根轨迹的条数和对称性。 n阶系统有n条根轨迹。根轨迹关于实轴对称。
规则3: 实轴上的根轨迹分布。
由实数开环零、极点将实轴分为若干段,如某段右边 开环零、极点(包括该段的端点)数之和为奇数,则该段就 是根轨迹,否则不是。如下图所示。
又因为开环传函的零极点表达式为:
m
GK (s)
G(s)H(s)
K
n
(s
×
p4 z 2
×
p3
×
×
p 2 z1 p1
σ
规则4:根轨迹的分会点(分离点和会合点)d。 (1)定义:分会点是指根轨迹离开实轴进入复平面的点(分 离点)或由复平面进入实轴的点(汇合点),位于相邻两极点 或两零点之间。
(2)位置:大部分的分会点在实轴上,若出现在复平面内时,则 成对出现。
(3)特点:分会点对应于闭环特征方程有重根的点;根轨迹离开
(4)与虚轴的交点:
方法1:闭环特征方程为s3 + 6s2 + 8s + K*= 0 令s = jω得:-jω3 -6ω2 + j8ω + K* = 0
-6ω2 + K* = 0 即
-ω3 + 8ω= 0
K* = 48 ω= 2.8 s-1
方法2:闭环特征方程为 s3 + 6s2 + 8s + K*= 0 列劳斯表如下:
规则1:根轨迹的起点和终点。 根轨迹起始于开环极点,终止开环零点或无穷远。
m
i 1
s
zi
n
s
l 1
pl
1 K
K
K
0 s pl
s s
zi , m条 (, n
m)条
规则2: 根轨迹的条数和对称性。 n阶系统有n条根轨迹。根轨迹关于实轴对称。
规则3: 实轴上的根轨迹分布。
由实数开环零、极点将实轴分为若干段,如某段右边 开环零、极点(包括该段的端点)数之和为奇数,则该段就 是根轨迹,否则不是。如下图所示。
又因为开环传函的零极点表达式为:
m
GK (s)
G(s)H(s)
K
n
(s
第四章控制系统的根轨迹分析法
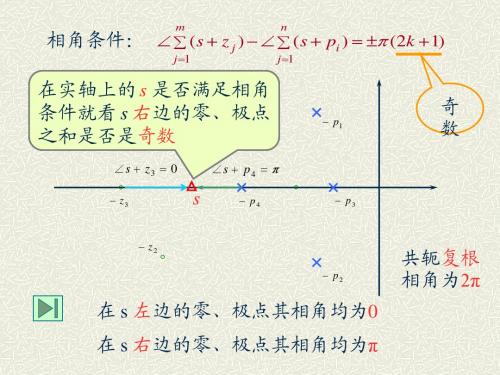
○
− p4
− p3
∠s + z 2
∠s + p2
− p2
共轭复根 相; ∠s + p2 = 2π 在 s 左边的零、极点其相角均为0
∠s + z1 + ∠s + z2 = 2π 在 s 右边的零、极点其相角均为π
n m 0 出射角公式: 出射角公式: θ pc =180 + ∑θzj − ∑θ pi j =1 i=1
ζ = 0.707
s’ s’
-2 0
K −1
Re
-1
根轨迹法的分析基本思路: 根轨迹法的分析基本思路 目的: 目的
①解决高阶系统求解特征根比较困难 的实现; 寻找到一种方便、 的实现 ②寻找到一种方便、有效的描述 系统的根轨迹的方法。 系统的根轨迹的方法。
方法: 方法
① 根据开环零极点的分布绘制出系统 的根轨迹图; 的根轨迹图;②利用根轨迹法来分析和设 计系统. 计系统
S1
0 -1 -1+j -1+j∞
∞ ↑ K
S2
-2 -1 -1-j -1-j∞ jω
1 S1 0 σ -1
闭环特征方程式 S2+2S+K= 0
S2 -2
特征方程的根 S1.2 = -1± 1-K ±
K变化时,闭环特征根 变化时,
在S平面上的轨迹图形
-1 K ∞ ↑
系统特征方程为 求得两个极点: 求得两个极点:
jω
z1 p3 -2 p2 -1 z2 1 p
1 0
-1
3、实轴上的根轨迹 、
实轴上某区间存在根轨迹, 实轴上某区间存在根轨迹,则 该区间右边的开环零、 该区间右边的开环零、极点数之和 必为奇数。 必为奇数。
− p4
− p3
∠s + z 2
∠s + p2
− p2
共轭复根 相; ∠s + p2 = 2π 在 s 左边的零、极点其相角均为0
∠s + z1 + ∠s + z2 = 2π 在 s 右边的零、极点其相角均为π
n m 0 出射角公式: 出射角公式: θ pc =180 + ∑θzj − ∑θ pi j =1 i=1
ζ = 0.707
s’ s’
-2 0
K −1
Re
-1
根轨迹法的分析基本思路: 根轨迹法的分析基本思路 目的: 目的
①解决高阶系统求解特征根比较困难 的实现; 寻找到一种方便、 的实现 ②寻找到一种方便、有效的描述 系统的根轨迹的方法。 系统的根轨迹的方法。
方法: 方法
① 根据开环零极点的分布绘制出系统 的根轨迹图; 的根轨迹图;②利用根轨迹法来分析和设 计系统. 计系统
S1
0 -1 -1+j -1+j∞
∞ ↑ K
S2
-2 -1 -1-j -1-j∞ jω
1 S1 0 σ -1
闭环特征方程式 S2+2S+K= 0
S2 -2
特征方程的根 S1.2 = -1± 1-K ±
K变化时,闭环特征根 变化时,
在S平面上的轨迹图形
-1 K ∞ ↑
系统特征方程为 求得两个极点: 求得两个极点:
jω
z1 p3 -2 p2 -1 z2 1 p
1 0
-1
3、实轴上的根轨迹 、
实轴上某区间存在根轨迹, 实轴上某区间存在根轨迹,则 该区间右边的开环零、 该区间右边的开环零、极点数之和 必为奇数。 必为奇数。
第4章 控制系统的根轨迹分析

绘制根轨迹如图4-13所示。
第4章 控制系统的根轨迹分析
图4-13 例4-5系统的根轨迹
第4章 控制系统的根轨迹分析
图中根轨迹与虚轴的交点可从系统临界稳定的条件
得到τ=1。τ=1时系统的特征方程为
得与虚轴交点的坐标为jω=±j。从根轨迹得到系统稳定时τ
的取值范围为0<τ<1。
第4章 控制系统的根轨迹分析
θj(j=1,2,3,4)。选取实轴上一点s0,若s0为根轨迹上的点,必满足
相角条件,有
第4章 控制系统的根轨迹分析
图4-5 实轴上根轨迹相角示意
第4章 控制系统的根轨迹分析
下面分别分析开环零、极点对相角条件的影响,进而分
析对实轴上根轨迹的影响。
(1)共轭复数极点p4和p5到点s0的向量的相角和为
φ4+φ5=2π,共轭复数零点到s0点的向量的相角和也为2π。
(2)实轴上,s0点左侧的开环极点p3和开环零点z2到点s0所
构成的向量的夹角φ3和θ2均为零度。
(3)实轴上,s0点右侧的开环极点p1、p2和开环零点z1到点
s0 所构成的向量的夹角φ1、φ2和θ1均为π。
第4章 控制系统的根轨迹分析
第4章 控制系统的根轨迹分析
若系统稳定,由劳斯表的第一列系数,有以下不等式成立:
得0<K* <78.47。
由此可知,当 Kc* =78.47时,系统临界稳定,此时根轨迹穿
过虚轴。K* =78.4ω 值由以下辅助方程确定:
将 K* =78.47代入辅助方程,得
解得s=±j2.16。
第4章 控制系统的根轨迹分析
对于例4-1,其在实轴上的根轨迹一条始于开环极点,止于
开环零点(根轨迹位于-2到-5之间),另两条始于开环极点,止于
自动控制原理--控制系统的根轨迹分析及特殊根轨迹

j1
s0
j1
jk
s sk
j1
jk
单位阶跃响应为
n
y(t) A0 Akeskt k 1
m
m
Ks zi Kzi
A0
i1 n
s sj
i1 n
GB(0)
sj
j1
s0
j1
m
m
K s zi
Ak
i1 n
s sj
1 s
K sk zi
i1 n
sk sk sj
jk
1
s2
100 8s 100
4 3
os1
1.5
1.7
可求得 0.4, ,n 10
s3
所以 % e 1 2 100% 25%,ts (s3.)5 n 3.5 4 0.9
j
0
利用根轨迹分析控制系统的性能
例11 分析K的变化对系统稳定性的影响
K (s 3) G(s)H (s) s(s 5)(s 6)(s2 2s 2)
增加开环极点的影响 增加极点对根轨迹形状的影响
增加开环零点的影响 增加零点对根轨迹形状的影响
例9 已知某系统闭环传递函数
GB (s) 0.67s 1
1 0.01s2
0.08s 1
试计算在单位阶跃输入时的系统输出超调量 % 和调节时间t。s
解:该闭环系统有三个极点,s1 1.5, s2,3 零4 、j9.2极点 分布如右图。
系统稳定的K的范围为: 0<K<35
例12 分析K的变化对系统的影响。设负反馈系统的开环传递函数为
K s z G(s)H(s) ss p
z p
求系统闭环根轨迹,并分析 p 2, 时z系 统4 的动态性能。
第4章 线性系统的根轨迹法(《自动控制原理》课件)

如果用试凑的方法由相角条件来绘制根轨迹, 如果用试凑的方法由相角条件来绘制根轨迹 将会非常不方 人们利用前面介绍的几个式子, 便. 人们利用前面介绍的几个式子 导出一些绘制根轨迹的法则 利用导出的法则, 可方便地绘制出根轨迹的大至形状, 利用导出的法则 可方便地绘制出根轨迹的大至形状 叫概略根 轨迹, 轨迹 这在利用根轨迹对系统进行初步分析和设计时已基本可用 了.
(2) 当0<K<=0.25时, 一个根的绝对值随 的增大而增大 另 的增大而增大, 时 一个根的绝对值随K的增大而增大 一个根的绝对值随K的增大而减小 两根的变化轨迹如下图所示: 的增大而减小, 一个根的绝对值随 的增大而减小 两根的变化轨迹如下图所示 jω ω σ -2 -1.5 -1 0
当K=0.25时, 两根相等 均为 时 两根相等, 均为-1.5 (3) 0.25<K<+∞ 时, 两根为共軛复根 且其实部均为 两根为共軛复根, 且其实部均为-1.5 , 而 +∞ 虚部的绝对值随K的增大而增大 两根的变化轨迹如下图所示: 的增大而增大, 虚部的绝对值随 的增大而增大 两根的变化轨迹如下图所示 jω ω σ
4-2 根轨迹绘制的基本法则
本节通过一个例子, 介绍绘制根轨迹的七条法则, 本节通过一个例子 介绍绘制根轨迹的七条法则 但对法则 不予推导和证明. 不予推导和证明 需指出的是, 需指出的是 绘制根轨迹的前提是必须已知闭环系统的开环 传递函数的零点和极点的具体数值, 一般以K’为参变量 为参变量. 传递函数的零点和极点的具体数值 一般以 为参变量 某闭环系统的开环传递函数为: 例: 某闭环系统的开环传递函数为
阶数. 阶数 K叫开环系统的增益 K’叫开环系统的根轨迹增益 叫开环系统的增益, 叫开环系统的根轨迹增益, 叫开环系统的增益 叫开环系统的根轨迹增益 K与K’的本质相同 仅它们间的值有一系数关系, 即: 与 的本质相同, 仅它们间的值有一系数关系 的本质相同
东南大学成贤学院自动控制原理ppt程鹏主编第二版
(4)当0.25<Kg<∞时,s1,2 =-0.5±j0.5 4Kg 1, 两个闭环极点变为一对共轭复数极点。s1、s2旳实 部不随Kg变化,其位于过(-1,0)点且平行于虚 轴旳直线上。
(5)当Kg→∞时, s1 = -0.5+ j∞、s2 = -0.5- j∞,此时s1、s2将趋于无限远处。
EXIT
EXIT
第4章第28页
m
n
(s zi ) (s p j ) 180 (2k 1) , k 0,1,2,
i 1
j 1
②位于s1右边旳实数零、极点: 每个零、极点提供180°相角。
③位于s1左边旳实数零、极点:(s1 z1)、(s1 p4 ) 向量引起旳 相角为0°
∴ 判断 s1是否落在根轨迹上,位于s1左边旳零、极点不 考虑。
m
s zi
i 1
n
s pj j 1
1
Kg
1. 起点:Kg=0,等式右边→∞,仅当
nm
s p j ( j 1, 2, , n)
成立,∴n条根轨迹起始于系统旳n个开环极点。
EXIT
第4章第23页
2.终点:Kg →∞ ,等式右边=0 ①当
s zi (i 1, 2, , m)
m
s zi
闭环特征方程为: D(s) = s2 +s + Kg = 0 解得闭环特征根(亦即闭环极点)
s1 0.5 0.5 1 4Kg , s2 0.5 0.5 1 4Kg
可见,当Kg 变化,两个闭环极点也随之连续变化。 当Kg 从0→∞变化时,直接描点作出两个闭环极点旳变 化轨迹。
EXIT
第4章第8页
3
1
60 180
300
k 0 k 1 k 2
(5)当Kg→∞时, s1 = -0.5+ j∞、s2 = -0.5- j∞,此时s1、s2将趋于无限远处。
EXIT
EXIT
第4章第28页
m
n
(s zi ) (s p j ) 180 (2k 1) , k 0,1,2,
i 1
j 1
②位于s1右边旳实数零、极点: 每个零、极点提供180°相角。
③位于s1左边旳实数零、极点:(s1 z1)、(s1 p4 ) 向量引起旳 相角为0°
∴ 判断 s1是否落在根轨迹上,位于s1左边旳零、极点不 考虑。
m
s zi
i 1
n
s pj j 1
1
Kg
1. 起点:Kg=0,等式右边→∞,仅当
nm
s p j ( j 1, 2, , n)
成立,∴n条根轨迹起始于系统旳n个开环极点。
EXIT
第4章第23页
2.终点:Kg →∞ ,等式右边=0 ①当
s zi (i 1, 2, , m)
m
s zi
闭环特征方程为: D(s) = s2 +s + Kg = 0 解得闭环特征根(亦即闭环极点)
s1 0.5 0.5 1 4Kg , s2 0.5 0.5 1 4Kg
可见,当Kg 变化,两个闭环极点也随之连续变化。 当Kg 从0→∞变化时,直接描点作出两个闭环极点旳变 化轨迹。
EXIT
第4章第8页
3
1
60 180
300
k 0 k 1 k 2
控制系统的根轨迹分析方法 自控原理 教学PPT课件

P3×
分别起始于p1, p2, p3,4,
P2
终止于无穷远。
×
-2
Im(s)
× 0 P1
Re(s)
根据规则四、实轴上存在
根轨迹是从-2到0之间。
P4×
例4-2-6
p1=0, p2= -2, p3,4= -1±j2
根据规则五、n-m=4条渐近线
与实轴交点: 渐近线相角分别为:
P3×
Im(s)
P2 ×
j5.66
×
-j5.66
例4-2-5 作
的根轨迹。
该系统 n=3 ,m=1。
有三个开环极点:
一个零点:
根据规则一、二、三: 该根轨迹有三个分支,
分别起始于p = 0(两条)和p = -12处,
有一个分支终止于z = -1,
另两个分支趋于无穷远。
× -12 -6 -4
根据规则四:
实轴上存在根轨迹是从-12到-1之间。
s1是分离点,s2是会合点。 ×
-12 -6
作完业整:的A绘-4-出7,根A轨-4-迹11,如图4-9所示。
看书p130,表4-1常规根轨迹。
●× -4 -2
图4-9
例4-2-6
分析:n=4,m=0。
根据规则一、二、三、有四个极点:
p1=0, p2= -2, p3,4= -1±j2
该根轨迹共有四个分支,
例如系统的开环零、极点分布如图。
要判断 和 之间的线段是否存
在根轨迹,取实验点
开环共轭极点和零点提供的相角 相互抵消,G(s0)的相角由实轴上的 开环零极点决定。 。
×
● ● × ××
﹣5
﹣2 ﹣1 0
处在G(s0)左边的开环零极点提供的角度 × 均为零, 相角条件由其右边的零极点决定。
《自动控制理论(第版)》邹伯敏课件第4章

i1
n
n
s n pl s n1
pl
l 1
l 1
3、用分子除以分母得
GsH s
K0
s nm
n l 1
pl
m i 1
zi s nm1
2020/5/4
第四章 根轨迹法
14
自动控制理论
当s 时,
令某系统的开环传递函数为W s
s
K0
A
nm
K0
snm
n
m
s nm1
A
1 W s 0,有n m条根轨迹分支,它们是由实轴上s σA点出发的射线,
图4-4 一阶系统
2020/5/4
图4-5 图4-4系统的等增益轨迹和根轨迹
第四章 根轨迹法
6
自动控制理论
结论:
根轨迹就是s 平面上满足相角条件点的集合。由于相角条件是绘制根轨迹 的基础,因而绘制根轨迹的一般步骤是:
➢找出s 平面上满足相角条件的点,并把它们连成曲线 ➢根据实际需要,用幅值条件确定相关点对应的K值
例4-4
已知GsH s
ss
K0
4s 2
4s
20
求根的分离点
图4-12 例4-4的根轨迹
解:1)有4条根轨迹分支,它们的始点分别为0,-4,-2±j4
2) 渐近线与正实轴的夹角
2k 1 , 3 , 5 , 7 , k 0,1,2,3
4
44 4 4
渐近线与实轴的交点为
2020/5/4
-A
422 4 第四章
规则2:根轨迹的分支数及其起点和终点
闭环特征方程:
n
m
s pl K 0 s zi 0
l 1
控制系统的根轨迹分析法资料PPT课件

由:
D' (s)
k gd
N '(s)
|s d
可以求得分离点s=-2.3557 。
近似求法:分离点在[-4,0]之间。
s0
-0.5 -1 -1.5 -2.0 -2.5 -3 -3.5 -4
kgd 0
1.628 3
5.971 8.80 9.375 7.457 3.949
kgd 的最大值为9.375,这时s=-2.5,是近似分离点。 第12页/共43页
s3
-7.6 -6 -4
Im
s1 2.08
-1.2
Re
0
s2 -2.08
(1) 判断闭环极点-1.20±j2.08是不是系统的主导极点: Im
Gk (s1 ) 1 2 3 s1 (s1 4) (s1 6)
s1 2.08
(180 tg 1 2.08 tg 1 2.08 tg 1 2.08 ) 180
对应根轨迹增益的计算:
|
s(s
kg 4)( s
6)
| 1 s1.2 j 2.08
k g 44
第20页/共43页
4.4.3 利用根轨迹估算系统的性能
(2) 估算系统的性能指标:
系统的闭环传递函数为
(s)
44
(s 1.2 j2.08)(s 1.2 j2.08)(s 7.6)
化简为
(s)
利用根轨迹可以清楚的看出开环根轨迹增益或其他开环系
统参数变化时,闭环系统极点位置及其瞬态性能的改变情况。
以二阶系统为例:开环传递函数为 Gk
闭环传递函数为(s)
s2
n2 2 n s
n2
(s)
n2 s(s 2
)
自动控制原理课件第四章根轨迹法ppt

2013-8-11 自动控制原理 16
nm s
Kg
sz
i
在实际系统通常是 n m ,则还有 (n m) 条根轨迹终止于s平 面的无穷远处,这意味着在无穷远处有 (n m) 个无限远(无穷) 零点。
Kg 0
nm
Kg 0
nm
0
Kg
有两个无穷远处的终点
_
K s ( s 1)
C(s)
特征根:S
s sK 0
1, 2
1 1 4K 2
K:0 ~ ∞
1 2
......
K
0 0
1 8
1 4
0.5 j
s1
0.146 0.5 0.5 j 0.5
......
s2 1 0.854 0.5 0.5 j 0.5
第4章 根轨迹法
4.1 根轨迹法的概念 4.2 根轨迹方程 4.3 常规根轨迹及其绘制 4.4 广义根轨迹及其绘制 4.5 按根轨迹分析控制系统 4.6 用MATLAB绘制根轨迹
2013-8-11
自动控制原理
1
4.1
根轨迹法的概念
R(s)
根轨迹的概念
K ( s) 2 闭环传递函数: s sK 特征方程: 2
2013-8-11
自动控制原理
18
规则2:根轨迹的分支数、连续性和对称性
根轨迹的分支数即根轨迹的条数。既然根轨迹是描述闭环 系统特征方程的根(即闭环极点)在S平面上的分布,那么,根 轨迹的分支数就应等于系统特征方程的阶数。 根轨迹方程: ( s p ) K ( s z ) 0 系统开环根轨迹增益(实变量)与复变量s有一一对应的关 系,当 K g 由零到无穷大连续变化时,描述系统特征方程根的复 变量s在平面上的变化也是连续的,因此,根轨迹是n条连续的 曲线。 由于实际的物理系统的参数都是实数,若它的特征方程有复 数根,一定是对称于实轴的共轭复根,因此,根轨迹总是对称 于实轴的。
nm s
Kg
sz
i
在实际系统通常是 n m ,则还有 (n m) 条根轨迹终止于s平 面的无穷远处,这意味着在无穷远处有 (n m) 个无限远(无穷) 零点。
Kg 0
nm
Kg 0
nm
0
Kg
有两个无穷远处的终点
_
K s ( s 1)
C(s)
特征根:S
s sK 0
1, 2
1 1 4K 2
K:0 ~ ∞
1 2
......
K
0 0
1 8
1 4
0.5 j
s1
0.146 0.5 0.5 j 0.5
......
s2 1 0.854 0.5 0.5 j 0.5
第4章 根轨迹法
4.1 根轨迹法的概念 4.2 根轨迹方程 4.3 常规根轨迹及其绘制 4.4 广义根轨迹及其绘制 4.5 按根轨迹分析控制系统 4.6 用MATLAB绘制根轨迹
2013-8-11
自动控制原理
1
4.1
根轨迹法的概念
R(s)
根轨迹的概念
K ( s) 2 闭环传递函数: s sK 特征方程: 2
2013-8-11
自动控制原理
18
规则2:根轨迹的分支数、连续性和对称性
根轨迹的分支数即根轨迹的条数。既然根轨迹是描述闭环 系统特征方程的根(即闭环极点)在S平面上的分布,那么,根 轨迹的分支数就应等于系统特征方程的阶数。 根轨迹方程: ( s p ) K ( s z ) 0 系统开环根轨迹增益(实变量)与复变量s有一一对应的关 系,当 K g 由零到无穷大连续变化时,描述系统特征方程根的复 变量s在平面上的变化也是连续的,因此,根轨迹是n条连续的 曲线。 由于实际的物理系统的参数都是实数,若它的特征方程有复 数根,一定是对称于实轴的共轭复根,因此,根轨迹总是对称 于实轴的。
《自动控制原理》PPT课件

i1
j1
i1
j1
f
G(s)
K G (1s 1)(22s2 22s 1) s (T1s 1)(T22s2 2T2s 1)
KG'
(s zi )
i1 q
(s pi )
i1
前向通道增益 前向通道根轨迹增益
KG'
KG
1 2 2 T1T2 2
反馈通道根轨迹增益
l
(s z j )
H(s) K H '
狭义根轨迹(通常情况):
变化参数为开环增益K,且其变化取值范围为0到∞。
G(s)H (s) K s(s 1)
(s) C(s) K R(s) s2 s K
D(s) s2 s K 0
s1,2
1 2
1 2
1 4K
K=0时 s1 0 s2 1
0 K 1/ 4 两个负实根
K值增加 相对靠近移动
i1
i1
负实轴上都是根轨迹上的点!
m
n
(s zi ) (s pi ) | s2 p1 135
i1
i1
负实轴外的点都不是根轨迹上的点!
二、绘制根轨迹的基本规则
一、根轨迹的起点和终点 二、根轨迹分支数 三、根轨迹的连续性和对称性 四、实轴上的根轨迹 五、根轨迹的渐近线 六、根轨迹的分离点 七、根轨迹的起始角和终止角 八、根轨迹与虚轴的交点 九、闭环特征方程根之和与根之积
a
(2k 1)180 nm
渐近线与实轴交点的坐标值:
n
m
pi zi
a= i1
i1
nm
证明
G(s)H (s) K '
m
(s zi )
i 1 n
控制系统根轨迹分析法课件

根轨迹的概念与分类
根轨迹定义
根轨迹是控制系统中的一种图示方法,用来表示系统的极点 与零点随系统参数变化的关系。根轨迹可以用来分析系统的 稳定性、响应速度和阻尼特性等。
根轨迹分类
根据根轨迹的性质和应用,可以将其分为常规根轨迹和广义 根轨迹。常规根轨迹通常用于分析线性时不变系统的稳定性 ,而广义根轨迹则可以用来分析更复杂的非线性、时变和离 散系统。
优化目标
通过优化控制系统的参数,使得 系统的根轨迹具有更好的分布, 从而提高系统的稳定性和性能。
优化方法
采用遗传算法、粒子群算法等优化 算法对控制系统的参数进行优化。
应用
用于优化控制系统的设计,提高控 制系统的性能和鲁棒性。
05
CHAPTER
控制系统根轨迹分析法的软 件实现
使用MATLAB进行控制系统根轨迹分析
系统的稳定性
稳定性定义
如果一个系统受到外部干扰后能够自我调节并恢复到原始状态,那么这个系统 被认为是稳定的。在控制系统中,稳定性是保证系统正常运行的重要条件。
稳定性判别方法
判断控制系统稳定性的方法有多种,包括劳斯判据、赫尔维茨判据、奈奎斯特 判据等。这些方法可以用来判断系统的稳定性,并指导设计者进行系统参数的 调整。
MATLAB软件介绍
MATLAB是一种科学计算软件,广泛应用于控制系统的设计和分析。
MATLAB在控制系统根轨迹分析中的应用
使用MATLAB的Control System Toolbox可以进行控制系统的根轨迹分析,通过调用相 关函数,可以方便地绘制根轨迹图并进行系统性能的分析。
MATLAB根轨迹分析实例
使用Simulink的Control Design Toolbox可以进行控制系统的根轨迹分析,通过搭建系统模型并设置相应的参数, 可以方便地进行根轨迹分析和系统优化。
根轨迹ppt课件.ppt

3.分析方法及思路 1)从数学模型的建立看开环传递函数的特点: 物理元件→典型环节→开环结构→闭环结构→系统数学模型
(1)开环结构中的典型环节直接对应着开环传递函数的零极 点,-------很容易获得;
(2)各个典型环节中的参数可以直接反映系统的物理参数, 这一点对分析系统和改造系统非常有利; (3)可以直接求取稳态误差; (4)同各种传递函数(如闭环传递函数和误差传递函数)有 简单的关系。 2)一个美好的愿望: 开环零极点图+开环增益→闭环零极点全部可能的分布图→ 分析系统的三大类性能。
j 1 n i 1
)
(s z
j 1 n i 1
j
)
s ( s pi )
(s p )
i
则幅值条件和相角条件可以进一步写成如下实用形式:
幅值条件:
G1 ( s ) H1 ( s )
sz
j 1 n i 1
m
j
s p
1 K*
基本公式
i
幅值条件:
第四章 根轨迹法
4.1 4.2 4.3 4.4 根轨迹法的基本概念 根轨迹绘制的基本规则 广义根轨迹 线性系统性能的根轨迹分析法
一、本章内容提要: 1.介绍已知系统开环传递函数的极点、零 点的条件下确定闭环系统的根轨迹法,并分 析系统参量变化时对闭环极点位置的影响; 2.根据闭环特征方程得到相角条件和幅值 条件由此推出绘制根轨迹的基本法则; 3.根轨迹绘制:常规根轨迹、参数根轨迹 、根轨迹曲线族、零度根轨迹; 4.根轨迹法分析系统性能
三、本章重点、关键、难点 1.重点:根轨迹的绘制和利用根轨迹 图分析控制系统 2.关键点:根轨迹方程,幅值条件, 相角条件 3.难点:广义根轨迹的绘制
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
规则二:根轨迹起始于开环极点,终于开环零点;
规则三:根轨迹是连续的,并且关于实轴对称;
规则四:实轴上的根轨迹区域右侧实轴上开环零极点
的个数是奇数;
n
m
规则五:根轨迹的渐近线有n-m条,交与实轴
pi z j
i 1
j 1
与实轴正向夹角为 2k 1 ;
nm
nm
规则六:根轨迹的分离点d在实轴上且满足
m
R(s)
B(s) -
G(s)
C(s)
H(s)
系统的特征方程为:1 G(s)H (s) 0 G(s)H (s) 1
m
(s zj )
K * j1 n
1
(s pi )
i1
为根轨迹方程
-
6
m
(s zj )
K * j1 n
1
(s pi )
i1 n
m
(s zj )
K * j1 n
1(2k 1)
2
a
(2k 1)
2 1
⑤求分离点坐标d
1 1 1 d 1.5 j1 d 1.5 j1 d 1
-
d1 2.12, d2 0.12 (舍去)
14
-
15
4.3 特殊根轨迹
4.3.1 广义根轨迹
设系统开环传递函数为 G(s)H (s)
闭环特征方程为 G(s)H (s) 1 0
等效变换成
A P(s) 1 0 Q(s)
等效开环传递函数为
G1
(s)H1
(s)
Ta s2
s2 (s 1) sK
等效开环传递函数有3个零点,即0,0,-1;2个极点, 不同K值可计算出不同极点。
按照常规根轨迹的绘制法则可绘制出广义根轨迹如图
-
17
-
18
4.3.2 零度根轨迹
特征方程 D s 1 G s H s
根轨迹方程 GsH s 1
(s pi )
i 1
| s pi |
所以
K*
i 1 m
为幅值条件
| s zj |
m
nj 1
(s z j ) (s pi ) (2k 1) 为相角条件
j 1
i 1
同时满足幅值条件与相角条件的s值即为特征根, 即系统的闭环极点。
-
7
4.2 绘制根轨迹的基本法则
规则一:根轨迹的分支数等于开环极点数n;
幅值方程: 相角方程:
m
szi
K i1 n
1
s pi
m
i 1
n
s zi s pi 2k
i 1
i 1
-
19
使用常规根轨迹法绘制零度根轨迹时,对 于与相角方程有关的某些法则要修改
• 实轴上某一区域,若其右方开环实数零、 极点个数之和为偶数,则该区域必是根轨 迹。
• 根轨迹的渐近线
s(s 1)
-
3
R(s)
k
C(s)
-
s(s 1)
可知系统的特称方程为:
K 0, S1 0, S2 1
1
1
K 4 , S1 S2 2
K
1 2
,
S1
1 2
j
1 2
,
S2
1 2
j
1 2
K
, S1
1 2
j, S2
1 2
j
-
4
4.1.2 根轨迹与系统性能
jω
将K值从零增大到正无穷时,系
统特征根的变化情况绘制在s平
面上如图所示。
K=0.5
K=0
K=0.25
K=0
-1
O -0.5
K=0.5
-
稳定性:特征根都在s左半平面;
稳态性能:根据系统的稳态误差要 σ 求,可以由根轨迹图确定闭环极点
位置的允许范围;
动态性能:由根轨迹图可知,当 0<K<0.5时,特征根都在负实轴上, 单位阶跃响应为非周期响应…..
5
4.1.3 根轨迹的幅值条件与幅角条件
第四章 控制系统的根轨迹分析法
本章学习目标: 明确根轨迹的概念及基本法则,熟练掌握 常规根轨迹的绘制; 能够利用根轨迹分析系统的性能; 了解特殊根轨迹的有关概念。
-
1
闭环控制系统的稳定性和性能指标主要由闭环系统极 点在复平面的位置决定,因此,分析或设计系统时确 定出闭环极点位置是十分有意义的。
根轨迹法根据反馈控制系统的开、闭环传
A
2k
nm
-
a 计算公式不变。
20
根轨迹的起始角与终止角
m
n
pi 2k z j pi pj pi
j 1
j 1
ji
m
m
zi 2k z jzi pjzi
j 1
j 1
ji
分离角与会合角
除上述四个法则外,其他法则不变
-
21
例:某正反馈系统,其中
G(s)
(s
K *(s 2) 3)(s2 2s
终于有限零点-1,另一条趋于无穷远处。 ③ 法则四,在负实轴上,0到-1区间和-2到负无穷区间
是根轨迹。
最后绘制出根轨迹如图所示。
-
10
-
11
例2: •已知系统的开环传递函数
G(s)H (s) K*(s 1) s2 3s 3.25
试求闭环系统的根轨迹分离点坐标d,并概 略绘制出根轨迹图。
-
2)
, H (s) 1
试绘制开环系统根轨迹增益 K * 0 变化时的根轨迹。
解:该系统是正反馈系统。
当 K * 0 变化时的根轨迹是零度根轨迹。利用零度根轨
迹法则绘制该系统的闭环根轨迹。
•实轴根轨迹在(3, )和(2, )区间内。
起始于开环极点 p1 3, p2 1 j1, p3 1 j1
令:
G1
(s)H1
(s)
A
P(s) Q(s)
-
16
例:已知系统的开环传递函数为 G(s)H (s)
K
试绘制当开环增益K为 化时的根轨迹。
1 2
s(s
,1时, 2,时间常数
1)(Ta s 1)
Ta 变 0
解: 题目显然是求广义根轨迹问题。
系统特征方程为 D(s) s(s 1)(Ta s 1) K 0
递函数之间的关系,直接由开环传递函数零、 极点求出闭环极点(闭环特征根)。这给系
统的分析与设计带来了极大的方便。
-
2
4.1 根轨迹的基本概念
所谓根轨迹,就是指开环传递函数某个参数(如开环 增益K)从零变化到无穷大时,闭环系统特征根在s平 面上变化的轨迹。
4.1.1 根轨迹的概念
R(s)
k
C(s)
-
12
解:根据系统开环传递函数求出开环极点
p1 1.5 j1, p2 1.5 j1
按步骤:
①n=2,m=1,有两条根轨迹
②两条根轨迹分别起于开环极点,终于开环 零点和无穷远零点
③实轴上根轨迹位于有限零点-1和无穷零点
-
之间,因此判断有分离点
13
④渐近线
a
1.5
j11.5 2 1
j1 1
1
n
1
j1 d z j i1 d pi
-
8
例1: •设一单位负反馈系统的开环传递函数为 G(s)=K(s+1)/[s(0.5s+1)],求 K 0 时的闭环根轨迹。
•解:将开环传递函数写成零、极点形式
G(s) 2K (s 1) s(s 2)
-
9
按绘制根规迹法则逐步进行:
① 法则一,有两条根轨迹 ② 法则三,两条根轨迹分别起始于开环极点0、-2,一条
