完整word版,Mathematic入门教程(整理版)
mathematic使用指南
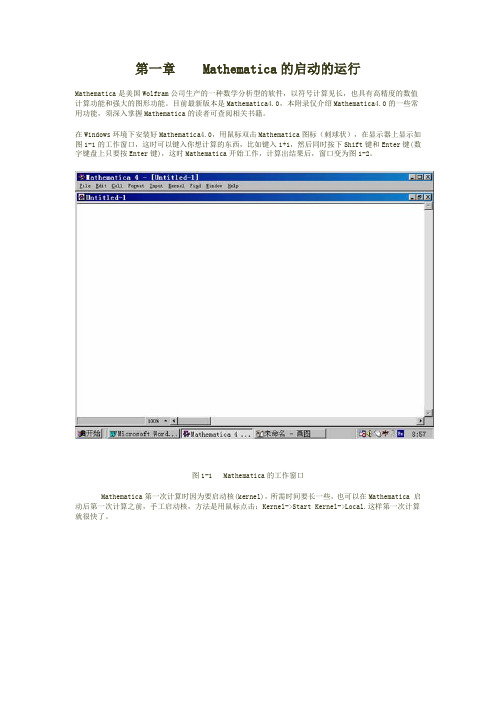
第一章Mathematica的启动的运行Mathematica是美国Wolfram公司生产的一种数学分析型的软件,以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。
目前最新版本是Mathematica4.0,本附录仅介绍Mathematica4.0的一些常用功能,须深入掌握Mathematica的读者可查阅相关书籍。
在Windows环境下安装好Mathematica4.0,用鼠标双击Mathematica图标(刺球状),在显示器上显示如图1-1的工作窗口,这时可以键入你想计算的东西,比如键入1+1,然后同时按下Shift键和Enter键(数字键盘上只要按Enter键),这时Mathematica开始工作,计算出结果后,窗口变为图1-2。
图1-1 Mathematica的工作窗口Mathematica第一次计算时因为要启动核(kernel),所需时间要长一些,也可以在Mathematica 启动后第一次计算之前,手工启动核,方法是用鼠标点击:Kernel->Start Kernel->Local.这样第一次计算就很快了。
图1-2 完成运算后的Mathematica的窗口图1-2中的“In[1]:=”表示第一个输入;“Out[1]=”表示第一个输出结果。
接下来可键入第二个输入,按这样的方式可利用Mathematica进行“会话式”计算。
要注意的是:“In[1]:= ”和“Out[1]=”是系统自动添加的,不需用户键入。
Mathematica还提供“批处理”运行方式,即可以将Mathematica作为一种算法语言,编写程序,让计算机执行,这在第七章将会作简要介绍。
第二章 Mathematica的基本运算功能2.1 算术运算Mathematica最基本的功能是进行算术运算,包括加(+),减(-),乘(*),除(/),乘方(^),阶乘(!)等。
注意:1 在Mathematica中,也可用空格代表乘号;数字和字母相乘,乘号可以省去,例如:3*2可写成3 2,2*x可写成2x,但字母和字母相乘,乘号不能省去。
mathematica教程

Mathematica 5.0使用教程目录第1章Mathematica概述 (3)1.1 运行和启动:介绍如何启动Mathematica软件,如何输入并运行命令 (3)1.2 表达式的输入:介绍如何使用表达式 (5)1.3 帮助的使用:如何在mathematica中寻求帮助 (6)第2章Mathematica的基本量 (8)2.1 数据类型和常量:mathematica中的数据类型和基本常量 (8)2.2 变量:变量的定义、变量的替换、变量的清除等 (10)2.3 函数:函数的概念,系统函数,自定义函数的方法 (12)2.4 表:表的创建,表元素的操作,表的应用 (15)2.5 表达式:表达式的操作 (16)2.6 常用符号:经常使用的一些符号的意义 (19)第3章Mathematica的基本运算 (19)3.1 多项式运算:多项的四则运算,多项式的化简等 (19)3.2 方程求解:求解一般方程,条件方程,方程数值解以及方程组的求解 (21)3.3 求积、求和:求积与求和 (24)第4章函数作图 (25)4.1 二维函数作图:一般函数的作图,参数方程的绘图 (25)4.2 二维图形元素:点、线等图形元素的使用 (29)4.3 图形样式:图形的样式,对图形进行设置 (31)4.4 图形的重绘和组合:重新显示所绘图形,将多个图形组合在一起 (33)4.5 三维图形的绘制:三维图形的绘制,三维参数方程的图形,三维图形的设置 (36)第5章微积分的基本操作 (42)5.1 函数的极限:如何求函数的极限 (42)5.2 导数与微分:如何求函数的导数、微分 (43)5.3 定积分与不定积分:如何求函数的不定积分和定积分,以及数值积分 (45)5.4 多变量函数的微分:如何求多元函数的偏导数、微分 (47)5.5 多变量函数的积分:如何计算重积分 (49)第6章微分方程的求解 (51)6.1 微分方程的解:微分方程的求解 (51)6.2 微分方程的数值解:如何求微分方程的数值解 (53)第7章Mathematica程序设计 (54)7.1 模块:模块的概念和定义方法 (54)7.2 条件结构:条件结构的使用和定义方法 (56)7.3 循环结构:循环结构的使用 (59)7.4 流程控制 (61)第8章Mathematica中的常用函数 (63)8.1 运算符和一些特殊符号:常用的和不常用一些运算符号 (63)8.2 系统常数:系统定义的一些常量及其意义 (63)8.3 代数运算:表达式相关的一些运算函数 (64)8.4 解方程:和方程求解有关的一些操作 (65)8.5 微积分相关函数:关于求导、积分、泰勒展开等相关的函数 (65)8.6 多项式函数:多项式的相关函数 (66)8.7 随机函数:能产生随机数的函数函数 (67)8.8 数值函数:和数值处理相关的函数,包括一些常用的数值算法 (67)8.9 表相关函数:创建表,表元素的操作,表的操作函数 (68)8.10 绘图函数:二维绘图,三维绘图,绘图设置,密度图,图元,着色,图形显示等函数 (69)8.11 流程控制函数 (72)第1章Mathematica概述1.1 Mathematica的启动和运行Mathematica是由美国物理学家Stephen Wolfram领导的一个小组开发进行量子力学研究的,软件开发成功促使Stephen Wolfram与1987年创建Wolfram研究公司,并推出了Mathematica1.0。
第1讲 Mathematica入门

1. 集合的定义 直接定义: 直接定义 直接用{}将相关元素放在一起就得到一个集 合.例如: 例22 In[1]:= t1={1,2,3,4,5,6} In[2]:= t2={Sin[x],Cos[x]} 语句定义: 可用Range与Table语句来定义集合. 语句定义 Range[imin,imax,di]给出的是一个数的集合,第一项为 imin,最后一项不超过imax,步长为di. 例如: 例23 In[3]:= t3=Range[1,30,3] Out[3]= {1,4,7,10,13,16,19,22,25,28}
除了上面的这种赋值形式(称为即时赋值)以外,还有 一种延迟赋值。 例10 In[4]:= t:=4 延迟赋值并不显示结果,只有调用变量时,才进行计 算并赋值。下面的例子可以看出即时赋值与延迟赋值的 区别。 例11 In[5]:= r=Random[ ]; s={r,r} Out[6]= {0.455181, 0.455181} In[7]:= r:=Random[ ]; s={r,r} Out[8]= {0.967234, 0.526599}
这些常数可以参与运算。
例6 In[1]:= 2*E Out[1]= 2E In[2]:= N[Pi,30] Out[2]= 3.14159265358979323846264338328 函数N[x,n]给出x的n位有效数字。 Mathematica提供了许多数学上的函数,表3给出了 一些常用的数学函数。
例15 In[15]:= x=2.0; u[x_]:=Sin[x]; v[x_]=Sin[x] Out[15]= 0.909297 In[16]:= ?u Global`u u[x_]=Sin[x] In[17]:= ?v Global`v v[x_]=0.909297 可以看出,上例中函数u[x]被定义为Sin[x],而v[x]被 定义为常函数0.909297(=sin2.0).
mathmatic教程

第 3 章 Mathem 章 Mathematica 概述
1.1 运行和启动:介绍如何启动 Mathematica 软件,如何输入并运行命令 1.2 表达式的输入:介绍如何使用表达式 1.3 帮助的使用:如何在 mathematica 中寻求帮助
第 2 章 Mathematica 的基本量
1.3 Mathematica 的联机帮助系统
用 Mathematica 的过程中, 常常需要了解一个命令的详细用法, 或者想知系统中是否有 完成某一计算的命令,联机帮助系统永远是最详细、最方便的资料库。
1.获取函数和命令的帮助
在 Notebook 界面下,用 ?或 ?? 可向系统查询运算符、函数和命令的定义和用法,获 取简单而直接的帮助信息。 例如, 向系统查询作图函数 Plot 命令的用法 ?Plot 系统将给 出调用 Plot 的格式以及 Plot 命令的功能(如果用两个问号 “??” , 则信息会更详细一 些)。? Plot* 给出所有以 Plot 这四个字母开头的命令。
8.1 8.2 8.3 8.4 8.5 8.6 8.7 8.8 8.9 8.10 运算符和一些特殊符号:常用的和不常用一些运算符号 系统常数:系统定义的一些常量及其意义 代数运算:表达式相关的一些运算函数 解方程:和方程求解有关的一些操作 微积分相关函数:关于求导,积分,泰勒展开等相关的函数 多项式函数:多项式的相关函数 随机函数:能产生随机数的函数函数 数值函数:和数值处理相关的函数,包括一些常用的数值算法 表相关函数:创建表,表元素的操作,表的操作函数 绘图函数:二维绘图,三维绘图,绘图设置,密度图,图元,着色,图 形显示等函数 8.11 流程控制函数
数学软件Mathematica详解教程

生成 n 元列表 {expr,expr,...,expr}
{expr|i 在列表 list 中变化}
Table[expr,{i,a,b,h}] {expr|i 在 Range[a,b,h]中变化}
Table 中的 expr 一般给的是通项公式
RandomInteger[range,n] 生成 n 个伪随机整数,range 表示取值范围
ToExpression[str]
ToString[expr]
转化为表达式
将表达式转化为字符串
更多字符串相关函数参见 “参考资料中心”
26
列表
列表
是 Mathematica 的基本对象,可用来表示集合,数组等 分为标准列表和稀疏列表
标准列表: 用大括号括起来的有限个元素,元素之间用逗号分隔
求最大值
求最小值
19
常用初等函数
Re[x], Im[x]
Conjugate[x] Arg[x]
提取实部和虚部
取共轭 辐角
Mod[m,n]
Quotient[m,n] Sin[x], Cos[x], ... ArcSin[x], ArcCos[x], ... Sinh, Cosh, ...,
m 除以 n 的余数
In[1]:= Clear[x,y]; In[2]:= f=2*x+y; In[3]:= f./{x->2,y->3} (* f(2,3) 的值 *)
In[3]:= f./{2->5}
(*把 2 替换成 5*)
15
数的基本运算
Mathematica 中的实数分精确数和双精度数
N[x,n] N[x] IntegerPart[x] FractionalPart[x] Floor[x] Round[x] Ceil[x] Precision[expr] x 的带 n 位有效数字的近似值 x 的双精度近似值 整数部分 小数部分 取整:不大于 x 的最大整数 取整:四舍五入 取整:不小于 x 的最小整数 显示计算精度
(整理)Mathematica入门教程.

(整理)Mathematica入门教程.Mathematica入门教程Mathematica的基本语法特征如果你是第一次使用Mathematica,那么以下几点请你一定牢牢记住:Mathematica中大写小写是有区别的,如Name、name、NAME等是不同的变量名或函数名。
系统所提供的功能大部分以系统函数的形式给出,内部函数一般写全称,而且一定是以大写英文字母开头,如Sin[x],Conjugate[z]等。
乘法即可以用*,又可以用空格表示,如2 3=2*3=6 ,x y,2 Sin[x]等;乘幂可以用“^”表示,如x^0.5,T an[x]^y。
自定义的变量可以取几乎任意的名称,长度不限,但不可以数字开头。
当你赋予变量任何一个值,除非你明显地改变该值或使用Clear[变量名]或“变量名=.”取消该值为止,它将始终保持原值不变。
一定要注意四种括号的用法:()圆括号表示项的结合顺序,如(x+(y^x+1/(2x)));[]方括号表示函数,如Log[x],BesselJ[x,1];{}大括号表示一个“表”(一组数字、任意表达式、函数等的集合),如{2x,Sin[12Pi],{1+A,y*x}};[[]]双方括号表示“表”或“表达式”的下标,如a[[2,3]]、{1,2,3}[[1]]=1。
Mathematica的语句书写十分方便,一个语句可以分为多行写,同一行可以写多个语句(但要以分号间隔)。
当语句以分号结束时,语句计算后不做输出(输出语句除外),否则将输出计算的结果。
一.数的表示及计算1.在Mathematica中你不必考虑数的精确度,因为除非你指定输出精度,Mathematica总会以绝对精确的形式输出结果。
例如:你输入In[1]:=378/123,系统会输出Out[1]:=126/41,如果想得到近似解,则应输入In[2]:=N[378/123,5],即求其5位有效数字的数值解,系统会输出Out[2]:=3.0732,另外Mathematica还可以根据你前面使用的数字的精度自动地设定精度。
mathematica教程

Mathematica 5.0使用教程目录第1章Mathematica概述 (3)1.1 运行和启动:介绍如何启动Mathematica软件,如何输入并运行命令 (3)1.2 表达式的输入:介绍如何使用表达式 (5)1.3 帮助的使用:如何在mathematica中寻求帮助 (6)第2章Mathematica的基本量 (8)2.1 数据类型和常量:mathematica中的数据类型和基本常量 (8)2.2 变量:变量的定义、变量的替换、变量的清除等 (10)2.3 函数:函数的概念,系统函数,自定义函数的方法 (12)2.4 表:表的创建,表元素的操作,表的应用 (15)2.5 表达式:表达式的操作 (16)2.6 常用符号:经常使用的一些符号的意义 (19)第3章Mathematica的基本运算 (19)3.1 多项式运算:多项的四则运算,多项式的化简等 (19)3.2 方程求解:求解一般方程,条件方程,方程数值解以及方程组的求解 (21)3.3 求积、求和:求积与求和 (24)第4章函数作图 (25)4.1 二维函数作图:一般函数的作图,参数方程的绘图 (25)4.2 二维图形元素:点、线等图形元素的使用 (29)4.3 图形样式:图形的样式,对图形进行设置 (31)4.4 图形的重绘和组合:重新显示所绘图形,将多个图形组合在一起 (33)4.5 三维图形的绘制:三维图形的绘制,三维参数方程的图形,三维图形的设置 (36)第5章微积分的基本操作 (42)5.1 函数的极限:如何求函数的极限 (42)5.2 导数与微分:如何求函数的导数、微分 (43)5.3 定积分与不定积分:如何求函数的不定积分和定积分,以及数值积分 (45)5.4 多变量函数的微分:如何求多元函数的偏导数、微分 (47)5.5 多变量函数的积分:如何计算重积分 (49)第6章微分方程的求解 (51)6.1 微分方程的解:微分方程的求解 (51)6.2 微分方程的数值解:如何求微分方程的数值解 (53)第7章Mathematica程序设计 (54)7.1 模块:模块的概念和定义方法 (54)7.2 条件结构:条件结构的使用和定义方法 (56)7.3 循环结构:循环结构的使用 (59)7.4 流程控制 (61)第8章Mathematica中的常用函数 (63)8.1 运算符和一些特殊符号:常用的和不常用一些运算符号 (63)8.2 系统常数:系统定义的一些常量及其意义 (63)8.3 代数运算:表达式相关的一些运算函数 (64)8.4 解方程:和方程求解有关的一些操作 (65)8.5 微积分相关函数:关于求导、积分、泰勒展开等相关的函数 (65)8.6 多项式函数:多项式的相关函数 (66)8.7 随机函数:能产生随机数的函数函数 (67)8.8 数值函数:和数值处理相关的函数,包括一些常用的数值算法 (67)8.9 表相关函数:创建表,表元素的操作,表的操作函数 (68)8.10 绘图函数:二维绘图,三维绘图,绘图设置,密度图,图元,着色,图形显示等函数 (69)8.11 流程控制函数 (72)第1章Mathematica概述1.1 Mathematica的启动和运行Mathematica是由美国物理学家Stephen Wolfram领导的一个小组开发进行量子力学研究的,软件开发成功促使Stephen Wolfram与1987年创建Wolfram研究公司,并推出了Mathematica1.0。
mathmatic教程-入门级别-一看就会Word版

Mathematica5教程第1章Mathematica概述1.1 运行和启动:介绍如何启动Mathematica软件,如何输入并运行命令1.2 表达式的输入:介绍如何使用表达式1.3 帮助的使用:如何在mathematica中寻求帮助第2章Mathematica的基本量2.1 数据类型和常量:mathematica中的数据类型和基本常量2.2 变量:变量的定义,变量的替换,变量的清除等2.3 函数:函数的概念,系统函数,自定义函数的方法2.4 表:表的创建,表元素的操作,表的应用2.5 表达式:表达式的操作2.6 常用符号:经常使用的一些符号的意义第3章Mathematica的基本运算3.1 多项式运算:多项的四则运算,多项式的化简等3.2 方程求解:求解一般方程,条件方程,方程数值解以及方程组的求解3.3 求积求和:求积与求和第4章函数作图4.1 二维函数作图:一般函数的作图,参数方程的绘图4.2 二维图形元素:点,线等图形元素的使用4.3 图形样式:图形的样式,对图形进行设置4.4 图形的重绘和组合:重新显示所绘图形,将多个图形组合在一起4.5 三维图形的绘制:三维图形的绘制,三维参数方程的图形,三维图形的设置第5章微积分的基本操作5.1 函数的极限:如何求函数的极限5.2 导数与微分:如何求函数的导数,微分5.3 定积分与不定积分:如何求函数的不定积分和定积分,以及数值积分5.4 多变量函数的微分:如何求多元函数的偏导数,微分5.5 多变量函数的积分:如何计算重积分5.6 无穷级数:无穷级数的计算,敛散性的判断第6章微分方程的求解6.1 微分方程的解:微分方程的求解6.2 微分方程的数值解:如何求微分方程的数值解第7章Mathematica程序设计7.1 模块:模块的概念和定义方法7.2 条件结构:条件结构的使用和定义方法7.3 循环结构:循环结构的使用7.4 流程控制第8章Mathematica中的常用函数8.1 运算符和一些特殊符号:常用的和不常用一些运算符号8.2 系统常数:系统定义的一些常量及其意义8.3 代数运算:表达式相关的一些运算函数8.4 解方程:和方程求解有关的一些操作8.5 微积分相关函数:关于求导,积分,泰勒展开等相关的函数8.6 多项式函数:多项式的相关函数8.7 随机函数:能产生随机数的函数函数8.8 数值函数:和数值处理相关的函数,包括一些常用的数值算法8.9 表相关函数:创建表,表元素的操作,表的操作函数8.10 绘图函数:二维绘图,三维绘图,绘图设置,密度图,图元,着色,图形显示等函数8.11 流程控制函数第1章Mathematica概述1.1 Mathematica的启动和运行Mathematica是美国Wolfram研究公司生产的一种数学分析型的软件,以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。
Mathematica入门教程

Mathematica入门教程Mathematica入门教程Mathematica入门教程Mathematica的基本语法特征如果你是第一次使用Mathematica,那么以下几点请你一定牢牢记住:Mathematica中大写小写是有区别的,如Name、name、NAME等是不同的变量名或函数名。
系统所提供的功能大部分以系统函数的形式给出,内部函数一般写全称,而且一定是以大写英文字母开头,如Sin[x],Conjugate[z]等。
乘法即可以用*,又可以用空格表示,如2 3=2*3=6 ,x y,2 Sin[x]等;乘幂可以用“^”表示,如x^0.5,Tan[x]^y。
自定义的变量可以取几乎任意的名称,长度不限,但不可以数字开头。
当你赋予变量任何一个值,除非你明显地改变该值或使用Clear[变量名]或“变量名=.”取消该值为止,它将始终保持原值不变。
一定要注意四种括号的用法:()圆括号表示项的结合顺序,如(x+(y^x+1/(2x)));[]方括号表示函数,如Log[x],BesselJ[x,1];{}大括号表示一个“表”(一组数字、任意表达式、函数等的集合),如{2x,Sin[12 Pi],{1+A,y*x}};[[]]双方括号表示“表”或“表达式”的下标,如a[[2,3]]、{1,2,3}[]=1。
Mathematica的语句书写十分方便,一个语句可以分为多行写,同一行可以写多个语句(但要以分号间隔)。
当语句以分号结束时,语句计算后不做输出(输出语句除外),否则将输出计算的结果。
一、数的表示及计算1.在Mathematica中你不必考虑数的精确度,因为除非你指定输出精度,Mathematica总会以绝对精确的形式输出结果。
例如:你输入In:=378/123,系统会输出Out:=126/41,如果想得到近似解,则应输入In:=N[378/123,5],即求其5位有效数字的数值解,系统会输出Out:=3.073 2,另外Mathematica还可以根据你前面使用的数字的精度自动地设定精度。
Mathematica简易教程

Page 21
使用条件运算符,基本格式为:f[x_]:=expr/;condition,当condition条件满足 时才把expr赋给f(x)。
Page 22
当然,使用If命令也可以定义上面的函数,If语句的格式为If[条件,值1,值 2],如果条件成立取“值1”,否则取“值2”,用If语句定义如下:
mathematicapage目录第一章mathematica简介第二章mathematica的基本量第三章mathematica的基本运算第四章函数作图第五章微积分的基本操作page第一章mathematica简介mathematica由美国物理学家stephenwolfram领导开发的他们组建wolfram研究公司mathematica是一个计算机代数系统把符号运算数值计算与图形显示集一体可以完成上述三项功能更重要的是它把这些功能融合在一个系统里使它们成为一个整体
3.2.4 解条件方程
在作方程计算时,可以把一个方程看做你要处理的主要方程,而把其 他方程作为必须满足的辅助条件,你就会发现这样处理很方便。 在Mathematica中,我们通常是首先命名辅助条件组,然后用名字把辅 助条件包含在你要用函数Solve[]求解的方程组中。
Page 40
3.3 求和与求积
Mathematica简介与入门
目录
第一章 Mathematica简介 第二章 Mathematica的基本量
第三章 Mathematica的基本运算
第四章 函数作图 第五章 微积分的基本操作
Page 2
第一章 Mathematica简介
Mathematica由美国物理学家Stephen Wolfram领导开发的,他们组建Wolfram 研究公司 Mathematica是一个计算机代数系统,把 符号运算、数值计算与图形显示集一体, 可以完成上述三项功能,更重要的是它把 这些功能融合在一个系统里,使它们成为 一个整体.此外,Mathematica还是一个 易于扩充的系统,即实际上提供了功能强 大的程序设计语言,可以定义用户需要的 各种函数,完成用户需要的各种工作,系 统本身还提供了一大批用这个语言写出的 专门程序或软件包 Mathematica的发布标志着现代科技计算 的开始。Mathematica是世界上通用计算 系统中最强大的系统。自从1988发布以来, 它已经对如何在科技和其它领域运用计算 机产生了深刻的影响
Mathematica软件使用入门

Mathematica软件使用入门目录第一章基本知识与基本操作 (3)1.1 Mathematica的基本语法特征 (3)1.2 Mathematica的启动、基本操作 (4)1.3 操作小技巧 (7)1.4 数值计算 (8)1.5 赋值与替换 (9)1.6 自定义函数 (10)1.7 方程与方程组解 (11)1.8 解不等式与不等式组 (12)1.9 由递推式求数列的通项公式 (13)1.10 作函数图像 (14)第二章运用Mathematica实现高等数学中的基本运算 (16)2.1 求极限运算 (16)2.2 求导数与微分 (18)2.3 求不定积分 (25)2.4 求定积分 (25)第三章实验练习题 (28)Mathematica是当今世界上最为流行的计算机代数系统之一.Mathematica系统是美国物理学家Stephen.Wolfram领导的一个小组开发的,后来他们成立了Wolfram研究公司.1987年推出了系统的1.0版;现在的最新版本是8.0版.Mathematica可以做:●符号计算和数值计算问题,如:能做多项式的计算、因式分解和展开等;●做各种有理式计算,求多项式、有理式方程和超越方程的精确解和近似解;●做向量、矩阵的各种计算;●求极限、导数、积分,做幂级数展开,求解某些微分方程等;●做任意位数的整数或分子分母为任意大整数的有理数的精确计算,做具有任意位精度的数值(实、复数值)的计算.●可以很方便地画出用各种方式表示的一元和二元函数的图形,通过图形,可以立即形象地掌握函数的某些特性,而这些特性一般是很难从函数的符号表达式中看清楚.第一章 基本知识与基本操作1.1 Mathematica 的基本语法特征使用Mathematica ,一定要牢牢记住:● Mathematica 中大写小写是有区别的,如Name 、name 、NAME 等是不同的变量名或函数名;● 系统所提供的功能大部分以系统函数的形式给出, 内部函数一般写全称, 而且一定是以大写英文字母开头, 如Sin[x], Cos[z]等;● 乘法即可以用*,又可以用空格表示,如2 3=2*3=6 , 2 Sin[x]=2* Sin[x] ● 乘幂可以用“^”表示,如x^0.5 表示: Tan[x]^y 表示: ● 自定义的变量可以取几乎任意的名称,长度不限,但不可以数字开头. ● 当你赋予变量任何一个值,除非你:明显地改变该值或 使用Clear[变量名] 或 使用“变量名=.”取消该值,否则它将始终保持原值不变.● 一定要注意四种括号的用法:0.5x yTan[x]( ):表示项的结合顺序,如: (x+(y^x+1/(2x)));[ ]:表示函数,如:Log[x], Sin[x];{ }:表示一个“表”(即是一组数字、或任意表达式、或函数等的一个有序集合),如:{2x,Sin[12 Pi],A,1}, {1+A,y*x,1,2};[[ ]]:双方括号表示“表”或“表达式”的下标,如:a; {3,5,7}[[2]]=5.a[[2,3]]表示:23●Mathematica的语句书写十分方便,一个语句可以分为多行写,同一行可以写多个语句(但要以分号间隔).●当语句以分号结束时,语句计算后不做输出(输出语句除外),否则将输出计算的结果.●Mathematica命令中的标点符号必须是英文的.1.2 Mathematica的启动、基本操作1.2.1 启动“Mathematica”:在windows操作系统中安装了Mathematica后,与其他的常用软件一样,可从“开始”→“程序”→“Mathematica5” Mathematica的主窗口并出现第一个notebook窗口(Untitled-1):1.2.2 简单使用:例1.1 计算+33的值①在“Untitled-1”窗口中输入:329/412+3^3②按下“Shift+Enter”(或数字键盘上的Enter键),就得到计算结果:其中“In[1]:=”是Mathematica自动加上的,表示第一个输入;“Out[1]:=”表示第一个输出.一般地:In[n]:= 表示第n个输入Out[n]:=表示第n个输出.注意:“In[n]:=”自动加上的,不能人工输入!1.2.3 保存结果:保存方法同一般的Windows软件:“文件”→“保存”⇒“另存为”窗口→在“查找范围”内找到目标文件夹→输入文件名(比如输入“1”)→“”.Mathematica 4或Mathematica 5的文件的后缀是“nb”,当输入“1”时,即产生文件“1.nb”.1.2.4打开文件1.nb启动Mathematica →“文件”→“打开”⇒打开”窗口:→在“查找范围”内找到文件“1.nb”→“”即可.1.2.5 退出Mathematica:与一般应用软件一样,单击右上方的“”按钮(或用菜单:“文件”→“退出”).1.3 操作小技巧1.3.1Ctrl+K的用途如果只知道命令的首写字母,可在输入该首写字母(要大写),再按下“Ctrl+K”组合键,则所有以该字母为首的命令都列出来,只要用鼠标双1.3.2使用前面已有的结果举例如下:例1.2 做如下操作:①输入:Integrate[x^2*(11-Sin[x]),{x,-1,1}]按:“Shift+Enter”;②输入:%+1,按:“Shift+Enter”;③输入:%+1,按:“Shift+Enter”;④输入:%1+1,按:“Shift+Enter”;⑤输入:%3+1,按:“Shift+Enter”,计算结果如下:可见,“%”表示前一个计算结果;“%n ”表示第n 个计算结果. 1.3.3 删除行:见下图示1.4 数值计算请看下例:1.5 赋值与替换X=. 或Clear[x] 清除赋给x 的值expr/.{x->xval,y->yval} 用xval 、yval 分别替换expr 中的x 、y . 例1.3 输入:x=3;y=4;w=x+y 输入:Clear[x,y]; 计算输入:z=(x+y)^2 计算输入:z/.x->5 计算输入:Clear[x,y]; 计算输入:u=x+y 计算输入:u/.{x->5,y->6} 计算 计算结果如下:1.6 自定义函数用户可以自行定义函数,一个函数一旦被定义好之后就可以象系的内部函数一样使用.例1.4 如要定义函数f(x)=x 2+3x-2只要键入:即可.又如要定义分段函数2+1 < 0()= 2sin 0x x g x x x ⎧⎨≥⎩可键入:g[x_]:= Which[x<0,x^2+1,x>=0,2Sin[x]]或g[x_]:=If[x<0,x^2+1,2Sin[x]]请见以下计算结果:1.7 方程与方程组解例1.5 ① 解方程:0652=+-x x输入:Solve[x^2-5x+6==0,x]即可.② 解方程组 输入:即可(结果见下图).22131x y x y +=⎧⎨-=⎩1.8例1.6 ① ⎪⎩⎪⎨⎧>---01222x x x 输入即可.② 解不等式)3(12>--x x 输入:即可(结果见下图)注: Mathematica系统有内部函数.还有一些系统扩展的功能但不是作为内部函数的、以文件的形式存储在磁盘上的文件,要使用它们,必须用一定的方式来调用这些文件,这些文件我们称之为程序包. 调用方式之一如上所述:或用:Needs["Algebra`InequalitySolve`"] 1.9 由递推式求数列的通项公式例1.7 设求数列的通项公式只要输入:11,1,n na na a-==1.10 作函数图像例1.8在同一坐标系中作出2-1y x 和y=sinx在[-2,2]内的图像.输入: Plot[{x^2-1,Sin[x]},{x,-2,2}] 结果见下图例1.9作出sinxcosy的三维图形输入:Plot3D[Sin[x]*Cos[y],{x,-2Pi,2Pi},{y,-即可(结果见下图)第二章 运用Mathematica 实现高等数学中的基本运算极限、导数和积分是高等数学中的主要概念和基本运算,如果你在科研中遇到较复杂的求极限、求导数或求积分问题,Mathematica 可以帮你快速解决这些问题。
1.2 MATHEMATICA软件入门

第一讲 MATHEMATICA软件入门Mathematica是当今世界上最为流行的计算机代数系统之一.Mathematica系统是美国物理学家Stephen.Wolfram领导的一个小组开发的,后来他们成立了Wolfram研究公司.1987年推出了系统的1.0版;现在的最新版本是6.0版.Mathematica可以做:●符号计算和数值计算问题,如:能做多项式的计算、因式分解和展开等;●做各种有理式计算,求多项式、有理式方程和超越方程的精确解和近似解;●做向量、矩阵的各种计算;●求极限、导数、积分,做幂级数展开,求解某些微分方程等;●做任意位数的整数或分子分母为任意大整数的有理数的精确计算,做具有任意位精度的数值(实、复数值)的计算.●可以很方便地画出用各种方式表示的一元和二元函数的图形,通过图形,可以立即形象地掌握函数的某些特性,而这些特性一般是很难从函数的符号表达式中看清楚.1.1 Mathematica的基本语法特征使用Mathematica,一定要牢牢记住:● Mathematica中大写小写是有区别的,如Name、name、NAME等是不同的变量名或函数名;● 系统所提供的功能大部分以系统函数的形式给出, 内部函数一般写全称, 而且一定是以大写英文字母开头, 如Sin[x], Cos[z]等;● 乘法即可以用*,又可以用空格表示,如2 3=2*3=6 , 2 Sin[x]=2* Sin[x] ● 乘幂可以用“^”表示,如x^0.5 表示: Tan[x]^y 表示: ● 自定义的变量可以取几乎任意的名称,长度不限,但不可以数字开头. ● 当你赋予变量任何一个值,除非你:明显地改变该值或 使用Clear[变量名] 或 使用“变量名=.”取消该值,否则它将始终保持原值不变.● 一定要注意四种括号的用法:( ): 表示项的结合顺序,如: (x+(y^x+1/(2x))); [ ]: 表示函数,如:Log[x], Sin[x];{ }: 表示一个“表”(即是一组数字、或任意表达式、或函数等的一个有序集合),如:{2x,Sin[12 Pi],A ,1}, {1+A,y*x ,1,2};[[ ]]: 双方括号表示“表”或“表达式”的下标,如:a[[2,3]]表示:23a ; {3,5,7}[[2]]=5.0.5xyTan[x]●Mathematica的语句书写十分方便,一个语句可以分为多行写,同一行可以写多个语句(但要以分号间隔).●当语句以分号结束时,语句计算后不做输出(输出语句除外),否则将输出计算的结果.●Mathematica命令中的标点符号必须是英文的.1.2 Mathematica的启动、基本操作1.2.1 启动“Mathematica”:在windows操作系统中安装了Mathematica后,与其他的常用软件一样,可从“开始”→“程序”→“Mathematica5” Mathematica的主窗口并出现第一个notebook窗口(Untitled-1):1.2.2 简单使用:例1 计算+33的值①在“Untitled-1”窗口中输入:329/412+3^3②按下“Shift+Enter”(或数字键盘上的Enter键),就得到计算结果:其中“In[1]:=”是Mathematica自动加上的,表示第一个输入;“Out[1]:=”表示第一个输出.一般地:In[n]:= 表示第n个输入Out[n]:=表示第n个输出.注意:“In[n]:=”自动加上的,不能人工输入!1.2.3 保存结果:保存方法同一般的Windows软件:“文件”→“保存” “另存为”窗口→在“查找范围”内找到目标文件夹→输入文件名(比如输入“1”)→“”.Mathematica 4或Mathematica 5的文件的后缀是“nb”,当输入“1”时,即产生文件“1.nb”.1.2.4打开文件1.nb启动Mathematica →“文件”→“打开” 打开”窗口:→在“查找范围”内找到文件“1.nb”→“”即可.1.2.5 退出Mathematica:与一般应用软件一样,单击右上方的“”按钮(或用菜单:“文件”→“退出”).1.3操作小技巧1.3.1Ctrl+K的用途如果只知道命令的首写字母,可在输入该首写字母(要大写),再按下“Ctrl+K”组合键,则所有以该字母为首的命令都列出来,只要用鼠标双1.3.2使用前面已有的结果举例如下:例2 做如下操作:①输入:Integrate[x^2*(11-Sin[x]),{x,-1,1}]按:“Shift+Enter”;②输入:%+1,按:“Shift+Enter”;③输入:%+1,按:“Shift+Enter”;④输入:%1+1,按:“Shift+Enter”;⑤输入:%3+1,按:“Shift+Enter”,计算结果如下:可见,“%”表示前一个计算结果;“%n ”表示第n 个计算结果. 1.3.3 删除行:见下图示1.4 数值计算请看下例:1.5 赋值与替换X=. 或Clear[x] 清除赋给x 的值expr/.{x->xval,y->yval} 用xval 、yval 分别替换expr 中的x 、y . 例3 输入:x=3;y=4;w=x+y输入:Clear[x,y]; 计算输入:z=(x+y)^2 计算输入:z/.x->5 计算输入:Clear[x,y]; 计算输入:u=x+y 计算输入:u/.{x->5,y->6} 计算计算结果如下:1.6 自定义函数用户可以自行定义函数,一个函数一旦被定义好之后就可以象系的内部函数一样使用. 例4 如要定义函数f(x)=x 2+3x-2只要键入:即可.又如要定义分段函数2+1 < 0()= 2sin 0x x g x x x ⎧⎨≥⎩可键入:g[x_]:= Which[x<0,x^2+1,x>=0,2Sin[x]]或g[x_]:=If[x<0,x^2+1,2Sin[x]]请见以下计算结果:1.7 方程与方程组解 例5 ① 解方程:0652=+-x x输入:Solve[x^2-5x+6==0,x]即可.② 解方程组 输入:即可(结果见下图).1.8例6 ① 解不等式组⎪⎩⎪⎨⎧>---01222x x x 输入2213x y x y +=⎧⎨-=⎩即可.② 解不等式)3(12>--x x 输入:即可(结果见下图)注:Mathematica 系统有内部函数.还有一些系统扩展的功能但不是作为内部函数的、以文件的形式存储在磁盘上的文件,要使用它们,必须用一定的方式来调用这些文件,这些文件我们称之为程序包. 调用方式之一如上所述:或用: Needs["Algebra`InequalitySolve`"]1.9 由递推式求数列的通项公式例7 设求数列的通项公式 11,1,n n a na a -==只要输入:1.10 作函数图像例8、在同一坐标系中作出2-1y x 和y=sinx 在[-2,2]内的图像. 输入: Plot[{x^2-1,Sin[x]},{x,-2,2}]结果见下图例9 作出Sin[x]*Cos[y]的三维图形输入: Plot3D[Sin[x]*Cos[y],{x,-2Pi,2Pi},{y,-即可(结果见下图)。
01第一篇Mathematica入门

01第⼀篇Mathematica⼊门第⼀篇Mathematica⼊门⼀、MathematicaMathematica是集⽂本编辑、数值计算、逻辑分析、图形、声⾳、动画于⼀体的⾼度优化的专家系统.它是⽬前⽐较流⾏的数学软件之⼀.Mathematica最显著的特点是⾼精度的运算功能、强⼤的作图功能以及逻辑编程功能.Mathematica是美国WolframResearch公司开发的⼀套专门⽤于进⾏数学计算的软件.从1988年问世⾄今,已⼴泛运⽤到⼯程技术、应⽤数学、计算机科学、财经、⽣物、⽣命科学、以及太空等领域,数以万计的论⽂、科学报告、计算机绘图等都是Mathematica的杰作. 1995年发表的Mathematica3.0版是数学软件史的⼀⼤创新,⽽现在的Mathematica4.1版,则达到了这类软件的顶峰. Mathematica除了提供数值处理与绘图的功能外,还具有符号计算以及处理多项式的各种运算、函数的微分、积分、解微分⽅程、统计、编程,甚⾄可以制作电脑动画及⾳效等等.Mathematica的基本系统是使⽤C语⾔编写的,因此能⽅便地移植到各种计算机系统上.尽管Mathematica有各种各样的版本,但它们有⼀个共同的内核,Mathematica的各种运算都是由内核来完成的.给内核配置不同的前端处理器,就成为适⽤于各种环境的版本.它的DOS版本的特点是运算速度快,对系统的配置要求较低;它在Windows环境下的特点是图⽂并茂,操作⽅便.这⾥介绍的是在Windows环境下的Mathematica4.1版本.Mathematica4.1对计算机的硬件要求如下:1.操作系统:Windows95以上.2.CPU:Inter586级以上的中央处理器.3.硬盘空间:除了要具备120MB的硬盘空间安装Mathematica4.1外,还需具有100MB左右的剩余硬盘空间⽤于进⾏交换⽂件和复杂的运算.4.内存:64MB以上.⼆、Mathematica界⾯简介双击Mathematica的图标即可运⾏Mathematica的主程序.主程序会同时打开⼀个新的⼯作窗⼝和⼀个基本输⼊模板(Basic Input palette).每⼀个⼯作窗⼝代表⼀个⽂件,⽂件名显⽰在⼯作窗⼝的标题栏上,默认的⽂件名为Untitled-1.nb.位于标题栏下的是菜单栏,包括(File,Edit,Cell,Format,Input,Kernel,Find,Window,Help项). ⽤户可以同时打开多个⼯作区,并且可以对每⼀个⼯作区使⽤不同的名字保存.Mathematica将它们分别命名为Untitled-1;Untitled-2;Untitled-3;….1.⼯作区窗⼝⼯作区是显⽰⼀切输⼊、输出窗⼝.⽆论直接输⼊各种算式或命令,还是已经编好的程序,所有的操作都在这个窗⼝运⾏.⼯作区窗⼝也称作Notebook.2.基本输⼊模板基本输⼊模板由⼀系列按钮组成,⽤以输⼊特殊符号、运算符号、常⽤表达式等.⽤⿏标左键单击⼀个按钮,就可以将它所表⽰的符号输⼊到当前的⼯作区窗⼝中.当启动Mathematica4.1之后,基本输⼊模板会显⽰在屏幕的右边,如果没有,则选择File 下拉菜单中的palette -Basic Input命令激活它.3.主菜单Mathematica的菜单项很多,以下只介绍⼀些最实⽤的菜单项.(1)File菜单File下拉菜单项中的New,Open,Close及Save命令⽤于新建、打开、关闭及保存⽤户的⽂件,这些选项与Word相同.另外有⼏个选项是Mathematica特有的,其中最有⽤的是:●Palettes⽤于打开各种模板;●Generate Palette from Selection⽤于⽣成⽤户⾃制的模板;●Notebooks记录最近使⽤过的⽂件.●模板单击Palettes项,会弹出7个英⽂选项,其中第三项BasicInput(基本输⼊模板)就是启动时已经显⽰在屏幕上的模板.其余最有⽤的选项是第⼆项BasicCalculations(基本计算模板).这个模板分类给出了各种基本计算的按钮.单击各项前⾯的⼩三⾓,会⽴即显⽰该项所包含的⼦项.再次单击各⼦项前⾯的⼩三⾓,则显⽰出⼦项中的各种按钮.若单击其中的某个按钮就可以把该运算命令(函数)输⼊到⼯作区窗⼝中,然后在各个⼩⽅块中键⼊数学表达式,就可以让Mathematica进⾏计算了.有了这两个模板,使得⽤户⽆须死记⼤量的命令和相关的参数,便于查询和输⼊.(2) cell(单元)●单元的样式Mathematica4.1的⼯作窗⼝由不同的单元(cell)组成.例如,输⼊表达式的单元称为输⼊单元(input cell),输出表达式的单元称为输出单元(output cell).每⼀个单元都有其特定的样式(style). 输⼊单元默认的样式名称为input,输出单元默认的样式名称为output.注:在新建⼀个单元时,默认为input.●单元的打开与关闭双击最外层单元的括号,即可关闭该单元,只显⽰最外层.同样只要双击已关闭单元的括号,即可打开该单元.●单元的删除选中所要删除单元的括号,按Delete键即可删除所选单元的内容.(3)Help(帮助)在Mathematica4.1中增加了Help Browser帮助系统.在Help Browser中不但汇集了Mathematica4.1的所有命令和使⽤⽅法,⽽且包含了其完整的使⽤⼿册及各种⼯具栏的使⽤⽅法.单击Help菜单中的Help命令,即可激活Help Browser帮助系统.Help Browser共分六⼤帮助信息:1.Built-in Functions 查询Mathematica4.1的所有内部命令与函数的使⽤⽅法.2.Add-ons 查询Mathematica4.1所带的函数库(packages)命令与函数的⽤法.3.The Mathematica Book Mathematica的完整⼿册.4.Getting Started/Demos初学者使⽤说明与范例.5.Other Information 其他信息,如数学表达式的⼆维格式的输⼊⽅法等.6.Master Index⽤索引的⽅法查询Mathematica的关键词.选择搜索主题的类别之后,输⼊关键词,单击Go To按钮开始搜索主题,或者在最左边的选择列表中选择搜索主题的类别之后,再逐渐缩⼩查询范围.例如:要查询Limit命令的使⽤⽅法,可以直接在Help Browser中输⼊Limit再单击Go To按钮,或选择Algebraic Computation-Calculus-Limit找到有关Limit命令的说明.4.退出Mathematica当结束⼯作时,可以选择“File”菜单中的“Exit”选项或单击关闭按纽. Mathematica 会询问是否保存对打开⼯作区内容的修改,选择“Yes”,系统要求指定⽂件名,⽤户可以任意给定⼀个⽂件名并指定位置,确认后系统将该⽂件保存在⽤户所指定的位置,再次打开该⽂件可以继续上次的运算;选择“Don’t Save”放弃保存;选择“Cancel”取消这次操作并返回Mathematica.三、⾃制模板由于BasicCalculations(基本计算模板)的内容太多,查找不⽅便,因此⾃制模板是⼀个⾮常重要的内容.⾃制模板的步骤如下:1.单击主菜单的input项,弹出⼦菜单.选中⼦菜单中的CreateTabel/Matrix/Palette(建⽴表、矩阵、模板)选项出现对话框.2.在对话框中,选中Make: Palette,在键⼊⾏数和列数,则在窗⼝⽣成⼀个可编辑的原始模板.3.⽤⿏标左键单击原始模板中的第⼀个⼩⽅块,然后在打开的BasicCalculations模板中单击⼀个今后经常使⽤的按钮,就可以将它复制到原始模板中.如此循环往复直⾄全部输⼊完成.4.单击File菜单中的Generate Palette from Selection项,就可以建⽴⼀个⾃⼰的模板了.5.单击⾃制模板右上⾓的关闭按钮,Mathematica将询问是否保存⾃制模板,若保存,则出现对话框,将对话框中显⽰的⽂件名“Untitled-1.nb”改成“⾃定义模板.nb”保存到存放Mathematica模板的⽬录D:\Mathematica\4.1\SystemFiles\FrontEnd\Palettes 下,再次启动时,这个模板的名字就会出现在File菜单的Palette选项中,可与Mathematica的模板⼀样使⽤.四、Mathematica 的常⽤语法1.Mathematica 的基本运算Mathematica 的基本运算包括加(+) ;减(-) ;乘(*) 、除(/) 、乘⽅(?) 等.我们可以按照⼀般数学表达式的⼿写格式输⼊这些基本运算,然后按下Shift+Enter 组合键得到输出结果.例如:In[1]:=Out[1]:= 6 In[2]:= 3^2 Out[2]:= 9说明:(1)Mathematica 将输⼊的指令⽤标题“In[n]:=”标识,输出结果⽤“Out[n]:=”标识,其中“n ”表⽰已经输⼊的指令数.(2)Shift+Enter 在Mathematica 中是执⾏运算的命令.2.输⼊和计算数学表达式(1)键盘直接输⼊和运⾏expr : 直接输⼊表达式.例如:在⼯作窗中输⼊,再按Shift+Enter 组合键,执⾏运算.这时,⼯作32)63(2-+?窗会显⽰如下运算:In[1]:=-??3Out[1]:= ??N[expr] 计算表达式的近似数值,Mathematica 默认的有效数字位数为16位,但按标准输出只显⽰前6位有效数字,若要全部显⽰,则⽤N[expr]//InputForm 命令.N[expr ,n] 计算表达式的具有任意指定数字位数的近似值(指定的数字位数n 应该⼤于16),结果在末位是四舍五⼊的. NumberForm[expr , n] 将表达式⽤n 个有效数字表⽰.例1 求的近似值,有效数字分别为6位、8位、16位、32位.e 解: In[1]:= N ??Out[1]:= 2.71828In[2]:= N u m b e r F o r m ?N ,8?Out[2]:= 2.7182818 In[3]:= N[ ]//InputForm Out[3]:= 2.718281828459045 In[4]:= N[ ,32]Out[4]:= 2.7182818284590452353602874713527(2)利⽤基本输⼊模板直接输⼊我们可以利⽤基本输⼊模板所提供的⼀些特殊符号、运算符号、常⽤表达式来输⼊表达式.3.简单的调⽤⽅式有时在后⾯的计算要调⽤到前⾯已经计算过的结果,这时Mathematica 提供了⼀种简单的调⽤⽅式:命令意义%%%%%…% (个%),或 %n n读取前⼀个输出结果.读取前第⼆个输出结果.读取前第个输出结果.n 例如 In[1]:= 3^4Out[1]:= 81 In[2]:= %?5 Out[2]:= 405 In[3]:= %1?%2Out[3]:= 4864.长表达式的输⼊Mathematica 是允许⼀个表达式占⽤多个输⼊⾏的,但需注意的是:必须在指令或语法告⼀段落⽽⼜不完整的地⽅使⽤Enter 键进⾏换⾏.5.有关代数式的⼏个命令(1)多项式的展开与因式分解命令意义[多项式]Expand 对多项式进⾏展开运算.[多项式]Factor 对多项式进⾏因式分解.例2 将多项式展开5)1(y x ++解 In[1]:= Expand[(1+x+y)^5]Out[1]:= 1?5x ?10x 2?10x 3?5x 4?x 55y 20xy例3 将多项式分解因式2223-+-x x x 通过管线不仅可以解路须同时切断习题电源,线缆敷设完毕,要进⾏检查和检测处理。
Mathematic入门教程整理版

(1)简介数学系给本科生开设一门课: "符号计算系统", 主要简单讲授mathematica(以下简称math)软件的使用和其编程,赶兴趣的同学可以找本math书以求更深入的了解.我们平日用到编程语言时, 大家都知道编程中用到的整型, 实型, 甚至双精度数, 都只是一个近似的数, 其精度有限, 有效数字有限, 在很多时候达不到实际需要的要求. 符号计算与数值计算的区别就在于符号计算以准确值记录计算的每一步的结果, 如果需要时, 可以将精确表示按需要计算成任意位数的小数表示出来(只要机器内存足够大).最常见的符号计算系统有maple, mathematica, redues等, 这些软件各有侧重, 比如,maple内存管理和速度比math好, 但是图形方面不如math; redues没找到, 没用过, 未明; 而用得较多的matlab 编程环境特好, 和C语言接口极其简单, 遗憾的是它不是符号计算, 只是数值计算. 所以, 就实用而全面来说, math是一个很好用的软件.math软件不仅能够进行一般的+-*/和科学函数如Sin, Log 等计算, 而且能进行因式分解, 求导, 积分, 幂级数展开, 求特征值等符号计算, 并且, math有较强的图元作图, 函数作图, 三维作图和动画功能.(2)mathematica入门mathematica自发布以来, 目前比较常见的有math 1.2 for DOS, math 2.2 for Windows, math 3.0 for win95, math 3.0 for UNIX.DOS下的math的好处就是系统小, 对机器要求低, 在386机器4M内存下就能运行得很好(机器再低点也是可以用的, 比如说286/2M). 在DOS下直接键入math<回车>即可进入math系统, 出现的提示符In[1]:=, 这时就可以进行计算了, 键入math函数, 回车即可进行运算. 如果输入的Quit, 则退出math. 这里要注意的是, math区分大小写的, 一般math的函数均以大写字母开始的.windows下的math对机器要求就要高一些了, math3.0更是庞大, 安装完毕有100M之多(2.2大约十多兆). 同windows下的其他软件一样, math可以双击图标运行, 在File菜单下有退出这一项. windows下的math有其优越性, 就是可以在windows下随心所欲地拷贝粘贴图形. math3.0更是能输入和显示诸如希腊字母, 积分符号, 指数等数学符号. DOS的math与windows下的一个区别是DOS的以回车结束一句输入, 而windows的以+<回车>结束一句输入. DOS下的提示符显示为In[数字]:=, 而windows下在结束输入后才显示出In[数字]:=和Out[数字]:=字样. (Out为输出提示符) 下面试试几个例子:(In[数字]:=为提示符, 不用键入)In[1]:= 2^100 计算2的100次方In[2]:= s={{3,7,9},{7,4,3},{1,3,8}} 定义矩阵sIn[3]:= Eigenvalues[s] 计算s的特征值In[4]:= Plot[Sin[x],{x,0,Pi}] 在0,Pi间画SinIn[5]:= Plot[Cos[x],{x,0,Pi}] CosIn[6]:= Plot3D[Sin[x]Sin[y],{x,0,1},{y,0,2}] 三维作图以In[6]为例说明: math的函数都以大写字母开头的单词为函数名, Plot3D, Plot, Eigenvalues, Sin等, 常数也是如此, 如Pi. 函数名后的参数用[]括起, 逗号隔开.math的输出可以作为函数的输入对象, 你可以再试一个: In[7]:=Show[%%,%%%] 这里一个%代表上一个输出, 两个代表上两个... 也可以直接用Out[n]代表第n个输出.这里需要补充的是!command 执行DOS命令?name 关于name(函数等)的信息(可以使用通配符)??name 关于name的额外信息(3)基本计算1. 算术运算符+加-减*乘/除^指数(乘也可用空格)N[expr]或expr //N 计算expr的数值(6位有效数字)N[expr, n] n表示小数的位数2. 数学函数Sqrt[x] x开方Exp[x] e的x方Log[x] x的自然对数Log[b,x] 以b为底, x的对数Sin[x], Cos[x], Tan[x], ArcSin[x], ArcCos[x] 三角函数Round[x] 离x最近的整数Floor[x] 不超过x的最大整数Quotient[n,m] n/m的整数部分Mod[n,m] n/m的余数Random[] 0,1间随机数Max[x,y,...] Min[x,y,...] 最大数和最小数3. 常数Pi Pi=3.1493...E e=2.71828...Degree Pi/180I i=Sqrt[-1]Infinity 无穷大Catalan Catalan常数.=0.915966ComplexInfinity 复无穷DirectedInfinity 有向的无穷EulerGamma 欧拉常数gamma=0.5772216 GoldenRatio 黄金分割(Sqrt[5]-1)/2Indeterminate 不定值4. 逻辑运算符==, !=, >, >=, <, <=, !, &&, ||Xor 异或If[条件,式1,式2] 如果条件成立, 值式1; 否则得式25. 变量a) 变量名以字母(一般小写)开头; 字母数字组成.(如x2为变量名; 而2x, 2*x, 2 x, x*2, x 2均是x乘以2).b) 赋值x=value; x=y=value; x=.(清除x值)c) 代换expr /. x->value 将式中x代换为valueexpr /. {x->xval, y->yval}下面就让我们以几个例子来结束本节:(大家还是注意, DOS下的Math, 只要输入In[num]:=后的指令后按回车, 而windows下则是按+回车.) 大家看看都有什么输出.In[1]:= 2.7+5.23In[2]:= 1/3+2/7In[3]:= 1/3+2/7 //NIn[4]:= N[Pi,100]曾经有人问我, 你是怎么算出Pi的1000位而没有错误的, 其实很简单, 大家只要把上式的100改为1000即可.In[5]:= Sin[Pi/2]+Exp[2]+Round[1.2]In[6]:= 10<7In[7]:= x=5;如果在输入之后加上一个";", 则只运算不输出.IN[8]:= y=0(所以In[7]和8完全可以合成一条x=5;y=0, 假如我不需要x=5的输出)In[9]:= x>yIn[10]:= t=1+m^2In[11]:= t /. m->2In[12]:= t /. m->5aIn[13]:= t /. m->Pi //N(4)代数变换上一节我们已经学习了Math里的基本运算和逻辑运算, 常用数学函数, 几个常见的常数, 以和变量的使用. 这一节, 我们来学学基本代数变换: Apart, Cancel, Coefficient, Collect, Denominator, Expand, ExpandAll, Exponent, Factor, Numerator, Short, Simplify, Together.Expand[expr] 多项式expr按项展开Factor[expr] 因子形式Simplify[expr] 最简形式In[1]:= Expand[(1+x)^2]In[2]:= Factor[%]我们以前说过的哦, %是上一个输出, %%是上上个, %%%是上上上个, ..., %n是第n个输出(即Out[n])In[3]:= Simplify[%%]In[4]:= Integrate[x^2/(x^4-1),x] 这是积分运算, 详情后叙In[5]:= D[%,x] 求导In[6]:= Simplify[%]ExpandAll[expr] 所有项均展开Together[expr] 通分Apart[expr] 分离成具有最简分母的各项Cancel[expr] 约去分子,分母的公因子Collect[expr] 合并In[1]:= e=(x-1)^2 (2+x)/((1+x)(x-3)^2)In[2]:= Expand[e]In[3]:= ExpandAll[e]In[4]:= Together[e]In[5]:= Apart[%]In[6]:= Factor[%]Coefficient[expr, form] 表达式中form项的系数Exponent[expr, form] form的最高幂次Numerator[expr] 取分子Denominator[expr] 取分母expr //Short 以简短形式输出In[1]:= e=Expand[(1+3x+4y^2)^2]In[2]:= Coefficient[e, x]In[3]:= Exponent[e, y]In[4]:= q=(1+x)/(2(2-y))In[5]:= Denominator[%]In[6]:= Expand[(x+5y+10)^4]In[7]:= %//Short 把上式输出, 中间项省去, 以<<数字>>表示省去的项数.最后, 我们以例子来看看用符号名做客体的标志的好处In[1]:= 12metersIn[2]:= %+5.3metersIn[3]:= %/(25seconds)In[4]:= %/.meters->3.78084feet 一下子就把米制变为英尺了.(5)微积分运算(2-1)学到上一节, 大家会发现怎么还停留在中学的计算中呢, 这一节, 大家就会看到微分D, Dt; 积分Integrate, NIntegrage; 和与积Sum, Product, NSum, NProduct. 下一节我们介绍解方程Solve, Eliminate, Reduce, NRoot, FindRoot, FindMinimum; 幂级数Series, Normal; 极限Limit; 特殊函数Fourier, InverseFourier, ...微分D[f, x] f对x求导D[f, x_1, x_2, ...] f对x_1, x_2, ...求导D[f, {x, n}] f对x求n次导Dt[f] 全微分dfDt[f, x] 全微商df/dxIn[1]:= D[x^n,x]In[2]:= D[f[x],x]In[3]:= D[2x f[x^2],x]In[4]:= D[x^n, {x, 3}]In[5]:= D[x^2 y^3, x, y]In[6]:= Dt[x^n]In[7]:= Dt[x y, x]积分Integrate[f,x] f对x积分Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}, ...] 定积分NIntegrate[f, {x, xmin, xmax}, {y, ymin, ymax}, ...]计算积分的数值解In[1]:= Integrate[Sin[Sin[x]],x] 嘻嘻, 无法计算, 原样输出In[2]:= Integrate[Log[x], {x,0,6}] 啊, 广义积分也一样算In[3]:= Integrate[x^2+y^2, {x,0,1}, {y,0,1}]In[4]:= In[3]//N 如果你的上一条输入不是In[3], 注意调整这一条的输入哦In[5]:= Integrate[Sin[Sin[x]], {x,0,1}] 怎么还没法计算啊In[6]:= N[%] 或NIntegrate[Sin[Sin[x]], {x,0,1}] 呵,终于可以计算了.和与积Sum[f, {i, imin, imax}, {j, jmin, jmax}, ...]f对i, j, ...分别从imin到imax,jmin到jmax,...求和Sum[f, {i, imin, imax, di}] 求和的步长为diProduct[f, {i, imin, imax}, {j, jmin, jmax}, ...] 求积NSum 数值解NProduct 数值解In[1]:= Sum[x^i/i, {i,1,4}]In[2]:= Sum[x^i/i, {i,1,5,2}]In[3]:= Sum[a/i^3, {i,1,10}]In[4]:= N[%] 或NSum[a/i^3, {i,1,10}]In[5]:= Sum[1/i^3, {i,1,Infinity}] 可能原样输出, 也可能输出Zeta[3](依math的版本不同而异)In[6]:= N[%]In[7]:= Sum[x^i*y^j, {i,1,3}, {j,1,i}]注: 如果想要求带符号上下限的Sum, 在math3.0中, 直接使用Sum函数即可:In[8]:= Sum[1/Sin[i], {i,1,n}]而如果在旧版本的math, 则可能需要调入包(package) "gospersu.m", 调入格式一般为In[8]:= <<"盘符:\\math路径\\packages\\algebra\\gospersu.m"(不同安装目录可能出现不一样)然后使用函数GosperSum[](6)微积分运算(2-2)上一节, 我们一起学习了微分D, Dt; 积分Integrate, NIntegrage;和与积Sum, Product, NSum, NProduct. 这一节我们将介绍解方程Solve,Eliminate, Reduce, NRoot, FindRoot, FindMinimum; 幂级数Series,Normal; 极限Limit; 特殊函数Fourier, InverseFourier, ...最后, 我们说明一下math的函数的定义, 别名的使用, 以和不同输出格式解方程Solve[{lhs1==rhs1, lhs2==rhs2,...}, {x,y,...}]解关于x,y,...的方程组{lhs1==rhs1, lhs2==rhs2,...}Eliminate[{lhs1==rhs1, lhs2==rhs2,...}, {x,y,...}]在联立方程中消去x,y,...Reduce[{lhs1==rhs1, lhs2==rhs2,...}, {x,y,...}]给出一组化简后的方程, 包括可能的解NRoot[poly==0, x] 给出多项式的根的数值逼近FindRoot[lhs==rhs, {x, x0}] 从x0出发, 求方程的数值解FindMinimum[f, {x,x0}] 在x0附近找f的极小值In[1]:= Solve[x^2+2x-7==0, x]In[2]:= Solve[2-4x+x^5==0, x] 呵呵~~~ 输出结果你会发现和没解一样In[3]:= N[%] 啊, 要数值解啊, 不早说. 这不是么.In[4]:= Solve[{a*x+y==0, 2x+(1-a)y==1},{x,a}]In[5]:= Eliminate[{3x+2y+z==3, 2x-2y-2z==5,x+y-7z==9}, {x,z}] In[6]:= Reduce[a*x+b==0, x] 哇, 好COOL. a==0, 怎么怎么; a!=0, ...In[7]:= FindRoot[Cos[x]==x,{x,1}]In[8]:= FindMinimum[x Sin[x], {x,2Pi}]幂级数Series[expr, {x, x0, n}] 求expr在x0的n阶幂级数Normal[series] 按标准形式In[1]:= Series[(1+x)^n, {x,0,3}] 最后还有近似量级呢(大喔O[x]^4)In[2]:= Normal[%]In[3]:= %^2 (1+%) 把大喔量级不要了, 多项式当然可以这么运算极限Limit[expr, x->x0] expr中x趋于x0 In[1]:= t=Sin[x]/xIn[2]:= t/.x->0 错了吧. 0不能当分母的In[3]:= Limit[t,x->0] 求极限总可以了吧特殊函数Fourier[] 傅利叶变换InverseFourier[] 反傅利叶变换In[1]:= {1,1,1,1,-1,-1,-1,-1}In[2]:= Fourier[%]In[3]:= InverseFourier[%]RungeKutta[], ... 等函数定义函数如下In[1]:= f[x_]:=x^2+1 math中定义函数:变量后跟_, 然后用:=In[2]:= f[x_, y_]:=x+y 以上两个定义同时存在并不矛盾, 当f仅使用一个参数, 自动用一式; 为两个参数, 则用二式In[3]:= f[3]In[4]:= f[3,2]定义别名In[1]:= para:=ParametricPlot 用:=来定义别名In[2]:= para[{Cos[t],t}, {t,0,Pi}]In[3]:= Alas[para] 查看para是什么的别名(7)矩阵/表的运算矩阵的定义Table, Array, IdentityMatrix, DiagonalMatrix; 输出输入TalbeForm, ColumnForm, MatrixForm, list(其他输出TeXForm, FortranForm, CForm); 和运算: 数乘, 矩阵乘法, Inverse, Transpose, Det, MatrixPower, Eigenvalues, Eigenvectors, 矩阵定义使用的一点说明.矩阵的定义Table[f, {imax}] 包含imax个f的元素(f是规则)Table[f, {i, imin, imax, istep}, {j, ...}, ...]istep=1可省, imin=1也等于1可再省Array[a, n] 建立向量a[1], a[2], ..., a[n]Array[a, {m, n}] 建mxn矩阵aArray[a, {m1, m2, ..., mn}] n维张量IdentityMatrix[n] 生成n维单位矩阵DiagonalMatrix[list] list元素为对角元In[1]:= Table[x, {4}]In[2]:= Table[i^2, {i, 1, 4}]In[3]:= x^%-1 看看表在运算符作用后的结果In[4]:= D[%, x] 求导也可以In[5]:= % /. x->3 代入值看看In[6]:= Array[a, {3, 2}] 看个2维的(3x2)矩阵In[7]:= DiagonalMatrix[{1,2,3}] 生成对角元是1,2,3的方阵矩阵的输出/输入TableForm[list] 以表列格式显示一个表ColumnForm[list] 写成一列MatrixForm[list] 按矩阵形式list[[i]] 第i个元素(一维); 第i行元素(二维)list[[i,j]] list的第i行, 第j列元素.In[1]:= a=Table[i+2*j, {i, 1, 3}, {j, 1, 2}]In[2]:= TableForm[%] 看看表格式In[3]:= ColumnForm[%%] 写成一列In[4]:= MatrixForm[%%%} 再看看矩阵形式In[5]:= %[[2]] 把上面的矩阵的第二行(是一维的表了哦)去来In[6]:= %%[[2,1]] 取第二行第一列元素(是一个数)注: In[5],In[6]也可用a[[2]]和a[[2,1]]的典型写法.其他输出格式TeXForm, FortranForm, CFormTeX(数学排版)格式, Fortran语言, C语言格式输出In[1]:= (Sqrt[x^3-1]+Exp[y])/Log[x]In[2]:= TeXForm[%] 注意TeX中T和X是大写, e是小写In[3]:= CForm[%]矩阵的数学运算cm 数乘(c标量, m是Table或Array定义的矩阵)a.b 矩阵相乘(注意矩阵乘法的规则)Inverse[m] 逆矩阵(当然要对方阵来说了)Transpose[m] 转置Det[m] m(方阵)的行列式MatrixPower[m,n] m(方阵)的n次幂Eigenvalues[m] m(方阵)的特征值Eigenvectors[m] m(方阵)的特征向量Eigenvalues[N[m]], Eigenvectors[N[m]] 数值解In[1]:= a=Table[i+2*j, {i, 1, 3}, {j, 1, 2}]In[2]:= 5a 看看乘积In[3]:= b=Table[3*i-2^j, {i, 1, 3}, {j, 1, 3}]In[4]:= b.a 矩阵乘法(注意,此例a.b没有意义)In[4]:= Transpose[%] 转置In[5]:= Inverse[b] 求一下矩阵的逆(天哪, 是方阵还不行, 还要行列式不为0)In[6]:= Det[b] 果然行列式为0In[7]:= c=b+{{1,0,0},{0,0,0},{0,0,0}}In[8]:= Inverse[c] 终于可以求逆了In[9]:= MatrixPower[b,3] b的3次方In[10]:= Eigenvalues[b] 特征值In[11]:= Eigenvectors[b] 特征向量一点说明: 矩阵可以先使用, 再定义; 局部定义和整体定义的顺序也自由. 如:In[1]:= d[1,1]=w; d[1,2]=e; d[2,1]=21; d[2,2]=22;In[2]:= Array[d,{3,3}] 你就会发现, 定义过的有值了, 没定义的还没有值.(8)表的运算.2表的结构VertorQ, MatrixQ, MemberQ, FreeQ, Length, TensorRank, Dimensions, Count, Position; 取表元First, Last, list[[]], Take, Rest, Drop, Select; 插入元素Prepend, Append, Insert, Join; 表的集合Union, Intersection, Complement; 表的重排Sort, Union, Reverse, RotateLeft, RotateRight, Transpose, Flatten, Partition, Permutations, Apply计算表的有关结构VectorQ[list] 检验list是否为向量结构MatrixQ[list] 检验list是否为矩阵结构MemberQ[list, form] 检验form是否为list的元素FreeQ[list, form] 检验form是否不是list的元素Length[list] list中元素的数目TensorRank[list] list的深度(看成张量的秩)Dimensions[list] list作为向量或矩阵的维数Count[list, form] form在list中出现的次数Position[list, form] form在list中的位置In[1]:= t={{1,2},3} t是一个表In[2]:= VectorQ[t] 不是向量In[3]:= MemberQ[t,3] 3是它的元素In[4]:= MemberQ[t,2] 2不是它的元素In[5]:= Length[t] t的长度是2In[6]:= TensorRank[t] t的深度是1In[7]:= Dimensions[t] 作为向量,是2维: {1,2}和3In[8]:= Position[t,3] 3在表t中的位置是{{2}}在表中取部分元素First[list] list的首元素Last[list] list的最后一个元素list[[n]] list的第n个元素list[[-n]] list的倒数第n个元素(以后二者合写为n/-n) list[[n1,n2,...,nm]] 相当list[[n1]][[n2]]...[[nm]]list[[{n1,n2,...,nm}]] list第n1,n2,...,nm元组成新表list[[{i1,i2,...},{j1,j2,...}]]list的i1,i2...行,j1,j2,...列Take[list, n/-n] 取list的前/后n个元素Rest[list] 去掉首元的listDrop[list, n/-n] 去掉前/后n个元素的listSelect[list, crit] 从list中选出满足crit的元素In[1]:= t={{2,1},{1}};In[2]:= VectorQ[t] 函数名最后字母为Q,其值为True/False In[3]:= aa={{a,b,c,d},{e,f,g,h},{i,j,k,l}};In[4]:= aa[[1]] 看看以下几个, 体会一下取元素/子表In[5]:= aa[[1]][[2]]In[6]:= aa[[1,2]]In[7]:= aa[[{1,2}]]In[8]:= aa[[{1},{2}]]In[9]:= Select[{a,23,12,0,3.5},EvenQ] 看看Select怎么用这里EvenQ[expr]判断expr是否偶数; OddQ[.]奇数?; NumberQ[.]数?;IntegerQ[.]整数?; PrimeQ[.]素数? AtomQ[.]简单表达式?...表中插入元素Prepend[list, elem] 表头加elem(PrependTo函数修改list)Append[list, elem] 在表尾加elem(AppendTo修改list)Insert[list, elem, n/-n] 在正/倒数第n个位置插入elemJoin[list1, list2, ...] 连接list1, list2, ...In[1]:= Prepend[{a,b,c},x] 在{a,b,c}前加x元素In[2]:= Insert[{a,b,c},x,2] 在{a,b,c}的第2个位置插入xIn[3]:= Join[{1,2,3},{xy},{m,{2,3},3}] 看看Join集合函数Union[list1, list2, ...] 去掉重复元并排序后的JoinIntersection[list1, list2, ...] 取各list的公共元Complement[t, list1, list2, ...] 在t中, 不在各list中的元素In[4]:= Union[{1,2,3},{xy},{m,{2,3},3}] 看看UnionIn[5]:= Complement[{a,b,c,d,e},{a,d},{e,f}] 看看Complement 表的重排Sort[list] 将list排序Union[list] 去掉重复元Reverse[list] 倒序RotateLeft[list, n/-n] 将list向左/右转n个元素(n=1可省) RotateRight[list, n/-n] 将list向右/左转n个元素(n=1可省) Transpose[list] 交换表的最上面两层Transpose[list, n] 交换表的顶层与第n层Flatten[list] 将list所有层变为一层Flatten[list, n] 将list的最上面n层变为一层Partition[list, n] 将list分成由n元组成的块(多余舍去)Partition[list, n, d] 各块中有偏移dPermutations[list] 给出list一切可能的排列Apply[Plus, list] 求和list[[i]]Apply[Times, list] 求积list[[i]]In[1]:= RotateLeft[{a,b,c,d,e},2] 得到{c,d,e,a,b}In[2]:= Flatten[{{a,b},c,{c,d}}] 得到{a,b,c,c,d}In[3]:= Table[i^2+j^2+k^2,{i,2},{j,2},{k,2}]In[4]:= Flatten[%,1] 展开一层In[5]:= Apply[Plus,%] 求和得到{24,36}In[6]:= Partition[{a,b,c,d,e,f,g},3,1] 看看Partition(9)二维图形二维函数作图Plot, 选项; 图的重现Show, Options, SetOptions, InputForm, Head; 参数绘图ParametricPlot; 线宽Thickness, 线型Dashing. 二维图形函数作图Plot[f[x],{x,xmin,xmax}] 在{xmin,xmax}间画出f[x]的图形Plot[{f1[x],f2[x],...},{x,xmin,xmax}] 画出fi[x]Plot[Release[f],{x,xmin,xmax}] 有时f的表达式很复杂,直接用Plot计算量大,可能得不出结果,可以先求f的值,再画Plot选项设置(格式: 选项->值)PlotRange Automatic {ymin,ymax}或{{xmin,xmax},{ymin,ymax}}AxesLabel轴标None {"x轴标","y轴标"}Frame框False TrueAxesOrigin原点Automatic {x,y}Axes轴Automatic None不画Ticks刻度Automatic None或{{xticks(,...)},{yticks(,...)}} GridLines网格None All或{{xlines...},{ylines}}AspectRatio 1/GodenRatio 正实数(高/宽)PlotPoints 15 Plot的作图精度In[1]:= Plot[Sin[x^2], {x,0,3}]In[2]:= Plot[Sin[x^2], {x,0,3}, PlotRange->{0,1.2}]In[3]:= Plot[Sin[x^2], {x,0,3}, AxesLabel->{"x","Sin[x^2]"}]In[4]:= Plot[Sin[x^2], {x,0,3}, Axes->None]In[5]:= Plot[Sin[x^2], {x,0,3}, PlotPoints->40]图形的重现Show[p] 重画图pShow[p1,p2,...] 把p1,p2,...重画在一起Show[p,option->value] 改变选项重画p(选项大多同上)(没有PlotPoits选项)Options[p] 显示图p的选项InputForm[p] 显示图p的有关存储信息SetOptions[函数名,option->value] 改变函数选项默认值Head[p] p的类型,如果p是图,则值为GraphicsIn[1]:= t1=Plot[BesselJ[1,x],{x,1,20}]In[2]:= t2=Plot[Sin[x],{x,0,15}]In[3]:= Show[t1,%]In[4]:= Show[%,Axes->None]In[5]:= Show[%,Frame->True]In[6]:= Options[%]In[7]:= InputForm[t2]参数绘图ParametricPlot[{fx,fy},{t,tmin,tmax}]ParametricPlot[{{fx,fy},{gx,gy},...},{t,tmin,tmax}]{fx,fy}的几种特殊情形{r[t]Cos[t],r[t]Sin[t]} 极坐标{Re[f],Im[f]} 复函数的相角图{Log[f],Log[g]} log-log图注意: 有时需要把AspectRatio->1才能更好地显示y/x比例, 如画圆.In[1]:= ParametricPlot[{Sin[t],Sin[2t]},{t,0,2Pi}]In[2]:= ParametricPlot[{Sin[t],Cos[t]},{t,0,2Pi}]In[3]:= Show[%,AspectRatio->Automatic]AspectRatio是1或Automatic是y/x的比例才是1选项,改变线宽和线型(虚线):在Plot的选项里使用PlotStyle->Thickness[0到1的值] 在math3.0下,使用0.005足矣PlotStyle->Dashing[{画,空}]在Show中,在Graphics[Thickness[.]]或Graphics[Dashing[.]] 之后的线宽或线型依此改变.In[1]:= Plot[Sin[x^2],{x,0,3},PlotStyle->Thickness[0.01]]In[2]:= Plot[Sin[x^2],{x,0,3},PlotStyle->Dashing[{0.01,0.01}]] In[3]:= t1=Plot[Sin[(3x)^2],{x,-1,1}]In[4]:= t2=ParametricPlot[{Sin[t],Sin[2t]},{t,0,2Pi}]In[5]:= Show[t1,Graphics[Dashing[{0.01,0.01}]],t2]In[6]:= Show[t1,Graphics[Thickness[0.01]],t2](10)三维图形三维函数作图Plot3D, 选项; 参数作图ParametricPlot3D; 等值线图ContourPlot; 密度图DensityPlot; 数据绘图ListPlot,ListPlot3D.三维作图函数作图Plot3D[f[x,y],{x,xmin,xmax},{y,ymin,ymax}]在{xmin,xmax}间画出f[x]的Surface图形Show[p] 重画图p,用法同二维Show[Gaphics3D[p]] 将图p(可能是SurfaceGraphics)转为Graphics3D,并重画三维作图选项PlotRange Automatic {zmin,zmax}或{{xmin,xmax},{y...},{z...}}Axes轴Automatic NoneAxesLabel None {"x轴标","y轴标","z轴标"}Ticks Automatic 刻度PlotLabel图标None 图的标记Boxed盒子True FalseBoxRatios {1,1,0.4} {x,y,z}HiddenSurface True False是否隐去曲面被挡部分Shading True False是否涂阴影(颜色)Mesh True False是否在曲面上画网格LightSources 三个光源设光源{{x,y,z},RGBColor[r,g,b]} FaceGrids None All或坐标网格ViewPoint视点{1.3,-2.4,2.} {x,y,z}{0,-2,0}正前方; {0,-2,2}前上方; {0,-2,-2}前下方;{2,-2,0}正右角; {0,0,2}正上方; ...PlotPoints 15 作图精度(PlotPoints为Plot3D,ParametricPlot3D,ContourPlot等plot函数选项)In[1]:= Plot3D[Sin[x]y^2,{x,-3,4},{y,-2,2}]In[2]:= Plot3D[Sin[x]y^2,{x,-3,4},{y,-2,2},PlotPoints->30]In[2]:= Show[%, Mesh->False,Boxed->False,Axes->None]参数绘图ParametricPlot3D[{fx,fy,fz},{u,umin,umax},{v,vmin,vmax}] 等值线图ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}]选项Contours 10 从zmin到zmax等值线条数密度图DensityPlot[f,{x,xmin,xmax},{y,ymin,ymax}]In[1]:= ParametricPlot3D[{Cos[5t],Sin[3t],Sin[t]},{t,0,2Pi}]In[2]:= ParametricPlot3D[{u,u+v,v^2},{u,0,2},{v,-1,1}]In[3]:= ContourPlot[Sin[x]Cos[y],{x,-2,2},{y,-2,2}]In[4]:= Show[%,Contours->30]In[5]:= DensityPlot[Sin[x]Cos[y],{x,-2,2},{y,-2,2}]数据绘图ListPlot[{y1,y2,...}] 画(1,y1),(2,y2),...ListPlot[{{x1,y1},{x2,y2},...}]ListPlot[...,PlotJoined->True] 连线ListPlot3D[array]In[1]:= t=Table[i^2,{i,10}]In[2]:= ListPlot[t]In[3]:= ListPlot[t,PlotJoined->True]In[4]:= tt=Table[Mod[y,x],{x,20},{y,20}]In[5]:= ListPlot3D[%,ViewPoint->{1.5,-0.5,1}](11)基本图元作图二维基本图元Point, Line, Rectangle, Polygon, Circle, Disk, Text, Graphics[]; 三维基本图元Point, Line, Polygon, Cuboid, Text, Graphics3D[]; 一些PlotStyle: Thickness, Dashing, PointSize, GrayLevel, RGBColor.基本图元绘图二维基本图元Point[{x,y}] 点(x,y)Line[{{x1,y1},{x2,y2},...}] 连线Rectangle[{xmin,ymin},{xmax,ymax}] 矩形Polygon[{{x1,y1},{x2,y2},...}] 多边形Circle[{x,y},r] 圆:圆心(x,y),半径rDisk[{x,y},r] 圆盘:圆心(x,y),半径rCircle[{x,y},{rx,ry},{a1,a2}] 椭圆:圆心(x,y),长短轴rx,ry,起始角a1,终止角a2Disk[{x,y},{rx,ry},{a1,a2}] 椭圆盘Text[expr,{x,y}] 文本输出在(x,y)Text[expr,{x,y},{x1,y1}] 文本输出{x1,y1}为{-1,0},{1,0},{0,1},{0,-1}, 则文本输出以(x,y)为左端点, 右端点, 上端点, 下端点; 其他-1到1的数为相对位移In[1]:= s1=Line[Table[{n,(-1)^n},{n,6}]]In[2]:= Show[Graphics[s1]]In[3]:= g1=Show[%, Axes->Automatic]In[4]:= Show[g1,Graphics[Text["f(x)",{4.5,0.8}]]]In[5]:=s2={Rectangle[{1,-1},{2,-0.6}],Polygon[ {{1,0},{3,1},{4,0.5},{5,1}}]} In[6]:= Show[g1,Graphics[s2]]In[7]:= Show[Graphics[Table[Circle[{3n,0},n/4],{n,4}]], AspectRatio->Automatic]In[8]:=Show[Graphics[Disk[{1,1},{1,2},{10Degree,325Degree}]],AspectRatio->Automatic]三维图元Point[{x,y,z}] 点(x,y,z)Line[{{x1,y1,z1},{x2,y2,z2},...}] 连线Polygon[{{x1,y1,z1},{x2,y2,z2},...}] 多边形Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}] 立方体Text[expr,{x,y,z}] 文本输出一些PlotStyleThickness[r] 线宽Dashing[{r1,r2,...}] 虚线{实虚实虚...}PointSize[r] 点的大小GrayLevel[r] 灰度0<=r<=1RGBColor[r,g,b] RGB颜色([0,1]间)[1,0,0]红; [0,1,0]绿; [0,0,1]蓝; [1,1,0]黄In[1]:= Plot[Sin[x^2],{x,0,3},PlotStyle->RGBColor[1,0,0]]In[2]:=Show[%,Graphics[PointSize[0.05]],Graphics[Point[{2,1}]]] In[3]:=Show[Graphics3D[RGBColor[1,0,0]],Graphics3D[ Line[{{0,0,0},{1, 2,3},{3,2,1}}]]](12)表达式与纯函数表达式形式FullForm, TreeForm, Head; 表达式的书写形式@,//, ~f~; 表达式的项expr[[n]]; 表达式操作Apply(@@), Nest, Map(/@), MapAll(//@), MapAt; 纯函数&, #, ##.表达式形式FullForm[expr] 给出表达式的完全形式TreeForm[expr] 给出表达式的完全形式Head[expr] 给出表达式的头部In[1]:= FullForm[x+y+z] x+y+z的FullForm是Plus[x,y,z]In[2]:= FullForm[1+(x y)^2+(y+z)^3]In[3]:= TreeForm[%]In[4]:= Head[%]In[5]:= Head[215]In[6]:= Head[21.5]In[7]:= Head[Plot[Sin[x],{x,0,1}]]表达式的四种书写形式f[x,y] 标准形式f@x f[x]的前缀形式x//f f[x]的后缀形式x~f~y f[x,y]的中间形式In[1]:= Pi^2//N 相当于N[Pi^2](//级别低)In[2]:= N@Pi^2In[3]:= {a,b,c}~Join~{c,d}表达式的项expr[[n]] expr的第n项expr[[-n]] expr倒数第n项expr[[n1,n2,...]] 树结构索引的expr的项expr[[n]]=expr2 项赋值Position[expr,form] 寻找expr中form的位置In[1]:= t=1+(3+x)^2+z;In[2]:= t[[2]] 得(3+x)^2(类似于取List的元素)In[3]:= t[[2,1]] 再取子表得到Power函数的(3+x)In[4]:= t[[4]] 出错,不存在In[5]:= t[[3]]=y*z 试试直接赋值In[6]:= t 看看t变成什么了表达式的操作Apply[f,list] 对list施加函数f (@@)Nest[f,x,n] 将f对x作用n次Map[f,expr] 将f作用于expr的第一层(/@) Map[f,expr,n] 将f作用于expr直到第n层MapAll[f,expr] 将f作用于expr的所有项(//@) MapAt[f,expr,{polist}] 将f作用于expr的polist位置上In[1]:= Apply[f,{a,b,c}] 得到f[a,b,c](同f@@{a,b,c})In[2]:= Nest[f,x,3] 得f[f[f[x]]]In[3]:= u=x+(x+2)^2/xIn[4]:= Map[f,u] 同f/@uIn[5]:= Map[f,u,2]In[6]:= MapAll[f,u] 同f//@uIn[7]:= MapAt[f,u,Position[u,x]] 所有x都换成f[x]纯函数& Function纯函数# 纯函数的第一个变量#n 纯函数的第n个变量##n 从第n个起的变量序列## ##1Function[x,expr] 有一个变量的纯函数Function[{x1,x2,...},expr] 列表参数的纯函数In[1]:= Map[#^2&, {a,b,c}] 甚至#^2& /@ {a,b,c} 即将函数#^2作用于{a,b,c}得到{a^2,b^2,c^2} In[2]:= (#1^2+#2^#3)&[x,y,3] 即x^2+y^3In[3]:= g[##,##]&[x,y] 得g[x,y,x,y](13)转化规则与参数转换规则f[x]=, f[x_]=, Clear; 模式与匹配; 赋值=和:=; /; , -> , :> , /. , //. , Replace, /: ; 参数的含义_, __, ___, _head, _:xdef.转换规则f[x]=expr 定义f在x的值f[x_]:=expr 定义f[x](区别=与:=)Clear[f]或f[x_]=. 清除f的定义Remove[f] 彻底清除变量或函数fIn[1]:= f[x]=x^2 定义f在x为x^2In[2]:= f[2]+f[x] f[2]未定义,所以得到f[2]+x^2In[3]:= g[x_]=x^2 定义g[x](这里x没有值,:=与=一样) In[4]:= g[2]+g[x] 得到4+x^2 (注意看f和g的区别) In[5]:= f[3]=10 再定义一个f[3]In[6]:= ?f 看看f模式与匹配f[n_], f[m_,n_], f[n_,n_]In[1]:= f[m_,n_]:=m+nIn[2]:= f[n_,n_]:=3*nIn[3]:= f[n_]:=2*nIn[4]:= f[2,2]+f[6,8] f[2,2]用的是f[n,n]而不是f[m,n]In[5]:= f[2]+f[6,8] f[2]用单参数规则,f[6,8]用双参数规则赋值= 立即赋值:= 到使用时再赋值In[1]:= y=2In[2]:= h[y_]=y^3 即时赋值In[3]:= h[1] =8In[4]:= h2[y_]:=y^3 使用时再赋值,这里只定义规则In[5]:= h2[1] =1 (注意h2与h的区别)In[6]:= ?hIn[7]:= ?h2 分别看看就知道了In[8]:= 3! 下面再熟练一下=和:=的区别In[9]:= f[x_]:=%+2xIn[10]:= 1+y^2In[11]:= g[x_]:=%+2xIn[12]:= 2+zIn[13]:= f[a]+g[a]In[14]:= f[a]*g[a]/; (表达式/;条件) 满足条件使用表达式-> (lhs -> rhs) 在定义时,lhs用rhs代替:> (lhs :> rhs) 在使用时,lhs用rhs代替/. (expr /. rule) 对expr所有项使用规则一次//. (expr //. rule) 对expr所有项使用规则直到结果不变化Replace[expr,rule] 对整体expr使用规则一次/: (g/:lhs:=rhs) 定义一个转换规则,与g相关联In[1]:= f[x_]:=1 /; -1<=x<=1 当-1<=x<=1时, f[x]=1In[2]:= f[x_]:=-1 其他时候f[x]=-1In[3]:= f[2]In[4]:= f[0.5] 分段函数耶In[5]:= Plot[f[x],{x,-2,2}] 画图看看, 不错不错In[6]:= x+y /. x->2 得到2+y(:>和->的区别类似于:=与=) In[7]:= Clear[f]In[8]:= f[5] /. {f[1]->1,f[x_]->x*f[x-1]}In[9]:= f[5] //. {f[1]->1,f[x_]->x*f[x-1]}In[10]:= ss /: math[ss]=96In[11]:= ss /: phys[ss]=95In[12]:= ?ss参数x_ 单个表达式xx__ 一个或多个表达式序列xx___ 0个或多个表达式序列xx_h (或x__h) Head是h的表达式(序列)x_:xdef 可省参数的缺省值In[1]:= nt[t_,lt__]:=t*ltIn[2]:= c={1,2,3,4}In[3]:= nt[3,c] 这里就使用c是列表参数In[4]:= li[x_,xi_,xj__]:=(x-xj)/(xi-xj)In[5]:= li[x,xi,{1,2}] 再看个例子In[6]:= h[x_Real]:=x^2 定义h,当x是Real时In[7]:= h[4.5] h[4.5]的值为20.25In[8]:= h[a] a的Head不是Real,未定义,得h[a] In[9]:= fac[0]=1 以下看看函数facIn[10]:= fac[n_Integer?Positive]:=n*fac[n-1]In[11]:= fac[5] 120(注意上面条件用?间隔)In[12]:= h2[x_?NumberQ]:=x^3 看看这个条件的使用In[13]:= f[x_,y_:1,z_:2]:=g[x,y,z]In[14]:= f[a1,b1,c1] 都有参数则按参数代入In[15]:= f[a1,b1] 少一个参数,使用缺省值In[16]:= f[a1] 只有一个参数,两个参数使用缺省(14)mathematica过程编程一般过程, Block; 循环Do, While, For, Nest, FixedPoint; 条件If, Which, Switch; 转向Return, Break, Continue, Goto, Label.一般过程Command; Command; ... 一串命令Block[{x,y,...},procedure] x,y,...为局部参数Block[{x=x0,y=y0,...},proc] 局部参数赋初值In[1]:= g[x_]:= Block[{u},u=(1+x)^2;u=Expand[u]]In[2]:= g[a+b] 看看g[a+b]=?In[3]:= u 而这时u不发生改变循环结构Do[expr,{i,imin,imax,istep}]计算expr,i从imin到imax,步长istepDo[expr,{i,imin,imax}] istep=1Do[expr,{i,imax}] imin=1,istep=1Do[expr,{n}] 计算expr n次Do[expr, {i...}, {j...}...] 多重循环(前面的外重循环)While[test,expr] 当test成立, 计算exprFor[start,test,increment,body]相当于C语言for(start;test;increment) body Nest[f,expr,n] f对expr作用n次FixedPoint[f,expr] 重复使用f,直到expr不再变化用于循环的表达式i++, i--, ++i, --i, i+=di, i-=di, i*=di, i/=di,{x,y}={y,x} x,y值交换In[1]:= Do[Print[i^2],{i,4}] 循环Print[i^2]In[2]:= t=x;Do[t=1/(1+k*t),{k,2,4}];tIn[3]:= Do[Print[{i,j}],{i,4},{j,i-1}]In[4]:= Nest[Function[t,1/(1+t)],x,3] 注意虚函数的使用In[5]:= FixedPoint[Function[t,Print[t];Floor[t/2]],67]In[6]:= n=17;While[(n=Floor[n/2])!=0,Print[n]]In[7]:= For[i=1,i<4,i++,Print[i]]In[8]:= For[i=1;t=x,i^2<10,i++,t=t^2+i;Print[t]]大家注意练习上面例子, 考虑并看看运行结果, 熟练Math的循环语句的使用.条件语句If[test,expr] if (test) exprIf[test,expr1,expr2] if (test) expr1 else expr2If[test,expr1,expr2,expr3] 无法判断时得值expr3Which[test1,value1,test2,value2,...True,value]test1为真,得value1;否则判断test2...;若全不满足,得Null Switch[expr,form1,value1,form2,value2,...]expr的值为form1,得value1; 为form2,得value2,...In[1]:= f[x_]:=If[x>0,1,-1]In[2]:= Plot[f[x],{x,-2,2}] 还是画图形象In[3]:= g[x_]:=Which[x>1,x+2,x<-5,x-2]In[4]:= g[0] 没有输出In[5]:= Print[g[0]] 看到了,是NullIn[6]:= g[-6]In[7]:= g[2] 这两个g值都有意义In[8]:= h[x_]:=Switch[Mod[x,3],0,a,1,b,2,c]In[9]:= h[4] 也可以看看h[5],h[6]等值转向控制Return[] 返回,当前函数值NullReturn[expr] 返回expr的值Break[] 和Continue[] 这两函数只用于For,While.(Do不使用)Goto[标志]和Label[标志](15)程序包程序包的结构, 上下文, 程序注释, 输出, 输入程序包的结构BeginPackage["self`"] 激活或建立self上下文f::ussage="...." f的用法说明Begin["`Private`"] 开始包的私有上下文....f[args]=.......End[] 结束自身的上下文EndPackage[] 结束包,将self`放在全局上下文路径的最前面如果第一句为BeginPackage["self`","f1`","f2`"], 则在定义包self时, 同时打开f1.m, f2.m, 调入f1`, f2`.名字和上下文上下文表示为字符串`name 在当前上下文或搜索路径中最先找到的符号context`name 在指定上下文中的符号`name 在当前上下文中的符号Unique[ss] 生成以ss开头的没用过的符号Clear[s] 清除s的值Remove[s] 清除符号sRemove["context`*"] 清除context上下文中的所有符号这里要提一下两个系统变量: $Context和$ContextPath, 前者为当前上下文, 后者为当前上下文路径. 关于上下文, 大家看看以下例子, 体会一下.In[1]:= $Context 当前上下文是Global`In[2]:= z=6 定义z=6In[3]:= Begin["new1`"] 开始new1上下文IN[4]:= new1`z=9 new1上下文中的z=9In[5]:= $Context 当前上下文是new1`In[6]:= z 看看z=9In[7]:= ?*`z 看看有几个z,其中有z和Global`zIn[8]:= EndAdd[] 结束new1`,并将new1`放在路径最前面In[9]:= $ContextPath 看看路径In[10]:= ?*`z 看看有几个z,其中有z和new1`zIn[11]:= z 看看现在z的值是Global的z值了In[12]:= $Context 当前上下文In[13]:= Remove[z] 清除变量zIn[14]:= z Global的z清除了,这时显示的z=9In[15]:= Remove[z] 再Remove就清除new1中的z了程序注释f::ussage="text..." 关于一个函数的说明(* 注释内容*) 出现在程序包的任何地方如If[x>y,(* then *)x,(* else *) y]和If[x>y,x,y]是一样的.输出Print[expr1,expr2,...] 在屏幕上输出expr1,expr2,...StringForm[string,expr1,expr2,...] 将string中成对的``依次用expr1,expr2,...代替. 若string中是`n`, n为整数, 则用第n个expr代替.如StringForm["`` is not ``.",x+1,y]输出x+1 is not y.Message[s::tag] 输出tagOff[s::tag] / On[s::tag] 屏蔽/打开tag信息In[1]:= f::"overflow"="Factorial argument `1` too large."In[2]:= f[x_]:=If[x>10,Message[f::"overflow",x];Infinity,x!]In[3]:= f[20] 输出错误信息In[4]:= Off[f::"overflow"] 屏蔽overflow信息In[5]:= f[20]表达式输出到文件expr >> file 把表达式的值写入新文件fileexpr >>> file 把表达式的值追加到file中!!file 显示文件输入Input[] 键盘输入完整表达式作为Input的返回值Input[提示] 显示提示,接受输入InputString[] 输入字符串Read[文件名,类型描述] 按类型描述读入文件,参看帮助。
mathematic入门教程1

y=2*x^2-1;
y/.x->Pi-x
x->Pi-x中的“->”是由键盘上的减号及大于号组成的,以后各节中不在说明.
变量的清除,当一个变量a无用时,可以用命令Clear[a]加以清除
1.5
“表”{}即可以作为数组,又可以作为矩阵;还可以把任意一组表达式用一个或一组{}括起来,进行运算、存储。另外可通过下表操作符[[]](双方括号)来访问它的每一个元素。
Mathematica中的普通数有整数、有理数、实数、复数四种类型
类型
描述
实例
特征说明
整数
Integer
33889
任意长度的精确数
有理数
Rational
27/79
化简过的分数
实数
Real
109.0
任意精确度的近似数
复数
Complex
12.0+2I
实部、虚部可为整数、有理数、实数
常数
常量名
数学含义
解释
2
Mathematica的一个重要的功能是进行代数公式演算,即符号运算.
Factor[多项式]表示将其括号内的多项式分解因式;Expand[多项式]表示将其括号内的多项式展开成按升幂排列的单项式之和的形式.
2.将多项式
3.式 积.
三、函数运算
3.1
(a)三角函数、复数函数、随机函数(Random[n])、特殊函数(如贝塞尔函数系、椭圆函数等),矩阵运算函数(如求特征值特征向量的EigenVector[],EigenValue[],求逆的Inverse[]等)。
Prepend[表,表达式]添加表达式于表后
第三讲MatheMatica入门

Which[条件1,表达式 1,条件2,表达式 2,……]
Which[条件1,表达式 依次计算每个条件的值,将第一个为True的条件对 1,…条件n,表达 应的表达式作为整个语句的值.用True作为Which 式n,True,表达式] 的最后一个条件时,可用于处理其他情况
x sin x 例7:分段函数 h( x) x 2 0
ch308_1.nb
再求函数值 , 输入: {h[-1],h[1],h[7],h[11]}
Mathematica程序:
求得: Out[]:={1,sin1,7/2,0}
ch308_2.nb
五、mathematica程序流程的控制
在正常情况下,系统对表达式的求值总是按照规定的顺序 和方式进行。但是,在有些情况下,人们需要改变这种正常 的顺序,以便程序的设计,是计算流程更加自然,或者为了 提高程序的执行效率,等等。为此,Mathematcia提供了一 些特殊的程序流程控制结构。 函数 Break 说明 退出最近的一层循环
二、Mathematica中的顺序控制结构
Mathematica中的顺序控制结构就是复合表达式,根据 求解问题的需要把一个系统的表达式按顺序排列,在一个表 达式后面写一个分号(;)接着写其他表达式,就构成了复 合表达式。一个复合表达式的值就是它的最后一表达式的值。 例5:求函数f(x)=2x3-6x2-18x+7的驻点。 Clear[f]; f[x_]:=2x^3-6x^2-18x+7; diff=D[f[x],x]; Solve[diff==0,x] Out[]={{x->-1},{x->3}}
三、Mathematica的输入、输出和运行
1、Mathematica的输入方式:通过键盘直接输入 2、Mathematica的运行 在Mathematica的工作区窗口,输入一行或多行表达 式,例如:输入1+1,然后按下Shif+Enter键,这时系统 开始计算并输出计算结果,并给输入和输出附上次序标识 In[1]和Out[1],注意In[1]是计算后才出现的。 3、控制系统结果输出的方法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)简介数学系给本科生开设一门课: "符号计算系统", 主要简单讲授mathematica(以下简称math)软件的使用及其编程,赶兴趣的同学可以找本math书以求更深入的了解.我们平日用到编程语言时, 大家都知道编程中用到的整型, 实型, 甚至双精度数, 都只是一个近似的数, 其精度有限, 有效数字有限, 在很多时候达不到实际需要的要求. 符号计算与数值计算的区别就在于符号计算以准确值记录计算的每一步的结果, 如果需要时, 可以将精确表示按需要计算成任意位数的小数表示出来(只要机器内存足够大).最常见的符号计算系统有maple, mathematica, redues等, 这些软件各有侧重, 比如,maple内存管理及速度比math好, 但是图形方面不如math; redues没找到, 没用过, 未明; 而用得较多的matlab编程环境特好, 和C语言接口极其简单, 遗憾的是它不是符号计算, 只是数值计算. 所以, 就实用而全面来说, math是一个很好用的软件.math软件不仅能够进行一般的+-*/及科学函数如Sin, Log 等计算, 而且能进行因式分解, 求导, 积分, 幂级数展开, 求特征值等符号计算, 并且, math有较强的图元作图, 函数作图, 三维作图及动画功能.(2)mathematica入门mathematica自发布以来, 目前比较常见的有math 1.2 for DOS, math 2.2 for Windows, math 3.0 for win95, math 3.0 for UNIX.DOS下的math的好处就是系统小, 对机器要求低, 在386机器4M内存下就能运行得很好(机器再低点也是可以用的, 比如说286/2M). 在DOS下直接键入math<回车>即可进入math系统, 出现的提示符In[1]:=, 这时就可以进行计算了, 键入math函数, 回车即可进行运算. 如果输入的Quit, 则退出math. 这里要注意的是, math区分大小写的, 一般math 的函数均以大写字母开始的.windows下的math对机器要求就要高一些了, math3.0更是庞大, 安装完毕有100M之多(2.2大约十多兆). 同windows下的其他软件一样, math可以双击图标运行, 在File菜单下有退出这一项. windows下的math有其优越性, 就是可以在windows下随心所欲地拷贝粘贴图形. math3.0更是能输入和显示诸如希腊字母, 积分符号, 指数等数学符号. DOS的math与windows下的一个区别是DOS的以回车结束一句输入, 而windows的以+<回车>结束一句输入. DOS下的提示符显示为In[数字]:=, 而windows下在结束输入后才显示出In[数字]:=及Out[数字]:=字样. (Out为输出提示符) 下面试试几个例子:(In[数字]:=为提示符, 不用键入)In[1]:= 2^100 计算2的100次方In[2]:= s={{3,7,9},{7,4,3},{1,3,8}} 定义矩阵sIn[3]:= Eigenvalues[s] 计算s的特征值In[4]:= Plot[Sin[x],{x,0,Pi}] 在0,Pi间画SinIn[5]:= Plot[Cos[x],{x,0,Pi}] CosIn[6]:= Plot3D[Sin[x]Sin[y],{x,0,1},{y,0,2}] 三维作图以In[6]为例说明: math的函数都以大写字母开头的单词为函数名, Plot3D, Plot, Eigenvalues, Sin等, 常数也是如此, 如Pi. 函数名后的参数用[]括起, 逗号隔开.math的输出可以作为函数的输入对象, 你可以再试一个: In[7]:=Show[%%,%%%] 这里一个%代表上一个输出, 两个代表上两个... 也可以直接用Out[n]代表第n个输出.这里需要补充的是!command 执行DOS命令?name 关于name(函数等)的信息(可以使用通配符)??name 关于name的额外信息(3)基本计算1. 算术运算符+加-减*乘/除^指数(乘也可用空格)N[expr]或expr //N 计算expr的数值(6位有效数字)N[expr, n] n表示小数的位数2. 数学函数Sqrt[x] x开方Exp[x] e的x方Log[x] x的自然对数Log[b,x] 以b为底, x的对数Sin[x], Cos[x], Tan[x], ArcSin[x], ArcCos[x] 三角函数Abs[x] |x|Round[x] 离x最近的整数Floor[x] 不超过x的最大整数Quotient[n,m] n/m的整数部分Mod[n,m] n/m的余数Random[] 0,1间随机数Max[x,y,...] Min[x,y,...] 最大数和最小数3. 常数Pi Pi=3.141592653589793...E e=2.71828...Degree Pi/180I i=Sqrt[-1]Infinity 无穷大Catalan Catalan常数.=0.915966ComplexInfinity 复无穷DirectedInfinity 有向的无穷EulerGamma 欧拉常数gamma=0.5772216GoldenRatio 黄金分割(Sqrt[5]-1)/2Indeterminate 不定值4. 逻辑运算符==, !=, >, >=, <, <=, !, &&, ||Xor 异或Implies 隐含If[条件,式1,式2] 如果条件成立, 值式1; 否则得式25. 变量a) 变量名以字母(一般小写)开头; 字母数字组成.(如x2为变量名; 而2x, 2*x, 2 x, x*2, x 2均是x乘以2).b) 赋值x=value; x=y=value; x=.(清除x值)c) 代换expr /. x->value 将式中x代换为valueexpr /. {x->xval, y->yval}下面就让我们以几个例子来结束本节:(大家还是注意, DOS下的Math, 只要输入In[num]:=后的指令后按回车, 而windows下则是按+回车.) 大家看看都有什么输出.In[1]:= 2.7+5.23In[2]:= 1/3+2/7In[3]:= 1/3+2/7 //NIn[4]:= N[Pi,100]曾经有人问我, 你是怎么算出Pi的1000位而没有错误的, 其实很简单, 大家只要把上式的100改为1000即可.In[5]:= Sin[Pi/2]+Exp[2]+Round[1.2]In[6]:= 10<7In[7]:= x=5;如果在输入之后加上一个";", 则只运算不输出.IN[8]:= y=0(所以In[7]和8完全可以合成一条x=5;y=0, 假如我不需要x=5的输出) In[9]:= x>yIn[10]:= t=1+m^2In[11]:= t /. m->2In[12]:= t /. m->5aIn[13]:= t /. m->Pi //N(4)代数变换上一节我们已经学习了Math里的基本运算及逻辑运算, 常用数学函数, 几个常见的常数, 以及变量的使用. 这一节, 我们来学学基本代数变换: Apart, Cancel, Coefficient, Collect, Denominator, Expand, ExpandAll, Exponent, Factor, Numerator, Short, Simplify, Together.Expand[expr] 多项式expr按项展开Factor[expr] 因子形式Simplify[expr] 最简形式In[1]:= Expand[(1+x)^2]In[2]:= Factor[%]我们以前说过的哦, %是上一个输出, %%是上上个, %%%是上上上个, ..., %n是第n个输出(即Out[n])In[3]:= Simplify[%%]In[4]:= Integrate[x^2/(x^4-1),x] 这是积分运算, 详情后叙In[5]:= D[%,x] 求导In[6]:= Simplify[%]ExpandAll[expr] 所有项均展开Together[expr] 通分Apart[expr] 分离成具有最简分母的各项Cancel[expr] 约去分子,分母的公因子Collect[expr] 合并In[1]:= e=(x-1)^2 (2+x)/((1+x)(x-3)^2)In[2]:= Expand[e]In[3]:= ExpandAll[e]In[4]:= Together[e]In[5]:= Apart[%]In[6]:= Factor[%]Coefficient[expr, form] 表达式中form项的系数Exponent[expr, form] form的最高幂次Numerator[expr] 取分子Denominator[expr] 取分母expr //Short 以简短形式输出In[1]:= e=Expand[(1+3x+4y^2)^2]In[2]:= Coefficient[e, x]In[3]:= Exponent[e, y]In[4]:= q=(1+x)/(2(2-y))In[5]:= Denominator[%]In[6]:= Expand[(x+5y+10)^4]In[7]:= %//Short 把上式输出, 中间项省去, 以<<数字>>表示省去的项数.最后, 我们以例子来看看用符号名做客体的标志的好处In[1]:= 12metersIn[2]:= %+5.3metersIn[3]:= %/(25seconds)In[4]:= %/.meters->3.78084feet 一下子就把米制变为英尺了.(5)微积分运算(2-1)学到上一节, 大家会发现怎么还停留在中学的计算中呢, 这一节, 大家就会看到微分D, Dt; 积分Integrate, NIntegrage; 和与积Sum, Product, NSum, NProduct. 下一节我们介绍解方程Solve, Eliminate, Reduce, NRoot, FindRoot, FindMinimum; 幂级数Series, Normal; 极限Limit; 特殊函数Fourier, InverseFourier, ...微分D[f, x] f对x求导D[f, x_1, x_2, ...] f对x_1, x_2, ...求导D[f, {x, n}] f对x求n次导Dt[f] 全微分dfDt[f, x] 全微商df/dxIn[1]:= D[x^n,x]In[2]:= D[f[x],x]In[3]:= D[2x f[x^2],x]In[4]:= D[x^n, {x, 3}]In[5]:= D[x^2 y^3, x, y]In[6]:= Dt[x^n]In[7]:= Dt[x y, x]积分Integrate[f,x] f对x积分Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}, ...] 定积分NIntegrate[f, {x, xmin, xmax}, {y, ymin, ymax}, ...]计算积分的数值解In[1]:= Integrate[Sin[Sin[x]],x] 嘻嘻, 无法计算, 原样输出In[2]:= Integrate[Log[x], {x,0,6}] 啊, 广义积分也一样算In[3]:= Integrate[x^2+y^2, {x,0,1}, {y,0,1}]In[4]:= In[3]//N 如果你的上一条输入不是In[3], 注意调整这一条的输入哦In[5]:= Integrate[Sin[Sin[x]], {x,0,1}] 怎么还没法计算啊In[6]:= N[%] 或NIntegrate[Sin[Sin[x]], {x,0,1}] 呵,终于可以计算了.和与积Sum[f, {i, imin, imax}, {j, jmin, jmax}, ...]f对i, j, ...分别从imin到imax,jmin到jmax,...求和Sum[f, {i, imin, imax, di}] 求和的步长为diProduct[f, {i, imin, imax}, {j, jmin, jmax}, ...] 求积NSum 数值解NProduct 数值解In[1]:= Sum[x^i/i, {i,1,4}]In[2]:= Sum[x^i/i, {i,1,5,2}]In[3]:= Sum[a/i^3, {i,1,10}]In[4]:= N[%] 或NSum[a/i^3, {i,1,10}]In[5]:= Sum[1/i^3, {i,1,Infinity}] 可能原样输出, 也可能输出Zeta[3](依math的版本不同而异)In[6]:= N[%]In[7]:= Sum[x^i*y^j, {i,1,3}, {j,1,i}]注: 如果想要求带符号上下限的Sum, 在math3.0中, 直接使用Sum函数即可: In[8]:= Sum[1/Sin[i], {i,1,n}]而如果在旧版本的math, 则可能需要调入包(package) "gospersu.m", 调入格式一般为In[8]:= <<"盘符:\\math路径\\packages\\algebra\\gospersu.m"(不同安装目录可能出现不一样)然后使用函数GosperSum[](6)微积分运算(2-2)上一节, 我们一起学习了微分D, Dt; 积分Integrate, NIntegrage;和与积Sum, Product, NSum, NProduct. 这一节我们将介绍解方程Solve, Eliminate, Reduce, NRoot, FindRoot, FindMinimum; 幂级数Series, Normal; 极限Limit; 特殊函数Fourier, InverseFourier, ...最后, 我们说明一下math的函数的定义, 别名的使用, 以及不同输出格式解方程Solve[{lhs1==rhs1, lhs2==rhs2,...}, {x,y,...}]解关于x,y,...的方程组{lhs1==rhs1, lhs2==rhs2,...}Eliminate[{lhs1==rhs1, lhs2==rhs2,...}, {x,y,...}]在联立方程中消去x,y,...Reduce[{lhs1==rhs1, lhs2==rhs2,...}, {x,y,...}]给出一组化简后的方程, 包括可能的解NRoot[poly==0, x] 给出多项式的根的数值逼近FindRoot[lhs==rhs, {x, x0}] 从x0出发, 求方程的数值解FindMinimum[f, {x,x0}] 在x0附近找f的极小值In[1]:= Solve[x^2+2x-7==0, x]In[2]:= Solve[2-4x+x^5==0, x] 呵呵~~~ 输出结果你会发现和没解一样In[3]:= N[%] 啊, 要数值解啊, 不早说. 这不是么. In[4]:= Solve[{a*x+y==0, 2x+(1-a)y==1},{x,a}]In[5]:= Eliminate[{3x+2y+z==3, 2x-2y-2z==5,x+y-7z==9}, {x,z}]In[6]:= Reduce[a*x+b==0, x] 哇, 好COOL. a==0, 怎么怎么; a!=0, ... In[7]:= FindRoot[Cos[x]==x,{x,1}]In[8]:= FindMinimum[x Sin[x], {x,2Pi}]幂级数Series[expr, {x, x0, n}] 求expr在x0的n阶幂级数Normal[series] 按标准形式In[1]:= Series[(1+x)^n, {x,0,3}] 最后还有近似量级呢(大喔O[x]^4)In[2]:= Normal[%]In[3]:= %^2 (1+%) 把大喔量级不要了, 多项式当然可以这么运算极限Limit[expr, x->x0] expr中x趋于x0In[1]:= t=Sin[x]/xIn[2]:= t/.x->0 错了吧. 0不能当分母的In[3]:= Limit[t,x->0] 求极限总可以了吧特殊函数Fourier[] 傅利叶变换InverseFourier[] 反傅利叶变换In[1]:= {1,1,1,1,-1,-1,-1,-1}In[2]:= Fourier[%]In[3]:= InverseFourier[%]RungeKutta[], ... 等函数定义函数如下In[1]:= f[x_]:=x^2+1 math中定义函数:变量后跟_, 然后用:=In[2]:= f[x_, y_]:=x+y 以上两个定义同时存在并不矛盾, 当f仅使用一个参数, 自动用一式; 为两个参数, 则用二式In[3]:= f[3]In[4]:= f[3,2]定义别名In[1]:= para:=ParametricPlot 用:=来定义别名In[2]:= para[{Cos[t],t}, {t,0,Pi}]In[3]:= Alas[para] 查看para是什么的别名(7)矩阵/表的运算矩阵的定义Table, Array, IdentityMatrix, DiagonalMatrix; 输出输入TalbeForm, ColumnForm, MatrixForm, list(其他输出TeXForm, FortranForm, CForm); 及运算: 数乘, 矩阵乘法, Inverse, Transpose, Det, MatrixPower, Eigenvalues, Eigenvectors, 矩阵定义使用的一点说明.矩阵的定义Table[f, {imax}] 包含imax个f的元素(f是规则)Table[f, {i, imin, imax, istep}, {j, ...}, ...]istep=1可省, imin=1也等于1可再省Array[a, n] 建立向量a[1], a[2], ..., a[n]Array[a, {m, n}] 建mxn矩阵aArray[a, {m1, m2, ..., mn}] n维张量IdentityMatrix[n] 生成n维单位矩阵DiagonalMatrix[list] list元素为对角元In[1]:= Table[x, {4}]In[2]:= Table[i^2, {i, 1, 4}]In[3]:= x^%-1 看看表在运算符作用后的结果In[4]:= D[%, x] 求导也可以In[5]:= % /. x->3 代入值看看In[6]:= Array[a, {3, 2}] 看个2维的(3x2)矩阵In[7]:= DiagonalMatrix[{1,2,3}] 生成对角元是1,2,3的方阵矩阵的输出/输入TableForm[list] 以表列格式显示一个表ColumnForm[list] 写成一列MatrixForm[list] 按矩阵形式list[[i]] 第i个元素(一维); 第i行元素(二维)list[[i,j]] list的第i行, 第j列元素.In[1]:= a=Table[i+2*j, {i, 1, 3}, {j, 1, 2}]In[2]:= TableForm[%] 看看表格式In[3]:= ColumnForm[%%] 写成一列In[4]:= MatrixForm[%%%} 再看看矩阵形式In[5]:= %[[2]] 把上面的矩阵的第二行(是一维的表了哦)去来In[6]:= %%[[2,1]] 取第二行第一列元素(是一个数)注: In[5],In[6]也可用a[[2]]和a[[2,1]]的典型写法.其他输出格式TeXForm, FortranForm, CFormTeX(数学排版)格式, Fortran语言, C语言格式输出In[1]:= (Sqrt[x^3-1]+Exp[y])/Log[x]In[2]:= TeXForm[%] 注意TeX中T和X是大写, e是小写In[3]:= CForm[%]矩阵的数学运算cm 数乘(c标量, m是Table或Array定义的矩阵)a.b 矩阵相乘(注意矩阵乘法的规则)Inverse[m] 逆矩阵(当然要对方阵来说了)Transpose[m] 转置Det[m] m(方阵)的行列式MatrixPower[m,n] m(方阵)的n次幂Eigenvalues[m] m(方阵)的特征值Eigenvectors[m] m(方阵)的特征向量Eigenvalues[N[m]], Eigenvectors[N[m]] 数值解In[1]:= a=Table[i+2*j, {i, 1, 3}, {j, 1, 2}]In[2]:= 5a 看看乘积In[3]:= b=Table[3*i-2^j, {i, 1, 3}, {j, 1, 3}]In[4]:= b.a 矩阵乘法(注意,此例a.b没有意义)In[4]:= Transpose[%] 转置In[5]:= Inverse[b] 求一下矩阵的逆(天哪, 是方阵还不行, 还要行列式不为0) In[6]:= Det[b] 果然行列式为0In[7]:= c=b+{{1,0,0},{0,0,0},{0,0,0}}In[8]:= Inverse[c] 终于可以求逆了In[9]:= MatrixPower[b,3] b的3次方In[10]:= Eigenvalues[b] 特征值In[11]:= Eigenvectors[b] 特征向量一点说明: 矩阵可以先使用, 再定义; 局部定义和整体定义的顺序也自由. 如:In[1]:= d[1,1]=w; d[1,2]=e; d[2,1]=21; d[2,2]=22;In[2]:= Array[d,{3,3}] 你就会发现, 定义过的有值了, 没定义的还没有值.(8)表的运算.2表的结构VertorQ, MatrixQ, MemberQ, FreeQ, Length, TensorRank, Dimensions, Count, Position; 取表元First, Last, list[[]], Take, Rest, Drop, Select; 插入元素Prepend, Append, Insert, Join; 表的集合Union, Intersection, Complement; 表的重排Sort, Union, Reverse, RotateLeft, RotateRight, Transpose, Flatten, Partition, Permutations, Apply计算表的有关结构VectorQ[list] 检验list是否为向量结构MatrixQ[list] 检验list是否为矩阵结构MemberQ[list, form] 检验form是否为list的元素FreeQ[list, form] 检验form是否不是list的元素Length[list] list中元素的数目TensorRank[list] list的深度(看成张量的秩)Dimensions[list] list作为向量或矩阵的维数Count[list, form] form在list中出现的次数Position[list, form] form在list中的位置In[1]:= t={{1,2},3} t是一个表In[2]:= VectorQ[t] 不是向量In[3]:= MemberQ[t,3] 3是它的元素In[4]:= MemberQ[t,2] 2不是它的元素In[5]:= Length[t] t的长度是2In[6]:= TensorRank[t] t的深度是1In[7]:= Dimensions[t] 作为向量,是2维: {1,2}和3In[8]:= Position[t,3] 3在表t中的位置是{{2}}在表中取部分元素First[list] list的首元素Last[list] list的最后一个元素list[[n]] list的第n个元素list[[-n]] list的倒数第n个元素(以后二者合写为n/-n)list[[n1,n2,...,nm]] 相当list[[n1]][[n2]]...[[nm]]list[[{n1,n2,...,nm}]] list第n1,n2,...,nm元组成新表list[[{i1,i2,...},{j1,j2,...}]]list的i1,i2...行,j1,j2,...列Take[list, n/-n] 取list的前/后n个元素Rest[list] 去掉首元的listDrop[list, n/-n] 去掉前/后n个元素的listSelect[list, crit] 从list中选出满足crit的元素In[1]:= t={{2,1},{1}};In[2]:= VectorQ[t] 函数名最后字母为Q,其值为True/FalseIn[3]:= aa={{a,b,c,d},{e,f,g,h},{i,j,k,l}};In[4]:= aa[[1]] 看看以下几个, 体会一下取元素/子表In[5]:= aa[[1]][[2]]In[6]:= aa[[1,2]]In[7]:= aa[[{1,2}]]In[8]:= aa[[{1},{2}]]In[9]:= Select[{a,23,12,0,3.5},EvenQ] 看看Select怎么用这里EvenQ[expr]判断expr是否偶数; OddQ[.]奇数?; NumberQ[.]数?;IntegerQ[.]整数?; PrimeQ[.]素数? AtomQ[.]简单表达式?...表中插入元素Prepend[list, elem] 表头加elem(PrependTo函数修改list) Append[list, elem] 在表尾加elem(AppendTo修改list)Insert[list, elem, n/-n] 在正/倒数第n个位置插入elemJoin[list1, list2, ...] 连接list1, list2, ...In[1]:= Prepend[{a,b,c},x] 在{a,b,c}前加x元素In[2]:= Insert[{a,b,c},x,2] 在{a,b,c}的第2个位置插入xIn[3]:= Join[{1,2,3},{xy},{m,{2,3},3}] 看看Join集合函数Union[list1, list2, ...] 去掉重复元并排序后的JoinIntersection[list1, list2, ...] 取各list的公共元Complement[t, list1, list2, ...] 在t中, 不在各list中的元素In[4]:= Union[{1,2,3},{xy},{m,{2,3},3}] 看看UnionIn[5]:= Complement[{a,b,c,d,e},{a,d},{e,f}] 看看Complement 表的重排Sort[list] 将list排序Union[list] 去掉重复元Reverse[list] 倒序RotateLeft[list, n/-n] 将list向左/右转n个元素(n=1可省) RotateRight[list, n/-n] 将list向右/左转n个元素(n=1可省) Transpose[list] 交换表的最上面两层Transpose[list, n] 交换表的顶层与第n层Flatten[list] 将list所有层变为一层Flatten[list, n] 将list的最上面n层变为一层Partition[list, n] 将list分成由n元组成的块(多余舍去) Partition[list, n, d] 各块中有偏移dPermutations[list] 给出list一切可能的排列Apply[Plus, list] 求和list[[i]]Apply[Times, list] 求积list[[i]]In[1]:= RotateLeft[{a,b,c,d,e},2] 得到{c,d,e,a,b}In[2]:= Flatten[{{a,b},c,{c,d}}] 得到{a,b,c,c,d}In[3]:= Table[i^2+j^2+k^2,{i,2},{j,2},{k,2}]In[4]:= Flatten[%,1] 展开一层In[5]:= Apply[Plus,%] 求和得到{24,36}In[6]:= Partition[{a,b,c,d,e,f,g},3,1] 看看Partition(9)二维图形二维函数作图Plot, 选项; 图的重现Show, Options, SetOptions, InputForm, Head; 参数绘图ParametricPlot; 线宽Thickness, 线型Dashing. 二维图形函数作图Plot[f[x],{x,xmin,xmax}] 在{xmin,xmax}间画出f[x]的图形Plot[{f1[x],f2[x],...},{x,xmin,xmax}] 画出fi[x]Plot[Release[f],{x,xmin,xmax}] 有时f的表达式很复杂,直接用Plot计算量大,可能得不出结果,可以先求f的值,再画Plot选项设置(格式: 选项->值)PlotRange Automatic {ymin,ymax}或{{xmin,xmax},{ymin,ymax}}AxesLabel轴标None {"x轴标","y轴标"}Frame框False TrueAxesOrigin原点Automatic {x,y}Axes轴Automatic None不画Ticks刻度Automatic None或{{xticks(,...)},{yticks(,...)}}GridLines网格None All或{{xlines...},{ylines}}AspectRatio 1/GodenRatio 正实数(高/宽)PlotPoints 15 Plot的作图精度In[1]:= Plot[Sin[x^2], {x,0,3}]In[2]:= Plot[Sin[x^2], {x,0,3}, PlotRange->{0,1.2}]In[3]:= Plot[Sin[x^2], {x,0,3}, AxesLabel->{"x","Sin[x^2]"}]In[4]:= Plot[Sin[x^2], {x,0,3}, Axes->None]In[5]:= Plot[Sin[x^2], {x,0,3}, PlotPoints->40]图形的重现Show[p] 重画图pShow[p1,p2,...] 把p1,p2,...重画在一起Show[p,option->value] 改变选项重画p(选项大多同上)(没有PlotPoits选项)Options[p] 显示图p的选项InputForm[p] 显示图p的有关存储信息SetOptions[函数名,option->value] 改变函数选项默认值Head[p] p的类型,如果p是图,则值为Graphics In[1]:= t1=Plot[BesselJ[1,x],{x,1,20}]In[2]:= t2=Plot[Sin[x],{x,0,15}]In[3]:= Show[t1,%]In[4]:= Show[%,Axes->None]In[5]:= Show[%,Frame->True]In[6]:= Options[%]In[7]:= InputForm[t2]参数绘图ParametricPlot[{fx,fy},{t,tmin,tmax}]ParametricPlot[{{fx,fy},{gx,gy},...},{t,tmin,tmax}]{fx,fy}的几种特殊情形{r[t]Cos[t],r[t]Sin[t]} 极坐标{Re[f],Im[f]} 复函数的相角图{Log[f],Log[g]} log-log图注意: 有时需要把AspectRatio->1才能更好地显示y/x比例, 如画圆. In[1]:= ParametricPlot[{Sin[t],Sin[2t]},{t,0,2Pi}]In[2]:= ParametricPlot[{Sin[t],Cos[t]},{t,0,2Pi}]In[3]:= Show[%,AspectRatio->Automatic]AspectRatio是1或Automatic是y/x的比例才是1选项,改变线宽和线型(虚线):在Plot的选项里使用PlotStyle->Thickness[0到1的值] 在math3.0下,使用0.005足矣PlotStyle->Dashing[{画,空}]在Show中,在Graphics[Thickness[.]]或Graphics[Dashing[.]]之后的线宽或线型依此改变.In[1]:= Plot[Sin[x^2],{x,0,3},PlotStyle->Thickness[0.01]]In[2]:= Plot[Sin[x^2],{x,0,3},PlotStyle->Dashing[{0.01,0.01}]]In[3]:= t1=Plot[Sin[(3x)^2],{x,-1,1}]In[4]:= t2=ParametricPlot[{Sin[t],Sin[2t]},{t,0,2Pi}]In[5]:= Show[t1,Graphics[Dashing[{0.01,0.01}]],t2]In[6]:= Show[t1,Graphics[Thickness[0.01]],t2](10)三维图形三维函数作图Plot3D, 选项; 参数作图ParametricPlot3D; 等值线图ContourPlot; 密度图DensityPlot; 数据绘图ListPlot,ListPlot3D.三维作图函数作图Plot3D[f[x,y],{x,xmin,xmax},{y,ymin,ymax}]在{xmin,xmax}间画出f[x]的Surface图形Show[p] 重画图p,用法同二维Show[Gaphics3D[p]] 将图p(可能是SurfaceGraphics)转为Graphics3D,并重画三维作图选项PlotRange Automatic {zmin,zmax}或{{xmin,xmax},{y...},{z...}} Axes轴Automatic NoneAxesLabel None {"x轴标","y轴标","z轴标"}Ticks Automatic 刻度PlotLabel图标None 图的标记Boxed盒子True FalseBoxRatios {1,1,0.4} {x,y,z}HiddenSurface True False是否隐去曲面被挡部分Shading True False是否涂阴影(颜色)Mesh True False是否在曲面上画网格LightSources 三个光源设光源{{x,y,z},RGBColor[r,g,b]} FaceGrids None All或坐标网格ViewPoint视点{1.3,-2.4,2.} {x,y,z}{0,-2,0}正前方; {0,-2,2}前上方; {0,-2,-2}前下方;{2,-2,0}正右角; {0,0,2}正上方; ...PlotPoints 15 作图精度(PlotPoints为Plot3D,ParametricPlot3D,ContourPlot等plot函数选项)In[1]:= Plot3D[Sin[x]y^2,{x,-3,4},{y,-2,2}]In[2]:= Plot3D[Sin[x]y^2,{x,-3,4},{y,-2,2},PlotPoints->30]In[2]:= Show[%, Mesh->False,Boxed->False,Axes->None]参数绘图ParametricPlot3D[{fx,fy,fz},{u,umin,umax},{v,vmin,vmax}] 等值线图ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}]选项Contours 10 从zmin到zmax等值线条数密度图DensityPlot[f,{x,xmin,xmax},{y,ymin,ymax}]In[1]:= ParametricPlot3D[{Cos[5t],Sin[3t],Sin[t]},{t,0,2Pi}]In[2]:= ParametricPlot3D[{u,u+v,v^2},{u,0,2},{v,-1,1}]In[3]:= ContourPlot[Sin[x]Cos[y],{x,-2,2},{y,-2,2}]In[4]:= Show[%,Contours->30]In[5]:= DensityPlot[Sin[x]Cos[y],{x,-2,2},{y,-2,2}]数据绘图ListPlot[{y1,y2,...}] 画(1,y1),(2,y2),...ListPlot[{{x1,y1},{x2,y2},...}]ListPlot[...,PlotJoined->True] 连线ListPlot3D[array]In[1]:= t=Table[i^2,{i,10}]In[2]:= ListPlot[t]In[3]:= ListPlot[t,PlotJoined->True]In[4]:= tt=Table[Mod[y,x],{x,20},{y,20}]In[5]:= ListPlot3D[%,ViewPoint->{1.5,-0.5,1}](11)基本图元作图二维基本图元Point, Line, Rectangle, Polygon, Circle, Disk, Text, Graphics[]; 三维基本图元Point, Line, Polygon, Cuboid, Text, Graphics3D[]; 一些PlotStyle: Thickness, Dashing, PointSize, GrayLevel, RGBColor.基本图元绘图二维基本图元Point[{x,y}] 点(x,y)Line[{{x1,y1},{x2,y2},...}] 连线Rectangle[{xmin,ymin},{xmax,ymax}] 矩形Polygon[{{x1,y1},{x2,y2},...}] 多边形Circle[{x,y},r] 圆:圆心(x,y),半径rDisk[{x,y},r] 圆盘:圆心(x,y),半径rCircle[{x,y},{rx,ry},{a1,a2}] 椭圆:圆心(x,y),长短轴rx,ry,起始角a1,终止角a2Disk[{x,y},{rx,ry},{a1,a2}] 椭圆盘Text[expr,{x,y}] 文本输出在(x,y)Text[expr,{x,y},{x1,y1}] 文本输出{x1,y1}为{-1,0},{1,0},{0,1},{0,-1}, 则文本输出以(x,y)为左端点, 右端点, 上端点, 下端点; 其他-1到1的数为相对位移In[1]:= s1=Line[Table[{n,(-1)^n},{n,6}]]In[2]:= Show[Graphics[s1]]In[3]:= g1=Show[%, Axes->Automatic]In[4]:= Show[g1,Graphics[Text["f(x)",{4.5,0.8}]]]In[5]:= s2={Rectangle[{1,-1},{2,-0.6}],Polygon[ {{1,0},{3,1},{4,0.5},{5,1}}]}In[6]:= Show[g1,Graphics[s2]]In[7]:= Show[Graphics[Table[Circle[{3n,0},n/4],{n,4}]], AspectRatio->Automatic]In[8]:=Show[Graphics[Disk[{1,1},{1,2},{10Degree,325Degree}]], AspectRatio->Automatic] 三维图元Point[{x,y,z}] 点(x,y,z)Line[{{x1,y1,z1},{x2,y2,z2},...}] 连线Polygon[{{x1,y1,z1},{x2,y2,z2},...}] 多边形Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}] 立方体Text[expr,{x,y,z}] 文本输出一些PlotStyleThickness[r] 线宽Dashing[{r1,r2,...}] 虚线{实虚实虚...}PointSize[r] 点的大小GrayLevel[r] 灰度0<=r<=1RGBColor[r,g,b] RGB颜色([0,1]间)[1,0,0]红; [0,1,0]绿; [0,0,1]蓝; [1,1,0]黄In[1]:= Plot[Sin[x^2],{x,0,3},PlotStyle->RGBColor[1,0,0]]In[2]:= Show[%,Graphics[PointSize[0.05]],Graphics[Point[{2,1}]]]In[3]:= Show[Graphics3D[RGBColor[1,0,0]],Graphics3D[ Line[{{0,0,0},{1,2,3},{3,2,1}}]]](12)表达式与纯函数表达式形式FullForm, TreeForm, Head; 表达式的书写形式@, //, ~f~; 表达式的项expr[[n]]; 表达式操作Apply(@@), Nest, Map(/@), MapAll(//@), MapAt; 纯函数&, #, ##.表达式形式FullForm[expr] 给出表达式的完全形式TreeForm[expr] 给出表达式的完全形式Head[expr] 给出表达式的头部In[1]:= FullForm[x+y+z] x+y+z的FullForm是Plus[x,y,z]In[2]:= FullForm[1+(x y)^2+(y+z)^3]In[3]:= TreeForm[%]In[4]:= Head[%]In[5]:= Head[215]In[6]:= Head[21.5]In[7]:= Head[Plot[Sin[x],{x,0,1}]]表达式的四种书写形式f[x,y] 标准形式f@x f[x]的前缀形式x//f f[x]的后缀形式x~f~y f[x,y]的中间形式In[1]:= Pi^2//N 相当于N[Pi^2](//级别低)In[2]:= N@Pi^2In[3]:= {a,b,c}~Join~{c,d}表达式的项expr[[n]] expr的第n项expr[[-n]] expr倒数第n项expr[[n1,n2,...]] 树结构索引的expr的项expr[[n]]=expr2 项赋值Position[expr,form] 寻找expr中form的位置In[1]:= t=1+(3+x)^2+z;In[2]:= t[[2]] 得(3+x)^2(类似于取List的元素)In[3]:= t[[2,1]] 再取子表得到Power函数的(3+x)In[4]:= t[[4]] 出错,不存在In[5]:= t[[3]]=y*z 试试直接赋值In[6]:= t 看看t变成什么了表达式的操作Apply[f,list] 对list施加函数f (@@)Nest[f,x,n] 将f对x作用n次Map[f,expr] 将f作用于expr的第一层(/@) Map[f,expr,n] 将f作用于expr直到第n层MapAll[f,expr] 将f作用于expr的所有项(//@)MapAt[f,expr,{polist}] 将f作用于expr的polist位置上In[1]:= Apply[f,{a,b,c}] 得到f[a,b,c](同f@@{a,b,c})In[2]:= Nest[f,x,3] 得f[f[f[x]]]In[3]:= u=x+(x+2)^2/xIn[4]:= Map[f,u] 同f/@uIn[5]:= Map[f,u,2]In[6]:= MapAll[f,u] 同f//@uIn[7]:= MapAt[f,u,Position[u,x]] 所有x都换成f[x]纯函数& Function纯函数# 纯函数的第一个变量#n 纯函数的第n个变量##n 从第n个起的变量序列## ##1Function[x,expr] 有一个变量的纯函数Function[{x1,x2,...},expr] 列表参数的纯函数In[1]:= Map[#^2&, {a,b,c}] 甚至#^2& /@ {a,b,c} 即将函数#^2作用于{a,b,c}得到{a^2,b^2,c^2}In[2]:= (#1^2+#2^#3)&[x,y,3] 即x^2+y^3In[3]:= g[##,##]&[x,y] 得g[x,y,x,y](13)转化规则与参数转换规则f[x]=, f[x_]=, Clear; 模式与匹配; 赋值=和:=; /; , -> , :> , /. , //. , Replace, /: ; 参数的含义_, __, ___, _head, _:xdef.转换规则f[x]=expr 定义f在x的值f[x_]:=expr 定义f[x](区别=与:=)Clear[f]或f[x_]=. 清除f的定义Remove[f] 彻底清除变量或函数fIn[1]:= f[x]=x^2 定义f在x为x^2In[2]:= f[2]+f[x] f[2]未定义,所以得到f[2]+x^2In[3]:= g[x_]=x^2 定义g[x](这里x没有值,:=与=一样) In[4]:= g[2]+g[x] 得到4+x^2 (注意看f和g的区别)In[5]:= f[3]=10 再定义一个f[3]In[6]:= ?f 看看f模式与匹配f[n_], f[m_,n_], f[n_,n_]In[1]:= f[m_,n_]:=m+nIn[2]:= f[n_,n_]:=3*nIn[3]:= f[n_]:=2*nIn[4]:= f[2,2]+f[6,8] f[2,2]用的是f[n,n]而不是f[m,n]In[5]:= f[2]+f[6,8] f[2]用单参数规则,f[6,8]用双参数规则赋值= 立即赋值:= 到使用时再赋值In[1]:= y=2In[2]:= h[y_]=y^3 即时赋值In[3]:= h[1] =8In[4]:= h2[y_]:=y^3 使用时再赋值,这里只定义规则In[5]:= h2[1] =1 (注意h2与h的区别)In[6]:= ?hIn[7]:= ?h2 分别看看就知道了In[8]:= 3! 下面再熟练一下=和:=的区别In[9]:= f[x_]:=%+2xIn[10]:= 1+y^2In[11]:= g[x_]:=%+2xIn[12]:= 2+zIn[13]:= f[a]+g[a]In[14]:= f[a]*g[a]/; (表达式/;条件) 满足条件使用表达式-> (lhs -> rhs) 在定义时,lhs用rhs代替:> (lhs :> rhs) 在使用时,lhs用rhs代替/. (expr /. rule) 对expr所有项使用规则一次//. (expr //. rule) 对expr所有项使用规则直到结果不变化Replace[expr,rule] 对整体expr使用规则一次/: (g/:lhs:=rhs) 定义一个转换规则,与g相关联In[1]:= f[x_]:=1 /; -1<=x<=1 当-1<=x<=1时, f[x]=1In[2]:= f[x_]:=-1 其他时候f[x]=-1In[3]:= f[2]In[4]:= f[0.5] 分段函数耶In[5]:= Plot[f[x],{x,-2,2}] 画图看看, 不错不错In[6]:= x+y /. x->2 得到2+y(:>和->的区别类似于:=与=) In[7]:= Clear[f]In[8]:= f[5] /. {f[1]->1,f[x_]->x*f[x-1]}In[9]:= f[5] //. {f[1]->1,f[x_]->x*f[x-1]}In[10]:= ss /: math[ss]=96In[11]:= ss /: phys[ss]=95In[12]:= ?ss参数x_ 单个表达式xx__ 一个或多个表达式序列xx___ 0个或多个表达式序列xx_h (或x__h) Head是h的表达式(序列)x_:xdef 可省参数的缺省值In[1]:= nt[t_,lt__]:=t*ltIn[2]:= c={1,2,3,4}In[3]:= nt[3,c] 这里就使用c是列表参数In[4]:= li[x_,xi_,xj__]:=(x-xj)/(xi-xj)In[5]:= li[x,xi,{1,2}] 再看个例子In[6]:= h[x_Real]:=x^2 定义h,当x是Real时In[7]:= h[4.5] h[4.5]的值为20.25In[8]:= h[a] a的Head不是Real,未定义,得h[a]In[9]:= fac[0]=1 以下看看函数facIn[10]:= fac[n_Integer?Positive]:=n*fac[n-1]In[11]:= fac[5] 120(注意上面条件用?间隔)In[12]:= h2[x_?NumberQ]:=x^3 看看这个条件的使用In[13]:= f[x_,y_:1,z_:2]:=g[x,y,z]In[14]:= f[a1,b1,c1] 都有参数则按参数代入In[15]:= f[a1,b1] 少一个参数,使用缺省值In[16]:= f[a1] 只有一个参数,两个参数使用缺省(14)mathematica过程编程一般过程, Block; 循环Do, While, For, Nest, FixedPoint; 条件If, Which, Switch; 转向Return, Break, Continue, Goto, Label.一般过程Command; Command; ... 一串命令Block[{x,y,...},procedure] x,y,...为局部参数Block[{x=x0,y=y0,...},proc] 局部参数赋初值In[1]:= g[x_]:= Block[{u},u=(1+x)^2;u=Expand[u]]In[2]:= g[a+b] 看看g[a+b]=?In[3]:= u 而这时u不发生改变循环结构Do[expr,{i,imin,imax,istep}]计算expr,i从imin到imax,步长istepDo[expr,{i,imin,imax}] istep=1Do[expr,{i,imax}] imin=1,istep=1Do[expr,{n}] 计算expr n次Do[expr, {i...}, {j...}...] 多重循环(前面的外重循环)While[test,expr] 当test成立, 计算exprFor[start,test,increment,body]相当于C语言for(start;test;increment) body Nest[f,expr,n] f对expr作用n次FixedPoint[f,expr] 重复使用f,直到expr不再变化用于循环的表达式i++, i--, ++i, --i, i+=di, i-=di, i*=di, i/=di,{x,y}={y,x} x,y值交换In[1]:= Do[Print[i^2],{i,4}] 循环Print[i^2]In[2]:= t=x;Do[t=1/(1+k*t),{k,2,4}];tIn[3]:= Do[Print[{i,j}],{i,4},{j,i-1}]In[4]:= Nest[Function[t,1/(1+t)],x,3] 注意虚函数的使用In[5]:= FixedPoint[Function[t,Print[t];Floor[t/2]],67]In[6]:= n=17;While[(n=Floor[n/2])!=0,Print[n]]In[7]:= For[i=1,i<4,i++,Print[i]]In[8]:= For[i=1;t=x,i^2<10,i++,t=t^2+i;Print[t]]大家注意练习上面例子, 考虑并看看运行结果, 熟练Math的循环语句的使用.条件语句If[test,expr] if (test) exprIf[test,expr1,expr2] if (test) expr1 else expr2If[test,expr1,expr2,expr3] 无法判断时得值expr3Which[test1,value1,test2,value2,...True,value]test1为真,得value1;否则判断test2...;若全不满足,得Null Switch[expr,form1,value1,form2,value2,...]expr的值为form1,得value1; 为form2,得value2,...In[1]:= f[x_]:=If[x>0,1,-1]In[2]:= Plot[f[x],{x,-2,2}] 还是画图形象In[3]:= g[x_]:=Which[x>1,x+2,x<-5,x-2]In[4]:= g[0] 没有输出In[5]:= Print[g[0]] 看到了,是NullIn[6]:= g[-6]In[7]:= g[2] 这两个g值都有意义In[8]:= h[x_]:=Switch[Mod[x,3],0,a,1,b,2,c]In[9]:= h[4] 也可以看看h[5],h[6]等值转向控制Return[] 返回,当前函数值NullReturn[expr] 返回expr的值Break[] 和Continue[] 这两函数只用于For,While.(Do不使用)Goto[标志]和Label[标志](15)程序包程序包的结构, 上下文, 程序注释, 输出, 输入程序包的结构BeginPackage["self`"] 激活或建立self上下文f::ussage="...." f的用法说明Begin["`Private`"] 开始包的私有上下文....f[args]=.......End[] 结束自身的上下文EndPackage[] 结束包,将self`放在全局上下文路径的最前面如果第一句为BeginPackage["self`","f1`","f2`"], 则在定义包self时, 同时打开f1.m, f2.m, 调入f1`, f2`.名字和上下文上下文表示为字符串`name 在当前上下文或搜索路径中最先找到的符号context`name 在指定上下文中的符号`name 在当前上下文中的符号Unique[ss] 生成以ss开头的没用过的符号Clear[s] 清除s的值Remove[s] 清除符号sRemove["context`*"] 清除context上下文中的所有符号这里要提一下两个系统变量: $Context和$ContextPath, 前者为当前上下文, 后者为当前上下文路径. 关于上下文, 大家看看以下例子, 体会一下.In[1]:= $Context 当前上下文是Global`In[2]:= z=6 定义z=6In[3]:= Begin["new1`"] 开始new1上下文IN[4]:= new1`z=9 new1上下文中的z=9In[5]:= $Context 当前上下文是new1`In[6]:= z 看看z=9In[7]:= ?*`z 看看有几个z,其中有z和Global`zIn[8]:= EndAdd[] 结束new1`,并将new1`放在路径最前面In[9]:= $ContextPath 看看路径In[10]:= ?*`z 看看有几个z,其中有z和new1`zIn[11]:= z 看看现在z的值是Global的z值了In[12]:= $Context 当前上下文In[13]:= Remove[z] 清除变量zIn[14]:= z Global的z清除了,这时显示的z=9In[15]:= Remove[z] 再Remove就清除new1中的z了程序注释f::ussage="text..." 关于一个函数的说明(* 注释内容*) 出现在程序包的任何地方如If[x>y,(* then *)x,(* else *) y]和If[x>y,x,y]是一样的.输出Print[expr1,expr2,...] 在屏幕上输出expr1,expr2,...StringForm[string,expr1,expr2,...] 将string中成对的``依次用expr1,expr2,...代替. 若string中是`n`, n为整数, 则用第n个expr代替.如StringForm["`` is not ``.",x+1,y]输出x+1 is not y.Message[s::tag] 输出tagOff[s::tag] / On[s::tag] 屏蔽/打开tag信息In[1]:= f::"overflow"="Factorial argument `1` too large."In[2]:= f[x_]:=If[x>10,Message[f::"overflow",x];Infinity,x!]In[3]:= f[20] 输出错误信息In[4]:= Off[f::"overflow"] 屏蔽overflow信息In[5]:= f[20]表达式输出到文件expr >> file 把表达式的值写入新文件fileexpr >>> file 把表达式的值追加到file中!!file 显示文件输入Input[] 键盘输入完整表达式作为Input的返回值Input[提示] 显示提示,接受输入InputString[] 输入字符串Read[文件名,类型描述] 按类型描述读入文件,参看帮助。
