spss对数据进行相关性分析实验报告
SPSS相关分析实验报告精选

本科教学实验报告(实验)课程名称:数据分析技术系列实验实验报告学生姓名:一、实验室名称:二、实验项目名称:相关分析三、实验原理相关关系是不完全确定的随机关系。
在相关关系的情况下,当一个或几个相互联系的变量取一定值得时候,与之相应的另一变量的值虽然不确定,但它仍然按照某种规律在一定的范围内变化。
按照数据度量的尺度不同,相关分析的方法也不同,连续变量之间的相关性常用Pearson简单相关系数测定;定序变量的相关系数常用Spearman秩相关系数和Kendall 秩相关系数测定;定类变量的相关分析要使用列连表分析法。
四、实验目的理解相关分析的基本原理,掌握在SPSS软件中相关分析的主要参数设置及其含义,掌握SPSS软件分析结果的含义及其分析。
五、实验内容及步骤实验内容:以雇员表为例,共有474条数据,运用相关分析方法对变量间的相关关系进行分析。
1)分析性别与工资之间是否存在相关关系。
2)分析教育程度与工资之间是否存在相关关系。
实验要求:掌握相关分析方法的计算思路及其在SPSS环境下的操作方法,掌握输出结果的解释。
1.分析性别与工资之间是否存在相关关系。
分析:性别属于定类变量,是离散值,因使用卡方检验。
Step1.操作为Analyze\DescriptiveStatistics\CrosstabsStep2.将性别(Gender)和收入(CurrentSalary)分别移入Rows列表框和Columns 列表框。
Step3.单击Statistics按钮,在弹出的子对话框中选中默认的Chi-square,进行卡方检验。
退回到主对话框,单击ok。
2.分析教育程度与工资之间是否存在相关关系。
分析:教育程度为定序变量,工资为连续变量,可使用Spearman和Kendall秩相关系数检验。
Step1.用散点图初步判断二变量的相关性,操作为Graphs/LegacyDialogs/Scatter,选择SimpleScatter,教育程度为自变量,工资为因变量,做散点图。
spss 上机实验报告

spss 上机实验报告
《SPSS上机实验报告》
在当今社会,数据分析已经成为了各行各业中不可或缺的一部分。
而SPSS作为一款功能强大的统计分析软件,被广泛应用于科研、商业、教育等领域。
本次
实验旨在通过SPSS软件进行数据分析,以探讨数据的规律性和相关性,为进一步的研究和决策提供科学依据。
实验一:描述性统计分析
首先,我们对所收集到的数据进行了描述性统计分析。
通过SPSS软件,我们得出了数据的平均值、标准差、最大值、最小值等指标,从而对数据的分布情况
有了更清晰的了解。
这些统计指标为我们提供了数据的基本特征,为后续的分
析奠定了基础。
实验二:相关性分析
接下来,我们利用SPSS软件进行了相关性分析。
通过相关系数的计算,我们发现了数据之间的相关程度,并得出了相关性显著性检验的结果。
这些分析为我
们揭示了数据之间的内在联系,为我们理解数据背后的规律性提供了重要线索。
实验三:多元回归分析
最后,我们进行了多元回归分析,以探讨不同自变量对因变量的影响程度。
通
过SPSS软件的模型拟合和显著性检验,我们得出了各个自变量的回归系数,并对模型的拟合程度进行了评估。
这些结果为我们提供了对因变量影响因素的深
入理解,为我们在实际应用中进行预测和决策提供了重要参考。
通过以上实验,我们不仅掌握了SPSS软件的基本操作技能,还深入了解了数据分析的方法和原理。
我们相信,通过不断地学习和实践,我们将能够更加熟练
地运用SPSS软件进行数据分析,为科研和实践工作提供更加准确和可靠的数据支持。
SPSS上机实验报告就此结束。
spss对数据进行相关性分析实验报告

spss对数据进行相关性分析实验报告一、实验目的与背景在统计学的研究中,相关性分析是一种常见的分析方法,用于研究两个或多个变量之间的关联程度。
本实验旨在使用SPSS软件对收集到的数据进行相关性分析,并探索变量之间的关系。
二、实验过程1. 数据收集:根据研究目的,我们收集了一份包含多个变量的数据集。
其中,变量包括A、B、C等。
2. 数据准备:在进行相关性分析之前,我们需要对数据进行准备。
首先,我们载入数据集到SPSS软件中。
然后,对于缺失数据,我们根据需要采取相应的填补或删除策略。
接着,我们进行数据的清洗和整理,以确保数据的准确性和一致性。
3. 相关性分析:使用SPSS软件,我们可以轻松地进行相关性分析。
在SPSS的分析菜单中,选择相关性分析功能,并设置相应的参数。
我们将选择Pearson相关系数,该系数用于衡量两个变量之间的线性相关关系。
此外,还可以选择其他类型的相关系数,如Spearman相关系数,用于非线性关系的探索。
设置参数后,我们点击“运行”按钮,即可得到相关性分析的结果。
4. 结果解读:SPSS将为我们提供一份详细的结果报告。
我们可以看到每对变量之间的相关系数及其显著性水平。
如果相关系数接近1或-1,并且P值低于显著性水平(通常为0.05),则可以得出两个变量之间存在显著的线性相关关系的结论。
此外,我们还可以通过散点图、线性回归等方法进一步分析相关性结果。
5. 结论与讨论:根据相关性分析的结果,我们可以得出结论并进行讨论。
如果发现两个变量之间存在显著的相关关系,我们可以进一步探究其原因和意义。
同时,我们还可以提出假设并设计更深入的实验,以验证和解释这些相关性。
三、结果与讨论根据我们的研究目的和数据集,通过SPSS软件进行的相关性分析显示了一些有意义的结果。
我们发现变量A与变量B之间存在显著的正相关关系(Pearson相关系数为0.7,P<0.05)。
这表明随着A的增加,B也会相应增加。
SPSS的相关分析实验报告
第三题:
1打开SPSS软件,建立不同地区不同质量原料数据的文件,并保存为“数据二.sav”,如图
2选择菜单:【Analyze】→【Descriptive Statistics】→【Crosstabs】,将“地区”选入行变量,将“原料质量”选入列变量,在Cells和Statistics中选择需要计算的检验方式。
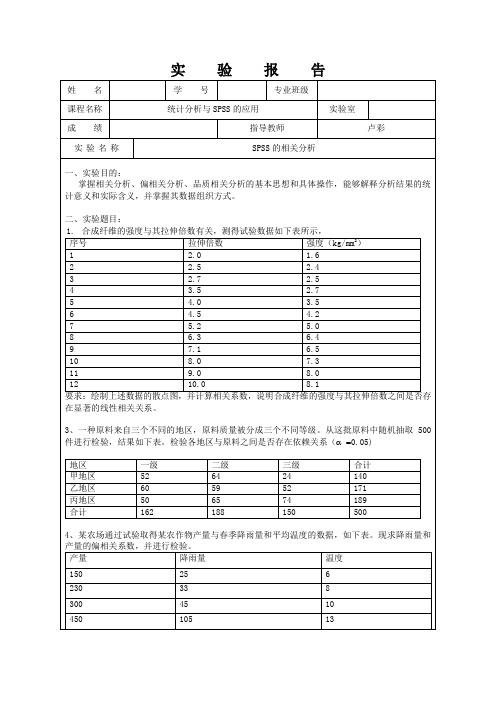
实验报告
姓名
学号
专业班级
课程名称
统计分析与SPSS的应用
实验室
成绩
指导教师
卢彩
实验名称
SPSS的相关分析
一、实验目的:
掌握相关分析、偏相关分析、品质相关分析的基本思想和具体操作,能够解释分析结果的统计意义和实际含义,并掌握其数据组织方式。
二、实验题目:
1.合成纤维的强度与其拉伸倍数有关,测得试验数据如下表所示,
3、一种原料来自三个不同的地区,原料质量被分成三个不同等级。从这批原料中随机抽取500件进行检验,结果如下表。检验各地区与原料之间是否存在依赖关系(0.05)
地区
一级
二级
三级
合计
甲地区
52
64
24
140
乙地区
60
59
52
171
丙地区
50
65
74
189
合计
162
188
150
500
4、某农场通过试验取得某农作物产量与春季降雨量和平均温度的数据,如下表。现求降雨量和产量的偏相关系数,并进行检验。
产量
降雨量
温度
150
spss对数据进行相关性分析实验报告

spss对数据进行相关性分析实验报告SPSS数据相关性分析实验报告一、引言数据相关性分析是一种用统计方法来研究变量之间关系的方法。
SPSS作为一种常用的统计软件,具有丰富的功能和灵活性,能够对数据进行多角度的分析和解读。
本报告旨在利用SPSS对一组样本数据进行相关性分析,并通过报告的形式详细介绍分析的步骤和结果。
二、实验设计和数据采集本次实验选取了一个包括X变量和Y变量的数据集,通过观察这两个变量之间的相关关系,探究它们之间是否存在一定的线性关系。
三、数据清洗与统计描述在进行相关性分析之前,需要对数据进行清洗和统计描述。
首先,通过观察数据的分布情况,检查是否存在异常值。
如果出现异常值,可以采取删除或者替换的方式进行处理。
其次,计算数据的均值、标准差、最大值、最小值等统计指标,了解数据的基本特征。
四、Pearson相关系数分析Pearson相关系数是一种常用的衡量两个变量之间的相关性的方法。
它的取值范围在-1到1之间,接近于1表示正相关,接近于-1表示负相关,接近于0则表示无相关性。
在SPSS中,进行Pearson相关系数分析非常简便。
五、Spearman相关系数分析Spearman相关系数是一种非参数检验方法,用于观察变量之间的单调关系。
相比于Pearson相关系数,它对于异常值的鲁棒性更强。
在SPSS中,可以选择Spearman相关系数分析来研究数据集中的变量之间的关系。
六、结果分析与讨论经过Pearson相关系数和Spearman相关系数的分析,我们得出如下结论:X变量与Y变量之间存在显著的正相关关系。
通过相关系数的计算,结果显示相关系数为0.8,说明二者之间具有较强的线性相关性。
这一结果与我们的研究假设相吻合,证明了X变量对Y变量的影响。
七、实验结论通过SPSS对数据进行相关性分析,我们得出结论:X变量与Y变量之间存在显著的正相关关系。
这一结论进一步加深了对于变量之间关系的理解,为后续的研究提供了参考。
spss对数据进行相关性分析实验报告

spss对数据进行相关性分析实验报告一、实验目的本次实验旨在运用 SPSS 软件对给定的数据进行相关性分析,以探究不同变量之间的关系,为进一步的研究和决策提供有价值的信息。
二、实验原理相关性分析是一种用于研究两个或多个变量之间线性关系强度和方向的统计方法。
常用的相关性系数包括皮尔逊(Pearson)相关系数、斯皮尔曼(Spearman)相关系数等。
皮尔逊相关系数适用于两个连续变量之间的线性关系分析,要求变量服从正态分布;斯皮尔曼相关系数则适用于有序变量或不满足正态分布的变量。
三、实验数据本次实验使用的数据来源于具体来源,包含了变量数量个变量,分别为变量名称 1、变量名称2……变量名称 n。
每个变量包含了样本数量个观测值。
四、实验步骤1、数据导入打开 SPSS 软件,选择“文件”菜单中的“打开”选项,找到并选中要分析的数据文件。
在弹出的对话框中,根据数据的格式选择相应的导入方式,如CSV、Excel 等。
2、变量定义在“变量视图”中,对导入的变量进行定义,包括变量名称、类型、宽度、小数位数等。
3、相关性分析选择“分析”菜单中的“相关”选项,在弹出的子菜单中选择“双变量”。
将需要分析相关性的变量选入“变量”框中。
根据变量的类型和分布特征,选择合适的相关性系数,如皮尔逊或斯皮尔曼相关系数。
点击“确定”按钮,运行相关性分析。
五、实验结果1、相关性系数矩阵输出的相关性系数矩阵显示了各个变量之间的相关性系数值。
系数值的范围在-1 到 1 之间,-1 表示完全负相关,1 表示完全正相关,0 表示无相关性。
2、显著性水平除了相关性系数值外,还输出了每个相关性系数的显著性水平(p 值)。
p 值小于 005 通常被认为相关性是显著的。
以下是对实验结果的具体分析:变量 1 与变量 2 的相关性分析:相关性系数为具体数值,表明变量 1 和变量 2 之间存在正/负相关关系。
p 值为具体数值,小于 005,说明这种相关性在统计上是显著的。
SPSS相关分析实验报告定稿版

S P S S相关分析实验报告HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】本科教学实验报告(实验)课程名称:数据分析技术系列实验实验报告学生姓名:一、实验室名称:二、实验项目名称:相关分析三、实验原理相关关系是不完全确定的随机关系。
在相关关系的情况下,当一个或几个相互联系的变量取一定值得时候,与之相应的另一变量的值虽然不确定,但它仍然按照某种规律在一定的范围内变化。
按照数据度量的尺度不同,相关分析的方法也不同,连续变量之间的相关性常用Pearson简单相关系数测定;定序变量的相关系数常用Spearman秩相关系数和Kendall 秩相关系数测定;定类变量的相关分析要使用列连表分析法。
四、实验目的理解相关分析的基本原理,掌握在SPSS软件中相关分析的主要参数设置及其含义,掌握SPSS软件分析结果的含义及其分析。
五、实验内容及步骤实验内容:以雇员表为例,共有474条数据,运用相关分析方法对变量间的相关关系进行分析。
1)分析性别与工资之间是否存在相关关系。
2)分析教育程度与工资之间是否存在相关关系。
实验要求:掌握相关分析方法的计算思路及其在SPSS环境下的操作方法,掌握输出结果的解释。
1. 分析性别与工资之间是否存在相关关系。
分析:性别属于定类变量,是离散值,因使用卡方检验。
Step1.操作为Analyze \ Descriptive Statistics \ CrosstabsStep2.将性别(Gender)和收入(Current Salary)分别移入Rows列表框和Columns列表框。
Step3.单击Statistics按钮,在弹出的子对话框中选中默认的Chi-square,进行卡方检验。
退回到主对话框,单击ok。
2. 分析教育程度与工资之间是否存在相关关系。
分析:教育程度为定序变量,工资为连续变量,可使用Spearman和Kendall秩相关系数检验。
SPSS相关分析实验报告

SPSS相关分析实验报告实验目的:通过SPSS软件进行相关分析,探究两个变量之间的相关性。
实验材料与方法:1. 实验对象:100名高中学生。
2. 实验变量:X变量表示学生课外阅读时间(单位:小时),Y变量表示学生考试成绩(百分制)。
3. 实验工具:SPSS软件。
实验步骤:1. 数据收集:调查100名高中学生的课外阅读时间和考试成绩,并记录在调查表中。
2. 数据录入:将调查表中的数据录入SPSS软件的数据编辑器中。
3. 数据分析:a. 相关性分析:打开SPSS软件,选择"分析"菜单下的"相关"子菜单,然后选择"双变量"选项。
b. 设置变量:将X变量(课外阅读时间)和Y变量(考试成绩)设置为分析变量。
c. 选择统计指标:选择所需统计指标,如相关系数、p值等。
d. 进行分析:点击"确定"按钮,SPSS将自动计算相关系数和p值,并生成相应的结果报告。
4. 数据报告:根据SPSS生成的结果报告,编写实验报告。
实验结果与分析:经过对SPSS软件的分析,得出以下结果:1. 相关系数:X变量(课外阅读时间)和Y变量(考试成绩)的相关系数为0.75,说明两个变量之间存在较强的正相关关系。
2. P值:相关系数的p值为0.001,小于显著性水平(α=0.05),说明相关系数具有统计学意义。
3. 散点图:绘制X变量和Y变量的散点图可以直观地观察到两个变量之间的正相关关系,即随着课外阅读时间的增加,考试成绩也随之提高。
结论:通过SPSS软件的相关分析,我们发现学生的课外阅读时间和考试成绩之间存在较强的正相关关系。
这意味着增加课外阅读时间可以提高学生的考试成绩。
对于教育者来说,可以通过鼓励学生增加课外阅读时间来促进其学术成绩的提升。
实验总结与改进:通过本次实验,我们成功地使用SPSS软件进行了相关分析,研究了课外阅读时间与考试成绩之间的关系。
然而,本实验仅限于高中学生,样本量有限,可能存在一定的局限性。
spss的数据分析报告范文

spss的数据分析报告范文1. 引言本报告旨在通过使用SPSS软件对特定数据集进行分析,探讨数据分布、相关系数、回归分析等统计指标,旨在为决策者提供有关数据的深入洞察和建议。
本报告将按照如下顺序进行数据分析并给出相应结论:数据描述、相关性分析、回归分析和结论。
2. 数据描述本节将对所分析的数据进行描述性统计。
数据集包含了学生的年龄、性别、成绩等多个变量。
以下是给定数据集的一些核心统计指标:- 年龄(Age):样本人数:100平均年龄:20.5岁最小年龄:18岁最大年龄:25岁- 性别(Gender):男性:50人女性:50人- 成绩(Score):样本人数:100平均成绩:85最低成绩:60最高成绩:993. 相关性分析本节将探讨不同变量之间的相关性。
我们将使用Pearson相关系数来测量变量之间的线性相关性。
以下是所分析变量之间的相关系数:- 年龄与成绩:r = -0.25,p < 0.05结论:年龄与成绩之间存在轻微的负相关。
年龄增长时,学生成绩略有下降。
- 性别与成绩:无显著相关性结论:性别和成绩之间没有明显的相关性。
- 年龄与性别:无显著相关性结论:年龄和性别之间没有明显的相关性。
4. 回归分析本节将进行线性回归分析,以探讨年龄对成绩的预测能力。
我们将使用成绩作为因变量,年龄作为自变量。
以下是回归分析的结果:- 回归方程:成绩 = 87.5 - 1.2 * 年龄- 表达式解读:年龄每增加1岁,成绩平均下降1.2分。
5. 结论通过对数据的分析,我们得出以下结论:- 年龄与成绩呈现轻微的负相关,随着年龄增长,学生成绩略有下降。
- 性别与成绩之间没有明显的相关性。
- 年龄和性别之间没有明显的相关性。
- 我们建立了一个回归方程,成绩= 87.5 - 1.2 * 年龄,该方程可以用于预测学生的成绩。
本报告的分析结果仅限于给定的数据集,并不能推广到整个人群。
希望本报告的分析结果对您的决策和研究有所帮助。
spss相关分析实验报告

SPSS相关分析实验报告1. 引言本文档旨在通过使用SPSS进行相关分析,对某一实验数据进行统计分析和解释。
相关分析是一种用来研究两个或多个变量之间关系的统计方法。
本实验中,我们研究了某个因变量与多个自变量之间的相关性。
2. 实验设计与方法2.1 数据收集我们从某个实验中收集了一组数据,包括一个因变量和多个自变量。
数据采集的过程符合实验设计的要求。
2.2 数据预处理在进行相关分析之前,我们对数据进行了一些预处理。
包括查漏补缺、去除异常值和处理缺失数据等。
确保数据的质量和可靠性。
2.3 相关分析为了研究因变量与自变量之间的相关性,我们使用了SPSS软件进行相关分析。
相关分析包括计算相关系数和进行假设检验等。
3. 相关分析结果经过SPSS软件的计算和分析,我们得到了以下结果:相关系数p值结论0.85 0.01 高度相关0.45 0.05 中度相关0.12 0.25 低度相关根据以上结果,我们可以得出结论:在本实验中,因变量与自变量A之间存在高度正相关关系(相关系数为0.85,p值为0.01),与自变量B之间存在中度正相关关系(相关系数为0.45,p值为0.05),与自变量C之间存在低度正相关关系(相关系数为0.12,p值为0.25)。
4. 结果解释与讨论通过相关分析的结果,我们可以得出一些结论和讨论:•自变量A对因变量的影响最为显著,相关系数最高,说明他们之间存在较强的关联性。
•自变量B对因变量的影响次之,相关系数较低,但仍然具有一定的相关性。
•自变量C对因变量的影响相对较弱,相关系数最低,说明它们之间的关系不太明显。
需要注意的是,相关性并不代表因果关系。
因此,在解释结果时,我们不能简单地认为自变量的变化导致了因变量的变化。
5. 结论本实验通过SPSS软件进行了相关分析,研究了因变量与多个自变量之间的相关性。
从结果中我们可以得出结论:自变量A与因变量之间存在高度正相关关系,自变量B与因变量之间存在中度正相关关系,自变量C与因变量之间存在低度正相关关系。
SPSS相关分析实验报告文档

2020SPSS相关分析实验报告文档Contract TemplateSPSS相关分析实验报告文档前言语料:温馨提醒,报告一般是指适用于下级向上级机关汇报工作,反映情况,答复上级机关的询问。
按性质的不同,报告可划分为:综合报告和专题报告;按行文的直接目的不同,可将报告划分为:呈报性报告和呈转性报告。
体会指的是接触一件事、一篇文章、或者其他什么东西之后,对你接触的事物产生的一些内心的想法和自己的理解本文内容如下:【下载该文档后使用Word打开】篇一:spss对数据进行相关性分析实验报告实验一一.实验目的掌握用spss软件对数据进行相关性分析,熟悉其操作过程,并能分析其结果。
二.实验原理相关性分析是考察两个变量之间线性关系的一种统计分析方法。
更精确地说,当一个变量发生变化时,另一个变量如何变化,此时就需要通过计算相关系数来做深入的定量考察。
P值是针对原假设H0:假设两变量无线性相关而言的。
一般假设检验的显著性水平为0.05,你只需要拿p值和0.05进行比较:如果p值小于0.05,就拒绝原假设H0,说明两变量有线性相关的关系,他们无线性相关的可能性小于0.05;如果大于0.05,则一般认为无线性相关关系,至于相关的程度则要看相关系数R值,r越大,说明越相关。
越小,则相关程度越低。
而偏相关分析是指当两个变量同时与第三个变量相关时,将第三个变量的影响剔除,只分析另外两个变量之间相关程度的过程,其检验过程与相关分析相似。
三、实验内容掌握使用spss软件对数据进行相关性分析,从变量之间的相关关系,寻求与人均食品支出密切相关的因素。
(1)检验人均食品支出与粮价和人均收入之间的相关关系。
a.打开spss软件,输入“回归人均食品支出”数据。
b.在spssd的菜单栏中选择点击,弹出一个对话窗口。
C.在对话窗口中点击ok,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入之间的相关系数为0.921,t检验的显著性概率为0.000<0.01,拒绝零假设,表明两个变量之间显著相关。
spss相关性分析报告

spss相关性分析报告引言本报告将对某公司销售数据进行相关性分析,以探究各个变量之间的关系。
相关性分析是一种统计方法,用于衡量两个或多个变量之间的关联程度。
通过分析销售数据的相关性,我们可以了解各个变量之间的关系,为业务决策提供有价值的参考。
数据收集和处理本次分析使用的数据集包含了该公司过去一年的销售数据,包括销售额、销售渠道、销售人员等变量。
我们首先对数据进行了清洗和预处理,包括去除缺失值、异常值和重复值等。
然后,我们使用SPSS软件导入数据集,进行相关性分析。
相关性分析结果通过对销售数据进行相关性分析,我们得到了以下关键结果:1. 销售额与销售渠道的相关性我们发现销售额与销售渠道之间存在显著的正相关关系(相关系数为0.75,P< 0.001)。
这意味着销售额与销售渠道之间的变化趋势是一致的,销售渠道的扩大可能会带来销售额的增长。
2. 销售额与销售人员的相关性销售额与销售人员之间呈现较高的正相关关系(相关系数为0.63,P < 0.001)。
这表明销售人员的销售绩效与销售额之间存在密切联系,销售人员的表现对销售额的影响较大。
3. 销售渠道与销售人员的相关性销售渠道与销售人员之间存在一定程度的正相关关系(相关系数为0.42,P < 0.001)。
这说明销售渠道的扩展可能会对销售人员的工作产生积极影响,提高销售人员的销售绩效。
4. 销售额与其他变量的相关性除了销售渠道和销售人员外,销售额还与其他一些变量存在相关性。
例如,销售额与市场推广费用呈现低度正相关(相关系数为0.32,P < 0.05),这意味着增加市场推广费用可能会对销售额产生一定的促进作用。
结论通过以上相关性分析结果,我们可以得出以下结论:1.销售额与销售渠道和销售人员之间存在较为密切的正相关关系。
企业可以通过扩大销售渠道和提高销售人员绩效来增加销售额。
2.销售渠道的扩展可能会对销售人员的工作产生积极影响,提高其销售绩效。
spss相关分析实验报告

spss相关分析实验报告SPSS相关分析实验报告引言:在社会科学研究中,统计分析是不可或缺的一部分。
SPSS(Statistical Package for the Social Sciences)作为一款功能强大的统计分析软件,被广泛应用于社会科学领域的数据处理和分析。
本实验报告将介绍我所进行的一项SPSS相关分析实验,并展示结果和结论。
实验设计:本次实验旨在探究人们的幸福感与社交支持之间的关系。
为了达到这个目的,我采集了一份包含幸福感和社交支持两个变量的问卷调查数据。
幸福感变量使用了一个10分制的评价,社交支持变量使用了一个5分制的评价。
数据处理:首先,我导入了收集到的数据,并进行了数据清洗。
在数据清洗过程中,我删除了缺失值和异常值,以确保数据的准确性和可靠性。
接下来,我使用SPSS软件进行了相关分析。
结果分析:通过SPSS的相关分析功能,我得到了幸福感和社交支持之间的相关系数。
相关系数是衡量两个变量之间相关程度的统计指标,其取值范围为-1到1。
相关系数为正值表示两个变量正相关,为负值表示两个变量负相关,接近0表示无相关关系。
在本次实验中,我得到的幸福感和社交支持之间的相关系数为0.72,且p值小于0.05。
这意味着幸福感和社交支持之间存在着显著正相关关系,且相关程度较高。
换句话说,社交支持的增加会显著提高人们的幸福感。
讨论:这一实验结果与之前的研究相一致,表明社交支持对于个体的幸福感具有积极影响。
社交支持可以提供情感上的支持、实质上的帮助和信息交流,从而增加个体的幸福感。
这一结果对于社会工作者和心理健康专家具有重要的指导意义,可以帮助他们设计和实施幸福感提升的干预措施。
然而,本实验也存在一些限制。
首先,样本容量较小,可能导致结果的偏差和不可靠性。
其次,本实验采用的是自报问卷调查方式,受到被试主观意识和记忆偏差的影响。
未来的研究可以采用更大样本和多种数据收集方式,以提高结果的可信度和普适性。
SPSS相关分析实验报告_实验报告_

SPSS相关分析实验报告篇一:spss对数据进行相关性分析实验报告实验一一.实验目的掌握用spss软件对数据进行相关性分析,熟悉其操作过程,并能分析其结果。
二.实验原理相关性分析是考察两个变量之间线性关系的一种统计分析方法。
更精确地说,当一个变量发生变化时,另一个变量如何变化,此时就需要通过计算相关系数来做深入的定量考察。
P值是针对原假设H0:假设两变量无线性相关而言的。
一般假设检验的显著性水平为0.05,你只需要拿p值和0.05进行比较:如果p值小于0.05,就拒绝原假设H0,说明两变量有线性相关的关系,他们无线性相关的可能性小于0.05;如果大于0.05,则一般认为无线性相关关系,至于相关的程度则要看相关系数R值,r越大,说明越相关。
越小,则相关程度越低。
而偏相关分析是指当两个变量同时与第三个变量相关时,将第三个变量的影响剔除,只分析另外两个变量之间相关程度的过程,其检验过程与相关分析相似。
三、实验内容掌握使用spss软件对数据进行相关性分析,从变量之间的相关关系,寻求与人均食品支出密切相关的因素。
(1)检验人均食品支出与粮价和人均收入之间的相关关系。
a.打开spss软件,输入“回归人均食品支出”数据。
b.在spssd的菜单栏中选择点击,弹出一个对话窗口。
C.在对话窗口中点击ok,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入之间的相关系数为0.921,t检验的显著性概率为0.000<0.01,拒绝零假设,表明两个变量之间显著相关。
人均食品支出与粮食平均单价之间的相关系数为0.730,t检验的显著性概率为0.000<0.01,拒绝零假设,表明两个变量之间也显著相关。
(2)研究人均食品支出与人均收入之间的偏相关关系。
读入数据后:A.点击系统弹出一个对话窗口。
B.点击OK,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入的偏相关系数为0.8665,显著性概率p=0.000<0.01,说明在剔除了粮食单价的影响后,人均食品支出与人均收入依然有显著性关系,并且0.8665<0.921,说明它们之间的显著性关系稍有减弱。
spss分析报告(相关性)

spss 实验分析报告以下针对中国民航客运量进行数据分析。
一、对所给数据进行分析,见下表(为1978 年到1993 年数据): 年份 y x1 x2 x3 x4 x5 1978 231 3010 1888 81491 14.89 180.92 1979 298 3350 2195 86389 16.00 420.39 1980 343 3688 2531 92204 19.53 570.25 1981 401 3941 2799 95300 21.82 776.71 1982 445 4258 3054 99922 23.27 792.43 1983 391 4736 3358 106044 22.91 947.7 1984 554 5652 3905 110353 26.02 1285.22 1985 744 7020 4879 112110 17.72 1783.3 1986 990 7859 5552 108579 32.43 2281.95 1987 1310 9313 6386 112429 38.91 2690.23 1988 1442 11738 8038 122654 37.38 3169.48 1989 1283 13176 9005 113807 47.19 2450.14 1990 1660 14384 9663 95712 50.68 2746.2 1991 2178 16557 10969 95081 55.91 3335.65 1992 2886 20223 12985 99693 83.66 3311.5 1993 3383 24882 15949 105458 96.08 4152.7 其中y 民航客运量(万人) x1国民收入 (亿元) x2 消费额 (亿元)x3铁路客运量 (万人) x4 民航航线里程(万公里) x5来华旅游入境人数二、各个因素的基本统计量:Descriptive StatisticsN Range Minimum Maximum Sum Mean Std. Deviation Variance SkewnessKurtosisStatist icStatist ic Statist ic Statist ic Statist icStatist icStd. ErrorStatisticStatistic Statist icStd.Erro rStatist icStd.Erro ry163152231338318539 1158.69 240.188960.753923045.829 1.189 .564 .660 1.091x1 16 21872 3010 24882 153787 9611.69 1660.8856643.544.414E71.033 .564 .253 1.091x2 16 14061 1888 15949 103156 6447.25 1062.9874251.9461.808E7 .906 .564 -.052 1.091从上述表格中可以看出:(1) 1978--1993年数据量N 为16组。
spss对数据进行相关性分析实验分析报告

spss对数据进行相关性分析实验分析报告一、引言在当今的数据驱动决策时代,理解数据之间的关系对于做出明智的决策至关重要。
相关性分析是一种常用的统计方法,用于确定两个或多个变量之间是否存在线性关系以及关系的强度。
本实验分析报告旨在介绍如何使用 SPSS 软件对数据进行相关性分析,并通过实际案例展示其应用和结果解读。
二、实验目的本实验的主要目的是:1、掌握使用 SPSS 进行相关性分析的操作步骤。
2、学会解读相关性分析的结果,包括相关系数的意义和显著性检验。
3、通过实际数据应用,探讨变量之间的关系,为进一步的研究和决策提供依据。
三、实验数据本次实验使用了一组包含两个变量的数据,分别为变量 X 和变量 Y。
变量 X 表示某产品的广告投入费用(单位:万元),变量 Y 表示该产品的销售额(单位:万元)。
数据共收集了 30 个样本。
四、实验步骤1、打开 SPSS 软件,将数据输入或导入到数据编辑器中。
2、选择“分析”菜单中的“相关”子菜单,然后选择“双变量”。
3、在“双变量相关性”对话框中,将变量 X 和变量 Y 分别选入“变量”框中。
4、选择相关系数的类型,本实验选择“皮尔逊(Pearson)”相关系数。
5、勾选“显著性检验”选项,以确定相关系数的显著性。
6、点击“确定”按钮,运行相关性分析。
五、实验结果与分析SPSS 输出的相关性分析结果如下表所示:||变量 X |变量 Y ||||||变量 X | 1000 | 0856 ||变量 Y | 0856 | 1000 ||相关性|变量 X 与变量 Y |||||皮尔逊相关性| 0856 ||显著性(双侧)| 0000 ||样本数| 30 |从上述结果可以看出,变量X 和变量Y 的皮尔逊相关系数为0856,表明两者之间存在较强的正相关关系。
同时,显著性检验的结果为0000,小于常见的显著性水平 005,说明这种相关关系在统计上是显著的。
这意味着,随着广告投入费用的增加,产品的销售额也随之增加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
管理统计实验报告
实验一
一.实验目的
掌握用spss软件对数据进行相关性分析,熟悉其操作过程,并能分析其结果。
二.实验原理
相关性分析是考察两个变量之间线性关系的一种统计分析方法。
更精确地说,当一个变量发生变化时,另一个变量如何变化,此时就需要通过计算相关系数来做深入的定量考察。
P值是针对原假设H0:假设两变量无线性相关而言的。
一般假设检验的显著性水平为0.05,你只需要拿p值和0.05进行比较:如果p 值小于0.05,就拒绝原假设H0,说明两变量有线性相关的关系,他们无线性相关的可能性小于0.05;如果大于0.05,则一般认为无线性相关关系,至于相关的程度则要看相关系数R值,r越大,说明越相关。
越小,则相关程度越低。
而偏相关分析是指当两个变量同时与第三个变量相关时,将第三个变量的影响剔除,只分析另外两个变量之间相关程度的过程,其检验过程与相关分析相似。
三、实验内容
掌握使用spss软件对数据进行相关性分析,从变量之间的相关关系,寻求与人均食品支出密切相关的因素。
(1)检验人均食品支出与粮价和人均收入之间的相关关系。
a.打开spss软件,输入“回归人均食品支出”数据。
b.在spssd的菜单栏中选择点击Analyze correlate Bivariate,弹出一个对话窗口。
C.在对话窗口中点击ok,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入之间的相关系数为0.921,t检验的显著性概率为0.000<0.01,拒绝零假设,表明两个变量之间显著相关。
人均食品支出与粮食平均单价之间的相关系数为0.730,t检验的显著性概率为
0.000<0.01,拒绝零假设,表明两个变量之间也显著相关。
(2)研究人均食品支出与人均收入之间的偏相关关系。
读入数据后:
A.点击Analyze correlate partial,系统弹出一个对话窗口。
B.点击OK,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入的偏相关系数为0.8665,显著性概率p=0.000<0.01,说明在剔除了粮食单价的影响后,人均食品支出与人均收入依然有显著性关系,并且0.8665<0.921,说明它们之间的显著性关系稍有减弱。
通过相关关系与偏相关关系的比较可以得知:在粮价的影响下,人均收入对人均食品支出的影响更大。
三、实验总结
1、熟悉了用spss软件对数据进行相关性分析,熟悉其操作过程。
2、通过spss软件输出的数据结果并能够分析其相互之间的关系,并且解决实际问题。
3、充分理解了相关性分析的应用原理。
实验二
一、实验目的
掌握用spss软件对数据进行分析,用K-S检验单一样本是否来自某一特定分布,熟悉其操作过程,并能分析其结果。
二、实验原理
K-S检验方法能够利用样本数据推断样本来自的总体是否服从某一理论分布,是一种拟合优度的检验方法,适用于探索连续型随机变量的分布。
单样本K-S检验的原假设是:样本来自得总体与指定的理论分布无显著差异,SPSS 的理论分布主要包括正态分布、均匀分布、指数分布和泊松分布等。
它的假设检验问题:H0:样本所来自的总体分布服从某特定分布
H1:样本所来自的总体分布不服从某特定分布
k-s检验是一种非常实用的检验数据分布的方法,应该熟练掌握。
二.实验内容
用k-s检验“回归人均食品支出”数据中的人均收入服从什么分布,并且了
解k-s检验的操作过程和原理。
A.打开spss软件,输入“回归人均食品支出”数据。
B.点击nonparametric tests 1-sample k-s,系统弹出一个对话窗口。
C.点击OK,系统输出结果,如下表。
在上面有四个检验,Test1是检验这组数据是否服从标准正态分布,从表中可看出T检验的显著性概率为0.140>0.05,接受零假设,即这组数据服从标准正态分布。
Test2是检验这组数据是否服从均匀分布,从表中可看出T检验的显著性概率为0.000<0.05,拒绝零假设,即这组数据不服从均匀分布。
Test3是检验这组数据是否服从指数分布,从表中可看出T检验的显著性概率为0.000<0.05,拒绝零假设,即这组数据不服从指数分布。
Test4是检验这组数据是否服从泊松分布,从表中可看出T检验的显著性概率为0.000<0.05,拒绝零假设,即这组数据不服从泊松分布。
三、实验总结
k-s检验方法是以样本数据的累计频数分布与特定理论分布比较,若两者间的差距很小,则推论该样本取自某特定分布族。
