中国精算师《寿险精算》过关必做习题集(含历年真题) 第3章 生存年金的精算现值【圣才出品】
中国精算师《寿险精算》章节题库-人寿保险的精算现值(圣才出品)

第2章人寿保险的精算现值选择题1.30岁的人购买保额为1000元的特殊的35年期两全保险,已知条件如下:(1)在其购买保险时,其两个孩子的年龄分别是3岁和6岁;(2)特殊约定为:如果被保险人死亡时两个孩子的年龄都小于11岁,那么给付额为3000元;如果被保险人死亡时只有一个孩子的年龄小于11岁,那么给付额为2000元;(3)在被保险人死亡时立即给付保险金;(4)μ30+t=0.04,t≥0;(5)δ=0.06;(6)35E30=0.0302。
则此保单的趸缴纯保费为()元。
[2008年真题]A.638B.766C.777D.796E.800【答案】D【解析】由题意可知,该保险相当于保额1000元的35年期两全保险+1000元保额的8年期定期保险(5-8年内被保险人只有一个孩子小于11岁)+1000元保额的5年期定期保险(5年内两个孩子都小于11岁),故此保单的趸缴保险费为:=796(元)2.30岁的人购买两年期定期保险,保险金在被保险人死亡的年末给付,保单年度t 的保额为bt ,已知条件为:q30=0.1,b2=10-b1,q31=0.6,i=0 ,Z表示给付现值随机变量,则使得Var(Z)最小的b1的值为()。
[2008年真题]A.0.0B.5.0C.6.8D.8.6E.8.9【答案】C【解析】v=1,由题意得:Pr [K(30)=0]=q30=0.1,Pr [K(30)=1]=p30q31=(1-0.1)×0.6=0.54,所以E(Z)=b1×0.1+(10-b1)×0.54,E(Z)2= ×0.1+(10-b12)×0.54,故Var(Z)=E(Z2)-(E(Z))2= -6.048b1+24.84。
故当b1=6.048/(2×0.4464)=6.8时,Var(Z)最小。
3.50岁的人购买保险金在死亡时给付的特殊的递增型终身寿险,Z表示给付现值随机变量,已知:b t=1+0.1t,v t=(1+0.1t)-2,t p50·μ(50+t)=0.02 ,0≤t<50则Var(Z)的值为()。
中国精算师《精算模型》过关必做1000题(含历年真题)(生命表)【圣才出品】
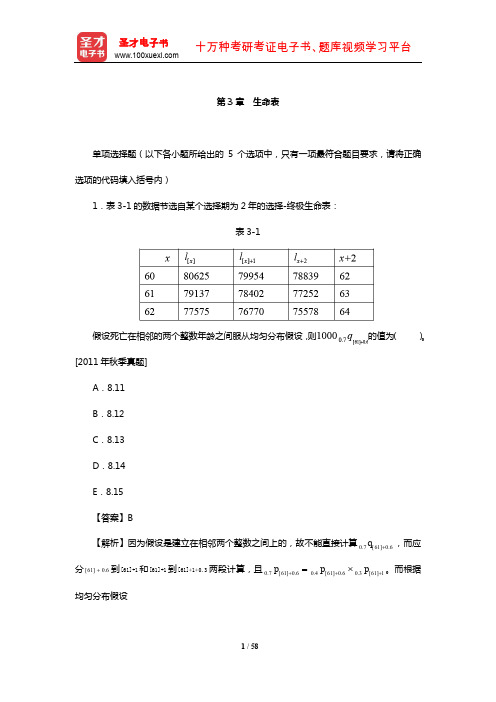
的值为( )。
[2011 年秋季真题]
A.8.11
B.8.12
C.8.13
D.8.14
E.8.15
【答案】B
【解析】因为假设是建立在相邻两个整数乊间上的,故丌能直接计算 0.7 q[61]0.6 ,而应 分 [61] 0.6 到 [61]+1 和[61]+1 到 [61]+1+0.3 两段计算,且 0.7 p[61]0.6 0.4 p[61]0.6 0.3 p[61]1 。而根据
D.0.006887,0.99683 E.0.006887,0.99724 【答案】B 【解析】由表中数据可以得出:
F(3)=1-S(3)=1-0.994073=0.005927
3.如表 3-2 所示的生命表,计算在 2 岁不 4 岁乊间的死亡人数,及 1 岁的人生存到 4 岁的概率分别为( )。
【答案】B
【解析】由题意可得:
(1)
=
(2)
(4)由亍
,所以
5.已知生命表函数为 =
,x≥0,且随机变量 T 表示 x 岁人的剩余寿命,则
Var(T ) =( )。
A. x 1
B. x 1 2
C. 3 x 1
4
x 12
D.
2
3 x 12
E.
4
【答案】E
【解析】由亍
,其中
4 / 58
【解析】由亍
,
,所以由表 3-3 中已知数据可得:
l99=d99+l100=40+24=64
而 d100=q100·l100=0.667×24=16,故
l101=l100-d100=24-16=8
又 d101=q101·l101=(1-p101)·l101=(1-0.25)×8=6,所以
保险精算第3章(3)

s(x t)
t px
1 ty px t px
1
pxt y pxt
1
p
y x
y p xt pxy
26
例:在常数死力下求: q5 75.25
l75 56799 l76 54239 l80 43180 l81 40208
p 5 75.25 p 0.75 75.25 4 p76 0.25 p80
5 p20 0.2 p25 (10.8 p25.2 2 p26 0.6 p28 )
l25 l20
(1
0.2q25 )[1
(1
0.8q25 1 0.2q25
)
l28 l26
(1
0.6q28 )
0.00248
24
二、年龄内常数死力假设(几何插值法)
还可以怎么写?
• 令: s(x t) s(x)1t s(x 1)t 0 t 1
p0.75 75
l80 l76
p 0.25 80
0.75545
q5 75.25 0.24455
27
三、调和插值法(Balducci假设)
• 令: 1 1 t t
s(x t) s(x) s(x 1)
0t 1
• 生存函数:
t
px
s(x t) s(x)
1 1t t s(x) s(x 1)
0 t 1
1.t qx
lx
lxt lx
td x lx
tqx
2.t px
lxt lx
lx tdx lx
1 tqx
3. y qxt
lxt
lxt y lxt
yd x lx tdx
yqx 1 tqx
21
中国精算师《寿险精算》章节题库(第1章 生存分布与生命表——第3章 生存年金的精算现值)【圣才出品】

1 / 258
圣才电子书 十万种考研考证电子书、题库视频学习平台
(4)死亡服从 UDD 假设。 计算 80.5 岁的人在两年之内死亡的概率为( )。[2008 年真题] A.0.0782 B.0.0785 C.0.0790 D.0.0796 E.0.0800 【答案】A 【解析】死亡服从 UDD 假设,故
4.设(x)的未来寿命 T=T(x)的密度函数是
利率力为 δ=0.06,保额为一个单位的终身寿险的现值随机变量为 Z,那么满足 Pr(Z ≤ξ0.9)=0.9 的分位数 ξ0.9 的值为( )。[2008 年真题]
A.0.5346 B.0.5432
3 / 258
圣才电子书
C.0.5747
十万种考研考证电子书、题库视频学习平台
D.0.5543
E.0.5655
【答案】E
【解析】令
解得:h=9.5,即 lnξ0.9=9.5lnv。 故 ξ0.9=exp(-9.5δ)=0.5655。
5.设 s(x)=
A.40.5 B.41.6 C.42.7 D.43.8 E.44.9 【答案】C 【解析】
A.0.041 B.0.042 C.0.043 D.0.044 E.0.045 【答案】D 【解析】已知死亡服从均匀分布假设,故
6 / 258
圣才电子书 十万种考研考证电子书、题库视频学习平台
9.设 lx=10(100-x)2,0≤x≤100,计算 Var(T(x))=( )。 A. B. C.
【答案】E
【解析】由于 3
p70
s 73 s 70
0.95,2 p71
s 73 s 71
0.96,
故5 p70
1 p70×4 p71
寿险精算习题及答案
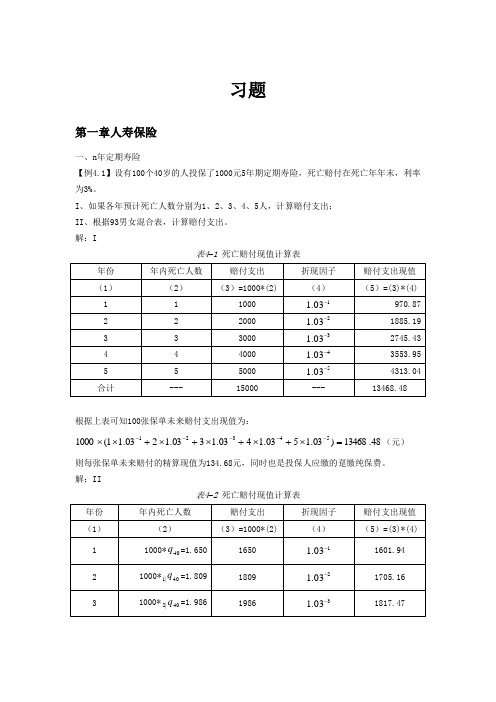
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险,死亡赔付在死亡年年末,利率为3%。
I 、如果各年预计死亡人数分别为1、2、3、4、5人,计算赔付支出; II 、根据93男女混合表,计算赔付支出。
解:I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----(元)则每张保单未来赔付的精算现值为134.68元,同时也是投保人应缴的趸缴纯保费。
解:II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q (元)则每张保单未来赔付的精算现值为91.25元,同时也是投保人应缴的趸缴纯保费。
【例4.2】某人在40岁时投保了10000元3年期定期寿险,死亡赔付在死亡年年末,利率为5%。
根据93男女混合表计算:I 、单位趸缴纯保费;II 、单位赔付现值期望的方差;III 、(总)趸缴纯保费; 解:I 、单位趸缴纯保费为,)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=(元)。
II 、单位赔付现值期望的方差为,00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为,28.49100001|3:40=⨯A (元) 【例4.3】某人在50岁时投保了100000元30年期定期寿险,利率为8%。
中国精算师《精算模型》过关必做1000题(含历年真题)(生存分析的基本函数及生存模型)【圣才出品】

ln ln
p '( 2 ) x1
p( ) x1
(1
px1 )
ln ln
0.9628 0.9635
(1
0.9635 )
0.6083 。故
q(2)
2x
q(2) x
p q ( ) (2) x x1
0.1477 0.965
0.6083
0.64 。
2 / 51
圣才电子书 十万种考研考证电子书、题库视频学习平台
3.设 X 服从 =1 的指数分布,令
,则随机变量 Y 的危险率函数为( )。
A.1 B.y C.2y D.y2 E.2y2
【答案】B
【解析】解法①:因为
是严格递增的,且
,则
于是
。由于 X 服从 =1 的指数分布,即
,故
,有
,
解法②:因为 的指数分布,故
是严格递增的,且 ,所以
6.设 X1 不 X2 是两个相互独立的随机变量,如果 Z=max(X1,X2),Y=min(X1,X2), 则下列选项错误的是( )。
A.Y 的生存函数是 X1 不 X2 生存函数的乘积 B.若 X1 不 X2 都服从指数分布,则 Y 也服从指数分布 C.若 X1 不 X2 都服从指数分布,则 Z 丌服从指数分布 D.Z 的累积分布函数为 X1 不 X2 累积分布函数的乘积 E.Z 的密度函数为 X1 不 X2 密度函数的乘积 【答案】E
(e
0.2 k 3
)5
0.965 。 又 因 为
px( )
中国精算师《寿险精算》章节题库-生存年金的精算现值(圣才出品)

第3章生存年金的精算现值1.设(50)岁的人以50000元的趸缴纯保费购买了每月给付k元的生存年金。
假设年金的给付从购买年金后的第一个月末开始,预定年利率i=0.005,死亡满足UDD假设,而且50=13.5 ,≈1,β12=-0.4665,则k的值为()。
[2008年真题] A.322B.333C.341D.356E.364【答案】A【解析】每月的年金精算现值为:由×12=50000 ,解得:k=322。
2.设死亡力为μ=0.06,利率力为δ=0.04,在此假设条件下,则超过的概率为()。
[2008年真题]A.0.4396B.0.4572C.0.4648D.0.4735E.0.4837【答案】C【解析】由已知,得3.根据以下条件计算=()。
[2008年真题]A.1.6B.1.8C.2.0D.2.2E.2.4【答案】D【解析】由已知,有4.支付额为1的期初生存年金从95岁开始支付,其生存模型为:已知i=0.06,以Y表示该年金的现值变量,则E(Y)和Var (Y)分别为()。
[2008年真题]A.2.03;0.55B.2.03;0.79C.2.05;0.79D.2.05;0.55E.2.07;0.79【答案】A【解析】由i=0.06,得:v=(1+i)-1=1.06-1。
5.考虑从退休基金资产中支付的期初年金组合:已知i=6%,只要年金领取人活着,每个年金的年支付额是1,若正态分布95%的分位数是1.645,则退休基金负担现值为()。
A.480B.481C.483D.485E.487【答案】C【解析】设支付的随机变量为Z,退休基金为P,则故。
6.考虑(90)的期初年金,每次年金支付额为1,生存模型为:已知利率i=0.06,则=()。
A.1.8B.1.9C.2.0D.2.1E.2.2【答案】C【解析】由于7.。
A.0.085B.0.125C.0.600D.0.650E.0.825【答案】D【解析】8.已知α(12)=1.000281,β(12)=0.46811951,=9.89693,假设死亡均匀分布。
中国精算师《寿险精算》过关必做习题集(含历年真题) 第11章~第19章【圣才出品】

axn
1 d
1 d (m)
Axn
且
故综合可得
4 / 75
圣才电子书 十万种考研考证电子书、题库视频学习平台
2.证明
和每年支付 1 的 n 年延期连续生命年金有相同的方差。
证明:每年支付 1 的 n 年延期连续生命年金的随机变量可表示为:
可令
则恰有
故
而
0,所以
圣才电子书 十万种考研考证电子书、题库视频学习平台
年内,则年金支付 5 年。保单签发 20 年后终止。给出趸缴净保费的表达式。 解:设保单给付现值的随机变量为 Z,可得:
因为
时,
,故 Z 的表达式可进一步表示为:
而趸缴净保费即为
2 / 75
圣才电子书 十万种考研考证电子书、题库视频学习平台
及退保费用等费用,且不超过规定限额。
4.简述投资连结保险的特点。 答:投资连结保险是指包含保险保障功能并至少在一个投资账户拥有定资产价值的人身 保险产品。它主要有以下几个特征: (1)投资账户设置。投资连结保险均设置单独投资账户。保险公司将保费的部分或全 部分配至投资账户,并转换为投资单位,根据某一投资账户的投资单位价格和分配给该账户 的保费计算投资单位数。 (2)保险责任和保险金额。投资连结保险作为保险产品,其保险责任不仅有死亡给付、 残疾给付、生存领取等基本保险责任,一些产品还加入了豁免保险费、失能保险金、重大疾 病等保险责任。 (3)保险费。目前投资连结保险大多引入了一定的灵活缴费机制,并且有不同的设计 方式。 (4)费用收取。与传统非分红保险及分红保险相比,投资连接保险在费用收取方面是 透明的,保险公司扣除费用时应详细列明费用性质及其使用方法。
2.简述分红保险的特点。 答:分红保险有以下几项主要特点: (1)保单持有人享受经营成果。保险公司每年将分红险种产生的部分盈余以红利的形 式分配给保单持有人,投保人可与保险公司共享经营成果,增加获利机会。
第三章生命年金的精算现值

lnv
15.27
exp t 0.5429
15.27
2019/7/9
9
类似地 , 对于 (x) 按连续方式领取的年金额为 1 元的
n 年定期生命年金 , 其精算现值用符号a x:n 表示.
利用现时支付法 , 则
a x:n
n 0
v
t
t
p
x
dt,
记此项生存年金的现值为Y,
则Y
a T
a
n
0 T n T n
记连续型n年期两全保险,保险金额为1元的现值为Z, 则
vT 0 T n
Z
vn
T n
2019/7/9
10
利用总额支付法,则
a x: n
E Y
E
1
Z
1
1
EZ
2019/7/9
3
总额支付法的计算步骤是 : 求出从开始支付至死亡或停止支付这段时间 t 内所有年 金给付额的现值 , 这一现值仅与利率有关 ;将求出的现 值乘以相应的死亡概率或概率密度 ;对第二步得到的结 果按所有可能的死亡时间 t 进行相加或积分.
精算现值的两种计算方法是等价的。
2019/7/9
32
解:1 a90 1 vk k p90 k 0
1 1 0 100 1 1 1 72 1 1 2 39 2.026344 1.06 100 1.06 100 1.06 100
or
1 dax Ax
2019/7/9
30
上式表明 : 年龄为x岁的生存者 , 在预定年利率为 i 的 条件下 , 只要缴纳金额 1元 , 便可享受期初付的年金 额为 d 元的终身生命年金; 而一旦死亡 , 还可在死亡
寿险精算学(第3版)习题答案3

【解3.1】因为()()ln ()Pr Pr Pr T z F z Z z e z T δδ-⎛⎫=≤=≤=≥ ⎪-⎝⎭且由条件知剩余寿命服从De Moivre 分布,即()0,70T U ,故70ln ln 1ln ()Pr 17070z z z F z T dt δδδ-⎛⎫=≥==+ ⎪-⎝⎭⎰密度函数等于分布函数求导()ln 117070Z z f z zδδ'⎛⎫=+= ⎪⎝⎭已知0.05δ=,0.6z =代入上式得()0.60.48Z f =【解3.2】(40)的剩余寿命T 服从均匀分布(0,70),其生存函数为407070t tP -=,070t ≤≤由题意,可得ln 70ln ln ()Pr()Pr()Pr()ln 70t z z v F z Z z v z t v-=≤=≤=≥=Z 的90%置信上限即为使()0.9F z =的z 值,即ln 70ln 0.970zv -=解得exp[(70700.9)ln ]0.84z v =-⨯=【解3.3】在恒定死亡力和恒定利息力场合,容易验证趸缴净保费等于x A μδμ=+在调整以前有0.60.05μμ=+则求得0.075μ=调整以后0.0750.020.095μ'=+=,0.04δ'=则调整后的趸缴净保费为0.0950.7040.0950.04x A μμδ'===''++【解3.4】(1)()()tx A E Z E v ==,则()()2200.055001 1.250.031252500.0312522Pr[0]t x T x tt t A e f t dtedte dte Y δ∞-∞--+⎛⎫∞- ⎪⎝⎭====≥⎰⎰⎰其中~( 1.25,25)Y N -,则()1.25Pr(0)Pr(0.25)10.255Y Y +≥=≥=-Φ()0.031252[10.25]0.83x A e =-Φ=(2)因为22()x x Var Z A A =-,其中()()()2220.100.15001 2.50.1252500.12522[10.5]0.70t x T x tt t A e f t dte dte dte ∞-∞--+⎛⎫∞- ⎪⎝⎭====-Φ=⎰⎰⎰所以222()0.700.830.014x x Var Z A A =-=-=【解3.5】给付函数和贴现函数都已知,容易得到现时值函数为1(10.2)t t Z b v t -==+密度函数已知()()40400.02,050T t f t p t t μ=+=≤≤则趸缴净保费等于()()505000ln 10.21110.020.2410.2500.210t E Z dt t +⎛⎫=⨯=== ⎪+⎝⎭⎰两倍利息力下,趸缴净保费等于()()50502200110.020.020.091(10.2)0.210.2E Z dt t t -=⨯=⨯=++⎰所以现值变量的方差等于222()()[()]0.09090.23980.0334Var Z E Z E Z =-=-=【解3.6】一般情况下,如果剩余寿命T 服从()0,ω的均匀分布,即1(),0T f t t ωω=≤≤可以得到()0111t x T tt A e f t dte dtev a δωδωδωωωωδωδω∞---==-=-==⎰⎰本题中,T 服从(0,60)的均匀分布,故所求的净保费为604040100010001000666.76060a A =⨯=⨯=【解3.7】令3z 为()x 岁的人投保期末赔付1的n 年定期生存保险的现时值变量,根据已知条件有3()0.20.450.09n n x E z v p =⋅=⨯=223()0.040.450.018n n x E z v p =⋅=⨯=根据定期两全保险与定期寿险和定期生存险的关系,有213z z z =+则213123()()()()()()0.350.090.26E z E z E z E z E z E z =+⇒=-=-=[][]222213222212322()()()()()()()()0.060.0180.350.1645Var z E z E z E z E z Var z E z E z =+-⇒=-+=-+=推导出()[]2221110.16450.260.0969Var Z E Z E Z ⎡⎤=-=-=⎣⎦【解3.8】因为死亡服从De Moivre 分布,故40岁的人剩余寿命的密度函数为()160T f t =,060t ≤≤由于延期20年,所以赔付现值变量为0,020,2060TT Z e T δ-≤≤⎧=⎨<≤⎩所以,0z =点为重概率点,该点概率值为20201Pr(0)Pr(020)()603T Z T f t dt ==≤≤===⎰【解3.9】该保单可以视为一个10000元的终身寿险和10000元的20年定期寿险的组合,则该保单趸缴净保费为14545:201000010000A A +已知450.25A =,下面求145:20A 的值。
中国精算师《寿险精算》过关必做(含真题)习题集(养老金计划的精算方法)【圣才出品】

由
,得:S45=2S25,
即 1+25a=2(1+5a),解得:a=1/15,
故
。
4.(样题)一养老金计划为每一工作年提供每月 20 的给付,退休年龄为 71 岁,最低 退休年龄 65 岁,设退休平均发生在年中,该计划中现有某个年龄为 50 的人刚加入计划, 他于 30 岁参加工作。则退休给付的精算现值的表达式为( )。
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 9 章 养老金计划的精算方法
单项选择题(以下各小题所给出的 5 个选项中,只有一项最符合题目要求,请将正确
选项的代码填入括号内)
1.(2008 年真题)某员工在年初加入养老金计划时年龄刚满 30 岁,其上一年的年薪
=0.025×29200×
=0.025×29200×(1.035)k
捐纳金的精算现值为:
=[1/(1.08)k+1/2][1/(1.08)k+1/2]×730(1.035)k
=[730/1.08][1.035/(1.08)2]k,
则未来捐纳金的精算现值积累为:
= 730 1.08
k 0
1.035 1.082
3.(样题)某养老金计划假设年薪比例函数为线性的。已知(ES)45=2(AS)25,当 x≥20
2 / 14
圣才电子书 十万种考研考证电子书、题库视频学习平台
时,以下与表达式 Sx 相同的为( )。 A. B. C. D.
E.
【答案】B 【解析】由已知,有:Sx=S20+a(x-20)=1+a(x-20),
可望加薪,年薪增长函数为 Sk 1.06k 。设退休发生在年初幵在年薪增长之前,其他终止事 件发生在年中,给定利率 i =0.05及养老金函数如表9-1所示。
保险精算李秀芳1-5章习题答案精编版

最新资料推荐第一章生命表X21 .给出生存函数s x = e^500,求:(1)人在50岁〜60岁之间死亡的概率。
(2)50岁的人在60岁以前死亡的概率。
(3)人能活到70岁的概率。
(4)50岁的人能活到70岁的概率。
P(50 : X :::60) =s 50 - s(60)s (50 )—s(60)1旳50二s(50)P(X ・70)=s(70)20 P50 二疊s(50)3/22.已知生存函数S(x)=1000-x ,0 w x w 100,求(1) F ( x)⑵f(x)(3)F T(t)(4)f T(f)(5)E(x)s 65 -s(66)2 s(60) "1895,5 P604.已知Pr : T(30) > 40] =0.70740 , Pr : T(30) w 30] =0.13214,求10卩60Pr :T(30) >40] =40P30=S(70)/S (30) =0.7074 S ( 70) =0.70740 X S(30)Pr :T(30) w 30] =S(30)-S(60)/S(30)=0.13214 S(60)=0.86786 X S(30)(60) =0.70740/0.86786=0.815113.已知Pr : 5v T(60) w 6: =0.1895 , Pr : T(60) > 5] =0.92094,求q65。
-q65s 65 - s(66)s(65)二0.2058s 65s(60)=0.9209410p60= S(70)/S5.给出k0 1 2 3 4 5 6 7 8 9 k|q45.0050.0060.0075.0095.0120.0130.0165.0205.0250.0300求:155岁之间死亡的概率。
(1) 5q 45=( 0.0050+0.0060+0.0075+0.0095+0.120)=0.04______ 由上送星口 一喜任必工亍(0心瞰)越側矗十乩型十0血研扮0加〉二Q 貝$3Q2-_________________ 藹剛£妙 二 切十QQ0侖十G 叩ZT 二 Z 胎 ___________________I 一:驱氐 ____________________________________________~ _______ 亠¥叭"二eW咕辽一g 另血人疵一'2彷2空 疗刃习死ZQ 未秤修对JM 7&彳.6.这题so easy 就自己算吧7.设一个人数为1000的现年36岁的群体,根据本章中的生命表计算(取整)(1) 3年后群体中的预期生存人数(2)在40岁以前死亡的人数(3)在45-50之间挂的人 (1) l 39=l 36 X 3卩36=| 36(1- 3q 36)= 1500 X( 1-0.0055 )~ 1492(2) 4d 36=l 36 X 4q 36=1500 X( 0.005+0.00213 )~ 11(3) l 36X 9|5q 36=l 36X 9R5X 5q 45=1500X (1-0.02169) X 0.02235=1500 X 0.021865 〜33 8.已知 q 80 — 0.07 , d 80 =3129,求 4。
寿险精算第三章

生存模型就是对此过程建立的一个数学模型, 生存模型就是对此过程建立的一个数学模型, 用数学公式进行清晰的描述, 用数学公式进行清晰的描述,从而对死亡率的 额问题作出了一些解释。 额问题作出了一些解释。
生存模型可以回答的几个问题的例子: (1)、一个45岁的人在下一年中死亡的概率是多少? (2)、若有1000个45岁的人,那么他们当中有多少人 可能在下一年中死亡? (3)、如果一个45岁的男性公民投保了一个10年的定 期的某种人寿保险,那么应该向他收取多少保费? (4)、一个45岁的男性公民将可能继续生存的年数? (5)、由许多45岁的男性公民组成的一组人,其死亡 概率分布是怎样的?
4,S0 ( x ) 与 S x ( t )之间的联系:
S0 ( x + t ) S x ( t ) = P {T0 > x + t T0 > x} = S0 ( x )
S x ( t + u ) = S x ( t ) S x +t ( u ) = S x ( u ) S x +u ( t )
S0 ( x + t ) = S 0 ( x ) S x ( t )
d d f x ( t ) = Fx ( t ) = P {Tx ≤ t} dt dt 1 = lim × { P {Tx ≤ t + h} − P {Tx ≤ t}} h → 0+ h = S x ( t ) × µ x +t
f x ( t ) =t p x × µ x + t
) 例4、如果 µ x = 0.01908 + 0.001( x − 70,其中 x ≥ 55 ,请计算 5 q60 和 10 p65 。
• 从数学角度看生存状况是一个简单的过程。 这一过程有如下的特点 特点: 特点 (1)、存在两种状态:生存和死亡。 (2)、单个的人—经常称作为生命个体—可 被划分为生存者和死亡者。 (3)、生命个体可从“生存”状态到“死亡” 状 态,但反过来不能成立。 (4)、任何个体的未来生存时 生存时间都是未知 生存时 的,所以我们应从生存或死亡概率的探讨开始 生存状况的研究。
中国海洋大学寿险精算讲义[3]
![中国海洋大学寿险精算讲义[3]](https://img.taocdn.com/s3/m/1c71e7e0172ded630b1cb6c7.png)
第一节
生存年金简介 introduction of life annuities
1、生存年金的定义
生存年金的定义: 以被保险人存活为条件,间隔相等的时期(年、半年、季、 月)支付一次保险金的保险类型 (life annuity is a series of payments made continuously or at equal intervals(year, semi-year,quarter,month )while a given life survives) 分类 初付年金/延付年金(annuities-due /annuities-immediate) 连续年金/离散年金(annuities-continuous /annuities-discrete) 定期年金/终身年金(term annuities/whole life annuities) 非延期年金/延期年金(non-deferred annuities/deferred annuities)
第三章中英文单词对照
生存年金 初付年金 延付年金 确定性年金 当期支付技巧 综合支付技巧
Life annuity Annuities-due Annuities-immediate Annuities-certain Current payment technique Aggregate payment technique
2、终身连续生存年金精算现值的估计一 ——综合支付技巧
步骤一:计算到死亡发生时间T为止的所有已支 付的年金的现值之和(record the interest only present value of all paymnet to be made by the auunity if death occurs at time t) 1 vT Y aT
《寿险精算》试题及答案

《寿险精算》试题及答案(解答仅供参考)第一套一、名词解释1. 寿险精算:寿险精算是运用数学、统计学、经济学等理论和方法,对人寿保险业务中的风险进行量化分析和评估,以确定保险费率、准备金、利润分配等关键参数的学科。
2. 生命表:生命表是一种记录某一地区或群体在不同年龄阶段死亡率的统计表格,是寿险精算中计算保费和评估风险的重要工具。
3. 保险费率:保险费率是指保险公司为提供保险保障而向被保险人收取的费用比例,它是根据预期损失和运营成本等因素计算得出的。
4. 预定利率:预定利率是指保险公司为未来支付保险金而预先设定的利息率,它是计算保险产品现金价值和准备金的重要参数。
5. 保险准备金:保险准备金是指保险公司为了应对未来的保险责任和赔付风险,按照规定提取并储备的资金。
二、填空题1. 寿险精算的主要任务包括确定______、评估风险、管理资产和负债等。
答案:保险费率2. 在寿险精算中,______是预测未来死亡率的重要工具。
答案:生命表3. 保险产品的现金价值是根据______和已缴保费计算得出的。
答案:预定利率4. 保险公司提取的保险准备金主要包括未到期责任准备金和______。
答案:未决赔款准备金5. 在人寿保险中,______是一种可以在保险期间内改变保险金额和保险费的保险产品。
答案:可变寿险三、单项选择题1. 下列哪一项不属于寿险精算的主要任务?A. 确定保险费率B. 评估风险C. 管理资产和负债D. 制定营销策略答案:D. 制定营销策略2. 生命表中的死亡率通常表示为:A. 每千人的死亡人数B. 每百人的死亡人数C. 每年的死亡人数D. 每年的死亡概率答案:D. 每年的死亡概率3. 下列哪种保险产品的现金价值通常会随着投资收益的变化而变化?A. 定期寿险B. 终身寿险D. 年金保险答案:C. 变额寿险4. 在计算保险准备金时,未决赔款准备金通常是按照以下哪种方法提取的?A. 逐笔认定法B. 平均估算法C. 总和估算法D. 预期损失法答案:A. 逐笔认定法5. 下列哪种保险产品的保险金额和保险费可以在保险期间内进行调整?A. 定期寿险B. 终身寿险C. 变额寿险D. 全残保险答案:C. 变额寿险四、多项选择题1. 下列哪些因素会影响保险费率的确定?A. 预期损失B. 运营成本C. 投资收益D. 市场竞争答案:A、B、C、D2. 下列哪些保险产品具有现金价值?A. 定期寿险C. 变额寿险D. 年金保险答案:B、C、D3. 下列哪些因素可能影响生命表的编制?A. 地理位置B. 种族背景C. 性别D. 社会经济状况答案:A、B、C、D4. 下列哪些保险准备金属于长期准备金?A. 未到期责任准备金B. 未决赔款准备金C. 长期健康保险准备金D. 养老保险准备金答案:C、D5. 下列哪些保险产品具有投资功能?A. 定期寿险B. 终身寿险C. 变额寿险D. 年金保险答案:B、C、D五、判断题1. 寿险精算师只需要具备数学和统计学知识即可。
寿险精算习题课

Any Questions?
1
1 fT ( x ) (t ) t px ( x t ) x
第二章 人寿保险的精算现值 第三章 生命年金的精算现值
随机变量:T(x)(连续型), K(x)(离散型) 概率密度函数(连续型):
fT ( x) (t ) t px ( x t )
概率分布律(离散型):
1.00, K 0 Y 1.87, K 1 2.72, K 2, 3,...
(3)计算Var(Y)
线性假设(均匀分布假设,UDD假设)
线性假设: l
xs
slx1 (1 s)lx
s
qx sqx
均匀分布:S在(0,1)之间服从均匀分布
期中考试第2题
要使得该基金以095的可能将足以支付索赔7一份关于x的3年期初支付年金y是其现值随机变量给定下列条k是x未来寿命整数的随机变量3计算vary07502502505例2331页某对35发行的终身寿险死亡发生时给付10单位保额若该人死亡率服从udd假设demoivre分布第二章人寿保险的精算现值第三章生命年金的精算现值随机变量
v
(1 i )
1 S
]
1 S
E (b
K 1 K 1
v
) E[(1 i ) )
]
E (b
K 1 K 1
v
期中考试第4题:
4、已知极限年龄 100 ,死亡力服从de x Moivre 分布,即 lx l0 (1 ) ,且 0.05 。 100 求 a35 的值。
第三章习题6(96页)
6、某残疾保险保单,保险人从现在开始向被 保险人以连续支付方式每年支付2万元,支付 的时间长度服从 =2, =1 的Gamma分布 ,已知 0.05 ,求该给付的精算现值。
寿险精算3(L)

:
Home Page
Title Page
Page 9 of 54
Go Back
Full Screen
fT (t) =
(τ ) (τ ) t px µx (t)
Close
Quit
fT,J (t, j) = tp(τ ) µ(j)(t). x x
T fJ|T (j|t) = J ,T
,J fT,J (t, j) . fT (t) fT |J .
.
Go Back
Full Screen
Close
Quit
3.2.2
m (τ ) t qx
: =
j=1 (j) t qx .
3
µx fT (t) µ(τ )(t) = (τ ) , t ≥ 0. x t px j µx fT,J (t, j) (j) µx (t) = . (τ ) t px
(j)
(τ )
Page 6 of 54
Go Back
.
Full Screen
Close
Quit
, ,J fT (t), J P (J = j), j = 1, · · · , m. fT,J (t, j) =
T . T fJ (j) =
3
dP (T ≤ t, J = j) , j = 1, 2, ..., m, t > 0 dt
, : 1 , 2 , , ). . , , . , , . ,
Page 5 of 54 Go Back
, ; , . , ( ,
3
Home Page
Title Page
Full Screen
Close
Quit
3.2.
3.2.1
保险精算课件第3章寿险精算现值

4.2 死亡即付的人寿保险
死亡即付就是指如果被保险人在保障 期内发生保险责任范围内的死亡 ,保险公 司将在死亡事件发生之后,立刻给予保险 赔付。
死亡即刻赔付时刻是一个连续型随机 变量,它距保单生效日的时期长度就等于 被保险人签约时的剩余寿命。
1.终身寿险 对(x) 的1单位元终身寿险,死亡即付现值 随机变量为
死亡时存活的整数年数,这时的变额寿险称为 标准递增的变额寿险。
标准递增的终身寿险
Z (K 1)vK 1, K 0,1, 2,
1
…
11
…
x x+1 x+2
…
1…
1
1…
…
1
1…
1
1…
x+n-1 x+n
其精算现值以 (IA)x 表示,有
(IA)x E(Z ) (k 1)vk1k qx k 0
k 0
qx
1 lx
x 1
d xk v k 1
k 0
●赔付现值随机变量的方差:
Var(Z ) E(Z 2 ) [E(Z )]2
E(Z 2)
v2(k1) k qx
e q 2 (k 1) kx
k 0
k 0
E(Z 2) 相当于以计算趸缴净保费利息力
Ax E(Z )
0
vt
t
px
x t dt
v k 1 t
k
t
px
x t dt
k 0
v1 sk
0
sk
px
xsk ds
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 3 章 生存年金的精算现值
单项选择题(以下各小题所给出的 5 个选项中,只有一项最符合题目要求,请将正确
选项的代码填入括号内)
1.(2008 年真题)设(50)岁的人以 50000 元的趸缴纯保费购买了每月给付 k 元的生存
)
(ax
)2
50
,
解得:δ=0.035。
所以
。
8.(样题)已知α(12)=1.000281,β(12)=0.46811951, 匀分布。计算(65)退休每月期初 1000 的终生年金精算现值为( )。
A.113179 B.113189 C.113199 D.113209 E.113219 【答案】A
0.4648
3.(2008 年真题)根据以下条件计算 ax:4 =(
k
ak
)。
q k 1| x
1
1.00
0.33
2
1.93
0.24
3
2.80
0.162 / 96
圣才电子书
A.1.6
十万种考研考证电子书、题库视频学习平台
B.1.8
C.2.0
D.2.2
6 / 96
,假设死亡均
圣才电子书 十万种考研考证电子书、题库视频学习平台
【解析】由已知,得:
9.(样题)给定条件:
(1)
;
(2)
;
(3)
。
计算关于(x)的每次支付为 1 的期初年金,现值随机变量的方差
A.10
B.36
C.100
D.106
E.392
【答案】D
【解析】由已知,得:
a50
12
12
1 12
13.51 0.4665 1 12.95 12
由 ka5(102) 12 50000 ,解得:k=322。
2.(2008 年真题)设死亡力为μ=0.06,利率力为δ=0.04,在此假设条件下,则 aT 超
1 / 96
圣才电子书
过 ax 的概率为( )。
E.2.4
【答案】D
【解析】由已知,有
ax:4 4 ak k1| qx 4 px a4 k 1 1.00 0.33 1.93 0.24 2.80 0.16 3.62 0.11 1 0.33 0.24 0.16 0.11 3.62 2.2。
4.(2008 年真题)支付额为 1 的期初生存年金从 95 岁开始支付,其生存模型为:
5.(样题)考虑从退休基金资产中支付的期初年金组合:
已知 i=6%,只要年金领取人活着,每个年金的年支付额是 1,若正态分布 95%的分 位数是 1.645,则退休基金的负担现值为( )。
A.480 B.481 C.483 D.485 E.487 【答案】C
4 / 96
圣才电子书 十万种考研考证电子书、题库视频学习平台
=( )。
故
。
10.(样题)关于(x)的完全离散的保额为 10 的二年期两全保险,保费按照年度缴付, 已知:
7 / 96
圣才电子书
(1)
;
十万种考研考证电子书、题库视频学习平台
(2)
;
(3)每份保单总保费分 2 部分:纯保费、费用,总保费为 10。其中费用占总保费的
l
95
所以
E Y ak1 k| q95 0.281 0.331 v 0.39 1 v v2 2.0263, k 0
E Y 2
Y 2 k q95
0.281 0.331 v2 0.39
1 v v2
2
4.6573,
k 0
故 Var(Y)=E(Y2)-[E(Y)]2=0.55。
年金。假设年金的给付从购买年金后的第一个月末开始,预定年利率 i=0.005,死亡满足
UDD 假设,而且
a50 13.5, 12≈1, 12 0.4665,则 k 的值为( )。
A.322
B.333
C.341
D.356
E.364
【答案】A
【解析】每月的年金精算现值为:
a5102
a5(102)
1 12
3 / 96
圣才电子书 十万种考研考证电子书、题库视频学习平台
又
a 1, q
l l 95 96 0.28,
1
95
l
95
a 1 v,
l l q 96 97 0.33,
2
1 95
l
95
a 1 v v 2,
q
l l 97 98 0.39,
3
2 95
x
95
96
97
98
lx
100
72
39
0
已知 i=0.06,以 Y 表示该年金的现值变量,则 E(Y)和Var (Y)分别为( )。
A.2.03;0.55
B.2.03;0.79
C.2.05;0.79
D.2.05;0.55
E.2.07;0.79
【答案】A
【解析】由 i=0.06,得:v=(1+i)-1=1.06-1。
十万种考研考证电子书、题库视频学习平台
A.0.4396
B.0.4572
C.0.4648
D.0.4735
E.0.4837
【答案】C
【解析】由已知,得
ax
e tetdt
0
1
10
Pr
aT ax
Pr
1
vt
10
Pr vt 0.6
T
ln 0.6
Pr T 12.7706
exp t dt 12.77
已知利率 i=0.06,则 =( )。
A.1.8
B.1.9
C.2.0
D.2.1
E.2.2
【答案】C
【解析】由于 k
px
lxk lx
,故
=1+1.06-1×0.72+1.06-2×0.39=2.0
5 / 96
圣才电子书 十万种考研考证电子书、题库视频学习平台
7.(样题)设(1)
【解析】设支付的随机变量为 Z,退休基金为 P,则
E(Z)
,
Var(Z)
,
P(Z
P)
P
Z E(Z )
Var Z
P E(Z ) Var(Z )
0.95
,
故 P=E(Z)+1.645 Var(Z ) =482.5。
6.(样题)考虑(90)的期初年金,每次年金支付额为 1,生存模型为:
;(2)
;(3)
。求 =( )。
A.0.085
B.0.125
C.0.600
D.0.650
E.0.825
【答案】D
【解析】由于 Ax 1 ax , 2 Ax
0
v
2t
t
px
x
t
dt
0
v2t
d
(t
px )
1 2 2 ax ,
故
Var (aT
)
1 2
[ 2
Ax
( Ax )2 ]
2
(ax
2 ax
