2020中考数学复习分类汇编专题4:二次函数与直角三角形以及矩形问题
专题四 二次函数综合题(含答案)2025年中考数学一轮题型专练(陕西)

专题四 二次函数综合题题型1 二次函数的实际应用二次函数的实际应用问题,在陕西中考2022,2023,2024年连续三年进行考查,其考查本质为二次函数表达式的应用,其主要为顶点式的考查,在表达式的基础上进行实践应用的考查,知x求y或知y求x,利用二次函数性质求最值,感受数学在实际问题中的应用.类型1 抛物线运动轨迹问题(2024·西安市莲湖区模拟)如图,在一场校园羽毛球比赛中,小华在点P选择吊球进行击球,当羽毛球飞行的水平距离是1 m时,达到最大高度3.2 m,建立如图所示的平面直角坐标系.羽毛球在空中的运行轨迹可以近似地看成抛物线的一部分,队友小乐则在点P选择扣球进行击球,羽毛球的飞行高度y1(单位:m)与水平距离x(单位:m)近似地满足一次函数关系y1=-0.4x+2.8.(1)根据如图所示的平面直角坐标系,求吊球时羽毛球满足的二次函数表达式.(2)在(1)的条件下,已知球网AB与y轴的水平距离OA=3 m,CA=2 m,且点A,C都在x轴上,实践发现击球和吊球这两种方式都能使羽毛球过网.要使球的落地点到点C的距离更近,请通过计算判断应该选择哪种击球方式?解题指南 (1)抓住最大高度这一特征,设出顶点式:y=a(x-h)2+k,然后将点P的坐标代入即可.(2)分别令一次函数与二次函数的y为0,对比两种方式在x轴的交点的横坐标到点C的横坐标的距离大小即可.类型2 以建筑为背景的“过桥”问题(2024·西工大模拟)陕北窑洞,具有十分浓厚的民俗风情和乡土气息.如图,某窑洞口的下部近似为矩形OABC,上部近似为一条抛物线.已知OA=3 m,AB=2 m,m.窑洞的最高点M(抛物线的顶点)离地面OA的距离为258(1)建立如图所示的平面直角坐标系,求抛物线的表达式.(2)若在窑洞口的上部要安装一个正方形窗户DEFG,使得点D,E在矩形OABC的边BC上,点F,G在抛物线上,那么这个正方形窗户DEFG的边长为多少米?解题指南 (1)借助点M为顶点,设出顶点式,然后将点B坐标代入顶点式即可.(2)设出小正方形DEFG的边长,然后用所设边长表示出点G的横坐标、纵坐标,最后代入(1)中抛物线的表达式解方程即可.(2024·西安新城区模拟)某地想将新建公园的正门设计为一个抛物线型拱门,设计部门给出了如下方案:将拱门图形放入平面直角坐标系中,如图,抛物线型拱门的跨度ON=24 m,拱高PE=8 m.其中,点N在x轴上,PE⊥ON,OE=EN.(1)求该抛物线的函数表达式.(2)现要在拱门中设置矩形框架,其周长越小越好(框架粗细忽略不计).设计部门给出了两个设计方案:方案一:矩形框架ABCD的周长记为C1,点A、D在抛物线上,边BC在ON上,其中AB=6 m.方案二:矩形框架A'B'C'D'的周长记为C2,点A',D'在抛物线上,边B'C'在ON上,其中A'B'=4 m.求这两个方案中,矩形框架的周长C1,C2,并比较C1,C2的大小.类型3 以“悬挂线”为背景解决高度问题如图,在一个斜坡上架设两个塔柱AB,CD(可看作两条竖直的线段),塔柱间挂起的电缆线下垂可以近似地看成抛物线的形状.两根塔柱的高度满足AB=CD=27 m,塔柱AB与CD之间的水平距离为60 m,且两个塔柱底端点D与点B的高度差为12 m.以点A为坐标原点,1 m为单位长度构建平面直角坐标系. (1)求点B,C,D的坐标.x2一样,且电(2)经过测量,AC段所挂电缆线对应的抛物线的形状与抛物线y=1100缆线距离斜坡面竖直高度至少为15.5 m时,才符合设计安全要求.请结合所学知识判断上述电缆线的架设是否符合安全要求?并说明理由.(2024·陕师大附中模拟)在元旦来临之际,学校安排各班在教室进行联欢.八(2)班同学准备装点一下教室.他们在屋顶对角A,B两点之间拉了一根彩带,彩带自然下垂后呈抛物线形状.若以两面墙交线AO为y轴,以点A正下方的墙角点O为原点建立平面直角坐标系,此时彩带呈现出的抛物线表达式为y=ax2-0.6x+3.5.已知屋顶对角线AB长12 m.(1)a= ,该抛物线的顶点坐标为.(2)小军想从屋顶正中心C(C为AB的中点)系一根绳子CD.将正下方彩带最低点向上提起,这样两侧的彩带就形成了两个对称的新抛物线形状(如图所示).要使两个新抛物线彩带最低点之间的水平距离为5 m,且比之前的最低点提高0.3 m.求这根绳子的下端D到地面的距离.题型2 图形面积探究类型1 面积、线段最值探究二次函数中面积问题,基本上都可以转化为线段相关问题,线段的三种表示方式:①水平型,②垂直型,③斜型.以边为分类标准,可采取不同方法进行面积的求解,现对不同类型线段的表示作以说明.(1)线段AB∥y轴时,点A,B横坐标相等,则AB=|y1-y2|=|y2-y1|=y1-y2.(2)线段BC∥x轴时,点B,C纵坐标相等,则BC=|x2-x1|=|x1-x2|=x2-x1.(3)线段AC与x轴,y轴不平行时,在Rt△ABC中,AC=AB2+BC2=(x1-x2)2+(y1-y2)2.第一步,过动点向x轴作垂线,与定边产生交点第二步,设动点坐标,表示交点坐标第三步,表示纵向线段长度|y上-y下|第四步,利用水平宽铅垂高表示三角形面积:S=12(y 上-y 下)(x 右-x 左)【原创好题】“水平宽”与“铅垂高”的运用:已知△ABC 的三个顶点坐标分别为A(x A ,y A ),B(x B ,y B ),C(x C ,y C ),用含有A,B,C 坐标的方式表示出△ABC 的面积.解题指南 (1)在平面直角坐标系中作△ABC,要求点A,B 在点C 的左、右两侧,经过点C 作x 轴的垂线交AB 于点D,则△ABC 被分成两部分,即S △ABC =S △ACD +S △BCD .(2)过点A 作△ADC 的高h 1,过点B 作△DBC 的高h 2,所以△ACD 与△BCD 的面积表示为S △ADC =12CD·h 1,S △BCD =12CD·h 2.(3)所以S △ABC =S △ADC +S △BCD =12CD·h 1+12CD·h 2=12CD·(h 1+h 2).(4)其中h 1与h 2的和可以看作点A 与点B 的水平间的距离,因此称之为“水平宽”,h 1+h 2=|x B -x A |,CD 是点C 与点D 的竖直间的距离,称之为“铅垂高”,即CD=|y D -y C |,故S △ABC =S △ACD +S △BCD =12|y D -y C |·|x B -x A |.1.如图,在平面直角坐标系xOy 中,直线y=x+4与坐标轴分别交于A,B 两点,抛物线y=-x 2+bx+c 过A,B 两点,D 为线段AB 上一动点,过点D 作CD ⊥x 轴于点C,交抛物线于点E.(1)求抛物线的表达式.(2)求△ABE 面积的最大值.2.如图,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC.(1)求A,B,C三点的坐标.(2)若P为线段BC上的一点(不与点B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N.当线段PM的长度最大时,求点M的坐标.类型2 面积关系探究(2018.T24)x2+bx与x轴交于O,A 【改编】在平面直角坐标系xOy中,已知抛物线y=-43两点,B(1,4)在抛物线上.若P是抛物线上一点,且在直线AB的上方,且满足△OAB 的面积是△PAB面积的2倍,求点P的坐标.解题指南 (1)第一步,将点B的坐标代入抛物线的表达式,求出b的值,根据A,B两点的坐标,求出直线AB的表达式;(2)第二步,借助三角形的面积公式,求出△OAB的面积,根据△OAB与△PAB的面积关系求出△PAB的面积;(3)第三步,设点P的坐标为t,-43t2+163t,过点P作x轴的垂线,与AB交于点N,并结合直线AB的表达式,表示出点N的坐标;(4)第四步,借助“水平宽,铅垂高”,求出PN的长度,用含有t的式子表示出PN的长度,构造方程求解即可.1.如图,抛物线y=-x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为x+3交于C,D两点,连接BD,AD.(3,0),抛物线与直线y=-32(1)求m的值.(2)求A,D两点的坐标.(3)若抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.2.如图,在平面直角坐标系中,点A(0,-1),抛物线y=-x2+bx+c经过点B(4,5)和C(5,0).(1)求抛物线的表达式.(2)连接AB,BC,求∠ABC的正切值.(3)在抛物线的对称轴上,是否存在点D,使得S△ABD=S△ABC?若存在,直接写出点D 的坐标;若不存在,请说明理由.3.已知抛物线y=-x2+bx+c过点A(-1,0),B(3,0),与y轴交于点C.(1)求抛物线的解析式.(2)P为抛物线对称轴上一动点,当△PCB是以BC为底边的等腰三角形时,求点P 的坐标.(3)在(2)的条件下,是否存在M为抛物线第一象限上的点,使得S△BCM=S△BCP?若存在,求出点M的横坐标;若不存在,请说明理由.解题指南 (1)由交点式可直接得出抛物线的解析式.(2)设P(1,m),根据列出方程,进而求得点P的坐标.(3)作PQ∥BC交y轴于点Q,作MN∥BC交y轴于点N,先求出PQ的解析式,进而求得MN的解析式,进一步求得结果. 借助“同底等高”找等面积的方法在平面直角坐标系中有△ABC,分别在BC所在直线的两侧找出一点P和Q,使得S△PBC=S△QBC=S△ABC.操作方式:(1)根据要求可知△PBC和△QBC均与△ABC具有共同的底边BC,要使它们的面积相等,只需要它们的高相等即可,因此可以设△PBC与△QBC的高均为h;(2)确定高以后,过点A作BC的平行线,则在所作平行线上存在一点P满足S△PBC=S△ABC;(3)如图,将BC所在直线向下平移AO'个单位长度,过A'作BC的平行线,则该直线上存在一点Q满足S△QBC=S△ABC;(4)运用“同底等高”法时,务必考虑不同位置的情况;(5)进行面积计算时,可以直接利用三角形面积公式求解.题型3 特殊三角形问题探究类型1 等腰三角形问题探究等腰三角形存在问题,可以分为两个方向来解决,几何法和代数法,其中几何法的优势在于比较直观地得到结果,对几何图形要求较高;代数法以解析几何为背景可更快地找到等量关系,方法较为单一,等腰三角形问题做完之后一定要验证是否出现三点共线的情况.方法一 几何法(1)两圆一线找出点;(2)利用勾股、相似、三角函数等求线段长,由线段长求得点坐标方法二 代数法(1)表示出三个点坐标A,B,C;(2)由点坐标表示出三条线段AB,AC,BC;(3)分类讨论①AB=AC;②AB=BC;③AC=BC;(4)列出方程求解(2024·铁一中模拟)如图,在平面直角坐标系中,抛物线L的顶点E的坐标为(-2,8),且过点B(0,6),与x轴交于M,N两点.(1)求该抛物线L的表达式.(2)设抛物线L关于y轴对称后的抛物线为L',其顶点记为点D,连接MD,在抛物线L'对称轴上是否存在点Q,使得以点M,D,Q为顶点的三角形为等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.(2024·西咸新区模拟)如图,抛物线L:y=ax2+bx-3(a、b为常数,且a≠0)与x轴交于点A(-1,0),B(3,0),与y轴交于点C.将抛物线L向右平移1个单位长度得到抛物线L'.(1)求抛物线L的函数表达式.(2)连接AC,探究抛物线L'的对称轴直线l上是否存在点P,使得以点A,C,P为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.类型2 直角三角形问题探究直角三角形存在问题,菱形中对角线垂直,矩形中的内角为直角,有下列两个方向可以帮助解决问题,不同的方法适用不同方向的题目,注意区分其方法.一、勾股定理若AC2+BC2=AB2,则△ABC为直角三角形二、构造“K”字型相似过直角顶点作坐标轴的平行线,过其他两点向平行线作垂直,出现“一线三等角”模型,利用“一线三等角”的相似模型,构建方程解决问题已知抛物线L:y=ax2-2ax-8a(a≠0)与x轴交于点A,点B,且点A在点B的左侧,与y轴交于点C.(1)求出点A与点B的坐标.(2)当△ABC是以AB为斜边的直角三角形时,求抛物线L的表达式.如图,在平面直角坐标系中,抛物线C1:y=ax2+bx+c(a≠0)交x轴于点A(-5,0),B(-1,0),交y轴于点C(0,5).(1)求抛物线C1的表达式和顶点D的坐标.(2)将抛物线C1关于y轴对称的抛物线记作C2,E为抛物线C2上一点,若△DOE是以DO为直角边的直角三角形,求点E的坐标. 直角三角形中的找点方法和计算方法找点方法:示例:如图,在平面内有A,B两点,试着找出一点C,使得A,B,C三点构成的三角形为直角三角形.分两种情况讨论:当AB为直角边时,{过点A作AB的垂线l1,过点B作AB的垂线l2;当AB为斜边时,以AB为直径作圆.如图,在直线l1,l2上的点C满足△ABC为直角三角形,但要注意一点:点C不与A,B两点重合.我们将这种找点C的方法称为“两线一圆”.计算方法:(1)利用勾股定理构造方程求解;(2)以“K”字型搭建相似三角形,列比例式构造方程求解.类型3 等腰直角三角形问题探究等腰直角三角形相关问题,以等腰直角三角形和正方形问题,主要解题方法相对统一,注意如何构图能直观得到“K”字全等是解决问题的关键之处.(1)过直角顶点作坐标轴平行线,构造“K”字全等(2)方法一:设某小边长度.方法二:设点坐标,表示直角三角形中的直角边(3)利用某纵向或横向线段构建等式(x+1)(x-5)与x轴交于A,B两点,与y轴交于点C.如果P是如图,抛物线y=-25抛物线上一点,M是该抛物线对称轴上的点,当△OMP是以OM为斜边的等腰直角三角形时,求点P的坐标.解题指南 第一步,过直角顶点作平行y轴的垂线,分别过另两个顶点作垂直,构造“K”字全等;第二步,利用坐标分别表示两直角三角形的直角边;第三步,利用某边相等构造方程.(2024·高新一中模拟)如图,在平面直角坐标系中,抛物线L:y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,3).(1)求出抛物线L的表达式和顶点的坐标.(2)P是抛物线L的对称轴右侧图象上的一点,过点P作x的垂线交x轴于点Q,作抛物线L关于直线PQ对称抛物线L',则C关于直线PQ的对称点为C',若△PCC'为等腰直角三角形,求出抛物线L'的表达式.题型4 三角形关系问题类型1 与相似三角形结合问题三角形的关系问题是陕西考试中非常常见的一个类型,中考中多次连续出现,相似问题的处理方法也相对较为固定,以固定三角形为参照,找到定角,以边为分类标准,进行分类讨论.主要有两个方法.方法一:利用一角相等,邻边成比例证明相似方法二:两组角相等的三角形相似分析目标三角形:第一类:找一角相等,用邻边成比例.第二类:找一角相等(多为90°问题),找另一角相等.方法总结:(1)分动、定三角形;(2)找等角;(3)表示边或者找另一角相等.(2024·曲江一中模拟)如图,抛物线y=ax 2+bx 经过坐标原点O 与点A(3,0),正比例函数y=kx 与抛物线交于点B 72,74.(1)求该抛物线的函数表达式.(2)P 是第四象限抛物线上的一个动点,过点P 作PM ⊥x 轴于点N,交OB 于点M,是否存在点P,使得△OMN 与以点N,A,P 为顶点的三角形相似?若存在,请求出点P 的坐标;若不存在,请说明理由.(2024·陕师大附中模拟)已知抛物线L 1:y=x 2+bx+c 与x 轴交于点A,B(点A 在点B 的左侧),与y 轴交于点C(0,-3),对称轴为直线x=1.(1)求此二次函数表达式和点A,B 的坐标.(2)P 为第四象限内抛物线L 1上一动点,将抛物线L 1平移得到抛物线L 2,抛物线L 2的顶点为点P,抛物线L 2与y 轴交于点E,过点P 作y 轴的垂线交y 轴于点D.是否存在点P,使以点P,D,E 为顶点的三角形与△AOC 相似?如果存在,请写出平移过程,并说明理由.类型2 与全等三角形结合问题1.全等为特殊的相似,相似比为1,方法与相似一致.2.注意相等角的邻边分类情况.【改编】如图,抛物线y=-23x 2+103x+4的图象与x 轴交于A,B 两点,与y 轴的正半轴交于点C,过点C 的直线y=-43x+4与x 轴交于点D.若M 是抛物线上位于第一象限的一动点,过点M 作ME ⊥CD 于点E,MF ∥x 轴交直线CD 于点F,当△MEF ≌△COD 时,求出点M 的坐标.解题指南 当△MEF ≌△COD 时,(1)找准对应角、边.结合关系式可知,∠MEF=∠COD,∠MFE=∠CDO,MF=CD.(2)根据直线CD 的表达式求出线段CD 的长度.由点M 在抛物线上,可以设点M的坐标为m,-23m 2+103m+4,再由MF ∥x 轴,得点F 的纵坐标.根据全等三角形的对应边相等可以得出点F 的横坐标为m-5.(3)由点F 在直线CD 上,将点F 的坐标代入直线CD 的表达式中,求出m 的值.已知经过原点O 的抛物线y=-x 2+4x 与x 轴的另一个交点为A.(1)求点A 的坐标及抛物线的对称轴.(2)B 是OA 的中点,N 是y 轴正半轴上一点,在第一象限内的抛物线上是否存在点M,使得△OMN 与△OBM 全等,且点B 与点N 为对应点?若存在,请求出点M 的坐标;若不存在,请说明理由. 与全等三角形结合问题的求解步骤(1)全等三角形的问题与相似三角形的问题步骤类似,均是先列出三角形的对应关系式,再根据关系式找出对应边相等;(2)借助对应边相等,将边与边的长度关系用点的坐标进行表示,然后运用“两点间距离公式”构造方程求解.题型5 特殊四边形问题探究类型1 平行四边形问题探究平行四边形问题,一般分为三定一动,两定两动问题,选取固定的两个点为分类标准,①以某边为边时;②以某边为对角线时.第一步,寻找分类标准;第二步,平移点,找关系(注意:从A到B和从B到A);第三步,代入关系求值(2024·西工大附中模拟)如图,抛物线y=ax2-2x+c与直线y=kx+b都经过A(0,3),B(-3,0)两点,该抛物线的顶点为C.(1)求此抛物线和直线AB的表达式.(2)设直线AB与该抛物线的对称轴交于点E,在射线EB上是否存在一点M,过点M作x轴的垂线交抛物线于点N.使点M,N,C,E是平行四边形的四个顶点?若存在,求出点M的坐标;若不存在,请说明理由.【改编】已知点A(-1,0)在抛物线L:y=x2-x-2上,抛物线L'与抛物线L关于原点对称,点A的对应点为点A',是否在抛物线L上存在一点P,在抛物线L'上存在一点Q,使得以AA'为边,且以A,A',P,Q为顶点的四边形是平行四边形?若存在,求出点P 的坐标;若不存在,请说明理由. 平行四边形中坐标的计算如图1,在平行四边形ABDC 中,关于坐标的计算——平移法则:x B -x A =x D -x C ,y B -y A =y D -y C ,x A -x C =x B -x D ,y A -y C =y B -y D .如图2,在平行四边形ADBC 中,关于坐标的计算——中点坐标公式:x M =x A +x B 2=x C +x D 2,y M =y A +y B 2=y C +y D 2.类型2 菱形问题探究菱形存在问题,主要分两类. 第一类:以平行四边形为背景,在平行四边形的基础上增加对角线垂直或邻边相等即可得菱形.(1)选一定点,再将这一定点与另外点的连线作为对角线,分类讨论.(2)利用中点坐标公式列方程:x A +x C 2=x B +x D 2;y A +y C 2=y B +y D 2.(3)对角线垂直:可参照直角存在问题.邻边相等:可参照等腰存在问题.(4)平移型:先平行四边形,再菱形.翻折型:先等腰,再菱形.第二类:若出现在平面内任意一点存在性问题,则去掉此点,转化为等腰存在问题,可以利用等腰存在问题策略解决问题如图,抛物线y=x 2+bx+c 与x 轴交于A,B 两点,与y 轴交于点C,OA=2,OC=6,连接AC 和BC.(1)求抛物线的函数表达式.(2)若M是y轴上的动点,在坐标平面内是否存在点N,使以A,C,M,N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.类型3 矩形问题探究矩形存在性问题,主要分两类. 第一类:以平行四边形为背景,在平行四边形的基础上增加对角线相等或一内角为90°即可得到矩形.(1)选一定点,再将这一定点与另外点的连线作为对角线,分类讨论.(2)利用中点坐标公式列方程:x A+x C=x B+x D;y A+y C=y B+y D.(3)方向一 对角线相等:(x A-x C)2+(y A-y C)2=(x B-x D)2+(y B-y D)2.方向二 有一角为90°.第二类:若出现在平面内任意一点存在性问题,则去掉此点,转化为直角存在问题,可以利用直角存在问题策略解决问题已知抛物线L:y=ax2+bx(a≠0)经过点B(6,0),C(3,9).(1)求抛物线L的表达式.(2)若抛物线L'与抛物线L关于x轴对称,P,Q(点P,Q不与点O,B重合)分别是抛物线L,L'上的动点,连接PO,PB,QO,QB,问四边形OPBQ能否为矩形?若能,求出满足条件的点P和点Q的坐标;若不能,请说明理由.已知抛物线L:y=-x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.(1)求A,B,C三点的坐标.(2)抛物线L平移后得到抛物线L',点A,C在抛物线L'上的对应点分别为点A',C',若以A,C,A',C'为顶点的四边形是面积为20的矩形,求平移后的抛物线L'的表达式.类型4 正方形问题探究(在菱形的基础上增加对角线相等)(1)选一定点,再将这一定点与另外点的连线作为对角线,分类讨论.(2)利用中点坐标公式列方程:x A+x C=x B+x D;y A+y C=y B+y D.(3)平行四边形题基础上加等腰直角三角形问题.,正方形ABCD的边AB 如图,一条抛物线y=ax2+bx(a≠0)的顶点坐标为2,83落在x轴的正半轴上,点C,D在这条抛物线上.(1)求这条抛物线的表达式.(2)求正方形ABCD的边长.解题指南 (1)已知顶点,可直接设抛物线的顶点式:y=a(x-h)2+k,将点的坐标代入计算即可.(2)①在正方形中,四条边均相等;②设出正方形的边长,并根据所设边长表示出正方形ABCD的顶点坐标;③注意观察正方形ABCD的顶点C,D在抛物线上;④代入相应点的坐标求出所设的边长即可.x2+bx+c的图象L经过原点,且与x轴的另一个交点为(8,0).已知二次函数y=-13(1)求该二次函数的表达式.(2)作x轴的平行线,交L于A,B两点(点A在点B的左侧),过A,B两点分别作x 轴的垂线,垂足分别为D,C.当以A,B,C,D为顶点的四边形是正方形时,求点A的坐标. 借助抛物线判定正方形的思路步骤1.明确在抛物线上的正方形的两个顶点;2.借助抛物线表达式y=ax2+bx+c(a≠0),设出其中一个顶点坐标为(x,ax2+bx+c),然后利用抛物线对称轴表示出另一个顶点坐标;3.根据正方形四条边相等构造一元二次方程求解即可.题型6 角度问题探究角相关问题是二次函数中相对较为综合性的问题,在近几年中考中也常出现在各个省市的中考题中,问题最终都会落到以下问题上来.等角问题,可直接用等角的性质来处理问题.解决策略:(1)寻找相似,出现等角;(2)利用三角函数找等角;(3)利用轴对称来找等角.【改编】在平面直角坐标系xOy中,已知抛物线y=-x2+4x-3与x轴分别交于A,B两点,且点A在点B的左侧.在抛物线上是否存在一点D,使得∠DOA=45°?若存在,求出点D的坐标;若不存在,请说明理由.解题指南 以平面直角坐标系为背景来探究角度问题,常用的思路为借助三角函数构造方程求解.本题具体步骤如下:第一步,根据∠DOA=45°,联想tan∠DOA=1;第二步,根据点D在抛物线上,可以过点D作x轴的垂线,记垂足为H,在△DOH中,tan∠DOH=DH OH;第三步,由点D在抛物线上,设点D的坐标为(t,-t2+4t-3);第四步,根据DH=|y D|=|-t2+4t-3|,OH=|t|,构造方程求解即可.已知抛物线L:y=-23x2+bx+c,与y轴的交点为C(0,2),与x轴的交点分别为A(3,0),B(点A在点B右侧).(1)求抛物线的表达式.(2)将抛物线沿x轴向左平移m(m>0)个单位长度,所得的抛物线与x轴的左交点为M,与y轴的交点为N,若∠NMO=∠CAO,求m的值.参考答案题型1 二次函数的实际应用类型1 抛物线运动轨迹问题例1 解析:(1)在y 1=-0.4x+2.8中,令x=0,则y 1=2.8,∴P (0,2.8).根据题意,二次函数图象的顶点坐标为(1,3.2).设二次函数的表达式为y=a (x-1)2+3.2,把P (0,2.8)代入y=a (x-1)2+3.2,得a+3.2=2.8,解得a=-0.4,∴吊球时羽毛球满足的二次函数表达式y=-0.4(x-1)2+3.2.(2)吊球时,令y=0,则-0.4(x-1)2+3.2=0,解得x 1=1+22,x 2=1-22(舍去),扣球时,令y=0,则-0.4x+2.8=0,解得x=7.∵OA=3 m,CA=2 m,∴OC=OA+AC=5.∵7-5=2,|22+1-5|=4-22<2,∴选择吊球时,球的落地点到点C 的距离更近.类型2 以建筑为背景的“过桥”问题例2 解析:(1)由题意得点M ,B 的坐标分别为32,258,(3,2).设抛物线的表达式为y=a x-322+258,将点B 的坐标代入上式得2=a 3-322+258,解得a=-12,∴抛物线的表达式为y=-12x-322+258.(2)设正方形的边长为2m.把点G 32-m ,2+2m 代入抛物线表达式,得2+2m=-1232-m-322+258,解得m=12(负值已舍去),∴正方形窗户DEFG 的边长为1 m .变式设问 解析:(1)由题意得抛物线的顶点坐标为(12,8),N (24,0).设y=a (x-12)2+8,把N (24,0)代入表达式中,得a=-118,∴该抛物线的函数表达式为y=-118(x-12)2+8.(2)方案一:令y=6,即6=-118(x-12)2+8.解得x 1=6,x 2=18,∴BC=AD=12.又∵AB=CD=6,∴矩形ABCD 的周长C 1=2×12+2×6=36(m).方案二:令y=4,即4=-118(x-12)2+8,解得x 1=12-62,x 2=12+62,∴B'C'=A'D'=12+62-(12-62)=122.又∵A'B'=C'D'=4,∴矩形A'B'C'D'的周长C 2=2×122+2×4=(242+8)m .∵C 1=36=28+8=4×7+8,C 2=242+8=4×62+8,∴36<242+8,即C 1<C 2.类型3 以“悬挂线”为背景解决高度问题例3 解析:(1)如图,过点C 作CE ⊥y 轴,垂足为E ,过点D 作DF ⊥y 轴,垂足为F.记CD 与x 轴相交于点G.根据题意,得点B 的坐标是(0,-27).∵FB=12,则GD=OF=OB-FB=27-12=15,OG=FD=EC=60,CG=CD-GD=27-15=12,∴点C 的坐标是(60,12),点D 的坐标是(60,-15).(2)符合安全要求.理由:设AC 段所挂电缆线对应的抛物线的函数表达式为y=1100x 2+bx ,将点C (60,12)代入表达式中,得12=1100×602+60b ,解得b=-25,∴y=1100x 2-25x.由点B (0,-27),D (60,-15)可知直线BD 的表达式为y=15x-27.记M 为抛物线上一点,过点M 作x 轴的垂线与BD 交于点N.设点M m ,1100m 2-25m ,则点N m ,15m-27,故MN=1100m 2-25m-15m-27=1100(m-30)2+18≥18>15.5,∴电缆线距离斜坡面竖直高度的最小值为18 m,高于安全需要的距离15.5 m,故符合安全要求.变式设问 解析:(1)0.05;(6,1.7).提示:由题意得抛物线的对称轴为直线x=6,则A (0,3.5),B (12,3.5),∴144a-7.2+3.5=3.5,解得a=0.05,∴抛物线的表达式为y=0.05x 2-0.6x+3.5.当x=6时,y=0.05x 2-0.6x+3.5=1.7,即该抛物线的顶点坐标为(6,1.7),(2)∵两个新抛物线彩带最低点之间的水平距离为5 m,且比之前的最低点提高0.3 m,∴左边新抛物线的顶点坐标为(3.5,2).设左边新抛物线的表达式为y=a'(x-3.5)2+2,将点A 的坐标代入上式得3.5=a'(0-3.5)2+2,解得a'=649,∴左侧抛物线的表达式为y=649(x-3.5)2+2.当x=6时,y=649(6-3.5)2+2=27198,∴这根绳子的下端D 到地面的距高为27198m .题型2 图形面积探究类型1 面积、线段最值探究例1 解析:如图,过点C 作垂直于x 轴的直线,与AB 交于点D ,分别过点A ,B 作CD 的垂线段h 1,h 2,即S △ABC =S △ACD +S △BCD .∵S △ADC =12CD ·h 1,S △BCD =12CD ·h 2,∴S △ABC =S △ACD +S △BCD =12CD ·(h 1+h 2).又∵CD=|y D -y C |,h 1+h 2=|x B -x A |,∴S △ABC =S △ACD +S △BCD =12(y D -y C)(x B -x A ).变式设问 1.解析:(1)在一次函数y=x+4中,令x=0,得y=4,令y=0,得x=-4,∴A (-4,0),B (0,4).∵点A (-4,0),B (0,4)在抛物线y=-x 2+bx+c 上,∴{-16-4b +c =0,c =4,解得{b =-3,c =4,∴抛物线的表达式为y=-x 2-3x+4.(2)设点C 的坐标为(m ,0)(-4≤m ≤0),则点E 的坐标为(m ,-m 2-3m+4),点D 的坐标为(m ,m+4),。
初三数学压轴题二次函数与等腰三角形、直角三角形、平行四边形、最值专题
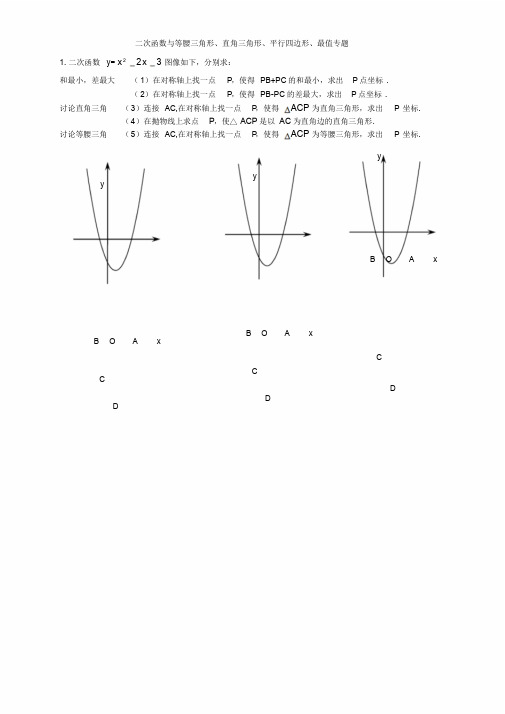
二次函数与等腰三角形、直角三角形、平行四边形、最值专题1. 二次函数y= x2 2x 3图像如下,分别求:和最小,差最大(1)在对称轴上找一点P,使得PB+PC的和最小,求出P 点坐标.(2)在对称轴上找一点P,使得PB-PC的差最大,求出P 点坐标.讨论直角三角(3)连接AC,在对称轴上找一点P,使得ACP 为直角三角形,求出P坐标.(4)在抛物线上求点P,使△ACP是以AC为直角边的直角三角形.讨论等腰三角(5)连接AC,在对称轴上找一点P,使得ACP 为等腰三角形,求出P坐标.yyyB O A xB O A xB O A xCCCDDD122.已知抛物线y=ax +bx+c 经过A( -1,0) 、B(3 ,0) 、C(0 ,3) 三点,直线l 是抛物线的对称轴.(1) 求抛物线的函数关系式;(2) 设点P是直线l 上的一个动点,当△PAC的周长最小时,求点P的坐标;(3) 在直线l 上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.2. 已知:如图一次函数y=1x+1 的图象与x 轴交于点A,与y 轴交于点B;二次函数y=2 1 x22+bx+c 的图象与一次函数y=(1)求二次函数的解析式;1x+1 的图象交于B、C两点,与x 轴交于D、E两点且D点坐标为(1,0)2(2)求四边形BDEC的面积S;(3)在x 轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.yC 2BxA O D E22、(2013?连云港)如图,抛物线y=-x 2+mx+n与x 轴分别交于点A(4,0),B(-2 ,0),与y 轴交于点C.(1)求该抛物线的解析式;(2)M为第一象限内抛物线上一动点,点M在何处时,△ACM的面积最大;(3)在抛物线的对称轴上是否存在这样的点P,使得△PAC为直角三角形?若存在,请求出所有可能点P 的坐标;若不存在,请说明理由.4、(西宁)在平面直角坐标系中,现将一块等腰直角三角板A BC 放在第二象限,斜靠在两坐标轴上,点C 为(-1,0).如图所示, B 点在抛物线y=12 x2+2+12x-2 图象上,过点 B 作BD ⊥x 轴,垂足为D,且B 点横坐标为-3.(1)求证:△BDC ≌△COA;(2)求BC 所在直线的函数关系式;(3)抛物线的对称轴上是否存在点P,使△ACP 是以AC 为直角边的直角三角形?若存在,求出所有点P 的坐标;若不存在,请说明理由.39、(潼南)如图,在平面直角坐标系中,△ABC 是直角三角形,∠ACB=90 °,AC=BC ,OA=1,OC=4,抛物线y=x 2+bx+c 经过A,B 两点,抛物线的顶点为D.(1)求b,c 的值;(2)点 E 是直角三角形ABC 斜边AB 上一动点(点A、B 除外),过点 E 作x 轴的垂线交抛物线于点F,当线段EF 的长度最大时,求点 E 的坐标;(3)在(2)的条件下:①求以点E、B、F、D 为顶点的四边形的面积;②在抛物线上是否存在一点P,使△EFP 是以EF 为直角边的直角三角形?若存在,求出所有点P 的坐标;若不存在,说明理由.2 bx c a6.如图,已知抛物线y ax ( 0)的顶点坐标为Q 2, 1 ,且与y 轴交于点 C 0,3 ,与x轴交于A、B 两点(点A在点 B 的右侧),点P 是该抛物线上一动点,从点C沿抛物线向点 A 运动(点P 与A不重合),过点P作PD∥y 轴,交AC于点D.(1) 求该抛物线的函数关系式;(2) 当△ADP是直角三角形时,求点P 的坐标;(3) 在问题(2) 的结论下,若点E在x轴上,点 F 在抛物线上,问是否存在以A、P、E、F 为顶点的平行四边形?若存在,求点 F 的坐标;若不存在,请说明理由.4。
中考复习专题2二次函数与直角三角形问题(含解析)

专题2二次函数与直角三角形问题我们先看三个问题:1.已知线段AB,以线段AB为直角边的直角三角形ABC有多少个?顶点C的轨迹是什么?2.已知线段AB,以线段AB为斜边的直角三角形ABC有多少个?顶点C的轨迹是什么?3.已知点A(4,0),如果△OAB是等腰直角三角形,求符合条件的点B的坐标.图1图2图3如图1,点C在垂线上,垂足除外.如图2,点C在以AB为直径的圆上,A、B两点除外.如图3,以OA为边画两个正方形,除了O、A两点以外的顶点和正方形对角线的交点,都是符合题意的点B,共6个.如图4,已知A(3,0),B(1,-4),如果直角三角形ABC的顶点C在y轴上,求点C的坐标.我们可以用几何的方法,作AB为直径的圆,快速找到两个符合条件的点C.如果作BD⊥y轴于D,那么△AOC∽△CDB.设OC=m,那么341m m-=.这个方程有两个解,分别对应图中圆与y轴的两个交点.对于代数法,可以采用两条直线的斜率之积来解决.【例1】.(2022•滨州)如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴相交于点A、B(点A 在点B的左侧),与y轴相交于点C,连接AC、BC.(1)求线段AC的长;(2)若点P为该抛物线对称轴上的一个动点,当PA=PC时,求点P的坐标;(3)若点M为该抛物线上的一个动点,当△BCM为直角三角形时,求点M的坐标.【分析】(1)根据坐标轴上点的特点求出点A,C的坐标,即可求出答案;(2)设出点P的坐标,利用PA=PC建立方程求解,即可求出答案;(3)分三种情况,利用等腰直角三角形的性质求出前两种情况,利用三垂线构造出相似三角形,得出比例式,建立方程求解,即可求出答案.【解析】(1)针对于抛物线y=x2﹣2x﹣3,令x=0,则y=﹣3,∴C(0,﹣3);令y=0,则x2﹣2x﹣3=0,∴x=3或x=﹣1,∵点A在点B的左侧,∴A(﹣1,0),B(3,0),∴AC==;(2)∵抛物线y=x2﹣2x﹣3的对称轴为直线x=﹣=1,∵点P为该抛物线对称轴上,∴设P(1,p),∴PA==,PC==,∵PA=PC,∴=,∴p=﹣1,∴P(1,﹣1);(3)由(1)知,B(3,0),C(0,﹣3),∴OB=OC=3,设M(m,m2﹣2m﹣3),∵△BCM为直角三角形,∴①当∠BCM=90°时,如图1,过点M作MH⊥y轴于H,则HM=m,∵OB=OC,∴∠OCB=∠OBC=45°,∴∠HCM=90°﹣∠OCB=45°,∴∠HMC=45°=∠HCM,∴CH=MH,∵CH=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,∴﹣m2+2m=m,∴m=0(不符合题意,舍去)或m=1,∴M(1,﹣4);②当∠CBM=90°时,过点M作M'H'⊥x轴,同①的方法得,M'(﹣2,5);③当∠BMC=90°时,如图2,Ⅰ、当点M在第四象限时,过点M作MD⊥y轴于D,过点B作BE⊥DM,交DM的延长线于E,∴∠CDM=∠E=90°,∴∠DCM+∠DMC=90°,∵∠DMC+∠EMB=90°,∴∠DCM=∠EMB,∴△CDM∽△MEB,∴,∵M(m,m2﹣2m﹣3),B(3,0),C(0,﹣3),∴DM=m,CD=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,ME=3﹣m,BE=﹣(m2﹣2m﹣3)=﹣m2+2m+3,∴,∴m=0(舍去)或m=3(点B的横坐标,不符合题意,舍去)或m=(不符合题意,舍去)或m=,∴M(,﹣),Ⅱ、当点M在第三象限时,M(,﹣),即满足条件的M的坐标为(1,﹣4)或(﹣2,5)或(,﹣),或(,﹣).【例2】.(2022•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.(1)求抛物线的解析式;(2)当点D在第二象限且=时,求点D的坐标;(3)当△ODF为直角三角形时,请直接写出点D的坐标.【分析】(1)将点A(﹣4,0),C(0,4)代入y=ax2﹣3x+c,即可求解;(2)过点D作DG⊥AB交于G,交AC于点H,设D(n,﹣n2﹣3n+4),H(n,n+4),由DH∥OC,可得==,求出D(﹣1,6)或(﹣3,4);(3)设F(t,t+4),当∠FDO=45°时,过点D作MN⊥y轴交于点N,过点F作FM⊥MN交于点M,证明△MDF≌△NOD(AAS),可得D点纵坐标为2,求出D点坐标为(,2)或(,2);当∠DFO=90°时,过点F作KL⊥x轴交于L点,过点D作DK⊥KL交于点K,证明△KDF≌△LFO(AAS),得到D点纵坐标为4,求得D(0,4)或(﹣3,4).【解析】(1)将点A(﹣4,0),C(0,4)代入y=ax2﹣3x+c,∴,解得,∴y=﹣x2﹣3x+4;(2)过点D作DG⊥AB交于G,交AC于点H,设直线AC的解析式为y=kx+b,∴,解得,∴y=x+4,设D(n,﹣n2﹣3n+4),H(n,n+4),∴DH=﹣n2﹣4n,∵DH∥OC,∴==,∵OC=4,∴DH=3,∴﹣n2﹣4n=3,解得n=﹣1或n=﹣3,∴D(﹣1,6)或(﹣3,4);(3)设F(t,t+4),当∠FDO=45°时,过点D作MN⊥y轴交于点N,过点F作FM⊥MN交于点M,∵∠DOF=45°,∴DF=DO,∵∠MDF+∠NDO=90°,∠MDF+∠MFD=90°,∴∠NDO=∠MFD,∴△MDF≌△NOD(AAS),∴DM=ON,MF=DN,∴DN+ON=﹣t,DN=ON+(﹣t﹣4),∴DN=﹣t﹣2,ON=2,∴D点纵坐标为2,∴﹣x2﹣3x+4=2,解得x=或x=,∴D点坐标为(,2)或(,2);当∠DFO=90°时,过点F作KL⊥x轴交于L点,过点D作DK⊥KL交于点K,∵∠KFD+∠LFO=90°,∠KFD+∠KDF=90°,∴∠LFO=∠KDF,∵DF=FO,∴△KDF≌△LFO(AAS),∴KD=FL,KF=LO,∴KL=t+4﹣t=4,∴D点纵坐标为4,∴﹣x2﹣3x+4=4,解得x=0或x=﹣3,∴D(0,4)或(﹣3,4);综上所述:D点坐标为(,2)或(,2)或(0,4)或(﹣3,4).【例3】(2022•广安)如图,在平面直角坐标系中,抛物线y=ax2+x+m(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,﹣4),点C坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.【分析】(1)把点B,C两点坐标代入抛物线的解析式,解方程组,可得结论;(2)存在.如图1中,设D(t,t2+t﹣4),连接OD.构建二次函数,利用二次函数的性质,解决问题;(3)如图2中,设抛物线的对称轴交x轴于点N,过点B作BM⊥抛物线的对称轴于点M.则N(﹣1.0).M (﹣1,﹣4),分三种情形:∠PAB=90°,∠PBA=90°,∠APB=90°,分别求解可得结论.【解析】(1)∵抛物线y=ax2+x+m(a≠0)的图象经过点B(0,﹣4),点C(2,0),∴,解得,∴抛物线的解析式为y=x2+x﹣4;(2)存在.理由:如图1中,设D(t,t2+t﹣4),连接OD.令y=0,则x2+x﹣4=0,解得x=﹣4或2,∴A(﹣4,0),C(2,0),∵B(0,﹣4),∴OA=OB=4,=S△AOD+S△OBD﹣S△AOB=×4×(﹣﹣t+4)+×4×(﹣t)﹣×4×4=﹣t2﹣4t=﹣∵S△ABD(t+2)2+4,∵﹣1<0,∴t=﹣2时,△ABD的面积最大,最大值为4,此时D(﹣2,﹣4);(3)如图2中,设抛物线的对称轴交x轴于点N,过点B作BM⊥抛物线的对称轴于点M.则N(﹣1.0).M (﹣1,﹣4);∵OA=OB=4,∠AOB=90°,∴∠OAB=∠OBA=45°,当∠P1AB=90°时,△ANP1是等腰直角三角形,∴AN=NP1=3,∴P1(﹣1,3),当∠ABP2=90°时,△BMP2是等腰直角三角形,可得P2(﹣1,﹣5),当∠APB=90°时,设P(﹣1,n),设AB的中点为J,连接PJ,则J(﹣2,﹣2),∴PJ=AB=2,∴12+(n+2)2=(2)2,解得n=﹣2或﹣﹣2,∴P3(﹣1,﹣2),P4(﹣1,﹣﹣2),综上所述,满足条件的点P的坐标为(﹣1,3)或(﹣1,﹣5)或(﹣1,﹣2)或(﹣1,﹣﹣2).【例4】.(2022•柳州)已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(m,0)两点,与y轴交于点C(0,5).(1)求b,c,m的值;(2)如图1,点D是抛物线上位于对称轴右侧的一个动点,且点D在第一象限内,过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作EF⊥x轴,垂足为点F,当四边形DEFG 的周长最大时,求点D的坐标;(3)如图2,点M是抛物线的顶点,将△MBC沿BC翻折得到△NBC,NB与y轴交于点Q,在对称轴上找一点P,使得△PQB是以QB为直角边的直角三角形,求出所有符合条件的点P的坐标.【分析】(1)把A(﹣1,0),C(0,5)代入y=﹣x2+bx+c,解二元一次方程组即可得b,c的值,令y =0即可得m的值;(2)设D(x,﹣x2+4x+5),则E(4﹣x,﹣x2+4x+5),表示出四边形DEFG的周长,根据二次函数的最值即可求解;(3)过点C作CH⊥对称轴于H,过点N作NK⊥y轴于K,证明△MCH≌△NCK,根据全等三角形的性质得NK=MH=4,CK=CH=2,则N(﹣4,3),利用待定系数法可得直线BN的解析式为y=﹣x+,可得Q(0,),设P(2,p),利用勾股定理表示出PQ2、BP2、BQ2,分两种情况:①当∠BQP=90°时,②当∠QBP=90°时,利用勾股定理即可求解.【解析】(1)把A(﹣1,0),C(0,5)代入y=﹣x2+bx+c,得,解得.∴这个抛物线的解析式为:y=﹣x2+4x+5,令y=0,则﹣x2+4x+5=0,解得x1=5,x2=﹣1,∴B(5,0),∴m=5;(2)∵抛物线的解析式为:y=﹣x2+4x+5=﹣(x﹣2)2+9,∴对称轴为x=2,设D(x,﹣x2+4x+5),∵DE∥x轴,∴E(4﹣x,﹣x2+4x+5),∵过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作EF⊥x轴,∴四边形DEFG是矩形,∴四边形DEFG的周长=2(﹣x2+4x+5)+2(x﹣4+x)=﹣2x2+12x+2=﹣2(x﹣3)2+20,∴当x=3时,四边形DEFG的周长最大,∴当四边形DEFG的周长最大时,点D的坐标为(3,8);(3)过点C作CH⊥对称轴于H,过点N作NK⊥y轴于K,∴∠NKC=∠MHC=90°,由翻折得CN=CM,∠BCN=∠BCM,∵B(5,0),C(0,5).∴OB=OC,∴∠OCB=∠OBC=45°,∵CH⊥对称轴于H,∴CH∥x轴,∴∠BCH=45°,∴∠BCH=∠OCB,∴∠NCK=∠MCH,∴△MCH≌△NCK(AAS),∴NK=MH,CK=CH,∵抛物线的解析式为:y=﹣x2+4x+5=﹣(x﹣2)2+9,∴对称轴为x=2,M(2,9),∴MH=9﹣5=4,CH=2,∴NK=MH=4,CK=CH=2,∴N(﹣4,3),设直线BN的解析式为y=mx+n,∴,解得,∴直线BN的解析式为y=﹣x+,∴Q(0,),设P(2,p),∴PQ2=22+(p﹣)2=p2﹣p+,BP2=(5﹣2)2p2=9+p2,BQ2=52+()2=25+,分两种情况:①当∠BQP=90°时,BP2=PQ2+BQ2,∴9+p2=p2﹣p++25+,解得p=,∴点P的坐标为(2,);②当∠QBP=90°时,P′Q2=BP′2+BQ2,∴p2﹣p+=9+p2+25+,解得p=﹣9,∴点P′的坐标为(2,﹣9).综上,所有符合条件的点P的坐标为(2,),(2,﹣9).1.(2022•公安县模拟)如图,已知二次函数y=﹣x2+bx+c经过A,B两点,BC⊥x轴于点C,且点A(﹣1,0),C(2,0),AC=BC.(1)求抛物线的解析式;的最大值以及此时E点的坐标;(2)点E是抛物线AB之间的一个动点(不与A,B重合),求S△ABE(3)根据问题(2)的条件,判断是否存在点E使得△ABE为直角三角形,如果存在,求出E点的坐标,如果不存在,说明理由.【分析】(1)先求得点B的坐标,然后将点A和点B的坐标代入抛物线的解析式可得到关于b、c的方程组,从而可求得b、c的值;(2)过点E作EF∥y轴交线段AB于点F,设点E(t,﹣t2+2t+3),则F(t,t+1),则可得到EF与x 的函数关系式,利用配方法可求得EF的最大值以及点E的坐标,最后根据EF的最大值可得△ABE的面积;(3)存在,设E(m,﹣m2+2m+3),分三种情况:分别以A,B,E为直角顶点,作出辅助线,构造相似列出方程,解方程即可.【解析】(1)∵点A(﹣1,0),C(2,0),∴AC=3,OC=2,∵AC=BC=3,∴B(2,3),把A(﹣1,0)和B(2,3)代入二次函数y=x2+bx+c中得:,解得:,∴二次函数的解析式为:y=﹣x2+2x+3;(2)∵直线AB经过点A(﹣1,0),B(2,3),设直线AB的解析式为y=kx+b′,∴,解得:,∴直线AB的解析式为:y=x+1,如图,过点E作EF∥y轴交线段AB于点F,∴设点E(t,﹣t2+2t+3),则F(t,t+1),∴EF=﹣t2+2t+3﹣(t+1)=﹣(t﹣)2+,∴当t=时,EF的最大值为,∴点E的坐标为(,),最大,S△ABE=•EF•(x B−x A)=××(2+1)=.∴此时S△ABE(3)在问题(2)的条件下,存在点E使得△ABE为直角三角形;设E(m,﹣m2+2m+3),①当点A为直角顶点,过点A作AB的垂线,与AB之间的抛物线无交点,故不可能存在点E使得△ABE为以点A为直角顶点的直角三角形,②当点B为直角顶点,如下图,此时∠EBA=90°,过点E作EG⊥CB,交CB延长线于点G,∵BC⊥x轴于点C,且AC=BC,∴△ABC是等腰直角三角形,∠ABC=45°,∴∠EBG=45°,∴△BEG是等腰直角三角形,EG=BG,∵EG的长为点E与直线BC的距离,即2﹣m,且BG=CG﹣BC=﹣m2+2m+3﹣3=﹣m2+2m,∴2﹣m==﹣m2+2m,解得m=1或m=2(舍),∴E(1,4);③如下图,此时∠AEB=90°,作EM∥x轴,交CB的延长线于点M,过点A作AN⊥x轴交ME的延长线于点N,∴∠BEM+∠AEN=90°,∵在Rt△AEN中,∠EAN+∠AEN=90°,∴∠BEM=∠EAN,∴△AEN∽△BEM,∴BM:EN=EM:AN,∴(﹣m2+2m):(m+1)=(2﹣m):(﹣m2+2m+3),即﹣m(2﹣m)(m+1)(m﹣3)=(2﹣m)(m+1),∵2﹣m≠0,m+1≠0,∴m2﹣3m+1=0,解得m=或m=(舍).∴E(,)综上,根据问题(2)的条件,存在点E(1,4)或(,)使得△ABE为直角三角形.2.(2022•高邮市模拟)如图,抛物线y=ax2+bx﹣3经过A(﹣1,0),与y轴交于点C,过点C作BC∥x 轴,交抛物线于点B,连接AC、AB,AB交y轴于点D,若.(1)求点B的坐标;(2)点P为抛物线对称轴上一点,且位于x轴上方,连接PA、PC,若△PAC是以AC为直角边的直角三角形,求点P的坐标.【分析】(1)根据A(﹣1,0),得到OA=l,对于y=ax2+bx﹣3,令x=0,则y=﹣3,得到C(0,﹣3),OC=3,根据BC∥x轴,得到△AOD∽△BCD,推出,得到BC=2,即可得B(2,﹣3);(2)把A(﹣1,0),B(2,﹣3)代入y=ax2+bx﹣3,求得a=1,b=﹣2,得到抛物线解析式并配方为y=x2﹣2x﹣3=(x﹣1)2﹣4,得到抛物线的对称轴是直线x=1,设P(1,m),写出PA2=m2+22=m2+4.PC2=(m+3)2+12=(m+3)2+1.AC2=12+32=10.根据△PAC是以AC为直角边的直角三角形,当∠PAC=90°时,PA2+AC2=PC2.得到m2+4+10=(m+3)2+1,求得m=;当∠PCA=90°时,PC2+AC2=AP2,得到(m+3)2+1+10=m2+4,求出m=﹣;即可得点P的坐标.【解析】∵A(﹣1,0),∴OA=l,在y=ax2+bx﹣3中,令x=0,则y=﹣3,∴C(0,﹣3),∴OC=3,∵BC∥x轴,∴△AOD∽△BCD,∴,∴BC=2,∴B(2,﹣3);(2)把A(﹣1,0),B(2,﹣3)代入y=ax2+bx﹣3,∴,解得,∴抛物线解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴是直线x=1,设P(1,m),∴PA2=m2+22=m2+4.PC2=(m+3)2+12=(m+3)2+1.AC2=12+32=10.∵△PAC是以AC为直角边的直角三角形,当∠PAC=90°时,PA2+AC2=PC2.∴m2+4+10=(m+3)2+1,解得m=;当∠PCA=90°时,PC2+AC2=AP2,∴(m+3)2+1+10=m2+4,解得m=﹣(不符合题意,舍去).∴P(1,).3.(2022•碑林区校级模拟)如图,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣2,0),B(4,0)两点.(1)求b,c的值;(2)点E为抛物线y=﹣x2+bx+c上一点,且点E在x轴上方,连接BE,以点E为直角顶点,BE为直角边,作等直角△BED,使得点D恰好落在直线y=x上,求出满足条件的所有点E的坐标.【分析】(1)运用待定系数法即可求得答案;(2)设D(m,m),E(n,﹣n2+2n+8),分两种情况:当点E1在点D左侧,∠DE1B=90°,BE1=D1E1时,当点E2在点D2右侧,∠D2E2B=90°,BE2=D2E2时,利用等腰直角三角形性质,添加辅助线构造全等三角形,再利用全等三角形的性质建立方程求解即可得出答案.【解析】(1)∵抛物线y=﹣x2+bx+c与x轴交于A(﹣2,0),B(4,0)两点,∴,解得:,∴b=2,c=8;(2)∵点D在直线y=x上,点E在抛物线解析式为y=﹣x2+2x+8上,∴设D(m,m),E(n,﹣n2+2n+8),当点E1在点D左侧,∠DE1B=90°,BE1=D1E1时,如图,过点E1作E1G∥x轴,过点B作BF⊥EG 于点F,过点D1作D1G⊥E1G于点G,则∠BFE1=∠E1GD1=90°,BF=﹣n2+2n+8,E1F=4﹣n,E1G=m﹣n,D1G=m﹣(﹣n2+2n+8)=n2﹣2n﹣8+m,∴∠E1BF+∠BE1F=90°,∵∠D1E1G+∠BE1F=90°,∴∠E1BF=∠D1E1G,在△BE1F和△E1D1G中,,∴△BE1F≌△E1D1G(AAS),∴E1F=D1G,BF=E1G,∴,解得:,当n=2时,﹣n2+2n+8=﹣22+2×2+8=8,∴E1(2,8);当点E2在点D2右侧,∠D2E2B=90°,BE2=D2E2时,如图,过点E2作E2H⊥x轴于点H,过点D2作D2K⊥E2H于点K,则∠BHE2=∠E2KD2=90°,BH=4﹣n,E2H=﹣n2+2n+8,E2K=﹣n2+2n+8﹣m,D2K=n﹣m,同理可得△BE2H≌△E2D2K(AAS),∴E2H=D2K,BH=E2K,∴,解得:或,∴E(1+,2)或(1﹣,2);综上所述,满足条件的所有点E的坐标为(2,8)或(1+,2)或(1﹣,2).4.(2022•雁峰区校级模拟)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴交于点C,直线y=x+1与x轴交于点E,与y轴交于点D.(1)求抛物线的解析式;(2)P为抛物线上的点,连接OP交直线DE于Q,当Q是OP中点时,求点P的坐标;(3)M在直线DE上,当△CDM为直角三角形时,求出点M的坐标.【分析】(1)根据抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,列方程组,于是得到答案;(2)令x=0,则y=x+1=1,求得OD=1,作PH⊥OB,垂足为H,得到∠COA=∠PHO=90°,根据平行线的性质得到∠P=∠DOQ,∠PFQ=∠ODQ,根据全等三角形的性质得到PF=OD=1,设P点横坐标为x,得到方程﹣x2+2x+3﹣(x+1)=1,求得x1=2,x2=﹣,当x=2时,y=3,当x=﹣时,y=,于是得到答案;(3)求得CD=OC﹣OD=2,设M(a,a+1),分两种情况①当∠CMD=90°时,②当∠DCM=90°时,根据勾股定理即可得到结论.【解析】(1)∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,∴,解得:,∴抛物线的解析式是y=﹣x2+2x+3;(2)令x=0,则y=x+1=1,∴OD=1,如图,作PH⊥OB,垂足为H,交ED于F,则∠COA=∠PHO=90°,∴PH∥OC,∴∠OPF=∠DOQ,∠PFQ=∠ODQ,又Q是OP中点,∴PQ=OQ,∴△PFQ≌△ODQ(AAS),∴PF=OD=1设P点横坐标为x,则﹣x2+2x+3﹣(x+1)=1,解得:x1=2,x2=﹣,当x=2时,y=3,当x=﹣时,y=,∴点P的坐标是(2,3)或(﹣,);(3)令x=0,则y=﹣x2+2x+3=3,∴OC=3,∴CD=OC﹣OD=2,设M(a,a+1),∴CM2=a2+(3﹣a﹣1)2=a2﹣2a+4,DM2=a2+(a+1﹣1)2=a2,①当∠CMD=90°时,∴CD2=CM2+DM2,∴22=a2﹣2a+4+a2,解得:a1=,a2=0(舍去),当a=时,a+1=,∴M(,);②当∠DCM=90°时,∴CD2+CM2=DM2,∴22+a2﹣2a+4=a2,解得:a=4,当a=4时,a+1=3,∴M(4,3);解法二:∵∠DCM=90°,∴CM∥x轴,∴a+1=3,解得a=4,∴M(4,3);综上所述:点M的坐标为(,)或(4,3).5.(2022•平南县二模)如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且A (﹣1,0),对称轴为直线x=2.(1)求该抛物线的表达式;(2)直线l过点A与抛物线交于点P,当∠PAB=45°时,求点P的坐标;(3)在抛物线的对称轴上是否存在一点Q,使得△BCQ是直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.【分析】(1)设y=(x﹣2)2+k,用待定系数法可得抛物线的解析式为y=x2﹣4x﹣5;(2)过点P作PM⊥x轴于点M,设P(m,m2﹣4m﹣5),根据∠PAB=45°知AM=PM,即|m2﹣4m﹣5|=m+1,解得m的值,即可得P的坐标是(6,7)或P(4,﹣5);(3)由y=x2﹣4x﹣5求出B(5,0),C(0,﹣5),设Q(2,t),有BC2=50,BQ2=9+t2,CQ2=4+(t+5)2,分三种情况:当BC为斜边时,9+t2+4+(t+5)2=50,当BQ为斜边时,50+4+(t+5)2=9+t2,当CQ为斜边时,50+9+t2=4+(t+5)2,分别解得t的值,即可求出相应Q的坐标.【解析】(1)设y=(x﹣2)2+k,把A(﹣1,0)代入得:(﹣1﹣2)2+k=0,解得:k=﹣9,∴y=(x﹣2)2﹣9=x2﹣4x﹣5,答:抛物线的解析式为y=x2﹣4x﹣5;(2)过点P作PM⊥x轴于点M,如图:设P(m,m2﹣4m﹣5),则PM=|m2﹣4m﹣5|,∵A(﹣1,0),∴AM=m+1∵∠PAB=45°∴AM=PM,∴|m2﹣4m﹣5|=m+1,即m2﹣4m﹣5=m+1或m2﹣4m﹣5=﹣(m+1),当m2﹣4m﹣5=m+1时,解得:m1=6,m2=﹣1(不合题意,舍去),当m2﹣4m﹣5=﹣(m+1),解得m3=4,m4=﹣1(不合题意,舍去),∴P的坐标是(6,7)或P(4,﹣5);(3)在抛物线的对称轴上存在一点Q,使得△BCQ是直角三角形,理由如下:在y=x2﹣4x﹣5中,令x=0得y=﹣5,令y=0得x=﹣1或x=5,∴B(5,0),C(0,﹣5),由抛物线y=x2﹣4x﹣5的对称轴为直线x=2,设Q(2,t),∴BC2=50,BQ2=9+t2,CQ2=4+(t+5)2,当BC为斜边时,BQ2+CQ2=BC2,∴9+t2+4+(t+5)2=50,解得t=﹣6或t=1,∴此时Q坐标为(2,﹣6)或(2,1);当BQ为斜边时,BC2+CQ2=BQ2,∴50+4+(t+5)2=9+t2,解得t=﹣7,∴此时Q坐标为(2,﹣7);当CQ为斜边时,BC2+BQ2=CQ2,∴50+9+t2=4+(t+5)2,解得t=3,∴此时Q坐标为(2,3);综上所述,Q的坐标为(2,3)或(2,﹣7)或(2,1)或(2,﹣6).6.(2022•太原一模)综合与实践如图,抛物线y=x2+2x﹣8与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.点D在直线AC 下方的抛物线上运动,过点D y轴的平行线交AC于点E.(1)求直线AC的函数表达式;(2)求线段DE的最大值;(3)当点F在抛物线的对称轴上运动,以点A,C,F为顶点的三角形是直角三角形时,直接写出点F的坐标.【分析】(1)分别令x=0,y=0,求得点C、A的坐标,再运用待定系数法即可求得答案;(2)设D(m,m2+2m﹣8),则E(m,﹣2m﹣8),可得DE=﹣2m﹣8﹣(m2+2m﹣8)=﹣m2﹣4m=﹣(m+2)2+4,运用二次函数的性质即可求得线段DE的最大值;(3)设F(﹣1,n),根据两点间距离公式可得:AF2=32+n2=n2+9,AC2=42+82=80,CF2=12+(n+8)2=n2+16n+65,分三种情况:①当∠AFC=90°时,②当∠CAF=90°时,③当∠ACF=90°时,分别建立方程求解即可.【解析】(1)在y=x2+2x﹣8中,令x=0,得y=﹣8,∴C(0,﹣8),令y=0,得x2+2x﹣8=0,解得:x1=﹣4,x2=2,∴A(﹣4,0),B(2,0),设直线AC的解析式为y=kx+b,则,解得:,∴直线AC的解析式为y=﹣2x﹣8;(2)设D(m,m2+2m﹣8),则E(m,﹣2m﹣8),∵点D在点E的下方,∴DE=﹣2m﹣8﹣(m2+2m﹣8)=﹣m2﹣4m=﹣(m+2)2+4,∵﹣1<0,∴当m=﹣2时,线段DE最大值为4;(3)∵y=x2+2x﹣8=(x+1)2﹣9,∴抛物线的对称轴为直线x=﹣1,设F(﹣1,n),又A(﹣4,0),C(0,﹣8),∴AF2=32+n2=n2+9,AC2=42+82=80,CF2=12+(n+8)2=n2+16n+65,①当∠AFC=90°时,∵AF2+CF2=AC2,∴n2+9+n2+16n+65=80,解得:n1=﹣4﹣,n2=﹣4+,∴F(﹣1,﹣4﹣)或(﹣1,﹣4+);②当∠CAF=90°时,∵AF2+AC2=CF2,∴n2+9+80=n2+16n+65,解得:n=,∴F(﹣1,);③当∠ACF=90°时,∵CF2+AC2=AF2,∴n2+16n+65+80=n2+9,解得:n=﹣,∴F(﹣1,﹣);综上所述,点F的坐标为(﹣1,﹣4﹣)或(﹣1,﹣4+)或(﹣1,)或(﹣1,﹣).7.(2022•桐梓县模拟)在平面直角坐标系xOy中,已知抛物线y=﹣与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,它的对称轴与x轴交于点D,直线L经过C,D两点,连接AC.(1)求A,B两点的坐标及直线L的函数表达式;(2)探索直线L上是否存在点E,使△ACE为直角三角形,若存在,求出点E的坐标;若不存在,说明理由.【分析】(1)令x=0,y=0,可分别求出A、B、C三点坐标,在求出函数的对称轴即可求D点坐标,利用待定系数法求直线解析式即可;(2)设E(t,﹣t+2),分三种情况讨论:①当∠CAE=90°时,AC2+AE2=CE2,②当∠ACE =90°时,AC2+CE2=AE2,③当∠AEC=90°时,AE2+CE2=AC2,分别利用勾股定理求解即可.【解析】(1)令y=0,则﹣=0,解得x=﹣2或x=6,∴A(﹣2,0),B(6,0),令x=0,则y=2,∴C(0,2),∵y=﹣=﹣(x﹣2)2+,∴抛物线的对称轴为直线x=2,∴D(2,0),设直线CD的解析式为y=kx+b,∴,解得,∴y=﹣x+2;(2)在点E,使△ACE为直角三角形,理由如下:设E(t,﹣t+2),∴AC2=16,AE2=4t2﹣8t+16,CE2=4t2,①当∠CAE=90°时,AC2+2CE2,∴16+4t2﹣8t+16=4t2,∴t=4,∴E(4,2);②当∠ACE=90°时,AC2+CE2=AE2,∴16+4t2=4t2﹣8t+16,∴t=0(舍);③当∠AEC=90°时,AE2+CE2=AC2,∴4t2﹣8t+16+4t2=16,∴t=0(舍)或t=1,∴E(1,);综上所述:E点坐标为(4,2)或(1,).8.(2022•沈阳模拟)如图1,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0),与y轴交于点C(0,﹣3).(1)求抛物线的解析式.(2)若点M是抛物线上B,C之间的一个动点,线段MA绕点M逆时针旋转90°得到MN,当点N恰好落在y轴上时,求点M,点N的坐标.(3)如图2,若点E坐标为(2,0),EF⊥x轴交直线BC于点F,将△BEF沿直线BC平移得到△B'E'F',在△B'E'F'移动过程中,是否存在使△ACE'为直角三角形的情况?若存在,请直接写出所有符合条件的点E′的坐标;若不存在,请说明理由.【分析】(1)将A(﹣1,0),B(3,0),C(0,﹣3)代入y=ax2+bx+c,即可求解;(2)过点M作HG∥y轴,交H,过点N作NG⊥HG交于点G,证明△AMH≌△MNG(AAS),设M(t,t2﹣2t﹣3),由HM=NG,可求t=即可求M、N点的坐标;(3)设△BEF沿x轴方向平移t个单位长,则沿y轴方向平移t个单位长,则E'(2+t,t),分三种情况讨论:①当∠ACE'=90°时,过点E'作E'H⊥y轴交于点H,可得△ACO∽△CE'H,利用相似比可求E'(﹣,﹣);当N点与E'重合时,也符合题意;②当∠CAE'=90°时,过点A作MN⊥x轴,过点C作CN⊥MN交于N点,过点E'作E'M⊥MN交于M点,可得△AME'∽△CNA,利用相似比可求E'(,);③当∠AE'C=90°时,过点E'作ST⊥x轴交于S点,过点C作CT⊥ST交于T点,可得△ASE'∽△E'TC,利用相似比可求E'(1,﹣1).【解析】(1)将A(﹣1,0),B(3,0),C(0,﹣3)代入y=ax2+bx+c,∴,∴,∴y=x2﹣2x﹣3;(2)过点M作HG∥y轴,交x轴于点H,过点N作NG⊥HG交于点G,∴∠AMH+∠NMG=90°,∵∠AMH+∠MAH=90°,∴∠NMG=∠MAH,∵AM=MN,∴△AMH≌△MNG(AAS),∴AH=MG,HM=NG,设M(t,t2﹣2t﹣3),∴HM=﹣t2+2t+3,NG=t,∴﹣t2+2t+3=t,∴t=,∵点M是抛物线上B,C之间,∴0<t<3,∴t=,∴M(,﹣),∴AH=1+=,∴HG=+=2+,∴N(0,﹣2﹣);(3)存在使△ACE'为直角三角形,理由如下:∵OB=OC,∴∠OBC=45°,设△BEF沿x轴方向平移t个单位长,则沿y轴方向平移t个单位长,∵E(2,0),∴E'(2+t,t),①如图2,当∠ACE'=90°时,过点E'作E'H⊥y轴交于点H,∴∠ACO+∠E'CH=90°,∵∠ACO+∠CAO=90°,∴∠E'CH=∠CAO,∴△ACO∽△CE'H,∴=,∵AO=1,CO=3,CH=﹣3﹣t,E'H=﹣2﹣t,∴=,解得t=﹣,∴E'(﹣,﹣);②如图3,当∠CAE'=90°时,过点A作MN⊥x轴,过点C作CN⊥MN交于N点,过点E'作E'M⊥MN交于M点,∴∠MAE'+∠NAC=90°,∵∠MAE'+∠ME'A=90°,∴∠NAC=∠ME'A,∴△AME'∽△CNA,∴=,∵NC=1,AN=3,AM=t,ME'=3+t,∴=,解得t=,∴E'(,);当E'点与N重合时,△ACE'为直角三角形,∴E'(﹣1,﹣3);③如图3,当∠AE'C=90°时,过点E'作ST⊥x轴交于S点,过点C作CT⊥ST交于T点,∴∠AE'S+∠CE'T=90°,∵∠AE'S+∠E'AS=90°,∴∠CE'T=∠E'AS,∴△ASE'∽△E'TC,∴=,∵AS=3+t,SE'=﹣t,CT=2+t,E'T=t+3,∴=,解得t=﹣1,∴E'(1,﹣1);综上所述:E'的坐标为(﹣,﹣)或(,)或(1,﹣1)或(﹣1,﹣3).9.(2022•东坡区校级模拟)如图,抛物线y=x2﹣(m+2)x+4的顶点C在x轴的正半轴上,直线y=x+2与抛物线交于A,B两点,且点A在点B的左侧.(1)求m的值;(2)点P是抛物线y=x2﹣(m+2)x+4上一点,当△PAB的面积是△ABC面积的2倍时,求点P的坐标;(3)将直线AB向下平移k(k>0)个单位长度,平移后的直线与抛物线交于D,E两点(点D在点E 的左侧),当△DEC为直角三角形时,求k的值.【分析】(1)令y=0得x2﹣(m+2)x+4=0,由Δ=0求得;(2)作CD∥AB交y轴于D,求得CD的函数表达式是y=x﹣2,在DF的延长线上截取EF=2DF=8,过点E作EG∥AB,求得EG的函数表达式,与抛物线函数表达式联立求得;(3)当∠CDE=90°时,可得直线CD的函数表达式是:y=﹣x+2,求出它与抛物线的交点即可,当∠DCE=90°时,设平移后的表达式是y=x+b,与抛物线的表达式联立求得D和E的坐标,再求出DE中点坐标,根据DE=2CI,进而求得b,根据平移的距离得出k值.【解析】(1)令y=0,∴x2﹣(m+2)x+4=0,∵Δ=(m+2)2﹣4×1×4=0,∴m=2或m=﹣6,又﹣,∴m>﹣2,∴m=2;(2)当m=2时,y=x2﹣4x+4=(x﹣2)2,如图1,作CD∥AB交y轴于D,∴CD的函数表达式是y=x﹣2,∴D(0,﹣2),∵y=x+=2与y轴交点F(0,2),∴DF =4,在DF 的延长线上截取EF =2DF =8,过点E 作EG ∥AB ,∴EG 的函数表达式是:y =x +10,由x 2﹣4x +4=x +10得,x =﹣1或x =6,当x =﹣1时,y =﹣1+10=9,当x =6时,y =6+10=16,∴P (﹣1,9)或P (6,16);作CM ⊥AB 于M 交EG 于N ,∵CD ∥AB ∥EG ,∴==,∴点P 到AB 的距离是点C 到AB 距离的2倍,∴△PAB 的面积是△ABC 面积的2倍.(3)当∠CDE =90°时,∴直线CD 的函数表达式是:y =﹣x +2,由x 2﹣4x +4=﹣x +2得,x =1或x =2(舍去),当x =1时,y =﹣1+2=1,∴y =x +(2﹣k )过(1,1),∴1+(2﹣k )=1,∴k =2,当∠DCE =90°时,设平移后的表达式是y =x +b ,由x 2﹣4x +4=x +b 得,化简得,x 2﹣5x +(4﹣b )=0,∴x 1=,x 2=,∴x1+x2=5,y1+y2=5+2b,∴DE的中点I(,),∴x1﹣x2=,∴y1﹣y2=x1+b﹣(x2+b)=x1﹣x2=,∵DE2=(x1﹣x2)2+(y1﹣y2)2=()2+()2=2(9+4b),CI2=(﹣2)2+()2=,由DE=2CI得,2(9+4b)=16+4b2+20b,∴b=﹣1或b=﹣2(舍去),∴k=3,综上所述,k=2或3.10.(2022•海沧区二模)抛物线y1=ax2﹣2ax+c(a<2且a≠0)与x轴交于A(﹣1,0),B两点,抛物线的对称轴与x轴交于点D,点M(m,n)在该抛物线上,点P是抛物线的最低点.(1)若m=2,n=﹣3,求a的值;(2)记△PMB面积为S,证明:当1<m<3时,S<2;(3)将直线BP向上平移t个单位长度得直线y2=kx+b(k≠0),与y轴交于点C,与抛物线交于点E,当x<﹣1时,总有y1>y2.当﹣1<x<1时,总有y1<y2.是否存在t≥4,使得△CDE是直角三角形,若存在,求t的值;若不存在,请说明理由.【分析】(1)将点A(﹣1,0)代入抛物线y1=ax2﹣2ax+c中,可得c=﹣3a,所以抛物线y1=ax2﹣2ax ﹣3a.当m=2,n=﹣3时,M(2,﹣3),将点M的坐标代入函数解析式,求解即可;(2)过点M作x轴的垂线,交直线BP于点Q,根据题意可知,P(a,﹣4a),B(3,0),所以直线BP 的解析式为:y=2ax﹣6a,设M(m,am2﹣2am﹣3a),则Q(m,2am﹣6a),根据三角形的面积公式可得出S和a的函数关系式,再根据二次函数的性质求解即可;(3)由平移可知,y2=2ax+2a,点C(0,2a),联立可得E(5,12a).根据题意当△ECD是直角三角形时,需要分三种情况讨论:①当∠ECD=90°时,过点E作y轴的垂线交y轴于点F,②当∠CDE =90°时,过点E作x轴的垂线于点F,③当∠CED=90°时,分别求解即可.【解答】(1)解:将点A(﹣1,0)代入抛物线y1=ax2﹣2ax+c中,∴a+2a+c=0,∴c=﹣3a,∴抛物线y1=ax2﹣2ax﹣3a.当m=2,n=﹣3时,M(2,﹣3),∴4a﹣4a﹣3a=﹣3,解得a=1;(2)证明:过点M作x轴的垂线,交直线BP于点Q,∵点P为y1=ax2﹣2ax﹣3a的最低点,∴P(a,﹣4a),令y1=ax2﹣2ax﹣3a=0,解得x=﹣1或x=3,∴B(3,0),∴直线BP的解析式为:y=2ax﹣6a,设M(m,am2﹣2am﹣3a),∴Q(m,2am﹣6a),∴QM=2am﹣6a﹣(am2﹣2am﹣3a)=﹣am2+4am﹣3a,∴S=|x B﹣x P|•QM=﹣am2+4am﹣3a=﹣a(m﹣2)2+a,∵﹣a<0,开口向下,∴当m=2时,S的最大值为a,∵a<2,∴当1<m<3时,S=a<2.(3)解:∵当x<﹣1时,总有y1<y2,∴直线l必经过点A(﹣1,0),将点A代入直线l:y2=kx+b,∴﹣k+b=0,∵直线l:y2=kx+b由直线PB:y=2ax﹣6a向上平移t个单位长度得到,∴k=b=2a,b=﹣6a+t=2a,∴t=8a,∴y2=2ax+2a,点C(0,2a),令2ax+2a=ax2﹣2ax﹣3a,解得x=﹣1或x=5,∴E(5,12a).①当∠ECD=90°时,过点E作y轴的垂线交y轴于点F,∴△FEC∽△OCD,∴EF:OC=CF:OD,即5:2a=10a:1,∴a=或a=﹣(舍);∴t=8a=4≥4,符合题意;②当∠CDE=90°时,过点E作x轴的垂线于点F,∴△OCD∽△FDE,∴EF:OD=DF:OC,即12a:1=4:2a,解得a=或a=﹣(舍),∴t=8a=<=4,不符合题意;③当∠CED=90°时,显然不存在.综上,存在,且t的值为.11.(2021•葫芦岛模拟)如图,在平面直角坐标系中,矩形OABC,点A在y轴上,点C在x轴上,其中B (﹣2,3),已知抛物线y=﹣x2+bx+c经过点A和点B.(1)求抛物线解析式;(2)如图1,点D(﹣2,﹣1)在直线BC上,点E为y轴右侧抛物线上一点,连接BE、AE,DE,若S△BDE=4S△ABE,求E点坐标;(3)如图2,在(2)的条件下,P为射线DB上一点,作PQ⊥直线DE于点Q,连接AP,AQ,PQ,若△APQ为直角三角形,请直接写出P点坐标.【分析】(1)求出A点坐标,将A、B点坐标代入y=﹣x2+bx+c即可求解;==2(m+2),S△ABE=m2+m,再由已知得到方程2(m+2)(2)设E(m,﹣m2﹣m+3),求得S△BDE=4(m2+m),求出m的值即可求E点坐标;(3)先求出直线DE的解析式为y=x+1,分三种情况讨论:①当P点与B点重合,此时△APQ为等腰直角三角形,则P(﹣2,3);②过点Q作QM⊥AB交BA的延长线于点M,证明△PAB∽△AQM,设P(﹣2,t),则Q(,),分别求出PB=t﹣3,AB=2,AM=,QM=﹣3=,再由三角形相似可得=,求出t即可求P点坐标;当PQ⊥AP时,AP∥DE,则直线AP的解析式为y=x+3,即可求P点坐标.【解答】解:(1)∵B(﹣2,3),矩形OABC,∴A(0,3),∵抛物线y=﹣x2+bx+c经过点A和点B,∴,∴,∴y=﹣x2﹣x+3;(2)∵D(﹣2,﹣1),∴BD=4,设E(m,﹣m2﹣m+3),=×4×(m+2)=2(m+2),∴S△BDE∵AB=2,=×2×(3+m2+m﹣3)=m2+m,∴S△ABE=4S△ABE,∵S△BDE∴2(m+2)=4(m2+m),解得m=﹣2或m=,∵E点在y轴由侧,∴m=,∴E(,);(3)∵E(,),D(﹣2,﹣1),设直线DE的解析式为y=kx+b,∴,∴,∴y=x+1,∴直线与y轴的交点为(0,1),如图1,当P点与B点重合,Q点为(0,1),此时△APQ为等腰直角三角形,∴P(﹣2,3);如图2,过点Q作QM⊥AB交BA的延长线于点M,∵∠PAQ=90°,∠PBA=90°,∠QME=90°,∴∠PAB=∠AQM,∴△PAB∽△AQM,∴=,设P(﹣2,t),∵直线DE的解析式为y=x+1,PQ⊥DE,∴∠PDQ=45°,∴Q(,),∴PB=t﹣3,AB=2,AM=,QM=﹣3=,∴=,∴t=9,∴P(﹣2,9);如图3,当PQ⊥AP时,∵∠PAQ+∠AQP=90°,∠∠AQE=90°,∴∠APQ=∠AQE,∴AP∥DE,∴直线AP的解析式为y=x+3,∴P(﹣2,1);综上所述:P点的坐标为(﹣2,1)或(﹣2,3)或(﹣2,9).12.(2021•和平区一模)如图,抛物线y=ax2+bx﹣,交y轴于点A,交x轴于B(﹣1,0),C(5,0)两点,抛物线的顶点为D,连接AC,CD.(1)求直线AC的函数表达式;(2)求抛物线的函数表达式及顶点D的坐标;(3)过点D作x轴的垂线交AC于点G,点H为线段CD上一动点,连接GH,将△DGH沿GH翻折到△GHR(点R,点G分别位于直线CD的两侧),GR交CD于点K,当△GHK为直角三角形时.①请直接写出线段HK的长为;②将此Rt△GHK绕点H逆时针旋转,旋转角为α(0°<α<180°),得到△MHN,若直线MN分别与直线CD,直线DG交于点P,Q,当△DPQ是以PQ为腰的等腰三角形时,请直接写出点P的纵坐标为﹣或﹣.【分析】(1)先根据抛物线y=ax2+bx﹣,交y轴于点A,求出点A坐标,再运用待定系数法求直线AC的函数表达式即可;(2)将B(﹣1,0),C(5,0)代入抛物线y=ax2+bx﹣求出a,b,即可得抛物线解析式,运用配方法将抛物线解析式化为顶点式即可得出顶点坐标;(3)①根据△GHK为直角三角形,且点R,点G分别位于直线CD的两侧,可分三种情况:∠GHK=90°或∠HGK=90°或∠GKH=90°,经分析仅有∠GKH=90°符合题意,过点H作HL⊥DG于点L,则HL=HK,先证明△GDK∽△CDF,再运用面积法即可求出答案;②由△DPQ是以PQ为腰的等腰三角形,可分两种情况:PQ=DQ或PQ=DP,分别求出点P的纵坐标即可.【解答】解:(1)设直线AC的函数表达式为:y=kx+c,∵抛物线y=ax2+bx﹣,交y轴于点A,∴A(0,﹣),将A(0,﹣),C(5,0)分别代入y=kx+c,得:,解得:,∴直线AC的函数表达式为:y=x﹣,(2)∵抛物线y=ax2+bx﹣经过B(﹣1,0),C(5,0)两点,∴,解得:,∴抛物线的解析式为y=x2﹣x﹣,∵y=x2﹣x﹣=(x﹣2)2﹣4,∴顶点D的坐标为(2,﹣4);(3)①如图1,∵△GHK为直角三角形,且点R,点G分别位于直线CD的两侧,∴∠GHK=90°或∠HGK=90°或∠GKH=90°,当∠GHK=90°时,∠GHD=90°,点R落在直线DC上,不符合题意,当∠HGK=90°时,∠DGH=∠HGK=90°,点R,点G位于直线CD的同侧,不符合题意,当∠GKH=90°时,点R,点G分别位于直线CD的两侧,符合题意,∴∠GKH=90°,∠DGH=∠RGH,过点H作HL⊥DG于点L,则HL=HK,∵D(2,﹣4),DG⊥x轴,∴G (2,﹣),F (2,0),∴DG =﹣﹣(﹣4)=,CF =5﹣2=3,DF =4,∴CD ===5,∵∠DFC =∠GKH =90°,∠GDK =∠CDF ,∴△GDK ∽△CDF ,∴==,即==,∴GK =,DK =,∵S △GKH +S △GDH =S △GDK ,∴××HK +××HL =××,故答案为:;②∵△DPQ 是以PQ 为腰的等腰三角形,∴PQ =DQ 或PQ =DP ,当PQ =DQ 时,如图2,由旋转知:点H 到PQ 、DQ 的距离相等,∴QH ⊥DP ,DH =HP ,由①知HL =HK =,∵HL ∥CF ,∴=,即=,∴DL =,∴L 的纵坐标为﹣4=﹣,即H 的纵坐标为﹣,∵H 为D 、P 的中点,∴P 的纵坐标为﹣,当PQ =DP 时,如图3,点P 为DQ 的垂直平分线与CD 的交点,∵H (,﹣),∴经过点H平行MN的直线为y=﹣x+,∵点H到直线MN的距离为,∴直线MN的解析式为y=﹣x﹣,∵直线CD的解析式为y=x﹣,∴P(,﹣);综上所述,点P的纵坐标为﹣或﹣.13.(2021•莱芜区三模)二次函数y=ax2+bx+c交x轴于点A(﹣1,0)和点B(﹣3,0),交y轴于点C(0,﹣3).(1)求二次函数的解析式;(2)如图1,点E为抛物线的顶点,点T(0,t)为y轴负半轴上的一点,将抛物线绕点T旋转180°,得到新的抛物线,其中B,E旋转后的对应点分别记为B′,E′,当四边形BEB'E'的面积为12时,求t 的值;(3)如图2,过点C作CD∥x轴,交抛物线于另一点D.点M是直线CD上的一个动点,过点M作x 轴的垂线,交抛物线于点P.当以点B、C、P为顶点的三角形是直角三角形时,求所有满足条件的点M 的坐标.【分析】(1)根据抛物线与x轴的交点坐标,设抛物线解析式为y=a(x+1)(x+3),将C(0,﹣3)代(2)如图1,连接EE′、BB′,延长BE,交y轴于点Q.利用待定系数法求出直线BE的解析式,根据抛物线y=﹣x2﹣4x﹣3绕点T(0,t)旋转180°,可得四边形BEB′E′是平行四边形,运用平行四边形性质即可求得答案;(3)设P(x,﹣x2﹣4x﹣3),根据以点B、C、P为顶点的三角形是直角三角形,分三种情况分别讨论即可:①当∠BP1C=90°时,③当∠P3BC=90°时,③当∠P3BC=90°时,④当∠BCP4=90°时.【解答】解:(1)∵二次函数过点A(﹣1,0),B(﹣3,0),∴设抛物线解析式为y=a(x+1)(x+3),将C(0,﹣3)代入,得:3a=3,解得:a=﹣1,∴二次函数的解析式为:y=﹣x2﹣4x﹣3;(2)如图1,连接EE′、BB′,延长BE,交y轴于点Q.由(1)得y=﹣x2﹣4x﹣3=﹣(x+2)2+1,。
2020年中考数学二次函数真题汇编(带答案)

2020年中考数学二次函数真题汇编(名师精选全国真题,值得下载练习)一、单选题1.如图,一段抛物线y=﹣x 2+4(﹣2≤x≤2)为C 1 , 与x 轴交于A 0 , A 1两点,顶点为D 1;将C 1绕点A 1旋转180°得到C 2 , 顶点为D 2;C 1与C 2组成一个新的图象,垂直于y 轴的直线l 与新图象交于点P 1(x 1 , y 1),P 2(x 2 , y 2),与线段D 1D 2交于点P 3(x 3 , y 3),设x 1 , x 2 , x 3均为正数,t=x 1+x 2+x 3 , 则t 的取值范围是( )A. 6<t≤8 B. 6≤t≤8 C. 10<t≤12 D. 10≤t≤12 【答案】D【解析】【解答】解:翻折后的抛物线的解析式为y=(x ﹣4)2﹣4=x 2﹣8x+12, ∵设x 1 , x 2 , x 3均为正数,∴点P 1(x 1 , y 1),P 2(x 2 , y 2)在第四象限, 根据对称性可知:x 1+x 2=8, ∵2≤x 3≤4,∴10≤x 1+x 2+x 3≤12即10≤t≤12, 故答案为:D .【分析】根据题意可求出翻折后的抛物线的解析式,设x 1 , x 2 , x 3均为正数,可得出点P 1(x 1 , y 1),P 2(x 2 , y 2)在第四象限,根据对称性可求出x 1+x 2=8,由2≤x 3≤4,可得出x 1+x 2+x 3的取值范围,从而得出t 的取值范围。
2.已知,平面直角坐标系中,直线y 1=x+3与抛物线y=-x x 的图象如图,点P 是y 2上的一个动点,则点P 到直线y 1的最短距离为( )A.B.C. D.【答案】D【解析】【解答】解、∵点P 到直线y 1的距离最短, ∴点P 是直线与抛物线相切时的交点。
设直线y 1平移k 个单位长度,则此时的解析式为 =x+3+k , 把 =x+3+k 代入y=-x 2+2x 整理得,-x 2+x-3-k=0,△=b 2-4ac=1-4 (-) (-3-k)=0,解得k=-,即直线y 1向下平移个单位长度与抛物线相切, 把k=-代入解析式解方程组可求得点P 的坐标为(1,);过点P 作PD ⊥直线y 1于点D ,则直线PD 的解析式可设为y 3=-x+b ,把点P (1,)代入可求得b=,即直线PD 的解析式为y 3=-x+,将y 1和y 3的解析式联立解方程组可求得点D 的坐标为(-,);若直线PD与x轴相较于点C,直线y1=x+3与x、y轴分别相较于点A、B,易得点A (-3,0)、B(0,3),∴∠BAC==∠DCA,由勾股定理可得:CD=,CP=,∴PD=CD-CP=。
2020年中考数学二轮专题——二次函数与几何图形综合(压轴)题型(含详细解答)

2020年中考数学二轮专题——二次函数与几何图形综合(压轴)题型一、基础过关1. (2019宿迁)如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,-3).(1)求抛物线的函数表达式;(2)如图①,连接AC,点P在抛物线上,且满足∠P AB=2∠ACO.求点P的坐标;(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.第1题图2. (2019贺州)如图,在平面直角坐标系中,已知点B的坐标为(-1,0),且OA=OC=4OB,抛物线y =ax2+bx+c(a≠0)图象经过A,B,C三点.(1)求A,C两点的坐标;(2)求抛物线的解析式;(3)若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P 的坐标及PD的最大值.第2题图二、能力提升1. (2019菏泽)如图,抛物线与x 轴交于A ,B 两点,与y 轴交于点C (0,-2),点A 的坐标是(2,0),P 为抛物线上的一个动点,过点P 作PD ⊥x 轴于点D ,交直线BC 于点E ,抛物线的对称轴是直线x =-1.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且PE =14OD ,求△PBE 的面积;(3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的上方,是否存在点M ,使△BDM 是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.第1题图三、满分冲关1. (2019襄阳)如图,在直角坐标系中,直线y =-12x +3与x 轴,y 轴分别交于点B ,点C ,对称轴为x=1的抛物线过B , C 两点,且交x 轴于另一点A ,连接A C.(1)直接写出点A ,点B ,点C 的坐标和抛物线的解析式;(2)已知点P 为第一象限内抛物线上一点,当点P 到直线BC 的距离最大时,求点P 的坐标; (3)抛物线上是否存在一点Q (点C 除外),使以点Q ,A ,B 为顶点的三角形与△ABC 相似?若存在,求出点Q 的坐标;若不存在,请说明理由.第1题图2、(2019滨州)如图①,抛物线y =-18x 2+12x +4与y 轴交于点A ,与x 轴交于点B ,C ,将直线AB 绕点A 逆时针旋转90°,所得直线与x 轴交于点D .(1)求直线AD 的函数解析式;(2)如图②,若点P 是直线AD 上方抛物线上的一个动点. ①当点P 到直线AD 的距离最大时,求点P 的坐标和最大距离; ②当点P 到直线AD 的距离为524时,求sin ∠P AD 的值.3、(2019金牛区一诊)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c (a ≠0)与x 轴的两个交点分别为A (-3,0)、B (1,0),与y 轴交于点D (0,3),过顶点C 作CH ⊥x 轴于点H .(1)求抛物线的解析式和顶点C 的坐标;(2)连接AD 、CD ,若点E 为抛物线上一动点(点E 与顶点C 不重合),当△ADE 与△ACD 面积相等时,求点E 的坐标;(3)若点P 为抛物线上一动点(点P 与顶点C 不重合),过点P 向CD 所在的直线作垂线,垂足为点Q ,以P 、C 、Q 为顶点的三角形与△ACH 相似时,求点P 的坐标.第1题图备用图参考答案一、基础过关1. 解:(1)把A (1,0),C (0,-3)代入y =x 2+bx +c 得,⎩⎪⎨⎪⎧1+b +c =0c =-3,解得⎩⎪⎨⎪⎧b =2c =-3, ∴抛物线的函数表达式为y =x 2+2x -3;(2)如解图,作点A 关于y 轴的对称点A ′,连接A ′C ,作AD ⊥A ′C 于点D , ∴点A ′的坐标为(-1,0), 则AA ′=2,OC =3,A ′C =10, ∵S △A ′AC =12AA ′·OC =12A ′C ·AD ,∴AD =AA ′·OC A ′C =3105,在Rt △A ′AD 中,∵A ′D 2+AD 2=A ′A 2, ∴A ′D 2+(3105)2=22.解得A ′D =105(负值已舍去), ∴DC =4105,∴tan ∠ACA ′=AD DC =34. 由对称可得∠ACD =2∠ACO ,则∠P AB =∠ACA ′, 设P (a ,a 2+2a -3),①如解图,当点P 在x 轴的上方时,作P 1H 1⊥x 轴于点H 1, ∴tan ∠P 1AB =P 1H 1AH 1=a 2+2a -31-a =34,解得a 1=1(舍),a 2=-154,把a =-154代入得P (-154,5716);②如解图,当点P 在x 轴的下方时,作P 2H 2⊥x 轴于点H 2, ∴tan ∠P 2AB =P 2H 2AH 2=-a 2-2a +31-a =34,解得a 3=1(舍),a 4=-94,把a =-94代入得P (-94,-3916),综上所述,点P 的坐标为(-154,5716)或(-94,-3916);第1题解图(3)是.设Q (m ,m 2+2m -3),则-3<m <1. 设直线AQ 的解析式为y =k 1x +b 1,把A (1,0),Q (m ,m 2+2m -3),代入解析式解得⎩⎪⎨⎪⎧k 1=m +3b 1=m -3, ∴y =(m +3)x -m -3, 当x =-1时,y =-2m -6, 设直线BQ 的解析式为y =k 2x +b 2,把B (-3,0),Q (m ,m 2+2m -3)代入y =k 2x +b 2,解得⎩⎪⎨⎪⎧k 2=m -1b 2=3m -3,∴y =(m -1)x +3m -3, 当x =-1时,y =2m -2, ∴DM =2m +6,DN =-2m +2, ∴DM +DN =2m +6-2m +2=8. 2. 解:(1)∵B (-1,0), ∴OB =1.又∵OA =OC =4OB , ∴OA =OC =4, ∴A (4,0),C (0,-4);(2)将A 、B 、C 三点坐标代入y =ax 2+bx +c 得,⎩⎪⎨⎪⎧16a +4b +c =0a -b +c =0c =-4,解得⎩⎪⎨⎪⎧a =1b =-3c =-4, ∴抛物线的解析式为y =x 2-3x -4;(3)如解图,过点P 作PE ⊥x 轴交AC 于点E , ∴PE ∥y 轴. ∵OA =OC ,∴∠PED =∠OCA =45°, ∴△DEP 为等腰直角三角形, ∴PD =22PE , ∴当PE 取得最大值时,PD 取得最大值, 易得直线AC 的解析式为y =x -4, 设P (x ,x 2-3x -4),则E (x ,x -4),则PE =(x -4)-(x 2-3x -4)=-x 2+4x =-(x -2)2+4, ∵0<x <4,∴当x =2时,PE 取得最大值,最大值为4, 此时PD 取得最大值,最大值为4×22=22,∴点P 的坐标为(2,-6).第2题解图二、能力提升1. 解:(1)∵抛物线与x 轴交于A ,B 两点,点A 的坐标为(2,0),抛物线的对称轴为直线x =-1, ∴点B 的坐标为(-4,0).∴设抛物线的函数表达式为y =a (x +4)(x -2),将点C (0,-2)代入得-8a =-2,解得a =14.∴抛物线的函数表达式为y =14(x +4)(x -2)=14x 2+12x -2;(2)设点P 的坐标为(x ,14x 2+12x -2),则点D 的坐标为(x ,0),设BC 所在直线的表达式为y =kx +b , 将B (-4,0),C (0,-2)代入得,⎩⎪⎨⎪⎧-4k +b =0b =-2,解得⎩⎪⎨⎪⎧k =-12b =-2, ∴BC 所在直线的表达式为y =-12x -2.∴点E 的坐标为(x ,-12x -2).∴PE =14x 2+x .∵PE =14OD ,∴14x 2+x =-14x ,即14x 2+54x =0, 解得x =-5或x =0(舍). ∴PE =54,BD =1,∴S △PBE =12PE ·BD =12×54×1=58;(3)存在.①当DM =DB =1时,如解图①,过点M 作MF ⊥x 轴于点F , 设M (m ,-12m -2),则MF =-12m -2,DF =-m -5,∵MF 2+DF 2=DM 2,∴(-12m -2)2+(-m -5)2=1,解得m =-285或m =-4(舍去).∴点M 的坐标为(-285,45);第1题解图①②当BD =BM =1时,如解图②,过点M 作x 轴的垂线,垂足为N , ∵DE ⊥x 轴, ∴DE ∥MN ,∴BN ∶BD =BM ∶BE ,∴BN ∶1=1∶BE . ∵E (-5,12),∴DE =12,∴BE =52, ∴BN ∶1=1∶52,解得BN =255. ∴点M 的横坐标为-4-255,将x =-4-255代入y =-12x -2,得y =55,即点M 的坐标为(-4-255,55).综上所述,点M 的坐标为(-285,45)或(-4-255,55).第1题解图②三、满分冲关1. 解:(1)A (-4,0),B (6,0),C (0,3),抛物线的解析式为y =-18x 2+14x +3;【解法提示】令y =-12x +3=0,解得x =6,令x =0,得y =3,∴B (6,0),C (0,3).∵抛物线的对称轴为x =1,且过点B 、A ,∴抛物线与x 轴的另一交点A 坐标为(-4,0),设抛物线的解析式为y =a (x +4)(x -6),将点C (0,3)代入得-24a =3,解得a =-18.∴y =-18(x +4)(x -6)=-18x 2+14x +3(2)如解图①,过点P 作PG ⊥x 轴于点G ,交BC 于点Q ,过点P 作PH ⊥BC 于点H . ∵OC =3,OB =6, ∴BC =OC 2+OB 2=3 5. 又∵∠HQP =∠GQB , ∴∠HPQ =∠CBO , ∴sin ∠HPQ =sin ∠CBO =55. 故点P 到直线BC 的距离最大,即PQ 最大. 设P (m ,-18m 2+14m +3),Q (m ,-12m +3),∴PQ =-18m 2+14m +3-(-12m +3)=-18(m -3)2+98.∵-18<0,∴当m =3时,PQ 有最大值为98.∴P (3,218);第1题解图①(3)存在.由(1)得A (-4,0)、B (6,0)、C (0,3), ∴AB =10,AC =32+42=5. 分为两种情况分类讨论:①当△ABC ∽△AQB 时,如解图②所示. ∴AC AB =ABAQ,∠CAB =∠BAQ . ∴AQ =AB 2AC =1025=20,过点Q 作QD ⊥x 轴,垂足为点D , ∴QD =AQ ·sin ∠BAQ =20×35=12,AD =AQ ·cos ∠BAQ =20×45=16.∴Q (12,-12).第1题解图②②当△ABC ∽△BQA 时,如解图③所示, ∴AB BQ =ACAB,∠CAB =∠ABQ . ∴BQ =AB 2AC=20,过点Q 作QE ⊥x 轴,垂足为E ,同理可得QE =BQ ·sin ∠ABQ =20×35=12,BE =BQ ·cos ∠ABQ =20×45=16, ∴Q (-10,-12).综上所述,点Q 的坐标是(12,-12)或(-10,-12).第1题解图③2、解:(1)抛物线y =-18x 2+12x +4, 令x =0,可得A 点的坐标为(0,4),令y =0,可得B 点的坐标为(-4,0),C 点的坐标为(8,0).易得直线AB 的函数解析式为y =x +4,∵OA =OB ,∴∠BAO =45°.又∵直线AD 由直线AB 逆时针旋转90°而来,∴∠BAD =90°,∴∠OAD =45°,△OAD 为等腰直角三角形,∴OD =OA =4,D (4,0),易得直线AD 的函数解析式为y =-x +4;(2)①如解图①,过点P 作PE ⊥x 轴交AD 于点E ,PF ⊥AD 于点F ,第1题解图①易得△PEF 为等腰直角三角形,∴PF =22PE , ∴当PE 取得最大值时,PF 取得最大值,设P (x ,-18x 2+12x +4), 则E (x ,-x +4),∴PE =-18x 2+12x +4-(-x +4)=-18x 2+32x =-18(x -6)2+92, ∴当x =6时,PE 有最大值92, 此时PF 有最大值924, ∴当x =6时,-18x 2+12x +4=52, ∴当点P 到直线AD 的距离最大时,点P 的坐标为(6,52),最大距离为924; ②如解图②,连接AP ,过点P 作PE ⊥x 轴,交AD 于点E ,PF ⊥AD 于点F ,当点P 到AD 的距离为524时,PF =524, 则此时PE =2PF =52, 将PE =52代入PE =-18(x -6)2+92中, 解得x 1=10,x 2=2,∴此时点P 的坐标为(10,-72)或(2,92), 当点P 的坐标为(2,92)时,AP =22+(92-4)2=172, ∴sin ∠P AD =524172=53434; 当点P 的坐标为(10,-72)时, AP =102+(-72-4)2=252, ∴sin ∠P AD =PF AP =524252=210. 综上,sin ∠P AD 的值是53434或210.3、1. 解:(1)把点A 、B 、D 的坐标分别代入抛物线的解析式中得:⎩⎪⎨⎪⎧a +b +c =09a -3b +c =0c =3,解得⎩⎪⎨⎪⎧a =-1b =-2c =3,∴抛物线的解析式为y =-x 2-2x +3,∴抛物线的对称轴为直线x =-b 2a=-1, ∴点C 的坐标为(-1,4);(2)如解图①,过点C 作CE ∥AD 交抛物线于点E ,交y 轴于点T ,则△ADE 与△ACD 面积相等,直线AD 过点D ,设其解析式为y =mx +3,将点A 的坐标代入得:0=-3m +3,解得m =1,则直线AD 的解析式为y =x +3,∵CE ∥AD ,设直线CE 的解析式为y =x +n ,将点C 的坐标代入上式得:4=-1+n ,解得n =5,则直线CE 的解析式为y =x +5,则点T 的坐标为(0,5),联立⎩⎪⎨⎪⎧y =-x 2-2x +3y =x +5, 解得x =-1或x =-2(x =-1为点C 的横坐标),即点E 的坐标为(-2,3);在y 轴取一点H ′,使DT =DH ′=2,过点H ′作直线E ′E ″∥AD ,则△ADE ′和△ADE ″都与△ACD 面积相等,同理可得直线E ′E ″的解析式为y =x +1,联立⎩⎪⎨⎪⎧y =-x 2-2x +3y =x +1, 解得x =-3±172, ∴点E ″、E ′的坐标分别为(-3+172,-1+172)、(-3-172,-1-172), 综上,满足要求的点E 的坐标为(-2,3)或(-3+172,-1+172)或(-3-172,-1-172);第1题解图①(3)如解图②,设点P 的坐标为(m ,n ),则n =-m 2-2m +3,把点C 、D 的坐标代入一次函数的解析式y =kx +b 得:⎩⎪⎨⎪⎧4=-k +b b =3, 解得⎩⎪⎨⎪⎧k =-1b =3, 即直线CD 的解析式为y =-x +3,由(1)得,直线AD 的解析式为y =x +3,∴AD ⊥CD ,而直线PQ ⊥CD ,故直线PQ 的解析式中的k 值与直线AD 的解析式中的k 值相同, 同理可得直线PQ 的解析式为y =x +(n -m ),联立⎩⎪⎨⎪⎧y =-x +3y =x +(n -m ), 解得x =3+m -n 2,即点Q 的坐标为(3+m -n 2,3-m +n 2), 则PQ 2=(m -3+m -n 2)2+(n -3-m +n 2)2=(m +n -3)22=12(m +1)2·m 2, 同理可得:PC 2=(m +1)2[1+(m +1)2],AH =2,CH =4,则AC =25,当△ACH ∽△CPQ 时,PC PQ =AC CH =52, 即4PC 2=5PQ 2,整理得3m 2+16m +16=0,解得m =-4或m =-43, ∴点P 的坐标为(-4,-5)或(-43,359); 当△ACH ∽△PCQ 时,同理可得,点P 的坐标为(-23,359)或(2,-5), 综上所述,点P 的坐标为(-4,-5)或(-43,359)或(-23,359)或(2,-5).第1题解图②。
2020中考数学 压轴专题:二次函数与几何综合(含答案)

又∵抛物线的对称轴为 x=b2=1,即 b=2,
∴m-2+2m+1=2,解得 m=1,
∴c=3,
∴抛物线的解析式为 y=-x2+2x+3;
y=-x2+2x+3
(2)由y=kx+2
可得:x2+(k-2)x-1=0,
∴x1+x2=2-k,x1x2=-1,
∴|x1-x2|= (x1+x2)2-4x1x2= (2-k)2+4≥2,
1 / 18
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
=O′C,∴CO′+PB′=P′O′+O′C′≥P′C′, 又由(1)易知 P(1,4), ∵P′P=O′B′=OB=3,C(0,3), ∴P′(-2,4),C′(0,-3),PC= 2, ∴直线 P′C′的解析式为 y=-72x-3, 直线 P′C′与 x 轴的交点为(-67,0), ∵PC,O′B′为定值, ∴当 CO′+PB′取最小值 P′C′时 L 最小, 此时 O′(-67,0),则 B′(175,0). 又∵P′C′= (4+3)2+22= 53, ∴L 最小值=P′C′+PC+O′B′= 53+ 2+3.
第 3 题解图② ①当∠AFP=90°时,即∠AF1P1=90°, ∴点 P1 既在 x 轴上,又在抛物线上,则点 P1 与点 B 重合,点 P1 的坐标为(1,0); ②当∠FAP=90°时,即∠F2AP2=90°,则∠P2AO=45°,设 AP2 与 y 轴的交点为点 N, ∴OA=ON=3,则 N(0,-3), ∴直线 AP2 的解析式为 y=-x-3,
y=-x-3 联立抛物线与直线 AP2 的解析式,得方程组y=-x2-2x+3,
x=-3 x=2 解得y=0 或y=-5, ∵A(-3,0), ∴P2(2,-5); ③当∠APF=90°时,即∠AP3F3=90°,点 P3 既在 x 轴上,又在抛物线上,则点 P3 与点 B 重合,点 P3 的坐标为(1,0).
中考复习专题8二次函数与矩形存在性问题(含解析)

专题8二次函数与矩形存在性问题1.矩形的判定:(1)有一个角是直角的平行四边形是矩形;(2)对角线相等的平行四边形是矩形;(3)有三个角为直角的四边形是矩形.2.题型分析矩形除了具有平行四边形的性质之外,还有“对角线相等”或“一个角为直角”,因此相比起平行四边形,坐标系中的矩形满足以下3个等式:因此在矩形存在性问题最多可以有3个未知量,代入可以得到三元一次方程组,可解.确定了有3个未知量,则可判断常见矩形存在性问题至少有2个动点,多则可以有3个.下:同时,也可以先根据A、B的坐标求出直线AB的解析式,进而得到直线AD或BC的解析式,从而确定C 或D的坐标.【例1】(2022•泸州)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+x+c经过A(﹣2,0),B(0,4)两点,直线x=3与x轴交于点C.(1)求a,c的值;(2)经过点O的直线分别与线段AB,直线x=3交于点D,E,且△BDO与△OCE的面积相等,求直线DE的解析式;(3)P是抛物线上位于第一象限的一个动点,在线段OC和直线x=3上是否分别存在点F,G,使B,F,G,P为顶点的四边形是以BF为一边的矩形?若存在,求出点F的坐标;若不存在,请说明理由.【分析】(1)把A(﹣2,0),B(0,4)两点代入抛物线y=ax2+x+c中列方程组解出即可;(2)利用待定系数可得直线AB的解析式,再设直线DE的解析式为:y=mx,点D是直线DE和AB的交点,列方程可得点D的横坐标,根据△BDO与△OCE的面积相等列等式可解答;(3)设P(t,﹣t2+t+4),分两种情况:作辅助线构建相似三角形,证明三角形相似或利用等角的三角函数列等式可解答.【解答】解:(1)把A(﹣2,0),B(0,4)两点代入抛物线y=ax2+x+c中得:解得:;(2)由(1)知:抛物线解析式为:y=﹣x2+x+4,设直线AB的解析式为:y=kx+b,则,解得:,∴AB的解析式为:y=2x+4,设直线DE的解析式为:y=mx,∴2x+4=mx,∴x=,当x=3时,y=3m,∴E(3,3m),∵△BDO与△OCE的面积相等,CE⊥OC,∴•3•(﹣3m)=•4•,∴9m2﹣18m﹣16=0,∴(3m +2)(3m ﹣8)=0,∴m 1=﹣,m 2=(舍),∴直线DE 的解析式为:y =﹣x ;(3)存在,B ,F ,G ,P 为顶点的四边形是以BF 为一边的矩形有两种情况:设P (t ,﹣t 2+t +4),①如图1,过点P 作PH ⊥y 轴于H ,∵四边形BPGF 是矩形,∴BP =FG ,∠PBF =∠BFG =∴∠CFG +∠BFO =∠BFO +∠OBF =∠CFG +∠CGF =∠OBF +∠PBH =90°,∴∠PBH =∠OFB =∠CGF ,∵∠PHB =∠FCG =90°,∴△PHB ≌△FCG (AAS ),∴PH =CF ,∴CF =PH =t ,OF =3﹣t ,∵∠PBH =∠OFB ,∴=,即=,解得:t 1=0(舍),t 2=1,∴F (2,0);②如图2,过点G作GN⊥y轴于N,过点P作PM⊥x轴于M,同①可得:NG=FM=3,OF=t﹣3,∵∠OFB=∠FPM,∴tan∠OFB=tan∠FPM,∴=,即=,解得:t1=,t2=(舍),∴F(,0);综上,点F的坐标为(2,0)或(,0).【例2】(2022•绥化)如图,抛物线y=ax2+bx+c交y轴于点A(0,﹣4),并经过点C(6,0),过点A作AB⊥y轴交抛物线于点B,抛物线的对称轴为直线x=2,D点的坐标为(4,0),连接AD,BC,BD.点E从A点出发,以每秒个单位长度的速度沿着射线AD运动,设点E的运动时间为m秒,过点E作EF⊥AB于F,以EF为对角线作正方形EGFH.(1)求抛物线的解析式;(2)当点G随着E点运动到达BC上时,求此时m的值和点G的坐标;(3)在运动的过程中,是否存在以B,G,C和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G的坐标,如果不存在,请说明理由.【分析】(1)根据抛物线的对称轴为直线x=2,可得出抛物线与x轴的另一个交点的坐标为(﹣2,0),列出交点式,再将点A(0,﹣4)可得出抛物线的解析式;(2)根据可得出△ABD是等腰直角三角形,再根据点E的运动和正方形的性质可得出点H,F,G的坐标,根据点B,C的坐标可得出直线BC的解析式,将点G代入直线BC的解析式即可;(3)若存在,则△BGC是直角三角形,则需要分类讨论,当点B为直角顶点,当点G为直角顶点,当点C为直角顶点,分别求解即可.【解答】解:(1)∵抛物线的对称轴为直线x=2,D点的坐标为(4,0),∴抛物线与x轴的另一个交点为(﹣2,0),∴抛物线的解析式为:y=a(x+2)(x﹣6),将点A(0,﹣4)解析式可得,﹣12a=﹣4,∴a=.∴抛物线的解析式为:y=(x+2)(x﹣6)=x2﹣x﹣4.(2)∵AB⊥y轴,A(0,﹣4),∴点B的坐标为(4,﹣4).∵D(4,0),∴AB=BD=4,且∠ABD=90°,∴△ABD是等腰直角三角形,∠BAD=45°.∵EF⊥AB,∴∠AFE=90°,∴△AEF是等腰直角三角形.∵AE=m,∴AF=EF=m,∴E(m,﹣4+m),F(m,﹣4).∵四边形EGFH是正方形,∴△EHF是等腰直角三角形,∴∠HEF=∠HFE=45°,∴FH是∠AFE的角平分线,点H是AE的中点.∴H(m,﹣4+m),G(m,﹣4+m).∵B(4,﹣4),C(6,0),∴直线BC的解析式为:y=2x﹣12.当点G随着E点运动到达BC上时,有2×m﹣12=﹣4+m.解得m=.∴G(,﹣).(3)存在,理由如下:∵B(4,﹣4),C(6,0),G(m,﹣4+m).∴BG2=(4﹣m)2+(m)2,BC2=(4﹣6)2+(﹣4)2=20,CG2=(6﹣m)2+(﹣4+m)2.若以B,G,C和平面内的另一点为顶点的四边形是矩形,则△BGC是直角三角形,∴分以下三种情况:①当点B为直角顶点时,BG2+BC2=CG2,∴(4﹣m)2+(m)2+20=(6﹣m)2+(﹣4+m)2,解得m=,∴G(,﹣);②当点C为直角顶点时,BC2+CG2=BG2,∴20+(6﹣m )2+(﹣4+m )2=(4﹣m )2+(m )2,解得m =,∴G (,﹣);③当点G 为直角顶点时,BG 2+CG 2=BC 2,∴(4﹣m )2+(m )2+(6﹣m )2+(﹣4+m )2=20,解得m =或2,∴G (3,﹣3)或(,﹣);综上,存在以B ,G ,C 和平面内的另一点为顶点的四边形是矩形,点G 的坐标为(,﹣)或(,﹣)或(3,﹣3)或(,﹣).【例3】(2022•黔东南州)如图,抛物线y =ax 2+2x +c 的对称轴是直线x =1,与x 轴交于点A ,B (3,0),与y 轴交于点C ,连接AC .(1)求此抛物线的解析式;(2)已知点D 是第一象限内抛物线上的一个动点,过点D 作DM ⊥x 轴,垂足为点M ,DM 交直线BC 于点N ,是否存在这样的点N ,使得以A ,C ,N 为顶点的三角形是等腰三角形.若存在,请求出点N 的坐标,若不存在,请说明理由;(3)已知点E 是抛物线对称轴上的点,在坐标平面内是否存在点F ,使以点B 、C 、E 、F 为顶点的四边形为矩形,若存在,请直接写出点F 的坐标;若不存在,请说明理由.【分析】(1)由抛物线的对称轴为直线x =1,抛物线经过点B (3,0),可得A (﹣1,0),用待定系数法即可求解;(2)求出直线BC的解析式,设点D坐标为(t,﹣t2+2t+3),则点N(t,﹣t+3),利用勾股定理表示出AC2,AN2,CN2,然后分①当AC=AN时,②当AC=CN时,③当AN=CN时三种情况进行讨论,列出关于t的方程,求出t的值,即可写出点N的坐标;(3)分两种情形讨论:①当BC为对角线时,②当BC为边时,先求出点E的坐标,再利用平行四边形的中心对称性求出点F的坐标即可.【解答】解:(1)抛物线y=ax2+2x+c的对称轴是直线x=1,与x轴交于点A,B(3,0),∴A(﹣1,0),∴,解得,∴抛物线的解析式y=﹣x2+2x+3;(2)∵y=﹣x2+2x+3,∴C(0,3),设直线BC的解析式为y=kx+3,将点B(3,0)代入得:0=3k+3,解得:k=﹣1,∴直线BC的解析式为y=﹣x设点D坐标为(t,﹣t2+2t+3),则点N(t,﹣t+3),∵A(﹣1,0),C(0,3),∴AC2=12+32=10,AN2=(t+1)2+(﹣t+3)2=2t2﹣4t+10,CN2=t2+(3+t﹣3)2=2t2,①当AC=AN时,AC2=AN2,∴10=2t2﹣4t+10,解得t1=2,t2=0(不合题意,舍去),∴点N的坐标为(2,1);②当AC=CN时,AC2=CN2,∴10=2t2,解得t1=,t2=﹣(不合题意,舍去),∴点N的坐标为(,3﹣);③当AN=CN时,AN2=CN2,∴2t2﹣4t+10=2t2,解得t=,∴点N的坐标为(,);综上,存在,点N的坐标为(2,1)或(,3﹣)或(,);(3)设E(1,a),F(m,n),∵B(3,0),C(0,3),∴BC=3,①以BC为对角线时,BC2=CE2+BE2,∴(3)2=12+(a﹣3)2+a2+(3﹣1)2,解得:a=,或a=,∴E(1,)或(1,),∵B(3,0),C(0,3),∴m+1=0+3,n+=0+3或n+=0+3,∴m=2,n=或n=,∴点F的坐标为(2,)或(2,);②以BC为边时,BE2=CE2+BC2或CE2=BE2+BC2,∴a2+(3﹣1)2=12+(a﹣3)2+(3)2或12+(a﹣3)2=a2+(3﹣1)2+(3)2,解得:a=4或a=﹣2,∴E(1,4)或(1,﹣2),∵B(3,0),C(0,3),∴m+0=1+3,n+3=0+4或m+3=1+0,n+0=3﹣2,∴m=4,n=1或m=﹣2,n=1,∴点F的坐标为(4,1)或(﹣2,1),综上所述:存在,点F的坐标为(2,)或(2,)或(4,1)或(﹣2,1).【例4】(2022•梁山县一模)如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.(1)试求抛物线的解析式;(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=,试求m的最大值及此时点P的坐标;(3)在(2)的条件下,m取最大值时,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.【分析】(1)因为抛物线y=ax2+bx+c经过A(﹣2,0)、B(4,0)两点,所以可以假设y=a(x+2)(x ﹣4),求出点C坐标代入求出a即可;(2)由△CMD∽△FMP,可得m==,根据关于m关于x的二次函数,利用二次函数的性质即可解决问题;(3)存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形.分两种情形分别求解即可:①当DP是矩形的边时,有两种情形;②当DP是对角线时;【解答】解:(1)因为抛物线y=ax2+bx+c经过A(﹣2,0)、B(4,0)两点,所以可以假设y=a(x+2)(x﹣4),∵OC=2OA,OA=2,∴C(0,4),代入抛物线的解析式得到a=﹣,∴y=﹣(x+2)(x﹣4)或y=﹣x2+x+4或y=﹣(x﹣1)2+.(2)如图1中,由题意,点P在y轴的右侧,作PE⊥x轴于E,交BC于F.∵CD∥PE,∴△CMD∽△FMP,∴m==,∵直线y=kx+1(k>0)与y轴交于点D,则D(0,1),∵BC的解析式为y=﹣x+4,设P(n,﹣n2+n+4),则F(n,﹣n+4),∴PF=﹣n2+n+4﹣(﹣n+4)=﹣(n﹣2)2+2,∴m==﹣(n﹣2)2+,∵﹣<0,∴当n=2时,m有最大值,最大值为,此时P(2,4).(3)存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形.①当DP是矩形的边时,有两种情形,a、如图2﹣1中,四边形DQNP是矩形时,有(2)可知P(2,4),代入y=kx+1中,得到k=,∴直线DP的解析式为y=x+1,可得D(0,1),E(﹣,0),由△DOE∽△QOD可得=,∴OD2=OE•OQ,∴1=•OQ,∴OQ=,∴Q(,0).根据矩形的性质,将点P向右平移个单位,向下平移1个单位得到点N,∴N(2+,4﹣1),即N(,3)b、如图2﹣2中,四边形PDNQ是矩形时,∵直线PD的解析式为y=x+1,PQ⊥PD,∴直线PQ的解析式为y=﹣x+,∴Q(8,0),根据矩形的性质可知,将点D向右平移6个单位,向下平移4个单位得到点N,∴N(0+6,1﹣4),即N(6,﹣3).②当DP是对角线时,设Q(x,0),则QD2=x2+1,QP2=(x﹣2)2+42,PD2=13,∵Q是直角顶点,∴QD2+QP2=PD2,∴x2+1+(x﹣2)2+16=13,整理得x2﹣2x+4=0,方程无解,此种情形不存在,综上所述,满足条件的点N坐标为(,3)或(6,﹣3).1.(2022•武功县模拟)在平面直角坐标系中,已知抛物线L1:y=﹣x2+bx+c(b、c为常数)与x轴交于A (﹣6,0)、B(2,0)两点.(1)求抛物线L1的函数表达式;(2)将该抛物线L1向右平移4个单位长度得到新的抛物线L2,与原抛物线L1交于点C,点D是点C 关于x轴的对称点,点N在平面直角坐标系中,请问在抛物线L2上是否存在点M,使得以点C、D、M、N为顶点的四边形是以CD为边的矩形?若存在,求出点M的坐标;若不存在,请说明理由.【分析】(1)利用待定系数法直接求解即可;(2)存在,根据题意求得抛物线L2的表达式,再与抛物线L1联立,求得点C的坐标,进而求得点D的坐标;要使得以点C、D、M、N为顶点的四边形是以CD为边的矩形,分当M在x轴上方时和当M在x轴下方时,两种情况讨论,根据矩形的性质列出方程,求解即可.【解答】解:(1)把A(﹣6,0)、B(2,0)代入y=﹣x2+bx+c中,得,解得,∴抛物线L1的函数表达式为y=﹣x2﹣4x+12;(2)存在,理由如下:∵y=﹣x2﹣4x+12=﹣(x+2)+16,∴抛物线L2的函数表达式为y=﹣(x+2﹣4)2+16=﹣(x﹣2)2+16=﹣x2+4x+12,令﹣x2﹣4x+12=﹣x2+4x+12,解得:x=0,当x=0时,y=﹣x2﹣4x+12=12,∴点C的坐标为(0,12),∵点D是点C关于x轴的对称点,∴点D坐标为(0,﹣12),①当M在x轴上方时,要使得以点C、D、M、N为顶点的四边形是以CD为边的矩形,则y M=y C,即﹣x2+4x+12=12,解得:x1=0,x2=4,∴M1(4,12);②当M在x轴下方时,要使得以点C、D、M、N为顶点的四边形是以CD为边的矩形,则y M=y D,即﹣x2+4x+12=﹣12,解得:x1=2+2,x2=2﹣2,M2(2+2,﹣12),M3(2﹣2,﹣12).综上所述,在抛物线L2上是否存在点M,使得以点C、D、M、N为顶点的四边形是以CD为边的矩形,点M的坐标为(4,12)或(2+2,﹣12)或(2﹣2,﹣12).2.(2022•东莞市校级一模)如图,在平面直角坐标系中,抛物线y=+bx+c与x轴的正半轴交于点D,与y轴交于点C,点A在抛物线上,AB⊥y轴于点B.△ABC绕点B逆时针旋转90°得到△OBE,连接DE.当+bx+c<0时,x的取值范围是﹣<x<2.(1)求该抛物线的解析式;(2)求证:四边形OBED是矩形;(3)在线段OD上找一点N,过点N作直线m垂直x轴,交OE于点F,连接DF,当△DNF的面积取得最大值时,求点N的坐标,在此基础上,在直线m上找一点P,连接OP、DP.使得∠OPD+∠DOE =90°,求点P的坐标.【分析】(1)由题意可知抛物线与x轴的两个交点为(2,0),(﹣,0),再将两个点代入解析式即可求解;(2)由旋转是性质,可得OB=AB,则设A(﹣m,m),求出A点坐标,由此可得BE=OD,再由BE ∥OD,OB⊥OD即可证明;(3)设N(n,0),则F(n,n),则S=﹣(n﹣1)2+,可知当n=1时,S有最大值,此时N(1,0),F(1,),通过已知可推导出∠OPN=∠POE,从而得到PF=OF,设P(1,t),则|t﹣|=,求出t的值即可求点P的坐标.【解答】(1)解:∵当+bx+c<0时,x的取值范围是﹣<x<2,∴抛物线与x轴的两个交点为(2,0),(﹣,0),∴,解得,∴y=﹣x﹣1;(2)证明:由(1)可知D(2,0),C(0,﹣1),∴OD=2,OC=1,∵AB⊥y轴,∴△ABC是直角三角形,∵△ABC绕点B逆时针旋转90°得到△OBE,∴OB⊥BE,AB=OB,设A(﹣m,m),∴m=m2﹣m﹣1,解得m=﹣1或m=,∴A(﹣1,1),∴BO=1,∴BC=BE=2,∴BE=OD,∵∠BOD=90°,∴BE∥OD,∴四边形OBED是矩形;(3)∵E(2,1),∴直线OE的解析式为y=x,设N(n,0),则F(n,n),∴S=×DN×FN=×(2﹣n)×n=﹣(n﹣1)2+,∵N在线段OD上,∴0≤n≤2,∴当n=1时,S有最大值,此时N(1,0),F(1,),∵∠PNO=90°,∴∠EOD+∠POE=90°,∵∠OPD+∠DOE=90°,∴∠POE+∠OPN=∠OPD,∵O点与D点关于l对称,∴∠OPN=∠NPD,∴∠OPN=∠POE,∴PF=OF,设P(1,t),∴|t﹣|=,∴t=+或t=﹣+,∴P点坐标为(1,+)或(1,﹣+).3.(2022•石家庄二模)如图,抛物线y=﹣x2+bx+c(c≠0)与x轴交于点A(﹣1,0),B(点A在点B左侧),与y轴交于点C,连接BC.(1)点C的纵坐标为b+1(用含b的式子表示),∠OBC=45度;(2)当b=1时,若点P为第一象限内抛物线上一动点,连接BP,CP,求△BCP面积的最大值,并求出此时点P的坐标;(3)已知矩形ODEF的顶点D,F分别在x轴、y轴上,点E的坐标为(3,2).①抛物线的顶点为Q,当AQ的中点落在直线EF上时,求点Q的坐标;②当抛物线在矩形内部的部分对应的函数值y随x的增大而减小时,请直接写出b的取值范围.【分析】(1)将(﹣1,0)代入解析式可得c与b的关系,从而可得OB=OC,进而求解.(2)由b=1可得抛物线解析式及点B,C坐标,根据待定系数法求出直线BC解析式,设点P坐标为(m,﹣m2+m+2),作PE⊥x轴交BC于点E,连接PC,PB,由S△BCP=S△CEP+S△BEP求解.(3)①将二次函数解析式化为顶点式可得点Q坐标,由点A,Q坐标可得A,Q中点坐标,进而求解.②根据抛物线与y轴交点的位置及抛物线对称轴的位置,结合图象求解.【解答】解:(1)将(﹣1,0)代入y=﹣x2+bx+c得0=﹣1﹣b+c,解得c=b+1,∴y=﹣x2+bx+b+1,设点B坐标为(x2,0),则抛物线对称轴为直线x==,解得x2=b+1,∴点B坐标为(b+1,0),∴OC=OB=b+1,∴∠OBC=45°,故答案为:b+1,45.(2)当b=1时,y=﹣x2+x+2,作PE⊥x轴交BC于点E,连接PC,PB,设直线BC解析式为y=kx+b,将B(2,0),(0,2)代入y=kx+b得,解得,∴y=﹣x+2.设点P坐标为(m,﹣m2+m+2),则点E坐标为(m,﹣m+2),∴PE=﹣m2+2m,=S△CEP+S△BEP=PE•x P+PE(x B﹣x P)=PE•x B=﹣m2+2m=﹣(m﹣1)2+1,∵S△BCP∴m=1时,△BCP面积的最大为1,此时点P坐标为(1,2).(3)①∵y=﹣x2+bx+b+1=﹣(x﹣)2++b+1,∴点Q坐标为(,+b+1),∵A(﹣1,0),∴点A,Q中点坐标为(﹣+,++),∴++=2,解得b=2或b=﹣6,当b=2时,点Q坐标为(1,4),当b=﹣6时,点Q坐标为(﹣3,4).②∵E(3,2),∴点F坐标为(0,2),将(0,2)代入y=﹣x2+bx+b+1得b+1=2,解得b=1,将E(3,2)代入y=﹣x2+bx+b+1得2=﹣9+4b+1,解得b=,∴1≤b<,满足题意.当抛物线顶点Q(,+b+1)落在y轴上时,=0,解得b=0,当抛物线经过原点时,0=b+1,解得b=﹣1,∴﹣1<b≤0符合题意.综上所述,1≤b<或﹣1<b≤0.4.(2022•滨海县一模)如图1,在平面直角坐标中,抛物线与x轴交于点A(﹣1,0)、B (4,0)两点,与y轴交于点C,连接BC,直线BM:y=2x+m交y轴于点M.P为直线BC上方抛物线上一动点,过点P作x轴的垂线,分别交直线BC、BM于点E、F.(1)求抛物线的表达式:(2)当点P落在抛物线的对称轴上时,求△PBC的面积:(3)①若点N为y轴上一动点,当四边形BENF为矩形时,求点N的坐标;②在①的条件下,第四象限内有一点Q,满足QN=QM,当△QNB的周长最小时,求点Q的坐标.【分析】(1)根据抛物线与x轴交于点A(﹣1,0)、B(4,0)两点,即知抛物线的表达式为:y=﹣(x+1)(x﹣4),即y=﹣x2+x+2;(2)由y=﹣x2+x+2求出P(,),由B(4,0),C(0,2)得直线BC的表达式为y=﹣x+2,从而可得E(,),PE=﹣=,即可得△PBC的面积是;(3)①过点N作NG⊥EF于点G,求得直线BM的表达式为:y=2x﹣8即知M(0,﹣8),设E(a,﹣a+2),则F(a,2a﹣8),证明△NEG≌△BFH(AAS),可得NG=BH,EG=FH,即有a=4﹣a,解得F(2,﹣4),E(2,1),从而可得N(0,﹣3);②取MN的中点D,由QN=QM,知点Q在MN的垂直平分线上,又C△QNB=BQ+NQ+BN=BQ+NQ+5最小,只需BQ+MQ最小,即点B、Q、M共线,此时,点Q即为MN的垂=BQ+MQ+5,故要使C△QNB直平分线与直线BM的交点,由N(0,﹣3),M(0,﹣8),得D(0,﹣),即可得Q(,﹣).【解答】解:(1)∵抛物线与x轴交于点A(﹣1,0)、B(4,0)两点,∴抛物线的表达式为:y=﹣(x+1)(x﹣4),即y=﹣x2+x+2;(2)如图:∵点P落在抛物线y=﹣x2+x+2的对称轴上,∴P为抛物线y=﹣x2+x+2的顶点,∵y=﹣x2+x+2=﹣(x﹣)2+,∴P(,),在y=﹣x2+x+2中,令x=0得y=2,∴C(0,2)由B(4,0),C(0,2)得直线BC的表达式为y=﹣x+2,把x=代入y=﹣x+2得y=,∴E(,),∴PE=﹣=,=PE•|x B﹣x C|=××4=,∴S△PBC答:△PBC的面积是;(3)①过点N作NG⊥EF于点G,如图:∵y=2x+m过点B(4,0),∴0=2×4+m,解得m=﹣8,∴直线BM的表达式为:y=2x﹣8,∴M(0,﹣8),设E(a,﹣a+2),则F(a,2a﹣8),∵四边形BENF为矩形,∴∠NEG=∠BFH,NE=BF,又∠NGE=90°=∠BHF,∴△NEG≌△BFH(AAS),∴NG=BH,EG=FH,而NG=a,BH=OB﹣OH=4﹣a,∴a=4﹣a,解得a=2,∴F(2,﹣4),E(2,1),∴EH=1,∵EG=FH,∴EF﹣EG=EF﹣FH,即GF=EH=1,∵F(2,﹣4),∴G(2,﹣3),∴N(0,﹣3);②取MN的中点D,如图:∵QN=QM,∴点Q在MN的垂直平分线上,又∵B(4,0),N(0,﹣3),∴BN=5,=BQ+NQ+BN=BQ+NQ+5=BQ+MQ+5,∴C△QNB最小,只需BQ+MQ最小,∴要使C△QNB∴当点B、Q、M共线时,△QNB的周长最小,此时,点Q即为MN的垂直平分线与直线BM的交点,∵N(0,﹣3),M(0,﹣8),∴D(0,﹣),在y=2x﹣8中,令y=﹣得:﹣=2x﹣8,解得x=,∴Q(,﹣).5.(2022•石家庄模拟)某公园有一个截面由抛物线和矩形构成的观景拱桥,如图1所示,示意图如图2,且已知图2中矩形的长AD为12米,宽AB为4米,抛物线的最高处E距地面BC为8米.(1)请根据题意建立适当的平面直角坐标系,并求出抛物线的函数解析式;(2)若观景拱桥下放置两根长为7米的对称安置的立柱,求这两根立柱之间的水平距离;(3)现公园管理处打算在观景桥侧面搭建一个矩形“脚手架”PQMN(如图2),对观景桥表面进行维护,P,N点在抛物线上,Q,M点在BC上,为了筹备材料,需求出“脚手架”三根支杆PQ,PN,MN的长度之和的最大值,请你帮管理处计算一下.【分析】(1)以CB所在的直线为x轴,点E为顶点建立直角坐标系,用待定系数法求解即可;(2)确定立柱的纵坐标,解方程可得答案;(3)设N(m,﹣m2+8),则PN=2m,MN=PQ=﹣m2+8,三根支杆的总长度w=﹣m2+2m+16,【解答】解:(1)如图,以CB所在的直线为x轴,点E为顶点建立直角坐标系,由题意得,E(0,8),A(﹣6,4),设抛物线的解析式为y=ax2+c,代入可得,解得,∴y=﹣x2+8;(2)依题意可得﹣x2+8=7,解得x=±3,∴3﹣(﹣3)=6(米),答:这两根立柱之间的水平距离是6米;(3)设N(m,﹣m2+8),则PN=2m,MN=PQ=﹣m2+8,∴三根支杆的总长度w=PQ+PN+MN+2m+2(﹣m2+8)=﹣m2+2m+16,∵a=﹣<0,∴m=﹣=4.5时,w最大=20.5,∴三根支杆PQ,PN,MN的长度之和的最大值为20.5米.6.(2022•朝阳区校级一模)已知二次函数y=x2﹣2mx﹣m与y轴交于点M,直线y=m+5与y轴交于点A,与直线x=4交于点B,直线y=﹣2m与y轴交于点D(A与D不重合),与直线x=4交于点C,构建矩形ABCD.(1)当点M在线段AD上时,求m的取值范围.(2)求证:抛物线y=x2﹣2mx﹣m与直线y=m+5恒有两个交点.(3y随着x的增大而增大或y随x的增大而减小时,求m的取值范围.(4)当抛物线在矩形内部(包括边界)最高点的横坐标等于点B到x轴距离的时,直接写出m的取值范围.【分析】(1)由题意得:M(0,﹣m),A(0,m+5),D(0,﹣2m),分两种情况:当m+5>﹣2m,即m>﹣时,当m+5<﹣2m,即m<﹣时,分别根据“点M在线段AD上”,列出不等式求解即可;(2)由题意得:x2﹣2mx﹣2m﹣5=0,根据根的判别式即可证得结论;(3)由题意得:抛物线的对称轴为直线x=m,顶点坐标为(m,﹣m2﹣m),开口向上,分三种情况:①当m+5<﹣2m,即m<﹣时,②当m+5>﹣2m,即﹣<m≤0时,③当16﹣9m≤﹣2m,即m≥时,分别画出图形讨论即可;(4)由题意得:抛物线y=x2﹣2mx﹣m在矩形ABCD中的最高点的横坐标x的范围是0≤x≤4,点B(4,m+5)到x轴的距离为|m+5|,根据“抛物线在矩形内部(包括边界)最高点的横坐标等于点B到x轴距离的”分三种情况:①当m <﹣5时,抛物线在矩形内部(包括边界)最高点的坐标为(﹣m ﹣,﹣2m ),②当﹣5≤m <时,抛物线在矩形内部(包括边界)最高点的坐标为(m +,﹣2m ),③当m >﹣,且16﹣9m ≥m +5,即﹣<m ≤时,抛物线在矩形内部(包括边界)最高点的坐标为(m +,m +5),分别代入抛物线解析式求解即可.【解答】(1)解:由题意得:M (0,﹣m ),A (0,m +5),D (0,﹣2m ),当m +5>﹣2m ,即m >﹣时,∵点M 在线段AD 上,∴﹣2m <﹣m <m +5,∴m >0;当m +5<﹣2m ,即m <﹣时,∵点M 在线段AD 上,∴m +5<﹣m <﹣2m ,∴m <;综上所述,m 的取值范围为m >0或m <.(2)证明:当x 2﹣2mx ﹣m =+5时,整理得:x 2﹣2mx ﹣2m ﹣5=0,Δ=(﹣2m )2﹣4×1×(﹣2m ﹣5)=4(m +1)2+16,∵4(m +1)2≥0,∴4(m +1)2+16>0,∴抛物线y =x 2﹣2mx ﹣m 与直线y =m +5恒有两个交点.(3)解:∵y =x 2﹣2mx ﹣m =(x ﹣m )2﹣m 2﹣m ,∴该抛物线的对称轴为直线x =m ,顶点坐标为(m ,﹣m 2﹣m ),开口向上,与y 轴的交点M (0,﹣m ),①当m +5<﹣2m ,即m <﹣时,如图1,此时抛物线在矩形内部的函数值y随着x的增大而增大;②当m+5>﹣2m,即﹣<m≤0时,如图2,此时抛物线在矩形内部的函数值y随着x的增大而增大;③当m>0时,如图3,令x=4,则y=16﹣8m﹣m=16﹣9m,当16﹣9m≤﹣2m,即m≥时,抛物线在矩形内部(不包括边界)的函数值y随着x的增大而减小;综上,m的取值范围为m<﹣或﹣<m≤0或m≥.(4)解:由题意得:抛物线y=x2﹣2mx﹣m在矩形ABCD中的最高点的横坐标x的范围是0≤x≤4,点B(4,m+5)到x轴的距离为|m+5|,当x=4时,y=16﹣9m,∵抛物线在矩形内部(包括边界)最高点的横坐标等于点B到x轴距离的,∴抛物线在矩形内部(包括边界)最高点的横坐标为|m+5|,①当m<﹣5时,抛物线在矩形内部(包括边界)最高点的坐标为(﹣m﹣,﹣2m),∴﹣2m=(﹣m﹣)2﹣2m(﹣m﹣)﹣m,解得:m=,∵m<﹣5,∴m=﹣;②当﹣5≤m<时,抛物线在矩形内部(包括边界)最高点的坐标为(m+,﹣2m),∴﹣2m=(m+)2﹣2m(m+)﹣m,解得:m=﹣1,∵﹣5≤m<,∴m=﹣1﹣;③当m>﹣,且16﹣9m≥m+5,即﹣<m≤时,抛物线在矩形内部(包括边界)最高点的坐标为(m +,m +5),∴m +5=(m +)2﹣2m (m +)﹣m ,解得:m =﹣3,∵﹣<m ≤,∴m =﹣3+;综上所述,m 的值为﹣或﹣1﹣或﹣3+.7.(2022•长春一模)已知抛物线y =x 2﹣2mx +2m +1.(1)写出抛物线y =x 2﹣2mx +2m +1的顶点坐标(用含m 的式子表示).(2)当x ≥1时,y 随x 的增大而增大,则m 的取值范围是m ≤1.(3)当﹣1≤x ≤2时,函数y =x 2﹣2mx +2m +1的图象记为G ,设图象G 的最低点的纵坐标为y 0.当y 0=﹣1时,求m 的值.(4)当m >0时,分别过点A (2,1)、B (2,4)作y 轴垂线,垂足分别为点D 、点C ,抛物线在矩形ABCD 内部的图象(包括边界)的最低点到直线y =﹣2的距离等于最高点到x 轴的距离,直接写出m 的值.【分析】(1)由y =(x ﹣m )2﹣m 2+2m +1,即可求解;(2)由抛物线的图象可得m ≤y 随x 的增大而增大;(3)分三种情况讨论:当m <﹣1时,y 0=2+4m =﹣1,解得m =﹣(舍);当m >2时,x =2,函数有最小值,y 0=5﹣2m =﹣1,解得m =3;当﹣1≤m ≤2时,y 0=﹣m 2+2m +1=﹣1,解得m =+1(舍)或m =﹣+1;(4)分五种情况讨论:当0<m ≤时,﹣m 2+2m +1+2=4,解得m =1(舍);当<m ≤1时,﹣m 2+2m +1+2=4﹣2m +1,解得m =+2(舍)或m =﹣+2;当1<m ≤时,﹣m 2+2m +1+2=2m +1,解得m =或m =﹣(舍);当<m ≤2时,﹣m 2+2m +1+2=4,解得m =1(舍);当m >2时,最高点纵坐标是4,最低点纵坐标是1,此时不符合题意.【解答】解:(1)∵y =x 2﹣2mx +2m +1=(x ﹣m )2﹣m 2+2m +1,∴顶点坐标为(m ,﹣m 2+2m +1);(2)∵抛物线开口向上,∴m≤1时,y随x的增大而增大,故答案为:m≤1;(3)当m<﹣1时,x=﹣1,函数有最小值,∴y0=2+4m,∵y0=﹣1,∴2+4m=﹣1,解得m=﹣(舍);当m>2时,x=2,函数有最小值,∴y0=5﹣2m,∵y0=﹣1,∴5﹣2m=﹣1,解得m=3;当﹣1≤m≤2时,x=m,函数有最小值,∴y0=﹣m2+2m+1,∵y0=﹣1,∴﹣m2+2m+1=﹣1,解得m=+1(舍)或m=﹣+1;综上所述:m的值为3或﹣+1;(4)当0<m≤时,﹣m2+2m+1+2=4,解得m=1(舍);当<m≤1时,﹣m2+2m+1+2=4﹣2m+1,解得m=+2(舍)或m=﹣+2;当1<m≤时,﹣m2+2m+1+2=2m+1,解得m=或m=﹣(舍);当<m≤2时,﹣m2+2m+1+2=4,解得m=1(舍);当m>2时,最高点纵坐标是4,最低点纵坐标是1,∴3≠4,∴此时不符合题意;综上所述:m的值为或2﹣.8.(2021•咸丰县一模)如图,在平面直角坐标系中,抛物线与x轴正半轴交于点A,且点A的坐标为(3,0),过点A作垂直于x轴的直线l,P是该抛物线上一动点,其横坐标为m,过点P作PQ⊥l于点Q,M是直线l上的一点,其纵坐标为.以PQ,QM为边作矩形PQMN.(1)求抛物线的解析式;(2)当点Q与点M的值;(3)当矩形PQMN是正方形,且抛物线的顶点在该正方形内部时,求m的值;(4)当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小时,求m的取值范围.【分析】(1)利用待定系数法求解即可.(2)根据点M与点P的纵坐标相等构建方程求解即可.(3)根据PQ=MQ,构建方程求解即可.(4)当点P在直线l的左边,点M在点Q是下方下方时,抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小,则有﹣m+<﹣m2+m+,解得0<m<4,观察图象可知.当0<m<3时,抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小,如图4﹣1中.当m>4时,点M 在点Q的上方,也满足条件,如图4﹣2中.【解答】解:(1)∵抛物线的图象经过点A(3,0),∴=0,解得b=1.∴抛物线解析式为:.(2)∵P点的横坐标为m,且P点在抛物线y=的图象上,∴P点的坐标为(m,),∵PQ⊥l,l过A点且垂直于x轴,∴Q点的坐标为(3,),∵M点的坐标为(3,﹣m+),∵Q点与M点重合,∴=﹣m+,解方程得:m=0或m=4.(3)∵抛物线=﹣(x﹣1)2+2,∴抛物线的顶点坐标为(1,2).∵N点的坐标为N(m,﹣m+),要使顶点(1,2)在正方形PQMN内部,∴﹣m+>2,得m<﹣.∴PN=﹣m+﹣()=m2﹣2m,PQ=3﹣m.∵四边形PQMN是正方形,∴m2﹣2m=3﹣m,解得m=1+(舍去)或m=1﹣.∴当m=1﹣时,抛物线顶点在正方形PQMN内部.(4)∵M点的纵坐标﹣m+,随P点的横坐标m的增大而减小,根据(1)的结果得:当m=0时,M,Q两点重合;m=3时,P,Q重合;m=4时,M,Q重合,矩形PQMN不存在;当m<0时,直线MN在直线PQ上方,抛物线顶点在矩形PQMN内部,不合题意.当0<m<4时,直线MN在直线PQ下方,如图4﹣1,当3<m<4时,矩形内部没有抛物线图象,不合题意;当m>4时,直线MN在直线PQ上方,矩形内部有抛物线,且为对称轴右侧,y随x的增大而减小,如图4﹣2;综上:当0<m<3或m>4时,抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小.9.(2022•白山模拟)在平面直角坐标系中,抛物线y=﹣x2+2x+b(b为常数,b≠0)与y轴交于点A,且点A的坐标为(0,3),过点A作垂直于y轴的直线l.P是该抛物线上的任意一点,其横坐标为m,过点P作PQ⊥l于点Q,M是直线l上的一点,其横坐标为﹣m+1.以PQ,QM为边作矩形PQMN.(1)求b的值;(2)当点Q与点M重合时,求m的值;(3)当矩形PQMN为正方形时,求m的值;(4)当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而增大时,直接写出m的取值范围.【分析】(1)利用待定系数法求解即可.(2)根据点Q与点M的横坐标相等构建方程求解即可.(3)根据PQ=MQ,构建方程求解即可.(4)当点P在直线l的下边,点M在点Q右侧时,抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而增大,则有﹣m+1≤2,解得﹣1≤m<0;当点Q在点M右边时,存在两段,不合题意;当0<m<2时,点P在l的上方,当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而增大时,有<m<2.【解答】解:(1)把点A(0,3)代入y=﹣x2+2x+b,得到b=3.(2)∵抛物线的解析式为y=﹣x2+2x+3,∴P(m,﹣m2+2m+3),∵PQ⊥l,且l⊥y轴,∴PQ∥y,∴Q(m,3);∵点M(﹣m+1,3)与点Q重合,∴﹣m+1=m,解得m=.(3)y=﹣x2+2x+3=﹣(x﹣1)2+4,∴抛物线的顶点坐标为(1,4),由题意PQ=MQ,∴|﹣m2+2m+3﹣3|=|﹣m+1﹣m|解得,m=1或m=﹣1或m=2+或m=2﹣.(4)根据题意可知,需要分类讨论:当点P在直线l的下边,点M在点Q右侧时,抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而增大,如图1,此时﹣m+1≤2,解得﹣1≤m<0;当点P在直线l的下边,点Q在点M右边时,如图2,存在两段,不合题意;当点P在l上方时,如图3和4,当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而增大时,当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而增大时,有<m<2.综上,当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而增大时,﹣1≤m<0或<m<2.10.(2021•吉林四模)如图,在平面直角坐标系中,抛物线y=x2+bx﹣与x轴交于点A(5,0),与该抛物线的对称轴l交于点B,作直线AB.P是该抛物线上的任意一点,其横坐标为m,过点P作x轴的垂线交AB于点Q,过点P作PN⊥l于点N,以PQ、PN为边作矩形PQMN.(1)求抛物线的解析式;(2)求直线AB的解析式;(3)当该抛物线被矩形PQMN截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2时,求点P 的坐标;(4)当该抛物线与坐标轴的交点到直线MQ的距离相等时,直接写出m的值.【分析】(1)把点A(5,0)代入抛物线y=x2+bx﹣中可解答;(2)根据配方法可得抛物线顶点B的坐标,利用待定系数法可得直线AB的解析式;(3)分两种情况:①点P在对称轴的左侧;②点P在对称轴的右侧;根据该抛物线被矩形PQMN截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2列方程可解答;(4)先求抛物线与y轴交点的坐标,根据该抛物线与坐标轴的交点到直线MQ的距离相等可知:点Q的纵坐标为﹣,将y=﹣代入直线AB的解析式可得答案.【解答】解:(1)把点A(5,0)代入抛物线y=x2+bx﹣中得:+5b﹣=0,解得:b=﹣2,∴抛物线的解析式为:y=x2﹣2x﹣;(2)∵y=x2﹣2x﹣=(x﹣2)2﹣,∴B(2,﹣),设直线AB的解析式为:y=kx+n,则,解得:,∴直线AB的解析式为:y=x﹣;(3)由题意得:P (m ,m 2﹣2m ﹣),∴Q (m ,m ﹣),分两种情况:①如图1,当点P 在对称轴的左侧时,∵抛物线被矩形PQMN 截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2,∴m 2﹣2m ﹣+=2,解得:m 1=0,m 2=4(舍),∴P (0,﹣);②如图2,当点P 在对称轴的右边时,∵抛物线被矩形PQMN 截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2,∴m 2﹣2m ﹣﹣m +=2,解得:m 1=6,m 2=1(舍),∴P (6,3.5);综上,点P 的坐标为(0,﹣)或(6,3.5);(4)如图3,当x =0时,y =﹣∵该抛物线与坐标轴的交点到直线MQ 的距离相等,即点D 与C 到直线MQ 的距离相等,∴点Q的纵坐标为﹣,当y=﹣时,m﹣=﹣,解得:m=.11.(2021•南关区校级二模)在平面直角坐标系中,抛物线y=x2﹣2ax﹣a(a为常数).(1)当(﹣,m)在抛物线上,求m的值.(2)当抛物线的最低点到x轴的距离恰好是时,求a的值.(3)已知A(﹣1,1)、B(﹣1,2a﹣),连接AB.当抛物线与线段AB有交点时,记交点为P(点P 不与A、B重合),将线段PB绕点P顺时针旋转90°得到线段PM,以PM、PA为邻边构造矩形PMQA.①若抛物线在矩形PMQA内部的图象的函数值y随自变量x的增大而减小时,求a的取值范围.②当抛物线在矩形PMQA内部(包含边界)图象所对应的函数的最大值与最小值的差为时,直接写出a的值.【分析】(1)将(﹣,m)代入y=x2﹣2ax﹣a求解.(2)求出顶点坐标,通过顶点纵坐标为±求解.(3)①通过数形结合,讨论抛物线对称轴与矩形边的位置关系与抛物线经过临界点时的值求解.②分类讨论点B在A上方与点B在A下方两种情况,分别求出最高点与最低点坐标作差求解.【解答】解:(1)将(﹣,m)代入y=x2﹣2ax﹣a可得:m=+a﹣a,∴m=.(2)∵y=x2﹣2ax﹣a=(x﹣a)2﹣a2﹣a,∴抛物线顶点坐标为(a,﹣a2﹣a),当﹣a2﹣a=时,解得a=﹣,当﹣a2﹣a=﹣时,解得a=或a=.。
2020届中考数学专题复习二次函数_二次函数解决实际问题专题训练及参考答案

二次函数--二次函数解决实际问题1. 如图,用长8m 的铝合金条制成矩形窗框,使窗户的透光面积最大,那么这个窗户的最大透光面积是( )A.6425m2B.43m2C.83m2 D.4m2 2. 某广场有一喷水池,水从地面喷出,如图,以水平地面为x 轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y =-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )A.4米B.3米C.2米D.1米3. 某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要每间隔0.4m 加设一根不锈钢的支柱,防护栏的最高点距底部0.5m ,如图所示,则防护栏不锈钢支柱的总长度至少为( )A.50mB.100mC.160mD.200m4. 河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为y=-125x2,当水面离桥拱顶的高度DO 是4m 时,这时水面宽度AB 为( )A.-20mB.10mC.20mD.-10m5. 某幢建筑物,从10米高的窗口A 用水管向外喷水,喷的水流呈抛物线,抛物线所在平面与墙面垂直(如图),如果抛物线的最高点M 离墙1米,离地面403米,则水流下落点B 离墙距离OB 是( )A.2米B.3米C.4米D.5米6. 如图,有一块边长为6cm 的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )A.3cm2B.323cm2C.923cm2D.2723cm2 7. 若某商品的利润y(元)与售价x(元)之间的函数关系式是y =-x2+8x +9,且售价x 的范围是1≤x≤3,则最大利润是( )A.16元B.21元C.24元D.25元8. 一件工艺品进价为100元,标价135元售出,每天可售出100件,根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价的钱数为( )A.5元B.10元C.0元D.3600元9. 如图,隧道的截面是抛物线,可以用y =-116x2+4表示,该隧道内设双行道,限高为3m ,那么每条行道宽是( )A.不大于4mB.恰好4mC.不小于4mD.大于4m ,小于8m10. 如图所示,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50m 长的篱笆围成中间有一道篱笆的养鸡场,设它的长为xm ,要使鸡场的面积最大,鸡场的长为 m.11. 比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系式y =-29x2+89x +109,则羽毛球飞出的水平距离为 米.12. 如图,有一抛物线形的立交拱桥,这个拱桥的最大高度为16m ,跨度为40m ,现把它的图形放在坐标系中.若在离跨度中心M 点5m 处垂直竖立一根铁柱支撑拱顶,这根铁柱应取 m.13. 如图,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD ,设AB 边长为x 米,则菜园的面积y(单位:米2),当x = 米时菜园的面积最大.14. 将一条长为20cm 的铁丝剪成两段,并以每一段铁丝的长度为周长各做一个正方形,则这两个正方形面积之和的最小值是__________cm2.15. 已知某人卖盒饭的盒数x(盒)与所获利润y(元)满足关系式:y =-x2+1200x -357600,则卖出盒饭数量为________盒时,获得最大利润为________元.16. 某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天销售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为____________元时,该服装店平均每天的销售利润最大17. 杂技团进行杂技表演,演员从跷跷板右端A 处弹跳到人梯顶端椅子B 处,其身体(看成一点)的路线是抛物线y =-35x2+3x +1的一部分,如图所示.(1)求演员弹跳离地面的最大高度;(2)已知人梯高BC =3.4米,在一次表演中,人梯到起跳点A 的水平距离是4米,问这次表演是否成功?请说明理由.18. 一种进价为每件40元的T 恤,若销售单价为60元,则每周可卖出300件,可提高利润,欲对该T 恤进行涨价销售.经过调查发现:每涨价1元,每周要少卖出10件.请确定该T 恤涨价后每周的销售利润y(元)与销售单价x(元)之间的函数关系式,并求销售单价为多少元时,每周的销售利润最大?19. 如图,某足球运动员站在点O 练习射门,将足球从离地面0.5m 的A 处正对球门踢出(点A 在y 轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y =at2+5t +c ,已知足球飞行0.8s 时,离地面的高度为3.5m.(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x =10t ,已知球门的高度为2.44m ,如果该运动员正对球门射门时,离球门的水平距离为28m ,他能否将球直接射入球门?20. 如图,隧道的截面由抛物线和长方形构成,长方形的长是12m ,宽是4m.按照图中所示的直角坐标系,抛物线可以用y =-16x2+bx +c 表示,且抛物线时的点C 到墙面OB 的水平距离为3m ,到地面OA 的距离为172m.(1)求该抛物线的函数关系式,并计算出拱顶D 到地面OA 的距离;(2)一辆货运汽车载一长方体集装箱后高为6m ,宽为4m ,如果隧道内设双向行车道,那么这辆货车能否安全通过?(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m ,那么两排灯的水平距离最小是多少米?参考答案:1—9 CACCB CCAA10. 2511. 512. 1513. 1514. 25215. 600 240016. 2217. 解:(1)y =-35x2+3x +1=-35(x -52)2+194,∵-35<0,∴函数的最大值是194.答:演员弹跳的最大高度是194米; (2)当x =4时,y =-35×42+3×4+1=3.4=BC ,所以这次表演成功. 18. 解:由题意,得y =(x -40)[300-10(x -60)],即y =-10x2+1300x -36000(60≤x≤90).配方,得y =-10(x -65)2+6250.∵-10<0,∴当x =65时,y 有最大值6250,因此,当该T 恤销售单价为65元时,每周的销售利润最大.19. 解:(1)由题意得:函数y =at2+5t +c 的图象经过(0,0.5)(0.8,3.5),∴⎩⎪⎨⎪⎧ 0.5=c 3.5=0.82a -5×0.8+c ,解得:⎩⎪⎨⎪⎧ a =-2516c =12,∴抛物线的解析式为:y =-2516t2+5t +12,∴当t =85时,y 最大=4.5;(2)把x =28代入x =10t 得t =2.8,∴当t =2.8时,y =-2516×2.82+5×2.8+12=2.25<2.44,∴他能将球直接射入球门.20. 解:(1)根据题意得B(0,4),C(3,172),把B(0,4),C(3,172)代入y =-16x2+bx +c 得⎩⎪⎨⎪⎧ c =4-16×32+3b +c =172,解得⎩⎪⎨⎪⎧ b =2c =4,所以抛物线解析式为y =-16x2+2x +4,则y =-16(x -6)2+10,所以D(6,10),所以拱顶D 到地面OA 的距离为10m ;(2)由题意得货运汽车最外侧于地面OA 的交点为(2,0)或(10,0),当x =2或x =10时,y =223>6,所以这辆货车能安全通过;(3)令y =0,则-16(x -6)2+10=8,解得x1=6+23,x2=6-23,则x1-x2=43,所以两排灯的水平距离最小是43m.。
2020年江苏省中考数学试题分类汇编(4)——二次函数(含答案)

2020年江苏省中考数学试题分类(4)——二次函数一.二次函数的性质(共4小题)1.(2020•镇江)点P (m ,n )在以y 轴为对称轴的二次函数y =x 2+ax +4的图象上.则m ﹣n 的最大值等于( )A .154B .4C .−154D .−174 2.(2020•无锡)请写出一个函数表达式,使其图象的对称轴为y 轴: .3.(2020•无锡)二次函数y =ax 2﹣3ax +3的图象过点A (6,0),且与y 轴交于点B ,点M 在该抛物线的对称轴上,若△ABM 是以AB 为直角边的直角三角形,则点M 的坐标为 .4.(2020•淮安)二次函数y =﹣x 2﹣2x +3的图象的顶点坐标为 .二.二次函数图象与几何变换(共2小题)5.(2020•宿迁)将二次函数y =(x ﹣1)2+2的图象向上平移3个单位长度,得到的拋物线相应的函数表达式为( )A .y =(x +2)2﹣2B .y =(x ﹣4)2+2C .y =(x ﹣1)2﹣1D .y =(x ﹣1)2+56.(2020•南京)下列关于二次函数y =﹣(x ﹣m )2+m 2+1(m 为常数)的结论:①该函数的图象与函数y =﹣x 2的图象形状相同;②该函数的图象一定经过点(0,1);③当x >0时,y 随x 的增大而减小;④该函数的图象的顶点在函数y =x 2+1的图象上.其中所有正确结论的序号是 .三.抛物线与x 轴的交点(共3小题)7.(2020•南通)已知抛物线y =ax 2+bx +c 经过A (2,0),B (3n ﹣4,y 1),C (5n +6,y 2)三点,对称轴是直线x =1.关于x 的方程ax 2+bx +c =x 有两个相等的实数根.(1)求抛物线的解析式;(2)若n <﹣5,试比较y 1与y 2的大小;(3)若B ,C 两点在直线x =1的两侧,且y 1>y 2,求n 的取值范围.8.(2020•盐城)若二次函数y =ax 2+bx +c 的图象与x 轴有两个交点M (x 1,0),N (x 2,0)(0<x 1<x 2),且经过点A (0,2).过点A 的直线l 与x 轴交于点C ,与该函数的图象交于点B (异于点A ).满足△ACN 是等腰直角三角形,记△AMN 的面积为S 1,△BMN 的面积为S 2,且S 2=52S 1.(1)抛物线的开口方向 (填“上”或“下”);(2)求直线l 相应的函数表达式;(3)求该二次函数的表达式. 9.(2020•苏州)如图,二次函数y =x 2+bx 的图象与x 轴正半轴交于点A ,平行于x 轴的直线l 与该抛物线交于B 、C 两点(点B 位于点C 左侧),与抛物线对称轴交于点D (2,﹣3).(1)求b 的值;(2)设P 、Q 是x 轴上的点(点P 位于点Q 左侧),四边形PBCQ 为平行四边形.过点P 、Q 分别作x 轴的垂线,与抛物线交于点P '(x 1,y 1)、Q '(x 2,y 2).若|y 1﹣y 2|=2,求x 1、x 2的值.四.二次函数的应用(共4小题)10.(2020•连云港)加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式y=﹣0.2x2+1.5x﹣2,则最佳加工时间为min.11.(2020•宿迁)某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:55 60 65 70销售单价x(元/千克)销售量y(千克)70 60 50 40(1)求y(千克)与x(元/千克)之间的函数表达式;(2)为保证某天获得600元的销售利润,则该天的销售单价应定为多少?(3)当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?12.(2020•南京)小明和小丽先后从A地出发沿同一直道去B地.设小丽出发第xmin时,小丽、小明离B 地的距离分别为y1m、y2m.y1与x之间的函数表达式是y1=﹣180x+2250,y2与x之间的函数表达式是y2=﹣10x2﹣100x+2000.(1)小丽出发时,小明离A地的距离为m.(2)小丽出发至小明到达B地这段时间内,两人何时相距最近?最近距离是多少?13.(2020•无锡)有一块矩形地块ABCD,AB=20米,BC=30米.为美观,拟种植不同的花卉,如图所示,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形AEHD 和BCGF中种植甲种花卉;在等腰梯形ABFE和CDHG中种植乙种花卉;在矩形EFGH中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米2、60元/米2、40元/米2,设三种花卉的种植总成本为y元.(1)当x=5时,求种植总成本y;(2)求种植总成本y与x的函数表达式,并写出自变量x的取值范围;(3)若甲、乙两种花卉的种植面积之差不超过120平方米,求三种花卉的最低种植总成本.五.二次函数综合题(共8小题)14.(2020•镇江)如图①,直线l经过点(4,0)且平行于y轴,二次函数y=ax2﹣2ax+c(a、c是常数,a <0)的图象经过点M(﹣1,1),交直线l于点N,图象的顶点为D,它的对称轴与x轴交于点C,直线DM、DN分别与x轴相交于A、B两点.(1)当a =﹣1时,求点N 的坐标及AA AA 的值; (2)随着a 的变化,AA AA 的值是否发生变化?请说明理由;(3)如图②,E 是x 轴上位于点B 右侧的点,BC =2BE ,DE 交抛物线于点F .若FB =FE ,求此时的二次函数表达式.15.(2020•宿迁)二次函数y =ax 2+bx +3的图象与x 轴交于A (2,0),B (6,0)两点,与y 轴交于点C ,顶点为E ..(1)求这个二次函数的表达式,并写出点E 的坐标;(2)如图①,D 是该二次函数图象的对称轴上一个动点,当BD 的垂直平分线恰好经过点C 时,求点D 的坐标;(3)如图②,P 是该二次函数图象上的一个动点,连接OP ,取OP 中点Q ,连接QC ,QE ,CE ,当△CEQ 的面积为12时,求点P 的坐标. 16.(2020•徐州)如图,在平面直角坐标系中,函数y =﹣ax 2+2ax +3a (a >0)的图象交x 轴于点A 、B ,交y 轴于点C ,它的对称轴交x 轴于点E .过点C 作CD ∥x 轴交抛物线于点D ,连接DE 并延长交y 轴于点F ,交抛物线于点G .直线AF 交CD 于点H ,交抛物线于点K ,连接HE 、GK .(1)点E 的坐标为: ;(2)当△HEF 是直角三角形时,求a 的值;(3)HE 与GK 有怎样的位置关系?请说明理由.17.(2020•淮安)如图①,二次函数y=﹣x2+bx+4的图象与直线l交于A(﹣1,2)、B(3,n)两点.点P 是x轴上的一个动点,过点P作x轴的垂线交直线l于点M,交该二次函数的图象于点N,设点P的横坐标为m.(1)b=,n=;(2)若点N在点M的上方,且MN=3,求m的值;(3)将直线AB向上平移4个单位长度,分别与x轴、y轴交于点C、D(如图②).①记△NBC的面积为S1,△NAC的面积为S2,是否存在m,使得点N在直线AC的上方,且满足S1﹣S2=6?若存在,求出m及相应的S1,S2的值;若不存在,请说明理由.②当m>﹣1时,将线段MA绕点M顺时针旋转90°得到线段MF,连接FB、FC、OA.若∠FBA+∠AOD﹣∠BFC=45°,直接写出直线OF与该二次函数图象交点的横坐标.18.(2020•常州)如图,二次函数y=x2+bx+3的图象与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,抛物线过点C(1,0),且顶点为D,连接AC、BC、BD、CD.(1)填空:b=;(2)点P是抛物线上一点,点P的横坐标大于1,直线PC交直线BD于点Q.若∠CQD=∠ACB,求点P的坐标;(3)点E在直线AC上,点E关于直线BD对称的点为F,点F关于直线BC对称的点为G,连接AG.当点F在x轴上时,直接写出AG的长.19.(2020•泰州)如图,二次函数y 1=a (x ﹣m )2+n ,y 2=6ax 2+n (a <0,m >0,n >0)的图象分别为C 1、C 2,C 1交y 轴于点P ,点A 在C 1上,且位于y 轴右侧,直线P A 与C 2在y 轴左侧的交点为B .(1)若P 点的坐标为(0,2),C 1的顶点坐标为(2,4),求a 的值;(2)设直线P A 与y 轴所夹的角为α.①当α=45°,且A 为C 1的顶点时,求am 的值;②若α=90°,试说明:当a 、m 、n 各自取不同的值时,AA AA 的值不变;(3)若P A =2PB ,试判断点A 是否为C 1的顶点?请说明理由.20.(2020•连云港)在平面直角坐标系xOy 中,把与x 轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线L 1:y =12x 2−32x ﹣2的顶点为D ,交x 轴于点A 、B (点A 在点B 左侧),交y 轴于点C .抛物线L 2与L 1是“共根抛物线”,其顶点为P .(1)若抛物线L 2经过点(2,﹣12),求L 2对应的函数表达式;(2)当BP ﹣CP 的值最大时,求点P 的坐标;(3)设点Q 是抛物线L 1上的一个动点,且位于其对称轴的右侧.若△DPQ 与△ABC 相似,求其“共根抛物线”L 2的顶点P 的坐标. 21.(2020•无锡)在平面直角坐标系中,O 为坐标原点,直线OA 交二次函数y =14x 2的图象于点A ,∠AOB=90°,点B 在该二次函数的图象上,设过点(0,m )(其中m >0)且平行于x 轴的直线交直线OA 于点M ,交直线OB 于点N ,以线段OM 、ON 为邻边作矩形OMPN .(1)若点A 的横坐标为8.①用含m的代数式表示M的坐标;②点P能否落在该二次函数的图象上?若能,求出m的值;若不能,请说明理由.(2)当m=2时,若点P恰好落在该二次函数的图象上,请直接写出此时满足条件的所有直线OA的函数表达式.2020年江苏省中考数学试题分类(4)——二次函数参考答案与试题解析一.二次函数的性质(共4小题)1.【解答】解:∵点P (m ,n )在以y 轴为对称轴的二次函数y =x 2+ax +4的图象上,∴a =0,∴n =m 2+4,∴m ﹣n =m ﹣(m 2+4)=﹣m 2+m ﹣4=﹣(m −12)2−154,∴当m =12时,m ﹣n 取得最大值,此时m ﹣n =−154,故选:C .2.【解答】解:∵图象的对称轴是y 轴,∴函数表达式y =x 2(答案不唯一),故答案为:y =x 2(答案不唯一).3.【解答】解:∵抛物线的对称轴为x =−122×(−16)=32, 设点M 的坐标为:(32,m ),当∠ABM =90°,过B 作BD 垂直对称轴于D ,则∠1=∠2,∴tan ∠2=tan ∠1=63=2, ∴AA AA =2,∴DM =3, ∴M (32,6),当∠M ′AB =90°时,∴tan ∠3=A′A AA =tan ∠1=63=2, ∴M ′N =9, ∴M ′(32,﹣9),综上所述,点M 的坐标为(32,﹣9)或(32,6).故答案为:(32,﹣9)或(32,6). 4.【解答】解:∵y =﹣x 2﹣2x +3=﹣(x 2+2x +1﹣1)+3=﹣(x +1)2+4,∴顶点坐标为(﹣1,4).故答案为:(﹣1,4).二.二次函数图象与几何变换(共2小题)5.【解答】解:由“上加下减”的原则可知,将二次函数y =(x ﹣1)2+2的图象向上平移3个单位长度,所得抛物线的解析式为:y =(x ﹣1)2+2+3,即y =(x ﹣1)2+5;故选:D .6.【解答】解:①∵二次函数y =﹣(x ﹣m )2+m +1(m 为常数)与函数y =﹣x 2的二次项系数相同, ∴该函数的图象与函数y =﹣x 2的图象形状相同,故结论①正确;②∵在函数y =﹣(x ﹣m )2+m 2+1中,令x =0,则y =﹣m 2+m 2+1=1,∴该函数的图象一定经过点(0,1),故结论②正确;③∵y =﹣(x ﹣m )2+m 2+1,∴抛物线开口向下,对称轴为直线x =m ,当x >m 时,y 随x 的增大而减小,故结论③错误;④∵抛物线开口向下,当x =m 时,函数y 有最大值m 2+1,∴该函数的图象的顶点在函数y =x 2+1的图象上.故结论④正确,故答案为①②④.三.抛物线与x 轴的交点(共3小题)7.【解答】解:(1)∵抛物线y =ax 2+bx +c 经过A (2,0),∴0=4a +2b +c ①,∵对称轴是直线x =1,∴−A 2A =1②, ∵关于x 的方程ax 2+bx +c =x 有两个相等的实数根,∴△=(b ﹣1)2﹣4ac =0③,由①②③可得:{A =−12A =1A =0,∴抛物线的解析式为y =−12x 2+x ;(2)∵n <﹣5,∴3n ﹣4<﹣19,5n +6<﹣19∴点B ,点C 在对称轴直线x =1的左侧,∵抛物线y =−12x 2+x ,∴−12<0,即y 随x 的增大而增大,∵(3n ﹣4)﹣(5n +6)=﹣2n ﹣10=﹣2(n +5)>0,∴3n ﹣4>5n +6,∴y 1>y 2;(3)若点B 在对称轴直线x =1的左侧,点C 在对称轴直线x =1的右侧时,由题意可得{3A −4<15A +6>11−(3A −4)<5A +6−1, ∴0<n <53, 若点C 在对称轴直线x =1的左侧,点B 在对称轴直线x =1的右侧时,由题意可得:{3A −4>15A +6<13A −4−1<1−(5A +6),∴不等式组无解,综上所述:0<n <53.8.【解答】解:(1)如图,如二次函数y =ax 2+bx +c 的图象与x 轴有两个交点M (x 1,0),N (x 2,0)(0<x 1<x 2),且经过点A (0,2).∴y =ax 2+bx +2,令y =0,则ax 2+bx +2=0,∵0<x 1<x 2,∴2A >0,∴a >0,∴抛物线开口向上,故答案为:上;(2)①若∠ACN =90°,则C 与O 重合,直线l 与抛物线交于A 点,因为直线l 与该函数的图象交于点B (异于点A ),所以不合题意,舍去;②若∠ANC =90°,则C 在x 轴的下方,与题意不符,舍去;③若∠CAN =90°,则∠ACN =∠ANC =45°,AO =CO =NO =2,∴C (﹣2,0),N (2,0),设直线l 为y =kx +b ,将A (0,2)C (﹣2,0)代入得{A =2−2A +A =0, 解得{A =1A =2, ∴直线l 相应的函数表达式为y =x +2;(3)过B 点作BH ⊥x 轴于H ,S 1=12AA ⋅AA ,S 2=12AA ⋅AA ,∵S 2=52S 1, ∴BH =52OA , ∵OA =2,∴BH =5,即B 点的纵坐标为5,代入y =x +2中,得x =3,∴B (3,5),将A 、B 、N 三点的坐标代入y =ax 2+bx +c 得{A =24A +2A +A =09A +3A +A =5,解得{A =2A =−5A =2,∴抛物线的解析式为y =2x 2﹣5x +2.9.【解答】解:(1)直线与抛物线的对称轴交于点D (2,﹣3),故抛物线的对称轴为x =2,即−12b =2,解得:b =﹣4,(2)∵b =﹣4∴抛物线的表达式为:y =x 2﹣4x ;把y =﹣3代入y =x 2﹣4x 并解得x =1或3,故点B 、C 的坐标分别为(1,﹣3)、(3,﹣3),则BC =2,∵四边形PBCQ 为平行四边形,∴PQ =BC =2,故x 2﹣x 1=2,又∵y 1=x 12﹣4x 1,y 2=x 22﹣4x 2,|y 1﹣y 2|=2,故|(x 12﹣4x 1)﹣(x 22﹣4x 2)|=2,|x 1+x 2﹣4|=1.∴x 1+x 2=5或x 1+x 2=3,由{A 2−A 1=2A 1+A 2=5,解得{A 1=32A 2=72; 由{A 2−A 1=2A 1+A 2=3,解得{A 1=12A 2=52. 四.二次函数的应用(共4小题)10.【解答】解:根据题意:y =﹣0.2x 2+1.5x ﹣2,当x =−1.52×(−0.2)=3.75时,y 取得最大值, 则最佳加工时间为3.75min .故答案为:3.75.11.【解答】解:(1)设y 与x 之间的函数表达式为y =kx +b (k ≠0),将表中数据(55,70)、(60,60)代入得:{55A +A =7060A +A =60, 解得:{A =−2A =180. ∴y 与x 之间的函数表达式为y =﹣2x +180.(2)由题意得:(x ﹣50)(﹣2x +180)=600,整理得:x 2﹣140x +4800=0,解得x 1=60,x 2=80.答:为保证某天获得600元的销售利润,则该天的销售单价应定为60元/千克或80元/千克.(3)设当天的销售利润为w 元,则:w =(x ﹣50)(﹣2x +180)=﹣2(x ﹣70)2+800,∵﹣2<0,∴当x =70时,w 最大值=800.答:当销售单价定为70元/千克时,才能使当天的销售利润最大,最大利润是800元.12.【解答】解:(1)∵y 1=﹣180x +2250,y 2=﹣10x 2﹣100x +2000,∴当x =0时,y 1=2250,y 2=2000,∴小丽出发时,小明离A 地的距离为2250﹣2000=250(m ),故答案为:250;(2)设小丽出发第xmin 时,两人相距sm ,则s =(﹣180x +2250)﹣(﹣10x 2﹣100x +2000)=10x 2﹣80x +250=10(x ﹣4)2+90,∴当x =4时,s 取得最小值,此时s =90,答:小丽出发第4min 时,两人相距最近,最近距离是90m .13.【解答】解:(1)当x =5时,EF =20﹣2x =10,EH =30﹣2x =20,y =2×12(EH +AD )×20x +2×12(GH +CD )×x ×60+EF •EH ×40=(20+30)×5×20+(10+20)×5×60+20×10×40=22000;(2)EF =(20﹣2x )米,EH =(30﹣2x )米,参考(1),由题意得:y =(30+30﹣2x )•x •20+(20+20﹣2x )•x •60+(30﹣2x )(20﹣2x )•40=﹣400x +24000(0<x <10);(3)S 甲=2×12(EH +AD )×x =(30﹣2x +30)x =﹣2x 2+60x , 同理S 乙=﹣2x 2+40x ,∵甲、乙两种花卉的种植面积之差不超过120米2,∴﹣2x 2+60x ﹣(﹣2x 2+40x )≤120,解得:x ≤6,故0<x ≤6,而y =﹣400x +24000随x 的增大而减小,故当x =6时,y 的最小值为21600,即三种花卉的最低种植总成本为21600元.五.二次函数综合题(共8小题)14.【解答】解:(1)分别过点M 、N 作MG ⊥CD 于点E ,NT ⊥DC 于点T ,∵MG ∥TN ∥x 轴,∴△DMG ∽△DAC ,△DCB ∽△DTN ,∴AA AA =AA AA ,AA AA =AA AA ,∵a =﹣1,则y =﹣x 2+2x +c ,将M (﹣1,1)代入上式并解得:c =4,∴抛物线的表达式为:y =﹣x 2+2x +4,则点D (1,5),N (4,﹣4),则MG =2,DG =4,DC =5,TN =3,DT =9,∴2AA =45,AA 3=59,解得:AC =52,BC =53, ∴AA AA =32;(2)不变,理由:第(2)问有错误MG =2,DG =4a∵y =ax 2﹣2ax +c 过点M (﹣1,1),则a +2a +c =1,解得:c =1﹣3a ,∴y =ax 2﹣2ax +(1﹣3a ),∴点D (1,1﹣4a ),N (4,1+5a ),∴MG =2,DG =4a ,DC =1﹣4a ,FN =3,DF =﹣9a ,由(1)的结论得:AC =1−4A −2A ,BC =1−4A −3A ,∴AA AA =32;(3)过点F 作FH ⊥x 轴于点H ,则FH ∥l ,则△FHE ∽△DCE ,∵FB =FE ,FH ⊥BE ,∴BH =HE ,∵BC =2BE ,则CE =6HE ,∵CD =1﹣4a ,∴FH =1−4A 6, ∵BC =4A −13A , ∴CH =54×4A −13A =20A −512A ,∴F (53−512A +1,16−23a ), 将点F 的坐标代入y =ax 2﹣2ax +(1﹣3a )=a (x +1)(x ﹣3)+1得: 16−23a =a (53−512A +1+1)(53−512A +1﹣3)+1,解得:a =−54或14(舍弃), 经检验a =−54,故y =−54x 2+52x +194. 15.【解答】解:(1)将A (2,0),B (6,0)代入y =ax 2+bx +3, 得{4A +2A +3=036A +6A +3=0, 解得{A =14A =−2 ∴二次函数的解析式为y =14A 2−2x +3.∵y =14A 2−2A +3=14(A −4)2−1,∴E (4,﹣1).(2)如图1,图2,连接CB ,CD ,由点C 在线段BD 的垂直平分线CN 上,得CB =CD .设D (4,m ),∵C (0,3),由勾股定理可得:42+(m ﹣3)2=62+32.解得m =3±√29.∴满足条件的点D 的坐标为(4,3+√29)或(4,3−√29).(3)如图3,设CQ 交抛物线的对称轴于点M ,设P (n ,14A 2−2n +3),则Q (12A ,18A 2−A +32), 设直线CQ 的解析式为y =kx +3,则18A 2−A +32=12nk +3. 解得k =14A −2−3A ,于是CQ :y =(14A −2−3A )x +3,当x =4时,y =4(14A −2−3A )+3=n ﹣5−12A, ∴M (4,n ﹣5−12A ),ME =n ﹣4−12A .∵S △CQE =S △CEM +S △QEM =12×12A ⋅AA =12⋅12A ⋅(A −4−12A )=12. ∴n 2﹣4n ﹣60=0,解得n =10或n =﹣6,当n =10时,P (10,8),当n =﹣6时,P (﹣6,24).综合以上可得,满足条件的点P 的坐标为(10,8)或(﹣6,24).16.【解答】解:(1)对于抛物线y =﹣ax 2+2ax +3a ,对称轴x =−2A −2A=1, ∴E (1,0),故答案为(1,0).(2)如图,连接EC .对于抛物线y =﹣ax 2+2ax +3a ,令x =0,得到y =3a ,令y =0,﹣ax 2+2ax +3a =0,解得x =﹣1或3,∴A (﹣1,0),B (3,0),C (0,3a ),∵C ,D 关于对称轴对称,∴D (2,3a ),CD =2,EC =DE ,当∠HEF =90°时,∵ED =EC ,∴∠ECD =∠EDC ,∵∠DCF =90°,∴∠CFD +∠EDC =90°,∠ECF +∠ECD =90°,∴∠ECF =∠EFC ,∴EC =EF =DE ,∵EA ∥DH ,∴F A =AH ,∴AE =12DH ,∵AE =2,∴DH =4,∵HE ⊥DFEF =ED ,∴FH =DH =4,在Rt △CFH 中,则有42=22+(6a )2,解得a =√33或−√33(不符合题意舍弃),∴a =√33.当∠HFE =90°时,∵OA =OE ,FO ⊥AE ,∴F A =FE ,∴OF =OA =OE =1,∴3a =1,∴a =13, 综上所述,满足条件的a 的值为√33或13.(3)结论:EH ∥GK .理由:由题意A (﹣1,0),F (0,﹣3a ),D (2,3a ),H (﹣2,3a ),E (1,0),∴直线AF 的解析式y =﹣3ax ﹣3a ,直线DF 的解析式为y =3ax ﹣3a ,由{A =−3AA −3A A =−AA 2+2AA +3A ,解得{A =−1A =0或{A =6A =−21A , ∴K (6,﹣21a ),由{A =3AA −3A A =−AA 2+2AA +3A ,解得{A =2A =3A 或{A =−3A =−12A , ∴G (﹣3,﹣12a ),∴直线HE 的解析式为y =﹣ax +a ,直线GK 的解析式为y =﹣ax ﹣15a ,∵k 相同,a ≠﹣15a ,∴HE ∥GK .17.【解答】解:(1)将点A (﹣1,2)代入二次函数y =﹣x 2+bx +4中,得﹣1﹣b +4=2,∴b =1,∴二次函数的解析式为y =﹣x 2+x +4,将点B (3,n )代入二次函数y =﹣x 2+x +4中,得n =﹣9+3+4=﹣2,故答案为:1,﹣2;(2)设直线AB 的解析式为y =kx +a ,由(1)知,点B (3,﹣2),∵A (﹣1,2),∴{−A +A =23A +A =−2, ∴{A =−1A =1, ∴直线AB 的解析式为y =﹣x +1,由(1)知,二次函数的解析式为y =﹣x 2+x +4,∵点P (m ,0),∴M (m ,﹣m +1),N (m ,﹣m 2+m +4),∵点N 在点M 的上方,且MN =3,∴﹣m 2+m +4﹣(﹣m +1)=3,∴m =0或m =2;(3)①如图1,由(2)知,直线AB 的解析式为y =﹣x +1,∴直线CD 的解析式为y =﹣x +1+4=﹣x +5,令y =0,则﹣x +5=0,∴x =5,∴C (5,0),∵A (﹣1,2),B (3,﹣2),∴直线AC 的解析式为y =−13x +53,直线BC 的解析式为y =x ﹣5,过点N 作y 轴的平行线交AC 于K ,交BC 于H ,∵点P (m ,0),∴N (m ,﹣m 2+m +4),K (m ,−13m +53),H (m ,m ﹣5),∴NK =﹣m 2+m +4+13m −53=−m 2+43m +73,NH =﹣m 2+9,∴S 2=S △NAC =12NK ×(x C ﹣x A )=12(﹣m 2+43m +73)×6=﹣3m 2+4m +7,S 1=S △NBC =12NH ×(x C ﹣x B )=﹣m 2+9,∵S 1﹣S 2=6,∴﹣m 2+9﹣(﹣3m 2+4m +7)=6,∴m =1+√3(由于点N 在直线AC 上方,所以,舍去)或m =1−√3;∴S 2=﹣3m 2+4m +7=﹣3(1−√3)2+4(1−√3)+7=2√3−1,S 1=﹣m 2+9=﹣(1−√3)2+9=2√3+5;②如图2,记直线AB 与x 轴,y 轴的交点为I ,L ,由(2)知,直线AB 的解析式为y =﹣x +1,∴I (1,0),L (0,1),∴OL =OI ,∴∠ALD =∠OLI =45°,∴∠AOD +∠OAB =45°,过点B 作BG ∥OA ,∴∠ABG =∠OAB ,∴∠AOD +∠ABG =45°,∵∠FBA =∠ABG +∠FBG ,∠FBA +∠AOD ﹣∠BFC =45°,∴∠ABG +∠FBG +∠AOD ﹣∠BFC =45°,∴∠FBG =∠BFC ,∴BG ∥CF ,∴OA ∥CF ,∵A (﹣1,2),∴直线OA 的解析式为y =﹣2x ,∵C (5,0),∴直线CF 的解析式为y =﹣2x +10,过点A ,F 分别作过点M 平行于x 轴的直线的垂线,交于点Q ,S ,由旋转知,AM =MF ,∠AMF =90°,∴△AMF 是等腰直角三角形,∴∠F AM =45°,∵∠AIO =45°,∴∠F AM =∠AIO ,∴AF ∥x 轴,∴点F 的纵坐标为2,∴F (4,2),∴直线OF 的解析式为y =12x ①,∵二次函数的解析式为y =﹣x 2+x +4②, 联立①②解得,{A =1+√654A =1+√658或{A =1−√654A =1−√658, ∴直线OF 与该二次函数图象交点的横坐标为1+√654或1−√654.18.【解答】解:(1)∵抛物线y=x2+bx+3的图象过点C(1,0),∴0=1+b+3,∴b=﹣4,故答案为:﹣4;(2)∵b=﹣4,∴抛物线解析式为y=x2﹣4x+3∵抛物线y=x2﹣4x+3的图象与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,∴点A(0,3),3=x2﹣4x+3,∴x1=0(舍去),x2=4,∴点B(4,3),∵y=x2﹣4x+3=(x﹣2)2﹣1,∴顶点D坐标(2,﹣1),如图1,当点Q在点D上方时,过点C作CE⊥AB于E,设BD与x轴交于点F,∵点A(0,3),点B(4,3),点C(1,0),CE⊥AB,∴点E(1,3),CE=BE=3,AE=1,∴∠EBC=∠ECB=45°,tan∠ACE=AAAA=13,∴∠BCF=45°,∵点B(4,3),点C(1,0),点D(2,﹣1),∴BC=√9+9=3√2,CD=√1+1=√2,BD=√(4−2)2+(3+1)2=2√5,∵BC2+CD2=20=BD2,∴∠BCD=90°,∴tan ∠DBC =AA AA =√23√2=13=tan ∠ACE , ∴∠ACE =∠DBC ,∴∠ACE +∠ECB =∠DBC +∠BCF ,∴∠ACB =∠CFD ,又∵∠CQD =∠ACB ,∴点F 与点Q 重合,∴点P 是直线CF 与抛物线的交点,∴0=x 2﹣4x +3,∴x 1=1,x 2=3,∴点P (3,0);当点Q 在点D 下方上,过点C 作CH ⊥DB 于H ,在线段BH 的延长线上截取HF =QH ,连接CQ 交抛物线于点P ,∵CH ⊥DB ,HF =QH ,∴CF =CQ ,∴∠CFD =∠CQD ,∴∠CQD =∠ACB ,∵CH ⊥BD ,∵点B (4,3),点D (2,﹣1),∴直线BD 解析式为:y =2x ﹣5,∴点F (52,0), ∴直线CH 解析式为:y =−12x +12, ∴{A =−12A +12A =2A −5,解得{A =115A =−35, ∴点H 坐标为(115,−35), ∵FH =QH ,∴点Q (1910,−65), ∴直线CQ 解析式为:y =−43x +43, 联立方程组{A =−43A +43A =A 2−4A +3,解得:{A 1=1A 1=0或{A 2=53A 2=−89,∴点P (53,−89); 综上所述:点P 的坐标为(3,0)或(53,−89);(3)如图,设直线AC 与BD 的交点为N ,作CH ⊥BD 于H ,过点N 作MN ⊥x 轴,过点E 作EM ⊥MN ,连接CG ,GF ,∵点A (0,3),点C (1,0),∴直线AC 解析式为:y =﹣3x +3,∴{A =−3A +3A =2A −5, ∴{A =85A =−95, ∴点N 坐标为(85,−95),∵点H 坐标为(115,−35), ∴CH 2=(115−1)2+(35)2=95,HN 2=(115−85)2+(−35+95)2=95, ∴CH =HN ,∴∠CNH =45°,∵点E 关于直线BD 对称的点为F ,∴EN =NF ,∠ENB =∠FNB =45°,∴∠ENF =90°,∴∠ENM +∠FNM =90°,又∵∠ENM +∠MEN =90°,∴∠MEN =∠FNM ,∴△EMN ≌△NKF (AAS )∴EM =NK =95,MN =KF ,∴点E 的横坐标为−15,∴点E (−15,185), ∴MN =275=KF ,∴CF =85+275−1=6, ∵点F 关于直线BC 对称的点为G ,∴FC =CG =6,∠BCF =∠GCB =45°,∴∠GCF =90°,∴点G (1,6),∴AG =√12+(6−3)2=√10.19.【解答】解:(1)由题意m =2,n =4,∴y 1=a (x ﹣2)2+4,把(0,2)代入得到a =−12.(2)①如图1中,过点A 作AN ⊥x 轴于N ,过点P 作PM ⊥AN 于M . ∵y 1=a (x ﹣m )2+n =ax 2﹣2amx +am 2+n ,∴P (0,am 2+n ),∵A (m ,n ),∴PM =m ,AN =n ,∵∠APM =45°,∴AM =PM =m ,∴m +am 2+n =n ,∵m >0,∴am =﹣1.②如图2中,由题意AB ⊥y 轴, ∵P (0,am 2+n ),当y =am 2+n 时,am 2+n =6ax 2+n ,解得x =±√66m , ∴B (−√66m ,am 2+n ),∴PB =√66m ,∵AP =2m ,∴AA AA =√66A =2√6.(3)如图3中,过点A 作AH ⊥x 轴于H ,过点P 作PK ⊥AH 于K ,过点B 作BE ⊥KP 交KP 的延长线于E .设B (b ,6ab 2+n ),∵P A =2PB ,∴点A 的横坐标为﹣2b ,∴A [﹣2b ,a (﹣2b ﹣m )2+n ],∵BE ∥AK , ∴AAAA =AAAA =12, ∴AK =2BE ,∴a (﹣2b ﹣m )2+n ﹣am 2﹣n =2(am 2+n ﹣6ab 2﹣n ),整理得:m 2﹣2bm ﹣8b 2=0,∴(m ﹣4b )(m +2b )=0,∵m ﹣4b >0,∴m +2b =0,∴m =﹣2b ,∴A (m ,n ),∴点A 是抛物线C 1的顶点.20.【解答】解:(1)当y =0时,12x 2−32x ﹣2=0,解得x =﹣1或4,∴A (﹣1,0),B (4,0),C (0,﹣2),由题意设抛物线L 2的解析式为y =a (x +1)(x ﹣4),把(2,﹣12)代入y =a (x +1)(x ﹣4),﹣12=﹣6a ,解得a =2,∴抛物线的解析式为y =2(x +1)(x ﹣4)=2x 2﹣6x ﹣8.(2)∵抛物线L 2与L 1是“共根抛物线”,A (﹣1,0),B (4,0),∴抛物线L 1,L 2的对称轴是直线x =32, ∴点P 在直线x =32上,∴BP =AP ,如图1中,当A ,C ,P 共线时,BP ﹣PC 的值最大,此时点P 为直线AC 与直线x =32的交点,∵直线AC 的解析式为y =﹣2x ﹣2,∴P (32,﹣5)(3)由题意,AB =5,CB =2√5,CA =√5,∴AB 2=BC 2+AC 2,∴∠ACB =90°,CB =2CA ,∵y =12x 2−32x ﹣2=12(x −32)2−258,∴顶点D (32,−258), 由题意,∠PDQ 不可能是直角,第一种情形:当∠DPQ =90°时,①如图3﹣1中,当△QDP ∽△ABC 时,AA AA =AA AA =12, 设Q (x ,12x 2−32x ﹣2),则P (32,12x 2−32x ﹣2),∴DP =12x 2−32x ﹣2﹣(−258)=12x 2−32x +98,QP =x −32, ∵PD =2QP ,∴2x ﹣3=12x 2−32x +98,解得x =112或32(舍弃), ∴P (32,398).②如图3﹣2中,当△DQP ∽△ABC 时,同法可得PQ =2PD ,x −32=x 2﹣3x +94,解得x =52或32(舍弃), ∴P (32,−218). 第二种情形:当∠DQP =90°.①如图3﹣3中,当△PDQ ∽△ABC 时,AA AA =AA AA =12, 过点Q 作QM ⊥PD 于M .则△QDM ∽△PDQ ,∴AA AA =AA AA =12,由图3﹣3可知,M (32,398),Q (112,398), ∴MD =8,MQ =4,∴DQ =4√5,由AA AA =AA AA ,可得PD =10, ∵D (32,−258) ∴P (32,558).②当△DPQ ∽△ABC 时,过点Q 作QM ⊥PD 于M .同法可得M (32,−218),Q (52,−218), ∴DM =12,QM =1,QD =√52,由AA AA =AA AA ,可得PD =52, ∴P (32,−58). 综上所述:P 点坐标为(32,398)或(32,−218)或(32,558)或(32,−58). 21.【解答】解:(1)①∵点A 在y =14x 2的图象上,横坐标为8, ∴A (8,16),∴直线OA 的解析式为y =2x ,∵点M 的纵坐标为m ,∴M (12m ,m ).②假设能在抛物线上,连接OP .∵∠AOB =90°,∴直线OB 的解析式为y =−12x ,∵点N 在直线OB 上,纵坐标为m ,∴N (﹣2m ,m ),∴MN 的中点的坐标为(−34m ,m ),∴P (−32m ,2m ),把点P 坐标代入抛物线的解析式得到m =329.(2)①当点A 在y 轴的右侧时,设A (a ,14a 2),∴直线OA 的解析式为y =14ax , ∴M (8A,2),∵OB ⊥OA , ∴直线OB 的解析式为y =−4A x ,可得N (−A 2,2),∴P (8A −A 2,4),代入抛物线的解析式得到,8A −A 2=±4,解得,a =4√2±4,∴直线OA 的解析式为y =(√2±1)x .②当点A 在y 轴的左侧时,即为①中点B 的位置,∴直线OA的解析式为y=−4A x=﹣(√2±1)x,综上所述,满足条件的直线OA的解析式为y=(√2±1)x或y=﹣(√2±1)x.。
2020中考数学复习分类汇编专题4:二次函数与直角三角形以及矩形问题(含答案)

专题:二次函数与直角三角形、矩形问题1. 如图,抛物线y =14x 2-32x -4与x 轴交于A ,B 两点(点B 在点A 右侧),与y 轴交于点C.连接BC ,以BC 为一边,点O 为对称中心作菱形BDEC ,点P 是x 轴上的一个动点,设点P 的坐标为(m ,0),过点P 作x 轴的垂线l 交抛物线于点Q .(1)求点A ,B ,C 的坐标;(2)点P 在线段OB 上运动时,直线l 分别交BD ,BC 于点M ,N .试探究m 为何值时,四边形CQMD 是平行四边形,此时,请判断四边形CQBM 的形状,并说明理由;(3)当点P 在线段EB 上运动时,是否存在点Q ,使△BDQ 为直角三角形,若存在,请直接写出....点Q 的坐标;若不存在,请说明理由.2. 如图,直线y =-12x +n 与x 轴交于点A ,与y 轴交于点B (0,4),抛物线y =-12x 2+bx +c 经过A 、B 两点,点C 为点B 关于x 轴的对称点,连接A C.(1)求点A 的坐标及抛物线的表达式;(2)点P 为直线AB 上方抛物线上一动点,过点P 作x 轴的垂线l ,与x 轴交于点E ,与AC 交于点M ,设点P 的横坐标为m .①求四边形PBCA 的最大面积;②是否存在点P ,使得△P AM 是直角三角形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.3.如图,抛物线y =ax 2+2x +c 与x 轴交于 A ,B 两点,与y 轴交于点C ,且点B 与点C 的坐标分别为B (3,0),C (0,3),点M 是抛物线的顶点.(1)求抛物线的表达式;(2)点P 是线段MB 上一个动点,且点P 的横坐标为m ,过点P 作PD ⊥x 轴于点D ,交抛物线于点E ,求线段PE 的最大值,并求出此时点E 的坐标;(3)在(2)的条件下,若在线段MB 上存在点P ,使得△PCD 为直角三角形,请直接写出点P 的坐标.4. 如图,一次函数y =ax +b 的图象与x 轴交于点A ,二次函数y =12x 2-32x +1的图象与一次函数y =ax +b 的图象交于B (0,1)、C (4,3)两点,与x 轴交于D 、E 两点,且OD =1.(1)求一次函数的表达式及点A 的坐标;(2)若抛物线上存在点P ,使S △BDC =S △PBC ,求出P 点坐标(不与已知点重合); (3)若N 为x 轴上一点,平面内是否存在点M ,使得以点B 、C 、M 、N 为顶点的四边形为矩形,若存在,请求出点M 的坐标;若不存在,请说明理由.5.如图,二次函数y=kx2-3kx-4k(k≠0)的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C,OC=O A.(1)求点A的坐标和抛物线的解析式;(2)在抛物线上是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)过抛物线上的点Q作垂直于y轴的直线,交y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,直接写出点Q的坐标.6. 如图①,已知抛物线y =ax 2+bx +c 的图象经过点A (0,3)、B (1,0),其对称轴为直线l :x =2,过点A 作AC ∥x 轴交抛物线于点C ,∠AOB 的平分线交线段AC 于点E ,点P 是抛物线上的一个动点,设其横坐标为m .(1)求抛物线的解析式;(2)若动点P 在直线OE 下方的抛物线上,连接PE 、PO ,当m 为何值时,四边形AOPE 面积最大,并求出其最大值;(3)如图②,F 是抛物线的对称轴l 上的一点,在抛物线上是否存在点P 使△POF 成为以点P 为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.7. 如图,抛物线y =-49x 2+bx +c 与y 轴交于点A (0,8),与x 轴交于点B (6,0),C ,过点A 作AD ∥x 轴与抛物线交于另一点D.(1)求抛物线的表达式;(2)连接AB ,点P 为AB 上一个动点,由点A 以每秒1个单位长度的速度沿AB 运动(不与点B 重合),运动时间为t ,过点P 作PQ ∥y 轴交抛物线于点Q ,求PQ 与t 的函数关系式;(3)点M 是y 轴上的一个点,点N 是平面直角坐标系内一点,是否存在这样的点M 、N ,使得以B 、D 、M 、N 为顶点的四边形是矩形?若存在,请直接写出点N 的坐标;若不存在,请说明理由.参考答案1. 解:(1)当y =0时,则14x 2-32x -4=0,解得,x 1=-2,x 2=8,∵点B 在点A 的右侧,∴点A 、B 的坐标分别为(-2,0)、(8,0), 当x =0时,y =-4, ∴点C 的坐标为(0,-4);(2)四边形CQBM 的形状是平行四边形,理由如下: 由菱形的对称性可知,点D 的坐标为(0,4).设直线BD 的表达式为y =kx +b (k ≠0),将B (8,0),D (0,4)代入解析式,得⎩⎪⎨⎪⎧8k +b =0,b =4,解得⎩⎪⎨⎪⎧k =-12,b =4.∴直线BD 的表达式为y =-12x +4.(4分)∵l ⊥x 轴,∴点M ,Q 的坐标分别是(m ,-12m +4),(m ,14m 2-32m -4).当MQ =DC 时,四边形CQMD 是平行四边形, ∴(-12m +4)-(14m 2-32m -4)=4-(-4)=8,化简得m 2-4m =0.解得m 1=0(舍去)或m 2=4, ∴当m =4时,四边形CQMD 是平行四边形, 此时,四边形CQBM 是平行四边形. 解法一:∵m =4,∴点P 是OB 中点, ∵l ⊥x 轴,∴l ∥y 轴, ∴△BPM ∽△BOD ,∴BP BO =BM BD =12,∴BM =DM ∵四边形CQMD 是平行四边形, ∴DM ∥CQ 、DM =CQ , ∴BM ∥CQ ,BM =CQ , ∴四边形CQBM 是平行四边形;解法二:设直线BC 的表达式y =k 1x +b 1,(k 1≠0)将B (8,0),C (0,-4)代入表达式,得⎩⎪⎨⎪⎧8k 1+b 1=0,b 1=-4, 解得⎩⎪⎨⎪⎧k 1=12,b 1=-4.∴直线BC 的表达式为y =12x -4.又∵l ⊥x 轴交BC 于点N , ∴当x =4时,y =-2. ∴点N 的坐标为(4,-2).由上述可知,点M ,Q 的坐标分别为M (4,2),Q (4,-6), ∴MN =2-(-2)=4, NQ =-2-(-6)=4, ∴MN =QN ,又∵四边形CQMD 是平行四边形, ∴DB ∥CQ , ∴∠MBN =∠QCN , 又∵∠MNB =∠QNC , ∴△BMN ≌△CQN ,∴BN =CN ,∴四边形CQBM 为平行四边形(3)存在.点Q 坐标为(-2,0)或(6,-4).【解法提示】①当∠BDQ 为直角时(如解图①),由点A 、B 、D 的坐标可知,此时点Q 与A 重合,即点Q 的坐标为(-2,0);第1题解图①②当∠DBQ 为直角时(如解图②),此时有两种方法可以解决问题,一种是利用BD 与BQ 的垂直关系求直线BQ 的表达式,将直线BQ 的表达式和抛物线的表达式联立方程组,通过计算求点Q 的坐标.由BD ⊥BQ ,且由(2)知直线BD 的表达式为y =-12x +4,设BQ的表达式为y =2(x -a ),∵直线BQ 过点B (8,0),代入得a =8, 则直线BQ 的表达式为y =2x -16,联立二次函数与直线BQ 的表达式⎩⎪⎨⎪⎧y =2x -16y =14x 2-32x -4,解得⎩⎪⎨⎪⎧x 1=6y 1=-4,⎩⎪⎨⎪⎧x 2=8y 2=0, ∴Q 点坐标为(6,-4);第1题解图②③当∠DQB 为直角时,以BD 为直径作圆与抛物线没有交点,因此此时点Q 不存在. 综上所述,抛物线上存在点Q 使得△BDQ 为直角三角形,点Q 的坐标为(-2,0)或(6,-4).2. 解:(1)∵直线y =-12x +n 与y 轴交于点B (0,4),∴n =4,∴直线AB 的表达式为y =-12x +4,当y =0时,有-12x +4=0,解得x =8,∴点A 的坐标为(8,0),将点A (8,0)、B (0,4)代入y =-12x 2+bx +c ,得⎩⎪⎨⎪⎧-32+8b +c =0,c =4,解得⎩⎪⎨⎪⎧b =72,c =4.∴抛物线的表达式为y =-12x 2+72x +4;(2)①设直线l 与AB 交于点F ,如解图, ∵点P 的横坐标为m (0<m <8),∴点P 的坐标为(m ,-12m 2+72m +4),点F 的坐标为(m ,-12m +4),∴PF =(-12m 2+72m +4)-(-12m +4)=-12m 2+4m ,∴S四边形PBCA=S △PBF +S △P AF +S △OAB +S △OAC =12PF ·OE +12PF ·AE +12OA ·OB +12OA ·OC =12PF ·OA +OA ·OB =12×8×(-12m 2+4m )+8×4=-2m 2+16m +32=-2(m -4)2+64, ∵-2<0,∴当m =4时,四边形PBCA 的面积取最大值,最大值为64;第2题解图②存在点P ,使得△P AM 是直角三角形,点P 坐标为(3,10). 【解法提示】∵PM ⊥x 轴,AP 、AM 均不与x 轴重合, ∴若△P AM 为直角三角形,只能是∠P AM =90°.∵点C 为点B 关于x 轴的对称点,直线AB 的表达式为y =-12x +4,∴直线AC 的表达式为y =12x -4,∵AP ⊥AM ,点A 的坐标为(8,0),直线AM 的表达式为y =12x -4,∴直线AP 的表达式为y =-2(x -8)=-2x +16. 联立直线AP 及抛物线表达式, 得⎩⎪⎨⎪⎧y =-2x +16,y =-12x 2+72x +4, 解得⎩⎪⎨⎪⎧x 1=3,y 1=10,⎩⎪⎨⎪⎧x 2=8,y 2=0.(舍去)∴存在点P ,使得△P AM 为直角三角形,点P 的坐标为(3,10). 3. 解:(1)将点B (3,0)、C (0,3)分别代入抛物线y =ax 2+2x +c 中,得⎩⎪⎨⎪⎧9a +6+c =0,c =3,解得⎩⎪⎨⎪⎧a =-1,c =3,∴抛物线的表达式为y =-x 2+2x +3; (2)∵y =-x 2+2x +3=-(x -1)2+4, ∴M (1,4).设直线BM 的表达式为y =kx +n (k ≠0),把点B (3,0),M (1,4)分别代入,得⎩⎪⎨⎪⎧3k +n =0,k +n =4,解得⎩⎪⎨⎪⎧k =-2,n =6,∴直线BM 的表达式为y =-2x +6. ∵点P 的横坐标为m ,∴P (m ,-2m +6),E (m ,-m 2+2m +3),∴PE =-m 2+2m +3-(-2m +6)=-m 2+4m -3=-(m -2)2+1, ∴当m =2时,PE 有最大值,最大值为1, 此时点E 的坐标为(2,3);(3)点P 的坐标为(32,3)或(-3+32,12-62).【解法提示】根据题意可得∠PDC 不可能为90°; (ⅰ)当∠DPC =90°时,则PD =OC =3,即-2m +6=3, 解得m =32,此时点P 的坐标为(32,3);(ⅱ)当∠PCD =90°时,则PC 2+CD 2=PD 2, 即m 2+(-2m +3)2+32+m 2=(-2m +6)2,整理得m 2+6m -9=0,解得m =-3-32(舍去)或m =-3+32,当m =-3+32时,y =-2m +6=12-62,此时点P 的坐标为(-3+32,12-62), 综上所述,点P 的坐标为(32,3)或(-3+32,12-62).4. 解:(1)将B (0,1)、C (4,3)代入y =ax +b ,得⎩⎪⎨⎪⎧b =1,4a +b =3,解得⎩⎪⎨⎪⎧a =12,b =1,∴一次函数的表达式为y =12x +1,令y =0,得x =-2, ∴A (-2,0)(2)如解图①,过点D 作y 轴平行线交BC 与点F ,过点P 作PG ∥y 轴,交BC 于点G .将x =1代入直线BC 的表达式得y =32.设点P (x ,12x 2-32x +1),则G (x ,12x +1).∴GP =|12x +1-(12x 2-32x +1)|=|-12x 2+2x |=|12x 2-2x |.∵S △PBC =S △DBC ,∴DF =GP ,即|12x 2-2x |=32;当12x 2-2x =32时,解得x =2+7或x =2-7. ∴点P 的坐标为(2+7,7+72)或(2-7,7-72).当12x 2-2x =-32时,解得x =3或x =1(舍去). ∴点P 的坐标为(3,1).综上所述,点P 的坐标为(3,1)或(2+7,7+72)或(2-7,7-72); (3)存在.如解图②,当∠CBN =90°时,BN 的表达式为y =-2x +1.将y =0代入得-2x +1=0, 解得x =12.∴点N 的坐标为(12,0).设点M 的坐标为(x ,y ). ∵四边形BNMC 为矩形, ∴12+42=0+x 2,0+32=1+y 2,解得x =92,y =2.∴点M 的坐标为(92,2);如解图,当∠CNM =90°时,设CN 的表达式为y =-2x +n ,将点C 的坐标代入得-8+n =3,解得n =11, ∴CN 的表达式为y =-2x +11.将y =0代入得-2x +11=0,解得x =112.∴点N 的坐标为(112,0).设点M 的坐标为(x ,y ). ∵四边形BMNC 为矩形,∴0+1122=4+x 2,1+02=3+y 2,解得x =32,y =-2.∴点M 的坐标为(32,-2);如解图④,当∠BNC =90°时,过点C 作CF ⊥x 轴,垂足为F .设ON =a ,则NF =4-a .∵∠BNO +∠OBN =90°,∠BNO +∠CNF =90°, ∴∠OBN =∠CNF . 又∵∠BON =∠CFN , ∴△BON ∽△NFC . ∴ON FC =OB FN ,即a 3=14-a,解得a =1或a =3, 当a =1时,点N 的坐标为(1,0),设点M 的坐标为(x ,y ). ∵四边形BNCM 为矩形,∴0+42=1+x 2,1+32=0+y2, 解得x =3,y =4. ∴点M 的坐标为(3,4);当a =3时,点N 的坐标为(3,0),设点M 的坐标为(x ,y ). ∵四边形BNCM 为矩形, ∴0+42=3+x 2,1+32=0+y 2, 解得x =1,y =4. ∴点M 的坐标为(1,4).综上所述,点M 的坐标为(92,2)或(32,-2)或(3,4)或(1,4).5. 解:(1)当y =0时,kx 2-3kx -4k =0, ∵k ≠0,∴x 2-3x -4=0, 解得x 1=-1,x 2=4, ∵点A 在点B 右侧, ∴B (-1,0),A (4,0), ∵OA =OC ,∴C (0,4),把x =0,y =4代入y =kx 2-3kx -4k ,得k =-1, 故抛物线的解析式为y =-x 2+3x +4;(2)存在,①当∠PCA =90°时,如解图,过点P 作PM ⊥y 轴于点M .∴∠MCP +∠ACO =90°,∵∠OAC+∠ACO=90°,∴∠MCP=∠OAC,∵OA=OC,∴∠MCP=∠OAC=45°,∴∠MPC=∠MCP=45°,∴MC=MP,设P(m,-m2+3m+4),则PM=CM=m,OM=-m2+3m+4,∴m+4=-m2+3m+4,解得m1=0(舍去),m2=2,∴-m2+3m+4=6,即P(2,6);②当∠P AC=90°时,如解图②,过点P作PN⊥y轴于点N,设AP与y轴交于点F,则有PN∥x轴,∴∠FPN=∠OAP,∵∠CAO=45°,∴∠OAP=45°,∴∠FPN=45°,OF=AO=4,∴PN=NF,设P(n,-n2+3n+4),则PN=-n,ON=n2-3n-4,∴-n=n2-3n-4-4,即n 2-2n -8=0,解得n 1=-2,n 2=4(舍去), ∴-n 2+3n +4=-6, 即P (-2,-6),综上所述,点P 的坐标是(2,6)或(-2,-6);(3)当点Q 的坐标是(3+172,2)或(3-172,2)时,EF 最短.【解法提示】如解图,∵∠OED =∠DFO =∠EOF =90°, ∴四边形OEDF 是矩形, ∴EF =OD ,∴当线段EF 的长度最短时,OD 最小,此时OD ⊥AC , ∵OA =OC ,∴∠COD =∠AOD =45°,CD =AD , ∵DF ∥OC , ∴△ADF ∽△ACO , ∴DF OC =AD AC =12, ∴DF =12OC =2,∴y Q =2,∴令y =2,即-x 2+3x +4=2,解得x 1=3+172,x 2=3-172,∴点Q 的坐标是(3+172,2)或(3-172,2).6. 解:(1)∵抛物线y =ax 2+bx +c 的图象经过点A (0,3)、B (1,0),对称轴为直线l :x =2,∴⎩⎪⎨⎪⎧c =3,a +b +c =0,-b 2a =2,解得⎩⎪⎨⎪⎧a =1,b =-4,c =3.∴抛物线的解析式为y =x 2-4x +3;(2)如解图①,过点P 作y 轴的平行线与OE 交于点Q ,与AE 交于点F ,设点P 的坐标为(m ,m 2-4m +3), ∵∠AOB 的平分线交线段AC 于点E , ∴直线OE 的解析式为y =x , 则点Q 的坐标为(m ,m ), ∴S四边形AOPE =S △OAE +S △OPQ +S △EPQ =12OA ·AE +12PQ ·AF +12PQ ·EF =12OA ·AE +12PQ ·AE =12×3×3+12(m -m 2+4m -3)×3=-32m 2+152m =-32(m -52)2+758, ∵-32<0,∴当m =52时,四边形AOPE 的面积最大,最大值是758;(3)存在,点P 的坐标为(3+52,1-52)或(3-52,1+52)或(5+52,1+52)或(5-52,1-52). 【解法提示】如解图②,过点P 作x 轴的平行线,交y 轴于点M ,交对称轴于点N ,设P (m ,m 2-4m +3).∴∠OMP =∠PNF =90°,∵△POF 是以点P 为直角顶点的等腰直角三角形, ∴∠OPF =90°,OP =PF ,∴∠MOP +∠OPM =90°,∠OPM +∠NPF =90°, ∴∠MOP =∠NPF , ∴△OPM ≌△PFN ,∴OM =PN ,即|m 2-4m +3|=|2-m |, 当m 2-4m +3=2-m 时,解得m =3±52,此时点P 的坐标为(3+52,1-52)或(3-52,1+52),当-(m 2-4m +3)=2-m 时,解得m =5±52,此时点P 的坐标为(5+52,1+52)或(5-52,1-52),综上所述,满足条件的点P 的坐标为(3+52,1-52)或(3-52,1+52)或(5+52,1+52)或(5-52,1-52).7. 解:(1)将A (0,8)、B (6,0)代入抛物线y =-49x 2+bx +c ,得⎩⎪⎨⎪⎧-49×36+6b +c =0,c =8,解得⎩⎪⎨⎪⎧b =43,c =8,∴抛物线的表达式为y =-49x 2+43x +8;(2)设直线AB 的解析式为y =kx +d ,将A ,B 两点坐标代入解析式得⎩⎪⎨⎪⎧d =8,6k +d =0,解得⎩⎪⎨⎪⎧d =8,k =-43,∴直线AB 的解析式为y =-43x +8.∵OA =8,OB =6, ∴AB =10,如解图①,过点P 作PE ⊥y 轴于点E ,则△AEP ∽△AOB ,∴AE ∶EP ∶AP =AO ∶OB ∶AB =4∶3∶5, 根据题意可知AP =t , ∴AE =45t ,EP =35t ,∴PQ =-49×(35t )2+43×35t +8-(-43×35t +8)=-425t 2+85t ,∴PQ 与t 的函数关系式为PQ =-425t 2+85t (0≤t <10);(3)存在.点N 的坐标为(3,-98)或(-3,234).【解法提示】要使以B 、D 、M 、N 为顶点的四边形是矩形,分以下两种情况讨论: 如解图②,过点B 作x 轴的垂线交AD 的延长线于点E ,则AE ⊥EB ,当y =8时, -49x 2+43x +8=8, 解得x =0或3, ∴点D 的坐标为(3,8), ∴AD =3,DE =3,①如解图②,当DM 为矩形的边时,过点N 作NK ⊥x 轴,交x 轴于点K ∵∠MAD =∠DEB =90°,∠ADM +∠BDE =90°,∠AMD +∠ADM =90°, ∴∠BDE =∠AMD , ∴△ADM ∽△EBD , ∴AM ED =AD EB ,即AM 3=38, ∴AM =98,同理,可求得△EBD ∽△KBN ,∴△ADM ∽△KBN .∵MD =NB ,∴△ADM ≌△KBN ,∴OK =KB =AD =3,AM =KN =98, ∴N (3,-98); ②如解图②,当DM ′为矩形的对角线时,过点N ′作N ′K ′⊥x 轴交DA 的延长线于点K ′. 同理可得△M ′BO ∽△DBE ,∴OM ′ED =OB EB, ∴OM ′3=68,∴OM ′=94, ∵DN ′=BM ′,∴易得△DN ′K ′≌△BM ′O .∴N ′K ′=M ′O =94,K ′D =OB =6. ∴AK ′=3,点N ′的纵坐标=OA -N ′K ′=8-94=234. ∴N ′(-3,234), ③当BD 为对角线时,取BD 中点I ,∵D (3,8),B (6,0),∴I (92,4). 以I 为圆心以BD 为半径作圆,假设⊙I 与y 轴有交点,设交点坐标为(0,t ),则有BD 2=(6-3)2+(8-0)2=73,DI 2=(8-t )2+(3-0)2=t 2-16t +73,BI 2=(6-0)2+(t -0)2=t 2+36,∴DI 2+BI 2=BD 2,即t 2-16t +73+t 2+36=73,整理得t 2-8t +18=0,∵b 2-4ac =(-8)2-4×1×18=8<0,∴原方程无解.∴⊙I 与y 轴无交点,∴以BD 为对角线这种情况不存在.综上所述,存在点M 、N ,使得以B 、D 、M 、N 为顶点的四边形是矩形,点N 的坐标为(3,-98)或(-3,234).。
2020年初三数学下册中考专题复习 二次函数的存在性问题【含答案】

2020年初三数学下册中考专题复习二次函数的存在性问题一.解答题(共20小题)1.如图,在▱OABC中,A、C两点的坐标分别为(4,0)、(﹣2,3),抛物线W经过O、A、C三点,点D是抛物线W的顶点.(1)求抛物线W的函数解析式及顶点D的坐标;(2)将抛物线W和▱OABC同时先向右平移4个单位长度,再向下平移m(0<m<3)个单位长度,得到抛物线W1和□O1A1B1C1,在向下平移过程中,O1C1与x轴交于点H,▱O1A1B1C1与▱OABC重叠部分的面积记为S,试探究:当m为何值时,S有最大值,并求出S的最大值;(3)在(2)的条件下,当S取最大值时,设此时抛物线W1的顶点为F,若点M是x 轴上的动点,点N是抛物线W1上的动点,是否存在这样的点M、N,使以D、F、M、N 为顶点的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.2.如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点A(1,0)、B(5,0)、C(0,4)三点.(1)求抛物线的解析式和对称轴;(2)P是抛物线对称轴上的一点,求满足PA+PC的值为最小的点P坐标(请在图1中探索);(3)在第四象限的抛物线上是否存在点E,使四边形OEBF是以OB为对角线且面积为12的平行四边形?若存在,请求出点E坐标,若不存在请说明理由(请在图2中探索)3.如图,抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点.(1)求抛物线的函数表达式;(2)如图1,P为抛物线上在第二象限内的一点,若△PAC面积为3,求点P的坐标;(3)如图2,D为抛物线的顶点,在线段AD上是否存在点M,使得以M,A,O为顶点的三角形与△ABC相似?若存在,求点M的坐标;若不存在,请说明理由.4.如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,﹣),与x轴交于A、B两点.(1)求抛物线的解析式.(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和的值.(3)点F(0,y)是y轴上一动点,当y为何值时,FC+BF的值最小.并求出这个最小值.(4)点C关于x轴的对称点为H,当FC+BF取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.5.如图1,抛物线C:y=ax2+bx经过点A(﹣4,0)、B(﹣1,3)两点,G是其顶点,将抛物线C绕点O旋转180°,得到新的抛物线C′.(1)求抛物线C的函数解析式及顶点G的坐标;(2)如图2,直线l:y=kx﹣经过点A,D是抛物线C上的一点,设D点的横坐标为m(m<﹣2),连接DO并延长,交抛物线C′于点E,交直线l于点M,若DE=2EM,求m的值;(3)如图3,在(2)的条件下,连接AG、AB,在直线DE下方的抛物线C上是否存在点P,使得∠DEP=∠GAB?若存在,求出点P的横坐标;若不存在,请说明理由.6.如图,抛物线y=ax2+bx+2交x轴于点A(﹣3,0)和点B(1,0),交y轴于点C.(1)求这个抛物线的函数表达式.(2)点D的坐标为(﹣1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP 面积的最大值.(3)点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,请直接写出点N的坐标;若不存在,请说明理由.7.已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线解析式;(2)当点P运动到什么位置时,△PAB的面积最大?(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.8.如图,抛物线y=ax2+2x+c经过A(﹣1,0),B两点,且与y轴交于点C(0,3),抛物线与直线y=﹣x﹣1交于A,E两点.(1)求抛物线的解析式;(2)坐标轴上是否存在一点Q,使得△AQE是以AE为底边的等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.(3)P点在x轴上且位于点B的左侧,若以P,B,C为顶点的三角形与△ABE相似,求点P的坐标.9.如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.(1)求抛物线的表达式;(2)如图1,连接BC,PB,PC,设△PBC的面积为S.求S关于t的函数表达式,并求出当t为何值时,△PBC的面积S有最大值;(3)如图2,设抛物线的对称轴为直线l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.10.综合与探究如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣3,0)、B两点,与y轴相交于点.当x=﹣4和x=2时,二次函数y=ax2+bx+c(a≠0)的函数值y相等,连接AC,BC.(1)求抛物线的解析式;(2)判断△ABC的形状,并说明理由;(3)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动,当运动时间为t秒时,连接MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,则t的值为,点P的坐标为;(4)抛物线对称轴上是否存在一点F,使得△ACF是以AC为直角边的直角三角形?若不存在,请说明理由;若存在,请直接写出点F的坐标.11.如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.(l)求抛物线的表达式;(2)如图l,若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求此时E点的坐标;(3)如图2,在x轴上是否存在一点D使得△ACD为等腰三角形?若存在,请求出所有符合条件的点D的坐标;若不存在,请说明理由.12.如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.(1)求二次函数的关系式;(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,①求S与m的函数关系式,写出自变量m的取值范围.②当S取得最值时,求点P的坐标;(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.13.如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,已知点P为抛物线第一象限上一动点,连接PB、PC、BC.(1)求抛物线的解析式,并直接写出抛物线的顶点坐标;(2)当△PBC的面积最大时,求出点P的坐标;(3)如图②,当点P与抛物线顶点重合时,过点B的直线与抛物线交于点E,在直线BE上方的抛物线上是否存在一点M,使得∠BEM=∠PBC?若存在,求出点M 的坐标;若不存在,请说明理由.14.如图,抛物线y=﹣x2+2x+3与坐标轴分别交于A,B,C三点,连接AC,BC.(1)直接写出A,B,C三点的坐标;(2)点M是线段BC上一点(不与B,C重合),过点M作x轴的垂线交抛物线于点N,连接CN.若点M关于直线CN的对称点M'恰好在y轴上,求出点M的坐标;(3)在平面内是否存在一点P,使△AOC关于点P的对称△A'O'C'(点A',O',C'分别是点A,O,C的对称点)恰好有两个顶点落在该抛物线上?若存在,求出点P的坐标;若不存在,说明理由.如果没有解题思路,可以这样考虑:变换后,A'O'与AO,O'C'与OC有什么样的位置关系?进而分析点O',A',C'的坐标关系!15.如图1,过原点的抛物线与x轴交于另一点A,抛物线顶点C的坐标为,其对称轴交x轴于点B.(1)求抛物线的解析式;(2)如图2,点D为抛物线上位于第一象限内且在对称轴右侧的一个动点,求使△ACD 面积最大时点D的坐标;(3)在对称轴上是否存在点P,使得点A关于直线OP的对称点A'满足以点O、A、C、A'为顶点的四边形为菱形.若存在,请求出点P的坐标;若不存在,请说明理由.16.综合与探究如图,已知抛物线y=ax2﹣2x+c与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,对称轴为直线l,顶点为D.(1)求抛物线的解析式及点D坐标;(2)在直线l上是否存在一点M,使点M到点B的距离与到点C的距离之和最小?若存在,求出点M的坐标;若不存在,请说明理由.(3)在x轴上取一动点P(m,0),﹣3<m<﹣1,过点P作x轴的垂线,分别交抛物线,AD,AC于点E,F,G.①判断线段FP与FG的数量关系,并说明理由②连接EA,ED,CD,当m为何值时,四边形AEDC的面积最大?最大值为多少?17.如图,抛物线y=ax2+bx(a>0)与双曲线y=相交于点A、B,已知点A坐标(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).(1)求实数a、b、k的值;(2)在该抛物线的对称轴上是否存在点P使得△POB为等腰三角形?若存在请求出所有的P点的坐标,若不存在请说明理由.(3)在坐标系内有一个点M,恰使得MA=MB=MO,现要求在y轴上找出点Q使得△BQM的周长最小,请求出M的坐标和△BQM周长的最小值.18.如图,已知,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,过点A的直线y=kx+k与该抛物线交于点C,点P是该抛物线上不与A,B重合的动点,过点P 作PD⊥x轴于D,交直线AC于点E.(1)求抛物线的解析式;(2)若k=﹣1,当PE=2DE时,求点P坐标;(3)当(2)中直线PD为x=1时,是否存在实数k,使△ADE与△PCE相似?若存在请求出k的值;若不存在,请说明你的理由.19.如图,抛物线y=ax2+bx﹣过点A(﹣,0)和点B(,2),连结AB交y轴于点C.(1)求抛物线的函数解析式;(2)点P在线段AB下方的抛物线上运动,连结AP,BP.设点P的横坐标为m,△ABP 的面积为s.①求s与m的函数关系式;②当s取最大值时,抛物线上是否存在点Q,使得S△ACQ=s.若存在,求点Q的坐标;若不存在,说明理由.20.如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交点C,抛物线y =﹣2x2+bx+c过A,C两点,与x轴交于另一点B.(1)求抛物线的解析式.(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当EF =BF时,求sin∠EBA的值.(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.详细答案一.解答题(共20小题)1.【解答】解:(1)设抛物线W的函数解析式为y=ax2+bx,图象经过A(4,0),C(﹣2,3)∴抛物线W的函数解析式为,顶点D的坐标为(2,﹣1);(2)根据题意,由O(0,0),C(﹣2,3),得O1(4,﹣m),C1(2,3﹣m)设直线O1C1的函数解析式为y=kx+b把O1(4,﹣m),C1(2,3﹣m)代入y=kx+b得:,直线O1C1与x轴交于点H∴过C1作C1E⊥HA于点E,∵0<m<3∴,∴,∵,抛物线开口向下,S有最大值,最大值为∴当时,;(3)当时,由D(2,﹣1)得F(6,)∴抛物线W1的函数解析式为,依题意设M(t,0),以D,F,M,N为顶点的四边形是平行四边形,分情况讨论:①以DF为边时∵D(2,﹣1),F点D,F横坐标之差是4,纵坐标之差是,若点M、N的横纵坐标与之有相同规律,则以D,F,M,N为顶点的四边形是平行四边形,∵M(t,0),∴把分别代入得t1=0,t2=4,t3=6,t4=14∴M1(0,0),M2(4,0),M3(6,0),M4(14,0)②以DF为对角线时,以点D,F,M,N为顶点不能构成平行四边形.综上所述:M1(0,0),M2(4,0),M3(6,0),M4(14,0).2.【解答】解:(1)将点A、B的坐标代入二次函数表达式得:y=a(x﹣1)(x﹣5)=a(x2﹣6x+5),则5a=4,解得:a=,抛物线的表达式为:y=(x2﹣6x+5)=x2﹣x+4,函数的对称轴为:x=3,顶点坐标为(3,﹣);(2)连接B、C交对称轴于点P,此时PA+PC的值为最小,将点B、C的坐标代入一次函数表达式:y=kx+b得:,解得:,直线BC的表达式为:y=﹣x+4,当x=3时,y=,故点P(3,);(3)存在,理由:四边形OEBF是以OB为对角线且面积为12的平行四边形,=OB×|y E|=5×|y E|=12,则S四边形OEBF点E在第四象限,故:则y E=﹣,将该坐标代入二次函数表达式得:y=(x2﹣6x+5)=﹣,解得:x=2或4,故点E的坐标为(2,﹣)或(4,﹣).3.【解答】解:(1)把A(﹣3,0),B(1,0),C(0,3)代入抛物线解析式y=ax2+bx+c 得,解得,所以抛物线的函数表达式为y=﹣x2﹣2x+3.(2)如解(2)图1,过P点作PQ平行y轴,交AC于Q点,∵A(﹣3,0),C(0,3),∴直线AC解析式为y=x+3,设P点坐标为(x,﹣x2﹣2x+3.),则Q点坐标为(x,x+3),∴PQ=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x.=,∴S△P AC∴,解得:x1=﹣1,x2=﹣2.当x=﹣1时,P点坐标为(﹣1,4),当x=﹣2时,P点坐标为(﹣2,3),综上所述:若△PAC面积为3,点P的坐标为(﹣1,4)或(﹣2,3),(3)如解(3)图1,过D点作DF垂直x轴于F点,过A点作AE垂直BC于E点,∵D为抛物线y=﹣x2﹣2x+3的顶点,∴D点坐标为(﹣1,4),又∵A(﹣3,0),∴直线AD为y=2x+6,AF=2,DF=4,tan∠DAB=2,∵B(1,0),C(0,3)∴tan∠ABC=3,BC=,sin∠ABC=,直线BC解析式为y=﹣3x+3.∵AB=4,∴AE=AB•sin∠ABC==,BE=,∴CE=,∴tan∠ACB=,∴tan∠ACB=tan∠DAB=2,∴∠ACB=∠DAB,∴使得以M,A,O为顶点的三角形与△ABC相似,则有两种情况,如解(3)图2Ⅰ.当∠AOM=∠CAB=45°时,△ABC∽△OMA,即OM为y=﹣x,设OM与AD的交点M(x,y)依题意得:,解得,即M点为(﹣2,2).Ⅱ.若∠AOM=∠CBA,即OM∥BC,∵直线BC解析式为y=﹣3x+3.∴直线OM为y=﹣3x,设直线OM与AD的交点M(x,y).则依题意得:,解得,即M点为(,),综上所述:存在使得以M,A,O为顶点的三角形与△ABC相似的点M,其坐标为(﹣2,2)或(,),4.【解答】解:(1)由题可列方程组:,解得:∴抛物线解析式为:y=x2﹣x﹣2;(2)如图1,∠AOC=90°,AC=,AB=4,设直线AC的解析式为:y=kx+b,则,解得:,∴直线AC的解析式为:y=﹣2x﹣2;当△AOC∽△AEB时=()2=()2=,=1,∴S△AEB=,∵S△AOC∴AB×|y E|=,AB=4,则y E=﹣,则点E(﹣,﹣);由△AOC∽△AEB得:∴;(3)如图2,连接BF,过点F作FG⊥AC于G,则FG=CF sin∠FCG=CF,∴CF+BF=GF+BF≥BE,当折线段BFG与BE重合时,取得最小值,由(2)可知∠ABE=∠ACO∴BE=AB cos∠ABE=AB cos∠ACO=4×=,|y|=OB tan∠ABE=OB tan∠ACO=3×=,∴当y=﹣时,即点F(0,﹣),CF+BF有最小值为;(4)①当点Q为直角顶点时(如图3):由(3)易得F(0,﹣),∵C(0,﹣2)∴H(0,2)设Q(1,m),过点Q作QM⊥y轴于点M.则Rt△QHM∽Rt△FQM∴QM2=HM•FM,∴12=(2﹣m)(m+),解得:m=,则点Q(1,)或(1,)当点H为直角顶点时:点H(0,2),则点Q(1,2);当点F为直角顶点时:同理可得:点Q(1,﹣);综上,点Q的坐标为:(1,)或(1,)或Q(1,2)或Q(1,﹣).5.【解答】解:(1)将A(﹣4,0)、B(﹣1,3)代入y=ax2+bx中,得解得∴抛物线C解析式为:y=﹣x2﹣4x,配方,得:y=﹣x2﹣4x=﹣(x+2)2+4,∴顶点为:G(﹣2,4);(2)∵抛物线C绕点O旋转180°,得到新的抛物线C′.∴新抛物线C′的顶点为:G′(2,﹣4),二次项系数为:a′=1∴新抛物线C′的解析式为:y=(x﹣2)2﹣4=x2﹣4x将A(﹣4,0)代入y=kx﹣中,得0=﹣4k﹣,解得k=,∴直线l解析式为y=x﹣,设D(m,﹣m2﹣4m),∵D、E关于原点O对称,∴OD=OE∵DE=2EM∴OM=2OD,过点D作DF⊥x轴于F,过M作MR⊥x轴于R,∴∠OFD=∠ORM,∵∠DOF=∠MOR∴△ODF∽△OMR∴===2∴OR=2OF,RM=2DF∴M(﹣2m,2m2+8m)∴2m2+8m=•(﹣2m)﹣,解得:m1=﹣3,m2=,∵m<﹣2∴m的值为:﹣3;(3)由(2)知:m=﹣3,∴D(﹣3,3),E(3,﹣3),OE=3,如图3,连接BG,在△ABG中,∵AB2=(﹣1+4)2+(3﹣0)2=18,BG2=2,AG2=20∴AB2+BG2=AG2∴△ABG是直角三角形,∠ABG=90°,∴tan∠GAB===,∵∠DEP=∠GAB∴tan∠DEP=tan∠GAB=,在x轴下方过点O作OH⊥OE,在OH上截取OH=OE=,过点E作ET⊥y轴于T,连接EH交抛物线C于点P,点P即为所求的点;∵E(3,﹣3),∴∠EOT=45°∵∠EOH=90°∴∠HOT=45°∴H(﹣1,﹣1),设直线EH解析式为y=px+q,则,解得∴直线EH解析式为y=﹣x,解方程组,得,,∴点P的横坐标为:或.6.【解答】解:(1)抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3)=ax2+2ax﹣3a,即﹣3a=2,解得:a=﹣,故抛物线的表达式为:y=﹣x2﹣x+2,则点C(0,2),函数的对称轴为:x=﹣1;(2)连接OP,设点P(x,﹣x2﹣x+2),=S△APO+S△CPO﹣S△ODC=×AO×y P+×OC×|x P|﹣×CO×OD 则S=S四边形ADCP=(﹣x2﹣x+2)×2×(﹣x)﹣=﹣x2﹣3x+2,∵﹣1<0,故S有最大值,当x=﹣时,S的最大值为;(3)存在,理由:△MNO为等腰直角三角形,且∠MNO为直角时,点N的位置如下图所示:①当点N在x轴上方时,点N的位置为N1、N2,N1的情况(△M1N1O):设点N1的坐标为(x,﹣x2﹣x+2),则M1E=x+1,过点N1作x轴的垂线交x轴于点F,过点M1作x轴的平行线交N1F于点E,∵∠FN1O+∠M1N1E=90°,∠M1N1E+∠EM1N1=90°,∴∠EM1N1=∠FN1O,∠M1EN1=∠N1FO=90°,ON1=M1N1,∴△M1N1E≌△N1OF(AAS),∴M1E=N1F,即:x+1=﹣x2﹣x+2,解得:x=(舍去负值),则点N1(,);N2的情况(△M2N2O):同理可得:点N2(,);②当点N在x轴下方时,点N的位置为N3、N4,同理可得:点N3、N4的坐标分别为:(,)、(,);综上,点N的坐标为:(,)或(,)或(,)或(,).7.【解答】解:(1)∵抛物线y=ax2+bx+3过点B(﹣3,0),C(1,0)∴解得:∴抛物线解析式为y=﹣x2﹣2x+3(2)过点P作PH⊥x轴于点H,交AB于点F∵x=0时,y=﹣x2﹣2x+3=3∴A(0,3)∴直线AB解析式为y=x+3∵点P在线段AB上方抛物线上∴设P(t,﹣t2﹣2t+3)(﹣3<t<0)∴F(t,t+3)∴PF=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t=S△P AF+S△PBF=PF•OH+PF•BH=PF•OB=(﹣t2﹣3t)=﹣(t+)∴S△P AB2+∴点P运动到坐标为(﹣,),△PAB面积最大(3)存在点P使△PDE为等腰直角三角形设P(t,﹣t2﹣2t+3)(﹣3<t<0),则D(t,t+3)∴PD=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t∵抛物线y=﹣x2﹣2x+3=﹣(x+1)2+4∴对称轴为直线x=﹣1∵PE∥x轴交抛物线于点E∴y E=y P,即点E、P关于对称轴对称∴=﹣1∴x E=﹣2﹣x P=﹣2﹣t∴PE=|x E﹣x P|=|﹣2﹣2t|∵△PDE为等腰直角三角形,∠DPE=90°∴PD=PE①当﹣3<t≤﹣1时,PE=﹣2﹣2t∴﹣t2﹣3t=﹣2﹣2t解得:t1=1(舍去),t2=﹣2∴P(﹣2,3)②当﹣1<t<0时,PE=2+2t∴﹣t2﹣3t=2+2t解得:t1=,t2=(舍去)∴P(,)综上所述,点P坐标为(﹣2,3)或(,)时使△PDE为等腰直角三角形.8.【解答】解:(1)将A(﹣1,0),C(0,3)代入y=ax2+2x+c,得,解得,,∴抛物线的解析式为:y=﹣x2+2x+3;(2)联立,解得,或,∴E(4,﹣5),如图1,当点Q在x轴上时,设Q(m,0),∵AE为底边,∴QA=QE,∴QA2=QE2,即(m+1)2=52+(m﹣4)2,解得,m=4,∴Q1(4,0);当点Q在y轴上时,设Q(0,n),∵AE为底边,∴QA=QE,∴QA2=QE2,即n2+12=42+(n+5)2,解得,n=﹣4,∴Q2(0,﹣4);综上所述,Q1(4,0),Q2(0,﹣4);(3)如图2,过点E作EH⊥x轴于点H,∵A(﹣1,0),E(4,﹣5),∴AH=EH=5,AE==5,∠BAE=45°,又OB=OC=3,∴∠ABC=45°,AB=4,BC==3,设P(t,0),则BP=3﹣t,∵∠BAE=∠ABC=45°,∴只可能存在△PBC∽△BAE和△PBC∽△EAB两种情况,当△PBC∽△BAE时,,∴=,∴t=,∴P1(,0);当△PBC∽△EAB时,,∴=,∴t=﹣,∴P2(﹣,0),综上所述,点P的坐标为(,0)或(﹣,0).9.【解答】解:(1)将A(﹣1,0)、B(3,0)代入y=﹣x2+bx+c,得,,解得,,∴抛物线的表达式为y=﹣x2+2x+3;(2)如图1,过点P作PF∥y轴,交BC于点F,设直线BC的解析式为y=mx+n(m≠0),将B(3,0)、C(0,3)代入y=mx+n,得,,解得,,∴直线BC的解析式为y=﹣x+3,∵点P的坐标为(t,﹣t2+2t+3),∴点F的坐标为(t,﹣t+3),∴PF=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t,∴S=PF•OB=﹣t2+t=﹣(t﹣)2+,∵﹣<0,∴当t=时,S取最大值,最大值为;(3)如图2,连接PC,交抛物线对称轴l于点E,∵抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,∴抛物线的对称轴为直线x=1,∵x D﹣x C=1,∴x P﹣x M=1,∴x P=2,∴P(2,3),在y=﹣x2+2x+3中,当x=0时,y=3,∴C(0,3),∴y C﹣y D=3,∴y M﹣y P=3,∴y M=6,∴点M的坐标为(1,6);当x P≠2时,不存在,理由如下,若四边形CDPM是平行四边形,则CE=PE,∵点C的横坐标为0,点E的横坐标为1,∴点P的横坐标t=1×2﹣0=2,又∵x P≠2,∴不存在,综上所述,点M的坐标为(1,6).10.【解答】解:(1)∵在抛物线y=ax2+bx+c中,当x=﹣4和x=2时,二次函数y=ax2+bx+c 的函数值y相等,∴抛物线的对称轴为x==﹣1,又∵抛物线y=ax2+bx+c与x轴交于A(﹣3,0)、B两点,由对称性可知B(1,0),∴可设抛物线的解析式为y=a(x+3)(x﹣1),将C(0,)代入y=a(x+3)(x﹣1),得,﹣3a=,解得,a=﹣,∴此抛物线的解析式为y=﹣(x+3)(x﹣1)=﹣x2﹣x+;(2)△ABC为直角三角形,理由如下:∵A(﹣3,0),B(1,0),C(0,),∴OA=3,OB=1,OC=,∴AB=OA+OB=4,AC==2,BC==2,∵AC2+BC2=16,AB2=16,∴AC2+BC2=AB2,∴△ABC是直角三角形;(3)∵点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,∴BM=BN=t,由翻折知,△BMN≌△PMN,∴BM=PM=BN=PN=t,∴四边形PMBN是菱形,∴PN∥AB,∴△CPN∽△CAB,设PM与y轴交于H,∴==,即==,解得,t=,CH=,∴OH=OC﹣CH=﹣=,∴y P=,设直线AC的解析式为y=kx+,将点A(﹣3,0)代入y=kx+,得,k=,∴直线AC的解析式为y=x+,将y P=代入y=x+,∴x=﹣1,∴P(﹣1,),故答案为:,(﹣1,);(4)设直线BC的解析式为y=kx+,将点B(1,0)代入y=kx+,得,k=﹣,∴直线BC的解析式为y=﹣x+,由(2)知△ABC为直角三角形,∠ACB=90°,如图2,当∠ACF=90°时,点B,C,F在一条直线上,在y=﹣x+中,当x=﹣1时,y=2,∴F1(﹣1,2);当∠CAF=90°时,AF∥BC,∴可设直线AF的解析式为y=﹣x+n,将点A(﹣3,0)代入y=﹣x+n,得,n=﹣3,∴直线AF的解析式为y=﹣x﹣3,在y=﹣x﹣3中,当x=﹣1时,y=﹣2,∴F2(﹣1,﹣2);∴点F的坐标为F1(﹣1,2),F2(﹣1,﹣2).11.【解答】解:(1)将点A(1,0),B(﹣3,0)代入y=ax2+bx+3,得,,解得,,∴抛物线表达式为y=﹣x2﹣2x+3;(2)如图1,过点E作EF⊥x轴于点F,设E(a,﹣a2﹣2a+3)(﹣3<a<0),∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,∴===,最大,且最大值为;∴当时,S四边形BOCE当时,,此时,点E坐标为;(3)如图2,连接AC,①当CA=CD时,此时CO为底边的垂直平分线,满足条件的点D1,与点A关于y轴对称,点D1坐标为(﹣1,0);②当AD=AC时,在Rt△ACO中,∵OA=1,OC=3,由勾股定理得,AC==,以点A为圆心,AC的长为半径作弧,交x轴于两点D2,D3,即为满足条件的点,此时它们的坐标分别为,;③当DA=DC时,线段AC的垂直平分线与x轴的交点D4,即为满足条件的点,设垂直AC的垂直平分线交y轴于点P,过AC中点Q,∵∠AOC=∠BOC=∠PQC=∠PQA=90°,∠D4PO=∠CPQ,∴∠ACO=∠OD4P,∴△D4AQ∽△CAO,∴=,即=,∴D4A=5,∴OD4=D4A﹣OA=4,∴点D4的坐标为(﹣4,0);综上所述,存在符合条件的点D,其坐标为D1(﹣1,0)或或或D 4(﹣4,0).12.【解答】解:(1)将点B(3,0),C(0,3)代入y=﹣x2+bx+c,得,解得,,∴二次函数的解析式为y=﹣x2+2x+3;(2)①∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点M(1,4),设直线BM的解析式为y=kx+b,将点B(3,0),M(1,4)代入,得,解得,∴直线BM的解析式为y=﹣2x+6,∵PD⊥x轴且OD=m,∴P(m,﹣2m+6),=PD•OD=m(﹣2m+6)=﹣m2+3m,∴S=S△PCD即S=﹣m2+3m,∵点P在线段BM上,且B(3,0),M(1,4),∴1≤m≤3;②∵S=﹣m2+3m=﹣(m﹣)2+,∵﹣1>0,∴当m=时,S取最大值,∴P(,3);(3)存在,理由如下:如图2﹣1,当∠CPD=90°时,∵∠COD=∠ODP=∠CPD=90°,∴四边形CODP为矩形,∴PD=CO=3,将y=3代入直线y=﹣2x+6,得,x=,∴P(,3);如图2﹣2,当∠PCD=90°时,∵OC=3,OD=m,∴CD2=OC2+OD2=9+m2,∵PD∥OC,∴∠PDC=∠OCD,∴cos∠PDC=cos∠OCD,∴=,∴DC2=PD•OC,∴9+m2=3(﹣2m+6),解得,m1=﹣3﹣3(舍去),m2=﹣3+3,∴P(﹣3+3,12﹣6),当∠PDC=90°时,∵PD⊥x轴,∴不存在,综上所述,点P的坐标为(,3)或(﹣3+3,12﹣6).13.【解答】解:(1)将点A(﹣1,0)、B(3,0)代入y=ax2+bx+3,得,解得,∴抛物线的解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,∴抛物线的顶点坐标为(1,4);(2)如图1,过点P作x轴的垂线,交BC于点N,在y=﹣x2+2x+3中,当x=0时,y=3,∴C(0,3),设直线BC的解析式为y=kx+3,将点B(3,0)代入y=kx+3,得3k+3=0,∴k=﹣1,∴直线BC的解析式为y=﹣x+3,设P(x,﹣x2+2x+3),则N(x,﹣x+3),∴PN=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x,=×PN×OB=(﹣x2+3x)×3=﹣(x﹣)2+,∴S△PBC∴当x=时,△PBC的面积最大,∴P(,);(3)存在,如图2,过点P作PH⊥x轴于H,设直线与y轴交于点Q,则Q(0,﹣),在Rt△OBQ中,tan∠OBQ===,在Rt△PHB中,tan∠BPH===,∴∠OBQ=∠BHP,∵∠BPH+∠PBH=90°,∴∠OBQ+∠PBH=90°,即∠PBE=90°,将点B(3,0)代入直线,得3k﹣=0,∴k=,∴y=x﹣,联立,解得,x1=3,x2=﹣,∴E(﹣,﹣),过点E作EF⊥BC于点F,则∠FEB+∠FBE=90°,∵∠PBC+∠FBE=90°,∴∠FEB=∠PBC,则此时射线EF与抛物线的交点即为所求的点M,∵BC==3,PC==,PB==2,∴BC2+PC2=PB2,∴△PCB为直角三角形,且∠PCB=90°,∴sin∠PBC===,∴sin∠FEB==,∵EB==,∴FB=,过点F作FD⊥x轴于点D,∵OB=OC=3,∴∠OBC=∠OCB=45°,∴∠DBF=∠DFB=45°,∴DB=DF=FB=,∴F(,),设直线EF的解析式为y=kx+b,将点E(﹣,﹣),F(,)代入y=kx+b,得,解得,∴直线EF的解析式为y=x﹣,联立,解得,x1=,x2=﹣,当x=时,y=,∴M(,).14.【解答】解:(1)在抛物线y=﹣x2+2x+3中,当y=0时,x1=﹣1,x2=3;当x=0时,y=3,∴A(﹣1,0),B(3,0),C(0,3)(2)∵点M'与点M关于直线CN对称,且点M'在y轴上,∴∠M'CN=∠MCN,∵MN∥y轴,∴∠M'CN=∠CNM,∴∠MCN=∠CNM,∴MN=CM,∵点C的坐标为(0,3),∴可设直线BC的解析式为y=kx+3,将点B(3,0)代入y=kx+3,得,3k+3=0,∴k=﹣1,∴直线BC的解析式为y=﹣x+3,设点M的横坐标为t,则M(t,﹣t+3),N(t,﹣t2+2t+3),∴MN=(﹣t2+2t+3)﹣(﹣t+3)=﹣t2+3t,,∴,∵t≠0,∴,∴,(3)根据题意,A'O'平行于x轴,O'C'平行于y轴,A'O'=1,O'C'=3,点A'在点O'的右边,点C'在点O'的下方,设点O'的横坐标为m,则A'的横坐标为m+1,点C'的横坐标为m,①若A'、O'在抛物线上,则﹣m2+2m+3=﹣(m+1)2+2(m+1)+3,∴,∴,则点P在OO'的中点处,∴;②若A'、C'在抛物线上,则﹣(m+1)2+2(m+1)+3=﹣m2+2m+3+3∴m=﹣1,∴O'(﹣1,3),则点P在OO'的中点处,∴,综上所述,存在点或,使△AOC关于点P的对称△A'O'C'恰好有两个顶点落在该抛物线上.15.【解答】解:(1)设抛物线解析式为y=a(x﹣h)2+k,(a≠0)∵顶点,∴,又∵图象过原点,∴,解出:,∴,即;(2)令y=0,即,解得:x1=0,x2=4,∴A(4,0),设直线AC的解析式为y=kx+b,将点A(4,0),代入,得,解得,∴直线AC的解析式为y=﹣x+4,过点D作DF∥y轴交AC于点F,设,则,∴,∴=,有最大值,∴当m=3时,S△ACD当m=3时,,∴;(3)∵∠CBO=∠CBA=90°,OB=AB=2,,∴,∴OA=OC=AC=4,∴△AOC为等边三角形,①如图3﹣1,当点P在C时,OA=AC=CA'=OA',∴四边形ACA'O是菱形,∴;②作点C关于x轴的对称点C',当点A'与点C'重合时,OC=AC=AA'=OA',∴四边形OCAA'是菱形,∴点P是∠AOA'的角平分线与对称轴的交点,记为P2,∴,∵∠OBP2=90°,OB=2,∴OP2=2BP2,∵∠OBP2=90°,OB=2,∴OP2=2BP2,设BP2=x,∴OP2=2x,又∵,∴(2x)2=22+x2,解得或,∴;综上所述,点P的坐标为或.16.【解答】解:(1)由抛物线y=ax2﹣2x+c与x轴交于A(﹣3,0),B(1,0)两点,得,解得,∴抛物线解析式为y=﹣x2﹣2x+3;由y=﹣x2﹣2x+3=﹣(x+1)2+4,得,点D坐标为(﹣1,4);(2)在直线l上存在一点M,到点B的距离与到点C的距离之和最小,根据抛物线对称性MA=MB,∴MB+MC=MA+MC,∴使MB+MC的值最小的点M应为直线AC与对称轴l:x=﹣1的交点,当x=0时,y=3,∴C(0,3),设直线AC解析式为直线y=kx+b,把A(﹣3,0)、C(0,3)分别代入y=kx+b,得,,解得,,∴直线AC解析式为y=x+3,把x=﹣1代入y=x+3得,y=2,∴M(﹣1,2),即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2);(3)①PF=2FG,理由如下,设直线AD解析式为y=k'x+b',把A(﹣3,0)、D(﹣1,4)分别代入直线y=k'x+b',得,,解得,∴直线AD解析式为y=2x+6,则点F的坐标为(m,2m+6),同理G的坐标为(m,m+3),则FG=(2m+6)﹣(m+3)=m+3,FP=2m+6=2(m+3),∴FP=2FG;②根据题意得点E的坐标为(m,﹣m2﹣2m+3),设直线l与x轴交于点N,EF=(﹣m2﹣2m+3)﹣(2m+6)=﹣m2﹣4m﹣3=﹣(m+2)2+1=S△AEF+S△EFD==∴S△AED,的最大值为1,∴当m为﹣2时,S△AED如图,过点D作DH∥x轴,交y轴于点H,在△DHC中,∠DHC=180°﹣∠AOB=90°,,在Rt△AOC中,,在Rt△ADN中,,∵,∴DC2+AC2=AD2,∴∠ACD=90°,∴,∴,∴当m为﹣2时,四边形AEDC的面积最大,最大值为4.17.【解答】解:(1)将A(1,4)代入y=,得,k=4,∴双曲线解析式为y=,设B(m,)(m<0),连接AB,交x轴于点C,设直线AB的解析式为y=kx+b,将点A(1,4),B(m,)代入,得,解得,,∴直线AB的解析式为y=﹣x+,当y=0时,x=m+1,∴C(m+1,0),OC=﹣m﹣1,=OC•(y A﹣y B)∴S△AOB=(﹣m﹣1)(4﹣),∵△AOB的面积为3,∴(﹣m﹣1)(4﹣)=3,整理,得2m2+3m﹣2=0,解得,m1=(舍去),m2=﹣2,∴B(﹣2,﹣2),将A(1,4),B(﹣2,﹣2)代入y=ax2+bx,得,,解得,,∴抛物线的解析式为y=x2+3x,∴a=1,b=3,k=4;(2)在抛物线y=x2+3x中,对称轴为x=﹣,设P(﹣,y),∵O(0,0),B(﹣2,﹣2),∴PO2=+y2,OB2=8,PB2=+(y+2)2,。
2020年九年级数学中考三轮压轴专题:《二次函数与三角形相似》(解析版)

三轮压轴专题:《二次函数与三角形相似》1.如图,在平面直角坐标系中,直线y=﹣x+n与x轴,y轴分别交于点B,点C,抛物线y=ax2+bx+(a≠0)过B,C两点,且交x轴于另一点A(﹣2,0),连接AC.(1)求抛物线的表达式;(2)已知点P为第一象限内抛物线上一点,且点P的横坐标为m,请用含m的代数式表示点P到直线BC的距离;(3)抛物线上是否存在一点Q(点C除外),使以点Q,A,B为顶点的三角形与△ABC 相似?若存在,直接写出点Q的坐标;若不存在,请说明理由.解:(1)点C(0,),则直线y=﹣x+n=﹣x+,则点B(3,0),则抛物线的表达式为:y=a(x﹣3)(x+2)=a(x2﹣x﹣6),故﹣6a=,解得:a=﹣,故抛物线的表达式为:y=﹣x2+x+…①;(2)过点P作y轴的平行线交BC于点G,作PH⊥BC于点H,则∠HPG=∠CBA=α,tan∠CBA===tanα,则cosα=,设点P(m,﹣m2+m+),则点G(m,﹣m+),则PH=PG cosα=(﹣m2+m++m﹣)=﹣m2+m;(3)①当点Q在x轴上方时,则点Q,A,B为顶点的三角形与△ABC全等,此时点Q与点C关于函数对称轴对称,则点Q(1,);②当点Q在x轴下方时,(Ⅰ)当∠BAQ=∠CAB时,△QAB∽△BAC,则=,由勾股定理得:AC=,AQ===10,过点Q作QH⊥x轴于点H,由△HAQ∽△OAC得:==,∵OC=,AQ=10,∴QH=6,则AH=8,OH=8﹣2=6,∴Q(6,﹣6);该点在抛物线上;根据点的对称性,当点Q在第三象限时,符合条件的点Q(﹣5,﹣6);故点Q的坐标为:(6,﹣6)或(﹣5,﹣6);(Ⅱ)当∠BAQ=∠CBA时,则直线AQ∥BC,直线BC表达式中的k为:﹣,则直线AQ的表达式为:y=﹣x﹣1…②,联立①②并解得:x=5或﹣2(舍去﹣2),故点Q(5,﹣),=,而=,故≠,即Q,A,B为顶点的三角形与△ABC不相似,故舍去,Q的对称点(﹣4,﹣)同样也舍去,即点Q的为:(﹣4,﹣)、(5,﹣)均不符合题意,都舍去;综上,点Q的坐标为:(1,)或(6,﹣6)或(﹣5,﹣6).2.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c 经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.①求PN的最大值;②若以B,P,N为顶点的三角形与△APM相似,请直接写出点M的坐标.解:(1)直线y=﹣x+c交于点A(3,0),与y轴交于点B,∴0=﹣2+c,解得c=2,∴B(0,2),∵抛物线y=﹣x2+bx+c经过点A,B,将点A、B的坐标代入抛物线表达式并解得:y=﹣x2+x+2;(2)①M(m,0),则P(m,),N(m,﹣m2+m+2),∴PN=﹣m2+m+2﹣=﹣m2+4m(0≤m≤3);当m=时,线段PN有最大值为3;②由(1)可知直线解析式为y=﹣x+2,∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,∴P(m,﹣m+2),N(m,﹣m2+m+2),∴PM=﹣m+2,AM=3﹣m,PN=﹣m2+m+2﹣(﹣m+2)=﹣m2+4m,∵△BPN和△APM相似,且∠BPN=∠APM,∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,当∠BNP=90°时,则有BN⊥MN,∴N点的纵坐标为2,∴﹣m2+m+2=2,解得m=0(舍去)或m=,∴M(,0);当∠NBP=90°时,过点N作NC⊥y轴于点C,则∠NBC+∠BNC=90°,NC=m,BC=﹣m2+m+2﹣2=﹣m2+m,∵∠NBP=90°,∴∠NBC+∠ABO=90°,∴∠ABO=∠BNC,∴Rt△NCB∽Rt△BOA,,∴=,解得m=0(舍去)或m=,∴M(,0);综上可知当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(,0)或(,0).3.已知抛物线y=x2+ax+b与x轴交于A(1,0),B(3,0)两点,与y轴交于点C.(1)填空:a=﹣4 b= 3 ;(2)如图1,已知E(,0),过点E的直线与抛物线交于点M、N,且点M、N关于点E对称,求直线MN的解析式;(3)如图2,已知D(0,1),P是第一象限内抛物线上一点,作PH⊥y轴于点H,若△PHD与△BDO相似,请求出点P的横坐标.解:(1)抛物线的表达式为:y=(x﹣1)(x﹣3)=x2﹣4x+3…①,故答案为:﹣4,3;(2)设点M、N的横坐标为m,n,直线MN的表达式为:y=k(x﹣)…②,联立①②并整理得:x2﹣(4+k)x+(3﹣k),则m+n=4+k,点M、N关于点E对称,则y M+y N=km﹣k+kn﹣k=k(m+n)﹣5k=0,即(4+k)k﹣5k=0,解得:k=0(舍去)或1,故直线MN的表达式为:y=x﹣;(3)设点P(m,m2﹣4m+3),则PH=m,HD=|m2﹣4m+3﹣1|,而OB=3,OD=1,则tan∠DOB=,若△PHD与△BDO相似,则tan∠HPD=或4,即=或4,即=或4,解得:m=或或.4.如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.(1)求抛物线的函数表达式;(2)如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;(3)如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.解:(1)将点A(0,1)和点B(3,﹣2)代入抛物物线y=﹣x2+bx+c中得,解得∴y=﹣x2+2x+1(2)如图1所示:过点D作DM∥y轴交AB于点M,设D(a,﹣a2+2a+1),则M(a,﹣a+1).∴DM=﹣a2+2a+1﹣(﹣a+1)=﹣a2+3a∴∵有最大值,当时,此时图1(3)∵OA=OC,如图2,CF∥y轴,∴∠ACE=∠ACO=45°,∴△BCD中必有一个内角为45°,由题意可知,∠BCD不可能为45°,①若∠CBD=45°,则BD∥x轴,∴点D与点B于抛物线的対称轴直线x=1対称,设BD与直线=1交于点H,则H(1,﹣2)B(3,﹣2),D(﹣1,﹣2)此时△BCD是等腰直角三角形,因此△ACE也是等腰直角三角形,(i)当∠AEC=90°时,得到AE=CE=1,∴E(1.1),得到t=1(ii)当∠CAE=90时,得到:AC=AE=,∴CE=2,∴E(1.2),得到t=2图2②若∠CDB=45°,如图3,①中的情况是其中一种,答案同上以点H为圆心,HB为半径作圆,则点B、C、D都在圆H上,设圆H与对称左侧的物线交于另一点D1,则∠CD1B=∠CDB=45°(同弧所对的圆周角相等),即D1也符合题意设由HD1=DH=2解得n1=﹣1(含去),n2=3(舍去),(舍去),∴,则,(i)若△ACE∽△CD1B,则,即,解得(舍去)(ii)△ACE∽△BD1C则,即,解得(舍去)综上所述:所有满足条件的t的值为t=1或t=2或或图35.如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).(1)求抛物线的解析式;(2)如图2,点P为直线BD上方抛物线上一点,若S△PBD=3,请求出点P的坐标.(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.解:(1)设抛物线的解析式为y=a(x﹣1)2+4,将点B(3,0)代入得,(3﹣1)2×a+4=0.解得:a=﹣1.∴抛物线的解析式为:y=﹣(x﹣1)2+4=﹣x2+2x+3.(2)过点P作PQ∥y轴交DB于点Q,∵抛物线的解析式为y=﹣x2+2x+3∴D(0,3).设直线BD的解析式为y=kx+b,∴,解得:,∴直线BD的解析式为y=﹣x+3.设P(m,﹣m2+2m+3),则Q(m,﹣m+3),∴PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.∵S△PBD=S△PQD+S△PQB,∴S△PBD=(3﹣m)=PQ=﹣m,∵S△PBD=3,∴﹣m=3.解得:m1=1,m2=2.∴点P的坐标为(1,4)或(2,3).(3)∵B(3,0),D(0,3),∴BD==3,设M(a,0),∵MN∥BD,∴△AMN∽△ABD,∴,即.∴MN=(1+a),DM==,∵△DNM∽△BMD,∴,∴DM2=BD•MN.∴9+a2=3(1+a).解得:a=或a=3(舍去).∴点M的坐标为(,0).6.如图,抛物线y=ax2+bx+c与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C (0,3),抛物线的对称轴与直线BC交于点D.(1)求抛物线的表达式;(2)在抛物线的对称轴上找一点M,使|BM﹣CM|的值最大,求出点M的坐标;(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,直接写出点E的坐标.解:(1)∵抛物线y=ax2+bx+c经过点A(1,0)、B(3,0)、C(0,3),∴,解得,∴抛物线的表达式为y=x2﹣4x+3;(2)∵抛物线对称轴是线段AB的垂直平分线,∴AM=BM,由三角形的三边关系,|BM﹣CM|=|AM﹣CM|<AC,∴点A、C、M三点共线时,|BM﹣CM|最大,设直线AC的解析式为y=mx+n,则,解得,∴直线AC的解析式为y=﹣3x+3,又∵抛物线对称轴为直线x=﹣=2,∴x=2时,y=﹣3×2+3=﹣3,故,点M的坐标为(2,﹣3);(3))∵OB=OC=3,OB⊥OC,∴△BOC是等腰直角三角形,∵EF∥y轴,直线BC的解析式为y=﹣x+3,∴△DEF只要是直角三角形即可与△BOC相似,∵D(2,1),A(1,0),B(3,0),∴点D垂直平分AB且到点AB的距离等于AB,∴△ABD是等腰直角三角形,∴∠ADB=90°,如图,①点F是直角顶点时,点F的纵坐标与点D的纵坐标相同,是1,∴x2﹣4x+3=1,整理得x2﹣4x+2=0,解得x=2±,当x=2﹣时,y=﹣(2﹣)+3=1+,当x=2+时,y=﹣(2+)+3=1﹣,∴点E1(2﹣,1+)E2(2+,1﹣),②点D是直角顶点时,易求直线AD的解析式为y=x﹣1,联立,解得,,当x=1时,y=﹣1+3=2,当x=4时,y=﹣4+3=﹣1,∴点E3(1,2),E4(4,﹣1),综上所述,存在点E1(2﹣,1+)或E2(2+,1﹣)或E3(1,2)或E4(4,﹣1),使以D、E、F为顶点的三角形与△BCO相似.7.如图,抛物线y=﹣x2+x+2与x轴交于点A,点B,与y轴交于点C,点D与点C 关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线1交抛物线于点Q.(1)求点A、点B、点C的坐标;(2)当点P在线段OB上运动时,直线1交直线BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(3)点P在线段AB上运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.解:(1)抛物线y=﹣x2+x+2,当x=0时,y=2,因此点C(0,2),当y=0时,即:﹣x2+x+2=0,解得x1=4,x2=﹣1,因此点A(﹣1,0),B (4,0),故:A(﹣1,0),B(4,0),C(0,2);(2)∵点D与点C关于x轴对称,∴点D(0,﹣2),CD=4,设直线BD的关系式为y=kx+b,把D(0,﹣2),B(4,0)代入得,,解得,k=,b=﹣2,∴直线BD的关系式为y=x﹣2,设M(m,m﹣2),Q(m,﹣m2+m+2),∴QM=﹣m2+m+2﹣m+2=﹣m2+m+4,当QM=CD时,四边形CQMD是平行四边形;∴﹣m2+m+4=4,解得m1=0(舍去),m2=2,答:m=2时,四边形CQMD是平行四边形;(3)在Rt△BOD中,OD=2,OB=4,因此OB=2OD,①若∠MBQ=90°时,如图1所示,当△QBM∽△BOD时,QP=2PB,设点P的横坐标为x,则QP=﹣x2+x+2,PB=4﹣x,于是﹣x2+x+2=2(4﹣x),解得,x1=3,x2=4(舍去),当x=3时,PB=4﹣3=1,∴PQ=2PB=2,∴点Q的坐标为(3,2);②若∠MQB=90°时,如图2所示,此时点P、Q与点A重合,∴Q(﹣1,0);③由于点M在直线BD上,因此∠QMB≠90°,这种情况不存在△QBM∽△BOD.综上所述,点P在线段AB上运动过程中,存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似,点Q(3,2)或(﹣1,0).8.如图,在平面直角坐标系中,直线y=﹣x+4分别与x轴、y轴相交于点B、C,经过点B、C的抛物线y=﹣+bx+c与x轴的另一个交点为A.(1)求出抛物线表达式,并求出点A坐标.(2)已知点D在抛物线上,且横坐标为3,求出△BCD的面积;(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于x轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.解:(1)由已知可求B(6,0),C(0,4),将点B(6,0),C(0,4)代入y=﹣+bx+c,则有,解得,∴y=﹣x2+x+4,令y=0,则﹣x2+x+4=0,解得x=﹣1或x=6,∴A(﹣1,0);(2)∵点D在抛物线上,且横坐标为3,∴D(3,8),过点D作y轴的垂线交于点E,过点B作BF⊥DE交ED的延长线于点F;∴E(0,8),F(6,8),∴S△BCD=S梯形ECBF﹣S△CDE﹣S△BFD=(EC+BF)×OB﹣×EC×ED﹣×DF×BF =×(4+8)×6﹣×4×3﹣×3×8=36﹣6﹣12=18;(3)设P(m,﹣m2+m+4),∵PQ垂直于x轴,∴Q(m,0),且∠PQO=90°,∵∠COB=90°,∴点A、P、Q为顶点的三角形与△BOC相似有两种情况:①△PAQ∽△CBO时,==,∴=,解得m=5或m=﹣1,∵点P是直线BC上方的抛物线上,∴0≤m≤6,∴m=5,∴P(5,4);②△PAQ∽△BCO时,==,∴=,解得m=﹣1或m=,∵点P是直线BC上方的抛物线上,∴0≤m≤6,∴m=,∴P(,);综上所述:P(5,4)或P(,)时,点A、P、Q为顶点的三角形与△BOC相似.9.如图,抛物线y=﹣+bx+c过点A(3,0)和B(0,2),点M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.(1)求此抛物线的解析式;(2)若点P是MN的中点,则求点P的坐标;(3)若以点B、N、P为顶点的三角形与△AMP相似,请直接写出点P的坐标.解:(1)抛物线经过点A(3,0),B(0,2),∴,解得,∴抛物线的解析式为:;(2)∵B(0,2),∴可设直线AB的解析式为y=kx+2,将点A(3,0)代入y=kx+2,得,3k+2=0,∴k=﹣,∴直线AB的解析式为,由M(m,0),设,,则,,点P是MN的中点,即NP=PM,∴,解得(舍),∴;(3)∵∠APM=∠NPB,∴若以点B、N、P为顶点的三角形与△AMP相似,则存在△AMP∽△NBP和△AMP∽△BNP两种情况,如图,过点P作PH∥x轴交y轴于H,则△BHP∽△BOA,∴=,∵OA=3,PH=m,BA==,∴BP=m,∴AP=AB﹣BP=﹣m=,①当△AMP∽△NBP时,=,∴=,解得,m1=3(舍去),m2=,∴P1(,);②当△AMP∽△BNP时,=,∴=,解得,m1=3(舍去),m2=,∴P2(,);∴点P的坐标为(,)或(,).10.如图,抛物线y=x2+mx+n与直线y=﹣x+3交于A、B两点,交x轴于D、C 两点,连接AC、BC,已知A(0,3),C(3,0).(1)抛物线的函数关系式为y=x2﹣x+3 ,tan∠BAC=;(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位的速度运动到E点,再沿线段EA以每秒个单位的速度运动到点A 后停止,当点E的坐标是多少时,点M在整个运动过程中用时最少?(3)P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使以A、P、Q为顶点的三角形与△ABC相似?若存在,求出所有符合条件的P点坐标,若不存在,请说明理由.解:(1)将A(0,3),C(3,0)代入y=x2+mx+n,得,解得,∴抛物线的解析式为y=x2﹣x+3;联立,解得或,∴点B的坐标为(4,1),如图1,过点B作BH⊥x轴于H,∵C(3,0),B(4,1),∴BH=1,OC=3,CH=4﹣3=1,∴BH=CH=1,∵∠BHC=90°,∴∠BCH=45°,BC=,同理,∠ACO=45°,AC=3,∴∠ACB=180°﹣45°﹣45°=90°,∴tan∠BAC===,故答案为:y=x2﹣x+3,;(2)如图2,过A作射线AF∥x轴,过D作射线DF∥y轴,DF与AC交于点E,∵A(0,3),C(3,0),∴可设直线AC的解析式为y=kx+3,将点C(3,0)代入y=kx+3,得3k+3=0,∴k=﹣1,∴直线AC的解析式为y=﹣x+3,∵OA=OC,∠AOC=90°,∴∠ACO=45°,∵AF∥OC,∴∠FAE=45°,∴EF=AE•sin45°=AE,∴当且仅当AF⊥DF时,DE+EF取最小值,点M在整个运动中用时最少,为:t=+=DE+AE=DE+EF,∵在y=x2﹣x+3中,当y=0时,x1=3,x2=2,∴D(2,0),则E点横坐标为2,将x=2代入直线y=﹣x+3,得,y=1,∴E(2,1);(3)存在点P,使得以A、P、Q为顶点的三角形与△ABC相似,过点P作PG⊥y轴于G,则∠PGA=90°,设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x,∵PQ⊥PA,∠ACB=90°,∴∠APQ=∠ACB=90°,若点G在点A的下方,①如图3﹣1,当∠PAQ=∠CAB时,则△PAQ∽△CAB,∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,∴△PGA∽△BCA,∴==,∴AG=3PG=3x,则P(x,3﹣3x),把P(x,3﹣3x)代入y=x2﹣x+3,得x2﹣x+3=3﹣3x,解得,x1=0(舍去),x2=﹣1(舍去);②如图3﹣2,当∠PAQ=∠CBA时,则△PAQ∽△CBA,同理可得,AG=PG=x,则P(x,3﹣x),把P(x,3﹣x)代入y=x2﹣x+3,得x2﹣x+3=3﹣x,解得,x1=0(舍去),x2=,∴P(,);若点G在点A的上方,①如图3﹣3,当∠PAQ=∠CBA时,则△PAQ∽△CBA,同理可得,AG=PG=x,则P(x,3+x),把P(x,3+x)代入y=x2﹣x+3,得x2﹣x+3=3+x,解得,x1=0(舍去),x2=,∴P(,);②如图3﹣4,当∠PAQ=∠CAB时,则△PAQ∽△CAB,同理可得,AG=3PG=3x,则P(x,3+3x),把P(x,3+3x)代入y=x2﹣x+3,得x2﹣x+3=3+3x,解得,x1=0(舍去),x2=11,∴P(11,36),综上所述,满足条件的点P的坐标为(,),(,),(11,36).11.如图已知直线y=x+与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣),交x轴正半轴于D点,抛物线的顶点为M.(1)求抛物线的解析式;(2)设点P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求△PAB的面积及点P的坐标;(3)若点Q为x轴上一动点,点N在抛物线上且位于其对称轴右侧,当△QMN与△MAD相似时,求N点的坐标.解:(1)将点B(4,m)代入y=x+,∴m=,将点A(﹣1,0),B(4,),C(0,﹣)代入y=ax2+bx+c,解得a=,b=﹣1,c=﹣,∴函数解析式为y=x2﹣x﹣;(2)设P(n,n2﹣n﹣),则经过点P且与直线y=x+垂直的直线解析式为y=﹣2x+n2+n﹣,直线y=x+与其垂线的交点G(n2+n﹣,n2+n+),∴GP=(﹣n2+3n+4),当n=时,GP最大,此时△PAB的面积最大,∴P(,),∵AB=,PG=,∴△PAB的面积=××=;(3)∵M(1,﹣2),A(﹣1,0),D(3,0),∴AM=2,AB=4,MD=2,∴△MAD是等腰直角三角形,∵△QMN与△MAD相似,∴△QMN是等腰直角三角形,设N(t,t2﹣t﹣)①如图1,当MQ⊥QN时,N(3,0);②如图2,当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,∵QN=MN,∠QNM=90°,∴△MNS≌△NMS(AAS)∴t﹣1=﹣t2+t+,∴t=±,∴t>1,∴t=,∴N(,1﹣);③如图3,当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点N作NR ∥x轴,与过M点的垂线分别交于点S、R;∵QN=MQ,∠MQN=90°,∴△MQR≌△QNS(AAS),∴SQ=QR=2,∴t+2=1+t2﹣t﹣,∴t=5,∴N(5,6);④如图4,当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,过点N作x轴的平行线,与两垂线交于点R、S;∵QN=MN,∠MNQ=90°,∴△MNR≌△NQS(AAS),∴SQ=RN,∴t2﹣t﹣=t﹣1,∴t=2±,∵t>1,∴t=2+,∴N(2+,1+);综上所述:N(3,0)或N(2+,1+)或N(5,6)或N(,1﹣).12.如图,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为D,对称轴交x轴于点Q.(1)求抛物线对应的二次函数的表达式;(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD 相切,求点P的坐标;(3)在抛物线的对称轴上是否存在一点M,使得△DCM与△BQC相似?如果存在,求出点M的坐标;如果不存在,请说明理由.解:(1)∵A(﹣1,0),B(3,0).代入y=﹣x2+bx+c,得,解得b=2,c=3.∴抛物线对应二次函数的表达式为:y=﹣x2+2x+3;(2)如图1,设直线CD切⊙P于点E.连结PE、PA,作CF⊥DQ于点F.∴PE⊥CD,PE=PA.由y=﹣x2+2x+3,得对称轴为直线x=1,C(0,3)、D(1,4).∴DF=4﹣3=1,CF=1,∴DF=CF,∴△DCF为等腰直角三角形.∴∠CDF=45°,∴∠EDP=∠EPD=45°,∴DE=EP,∴△DEP为等腰三角形.设P(1,m),∴EP2=(4﹣m)2.在△APQ中,∠PQA=90°,∴AP2=AQ2+PQ2=[1﹣(﹣1)]2+m2∴(4﹣m)2=[1﹣(﹣1)]2+m2.整理,得m2+8m﹣8=0解得,m=﹣4±2.∴点P的坐标为(1,﹣4+2)或(1,﹣4﹣2).(3)存在点M,使得△DCM∽△BQC.如图2,连结CQ、CB、CM,∵C(0,3),OB=3,∠COB=90°,∴△COB为等腰直角三角形,∴∠CBQ=45°,BC=3.由(2)可知,∠CDM=45°,CD=,∴∠CBQ=∠CDM.∴△DCM与△BQC相似有两种情况.当时,∴,解得DM=.∴QM=DQ﹣DM=4﹣=.∴M1(1,).当时,∴,解得DM=3,∴QM=DQ﹣DM=4﹣3=1.∴M2(1,1).综上,点M的坐标为或(1,1).13.已知抛物线y=ax2+bx+3与x轴分别交于点A(﹣3,0),B(1,0),交y轴于点C,抛物线的顶点为点D.(1)抛物线的表达式及顶点D的坐标.(2)若点F是线段AD上一个动点,①如图1,当FC+FO的值最小时,求点F的坐标;②如图2,以点A,F,O为顶点的三角形能否与△ABC相似?若能,求出点F的坐标;若不能,请说明理由.解:(1)抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),故﹣3a=3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2﹣2x+3…①,函数的对称轴为:x=﹣1,故顶点D的坐标为:(﹣1,4);(2)①点D的坐标为:(﹣1,4),点A(﹣3,0),点C(0,3),作点O关于直线AD的对称轴R,连接CR交AD于点F,则点F为所求点,FC+FO=FC+RF=CR为最小,连接AR,设直线OR交AD于点H,由点A、D的坐标得,直线AD的表达式为:y=2x+6,则tan∠DAO=2=tanα,设∠HOA=∠β,则tanβ=,则cosβ=,sinβ=,OH=AO•cosβ=,OR=2OH=,y R=OR sinβ=,同理x R=﹣,故点R(﹣,),由点R、C的坐标得,直线RC的表达式为:y=x+3…②,联立①②并解得:x=﹣,y=,则点F(﹣,);②在Rt△ACD中,tan∠CAD===,在Rt△OBC中,tan∠OCB==,∴∠ACD=∠OCB,∵OA=OC,∴∠OAC=∠OCA=45°,∴∠FAO=∠ACB,若以A,F,O为顶点的三角形与△ABC相似,则可分两种情况考虑:当∠AOF=∠ABC时,△AOF∽△CBA,∴OF∥BC,设直线BC的解析式为y=kx+b,将点B、C的坐标代入上式并解得:直线BC的解析式为y=﹣3x+3,∴直线OF的解析式为y=﹣3x,直线AD的解析式为y=2x+6,联立直线OF、AD的表达式并解得:x=﹣,故点F(﹣,);当∠AOF=∠CAB=45°时,△AOF∽△CAB,∵∠CAB=45°,∴OF⊥AC,∴直线OF的解析式为y=﹣x,将上式与y=2x+6联立并解得:x=﹣2,故点F(﹣2,2);综合以上可得F点的坐标为(﹣,)或(﹣2,2).14.如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴对折,点A 落到点C处,过点A、B的抛物线y=﹣x2+bx+c与直线BC交于点B、D.(1)求直线BD和抛物线的解析式;(2)在直线BD上方的抛物线上求一点E,使△BDE面积最大,求出点E坐标;(3)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标:若不存在,请说明理由.解:(1)令y=0,则x=﹣1,令x=0,则y=2,∴点A、B的坐标分别是:A(﹣1,0),B(0,2),根据对折的性质:点C的坐标是:(1,0),设直线BD解析式为y=kx+b,把B(0,2),C(1,0)代入y=kx+b,得,解得:k=﹣2,b=2,∴直线BD解析式为y=﹣2x+2,把A(﹣1,0),B(0,2)代入y=﹣x2+bx+c得,解得:b=1,c=2,∴抛物线的解析式为y=﹣x2+x+2;(2)解方程组得:和,∴点D坐标为(3,﹣4),作EF∥y轴交直线BD于F设E(x,﹣x2+x+2),F(x,﹣2x+2)∴EF=(﹣x2+x+2)﹣(﹣2x+2)=﹣x2+3x,△BDE面积S=×EF×x D=×(﹣x2+3x)=﹣(x﹣)2+,当x=时,三角形面积最大,此时,点E的坐标为:;(3)存在.∵点B、C的坐标分别是B(0,2)、C(1,0),∴BO=2,CO=1,①如图1所示,当△MON∽△BCO时,∴,即,∴MN=2ON,设ON=a,则M(a,2a),将M(a,2a)代入抛物线的解析式y=﹣x2+x+2得:﹣a2+a+2=2a,解得:a1=﹣2(不合题意,舍去),a2=1,∴点M的坐标为(1,2);②当△MON∽△CBO时,同理可得:,即,∴MN=ON,设ON=b,则M(b,b),将M(b,b)代入抛物线的解析式y=﹣x2+x+2得:∴,解得:(不合题意,舍去),,∴点M的坐标为(,),∴存在这样的点M(1,2)或.15.如图,抛物线y=ax2+2x+c经过A(﹣1,0),B两点,且与y轴交于点C(0,3),抛物线与直线y=﹣x﹣1交于A,E两点.(1)求抛物线的解析式;(2)坐标轴上是否存在一点Q,使得△AQE是以AE为底边的等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.(3)P点在x轴上且位于点B的左侧,若以P,B,C为顶点的三角形与△ABE相似,求点P的坐标.解:(1)将A(﹣1,0),C(0,3)代入y=ax2+2x+c,得,解得,,∴抛物线的解析式为:y=﹣x2+2x+3;(2)联立,解得,或,∴E(4,﹣5),如图1,当点Q在x轴上时,设Q(m,0),∵AE为底边,∴QA=QE,∴QA2=QE2,即(m+1)2=52+(m﹣4)2,解得,m=4,∴Q1(4,0);当点Q在y轴上时,设Q(0,n),∵AE为底边,∴QA=QE,∴QA2=QE2,即n2+12=42+(n+5)2,解得,n=﹣4,∴Q2(0,﹣4);综上所述,Q1(4,0),Q2(0,﹣4);(3)如图2,过点E作EH⊥x轴于点H,∵A(﹣1,0),E(4,﹣5),∴AH=EH=5,AE==5,∠BAE=45°,又OB=OC=3,∴∠ABC=45°,AB=4,BC==3,设P(t,0),则BP=3﹣t,∵∠BAE=∠ABC=45°,∴只可能存在△PBC∽△BAE和△PBC∽△EAB两种情况,当△PBC∽△BAE时,,∴=,∴t=,∴P1(,0);当△PBC∽△EAB时,,∴=,∴t=﹣,∴P2(﹣,0),综上所述,点P的坐标为(,0)或(﹣,0).。
中考数学专题复习分类练习 二次函数综合解答题含答案

一、二次函数 真题与模拟题分类汇编(难题易错题)1.如图1,抛物线y=ax 2+bx+c (a≠0)与x 轴交于点A (﹣1,0)、B (4,0)两点,与y 轴交于点C ,且OC=3OA .点P 是抛物线上的一个动点,过点P 作PE ⊥x 轴于点E ,交直线BC 于点D ,连接PC . (1)求抛物线的解析式;(2)如图2,当动点P 只在第一象限的抛物线上运动时,求过点P 作PF ⊥BC 于点F ,试问△PDF 的周长是否有最大值?如果有,请求出其最大值,如果没有,请说明理由. (3)当点P 在抛物线上运动时,将△CPD 沿直线CP 翻折,点D 的对应点为点Q ,试问,四边形CDPQ 是否成为菱形?如果能,请求出此时点P 的坐标,如果不能,请说明理由.【答案】(1) y=﹣234x +94x+3;(2) 有最大值,365;(3) 存在这样的Q 点,使得四边形CDPQ 是菱形,此时点P 的坐标为(73,256)或(173,﹣253).【解析】试题分析: (1)利用待定系数法求二次函数的解析式; (2)设P (m ,﹣34m 2+94m+3),△PFD 的周长为L ,再利用待定系数法求直线BC 的解析式为:y=﹣34x+3,表示PD=﹣2334m m ,证明△PFD ∽△BOC ,根据周长比等于对应边的比得:=PED PD BOC BC 的周长的周长,代入得:L=﹣95(m ﹣2)2+365,求L 的最大值即可;(3)如图3,当点Q 落在y 轴上时,四边形CDPQ 是菱形,根据翻折的性质知:CD=CQ ,PQ=PD ,∠PCQ=∠PCD ,又知Q 落在y 轴上时,则CQ ∥PD ,由四边相等:CD=DP=PQ=QC ,得四边形CDPQ 是菱形,表示P (n ,﹣23n 4 +94n+3),则D (n ,﹣34n+3),G (0,﹣34n+3),利用勾股定理表示PD 和CD 的长并列式可得结论. 试题解析:(1)由OC=3OA ,有C (0,3),将A (﹣1,0),B (4,0),C (0,3)代入y=ax 2+bx+c 中,得:016403a b c a b c c -+=⎧⎪++=⎨⎪=⎩, 解得:34943a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩,故抛物线的解析式为:y=﹣234x +94x+3; (2)如图2,设P (m ,﹣34m 2+94m+3),△PFD 的周长为L ,∵直线BC 经过B (4,0),C (0,3), 设直线BC 的解析式为:y=kx+b ,则403k b b +=⎧⎨=⎩解得:343k b ⎧=-⎪⎨⎪=⎩∴直线BC 的解析式为:y=﹣34x+3, 则D (m ,﹣334m +),PD=﹣2334m m +,∵PE ⊥x 轴,PE ∥OC , ∴∠BDE=∠BCO , ∵∠BDE=∠PDF , ∴∠PDF=∠BCO , ∵∠PFD=∠BOC=90°, ∴△PFD ∽△BOC ,∴=PED PDBOC BC的周长的周长,由(1)得:OC=3,OB=4,BC=5, 故△BOC 的周长=12,∴2334125m mL -+=,即L=﹣95(m ﹣2)2+365,∴当m=2时,L 最大=365; (3)存在这样的Q 点,使得四边形CDPQ 是菱形,如图3, 当点Q 落在y 轴上时,四边形CDPQ 是菱形,理由是:由轴对称的性质知:CD=CQ ,PQ=PD ,∠PCQ=∠PCD , 当点Q 落在y 轴上时,CQ ∥PD , ∴∠PCQ=∠CPD , ∴∠PCD=∠CPD , ∴CD=PD , ∴CD=DP=PQ=QC , ∴四边形CDPQ 是菱形, 过D 作DG ⊥y 轴于点G , 设P (n ,﹣234n +94n+3),则D (n ,﹣34n+3),G (0,﹣334n +), 在Rt △CGD 中,CD 2=CG 2+GD 2=[(﹣34n+3)﹣3]2+n 2=22516n , 而|PD|=|(﹣239344n n ++ 3n ++)﹣(﹣34n+3)|=|﹣234n +3n|,∵PD=CD , ∴﹣235344n n n +=①, ﹣235344n n n +=-②, 解方程①得:n=73或0(不符合条件,舍去), 解方程②得:n=173或0(不符合条件,舍去), 当n=73时,P (73,256),如图3,当n=173时,P (173,﹣253),如图4,综上所述,存在这样的Q 点,使得四边形CDPQ 是菱形,此时点P 的坐标为(73,256)或(173,﹣253).点睛: 本题是二次函数的综合题,考查了利用待定系数法求函数的解析式、菱形的性质和判定、三角形相似的性质和判定,将周长的最值问题转化为二次函数的最值问题,此类问题要熟练掌握利用解析式表示线段的长,并利用相似比或勾股定理列方程解决问题.2.在平面直角坐标系中,有两点(),A a b 、(),B c d ,若满足:当a b ≥时,c a =,2d b =-;当a b <时,c a <-,d b <,则称点为点的“友好点”.(1)点()4,1的“友好点”的坐标是_______.(2)点(),A a b 是直线2y x =-上的一点,点B 是点A 的“友好点”. ①当B 点与A 点重合时,求点A 的坐标.②当A 点与A 点不重合时,求线段AB 的长度随着a 的增大而减小时,a 的取值范围. 【答案】(1)()41-,;(2)①点A 的坐标是()2,0或()1,1-;②当1a <或322a ≤<时,AB 的长度随着a 的增大而减小; 【解析】 【分析】(1)直接利用“友好点”定义进行解题即可;(2)先利用 “友好点”定义求出B 点坐标,A 点又在直线2y x =-上,得到2b a =-;①当点A 和点B 重合,得2b b =-.解出即可,②当点A 和点B 不重合, 1a ≠且2a ≠.所以对a 分情况讨论,1°、当1a <或2a >时,()222313224AB b b a a a ⎛⎫=--=-+=--⎪⎝⎭,所以当a ≤32时,AB 的长度随着a 的增大而减小,即取1a <.2°当12a <<时,()22231+3224AB b b a a a ⎛⎫=--=--=--+⎪⎝⎭,当32a ≥时,AB 的长度随着a 的增大而减小,即取322a ≤<. 综上,当1a <或322a ≤<时,AB 的长度随着a 的增大而减小. 【详解】(1)点()4,1,4>1,根据“友好点”定义,得到点()4,1的“友好点”的坐标是()41-, (2)点(),A a b 是直线2y x =-上的一点,∴2b a =-.2a a >-,根据友好点的定义,点B 的坐标为()2,B a b -,①当点A 和点B 重合,∴2b b =-. 解得0b =或1b =-. 当0b =时,2a =;当1b =-时,1a =,∴点A 的坐标是()2,0或()1,1-.②当点A 和点B 不重合,1a ≠且2a ≠.当1a <或2a >时,()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭. ∴当a ≤32时,AB 的长度随着a 的增大而减小, ∴取1a <.当12a <<时, ()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭ .∴当32a ≥时,AB 的长度随着a 的增大而减小, ∴取322a ≤<. 综上,当1a <或322a ≤<时,AB 的长度随着a 的增大而减小. 【点睛】本题属于阅读理解题型,结合二次函数的基本性质进行解题,第二问的第二小问的关键是求出AB 的长用a 进行表示,然后利用二次函数基本性质进行分类讨论3.温州茶山杨梅名扬中国,某公司经营茶山杨梅业务,以3万元/吨的价格买入杨梅,包装后直接销售,包装成本为1万元/吨,它的平均销售价格y (单位:万元/吨)与销售数量x (2≤x ≤10,单位:吨)之间的函数关系如图所示.(1)若杨梅的销售量为6吨时,它的平均销售价格是每吨多少万元?(2)当销售数量为多少时,该经营这批杨梅所获得的毛利润(w )最大?最大毛利润为多少万元?(毛利润=销售总收入﹣进价总成本﹣包装总费用)(3)经过市场调查发现,杨梅深加工后不包装直接销售,平均销售价格为12万元/吨.深加工费用y (单位:万元)与加工数量x (单位:吨)之间的函数关系是y =12x +3(2≤x ≤10).①当该公司买入杨梅多少吨时,采用深加工方式与直接包装销售获得毛利润一样? ②该公司买入杨梅吨数在 范围时,采用深加工方式比直接包装销售获得毛利润大些?【答案】(1)杨梅的销售量为6吨时,它的平均销售价格是每吨10万元;(2)当x =8时,此时W 最大值=40万元;(3)①该公司买入杨梅3吨;②3<x ≤8. 【解析】 【分析】(1)设其解析式为y =kx +b ,由图象经过点(2,12),(8,9)两点,得方程组,即可得到结论;(2)根据题意得,w =(y ﹣4)x =(﹣12x +13﹣4)x =﹣12x 2+9x ,根据二次函数的性质即可得到结论;(3)①根据题意列方程,即可得到结论;②根据题意即可得到结论. 【详解】(1)由图象可知,y 是关于x 的一次函数. ∴设其解析式为y =kx +b ,∵图象经过点(2,12),(8,9)两点, ∴21289k b k b +=⎧⎨+=⎩,解得k =﹣12,b =13, ∴一次函数的解析式为y =﹣12x +13, 当x =6时,y =10,答:若杨梅的销售量为6吨时,它的平均销售价格是每吨10万元; (2)根据题意得,w =(y ﹣4)x =(﹣12x +13﹣4)x =﹣12x 2+9x , 当x =﹣2ba=9时,x =9不在取值范围内,∴当x=8时,此时W最大值=﹣12x2+9x=40万元;(3)①由题意得:﹣12x2+9x=9x﹣(12x+3)解得x=﹣2(舍去),x=3,答该公司买入杨梅3吨;②当该公司买入杨梅吨数在 3<x≤8范围时,采用深加工方式比直接包装销售获得毛利润大些.故答案为:3<x≤8.【点睛】本题是二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.4.如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B.抛物线过A、B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)如图1,设抛物线顶点为M,且M的坐标是(12,92),对称轴交AB于点N.①求抛物线的解析式;②是否存在点P,使四边形MNPD为菱形?并说明理由;(2)是否存在这样的点D,使得四边形BOAD的面积最大?若存在,求出此时点D的坐标;若不存在,请说明理由.【答案】(1)①y=﹣2x2+2x+4;;②不存在点P,使四边形MNPD为菱形;;(2)存在,点D的坐标是(1,4).【解析】【分析】(1)①由一次函数图象上点的坐标特征求得点B的坐标,设抛物线解析式为y=a21922x⎛⎫-+⎪⎝⎭,把点B的坐标代入求得a的值即可;②不存在点P,使四边形MNPD为菱形.设点P的坐标是(m,﹣2m+4),则D(m,﹣2m2+2m+4),根据题意知PD∥MN,所以当PD=MN时,四边形MNPD为平行四边形,根据该等量关系列出方程﹣2m2+4m=32,通过解方程求得m的值,易得点N、P的坐标,然后推知PN=MN是否成立即可;(2)设点D的坐标是(n,﹣2n2+2n+4),P(n,﹣2n+4).根据S四边形BOAD=S△BOA+S△ABD =4+S△ABD,则当S△ABD取最大值时,S四边形BOAD最大.根据三角形的面积公式得到函数S△ABD=﹣2(n﹣1)2+2.由二次函数的性质求得最值.【详解】解:①如图1,∵顶点M的坐标是19,22⎛⎫ ⎪⎝⎭,∴设抛物线解析式为y=21922a x⎛⎫-+⎪⎝⎭(a≠0).∵直线y=﹣2x+4交y轴于点B,∴点B的坐标是(0,4).又∵点B在该抛物线上,∴21922a⎛⎫-+⎪⎝⎭=4,解得a=﹣2.故该抛物线的解析式为:y=219222x⎛⎫--+⎪⎝⎭=﹣2x2+2x+4;②不存在.理由如下:∵抛物线y=219222x⎛⎫--+⎪⎝⎭的对称轴是直线x=12,且该直线与直线AB交于点N,∴点N的坐标是1,32⎛⎫ ⎪⎝⎭.∴93322MN=-=.设点P的坐标是(m,﹣2m+4),则D(m,﹣2m2+2m+4),∴PD=(﹣2m2+2m+4)﹣(﹣2m+4)=﹣2m2+4m.∵PD∥MN.当PD=MN时,四边形MNPD是平行四边形,即﹣2m2+4m=32.解得 m1=12(舍去),m2=32.此时P(32,1).∵PN∴PN≠MN,∴平行四边形MNPD不是菱形.∴不存在点P,使四边形MNPD为菱形;(2)存在,理由如下:设点D的坐标是(n,﹣2n2+2n+4),∵点P在线段AB上且直线PD⊥x轴,∴P(n,﹣2n+4).由图可知S四边形BOAD=S△BOA+S△ABD.其中S△BOA=12OB•OA=12×4×2=4.则当S△ABD取最大值时,S四边形BOAD最大.S△ABD=12(y D﹣y P)(x A﹣x B)=y D﹣y P=﹣2n2+2n+4﹣(﹣2n+4)=﹣2n2+4n=﹣2(n﹣1)2+2.当n=1时,S△ABD取得最大值2,S四边形BOAD有最大值.此时点D的坐标是(1,4).【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.5.如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.(1)求抛物线的解析式;(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE 面积最大,并求出其最大值;(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.【答案】(1)y=x2-4x+3.(2)当m=52时,四边形AOPE面积最大,最大值为758.(3)P点的坐标为:P13+5152-),P2(352,1+52),P3(52,1+52),P455-15-.【解析】分析:(1)利用对称性可得点D的坐标,利用交点式可得抛物线的解析式;(2)设P(m,m2-4m+3),根据OE的解析式表示点G的坐标,表示PG的长,根据面积和可得四边形AOPE的面积,利用配方法可得其最大值;(3)存在四种情况:如图3,作辅助线,构建全等三角形,证明△OMP≌△PNF,根据OM=PN列方程可得点P 的坐标;同理可得其他图形中点P的坐标.详解:(1)如图1,设抛物线与x轴的另一个交点为D,由对称性得:D(3,0),设抛物线的解析式为:y=a(x-1)(x-3),把A(0,3)代入得:3=3a,a=1,∴抛物线的解析式;y=x2-4x+3;(2)如图2,设P(m,m2-4m+3),∵OE平分∠AOB,∠AOB=90°,∴∠AOE=45°,∴△AOE是等腰直角三角形,∴AE=OA=3,∴E(3,3),易得OE的解析式为:y=x,过P作PG∥y轴,交OE于点G,∴G(m,m),∴PG=m-(m2-4m+3)=-m2+5m-3,∴S四边形AOPE=S△AOE+S△POE,=12×3×3+12PG•AE,=92+12×3×(-m2+5m-3),=-32m2+152m,=32(m-52)2+758,∵-32<0, ∴当m=52时,S 有最大值是758;(3)如图3,过P 作MN ⊥y 轴,交y 轴于M ,交l 于N ,∵△OPF 是等腰直角三角形,且OP=PF , 易得△OMP ≌△PNF , ∴OM=PN ,∵P (m ,m 2-4m+3), 则-m 2+4m-3=2-m , 解得:m=5+5或55-,∴P 的坐标为(5+5,1+5)或(55-,15-);如图4,过P 作MN ⊥x 轴于N ,过F 作FM ⊥MN 于M ,同理得△ONP ≌△PMF , ∴PN=FM ,则-m 2+4m-3=m-2, 解得:x=3+52或352; P 的坐标为(3+52,152-)或(352,1+52);综上所述,点P 的坐标是:(5+52,1+52)或(552-,152-)或(3+52,152-)或(352,1+52). 点睛:本题属于二次函数综合题,主要考查了二次函数的综合应用,相似三角形的判定与性质以及解一元二次方程的方法,解第(2)问时需要运用配方法,解第(3)问时需要运用分类讨论思想和方程的思想解决问题.6.如图,某足球运动员站在点O 处练习射门,将足球从离地面0.5m 的A 处正对球门踢出(点A 在y 轴上),足球的飞行高度y(单位:m )与飞行时间t(单位:s )之间满足函数关系y =at 2+5t +c ,已知足球飞行0.8s 时,离地面的高度为3.5m . (1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?(2)若足球飞行的水平距离x(单位:m )与飞行时间t(单位:s )之间具有函数关系x =10t ,已知球门的高度为2.44m ,如果该运动员正对球门射门时,离球门的水平距离为28m ,他能否将球直接射入球门?【答案】(1)足球飞行的时间是85s 时,足球离地面最高,最大高度是4.5m ;(2)能. 【解析】试题分析:(1)由题意得:函数y=at 2+5t+c 的图象经过(0,0.5)(0.8,3.5),于是得到,求得抛物线的解析式为:y=﹣t 2+5t+,当t=时,y 最大=4.5;(2)把x=28代入x=10t 得t=2.8,当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,于是得到他能将球直接射入球门.解:(1)由题意得:函数y=at 2+5t+c 的图象经过(0,0.5)(0.8,3.5), ∴,解得:,∴抛物线的解析式为:y=﹣t2+5t+,∴当t=时,y最大=4.5;(2)把x=28代入x=10t得t=2.8,∴当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,∴他能将球直接射入球门.考点:二次函数的应用.7.如图1,抛物线经过平行四边形的顶点、、,抛物线与轴的另一交点为.经过点的直线将平行四边形分割为面积相等的两部分,与抛物线交于另一点.点为直线上方抛物线上一动点,设点的横坐标为.(1)求抛物线的解析式;(2)当何值时,的面积最大?并求最大值的立方根;(3)是否存在点使为直角三角形?若存在,求出的值;若不存在,说明理由.【答案】(1)抛物线解析式为y=﹣x2+2x+3;(2)当t=时,△PEF的面积最大,其最大值为×,最大值的立方根为=;(3)存在满足条件的点P,t的值为1或【解析】试题分析:(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;(2)由A、C坐标可求得平行四边形的中心的坐标,由抛物线的对称性可求得E点坐标,从而可求得直线EF的解析式,作PH⊥x轴,交直线l于点M,作FN⊥PH,则可用t表示出PM的长,从而可表示出△PEF的面积,再利用二次函数的性质可求得其最大值,再求其最大值的立方根即可;(3)由题意可知有∠PAE=90°或∠APE=90°两种情况,当∠PAE=90°时,作PG⊥y轴,利用等腰直角三角形的性质可得到关于t的方程,可求得t的值;当∠APE=90°时,作PK⊥x 轴,AQ⊥PK,则可证得△PKE∽△AQP,利用相似三角形的性质可得到关于t的方程,可求得t的值.试题解析:(1)由题意可得,解得,∴抛物线解析式为y=﹣x2+2x+3;(2)∵A(0,3),D(2,3),∴BC=AD=2,∵B(﹣1,0),∴C(1,0),∴线段AC的中点为(,),∵直线l将平行四边形ABCD分割为面积相等两部分,∴直线l过平行四边形的对称中心,∵A、D关于对称轴对称,∴抛物线对称轴为x=1,∴E(3,0),设直线l的解析式为y=kx+m,把E点和对称中心坐标代入可得,解得,∴直线l的解析式为y=﹣x+,联立直线l和抛物线解析式可得,解得或,∴F(﹣,),如图1,作PH⊥x轴,交l于点M,作FN⊥PH,∵P点横坐标为t,∴P(t,﹣t2+2t+3),M(t,﹣t+),∴PM=﹣t2+2t+3﹣(﹣t+)=﹣t2+t+,∴S△PEF=S△PFM+S△PEM=PM•FN+PM•EH=PM•(FN+EH)=(﹣t2+t+)(3+)=﹣(t﹣)+×,∴当t=时,△PEF的面积最大,其最大值为×,∴最大值的立方根为=;(3)由图可知∠PEA≠90°,∴只能有∠PAE=90°或∠APE=90°,①当∠PAE=90°时,如图2,作PG⊥y轴,∵OA=OE,∴∠OAE=∠OEA=45°,∴∠PAG=∠APG=45°,∴PG=AG,∴t=﹣t2+2t+3﹣3,即﹣t2+t=0,解得t=1或t=0(舍去),②当∠APE=90°时,如图3,作PK⊥x轴,AQ⊥PK,则PK=﹣t2+2t+3,AQ=t,KE=3﹣t,PQ=﹣t2+2t+3﹣3=﹣t2+2t,∵∠APQ+∠KPE=∠APQ+∠PAQ=90°,∴∠PAQ=∠KPE,且∠PKE=∠PQA,∴△PKE∽△AQP,∴,即,即t2﹣t﹣1=0,解得t=或t=<﹣(舍去),综上可知存在满足条件的点P,t的值为1或.考点:二次函数综合题8.如图,抛物线与x轴交于点A(,0)、点B(2,0),与y轴交于点C(0,1),连接BC.(1)求抛物线的函数关系式;(2)点N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t (),求△ABN的面积S与t的函数关系式;(3)若且时△OPN∽△COB,求点N的坐标.【答案】(1);(2);(3)(,)或(1,2).【解析】试题分析:(1)可设抛物线的解析式为,用待定系数法就可得到结论;(2)当时,点N在x轴的上方,则NP等于点N的纵坐标,只需求出AB,就可得到S与t的函数关系式;(3)由相似三角形的性质可得PN=2PO.而PO=,需分和0<t<2两种情况讨论,由PN=2PO得到关于t的方程,解这个方程,就可得到答案.试题解析:(1)设抛物线的解析式为,把C(0,1)代入可得:,∴,∴抛物线的函数关系式为:,即;(2)当时,>0,∴NP===,∴S=AB•PN==;(3)∵△OPN∽△COB,∴,∴,∴PN=2PO.①当时,PN===,PO==,∴,整理得:,解得:=,=,∵>0,<<0,∴t=,此时点N的坐标为(,);②当0<t<2时,PN===,PO==t,∴,整理得:,解得:=,=1.∵<0,0<1<2,∴t=1,此时点N的坐标为(1,2).综上所述:点N的坐标为(,)或(1,2).考点:1.二次函数综合题;2.待定系数法求二次函数解析式;3.相似三角形的性质.9.已知抛物线27y x3x4=--的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.(1)求点A、B、C、D的坐标;(2)在y轴的正半轴上是否存在点P,使以点P、O、A为顶点的三角形与△AOC相似?若存在,求出点P的坐标;若不存在,请说明理由;(3)取点E(34-,0)和点F(0,),直线l经过E、F两点,点G是线段BD的中点.①点G是否在直线l上,请说明理由;②在抛物线上是否存在点M,使点M关于直线l的对称点在x轴上?若存在,求出点M 的坐标;若不存在,请说明理由.【答案】解:(1) D(32,﹣4)(2) P(0,74)或(0,17)(3)详见解析【解析】【分析】(1)令y=0,解关于x的一元二次方程求出A、B的坐标,令x=0求出点C的坐标,再根据顶点坐标公式计算即可求出顶点D的坐标.(2)根据点A、C的坐标求出OA、OC的长,再分OA和OA是对应边,OA和OC是对应边两种情况,利用相似三角形对应边成比例列式求出OP的长,从而得解.(3)①设直线l的解析式为y=kx+b(k≠0),利用待定系数法求一次函数解析式求出直线l的解析式,再利用中点公式求出点G的坐标,然后根据直线上点的坐标特征验证即可.②设抛物线的对称轴与x轴交点为H,求出OE、OF、HD、HB的长,然后求出△OEF和△HDB相似,根据相似三角形对应角相等求出∠OFE=∠HBD,然后求出EG⊥BD,从而得到直线l是线段BD的垂直平分线,根据线段垂直平分线的性质点D关于直线l的对称点就是B ,从而判断出点M 就是直线DE 与抛物线的交点.再设直线DE 的解析式为y=mx+n ,利用待定系数法求一次函数解析求出直线DE 的解析式,然后与抛物线解析式联立求解即可得到符合条件的点M . 【详解】解:(1)在27y x 3x 4=--中,令y=0,则27x 3x 04--=,整理得,4x 2﹣12x ﹣7=0, 解得x 1=12-,x 2=72.∴A (12-,0),B (72,0). 在27y x 3x 4=--中,令x=0,则y=74-.∴C (0,74-). ∵()227413b 334ac b 442a 2124a 41⎛⎫⨯⨯--- ⎪--⎝⎭-=-===-⨯⨯,,∴顶点D (32,﹣4). (2)在y 轴正半轴上存在符合条件的点P . 设点P 的坐标为(0,y ),∵A (12-,0),C (0,74-),∴OA=12,OC=74,OP=y , ①若OA 和OA 是对应边,则△AOP ∽△AOC ,∴OP OA OC OA =.∴y=OC=74,此时点P (0,74). ②若OA 和OC 是对应边,则△POA ∽△AOC ,∴OP OAOA OC=,即1y 21724=.解得y=17,此时点P (0,17).综上所述,符合条件的点P 有两个,P (0,74)或(0,17).(3)①设直线l 的解析式为y=kx+b (k≠0),∵直线l 经过点E (32-,0)和点F (0,34-),∴3k b 023b 4⎧-+=⎪⎪⎨⎪=-⎪⎩,解得1k 23b 4⎧=-⎪⎪⎨⎪=-⎪⎩,∴直线l 的解析式为13y x 24=--. ∵B (72,0),D (32,﹣4),∴[]1735104222222+=+-=-(),(),∴线段BD 的中点G 的坐标为(52,﹣2). 当x=52时,153y 2224=-⨯-=-,∴点G 在直线l 上. ②在抛物线上存在符合条件的点M .设抛物线的对称轴与x 轴交点为H ,则点H 的坐标为(32,0), ∵E (32-,0)、F (0,34-),B (72,0)、D (32,﹣4), ∴OE=32,OF=72,HD=4,HB=72﹣32=2. ∵,∠OEF=∠HDB ,∴△OEF ∽△HDB .∴∠OFE=∠HBD .∵∠OEF+∠OFE=90°,∴∠OEF+∠HBD=90°.∴∠EGB=180°﹣(∠OEF+∠HBD )=180°﹣90°=90°,∴直线l 是线段BD 的垂直平分线.∴点D 关于直线l 的对称点就是点B .∴点M 就是直线DE 与抛物线的交点.设直线DE 的解析式为y=mx+n ,∵D (32,﹣4),E (32-,0), ∴,解得.∴直线DE 的解析式为. 联立,解得,.∴符合条件的点M 有两个,是(32,﹣4)或(,).10.如图1,抛物线y=ax 2+2x+c 与x 轴交于A (﹣4,0),B (1,0)两点,过点B 的直线y=kx+23分别与y 轴及抛物线交于点C ,D . (1)求直线和抛物线的表达式; (2)动点P 从点O 出发,在x 轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t 秒,当t 为何值时,△PDC 为直角三角形?请直接写出所有满足条件的t 的值;(3)如图2,将直线BD 沿y 轴向下平移4个单位后,与x 轴,y 轴分别交于E ,F 两点,在抛物线的对称轴上是否存在点M ,在直线EF 上是否存在点N ,使DM+MN 的值最小?若存在,求出其最小值及点M ,N 的坐标;若不存在,请说明理由.【答案】(1)抛物线解析式为:y=228233x x +-,BD 解析式为y=﹣2233x +;(2)t 的值为4915129±、233.(3)N 点坐标为(﹣2,﹣2),M 点坐标为(﹣32,﹣54),213 【解析】分析:(1)利用待定系数法求解可得;(2)先求得点D 的坐标,过点D 分别作DE ⊥x 轴、DF ⊥y 轴,分P 1D ⊥P 1C 、P 2D ⊥DC 、P 3C ⊥DC 三种情况,利用相似三角形的性质逐一求解可得;(3)通过作对称点,将折线转化成两点间距离,应用两点之间线段最短.详解:(1)把A (﹣4,0),B (1,0)代入y=ax 2+2x+c ,得168020a ca c-+=⎧⎨++=⎩,解得:2383 ac⎧=⎪⎪⎨⎪=-⎪⎩,∴抛物线解析式为:y=228233x x+-,∵过点B的直线y=kx+23,∴代入(1,0),得:k=﹣23,∴BD解析式为y=﹣2233x+;(2)由2282332233y x xy x﹣⎧=+-⎪⎪⎨⎪=+⎪⎩得交点坐标为D(﹣5,4),如图1,过D作DE⊥x轴于点E,作DF⊥y轴于点F,当P1D⊥P1C时,△P1DC为直角三角形,则△DEP1∽△P1OC,∴DEPO=PEOC,即4t=523t-,解得15129±,当P2D⊥DC于点D时,△P2DC为直角三角形由△P2DB∽△DEB得DBEB=2P BDB,5252,解得:t=233; 当P 3C ⊥DC 时,△DFC ∽△COP 3,∴DF OC =3CF P O ,即523=103t, 解得:t=49, ∴t 的值为49、15129±、233. (3)由已知直线EF 解析式为:y=﹣23x ﹣103, 在抛物线上取点D 的对称点D′,过点D′作D′N ⊥EF 于点N ,交抛物线对称轴于点M过点N 作NH ⊥DD′于点H ,此时,DM+MN=D′N 最小.则△EOF ∽△NHD′设点N 坐标为(a ,﹣21033a -), ∴OE NH =OF HD ',即52104()33a ---=1032a -, 解得:a=﹣2,则N 点坐标为(﹣2,﹣2),求得直线ND′的解析式为y=32x+1, 当x=﹣32时,y=﹣54, ∴M 点坐标为(﹣32,﹣54), 此时,DM+MN 22D H NH '+2246+13点睛:本题是二次函数和几何问题综合题,应用了二次函数性质以及转化的数学思想、分类讨论思想.解题时注意数形结合.。
中考二次函数与直角三角形有关的问题知识解读

二次函数与直角三角形有关的问题知识解读【专题说明】二次函数之直角三角形存在性问题,主要指的是在平面直角坐标系下,已知一条边(或两个顶点)的直角三角形存在,求第三个顶点的坐标的题型.主要考察学生对转化思想、方程思想、几何问题代数化的数形结合思想及分类讨论思想的灵活运用。
【解题思路】直角三角形的存在性问题1.找点:在已知两定点,确定第三点构成直角三角形时,要么以两定点为直角顶点,要么以动点为直角顶点.以定点为直角顶点时,构造两条直线与已知直线垂直;以动点为直角顶点时,以已知线段为直径构造圆找点2.方法:(1)以两定点为直角顶点时,两直线互相垂直,则k1*k2=-1(2)以已知线段为斜边时,利用K型图,构造双垂直模型,最后利用相似求解,或者三条边分别表示之后,利用勾股定理求解下面主要介绍2种常用方法:【方法1 几何法】“两线一圆”(1)若∠A 为直角,过点A 作AB 的垂线,与x 轴的交点即为所求点C;(2)若∠B 为直角,过点B 作AB 的垂线,与x 轴的交点即为所求点C;(3)若∠C 为直角,以AB 为直径作圆,与x 轴的交点即为所求点C.(直径所对的圆周角为直角)如何求得点坐标?以C2为例:构造三垂直.),坐标为(故代入得:坐标得、由,易证0213232222C C C BN AM B A N MB BN AM BN AMB ===∆≈∆()),坐标为(,,坐标为故或故又即代入得:设,,坐标得、由求法相同,如下:易证、040231a ,4a ,3ab ,3ab 1N a,31,4333333343C C C C C C C C C C b b M BN AM B A NBM N AMNB AM ==+=======∆≈∆【方法2 代数法】点-线-方程23m 20352235110,m 135-m 1-m 35-m 11-m 22222122111=+=+=+=+==,解得:)代入得方程(,,,)表示线段:();,()、,(),又坐标为()表示点:设(:不妨来求下)()()()(BC C C C A AB B A【典例分析】【方法1 勾股定理】【典例1】(2021秋•建华区期末)抛物线y=x2+bx+c经过A、B(1,0)、C(0,﹣3)三点.点D为抛物线的顶点,连接AD、AC、BC、DC.(1)求抛物线的解析式;(2)在y轴上是否存在一点E,使△ADE为直角三角形?若存在,请你直接写出点E的坐标;若不存在,请说明理由.【解答】解(1)∵抛物线y=x2+bx+c经过B(1,0)、C(0,﹣3),∴,解得,∴抛物线的解析式为:y=x2+2x﹣3.(4)在y轴上存在点E,使△ADE为直角三角形,理由如下:∵抛物线的解析式为y=x2+2x﹣3=(x+1)2﹣4,∴D(﹣1,﹣4),设E点坐标为(0,m),∴AE2=m2+9,DE2=m2+8m+17,AD2=20,当∠EAD=90°时,有AE2+AD2=DE2,∴m2+9+20=m2+8m+17,解得m=,∴此时点E的坐标为(0,);当∠ADE=90°时,DE2+AD2=AE2,m2+8m+17+20=m2+9,解得m=﹣,∴此时点E的坐标为(0,﹣);当∠AED=90°时,AE2+DE2=AD2,m2+9+m2+8m+17=20,解得m=﹣1或m=﹣3,∴此时点E的坐标为(0,﹣1)或(0,﹣3).【变式1-1】(2022•灞桥区校级模拟)如图,抛物线与x轴交于点A(1,0),B(3,0),与y轴交于点C(0,3).(1)求二次函数的表达式及顶点坐标;(2)连接BC,在抛物线的对称轴上是否存在一点E,使△BCE是直角三角形?若存在,请直接写出点E的坐标;若不存在,请说明理由.【解答】解:(1)设抛物线的解析式为y=a(x﹣1)(x﹣3),将点C(0,3)代入y=a(x﹣1)(x﹣3),∴3a=3,∴a=1,∴y=(x﹣1)(x﹣3)=x2﹣4x+3,∵y=x2﹣4x+3=(x﹣2)2﹣1,∴顶点为(2,﹣1);(2)存在一点E,使△BCE是直角三角形,理由如下:∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的对称轴为直线x=2,设E(2,t),∵△BCE是直角三角形,∴BE⊥CE,∵B(3,0),C(0,3),∴BC=3,BE=,CE=,①当BC为斜边时,∴18=()2+()2,解得t=,∴E点坐标为(2,)或(2,);②当BE为斜边时,∴18+()2=()2,解得t=5,∴E点坐标为(2,5);③当CE为斜边时,∴18+()2=()2,解得t=﹣1,∴E点坐标为(2,﹣1);综上所述:E点坐标为(2,)或(2,)或(2,5)或(2,﹣1)【变式1-2】(2022•广安)如图,在平面直角坐标系中,抛物线y=ax2+x+m(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,﹣4),点C坐标为(2,0).(1)求此抛物线的函数解析式.(2)点P为该抛物线对称轴上的动点,使得△P AB为直角三角形,请求出点P的坐标.【解答】解:(1)∵抛物线y=ax2+x+m(a≠0)的图象经过点B(0,﹣4),点C(2,0),∴,解得,∴抛物线的解析式为y=x2+x﹣4;(2)如图2中,设抛物线的对称轴交x轴于点N,过点B作BM⊥抛物线的对称轴于点M.则N(﹣1.0).M(﹣1,﹣4);∵OA=OB=4,∠AOB=90°,∴∠OAB=∠OBA=45°,当∠P1AB=90°时,△ANP1是等腰直角三角形,∴AN=NP1=3,∴P1(﹣1,3),当∠ABP2=90°时,△BMP2是等腰直角三角形,可得P2(﹣1,﹣5),当∠APB=90°时,设P(﹣1,n),设AB的中点为J,连接PJ,则J(﹣2,﹣2),∴PJ=AB=2,∴12+(n+2)2=(2)2,解得n=﹣2或﹣﹣2,∴P3(﹣1,﹣2),P4(﹣1,﹣﹣2),综上所述,满足条件的点P的坐标为(﹣1,3)或(﹣1,﹣5)或(﹣1,﹣2)或(﹣1,﹣﹣2).【方法2 构造“K”字型利用相似作答】【典例2】(2022•碑林区校级四模)如图,在平面直角坐标系中,抛物线C1:y=ax2+bx+c 交x轴于点A(﹣5,0),B(﹣1,0),交y轴于点C(0,5).(1)求抛物线C1的表达式和顶点D的坐标.(2)将抛物线C1关于y轴对称的抛物线记作C2,点E为抛物线C2上一点若△DOE是以DO为直角边的直角三角形,求点E的坐标.【解答】解:(1)将点A(﹣5,0),B(﹣1,0),C(0,5)代入y=ax2+bx+c,∴,解得,∴y=x2+6x+5,∵y=x2+6x+5=(x+3)2﹣4,∴顶点D(﹣3,﹣4);(2)设抛物线C2上任意一点(x,y),则(x,y)关于y轴对称的点为(﹣x,y),∵点(﹣x,y)在抛物线C1上,∴抛物线记作C2的解析式为y=x2﹣6x+5,设E(t,t2﹣6t+5),过点D作DG⊥x轴交于点G,过点E作EH⊥x轴交于点H,∵∠DOE=90°,∴∠GOD+∠HOE=90°,∵∠GOD+∠GDO=90°,∴∠HOE=∠GDO,∴△GDO∽△HOE,∴=,∵DG=4,GO=3,HE=﹣t2+6t﹣5,OH=t,∴=,∴t=4或t=,∴E(4,﹣3)或E(,﹣).【变式2-1】(2022•济南)抛物线y=ax2+x﹣6与x轴交于A(t,0),B(8,0)两点,与y轴交于点C,直线y=kx﹣6经过点B.点P在抛物线上,设点P的横坐标为m.(1)求抛物线的表达式和t,k的值;(2)如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;【解答】解:(1)将B(8,0)代入y=ax2+x﹣6,∴64a+22﹣6=0,∴a=﹣,∴y=﹣x2+x﹣6,当y=0时,﹣t2+t﹣6=0,解得t=3或t=8(舍),∴t=3,∵B(8,0)在直线y=kx﹣6上,∴8k﹣6=0,解得k=,∴y=x﹣6;(2)作PM⊥x轴交于M,∵P点横坐标为m,∴P(m,﹣m2+m﹣6),∴PM=m2﹣m+6,AM=m﹣3,在Rt△COA和Rt△AMP中,∵∠OAC+∠P AM=90°,∠APM+∠P AM=90°,∴∠OAC=∠APM,∴△COA∽△AMP,∴=,即OA•MA=CO•PM,3(m﹣3)=6(m2﹣m+6),解得m=3(舍)或m=10,∴P(10,﹣);【变式2-2】(2022•滨州)如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接AC、BC.(1)求线段AC的长;(2)若点M为该抛物线上的一个动点,当△BCM为直角三角形时,求点M的坐标.【解答】解:(1)针对于抛物线y=x2﹣2x﹣3,令x=0,则y=﹣3,∴C(0,﹣3);令y=0,则x2﹣2x﹣3=0,∴x=3或x=﹣1,∵点A在点B的左侧,∴A(﹣1,0),B(3,0),∴AC==;(2)由(1)知,B(3,0),C(0,﹣3),∴OB=OC=3,设M(m,m2﹣2m﹣3),∵△BCM为直角三角形,∴①当∠BCM=90°时,如图1,过点M作MH⊥y轴于H,则HM=m,∵OB=OC,∴∠OCB=∠OBC=45°,∴∠HCM=90°﹣∠OCB=45°,∴∠HMC=45°=∠HCM,∴CH=MH,∵CH=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,∴﹣m2+2m=m,∴m=0(不符合题意,舍去)或m=1,∴M(1,﹣4);②当∠CBM=90°时,过点M作M'H'⊥x轴,同①的方法得,M'(﹣2,5);③当∠BMC=90°时,如图2,Ⅰ、当点M在第四象限时,过点M作MD⊥y轴于D,过点B作BE⊥DM,交DM的延长线于E,∴∠CDM=∠E=90°,∴∠DCM+∠DMC=90°,∵∠DMC+∠EMB=90°,∴∠DCM=∠EMB,∴△CDM∽△MEB,∴,∵M(m,m2﹣2m﹣3),B(3,0),C(0,﹣3),∴DM=m,CD=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,ME=3﹣m,BE=﹣(m2﹣2m﹣3)=﹣m2+2m+3,∴,∴m=0(舍去)或m=3(点B的横坐标,不符合题意,舍去)或m=(不符合题意,舍去)或m=,∴M(,﹣),Ⅱ、当点M在第三象限时,M(,﹣),即满足条件的M的坐标为(1,﹣4)或(﹣2,5)或(,﹣),或(,﹣).。
【2019-2020】中考数学试题分类汇编考点25矩形含解析

∵点P、Q是AO,AD的中点,
∴PQ是△AOD的中位线,
∴PQ= DO=2.5.
故答案为:2.5.
12.(20xx•嘉兴)如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是0或1<AF 或4.
【解答】解:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∵点E是边BC的中点,
∴BE= BC= AD,
∴△BEF∽△DAF,
∴ = ,
∴EF= AF,
∴EF= AE,
∵点E是边BC的中点,
∴由矩形的对称性得:AE=DE,
∴EF= DE,设EF=x,则DE=3x,
∴DF= =2 x,
∴tan∠BDE= = = ;
【解答】解:过点C1作C1N⊥x轴于点N,过点A1作A1M⊥x轴于点M,
由题意可得:∠C1NO=∠A1MO=90°,
∠1=∠2=∠3,
则△A1OM∽△OC1N,
∵OA=5,OC=3,
∴OA1=5,A1M=3,
∴OM=4,
∴设NO=3x,则NC1=4x,OC1=3,
则(3x)2+(4x)2=9,
解得:x=± (负数舍去),
故选:A.
3.(20xx•威海)矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )
A.1B. C. D.
【分析】延长GH交AD于点P,先证△APH≌△FGH得AP=GF=1,GH=PH= PG,再利用勾股定理求得PG= ,从而得出答案.
2020年中考数学二次函数压轴题核心考点突破14矩形存在性问题

引例:已知 A(1,1)、B(4,2),点 C 在 x 轴上,点 D 在坐标系中,且以 A、B、C、D 为顶点的四边形是矩形,求 D 点坐标.
y
A O
B x
【分析】 设 C 点坐标为(a,0),D 点坐标为(b,c),又 A(1,1)、B(4,2). 先考虑平行四边形存在性:
(1)AB
为对角线时,
C 的坐标为(0,3),点 C 与点 D 关于抛物线的对称轴对称.
(1)求抛物线的解析式;
(2)若点 P 为抛物线对称轴上一点,连接 BD,以 PD,PB 为边作平行四边形 PDNB,是
否存在这样的点 P,使得平行四边形 PDNB 是矩形?若存在,请求出 tan∠BDN 的值;
y
y
若不存在,请说明理由.
a 42 0 22 ,
a
4 3
综合以上可解得:
b
13 3
.故
C
14 3
,
0
、D
13 3
,1
.
c 1
【小结】这个方法是在 平行四边形基础上多加一个等式而已,剩 下的都是计算的故事.
【2018·铁岭中考(删减)】
如图,抛物线 y x2 bx c 交 x 轴于点 A ,B,交 y 轴于点 C.点 B 的坐标为(3,0)点
xA yA
xC yC
xB yB
xD yD
xA xC 2 yA yC 2
(AC 为对角线时)
xB xD 2 yB yD 2
因此在矩形存在性问题最多可以有 3 个未知量,代入可以得到三元一次方程组,可解. 确定了有 3 个未知量,则可判断常见矩形存在性问题至少有 2 个动点,多则可以有 3 个.
中物理
矩形存在性问题
2020中考数学复习分类汇编专题3:二次函数与线段及其最值问题(含答案)

专题:二次函数中的线段问题(含最值问题)1. 如图,抛物线y =ax 2+bx +c (a ≠0)与x 轴交于点A ,B (1,0),与y 轴交于点C ,直线y = x -2经过点A 、C .抛物线的顶点为D ,对称轴为直线l .(1) 求抛物线的表达式、顶点D 的坐标及对称轴l ; (2) 设点E 为x 轴上一点,且AE =CE ,求点E 的坐标;(3) 设点G 是y 轴上一点,是否存在点G ,使得GD +GB 的值最小,若存在,求出点G 的坐标;若不存在,请说明理由;(4) 在直线l 上是否存在一点F ,使得△BCF 的周长最小,若存在,求出点F 的坐标及△BCF 周长的最小值;若不存在,请说明理由;(5) 点S 为y 轴上任意一点,K 为直线AC 上一点,连接BS ,BK ,是否存在点S ,K 使得△BSK 的周长最小,若存在,求出S ,K 的坐标,并求出△BSK 周长的最小值;若不存在,请说明理由;(6) 在y 轴上是否存在一点S ,使得SD -SB 的值最大,若存在,求出点S 的坐标;若不存在,请说明理由; (7) 若点H 是抛物线上位于AC 上方的一点,过点H 作y 轴的平行线,交AC 于点K ,设点H 的横坐标为h ,线段HK =d .①求d 关于h 的函数关系式; ②求d 的最大值及此时H 点的坐标.122. 如图,抛物线y=-x2-2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.点D(m,0)为线段OA上一个动点(与点A,O不重合),过点D作x轴的垂线与线段AC交于点P,与抛物线交于点Q,连接BP,与y轴交于点E.(1)求A,B,C三点的坐标;(2)当点D是OA的中点时,求线段PQ的长;(3)在点D运动的过程中,探究下列问题:①是否存在一点D,使得PQ+22PC取得最大值?若存在,求此时m的值;若不存在,请说明理由;②连接CQ,当线段PE=CQ时,直接写出m的值.3. 如图,直线y =-34x +1与x 轴、y 轴分别交于A 、B 两点,抛物线y =-12x 2+bx +c 经过点B ,且与直线AB 的另一交点为C (4,n ).(1)求该抛物线的表达式及点C 的坐标;(2)设抛物线上的一个动点P 的横坐标为t (0<t <4),过点P 作PD ⊥AB 交直线AB 于点D ,作PE ∥y 轴交直线AB 于点E .①求线段PD 的长的最大值; ②当t 为何值时,点D 为BE 的中点.4. 已知抛物线y =ax 2+bx +2经过A (-1,0),B (2,0),C 三点.直线y =mx +12交抛物线于A ,Q 两点,点P 是抛物线上直线AQ 上方的一个动点,过点P 作PF ⊥x 轴,垂足为点F ,交AQ 于点N .(1)求抛物线的表达式;(2)如图①,在点P 运动过程中,当PN =2NF 时,求点P 的坐标;(3)如图②,线段AC 的垂直平分线交x 轴于点E ,垂足为点D ,点M 为抛物线的顶点,在直线DE 上是否存在一点G ,使△CMG 的周长最小?若存在,请求出点G 的坐标;若不存在,请说明理由.参考答案1. (1)解:对于直线y =21x -2, 令y =0,得x =4,令x =0,得y =-2, ∴点A (4,0),点C (0,-2),抛物线的解析式为y = -21x 2+25x -2 ∴顶点D 的坐标为(25,98 ),对称轴l 为直线x = 25(2)要求点E 的坐标,已知AE =CE ,设E 点坐标为(e ,0),用含e 的式子分别表示出AE 和CE ,建立等量关系求解即可.点E 的坐标为( 23,0)(3)要使GD +GB 的值最小,一般是通过轴对称作出对称点来解决. 解:存在.如解图②,要使GD +GB 的值最小,取点B 关于y 轴的对称点B ′,点B ′的坐标为(-1,0).连接B ′D ,直线B ′D 与y 轴的交点G 即为所求的点,点G 的坐标为(0, 289);(4)要使△BCF 周长最小,BC 长为定值,即要使CF +BF 的值最小.△BCF 周长的最小值为BC +AC =3 √5 ;(5)要求△BSK 周长的最小值,可分别作点B 关于y 轴和直线AC 的两个对称点B ′、B ″,连接B ′B ″与y 轴和直线AC 交点即为使得△BSK 的周长最小的点S 、K ,最小值即线段B ′B ″的长.存在点S (0,-43 ),点K (1, - 23 )使得△BSK 的周长最小,最小值为4;(6)当点S 在DB 的延长线上时,SD -SB 最大,最大值为BD , 即当点S 的坐标为(0,-43)时,SD -SB 的值最大;(7)平行于y 轴的直线上两点之间的距离为此两点的纵坐标之差的绝对值,如此问,由题可得点H 的横坐标为h ,①求出点H ,K 的纵坐标,再由点H 在点K 的上方,可得到d 关于h 的函数关系式;②利用二次函数的性质求最值,即可得d 的最大值及H 点的坐标.(1)d 关于h 的函数关系式为d =-21h 2+2h ; (2)当h =2时,d 最大,最大值为2,此时点H 的坐标为(2,1).参考答案2. 解:(1)在y =-x 2-2x +3中, 令y =0,得-x 2-2x +3=0, 解得x 1=-3,x 2=1. ∵点A 在点B 的左侧, ∴A (-3,0),B (1,0). 令x =0,得y =3, ∴点C 的坐标为(0,3);(2)设直线AC 的表达式为y =kx +b .将A ,C 两点的坐标(-3,0),(0,3)代入表达式,得⎩⎪⎨⎪⎧-3k +b =0,b =3,解得⎩⎪⎨⎪⎧k =1,b =3,∴直线AC 的表达式为y =x +3.(4分) ∵点D 是OA 的中点,∴OD =12OA =32,∴点D 的横坐标m =-32.∵PQ ⊥x 轴,∴把m =-32分别代入y =x +3和y =-x 2-2x +3,得P ,Q 两点的坐标分别为(-32,32)、(-32,154),∵DQ ⊥OA ,∴PQ =DQ -DP =y Q -y P . ∴PQ =154-32=94;(3)①存在点D ,使得PQ +22PC 取得最大值. 理由:∵点D 的横坐标为m ,PQ ⊥x 轴,且点P ,Q 分别在直线AC 和抛物线上, ∴P ,Q 两点的坐标分别为(m ,m +3),(m ,-m 2-2m +3). ∵DQ ⊥OA ,∴PQ =DQ -DP =y Q -y P ,∴PQ =-m 2-2m +3-(m +3)=-m 2-3m . 如解图,过点P 作PF ⊥y 轴于点F ,则PF =-m . 在Rt △AOC 中,OA =OC =3, ∴∠CAO =∠OCA =45°.∴sin ∠OCA =PF PC =22.∴PF =22PC ∴PQ +22PC =-m 2-3m -m =-m 2-4m =-(m +2)2+4, ∵PQ +22PC 是m 的二次函数,其中a =-1<0,而-3<m <0. ∴当m =-2时,PQ +22PC 取得最大值;②m =-1或m =- 5.【解法提示】∵△PFE ∽△BOE ,∴PF BO =EFEO.∵PF =-m ,OF =m +3,OB =1,∴EF =-mOE .∵OF =EF +OE ,∴m +3=(-m +1)OE ,则OE =m +3-m +1,EF =-m (m +3)-m +1,又∵CQ =PE ,PQ ∥CE ,∴|y Q -y C |=|y P -y E |=EF .∵|y Q -y C |=|-m 2-2m +3-3|=|m 2+2m |,∴-m (m +3)-m +1=|m 2+2m |.又∵-3<m <0,解得m =-1或m =- 5.3. 解:(1)把x =4,y =n 代入y =-34x +1中,得n =-34×4+1=-2∴点C 的坐标为(4,-2).将点C (4,-2)和点B (0,1)代入y =-12x 2+bx +c ,得⎩⎪⎨⎪⎧-8+4b +c =-2,c =1, 解得⎩⎪⎨⎪⎧b =54,c =1,∴抛物线的表达式为y =-12x 2+54x +1;(2)①∵PE =-12t 2+54t +1-(-34t +1)=-12t 2+2t ,如解图,过点E 作QE ⊥y 轴于点Q ,则QE =t , QB =1+34t -1=34t ,BE =QB 2+QE 2=(34t )2+t 2=54t ∵PE ∥y 轴, ∴∠PEB =∠EBQ , ∵∠BQE =∠PDE =90°, ∴△PED ∽△EBQ ,∴PE EB =PD EQ ,得-12t 2+2t 54t =PDt, PD =-25t 2+85t .∵-25<0,∴PD 有最大值, PD 最大=0-(85)24×(-25)=85;②∵点D 为BE 的中点,∴由PE EB =DE QB ,DE =12BE ,得12BE 2=PE ·QB ,代入得12×(54t )2=(-12t 2+2t )×34t ,整理得2532=-38t +32,解得t =2312,∴当t =2312时,点D 为BE 的中点.4. 解:(1)∵抛物线y =ax 2+bx +2经过A (-1,0),B (2,0),∴将点A 和点B 的坐标代入得⎩⎪⎨⎪⎧a -b +2=0,4a +2b +2=0,解得⎩⎪⎨⎪⎧a =-1,b =1,∴抛物线的表达式为y =-x 2+x +2;(2)直线y =mx +12交抛物线于A 、Q 两点,把A (-1,0)代入解析式得m =12,∴直线AQ 的表达式为y =12x +12.设点P 的横坐标为n ,则P (n ,-n 2+n +2),N (n ,12n +12),F (n ,0),∴PN =-n 2+n +2-(12n +12)=-n 2+12n +32,NF =12n +12.∵PN =2NF ,即-n 2+12n +32=2×(12n +12),解得n =-1或n =12,当n =-1时,点P 与点A 重合,不符合题意舍去.∴点P 的坐标为(12,94);(3)在直线DE 上存在一点G ,使△CMG 的周长最小;此时G (-38,1516).理由如下:∵y =-x 2+x +2=-(x -12)2+94,∴M (12,94).如解图,连接AM 交直线DE 于点G ,连接CG 、CM ,此时,△CMG 的周长最小. 设直线AM 的函数表达式为y =kx +b ,且过A (-1,0),M (12,94).根据题意得⎩⎪⎨⎪⎧-k +b =0,12k +b =94,解得⎩⎨⎧k =32,b =32.∴直线AM 的表达式为y =32x +32.∵D 为AC 的中点,∴D (-12,1).设直线AC 的表达式为y =kx +2,将点A 的坐标代入得-k +2=0,解得k =2, ∴AC 的表达式为y =2x +2.设直线DE 的表达式为y =-12x +c ,将点D 的坐标代入得:14+c =1,解得c =34,∴直线DE 的表达式为y =-12x +34.联立⎩⎨⎧y =-12x +34,y =32x +32,解得⎩⎨⎧x =-38,y =1516.∴在直线DE 上存在一点G ,使△CMG 的周长最小,此时G (-38,1516).。
2024年九年级中考数学专题复习: 二次函数与直角三角形综合压轴题(含答案)
2024年九年级中考数学专题复习:二次函数与直角三角形综合压轴题1.如图,抛物线与轴相交于两点,与轴相交于点,点的坐标是,点的坐标是,是抛物线的顶点.(1)求抛物线的解析式;(2)为线段上的一个动点,过点作轴于点,点坐标为.①在上是否存在点,使为直角三角形?如果存在,请求出点的坐标;如果不存在,请说明理由;②连接,若,求的值.2.已知抛物线,交x 轴于A ,B 两点,交y 轴于C 点,点F 为抛物线顶点,直线垂直于x 轴于E 点,点P 是线段BE 上的动点(除B ,E 外),过点P 作x 轴的垂线交抛物线于点D ,当时,.2y x bx c =-++x A B ,y C B ()20-,C ()02,M P MB P PD x ⊥D D ()0m ,MB P PCD P AC PCD OCA ∠=∠m 2y ax 2x c =++EF 0y ≥13x -≤≤(1)求抛物线的表达式;(2)如图1,当点P 的横坐标为2时,求四边形的面积(3)如图2,直线分别与抛物线对称轴交于M ,N 两点.试问,是否为定值?如果是,请求出这个定值;如果不是,请说明理由.(4)如图3,点在抛物线上,当是以为斜边的直角三角形时,求点P 的坐标.3.如图,抛物线经过点,与x 轴交于点,点C 是该抛物线的顶点.(1)求该抛物线的函数关系式和点C 坐标;(2)如图1,点P 是抛物线上在第一象限内的点,若为直角三角形,直接写出点P 的坐标;(3)如图 2,点Q 是抛物线上一点,过点Q 作抛物线对称轴的垂线,垂足为H ,点D 是ACFD AD BD ,EM EN +()2,3Q AQD AQ 2y ax bx =+()1,3()4,0A OCP △(1)求,的值;(2)抛物线的对称轴上是否存在一点长;若不存在,请说明理由;(3)抛物线的对称轴是上是否存在一点在,求出点的坐标,若不存在,请说明理由.a k N(1)求a ,k 的值.(2)求的面积.(3)抛物线的对称轴上是否存在一点N ,使是直角三角形?若存在,求出点N 的坐标,若不存在,请说明理由.7.如图,抛物线的顶点为,与轴交于点,与轴交于点、.(1)求此抛物线的解析式;(2)设是直线上方该抛物线上除点外的一点,且与的面积相等,求点的坐标;(3)在直线上方,抛物线上找一点,使得的面积最大,则点的坐标为________;(4)设是抛物线上一点,且为直角三角形,则点的横坐标为________.ACP △ABN ()1,4P y ()0,3C x A B Q BC P BCQ △BCP Q BC M BCM M E EBC E8.已知直线l 与轴、轴分别相交于、两点,抛物线经过点,交轴正半轴于点. (1)求直线的函数解析式和抛物线的函数解析式;(2)在第一象限内抛物线上取点,连接、,求面积的最大值及点的坐标.(3)抛物线上是否存在点使为直角三角形,如果存在,请直接写出点的坐标;如果不存在,请说明理由.9.如图,抛物线的对称轴为直线,并且经过点,交轴于另一点,交轴于点.x y (1,0)A (0,3)B 224y ax ax a =-++(0)a <B x C l M AM BM AMB M P CBP P 23y ax bx =++2x =()2,0A -x B y C(1)求抛物线的解析式;(2)在直线上方的抛物线上有一点P ,求点P 到直线距离的最大值及此时点P 的坐标;(3)在直线下方的抛物线上是否存在点Q ,使得为直角三角形?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.10.在平面直角坐标系中,为坐标原点,抛物线与轴交于点.(1)求抛物线的解析式.(2)如图,将抛物线向左平移1个单位长度,记平移后的抛物线顶点为,平移后的抛物线与轴交于两点(点在点的右侧),与轴交于点.判断以三点为顶点的三角形是否为直角三角形,并说明理由.BC BC BC QBC △O 2y x c =-+y ()0,4P 2y x c =-+Q x ,A B A B y C ,,B C Q(3)直线与抛物线交于两点(点在点的右侧),当轴上存在一点,能使以三点为顶点的三角形与相似时,请直接写出点的坐标.11.如图,在平面直角坐标系中,抛物线与轴交于两点,与轴交于点.(1)求抛物线的函数解析式及顶点的坐标;(2)连接,若点在线段上运动(不与点重合),过点作轴于点,对称轴交轴于点.设,当为何值时,与的面积之和最小?(3)将抛物线在轴左侧的部分沿轴翻折,保留其他部分得到新的图象,在图象上是否存在点,使为直角三角形?若存在,直接写出所有符合条件的点的坐标;若不存在,请说明理由.BC 2y x c =-+,M N N M x T ,,B N T ABC T 22y ax x b =++x ()30A B ,,y ()03C ,D BD E BD B D ,E EF x ⊥F x T EF m =m BFE △DEC 22y ax x b =++y y L L P BDP △P(1)求抛物线与直线的解析式;(2)如图1,连接,,,若是直角三角形,求点(3)如图2,若点在直线下方的抛物线上,过点的最大值.(1)用表示点、的坐标;AC AP PC APC △P BC P 12CQ PQ +m A D(1)求该抛物线的函数解析式;(2)当点的横坐标为1时,求四边形的面积;(3)连接,记的面积为,记的面积为点的坐标;(4)在(3)的条件下试探究:该拋物线上是否存在点在,请直接写出点的横坐标;若不存在,请说明理由.P BOCP ,PC AC DPC △1S DAC △P Q15.如图1,抛物线与x 轴交于,与y 轴交于点C .(1)求抛物线的解析式;(2)抛物线的顶点为P ,求四边形的面积;(3)如图2,点M 从点C 出发,沿的方向以每秒1个单位长度的速度向终点B 运动,同时点N 从B 出发,以每秒1个单位长度的速度沿的方向向终点C 运动,当其中一个点到达终点时,另一点也随之停止运动,设运动时间为t 秒.①当是直角三角形时,求t 的值;②在M 、N 运动的过程中,抛物线上存在点Q ,使四边形为平行四边形,请直接写出点Q 的坐标.24y ax bx =++()()1,0,3,0A B -PBOC CB B O C →→BMN CMNQ参考答案:。
中考数学倒计时4:二次函数中的矩形和Rt三角形问题分析

中考数学倒计时4:二次函数中的矩形和Rt三角形问题分析
原创满分辅导中学解题思维
2018-06-09
(1)将点A和B的坐标代入解析式,
求得b和c的值,也就得到了抛物线的解析式;
(2)
①当OMHN是矩形的时候,点N和点H的纵坐标相等,
那么假设M坐标为(t,0)的话,则N(0,t),
点H和M的横坐标相同,都为t,那么代入抛物线解析式得到H的纵坐标,
使H的纵坐标和点N的纵坐标相等,
解方程得到t的值,再求出H坐标即可;
②△PFB为直角三角形的情况,根据图形验证PC和PB不垂直可知只有∠PFB=90°这一种情况,
那么当PF⊥BC时,
方法一:
连接PF并延长,交x轴于点D,
根据∠OBC=45°可知∠PDB=45°,
那么可知点P到x轴的距离=点D到对称轴的距离,
从而得到点D坐标,
根据点D和P的坐标得到直线PD的解析式,
然后与BC相交求出点F坐标即可;
方法二:
根据直线BC的解析式,假设点F的坐标出来,
再根据两个坐标点之间的距离计算方法表示出PF、PB、BF,
利用勾股定理PF²+BF²=PB²,
解方程得到点F的坐标即可;
构造直角三角形与构造等腰三角形的方法有些许类似,所以同学们可以掌握这两种方法,以备不时之需。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:二次函数与直角三角形、矩形问题1. 如图,抛物线y =14x 2-32x -4与x 轴交于A ,B 两点(点B 在点A 右侧),与y 轴交于点C.连接BC ,以BC 为一边,点O 为对称中心作菱形BDEC ,点P 是x 轴上的一个动点,设点P 的坐标为(m ,0),过点P 作x 轴的垂线l 交抛物线于点Q .(1)求点A ,B ,C 的坐标;(2)点P 在线段OB 上运动时,直线l 分别交BD ,BC 于点M ,N .试探究m 为何值时,四边形CQMD 是平行四边形,此时,请判断四边形CQBM 的形状,并说明理由;(3)当点P 在线段EB 上运动时,是否存在点Q ,使△BDQ 为直角三角形,若存在,请直接写出....点Q 的坐标;若不存在,请说明理由.2. 如图,直线y =-12x +n 与x 轴交于点A ,与y 轴交于点B (0,4),抛物线y =-12x 2+bx +c 经过A 、B 两点,点C 为点B 关于x 轴的对称点,连接A C.(1)求点A 的坐标及抛物线的表达式;(2)点P 为直线AB 上方抛物线上一动点,过点P 作x 轴的垂线l ,与x 轴交于点E ,与AC 交于点M ,设点P 的横坐标为m .①求四边形PBCA 的最大面积;②是否存在点P ,使得△P AM 是直角三角形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.3.如图,抛物线y =ax 2+2x +c 与x 轴交于 A ,B 两点,与y 轴交于点C ,且点B 与点C 的坐标分别为B (3,0),C (0,3),点M 是抛物线的顶点.(1)求抛物线的表达式;(2)点P 是线段MB 上一个动点,且点P 的横坐标为m ,过点P 作PD ⊥x 轴于点D ,交抛物线于点E ,求线段PE 的最大值,并求出此时点E 的坐标;(3)在(2)的条件下,若在线段MB 上存在点P ,使得△PCD 为直角三角形,请直接写出点P 的坐标.4. 如图,一次函数y =ax +b 的图象与x 轴交于点A ,二次函数y =12x 2-32x +1的图象与一次函数y =ax +b 的图象交于B (0,1)、C (4,3)两点,与x 轴交于D 、E 两点,且OD =1.(1)求一次函数的表达式及点A 的坐标;(2)若抛物线上存在点P ,使S △BDC =S △PBC ,求出P 点坐标(不与已知点重合); (3)若N 为x 轴上一点,平面内是否存在点M ,使得以点B 、C 、M 、N 为顶点的四边形为矩形,若存在,请求出点M 的坐标;若不存在,请说明理由.5. 如图,二次函数y =kx 2-3kx -4k (k ≠0)的图象与x 轴交于A ,B 两点(点A 在点B 的右侧),与y 轴交于点C ,OC =O A.(1)求点A的坐标和抛物线的解析式;(2)在抛物线上是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)过抛物线上的点Q作垂直于y轴的直线,交y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,直接写出点Q的坐标.6. 如图①,已知抛物线y =ax 2+bx +c 的图象经过点A (0,3)、B (1,0),其对称轴为直线l :x =2,过点A 作AC ∥x 轴交抛物线于点C ,∠AOB 的平分线交线段AC 于点E ,点P 是抛物线上的一个动点,设其横坐标为m .(1)求抛物线的解析式;(2)若动点P 在直线OE 下方的抛物线上,连接PE 、PO ,当m 为何值时,四边形AOPE 面积最大,并求出其最大值;(3)如图②,F 是抛物线的对称轴l 上的一点,在抛物线上是否存在点P 使△POF 成为以点P 为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.7. 如图,抛物线y =-49x 2+bx +c 与y 轴交于点A (0,8),与x 轴交于点B (6,0),C ,过点A 作AD ∥x 轴与抛物线交于另一点D.(1)求抛物线的表达式;(2)连接AB ,点P 为AB 上一个动点,由点A 以每秒1个单位长度的速度沿AB 运动(不与点B 重合),运动时间为t ,过点P 作PQ ∥y 轴交抛物线于点Q ,求PQ 与t 的函数关系式;(3)点M 是y 轴上的一个点,点N 是平面直角坐标系内一点,是否存在这样的点M 、N ,使得以B 、D 、M 、N 为顶点的四边形是矩形?若存在,请直接写出点N 的坐标;若不存在,请说明理由.参考答案1. 解:(1)当y =0时,则14x 2-32x -4=0,解得,x 1=-2,x 2=8,∵点B 在点A 的右侧,∴点A 、B 的坐标分别为(-2,0)、(8,0), 当x =0时,y =-4, ∴点C 的坐标为(0,-4);(2)四边形CQBM 的形状是平行四边形,理由如下: 由菱形的对称性可知,点D 的坐标为(0,4).设直线BD 的表达式为y =kx +b (k ≠0),将B (8,0),D (0,4)代入解析式,得⎩⎪⎨⎪⎧8k +b =0,b =4,解得⎩⎪⎨⎪⎧k =-12,b =4.∴直线BD 的表达式为y =-12x +4.(4分)∵l ⊥x 轴,∴点M ,Q 的坐标分别是(m ,-12m +4),(m ,14m 2-32m -4).当MQ =DC 时,四边形CQMD 是平行四边形, ∴(-12m +4)-(14m 2-32m -4)=4-(-4)=8,化简得m 2-4m =0.解得m 1=0(舍去)或m 2=4, ∴当m =4时,四边形CQMD 是平行四边形, 此时,四边形CQBM 是平行四边形.解法一:∵m =4,∴点P 是OB 中点, ∵l ⊥x 轴,∴l ∥y 轴, ∴△BPM ∽△BOD , ∴BP BO =BM BD =12,∴BM =DM ∵四边形CQMD 是平行四边形, ∴DM ∥CQ 、DM =CQ , ∴BM ∥CQ ,BM =CQ , ∴四边形CQBM 是平行四边形;解法二:设直线BC 的表达式y =k 1x +b 1,(k 1≠0)将B (8,0),C (0,-4)代入表达式,得⎩⎪⎨⎪⎧8k 1+b 1=0,b 1=-4, 解得⎩⎪⎨⎪⎧k 1=12,b 1=-4.∴直线BC 的表达式为y =12x -4.又∵l ⊥x 轴交BC 于点N , ∴当x =4时,y =-2. ∴点N 的坐标为(4,-2).由上述可知,点M ,Q 的坐标分别为M (4,2),Q (4,-6), ∴MN =2-(-2)=4, NQ =-2-(-6)=4, ∴MN =QN ,又∵四边形CQMD 是平行四边形, ∴DB ∥CQ ,∴∠MBN =∠QCN , 又∵∠MNB =∠QNC , ∴△BMN ≌△CQN , ∴BN =CN ,∴四边形CQBM 为平行四边形(3)存在.点Q 坐标为(-2,0)或(6,-4).【解法提示】①当∠BDQ 为直角时(如解图①),由点A 、B 、D 的坐标可知,此时点Q 与A 重合,即点Q 的坐标为(-2,0);第1题解图①②当∠DBQ 为直角时(如解图②),此时有两种方法可以解决问题,一种是利用BD 与BQ 的垂直关系求直线BQ 的表达式,将直线BQ 的表达式和抛物线的表达式联立方程组,通过计算求点Q 的坐标.由BD ⊥BQ ,且由(2)知直线BD 的表达式为y =-12x +4,设BQ的表达式为y =2(x -a ),∵直线BQ 过点B (8,0),代入得a =8, 则直线BQ 的表达式为y =2x -16,联立二次函数与直线BQ 的表达式⎩⎪⎨⎪⎧y =2x -16y =14x 2-32x -4,解得⎩⎪⎨⎪⎧x 1=6y 1=-4,⎩⎪⎨⎪⎧x 2=8y 2=0, ∴Q 点坐标为(6,-4);第1题解图②③当∠DQB 为直角时,以BD 为直径作圆与抛物线没有交点,因此此时点Q 不存在. 综上所述,抛物线上存在点Q 使得△BDQ 为直角三角形,点Q 的坐标为(-2,0)或(6,-4).2. 解:(1)∵直线y =-12x +n 与y 轴交于点B (0,4),∴n =4,∴直线AB 的表达式为y =-12x +4,当y =0时,有-12x +4=0,解得x =8,∴点A 的坐标为(8,0),将点A (8,0)、B (0,4)代入y =-12x 2+bx +c ,得⎩⎪⎨⎪⎧-32+8b +c =0,c =4,解得⎩⎪⎨⎪⎧b =72,c =4.∴抛物线的表达式为y =-12x 2+72x +4;(2)①设直线l 与AB 交于点F ,如解图, ∵点P 的横坐标为m (0<m <8),∴点P 的坐标为(m ,-12m 2+72m +4),点F 的坐标为(m ,-12m +4),∴PF =(-12m 2+72m +4)-(-12m +4)=-12m 2+4m ,∴S四边形PBCA=S △PBF +S △P AF +S △OAB +S △OAC =12PF ·OE +12PF ·AE +12OA ·OB +12OA ·OC =12PF ·OA +OA ·OB =12×8×(-12m 2+4m )+8×4=-2m 2+16m +32=-2(m -4)2+64, ∵-2<0,∴当m =4时,四边形PBCA 的面积取最大值,最大值为64;第2题解图②存在点P ,使得△P AM 是直角三角形,点P 坐标为(3,10). 【解法提示】∵PM ⊥x 轴,AP 、AM 均不与x 轴重合, ∴若△P AM 为直角三角形,只能是∠P AM =90°.∵点C 为点B 关于x 轴的对称点,直线AB 的表达式为y =-12x +4,∴直线AC 的表达式为y =12x -4,∵AP ⊥AM ,点A 的坐标为(8,0),直线AM 的表达式为y =12x -4,∴直线AP 的表达式为y =-2(x -8)=-2x +16. 联立直线AP 及抛物线表达式, 得⎩⎪⎨⎪⎧y =-2x +16,y =-12x 2+72x +4, 解得⎩⎪⎨⎪⎧x 1=3,y 1=10,⎩⎪⎨⎪⎧x 2=8,y 2=0.(舍去)∴存在点P ,使得△P AM 为直角三角形,点P 的坐标为(3,10). 3. 解:(1)将点B (3,0)、C (0,3)分别代入抛物线y =ax 2+2x +c 中,得⎩⎪⎨⎪⎧9a +6+c =0,c =3,解得⎩⎪⎨⎪⎧a =-1,c =3, ∴抛物线的表达式为y =-x 2+2x +3; (2)∵y =-x 2+2x +3=-(x -1)2+4, ∴M (1,4).设直线BM 的表达式为y =kx +n (k ≠0),把点B (3,0),M (1,4)分别代入,得⎩⎪⎨⎪⎧3k +n =0,k +n =4,解得⎩⎪⎨⎪⎧k =-2,n =6,∴直线BM 的表达式为y =-2x +6. ∵点P 的横坐标为m ,∴P (m ,-2m +6),E (m ,-m 2+2m +3),∴PE =-m 2+2m +3-(-2m +6)=-m 2+4m -3=-(m -2)2+1, ∴当m =2时,PE 有最大值,最大值为1, 此时点E 的坐标为(2,3);(3)点P 的坐标为(32,3)或(-3+32,12-62).【解法提示】根据题意可得∠PDC 不可能为90°; (ⅰ)当∠DPC =90°时,则PD =OC =3,即-2m +6=3, 解得m =32,此时点P 的坐标为(32,3);(ⅱ)当∠PCD =90°时,则PC 2+CD 2=PD 2,即m 2+(-2m +3)2+32+m 2=(-2m +6)2,整理得m 2+6m -9=0,解得m =-3-32(舍去)或m =-3+32,当m =-3+32时,y =-2m +6=12-62,此时点P 的坐标为(-3+32,12-62), 综上所述,点P 的坐标为(32,3)或(-3+32,12-62).4. 解:(1)将B (0,1)、C (4,3)代入y =ax +b ,得⎩⎪⎨⎪⎧b =1,4a +b =3,解得⎩⎪⎨⎪⎧a =12,b =1,∴一次函数的表达式为y =12x +1,令y =0,得x =-2, ∴A (-2,0)(2)如解图①,过点D 作y 轴平行线交BC 与点F ,过点P 作PG ∥y 轴,交BC 于点G .将x =1代入直线BC 的表达式得y =32.设点P (x ,12x 2-32x +1),则G (x ,12x +1).∴GP =|12x +1-(12x 2-32x +1)|=|-12x 2+2x |=|12x 2-2x |.∵S △PBC =S △DBC ,∴DF =GP ,即|12x 2-2x |=32;当12x 2-2x =32时,解得x =2+7或x =2-7. ∴点P 的坐标为(2+7,7+72)或(2-7,7-72).当12x 2-2x =-32时,解得x =3或x =1(舍去). ∴点P 的坐标为(3,1).综上所述,点P 的坐标为(3,1)或(2+7,7+72)或(2-7,7-72); (3)存在.如解图②,当∠CBN =90°时,BN 的表达式为y =-2x +1.将y =0代入得-2x +1=0, 解得x =12.∴点N 的坐标为(12,0).设点M 的坐标为(x ,y ). ∵四边形BNMC 为矩形, ∴12+42=0+x 2,0+32=1+y 2,解得x =92,y =2.∴点M 的坐标为(92,2);如解图,当∠CNM =90°时,设CN 的表达式为y =-2x +n ,将点C 的坐标代入得-8+n =3,解得n =11, ∴CN 的表达式为y =-2x +11.将y =0代入得-2x +11=0,解得x =112.∴点N 的坐标为(112,0).设点M 的坐标为(x ,y ). ∵四边形BMNC 为矩形,∴0+1122=4+x 2,1+02=3+y 2,解得x =32,y =-2.∴点M 的坐标为(32,-2);如解图④,当∠BNC =90°时,过点C 作CF ⊥x 轴,垂足为F .设ON =a ,则NF =4-a .∵∠BNO +∠OBN =90°,∠BNO +∠CNF =90°, ∴∠OBN =∠CNF .又∵∠BON =∠CFN , ∴△BON ∽△NFC . ∴ON FC =OB FN ,即a 3=14-a,解得a =1或a =3, 当a =1时,点N 的坐标为(1,0),设点M 的坐标为(x ,y ). ∵四边形BNCM 为矩形, ∴0+42=1+x 2,1+32=0+y2, 解得x =3,y =4. ∴点M 的坐标为(3,4);当a =3时,点N 的坐标为(3,0),设点M 的坐标为(x ,y ). ∵四边形BNCM 为矩形, ∴0+42=3+x 2,1+32=0+y 2, 解得x =1,y =4. ∴点M 的坐标为(1,4).综上所述,点M 的坐标为(92,2)或(32,-2)或(3,4)或(1,4).5. 解:(1)当y =0时,kx 2-3kx -4k =0, ∵k ≠0,∴x 2-3x -4=0, 解得x 1=-1,x 2=4, ∵点A 在点B 右侧, ∴B (-1,0),A (4,0), ∵OA =OC ,∴C (0,4),把x =0,y =4代入y =kx 2-3kx -4k ,得k =-1, 故抛物线的解析式为y =-x 2+3x +4;(2)存在,①当∠PCA=90°时,如解图,过点P作PM⊥y轴于点M.∴∠MCP+∠ACO=90°,∵∠OAC+∠ACO=90°,∴∠MCP=∠OAC,∵OA=OC,∴∠MCP=∠OAC=45°,∴∠MPC=∠MCP=45°,∴MC=MP,设P(m,-m2+3m+4),则PM=CM=m,OM=-m2+3m+4,∴m+4=-m2+3m+4,解得m1=0(舍去),m2=2,∴-m2+3m+4=6,即P(2,6);②当∠P AC=90°时,如解图②,过点P作PN⊥y轴于点N,设AP与y轴交于点F,则有PN∥x轴,∴∠FPN=∠OAP,∵∠CAO=45°,∴∠OAP=45°,∴∠FPN =45°,OF =AO =4, ∴PN =NF ,设P (n ,-n 2+3n +4), 则PN =-n ,ON =n 2-3n -4, ∴-n =n 2-3n -4-4, 即n 2-2n -8=0,解得n 1=-2,n 2=4(舍去), ∴-n 2+3n +4=-6, 即P (-2,-6),综上所述,点P 的坐标是(2,6)或(-2,-6);(3)当点Q 的坐标是(3+172,2)或(3-172,2)时,EF 最短.【解法提示】如解图,∵∠OED =∠DFO =∠EOF =90°, ∴四边形OEDF 是矩形, ∴EF =OD ,∴当线段EF 的长度最短时,OD 最小,此时OD ⊥AC , ∵OA =OC ,∴∠COD =∠AOD =45°,CD =AD , ∵DF ∥OC , ∴△ADF ∽△ACO ,∴DF OC =AD AC =12, ∴DF =12OC =2,∴y Q =2,∴令y =2,即-x 2+3x +4=2, 解得x 1=3+172,x 2=3-172,∴点Q 的坐标是(3+172,2)或(3-172,2).6. 解:(1)∵抛物线y =ax 2+bx +c 的图象经过点A (0,3)、B (1,0),对称轴为直线l :x =2,∴⎩⎪⎨⎪⎧c =3,a +b +c =0,-b 2a =2,解得⎩⎪⎨⎪⎧a =1,b =-4,c =3.∴抛物线的解析式为y =x 2-4x +3;(2)如解图①,过点P 作y 轴的平行线与OE 交于点Q ,与AE 交于点F ,设点P 的坐标为(m ,m 2-4m +3), ∵∠AOB 的平分线交线段AC 于点E , ∴直线OE 的解析式为y =x , 则点Q 的坐标为(m ,m ), ∴S四边形AOPE =S △OAE +S △OPQ +S △EPQ =12OA ·AE +12PQ ·AF +12PQ ·EF =12OA ·AE +12PQ ·AE=12×3×3+12(m -m 2+4m -3)×3=-32m 2+152m =-32(m -52)2+758, ∵-32<0,∴当m =52时,四边形AOPE 的面积最大,最大值是758;(3)存在,点P 的坐标为(3+52,1-52)或(3-52,1+52)或(5+52,1+52)或(5-52,1-52). 【解法提示】如解图②,过点P 作x 轴的平行线,交y 轴于点M ,交对称轴于点N ,设P (m ,m 2-4m +3).∴∠OMP =∠PNF =90°,∵△POF 是以点P 为直角顶点的等腰直角三角形, ∴∠OPF =90°,OP =PF ,∴∠MOP +∠OPM =90°,∠OPM +∠NPF =90°, ∴∠MOP =∠NPF , ∴△OPM ≌△PFN ,∴OM =PN ,即|m 2-4m +3|=|2-m |, 当m 2-4m +3=2-m 时,解得m =3±52,此时点P 的坐标为(3+52,1-52)或(3-52,1+52),当-(m 2-4m +3)=2-m 时,解得m =5±52,此时点P 的坐标为(5+52,1+52)或(5-52,1-52),综上所述,满足条件的点P 的坐标为(3+52,1-52)或(3-52,1+52)或(5+52,1+52)或(5-52,1-52).7. 解:(1)将A (0,8)、B (6,0)代入抛物线y =-49x 2+bx +c ,得⎩⎪⎨⎪⎧-49×36+6b +c =0,c =8,解得⎩⎪⎨⎪⎧b =43,c =8,∴抛物线的表达式为y =-49x 2+43x +8;(2)设直线AB 的解析式为y =kx +d ,将A ,B 两点坐标代入解析式得⎩⎪⎨⎪⎧d =8,6k +d =0,解得⎩⎪⎨⎪⎧d =8,k =-43,∴直线AB 的解析式为y =-43x +8.∵OA =8,OB =6, ∴AB =10,如解图①,过点P 作PE ⊥y 轴于点E ,则△AEP ∽△AOB ,∴AE ∶EP ∶AP =AO ∶OB ∶AB =4∶3∶5, 根据题意可知AP =t , ∴AE =45t ,EP =35t ,∴PQ =-49×(35t )2+43×35t +8-(-43×35t +8)=-425t 2+85t ,∴PQ 与t 的函数关系式为PQ =-425t 2+85t (0≤t <10);(3)存在.点N 的坐标为(3,-98)或(-3,234).【解法提示】要使以B 、D 、M 、N 为顶点的四边形是矩形,分以下两种情况讨论: 如解图②,过点B 作x 轴的垂线交AD 的延长线于点E ,则AE ⊥EB ,当y =8时, -49x 2+43x +8=8, 解得x =0或3, ∴点D 的坐标为(3,8), ∴AD =3,DE =3,①如解图②,当DM 为矩形的边时,过点N 作NK ⊥x 轴,交x 轴于点K ∵∠MAD =∠DEB =90°,∠ADM +∠BDE =90°,∠AMD +∠ADM =90°, ∴∠BDE =∠AMD , ∴△ADM ∽△EBD ,∴AM ED =AD EB ,即AM 3=38, ∴AM =98, 同理,可求得△EBD ∽△KBN ,∴△ADM ∽△KBN .∵MD =NB ,∴△ADM ≌△KBN ,∴OK =KB =AD =3,AM =KN =98, ∴N (3,-98); ②如解图②,当DM ′为矩形的对角线时,过点N ′作N ′K ′⊥x 轴交DA 的延长线于点K ′. 同理可得△M ′BO ∽△DBE ,∴OM ′ED =OB EB, ∴OM ′3=68,∴OM ′=94, ∵DN ′=BM ′,∴易得△DN ′K ′≌△BM ′O .∴N ′K ′=M ′O =94,K ′D =OB =6. ∴AK ′=3,点N ′的纵坐标=OA -N ′K ′=8-94=234. ∴N ′(-3,234), ③当BD 为对角线时,取BD 中点I ,∵D (3,8),B (6,0),∴I (92,4). 以I 为圆心以BD 为半径作圆,假设⊙I 与y 轴有交点,设交点坐标为(0,t ),则有BD 2=(6-3)2+(8-0)2=73,DI 2=(8-t )2+(3-0)2=t 2-16t +73,BI 2=(6-0)2+(t -0)2=t 2+36,∴DI 2+BI 2=BD 2,即t 2-16t +73+t 2+36=73,整理得t 2-8t +18=0,∵b 2-4ac =(-8)2-4×1×18=8<0,∴原方程无解.∴⊙I 与y 轴无交点,∴以BD 为对角线这种情况不存在.综上所述,存在点M 、N ,使得以B 、D 、M 、N 为顶点的四边形是矩形,点N 的坐标为(3,-98)或(-3,234).。
