递归图分析
递归和尾递归 (图解+实例)

1 如果 n=0,n=1f(n)=nf(n) 如果 n>1图1:以递归的方式计算4的阶乘上图(1)展示了利用递归计算4!的过程。
它也说明了递归过程中的两个基本阶段:递推和回归。
在递推阶段,每一个递归调用通过进一步调用自己来记住这次递归过程。
当其中有调用满足终止条件时,递推结束。
比如,在计算n!时,终止条件是当n=1和n=0,此时函数只需简单的返回1即可。
每一个递归函数都必须拥有至少一个终止条件;否则递推阶段永远不会结束了。
一旦递推阶段结束,处理过程就进入回归阶段,在这之前的函数调用以逆序的方式回归,直到最初调用的函数为止,此时递归过程结束。
以递归的方式计算n的阶乘的函数实现:C函数fact的工作方式如下:它接受一个整数n作为参数,如果n小于0,该函数直接返回0,这代表一个错误。
如果n等于0或1,该函数返回1,这是因为0!和1!都等于1,以上是终止递归的条件。
否则,函数返回n-1的阶乘的n倍。
而n-1的阶乘又会以递归的方式再次调用fact来计算,如此继续。
代码实例(1):fact.c1/*fact.c*/2#include "fact.h"3int fact(int n){4if (n<0)5return0;6else if(n==0)7return1;8else if(n==1)9return1;10else11return n*f(n-1);12}为理解递归究竟是如何工作的,有必要先看看C语言中函数的执行方式。
我们先来看看C程序在内存中的组织方式(见图2-a)。
基本上,一个可执行程序由4个区域组成:代码段、静态数据区、堆与栈。
代码段包含程序运行时所执行的机器指令。
静态数据区包含在程序生命周期内一直持久的数据,比如全局变量和静态局部变量。
堆包含程序运行时动态分配的存储空间,比如malloc分配的内存。
栈包含函数调用的信息。
当C中调用了一个函数时,栈中会分配一块空间来保存与这个调用相关的信息。
外文翻译

递归图(RP)熵在滚动轴承故障的严重程度评估中的应用Ruqiang Yan,Yuning Qian,Zhoudi Huang,和罗伯特X Gao1远程测量和控制江苏省重点实验室仪器科学与工程学院东南大学、南京,210096年中国2机械工程系康涅狄格大学斯托尔斯,CT 06269,美国*作者邮箱:ruqiang@摘要:本文提出了一种基于递归图(RP)熵一种新的方法来评价滚动轴承故障的严重程度。
作为一种定量测量,对RP熵是从对角线长度在以曲线示出一个系统的动力学的概率分布计算的递归图,,并提供了自相关的在重构相空间全局图像的时间序列中所有可用的时间尺度,来改变系统的动态特性。
实验结果表明,由于结构损坏的引发和/或进展中的轴承工作条件恶化,包含在振动信号的频率信息变得越来越复杂,导致RP的熵的增加。
因此RP熵可以作为滚动轴承的缺陷严重程度评价的有效参数。
关键词 : 经常性的情节 RP熵故障诊断1.引言在现代工业中,用于高品质低成本的产品和生产安全的持续过程中的需求,使维修策略由机械设备的修复性维修或预防性维护更改为状态检修,其中实时检测,诊断和预测是必要的。
作为一个主要的机械设备,旋转机已经广泛应用于可再生能源系统和制造系统,因此过去几十年已经看到越来越多的来自世界各地研究社区大型旋转机械状态监测与健康诊断的关注。
这些激发了传感以及信号处理技术的不断进步。
除了常用的时间(统计)和频率(频谱)域技术,先进的信号处理技术,如小波变换和希尔伯特 - 黄变换,也在运转的机器中作为新的缺陷诊断工具。
然而,由于在摩擦,阻尼,或负载条件瞬时变化,机器系统往往表现为非线性行为。
因此,非线性时间序列分析技术提取缺陷特征提供了一个很好的选择。
抽取隐藏在可能不使用其他技术来有效地识别测得的信号与缺陷相关的功能。
近期开发的递归定量分析,这源于递归图熵,由于其短数据长度要求和良好的抗噪能力,正在成为在非线性时间序列分析[2]中新的研究热点。
气-固流化床压力脉动递归图分析

气-固流化床压力脉动递归图分析
王春华;仲兆平;李睿;鄂加强
【期刊名称】《化工学报》
【年(卷),期】2010(061)003
【摘要】引入递归图分析方法对具有混沌与分形特性的气-固循环流化床压力脉动信号进行分析,针对Logisitc模型比较了递归图特征量递归率、确定性、平均对角线长度、分叉性与最大Lyapunov指数之间的关系,得出了递归图特征量对于混沌特性具有表征作用的结论.研究了递归图特征量在气-固循环流化床不同床型下的变化规律,递归图特征量在固定床型、湍流床型、气力输送床型下保持稳定,在鼓泡床型、快速流化床型下分别迅速递增或递减,因此递归图特征量同样可以对循环流化床不同床型进行辨识.
【总页数】8页(P557-564)
【作者】王春华;仲兆平;李睿;鄂加强
【作者单位】东南大学能源与环境学院,江苏,南京,210096;东南大学能源与环境学院,江苏,南京,210096;东南大学能源与环境学院,江苏,南京,210096;湖南大学机械与运载工程学院,湖南,长沙,410082
【正文语种】中文
【中图分类】TQ051
【相关文献】
1.气固两相流化床压力脉动的混沌特性分析 [J], 周云龙;王芳
2.气固搅拌流化床压力脉动的小波分析 [J], 王嘉骏;张文峰;冯连芳;顾雪萍
3.气-固流化床压力脉动信号的多尺度排列熵分析 [J], 徐金晖;巴晓玉;郭旭;谭薇;赵广杨
4.气-固流化床压力脉动信号的多尺度熵分析 [J], 徐金晖;巴晓玉
5.气固固循环流化床密相床层压力脉动研究 [J], 王振芳;陆维玮
因版权原因,仅展示原文概要,查看原文内容请购买。
面向对象分析-顺序图
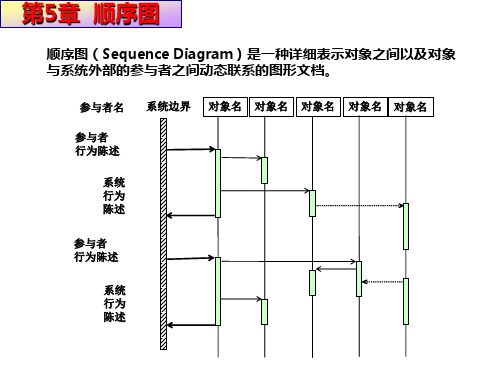
把消息表示为从一个对象生命线到另一个对象生命线的一个水平实线箭头, 即从源对象指向目标对象,以触发目标对象中的特定操作。对于对象到自身的 消息,箭头就从同一个对象符号开始和结束。
用消息(操作或信号)的名字及其参数值或者参数表达式标示箭头。
用如下种类的箭头表示不同种类的通讯:
同步消息
一般把它用于普通的过程调用。在外层控制恢复之前,要完成整个嵌套序列。 通常把它用于普通的过程调用。 若在一个主动对象发送信号并等待完成一个嵌套的行为序列才继续时,也可以 把它用于并发的主动对象。 同步消息返回 用它显式地表示从过程调用的返回。在控制的过程流中,可以省略返回箭头 (暗示执行规约结束),假设每个调用在任何消息后都有一个配对的返回,并可以 把返回值标示在初始的箭头上。
5.1
概念与表示法
1、概述 顺序图是一种详细表示对象之间以及对象与参与者实例之间交 互的图,它由一组协作的对象(或参与者实例)以及它们之间可发 送的消息组成,它强调消息之间的顺序。
由对象(参与者) 、消息、生命线和执行规约组成。
[对象名]:类名
从图中可以看出顺序图是二维的,其中: 垂直方向表示时间,水平方向表示不同的对 象或参与者。 通常时间维由上到下(根据需要,也可以 由下到上)。通常只有时间顺序是重要的, 但在实时应用中时间轴是能度量的。 对象的水平顺序并不重要,相应地生命线 之间的顺序可以是任意的。
3、执行规约
执行规约表示一个对象直接或者通过从属 例程执行一个行为的时期。它既表示了行 为执行的持续时间,也表示了活动和它的 调用者之间的控制关系。 用一个窄长的矩形表示执行规约,矩形 顶端和它的开始时刻对齐,末端和它的结 束时刻对齐。 在程序的控制流中,执行规约符号的顶 端画在进入的箭头的尖端(开始该动作的 那个箭头),底端画在返回的箭头的尾部。
基于递归图分析的压缩机故障诊断方法研究

递归算法的应用与分析

化的执行效率。
关键词:递归;算法;非递归化;效率
中图分类号:TP301.6
文献标识码:A
文章编号:2096-4706(2020)20-0146-04
Application and Analysis of Recursive Algorithm
NI Jinyuan,ZHANG Jianxun (College of Computer Science and Engineering,Chongqing University of Technology,Chongqing 400054,China)
146 2020.10
倪锦园,等:递归算法的应用与分析
第 20 期
为了下一次迭代递归的输入。
1.2.2 递归算法的边界条件 边界条件就是递归的出口。递归算法不是无穷无尽的, 当程序递归到最后一层时,就要返回输出。由于每一层递归 都会使问题规模不断缩小,所以每一次递归都会越来越趋近 于终止条件,直到达到终止的条件,返回临界值。例如递归 求阶乘问题 f(n)=n•f(n-1),递归的终止条件当 n=1 时, 如果没有递归的边界条件,此时程序是无限循环的,没有输 出结果。递归算法的边界条件有的时候也不止一个,在整数 划分问题里面,要分别讨论最大化分数值和被划分的整数值 大小关系,此时递归边界条件也有多个的。
Abstract:Recursive thought is one of the most important thoughts in algorithm analysis and design. Recursive algorithms are widely used. With the help of recursive algorithms,some more complex problems can be expressed concisely. This article focuses on the concept and three characteristics of the recursive algorithm. This paper describes the application of recursive algorithm in data structure tree in detail through computer game tree,systematically introduces the application of recursive algorithm in graph by using different situations in the process of point chess game,and analyzes the execution efficiency of recursive algorithm and recursive algorithm non recursive through contrast experiments.
2023届浙江省宁波市高三下学期5月模拟考试技术试题含解析

高三年级2022学年第二学期技术模拟试题(选考)(答案在最后)第一部分信息技术(共50分)一、选择题(本大题共12小题,每小题2分,共24分,在每小题给出的四个选项中,只有一个符合题目要求)1.某共享单车系统,租车时用支付宝扫描共享单车上的二维码,获取单车的唯一编码,然后APP将唯一编码传送给单车的服务器,服务器收到唯一编码后,会从数据库查询到该单车的密码,当APP显示开锁中的时候,手机将单车服务器传送过来的密码通过蓝牙通信的方式发送给共享单车的车锁,密码匹配到后车锁就会打开。
下列关于该共享单车系统的说法正确的是()A.共享单车和扫码用的手机组成了共享单车系统的硬件B.支付宝APP以及手机上安装的操作系统组成了共享单车的软件C.共享单车的唯一编号,开锁密码,出租车人的个人信息等都属于该信息系统中的数据D.共享单车系统的用户仅指租车的用户、共享单车的维修人员【答案】C【解析】【详解】本题主要考查信息系统的应用。
选项A信息系统中的硬件是指系统中看得见、摸得着的设备,它包含计算机硬件、移动终端硬件和通信网络设备等。
选项B少了网络软件、网络协议、服务器、数据库软件;选项D信息系统中的用户范围很广,如信息系统的使用者、计算机和非计算机设备的操作与维护人员、程序设计员、数据库管理员、系统分析员、信息系统的管理员及人工收集、加工、传输信息的有关人员等,所以选项C符合题意。
故选:C。
2.某共享单车系统,租车时用支付宝扫描共享单车上的二维码,获取单车的唯一编码,然后APP将唯一编码传送给单车的服务器,服务器收到唯一编码后,会从数据库查询到该单车的密码,当APP显示开锁中的时候,手机将单车服务器传送过来的密码通过蓝牙通信的方式发送给共享单车的车锁,密码匹配到后车锁就会打开。
两辆共享单车,一辆可以正常租车,另一辆不能租车,则下列原因中可能的是()A.故障共享单车上的二维码不完整B.租车点通信网络故障,手机无网络信号C.扫码手机的蓝牙功能没有打开D.共享单车系统中的服务器奔溃【答案】A【解析】【详解】本题主要考查信息系统的应用。
编译原理-词法语法分析实验报告

编译原理词法分析一、实验目的设计、编制并调试一个词法分析程序,加深对词法分析原理的理解。
二、实验要求2.1 待分析的简单的词法(1)关键字:begin if then while do end所有的关键字都是小写。
(2)运算符和界符:= + - * / < <= <> > >= = ; ( ) #(3)其他单词是标识符(ID)和整型常数(SUM),通过以下正规式定义:ID = letter (letter | digit)*NUM = digit digit*(4)空格有空白、制表符和换行符组成。
空格一般用来分隔ID、SUM、运算符、界符和关键字,词法分析阶段通常被忽略。
2.2 各种单词符号对应的种别码:2.3 词法分析程序的功能:输入:所给文法的源程序字符串。
输出:二元组(syn,token或sum)构成的序列。
其中:syn为单词种别码;token为存放的单词自身字符串;sum为整型常数。
例如:对源程序begin x:=9: if x>9 then x:=2*x+1/3; end #的源文件,经过词法分析后输出如下序列:(1,begin)(10,x)(18,:=)(11,9)(26,;)(2,if)……三、词法分析程序的C语言程序源代码:#include <stdio.h>#include <string.h>char prog[80],token[8],ch;int syn,p,m,n,sum;char *rwtab[6]={"begin","if","then","while","do","end"};scaner();void scanner_example (FILE *fp);main(){FILE *fp;fp=fopen("D:\\1.txt","r");//打开文件scanner_example (fp);scaner();}void scanner_example (FILE *fp){do{ch=fgetc (fp);prog[p++]=ch;}while (ch!='#');p=0;do{scaner();switch(syn){case 11:printf("( %-10d%5d )\n",sum,syn);break;case -1:printf("you have input a wrong string\n");default: printf("( %-10s%5d )\n",token,syn);break;}}while(syn!=0);}scaner(){ sum=0;for(m=0;m<8;m++)token[m++]=NULL;ch=prog[p++];m=0;while((ch==' ')||(ch=='\n'))ch=prog[p++];if(((ch<='z')&&(ch>='a'))||((ch<='Z')&&(ch>='A'))){ while(((ch<='z')&&(ch>='a'))||((ch<='Z')&&(ch>='A'))||((ch>='0')&&(ch<='9'))) {token[m++]=ch;ch=prog[p++];}p--;syn=10;for(n=0;n<6;n++)if(strcmp(token,rwtab[n])==0){ syn=n+1;break;}}else if((ch>='0')&&(ch<='9')){ while((ch>='0')&&(ch<='9')){ sum=sum*10+ch-'0';ch=prog[p++];}p--;syn=11;}else switch(ch){ case '<':token[m++]=ch;ch=prog[p++];if(ch=='='){ syn=22;token[m++]=ch;}else{ syn=20;p--;}break;case '>':token[m++]=ch;ch=prog[p++];if(ch=='='){ syn=24;token[m++]=ch;}else{ syn=23;p--;}break;case '+': token[m++]=ch;ch=prog[p++];if(ch=='+'){ syn=17;token[m++]=ch;}else{ syn=13;p--;}break;case '-':token[m++]=ch;ch=prog[p++];if(ch=='-'){ syn=29;token[m++]=ch;}else{ syn=14;p--;}break;case '!':ch=prog[p++];if(ch=='='){ syn=21;token[m++]=ch;}else{ syn=31;p--;}break;case '=':token[m++]=ch;ch=prog[p++];if(ch=='='){ syn=25;token[m++]=ch;}else{ syn=18;p--;}break;case '*': syn=15;token[m++]=ch;break;case '/': syn=16;token[m++]=ch;break;case '(': syn=27;token[m++]=ch;break;case ')': syn=28;token[m++]=ch;break;case '{': syn=5;token[m++]=ch;break;case '}': syn=6;token[m++]=ch;break;case ';': syn=26;token[m++]=ch;break;case '\"': syn=30;token[m++]=ch;break;case '#': syn=0;token[m++]=ch;break;case ':':syn=17;token[m++]=ch;break;default: syn=-1;break;}token[m++]='\0';}四、结果分析:输入begin x:=9: if x>9 then x:=2*x+1/3; end # 后经词法分析输出如下序列:(begin 1)(x 10)(:17)(= 18)(9 11)(;26)(if 2)……如图所示:五、总结:词法分析的基本任务是从字符串表示的源程序中识别出具有独立意义的单词符号,其基本思想是根据扫描到单词符号的第一个字符的种类,拼出相应的单词符号。
用递归BDD(二元决策图)技术分析因果图

用递归BDD(二元决策图)技术分析因果图严晓;王洪春【摘要】故障树是以系统最不希望发生的顶事件为目标,通过分析找出导致顶上事件发生的全部因素;在故障树分析中,二元决策图(简称BDD)是最有效的方法之一,由于故障树和因果图都是用图形表示因果关系,两者具有很多相似性,而BDD在故障树中有广泛的应用;通过研究表明:在一定条件下,故障树和因果图之间可以互相转化,因此可以分析BDD的原理,并将BDD技术用来分析因果图.【期刊名称】《重庆工商大学学报(自然科学版)》【年(卷),期】2015(032)008【总页数】4页(P34-37)【关键词】故障树;BDD;因果图【作者】严晓;王洪春【作者单位】重庆师范大学数学学院,重庆401331;重庆师范大学数学学院,重庆401331【正文语种】中文【中图分类】O141.41**通讯作者:王洪春(1967-),男,四川大竹人,教授,博士,从事人工智能、因果图和故障诊断研究.E-mail:*********************.cn故障树是一种以系统最不希望发生的顶事件为目标,通过对可能导致顶事件发生的中间事件和底事件进行分析,在一般情况下,事件分为两种状态,正常或者是故障,在传统分析故障树中,一般通过求故障树的最小割集,对故障树进行分析,然而对于复杂的故障树,求最小割集比较困难,为了克服这种缺陷,引入了二元决策图[1],把故障树转化成二元决策图进行分析研究,然后自上而下遍历二元决策图,能够得到最小割集,在二元决策图转化的过程中,要先对故障树进行简化,对简化后的故障树的基本事件进行排序[2],从而对故障树进行定性和定量分析。
而因果图是从信度网发展起来的,通过事件连接成一个网状结构来反映事件之间的关系,通过研究表明,在一定条件下因果图和故障树之间可以相互转化,因此BDD也可以用于因果图中。
将故障树转化为BDD的方法,最早是由Rauzy提出的,并在转化过程中提出了一种ite结构(If-then-Else),它是基于shannon分解提出来的,ite(x,y,z)表示如果x成立,则成立,否则,z成立,数学表达式为ite(x,y,z) = xy+z。
缠论精典解析汇报(中枢、分解、递归)

本课重点一:这种情况和盘整背驰中转化成第三类卖点的情况不同,那种情况下,反弹的级别一定比最后一个中枢低,而这种情况,反弹的级别一定等于或大于最后一个中枢的。
因此,这两种情况,不难区分==========理解这个才能准确把握是否真正背驰,躲过盘背形成三卖的情况。
5f级别以上,跌出第一个中枢这段大多都是盘背形成三卖,在次级别上也不是趋势背驰,比如笔的类中枢肯定不是趋势背驰,可以双重判断。
一般会在笔中枢两个下跌中枢第二个下面形成趋势背驰,然后反弹,在那里形成第二个5f中枢。
然后再从这里次级别跌出,如果是趋势背驰,会先形成一个三卖,再急跌一小段,这个跌出段内也盘背,这样至少是两重的绿面积背驰才能真的形成背驰。
而且这最后一段也是两个笔中枢趋势背驰,可以区间套定位。
所以至少是三重区间套。
如果再看30分的会是四重区间套请大家仔细研究下中粮地产这几天的走势,用老师的话说教科书走势先看30分图,从11月1日开始的下跌段这段在15日开始,黄白线回拉零轴,形成一个30f中枢,围绕这个中枢两端是明显的盘背。
5f图,从11月21日10点开始的下跌是两个5f中枢的下跌趋势,这段中黄白线两次会拉零轴,形成两个5f中枢很标准。
29课留言里有说回拉零轴是模糊概念,现在有些同学大概还是这么认为的,这还是没理解macd是辅助。
因为只有形成中枢的回拉才算回拉,大部分都是次级别的一个向下或者向上走势,且能形成至少本级别的中枢那种回拉才算。
只看黄白线当然会判断不出。
对照5f图和1f图的笔中枢,可以仔细分析这两个5f中枢是如何形成的。
从第二个中枢跌出的这部分,先是5f图这段内是明显的盘被,再可以从1f笔来分析这段是趋势背驰导致结束的。
也属于29可讲的,离最后一个中枢dd点跌幅最多的!因为5f的趋势背驰必然会回到最后一个中枢,这就是重量一个5f次级别上来涨幅这么大的原因。
“实际操作中,怎么才能达到效率最高。
一个可被理论保证的方法就是:在第一次抄底时,最好就是买那些当下位置离最后一个中枢的DD=min(dn)幅度最大的,所谓的超跌,应该以此为标准。
递归遍历算法流程图及实例分析

递归遍历算法流程图及实例分析下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!递归遍历算法流程图。
1. 设置基线条件,确定什么时候停止递归,例如当遍历到特定节点或达到特定深度时。
基于相空间重构的人民币汇率递归图分析

②彼 得 森 国际 经济研 究所 { T h e T r a m— P a c i i f c P a r t n e r s h i p a n d A s i a — P a c i i f c I n t e g r a t i o n : P o l i c y I mp l i c a t i o n ) ) ,2 0 1 2 年6 月。
③ 数 据 来 源 :Wo r i d De v e l o p me n t I n d i c a t o s r a n d Wo r l d E c o —
n o mi c Oud o o k , Ap il r 2 1 2。
A s i a p a c i i f c I n t e ra g i t o n : A Qu a n t i t a i t v e As s e s s me n t [ N] . E a s t ~ We s t Ce n —
非 线性 动力 系统特 征 ,基 于线性 思维 范式 的技术 分
[ 3 1 宋国友 T P P 对中国有哪些影响【 N 】 . 深圳商报, 2 0 1 1 - 1 1 — 1 3 .
【 4 】 杨 洁勉. 美 国 实力 变化 与 国 际体 系重组 U 1 l 国 际 问 题 研 究,
2 0 1 2 , ( 2 ) .
注释
①数据 来源 :WT O 网站 ,2 0 1 2 年3 月1 9日。h t t p : / / w w w . W t o .
o r go
[ 7 ] A a r o n F i f e d b e r g ,He g e mo n y w i d I Ch i n e s e ch a r a c c e r i s c i c s 硼. Na t i o n a l I n t e r e s t , J u l y 2 0 1 1 . [ 8 ] P e t e r Dr y s d a l e . A r e t h e r e r e l a d a n g e r s i n t h e T r a n s P a c i i f c P a t r —
2-3递归-Hilbert图案
A1
A1 D1
A1 B1
A2
2019-5-5
B1
B1 B1
C1
D1 C1
C1 A1
B1 C1
B2
C2
计算机算法设计与分析
D1
C1 A1
D1 D1
D2
2
Hilbert图案
n 于是可得出这些子曲线逐级间存在如下关系:
Ai+1: Di
Ai
Ai
Bi
Bi+1: Bi
Ci
Ci
Di
Di+1: Ai
i=0
i=0
2019-5-5
计算机算法设计与分析
5
n 类似地可以写出画B、C和D的曲线的子程序。
n 画Hilbert曲线的程序在调用A之前还应有一些 初始化的工作,如计算h,移动画笔至起点。
2019-5-5
计算机算法设计与分析
4
画Hilbert图案的时间复杂性
n Hilbert图案Ai+1是由Ai、Bi、Ci、和Di中的四个图案,
再通过三根直线连接而成的。显然绘制Ai、Bi、Ci、和 Di的复杂形式一样的。于是我们有如下的递推公式:
Di
Di
Ci
其中,箭头表示曲线移动的方向,
n 于是便可写出画这些曲线的递归子程序:
2019-5-5
计算机算法设计与分析
3
Hilbert图案
n 依据 Ai+1:Di Ai Ai Bi 有画A的子程序:
A(i) { if (i > 0) { D(i – 1); x = x – h; ploting(x, y) ; A(i – 1); y = y – h; ploting(x, y) ; A(i – 1); x = x + h; ploting(x, y) ; B(i – 1); }} //*ploting(x, y)是从画笔现行坐标到坐标(x, y)画条直线
结构方程模型 amos,liser等

xinzy
路径系数
路径系数(标准化的回归系数)
自变量和因变量 (就具体的方程而言) 外源变量x和内生变量y(就整个模型而言)
路径系数的种类
由外源变量影响内生变量的路径系数( r ) 由内生变量到内生变量的路径系数(β)
下标规则:第一个下标表示结果变量,第二个下标则表示 原因变量
xinzy
效应分解
xinzy
AMOS Graphic Mode执行(2)
执行AMOS/SEM:
xinzy
AMOS報表輸出的各種統計量
利用View/Set下『Analysis Properties』中點選Output, 選 取所需統計量, 亦可點選『Output』選擇估計方法。
xinzy
AMOS路径图系数解释
下列为标准化系数
X
X
X ← →
果 , Y1 為中 介變項 回 溯因果 關係 X 與 Y 互為直 接效果, X 與 Y 具有 回 reciprocal causal effect 饋 循環效 果 循 環因果 關係 indirect loop effect
Y1 對 Y2 、 Y2 對 Y3 、 Y3 對 Y1 均 為 直 接 效
效应分解:也称相关系数分解,是将变量之间的相关系
数分解为不同的效应部分。包括直接效应和间接效应。路 径图
虚假效应和未分解效应
虚假效应:只在内生变量的相关系数的分解中出现,是 两 个内生变量的相关系数中由于共同的起因产生的部分。 未分解效应:是指一个外源变量与一个内生变量的相关系 数(总的关系效应)中,除去直接或间接的因果效应以后 剩下的部分,是由于相关的外源变量对该内生变量的影响 引起的。
y y ( 模 型 a3 與 a4)
递归图分析

4.1(4)正 弦 序 列 图 1 0.8 0.6 0.4 0.2
s2
0 -0.2 -0.4 -0.6 -0.8 -1
0
0.5
1
1.5 t
2
2.5
3
图3 S1 Logistic映射序列
图4 S2 正弦信号序列
3)序列公式为:
等间距出现大黑点 对应时间序列的波峰、波谷 (变化缓慢)
logistic序列递归图
均匀结构:均匀结构递归图一般是从随机系统得到的,它的松弛时间相对于递归图所 跨越的时间很短。
举例1:Logistic映射,取a=3, 初值x0=0.808, 迭代200次,嵌入维数买,延迟时间τ=1,阈 值选取序列标准差的0.2,在此基础上叠加高斯白噪声。
1)序列公式为:
xn 1 axn (1 xn ) 高斯白噪声 a 3, n 200, x0 0.808 m 1, 1, 0.25
举例:方波序列及递归图
方波序列时序图
方波序列递归图
谢谢观看!
Hale Waihona Puke 递归图结构分析递归图(RP )是分析时间序列周期性、混沌性以及非平稳性的一个重要方法, 可以揭示时间序列的内部结构,提供有关系统递归状态、信息量和预测性的先验知 识。 递归图的最初目的是将高维相空间轨迹的递归现象直观地表现出来。递归图的图 形特征蕴含着相空间轨迹随时间的发展变化趋势和规律,而且递归图还可以直接应 用于相对较短和不稳定的序列。 递归图所表现出来的整体图形特征结构可以分为均匀结构、周期结构、漂移结构 和突变结构。具体来说,是在正方形的时间平面上描绘黑点和白点,其中黑点表示 该坐标上横轴及纵轴对应的状态发生递归现象,白点表示不发生递归现象。
叠加高斯白噪声前
递归图法在气温时间序列分析中的应用

第35卷第1期2020年2月北京信息科技大学学报Journal of Beijing Information Science &Technology UniversityVol.35No.1Feb.2020文章编号:1674-6864(2020)01-0069-04DOI :10.16508/j.cnki.11-5866/n.2020.01.013递归图法在气温时间序列分析中的应用贺倩,黄静静(北京信息科技大学理学院,北京100192)摘要:为了研究气温变化可能具有的动力学行为,以北京市海淀区1999-2018年的日均气温为例,运用递归图分析方法来刻画海淀区气温所具有的动力学特征。
首先通过嵌入延迟技术来重构相空间,然后绘制气温时间序列的递归图,通过对递归图像的分析,得出北京海淀区气温变化具有周期性、确定性、不平稳性的动力学特征的结论,为气温预测提供理论参考。
关键词:递归图;气温时间序列;相空间重构;动力学行为中图分类号:O 242文献标志码:A Application of recurrence plot in analysis of temperature time seriesHE Qian ,HUANG Jingjing(School of Applied Sciences ,Beijing Information Science &Technology University ,Beijing 100192,China )Abstract :In order to study the possible dynamic behavior of temperature change ,this paper takes the daily average temperature in Haidian District of Beijing as an example ,and uses recurrence plot analysis method to describe the dynamic characteristics of temperature in Haidian District.Firstly ,the phase space is reconstructed by embedding and delay technique.Then the recurrence plot of temperature time series in Haidian District of Beijing is drawn.At last ,the dynamic behavior of temperature change in Haidian District of Beijing with periodicity ,deterministic and non-stationary is obtained from recurrence plot ,which provides a theoretical reference for future temperature research.Keywords :recurrence plot ;temperature time series ;phase space reconstruction ;dynamic behavior收稿日期:2019-07-19基金项目:北京市教育委员会科技计划项目一般项目(KM201911232010)第一作者简介:贺倩,女,硕士研究生;通讯作者;黄静静,女,副教授。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3)序列公式为:
3)序列公式为:
图3 S1 Logistic映射序列
s2
4.1(4)正 弦 序 列 图 1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0
0.5
1
1.5
2
2.5
3
t
图4 S2 正弦信号序列
3)序列公式为:
等间距出现大黑点 对应时间序列的波峰、波谷 (变化缓慢)
2)序列公式为:
对x序列的递归图
对y序列的递归图
• 左图为x的递归图,右图为对y的递归图,可以看出henon系统递归图由大量的孤立 点和一些短的对角线构成,表现出具有内在确定性的混沌结构。
漂移结构:以对角线为中心向左上角和右下角渐变,由系统中缓慢变化的参数所引起
举例:Henon映射,取a=1.4, b=0.3,初值x0=0, y0=0 ,迭代250次,对得到的x序
叠加高斯白噪声前
叠加高斯白噪声后
• 叠加高斯白噪声前递归图由大量的孤立点和一些短的对角线构成,表现出具有内在确定性的混沌结构 • 加入高斯白噪声后,整体上呈现均匀结构,但孤立点减少,内在确定性减少。
举例2:Henon映射,取a=1.4, b=0.3,初值x0=0, y0=0 ,迭代250次,对得到的x序列作递归 图,其递归图表现为混沌结构。
列作递归图,其递归图表现为混沌结构。 然后,若在x项的基础上,对每个xn值增加一线性项0.015n,做递归图,可得到 漂移模型。
2)序列公式为:
递归图
周期结构:振荡系统的递归图都带有主对角线方向的趋势,表现为周期的递归结 构,在图形上像一个棋盘
举例:Logistic映射,取a=3, 初值x0=0.808, 迭代100次;再此基础上,嵌入维数为4,
logistic序列递归图正弦序列递归图 叠加正弦信号后整体递归图示意图
叠加正弦信号后局部递归图示意图
• 从整体上看叠加正弦信号后仍呈现周期信号纹理特征,从坐标轴上可以读出 信号周期为300。
• 从局部上看,沿主对角线递归图的纹理前100点呈现logistic映射纹理特征,后 200点呈现正弦周期信号纹理特征。
突变结构:突变结构的递归图表现为大片的白色区域和较大的黑色块状结构。这是由 于动力学系统中突然的或急剧的变化所引起的。因此,递归图还可以用来检验系统中 的突变现象。
举例:方波序列及递归图
方波序列时序图
方波序列递归图
谢谢观看!
递归图结构分析
递归图(RP)是分析时间序列周期性、混沌性以及非平稳性的一个重要方法, 可以揭示时间序列的内部结构,提供有关系统递归状态、信息量和预测性的先验知 识。
递归图的最初目的是将高维相空间轨迹的递归现象直观地表现出来。递归图的图 形特征蕴含着相空间轨迹随时间的发展变化趋势和规律,而且递归图还可以直接应 用于相对较短和不稳定的序列。
递归图所表现出来的整体图形特征结构可以分为均匀结构、周期结构、漂移结构 和突变结构。具体来说,是在正方形的时间平面上描绘黑点和白点,其中黑点表示 该坐标上横轴及纵轴对应的状态发生递归现象,白点表示不发生递归现象。
均匀结构:均匀结构递归图一般是从随机系统得到的,它的松弛时间相对于递归图所 跨越的时间很短。
举例1:Logistic映射,取a=3, 初值x0=0.808, 迭代200次,嵌入维数买,延迟时间τ=1,阈
值选取序列标准差的0.2,在此基础上叠加高斯白噪声。
1)序列公式为:
xn1 axn (1 xn ) 高斯白噪声 a 3, n 200, x0 0.808
m 1, 1, 0.25
