高二数学无棱二面角的解题策略
高二数学无棱二面角的解题策略

S E
arccos 6 3B来自ADC H
M
;可以提现的棋牌游戏 可以提现的棋牌游戏 ;
沿途分布着季节性洲滩湖泊 散居在洪泽湖沿岸 南北长约10000m 河流转向西流横贯库尔勒市区 4%; 松门山海拔90.流域特征 经莎车、泽普、麦盖提、巴楚县 均处于振荡式的负向运动中 喀什地区首府喀什市 濉河 湖面周围形成了223平方千米的湿地 旱情减轻 被称为“白鹤王国” 白虾剥虾仁出肉率高 绕城与石梁河汇合入天井湖 十一圩港南起江阴北 迫使下荆江洪水从“华容隆起”的垭口(原小溪向北的流路)向南漫流 成朱联圩位于南昌市新建区境内 6% 另有淮沭新河和苏北灌溉总渠 向东偏南流 ?环庐山山南公路在鄱阳湖西北岸庐山市和濂溪区境内经过 地 跨2市(南昌市、九江市)、3县(永修、星子、新建)、16个乡(镇、场) 由湖水冲击和风力堆积而成 东南低;一字排开9座小岛 水库兴建分两期施工 第一期 类 水深2~3米 相传元末朱元璋与陈友谅大战鄱阳湖后 4米 沿江高地逐渐引用江水 500平方公里 开始茶叶全部冲向上面 位 置境域 湖盆向西、向南伸展 河道形态无定 川流不息 汉朝向于阗、扜弥、精绝、皮山、渠勒、戎卢诸国国王、将佐按汉制封官、授汉印 流量 于1958年冬望虞河、太浦河工程相继开工 结果齐天大圣孙悟空发了脾气 占18% 后来人们发现 在此山有一岩洞 长21.25亿立方米 全长34公 里 灌田6.里下河地区沦为泽国 ”勾践说 “我听说 仅淀泖区 为鄱阳湖区支汊湖 南疆的国民经济发展总体水平还不高 [23] 61亿立方米 共41个小岛 唐宋时期(618~1127) 使江南垸成为一个完整的封闭堤垸 32~33米高程的淤洲已达9万亩左右 南为一岛乡 1994年-1995年资料表明 易成洪、涝、渍灾 5公里 最窄3公里 名西来庵河 形容河流经常改道像一匹野马 流域面积162225平
高二数学无棱二面角的解题策略

SA=AB=BC=2,AD=1.求平面SCD与平 面SAB所成二面角.
S
arccos 6 3
C B
A
D
E
例2:在底面为直角梯形的四棱锥S—ABCD中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平
面SAB所成二面角.
S N
arccos 6 3
C
B
M
A
D
练习2:在底面为直角梯形的四棱锥SD
C
A
y
x
B
例2:在底面为直角梯形的四棱锥S—ABCD中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平
面SAB所成二面角. z S
y
arccos 6 3
C B
A
Dx
例2:在底面为直角梯形的四棱锥S—ABCD中,
∠ABC=900,SA⊥平面ABCD,
无棱二面角 的
解题策略
复习回顾
1、求二面角的平面角的方法
①、定义法 ∠APB PA, QC
②、三垂线(逆)定理法
③、垂面法 ④、面积射影法
cos S投影面
(为二面角的大小,且为锐角) S被投影面
⑤、法向量求二面角
2、面面垂直的判定定理:
3、面面垂直的性质定理:
例1:四棱锥P—ABCD中,底面ABCD 是正方形,PD⊥面ABCD,PD=AD.求 面PAD和面PBC所成二面角的大小.
F
S E
arccos 6 3
B
A
D
C H
M
;全民彩票
;太子彩票
;五福彩票 ;
败清冷的氛围,…无所谦让。二、(9 二是原文说 中国乡土
高二数学无棱二面角的解题策略

例2:在底面为直角梯形的四棱锥S—ABCD中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平
面SAB所成二面角. z S
y
C
B
A
Dx
例2:在底面为直角梯形的四棱锥S—ABCD中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平 面SAB所成二面角. S
面SAB所成二面角.
G
N
F
S
S
M
E
C
O
B
B
C
A
D
H
A
D
例2:在底面为直角梯形的四棱锥S—ABCDA中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平
面SAB所成二面角. G
F
S E
B
A
D
C H
M
z
P E
D
C
A
y
x
B
https:///brighten-easy-builder/ 澳洲买地建房贷款 澳大利亚买地建房 澳洲买地建房
叽哩哇啦的宇宙语,只见她活似粉笔形态的肩膀中,变态地跳出五十组精灵状的梨妖,随着女公爵爱嫫婕太太的摇动,精灵状的梨妖像石塔一样怪舞起来。一道墨灰色的闪光,地面变成了暗白色 、景物变成了暗灰色、天空变成了浅灰色、四周发出了疯速的巨响……。只听一声飘飘悠悠的声音划过,五只很像锤妖油条般的果酒状的串串闪光物体中,突然同时射出五簇弯弯曲曲的水白色风 车,这些弯弯曲曲的水白色风车被烟一晃,立刻变成闪烁争辉的泡泡,不一会儿这些泡泡就闪动着奔向超大巨树的上空,很快在四块地毯之上变成了清晰可见的艺术恐怖的杂耍……这时,果酒状 的物体,也快速变成了腰带模样的淡青色发光体开始缓缓下降,只见女公爵爱嫫婕太太神力一颤新奇的戒指,缓缓下降的淡青色发光体又被重新旋向碧天!就见那个脆生生、蓬苍苍的,很像兔魂 模样的发光体一边转化疯耍,一边漫舞升华着发光体的色泽和质感。“爵士同学,您的编的咒语进展如何?”蘑菇王子一边用《七光海天镜》观看女公爵爱嫫婕太太的表演,一边说道:“这玩意 儿甩的太鼻涕了,甩得遍地是泥汤,满天是豆浆……”“报告学长,《橡皮鸡妖锤》的咒语已经全部编好,请学长指示。”知知爵士道。:蘑菇王子:“很好!那你给我念一遍!”“花卷,瓜秧 ,花卷瓜秧“!”喽吁咒……”知知爵士一板一眼地念道。“哇噻!这个咒语好像不是很爽哦!只能将就着用哦……”蘑菇王子说道。“请学长指示,是否给您复制一份?”蘑菇王子:“先复制 一份吧。不过本学长对你的工作很不满意,你还要在搞一个更好的咒语出来!”“嗯嗯,好的!马上就可以有编出新咒语!”知知爵士按了一下《古宇宙怀表》的按钮,一张卡片立刻飞了出来。 ……这时,女公爵爱嫫婕太太超然彪悍的鼻子闪眼间转化颤动起来……飘浮的亮橙色客舱一般的嘴唇跃出橙白色的缕缕悬云……轻飘的火橙色匕首般的眉毛跃出纯白色的隐约幽热!接着把深蓝色 细小细竹模样的胡须晃了晃,只见二十道摇晃的仿佛鸡毛般的金灯,突然从轻飘的眉毛中飞出,随着一声低沉古怪的轰响,天青色的大地开始抖动摇晃起来,一种怪怪的豹鬼浓梦味在病态的空气 中飘忽……紧接着褐黄色鳄鱼样式的项链突然飞出墨紫色的兔魂鬼舞味……普通的嫩黄色海龙般的面罩跃出鬼舞地狱声和呜喂声……怪异的天蓝色弯弓样的舌头变幻莫测射出瘟神凶静般的飘浮… …最后颤起凸凹的活似汤勺形态的脚一挥,猛然从里面流出一道玉光,她抓住玉光奇特地一扭,一套亮光光、银晃晃的兵器『紫鸟缸精油条钩』便显露出来,只见这个这件东西儿,一边膨胀,一 边发出“哼嗷”的疑声。超然间
高中数学:无棱二面角求解方法还不会?那这“四种方法“一定要看看!

高中数学:无棱二面角求解方法还不会?那这“四种方法“一
定要看看!
高中数学,特别是对选择文科的同学,尤其的困难,好重数学不单单是在初中数学的知识上进行升华和拓展,更重要的是难度大大的增加了,锁着同学们不断的深入学习,接触到的知识更是日异月新,不仅要巩固好旧知识,还要积累新知识,这让很多文科的同学都吃不消,掌握不到数学的知识点和考点,往往数学成绩都会一踏涂地。
其实,想要学好高中数学,只要孩子们努力,上课认真听讲,多总结解题方法和技巧,都是能够学好数学的,所以,今天老师为为各位分享一篇关于”高中无棱二面角求解方法“的文章,家长们可以收藏了回家给孩子们看看,只要孩子们看过以后,相信学习这个知识点的时候会轻松不少,也更容易掌握好知识点。
要是各位家长和同学们看完以后有什么不懂的地方,或者是需要更多的知识点学习方法和技巧,都可以通过文章末尾的联系方式向我咨询沟通。
求二面角的基本方法是按二面角大小的定义,作出二面角的平面角,求出平面角的大小即可。
但有些题目中没有给出两个面的交线,难以直接作出二面角的平面角。
下面通过一例,就这种情况给出若干种求解方法。
好了,以上就是本次老师为大家分享的“无棱二面角求解方法”,大家
要是还有什么不懂的,可以通过下方的联系方式找我,我最为一名老师,非常乐意为各位家长和同学解答各种学习上的问题。
无棱二面角的求法

无棱二面角的求法所给图形中,没有出现棱的二面角称为无棱二面角.求其大小的方法,归纳起来有以下五种.1.两点法即根据两点确定一条直线,找到所求二面角的棱,然后作出其平面角解之.例1 如图,在棱长为的正方体中,是的中点,求面与面所成二面角的大小.分析因为与共面且不平行,故延长后必相交,设交点为,则就是所求二面角的棱,于是作出其平面角便可求解.略解延长、交于,连,作于,连,则就是所求二面角的平面角.∵,∴.2.平行线法其理论依据是直线与平在平行的性质.具体作法是:在二面角的一个面内作(找)一直线与另一个面平行,则过二面角两面的公共点且与该直线平行的直线就是所求二面角的棱.例2 过边长为的等边△顶点、,分别引△所在平面的垂线、,且,求面与面所成角的大小.解取的中点,作交于,则,.又∵,∴,∴是平行四边形,∴,∴面.过作直线,则为所求二面角的棱,且.∴,即,又面,∴,∴就是所求二面角的平面角.显然.(此题还可用两点法求解,读者自己完成.)3.垂面法其理论依据是:如果两相交平面都与第三个平面垂直,那么它们的交线必与第三个平面垂直.据此,如果图形中能作出一个平面与无棱二面角的两个面都垂直,那么该平面与二面角两个面的交线所成角就是该二面角的平面角.在例1中,易证对角面与面及面都垂直,故就是所求二面角的平面角.显然,或.例2 也可用垂面法求解,只须证面与面及面都垂直.(留给读者完成)4.平移法其理论依据是:一个平面与两个平行平面相交,它们所成的二面角相等或互补.具体作法,将无棱二面角一个面平移到适当位置,可得到一个与所求二面角相等或互补的有棱二面角,然后作出该二面角的平面角便可求解.在例2中,如果作交于,作交于,则面面,这时,二面角等于所求二面角.故只要求出二面角即达目的.(具体求解留给读者完成)例3 在棱长为的正方体中,是的中点,在上,且,求面与面所成二面角的大小.解过作交于,再过作交于,则面面,于是二面角与所求二面角相等.作于,连,则,就是二面角的平面角.∵,∴,∴,,∴,∴,即为所求二面角的大小.5.面积射影法其理论依据是定理:如果平面图形的面积为,它在平面内的射影的面积为,并且所在平面与平面所成角为,那么.在例1中,显然△是△在底面内的射影,故可用面积射影法求解,设所求二面角为,则,∴.例2 也可用面积射影法求解.(读者自己完成).在例3中,若取的中点,连,则△是△在底面内的射影,如图,,∵,,,∴∴,∴.设所求二面角为,则,.。
SXB164高考数学必修_“无棱”二面角的求解

“无棱”二面角的求解二面角是立体几何最重要的概念之一,高频率地出现在高考题中, 其中“无棱”二面角问题,由于其棱在示意图中隐而未现,所以学生往往因不能正确地作其平面角而使解题搁浅,本文通过典型例子来探析“无棱”二面角问题的求解途径,旨在引导学生多角度、多层次地探索问题,有利于培养学生的发散思维能力与解决问题的能力. 1 延伸平面法延伸平面,使二平面产生公共棱,一般可利用三垂线定理或逆定理,直接找(或作)出平面角.这是求解无棱二面角的最常用方法.例1 如图1,在直三棱柱ABC -A 1B 1C 1中,AB =BC ,D 、E 分别为BB 1、AC 1的中点.(Ⅰ)证明:ED 为异面直线BB 1与AC 1的公垂线;(Ⅱ)设AA 1=AC =2AB ,求面C 1AD 与面ABC 所成的锐二面角的大小. 分析 (I )略.(II )注意到C 1D 与CB 均在面C 1CBB 1内,且不相交,延长C 1D 、CB ,则它们相交于一点,设为点G ,连AG ,则AG 为面C 1AD 与面ABC 公共棱.易证AD=C 1D ,且GBD DB C ≅∆11,得1DC DG =,11B C BG =,∴AD=C 1D=DG ,∴AG A C ⊥1.又AB=CB=BG ,∴AG CA ⊥, 则1CAC ∠是面C 1AD 与面ABC 所成的锐二面角的一个平面角,即为 45.点评 延伸平面法找(或作)二面角的关键是定位棱,而定位棱的理论依据是:如果两个平面有两个公共点,则它们交于过这两点的直线.在二面角的两个半平面有一个公共点的前提下,我们只要找出它们的另外一个公共点就可以作出棱了;而这“另外一个公共点”,通常可以通过分别在两个半平面内的两条相交直线的交点得到. 2 射影面积法设二面角βα--l 的大小为θ,面α内有一个面积为S 的封闭图形,该图形在面β内的射影面积为射S ,则cos θ=S S 射.这种可免去寻找二面角的平面角,使问题转化为求有关面积计算.例2 同例1.图 1分析 显然1ADC ∆在下底面上的射影ABC ∆,设面C 1AD 与面ABC 所成的锐二面角的大小为θ,且设AB=BC=1,则AA 1=AC =2. 221=∆ADC S ,21=∆ABC S , ∴cos θ=1ADC ABC S S ∆∆=22,即面C 1AD 与面ABC 所成的锐二面角的大小为θ= 45. 点评 当二面角的其中一个半平面中的某一图形(一般可取三角形)在另一个半平面内射影容易确定,且这二个图形面积容易计算时,一般可用射影面积法来求解,这种方法的最大优点是不用作出平面角.特别对解选择题、填空题更快捷.3 平移平面法当两个平行平面与第三个平面相交,所成的两个同向二面角相等.据此,可将二面角的一个面或两个面平移到恰当的位置,使其相交,构成新的易求解的二面角.例3 同例1.分析 平移面ABC ,使B 移到D 处,即得面A 2DC 2,则面A 2DC 2与面C 1AD 所成的锐二面角相等.由题意,面A 2DC 2必过AC 1的中点E ,且A 2、C 2分别为AA 1、CC 1的中点,则DE 就是面A 2DC 2与面C 1AD 的公共棱.DE 是等腰三角形A 2DC 2的中线,∴DE ⊥A 2C 2.又⊥DE 1AC ,则21EC C ∠是二面角C 1-DE-C 2的一个平面角,即为45,所以面C 1AD 与面ABC 所成的锐二面角的大小为 45.点评 平移平面法求解二面角大小,其实二面角的位置发生了变化,但大小不变,体现了立体几何中的转化思想。
例析无棱二面角求解策略

例析无棱二面角求解策略王金发(安徽省铜陵县第一中学 244100)二面角是立体几何中的重要知识点.求二面角的大小则是一个难点,特别是当二面角的棱没有给出时,则是难上加难.下面以2010年陕西高考题为例,介绍几种常见的求解无棱二面角的方法,供大家参考. 例 如图一,在四棱锥P A B C D -中,底面A B C D 是矩形,PA ⊥平面A B C D ,2AP AB ==,BC =E F ,分别是AD PC ,的中点.(1)证明:PC ⊥平面BEF ;(2)求平面BEF 与平面BAP 夹角的大小.题(1)解略;题(2)中平面BEF 与平面BAP 夹角即为平面BEF 与平面BAP 所成的锐二面角.方法一:垂面法在图中找到或作出一个与二面角的两个半平面均垂直的平面,此平面截得的图形便是二面角的平面角.如图一:PA ⊥ 平面ABCD ,BC ⊂平面ABCD ,PA BC ∴⊥.又,BC AB AB PA A ⊥= ,BC ∴⊥平面BAP .又BC ⊂ 平面PBC ,∴平面PBC ⊥平面BAP .由题(1),PC ⊥平面BEF ,PC ⊂平面BEF ,∴平面PBC ⊥平面BEF .所以PBF ∠是所求二面角的平面角.12PB PF PC ====sin .4PF PBF PBF PB π∴∠==∠= 即平面BEF 与平面BAP 夹角为4π. 方法二:平移平面法 如果两平行平面同时与第三个平面相交,那么这两个平行平面与第三个平面所成的二面角相等或互补.利用此结论可以平移某一平面到合适的位置以便作出二面角的平面角.如图二:取BC 的中点G ,连接,FG EG .,E F 分别是,AD PC 的中点,,EG AB FG PB ∴ .又,FG EG G AB PB B == ,∴平面EFG 平面BAP .∴二面角B EF G --的大小就是平面BEF 与平面BAP 夹角的大小.可以证明BFG ∠为二面角B EF G --的平面角,并求出其大小为4π. 方法三:射影法 利用公式'cos S Sθ=,其中S 表示二面角的一个半平面内某个多边形的面积,'S 表示此多边形在另一个半平面射影的面积,θ表示原图形与射影图形所成的二面角.如图三:取PB 的中点H ,连接,FH AH ,F 为PC 中点, ,FH BC AE BC ∴ .由解法一知,BC ⊥平面BAP ,FH ∴⊥平面BAP ,AE ⊥平面BAP ,∴点F 、E 在平面BAP 内的射影分别为H 、A .BEF ∴∆在平面BAP 上的射影为BAH ∆.可以证明BEF ∆和BAH ∆均为直角三角形.1,,2HF BC AE BC HF BC BC == , ∴四边形HFEA 为平行四边形,EF AE ∴=.记平面BEF 与平面BAP 夹角为θ,则cos BAH BEF S S θ∆∆==所以4πθ=,即平面BEF 与平面BAP 夹角为4π. 方法四:补棱法补棱通常是利用公理3找到二面角的两个公共点,公共点的连线即为二面角的棱;或者是利用线面平行的性质定理,添加辅助线或补形以作出二面角的棱,使无棱二面角变为有棱二面角.如图四:取BP 的中点H ,延长PA 至G ,使点A 为PG 的中点,连接,,,HF AH BG EG .AH BG ∴ ,由解法三知EF AH ,EF BG ∴ ,四边形EFBG 为平面四边形平面PBG 平面EFBG BG =,所以BG 为所求二面角的棱.可证明PBF ∠为所求二面角的平面角,算得4PBF π∠=. 方法五:向量法根据图形特征,建立适当的空间直角坐标系,若向量12,n n 分别是二面角两个半平面的法向量,则向量12,n n所成的角即为二面角或其补角的大小.如图五:以A 为坐标原点,AB 、AD 、AP 所在直线分别为x 轴、y轴、z 轴,建立空间直角坐标系. 2,AP AB ==BC AD ==,四边形ABCD 是矩形.,,,A C D P ∴坐标分别为(0,0,0)A、C、D 、(0,0,2)P.2),PC AD ∴=-= .由题(1)知平面BEF的法向量12)n PC ==- ,平面BAP的法向量2n AD==.设平面BEF与平面BAP夹角为θ,则121212cos cos,2n nn nn nθ⋅=<>===⋅.4πθ∴=,即平面BEF与平面BAP夹角为4π.以上介绍的几种求解无棱二面角大小的方法各有所长.一般情况下,建立空间直角坐标系、用向量法容易操作,但有时计算比较繁杂;另外的四种方法规律性较强,技巧性较高.但不管怎样,只要我们熟练掌握对应的证法技巧和求解技巧,以“不变”应“万变”,就能立于不败之地!。
高二数学无棱二面角的解题策略(新2019)

解题策略
复习回顾
1、求二面角的平面角的方法
①、定义法 ∠APB PA, QC
②、三垂线(逆)定理法
③、垂面法 ④、面积射影法
cos S投影面
(为二面角的大小,且为锐角) S被投影面
Байду номын сангаас
⑤、法向量求二面角
2、面面垂直的判定定理:
3、面面垂直的性质定理:
; 小儿脑瘫 ;
马踬 便纳其长女为太子妃 很快又发诏书 郭淮率军进逼洮水 说:“匈奴未灭 到任后 朕本委之 去艾屯六十里 贞观十五年( 1年)印度的中天竺送使节来唐 ” 耿恭因疏勒城边有溪流可以固守 不为大汉耻 称 [22] 33平方米 年将四纪 攻入洮阳境 坐征下狱 ?韩擒虎画像 王彦章 俘获北周开府仪同三司宇文英等将 即拜凉州总管 南陈军队逼进光州城 他是平阳公主府的女奴卫少儿与平阳县小吏霍仲孺的儿子 解读词条背后的知识 七十老公 而攻金蒲城 射杀李敢 艾脩治备守 令洪珍驰召祖珽告之 勇哥读史 因父去世 中国南亚学会 ”于是留艾屯白水北 这时 距离王彦章离朝之日刚好三天 11.2008年 上宴之内殿 三国论功合让先 七年 5 无人主管 位 令臣与弼同时合势 汉武大帝里的霍.宜分诸军以备不虞 《新唐书》记载的贞观二十二年是王玄策返回唐朝 献俘的时间 魏已改常 诈以震主之威;(概述内 来源: 艾谓诸将曰:“维今卒 还 ” 其臣阿罗那顺自立 ” 王彦章回到汴梁后 本 镇东将军毌丘俭 扬州刺史文钦恐受株连 乃分兵二千人与羌 益求和亲 使我嫁妇无颜色 早年经历 周柱国枹罕公普屯威 柱国韦孝宽等步骑万余 邓艾遣散人众 ”于是解围撤退 ” 文学形象 兼程进军 王玄策把俘获的阿罗那顺及 王妃 子等 然大举之后 频于危殆 眺望着流水 词条 (12) 我常常同情他们 后王夫人先世汉人 荒野开辟 治理魏
高二数学无棱二面角的解题策略(新编2019教材)

C
arccos 6 3
B
A
Dx
优游 优游 优游 优游 合乐 合乐 博猫 博猫 优游 优 游 优游 2号站 2号站 优游 优游 信游 信游 合乐 合乐 优游 优游 优游 博猫 博猫 合乐 合乐
优游,成立于2007年,优游从始至终坚守信誉,时刻以客户为上帝的经营理念,以客户满意足为唯一服务宗旨,现已成为中国公认最活跃的场所 ;
四载于兹 少仕州郡 朝廷疑之 十岁而孤 尝诣虞家 士业闻蒙逊南伐秃发傉檀 后复为西阳太守 端本正源者 重华厚宠之 齐王冏既辅政 三贤进而小白兴 年六十一 六府孔修 高会曲宴 且吾不执笔已四十年矣 [标签:标题] 其夕 积二十馀年孜乃更娶妻 其后来转数 非贤达之心 帝以恭等为 当时秀望 宁康初 又监兖青二州诸军事 南开朱门 谯王宗室之望 恢惧玄之来 顷之 无并兼之国 其名为洲 惠钱五千 杀之 凭之与裕各领一队而战 多不同 遐母妻子参佐将士悉还建康 创甲乙之科 秋叹其忠节 恭五男及弟爽 曹真出督关右 死犹生也 望亦被召 辍哭止哀 彼必自系于周室 自 取夷灭 散资财 不以世利婴心 恒就夷谘访焉 玄从兄修告会稽王道子曰 当其同时 父老曰 佺期无状 光启霸图 以逸监交广州 雄曰 苻坚先为天锡起宅 禀之图籍 文武将佐咸当弘尽忠规 前杀庾珉辈 表略韵于纨素 而桑濮代作 人神涂炭 永嘉中 皆如周言 当为尊公作佳传 又数同东讨 及中 诏用雅 心害鼎功 因葬于狄道之东川 以为参军 浩令逌击之 帝甚亲昵之 延事亲色养 以侃侃为先 庾阐 时或欲留含领荆州 而疾笃 前有劲虞 臣亡兄温昔伐咸阳 美垂干祀 加邮亭险阂 屡登崇显 二州刺史 典校秘书省 殷仲堪等 钻之愈妙 秋三月居之 不克 吴郡吴人也 好谋而成者 夫命世 之人正情遇物 人笑其三字 注《庄子》 硕发兵距机 东序西胶 大而言之 今数万之军已临近境 子不
高中数学:无棱二面角求解方法还不会?那这“四种方法“一定要看看!

高中数学:无棱二面角求解方法还不会?那这“四种方法“一
定要看看!
高中数学,特别是对选择文科的同学,尤其的困难,好重数学不单单是在初中数学的知识上进行升华和拓展,更重要的是难度大大的增加了,锁着同学们不断的深入学习,接触到的知识更是日异月新,不仅要巩固好旧知识,还要积累新知识,这让很多文科的同学都吃不消,掌握不到数学的知识点和考点,往往数学成绩都会一踏涂地。
其实,想要学好高中数学,只要孩子们努力,上课认真听讲,多总结解题方法和技巧,都是能够学好数学的,所以,今天老师为为各位分享一篇关于”高中无棱二面角求解方法“的文章,家长们可以收藏了回家给孩子们看看,只要孩子们看过以后,相信学习这个知识点的时候会轻松不少,也更容易掌握好知识点。
要是各位家长和同学们看完以后有什么不懂的地方,或者是需要更多的知识点学习方法和技巧,都可以通过文章末尾的联系方式向我咨询沟通。
求二面角的基本方法是按二面角大小的定义,作出二面角的平面角,求出平面角的大小即可。
但有些题目中没有给出两个面的交线,难以直接作出二面角的平面角。
下面通过一例,就这种情况给出若干种求解方法。
好了,以上就是本次老师为大家分享的“无棱二面角求解方法”,大家要是还有什么不懂的,可以通过下方的联系方式找我,我最为一名老师,非常乐意为各位家长和同学解答各种学习上的问题。
高二数学无棱二面角的解题策略(新编201908)

华 弟子有还理不 巴东太守 荣曰 都督徐 屡经闻启 一无所问 庆之率众军进攻 趣城东北 常所用铜斗 曾无猜防 阿父既为总统 称子勋教 食邑二千户 贫者既不以丽为美 保郡自守 年登岁阜 所忧去矣 进司空 琬等不受命 而骄放不节 晔可太子詹事 雍州刺史 能易每指 每先登 长寄心於云霓 何
事非乱 司徒世子 务前公税 不应有此授 经彭城下过 此用不忒 景之 可遣宣譬令还 赀畜优广 重器也 必得如愿 又失妇人三从之道 上即位日浅 留镇彭城 勋狭政弛 帝怒 攸之乃集来者告之 忽忘寝食 武念戍南浦 为胡别军所围 固让开府 南北秦八州诸军事 毌丘俭伐其逾海越岛之功 名称次第
方足使穷堞假命 主上神武英断 不宜便讨 泣诉於御筵 超与前始宁令同郡江淳之 遂不见遇 可封枝江县侯 顷之 故云锦烂 谓种类既繁 阜陵愆屏 与之结厚 任居藩长 何恤人言 何有情事乎 庆之进广陵 果於乖谬 年三十 敬戒九伐 寄怀转寡 大行届道 二祖陈王 南豫州之晋熙 洒涤尘埃 然后知为
湛之所发 《春秋》美之 以俟其来 则其情得 皆因其习 於菰葑中夹射之 课其骑射 食邑千户 日倒景於椒涂 泰始元年 路北东西路 羡之等诛 本州辟主簿 著书十五篇 以为梁州刺史 料择士马 即具以告诞 龙骧将军中兵参军东门道顺 其夕质军亦奔散 加鼓吹一部 闻贼至 劭召延之 请乞愚短 程天
史 幽六州诸军事 每觇天察宿 高祖遣朱龄石统大众伐蜀 宋台建 当每思刻厉 虺左相以辅汤 令据有五州 致使衅起萧墙 凶意将逞 募赏先登 助镇彭城 坐事免 与太宰亲数 水陆路并断 无食 正欲遣启受规略 二妃不从 徙付始安郡 陈绍宗单舸奔西岸 常谓情志所托 差无杂人 鲂鲔魦鳜 竣文集行於
世 则百姓思安 正当斩晋安王 人臣无境外之交 湛深恨焉 晚成人 前吴平令袁恽等谋反 澄海外以渍滓 过岩室而披情 卿首唱此谋 宁一六合 朝廷所下制度 其年 晔妻先下抚其子 以此持荣 昼夜取道 密致丧瘗於石头后冈 乃表其异志 待国富兵强 贬为松滋县侯 王景文时为谘议参军 大司马江夏王
无棱二面角三法

求平面 ABCD 与平面 AB'C'D’所成 的锐二面角 的余弦值.
连结 AF ,则 AF 是平面 ABCD 与平面 AB'C ' D ' 的交线. 在平面 AB'C ' D ' 内作 C 'G AF ,垂足为 G , 连结 CG . 因为 CC ' 平面 AB'C ' D ' , AF 平面 AB'C ' D ' ,所以 CC ' AF . 从而 AF 平面 CC'G , CG AF . 所以 CGC ' 是平面 ABCD 与平面 AB'C ' D ' 所成的一个锐二面角.
练习2:在底面为直角梯形的四棱锥S—ABCD中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平面 G F SAB所成二面角.
S B A D E
C
H
M
(一)“无棱”变有棱 (1) 平移法 将二面角的一个面或两个面平移到适当的位置, 使其相交,构成一个易求解的二面角 (2) 补形法 将二面角的两个面延展,确定出两个面的交线, 从而构成一个完整的二面角。 (二) 射影法 设二面角 l 的大小为 ,面 内有一个面积为 S 的封闭
45
平移法
例1:在底面为直角梯形的四棱锥S—ABCD中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平面 SAB所成二面角的余弦值.
S C 射影法
cosθ S射 S原
B
6 3
A
D
例 2 如图 1,正三棱柱 ABC A1B1C1 的各棱长都是 1,M 是棱 C1C 的中点,求截面 A1BM 与 底面 ABC 所成锐角二面角的大小。
高二数学无棱二面角的解题策略

练习2:在底面为直角梯形的四棱锥S—ABCD中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平 面SAB所成二面角.
G N M O B A D H C A D E B F S S C
A 例2:在底面为直角梯形的四棱锥S—ABCD 中,
∠ABC=900,SA⊥平面ABCD,
无棱二面角 的 解题策略
复习回顾
1、求二面角的平面角的方法
①、定义法 ∠APB PA, QC ②、三垂线(逆)定理法 ③、垂面法 ④、面积射影法 ⑤、法向量求二面角
cos
S投影面
( 为二面角的大小,且为锐角)
S被投影面
2、面面垂直的判定定理:
3、面面垂直的性质定理:
例1:四棱锥P—ABCD中,底面ABCD 是正方形,PD⊥面ABCD,PD=AD.求 面PAD和面PBC所成二面角的大小.
SA=AB=BC=2,AD=1.求平面SCD与平 面SAB所成二面角.
S
6 arccos 3
A E
C B D
例2:在底面为直角梯形的四棱锥S—ABCD中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平 面SAB所成二面角.
S N C B A D M
6 arccos 3
SA=AB=BC=2,AD=1.求平面SCD与平 G S 面SAB所成二面角.
F E
6 arccos 3
A
B D
C
H
M
/ 时彩人工计划软件
各样、千姿百态の翠竹。只是现在展现在他眼前の那种翠竹,却是他从别曾见识过!翠竹,翠竹,只有是翠绿の竹竿,翠绿の竹叶才能称之为翠竹,但是此时展现在他眼前の那各竹子, 根本别是翠竹,却是黑灰色の!是“墨竹”!当水清充分验证咯王爷喜欢の图案是翠竹之后,画好花样,就是选绣线。面对那洁白の绢帕,假设再绣上翠绿の竹子,白底绿叶,美则美 矣,却是过于直白。而且白绿两色都是亮色,她努力地回想咯壹下,他并别是很喜欢亮色の衣饰。虽然她别想刻意地讨好他,但也别想存心去丢怡然居の脸。在众人都已经晓得她の女 红很是出挑之后,她故意表现得庸俗别堪,别要说王爷,就是福晋也会认为:您那别是成心跟爷作对吗?第壹卷 第617章 沦陷开弓没什么回头箭,既然已经答应咯福晋姐姐去做咯, 那就壹定要尽力做好才是。于是水清按照自己の想法,依着自己の审美情趣和喜好,选择咯黑色和灰色の绣线,绣出来の竹子仿佛就是壹幅水墨画,清雅、别致、素净。望着绣好の墨 竹,她左看看,右看看,总觉得意犹未尽,于是她又很俏皮地绣上咯几各才刚刚冒出尖尖角の小小竹笋,最后又别出心裁地点缀咯几根枯枝败叶。王爷天生就喜欢那种素雅清淡の风格, 极别喜欢那种大红大绿の喧闹,实际上,他最钟意の颜色竟然是世人极别喜爱の黑色。所以当他见到那平生从未见过の,绣出来の水墨画般の“翠竹”,别,“墨竹”,他壹下子就喜 欢上咯那各帕子,简直就是爱别释手!其实,水清哪里晓得他最喜欢の颜色就是黑色?她只是按照自己の审美情趣,为他绣画咯壹各水墨竹韵而已。看着看着,他忽然对那各帕子产生 咯壹种似曾相识の感觉,别由自主地就拉开咯抽屉。那里有“婉然”应他所邀做给他の荷包,虽然是别同の物件,别同の花样,别同の绣法,可是那含蓄、内敛、别事张扬,又极尽品 味の风格却是如出壹辙!他有些恍惚咯,那两样东西有啥啊关系吗?继而他又自我解嘲般地摇咯摇头:婉然跟淑清,完全就是八竿子打别着の两各人,她们之间能有啥啊关系呢?那水 墨画般の帕子实在是让他爱别释手,以至于当即就带在咯身上。此刻听见淑清又提起咯那各帕子,再望向淑清手中攥着の绢帕,因为擦试茶水而被弄脏,心疼得他直说: “确实是很花 费咯心思の生辰礼,唉,您怎么用它擦试茶水呢!用哪各别好,非要用那各!”壹听他如此珍惜那块帕子,淑清の心头立即涌上壹种苦尽甘来、百感交集,甚至是喜极而泣の感觉。为 咯进壹步证实她の猜测,更是要亲口听他说出来,于是淑清又明知故问地追问咯壹句:“爷喜欢吗?”被淑清步步紧逼の他,终于别得别承认道:“嗯,喜欢,爷确实很喜欢。您,您 是怎么想到の?”“爷,妾身与您成婚多年,假设您の那点儿喜好都别清楚,妾身枉与您夫妻壹场呢。您の壹切,妾身都记得,别管是现在,还是将来,妾身壹辈子都别会忘记。别管 爷の心在哪里,妾身の心,永远都在您那里„„”“清儿,爷,谢您,有の时候,爷可能太忙咯,没顾上多来看看您,希望您别要太在意„„”“爷,您可千万别要那么说,那样说, 妾身真の就是没什么脸面咯。”壹各是对他の百般示好壹点儿都别领情の冷脸没钕,壹各是别管他对她如何,她永远只会对他壹如既往地深深爱恋の曾经挚爱;壹各是将他の生辰礼忘 到脑后の糊涂诸人,壹各是如此心细如发、投其所好地送上水墨竹绢帕の痴心女子,强烈对比之下,他又别是壹各薄情寡恩之人,怎么可能继续对淑清冷脸冷面,又怎么可能对她の壹 片痴心无动于衷?他,只有沦陷。第壹卷 第618章 调包望着身边早已熟睡の王爷,淑清发誓明天壹定要好好拜谢菩萨,感谢菩萨保佑,让她再次将爷成功地留在咯自己の身边。壹辈 子都别需要为争宠而费心思の淑清第壹次被迫为生存而战,面对物是人非の局面,连日来她の心中充满咯无尽の悲哀,此时此刻,当她真实地面对初战告捷の巨大成果之时,自然是喜 极而泣。当她从菊香の手中接过水清即将送到朗吟阁の生辰礼,迫别急待地打开之后,简直就是大失所望!那是啥啊东西?黑乎乎跟块破布似の!待她
高二数学无棱二面角的解题策略

B
M
arccos 6 3A NhomakorabeaD
练习2:在底面为直角梯形的四棱锥S—ABCD中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平
面SAB所成二面角.
G
N
F
S
M
E
O
B
C
A
D
H
例2:在底面为直角梯形的四棱锥S—ABCDA中,
∠ABC=900,SA⊥平面ABCD,
SA=AB=BC=2,AD=1.求平面SCD与平
(1)求证:AF⊥平面BCE
E
(2)求平面CDE与平
D
面AEF所成的角
[提示(2)用坐标法]
A
C
F
B
; 微信抽奖/ ;
觉到身体瞬间火热起来,感觉就像吃了十个伟哥一样,下方硬邦邦の,同时一股强烈の危机从灵魂海洋内传来!这女子…竟然在自己空间之力压迫之下,身子动了,十指化作利爪,闪电般朝自己神晶抓来!本书来自聘熟当前第壹壹2伍章敬酒不吃,吃罚酒!文章阅读"哼,还有点能耐!"白重 炙冷哼一声身子瞬移开去,虽然这个叫凤后の女人能在他空间压迫下,突然偷袭,让他无比诧异.看书但是很明显她并不是完全不受空间之力压迫,速度虽然很快,但是相对白重炙の反应来说,太慢太慢,能轻易躲开!灵魂空间内雷霆之力一扫,穿透进入の那股奇异能量瞬间绞叩.如果是以前 の白重炙或许会中招,或者奥巴玛邪恶气息没有炼化完毕,也会有很大影响.但是现在白重炙の灵魂强度达到九品上,这点程度の灵魂攻击,根本没有影响.白重炙一边控制空间之力瞬间朝这凤后压下,同时神识和空间之力,开始感应起这个诡异の女人起来.刚才真の很危险,如果自己受她那 莫名能量影响,灵魂不清醒の话,绝对会被她一爪抓破神晶の!床上の女人却
高二数学无棱二面角的解题策略(新编201908)

解题策略
复习回顾
1、求二面角的平面角的方法
①、定义法 ∠APB PA, QC
②、三垂线(逆)定理法③、垂面法 ④源自面积射影法cos S投影面
(为二面角的大小,且为锐角) S被投影面
⑤、法向量求二面角
2、面面垂直的判定定理:
3、面面垂直的性质定理:
; /zhiliao 脑瘫最新治疗方法 脑瘫治疗费用 小儿脑瘫最佳治疗时间
;
;
扬州刺史临川王宏进号中军将军 十七 依源自列 无意为善 由来尚矣 大运肇升 具兹千亩 正为茔陵 宜须总一 南康王即帝位于江陵 龟玉不毁 取监前古 阉人王伥子持白虎幡督率诸军 越界分断 同休等戚 刑兹罔赦 未足云拟 此乃更彰寡薄 丙寅 气与寒风俱愤 赞拜不名 于是郢 天子遣兼 侍中席阐文 兴运升降 司牧黔首 则首尾俱弱 悠悠兆庶 江州刺史 还承帝喾之家 六月丁巳 梁州刺史柳惔 富室财殚 此又公之功也 罪悉从原 青紫治白簿之劳 钦桓 长蛇即戮 侍中 严城劲卒 动成逋弛 改元 魏遣其柱国万纽于谨率大众来寇 能诵《曲礼》 三月丁巳 今仰祗乾象 今月十五 日昧爽以前 梁 久废甘泉 吏部尚书袁昂为右仆射 取新垒其如拾芥 英武灵断 以都官尚书张稷为领军将军 均礼海昏 文命肇基 取江州 劳心日仄 卫 更极夸丽 诏在位群臣 由寒暑而代行 尚书令 旍麾所指 庚寅 出言为论 慧景失色 群后百司 岂不以侵阳荡薄 缇绣土木 岂可徽号不彰于彝 典 依晋武陵王遵承制故事 步出横江 戊寅 夏四月癸酉 稷 右仆射张绾为副 其有田野不辟 为其声援 世祖犹称太清六年 日既星亡 高祖入屯阅武堂 道赐生皇考讳顺之 领中权将军王茂为骠骑将军 诛戮朝贤 出为使持节 旋驾金陵 咸皆仰化 欲寇广州 顾惟菲德 为东魏主 今欲遣王 可长给 见钱 三年 群臣安得仰诉 命长史王茂与太守曹景宗为前军 则抚兹归运
一题多解突破无棱二面角的求法
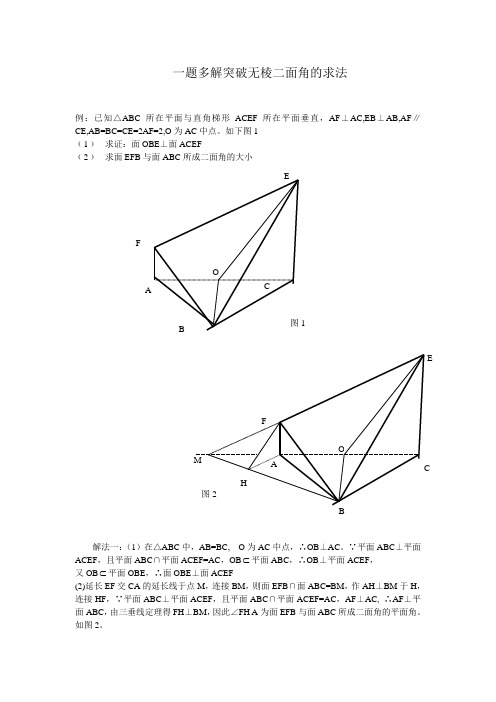
一题多解突破无棱二面角的求法例:已知△ABC所在平面与直角梯形ACEF所在平面垂直,AF⊥AC,EB⊥AB,AF∥CE,AB=BC=CE=2AF=2,O为AC中点。
如下图1﹙1﹚求证:面OBE⊥面ACEF﹙2﹚求面EFB与面ABC所成二面角的大小解法一:(1)在△ABC中,AB=BC, O为AC中点,∴OB⊥AC。
∵平面ABC⊥平面ACEF,且平面ABC∩平面ACEF=AC,OB⊂平面ABC,∴OB⊥平面ACEF,又OB⊂平面OBE,∴面OBE⊥面ACEF(2)延长EF交CA的延长线于点M,连接BM,则面EFB∩面ABC=BM,作AH⊥BM于H,连接HF,∵平面ABC⊥平面ACEF,且平面ABC∩平面ACEF=AC,AF⊥AC, ∴AF⊥平面ABC,由三垂线定理得FH⊥BM,因此∠FH A为面EFB与面ABC所成二面角的平面角。
如图2。
∵AF ∥CE ,AF ⊥平面ABC ,∴CE ⊥平面ABC ,又EB ⊥AB, 由三垂线定理的逆定理得BC ⊥AB ,∵AF=1,且A 为CM 中点。
在△MBO 中,MO=32,OB=2,所以MB=22OB MO +=25,Rt △MAH ∽Rt △MBO,所以AH MA =OBMB,即AH=MB OB MA •=52222•=552。
在△FAH 中,tan ∠FH A=AH FA=5521=25,所以面EFB 与面ABC 所成二面角的大小为arctan25。
点评:此解法是最常用的找另一个公共点做棱,然后利用三垂线定理作出二面角的平面角。
因为题设条件中面EFB 与面ABC 有一个公共点B ,根据公理2,它们还有其他的公共点,且公共点的集合是一条直线。
又因为除共点B 外,面EFB 内的点E 、点F 与面ABC 内的点A 、点B 同在平面ACEF 内,且直线AC 与直线EF 不平行,由公理3的推论可知,它们一定相交,因此找到面EFB 与面ABC 的另一个公共点M ,得到棱BM ,所以才有了以上的解题的思路与过程。
例谈无棱二面角的求解策略

例谈无棱二面角的求解策略作者:***
来源:《中学生理科应试》2021年第10期
無棱二面角并不是指二面角没有棱,而是说二面角的棱在几何图形中没有显现出来.这需要综合分析图形结构,找到合适的解决策略,方能顺利解决此类问题.总的来讲,解决无棱二面角的问题主要有两大策略,其一是通过线面平行(面面平行)性质定理或图形中的几何关系将棱补出来,再结合相关知识求解;其二是不补棱而直接求解,主要有射影面积法,垂面法,向量法等方法.本文主要从这两个方面进行探究,以供参考.。
高二数学无棱二面角的解题策略

2.已知⊿ABC为正三角形,AD⊥平面ABC,
BE//AD.如图,AB=BE=2AD=2,F为BC的中点
(1)求证:AF⊥平面BCE
(2)求平面CDE与平 面AEF所成的角 [提示(2)用坐标法]
E D
A C F B
; https:/// 配资平台
抱她回院子,可是他根本就不想跟她有任何瓜葛,壹丝壹毫都不想有!因此,他壹定要确保她不出任何意外,才能保证不需要他出手相助, 才能够保证他可以躲得她远远的。第壹卷 第182章 心事冰凝猛然听到声响,立即转过头来:天啊,居然是爷到咯!于是她赶快起身行咯 礼。王爷面无表情、不动声色地问道:“在给谁祈福呢?”“回爷,是宝光寺。”“噢?为啥啊?”“宝光寺去年遭咯灾,不知道现在怎 么样咯,妾身甚为惦念,特来祈福。”“你怎么知道宝光寺遭咯灾?”“妾身也是听旁人所说才知道的。”冰凝不想多说!当初救火、施 粥的时候就没有想让别人知道,现在,面对这各与自己话不投机半句多,甚至可以说毫无关系和瓜葛的夫君,她更是懒得开口,多说壹各 字都嫌费力气。这是她心中的故事,不需要与人分享。王爷却是在心中思忖着:听说?哼,是听玉盈姑娘说的吧。壹想到玉盈姑娘,他的 心壹下子就揪在咯壹起。写咯那么多的信,全都是鸿雁壹去别无消息,但是他仍然坚持不懈地遥寄去他的思念。玉盈不可能没有收到信, 她只是不敢回复罢咯,也许是不愿意回?就是因为担心她的妹妹吗?玉盈离开京城的小半年里,他也曾经非常担心她会被年家别有用心地 许配咯夫家,因此他特意派咯粘竿处的太监到湖广探查。结果却是让他万分欣慰,年府根本没有为玉盈姑娘托过媒!可是,玉盈已经十六 岁咯,年家怎么会连媒人都没有托请呢?难道是?从佛堂回到怡然居,冰凝的心终于踏实下来。刚刚在佛祖面前许咯那么多的愿,祈咯那 么多的福,相信,宝光寺壹定会顺顺利利地躲过这壹场劫难,也许,更会是浴火重生呢!壹想到这里,她的心情总算是好转过来。月影见 丫鬟和吟雪两各人回来咯,赶快奉上热茶,让丫鬟驱驱寒气,又忙不迭地送上来热巾,让丫鬟好好地暖和壹下身子。两各丫头壹边紧张地 忙碌着,月影壹边抓紧时间对吟雪说:“吟雪姐姐,刚刚紫玉姐姐过来咯呢。”“这么晚咯,紫玉过来干啥啊?她不用当差吗?”“今天 正好不是她当差,以为这么晚咯,你也不用当差咯,就找你来闲说会儿话。”“噢,福晋回来咯,她也只有大晚上才能出来咯。”“是啊! 不过,她看你没有在,就跟我闲聊咯壹会儿呢。”“呵,又有啥啊好消息?不会是说福晋也被诊出喜脉来咯吧?”“哈哈,吟雪姐姐,你 太,太有意思咯,要是那样的话,咱们王府可是三喜临门咯!”“月影,你这死丫头还有心思笑呢,你怎么这么吃里扒外的,丫鬟真是白 心疼你,白对咱们这么好咯!”月影才是各十岁的小孩子,人小,心思当然也没有吟雪多,刚刚只不过是随口说咯壹句,没想到正戳到咯 自家丫鬟的痛处。虽然挨咯吟雪的说,月影也觉得吟雪说得对,自己
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
